Abstract
Financial forecasting is a challenging task due to the complexity and nonlinear volatility that characterize modern financial markets. Machine learning algorithms are very effective at increasing prediction accuracy, thereby supporting data-driven decision making, optimizing pricing strategies, and improving financial risk management. In particular, combining machine learning techniques with metaheuristic algorithms often leads to significant performance improvements across various domains. This study proposes a hybrid framework for cryptocurrency price prediction, where Support Vector Regression (SVR) with radial basis function kernel is used to perform the prediction, while a Firefly algorithm is employed for correlation-based feature selection and hyperparameter tuning. To improve search performance, the parameters of the Firefly algorithm are optimized using the Fully Informed Search Algorithm (FISA) which is an improved version of the parameterless Rao algorithm. The model is applied to hourly data of Bitcoin, Ethereum, Binance, Solana and Ripple, separately. The model’s performance is evaluated by comparison with Gated Recurrent Unit (GRU), Multilayer Perceptron (MLP), and SVR methods using MSE, MAE, and MAPE metrics, along with statistical validation by Wilcoxon’s signed-rank test. The results show that the proposed model achieves a superior accuracy and demonstrate the critical importance of feature selection and hyperparameter tuning for achieving accurate predictions in volatile markets. Moreover, customizing both feature sets and model configurations for each cryptocurrency allows the model to capture distinct market characteristics and provides deeper insights into intra-day market dynamics.
1. Introduction
As of today, billions of dollars have been invested in the cryptocurrency market. Since the introduction of Bitcoin in 2009, many other cryptocurrencies have been developed, reflecting the rapid evolution of the digital currency landscape. Users can send tokens or coins directly without the need for an intermediary like a bank with the help of blockchain technology. Blockchain relies on cryptography to ensure secure, decentralized, verifiable, and transparent transactions [1]. Cryptocurrencies find uses worldwide in investment, online shopping, supply chain financing, and gaming. The global cryptocurrency market is expanding rapidly due to the growing number of use cases, increasing adoption among companies, innovations in blockchain technology, and ongoing regulatory developments. Some experts suggest that cryptocurrencies may act as a hedge against financial instability. Cryptocurrency provides many advantages for investors in terms of transaction costs, security, privacy, and inflation protection. However, Bitcoin and other cryptocurrencies are highly volatile and may be viewed as highly speculative assets. Therefore, cryptocurrency price prediction is a significantly challenging and complex problem by its nature.
Advanced machine learning and deep learning models have become prominent in financial market analysis and forecasting due to their ability to capture nonlinear behaviors, high volatility, and complex market dynamics [2,3,4,5,6]. Traditional statistical models, such as ARIMA, often struggle to model nonlinear dynamics and sudden market shocks that are typical in cryptocurrency markets, because these models typically rely on assumptions of linearity and stationarity. However, machine learning and deep learning methods, such as Support Vector Regression (SVR), Random Forest, and Long Short-Term Memory (LSTM) network, can learn complex nonlinear patterns and handle large and noisy datasets, making them well suited for predicting cryptocurrency price movements [3,5,6]. Very recently, several researchers have applied transformer-based approaches to model sequential and long-term temporal dependencies in cryptocurrency time series data [7,8,9].
In the wider forecasting literature, machine learning methods are frequently combined with metaheuristics to enhance model performance for solving complex real-world problems [10,11]. Metaheuristics may be used for different purposes in the machine learning domain, such as feature selection, hyperparameter optimization, model training, or model selection. The application of hybrid “Metaheuristics–Machine Learning” approaches in cryptocurrency prediction enhances the performance and robustness of a model [11,12,13]. Machine learning-based prediction in the cryptocurrency market is an emerging field that has shown promising results in short-term forecasting. Strumberger et al. [12] used a bidirectional long-short term memory (BiLSTM) network tuned by a hybrid adaptive reptile search algorithm. Kumar et al. [11] proposed a hybrid approach in which Ant Colony Optimization (ACO) and Binary Grasshopper Optimization algorithms are used for feature extraction, while a Convolutional Neural Network (CNN) was employed for predicting Bitcoin prices. Nayak et al. [13] used a hybrid approach based on an Artificial Neural Network (ANN) in which a fairly new population-based optimization method, the Rao algorithm, was used for tuning ANN parameters. All of these hybrid approaches achieved promising forecasting accuracies. Despite the growing body of literature in recent years, the rapid evolution and complexity of the cryptocurrency market necessitate further research, particularly on enhancing model robustness and generalizability, as well as exploring hybrid approaches that integrate multiple algorithms.
The aim of this paper is to develop a hybrid approach integrating Support Vector Regression (SVR), the Firefly algorithm, and the Fully Informed Search Algorithm (FISA) for predicting different cryptocurrency prices. SVR with a Radial Basis Function (RBF) kernel was applied to predict cryptocurrency close prices. SVR was selected due to its proven success in time series prediction problems [14,15]. The Firefly optimization algorithm was employed to jointly search the most relevant features and SVR hyperparameters corresponding to those features. Hyperparameter values of the Firefly algorithm were also optimized utilizing the FISA to increase the robustness and consistency of the model. FISA is an improved version of the Rao algorithm [16]. The Rao algorithm is a recent population-based metaphorless optimization algorithm, and does not require algorithm-specific learning parameters [13,16]. The simplicity, parameterless technique, and effective exploration and exploitation capability make it a very good candidate method for metaheuristic parameter tuning.
Past research shows that there is no single best model, and different algorithms may show different performances across multiple types of cryptocurrencies [2,13]. Hence, the proposed hybrid approach was applied for five popular cryptocurrencies: Bitcoin, Ethereum, Binance, Solana, and Ripple. The main input data consist of hourly OHLC (open, high, low, and close prices) and volume values from 1 October to 1 December 2024. The input data was gathered via the Binance API (https://developers.binance.com/docs/binance-spot-api-docs/rest-api, accessed on 8 June 2025). A total of 76 different features were created based on the OHLC data using 58 widely used technical indicators.
The findings reveal that the incorporation of feature selection and hyperparameter optimization substantially improves the accuracy of the SVR prediction model and increases its adaptability across different cryptocurrencies. A comprehensive set of results is provided by utilizing Gated Recurrent Unit (GRU), Multilayer Perceptron (MLP), and SVR without feature selection. The results show that the proposed hybrid model achieved a superior performance in terms of MAE, MAPE, and MSE for five cryptocurrencies. Testing the proposed model on five widely used cryptocurrency datasets validated the robustness and adaptability of the model in handling the non-stationary and volatile nature of different assets.
The contributions of this paper can be summarized as follows:
- (i)
- To the best of the author’s knowledge, this study is the first to propose a plug-in hybrid optimization framework combining the Firefly optimization algorithm and FISA for joint feature selection and parameter optimization, used here with SVR for cryptocurrency price prediction. The proposed modular structure can be easily integrated into other machine learning or deep learning models, enabling broader applicability and improved predictive performance.
- (ii)
- A wide set of technical indicators was used in the prediction model, and feature selection was applied using the proposed hybrid FISA and Firefly algorithm to improve prediction accuracy.
- (iii)
- A correlation-based feature selection technique was integrated into the Firefly algorithm to adapt the feature selection process for the target problem. Consequently, the algorithm selects different feature sets, offering deeper insights into the varying dynamics of different cryptocurrency markets.
- (iv)
- While most existing studies utilize daily data, this study used hourly data as the primary input for model training and forecasting, which is critical for intra-day trading in the cryptocurrency market.
2. Literature Review and Background
Cryptocurrency is a type of digital asset that uses cryptographic techniques to secure transactions, regulate the creation of new units, and verify asset transfers, typically operating on decentralized blockchain or distributed ledger systems. While Bitcoin continues to be the most recognized and widely adopted cryptocurrency, there are thousands of alternative cryptocurrencies in the market, each with specific consensus mechanisms, features, and use cases. Some common alternative coins, known as altcoins, include Ethereum, Litecoin, Tether, Ripple, Binance, Solana, etc. Cryptocurrencies provide many advantages such as cheaper and faster money transfer, decentralization, which reduces the security and market manipulation risk, and inflation protection. Therefore, they are increasingly used both for payments on e-commerce platforms and for investment purposes. However, besides the benefits, cryptocurrencies also have some disadvantages including high energy consumption for mining activities, the high volatility of the market, and inherent speculative nature.
Different methods have been used for predicting cryptocurrency prices and market trends accurately [see [4,5] for literature review]. Various conventional statistical methods, machine learning techniques, and deep learning algorithms have been used to predict cryptocurrency prices in the literature, e.g., ARIMA [3], GARCH [2], Facebook Prophet [17], MLP [3,18], LSTM [19,20,21], and SVR [15]. Some researchers have also attempted to understand the existence of different behavioral effects in the cryptocurrency market. As an example, Cao et al. [20] developed a metric to measure the herding effect and used LSTM for cryptocurrency price prediction. Muchtadi-Alamsyah et al. [15] developed SVR-based models by combining them with an autoregressive model and GARCH to predict cryptocurrency market risk through Value-at-Risk (VaR) and Expected Shortfall (ES) metrics. Rodrigues and Machado [6] compared Recurrent Neural Network (RNN), ARIMA, and Conventional Regression Algorithms, and found that the GRU architecture outperformed the other approaches.
Several researchers have applied transformer-based models for cryptocurrency prediction [7,8,9]. Deep learning methods, such as RNN, LSTM, and GRU, have been widely used to forecast sequential patterns. Despite their high accuracy, these methods require a high computational time. Transformer-based models have emerged as one of the most powerful deep learning architectures due to their self-attention mechanisms and parallel processing capabilities. Recent advances in this area have led to specialized architectures such as Informer, Autoformer, PatchTST, TST, and TimeMoE which are designed to improve the accuracy and efficiency of time series forecasting. They provide significant advantages across a wide range of domains, including natural language processing, but their application in the cryptocurrency area is fairly new. Younas et al. [8] proposed a new transformer model combining self-attention and auto-correlation, and compared their model’s performance with Autoformer, Informer, and FEDformer. Izadi and Hajizadeh [7] integrated the transformer model with a Convolutional Neural Network (CNN). They also proposed a novel data vectorization method to transform raw data, enabling more effective input into the model. Mahdi et al. [9] proposed a new hybrid transformer and GRU model to predict the closing prices of Bitcoin and Ethereum based on past prices, trading volumes, and the Fear and Greed Index.
Cryptocurrency prediction models mainly use historical price data (OHLC—open, high, low, close prices) as the primary input. Various features are also used to capture historical and real-time information about the cryptocurrency market, investor behavior, and macro-economic drivers. Common feature categories used in cryptocurrency price predictions may be listed as follows:
- Historical price data.
- Trading volume [14].
- Technical indicators [22,23].
- Social media and news sentiments [12,24].
- Macroeconomic and external features (e.g., inflation, interest rate, gold price, crude oil price) [22].
- Blockchain-specific variables [25].
Technical indicators are very useful for evaluating price movements, identifying trends, measuring market uncertainty, and making investment decisions. These indicators are mathematical calculations derived from historical market data, often Open High Low Close Volume (OHLCV). The most widely used technical indicators include moving averages (MAs), relative strength index (RSI), rate of change (ROC), Bollinger bands, moving average convergence divergence (MACD), and on-balance volume (OBV) [26].
Social media and other media channels influence cryptocurrency pricing and market trends, hence, some authors have used social media data to enrich their dataset for training models. Strumberger et al. [12] used a wide range of internal and external variables including the daily quantity of tweets concerning Bitcoin. They used a Bidirectional Long-Short Term Memory (BiLSTM) network tuned by a hybrid adaptive reptile search algorithm to forecast Bitcoin closing prices. Amirshahi and Lahmiri [27] used close prices and a large text dataset including more than sixteen million cryptocurrency-related tweets posted in 2021 as the input. They used a hybrid prediction model of LSTM and CNN and proposed a flexible input layer which can be customized for different cryptocurrencies.
Feature selection is a crucial step in cryptocurrency prediction models, as in other machine learning applications, enabling the identification of the most relevant and informative input variables. Feature selection techniques help to remove irrelevant and redundant features and prevent overfitting. Hence, it is applied by researchers to reduce the dimensionality of data, improve model accuracy, and lower computational costs. Kumar et al. [11] combined two swarm intelligence algorithms with machine learning to increase the accuracy of Bitcoin price prediction. In the pre-processing stage, they used the Ant Colony Optimization (ACO) and Binary Grasshopper Optimization (BGHO) algorithms for identifying the feature set. Then, the output of the BGHO algorithm was used as an input for the CNN to predict the Bitcoin price. Ghadiri and Hajizadeh [25] used the XGBoost algorithm to find the most relevant features among a large set of technical indicators, market variables, and blockchain-specific data. Then, they applied the Double Deep QNetwork algorithm that integrates LSTM, BiLSTM, and GRUs to decide trading actions. Cheng et al. [26] applied three algorithms to select the most critical indicators: Random Forest, Multilayer Perceptron Regression, and the Sparrow Search Algorithm. Their study reveals the importance of choosing the right technical indicators for improving predictive performance.
Numerous approaches have been proposed for cryptocurrency prediction, each with its own potential benefits and limitations. Gupta and Nalavade [22] listed the properties and drawbacks of some of the relevant literature, e.g., the accuracy, precision, generalizability, speed, robustness, over fitting, log volatility, and scope of the dataset. The previous literature highlighted that a single model is inadequate due to the complex nonlinear dynamics of cryptocurrency data. Researchers and practitioners can create robust models by combining metaheuristics and machine learning models for cryptocurrency prediction. They can be employed either as a unified model or with metaheuristics specifically applied for feature selection and hyperparameter optimization. Sharifi et al. [28] used the Chaotic Dolphin Swarm Algorithm (CDSA) to optimize the training stage of the LSTM model for predicting Bitcoin prices. CDSA helps the LSTM model to escape from becoming trapped in local optima. Gupta and Nalavade [22] developed a two-level ensemble classifier using SVM and ANN for Bitcoin price prediction.
The performance of most machine learning and deep learning algorithms is highly sensitive to the selection and tuning of their hyperparameters, especially due to the complex, noisy, and highly volatile nature of crypto markets. Hence, another fundamental point in machine learning-based cryptocurrency price prediction models is parameter optimization, which enhances both model accuracy and generalization capability. Misconfigured algorithm parameters may lead to problems including overfitting or underfitting, erroneous outputs, excessive training times, and missing important patterns due to poor data exploitation and utilization. Some studies have developed hybrid approaches that integrate metaheuristic algorithms to fine-tune the hyperparameters of machine learning models. Lahmiri et al. [14] used SVR to forecast changes in cryptocurrency trading volume and optimized the parameters of the SVR algorithm using Bayesian Optimization. The experimental results showed that the proposed model with RBF kernel outperforms the ARIMA, Lasso regression, and Gaussian regression models. Another contribution of their study is that they tried three different kernels and examined the effect of kernel selection on prediction accuracy. Nayak et al. [13] used the Rao algorithm for configuring ANN parameters (RA + ANN) and predicted six popular cryptocurrencies with the lowest MAPE and average relative variance values: Bitcoin, Litecoin, Ethereum, CMC 200, Tether, and Ripple. Hafidi et al. [29] developed a novel method that integrates the Genetic Algorithm for the hyperparameter optimization of LSTM networks. This hybrid approach enables the efficient exploration of the hyperparameter space for learning rate, the number of hidden layers, epochs, and window size. They also considered the strong interdependencies among cryptocurrencies as an input feature in their predictive model.
Cryptocurrency is expected to experience significant growth in the coming years, driven by increasing interest from investors, growing institutional adoption, and developing blockchain technology. Hence, researchers will continue to explore innovative approaches for forecasting price trends and market volatility. Besides traditional statistical models, machine learning and deep learning models, such as SVR and LSTM, have demonstrated highly accurate results due to their success in modeling complex and nonlinear patterns. The examination of the literature indicates that integrating metaheuristic and machine learning is a promising field in forecasting and optimization problems. Another promising research area is the application of the developed models to hourly data. Most of the existing literature is based on daily data [11,26], and only a limited number of researchers used an hourly forecasting horizon [30]. Hourly input data usage is appropriate to capture short-term fluctuations (intra-day volatility) and react to sudden market changes.
3. Research Methodology
This section presents the data collection process and introduces the proposed forecasting framework, along with the methodologies employed in developing the model.
3.1. Data Collection
There are thousands of cryptocurrencies in the marketplace today. These digital assets range from prominent cryptocurrencies such as Bitcoin to a wide variety of altcoins, each designed for specific purposes and targets different user communities. In this study, five popular and well-known cryptocurrencies were selected to evaluate the predictive power and adaptability of the proposed model across diverse market conditions. These cryptocurrencies are Binance (BNB), Bitcoin (BTC), Ethereum (ETH), Solana (SOL), and Ripple (XRP). Hourly open, low, high, close, and volume data from 1 October to 1 December 2024 were fetched through the Binance API. The summary statistics of these cryptocurrencies are given in Table 1, and the time series plots are represented in Figure 1.

Table 1.
Summary statistics of cryptocurrency time series data.
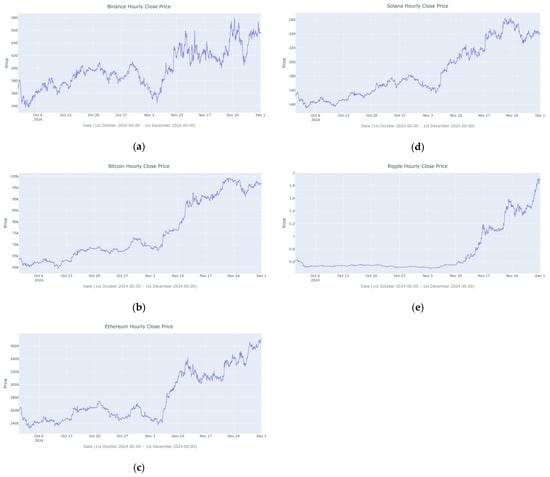
Figure 1.
Time series plots of hourly close prices for (a) Binance, (b) Bitcoin, (c) Ethereum, (d) Solana, (e) Ripple.
The dataset was assessed for completeness and data quality. No missing values were detected, and outlier analysis revealed no extreme observations, indicating complete and high-quality source data. The primary dataset was then split into training and test sets, with 70% allocated for training and the remaining 30% for testing. The input features were lagged by five hours to capture temporal dependencies in the hourly data. Lagging enables the model to leverage historical information, which is crucial in time series forecasting, where past observations strongly influence future values.
Technical indicators are fundamental tools in financial technical analysis, relying on mathematical calculations based on historical price and volume time series data. A total of 76 different features were created based on the OHLCV data utilizing 58 widely used technical indicators. TA-Lib Technical Analysis Library (https://ta-lib.org/, accessed on 8 June 2025), which is an open-source library widely used for the technical analysis of financial market data, was used to calculate these indicators in Python 3.12. Figure 2 provides a list of these 58 indicators under 5 categories. The final feature set includes 76 features because some technical indicators produce multiple outputs rather than a single value. For instance, the Bollinger Bands indicator produces three separate features as upper, middle, and lower bands. Prior to modeling, z-score normalization was applied to all features to ensure the proper functioning of the SVR model, which relies on distance-based kernel functions, such as the Radial Basis Function, that are sensitive to feature magnitudes. Additionally, since the Ripple price fluctuates within the 0–1 range, we scaled it by a factor of 1000 in our model before z-score normalization. This adjustment was necessary because the minimum value of the SVR’s c parameter is 1 in the Scikit learn package.
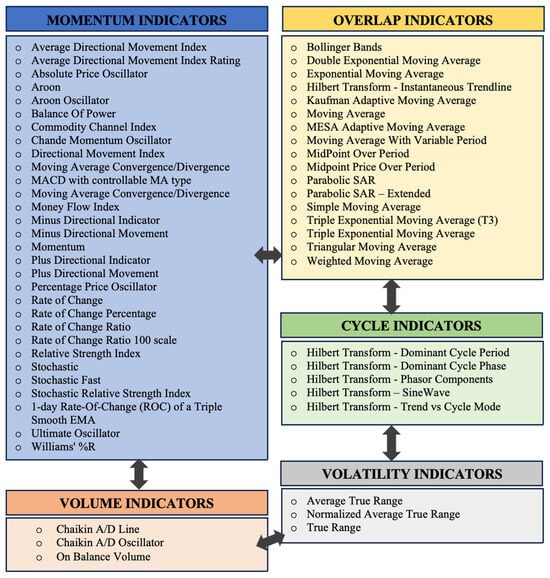
Figure 2.
Categorization of technical indicators used in the study (indicators list was gathered from https://ta-lib.org/, accessed on 8 June 2025).
The momentum indicators category includes the technical tools that measure the strength of price movements over a specific time period. They are generally used with other indicators because they do not identify the direction of the movement. Divergence between price and momentum provides early warnings of potential trend reversals, thereby assisting market participants in making more informed trading and risk management decisions. Overlap indicators are plotted on the price chart and use the same scale, enabling the simultaneous observation of price action and indicator signals, e.g., moving average. They are mainly used to identify trends, measure volatility, and show resistance levels.
Cycle indicators are used to identify repeating and cyclical price patterns in the market. While trend-following indicators primarily show the overall market direction, cycle indicators focus on timing. They help to detect turning points and optimize the timing of trading decisions. Volume indicators analyze the number of tokens traded and evaluate market interest and trends. A high volume often indicates a growing market interest. Volatility indicators show how much and how rapidly prices are changing. High volatility indicates a higher risk. These indicators help market traders to understand and respond to unpredictable price movements. Each of these categories reflects a different perspective of cryptocurrency market structure; therefore, combining them provides a complete picture of the market and enables more reliable analysis.
3.2. Methodological Background
This paper proposes a hybrid cryptocurrency prediction model combining two metaheuristics algorithms and a machine learning model to forecast hourly cryptocurrency close prices. The SVR algorithm is used to forecast the closing price, while the Firefly algorithm is used for simultaneous feature selection and SVR parameter optimization to build a flexible and robust SVR model. Due to the stochastic nature of the Firefly algorithm, the FISA is used to fine-tune its hyperparameters and maintain the best parameter configuration of the overall model. The working principles of these three methods are explained in the following sections.
3.2.1. Support Vector Regression
SVR is a supervised machine learning algorithm derived from the working principles of Support Vector Machine (SVM) [31]. SVM creates one or a series of hyperplanes in a high-dimensional space to split data points and select the one(s) that maximize the separation margin. These nearest points are called support vectors. If the data cannot be separated linearly well, SVM can use a technique called the “kernel trick” to perform nonlinear classification. The kernel trick technique utilizes a kernel function, transforming the data into coordinates in a higher-dimensional space where a linear separation is possible. Thus, the kernel trick implicitly maps the input data into a high-dimensional feature space. In mathematical terms, the basic SVR procedure can be represented as follows:
Assuming the hyperplane equation
where is the weight vector and is bias, SVR tries to predict values by fitting a hyperplane that keeps most of the prediction errors within a tolerance level [14].
Any hyperplane that satisfies the below constraint provides a better-fitting model in SVR training:
SVR is selected due to its proven success in financial forecasting problems [14]. The SVR algorithm is effective in capturing both linear and nonlinear relationships, robust to outliers, and performs well even in the presence of noise and high-dimensional feature spaces.
Feature selection and parameter optimization for the SVR model has a huge impact on the quality of the solution. Feature selection is a particularly crucial step in financial forecasting due to the high dimensionality of financial data. It helps to remove irrelevant and redundant variables to improve the model’s accuracy, combat overfitting, and enhance generalization of the machine learning model. Additionally, feature selection reduces computational complexity and accelerates the training process of the prediction model, which is critical for real-time decision making in dynamic trading environments. This step is especially necessary for this study, which focuses on hourly cryptocurrency prices. Secondly, feature selection results show the varying relevance of different indicators across cryptocurrencies, offering valuable insights for intra-day trading.
Kernel function and parameter selection have a huge impact on prediction accuracy. Kernel function defines a way to map input data into a higher-dimensional space. The Radial Basis Function (RBF) kernel was selected in this study due to the highly nonlinear and volatile structure of the cryptocurrency market. The regularization parameter (C) governs the trade-off between training error and model complexity. The epsilon () parameter defines the margin of tolerance, representing the width of the tube around the estimated function. The gamma (γ) parameter controls the influence of a single training example on the model. Since the predictive performance of the SVR algorithm is highly sensitive to its hyperparameter setting, this study employs the Firefly algorithm for both feature selection and SVR hyperparameter optimization corresponding to the selected feature set, aiming to enhance predictive accuracy and generalization performance.
3.2.2. Firefly Algorithm
The Firefly algorithm is used to find the most relevant features from the determined 76 features explained in Section 3.1 and tune the hyperparameters of the SVR model. The Firefly algorithm is a nature-inspired, population-based metaheuristic proposed by Xin-She Yang in 2007 [32]. The Firefly algorithm mimics the bioluminescent flashing behavior of fireflies [33]. These flashes are used as warning signals for hunting or attracting other fireflies for mating. The attractiveness of each firefly is determined by the brightness and a firefly will be attracted by a brighter one. The algorithm mimics this behavior by assigning a brightness value based on the solution’s quality and an attractiveness function that decreases with distance. The light intensity at a particular distance r from the light source complies with the inverse square law. In other words, the light intensity I decreases as the distance r increases in terms of I ∝ 1/r2. Therefore, most fireflies have a visual distance limit, usually several hundred meters at night, which facilitates communication between fireflies. The flashing characteristics of fireflies can be idealized into three rules which form the basis of the Firefly algorithm: mutual attraction of fireflies, relation of attraction with brightness, and determination of the brightness by the landscape objective function.
The Firefly algorithm involves the following steps [34]:
- Generate an initial population of fireflies.
- Apply the following iterative steps (main loop) until termination criteria are met:
- Calculate the brightness of each firefly based on the objective function.
- Move fireflies towards brighter ones, modifying their position according to attractiveness (population update).
- If there is a new one brighter than the previous iteration, determine this as the global best solution (best brighter).
- Display the global best solution.
The solution approach of the Firefly algorithm is explained in the following paragraphs based on Fister et al. [35]. Each firefly expresses a solution for the target problem. The candidate solution xi is expressed as follows:
A candidate solution is generated based on the following equation:
where represents a random number that varies uniformly in [0, 1]. and show the lower and upper bounds of the jth feature. Attractiveness is calculated based on distance r as follows:
where represents attractiveness at r = 0. The distance between the fireflies i and j ( is calculated based on the Euclidian distance. A firefly moves to another attractive firefly based on the following equation:
where is the step size scaling coefficient, γ is a fixed light absorption coefficient, and is the randomization parameter. To sum up, equations include the position of the firefly, movement of the firefly to more attractive one, and randomized movement. The Firefly algorithm is selected due to a number of strengths: (i) effective in exploring and exploiting complex search spaces, (ii) successful in finding optimal or near-optimal feature subsets, (iii) suitable for high-dimensional and complex feature spaces [34].
The step size coefficient (α) governs the scale of random movements in the search space, enabling the algorithm to explore diverse regions and avoid early convergence. The attractiveness parameter (β) dictates how strongly a firefly is drawn toward superior solutions, effectively steering the population toward high-quality areas of the search space. The light absorption coefficient (γ) controls the decay of attractiveness with distance, dynamically balancing local exploitation and global exploration to enhance the algorithm’s search efficiency and robustness.
3.2.3. FISA and Rao Algorithms
Parameter optimization is a very important step that affects the performance of metaheuristic algorithms. In this study, an improved version of the Rao algorithm, which is called the Fully Informed Search Algorithm—FISA [16], is used to tune the parameters of the Firefly algorithm. The Rao algorithm is a fairly new non-metaphor-based optimization algorithm that is proposed by Ravipudi Venkata Rao [36]. It is a population-based algorithm and updates the population through optimal and worst individuals in the population. The search mechanism is established on the differences between solutions. The Rao algorithm is selected due to its non-parameter-based working principle and its proven success in solving complex optimization problems [10]. Unlike other metaheuristics, such as PSO or GA, the Rao algorithm does not involve hyperparameters to regulate exploration and exploitation mechanisms. This property provides simplicity and an increased adaptation capability across diverse problem domains.
The working principle of the Rao algorithm may be explained as follows. For any iteration, the updated value is identified based on the best and worst candidate solutions by using the following equation [36]:
where and are the values of the variable j for the best and worst candidate solutions in the ith iteration. is the updated value of , and and are two random numbers within [0, 1]. Two candidate solutions are compared based on their fitness value. While the Rao-1 algorithm only considers the best and worst solution, the Rao-2 and Rao-3 algorithms also consider the interaction of the best and worst solutions with randomly selected solutions.
Ghasemi et al. [16] developed a new version of the basic Rao algorithm, called the Fully Informed Search Algorithm (FISA). They tried to improve the performance of the Rao algorithm in optimizing shifted functions. As in the Rao algorithm, the population moves toward better solutions; however, FISA modifies Rao’s update rule by placing single best and worst solutions with their means. Each member simultaneously moves away from the mean position of individuals having worse fitness values, and approaches to the mean position of ones having better fitness values, rather than being influenced by just a few extreme individuals [16]. So, the FISA approach leverages collective information and helps to achieve a balance between exploration and exploitation, while retaining Rao’s hallmark simplicity and non-parametric structure. This study employs Ghasemi et al. (2023)’s Rao version, FISA [16], to optimize the parameters of the Firefly algorithm. A Rao-based algorithm is selected due to its self-adaptive, parameterless structure, proven success, and flexibility for automatically optimizing the parameters of a metaheuristic algorithm.
3.3. General Framework of the Proposed Model
A novel hybrid approach has been developed that integrates machine learning with metaheuristic algorithms to effectively predict the closing prices of cryptocurrencies. The proposed model combines SVR with RBF kernel, Firefly algorithm, and FISA. An overview of the proposed framework is illustrated in Figure 3. The SVR algorithm is employed to predict the close price of cryptocurrencies with its performance strengthened through feature selection and parameter optimization. The proposed model includes two main improvement stages: (i) applying an improved Firefly algorithm to identify the most relevant features and optimize hyperparameters of the SVR algorithm, (ii) using FISA to fine-tune the parameters of the Firefly algorithm, thereby achieving a more effectively configured model with enhanced search capability.
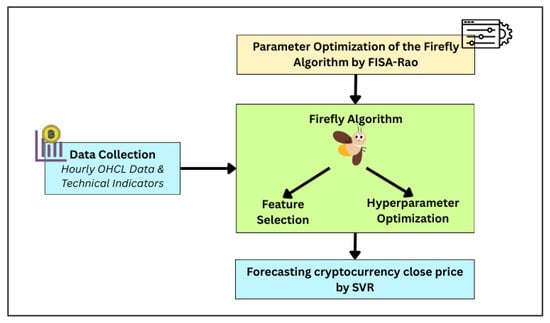
Figure 3.
Basic framework of the proposed model.
3.3.1. Firefly Algorithm Adaptation and Improvement for the Joint Optimization of Features and Hyperparameters
Feature selection and parameter optimization are two essential challenges in machine learning. In the proposed model, the Firefly algorithm was employed to address both tasks for the SVR-based forecasting framework. The Firefly algorithm searches in a joint space of feature subsets and SVR parameter configurations. Each solution represents an individual in the population and encodes both the feature subsets and parameters of the SVR model: C, ε, and γ. Each solution is represented as a one-dimensional vector with 79 elements. The first 76 elements denote the feature selection flags in the dataset, while the remaining 3 elements correspond to the SVR parameter values.
The solution vector is encoded as numerical values between lower and upper bounds. The boundary is set to [−100, 100] for the first 76 elements (feature selection flags) of the vector. The last three elements showing the SVR parameters are set to [Average standardized close price-3σ, Average standardized close price + 3σ], [0.001, 0.1], and [0.0000001, 0.00009], respectively, for C, ε, and γ. In the initialization stage, all solution vectors are randomly assigned values within the predefined boundaries.
The solution vector is decoded by using a binarization method for the first 76 elements of the solution vector. The binarization method works by calculating feature selection thresholds for each element and determining whether the corresponding feature is selected (included) or discarded (excluded). Instead of using a single global threshold value, the proposed process in this paper identifies different threshold values for each feature considering their correlation with the predicted feature. This process helps the algorithm tend to select the features having a higher correlation. The proposed model introduces a new parameter into the Firefly algorithm, named feature coefficient, to calculate feature selection thresholds. The feature selection thresholds are derived by multiplying the lower boundary, the correlation of each feature with the closing price (normalized), and feature coefficient (adjustment factor). In evaluating the solution, each element of the vector is compared against its feature selection thresholds, which determines whether to select or discard the corresponding feature. If the value in the solution vector is lower than the corresponding threshold value, this feature is excluded, otherwise it is included in the SVR prediction model. This approach allows the Firefly algorithm to focus on the most relevant features and helps to improve the overall predictive performance of the SVR model.
In every iteration, each individual of the population is decoded as described above. The SVR model is subsequently trained using the decoded solution and the mean square error (MSE) of the model for the test dataset is evaluated as the fitness value of the corresponding solution. The Firefly algorithm then iteratively generates a new population of solutions, leveraging these fitness evaluations to guide the search toward optimal feature subsets and hyperparameter configurations. The Firefly algorithm is run for 100 iterations with a population size of 25.
3.3.2. FISA-Rao Algorithm Adaption to Fine-Tune the Parameters of the Firefly Algorithm
The performance and convergence of the Firefly algorithm depend on three main parameters: (i) step size scaling coefficient (α), attractiveness (β), and light absorption coefficient (γ). These parameters directly affect the algorithm’s exploration and exploitation capabilities. The proposed model uses a parameterless optimization algorithm, an improved version of the Rao algorithm (Fully Informed Search Algorithm—FISA), to identify the best configuration of the Firefly algorithm parameters, thereby improving solution quality and convergence speed. The methodological approach of the entire model is summarized in Figure 4.
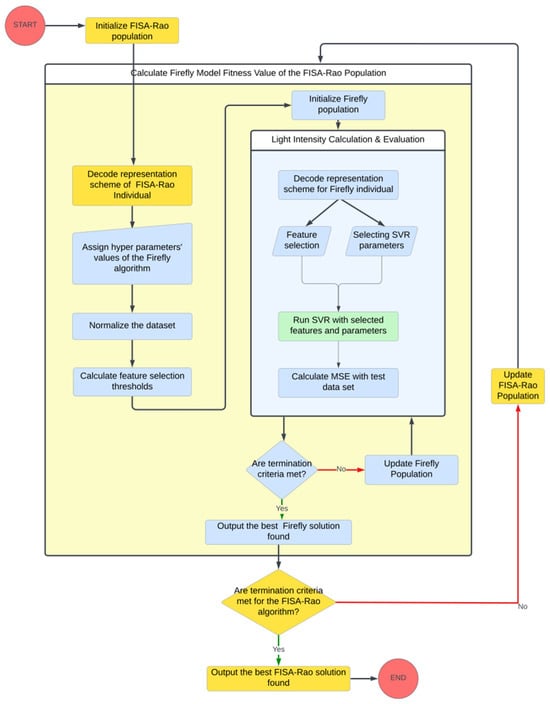
Figure 4.
Flowchart of the proposed model.
The Rao-based FISA is initialized with a randomly generated population of candidate solutions including α, β, γ, and feature coefficient. The feature coefficient is used in the feature selection process in the Firefly algorithm (Section 3.3.1). Each solution runs a Firefly algorithm with a configuration of 100 iterations with a population size of 25. The firefly stage returns the best solution’s MSE as its fitness value. The FISA updates the individuals of the population based on their fitness value. The FISA is executed for 50 iterations with a population size of 10. At the end of this process, the best configuration of the Firefly algorithm parameters is identified for each cryptocurrency.
4. Results and Discussion
The primary dataset was split into training and test sets, with 70% allocated for training and the remaining 30% for testing. The proposed SVR-based prediction approach enhanced by the FISA-Rao and Firefly algorithms was applied to the training set, and its performance was subsequently evaluated on the test set to assess its predictive capability. The closing price was assigned as the target variable, while the remaining 75 features were used as independent variables to predict it. The proposed hybrid model was coded and run using Python. Scikit learn package was used to implement the SVR model.
First, the FISA-Rao optimization algorithm was run for 50 iterations with a population size of 10 to determine the parameter values of the Firefly algorithm. Table 2 gives the α, β, and γ parameters and the feature coefficients identified by the FISA-Rao algorithm. The feature coefficient in the table is used in calculating the feature threshold value which determines the feature set.

Table 2.
Firefly optimization algorithm parameters identified by the FISA-Rao algorithm.
The Firefly algorithm was run 100 times using this hyperparameter configuration to select the features and optimize the three parameters of the SVR model. The total number of selected features and the corresponding settings of the SVR parameters are presented in Table 3. A detailed list of the selected features is given in Appendix A. Finally, the SVR model was run with this configuration to predict the cryptocurrency price movements over the test period.

Table 3.
SVR algorithm parameters identified by the firefly optimization algorithm.
4.1. Benchmark Results
The performance of the proposed hybrid model was compared to the Gated Recurrent Unit (GRU), Multilayer Perceptron (MLP), and SVR methods without a feature selection step. MLP is a widely used feedforward neural network for time series prediction. GRU is a type of recurrent neural network (RNN) designed to capture temporal dependencies in sequential data. MLP provides a baseline for nonlinear modeling, while GRU serves as a strong benchmark for modeling temporal dependencies, ensuring that the proposed model is evaluated against both traditional and sequence-sensitive approaches. The grid search method was also used to optimize the parameters of the regular SVR (C, ε, and γ) and parameters of the MLP algorithm (activation function and hidden layer sizes) to ensure fair and performance-maximized comparisons. The parameter values of the GRU method were gathered from Rodrigues and Machado [6]. The parameter values and configurations of the benchmark methods are given in Table 4. The Scikit learn Python package was used to run the algorithms.

Table 4.
Configuration of the benchmark methods for each cryptocurrency.
Figure 5 represents the time series plots of the forecasts generated by the proposed model and three benchmark methods for Binance, Bitcoin, Ethereum, Solana, and Ripple.
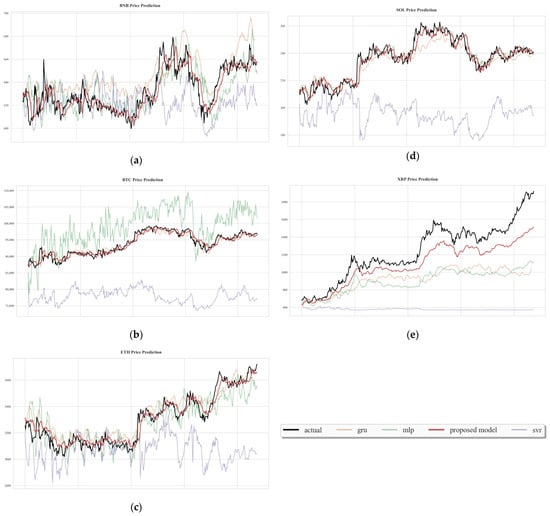
Figure 5.
Close price forecasts of employed methods for (a) Binance, (b) Bitcoin, (c) Ethereum, (d) Solana, (e) Ripple.
Table 5 shows the comparative results of the proposed model and benchmark methods for five different cryptocurrencies. The proposed SVR-based approach with a hybrid FISA-Rao and Firefly algorithm achieves a substantially better performance compared with “GRU, SVR, and MLP without feature selection process” in terms of accuracy and robustness across all five cryptocurrencies. The results clearly demonstrate the superior performance of the proposed hybrid model across all five cryptocurrencies. For each cryptocurrency type, the proposed model achieves the lowest MSE, MAE, and MAPE values, indicating more accurate and stable predictions relative to GRU, MLP, and SVR. While GRU and MLP occasionally provide competitive results—particularly for Solana and Ripple—the proposed model consistently outperforms them, showing both lower error magnitudes and an improved percentage accuracy. SVR exhibits a substantially weaker performance for all assets, suggesting that feature selection is important for the SVR model.

Table 5.
Comparison of results based on multiple performance metrics.
Overall, these findings confirm the robustness, generalization capability, and predictive advantage of the proposed hybrid architecture across heterogeneous market conditions and asset price levels. For the Ripple data, both our proposed model and the benchmark methods exhibit a comparatively lower prediction performance. This outcome may be attributed to the highly volatile and irregular behavior of Ripple’s price movements during the study period, which makes accurate forecasting particularly challenging. In addition to the superior performance in MAE, MAPE and MSE, the proposed model predicts the close prices with 24 features for Binance, 26 features for Bitcoin, 26 features for Ethereum, 33 features for Solana, and 33 features for Ripple cryptocurrency among 76 total features.
Figure 6 shows a graphical comparison of the MAPE performance metric of the four approaches for the selected five cryptocurrencies.
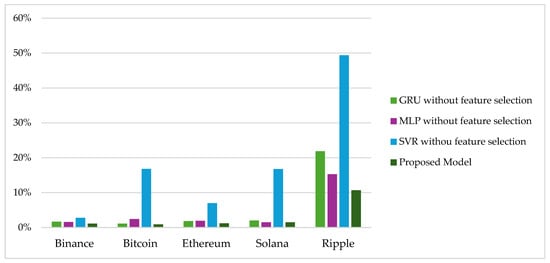
Figure 6.
Graphical comparison of the four methods based on MAPE metric.
We also employed the Wilcoxon signed-rank test to evaluate whether the performance differences among the compared algorithms are statistically significant. The Wilcoxon signed-rank test is a non-parametric statistical test that analyzes the paired performance scores of each algorithm and determines whether the median of the differences deviates significantly from zero [9]. This allows us to verify not only whether one algorithm outperforms another, but also whether the observed improvements are consistent and are not attributable to random fluctuations. As shown in Table 6, post hoc pairwise comparisons using the Wilcoxon signed-rank test revealed a strong and highly consistent performance advantage of the proposed hybrid model (SVR + Firefly + FISA-Rao) across nearly all coin types and benchmark algorithms. The results confirm the robustness of the proposed model across different cryptocurrencies. For Binance, Bitcoin, and Ethereum, all comparisons between the proposed model and baseline models (MLP, SVR, and GRU) yield p = 1.91 × 10−6 and stat = 0, which implies that all paired differences are in the same direction. This is the strongest possible result in a Wilcoxon’s test and suggests a consistently superior performance rather than an improvement observed by chance. Only for Solana did the comparison of the proposed model with MLP yield no statistically significant difference. This may show the asset-specific dynamics such as shorter and sharper volatility cycles of Solana. However, comparisons against SVR and GRU for Solana again confirm that the proposed model consistently outperforms the SVR and GRU models for this asset.

Table 6.
Comparison of the proposed model with benchmark models for close price prediction of different coins using Wilcoxon’s signed-rank test.
4.2. Analysis of the Selected Features for Different Cryptocurrencies
Feature selection helps to identify the most relevant variables, decreases computational efforts, and increases model generalizability. The assessment of the selected features also provides additional highlights about the incorporation of varying sets of technical indicators into the predictive model. Table 7 gives the distribution of the selected indicators per category for five cryptocurrency types. In total, the input feature dataset includes 3 OHLC, 30 momentum, 17 overlap, 5 cycle, 3 volatility, and 3 volume indicators. As is seen from the table, the feature selection process resulted in a varying number of selected features across different cryptocurrencies, reflecting the distinct market characteristics and price dynamics of each asset. The most striking observation is the difference in the number of selected features. While Binance required 24 features, Solana and Ripple needed as many as 33 features. This indicates that different coins exhibit different levels of market complexities. Momentum and overlap features are particularly dominant, reflecting their critical role in capturing the underlying price dynamics of the cryptocurrencies. Momentum features are technical indicators that show the strength and speed of price movements. Overlap indicators mainly highlight the trend direction. A detailed list of the selected features for each cryptocurrency is provided in Appendix A.

Table 7.
Number of selected features by category.
One of the strongest aspects of the proposed hybrid model is its highly adaptive structure to the diverse statistical and market characteristics of each cryptocurrency. The feature selection results reveal that the proposed model can uncover heterogenous predictive structures. Instead of relying on a fixed set of technical indicators, the model dynamically identifies the most informative features for each asset class, demonstrating both robustness and context-sensitivity. The model quickly converges to a minimal set of highly predictive features without overfitting.
Multi-collinearity among the selected features was also evaluated based on Pearson’s correlation. Strong correlation was discovered among some of the selected features. However, unlike linear models, SVR with an RBF kernel can capture nonlinear relationships among features. Therefore, strong linear correlations (multicollinearity) among features do not inherently affect the model. This emphasizes the strength of the proposed model to handle features with complex nonlinear relations.
5. Conclusions
Following the remarkable expansion in cryptocurrency valuations in recent years, cryptocurrencies have emerged as prominent investment assets, and there is a growing research stream in this area. However, cryptocurrencies are one of the most volatile assets in financial markets. The cryptocurrency market is robust to inflation and resilient to global economic and political crises. Consequently, accurate price prediction has become a critical focus for both individual and institutional investors. This has led to an increased interest in advanced forecasting techniques to cope with the volatility and risks of the market. Past studies showed the success of machine learning algorithms for cryptocurrency prediction. In particular, the incorporation of metaheuristics in machine learning techniques has a great ability to improve the accuracy of models. Metaheuristics may be utilized at different stages including feature selection, parameter/hyperparameter fine-tuning, training, etc.
In machine learning-based cryptocurrency price prediction, two critical challenges are feature selection and hyperparameter optimization for the chosen learning model to ensure accurate and robust predictions. This study proposed a hybrid approach integrating machine learning and metaheuristic algorithms to address these challenges. The proposed model uses SVR to predict the hourly closing price while the Firefly algorithm identifies the most relevant features and optimizes the parameters of the SVR algorithm. The Firefly algorithm was adapted to search the joint space of feature subsets and parameter configurations by designing the solution vector. While the first 76 elements correspond to the features in the dataset, the last 3 elements are hyperparameters of the SVR model which are c, ε, and γ. The performance of the Firefly algorithm was also enhanced by using FISA which is a recent version of the Rao algorithm. Momentum, overlap, cycle, volume, and volatility indicators were used in this study as each technical category captures a different dimension of price movement and market dynamics. They are used together to provide a more complete and reliable market analysis. The feature selection step aims to identify the most relevant input features for improving model performance, increasing robustness, reducing overfitting, and enhancing interpretability. Feature selection is also critical in this study, as hourly prediction demands faster model training and timely decision making.
The proposed hybrid model was tested on a diverse dataset including Bitcoin, Ethereum, Binance, Solana, and Ripple coins. Hence, the prediction performance, robustness, generalizability, and adaptability of the model was evaluated considering different market conditions. The proposed model achieved remarkably low prediction errors across all metrics, demonstrating its effectiveness in capturing the dynamics of different cryptocurrency markets. The model’s performance with diverse asset classes highlights its robustness and potential for broader financial forecasting applications. The results also show that both the feature selection process and the parameter optimization stage yield a different set of features and configurations for each cryptocurrency. The modular Firefly algorithm, enhanced by the FISA-Rao algorithm, dynamically extracts the most informative features for each asset. The results demonstrate the robustness, adaptability, and sensitivity of the proposed model to asset-specific market dynamics. Overall, the model highlights the critical role of feature selection and parameter optimization in achieving accurate predictions. By addressing both components within a unified framework, the proposed approach ensures that the selected features and optimized parameters reinforce each other, resulting in a more coherent, efficient, and performance-oriented predictive structure.
The performance of the proposed hybrid approach was also compared with other models including GRU, SVR, and MLP without feature selection. The proposed hybrid ML and metaheuristic-based approach outperformed all benchmarks in terms of MAE, MAPE, and MSE metrics for all cryptocurrency types. These findings suggest that the proposed framework is very well suited to address the dynamic and volatile nature of cryptocurrency markets, providing valuable insights for both academic research and practical trading applications.
The results showed that the incorporation of the two-level hierarchical optimization framework of SVR, Firefly, and FISA-Rao algorithms particularly enhanced model robustness across varying cryptocurrency behaviors. This study also contributes to the underexplored area of hourly (intra-day) cryptocurrency prediction, which is often overlooked despite the high volatility and rapid price fluctuations in the crypto market. Short-term predictions enable traders and automated trading systems to effectively manage risk, respond quickly to market fluctuations, and optimize trading strategies. The employed feature selection stage helps to reduce the complexity and noise in the dataset.
The increasing usage of cryptocurrencies by businesses and governments will make the cryptocurrency price prediction problem an important global economic issue. Hence, the importance of new and modern hybrid forecasting approaches is expected to achieve greater popularity in the future. A possible future research direction may be expanding the set of input features including macroeconomic factors, geopolitical factors, and sentiment analysis to capture the multifaceted influences on market behavior. Another promising future research direction may be integrating the proposed hybrid feature selection and parameter optimization framework with any deep learning model, which may further enhance predictive performance and model robustness.
Author Contributions
Conceptualization, Data curation, Methodology, Software, Validation, Visualization, Writing—original draft, Writing—review and editing, K.B.; Conceptualization, Formal analysis, Methodology, Investigation, Supervision, Validation, Visualization, Writing—original draft, Writing—review and editing, M.E.; Conceptualization, Supervision, S.Ü.O.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available on request.
Acknowledgments
This work is derived from the second author’s Master’s thesis, supervised by the first author and co-supervised by the third author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACO | Ant Colony Optimization |
| ANN | Artificial Neural Network |
| BNB | Binance |
| BTC | Bitcoin |
| ETH | Ethereum |
| FISA | Fully Informed Search Algorithm |
| GRU | Gated Recurrent Unit |
| MLP | Multi-Layer Perceptron |
| OHLC | Open High Low Close |
| OHLCV | Open High Low Close Volume |
| RBF | Radial Basis Function |
| SOL | Solana |
| SVR | Support Vector Regression |
| XRP | Ripple |
Appendix A

Table A1.
Selected features by the proposed algorithm for different cryptocurrencies.
Table A1.
Selected features by the proposed algorithm for different cryptocurrencies.
| No | Feature Technical Indicator Description | Binance | Bitcoin | Ethereum | Solana | Ripple |
|---|---|---|---|---|---|---|
| 1 | Open Price | X | X | |||
| 2 | High Price | X | X | X | X | |
| 3 | Low Price | X | X | X | X | |
| 4 | Volume | |||||
| 5 | Hilbert Transform—Dominant Cycle Period | X | X | |||
| 6 | Hilbert Transform—Dominant Cycle Phase | X | ||||
| 7 | Hilbert Transform—Phasor In-Phase Component | X | X | |||
| 8 | Hilbert Transform—Phasor Quadrature Component | X | X | |||
| 9 | Hilbert Transform—Sine Wave | X | ||||
| 10 | Hilbert Transform—Lead Sine Wave | X | ||||
| 11 | Hilbert Transform—Trend vs. Cycle Mode | X | X | |||
| 12 | Average Directional Movement Index | X | X | |||
| 13 | Average Directional Movement Index Rating | X | X | |||
| 14 | Absolute Price Oscillator | X | ||||
| 15 | Aroon Indicator—Aroon Down | |||||
| 16 | Aroon Indicator—Aroon Up | X | ||||
| 17 | Aroon Oscillator | X | X | X | ||
| 18 | Balance of Power | X | X | X | X | |
| 19 | Commodity Channel Index | X | X | |||
| 20 | Chande Momentum Oscillator | X | ||||
| 21 | Directional Movement Index | X | ||||
| 22 | MACD—MACD Line | X | ||||
| 23 | MACD—Signal Line | |||||
| 24 | MACD—Histogram | X | X | |||
| 25 | MACDEXT—MACD Line | X | ||||
| 26 | MACDEXT—Signal Line | X | ||||
| 27 | MACDEXT—Histogram | X | X | |||
| 28 | MACDFIX—MACD Line | X | X | |||
| 29 | MACDFIX—Signal Line | X | ||||
| 30 | MACDFIX—Histogram | X | ||||
| 31 | Money Flow Index | X | ||||
| 32 | Negative Directional Indicator (-DI) | X | X | |||
| 33 | Negative Directional Movement (-DM) | X | X | |||
| 34 | Momentum | X | ||||
| 35 | Positive Directional Indicator (+DI) | |||||
| 36 | Positive Directional Movement (+DM) | X | ||||
| 37 | Percentage Price Oscillator | |||||
| 38 | Rate of Change | |||||
| 39 | Rate of Change (Percentage) | |||||
| 40 | Rate of Change Ratio | X | X | X | ||
| 41 | Rate of Change Ratio (×100) | X | ||||
| 42 | Relative Strength Index | X | ||||
| 43 | Stochastic Oscillator—Slow %K | X | X | |||
| 44 | Stochastic Oscillator—Slow %D | |||||
| 45 | Stochastic Fast—%K | X | X | |||
| 46 | Stochastic Fast—%D | |||||
| 47 | Stochastic RSI—%K | X | X | |||
| 48 | Stochastic RSI—%D | X | ||||
| 49 | TRIX (Triple Exponential Average) | X | ||||
| 50 | Ultimate Oscillator | X | X | |||
| 51 | Williams %R | X | ||||
| 52 | Bollinger Bands—Upper Band | X | X | |||
| 53 | Bollinger Bands—Middle Band | X | X | X | ||
| 54 | Bollinger Bands—Lower Band | X | X | X | X | |
| 55 | Double Exponential Moving Average | X | X | X | X | |
| 56 | Exponential Moving Average | X | X | X | ||
| 57 | Hilbert Transform—Instantaneous Trendline | X | X | X | ||
| 58 | Kaufman Adaptive Moving Average | X | X | X | ||
| 59 | Moving Average | X | X | X | X | |
| 60 | MESA Adaptive Moving Average—MAMA | X | X | X | X | |
| 61 | MESA Adaptive Moving Average—FAMA (Following) | X | X | X | ||
| 62 | Midpoint (Average of Price) | X | X | X | X | |
| 63 | Midprice (Average of High and Low) | X | X | X | X | X |
| 64 | Parabolic SAR | X | X | X | ||
| 65 | Parabolic SAR Extended | X | ||||
| 66 | Simple Moving Average | X | X | X | X | |
| 67 | Triple Exponential Moving Average (T3) | X | X | X | ||
| 68 | Triple Exponential Moving Average (TEMA) | X | X | X | ||
| 69 | Triangular Moving Average | X | X | X | ||
| 70 | Weighted Moving Average | X | X | X | ||
| 71 | Average True Range | X | ||||
| 72 | Normalized Average True Range | |||||
| 73 | True Range | |||||
| 74 | Chaikin A/D Line | X | X | X | ||
| 75 | Chaikin A/D Oscillator | X | ||||
| 76 | On Balance Volume | X | X | X |
References
- Kuznetsov, O.; Kostenko, O.; Klymenko, K.; Hbur, Z.; Kovalskyi, R. Machine Learning Analytics for Blockchain-Based Financial Markets: A Confidence-Threshold Framework for Cryptocurrency Price Direction Prediction. Appl. Sci. 2025, 15, 11145. [Google Scholar] [CrossRef]
- Dudek, G.; Fiszeder, P.; Kobus, P.; Orzeszko, W. Forecasting cryptocurrencies volatility using statistical and machine learning methods: A comparative study. Appl. Soft Comput. 2024, 151, 111132. [Google Scholar] [CrossRef]
- Rajabi, S.; Roozkhosh, P.; Farimani, N. MLP-based Learnable Window Size for Bitcoin price prediction. Appl. Soft Comput. 2022, 129, 109584. [Google Scholar] [CrossRef]
- Khedr, A.M.; Arif, I.; Pravija, V.P.R.; El-Bannany, M.; Alhashmi, S.M.; Sreedharan, M. Cryptocurrency price prediction using traditional statistical and machine-learning techniques: A survey. Intell. Syst. Account. Financ. Manag. 2021, 28, 3–34. [Google Scholar] [CrossRef]
- Ren, Y.; Ma, C.; Kong, X.; Baltas, K.; Zureigat, Q. Past, present, and future of the application of machine learning in cryptocurrency research. Res. Int. Bus. Financ. 2022, 63, 101799. [Google Scholar] [CrossRef]
- Rodrigues, F.; Machado, M. High-Frequency Cryptocurrency Price Forecasting Using Machine Learning Models: A Comparative Study. Information 2025, 16, 300. [Google Scholar] [CrossRef]
- Izadi, M.A.; Hajizadeh, E. Time series prediction for cryptocurrency markets with transformer and parallel convolutional neural networks. Appl. Soft Comput. 2025, 177, 113229. [Google Scholar] [CrossRef]
- Younas, R.; Raza Ur Rehman, H.M.; Choi, G.S. Crypto foretell: A novel hybrid attention-correlation based forecasting approach for cryptocurrency. J. Big Data 2025, 12, 229. [Google Scholar] [CrossRef]
- Mahdi, E.; Martin-Barreiro, C.; Cabezas, X. A Novel Hybrid Approach Using an Attention-Based Transformer + GRU Model for Predicting Cryptocurrency Prices. Mathematics 2025, 13, 1484. [Google Scholar] [CrossRef]
- Calvet, L.; Armas, J.; Masip, D.; Juan, A. Learnheuristics: Hybridizing metaheuristics with machine learning for optimization with dynamic inputs. Open Math. 2017, 15, 261–280. [Google Scholar] [CrossRef]
- Kumar, A.; Priyanka, S.; Dhanashree, K.; Praveen, V.; Rekha, R. Efficient binary grasshopper optimization based neural network algorithm for bitcoin value prediction. Int. J. Nonlinear Anal. Appl. 2022, 13, 53–60. [Google Scholar] [CrossRef]
- Strumberger, I.; Zivkovic, M.; Thumiki, V.; Djordjevic, A.; Gajic, J.; Bacanin, N. Multivariate Bitcoin Price Prediction Based on Tuned Bidirectional Long Short-Term Memory Network and Enhanced Reptile Search Algorithm. In Information and Software Technologies (ICIST 2023); Lopata, A., Gudonienė, D., Butkienė, R., Eds.; Springer: Cham, Swizerland, 2024; Volume 1979, pp. 38–52. [Google Scholar]
- Nayak, S.; Nayak, S.; Das, S. Modeling and Forecasting Cryptocurrency Closing Prices with Rao Algorithm-Based Artificial Neural Networks: A Machine Learning Approach. FinTech 2022, 1, 47–62. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S.; Bezzina, F. Complexity analysis and forecasting of variations in cryptocurrency trading volume with support vector regression tuned by Bayesian optimization under different kernels: An empirical comparison from a large dataset. Expert. Syst. Appl. 2022, 209, 118349. [Google Scholar] [CrossRef]
- Muchtadi-Alamsyah, I.; Viltoriano, R.; Harjono, F.; Nazaretha, M.; Susilo, M.; Bayu, A.; Josaphat, B. Support vector regression-based heteroscedastic models for cryptocurrency risk forecasting. Appl. Soft Comput. 2024, 162, 111792. [Google Scholar] [CrossRef]
- Ghasemi, M.; Rahimnejad, A.; Akbari, E.; Rao, R.V.; Trojovský, P.; Trojovská, E.; Gadsden, S.A. A new metaphor-less simple algorithm based on Rao algorithms: A Fully Informed Search Algorithm (FISA). PeerJ Comput. Sci. 2023, 9, e1431. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Tiwari, S.; Khaled, D.; Mahendru, M.; Shahzad, U. Forecasting Bitcoin prices using artificial intelligence: Combination of ML, SARIMA, and Facebook Prophet models. Technol. Forecast. Soc. Change 2024, 198, 122938. [Google Scholar] [CrossRef]
- Peng, P.; Chen, Y.; Lin, W.; Wang, J. Attention-based CNN–LSTM for high-frequency multiple cryptocurrency trend prediction. Expert. Syst. Appl. 2024, 237, 121520. [Google Scholar] [CrossRef]
- Mizdrakovic, V.; Kljajic, M.; Zivkovic, M.; Bacanin, N.; Jovanovic, L.; Deveci, M.; Pedrycz, W. Forecasting bitcoin: Decomposition aided long short-term memory based time series modeling and its explanation with Shapley values. Knowl.-Based Syst. 2024, 299, 112026. [Google Scholar] [CrossRef]
- Cao, G.; Ling, M.; Wei, J.; Chen, C. Dynamic Market Behavior and Price Prediction in Cryptocurrency: An Analysis Based on Asymmetric Herding Effects and LSTM. Comput. Econ. 2024, 65, 3325–3360. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Z.; Dai, H.-N. Enhancing Bitcoin Price Fluctuation Prediction Using Attentive LSTM and Embedding Network. Appl. Sci. 2020, 10, 4872. [Google Scholar] [CrossRef]
- Gupta, R.; Nalavade, J. Metaheuristic Assisted Hybrid Classifier for Bitcoin Price Prediction. Cybern. Syst. 2023, 54, 1037–1061. [Google Scholar] [CrossRef]
- Htun, H.; Biehl, M.; Petkov, N. Survey of feature selection and extraction techniques for stock market prediction. Financ. Innov. 2023, 9, 26. [Google Scholar] [CrossRef]
- Htay, H.S.; Ghahremani, M.; Shiaeles, S. Enhancing Bitcoin Price Prediction with Deep Learning: Integrating Social Media Sentiment and Historical Data. Appl. Sci. 2025, 15, 1554. [Google Scholar] [CrossRef]
- Ghadiri, H.; Hajizadeh, E. Designing a cryptocurrency trading system with deep reinforcement learning utilizing LSTM neural networks and XGBoost feature selection. Appl. Soft Comput. 2025, 175, 113029. [Google Scholar] [CrossRef]
- Cheng, C.; Yang, J.; Dai, J. Verifying Technical Indicator Effectiveness in Cryptocurrency Price Forecasting: A Deep Learning Time Series Model Based on Sparrow Search Algorithm. Cogn. Comput. 2025, 17, 62. [Google Scholar] [CrossRef]
- Amirshahi, B.; Lahmiri, S. Investigating the effectiveness of Twitter sentiment incryptocurrency close price prediction by using deep learning. Expert. Syst. 2025, 42, 13428. [Google Scholar] [CrossRef]
- Sharifi, A.; Khalili Damghani, K.; Abdi, F.; Sardar, S. A Hybrid Model for Predicting Bitcoin Price Using Machine Learning and Metaheuristic Algorithms. J. Appl. Res. Ind. Eng. 2022, 9, 134–150. [Google Scholar] [CrossRef]
- Hafidi, N.; Khoudi, Z.; Nachaoui, M.; Lyaqini, S. Enhancing Cryptocurrency Price Prediction through Inter-Coin Volatility and Hyperparameter Optimization. Comput. Econ. 2025. [Google Scholar] [CrossRef]
- Patel, R.; Chauhan, J.; Tiwari, N.K.; Upaddhyay, V.; Bajpai, A. A Deep Learning Framework for Hourly Bitcoin Price Prediction Using Bi-LSTM and Sentiment Analysis of Twitter Data. SN Comput. Sci. 2024, 5, 767. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support Vector Regression. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Fister, I.; Fister, I.; Yang, X.; Brest, J. A comprehensive review of firefly algorithms. Swarm Evol. Comput. 2013, 13, 34–46. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, D. A Systematic Review on Firefy Algorithm: Past, Present, and Future. Arch. Comput. Methods Eng. 2021, 28, 3269–3291. [Google Scholar] [CrossRef]
- Fister, I.; Perc, M.; Kamal, S.; Fister, I. A review of chaos-based firefly algorithms: Perspectives and research challenges. Appl. Math. Comput. 2015, 252, 155–165. [Google Scholar] [CrossRef]
- Rao, R.V. Rao algorithms: Three metaphor-less simple algorithms for solving optimization problems. Int. J. Ind. Eng. Comput. 2020, 11, 107–130. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).