A Preliminary Design of a Novel Limb Mechanism for a Wheel–Legged Robot

Abstract

This paper presents a new approach to the dimensional synthesis of a robotic limb mechanism for a wheel-legged robot. The proposed kinematic structure enables independent control of wheel motions relative to the robot platform, allowing each drive to perform a distinct movement. The selection of the mechanism’s common dimensions simplifies platform levelling to a single-drive actuation. The hybrid limb design, which combines features of driving and walking systems, enhances platform stability on uneven terrain and is suitable for rescue, exploration, and inspection robots. The synthesis method defines the desired trajectory of the wheel centre and applies a genetic algorithm to determine mechanism dimensions that reproduce this motion. The stochastic optimisation process yields multiple feasible solutions, enabling the introduction of additional design criteria for optimal configuration selection. Analytical kinematic relations were developed for workspace and trajectory evaluation, solving both direct and inverse kinematic problems. The results confirm the effectiveness of evolutionary optimisation in synthesising complex kinematic mechanisms. The proposed approach can be adapted to other mobile robot structures. Future work will address dynamic modelling, adaptive control for real-time platform levelling, and comparative studies with other synthesis methods.

1. Introduction

Wheel–legged robots are hybrid mobile robots that combine the features of wheeled and walking robotic platforms [1]. They were created by combining walking robots, in which the feet were replaced with drive wheels. Thanks to the ability to choose the appropriate mode of locomotion, these robots can move more effectively in diverse terrains and environments.

The need to use mobile robots stems from the growing demand for process automation in a rapidly changing industrial and service environment. Mobile robots, thanks to their ability to move independently and adapt to their surroundings, enable increased operational efficiency, reduced labour costs and improved employee safety by eliminating the need to perform dangerous or monotonous tasks [2]. Furthermore, their use contributes to improving the precision and repeatability of technological processes, which is crucial in the context of Industry 4.0 [3]. With the development of artificial intelligence and vision systems, mobile robots are becoming increasingly autonomous, opening up new opportunities for their use in logistics, agriculture, medicine and transport [4].

The literature contains many examples of wheel–legged mobile robots with different numbers of limbs developed in many research centres. An example of a bipedal hybrid robot is Handle [5]. It is a balancing robot designed to carry loads in warehouses. To maintain stability on two wheels, the Handle is equipped with a movable counterweight system that compensates for the variable load on the limbs when carrying loads. Other examples of similar robots include Ascento [6] and WLR II [7]. The literature also contains examples of quadruped robots such as ANYmal on Wheels [8], which was based on a four-legged robot [9] similar to Spot [10]. ANYmal was equipped with wheels, which expanded its mobility. Another example is Centauro [11]. It is a humanoid robot connected to a platform that enables walking and driving. It was created to perform various activities in environments inaccessible to humans.

The Atlete robot [12] is a hexapod robotic platform developed by NASA for use in building a space base during future missions to the Moon.

The main design challenge is to develop the robot’s limb mechanism. The wheel guidance mechanism in the robot is a complex kinematic system that must provide both the movements necessary for walking and driving [13]. To perform gait, the limb mechanism must provide at least two movements: lifting and extending the wheel. Rolling and turning movements of the wheel are necessary for driving. The robots presented have a variety of limb structures with different degrees of mobility.

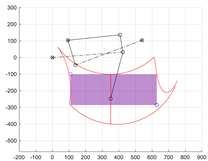
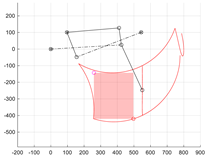
As part of research conducted at the Faculty of Mechanical Engineering of the Wrocław University of Science and Technology, prototypes of mobile robots with a wheel–legged structure were developed and tested [14]. The research covered issues related to the design methodology, kinematics, dynamics and control of this type of construction [15]. The theoretical analyses and laboratory experiments resulted in new design solutions and control algorithms, which constitute a significant contribution to the development of knowledge about mobile robotic systems and their practical applications in modern industries [16]. One of the research outcomes was the development of a novel, innovative wheel guidance mechanism for a mobile robot, enabling both driving and walking (Figure 1).

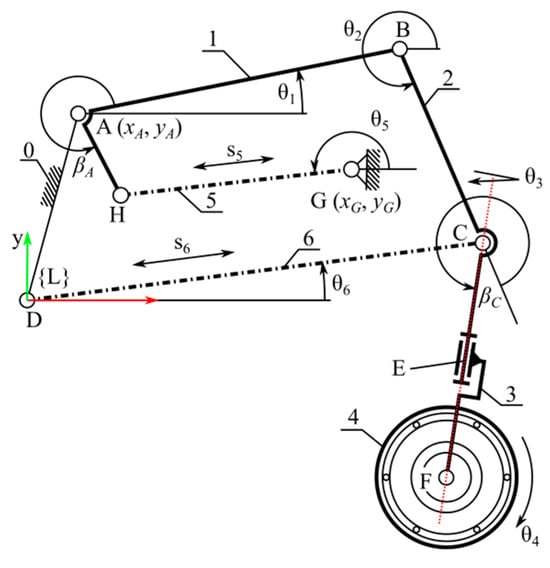
Figure 1. Kinematic scheme of designed hybrid wheel–legged mobile robot.

This work aims to develop a method for dimensional synthesis (dimension selection) of a limb mechanism that ensures proper wheel movements.

2. Materials and Methods

At Wrocław University of Science and Technology, as part of a project involving the construction of a four-limbed robot, a new wheel guidance limb for wheel–legged robots has been developed [17] (Figure 1). The mechanism has four degrees of freedom, which necessitates the use of four kinematic excitations (drives).

The primary advantage of the presented mechanism is that limb movements are performed by individual drives independently of one another. Two drives are designed for driving, and the other two for gait movements. Angular excitation θ₃ performs the steering manoeuvre, and θ₄ is responsible for the rolling of the wheel. The s₅ linear drive is responsible for the limb lifting movement. It forces the centre of the wheel to move along vertical trajectories. The s₆ linear drive (with the s₅ drive locked) is responsible for wheel extension, which is the horizontal movement of the wheel necessary to step over an obstacle. The combination of the movements of both drives enables the achievement of more complex wheel centre trajectories.

A wide range of strategies used in dimensional synthesis have already been explored [18,19,20]. The developed dimensional synthesis method focuses on determining the common dimensions of the limb to perform the intended walking and riding movements, i.e., the appropriate guidance of the centre of the wheel—point F. Two tasks of the wheel suspension mechanism have been identified:

• Guiding point F in the vertical axis to compensate for uneven terrain during driving to level robot platform;
• Moving the wheel horizontally during walking.

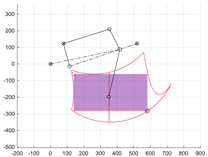
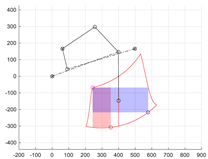
It was assumed that the axes of the wheel steering drive θ₃ and the driving drive θ₄ intersect at point F. It was also determined that the steering axis θ₃ is aligned along the CF segment (Figure 1 and Figure 2). As a result of this assumption, the movements of these drives do not affect the displacement of the wheel centre F relative to the limb coordinate system {L}. Therefore, in the subsequent stages of synthesis, the θ₃ and θ₄ drives were omitted, as they do not affect the movement of the wheel centre. After replacing members 2, 3 and 4 with a single replacement link 7 (Figure 1 and Figure 2), a two-degree-of-freedom (2 DoF) planar mechanism was obtained (Figure 2).

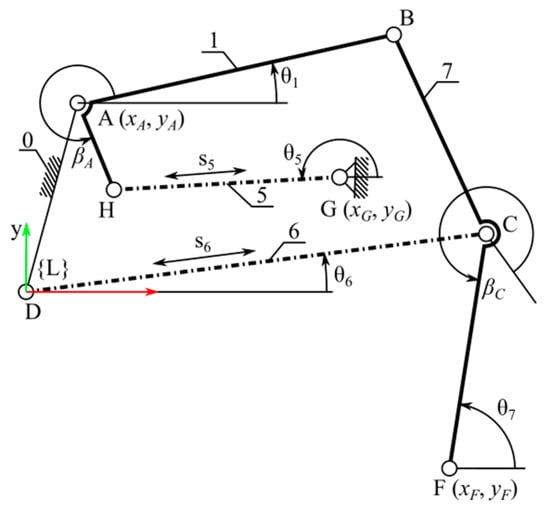
Figure 2. Scheme of simplified limb mechanism without steering and wheel drive.

This work aims to develop a method for dimensional synthesis of a limb that allows the dimensions of the mechanism to be selected to ensure the lifting movement of the wheel (point F) along a trajectory similar to a vertical section with the walking drive s₆ locked. The innovation of the wheel suspension used in the robot lies in the fact that by selecting the appropriate dimensions of the system components, vertical wheel movement can be achieved using only one drive, which significantly simplifies the robot control system in the case of levelling the platform while driving. The procedure for selecting the dimensions of the limb mechanism for the adopted synthesis objective requires determining the lengths of members AB, BC, AH, CF, angles β_A, β_C, the position of support points A(x_A, y_A) of member 1 and G(x_G, y_G) of member 5 attachment, and the ranges of motion of the s₅ wheel lift drive HG_MIN, HG_MAX and the s₆ wheel extension drive CD_MIN, CD_MAX. Assuming that both linear drives s₅ and s₆ will be identical, i.e., their ranges of motion will also be equal to s_MIN to s_MAX. Therefore, 10 geometric parameters of the mechanism need to be determined.

The following assumptions were made for the synthesis of the mechanism:

• Rectilinear trajectory of the centre of wheel F (with the s₆ extension drive locked in the fixed position CD_LEV);
• The workspace of the movement of the centre of wheel F of the limb mechanism will have a height h_s and a width l_s greater than the width and height of two standard stair sizes;
• The trajectory of the centre of wheel F will ensure uniform vertical guidance of the wheel, depending on the deflection of the levelling drive s₅.

Fundamentals of Dimensional Synthesis of Basic Limb Dimensions

The procedure for dimensional synthesis of the basic dimensions of the limb is divided into three main stages. The first stage involves determining the limb parameters required to achieve a vertical trajectory of the wheel centre F, with the wheel extension drive locked at s₆ = const. Movement along such a trajectory will be used when driving off-road to lift the wheel and compensate for uneven terrain. In the next stage of synthesis, by activating the wheel extension drive s₆, the boundary of the workspace of the mechanism was determined. Its dimensions were then analysed. In the final stage of synthesis, the parameters for mounting the levelling drive s₅ were selected and the vertical guidance of the wheel was evaluated.

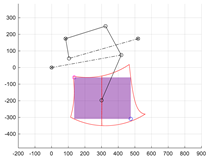
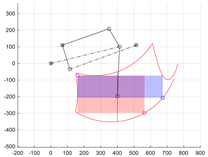
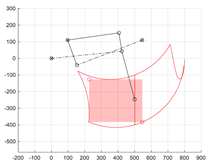
In the first stage, the linear parameters AB, BC, and CF, the angular parameter β_C, and the position of point A (x_A, y_A) were selected. For this purpose, a constant length of the stepping actuator s₆ = CD = CD_LEV was assumed, at which the trajectory of point F is to be vertical. The synthesis was performed with a fixed vertical movement of the centre of circle F. To achieve a one-degree-of-freedom (1 DoF) mechanism in this step, it was assumed that link AB has a variable length. The synthesis aimed to obtain a constant length of segment AB with the assumed movement of the centre of circle F (Figure 3).

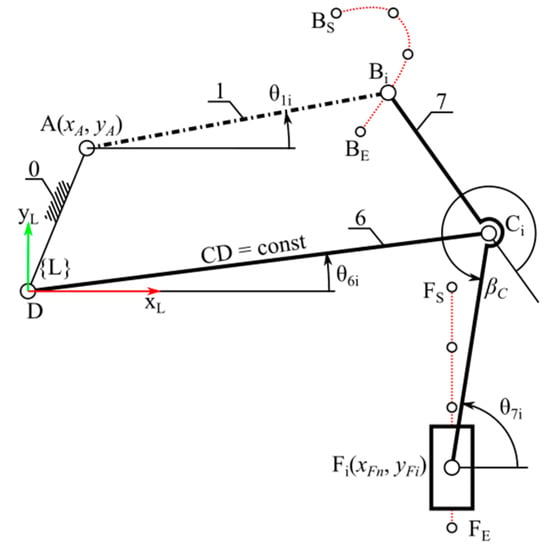
Figure 3. Desired wheel lift trajectory (point F), with fixed stroke of s₆ drive assumed.

A vertical section of the centre of the circle F was established between two given points, the starting point F_S (x_Fn, y_FS) and the end point F_E (x_Fn, y_FE). The assumed segment was divided into n-evenly spaced points F_i (x_Fn, y_Fi) for i = 1, …, n. For each position point F_i, the corresponding positions of point C_i were determined at the intersection of circles O₁ (with centre at D and radius CD) and O₂ (with centre at F_i and radius CF). The formula gives the position of point C_i:

$$\left({\mathrm{x}}_{\mathrm{C}\mathrm{i}},{\mathrm{y}}_{\mathrm{C}\mathrm{i}}\right)=\left({\mathrm{x}}_{\mathrm{D}},{\mathrm{y}}_{\mathrm{D}}\right)+\mathrm{C}\mathrm{D}\cdot \left(\cos {\mathsf{\theta }}_{6\mathrm{i}},\sin {\mathsf{\theta }}_{6\mathrm{i}}\right)$$

where θ_6i was determined based on the angles of the triangle F_iDC_i:

$${\mathsf{\theta }}_{6\mathrm{i}}={\tan }^{-1}\left({\displaystyle \frac{{\mathrm{y}}_{\mathrm{F}\mathrm{i}}-{\mathrm{y}}_{\mathrm{D}}}{{\mathrm{x}}_{\mathrm{F}\mathrm{n}}-{\mathrm{x}}_{\mathrm{D}}}}\right)+{\tan }^{-1}\left({\displaystyle \frac{\sqrt{{\left(2\cdot \mathrm{C}\mathrm{D}\cdot \mathrm{D}{\mathrm{F}}_{\mathrm{i}}\right)}^2-{\mathsf{\Delta }}_{12}^2}}{{\mathsf{\Delta }}_{12}}}\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {\mathsf{\Delta }}_{12}={\mathrm{D}\mathrm{F}}_{\mathrm{i}}^2+{\mathrm{C}\mathrm{D}}^2-{\mathrm{C}\mathrm{F}}_{\mathrm{i}}^2$$

The parameter Δ₁₂ is a discriminant of the equation that determines whether circles O₁ and O₂ intersect (Δ₁₂ > 0), are tangent to each other (Δ₁₂ = 0) or have no points of intersection (Δ₁₂ < 0). Subsequently, the orientation θ_7i of link 7 is determined based on point C_i:

$${\mathsf{\theta }}_{7\mathrm{i}}= {\tan }^{-1}\left({\displaystyle \frac{{\mathrm{y}}_{\mathrm{C}\mathrm{i}}-{\mathrm{y}}_{\mathrm{F}\mathrm{i}}}{{\mathrm{x}}_{\mathrm{C}\mathrm{i}}-{\mathrm{x}}_{\mathrm{F}\mathrm{n}}}}\right)$$

The designated angular positions θ_7i determine CF and, with the selected parameters BC and β_C, determine the set of points B_i (trace t_B) on the trajectory of point B. The formula gives the position of point B_i:

$$\left({\mathrm{x}}_{\mathrm{B}\mathrm{i}},{\mathrm{y}}_{\mathrm{B}\mathrm{i}}\right)=\left({\mathrm{x}}_{\mathrm{C}\mathrm{i}},{\mathrm{y}}_{\mathrm{C}\mathrm{i}}\right)+{\mathrm{B}\mathrm{C}}_{\mathrm{i}}\cdot \left(\cos \left({\mathsf{\theta }}_{7\mathrm{i}}-{\mathsf{\beta }}_{\mathrm{C}}\right),\sin \left({\mathsf{\theta }}_{7\mathrm{i}}-{\mathsf{\beta }}_{\mathrm{C}}\right)\right)$$

By assuming the position of a fixed point A (x_A, y_A), it is possible to determine the set of lengths AB_i corresponding to the successive positions of points B_i. The optimisation aimed to obtain a constant length AB for member 1. Therefore, the target function given by the formula was minimised:

$${\mathrm{F}}_{1\mathrm{T}\mathrm{A}\mathrm{R}\mathrm{G}\mathrm{E}\mathrm{T}}=\mathrm{r}\mathrm{m}\mathrm{s}\left(\mathrm{A}{\mathrm{B}}_{\mathrm{i}}-\overline{\mathrm{A}{\mathrm{B}}_{\mathrm{i}}}\right)$$

(1)

where ($\overline{\mathrm{A}{\mathrm{B}}_{\mathrm{i}}}$)—average value from the set of lengths AB_i, rms—function determining the root mean square error.

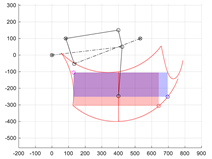
The optimisation results in the ABCD four-bar mechanism (Figure 4), where link 1 is the driver, link 6 is the rocker and link 7 is the coupler part. The length AB of member 1 is assumed to be equal to ($\overline{\mathrm{A}{\mathrm{B}}_{\mathrm{i}}}$). With a constant length CD of the wheel extension drive, s₆ = CD_LEV, this mechanism moves the coupler point F along a trajectory similar to the assumed straight line, which is necessary to level the platform while driving. The literature on the optimisation of four-bar mechanism is extensive and continues to be developed [21,22].

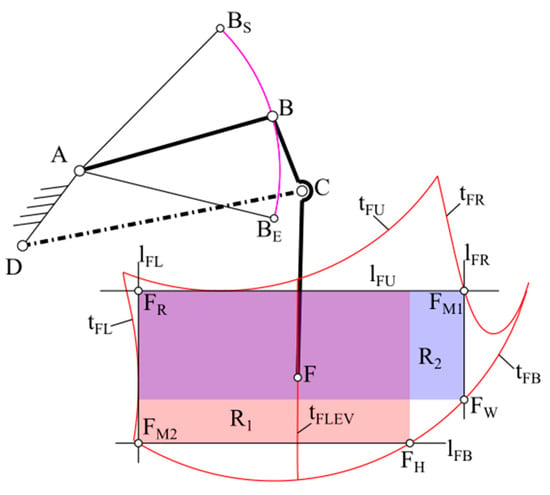
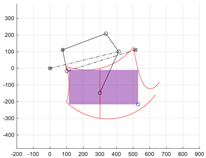
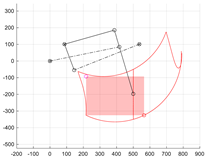
Figure 4. The workspace of the centre of wheel F of the robot limb mechanism.

The next step in the synthesis process was to evaluate the obtained solution. The first parameter examined was the rectilinearity of the trajectory of point F. Parameter θ₁ was temporarily adopted as the wheel levelling drive, as the parameters of support point G and attachment point H of the wheel lifting drive s₅ had not yet been determined. The angular range of movement of member AB was adopted based on the results obtained from the previous stage of synthesis, θ₁ = <θ_1S, θ_1E>. The angle θ_1S corresponds to the deflection of member 1 to point B_S (initial position), and the angle θ_1E corresponds to the position of member 1 so that point B coincides with point B_E (final position). The working range of the θ₁ drive was divided into m points. For each position θ_1j, the position of point B_j was determined:

$$\left({\mathrm{x}}_{\mathrm{B}\mathrm{j}},{\mathrm{y}}_{\mathrm{B}\mathrm{j}}\right)=\left({\mathrm{x}}_{\mathrm{A}},{\mathrm{y}}_{\mathrm{A}}\right)+\mathrm{A}\mathrm{B}\cdot \left(\cos {\mathsf{\theta }}_{1\mathrm{j}},\sin {\mathsf{\theta }}_{1\mathrm{j}}\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \mathrm{j}=1,\dots ,\mathrm{m}$$

At specific points B_j (x_Bj, y_Bj) and D (x_D, y_D), the position of point C_j (x_Cj, y_Cj) was determined at the intersection of two circles O₃ (with centre at B_j and radius BC) and O₄ (with centre at D and radius CD):

$$\left({\mathrm{x}}_{\mathrm{C}\mathrm{j}},{\mathrm{y}}_{\mathrm{C}\mathrm{j}}\right)=\left({\mathrm{x}}_{\mathrm{B}\mathrm{j}},{\mathrm{y}}_{\mathrm{B}\mathrm{j}}\right)+\mathrm{B}\mathrm{C}\cdot \left(\cos {\mathsf{\theta }}_{2\mathrm{j}},\sin {\mathsf{\theta }}_{2\mathrm{j}}\right),$$

(2)

where θ_2j is the orientation of member 2 (BC) determined by the angles of triangle BCD:

$${\mathsf{\theta }}_{2\mathrm{j}}={\tan }^{-1}\left({\displaystyle \frac{{\mathrm{y}}_{\mathrm{D}}-{\mathrm{y}}_{\mathrm{B}\mathrm{j}}}{{\mathrm{x}}_{\mathrm{D}}-{\mathrm{x}}_{\mathrm{B}\mathrm{j}}}}\right)+{\tan }^{-1}\left({\displaystyle \frac{\sqrt{{\left(2\cdot \mathrm{B}\mathrm{C}\cdot \mathrm{B}\mathrm{D}\right)}^2-{\mathsf{\Delta }}_{34}^2}}{{\mathsf{\Delta }}_{34}}}\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {\mathsf{\Delta }}_{34}={\mathrm{B}\mathrm{D}}^2+{\mathrm{B}\mathrm{C}}^2-{\mathrm{CD}}^2$$

Next, the position of point F_j was determined based on the position of point C_j and the parameters of member 2, i.e., the length CF and angle β_C:

$$\left({\mathrm{x}}_{\mathrm{F}\mathrm{j}},{\mathrm{y}}_{\mathrm{F}\mathrm{j}}\right)=\left({\mathrm{x}}_{\mathrm{C}\mathrm{j}},{\mathrm{y}}_{\mathrm{C}\mathrm{j}}\right)+\mathrm{C}\mathrm{F}\cdot \left(\cos \left({\mathsf{\theta }}_{2\mathrm{j}}+{\mathsf{\beta }}_{\mathrm{C}}\right),\sin \left({\mathsf{\theta }}_{2\mathrm{j}}+{\mathsf{\beta }}_{\mathrm{C}}\right)\right)$$

(3)

When the wheel extension drive is set to a fixed position s₆ = CD_LEV, the centre of wheel F moves along a trajectory similar to the specified vertical segment F_SF_E. The deviation of the position of points F_j in the horizontal x_Fj from the specified value x_Fn was determined. Based on the differences in the position of the centre of the wheel from the specified trajectory, the first coefficient C_OEFF1 was formulated, determining the quality of the solution:

$${\mathrm{C}}_{\mathrm{O}\mathrm{E}\mathrm{F}\mathrm{F}1}=\mathrm{r}\mathrm{m}\mathrm{s}({\mathrm{x}}_{\mathrm{F}\mathrm{j}}-{\mathrm{x}}_{\mathrm{F}\mathrm{n}})$$

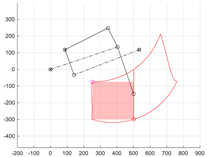
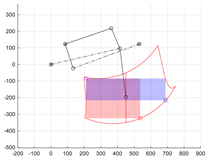
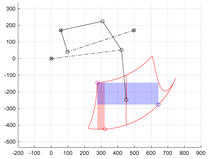
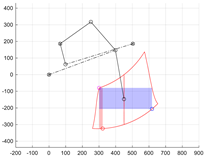
Then, after activating the wheel extension drive s₆, the size of the workspace of the centre of the wheel F of the limb mechanism was evaluated. The stroke range of the drive s₆ was set between lengths CD = <s_MIN, s_MAX>. The positions of point F for the extreme positions of drives θ₁ and s₆ were determined. The upper limit of the workspace of the centre of wheel F was obtained at a constant position of point B in position BS (when θ₁ = θ_1S) and at an actuator extension of s_MIN < s₆ < s_MAX. The working range of the actuator was divided into m points, thus determining the upper trace of point F—t_FU consisting of m points. Similarly, the trace of the bottom limit of the workspace t_FB was determined for the set position of point B in position B_E (θ₁ equal to θ_1E) and with a change in the length of segment CD in the full range. Subsequently, the right boundary of the workspace t_FR was created by a change in the angular position θ₁ in the full range from θ_1S to θ_1E and a constant length CD of the extension actuator s₆ = s_MIN. The left boundary t_FL corresponds to the trajectory of the centre of the wheel at a given drive s₆ with a length CD equal to s_MAX (Figure 4).

The resulting shape of the workspace should be assessed in terms of size (width and height). For assessment, it was assumed that a rectangle would be inscribed in the resulting area (Figure 4). The height and width of the rectangle will allow for an assessment of how high or wide obstacles, such as stairs, curbs or thresholds, the robot will be able to overcome. When controlling the limb in the task space (i.e., controlling the position of point F), the inscribed rectangle limits the movement capabilities of the mechanism to the ranges of the drives used. Additionally, it was assumed that the mechanism would not assume any dead or singular positions inside this rectangle.

The assessment procedure began with the definition of two tangent lines to the boundaries of the robot limb’s workspace. The first horizontal line l_FU is tangent to the upper boundary of the t_FU zone (Figure 4). The second vertical line l_FL is tangent to the left boundary of the t_FL working zone. The intersection of these tangents marks the first vertex FR of the rectangle being sought. Next, the intersection point F_M1 of the horizontal tangent l_FU with the right boundary of the workspace t_FR is determined. The vertical line l_FR drawn from this point F_M1 intersects the lower boundary of the trace t_FB, determining the lower right vertex F_W of the rectangle R₂ (F_R, F_W) marked in blue in Figure 4. Similarly, the intersection of the vertical tangent l_FL with the lower boundary of the t_FB zone marks the point F_M2. The horizontal line l_FB drawn from it intersects the boundary of the workspace, marking the vertex F_H of the second rectangle R₁ (F_R, F_H) inscribed in the area (marked in red in Figure 4). Rectangle R₁ has a greater height. Rectangle R₁ has a greater height, while rectangle R₂ has a greater width. The height of rectangle R₁ and the width of rectangle R₂ are coefficients that can be used to assess the size of the working zone of the limb mechanism:

$${\mathrm{C}}_{\mathrm{O}\mathrm{E}\mathrm{F}\mathrm{F}2}={\mathrm{x}}_{\mathrm{F}\mathrm{W}}-{\mathrm{x}}_{\mathrm{F}\mathrm{R}}$$

$${\mathrm{C}}_{\mathrm{O}\mathrm{E}\mathrm{F}\mathrm{F}3}={\mathrm{y}}_{\mathrm{F}\mathrm{H}}-{\mathrm{y}}_{\mathrm{F}\mathrm{R}}$$

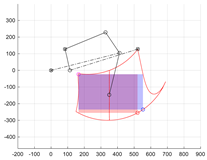
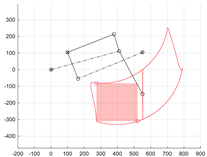
The final step of the synthesis was to select the parameters for mounting the s₅ actuator responsible for wheel lifting movement. These are the coordinates of support point G (x_G, y_G) and the length AH and angle β_A. It was assumed that the actuator is to rotate member 1 within the range (θ_1S, θ_1E) obtained in the first step of the synthesis. The s₅ actuator in the minimum stroke position, GH equal to s_MIN, is to force the orientation of member 1 equal to θ_1S, and the maximally extended stroke of s₅ actuator, GH equal to s_MAX, is to correspond to the position of the wheel at the lower limit of the workspace when θ₁ is equal to θ_1E. Furthermore, to fully utilise the actuator’s capabilities, the angle δ_H of actuator s₅ operation should be close to a right angle over the entire operating range of the actuator (Figure 5).

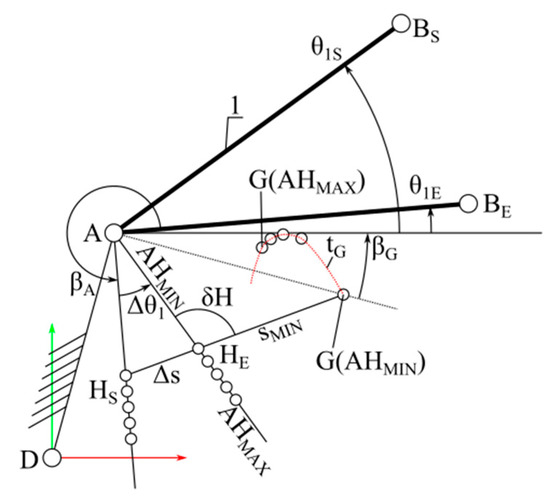
Figure 5. Limb dimensions determining the position of the s₅ drive mounting.

For the specified length AH and angle β_A, the starting point H_S was obtained, corresponding to the position of member 1 in the initial orientation θ_1S. The endpoint H_E corresponds to the position of member 1 determined by the specified angle θ_1E. At point H_S, actuator s₅ should be in its minimum stroke position s_MIN, while at point H_E, it should be in its maximum stroke position s_MAX. The intersection of circles O₅ (with centre at H_S and radius s_MIN) and O₆ (with centre at H_E and radius s_MAX) determines the position of point G. The minimum length of lever AH_MIN is that at which circles O₅ and O₆ are tangent to each other. Point G is then located on a straight line passing through points H_S and H_E, at a distance s_MIN from point H_S. The length AH_MIN was determined based on the isosceles triangle H_SAH_E, where the base of the triangle H_SH_E has a stroke length s₅ equal to Δs = s_MAX − s_MIN:

$$\mathrm{A}{\mathrm{H}}_{\mathrm{M}\mathrm{I}\mathrm{N}}=\sqrt{{\displaystyle \frac{\mathsf{\Delta }{\mathrm{s}}^2}{2\left(1-\cos \mathsf{\Delta }{\mathsf{\theta }}_1\right)}}}$$

It was assumed that angle β_A = 3/2 π and the trace t_G of point G was determined by taking n values of length AH from the determined AH_MIN to a certain fixed AH_MAX. The greater the length of member AH, the less force the levelling actuator s₅ will need to balance the loads of the wheel suspension system. However, the AH lever cannot be too long so that point H does not collide with the ground when the wheel is raised to its maximum height.

With the parameter β_A = 3/2π set, the trace of point G is determined by the change in the length of member AH. Changing the parameter β_A by a certain fixed angle Δβ_A simultaneously rotates the trace t_G relative to point A. The characteristic of angle δ_H therefore does not depend on angle β_A, because changing this parameter simultaneously rotates triangle H_SAH_E and trace t_G. Therefore, the length AH and the angle β_A can be selected independently. For each adopted value of AH_i, the characteristic of the angle δ_H of the levelling actuator s5 was determined. This characteristic is closest to the value 1/2 π when circles O5 and O6 are tangent to each other. It was therefore assumed that point G would be determined for the lever length AH = AH_MIN. It was marked as point G_REF (x_GREF, y_GREF).

When the angle β_A changes, the segment AG_REF rotates relative to point A. The value of angle β_A was selected so that point G is located at the same height as point A (y_G = y_A). The designated point GREF was rotated relative to point A by angle β_G, taking this rotation into account in the value of angle β_A:

$${\mathsf{\beta }}_{\mathrm{A}}=\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\mathsf{\pi }+{\mathsf{\beta }}_{\mathrm{G}},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {\mathsf{\beta }}_{\mathrm{G}}={\tan }^{-1}\left({\mathrm{y}}_{\mathrm{G}\mathrm{R}\mathrm{E}\mathrm{F}}/{\mathrm{x}}_{\mathrm{G}\mathrm{R}\mathrm{E}\mathrm{F}}\right)$$

After this stage of synthesis, all the basic dimensions of the mobile robot limb mechanism were obtained. The last coefficient, which was necessary for evaluating the obtained solution (including s₅ drive mount parameters), remained to be determined. In addition to the characteristic angle δ_H of actuator s₅, the synthesis aimed to obtain a linear characteristic of the vertical displacement of point F, dependent on the stroke of actuator s₅, for a fixed stroke of actuator s₆ (for CD = CD_LEV). Obtaining a linear characteristic y_F(s₅) with a slope coefficient m_F will significantly simplify the control system of the robot platform levelling while driving over uneven terrain. The slope parameter m_F has the following value:

$${\mathrm{m}}_{\mathrm{F}}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}={\displaystyle \frac{\mathsf{\Delta }{\mathrm{y}}_{\mathrm{F}}}{\mathsf{\Delta }\mathrm{s}}}={\displaystyle \frac{{\mathrm{y}}_{\mathrm{F}\mathrm{S}}-{\mathrm{y}}_{\mathrm{F}\mathrm{E}}}{{\mathrm{s}}_{\mathrm{M}\mathrm{A}\mathrm{X}}-{\mathrm{s}}_{\mathrm{M}\mathrm{I}\mathrm{N}}}}$$

(4)

In the next step of the synthesis, the influence of the stroke changes of the wheel lifting drive s₅ on the vertical position y_F of the wheel was determined. The previously determined Equation (3) defines the position of the centre of wheel F in relation to the value of angle θ₁. At this stage, the influence of the change in length GH, i.e., the wheel lift drive s₅, on the orientation of member 1 must be determined. For this purpose, point H was determined at the intersection of circle O₇ (with centre at G and radius GH) and circle O₈ (with centre at A and radius AH):

$$\left({\mathrm{x}}_{\mathrm{H}},{\mathrm{y}}_{\mathrm{H}}\right)=\left({\mathrm{x}}_{\mathrm{G}},{\mathrm{y}}_{\mathrm{G}}\right)+\mathrm{G}\mathrm{H}\cdot \left(\cos {\mathsf{\theta }}_5,\sin {\mathsf{\theta }}_5\right)$$

(5)

The inclination θ₅ of the wheel lifting actuator, depending on its length GH, is determined based on the angles of the triangle GHA:

$${\mathsf{\theta }}_5={\tan }^{-1}\left({\displaystyle \frac{{\mathrm{y}}_{\mathrm{A}}-{\mathrm{y}}_{\mathrm{G}}}{{\mathrm{x}}_{\mathrm{A}}-{\mathrm{x}}_{\mathrm{G}}}}\right)+{\tan }^{-1}\left({\displaystyle \frac{\sqrt{{\left(2\cdot \mathrm{G}\mathrm{H}\cdot \mathrm{A}\mathrm{G}\right)}^2-{\mathsf{\Delta }}_{78}^2}}{{\mathsf{\Delta }}_{78}}}\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {\mathsf{\Delta }}_{78}={\mathrm{G}\mathrm{H}}^2+{\mathrm{A}\mathrm{G}}^2-{\mathrm{A}\mathrm{H}}^2$$

(6)

The position of point H expresses the orientation θ₁:

$${\mathsf{\theta }}_1={\tan }^{-1}\left({\displaystyle \frac{{\mathrm{y}}_{\mathrm{H}}-{\mathrm{y}}_{\mathrm{A}}}{{\mathrm{x}}_{\mathrm{H}}-{\mathrm{x}}_{\mathrm{A}}}}\right)-{\mathsf{\beta }}_{\mathrm{A}}$$

(7)

Based on this relationship, the effect of the change in the length of the actuator on the lifting height of the wheel centre F was determined. The derivative of the vertical position of point F relative to the stroke of the wheel lifting drive s₅ was calculated:

$${\displaystyle \frac{\mathrm{d}{\mathrm{y}}_{\mathrm{F}}}{\mathrm{d}{\mathrm{s}}_5}}={\displaystyle \frac{\partial {\mathrm{y}}_{\mathrm{F}}}{\partial {\mathsf{\theta }}_1}}\cdot {\displaystyle \frac{\mathrm{d}{\mathsf{\theta }}_1}{\mathrm{d}{\mathrm{s}}_5}}$$

This derivative should have a constant value equal to m_F, then the wheel lift characteristic will be linear. The derivative of the vertical position of the wheel centre relative to the orientation of member 1 was determined based on relation 3:

$${\displaystyle \frac{\partial {\mathrm{y}}_{\mathrm{F}}}{\partial {\mathsf{\theta }}_1}}=\mathrm{A}\mathrm{B}\cos {\mathsf{\theta }}_1+\left(\mathrm{B}\mathrm{C}\cos {\mathsf{\theta }}_2+\mathrm{C}\mathrm{F}\cos \left({\mathsf{\theta }}_2+{\mathsf{\beta }}_{\mathrm{C}}\right)\right){\displaystyle \frac{\partial {\mathsf{\theta }}_2}{\partial {\mathsf{\theta }}_1}}$$

The derivative of angle θ₂ with respect to angle θ₁ was determined based on Equation (2):

$${\displaystyle \frac{\mathrm{d}{\mathsf{\theta }}_2}{\mathrm{d}{\mathsf{\theta }}_1}}={\displaystyle \frac{\mathrm{A}\mathrm{B}\cdot {\mathrm{x}}_{\mathrm{A}}\cdot \sin {\mathsf{\theta }}_1-\mathrm{A}\mathrm{B}\cdot {\mathrm{y}}_{\mathrm{A}}\cdot \cos {\mathsf{\theta }}_1+\mathrm{A}\mathrm{B}\cdot \mathrm{B}\mathrm{C}\cdot \sin \left({\mathsf{\theta }}_1-{\mathsf{\theta }}_2\right)}{\mathrm{B}\mathrm{C}\cdot {\mathrm{y}}_{\mathrm{A}}\cdot \cos {\mathsf{\theta }}_2-\mathrm{B}\mathrm{C}\cdot {\mathrm{x}}_{\mathrm{A}}\cdot \sin {\mathsf{\theta }}_2+\mathrm{A}\mathrm{B}\cdot \mathrm{B}\mathrm{C}\cdot \sin \left({\mathsf{\theta }}_1-{\mathsf{\theta }}_2\right)}}$$

Based on relations 5, 6 and 7, the derivative of orientation θ₁ with respect to drive length s₅ was determined:

$${\displaystyle \frac{\mathrm{d}{\mathsf{\theta }}_1}{\mathrm{d}{\mathrm{s}}_5}}={\displaystyle \frac{\mathrm{G}\mathrm{H}}{\mathrm{A}\mathrm{H}\cdot \left(\left({\mathrm{y}}_{\mathrm{A}}-{\mathrm{y}}_{\mathrm{G}}\right)\cos \left({\mathsf{\theta }}_1+{\mathsf{\beta }}_{\mathrm{A}}\right)+\left({\mathrm{y}}_{\mathrm{G}}-{\mathrm{y}}_{\mathrm{A}}\right)\sin \left({\mathsf{\theta }}_1+{\mathsf{\beta }}_{\mathrm{A}}\right)\right)}}$$

The parameter allowing the linearity of the wheel level characteristic y_F (s₅, s₆ = CD_LEV) to be assessed is as follows:

$${\mathrm{C}}_{\mathrm{O}\mathrm{E}\mathrm{F}\mathrm{F}4}=\mathrm{r}\mathrm{m}\mathrm{s}\left({\displaystyle \frac{\mathrm{d}{\mathrm{y}}_{\mathrm{F}}}{\mathrm{d}{\mathrm{s}}_5}}-{\mathrm{m}}_{\mathrm{F}}\right)$$

The synthesis of the robot limb mechanism focused on determining the common dimensions of the robot limb mechanism for the proper execution of wheel guidance movements to accomplish the two main tasks set for the mobile robot: maintaining a constant platform orientation when driving on uneven terrain and stepping over obstacles that the robot cannot overcome by driving on wheels.

The developed C_OEFFi coefficients allow for the evaluation of the obtained solution. The first and fourth coefficients evaluate the platform levelling task. The second and third coefficients allow us to determine whether the robot will be able to manipulate its limbs to overcome obstacles such as thresholds, curbs, or steps.

3. Results

The dimensional synthesis procedure developed and presented in Section 2 was used to select the fundamental dimensions of a new innovative mobile robot limb. The robot being built is designed to navigate public buildings, where it may encounter obstacles such as thresholds and steps, and must be able to walk up and down typical stairs.

The preliminary design assumptions stipulate that obstacles will have a height hp of no more than 0.15 m. This corresponds to the height of a standard staircase. The height of the levelling trajectory is set to cover two such stairs, enabling the robot to walk. To obtain a sufficiently large working space, it was assumed that the Δs strokes of the lifting and walking actuators would be 0.15 m. Based on a review of available linear drive models, the minimum drive length was determined to be s_MIN = 0.35 m. The maximum drive length s_MAX = s_MIN + Δs = 0.5 m. The length of the wheel extension drive s₆, at which the wheel trajectory is to be straight, was assumed to be in the middle of the CD_LEV = 0.425 m movement range.

The first optimisation objective in the synthesis procedure is to minimise the objective function F1_TARGET given by relation (7). Five basic dimensions of the limb mechanism are sought: lengths BC, CF, angle β_C, and coordinates of point A: x_A and y_A (Figure 3). The ranges of values for the sought parameters were adopted (Table 1).

Table 1. Ranges of desired basic dimensions of the limb mechanism.

	CF [m]	BC [m]	βC [°]	xA [m]	yA [m]
min.	0.1	0.1	−60	−0.1	0.1
max.	0.3	0.3	60	0.1	0.3

In the synthesis procedure, it was assumed that the common dimensions would take values from a fixed range with a fixed step. A genetic algorithm from Matlab’s “version 2024b” (MathWorks, Natick, MA, USA www.mathworks.com) optimisation toolbox was used to solve the problem. The advantage of this algorithm is its ability to obtain a solution in a short amount of time. The disadvantage is the stochastic nature of the search. The effect of random searching of the parameter space may be that the algorithm gets stuck in a local minimum of the objective function. To avoid this, it was assumed that the algorithm would operate on integer variables. Linear functions were established that map the integer value of the variable to the real value of the length or angle of the parameter being searched for. The ranges of the variables were selected so that the lengths and coordinates of the points took values with an accuracy of 0.001 m, and the angle values with an accuracy of 0.1°. Limiting the search to integer variables accelerated the algorithm’s operation. In cases where a task requires greater accuracy in searching for dimensions, it is sufficient to modify the functions that map integer variables to the actual values of the robot limb mechanism’s dimensions.

It was assumed that the vertical levelling trajectory of point F would be determined by two points: the starting point F_S and the end point F_E. Three values of the height y_FS of the starting point along the OY axis were assumed, equal to y_FS ∈ <0 m, −0.05 m, −0.1 m>. The height of the specified trajectory of point F was set at 0.3 m, which determines the position of the final point F_E. The position of the specified trajectory of point F along the OX axis was assumed to be in the range x_Fn ∈ <0.3 m; 0.55 m> with a step of 0.05 m. The specified section was divided into n = 10 points F_i, for which the positions of points B_i and the lengths of section AB_i were determined.

For each given section of the trajectory of point F, a genetic algorithm was run to search for a solution. As a result, 18 geometric solutions for the mechanism of a wheeled walking robot limb were obtained (Table 2). In each case, sets of five sought parameters (BC, CF, β_C, x_A, y_A) were obtained.

Table 2. Robot limb mechanisms obtained for different positions of the given trajectory of wheel F.

	yF ∈ <0; −0.3> m	yF ∈ <−0.05; −0.35> m	yF ∈ <−0.1; −0.4> m
xFn = 0.3 m
xFn = 0.35 m
xFn = 0.4 m
xFn = 0.45 m
xFn = 0.5 m
xFn = 0.55 m

The length of member AB was taken as the average value among the determined lengths AB_i. The range of angular position changes θ₁ of member 1 was taken as corresponding to points B_S and B_E (Figure 3). It was assumed that the movement of member 1 in the angular range θ₁ ∈ <θ_1S, θ_1E> and the movement of the wheel extension actuator s₆ in the range DC ∈ <s_MIN, s_MAX>.

For each mechanism, the values of the evaluation coefficients C_OEFF1, C_OEFF2 and C_OEFF3 were determined. Next, the support point of the wheel lifting actuator G (x_G, y_G) and the dimensions of the levers AH and β_A were determined. The evaluation coefficient C_OEFF4 was determined for the selected dimensions. Table 3 shows the common dimensions of the robot limb mechanism obtained for the assumed different positions of the trajectory of point F. A mechanism was sought that would minimise the coefficients evaluating the trajectory of the wheel lifting movement, C_OEFF1 and C_OEFF4, while maximising the coefficients evaluating the size of the workspace, C_OEFF2 and C_OEFF3.

Table 3. Common dimensions of the limb mechanisms obtained.

Lp.	AB [m]	BC [m]	CF [m]	AH [m]	βC [°]	βA [°]	xA [m]	yA = yG [m]	xG [m]
1	0.277	0.133	0.272	0.13	−60	−99	0.076	0.111	0.514
2	0.263	0.15	0.259	0.131	−48	−99	0.084	0.128	0.522
3	0.235	0.207	0.294	0.126	−43	−111	0.062	0.166	0.498
4	0.226	0.225	0.299	0.128	−31	−111	0.067	0.186	0.503
5	0.289	0.127	0.298	0.161	−8	−97	0.087	0.118	0.534
6	0.299	0.107	0.294	0.171	11	−90	0.099	0.104	0.55
7	0.25	0.198	0.297	0.121	−52	−98	0.084	0.174	0.519
8	0.288	0.137	0.292	0.142	−40	−93	0.078	0.123	0.52
9	0.297	0.125	0.298	0.152	−33	−92	0.069	0.11	0.513
10	0.293	0.132	0.296	0.154	−16	−91	0.085	0.123	0.53
11	0.311	0.105	0.294	0.166	0	−85	0.087	0.101	0.537
12	0.297	0.117	0.3	0.162	11	−83	0.1	0.113	0.548
13	0.309	0.114	0.3	0.151	−35	−80	0.095	0.111	0.539
14	0.315	0.106	0.289	0.156	−24	−79	0.093	0.104	0.539
15	0.32	0.103	0.298	0.161	−17	−81	0.083	0.1	0.531
16	0.256	0.207	0.3	0.136	−28	−85	0.057	0.17	0.497
17	0.311	0.112	0.3	0.161	6	−78	0.097	0.11	0.545
18	0.314	0.103	0.3	0.16	17	−73	0.097	0.101	0.544

In Table 4, cases where individual coefficients have minimum or maximum values are marked with bold. The trajectory of the centre of circle F, the levelling movement of the platform, is best in the case of mechanism No. 10.

Table 4. Values of C_OEFFi assessment coefficients as obtained solutions.

Lp.	yFS [m]	xFN [m]	COEFF1	COEFF4	COEFF2	COEFF3	CEOFF5 = COEFF2·COEFF3
1	0	0.3	0.8206	0.2742	0.4160	0.2063	0.0858
2		0.35	0.9679	0.1711	0.3876	0.2315	0.0897
3		0.4	0.3245	0.1295	0.3344	0.2402	0.0803
4		0.45	0.4274	0.105	0.3170	0.2442	0.0774
5		0.5	0.58	0.0923	-	0.2244	-
6		0.55	2.0503	0.1435	-	0.2282	-
7	−0.05	0.3	1.4042	0.2571	0.3394	0.2495	0.0847
8		0.35	2.0414	0.1596	0.4448	0.2242	0.0998
9		0.4	0.2755	0.087	0.5131	0.2243	0.1151
10		0.45	0.2229	0.0588	0.4774	0.2393	0.1143
11		0.5	0.6789	0.0845	-	0.2323	-
12		0.55	1.231	0.1623	-	0.2574	-
13	−0.1	0.3	0.9589	0.2125	0.4853	0.1723	0.0836
14		0.35	1.1773	0.1306	0.5188	0.1846	0.0958
15		0.4	0.7309	0.0653	0.5656	0.2010	0.1137
16		0.45	1.2464	0.1392	0.3681	0.2793	0.1028
17		0.5	1.2565	0.1091	-	0.2562	-
18		0.55	0.8824	0.2418	-	0.2770	-

Assessing the workspace size is no longer straightforward. The mechanisms designated for the x_FN parameter equal to 0.3 m and 0.35 m are characterised by rectangles R₁ and R₂ (Figure 4) of very similar sizes. However, the further the set trajectory of point F is from the centre of the system, the smaller the rectangle R₂, and in some cases, it could not be determined. To assess the size of the workspace, the C_OEFF5 parameter was introduced, which is the product of the width of rectangle R₁ (C_OEFF2) and the height of rectangle R₂ (C_OEFF3). The values are presented in Table 4.

The best solution, according to the additional C_EOFF5 coefficient, is mechanism No. 9. Limbs No. 10 and 15 have very similar C_OEFF5 values, which describe the size of the limb mechanism workspace. Mechanism No. 10 was therefore adopted as the dimensional synthesis solution for selecting the dimensions of the wheel–legged robot limb mechanism. It combines the characteristics of the desired wheel centre F trajectory for the platform levelling task with the appropriate workspace size necessary for walking.

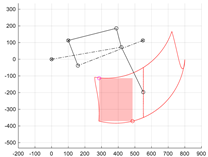
The results of the dimensional synthesis procedure presented above determined the dimensions of the new innovative limb of the wheel–legged robot. The selected solution is described in Table 3, row 10 (marked with bold), and presented in Figure 6a.

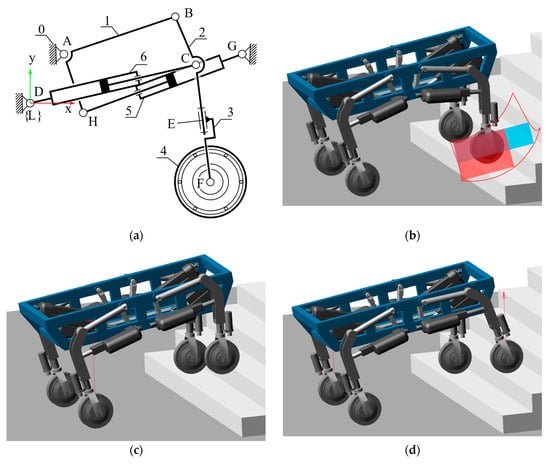
Figure 6. (a) A kinematic scheme of the new limb mechanism with dimensions (Table 3, row 10) obtained based on the developed synthesis procedure, (b) model of wheel–legged mobile robot designed based on the obtained limb mechanism, (c) wheel lifting motion over the step, and (d) wheel extension motion over the step while overcoming the stairs.

Figure 6b shows a model of a wheel–legged mobile robot designed based on the proposed synthesis prepared in MSC Adams “version 2024.2” (Newport Beach, CA, USA). The workspace and the rectangles described against the background of the stairs show the possibility of moving the wheel along the profile of the stairs. Figure 6c shows the process of lifting the wheel along a vertical line, and Figure 6d shows the movement of the wheel over an obstacle along a horizontal line.

Figure 7 illustrates the characteristics of the wheel lifting trajectory obtained using the new limb mechanism solution. Figure 7a presents a curve describing the distance of the centre of the wheel F from the desired trajectory in the horizontal OX axis x_FN – x_F. Figure 7b shows the derivative dy_F/ds₅ of the vertical position y_F of the wheel centre relative to the stroke of the wheel lifting actuator s₅. The coefficient mF, given by Equation (4), is equal to −2 (Δy_F was set at 0.3 m, and the selected actuators have a stroke of Δs = 0.15 m).

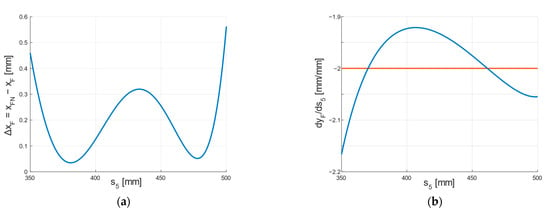
Figure 7. (a) The deviation of point F from the assumed straight trajectory used to level the robot platform, and (b) the derivative of vertical position y_F depending on actuator extension s₅ (blue), and it desired constant value (red) defined by Equation (4).

The quasi-linear trajectory of the centre of wheel F allows the platform to be levelled while driving, using only one drive (the wheel extension drive s6 is inactive). On the other hand, the constant characteristic dy_F/ds₅ allows us to assume that the vertical position of point F depends linearly on the extension of actuator s₅. In Figure 7b, the obtained characteristic deviates from the constant, assumed value only at the beginning (when the wheel is raised to its maximum height). Furthermore, it deviates from the value dy_F/ds₅ = m_F = −2 by only 0.1, which represents a 5% relative error. The proposed solution not only reduces the number of drives needed to maintain a constant platform orientation when driving on uneven terrain, but also significantly simplifies the drive control system by reducing kinematic equations to linear functions.

4. Conclusions

The current paper presents the design of a new mechanism for the limb of a wheel–legged robot. The innovative aspect of the solution lies in the selection of the kinematic structure of the limb mechanism, which allows for the independent execution of specific wheel movements relative to the robot platform. Each drive of the robot limb is responsible for performing different wheel movements. The presented selection of common mechanism dimensions has allowed for significant simplification of the platform levelling task, reducing it to the use of only one drive.

The developed mechanism can be utilised in mobile robots designed to operate in uneven terrain, where maintaining platform stability is crucial while driving. Thanks to its hybrid design, which combines the advantages of drive motors and walking motors, the designed limb can be used, for example, in rescue, exploration, or inspection robots.

In previous work [17], the authors focused on dividing the dimensional synthesis process into smaller steps so that a maximum of two parameters were selected at each stage. In this paper, the main parameters of the mechanism were optimised, and then coefficients C_OEFFi were presented to evaluate the solutions obtained. This allowed for the construction of an expert system where the selection of appropriate features allows for the choice of a solution.

The developed synthesis method involves determining the desired trajectory of the wheel’s centre and then, using a genetic algorithm, determining the dimensions of the mechanism that follows the given trajectory. The stochastic nature of genetic algorithms, combined with the varying positions of the given trajectory, allowed for the generation of a whole family of solutions. The synthesis results showed that for the adopted trajectory of point F, different mechanisms can be obtained by changing only the initial position of the trajectory. Such a variety of solutions allows the user to introduce additional criteria or design constraints, facilitating the selection of the optimal solution for the robot limb mechanism.

The optimisation task was formulated in such a way that the objective function F_1TARGET is single-criterion. The use of a genetic algorithm allowed for the effective identification of a set of mechanism parameters that meet the assumed kinematic criteria. The results obtained confirm that the method is highly flexible and capable of finding many alternative solutions, which allows for further optimisation depending on design requirements.

It is worth noting that the accuracy of the solutions obtained and the calculation time depend on the selection of genetic algorithm parameters, such as population size, number of iterations, and mutation and crossover probabilities. However, the impact of these parameters on the results obtained was not the subject of this study. Additionally, the limb structure presented in this paper consists solely of rigid members. It does not contain any flexible elements, such as springs and dampers, typical of classic suspension mechanisms that can compensate for the impact of uneven terrain on platform inclination changes.

The synthesis method is based on the selection of C_OEFFi coefficients evaluating the obtained solutions. The paper presents the relevant kinematic relationships analytically. In the case of the working zone assessment, a solution to the simple kinematics task of the limb mechanism was determined, which consisted of determining the position of point F based on the extension of actuators s₅ and s₆. To assess the trajectory used to level the robot platform, the inverse kinematics task was solved.

The results obtained confirm the possibility of using evolutionary optimisation methods in the process of synthesising complex kinematic mechanisms. The developed approach is a universal tool that can be adapted to the design of other types of mobile robots with complex limb geometry.

Further research directions may include the development of a synthesis method that incorporates a dynamic limb model, allowing for consideration of the influence of inertial forces, the mass of limb mechanism components, and external loads. An important stage of future work will also involve the development and implementation of a control system that enables adaptive levelling of the robot platform in real time, as well as the verification of the designed mechanism through experimental tests using a prototype. In addition, it is planned to compare the genetic algorithm used with other optimisation methods, enabling us to assess their effectiveness and accuracy in the process of synthesising the robot limb mechanism.