A Novel Bearing Fault Diagnosis Method Based on Singular Spectrum Decomposition and a Multi-Strategy Enhanced Cuckoo Search-Optimized Extreme Learning Machine

Abstract

Large background noise, difficulty in feature extraction, and low parameter-optimization efficiency of diagnosis models are key challenges in rolling bearing fault diagnosis. To address these issues, this paper proposes a fault diagnosis framework that combines Singular Spectrum Decomposition (SSD) with a Multi-Strategy Enhanced Cuckoo Search (MS-CS) algorithm to optimize an Extreme Learning Machine (ELM). First, the raw vibration signal is decomposed via SSD and each intrinsic component’s energy contribution is computed; components whose cumulative energy exceeds 90% are retained and reconstructed, thereby effectively suppressing noise while preserving critical fault features. Next, Multiscale Permutation Entropy (MPE) is extracted from the reconstructed signal to form a high-discriminability feature set. To overcome the traditional Cuckoo Search algorithm’s tendency to become trapped in local optima and its slow convergence, Cauchy mutation and adaptive Levy flight strategies are introduced to enhance global exploration and local exploitation. Finally, the improved MS-CS algorithm is employed to optimize the ELM’s input weights and hidden-layer biases, yielding a high-precision diagnostic model. Experimental results on benchmark bearing data demonstrate an average fault recognition rate of 96%, representing improvements of 6.67% over the conventional CS-ELM and 18% over the unoptimized ELM. These findings confirm the proposed method’s effectiveness and robustness in practical engineering applications.

1. Introduction

Rolling bearings serve as critical support components in a wide range of rotating machinery, and their operational state directly influences equipment safety, reliability, and productivity [1]. Extensive engineering experience demonstrates that bearing failures are among the primary causes of unplanned downtime and serious safety incidents; therefore, accurate and timely fault diagnosis is essential for ensuring the stable operation of industrial systems and reducing maintenance costs [2,3]. However, vibration signals collected under real-world operating conditions are often contaminated by mechanical friction, oil-film deformation, and environmental disturbances, exhibiting strong nonstationarity and nonlinearity that pose significant challenges to both feature extraction and diagnostic model construction [4,5].

Traditional time-domain and frequency-domain analyses can provide preliminary fault discrimination under simple operating conditions but frequently fail in the presence of high noise levels or variable speeds, as fault-induced signal components may be masked or distorted. To address these limitations, researchers have developed numerous adaptive signal decomposition and denoising techniques. Empirical Mode Decomposition (EMD) adaptively extracts intrinsic mode functions but suffers from mode mixing [6,7]; Variational Mode Decomposition (VMD) isolates modes by constrained optimization yet requires careful tuning of mode number and penalty parameters and may still degrade under heavy noise [8]; Empirical Wavelet Transform (EWT) [9] improves noise suppression through adaptive band splitting but remains sensitive to initial band allocation and often demands manual intervention.

In contrast, Singular Spectrum Decomposition (SSD) [10] constructs a trajectory matrix of the vibration signal and applies singular value decomposition to extract components according to their energy contribution, achieving effective noise attenuation while preserving fault-related features with greater robustness and reduced parameter sensitivity. SSD is particularly suitable for vibration analysis because it performs adaptive decomposition based on the intrinsic structure of the signal without requiring predefined basis functions or large-scale training data. This makes it a computationally efficient and interpretable approach for processing nonstationary industrial signals, especially when labeled samples are limited. Although advanced deep generative models such as TnGAN [11] and Spatiotemporal GAN [12] have demonstrated strong data-imputation and representation capabilities, their effectiveness typically depends on extensive training datasets, high computational costs, and complex hyperparameter tuning. In contrast, SSD provides a simpler yet robust framework that effectively extracts meaningful components from limited vibration data, which aligns better with the requirements of this study.

At the feature-extraction stage, the nonstationarity and nonlinearity of bearing vibration signals render single-scale or single-domain measures inadequate for fully characterizing fault patterns. Although techniques such as wavelet packet energy entropy [13] and spectral energy density [14] can reflect energy distribution changes to some extent, they are sensitive to noise and require a priori selection of decomposition levels. Entropic measures like singular spectrum entropy enhance information representation but neglect the multi-scale temporal structure of the signal. Multiscale Permutation Entropy (MPE) [15] addresses these shortcomings by reconstructing the signal at multiple scales and computing the permutation entropy at each resolution, thereby quantifying the complexity and regularity of the time series across scales and demonstrating strong noise resistance. MPE thus yields a high-discriminability feature set for fault recognition.

In terms of model construction and parameter optimization, the Extreme Learning Machine (ELM) [16,17] has attracted considerable attention owing to its single-hidden-layer architecture and rapid training via a closed-form solution. Nevertheless, the performance of ELM heavily depends on the random initialization of input weights and hidden biases, leading to unstable generalization and suboptimal diagnostic accuracy. To enhance ELM robustness and precision, swarm-intelligence algorithms such as Particle Swarm Optimization (PSO) [18] and Cuckoo Search (CS) [19] have been employed, yet both face challenges in high-dimensional search spaces, including loss of population diversity, entrapment in local optima, and slow convergence.

To overcome these issues, this paper proposes a Multi-Strategy Enhanced Cuckoo Search (MS-CS) algorithm that incorporates Cauchy mutation and adaptive Levy flight into the standard CS framework. In this study, Singular Spectrum Decomposition (SSD) is employed to reconstruct vibration signals and suppress noise, while the Extreme Learning Machine (ELM) is utilized for efficient classification. The integration of SSD-based signal decomposition and ELM learning not only enables more effective denoising and feature enhancement at the signal level but also allows the learning model to focus on fault-relevant information, thereby improving diagnostic accuracy and stability compared with using either approach alone. By dynamically adjusting the flight step size and introducing heavy-tailed mutation, MS-CS achieves a balance between global exploration and local exploitation, thereby efficiently optimizing the input weights and hidden biases of ELM. Compared with recent deep learning and transformer-based fault diagnosis models, which often require extensive labeled data and high computational resources, the proposed SSD–MPE–MS-CS–ELM framework offers a lightweight yet highly accurate alternative with significantly reduced training time and computational cost, making it more suitable for real-time industrial deployment. Combining SSD-based signal reconstruction with MPE feature extraction and MS-CS-optimized ELM, we develop a comprehensive bearing fault diagnosis framework. Experimental validation using benchmark bearing datasets demonstrates that MS-CS-ELM significantly outperforms both the unoptimized ELM and the conventional CS-ELM across multiple fault types, confirming the efficacy and robustness of the proposed methodology. The main contributions of this study can be summarized as follows: (1) a multi-strategy enhanced Cuckoo Search (MS-CS) algorithm integrating adaptive Lévy flight and Cauchy mutation is proposed to improve optimization efficiency and solution diversity; (2) a hybrid diagnostic framework combining Singular Spectrum Decomposition, Multiscale Permutation Entropy, and MS-CS-optimized ELM is developed to achieve high-precision and noise-robust bearing fault classification; and (3) extensive comparative experiments are conducted to verify the superior diagnostic accuracy and stability of the proposed model, highlighting its potential for practical industrial applications.

The remainder of this paper is organized as follows. Section 2 details the principles and implementation of SSD signal reconstruction and MPE feature extraction. Section 3 describes the design rationale and algorithmic steps of the MS-CS method. Section 4 introduces the construction of the MS-CS-ELM diagnostic model. Section 5 presents comparative simulations and performance analysis. Finally, Section 6 summarizes the contributions of this study and outlines directions for future research.

2. Singular Spectrum Decomposition Reconstruction and Multiscale Permutation Entropy Extraction

2.1. Singular Spectrum Decomposition

SSD is employed to isolate fault-related components from noise-corrupted vibration signals by constructing a trajectory (Hankel) matrix from embedded signal vectors and performing spectral decomposition [20]. The principal steps include signal embedding, covariance matrix construction, singular value decomposition (SVD), and component reconstruction, as detailed below.

(1)

Signal embedding and trajectory matrix construction.

Let the one-dimensional vibration signal of length N be:

$$x={[x_1,x_2,\dots ,x_N]}^{\mathrm{T}}$$

(1)

Choosing an embedding dimension (window length) L and a sliding step of one sample, one forms the trajectory matrix:

$$\mathrm{X}=\hspace{1em}\left[\begin{array}{cccc}{x}_1& x_2& \dots & x_K\\ x_2& x_3& \dots & x_{K+1}\\ ⋮& ⋮& \ddots & ⋮\\ x_L& x_{L+1}& \dots & x_N\end{array}\right], K = N-L+1,$$

(2)

where each column ${[X]}_{:,j}$ represents an L-dimensional time-delay embedding at time j. This procedure reconstructs the scalar time series into an L-dimensional phase space, providing a richer representation for spectral analysis.

(2)

Covariance matrix and singular value decomposition.

The normalized covariance matrix of X is computed as:

$$\mathrm{C}={\displaystyle \frac{1}{K}}{\mathrm{XX}}^{\mathrm{T}}$$

(3)

where $\mathrm{C}\in {ℝ}^{L\times L}$ encodes energy couplings among delayed components. Applying SVD to C yields:

$$\mathrm{C}=\mathrm{U}\mathrm{\Lambda }{\mathrm{U}}^{\mathrm{T}}$$

(4)

$$\mathrm{\Lambda }=\mathrm{diag}({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_L),\hspace{1em}{\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_L\ge 0,$$

(5)

where $\mathrm{U}=[{\mathrm{u}}_1,{\mathrm{u}}_2,\dots ,{\mathrm{u}}_L]$ is the orthonormal eigenvector matrix and λ is the corresponding eigenvalues. Large eigenvalues correspond to principal signal structures (including fault features), whereas smaller eigenvalues primarily reflect noise or random fluctuations.

(3)

Component grouping and time series reconstruction.

Based on either cumulative energy ratio or the “elbow” criterion of the eigenvalue spectrum, the first r eigenvectors are assigned to the signal subspace and the remaining L − r to the noise subspace [21]. The projection matrix onto the signal subspace is:

$$\mathrm{P}={\displaystyle \sum _{i=1}^r{\mathrm{u}}_i{\mathrm{u}}_i^{\mathrm{T}}}$$

(6)

Applying P to the trajectory matrix produces the signal component matrix:

$$X_s=\mathrm{PX}$$

(7)

Finally, diagonal averaging of ${\mathrm{X}}_s$ reconstructs the one-dimensional signal $x_r$ via:

$$x_r(t)={\displaystyle \frac{1}{N_t}}{\displaystyle \sum _{i+j=t+1}{\left[X_s\right]}_{i,j},t=1,2,\dots ,N,}$$

(8)

where $N_t$ normalizes by the number of elements on the (i,j) anti-diagonal. This procedure yields a multi-component time series reconstruction based on energy-spectrum selection.

(4)

Component selection and fault feature preservation.

The truncation index r is chosen such that the cumulative energy ratio of the first r singular values satisfies:

$${\displaystyle \frac{{\displaystyle \sum _{i=1}^r{\lambda }_i}}{{\displaystyle \sum _{i=1}^L{\lambda }_i}}}\ge \eta$$

(9)

where the threshold η is typically set between 0.8 and 0.95 to ensure retention of major signal structures.

Through these steps, SSD effectively suppresses random noise and enhances the signal-to-noise ratio of fault-related information, thus establishing a solid foundation for subsequent multiscale permutation entropy feature extraction.

2.2. Multiscale Permutation Entropy Extraction

MPE quantifies the complexity and regularity of nonstationary time series over multiple temporal resolutions. Unlike single-scale entropy measures, MPE employs a coarse-graining procedure that captures signal dynamics at various scales, thus providing a more comprehensive characterization of fault signatures [22].

Let the reconstructed one-dimensional signal be $x=[x_1,x_2,\dots ,x_N]$. For a given scale factor $\tau$, the coarse-grained series $y^{(\tau )}=[y_1^{(\tau )},y_2^{(\tau )},\dots ,y_{N_{\tau }}^{(\tau )}]$ of length $N_{\tau }=[N/\tau ]$ is defined by:

$$y_j^{(\tau )}={\displaystyle \frac{1}{\tau }}{\displaystyle \sum _{i=(j-1)\tau +1}^{j\tau }{x}_i},j=1,2,\dots ,N,$$

(10)

where $\tau$ controls the window size, averaging each block of $\tau$ samples to suppress high-frequency noise and emphasize lower-frequency components.

For each coarse-grained sequence $y^{(\tau )}$, select an embedding dimension m and time delay $l$ to construct the vector series:

$$v_i =[y_i^{(\tau )},y_{i+l}^{(\tau )}\hspace{1em},\dots ,y_{i+ml}^{(\tau )}],i=1,2,\dots ,N_{\tau }-(m-1)l.$$

(11)

Each vector $v_i$ is mapped to a permutation pattern $\pi$ of length $m$ according to the relative ordering of its elements. Denoting by $P=N_{\tau }-(m-1)l$ the total number of vectors, one obtains the probability distribution ${\left\{p_j\right\}}_{j=1}^{m!}$ of all $m!$ possible patterns, satisfying:

$${\displaystyle \sum _{j=1}^{m!}{p}_j}=1$$

(12)

The permutation entropy at scale $\tau$ is then defined as:

$${\mathrm{PE}}^{(\tau )}(m,l)={\displaystyle \sum _{\pi \in \prod }p(\pi )\ln p(\pi )}$$

(13)

Upon normalization by $\ln (m!)$, this yields:

$${\mathrm{NPE}}^{(\tau )}={\displaystyle \frac{{\mathrm{PE}}^{(\tau )}}{\ln (m!)}}\in [0,1],$$

(14)

where values approaching zero indicate greater regularity, and values approaching one indicate higher randomness.

By varying $\tau$ from 1 to a maximum scale ${\tau }_{\max }$ and computing ${\mathrm{NPE}}^{(\tau )}$ at each level, one constructs the multiscale feature vector:

$$\mathrm{F}=[{\mathrm{NPE}}^{(1)},{\mathrm{NPE}}^{(2)},\dots ,{\mathrm{NPE}}^{(\tau \max )}]$$

(15)

which encapsulates the signal’s complexity across multiple time scales. Applying MPE to the SSD-reconstructed signal thus yields a high-discriminability input set for the subsequent population-based optimization and diagnostic modeling.

3. Multi-Strategy Enhanced Cuckoo Search Algorithm (MS-CS): Design Principles and Implementation

3.1. Cuckoo Search Algorithm

The traditional CS algorithm is a population-based optimization method inspired by the brood parasitism of cuckoo species and Levy flight random walks [23]. Each candidate solution is represented by a d-dimensional real vector ${\mathrm{x}}_i\in {ℝ}^d$, and a population of n such vectors is initialized by uniform sampling within the search bounds L and U:

$${\mathrm{x}}_i^{(0)}=\mathrm{L}+(\mathrm{U}-\mathrm{L})\odot {\xi }_i, {\xi }_i\sim u{(0,1)}^d$$

(16)

where ⊙ denotes element-wise multiplication, ensuring a uniform spread of initial solutions.

During each iteration, new solutions are generated via Levy flights to simulate the long-range, heavy-tailed jumps of cuckoos. For the i-th individual at iteration t, the update rule is:

$${\mathrm{x}}_i^{(t+1)} = {\mathrm{x}}_i^{(t)} + \alpha \mathrm{Levy}(\lambda )({\mathrm{x}}_i^{(t)}-{\mathrm{x}}_{\ast }),$$

(17)

where $\alpha >0$ is a step-size scaling factor, ${\mathrm{x}}_{\ast }$ is the current global best solution, and Levy(λ) denotes a random step drawn from a Levy distribution characterized by:

$$p(u)\propto u^{-(1+\lambda )}, 1<\lambda \le 3.$$

(18)

which balances local exploitation and global exploration.

To mimic the host bird’s discovery of alien eggs, a fraction $p_a$ of the worst solutions is replaced by new ones drawn by uniform sampling. Specifically, if $I\subset \{1,\dots ,n\}$ is a randomly selected index set of size $\left|I\right|\approx p_{a}n$, then for each $i\in I$,

$${\mathrm{x}}_i^{(t+1)}=\mathrm{L}+(\mathrm{U}-\mathrm{L})\odot {\xi }_i^{\prime }, {\xi }_i\sim u{(0,1)}^d$$

(19)

The remaining individuals retain their Lévy-flight updates. The new solutions are evaluated and compared to the current ones, and the better of the two is retained. This process of Lévy flights, parasitic replacement, and greedy selection iterates until a convergence criterion or maximum iteration count is met, yielding the global optimum.

3.2. Multi-Strategy Enhancement of the Cuckoo Search Algorithm

Although the conventional Cuckoo Search (CS) algorithm excels at global exploration, it may suffer from loss of population diversity and premature convergence in high-dimensional or constrained problems, as well as slow convergence due to inappropriate step-size control [24]. To address these shortcomings, this study integrates Cauchy mutation and adaptive Lévy flight into the CS framework, yielding the Multi-Strategy Enhanced Cuckoo Search (MS-CS) algorithm. After initial population generation, each individual ${\mathrm{x}}_i^{(t)}$ in generation t undergoes Cauchy mutation to enhance diversity:

$${\overline{\mathrm{x}}}_j^{(t)}={\mathrm{x}}_i^{(t)}+\gamma \mathrm{Cauchy}(0,1)({\mathrm{x}}_i^{(t)}-{\mathrm{x}}_j^{(t)}\hspace{1em})$$

(20)

where $\gamma >0$ is the mutation strength factor, $\mathrm{Cauchy}(0,1)$ is a standard Cauchy random variable, and ${\mathrm{x}}_j^{(t)}$ is a randomly selected peer. The heavy tails of the Cauchy distribution facilitate large jumps early in the search, helping to escape local optima.

Building on this mutation, MS-CS introduces an adaptive mechanism for the Lévy flight parameters. Let $r=t/T$ denote the normalized iteration count (with $T$ the maximum number of iterations). The step-size factor $\alpha$ decays exponentially according to:

$${\alpha }^{(t)}={\alpha }_0\exp (-kr)$$

(21)

while the Lévy distribution parameter λ increases linearly:

$${\lambda }^{(t)}={\lambda }_{\min }+({\lambda }_{\max }-{\lambda }_{\min })r$$

(22)

These adjustments ensure broad exploration in early iterations and fine-grained local search in later stages. Accordingly, each mutated individual ${\overline{\mathrm{x}}}_i^{(t)}$ is updated via adaptive Lévy flight:

$$x_i^{(t+1)}={\overline{\mathrm{x}}}_i^{(t)}+{\alpha }^{(t)}\mathrm{Levy}({\lambda }^{(t)})({\overline{\mathrm{x}}}_i^{(t)}-x_{\ast })$$

(23)

where ${\mathrm{x}}_{\ast }$ is the current global best. MS-CS retains the CS probabilistic replacement of a fraction $p_a$ of the worst individuals and applies greedy selection to choose the better solutions. The coordination of Cauchy mutation, adaptive Levy flight, and parasitic replacement enables MS-CS to maintain population diversity while achieving rapid and accurate convergence.

3.3. Optimization of the ELM Network by the Enhanced Cuckoo Search Algorithm

For an ELM with training set $\{({\mathrm{x}}_j,{\mathrm{t}}_j)\left|j=1,\dots ,N\right.\}$, where ${\mathrm{x}}_j\in {ℝ}^d$ and ${\mathrm{t}}_j\in {ℝ}^m$, the single-hidden-layer output is given by:

$$y_j={\displaystyle \sum _{i=1}^L{\beta }_{i}g({\mathrm{w}}_i^T{\mathrm{x}}_j+b_i)}$$

(24)

where $L$ is the number of hidden neurons, ${\mathrm{w}}_i\in {ℝ}^d$ and $b_i\in ℝ$ are the input weight vector and bias of neuron $i$, ${\beta }_i\in {ℝ}^m$ is the output weight, and $g(\cdot )$ is the activation function. Aggregating the network responses yields the hidden-layer output matrix:

$$H=\left[\begin{array}{ccc}g({\mathrm{w}}_1^T{\mathrm{x}}_1+b_1)& \dots & g({\mathrm{w}}_L^T{\mathrm{x}}_1+b_L)\\ ⋮& \ddots & ⋮\\ g({\mathrm{w}}_1^T{\mathrm{x}}_N+b_1)& \dots & g({\mathrm{w}}_L^T{\mathrm{x}}_N+b_L)\end{array}\right]\in {ℝ}^{N\times L}$$

(25)

Traditionally, $\{{\mathrm{w}}_i,b_i\}$ are randomly initialized and the output weight matrix $\mathrm{B}\in {ℝ}^{L\times m}$ is solved by least squares:

$$\mathrm{B}={\mathrm{H}}^{†}\mathrm{T}$$

(26)

where $\mathrm{T}={[t_1,t_2,\dots ,t_N]}^{\mathrm{T}}$ and ${\mathrm{H}}^{†}$ is the Moore–Penrose pseudoinverse. Random initialization, however, may yield poorly conditioned $\mathrm{H}$, degrading generalization and stability.

To address this, MS-CS is employed to optimize the concatenated parameter vector:

$$\mathrm{z}={[{\mathrm{w}}_1^{\mathrm{T}},b_1,\dots ,{\mathrm{w}}_L^{\mathrm{T}},b_L]}^{\mathrm{T}}\in {ℝ}^{(d+1)L}$$

(27)

Using the training error sum of squares as the objective:

$$f(\mathrm{z})={‖{\mathrm{H}\left(\mathrm{z}\right)\mathrm{H}\left(\mathrm{z}\right)}^{†}\mathrm{T}-\mathrm{T}‖}_F^2$$

(28)

where ${‖\cdot ‖}_F^2$ denotes the Frobenius norm and $\mathrm{H}(\mathrm{z})$ emphasizes the dependence of $\mathrm{H}$ on $\mathrm{z}$.

During MS-CS optimization, candidate vectors ${\mathrm{z}}_i$ are generated via the multi-strategy mutation and adaptive Lévy flight. For each ${\mathrm{z}}_i$, one reconstructs $\mathrm{H}({\mathrm{z}}_i)$, computes ${\mathrm{B}}_i=\mathrm{H}{({\mathrm{z}}_i)}^{†}\mathrm{T}$, and evaluates $f({\mathrm{z}}_i)$.

MS-CS iteratively updates the population based on these objective values until convergence to the optimal ${\mathrm{z}}^{\ast }$. The resulting ELM, configured by ${\mathrm{z}}^{\ast }$, achieves maximal diagnostic accuracy and robustness. Through this approach, MS-CS-ELM combines the rapid analytic training of ELM with the global search capabilities of the enhanced CS, making it well suited for bearing fault diagnosis under noisy, complex conditions.

4. MS-CS-ELM Fault Diagnosis Model

The MS-CS-ELM fault diagnosis model integrates three core components—signal preprocessing, feature extraction, and intelligent optimization learning—to form a comprehensive pipeline from raw vibration data to fault classification. Initially, the acquired vibration signals are decomposed and reconstructed using SSD to suppress noise and amplify fault-related components. Next, MPE features are computed from the reconstructed signals, yielding feature vectors that capture dynamic complexity across multiple temporal scales. These feature vectors are then fed into an ELM, whose input weights and hidden-layer biases are optimized by the MS-CS algorithm to minimize training error. Finally, the optimized ELM model performs online diagnosis and classification of bearing fault types. A schematic of this diagnostic framework is presented in Figure 1.

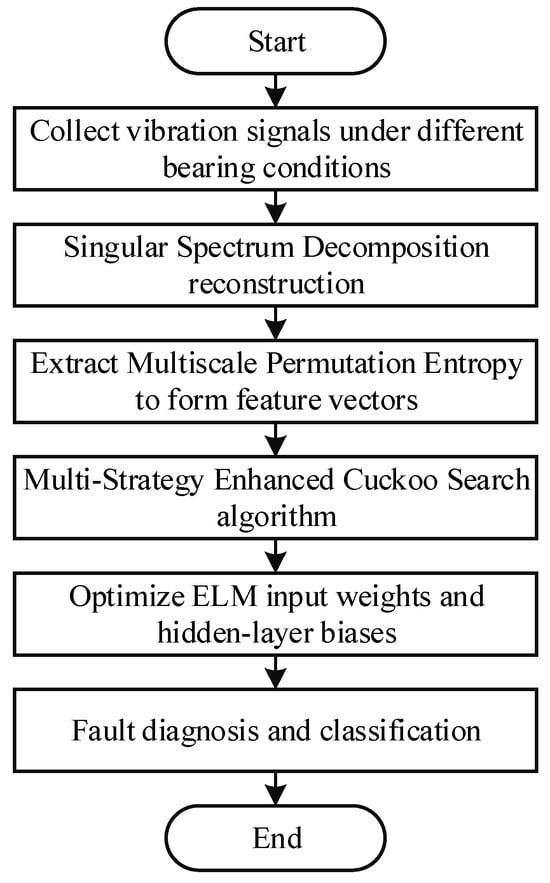
Figure 1. MS-CS-ELM fault diagnosis process.

5. Experimental Results and Comparative Analysis

5.1. Experimental Setup

The validation experiments were conducted on the widely used Xi’an Jiaotong University rolling bearing test rig, which comprises a digitally controlled hydraulic loading system, an AC motor coupled to a shaft through a motor speed controller, and support bearings mounting the test bearing under varying load conditions (Figure 2). A digital force display monitors the applied radial load, while vertical and horizontal accelerometers are mounted on the bearing housing to capture vibration responses. The test bearing itself can be configured in one of four distinct states—inner race fault, outer race fault, or cage fault—by introducing controlled defects of known dimensions and locations.

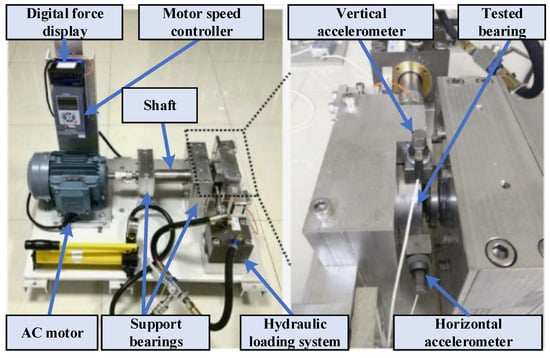
Figure 2. Diagram of experimental device.

During each run, the motor speed controller maintains a constant rotational speed while the hydraulic system applies predetermined radial loads. Vibration signals are recorded simultaneously from both accelerometers at a high sampling rate to ensure accurate capture of transient and steady-state features. This setup enables systematic collection of multi-condition bearing data under repeatable and well-controlled experimental conditions. The resulting dataset thus provides a robust benchmark for evaluating the proposed SSD–MPE–MS-CS–ELM diagnostic framework across normal and various fault scenarios.

The test bearing selected for this study is the LDK UER204 rolling bearing (LDK Bearings Co., Ltd. (Linqing, Shandong, China)), whose specifications are listed in Table 1. Three operating conditions were designed: Condition a at 2100 r/min and 12 kN radial load; Condition b at 2250 r/min and 11 kN; and Condition c at 2400 r/min and 10 kN. For each condition, five bearings were tested. This rig, under well-controlled speed and load parameters, emulates real-world operating influences on bearing vibration, thereby providing a reliable data foundation for subsequent fault diagnosis model development.

Table 1. Specifications of the LDK UER204 Bearing.

Parameter	Value	Parameter	Value
Inner raceway diameter (mm)	29.30	Ball diameter (mm)	7.92
Outer raceway diameter (mm)	39.80	Number of balls	8
Bearing pitch diameter (mm)	34.55	Contact angle (°)	0
Basic dynamic load rating (N)	12,820	Basic static load rating (kN)	6.65

5.2. SSD Signal Decomposition and Reconstruction

Vibration signals acquired under actual operating conditions are often contaminated by mechanical friction, oil-film deformation, and environmental disturbances, exhibiting significant nonstationarity and high noise levels. Consequently, direct application of time-domain or frequency-domain methods fails to extract fault features accurately. Furthermore, different fault types of manifests in distinct spectral components and energy distributions, making it difficult for conventional filtering to simultaneously preserve fault signatures and suppress noise. To address these challenges, this study applies Singular Spectrum Decomposition (SSD) to decompose the raw signal and reconstruct only those components whose cumulative singular value energy exceeds a threshold of 0.9. Figure 3 and Figure 4, respectively, show the original outer-race fault signal and its SSD-decomposed components.

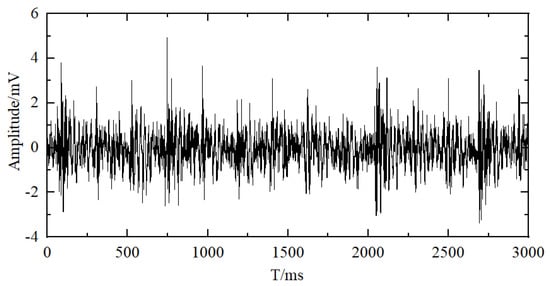
Figure 3. Original Outer-Race Fault Signal.

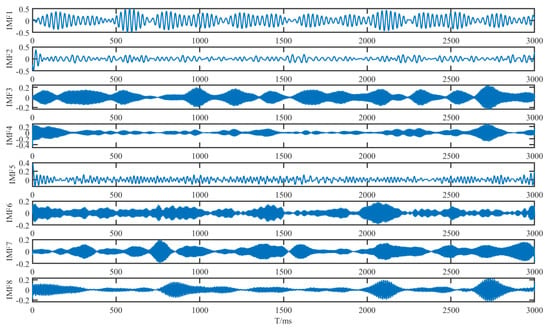
Figure 4. SSD Decomposed Components of Outer-Race Fault Signal.

As illustrated in the figures, the SSD-decomposed components exhibit markedly different energy contributions, with only the high-energy modes containing pertinent fault signatures, while the low-energy modes predominantly consist of random noise or background interference. Consequently, it is necessary to select components judiciously to avoid the influence of irrelevant modes on subsequent analysis. In this study, the singular value energy ratio method is adopted: the sum of the first r singular values, ordered in descending magnitude, is divided by the total sum of all singular values, and a threshold of 0.9 is imposed. This criterion ensures that the reconstructed signal retains the principal structural components of the original signal while effectively eliminating low-energy noise modes, thus achieving a balance between noise suppression and feature preservation. The signal subspace is formed by the eigenvectors corresponding to the first r singular values, and diagonal averaging is applied to map this subspace back to the time domain, yielding a high-signal-to-noise-ratio reconstructed signal, as shown in Figure 5.

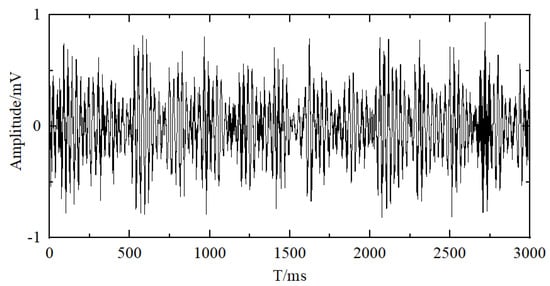
Figure 5. Reconstructed Outer-Race Fault Signal.

It should be noted that the SSD reconstruction process does not obscure or distort fault-related features; on the contrary, by suppressing random noise and retaining the dominant structural components, it enhances the clarity and separability of characteristic impulses, thereby facilitating more effective and reliable feature extraction in the subsequent MPE analysis. The reconstructed signal shows pronounced enhancement of fault impulses and clear periodicity in the time domain, while its signal-to-noise ratio (SNR) improves by approximately 5–8 dB over the raw signal, thereby boosting the accuracy and robustness of subsequent MPE feature extraction. Similar reconstruction results for inner race and cage faults are presented in Figure 6 and Figure 7.

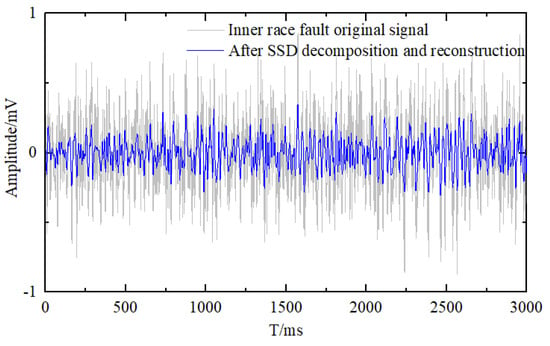
Figure 6. Inner Race Fault: Before and After SSD Reconstruction.

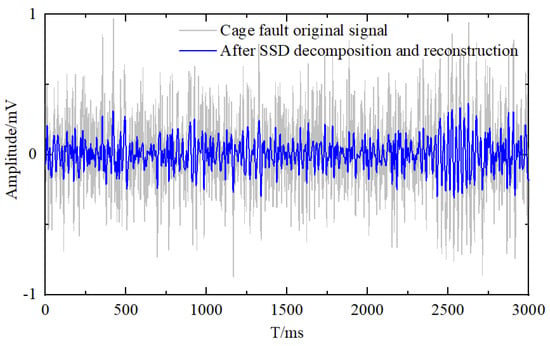
Figure 7. Cage Fault: Before and After SSD Reconstruction.

Overall, SSD reconstruction preserves key fault information while effectively suppressing random noise, providing high-quality input for the diagnostic algorithms.

5.3. Fault Diagnosis Comparative Experiments and Analysis

From the high-SNR reconstructed signals, Multiscale Permutation Entropy (MPE) is computed across multiple scale factors to form feature vectors that capture complexity at various time resolutions. For model training and testing, inner race faults, outer race faults, and cage faults are labeled as 1, 2, and 3, respectively. These feature vectors are then applied to three diagnostic methods—traditional ELM, CS-ELM (ELM optimized by conventional Cuckoo Search), and the proposed MS-CS-ELM—for comparative validation. The diagnostic results for each method are shown in Figure 8, Figure 9 and Figure 10.

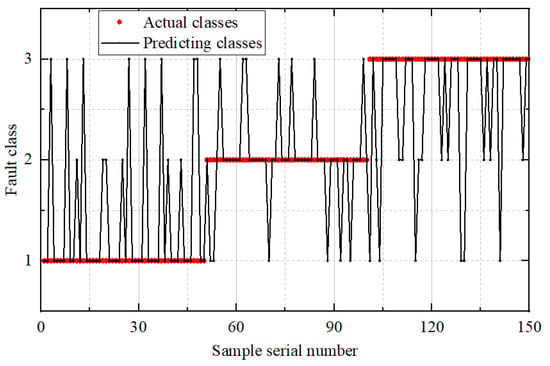
Figure 8. Diagnostic Results of the ELM Model.

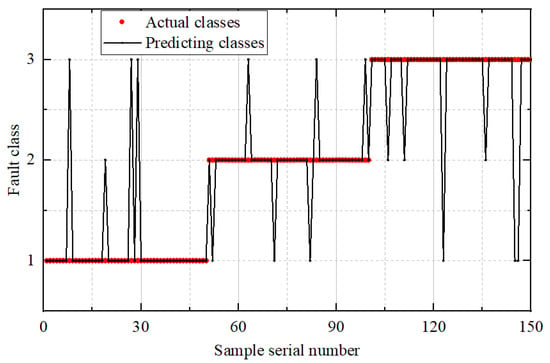
Figure 9. Diagnostic Results of the CS-ELM Mode.

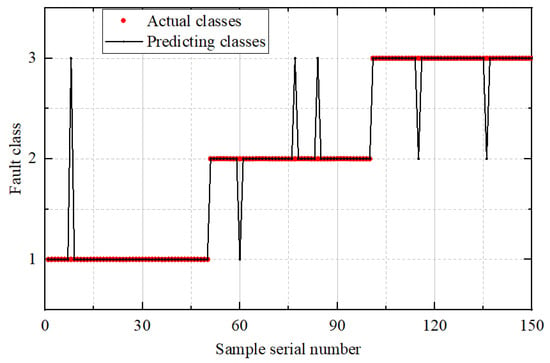
Figure 10. Diagnostic Results of the MS-CS-ELM Model.

In Figure 8, Figure 9 and Figure 10, the horizontal axis represents the sequence index of test samples, while the vertical axis denotes the fault category, labeled as 1, 2, and 3. The term actual class refers to the true fault label of each test sample, whereas predicting class indicates the category output by the diagnostic model. The noticeable peaks observed in the prediction plots correspond to misclassified samples—instances where the model’s predicted class differs from the actual fault type—thus serving as visual indicators of classification errors. The comparative results indicate that the proposed MS-CS -ELM framework substantially outperforms both the unoptimized ELM and the CS-ELM across all fault categories. Specifically, the baseline ELM yields relatively low classification accuracies of 0.72 for inner race faults and 0.74 for outer race faults, although it performs better on cage faults (0.88). When the conventional Cuckoo Search algorithm is employed to optimize the ELM parameters, the CS-ELM improves recognition rates markedly for inner and outer faults—achieving 0.92 and 0.88, respectively—while maintaining the same accuracy of 0.88 for cage faults. However, the multi-strategy enhancements introduced in MS-CS -ELM drive further gains: the inner race fault accuracy rises to 0.98, outer race recognition to 0.94, and cage fault detection to 0.96. These results demonstrate that the adaptive Levy flight and Cauchy mutation strategies in MS-CS effectively guide the search toward superior weight and bias configurations, thereby enhancing the model’s ability to capture subtle fault signatures and improving robustness against noise. Overall, MS-CS -ELM achieves relative improvements of 36% on inner race faults, 27% on outer race faults, and 9% on cage faults compared to the baseline ELM, confirming the efficacy of the proposed multi-strategy optimization in achieving high-precision bearing fault diagnosis.

The computational complexity of the proposed MS-CS algorithm mainly depends on the population size N, the maximum number of iterations T, and the dimension of the optimization problem D. Thus, the overall time complexity can be expressed as O (N × T × D), which is comparable to that of conventional population-based algorithms such as CS and PSO. Despite the introduction of additional adaptive mechanisms, the convergence speed remains efficient due to the dynamic step size control and heavy-tailed mutation strategy that accelerate convergence in later iterations.

In addition to the comparative analysis of ELM, CS-ELM and MS-CS -ELM, two further experiments were conducted to deepen the evaluation of the proposed framework. The first additional study assessed the diagnostic prowess of ELM by benchmarking it against two contemporary deep learning models: a one-dimensional convolutional neural network (1D-CNN) designed for end-to-end feature extraction and classification, and a deep belief network (DBN) that applies unsupervised pretraining on MPE features followed by supervised fine-tuning. The second additional study examined the generalizability of the MS-CS optimization strategy by comparing MS-CS -ELM with two other population-based optimization methods, namely Particle Swarm Optimization ELM (PSO-ELM) and Grey Wolf Optimizer ELM (GWO-ELM), under the same diagnostic conditions. To provide a more comprehensive evaluation of diagnostic performance, three additional metrics were introduced: Average precision (Ape), Sensitivity (Sen) and Specificity (Spe). The results of these experiments are summarized in Table 2.

Table 2. Diagnostic accuracy results of different models.

	Inner Race Fault	Outer Race Fault	Cage Fault	Ape	Sen	Spe	Training Time (s)	Inference Time (ms/Sample)
ELM	0.72	0.74	0.88	0.78	0.78	0.74	1.2	0.35
CS-ELM	0.92	0.88	0.88	0.8933	0.86	0.84	2.8	0.42
MS-CS-ELM	0.98	0.94	0.96	0.96	0.97	0.96	3.0	0.40
ID-CNN	0.9	0.92	0.86	0.89	0.88	0.90	48.5	2.30
DBN	0.84	0.8	0.86	0.8333	0.80	0.85	35.2	1.90
PSO-ELM	0.9	0.9	0.84	0.88	0.85	0.87	3.5	0.43
GWO-ELM	0.86	0.88	0.92	0.8867	0.89	0.86	3.4	0.41

When benchmarked against deep learning models, the MS-CS -ELM also outperforms the one-dimensional convolutional neural network (1D-CNN), which attains an average accuracy of 0.89, and the deep belief network (DBN), which achieves 0.8333 despite its unsupervised pretraining on MPE features. Furthermore, MS-CS -ELM surpasses other population-based optimization techniques: Particle Swarm Optimization-ELM yields 0.88 on average, while Grey Wolf Optimizer-ELM records 0.8867. These comparisons underscore that the proposed multi-strategy enhanced Cuckoo Search not only improves ELM’s parameter optimization but also delivers a more robust and accurate diagnostic model than both traditional deep learning classifiers and alternative swarm-intelligence-based ELM optimizations under identical experimental conditions. The consistently higher Ape, Sen, and Spe values further confirm that the proposed multi-strategy enhanced Cuckoo Search effectively improves ELM’s optimization performance, delivering a more accurate and reliable fault diagnosis model with efficient computational complexity and broad applicability in industrial scenarios. Moreover, the analysis of computational complexity and runtime efficiency indicates that the proposed MS-CS-ELM achieves an excellent balance between diagnostic accuracy and computational cost, requiring only marginally higher training time than CS-ELM while being significantly lighter and faster than deep learning-based counterparts such as 1D-CNN and DBN.

6. Conclusions and Future Works

In this work, the challenges of strong noise interference, non-stationarity and multi-fault feature extraction in practical rolling bearing vibration signals, as well as the instability and suboptimal convergence of ELM due to random initialization, have been systematically addressed by integrating SSD based signal reconstruction with MPE feature extraction and a MS-CS optimization of ELM parameters. SSD effectively suppresses noise and preserves fault-related components by selecting singular components whose cumulative energy exceeds 90%, while MPE captures the dynamic complexity of the reconstructed signals across multiple time scales. The subsequent MS-CS algorithm, incorporating Cauchy mutation and adaptive Levy flight, further refines ELM input weights and hidden biases. Comprehensive validation on the Xi’an Jiaotong University bearing dataset demonstrates that MS-CS -ELM achieves an average diagnostic accuracy of 0.96, significantly outperforming traditional ELM, CS-ELM, 1D-CNN, DBN, PSO-ELM and GWO-ELM, thereby confirming the synergistic benefits of the proposed signal-level and algorithmic-level enhancements.

The proposed MS-CS-ELM framework is suitable for fault diagnosis tasks involving non-stationary and nonlinear vibration signals, particularly in mechanical equipment such as bearings, gearboxes, and rotating machinery. Since the method relies on statistical feature extraction rather than extensive labeled data, it is also applicable to small-sample and noisy environments where deep learning methods often face performance degradation.

Looking ahead, the SSD, MPE and MS-CS-ELM framework will be extended to an online, real-time monitoring system where incremental learning and adaptive thresholding can facilitate rapid adaptation to evolving operational conditions and emerging compound fault modes. Future investigations will also evaluate the model’s performance under more challenging operating conditions, such as variable rotational speeds, heavy load fluctuations, and different bearing types, to further examine its generalization capability and robustness. In addition, to address data imbalance and long-term degradation in field applications, future research will explore the integration of transfer learning and deep domain adaptation techniques to further enhance model generalization and robustness in complex industrial environments. In our future work, these studies will be conducted on both laboratory and real industrial platforms to comprehensively validate the proposed method under diverse and realistic conditions.