Interplanetary Mission Performance Assessment of a TANDEM Electric Thruster-Based Spacecraft

Abstract

The aim of this paper is to analyze the transfer performance of a spacecraft equipped with a TANDEM electric propulsion system in a classical interplanetary mission scenario targeting Mars, Venus, or a near-Earth asteroid. The TANDEM concept is a coaxial, two-channel Hall-effect thruster recently proposed under ESA’s Technology Development Element program. This innovative propulsion system, currently undergoing experimental characterization, is designed to operate at power levels between $3\mathrm{kW}$ and $25\mathrm{kW}$, delivering a maximum thrust of approximately $1\mathrm{N}$. Its architecture allows operation using a single channel (internal or external) or both channels simultaneously to achieve maximum thrust. This inherent flexibility enables the definition of advanced control strategies for future missions employing such a propulsion system. In the context of a heliocentric mission scenario, this paper adopts a simplified thrust model based on actual thruster characteristics and a semi-analytical model for spacecraft mass breakdown. Transfer performance is evaluated within an optimization framework in terms of time of flight and the corresponding propellant mass consumption as functions of the main spacecraft design parameters.

1. Introduction

Since the successful NASA mission Deep Space 1 [1], which tested the effectiveness of the NSTAR ion engine in interplanetary space in the late 1990s [2], solar electric propulsion (SEP) has been considered a viable option for performing robotic missions aimed at exploring regions of the Solar System or visiting small celestial bodies that are difficult to reach using chemical (high-thrust) propulsion systems [3]. In this context, the SEP’s potential has been confirmed over the last decade by the JAXA missions Hayabusa and Hayabusa2 [4], which successfully returned samples from near-Earth asteroids, becoming the first missions ever to achieve this milestone [5]. More recently, the ESA/JAXA mission BepiColombo [6], launched in 2018 to reach Mercury, with its four QinetiQ-T6 ion thrusters [7], represents a typical example of how a complex interplanetary trajectory can be achieved with the aid of a SEP system composed of an array of advanced thrusters.

The potential of a newly proposed (low-thrust) electric propulsion system designed to equip a deep-space vehicle is usually assessed by analyzing, within a simplified and preliminary framework [8], its performance in an interplanetary mission scenario involving the transfer to an inner planet, such as Mars or Venus [9]. In the context of the heliocentric orbit transfer of a SEP-propelled vehicle, the preliminary trajectory is obtained by solving an appropriate optimal control problem [10], where the scalar term to be minimized is the required propellant mass, the flight time, or a suitable combination of these two key mission parameters. This typical optimization problem can be solved, in an approximate form and under some simplifying assumptions, using a semi-analytical approach such as that proposed in Ref. [11], or by employing a conventional technique based on the calculus of variations [12] (i.e., an indirect approach), or a more recent—though typically more computationally demanding—direct approach [13]. In this first phase of the mission’s study, a simplified modeling of the spacecraft’s dynamics is employed to reduce computational cost and enable the analysis of a large number of possible transfer trajectories within a short time frame.

Considering the context of preliminary trajectory design, this paper aims to investigate the performance of a spacecraft equipped with the newly proposed TANDEM Electric Propulsion System (TEPS) [14,15]. In particular, the potential of this thruster concept is assessed within a heliocentric mission scenario involving the transfer of a robotic vehicle from Earth’s orbit to that of Mars, Venus, or a near-Earth asteroid, such as the recently discovered [16] (and potentially hazardous [17]) asteroid 2024 YR4. The novel contribution of this paper is to provide the first analysis of the transfer performance of a spacecraft propelled by a TEPS within a defined (and important) set of heliocentric mission scenarios.

This work is based on two main assumptions. The first is closely related to the (typical) assumption of a two-body dynamical model for describing the heliocentric motion of the TEPS-propelled spacecraft. In this context, all orbital perturbations are neglected, and the spacecraft is assumed to be influenced only by the Sun’s gravitational attraction and the continuous thrust provided by the on-board primary propulsion system, i.e., the TANDEM. Moreover, the spacecraft state vector is assumed to be exactly known at any point along the transfer trajectory, so that possible uncertainties in this aspect (as well as in the characteristics of the thrust vector) are disregarded. Uncertainty analysis, in fact, can be considered a second-order approach to trajectory design, where the results obtained with the proposed procedure are refined using a more accurate mathematical model, which, on the other hand, requires increased computation time. The second important assumption concerns the concept of orbit-to-orbit transfer, where planetary ephemerides are not considered in the trajectory design in order to determine the global minimum flight time for a given parking and target orbit. Although this assumption may seem incompatible with the requirements of an orbital rendezvous, the results obtained in this case can be used to identify the most appropriate launch window to achieve transfer performance close to the optimal one.

The TEPS is a coaxial, two-channel Hall-effect thruster [18] recently proposed under ESA’s Technology Development Element program [19]. This innovative propulsion system, developed by the University of Pisa and Aerospazio Tecnologie s.r.l. (Siena, Italy), is currently undergoing experimental characterization in terms of classical propulsive performance, such as thrust magnitude and specific impulse, using either Xenon or Krypton as propellant [20,21]. The propulsion system is designed to operate at power levels between approximately $3\mathrm{kW}$ and $25\mathrm{kW}$ and can deliver a maximum thrust of $1093\mathrm{mN}$ with a specific impulse of about $2421\mathrm{s}$ and a total efficiency of $51\%$ when Xenon is used as propellant and the input power is $25.3\mathrm{kW}$ [22]. Notably, the specific design of TEPS allows this Hall-effect thruster to operate using a single channel (either internal or external) or both channels simultaneously to achieve maximum thrust for a given TEPS input power [22]. Conversely, when using Xenon (which is considered the reference propellant in the remainder of this paper), tests indicated that the minimum thrust magnitude is about $181\mathrm{mN}$, obtained with a specific impulse of $1508\mathrm{s}$ and a total efficiency of $40\%$ when the TEPS input power is $3\mathrm{kW}$.

Considering these two extreme thrust values, as described in Ref. [22], recent laboratory measurements have characterized TEPS performance at 11 potential operating points. These include operation with the inner channel only (IC mode), the outer channel only (OC mode), or both channels simultaneously (dual channel, DC mode). For each operating point, performance data—covering thrust, electric input power, specific impulse, and propellant mass flow rate—can be used to populate a representative thrust table for this propulsion system. This table enables the modeling of key characteristics of the spacecraft’s thrust vector during the interplanetary transfer, as illustrated in Ref. [23]. In that work, NASA’s Evolutionary Xenon Thruster (NEXT) thrust table, provided by Patterson and Benson [24], was used to investigate flight performance in a robotic mission to the inner Solar System’s regions. More recently, this approach was applied in Ref. [25] to analyze the heliocentric transfer of a CubeSat propelled by a BIT-3 RF ion thruster [26] developed by Busek Co. Inc. (Natick, MA, USA) [27]. A similar methodology was employed to analyze the transfer of a spacecraft equipped with more complex multimode propulsion system, such as a monopropellant–electrospray microthruster [28], which combines the advantages of both continuous-thrust and high-thrust propulsion modes in trajectory design [29].

In this paper, Section 2 illustrates a simplified thrust model suitable for implementation in an orbital simulator to study the optimal heliocentric trajectories of a TEPS-propelled interplanetary spacecraft across a set of mission scenarios. These scenarios are described in Section 3, which also briefly outlines the approach adopted for designing the spacecraft’s transfer trajectory which gives the total flight time. This approach is primarily based on the optimization method proposed about a decade ago in Ref. [23] for a conventional spacecraft and later validated for CubeSat-based mission scenarios. Accordingly, Section 3 does not present the mathematical approach used to optimize the spacecraft’s trajectory (summarized instead in the Appendix A), in order to focus on the novelties of this work, namely the results of numerical simulations discussed in Section 4.

In that section, the TEPS-based mission performance is assessed by analyzing the characteristics of the rapid transfer trajectory as functions of the vehicle’s initial mass and the reference electric power supplied by the solar array. The orbital simulations are then used to determine the propellant mass required to complete the transfer. This value is subsequently used as input to the simplified mass breakdown model proposed by Gerberich and Oleson [30], which employs a statistical approach to estimate the mass of the spacecraft’s key subsystems as a function of payload mass. The results of the numerical simulations are presented in graphical form, enabling a quick evaluation of transfer performance and the identification of an appropriate trade-off among the spacecraft’s initial total mass, installed electric power, flight time, and payload mass for a given mission scenario. This aspect is further discussed in Section 5, which provides the final remarks of the paper.

2. Simplified Thrust Modeling of TEPS for Preliminary Trajectory Analysis

This section introduces the thrust model adopted to analyze the dynamics of an interplanetary spacecraft equipped with a TEPS. The starting point is the experimental characterization of the TANDEM system, as reported in the recent and noteworthy work by Scaranzin et al. [22], which details the performance of this innovative thruster under laboratory conditions. In particular, assuming Xenon as the propellant, Table VI.1 in Ref. [22] summarizes the experimental measurements obtained during a test campaign covering eleven operating points. A subset of the data reported in that table is employed here to model the TEPS-induced thrust vector along an assigned interplanetary orbit transfer. Note that the procedure used in this work can be easily adapted to a context where the electric thruster operates with a greater number of levels than the 11 analyzed so far in the experimental framework.

From the perspective of preliminary mission design, the propulsion system is characterized by three key parameters: the thrust magnitude T, the propellant mass flow rate ${\dot{m}}_p$, and the electric input power P. It is also necessary to allow the thruster to be switched off, enabling the spacecraft to enter a coasting phase whose trajectory is essentially a Keplerian arc under the typical assumption of a two-body (heliocentric) dynamical model. To this end, in addition to the eleven operating points reported in Table VI.1 of Ref. [22], an additional (virtual) twelfth point is introduced, characterized by zero values of T, ${\dot{m}}_p$, and P. When this (virtual) operating point is selected, it indicates that the TEPS-propelled spacecraft transitions from a propelled phase to a coasting arc along the interplanetary trajectory. Accordingly, the TEPS performance model (for the preliminary trajectory analysis) considers 12 possible operating points, which are referenced throughout the paper using the dimensionless index $\mathrm{Id}\in [1,2,\dots ,12]$.

The three key parameters $\{T,{\dot{m}}_p,P\}$ used for simulating the spacecraft’s orbit around the Sun, together with the specific impulse $I_{\mathrm{sp}}$—reported here for completeness, as its value can be readily computed from the pair $\{T,{\dot{m}}_p\}$ using standard formulas—are summarized in Table 1 as functions of the thruster’s operating point $\mathrm{Id}$. In particular, the second column of that table specifies the TEPS operating mode, i.e., the channel employed to generate thrust (IC, OC, or DC), with $\mathrm{Id}=12$ corresponding to the propulsion system being switched off (no active channel). Figure 1 shows the bar plots of the thruster’s performance parameters $\{T,{\dot{m}}_p,P,I_{\mathrm{sp}}\}$ as a function of the dimensionless term $\mathrm{Id}$.

Table 1. Performance characteristics of the TEPS used to model the spacecraft’s thrust vector as a function of the operating point $\mathrm{Id}$. Data for the first eleven operating points are taken from Ref. [22]. The last row corresponds to the switched-off state.

Id	Operating Mode	T [mN]	P [kW]	${\dot{\mathit{m}}}_{\mathit{p}}$ [mg/s]	${\mathit{I}}_{\mathbf{sp}}$ [s]
1	IC	181	3.3	12.2	1508
2	IC	271	4.8	16.4	1687
3	OC	569	10.7	33.0	1758
4	DC	816	15.3	44.1	1888
5	IC	329	6.3	17.3	1938
6	OC	644	14.3	32.8	1999
7	DC	957	20.5	45.2	2160
8	DC	1090	20.2	49.4	2250
9	IC	346	7.3	16.6	2119
10	OC	786	18.5	34.1	2348
11	DC	1093	25.3	46.0	2421
12	off	0	0	0	0

The value of P reported in Table 1 is particularly relevant for trajectory design in a heliocentric scenario where solar arrays supply electric power. In fact, comparing P with the available electric power $P_{\mathrm{av}}$ determines which thruster’s operating points are effectively accessible at a given solar distance r. To this end, a simple model of $P_{\mathrm{av}}$ to operate the TEPS at a generic value of r is employed. In this simplified model, the available electric power $P_{\mathrm{av}}$ is expressed as a function of: (1) the reference (installed) power $P_0$ at a solar distance of 1 astronomical unit; (2) the Sun–spacecraft distance r; and (3) the electric power $P_{\mathrm{L}}$ allocated to other subsystems (e.g., for example, the communications system and the scientific payload), through the following equation:

$$P_{\mathrm{av}}=\left\{\begin{array}{cc}{P}_0{\left({\displaystyle \frac{1\mathrm{AU}}{r}}\right)}^2-P_{\mathrm{L}}\hfill & \mathrm{if}{P}_0{\left({\displaystyle \frac{1\mathrm{AU}}{r}}\right)}^2>P_{\mathrm{L}}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

Once the value of $P_{\mathrm{av}}$ is computed at a generic point along the spacecraft’s heliocentric trajectory trough Equation (1), the operating level $\mathrm{Id}$ requiring an input power equal to P can be used only if the condition

$$P_{\mathrm{av}}\ge P\left(\mathrm{Id}\right)$$

(2)

is satisfied. On the other hand, when $P_{\mathrm{av}}=0$, the only (virtual) operating point available is $\mathrm{Id}=12$, corresponding to the propulsion system being switched off and the spacecraft entering a coasting arc.

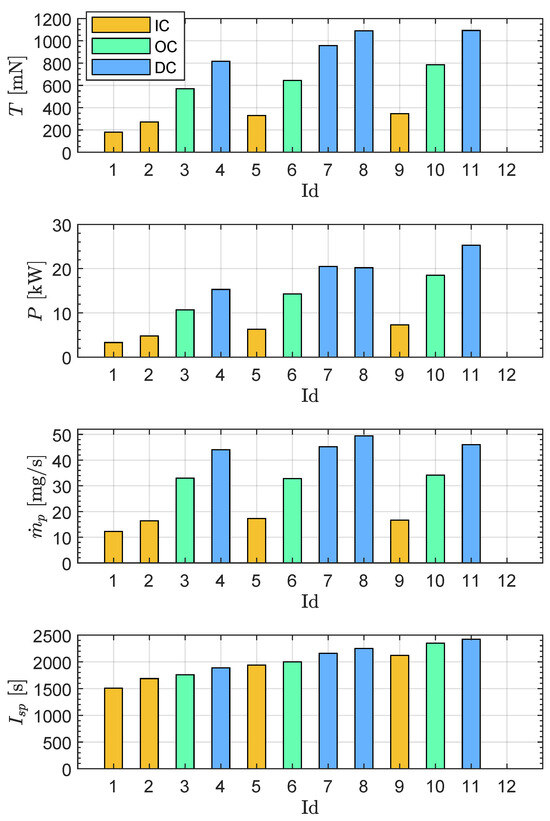
Figure 1. Bar plots of the performance data summarized in the TEPS thrust table, used to simulate the spacecraft’s heliocentric dynamics. The three colors represent the operating modes: green → outer channel (OC), orange → inner channel (IC), and blue → dual channel (DC).

The second column in Table 1, as well as the color used to fill the bars in Figure 1, indicates the TEPS operating mode for each operating point. In this regard, three subsets of operating points can be defined: ${\mathrm{Id}}_{\mathrm{IC}}=[1,2,5,9,12]$, ${\mathrm{Id}}_{\mathrm{OC}}=[3,6,10,12]$, and ${\mathrm{Id}}_{\mathrm{DC}}=[4,7,8,11,12]$, corresponding to IC, OC, and DC modes, respectively, including the off-mode identified by $\mathrm{Id}=12$. The three subsets $\{{\mathrm{Id}}_{\mathrm{IC}},{\mathrm{Id}}_{\mathrm{OC}},{\mathrm{Id}}_{\mathrm{DC}}\}$ can be used, for example, to analyze the spacecraft’s transfer performance under a more constrained scenario in which the operation mode along a generic propelled arc remains fixed as one of the three options (i.e., IC, OC, or DC) throughout the entire interplanetary transfer.

Bearing in mind that Table 1 provides the thrust magnitude and propellant mass flow rate as functions of the operating point $\mathrm{Id}$—i.e., $T=T\left(\mathrm{Id}\right)$ and ${\dot{m}}_p={\dot{m}}_p\left(\mathrm{Id}\right)$—which can be selected within a (discrete) interval whose limits depend on the solar distance r through the value of the available electric power $P_{\mathrm{av}}$, and following the approach discussed in Ref. [31], the TEPS-induced thrust vector $\mathit{T}$ is expressed as

$$\mathit{T}=\eta T\widehat{\mathit{u}}$$

(3)

where $\widehat{\mathit{u}}$ is the thrust unit vector, which will be determined (together with the operating point $\mathrm{Id}$) by solving a suitable optimal control problem described later in this paper, and $\eta$ is the duty cycle, defined according to Rayman and Williams [31] as “the fraction of time during deterministic thrust periods in which the thruster is actually active”. In this work, we assume $\eta =0.9$, a value consistent with that employed to design the trajectory of Deep Space 1, where $\eta =0.92$ [31]. Note that the recent work by Nurre and Taheri [32] provides an interesting discussion on the impact of the mathematical model used to describe the concept of duty cycle on mission performance during the preliminary trajectory design phase.

The concept of duty cycle is also employed in the differential equation governing the temporal variation of the spacecraft mass m. Using the definition of the propellant mass flow rate, expressed as a function of $\mathrm{Id}$ in Table 1, the temporal variation of the spacecraft mass can be written as

$$\dot{m}=-\eta {\dot{m}}_p$$

(4)

where the term $\eta$ is (again) introduced to scale the nominal value of ${\dot{m}}_p$ provided by the TEPS thrust table. According to Equations (3) and (4), in this simplified thrust model, the control terms are $\{\widehat{\mathit{u}},\mathrm{Id}\}$, which are used to determine the TEPS-induced thrust vector in the generic point along the spacecraft’s heliocentric trajectory. The values of the control terms are obtained by solving an optimization problem that minimizes the flight time $\Delta t$ required to complete a prescribed heliocentric orbit transfer, as described in the next section.

3. Mission Overview and Spacecraft Mass Breakdown Model

The performance of the TEPS-propelled spacecraft is evaluated during the heliocentric phase of a typical interplanetary transfer, in which the space vehicle departs from Earth’s orbit and reaches the orbit of a target celestial body, such as Venus, Mars, or the Apollo-type near-Earth asteroid 2024 YR4 [17]. In this study, both the departure and target heliocentric orbits are assumed to be Keplerian, with their orbital parameters obtained from the JPL Horizons system [33] as of 1 January 2025. More precisely, the Keplerian orbital elements of the celestial bodies involved in the analysis—namely the semimajor axis a, eccentricity e, inclination i, argument of perihelion $\omega$, and right ascension of the ascending node $\mathrm{\Omega }$—are reported in Table 2.

In this work, a rapid orbit-to-orbit transfer is considered, meaning that the optimal spacecraft trajectory connecting the three-dimensional heliocentric orbits (i.e., the parking and target orbits) is analyzed by minimizing the flight time $\Delta t$ without imposing ephemeris constraints. This assumption enables the determination of both the global minimum value of $\Delta t$ and the optimal geometrical configuration of the transfer. The latter can subsequently be used to identify the most favorable launch window in an actual ephemeris-constrained mission scenario. In this regard, the adopted procedure closely follows the first phase of the method presented by the author in Ref. [34], where the performance of an ideal reflective solar sail [35] was evaluated in a rendezvous scenario involving asteroid 2024 YR4. The details of the mathematical model used to compute the rapid transfer trajectory are summarized in the Appendix A.

Table 2. Orbit’s data used in the study. Data evaluated at 1 January 2025 using JPL’s Horizons system.

Cel. Body	a [AU]	e	i [deg]	$\mathit{\omega }$ [deg]	$\mathbf{\Omega }$ [deg]
Earth	1	$1.6712\times {10}^{-2}$	$3.2485\times {10}^{-3}$	$288.4904$	$174.4417$
Venus	$0.723328$	$6.7465\times {10}^{-3}$	$3.394$	$55.1507$	$76.6118$
Mars	$1.5237$	$9.3430\times {10}^{-2}$	$1.8475$	$286.7114$	$49.4867$
2024 YR4	$2.5172$	$6.6174\times {10}^{-1}$	$3.4089$	$134.3614$	$271.3710$

Table 2. Orbit’s data used in the study. Data evaluated at 1 January 2025 using JPL’s Horizons system.

Cel. Body	a [AU]	e	i [deg]	$\mathit{\omega }$ [deg]	$\mathbf{\Omega }$ [deg]
Earth	1	$1.6712\times {10}^{-2}$	$3.2485\times {10}^{-3}$	$288.4904$	$174.4417$
Venus	$0.723328$	$6.7465\times {10}^{-3}$	$3.394$	$55.1507$	$76.6118$
Mars	$1.5237$	$9.3430\times {10}^{-2}$	$1.8475$	$286.7114$	$49.4867$
2024 YR4	$2.5172$	$6.6174\times {10}^{-1}$	$3.4089$	$134.3614$	$271.3710$

In this optimization procedure, once the target celestial body is selected, the minimum flight time $\Delta t$ and the corresponding propellant mass $m_p$ are obtained as functions of the spacecraft’s initial mass $m_0$ at the beginning of the transfer, and the installed reference electric power $P_0$. In particular, the computed value $m_p=m_p(m_0,P_0)$ is used as input to the simplified mass breakdown model, based on statistical data, proposed by Gerberich and Oleson [30]. In that semi-analytical model, the total (initial) spacecraft mass $m_0$ is assumes as the sum of the so-called dry mass $m_{\mathrm{dry}}$ and the propellant mass $m_p$, viz.

$$m_0=m_{\mathrm{dry}}+m_p$$

(5)

The dry mass is given by the sum of the bus mass $m_{\mathrm{bus}}$—which includes all spacecraft subsystems except the scientific payload—and the payload mass $m_{\mathrm{pay}}$:

$$m_{\mathrm{dry}}=m_{\mathrm{bus}}+m_{\mathrm{pay}}$$

(6)

The bus mass $m_{\mathrm{bus}}$, in turn, is further partitioned among the remaining subsystems using a set of suitable mass fractions. These fractions are estimated through a statistical analysis of previous space missions involving spacecraft equipped with propulsion systems of a similar class. In this regard, Ref. [30] considers seven parts of $m_{\mathrm{bus}}$: the guidance, navigation, and control subsystem (subscript “GN&C”), the command and data handling subsystem (“C&DH”), the communications subsystem (“Comm”), the power subsystem (“Pow”), the thermal subsystem (“The”), the structure (“Str”), and the propulsion subsystem (“Pro”). Therefore, using the mass fractions reported in the first row of Table 1 in Ref. [30], the mass of each subsystem is computed as a function of $m_{\mathrm{bus}}$ as

$$\begin{array}{c}{m}_{\mathrm{G}\mathrm{N}\&\mathrm{C}}=0.047m_{\mathrm{bus}},m_{\mathrm{C}\&\mathrm{D}\mathrm{H}}=0.054m_{\mathrm{bus}},m_{\mathrm{Comm}}=0.05m_{\mathrm{bus}},\hfill \\ \hfill \hspace{1em}{m}_{\mathrm{Pow}}=0.28m_{\mathrm{bus}},m_{\mathrm{The}}=0.083m_{\mathrm{bus}},m_{\mathrm{Str}}=0.214m_{\mathrm{bus}},m_{\mathrm{Pro}}=0.272m_{\mathrm{bus}}\end{array}$$

(7)

However, the key concept behind the statistical model proposed by Gerberich and Oleson [30] is the use of an analytical expression that relates the spacecraft dry mass $m_{\mathrm{dry}}$ to its payload mass $m_{\mathrm{pay}}$. This function, $m_{\mathrm{dry}}=m_{\mathrm{dry}}\left(m_{\mathrm{pay}}\right)$, is derived through a best-fit approximation of historical data from similar space missions collected by the COMPASS team at NASA’s Glenn Research Center. More precisely, for interplanetary missions involving spacecraft propelled by electric propulsion systems, Ref. [30] suggests a linear relationship of the form

$$m_{\mathrm{dry}}=a_1{m}_{\mathrm{pay}}+a_0\mathrm{with}{a}_0=372.71\mathrm{kg}\mathrm{and}{a}_1=7.49$$

(8)

where $\{a_0,a_1\}$ are best-fit coefficients obtained through a linear interpolation of historical data; see for example Equation (2) in Ref. [30].

Combining Equations (5) and (8), the payload mass can be implicitly expressed as a function of the two trajectory design parameters $\{m_0,P_0\}$. The resulting relationship is given by

$$m_{\mathrm{pay}}=m_{\mathrm{pay}}(m_0,P_0)={\displaystyle \frac{m_0-m_p(m_0,P_0)-a_0}{a_1}}$$

(9)

where the value of $m_p(m_0,P_0)$ is an output of the optimization process which minimizes the flight time $\Delta t$. Similarly, the bus mass $m_{\mathrm{bus}}$—and, consequently, the masses of the other subsystems given by Equation (7)—can be expressed as a function of the two parameters $\{m_0,P_0\}$ as

$$m_{\mathrm{bus}}=m_{\mathrm{bus}}(m_0,P_0)=m_{\mathrm{dry}}-m_{\mathrm{pay}}\equiv (a_1-1)m_{\mathrm{pay}}+a_0$$

(10)

where $m_{\mathrm{pay}}(m_0,P_0)$ is given by Equation (9).

To summarize, for a given mission scenario (i.e., a specified target orbit) and a selected pair of design parameters $\{m_0,P_0\}$, the optimal control problem described in the Appendix A is numerically solved to determine the minimum flight time $\Delta t$ and the propellant mass $m_p$ required for the specific interplanetary transfer. The computed $m_p$ is then used to evaluate the payload mass $m_{\mathrm{pay}}$ through Equation (9), which, in turn, is employed to compute the masses of the other subsystems using Equations (7) and (10). The results of this numerical study of the transfer performance are illustrated in the next section.

4. Simulation Results and Parametric Analysis of Mission Performance

This section presents the results of numerical simulations for the rapid transfer of a TEPS-propelled spacecraft in three interplanetary (orbit-to-orbit, ephemeris-free) mission scenarios. In particular, the orbital elements of both the parking orbit (i.e., the Earth’s orbit) and the generic target orbit (i.e., the orbit of Mars, Venus, or asteroid 2024 YR4) are reported in Table 2. In each case, the minimum flight time, the propellant mass, and subsystem masses are evaluated as functions of the pair $\{m_0,P_0\}$, varying over an appropriate interval. In all simulations and mission scenarios, a fixed load electric power of $P_{\mathrm{L}}=500\mathrm{W}$ was assumed, in accordance with the procedure used in Ref. [23]. The numerical results also allow the evaluation of the mass fractions $f_p$, $f_{\mathrm{bus}}$, and $f_{\mathrm{pay}}$ corresponding to the three masses $\{m_p,m_{\mathrm{bus}},m_{\mathrm{pay}}\}$. These fractions are defined as

$$f_p={\displaystyle \frac{m_p}{m_0}},f_{\mathrm{bus}}={\displaystyle \frac{m_{\mathrm{bus}}}{m_0}},f_{\mathrm{pay}}={\displaystyle \frac{m_{\mathrm{pay}}}{m_0}}$$

(11)

4.1. Earth-Mars Mission

The spacecraft performance in this classical interplanetary three-dimensional transfer is computed by considering a large vehicle with an initial mass in the range $m_0\in [4000,5000]\mathrm{kg}$. For reference, the lower bound of this interval is consistent with the launch mass of the BepiColombo spacecraft, which was about $4100\mathrm{kg}$. Conversely, the upper bound of $4000\mathrm{kg}$ could represent a potential Mars cargo mission.

Keeping in mind the required input power summarized in Table 1, and considering the reduction of available power with increasing solar distance, a value of $P_0\in [25,50]\mathrm{kW}$ was selected for the simulations. This choice makes it possible to appreciate the impact of available electric power on transfer performance, even when $P_{\mathrm{av}}$ is insufficient to operate all thrust levels indicated in Table 1. In fact, recalling that $P_{\mathrm{L}}=500\mathrm{W}$ and using Equation (1), at a solar distance equal to the semimajor axis of Mars’ orbit (i.e., about $1.523\mathrm{AU}$), when $P_0=25\mathrm{kW}$ the available power is slightly above $10\mathrm{kW}$. This value, for example, is substantially sufficient to activate only the IC mode; see Figure 1.

The performance analysis was carried out parametrically by varying $m_0$ (or $P_0$) in steps of $50\mathrm{kg}$ (or $1\mathrm{kW}$). Accordingly, 500 optimization processes were solved to obtain the contour plot shown in Figure 2, which illustrates the variation of the minimum flight time $\Delta t$ as a function of the two design parameters $m_0$ and $P_0$.

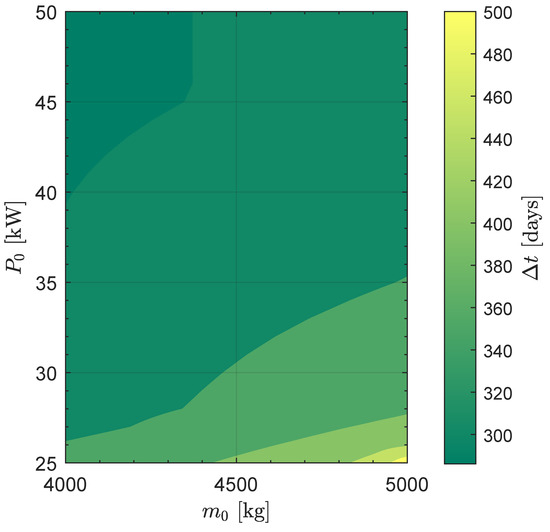
Figure 2. Minimum flight time $\Delta t$ for an Earth–Mars orbit-to-orbit transfer as a function of $m_0$ and $P_0$.

Figure 2 shows that a TEPS-propelled spacecraft with a launch mass of about $4100\mathrm{kg}$ (i.e., similar to BepiColombo) can potentially complete the interplanetary transfer in approximately $375\mathrm{days}$ if $P_0=25\mathrm{kW}$. For the same launch mass, increasing $P_0$ to $30\mathrm{kW}$ (or $35\mathrm{kW}$) reduces the flight time to $333\mathrm{days}$ (or $311\mathrm{days}$). Similar trends are observed in the figure for launch masses up to $5000\mathrm{kg}$.

The corresponding propellant mass $m_p$, which is an output of the optimization process, together with the payload mass $m_{\mathrm{pay}}$ obtained using Equation (9), is reported in Figure 3. Note that $m_p$ refers to a transfer where the performance index to be optimized is the flight time $\Delta t$. For example, from the figure, one can observe that a spacecraft with $m_0=4100\mathrm{kg}$ and $P_0=25\mathrm{kW}$ requires about $m_p=1060\mathrm{kg}$ of propellant to complete the transfer (the BepiColombo spacecraft, for comparison, carried $1400\mathrm{kg}$ of propellant at the beginning of its transfer), while the scientific payload mass obtained through the statistical model is slightly below $360\mathrm{kg}$.

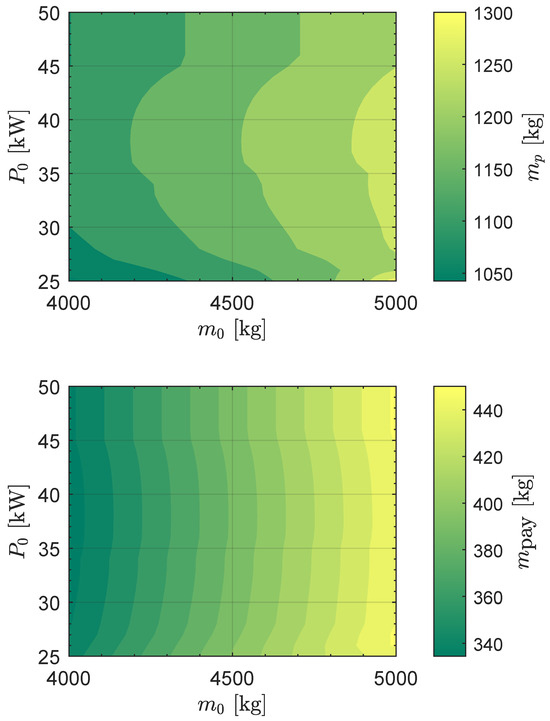
Figure 3. Propellant ($m_p$) and payload ($m_{\mathrm{pay}}$) mass for an Earth–Mars orbit-to-orbit transfer as a function of $m_0$ and $P_0$.

These values of $m_p$ and $m_{\mathrm{pay}}$ correspond to mass fractions of $f_p=25.8\%$ and $f_{\mathrm{pay}}=8.8\%$, respectively. This is confirmed by Figure 4, which also shows the variation of $f_{\mathrm{bus}}$ with the two design parameters $m_0$ and $P_0$. In particular, the same combination of launch mass and reference electric power gives about $f_{\mathrm{bus}}=65.4\%$.

4.2. Earth-Venus Mission

The same procedure illustrated in the previous subsection was used to parametrically investigate the transfer performance in an Earth–Venus scenario. In this case, the initial spacecraft mass still lies within the interval $m_0\in [4000,5000]\mathrm{kg}$, while—bearing in mind that the transfer is now toward an inner region of the Solar System—the reference electric power was selected in the range $P_0\in [15,25]\mathrm{kW}$.

The results of the numerical optimizations provide the minimum flight time, $\Delta t=\Delta t(m_0,P_0)$, shown in Figure 5. The trend of the level curves is similar to that observed in the Earth–Mars scenario (see Figure 2). For example, assuming again $m_0=4100\mathrm{kg}$, the flight time is about $310\mathrm{days}$ (or $260\mathrm{days}$) when $P_0=15\mathrm{kW}$ (or $25\mathrm{kW}$). Conversely, if the initial mass is $5000\mathrm{kg}$, the minimum flight time ranges between $416\mathrm{days}$ and $315\mathrm{days}$, with an excursion of about one hundred days.

The results in terms of propellant mass and payload mass are reported in Figure 6, where one can observe that $m_{\mathrm{pay}}\in [350,450]\mathrm{kg}$ and $m_p\in [1000,1350]\mathrm{kg}$. Finally, the mass fractions $\{f_{\mathrm{pay}},f_{\mathrm{bus}},f_p\}$ are shown in Figure 7.

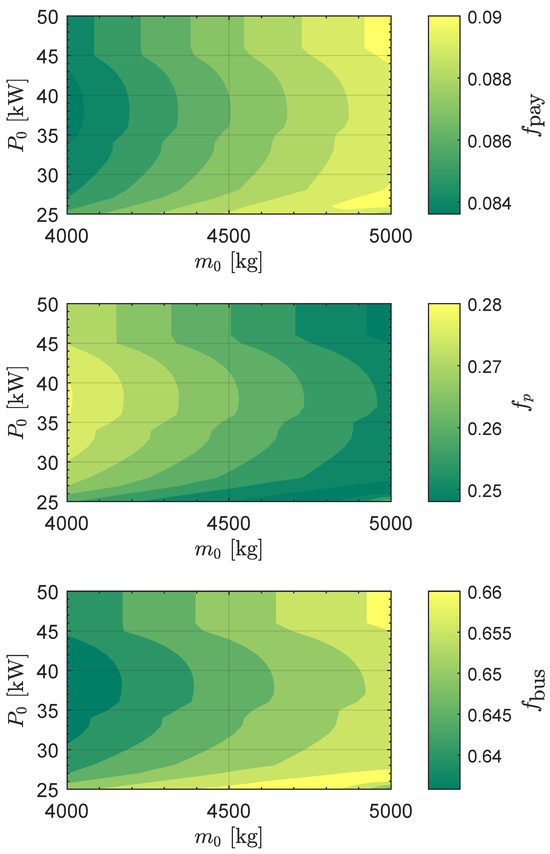
Figure 4. Mass fractions defined in Equation (11) for an Earth–Mars orbit-to-orbit transfer as a function of $m_0$ and $P_0$.

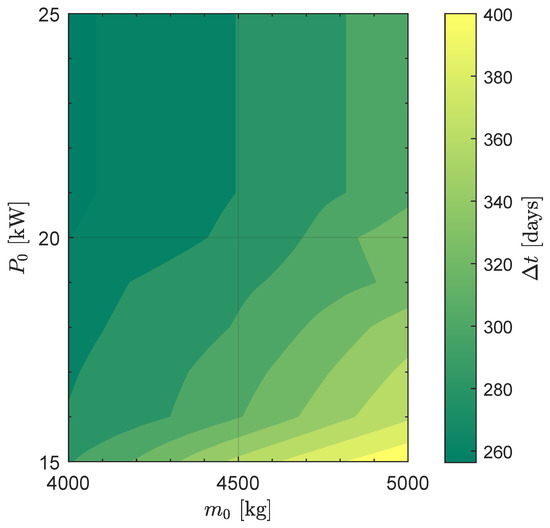
Figure 5. Minimum flight time $\Delta t$ for an Earth–Venus orbit-to-orbit transfer.

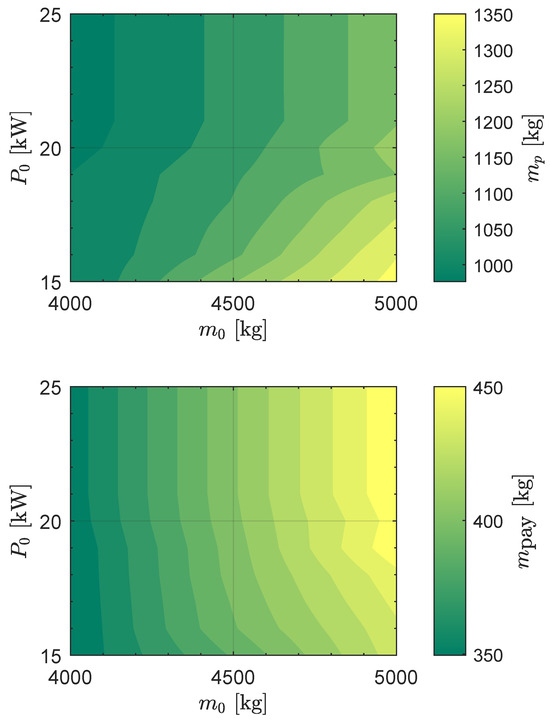
Figure 6. Propellant ($m_p$) and payload ($m_{\mathrm{pay}}$) mass for an Earth–Venus orbit-to-orbit transfer.

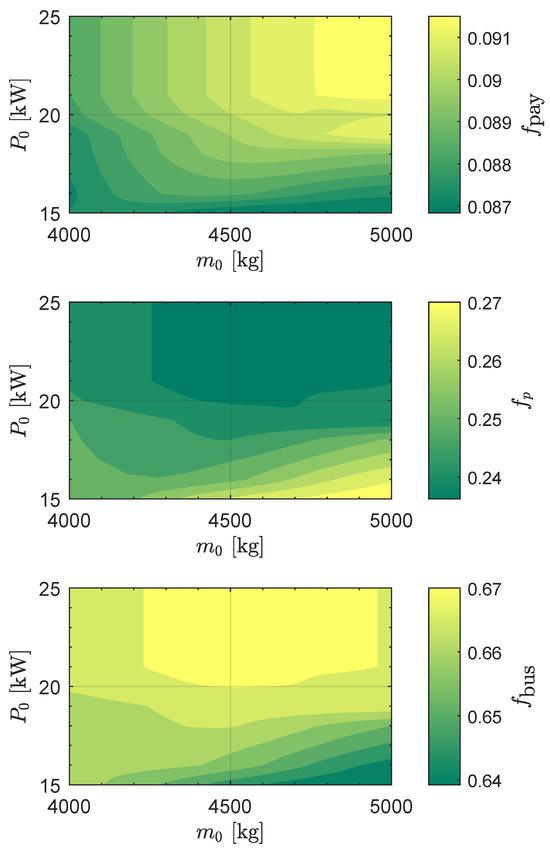
Figure 7. Mass fractions $\{f_{\mathrm{pay}},f_{\mathrm{bus}},f_p\}$ for an Earth–Venus orbit-to-orbit transfer.

4.3. Earth-Asteroid 2024 YR4 Mission

The asteroid-based mission scenario was analyzed by considering a singe (fixed) value of $P_0=30\mathrm{kW}$ to reduce the computational cost of the parametric study, and an initial spacecraft mass ranging within the interval $m_0\in [4000,4500]\mathrm{kg}$, with a step of $10\mathrm{kg}$. In this case, the minimum flight time ranges between $550\mathrm{days}$ and $630\mathrm{days}$, as shown in Figure 8. The corresponding propellant mass varies from about $1900\mathrm{kg}$ to $2100\mathrm{kg}$, while the payload mass is on the order of $250\mathrm{kg}$; see Figure 9. For instance, the solar sail-based mission scenario analyzed in Ref. [34] gives a flight time of about 7 years when the initial propulsive acceleration of the spacecraft is roughly $0.26\mathrm{mm}/{\mathrm{s}}^2$.

Consider the case study in which the initial spacecraft mass is $m_0=4100\mathrm{kg}$. In this specific scenario, the minimum flight time and the spacecraft mass breakdown (obtained using the simplified approach described in the previous section) are reported in Table 3. The resulting masses yield the following fractions: $f_p=47.6\%$, $f_{\mathrm{pay}}=5.8\%$, and $f_{\mathrm{bus}}=46.6\%$. The sketch of the optimal spacecraft transfer trajectory is reported in Figure 10, while Figure 11 shows the temporal variation of the control term $\mathrm{Id}$ during the rapid interplanetary transfer. In particular, Figure 11 shows that this specific rapid transfer requires four thrust levels, namely $\mathrm{Id}\in \{3,4,6,8\}$. In other words, the TEPS operates in both OC and DC modes during the flight.

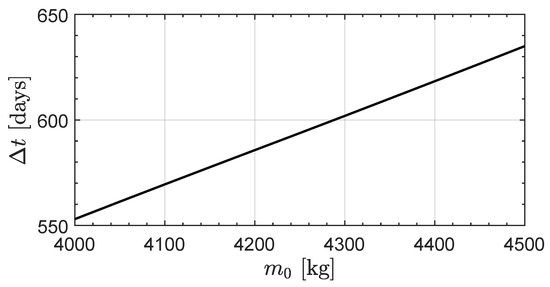
Figure 8. Minimum flight time for an Earth–asteroid 2025 YR4 transfer when $P_0=30\mathrm{kW}$.

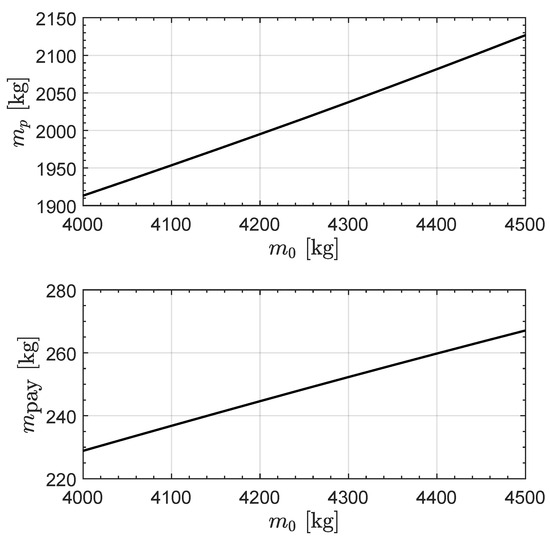
Figure 9. Propellant and payload mass for an Earth–asteroid 2025 YR4 transfer when $P_0=30\mathrm{kW}$.

Table 3. Results for the rapid Earth–asteroid 2025 YR4 transfer with $m_0=4100\mathrm{kg}$ and $P_0=30\mathrm{kW}$.

Term	Value
$\Delta t$	$569\mathrm{days}$
$m_p$	$1954\mathrm{kg}$
$m_{\mathrm{dry}}$	$2146\mathrm{kg}$
$m_{\mathrm{bus}}$	$1909\mathrm{kg}$
$m_{\mathrm{pay}}$	$237\mathrm{kg}$
$m_{\mathrm{G}\mathrm{N}\&\mathrm{C}}$	$90\mathrm{kg}$
$m_{\mathrm{C}\&\mathrm{D}\mathrm{H}}$	$103\mathrm{kg}$
$m_{\mathrm{Comm}}$	$95\mathrm{kg}$
$m_{\mathrm{Pow}}$	$534\mathrm{kg}$
$m_{\mathrm{The}}$	$159\mathrm{kg}$
$m_{\mathrm{Str}}$	$408\mathrm{kg}$
$m_{\mathrm{Pro}}$	$520\mathrm{kg}$

Table 3. Results for the rapid Earth–asteroid 2025 YR4 transfer with $m_0=4100\mathrm{kg}$ and $P_0=30\mathrm{kW}$.

Term	Value
$\Delta t$	$569\mathrm{days}$
$m_p$	$1954\mathrm{kg}$
$m_{\mathrm{dry}}$	$2146\mathrm{kg}$
$m_{\mathrm{bus}}$	$1909\mathrm{kg}$
$m_{\mathrm{pay}}$	$237\mathrm{kg}$
$m_{\mathrm{G}\mathrm{N}\&\mathrm{C}}$	$90\mathrm{kg}$
$m_{\mathrm{C}\&\mathrm{D}\mathrm{H}}$	$103\mathrm{kg}$
$m_{\mathrm{Comm}}$	$95\mathrm{kg}$
$m_{\mathrm{Pow}}$	$534\mathrm{kg}$
$m_{\mathrm{The}}$	$159\mathrm{kg}$
$m_{\mathrm{Str}}$	$408\mathrm{kg}$
$m_{\mathrm{Pro}}$	$520\mathrm{kg}$

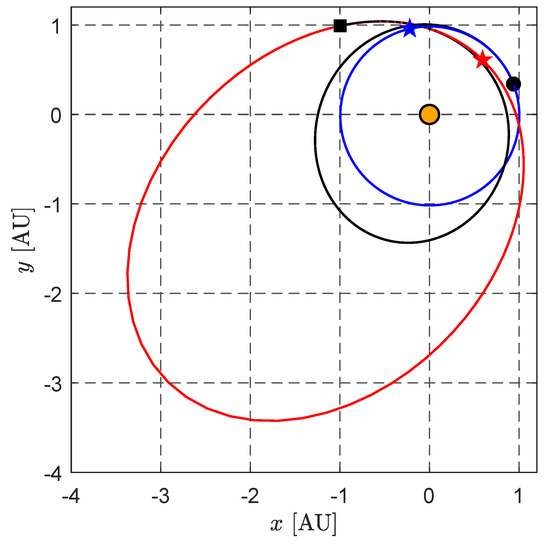
Figure 10. Rapid transfer trajectory for an Earth–asteroid 2025 YR4 transfer (ecliptic projection) when $m_0=4100\mathrm{kg}$ and $P_0=30\mathrm{kW}$. Orange dot → the Sun; black dot → start; black square → arrival; blue star → Earth’s perihelion; red star → asteroid orbit’s perihelion; blue line → Earth’s orbit; red line → asteroid’s orbit; black line → spacecraft trajectory.

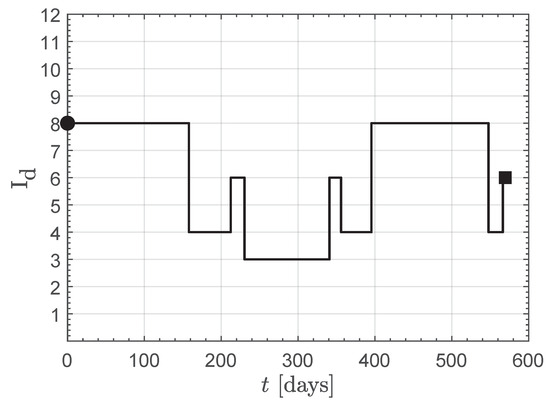
Figure 11. Optimal thrust level for an Earth–asteroid 2025 YR4 transfer when $m_0=4100\mathrm{kg}$ and $P_0=30\mathrm{kW}$. Black dot → start; black square → arrival.

5. Conclusions

This paper has analyzed the transfer performance of an interplanetary spacecraft equipped with a TANDEM electric propulsion system across a set of potential heliocentric mission scenarios. The specific capability of this Hall-effect thruster, which can operate in either single- or dual-channel mode, provides greater flexibility in selecting the most appropriate thrust level at any point along a heliocentric transfer trajectory.

In this context, the performance in terms of flight time and required propellant mass was investigated parametrically as a function of the spacecraft’s initial inertial characteristics and the reference electric power supplied by the solar array subsystem. The simulations indicate that a large spacecraft, with an initial (total) mass comparable to that of ESA/JAXA’s BepiColombo, requires a minimum flight time of about one year to reach Mars in a simplified orbit-to-orbit mission scenario. This transfer time should be regarded as the minimum admissible value, since in an ephemeris-constrained case the relative angular positions of the planets will degrade mission performance by increasing the flight time.

The results also show that the characteristics of the transfer trajectory depend on the reference (installed) electric power, which directly affects the number of thrust levels that can be selected at a given solar distance during the transfer. In this study, a simplified mathematical model for the variation of available electric power with Sun–spacecraft distance was adopted. A more refined model—accounting, for example, for the temporal degradation of the solar panels and possible constraints on array orientation during the flight—could be considered as a future extension of this work. In fact, if both the degradation of the solar cell film and potential attitude constraints on the solar panel orientation are included in the mathematical model, the result would be a reduction in the available thrust levels at any point along the transfer trajectory, given that the reference value of the electric power remains fixed. This, in turn, would affect the characteristics of the thrust vector and ultimately the flight time performance. Quantifying this type of performance degradation is difficult without a specific calculation of the optimal transfer trajectory.

Once such a refined model for calculating the available electric power is implemented, the transfer performance can be assessed in a more realistic, ephemeris-constrained scenario. This would enable the identification of the most suitable launch windows, starting from the ephemeris-free results obtained with the approach presented in this paper. Another potential extension of this work involves analyzing a more common geocentric mission scenario, where the TANDEM-based propulsion system equips a reusable orbital transfer vehicle, enabling the geocentric orbital transfer of small satellites.