Parametric Study and Hemocompatibility Assessment of a Centrifugal Blood Pump Based on CFD Simulation and Experimental Validation
Abstract
1. Introduction
2. Methods
2.1. Centrifugal Blood Pump Selection
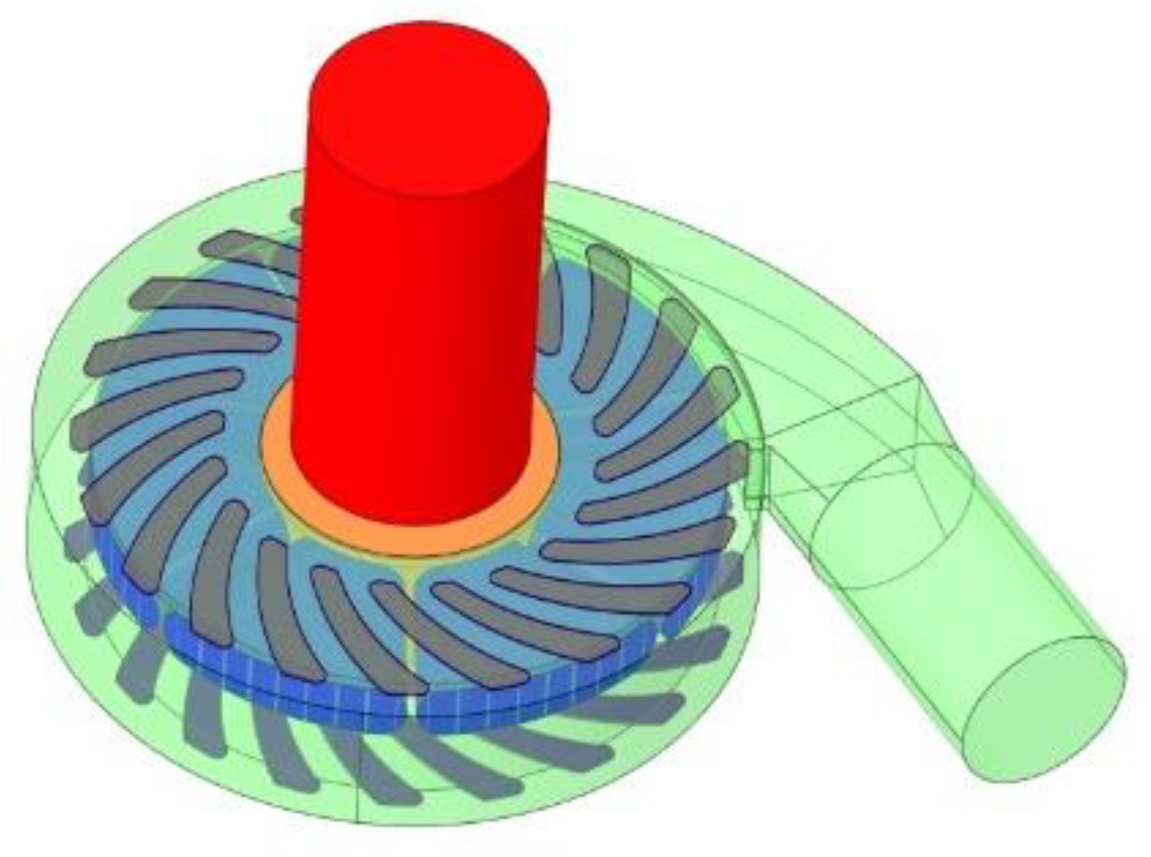
2.2. Centrifugal Blood Pump Model Construction
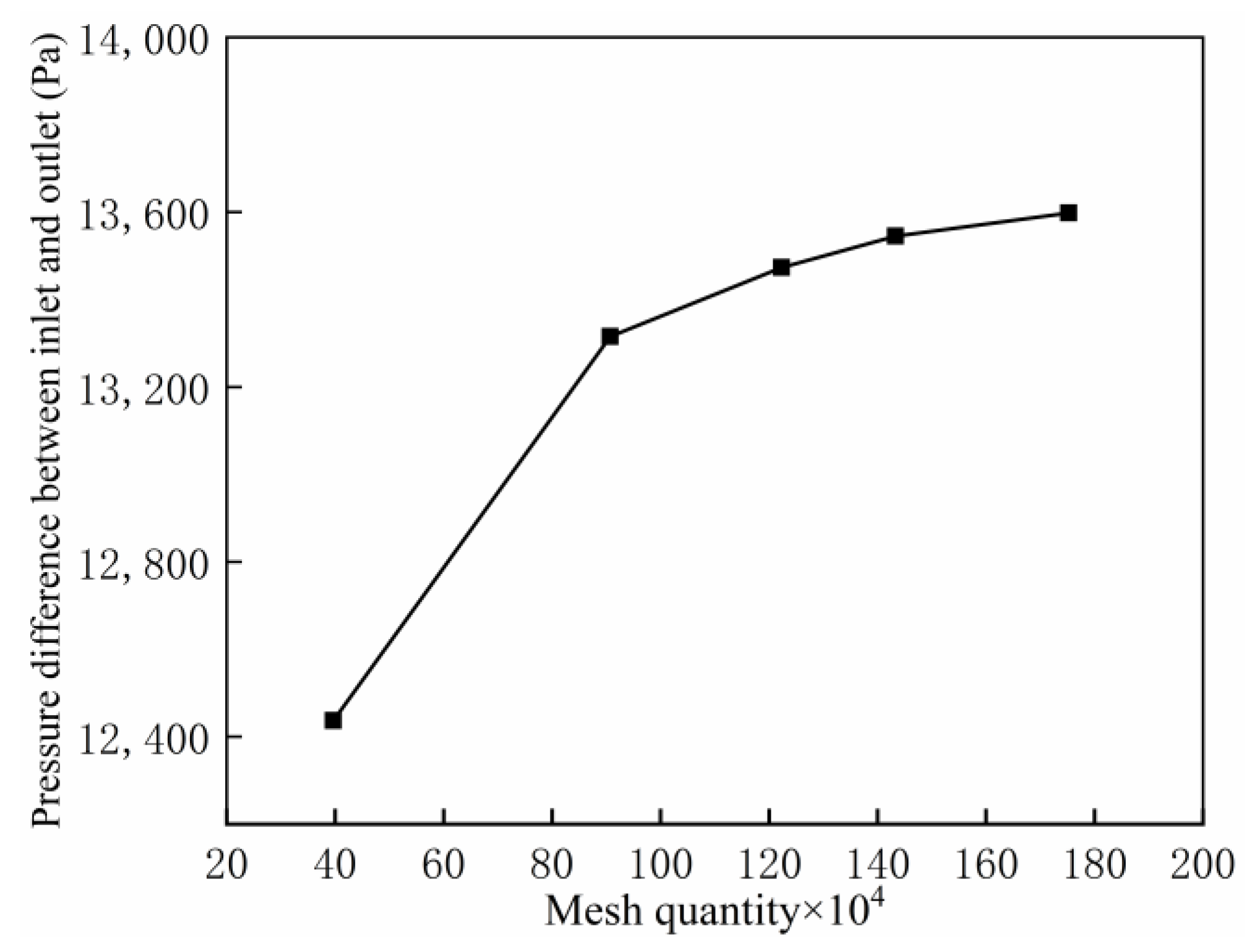
2.3. Mesh Generation and Grid Independence Verification
2.4. Numerical Method and Boundary Conditions
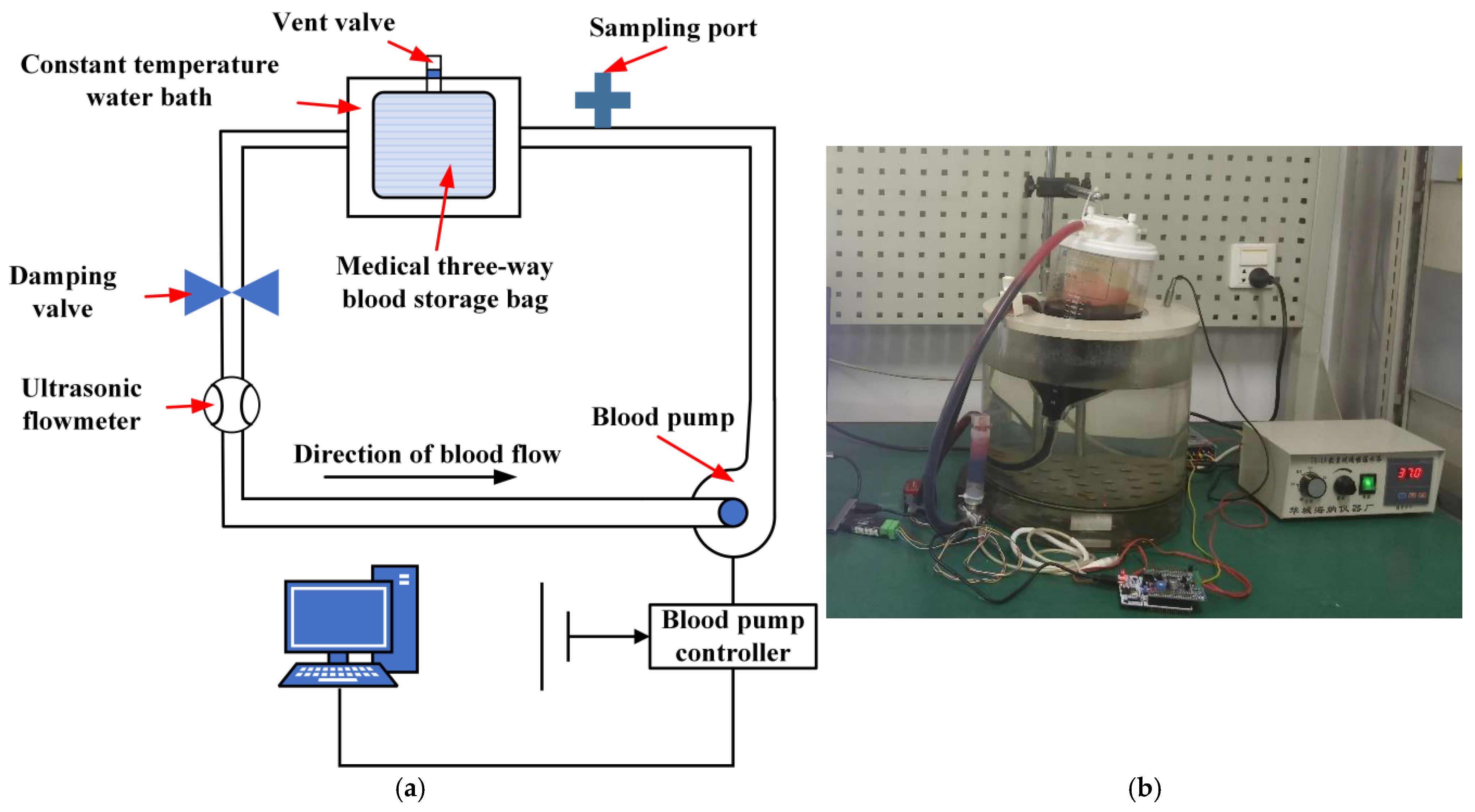
2.5. Centrifugal Blood Pump Hemolysis Experiment
3. Results
3.1. Influence of Blood Pump Parameters on the Performance of a Centrifugal Blood Pump
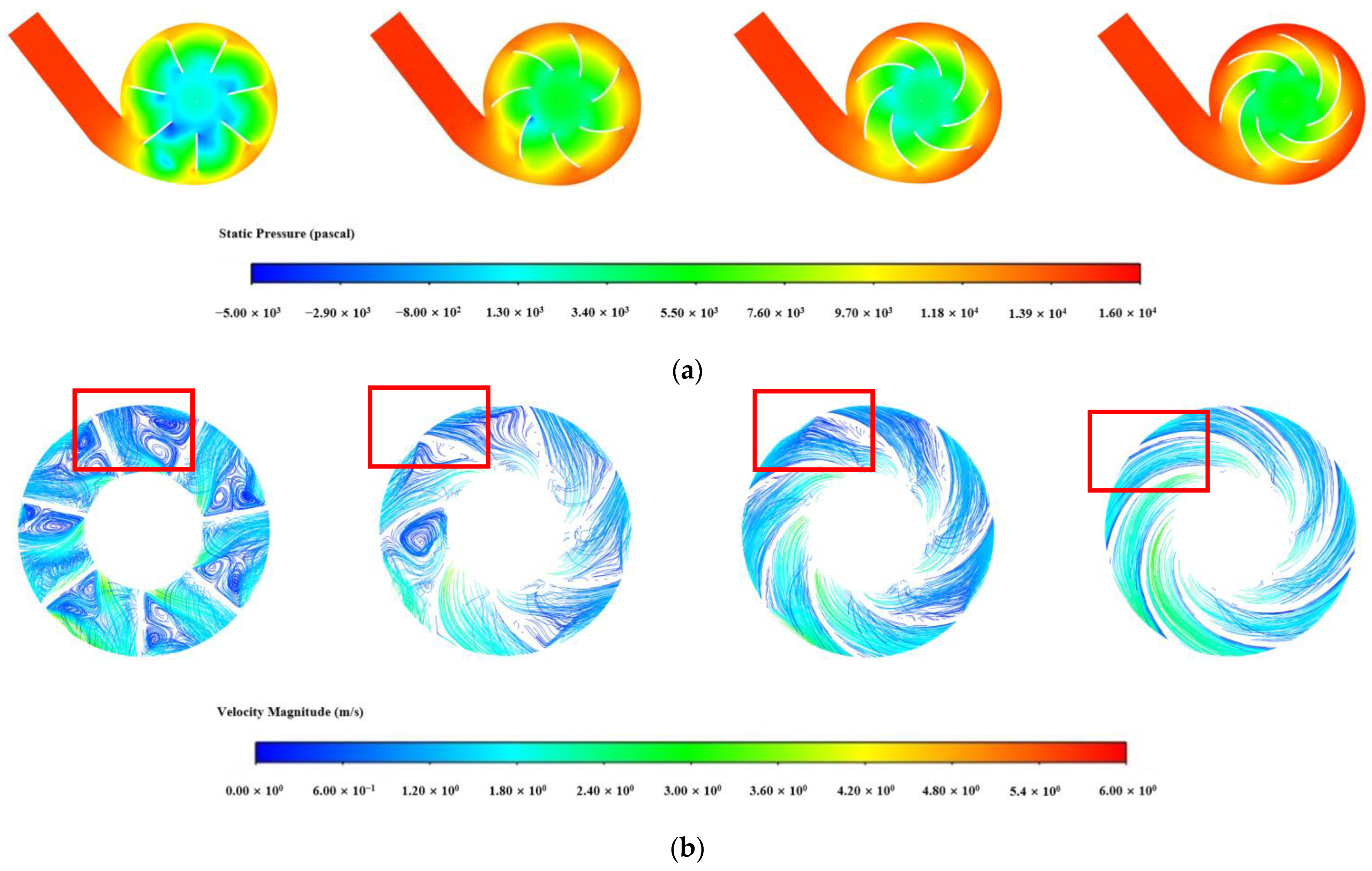
3.1.1. Influence of Blade Number in the Impeller
3.1.2. Influence of Blade Wrap Angle on Centrifugal Blood Pump Performance
3.1.3. Influence of Impeller Flow Path on Centrifugal Blood Pump Performance
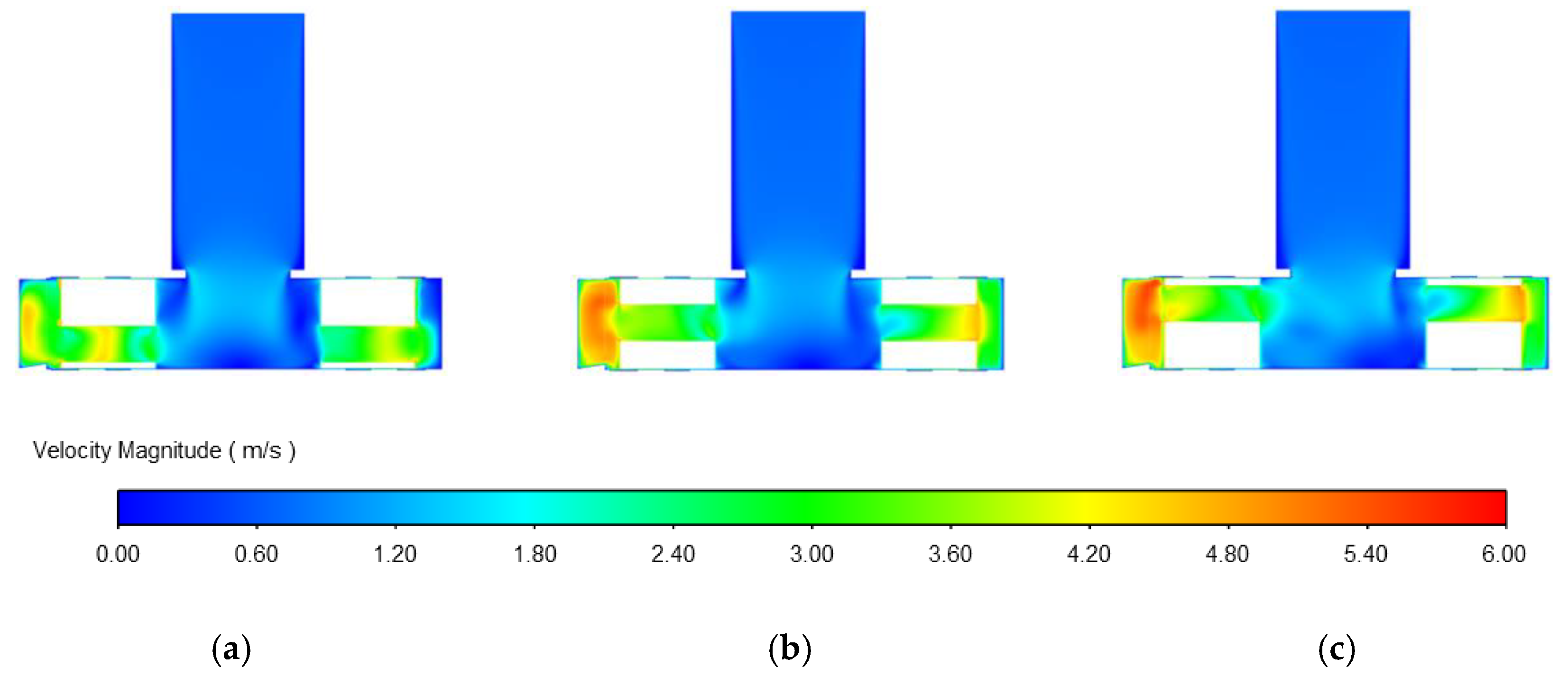
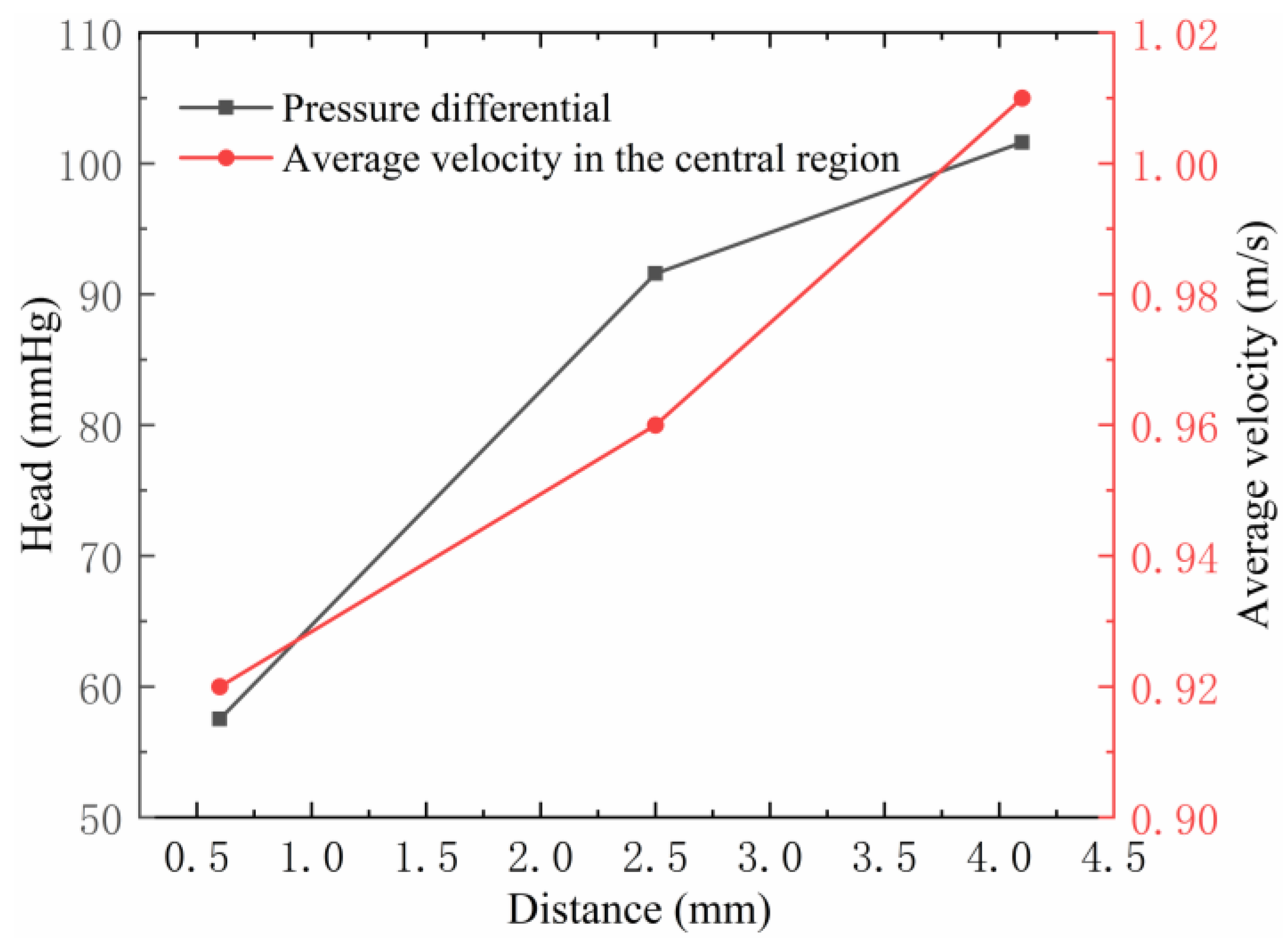
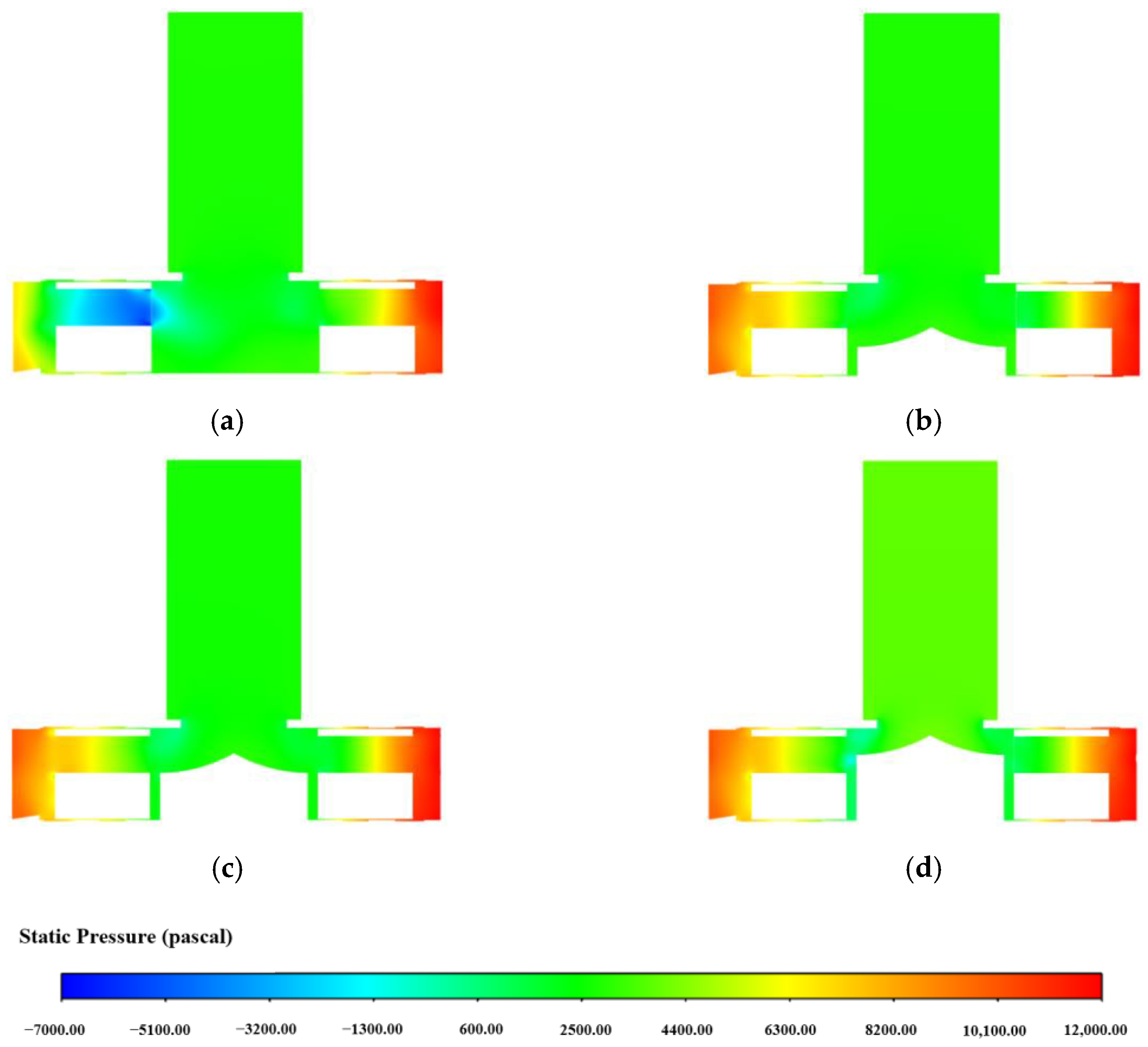
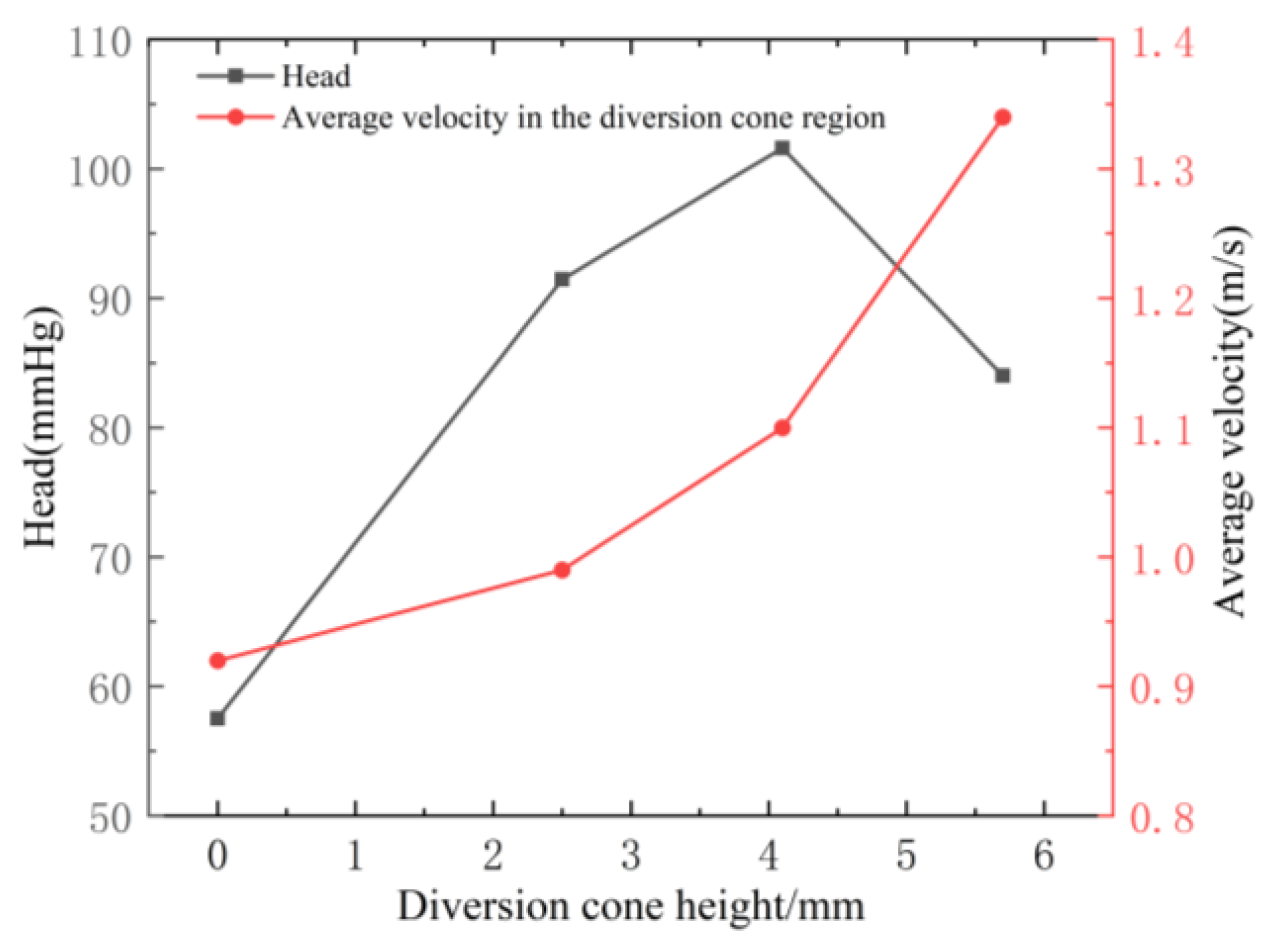
3.1.4. Influence of the Diversion Cone Height on Centrifugal Blood Pump Performance
3.2. Establishment and Flow-Field Numerical Simulation of the Screening Blood Pump Model
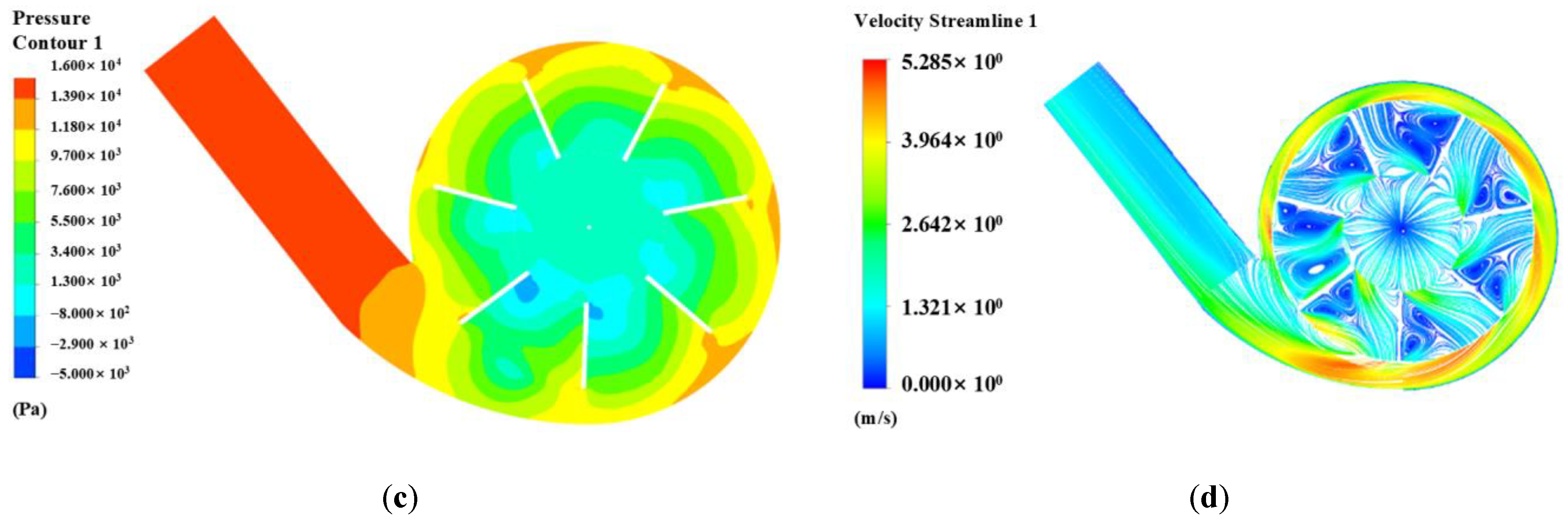
3.3. Evaluation of Hydraulic Characteristics
3.4. Hemocompatibility Results and Analysis
3.5. Verification Tests
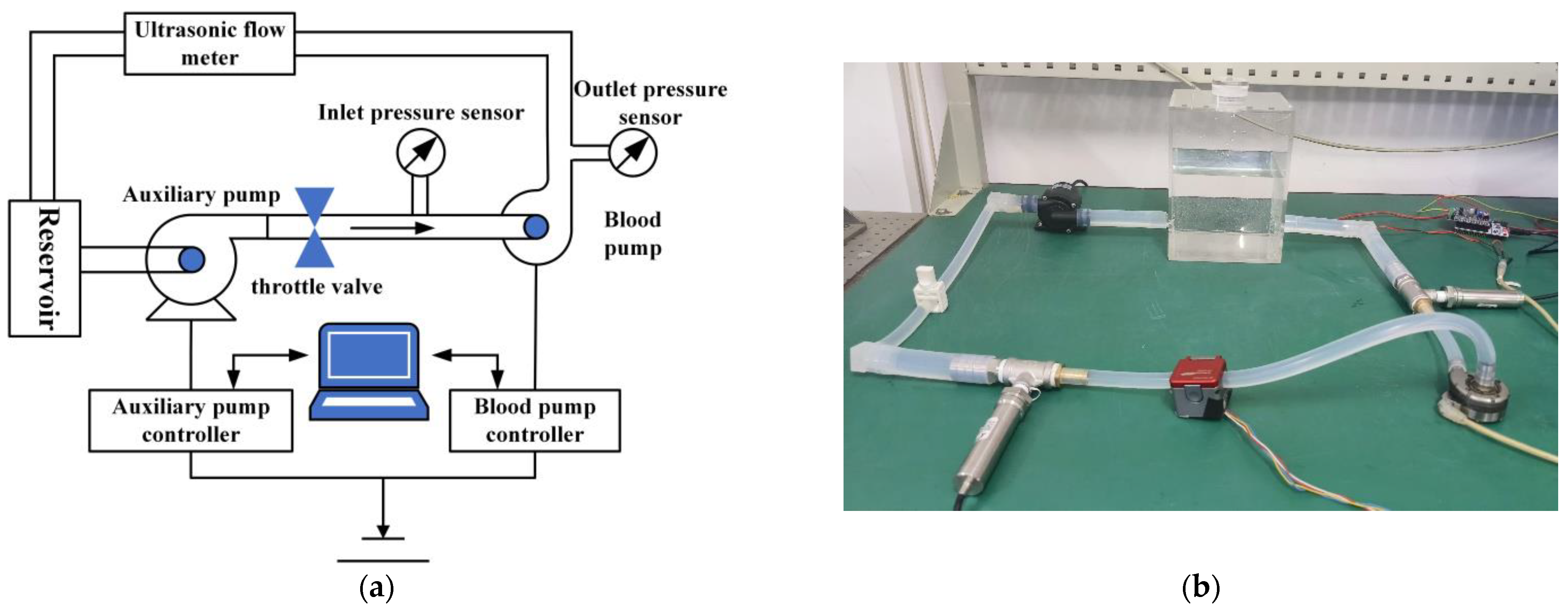
3.5.1. Working Principle and Construction of the Hydraulic Performance Test Platform
3.5.2. Hydraulic Performance Test Procedure
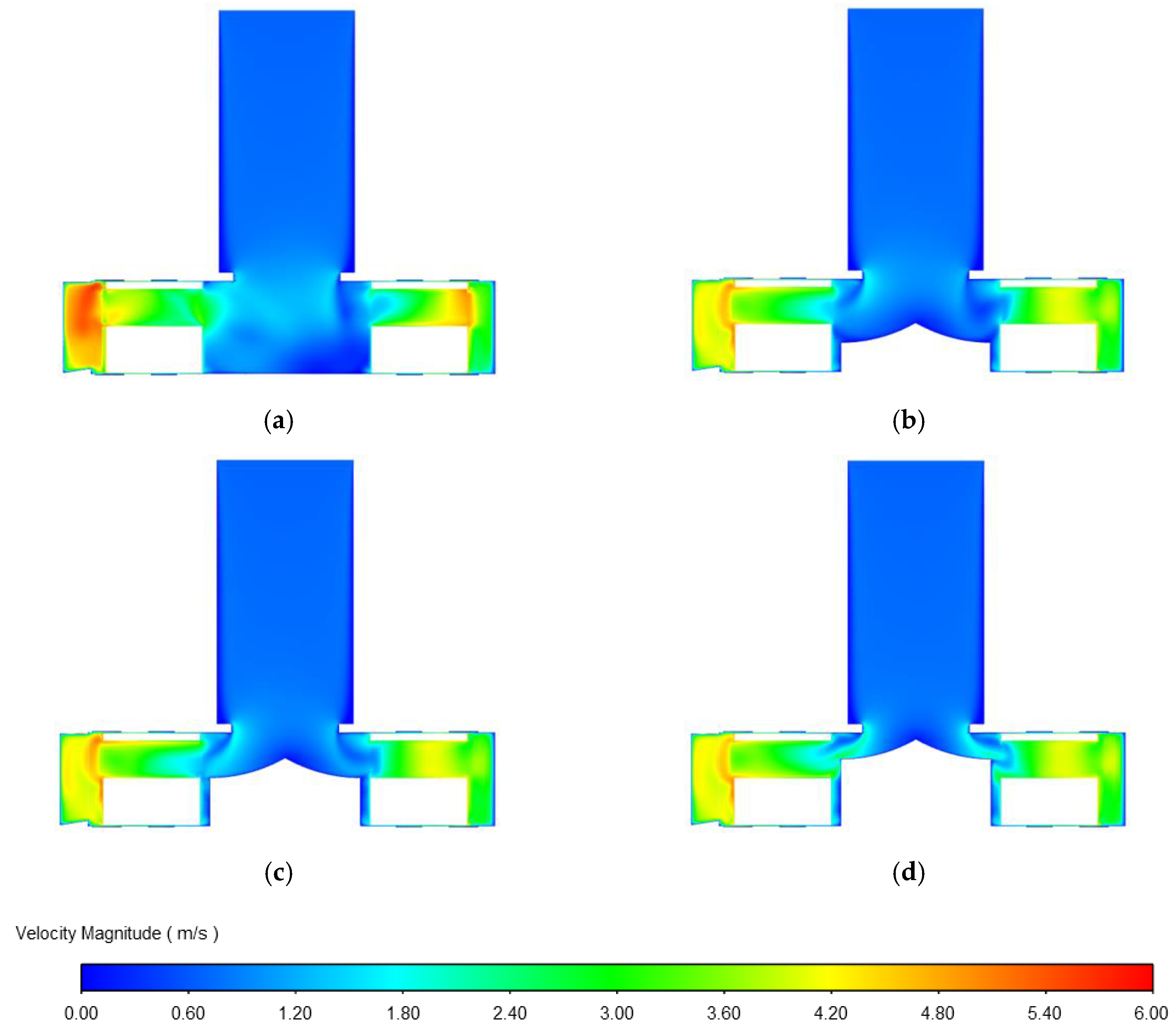
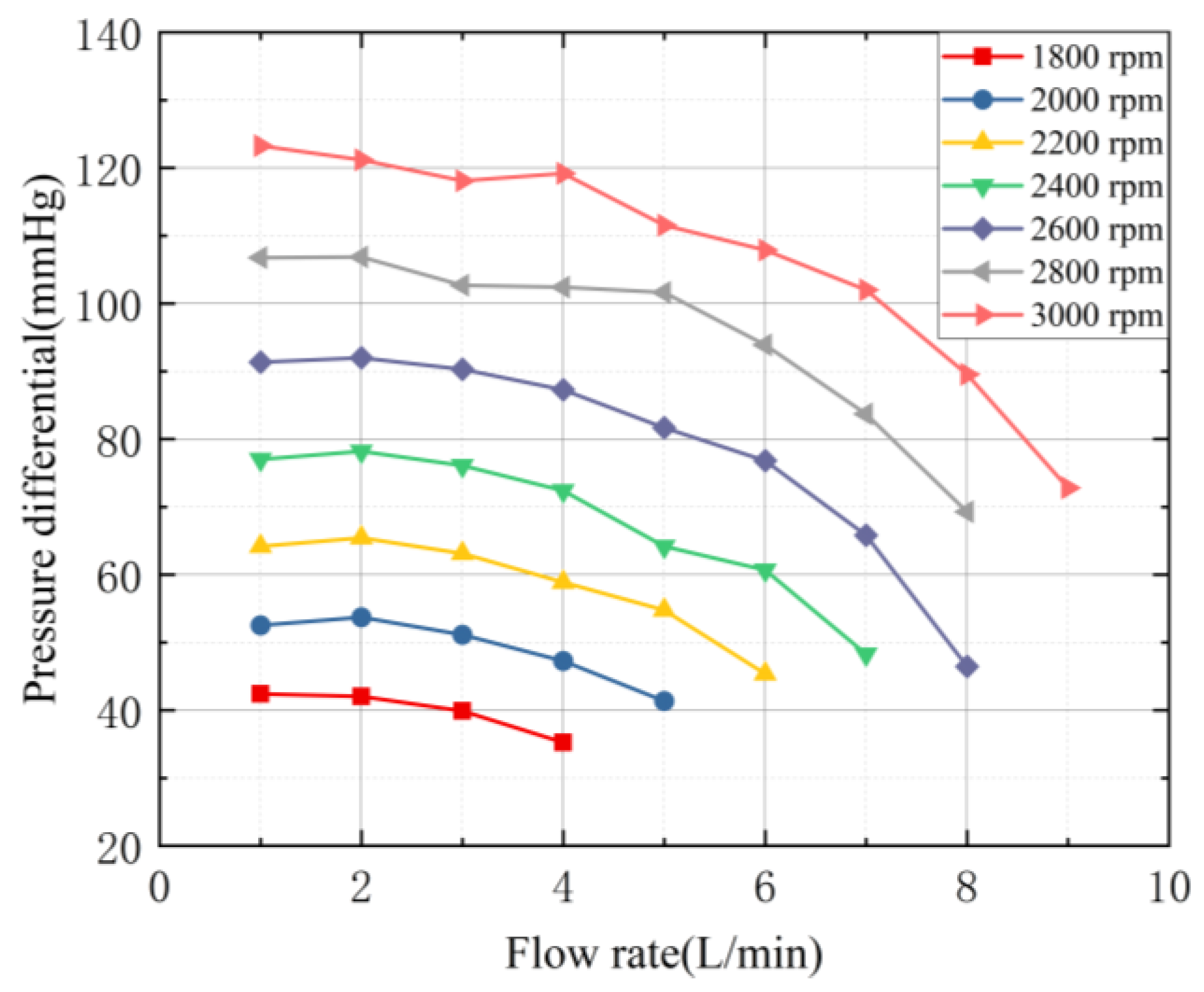
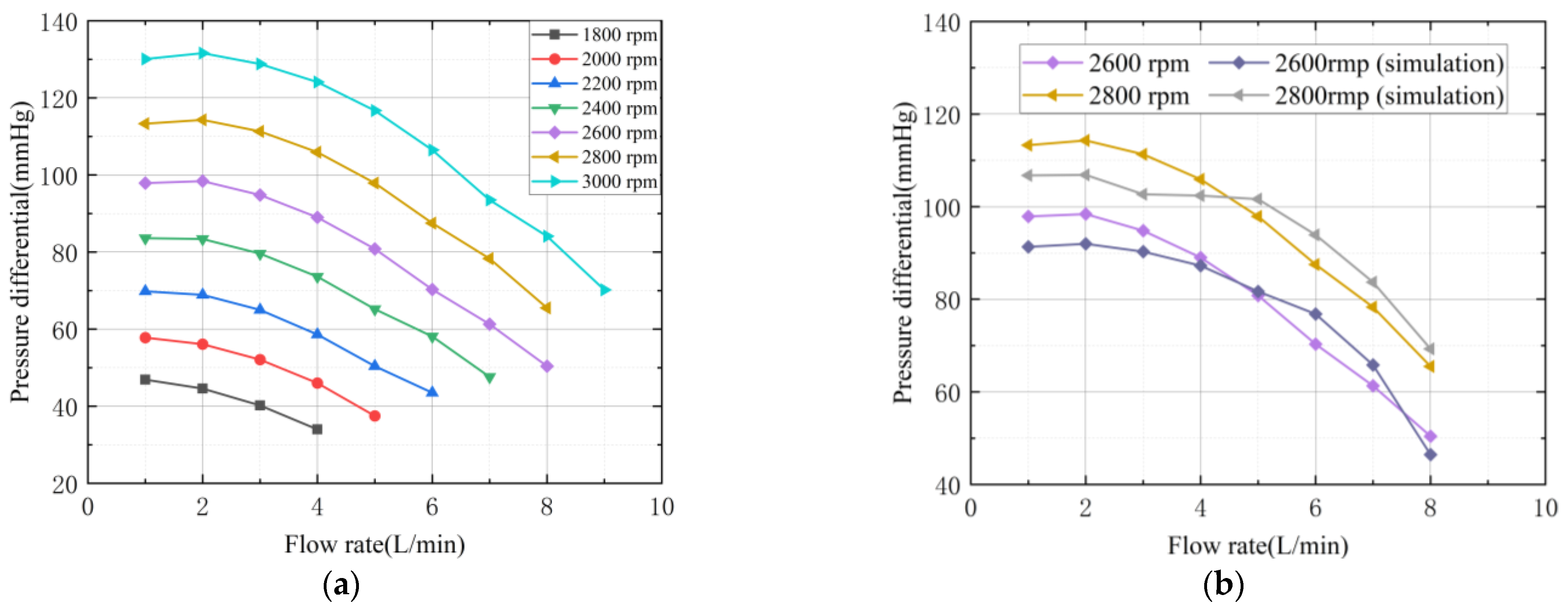
3.5.3. Comparison and Analysis of Hydraulic Performance Results
4. Discussion
4.1. Blood Pump Parametric Analysis
4.2. Innovation and Clinical Significance
4.3. Limitations and Future Prospects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SMLM | soft-magnetically levitated miniature centrifugal pump |
| VAD | ventricular assist device |
| CFD | computational fluid dynamics |
| vWF | von Willebrand Factor (vWF) |
References
- Wang, S.; Jia, T.; Liu, G.; Lu, X.; Yang, Q.; Zhu, C. Mapping the research trends and hot topics of ventricular arrhythmia: A bibliometric analysis from 2001 to 2020. Front. Cardiovasc. Med. 2022, 9, 856695. [Google Scholar] [CrossRef]
- Mi, S.; Huang, F.; Jiao, M.; Qian, Z.; Han, M.; Miao, Z.; Zhan, H. Inhibition of MEG3 ameliorates cardiomyocyte apoptosis and autophagy by regulating the expression of miRNA-129-5p in a mouse model of heart failure. Redox Rep. 2023, 28, 2224607. [Google Scholar] [CrossRef] [PubMed]
- Dandel, M. Cardiological Challenges Related to Long-Term Mechanical Circulatory Support for Advanced Heart Failure in Patients with Chronic Non-Ischemic Cardiomyopathy. J. Clin. Med. 2023, 12, 6451. [Google Scholar] [CrossRef] [PubMed]
- Bounouib, M.; Taha-Janan, M.; Maazouzi, W. Optimization of hemocompatibility metrics in ventricular assist device design using machine learning and CFD-based response surface analysis. Int. J. Artif. Organs 2025, 48, 367–383. [Google Scholar] [CrossRef] [PubMed]
- Oran, E.; Abo-Serie, E.; Jewkes, J.; Henry, M.; Oran, B. Design and optimisation of an Intra-Aortic Shrouded rotor axial pump. J. Biomech. 2024, 162, 111858. [Google Scholar] [CrossRef]
- Song, G.; Chua, L.P.; Lim, T.M. Numerical study of a centrifugal blood pump with different impeller profiles. ASAIO J. 2010, 56, 24–29. [Google Scholar] [CrossRef]
- Zhou, M.; Qi, Z.; Xia, Z.; Li, Y.; Ling, W.; Yang, J.; Yang, Z.; Pei, J.; Wu, D.; Huo, W.; et al. Miniaturized soft centrifugal pumps with magnetic levitation for fluid handling. Sci. Adv. 2021, 7, eabi7203. [Google Scholar] [CrossRef]
- Deng, Q.; Pei, J.; Wang, W.; Lin, B.; Zhang, C.; Zhao, J. Energy Loss and Radial Force Variation Caused by Impeller Trimming in a Double-Suction Centrifugal Pump. Entropy 2021, 23, 1228. [Google Scholar] [CrossRef]
- Hirschhorn, M.; Catucci, N.; Day, S.W.; Stevens, R.M.; Tchantchaleishvili, V.; Throckmorton, A.L. Channel impeller design for centrifugal blood pump in hybrid pediatric total artificial heart: Modeling, magnet integration, and hydraulic experiments. Artif. Organs 2022, 47, 680–694. [Google Scholar] [CrossRef]
- Diallo, A.B.; Çınar, H.; Yapıcı, R. Analysis of fluid forces impacting on the impeller of a mixed flow blood pump with computational fluid dynamics. Int. J. Artif. Organs 2024, 47, 894–907. [Google Scholar] [CrossRef]
- Ji, D.; Lu, W.; Xu, B.; Xu, L.; Lu, L. Study of Energy Loss Characteristics of a Shaft Tubular Pump Device Based on the Entropy Production Method. Entropy 2023, 25, 995. [Google Scholar] [CrossRef]
- Parente, R.; Fumagalli, M.R.; Di Claudio, A.; Rincón, C.L.C.; Erreni, M.; Zanini, D.; Iapichino, G.; Protti, A.; Garlanda, C.; Rusconi, R.; et al. A Multilayered Imaging and Microfluidics Approach for Evaluating the Effect of Fibrinolysis in Staphylococcus aureus Biofilm Formation. Pathogens 2023, 12, 1141. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Fang, Y.; Shen, Y.; Li, H.; Wang, Y.; Zhu, X.; Lu, X. Structural characteristics of corrugated sandwich rectangular pressure vessels. Sci. Rep. 2025, 15, 10646. [Google Scholar] [CrossRef] [PubMed]
- Hatoum, H.; Moore, B.L.; Dasi, L.P. On the Significance of Systolic Flow Waveform on Aortic Valve Energy Loss. Ann. Biomed. Eng. 2018, 46, 2102–2111. [Google Scholar] [CrossRef]
- Zhang, J.; Rothenberger, S.M.; Brindise, M.C.; Markl, M.; Rayz, V.L.; Vlachos, P.P. Wall Shear Stress Estimation for 4D Flow MRI Using Navier-Stokes Equation Correction. Ann. Biomed. Eng. 2022, 50, 1810–1825. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.C.; Saha, G. Effect of microplastics deposition on human lung airways: A review with computational benefits and challenges. Heliyon 2024, 10, e24355. [Google Scholar] [CrossRef]
- Peng, P.; Chen, H.; Che, B.; Li, X.; Fan, C.; Liu, L.; Luo, T.; Deng, L. Research on a portable electrical impedance tomography system for evaluating blood compatibility of biomaterials. Sheng Wu Yi Xue Gong Cheng Xue Za Zhi J. Biomed. Eng. Shengwu Yixue Gongchengxue Zazhi 2025, 42, 219–227. [Google Scholar] [CrossRef]
- Fu, M.; Liu, G.; Wang, W.; Gao, B.; Ji, B.; Chang, Y.; Liu, Y. Hemodynamic evaluation and in vitro hemolysis evaluation of a novel centrifugal pump for extracorporeal membrane oxygenation. Ann. Transl. Med. 2021, 9, 679. [Google Scholar] [CrossRef]
- Yun, Z.; Yao, J.; Wang, L.; Tang, X.; Feng, Y. The design and evaluation of the outflow structures of an interventional microaxial blood pump. Front. Physiol. 2023, 14, 1169905. [Google Scholar] [CrossRef]
- Gu, K.; Yang, K.; Zhao, C.; Shu, Q.; Lin, R. Optimizing the design of a pediatric blood pump through orthogonal experimentation. Heliyon 2025, 11, e42502. [Google Scholar] [CrossRef]
- Li, Y.; Yu, J.; Wang, H.; Xi, Y.; Deng, X.; Chen, Z.; Fan, Y. Investigation of the influence of blade configuration on the hemodynamic performance and blood damage of the centrifugal blood pump. Artif. Organs 2022, 46, 1817–1832. [Google Scholar] [CrossRef]
- Wang, J.; Nakata, T.; Liu, H. Development of Mixed Flow Fans with Bio-Inspired Grooves. Biomimetics 2019, 4, 72. [Google Scholar] [CrossRef]
- Sarkisyan, H.; Stevens, R.; Tchantchaleishvili, V.; Rossano, J.; Throckmorton, A. Integrated long-term multifunctional pediatric mechanical circulatory assist device. Artif. Organs 2020, 45, E65–E78. [Google Scholar] [CrossRef]
- Medina, R.; Sánchez, R.-V.; Cabrera, D.; Cerrada, M.; Estupiñan, E.; Ao, W.; Vásquez, R.E. Scale-Fractal Detrended Fluctuation Analysis for Fault Diagnosis of a Centrifugal Pump and a Reciprocating Compressor. Sensors 2024, 24, 461. [Google Scholar] [CrossRef]
- Peng, G.; Chen, Q.; Zhou, L.; Pan, B.; Zhu, Y. Effect of Blade Outlet Angle on the Flow Field and Preventing Overload in a Centrifugal Pump. Micromachines 2020, 11, 811. [Google Scholar] [CrossRef]
- Yu, N.; Yu, X.; Cai, Z.; Yang, X.; Tian, L.; Li, S. Research on multi-condition optimization of centrifugal compressor impeller meridian profile. PLoS ONE 2025, 20, e0318783. [Google Scholar] [CrossRef]
- Lloyd, A.; Fiala, D.; Heyde, C.; Havenith, G. A mathematical model for predicting cardiovascular responses at rest and during exercise in demanding environmental conditions. J. Appl. Physiol. 2022, 133, 247–261. [Google Scholar] [CrossRef]
- Mazimba, S.; Jeukeng, C.; Ondigi, O.; Mwansa, H.; E Johnson, A.; Elumogo, C.; Breathett, K.; Kwon, Y.; Mubanga, M.; Mwansa, V.; et al. Coronary perfusion pressure is associated with adverse outcomes in advanced heart failure. Perfusion 2022, 38, 1492–1500. [Google Scholar] [CrossRef]
- Reymond, P.; Bendjelid, K.; Giraud, R.; Richard, G.; Murith, N.; Cikirikcioglu, M.; Huber, C. To Balloon or Not to Balloon? The Effects of an Intra-Aortic Balloon-Pump on Coronary Artery Flow during Extracorporeal Circulation Simulating Normal and Low Cardiac Output Syndromes. J. Clin. Med. 2021, 10, 5333. [Google Scholar] [CrossRef]
- Olsen, D.B. The history of continuous-flow blood pumps. Artif. Organs 2000, 24, 401–404. [Google Scholar] [CrossRef]
- Carson, J.L.; Stanworth, S.J.; Dennis, J.A.; Trivella, M.; Roubinian, N.; Fergusson, D.A.; Triulzi, D.; Dorée, C.; Hébert, P.C. Transfusion thresholds for guiding red blood cell transfusion. Cochrane Database Syst. Rev. 2021, 12, Cd002042. [Google Scholar] [CrossRef]
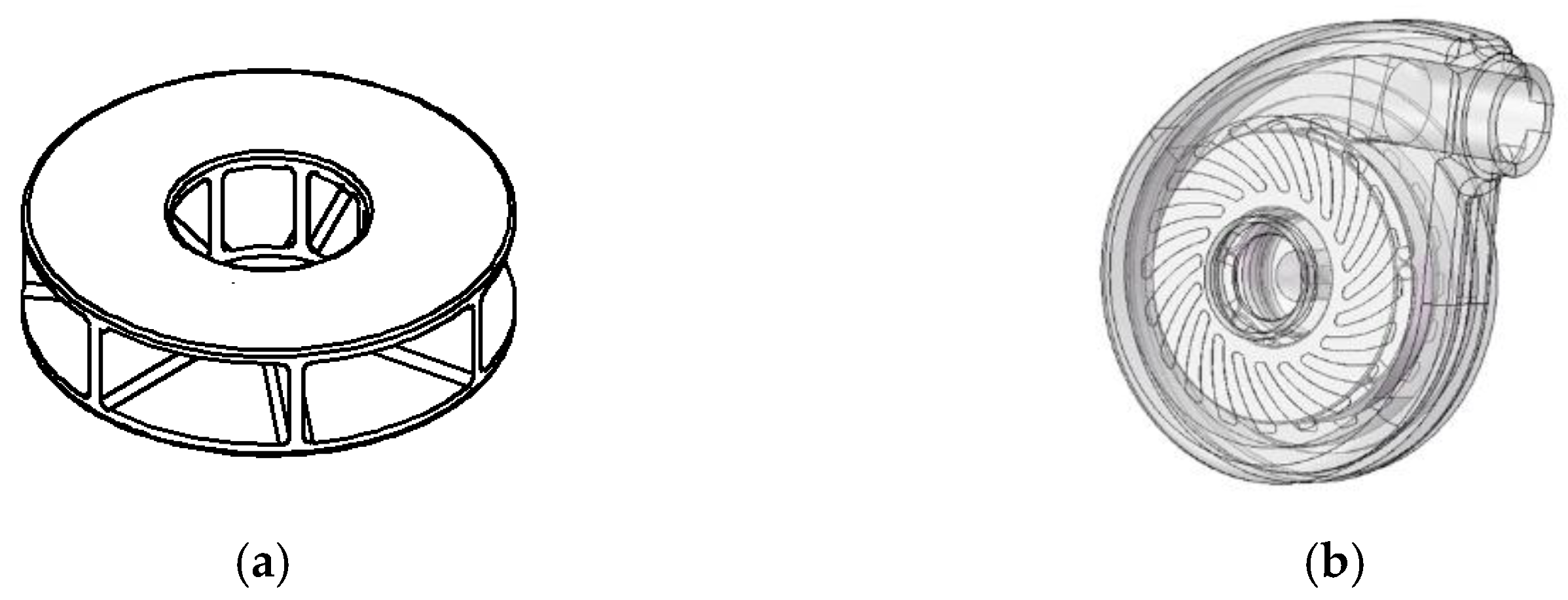







| Parameter | Value or Selection | Remarks |
|---|---|---|
| blood density | 1060 kg/m3 | Human normal blood density1050~1060 kg/m3 |
| blood viscosity | 3.5 × 10−3 Pa·s | The range of 0.0030.004 Pa·s |
| blood pressure value | 100 mmHg | The ranges from 80 to 120 mmHg |
| blood pump flow rate | 5 L/min | Cardiac output of an adult male |
| Inlet Boundary Conditions | Velocity inlet boundary | |
| Outlet Boundary Conditions | Pressure outlet boundary | Pressure difference value of the human heart |
| Turbulence Model | RNG k-ε model | |
| Wall Boundary Conditions | Rotating wall | The remaining walls are all stationary walls. |
| Impeller Rotational Speed | 2800 r/min | |
| Interface between the stationary and rotating regions | Inlet–Impeller liquid–liquid Impeller–Volute liquid–liquid | The interface between the stationary and rotating regions is treated using the interface method. |
| Solver | SIMPLEC algorithm | The pressure correction value is readily obtained. |
| Convergence Accuracy | 0.00001 | Convergence criterion based on the root-mean-square residual value |
| Blade Number | Head (mmHg) | Efficiency (%) |
|---|---|---|
| 6 | 90.74457 | 32.41 |
| 7 | 101.64041 | 34.53 |
| 8 | 106.54463 | 33.14 |
| Blade Wrap Angle (°) | Head (mmHg) | Efficiency (%) |
|---|---|---|
| 0° | 101.6 | 33.1 |
| 30° | 89.0 | 38.9 |
| 60° | 85.2 | 40.8 |
| 90° | 72.1 | 37.1 |
| Parameter | Numerical Value |
|---|---|
| Inner diameter of impeller | 7.5 mm |
| Outer diameter of impeller | 16 mm |
| Number of leaves | 7 |
| Wrap angle of blade | 0° |
| Position of the flow channel | 4.1 mm |
| Diversion cone height | 4.1 mm |
| Time (h) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Plasma free hemoglobin concentration (mg/L) | 37.52 | 50.96 | 88.35 | 113.75 | 148.23 | 201.75 | 226.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xin, L.; Weng, Q. Parametric Study and Hemocompatibility Assessment of a Centrifugal Blood Pump Based on CFD Simulation and Experimental Validation. Appl. Sci. 2025, 15, 11710. https://doi.org/10.3390/app152111710
Wang Y, Xin L, Weng Q. Parametric Study and Hemocompatibility Assessment of a Centrifugal Blood Pump Based on CFD Simulation and Experimental Validation. Applied Sciences. 2025; 15(21):11710. https://doi.org/10.3390/app152111710
Chicago/Turabian StyleWang, Yiwen, Libo Xin, and Qinghong Weng. 2025. "Parametric Study and Hemocompatibility Assessment of a Centrifugal Blood Pump Based on CFD Simulation and Experimental Validation" Applied Sciences 15, no. 21: 11710. https://doi.org/10.3390/app152111710
APA StyleWang, Y., Xin, L., & Weng, Q. (2025). Parametric Study and Hemocompatibility Assessment of a Centrifugal Blood Pump Based on CFD Simulation and Experimental Validation. Applied Sciences, 15(21), 11710. https://doi.org/10.3390/app152111710





