Emergency Relief Material Distribution Path Optimization Under Multiple Constraints

Abstract

To overcome the limitations of traditional methods in emergency response scenarios—such as limited adaptability during the search process and a tendency to fall into local optima, which reduce the overall efficiency of emergency supply distribution—this study develops a Vehicle Routing Problem (VRP) model that incorporates multiple constraints, including service time windows, demand satisfaction, and fleet size. A multi-objective optimization function is formulated to minimize the total travel time, reduce distribution imbalances, and maximize demand satisfaction. To solve this problem, a hybrid deep reinforcement learning framework is proposed that integrates an Adaptive Large Neighborhood Search (ALNS) with Proximal Policy Optimization (PPO). In this framework, ALNS provides the baseline search, whereas the PPO policy network dynamically adjusts the operator weights, acceptance criteria, and perturbation intensities to achieve adaptive search optimization, thereby improving global solution quality. Experimental validation of benchmark instances of different scales shows that, compared with two baseline methods—the traditional Adaptive Large Neighborhood Search (ALNS) and the Improved Ant Colony Algorithm (IACA)—the proposed algorithm reduces the average objective function value by approximately 23.6% and 25.9%, shortens the average route length by 7.8% and 11.2%, and achieves notable improvements across multiple performance indicators.

1. Introduction

The optimization of emergency supply distribution routes is a critical challenge in response to natural disasters, public health crises, and industrial accidents. Under limited resources and strict time constraints, the efficient scheduling of emergency supplies is essential to ensure the orderly progress of relief operations. This problem can be abstracted as a Vehicle Routing Problem (VRP), which is a classic topic in combinatorial optimization [1,2]. With the introduction of multiple constraints in complex environments, the VRP has become an even more challenging NP-hard problem. As the scale of the problem grows and the constraints increase in complexity, the solution difficulty rises accordingly, underscoring the urgent need for efficient optimization strategies.

In recent years, the role of VRP in emergency response has become increasingly critical. For example, during the catastrophic floods in Henan Province in 2021, 12 national highways were blocked, leaving several regions isolated [3]. The traditional scheduling methods faced significant delays in material delivery, highlighting the need for more responsive routing strategies. Similarly, during the 2023 Turkey earthquake, surface ruptures extended over 300 km, severely disrupting traditional route planning models for emergency supply transportation [4]. These cases clearly illustrate the limitations of traditional routing methods under complex constraints and emphasize the need for more intelligent and adaptive optimization approaches.

Against this background, traditional routing methods in emergency environments face three major challenges. (1) Limited adaptability: conventional approaches typically rely on fixed heuristic strategies in complex environments and lack global search mechanisms and dynamic parameter adjustments. As a result, they often become trapped in local optima during natural disasters, thereby reducing the overall scheduling effectiveness. (2) Response delays: Traditional methods depend on predefined routing strategies and lack mechanisms for adaptive adjustments to dynamic conditions. Consequently, they cannot promptly reconstruct transportation plans, which leads to insufficient responsiveness. (3) Low resource utilization: Conventional approaches struggle to handle multi-constraint optimization problems, often resulting in redundant services, material waste, and uneven distribution, which ultimately undermine transportation efficiency.

Previous studies have proposed various algorithms for VRP in both emergency and general contexts, which can broadly be categorized into heuristic methods and machine learning–based strategy optimization approaches. Among traditional algorithms, Dorigo et al. [5] first introduced the ant colony optimization (ACO) algorithm and successfully applied it to the classical Traveling Salesman Problem (TSP), laying the theoretical foundation for subsequent VRP research. Building on this, Kubil et al. [6] developed a multi-objective ACO algorithm for multi-depot VRP variants, while Miao et al. [7] incorporated adaptive mechanisms to enhance global search performance. Zhang et al. [8] proposed the MSALNS algorithm to solve the flexible time window and delivery location VRP of customer satisfaction, and introduced backtracking and correlation operators and simulated annealing acceptance mechanism to improve search performance. Cao et al. [9] addressed cold-chain distribution under traffic congestion by formulating a time-window-constrained routing model and designing an improved genetic algorithm to enhance solution stability and scheduling efficiency. Liu et al. [10] proposed a multi-objective emergency distribution model that considered the urgency of supplies during epidemic outbreaks and introduced a hybrid intelligent optimization algorithm to improve computational efficiency, demonstrating advantages in cost reduction and vehicle utilization. Yu et al. [11] and Tu et al. [12] applied simulated annealing and its improved variants to VRP in omni-channel retail distribution and under multiple time-window constraints, respectively. Wei et al. [13] modeled the routing problem for emergency distribution during epidemic lockdowns as a generalized VRP with complex constraints and proposed an improved ACO algorithm. Compared with standard ACO, their method achieved significantly better routing performance, verifying its effectiveness in disaster scenarios.

With the advancement of machine learning, an increasing number of studies have integrated machine learning into the VRP framework, leveraging adaptive decision-making capabilities to enhance intelligence and generalization. James et al. [14] tackled the route selection problem in last-mile delivery by employing reinforcement learning to model vehicle–environment interactions, thereby achieving optimal routing. Zong et al. [15] proposed an end-to-end reinforcement learning framework for the VRPTW, incorporating feature encoding and a time penalty mechanism to improve solution quality. Silva et al. [16] applied a multi-agent reinforcement learning framework to VRP with time-window constraints, enabling agents to dynamically adjust strategies based on environmental feedback. Kang et al. [17] addressed the routing of electric vehicles providing emergency power supply to shelters after earthquakes and designed a deep reinforcement learning algorithm with a multi-head attention mechanism, which demonstrated strong responsiveness and routing performance in complex environments. Arishi et al. [18] formulated a multi-agent VRP framework for multi-depot distribution scenarios, thereby enhancing system-level collaborative scheduling. Ahamed et al. [19] and Liu et al. [20] employed deep Q-networks and decision models, respectively, for supply chain route optimization and logistics efficiency improvement, both of which demonstrated strong policy-learning capabilities.

Existing research on VRP shows a trend toward the diversification of algorithm design. Some researchers have integrated metaheuristics with other algorithms to improve the adaptability and solution efficiency. Therefore, hybrid ALNS algorithms have become popular research topics. Recent research has focused on embedding learning mechanisms or other metaheuristic methods into the ALNS framework to improve the operator selection and search strategies. Reijnen et al. [21] proposed an adaptive large-neighborhood search algorithm (DR-ALNS) based on deep reinforcement learning. By learning the search state, it dynamically selects operators, adjusts parameters, and controls acceptance criteria, thereby adaptively optimizing the search process. Ma et al. [22] proposed an improved adaptive large neighborhood search algorithm (IALNS-SA) combined with simulated annealing for the vehicle routing problem with simultaneous delivery and pickup time windows. The algorithm improves the robustness by introducing supplementary damage and repair operators, and adopts the SA acceptance criterion to avoid falling into local optimality. Liu et al. [23] proposed an adaptive hybrid genetic and large neighborhood search algorithm (AHGSLNS) for a multi-attribute vehicle routing problem. By combining a genetic search with the ALNS, the parameters and acceptance criteria were adaptively adjusted to improve the stability and convergence of the algorithm.

These studies have improved the intelligence and adaptability of ALNS at the algorithmic level, but have mainly focused on improving operator selection and search mechanisms. In contrast, the ALNS-PPO algorithm proposed in this paper not only integrates the adaptive mechanism into the search strategy but also combines it with demand point satisfaction-oriented target modeling, expanding the research scope of the hybrid ALNS from both the model and algorithm dimensions.

Although existing VRP research has performed well in general scenarios, in complex environments and multi-constraint emergency scenarios, traditional algorithms that rely on fixed-domain search strategies are prone to falling into local optimality and have difficulty obtaining high-quality solutions. They are also highly dependent on manual experience for parameter settings and have limited adaptability and generalization capabilities. To overcome these limitations, this study aims to establish a multi-constrained emergency material scheduling and routing optimization model and proposes a hybrid optimization framework that integrates Adaptive Large Neighborhood Search (ALNS) with Proximal Policy Optimization (PPO) to enhance both the global search capability and adaptive decision-making ability in emergency logistics scheduling. By leveraging deep reinforcement learning mechanisms, the framework dynamically adjusts parameters to enable route reconstruction and adaptive optimization, thereby significantly enhancing the adaptability in complex disaster environments. Regarding the practical implications of this research, from an economic perspective, this model can significantly reduce transportation costs and material waste during large-scale relief operations by improving vehicle utilization and reducing redundant trips. From a social perspective, improved route efficiency can help deliver essential supplies to disaster-stricken areas more quickly and equitably, thereby improving the overall responsiveness and equity of disaster relief efforts. The results suggest that this approach has the potential to provide theoretical and practical value to real-world emergency logistics systems. The main contributions of this study are as follows.

(1)

Multi-constraint model construction: A VRP model was developed that incorporated multiple depots, vehicles, demand points, and real-world constraints, providing a theoretical foundation and modeling framework for route planning in complex emergency scenarios.

(2)

Collaborative hybrid optimization framework combining ALNS and PPO. Unlike existing reinforcement learning-based VRP research, using reinforcement learning as a standalone solver, this study establishes a dynamic interaction mechanism in which the PPO adaptively learns and adjusts the neighborhood search strategy in ALNS. Collaborative integration enhances global exploration capabilities and supports adaptive decision-making under multiple operational constraints.

(3)

Comprehensive evaluation and validation: The proposed approach was systematically evaluated using multiple public VRP benchmark datasets and compared with traditional heuristic algorithms. Experimental results demonstrate that it achieves superior routing performance and significant improvements across multiple performance indicators, underscoring its strong generalization capability and practical application value.

2. Problem Description and Modeling

This section presents a detailed description of the modeling process for the emergency supply distribution vehicle routing optimization problem, including the formulation of objective functions, the definition of constraints, and the specification of relevant parameters. The objective is to ensure that the model comprehensively and accurately captures the complexity and requirements of real-world emergency distribution scenarios.

2.1. Problem Description

In the aftermath of sudden disasters such as earthquakes, floods, or epidemic outbreaks, the rapid and efficient distribution of relief materials has become a critical component of emergency response operations. Unlike conventional logistics, emergency relief distribution is subject to multiple constraints. Its primary objective is not only to minimize transportation time but also to ensure the prompt and reliable delivery of critical supplies to affected regions in order to support life-saving operations. Therefore, to better characterize the logistical features of such emergency scenarios, it is necessary to establish a multi-constraint path optimization model for emergency relief material distribution.

Given several emergency supply depots and multiple affected demand points, the objective is to plan vehicle distribution routes under the constraints of vehicle capacity, road accessibility, and delivery time windows, so that materials are delivered efficiently to target areas in the shortest possible time, producing an optimal or near-optimal emergency distribution plan.

Model Assumptions:

• The demand quantities and location coordinates of all the demand points are known prior to scheduling and remain fixed throughout the optimization process.
• Each demand point has a strict service time window. If the delivery cannot be completed within the specified time, the task is considered unsuccessful and the distribution is invalid.
• All vehicles have identical loading capacities and travel speeds.
• Each vehicle is prohibited from returning to the depot for replenishment during a single trip; therefore, the entire loading and delivery processes must be completed in one operation.
• The inventory of each depot is known and non-replenished, and the depot locations are randomly distributed.
• The demand at each demand point must be fully served by a single vehicle and cannot be split among multiple vehicles.
• Each vehicle can carry multiple types of supplies. However, the total load must not exceed its maximum capacity.
• Both waiting time and service time at demand points are considered during transportation.

These simplified assumptions are adopted to preserve the model’s tractability and emphasize the core decision logic of the proposed optimization framework. Although this abstraction inevitably reduces the level of real-world detail, it allows for a clearer interpretation of the key routing relationships and constraint interactions.

Figure 1 shows a typical schematic of vehicle distribution route planning for emergency relief materials. The diagram illustrates the core workflow of emergency material distribution. Multiple vehicles depart from the depots, sequentially deliver materials to demand points while satisfying the constraints, and return to the depot, providing a visual representation of the VRP scenario addressed in this study.

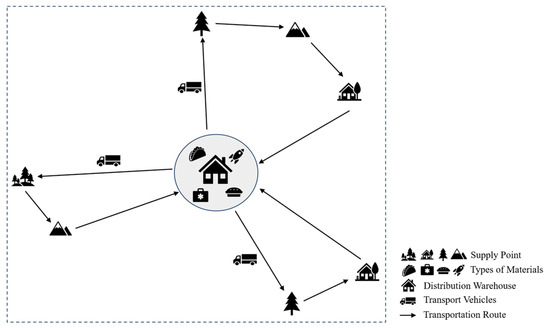
Figure 1. Schematic diagram of vehicle distribution route planning for emergency relief materials.

2.2. Modeling

To effectively address the practical problem of emergency supply vehicle routing optimization, a mathematical model is constructed based on the above assumptions, systematically describing and constraining the key factors in the emergency distribution process. By optimizing vehicle routes, the model minimizes a multi-objective function to ensure the efficient delivery of supplies from depots to demand points. In the modeling process, real-world constraints are comprehensively incorporated to allocate supply and vehicle resources effectively, thereby ensuring the timely delivery of materials and enhancing emergency response capability under disaster scenarios.

The parameters used in the model are defined as follows in Table 1:

Table 1. Meaning of parameters in the model.

Parameters	Meaning
$D=\{0,1,2,\dots ,m\}$	Depot set, where 0 denotes the default depot; m is the number of additional depots, $\forall f\in D$
$N=\{1,2,3,\dots ,n\}$	Demand point set; n is the number of demand points, $\forall i\in N$
$K=\{1,2,3,\dots ,p\}$	Transportation vehicle set; p is the number of available vehicles, $\forall k\in K$
$z_d$	Total volume of materials allocated by depot d, $\forall d\in D$
$S_d$	Initial supply inventory at depot d, $\forall d\in D$
$f_i$	Demand quantity at demand point i, $f_i\ge 0$, $\forall i\in N$
$f_c$	Demand volume at service point c for vehicles’ actual service needs, $f_c\ge 0$, $\forall c\in N$
$[e_i,l_i]$	Service time window of demand point i, $\forall i\in N$
$y_i^k$	Binary decision variable: 1 if demand point i is served by vehicle k; 0 otherwise, $\forall i\in N$, $\forall k\in K$
$Q_k$	Maximum load capacity of vehicle k, $\forall k\in K$
$L_k$	Actual loading capacity utilized by vehicle k, $\forall k\in K$
$M$	Total number of vehicles actually used, $M\ge 0$
$R_k$	Service route of vehicle k (sequence of depots and demand points), $\forall k\in K$
$T_{ij}$	Total travel time of vehicle k on edge $(i,j)$, $\forall (i,j)\in E’$
$x_{ij}^k$	Binary decision variable, equal to 1 if vehicle k travels along edge $(i,j)$, and 0 otherwise, $\forall (i,j)\in E’$, $\forall k\in K$
$t_i^k$	Arrival time of vehicle k at demand point i, $\forall i\in N$, $\forall k\in K$
$E’$	Set of feasible post-disaster paths, excluding those blocked or restricted by traffic control

All parameters are expressed in dimensionless form, and time and distance can be interpreted in minutes and kilometers, respectively, when applied to real emergency logistics cases.

Considering the problem description and the definitions of the relevant parameters, the objective functions and constraints are formulated as follows:

• Objective Function

$$\min Z=\alpha {\displaystyle \sum _{k\in K}{\displaystyle \sum _{(i,j)\in E’}{T}_{ij}}}{x}_{ij}^k+\gamma {\displaystyle \sum _{i\in N}\left|L_k-\frac{1}{\left|K\right|}{\displaystyle \sum _{i\in N}{f}_i}\right|}+\delta \left({\displaystyle \sum _{i\in N}{f}_i-{\displaystyle \sum _{k\in K}{\displaystyle \sum _{c\in R_k}{f}_c}}}\right)$$

(1)

The proposed optimization model aims to improve the efficiency and rationality of emergency supply distribution by considering multiple objectives. In particular, the objective function integrates three key components:

• ${\displaystyle \sum _{k\in K}{\displaystyle \sum _{(i,j)\in E’}{T}_{ij}}}{x}_{ij}^k$, which denotes the total travel time of all vehicles. Optimizing delivery routes while minimizing unnecessary detours and empty trips helps improve both overall transportation efficiency and emergency response speed.
• ${\displaystyle \sum _{i\in N}\left|L_k-\frac{1}{\left|K\right|}{\displaystyle \sum _{i\in N}{f}_i}\right|}$ denotes the total average deviation in the load distribution among vehicles. Here ${\displaystyle \frac{1}{\left|K\right|}}{\displaystyle \sum _{i\in N}{f}_i}$ is the expected load capacity per vehicle, which ensures that every demand point receives a sufficient supply of relief materials.
• $\left({\displaystyle \sum _{i\in N}{f}_i-{\displaystyle \sum _{k\in K}{\displaystyle \sum _{c\in R_k}{f}_c}}}\right)$ denotes the degree of demand satisfaction. The difference between the total demand of ${\displaystyle \sum _{i\in N}{f}_i}$ and the total number of demand points served ${\displaystyle \sum _{k\in K}{\displaystyle \sum _{c\in R_k}{f}_c}}$. The objective of maximizing the fulfillment of actual demand at each point and ensuring that material distribution adequately meets the required needs.

To balance the model’s multiple objectives, weighting coefficients α, γ, and δ are introduced. These coefficients are normalized such that α + γ + δ = 1 to ensure comparability across different indicators. Considering that, in emergency scenarios, “the needs of the disaster area must be met first” while also balancing transportation efficiency and vehicle resource waste, the weights are set to α = 0.3, γ = 0.2, and δ = 0.5.

The proposed model considers transportation efficiency, balance of material allocation, and demand satisfaction in route optimization. It integrates three indicators—total vehicle travel time, load distribution deviation, and unsatisfied demand—into a single aggregated objective function via a weighted summation, aiming to achieve overall optimization and a balanced trade-off among multiple objectives.

2.

Constraints

The model must comply with the following fundamental constraints to guarantee the rationality and feasibility of emergency material distribution:

• Constraint ensuring that each vehicle route forms a closed loop

  $${\displaystyle \sum _{i\in N\cup D}{x}_{di}^k}={\displaystyle \sum _{j\in N\cup D}{x}_{ij}^k}=1,\hspace{1em}\forall (i,j)\in E’,\forall k\in K$$

  (2)
• Constraint ensuring that the load carried by each vehicle does not exceed its capacity

  $${\displaystyle \sum _{i\in N}{f}_i{y}_i^k\le Q^k},\hspace{1em}\forall f\in D, \forall k\in K$$

  (3)
• Constraint ensuring that each delivery is made within the specified time window

  $$e_i\le t_i^k\le l_i,\hspace{1em}\forall i\in N,\forall k\in K$$

  (4)
• Constraint ensuring that the quantity of materials supplied does not exceed the available inventory

  $${\displaystyle \sum _{k\in K}{\displaystyle \sum _{i\in N}{f}_i}}{y}_i^k\le S_d,\hspace{1em}\forall f\in D,\forall i\in N$$

  (5)
• Constraint ensuring that each demand point is served by exactly one vehicle

  $${\displaystyle \sum _{k\in K}{y}_i^k}=1, \forall i\in N$$

  (6)

In the proposed model, Equation (2) ensures that each vehicle departs from and returns to the distribution center, maintaining route closure and operational feasibility. Equation (3) enforces that the vehicle load does not exceed its capacity, reflecting practical transportation limitations. Equation (4) requires that service at each demand point be completed within the specified time window, thereby satisfying the timeliness requirements of emergency logistics. Equation (5) limits the quantity of materials delivered in a single trip to the available inventory, ensuring supply feasibility. Equation (6) guarantees that each demand point is served by exactly one vehicle, promoting efficient resource utilization. Collectively, these constraints establish a multi-constraint vehicle routing optimization model for emergency material distribution, providing a robust theoretical foundation for the subsequent application of optimization algorithms.

3. Algorithm Design

This study proposes a hybrid deep reinforcement learning framework that integrates Adaptive Large Neighborhood Search (ALNS) with Proximal Policy Optimization (PPO), thereby enhancing both the adaptability and solution efficiency of the algorithm. The theoretical basis for the combination of ALNS and PPO stems from their complementary strengths: ALNS overcomes PPO’s inherent limitation of low solution feasibility in complex constraint scenarios, while PPO addresses ALNS’s flaw of rigid parameter settings leading to local optima. PPO, based on the policy gradient theory in deep reinforcement learning, leverages solution quality feedback to update its policy, which aligns with the iterative “break-and-repair” mechanism of ALNS, enabling ALNS to adjust core search parameters in real time based on the current solution state.

Figure 2 presents the overall flowchart, illustrating the main steps and execution process. The framework primarily consists of four stages: initial solution generation, feature extraction, PPO-based policy parameter output, and subsequent parameter update and solution optimization. Specifically, initial solutions are generated using the ALNS algorithm, while PPO is employed for parameter adjustment. The solution is iteratively refined until the termination criteria are satisfied, at which point the final results are obtained.

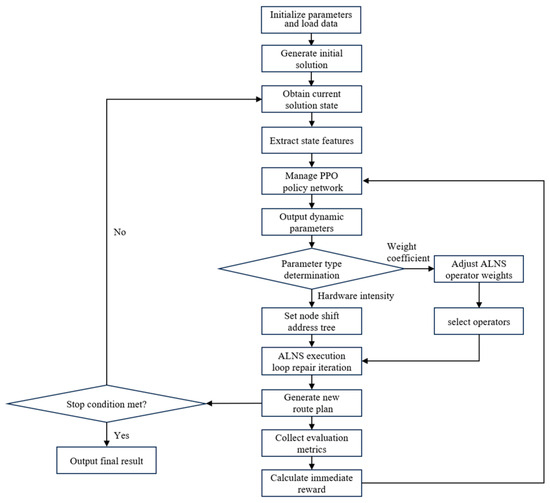
Figure 2. Overall flowchart of the ALNS-PPO hybrid algorithm.

3.1. Basic Algorithm Modules

3.1.1. Adaptive Large Neighborhood Search (ALNS)

The ALNS algorithm employs a destroy–repair mechanism in combination with a neighborhood generation strategy [24]. This study introduces three types of destruction operators: random removal (based on 10% removal), long-term conflict removal, and distance cluster removal, and three types of repair operators: minimum-redundant-time insertion, greedy insertion, and nearest-neighbor insertion. Each destruction–repair pair $\left(D_u,R_v\right)$ constitutes a candidate neighborhood. During the search process, the PPO module dynamically adjusts its selection probability based on recent performance feedback. The repair process enforces the vehicle capacity and time window constraints by recalculating the earliest and latest feasible arrival times after each insertion. This adaptive operator mechanism enables ALNS to explore diverse neighborhood structures while maintaining feasibility, thereby improving overall search capabilities.

As shown in Figure 3, during each iteration, the destroy operator first selects an appropriate destruction operator to remove a subset of nodes from the current solution, resulting in a partial solution. The repair operator then selects an appropriate repair operator to reinsert the removed nodes into the partial solution, thereby generating a new candidate solution. By collaboratively utilizing multiple destroy and repair operators, the ALNS algorithm can dynamically switch neighborhood structures throughout the search process. In particular, the destroy operator can adaptively adjust the removal strategy according to the real-time system requirements, whereas the repair operator considers multiple constraints when reinserting nodes.

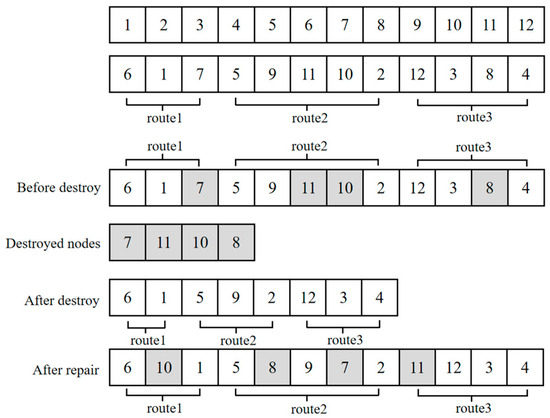
Figure 3. Schematic of the Destroy–Repair mechanism in the ALNS algorithm.

3.1.2. Proximal Policy Optimization (PPO)

Proximal Policy Optimization (PPO) is an efficient and stable policy-gradient deep reinforcement learning algorithm that employs a dual policy–value network architecture to improve the stability of policy updates in complex routing optimization scenarios [25].

In this study, the PPO module primarily functions as an adaptive controller within the ALNS framework rather than as a standalone end-to-end deep policy network. The PPO module employs a simplified actor–critic dual-network architecture. Both subnetworks consist of two fully connected layers with 48 and 24 hidden nodes, and the activation function used is ReLU. The output layer of the actor network generates five continuous control parameters, $\alpha =[r_d,w_r,w_d,\beta ,\delta ]$, corresponding to the key regulatory variables in the ALNS algorithm, and the critic network outputs a scalar state value that is used to evaluate the expected return of the current policy. To avoid gradient instability caused by inconsistent numerical scales, all the input features are normalized to the [0, 1] interval before entering the network. For action parameterization, the continuous actions produced by the PPO are represented in a bounded continuous space and mapped to the feasible range of ALNS parameters using a sigmoid function and linear scaling, ensuring that each action update corresponds to a valid search control variable.

The PPO algorithm implements an enhanced policy-gradient method that includes the following key steps:

Step 1: Data Collection. The interaction data are collected by implementing the current policy in the environment. The dataset includes states, actions, rewards, and the corresponding next states.

Step 2: Advantage Estimation. The GAE method is employed to evaluate the relative value of each action with respect to the average policy, facilitating subsequent gradient optimization. The core GAE formula is as follows:

$${\hat{A}}_t^{\mathrm{GAE}(\gamma ,\lambda )}={\displaystyle \sum _{l=0}^{\infty }{(\gamma \lambda )}^l}{\delta }_{t+l}$$

(7)

$\gamma$ denotes the discount factor that reflects the importance of long-term rewards.

$\lambda$ is the GAE parameter that controls the bias-variance trade-off and ${\delta }_{t+l}$ represents the temporal-difference error.

Step 3: Objective Function Optimization. The PPO algorithm utilizes a specifically designed objective function to guide policy updates in reinforcement learning. Its primary purpose is to constrain the step size of policy updates and prevent abrupt policy changes, thereby enhancing training stability and efficiency. The PPO objective is defined as follows:

$$L^{CLIP}(\theta ) ={\hat{\mathbb{E}}}_t\left[\min \left(r_t(\theta ){\hat{A}}_t,\mathrm{clip}(r_t(\theta ),1-ϵ,1+ϵ){\hat{A}}_t\right)\right]$$

(8)

Here, $r_t(\theta )$ denotes the probability ratio, that is, the ratio of the action probability under the current policy to that under the old policy. ${\hat{A}}_t$ represents the estimated advantage function, which indicates the relative value of taking a specific action compared to the average action in the current state.

Step 4: Policy Update. In the PPO algorithm, the policy parameters are updated using gradient descent. The overall loss function is first computed, after which the parameters θ are iteratively adjusted through gradient-based optimization, gradually approaching the optimal policy while maintaining update stability.

3.2. Design of the ALNS-PPO Hybrid Framework

The existing hybrid ALNS algorithms still exhibit two key limitations: first, the passive nature of operator selection and parameter adjustment, which creates a disconnect between the search direction and the core requirements of emergency tasks; and second, the single-dimensional handling of constraints, which limits adaptability to the complex and interdependent constraints typical of disaster scenarios. To overcome these challenges, the ALNS-PPO framework proposed in this study introduces two major innovations: (1) a multi-constraint collaborative control mechanism, which ensures the satisfaction of key constraints while dynamically balancing vehicle capacity and inventory limitations; and (2) a scenario-aware policy network, which extends the PPO feedback signal from pure search performance to multi-objective comprehensive benefits. This design enables the adaptive adjustment of operator weights and perturbation intensity to directly serve the core objectives of emergency logistics optimization.

To further illustrate the implementation logic of this collaborative optimization process, this study presents a framework design from two perspectives: a ‘hybrid architecture coordination mechanism’ and a ‘perception and feedback mechanism’.

3.2.1. Hybrid Architecture Coordination Mechanism

The proposed ALNS-PPO hybrid algorithm uses a hierarchical architecture to integrate traditional heuristic search methods with deep reinforcement learning. The ALNS layer quickly generates high-quality routing solutions through a destroy–repair mechanism, while the PPO layer outputs policy parameters via the policy network to guide the neighborhood search direction and scope within ALNS.

Figure 4 illustrates the core coordination mechanism of the proposed ALNS-PPO hybrid optimization framework, which systematically demonstrates the collaboration between deep reinforcement learning and heuristic search algorithms. The framework builds the main routing search structure using ALNS and integrates the PPO policy network as a control module. This framework adaptively guides the search process through state perception and reward feedback mechanisms.

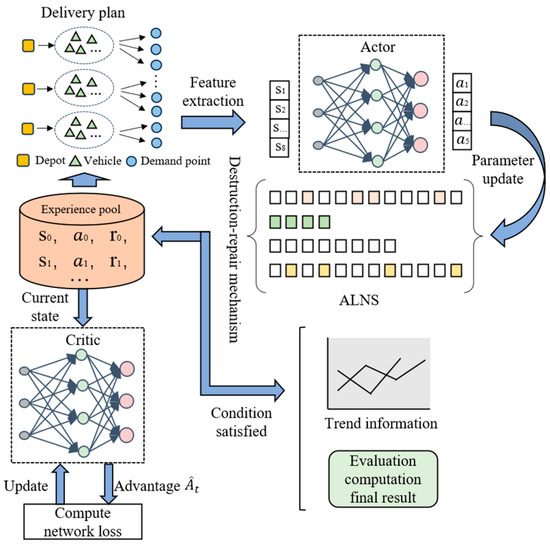
Figure 4. ALNS-PPO hybrid optimization architecture diagram.

(1)

Input phase:

Within this framework, the ALNS functions as the core component for route optimization, combining destruction and repair operators to iteratively perturb and reconstruct the current delivery routes. The system first extracts key emergency logistics information, including the number and geographic locations of warehouses, vehicle capacities, demand data for each demand point, and their corresponding time windows. Based on this information, ALNS utilizes its embedded route construction logic to generate an initial feasible delivery plan, which serves as the input for subsequent optimization within the framework.

(2)

Decision support phase:

Before each iteration, the PPO policy network perceives and analyzes the current solution state, encoding it into a state vector embedded within the Actor–Critic-based search framework. The Actor module extracts key routing features and outputs policy parameters—such as perturbation intensity and operator weights—that regulate the adaptive behavior of the ALNS process. These parameters dynamically adjust the execution strategies of the destruction and repair operators, thereby enhancing the effectiveness of exploration and guidance throughout the search.

After each path update, ALNS transmits the new solution structure to the evaluation module, which assesses both the feasibility and the quality of the solution. Based on the observed improvements, the system generates feedback signals used for subsequent deep reinforcement learning updates. The evaluation outcomes, together with the corresponding states and actions, form experience data that are stored in the experience pool for Critic network training.

The Critic module evaluates the current policy using a value function and provides feedback to improve the Actor’s decision making. Through this continuous cycle of state evaluation, policy refinement, and feedback integration, the PPO network offers dynamic and adaptive decision support, effectively guiding the ALNS toward high-quality solutions throughout the search process.

The overall framework illustrates the tight integration between deep reinforcement learning and heuristic search. The PPO module perceives the search state, generates control signals, and updates the policy based on feedback from the results, continuously guiding ALNS to adaptively explore high-quality solutions within the search space. This mechanism not only enhances the efficiency of route optimization but also improves the algorithm’s adaptability to complex and constrained environments.

3.2.2. Perception and Feedback Mechanism

In the ALNS-PPO hybrid optimization framework, the effectiveness of the policy network relies on an accurate perception of the search state and the proper construction of feedback information. The algorithm integrates state perception and a feedback mechanism to extract feature information from routing solutions and generate adaptive reward signals based on optimization outcomes.

This mechanism primarily consists of three core functions: (1) state-vector construction, which extracts multidimensional indicators from the current routing solution to represent the search state; (2) action-space output, which maps the key control parameters of the ALNS algorithm into the action space of the policy, enabling the policy network to dynamically adjust the search behavior in response to the current state; and (3) reward signal design, which provides feedback to the policy network based on the trend of objective value changes between the current solution and the historical best solution, guiding the optimization direction.

• State Space: In emergency material scheduling scenarios, route optimization must balance timeliness and coverage. To enable the PPO policy network to accurately perceive the dynamic environment, the state space is designed as an eight-dimensional vector, comprising the objective function value, vehicle utilization, proportion of customers violating time-window constraints, total delivery load, number of customers, average network distance, distance standard deviation, and number of distribution centers.
• Action Space: In the ALNS-PPO hybrid framework, the action space comprises five key dimensions, two of which control the intensity of ALNS destroy operations and multi-objective weighting in repair operations. The continuous action vector $\alpha =[r_d,w_r,w_d,\beta ,\delta ]$ output by the PPO undergoes nonlinear transformations to regulate the ALNS parameters. Specifically, $r_d$ denotes the destroy ratio; $w_r$ represents the selection weight for repair methods, adjusting the usage probability of multiple repair operators; $w_d$ is the selection weight for destroy methods; $\beta$ serves as a solution acceptance probability adjustment factor; and $\delta$ is an additional exploration factor that controls the perturbation intensity or magnitude.
• Reward Function: This study designs a reward mechanism based on improvements in the objective function to effectively guide the PPO policy network in learning high-quality search strategies. Given that the objective function already integrates multiple factors, including the total vehicle travel time, material allocation deviation, and demand satisfaction, the reward function is defined as the scaled difference between the objective function values of the current and previous solutions, and it is expressed as follows:

  $$r_t={\displaystyle \frac{C_{prev}-C_{curr}}{k}}$$

  (9)

Here, $C_{prev}$ denotes the best objective function value obtained in the previous iteration, $C_{curr}$ represents the objective function value of the new solution generated under the guidance of the PPO in the current iteration, and $k$ is a scaling factor used to balance the magnitude of the reward value to prevent training instability.

To ensure that the continuous action output of the PPO module can be effectively mapped to the discrete decision parameters of the ALNS, this study develops the corresponding action transformation and normalization functions within the hybrid framework. Each continuous action ${\alpha }_i$ output from the PPO is first mapped to the interval [0, 1] using a sigmoid function to ensure boundedness. The normalized results are scaled linearly. For the operator selection weights, because the sum of multiple operator weights must be one, a softmax function is applied for normalization. Through this transformation and normalization mechanism, the continuous action output of the PPO module can be smoothly and stably mapped to the control parameters of the ALNS, thereby achieving effective coupling between deep reinforcement learning and heuristic search.

Through the synergistic interaction of these three components, the deep reinforcement learning strategy continuously refines the search policy in complex environments, thereby effectively guiding the ALNS algorithm’s behavior.

4. Experiments and Analysis

4.1. Experimental Setup

The experiments were conducted on a Windows 10 platform equipped with an Intel Core i5-9300H @ 2.40 GHz processor and an NVIDIA GeForce GTX 1650 GPU. The algorithms were implemented in Python 3.8 and developed and debugged in the PyCharm (2024.1.4) environment. The classic Solomon and Homberger benchmark datasets were selected for the experiments to comprehensively evaluate the performance and adaptability of the proposed ALNS-PPO algorithm. To better reflect a real-world emergency logistics scenario, the original single-warehouse setting in the dataset was modified to a multi-warehouse configuration, and the vehicle capacity was adjusted. Examples of different scales and complexities were constructed to verify the solution effect and robustness of the algorithm under multiple constraints.

To ensure the reliability and reproducibility of the experiments, the parameters of the ALNS-PPO algorithm were appropriately configured. In the PPO module, the discount factor gamma was set to 0.985 to balance short-term and long-term rewards; strategy updates employed eps_clip with a weight of 0.3 to limit policy fluctuations and enhance training stability; the number of epochs was set to 4, the learning rate (lr) to 0.0003, and the Adam optimizer was adopted with a batch size of 32 to balance gradient estimation accuracy and computational efficiency. In the ALNS module, the degree parameter was set to 3 to control solution diversity and prevent premature convergence to local optima, while the number of iterations was set to 10,000 to ensure sufficient convergence of the algorithm.

4.2. Validation of Algorithm Effectiveness

To evaluate the performance of the proposed ALNS-PPO algorithm in emergency relief vehicle routing optimization, experiments were conducted from two perspectives: optimization effectiveness and parameter sensitivity analysis. These evaluations aimed to assess the algorithm’s solution quality and adaptability while also providing data for subsequent comparative studies. Twelve benchmark instances were selected for testing, including C101, C203, R102, R205, RC103, and RC207 from the Solomon dataset, and C121, C221, R122, R223, RC123, and RC225 from the Homberger dataset. In these instances, C-type cases feature clustered customer locations; R-type cases have dispersed customer locations with diverse time-window constraints; and RC-type cases combine both characteristics with more complex time-window restrictions, thereby closely reflecting the scheduling requirements of practical emergency distribution tasks.

For all experiments, the maximum number of iterations was set to 10,000. In the Solomon dataset, the problem scale is relatively small, with no more than 100 customer nodes, 3 depots, and 30 vehicles. In contrast, the Homberger dataset extends the Solomon dataset to larger scales, with up to 200 customer nodes, 5 depots, and 50 vehicles. Each instance was independently executed 10 times. The main evaluation metrics included total travel distance, number of vehicles used, demand fulfillment rate, and objective function value, to assess the algorithm’s robustness and optimization effectiveness under different demand distributions and time-window scenarios.

4.2.1. Parameter Sensitivity Analysis

In this section, a sensitivity analysis is performed on the key parameters of the algorithm to investigate their impact on solution quality. To assess the influence of these parameters, experiments were performed on the C101 instance of the Solomon dataset, and the convergence curves of the objective function values and key statistical indicators were recorded.

• Analysis of the Sensitivity to Destruction Intensity

In the damage intensity sensitivity analysis, the C101 instance from the Solomon dataset and the R221 instance from the Homberger dataset were selected as representative test cases. The damage intensity was set to 3, 10, and 20, respectively, while the other parameters remained constant, to evaluate the influence on the convergence of the algorithm. The convergence trend of the objective function value with respect to the number of iterations is illustrated in Figure 5, and comparative performance data for different damage intensities are summarized in Table 2.

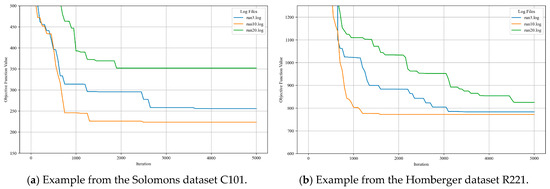
Figure 5. Convergence trend of the objective function under different damage intensities.

Table 2. Comparison of indicators at different damage intensities.

Dataset	Pr	Destruction Intensity	Runtime	Total Route Length	Vehicle Utilization	Demand Satisfaction Rate	Objective Function Value
Soloman	C101	3	200.36	3129.74	30/30	100%	254.25
		10	234.55	3294.86	30/30	100%	223.50
		20	194.13	3018.24	30/30	100%	351.91
Homberger	R221	3	551.68	8361.48	46/50	100%	783.57
		10	475.57	8759.13	48/50	100%	772.03
		20	455.49	8569.38	48/50	100%	825.33

The convergence curves indicate that, when the destruction intensity is set to 20, the algorithm converged the fastest; however, the objective function value remained relatively high, stabilizing after approximately 1900 iterations. With a destruction intensity of 3, the algorithm showed a rapid initial decrease, yet the final convergence value is slightly higher than that for an intensity of 10. At an intensity of 10, the convergence speed is slower than that at 20; however, the objective function value underwent a greater reduction. These results suggest that an excessively high destruction intensity can substantially disrupt the solution structure, and although convergence may occur faster, the local optimization capability may be reduced, making it more difficult for the algorithm to identify superior solutions.

• Analysis of Sensitivity to the Learning Rate

In the sensitivity analysis of the learning rate, the C101 instance from the Solomon dataset and the R221 instance from the Homberger dataset were chosen as representative test cases. The learning rate was set to 0.003, 0.0003, and 0.00003, respectively, while keeping other parameters constant, to assess its effect on the convergence behavior of the algorithm.

Figure 6 and Figure 7 show the sensitivity analysis results for different learning rates. They show variations in objective function values and algorithm runtimes across different settings. As can be seen, the learning rate has a clear influence on both convergence behavior and computational performance. A moderate learning rate (0.0003) provided a good balance between stability, convergence speed, and runtime efficiency. Detailed observations are shown in Figure 6 and Figure 7, and the corresponding quantitative results are summarized in Table 3.

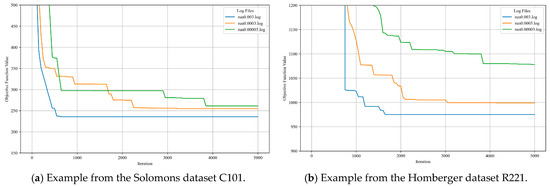
Figure 6. Convergence trend of the objective function under different learning rates.

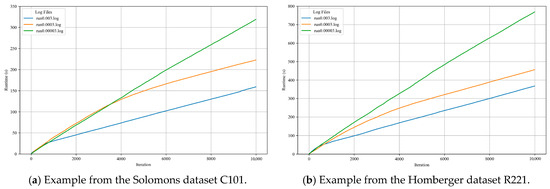
Figure 7. Algorithm runtime trends under different learning rates.

Table 3. Comparison of indicators at different learning rates.

Dataset	Pr	Learning Rate	Runtime	Total Route Length	Vehicle Utilization	Demand Satisfaction Rate	Objective Function Value
Soloman	C101	0.003	159.14	3104.46	30/30	100%	235.71
		0.0003	222.79	3048.43	30/30	100%	253.53
		0.00003	319.08	3199.62	30/30	100%	261.31
Homberger	R221	0.003	367.55	8537.98	50/50	100%	975.12
		0.0003	456.15	8692.60	50/50	100%	999.05
		0.00003	768.70	8499.74	50/50	100%	1077.18

For a relatively high learning rate (e.g., 0.003), the optimization process proceeded quickly, and the runtime increased moderately with the number of iterations. This indicates that a higher learning rate can accelerate convergence but may lead to unstable results and lower optimization precision per iteration. When the learning rate is reduced to 0.0003, the iteration precision improves. However, the overall convergence slows noticeably, resulting in a longer runtime. Further decreasing the learning rate to 0.00003 leads to an even slower convergence, with a significant increase in the required number of iterations and, consequently, in the total runtime. These results suggest that, although a smaller learning rate can enhance the solution accuracy, it requires considerably more computational time. Therefore, selecting an appropriate learning rate is critical for balancing computational efficiency and optimization precision.

• Analysis of the Sensitivity to Weight Coefficient

To assess the influence of the objective function’s weighting scheme on model performance, a sensitivity analysis of the weight coefficients was conducted using the C101 instance from the Solomon dataset. All other parameters were kept constant, and eight alternative combinations of weight values were tested to evaluate their effect on the experimental results.

Table 4 shows the comparison of indicators under different weight coefficient combinations. The results indicate that the multi-objective optimization results are sensitive to the weight coefficients (α, γ, δ), and different combinations reflect the multi-objective trade-off among “transportation efficiency, load balance, and demand satisfaction”.

Table 4. Comparison of indicators under different weight coefficients.

Weight Combination (α, γ, δ)	Objective Function Value	Total Route Length	Demand Satisfaction Rate	Vehicle Utilization	Average Load Deviation
(0.3, 0.1, 0.6)	309.49	3282.79	100%	26/30	3.21
(0.3, 0.2, 0.5)	271.29	3087.45	100%	30/30	2.73
(0.3, 0.3, 0.4)	283.84	3109.65	100%	30/30	2.63
(0.3, 0.4, 0.3)	295.63	3179.97	98.2%	30/30	2.49
(0.1, 0.2, 0.7)	306.35	3243.57	100%	27/30	2.85
(0.2, 0.2, 0.6)	297.79	3199.24	100%	29/30	2.82
(0.4, 0.2, 0.4)	287.53	3115.87	100%	30/30	2.77
(0.5, 0.2, 0.3)	301.11	3129.34	97.6%	30/30	2.89

When the demand satisfaction weight δ is dominant, the model gives priority to ensuring 100% demand satisfaction, but the total route is longer. Increasing the total transportation time weight α can shorten the route and optimize the objective function value, among which the combination (0.3, 0.2, 0.5) achieves the optimal balance among efficiency, service level, and resource utilization. Increasing the load balance weight γ can significantly reduce the average load deviation, and the insufficient vehicle utilization when δ is dominant is a reasonable adaptive performance of the algorithm to maintain service reliability.

Therefore, the proposed optimization framework exhibits notable robustness and interpretability, successfully capturing the inherent trade-offs among multiple objectives while maintaining stable solution performance.

4.2.2. Result Stability Analysis

To further validate the stability of the proposed ALNS-PPO hybrid optimization framework, we performed ten independent runs on selected instances from the Solomon and Homberger benchmark datasets. The resulting changes in the objective function values are shown in Figure 8 and Figure 9, respectively. The algorithm maintained relatively stable performance across multiple runs, with only minor fluctuations observed across different scenarios. This consistency demonstrates the robustness of the proposed framework under varying data distributions and constraint settings. Furthermore, the observed dispersion across runs serves as an implicit statistical validation of the algorithm’s reproducibility and generalization capabilities, providing supporting evidence for the reliability of the reported results.

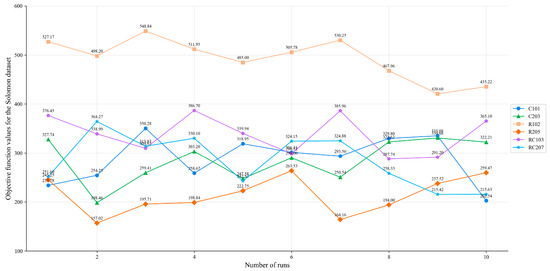
Figure 8. Objective function values for the Solomon dataset.

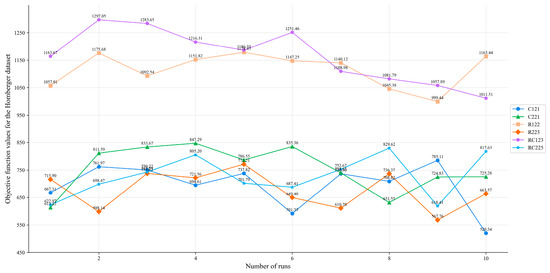
Figure 9. Objective function values for the Homberger dataset.

Furthermore, based on the stability verification, the algorithm’s performance was systematically evaluated across multiple independent runs. The mean, standard deviation, and coefficient of variation (CV) of the objective function were calculated for several representative examples. Given the randomness inherent in the algorithm’s initial solution generation and search path selection, analyzing fluctuations in the objective function value is crucial for evaluating the consistency of the algorithm’s performance. CV quantifies the relative variability of the results; smaller values indicate more stable algorithm performance.

As shown in Table 5, the ALNS-PPO algorithm demonstrates consistent performance in terms of the mean and standard deviation of the objective function across different problem instances. In the Solomon dataset, although the CV values for some small and medium-scale instances, such as R205 and RC207, are slightly higher, they remained within an acceptable range, reflecting the strong adaptability and stability of the algorithm across various problem structures. This is mainly related to the search characteristics of random heuristic algorithms in low-dimensional solution spaces. When the solution space is small and the number of feasible solutions is limited, random perturbations may cause the volatility of local search paths to be amplified, making the results deviate more from the mean. For large-scale and more complex instances from the Homberger dataset, the algorithm exhibits even more stable optimization results. For example, the CV values for RC225 and R223 are 10.38% and 11.44%, respectively, indicating a noticeably reduced fluctuation range. These results suggest that, in higher-dimensional search spaces and under more complex constraints, the deep reinforcement learning mechanism, combined with the global search strategy, effectively guides the search process and mitigates the risk of being trapped in local optima.

Table 5. Indicators for evaluating the stability of the objective function.

Dataset	Pr	Mean Objective Function Value	Standard Deviation	Coefficient of Variation
Solomon	R205	217.23	42.16	19.41%
Solomon	RC207	284.08	53.28	18.76%
Homberger	R223	672.23	76.89	11.44%
Homberger	RC225	727.68	74.56	10.38%

4.3. Algorithm Comparison

To evaluate the effectiveness and superiority of the proposed ALNS-PPO algorithm in solving the multi-depot, multi-constraint emergency logistics VRP, a series of systematic comparative experiments were conducted. The comparison algorithms included the traditional Adaptive Large Neighborhood Search (ALNS) and a representative heuristic method—the Improved Ant Colony Algorithm (IACA)—to comprehensively assess differences in solution quality and computational efficiency [26]. The experiments were performed on the standard Solomon and Homberger datasets, which encompass instances of varying scales, thereby thoroughly testing the algorithm’s adaptability and stability under multiple constraints and ensuring the generality and objectivity of the evaluation results.

Table 6 presents a comparison of the experimental results obtained using each algorithm under identical environmental and constraint settings across multiple independent runs. Taking the R205 and RC207 instances as examples, the objective function values of ALNS-PPO were reduced by 39.9% and 31.2%, respectively, compared with those of the traditional ALNS, and also show significant improvements over the IACA. These results demonstrate that the dynamic strategy adjustment enabled by the PPO effectively overcomes the local optimum limitations of the ALNS. Although ALNS-PPO uses slightly more vehicles than IACA in the C101 instance, it achieved a substantial reduction in the total route length through more refined route planning. This intelligent trade-off between resource utilization and route optimization highlights the decision-making advantages of deep reinforcement learning in multi-constraint optimization.

Table 6. Experimental comparison results on Solomon and Homberger datasets.

Dataset	Pr	Algorithm	Objective Function Value	Total Travel Distance	Number of Vehicles	Demand Satisfaction
Solomon	C101	ALNS	382.38	3161.95	29	100%
	C101	ALNS-PPO	287.52	3090.61	30	100%
	C101	IACA	369.49	3592.74	28	100%
	R205	ALNS	303.04	1835.38	24	100%
	R205	ALNS-PPO	181.95	1794.39	25	100%
	R205	IACA	293.07	2265.50	21	100%
	RC207	ALNS	372.76	2680.47	21	100%
	RC207	ALNS-PPO	256.35	2262.50	22	100%
	RC207	IACA	360.16	2926.34	22	100%
Homberger	C221	ALNS	1106.46	9058.61	44	93.5%
	C221	ALNS-PPO	820.67	9060.28	49	100%
	C221	IACA	1114.15	9144.43	46	92.6%
	R224	ALNS	997.39	6828.70	42	90.3%
	R224	ALNS-PPO	663.05	6490.95	38	100%
	R224	IACA	1025.53	6892.78	40	91.4%
	RC225	ALNS	948.06	7176.41	44	89.8%
	RC225	ALNS-PPO	665.81	6224.21	42	100%
	RC225	IACA	988.19	6892.08	45	90.7%

Although the proposed ALNS-PPO algorithm may occasionally increase the number of vehicles compared with traditional heuristic methods (e.g., in instances C101 and C221), this adjustment reflects a deliberate trade-off between delivery timeliness and vehicle utilization. In emergency material transportation, the operational objective is to prioritize the rapid and complete delivery of relief supplies to the affected areas. Increasing the number of vehicles significantly shortens delivery distances and ensures that all demands are fully met within strict service time windows. This behavior is operationally feasible in real disaster response scenarios, where vehicle deployment costs are often secondary to rescue efficiency and timeliness. Therefore, in some cases, an enlarged fleet size indicates a more realistic and effective allocation strategy rather than optimization inefficiency.

The experimental results further indicate that the proposed ALNS-PPO algorithm exhibits significant advantages in large-scale and highly complex instances of the Homberger dataset (e.g., RC225 and R224), achieving lower objective function values and a 100% demand satisfaction rate. This suggests that, in multi-constraint scenarios characterized by large task sizes and dispersed demand distributions, the integration of deep reinforcement learning strategies enables the algorithm to demonstrate a stronger global search capability and adaptability. In contrast, traditional algorithms such as ALNS and IACA perform reasonably well in small-scale and structurally regular instances of the Solomon dataset (e.g., C101 and C203) but are prone to local optima when addressing large-scale, multi-constraint problems, exhibiting weaker stability and generalization ability.

Therefore, the ALNS-PPO algorithm is better suited for large-scale emergency scheduling problems characterized by high complexity and stringent constraints, whereas traditional algorithms remain effective for medium- and small-scale problems with relatively regular structures.

To comprehensively evaluate the efficiency-quality trade-off of the proposed ALNS-PPO algorithm, it is crucial to address the key requirement of emergency logistics—rapidly generating feasible solutions during the golden post-disaster rescue period is crucial. However, a single metric cannot address both metrics. Therefore, this study introduced the “Unit-Time Improvement Rate (UTIR)” metric. The UTIR metric measures the improvement in the objective function value achieved by a given algorithm relative to the ALNS per unit computational time, and is defined as:

$$UTIR={\displaystyle \frac{Z_{ALNS}-Z}{T_{ALNS}+T}}\times 100\%$$

(10)

Here, Z denotes the objective function value and T represents the computational time. The ALNS algorithm serves as the baseline for evaluation. A larger UTIR value indicated a more significant performance improvement per unit time. Furthermore, since both the numerator and denominator are expressed as dimensionless percentages, UTIR is a dimensionless metric. As the denominator approaches zero, UTIR exhibits large positive values, representing an “efficient trade-off”—a significant improvement in quality at a minimal cost in time.

As shown in Table 7, the proposed ALNS-PPO algorithm is further validated in terms of its overall performance in balancing solution quality and computational efficiency. Across multiple instances, ALNS-PPO exhibits relatively high UTIR values, mostly ranging from 24% to 31%, indicating a favorable balance between optimization effectiveness and efficiency. For example, in instance C221, the UTIR of ALNS-PPO reaches 31.53%, demonstrating that the algorithm maintains strong optimization capability per unit time even in large-scale problems. In contrast, although the IACA achieves shorter computational times in some instances, its optimization performance is generally insufficient, resulting in lower UTIR values and even negative values in C221, R224, and RC225. This indicates that IACA is less efficient than ALNS-PPO in terms of performance per unit time. Overall, ALNS-PPO achieves more stable performance in both solution quality and efficiency, making it well-suited for highly complex multi-constraint routing optimization scenarios.

Table 7. UTIR metrics vs. calculation time.

Pr	ALNS	ALNS-PPO		IACA
	Time	Time	UTIR%	Time	UTIR%
C101	158.92	204.20	26.12%	182.83	3.77%
R205	209.33	255.43	26.05%	254.37	2.15%
RC207	184.53	262.99	26.01%	233.91	3.01%
C221	464.18	441.82	31.53%	476.40	−0.82%
R224	574.31	549.09	29.75%	585.97	−2.42%
RC225	615.74	553.02	24.14%	607.69	−3.28%

In addition to its numerical advantages, the proposed framework also has potential implications for real-world emergency logistics. However, the current model assumes static demand information and simplified road accessibility, which may limit its direct deployment in highly dynamic disaster environments. Future extensions could integrate dynamic updates to further enhance its applicability in real-world emergency scenarios.

Furthermore, compared to existing research such as reinforcement learning and heuristic algorithms, the proposed method demonstrates stronger solution stability and adaptability under multiple constraints, validating its effectiveness and scalability in complex path planning environments.

5. Conclusions

This study addressed the emergency material distribution path optimization problem under multiple constraints. A multi-constraint optimization model was developed by considering vehicle capacity, service time windows, distribution balance, and number of vehicles. The Adaptive Large Neighborhood Search (ALNS) algorithm was integrated with Proximal Policy Optimization (PPO) to enhance global exploration and adaptive decision-making capabilities. The experiments were performed on several representative instances from the Solomon and Homberger benchmark datasets. The results indicate that, compared with traditional heuristic methods, the proposed ALNS-PPO algorithm effectively reduces the total delivery distance and improves demand satisfaction. It also demonstrates strong stability and robustness in complex emergency logistics scenarios.

The findings provide valuable decision support for emergency logistics managers under time-critical conditions. The proposed method can assist in planning rapid-response operations, optimizing the balance between supply coverage and transportation efficiency, and reducing delivery delays. Furthermore, the hybrid framework offers scalability and practical potential for large-scale disaster response networks.

Despite these promising results, this study has several limitations. The current model assumes fixed demand quantities and single-trip vehicle routes, which may simplify the real-world logistics dynamics. In addition, iterative learning and repair mechanisms increased the computational cost as the problem size increased. Future work will consider dynamic or uncertain demand, multi-trip routing, and the integration of real-time traffic and terrain data. These improvements are expected to enhance the adaptability and practical applicability of the proposed method for large-scale and highly uncertain emergency response scenarios.