Abstract
In order to achieve the automated qualitative evaluation of Ephestia kuehniella eggs in mass industrialization and production, YOLOv10-CR is presented, with a modified circular representation based on YOLOv10. While existing methods like CircleNet struggle with overlapping objects, YOLOv10, though highly effective in general object detection, is not optimized for spherical objects. To address these limitations, we integrate YOLOv10’s efficient architecture with CircleNet’s circular representation, introducing a modified circle representation (xyy format) and an improved circle intersection over union (cIOU) algorithm. The proposed xyy circle representation reduces degrees of freedom by encoding circles through top and bottom boundary points, effectively disentangling overlapping eggs caused by adhesive mucus. The improved cIOU algorithm avoids singularity issues in nested or tangent circles, enhancing robustness under rotational variations. Experimental results demonstrate that the proposed YOLOv10-CR achieves better detection accuracy, computational efficiency, and rotation robustness with lower computational costs for the detection of Ephestia kuehniella eggs.
1. Introduction
Ephestia kuehniella is a critical species in biocontrol systems. Its eggs, with an average diameter of 0.5–0.7 mm and a spherical morphology covered by a thin adhesive layer, are widely used as factitious hosts for rearing predatory mites (Phytoseiidae) [1]. With the expansion of biocontrol technology, the mass industrialization and production of the eggs has expanded. In the current mass industrialization and production, automated qualitative evaluation is one of the key techniques. Moreover, precisely detecting the eggs is critical for automated qualitative evaluation. However, the adhesive property of the eggs often leads to overlapping clusters, posing significant challenges for automated detection and evaluation in industrial production. For ball-shaped object detection, CircleNet is an anchor-free detection method, which is optimized for glomeruli and nuclei detection, offering superior performance and rotation consistency [2,3]. CircleNet relies on center-radius representations, which struggle with overlapping objects due to ambiguous center predictions in dense clusters [4]. Quantitative analysis on the egg datasets shows that CircleNet achieves only 0.78 mAP50-95 under 50% overlap ratio, primarily due to its sensitivity to anchor point misalignment. Meanwhile, YOLOv10, a new real-time end-to-end object detector, achieves the state-of-the-art performance and efficiency across various model scales [5], but is not optimized for ball-shaped objects. Focusing on the detection of the eggs, a YOLOv10 based circular object detection model termed YOLOv10-CR is introduced in this paper, inspired by YOLOv10 and CircleNet [6,7]. Briefly, the contributions of this study are in two areas:
- Optimized Ephestia kuehniella egg object detection: The proposed YOLOv10-CR integrates the efficient and effective model architecture of YOLOv10 and a simple circle representation with less degree of freedom (DoF). It is a NMS-free and optimized approach for the detection of overlapping ball-shaped objects.
- Modified circle representation: We propose a modified circle representation applied to the architecture of YOLOv10 with superior detection performance for ball-shaped objects. We also introduce an improved circle intersection over union (cIOU) algorithm with enhanced generality and efficiency.
2. Architecture and Algorithm Improvement
2.1. Architecture
Inspired by the CircleNet and YOLOv10, a modified architecture is proposed for Ephestia kuehniella egg detection. As shown in Figure 1, compared with the YOLOv10-N architecture [5], the feature extraction network is retained, but the head is replaced by a prediction head with modified circle representation to generate circular object results. The full diagram is shown in [5]. Different from the circle representation proposed in [5], a new circle representation termed the xyy format is proposed.
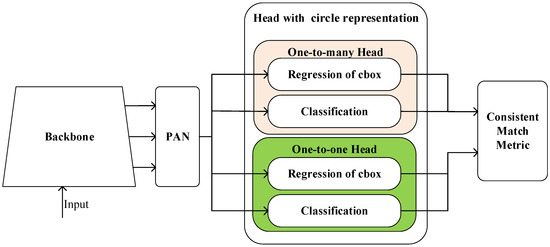
Figure 1.
The architecture of YOLOv10-CR.
As shown in Figure 2, a circle box can be represented by the top point and bottom point, which are defined as and , respectively. Then, the offset between the anchor point (For a detailed explanation, please refer to [5]) and top point is defined as the following:
where denotes the center point of the circle box. Note that .
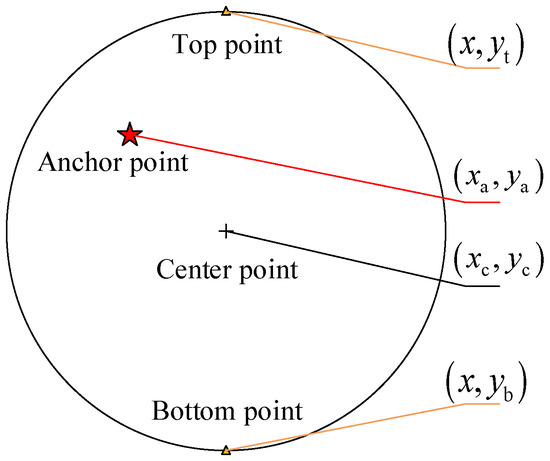
Figure 2.
Circle representation (xyy format).
Analogously, the offset between the anchor point and bottom point in y axis is defined as the following:
2.2. Circle IOU with Improved Algorithm
Referring to [3], the circle intersection over union (cIOU) is defined as the following:
Let the circle of ground truth and prediction be represented as A and B, respectively, and be defined as and in center coordinates, simultaneously define the radius as and . Then, the can be calculated for three different scenarios.
Case 1 , when the circles are separate, thus
Case 2 If , when one circle contains the other one, we have
Case 3 , when two circles intersect as shown in Figure 3, thus the distance between the center coordinates can be defined as the following:
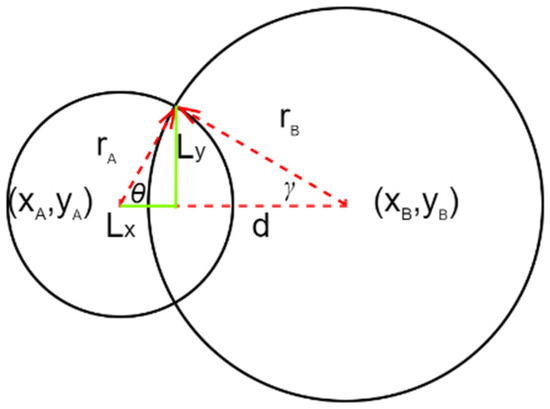
Figure 3.
The parameters used to calculate cIOU.
and can be derived by Cosine Law:
Hence, the area of intersection an area of union can be derived as
where is defined as
Compared with the algorithm in [3], the arccos function is adopted for calculating the central angle, instead of arcsin function. As illustrated in Figure 4, the arcsin function exhibits an inherent limitation in its output range of , which becomes problematic when calculating the central angle between two circles with significant radius discrepancies. Specifically, if the geometric relationship of the intersecting circles results in a central angle exceeding this restricted domain, supplementary computational interventions are required to handle boundary cases. In contrast, the arccos function inherently spans , thereby comprehensively encompassing all potential intersection scenarios, including partial overlaps, containment, and tangential contact, without necessitating ad hoc conditional checks or post-calculation corrections.

Figure 4.
The special case where two circles intersect.
2.3. Circle Box Estimator and DFL for Modified Circle Representation
The circle box estimator is the key component of the head, which establishes the relationship between the features and the circle box. Since the prediction range of the distribution focal loss (DFL) is defined between 0 and the maximum deviation [8,9], the x-axis deviation range in our proposed method does not align with DFL’s computational constraints. To address this, a linear transformation is applied to normalize the deviations in the xyy circular representation, ensuring compatibility with DFL’s operational range. By (1)–(3) and Figure 2, it can be derived that the offsets from the circle box to the location of the anchor point (,,) satisfy the criteria as
where is the upper bound of the offsets. Note that the offset has a different range from others, and it is unlike the situation in standard YOLOv10 [5], which cannot apply the regression operation method simply and directly.
In order to solve the offsets through Equations (14)–(16) efficiently, the geometric features will be utilized. Inspired by [6], we let , therefore
Consequently, we adopt the relative offsets (,,) as the regression targets, referring to [5,6]. Meanwhile, a group of xyy format bounding box regressions with the same structure is constructed, given the discrete label set as with the discrete distribution property , where denotes the distribution of label [7,10]. From the regression model, the general distribution will be learned. Then, through a softmax layer, the discrete distribution can be implemented easily. Consequently, the estimated regression value of the offsets can be presented as the following:
which delivers the statistics of the learned discrete distribution into a conventional operation.
At inference time, the estimated values can be recovered as follows:
where , , , respectively, are the estimated offsets of , , via Formula (18), and , , are the estimated values of , , .
Following [5,10], the DFL is adopted to improve the learning efficiency of the xyy format bounding box regression.
Finally, the overall training objective is
where , , are the box loss gain, class loss gain, and DFL loss gain, respectively, is the box loss, is the binary cross-entropy (BCE) classification loss of the prediction, and is the distribution focal loss [9].
3. Experimental Design
3.1. Experimental Details
The experiments are conducted on the same machine with an Intel® Core™ i7-8700 CPU, a GeForce GTX 1650 4G GPU, Windows 10, Pytorch 2.0.0, and CUDA 11.7.
Due to the limited availability of Ephestia kuehniella egg images, we applied a data augmentation strategy incorporating random combinations of translation, scaling, flipping, and rotation to expand the dataset. This process yielded a final dataset comprising 416 images with a resolution of 640 × 640 pixels, which was utilized to train the model and evaluate its detection performance. The YOLOv10-N is used as the baseline model, and the same training hyperparameters are adopted during the training of all the models. No pre-trained weights were used during training. The training process was set to 120 epochs, with a batch size of 16. The main hyperparameters are presented in Table 1.

Table 1.
Hyperparameters.
3.2. Evaluation Metrics
Following [10], precision (P), recall (R), mAP50, and mAP50-95 are employed to evaluate the detection performance. Additionally, the GFLOPs and the total number of parameters are employed to measure the computational complexity and model size. According to [5], cIOU behaves nearly the same as IOU, which ensures a fair comparison between YOLOv10 and the proposed method.
4. Results
4.1. Detection Experiments
As shown in Figure 5, the training and validation losses (box loss, classification loss, and DFL loss) converge stably, indicating the model’s robustness. The one-to-many (om) and one-to-one (oo) strategies exhibit distinct convergence patterns due to their optimization objectives.
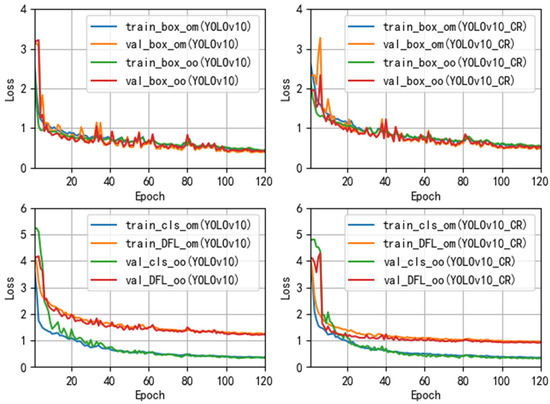
Figure 5.
The results of training and validation.
According to the results of detection accuracy presented in Table 2 and the computational complexity comparison in Table 3, it can be observed that when our model design is compared with the original model, it achieves 2.3% precision improvement, 4.0% recall improvement, 1.2% mAP50 improvement, and 9.9% mAP50-95 improvement, with a considerable training time reduction of 14.9%, 8.9% fewer parameters (0.23 M), 12.2% less FLOPs, and 8.8% less computational latency (1.3 ms averagely). Compared to the specialized spherical object detector CircleNet, our model demonstrates significant advantages in computational complexity while achieving higher precision and recall rates of 2.2% and 3.6%, respectively. CircleNet exhibits suboptimal performance when detecting overlapping targets, whereas our model outperforms it with 5.3% and 9.6% improvements in mAP50 and mAP50-95. It demonstrates that the proposed YOLOv10-CR obtains detection performance, latency improvements, and a lower computational cost.

Table 2.
Comparison of detection accuracy.

Table 3.
Comparison of computational complexity.
4.2. Rotation Robustness Experiments
The rotation robustness of the proposed YOLOv10-CR is evaluated by rotating the original test images. The original test images are rotated in two ways.
In the first experiments, the original test images were rotated by 90, 180, and 270 degrees anti-clockwise, respectively. This avoids the impact of intensity interpolation [3]. As shown in Figure 6a, the detection result of YOLOv10-CR is shown in the left panel (cIOU > 0.5), while the detection result of YOLOv10 is displayed in the right panel (IOU > 0.5). Evidently, they can detect the eggs in the original image correctly. Similarly, in Figure 6b (rotated by 90 degrees) and Figure 6d (rotated by 270 degrees), it can be observed that they have the same detection performance. As presented in Figure 6c, YOLOv10-CR detects the eggs correctly from the image rotated by 180 degrees as before, but YOLOv10 fails to detect two of the eggs.
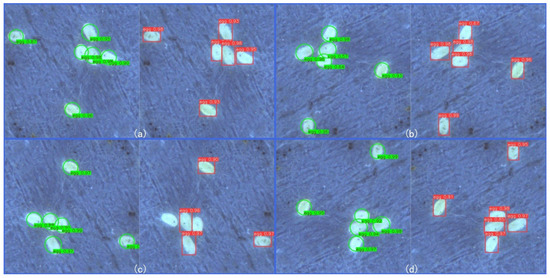
Figure 6.
Non-arbitrary rotation robustness comparison.
In the second experiments, the original test images were rotated by an arbitrary angle. Several results are demonstrated in Figure 7. As demonstrated in Figure 7a,c,d, they maintain the detection precision. While the proposed YOLOv10-CR has better detection precision than YOLOv10 in Figure 7b,e–g, from Figure 7b,g,h, despite the improvements offered by YOLOv10-CR, the detection of partially occluded objects remains a challenge for both the proposed and baseline model.

Figure 7.
Rotation robustness comparison.
Table 4 demonstrates the detection accuracy comparison of two experiments. It shows that the proposed YOLOv10-CR approach achieved better rotation robustness. The proposed method addresses a critical bottleneck in biocontrol production: efficient egg quantification under overlapping conditions. By improving detection accuracy, our approach directly enhances the scalability of predatory mite rearing systems, which rely on precise egg counts for population management.

Table 4.
Comparison of detection accuracy in the rotation robustness experiments.
5. Conclusions
In this paper, YOLOv10-CR is proposed, targeting Ephestia kuehniella egg detection. For target object detection, a modified detection head with xyy format circle representation and an improved cIOU algorithm are proposed, simplifying and optimizing egg detection. A modified circle box estimator and DFL are also designed. The proposed YOLOv10-CR not only advances object detection for spherical biological targets, but also provides a scalable solution for industrial biocontrol. By reducing computational latency by 8.8% (1.3 ms) and improving rotation robustness, this method significantly supports sustainable agricultural practices through automated pest management.
Author Contributions
Methodology and experiment, D.H., C.S.; Writing—original draft, D.H.; Writing—review & editing, C.S.; Supervision, Y.M., L.L., J.C. and Y.C.; Project administration, D.H., Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The research in this paper was funded by the Fujian University Industry–University Cooperation Science and Technology and Program (2022N5020) and the Fujian Provincial Natural Science Foundation (2022H6005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting this study are not publicly available to protect the privacy of the individuals involved. The corresponding author can provide the data upon reasonable request.
Conflicts of Interest
Author Yanxuan Zhang was employed by the company Fujian Yanxuan Biological Control Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Liu, J.F.; Zhang, Z.Q. Development, survival and reproduction of a New Zealand strain of Amblydromalus limonicus (Acari: Phytoseiidae) on Typha orientalis pollen, Ephestia kuehniella eggs, and an artificial diet. Int. J. Acarol. 2017, 43, 153–159. [Google Scholar] [CrossRef]
- Yang, H.; Deng, R.; Lu, Y.; Zhu, Z.; Chen, Y.; Roland, J.T.; Lu, L.; Landman, B.A.; Fogo, A.B.; Huo, Y. CircleNet: Anchor-free glomerulus detection with circle representation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Lima, Peru, 4–8 October 2020; Springer: New York, NY, USA, 2020; pp. 35–44. [Google Scholar]
- Nguyen, E.H.; Yang, H.; Deng, R.; Lu, Y.; Zhu, Z.; Roland, J.T.; Lu, L.; Landman, B.A.; Fogo, A.B.; Huo, Y.; et al. Circle Representation for Medical Object Detection. IEEE Trans. Med. Imaging 2022, 41, 746–754. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liang, P.; Sun, Z.; Song, B.; Cheng, E. CircleFormer: Circular Nuclei Detection in Whole Slide Images with Circle Queries and Attention. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, BC, Canada, 8–12 October 2023; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J.; Ding, G. Yolov10: Real-time end-to-end object detection. arXiv 2024, arXiv:2405.14458. [Google Scholar]
- Zhang, R.; Xu, L.; Yu, Z.; Shi, Y.; Mu, C.; Xu, M. Deep-IRTarget: An Automatic Target Detector in Infrared Imagery Using Dual-Domain Feature Extraction and Allocation. IEEE Trans. Multimed. 2022, 24, 1735–1749. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, B.; Xu, L.; Huang, Y.; Xu, X.; Zhang, Q.; Jiang, Z.; Liuy, Y. A Benchmark and Frequency Compression Method for Infrared Few-Shot Object Detection. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5001711. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection. arXiv 2020, arXiv:2006.04388. [Google Scholar] [CrossRef]
- Li, X.; Lv, C.; Wang, W.; Li, G.; Yang, L.; Yang, J. Generalized Focal Loss: Towards Efficient Representation Learning for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 3139–3153. [Google Scholar] [CrossRef] [PubMed]
- Glenn, J. Yolov8. Available online: https://github.com/ultralytics/ultralytics/tree/main (accessed on 20 February 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).