Room Temperature Fabry–Pérot Modes Microcavity Exciton–Polariton in CdS/CdS:SnS2 Superlattice Microwires
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of the CdS/CdS:SnS2 Superlattice Microwires
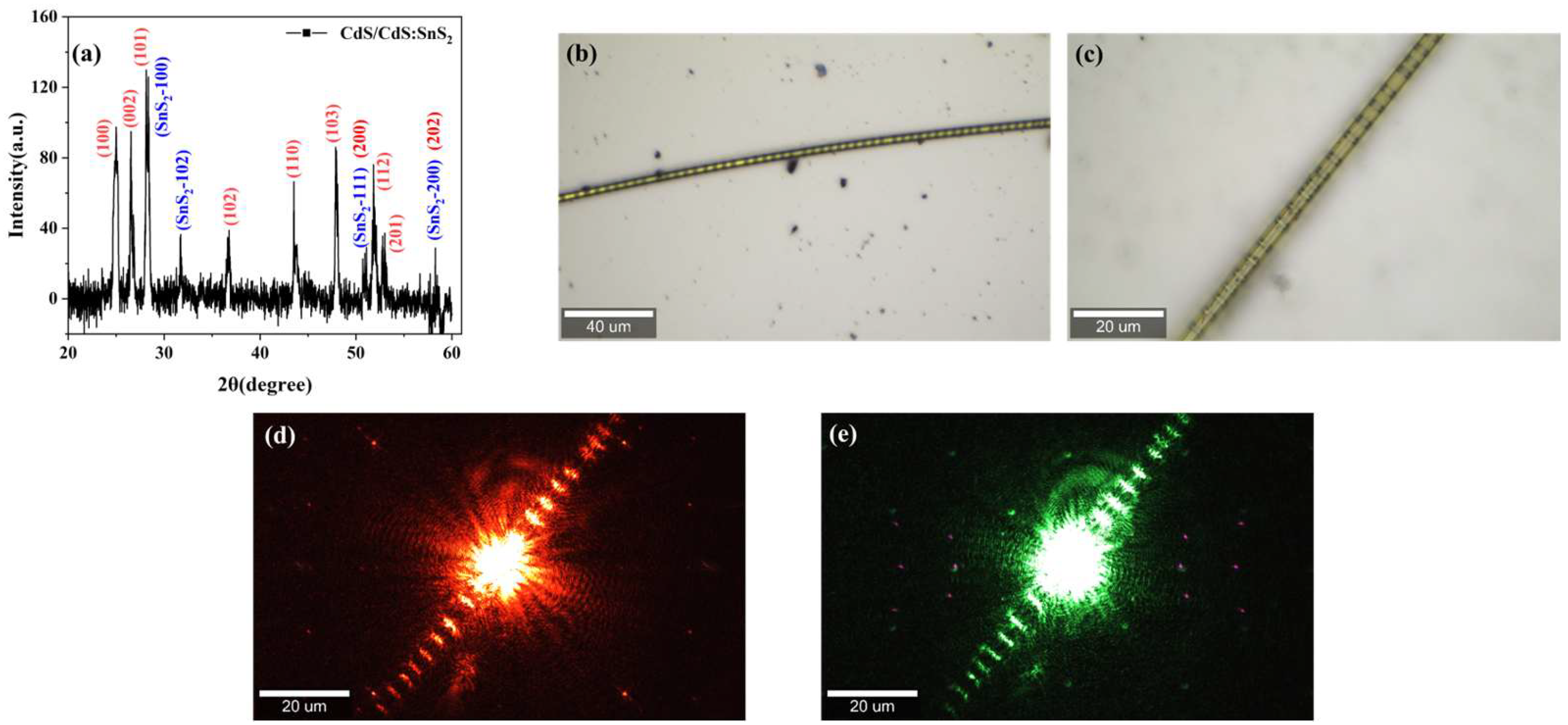
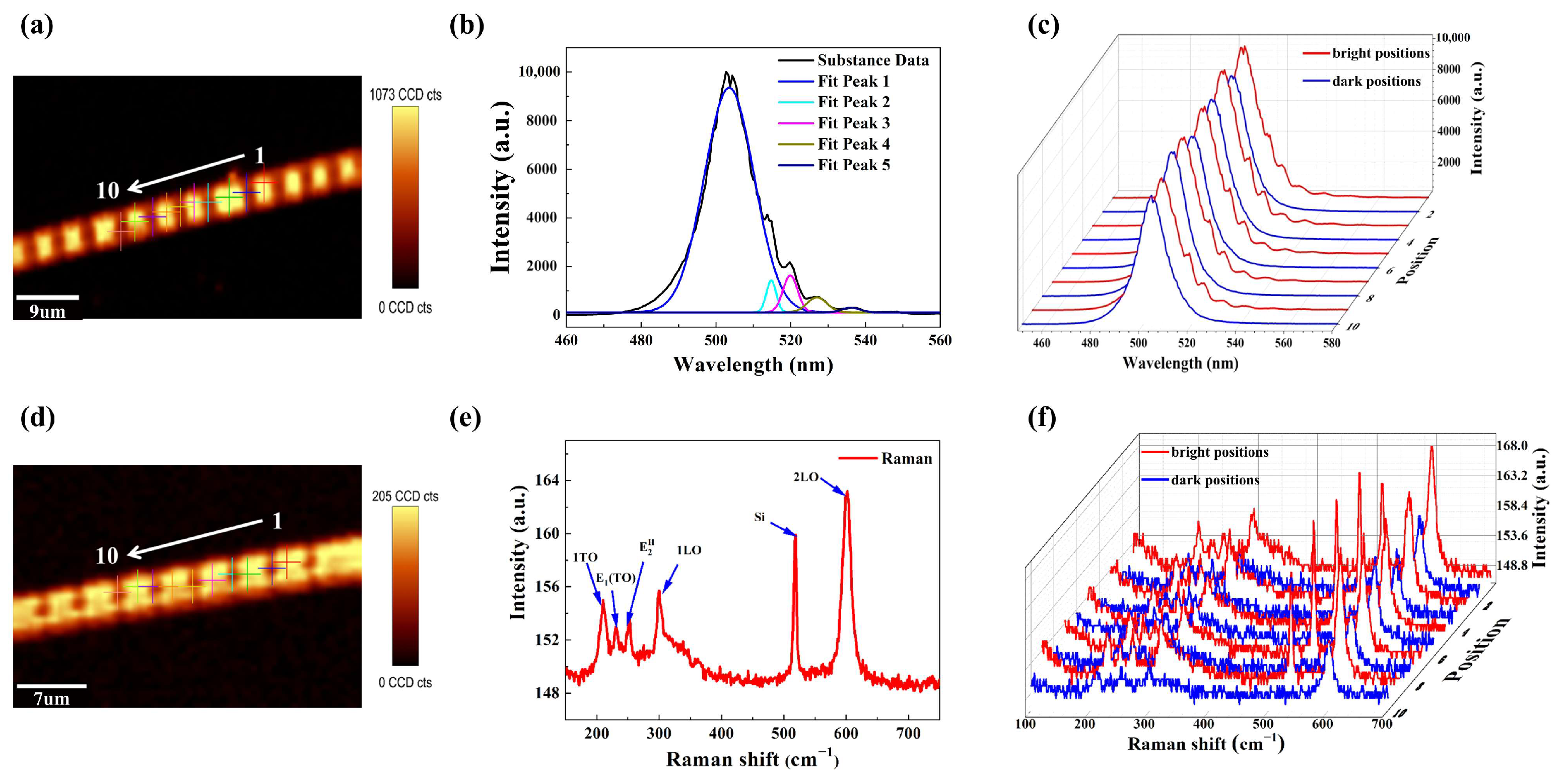
2.2. Characterization
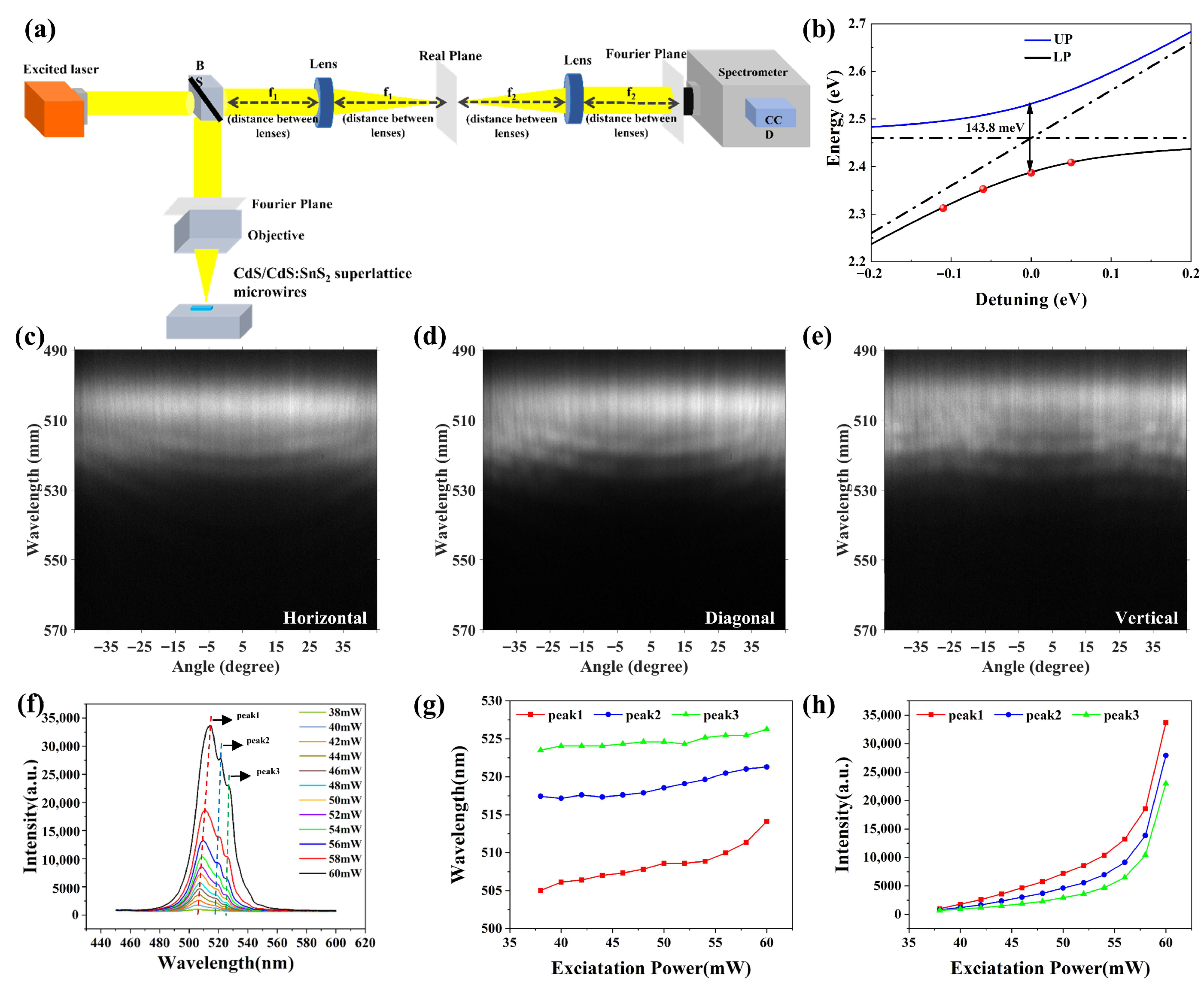
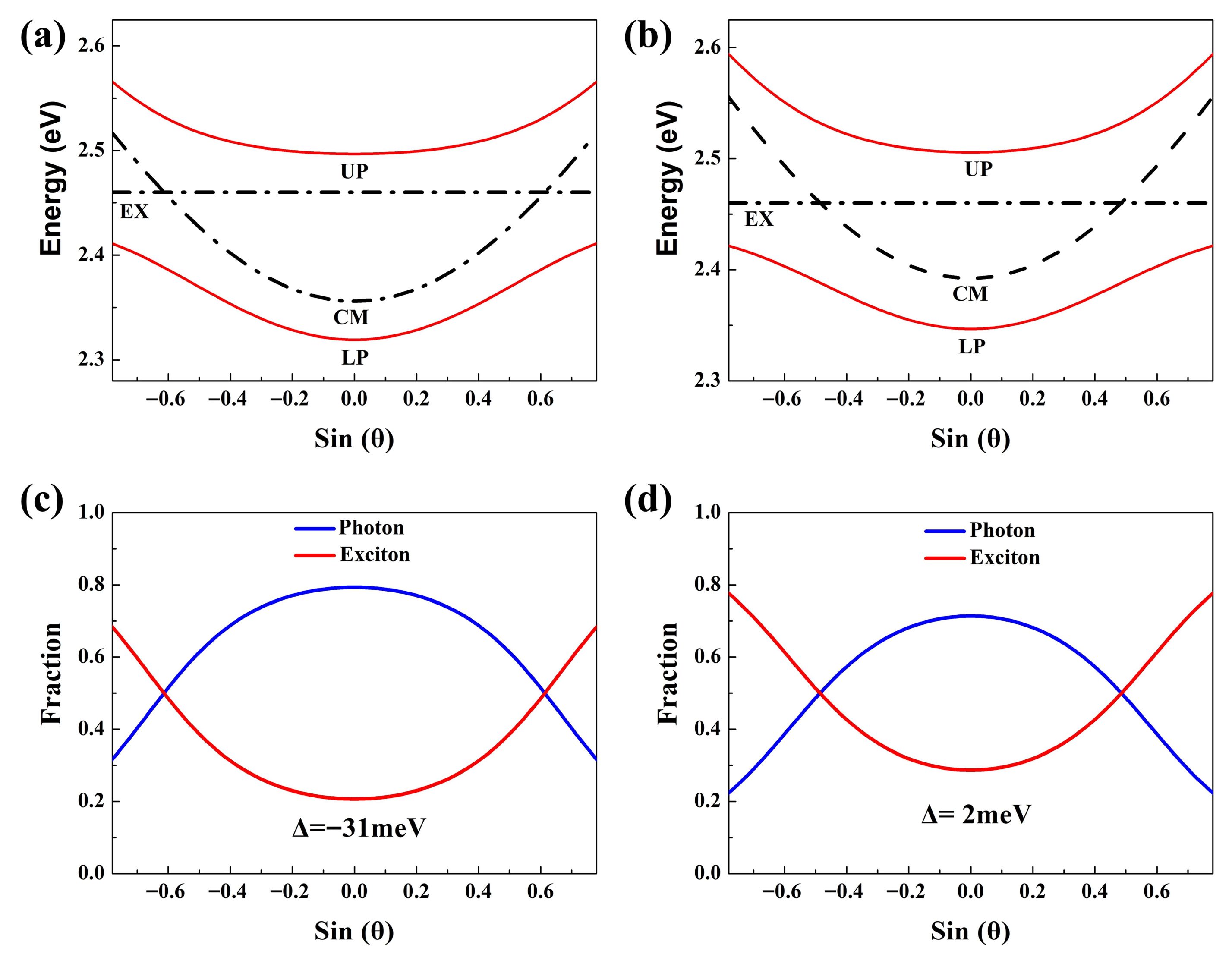
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, H.; Haug, H.; Yamamoto, Y. Exciton-polariton Bose-Einstein condensation. Rev. Mod. Phys. 2010, 82, 1489–1537. [Google Scholar] [CrossRef]
- Wang, T.; Zang, Z.; Gao, Y.; Lyu, C.; Gu, P.; Yao, Y.; Peng, K.; Watanabe, K.; Taniguchi, T.; Liu, X.; et al. Electrically Pumped Polarized Exciton-Polaritons in a Halide Perovskite Microcavity. Nano Lett. 2022, 22, 5175–5181. [Google Scholar] [CrossRef]
- Tumkur, T.; Zhu, G.; Noginov, M. Strong coupling of surface plasmon polaritons and ensembles of dye molecules. Opt. Express 2016, 24, 3921–3928. [Google Scholar] [CrossRef]
- Berghuis, A.M.; Castellanos, G.W.; Murai, S.; Pura, J.L.; Abujetas, D.R.; van Heijst, E.; Ramezani, M.; Sanchez-Gil, J.A.; Rivas, J.G. Room Temperature Exciton-Polariton Condensation in Silicon Metasurfaces Emerging from Bound States in the Continuum. Nano Lett. 2023, 23, 5603–5609. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, P.; Xiao, B.; Das, A.; Bhowmick, S.; Heo, J. Solid State Electrically Injected Exciton-Polariton Laser. Phys. Rev. Lett. 2013, 110, 206403. [Google Scholar] [CrossRef] [PubMed]
- Byrnes, T.; Kim, N.Y.; Yamamoto, Y. Exciton-polariton condensates. Nat. Phys. 2014, 10, 803–813. [Google Scholar] [CrossRef]
- Hoffmann, D.K.; Singh, V.P.; Paintner, T.; Jaeger, M.; Limmer, W.; Mathey, L.; Hecker Denschlag, J. Second sound in the crossover from the Bose-Einstein condensate to the Bardeen-Cooper-Schrieffer superfluid. Nat. Commun. 2021, 12, 7074. [Google Scholar] [CrossRef]
- Huang, Y.; Su, R.; Wang, Y.; Zhu, C.; Feng, J.; Zhao, J.; Liu, Z.; Xiong, Q. A Fano Cavity-Photon Interface for Directional Suppression of Spectral Diffusion of a Single Perovskite Nanoplatelet. Nano Lett. 2022, 22, 8274–8280. [Google Scholar] [CrossRef]
- Larionova, Y.; Stolz, W.; Weiss, C.O. Optical bistability and spatial resonator solitons based on exciton-polariton nonlinearity. Opt. Lett. 2008, 33, 321–323. [Google Scholar] [CrossRef]
- Schweiner, F.; Ertl, J.; Main, J.; Wunner, G.; Uihlein, C. Exciton-polaritons in cuprous oxide: Theory and comparison with experiment. Phys. Rev. B 2017, 96, 245202. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, S.; Song, J.; Deng, X.; Du, W.; Zeng, X.; Zhang, Y.; Zhang, Z.; Chen, Y.; Wang, Y.; et al. Exciton polariton condensation from bound states in the continuum at room temperature. Nat. Commun. 2024, 15, 3345. [Google Scholar] [CrossRef]
- Su, R.; Wang, J.; Zhao, J.; Xing, J.; Zhao, W.; Diederichs, C.; Liew, T.C.H.; Xiong, Q. Room temperature long-range coherent exciton polariton condensate flow in lead halide perovskites. Sci. Adv. 2018, 4, eaau0244. [Google Scholar] [CrossRef]
- Shang, Q.; Li, C.; Zhang, S.; Liang, Y.; Liu, Z.; Liu, X.; Zhang, Q. Enhanced optical absorption and slowed light of reduced-dimensional CsPbBr3 nanowire crystal by exciton–polariton. Nano Lett. 2020, 20, 1023–1032. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Zhang, S.; Zhang, Q.; Liu, X. Recent progress of strong exciton–photon coupling in lead halide perovskites. Adv. Mater. 2019, 31, 1804894. [Google Scholar] [CrossRef] [PubMed]
- Zaremba, M.; Kedziora, M.; Stanco, L.; Piskorski, K.; Kosiel, K.; Szerling, A.; Mazur, R.; Piecek, W.; Opala, A.; Sigurdsson, H.; et al. Optically Trapped Exciton-Polariton Condensates in a Perovskite Microcavity. Adv. Opt. Mater. 2025, 13, 2500304. [Google Scholar] [CrossRef]
- Kedziora, M.; Opala, A.; Mastria, R.; De Marco, L.; Krol, M.; Lempicka-Mirek, K.; Tyszka, K.; Ekielski, M.; Guziewicz, M.; Bogdanowicz, K.; et al. Predesigned perovskite crystal waveguides for room-temperature exciton-polariton condensation and edge lasing. Nat. Mater. 2024, 23, 1515–1522. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Shi, Y.; Ghosh, S.; Liu, H.; Xu, H.; Xiong, Q. Ultrafast neuromorphic computing driven by polariton nonlinearities. Elight 2025, 5, 9. [Google Scholar] [CrossRef]
- Sun, L.; Ren, M.-L.; Liu, W.; Agarwal, R. Resolving Parity and Order of Fabry-Perot Modes in Semiconductor Nanostructure Waveguides and Lasers: Young’s Interference Experiment Revisited. Nano Lett. 2014, 14, 6564–6571. [Google Scholar] [CrossRef]
- Tian, Y.; Yao, S.; Zou, B. Excitation-Power-Dependent Color Tuning in a Single Sn-Doped CdS Nanowire. Molecules 2024, 29, 5389. [Google Scholar] [CrossRef]
- Mi, Y.; Jin, B.; Zhao, L.; Chen, J.; Zhang, S.; Shi, J.; Zhong, Y.; Du, W.; Zhang, J.; Zhang, Q. High-quality hexagonal nonlayered CdS nanoplatelets for low-threshold whispering-gallery-mode lasing. Small 2019, 15, 1901364. [Google Scholar] [CrossRef]
- Wen, X.; Lu, Z.; Wang, G.-C.; Washington, M.A.; Lu, T.-M. Efficient and stable flexible Sb2Se3 thin film solar cells enabled by an epitaxial CdS buffer layer. Nano Energy 2021, 85, 106019. [Google Scholar] [CrossRef]
- Kennerud, K.L. Analysis of performance degradation in CdS solar cells. IEEE Trans. Aerosp. Electron. Syst. 2007, AES-5, 912–917. [Google Scholar] [CrossRef]
- Nizamoglu, S.; Mutlugun, E.; Akyuz, O.; Perkgoz, N.K.; Demir, H.V.; Liebscher, L.; Sapra, S.; Gaponik, N.; Eychmüller, A. White emitting CdS quantum dot nanoluminophores hybridized on near-ultraviolet LEDs for high-quality white light generation and tuning. New J. Phys. 2008, 10, 023026. [Google Scholar] [CrossRef]
- Van Vugt, L.K.; Piccione, B.; Cho, C.-H.; Nukala, P.; Agarwal, R. One-dimensional polaritons with size-tunable and enhanced coupling strengths in semiconductor nanowires. Proc. Natl. Acad. Sci. USA 2011, 108, 10050–10055. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Zhang, J.; Xiong, Q. Surface Depletion Induced Quantum Confinement in CdS Nanobelts. Acs Nano 2012, 6, 5283–5290. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Zhou, W.; Peng, Y.; Yin, Y.; Zhong, M.; Zhao, Z.; Zhang, Q.; Tang, D.; Zeng, R.; Zou, B. Surface polarons and optical micro-cavity modulated broad range multi-mode emission of Te-doped CdS nanowires. Nanotechnology 2018, 29, 465709. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Zhang, D.; Ge, C.; He, M.; Zeng, Z.; Wang, Y.; Liu, S.; Wang, X.; Pan, A. Enhancing circular polarization of photoluminescence of two-dimensional Ruddlesden-Popper perovskites by constructing van der Waals heterostructures. Appl. Phys. Lett. 2021, 119, 151101. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Y.; Xu, Z.; Li, L.; Zhang, D.; Zheng, W.; Liang, D.; Zheng, B.; Liu, H.; Sun, X.; et al. Magnetic Doping Induced Strong Circularly Polarized Light Emission and Detection in 2D Layered Halide Perovskite. Adv. Opt. Mater. 2022, 10. [Google Scholar] [CrossRef]
- Rashba, E.; Gurgenishvili, G. Edge absorption theory in semiconductors. Sov. Phys. Solid State 1962, 4, 759. [Google Scholar]
- Zhang, M.; Wille, M.; Röder, R.; Heedt, S.; Huang, L.; Zhu, Z.; Geburt, S.; Grützmacher, D.; Schäpers, T.; Ronning, C. Amphoteric nature of Sn in CdS nanowires. Nano Lett. 2014, 14, 518–523. [Google Scholar] [CrossRef]
- Khurgin, J.B. Pliable polaritons: Wannier exciton-plasmon coupling in metal-semiconductor structures. Nanophotonics 2019, 8, 629–639. [Google Scholar] [CrossRef]
- Li, S.; Deng, F.; Huang, L.; Zhang, Y.; Zhou, L.; Lan, S. Greatly enhanced exciton-photon coupling in a WS2-Si3N4 nanohole array-Ag film heterostructure. Appl. Surf. Sci. 2025, 702, 163356. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Yao, S.; Cheng, L.; Wen, H.; Guo, H.; Tang, J.; Liu, J.; Liu, X.; Zou, B. Room temperature exciton polariton condensation in high-quality Sn-doped CdS microsheet. Nano Res. 2025, 18, 94907525. [Google Scholar] [CrossRef]
- Dai, G.; Zou, B.; Wang, Z. Preparation and periodic emission of superlattice CdS/CdS:SnS2 microwires. J. Am. Chem. Soc. 2010, 132, 12174–12175. [Google Scholar] [CrossRef]
- Liu, R.; Li, Z.-A.; Zhang, C.; Wang, X.; Kamran, M.A.; Farle, M.; Zou, B. Single-step synthesis of monolithic comb-like CdS nanostructures with tunable waveguide properties. Nano Lett. 2013, 13, 2997–3001. [Google Scholar] [CrossRef]
- Zou, S.; Zhou, W.; Liu, R.; Zou, B. Cavity-enhanced microphotoluminescence in a core–shell n–p CdS/CdO micrometer wire and Its efficient surface photovoltage responses in the whole visible range. J. Phys. Chem. C 2017, 121, 14349–14358. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Guo, Y.; Wang, Y.; Liu, R.; Chen, B.; Zhong, H.; Zou, B. Growth of CdS nanotubes and their strong optical microcavity effects. Nanoscale 2019, 11, 5325–5329. [Google Scholar] [CrossRef]
- Ma, W.; Lu, J.; Yang, Z.; Peng, D.; Li, F.; Peng, Y.; Chen, Q.; Sun, J.; Xi, J.; Pan, C. Crystal-orientation-related dynamic tuning of the lasing spectra of CdS nanobelts by piezoelectric polarization. ACS Nano 2019, 13, 5049–5057. [Google Scholar] [CrossRef]
- Xu, J.; Zhuang, X.; Guo, P.; Zhang, Q.; Ma, L.; Wang, X.; Zhu, X.; Pan, A. Dilute tin-doped CdS nanowires for low-loss optical waveguiding. J. Mater. Chem. C 2013, 1, 4391–4396. [Google Scholar] [CrossRef]
- Abdi, A.; Titova, L.V.; Smith, L.M.; Jackson, H.E.; Yarrison-Rice, J.M.; Lensch, J.L.; Lauhon, L.J. Resonant Raman scattering from CdS nanowires—Art. No. 043118. Appl. Phys. Lett. 2006, 88, 043118. [Google Scholar] [CrossRef]
- Khoo, K.H.; Zayak, A.T.; Kwak, H.; Chelikowsky, J.R. First-Principles Study of Confinement Effects on the Raman Spectra of Si Nanocrystals. Phys. Rev. Lett. 2010, 105, 115504. [Google Scholar] [CrossRef]
- Evans, T.J.S.; Schlaus, A.; Fu, Y.; Zhong, X.; Atallah, T.L.; Spencer, M.S.; Brus, L.E.; Jin, S.; Zhu, X.Y. Continuous-Wave Lasing in Cesium Lead Bromide Perovskite Nanowires. Adv. Opt. Mater. 2018, 6. [Google Scholar] [CrossRef]
- Wang, X.; Shoaib, M.; Wang, X.; Zhang, X.; He, M.; Luo, Z.; Zheng, W.; Li, H.; Yang, T.; Zhu, X.; et al. High-Quality In-Plane Aligned CsPbX3 Perovskite Nanowire Lasers with Composition-Dependent Strong Exciton—Photon Coupling. Acs Nano 2018, 12, 6170–6178. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhong, Y.; Yang, F.; Cao, Q.; Du, W.; Shi, J.; Liu, X. Cavity engineering of two-dimensional perovskites and inherent light-matter interaction. Photonics Res. 2020, 8, A72–A90. [Google Scholar] [CrossRef]
- Lv, Q.; Shen, X.; Li, X.; Liu, J.; Shan, Z.; Xiao, L.; Guo, P.; Ho, J.C. Laser-induced phase segregation of inorganic halide perovskite alloy nanowires for optical switch. Nano Res. 2025, 18, 94907119. [Google Scholar] [CrossRef]
- Yang, X.; Wu, R.; Zheng, B.; Luo, Z.; You, W.; Liu, H.; Li, L.; Zhang, Y.; Tan, Q.; Liang, D.; et al. A Waveguide-Integrated Two-Dimensional Light-Emitting Diode Based on p-Type WSe2/n-Type CdS Nanoribbon Heterojunction. Acs Nano 2022, 16, 4371–4378. [Google Scholar] [CrossRef]
- Cao, B.; Tian, Y.; Wen, H.F.; Guo, H.; Wu, X.; Li, L.; Zhang, Z.; Liu, L.; Zhu, Q.; Tang, J. Recent progress on fabrication, spectroscopy properties, and device applications in Sn-doped CdS micro-nano structures. J. Semicond. 2024, 45, 091101. [Google Scholar] [CrossRef]
- Ouyang, C.; Li, Y.; Fu, X.; Zeng, Z.; Huang, L.; Liu, S.; Wang, X.; Gao, T.; Pan, A. Room temperature exciton-polaritons in high-quality 2D Ruddlesden–Popper perovskites (BA)2(MA)n−1PbnI3n+1 (n = 3, 4). Appl. Phys. Lett. 2020, 117, 221107. [Google Scholar] [CrossRef]
- Han, Q.; Wang, J.; Lu, J.; Sun, L.; Lyu, F.; Wang, H.; Chen, Z.; Wang, Z. Transition between exciton-polariton and coherent photonic lasing in all-inorganic perovskite microcuboid. ACS Photonics 2020, 7, 454–462. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Jia, C.; Sun, H.; Tian, Y. Room Temperature Fabry–Pérot Modes Microcavity Exciton–Polariton in CdS/CdS:SnS2 Superlattice Microwires. Appl. Sci. 2025, 15, 11243. https://doi.org/10.3390/app152011243
Wang J, Jia C, Sun H, Tian Y. Room Temperature Fabry–Pérot Modes Microcavity Exciton–Polariton in CdS/CdS:SnS2 Superlattice Microwires. Applied Sciences. 2025; 15(20):11243. https://doi.org/10.3390/app152011243
Chicago/Turabian StyleWang, Jia, Caiqin Jia, Heming Sun, and Ye Tian. 2025. "Room Temperature Fabry–Pérot Modes Microcavity Exciton–Polariton in CdS/CdS:SnS2 Superlattice Microwires" Applied Sciences 15, no. 20: 11243. https://doi.org/10.3390/app152011243
APA StyleWang, J., Jia, C., Sun, H., & Tian, Y. (2025). Room Temperature Fabry–Pérot Modes Microcavity Exciton–Polariton in CdS/CdS:SnS2 Superlattice Microwires. Applied Sciences, 15(20), 11243. https://doi.org/10.3390/app152011243




