Abstract
This paper presents a kinematics-constrained grid-based path planning algorithm that generates real-time, safe, and executable trajectories, thereby enhancing the performance and reliability of autonomous vehicle parking systems. The grid resolution adapts to the minimum turning radius and steering limits, ensuring feasible motion primitives. The cost function integrates path efficiency, direction-switching penalties, and collision risk to ensure smooth and feasible maneuvers. A cubic spline refinement produces curvature-continuous trajectories suitable for vehicle execution. Simulation and experimental results demonstrate that the proposed method achieves collision-free and curvature-bounded paths with significantly reduced computation time and improved maneuver smoothness compared with conventional A* and Hybrid A*. In both structured and dynamic parking environments, the planner consistently maintained safe clearance and stable tracking performance under variations in vehicle geometry and velocity. These results confirm the robustness and real-time feasibility of the proposed approach, effectively unifying kinematic feasibility, safety, and computational efficiency for practical autonomous parking systems.
1. Introduction
The rapid increase in the number of vehicles has greatly intensified the demand for parking spaces, particularly in urban areas where land availability is severely limited [1,2]. To maximize capacity, modern parking facilities are often designed with narrow lanes and compact layouts. Such environments make maneuvering more difficult and place a heavy cognitive burden on drivers, which has led to growing interest in autonomous parking assistance systems [3,4]. A reliable parking path planner must therefore generate trajectories that are not only geometrically valid but also feasible for real vehicles subject to nonholonomic constraints.
Early studies on parking path planning have largely relied on geometric methods, such as circular-arc approaches that consider the minimum turning radius of a vehicle [5,6,7]. Although computationally simple, these methods typically assume favorable initial conditions and cannot easily adapt to different vehicle specifications. More recently, advanced path planning techniques developed for mobile robots have been applied in the parking domain [8,9,10]. Sampling-based methods such as Probabilistic Roadmaps (PRM) [11,12,13,14,15] and Rapidly-Exploring Random Trees (RRT) [16,17,18,19,20,21] have demonstrated effectiveness in complex or high-dimensional spaces, but they often fail to guarantee optimality and require high computation time.
Search-based methods, such as Dijkstra’s algorithm and A*, have been widely studied in path planning. Dijkstra’s algorithm guarantees the shortest path by exhaustively exploring all nodes, but its high computational cost makes it impractical for real-time applications [22,23,24,25,26]. In contrast, A* improves efficiency by combining the actual travel cost and a heuristic estimate to the goal, reducing the search space while still ensuring optimality under an admissible heuristic [27,28,29,30,31,32]. This balance of optimality and efficiency has established A* as one of the most popular algorithms in robotics and autonomous driving research. However, the classical A* algorithm formulation is based on a uniform grid with fixed cell sizes, which is appropriate for holonomic robots capable of point rotations but is less suitable for vehicles with steering constraints and a limited turning radius [33,34]. To address these limitations, Hybrid A* incorporates vehicle kinematic constraints directly into the search process, enabling feasible path generation for real vehicles. Nevertheless, Hybrid A* requires dense sampling for continuous trajectories and frequent kinematic checks, which increase memory consumption and computation time [35,36,37,38,39,40,41].
Recent research on autonomous parking emphasizes three major challenges: improving computational efficiency for real-time operation, ensuring kinematically feasible trajectories, and enhancing safety through obstacle-aware planning. Various strategies have been explored, including deep learning-based adaptive heuristics, cost function modifications, and spline-based trajectory smoothing [42,43,44,45,46,47,48]. Despite these efforts, there remains a need for algorithms that can efficiently generate smooth, safe, and feasible parking paths across diverse environments.
This paper proposes an advanced parking path planning algorithm that incorporates vehicle kinematic characteristics into the grid design and introduces an enhanced cost function for efficient and feasible trajectory generation. The proposed grid adapts its resolution to the vehicle’s minimum turning radius and steering constraints, ensuring that the planned paths are directly executable by real vehicles. The cost function incorporates switching penalties, adaptive weighting based on distance to the destination, and collision costs, which together promote smooth, safe, and dynamically adjustable parking maneuvers. To improve trajectory fidelity, the search space is extended to 16 motion directions for finer steering control, and cubic spline interpolation is applied to produce continuous and trackable paths. Both simulation studies in various parking scenarios and experimental validation with a real steering-constrained vehicle demonstrate that the proposed algorithm generates collision-free and curvature-bounded paths with higher smoothness and lower computation time than conventional A* and Hybrid A*. The main contributions of this paper are as follows: (1) a kinematics-constrained grid formulation that embeds vehicle steering characteristics directly into the search space; (2) a parking-oriented cost function that balances efficiency, smoothness, and safety; and (3) a lightweight trajectory generation framework capable of producing curvature-continuous, executable paths in real time. These aspects collectively constitute the novelty of the proposed approach compared with conventional A* and Hybrid A* methods.
The remainder of this paper is organized as follows. Section 2 introduces the kinematics-constrained grid and explains its construction. Section 3 describes the proposed cost functions and feasible path generation scheme. Section 4 presents simulation results and experimental validation. Finally, Section 5 concludes the paper.
2. Vehicle Kinematics-Based Grid Construction
In parking path planning, the discretization of the search space is crucial to ensure that trajectories are both computationally efficient and physically realizable by a real vehicle. Conventional uniform grids, though effective for holonomic or point-rotating robots, fail to adequately reflect the nonholonomic constraints of passenger vehicles, such as limited steering angles and minimum turning radius. To address this limitation, the proposed algorithm designs the grid structure to explicitly incorporate vehicle kinematics.
2.1. Vehicle Kinematic Model
Parking maneuvers are typically performed at low speeds, where vehicle dynamics can be reasonably neglected. Especially, a constant low speed is assumed to simplify the kinematic modeling, as parking maneuvers are performed under quasi-static conditions where variations in longitudinal velocity have a negligible effect on the path geometry. This assumption focuses the analysis on the steering-related kinematic constraints that dominate low-speed parking behavior, while the resulting trajectories can later be followed by a velocity-adaptive controller in practical implementations. Under this assumption, the vehicle is modeled using a simplified bicycle model with three degrees of freedom. The states of the vehicle are described by its center position (x, y), heading angle θ, longitudinal velocity v, wheelbase L, and steering angle δ, as shown in Figure 1. The governing kinematic equations of the bicycle model are expressed as follows:
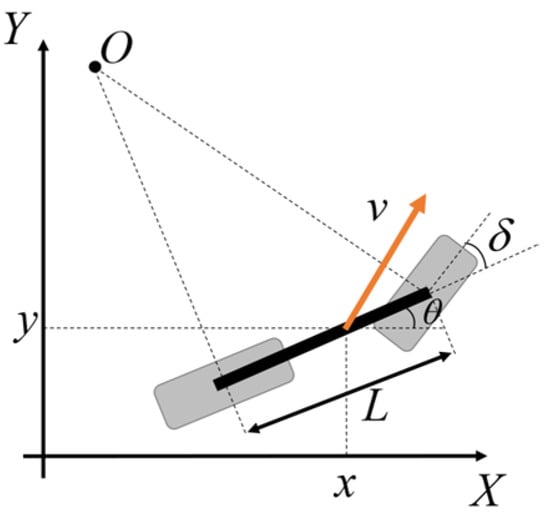
Figure 1.
Vehicle kinematic model.
Based on these kinematic equations, the minimum turning radius of the vehicle, R, can be derived as:
where δmax denotes the maximum steering angle. This parameter represents the fundamental limit of vehicle maneuverability and directly determines the spatial resolution of the search grid used for path planning.
2.2. Kinematics-Constrained Grid Formulation
The search space is discretized so that each transition between neighboring cells corresponds to a physically realizable maneuver. Unlike a uniform lattice with fixed spacing, the proposed grid adapts its resolution according to the vehicle’s steering limits and turning capability at different orientations.
For the horizontal grid, the grid dimensions (Δxh, Δyh) are derived from the achievable displacements under the minimum turning radius R, assuming constant vehicle speed over a short time horizon and a nonzero heading change Δθmax:
These values determine the resolution of the horizontal grid, which is applied when the vehicle heading is aligned with 0° or 180°.
To preserve geometric consistency, the vertical grid resolution is scaled proportionally to the horizontal grid. Therefore, the vertical grid dimensions (Δxv, Δyv) are given as:
where k is a proportionality factor empirically tuned from the vehicle length–width ratio and kept constant across headings, ensuring compatibility with vehicle kinematics. The vertical grid is applied when the vehicle heading is aligned with 90° or 270°, and its motion primitives include both forward and backward transitions.
Figure 2 shows the configurations of the horizontal and vertical grids, including their cell sizes and feasible motion primitives. The horizontal grid provides six options: straight, left, and right maneuvers in both forward and backward directions. The vertical grid provides three forward and three backward options. Each primitive corresponds to either straight-line motion or a curved motion under maximum steering input, ensuring consistency with nonholonomic constraints.
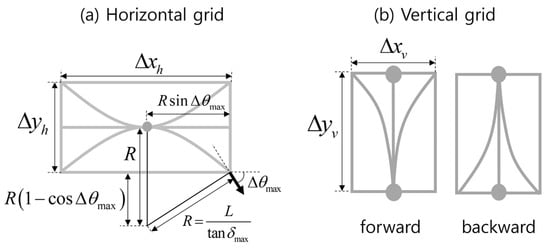
Figure 2.
Grid configurations reflecting vehicle kinematic constraints in horizontal and vertical orientations: (a) horizontal grid and (b) vertical grid.
As a result, the proposed grid is not a uniform geometric abstraction but a discretized representation of feasible motion space. This kinematics-constrained formulation provides the foundation for efficient and realistic path planning in parking environments.
3. Kinematics-Constrained Grid-Based Path Planning
The basic concept of the path planning algorithm assigns the considerable cost for each grid cell based on associated risk factors and then identifies the kinematically feasible grids. Therefore, the designed cost function for feasible and time-efficient parking is first introduced. Second, the optimal grids, that have the minimum cost function while pruning transitions that violate vehicle constraints within the feasible motion directions, are extracted within the discretized environments. Last, the resulting discrete path is post-processed using spline interpolation to generate a continuous trajectory that can be robustly tracked by the vehicle.
3.1. Cost Function Design
The proposed cost function F(n) is formulated to balance three critical requirements in autonomous parking scenarios: (i) minimizing the total path length, (ii) ensuring smooth maneuvers with minimal directional changes, and (iii) guaranteeing safe clearance from static obstacles:
where each term contributes a unique property, and together they establish a search strategy that is both theoretically grounded and practically applicable in constrained environments.
The first two terms, G(n) and H(n), originate from the A* algorithm and represent the travel cost and heuristic cost, respectively, which contribute to minimizing the total path length, as shown in Figure 3. G(n) denotes the accumulated travel cost from the start grid to the current grid n:
where gi is the cost of traversing grid i. By construction, G(n) is always non-decreasing since it aggregates positive transition costs between consecutive grids, therefore it provides a lower bound for any path passing through n.
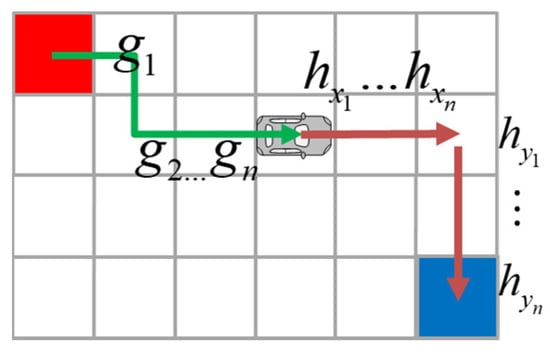
Figure 3.
Concept of travel cost and heuristic cost: the red cell and the blue cell indicate the starting grid and the goal, respectively.
The heuristic cost H(n) estimates the remaining cost from grid n to the destination grid g:
A weight factor w adaptively adjusts the influence of the heuristic term depending on the distance to the estimation, e.g., a larger weight is applied when the goal is far, while a smaller weight is used when the goal is near.
The term S(n) represents the switching cost, which penalizes frequent direction changes and promotes smoother paths with fewer reversals. In practice, frequent direction changes result in highly tortuous paths, which are undesirable for real vehicles due to steering constraints, energy inefficiency, and driver discomfort. Formally, the switching cost S(n) is defined as:
where Ns is the number of direction changes, and ws is a positive scaling factor that determines the penalty severity. For instance, in Figure 4, the vehicle experiences a direction change when transitioning from Grid 2 to Grid 3. At this point, the switching count Ns is incremented by one. Since Ns is an integer, S(n) increases in discrete steps. This discrete stepwise property creates smoothness layers in the search space. Paths with fewer turns lie in lower-cost layers, whereas tortuous paths are pushed into higher-cost regions. In practice, this reduces the likelihood of oscillatory behavior, where the planner alternates between directions unnecessarily. In addition, to avoid dominance over the base travel cost, S(n) is subject to the following upper bound, which ensures that switching penalties remain proportional to path length:
where k is the number of edges traversed to reach the grid n.
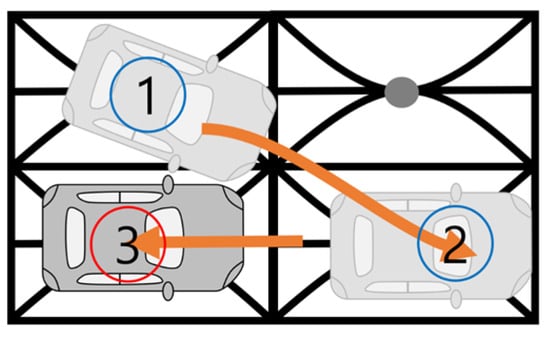
Figure 4.
An example of a switching cost.
The term C(n) represents the collision cost, which applies penalties to grids within a predefined safety buffer Ω around static obstacles:
where κ is set large enough to strongly discourage unsafe transitions while still preserving algorithm completeness, i.e., κ = max(G(n), wH(n)). By inflating costs in unsafe regions, the algorithm reduces the likelihood of risky transitions being selected during the search, thereby enhancing the overall feasibility of the computed trajectory.
By integrating these components, such as actual path length, heuristic guidance, direction-change penalties, and obstacle avoidance, the designed cost function guides the search toward short, smooth, and safe, feasible trajectories suitable for real parking scenarios.
3.2. Optimal Search Space Extraction
The planner evaluates the kinematically feasible neighbors of the current grid and selects the optimal one-step successor according to the cost function. Specifically, for the current grid n, the local selection rule is expressed as:
where denotes the set of feasible neighbors generated by motion primitives. Figure 5 shows the neighbor configuration: the gray cell at the center represents the current grid n, while the sixteen yellow cells correspond to the candidate directions to be evaluated for the next plan. These candidates include forward and backward straight transitions as well as curved maneuvers under maximum steering in both left and right directions. Each primitive ensures that a successor cell is physically reachable while respecting the minimum turning radius and the orientation-dependent grid spacing.

Figure 5.
Current grid (gray) and its sixteen neighboring candidate grids (yellow) forming the set .
Although the enlarged neighbor set increases the branching factor of the search, the cost terms regulate its use: the switching cost penalizes frequent reversals, thereby discouraging oscillatory paths, while the collision cost inflates the value of cells near obstacles, effectively steering the search away from unsafe regions. The global search proceeds under a priority-driven expansion until the destination grid is reached, producing a sequence of one-step optimal successors.
3.3. Final Path Generation
The discrete sequence of grids obtained from the search process produces a collision-free and kinematically feasible grid sequence, but the trajectory is still piecewise linear with abrupt changes in direction. Such discontinuities are impractical for real vehicles due to steering limitations and may lead to excessive control effort. To address this issue, the discrete path is refined through cubic spline interpolation, yielding a continuous and smooth trajectory suitable for vehicle tracking.
Let the discrete waypoints generated by the planner be represented as (x0, y0), (x1, y1), …, (xn, yn). For each interval [xi, xi+1], the trajectory is modeled as:
with coefficients ai, bi, ci, di determined by continuity and smoothness constraints. Specifically, the first and second derivatives of adjacent polynomials are required to be continuous at each waypoint, ensuring that both heading and curvature evolve smoothly along the path. To further enhance naturalness, the boundary conditions impose zero second derivatives at the start and destination positions, thereby minimizing curvature at the endpoints.
From a vehicle control perspective, the interpolated trajectory significantly reduces steering effort by avoiding abrupt curvature changes, which in turn enhances passenger comfort and reduces mechanical stress on steering actuators. Moreover, because the coefficients of cubic splines can be computed in closed form with linear complexity in the number of waypoints, the refinement step introduces only a negligible computational burden relative to the overall planning process, thereby preserving real-time feasibility.
Figure 6 shows an example of spline-based refinement, where the initially jagged polyline is transformed into a smooth curve without compromising feasibility. While spline interpolation may introduce slight overshoot near sharp corners, the influence is effectively mitigated by the kinematics-constrained grid design, which already enforces safe spacing from obstacles. Consequently, the proposed post-processing step bridges the gap between grid-based planning and practical execution, enabling the algorithm to generate trajectories that are smooth, dynamically compatible, and computationally efficient.
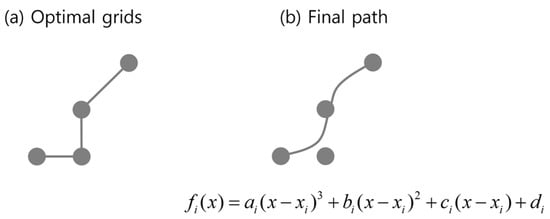
Figure 6.
Spline interpolation smooths the discrete polyline path (a) into a continuous trajectory (b).
4. Validation
To validate the effectiveness of the proposed parking path planning algorithm, simulation studies were first conducted in three representative environments: perpendicular parking, parallel parking, and a structured parking-aisle scenario. The proposed method was compared against the baseline A* and Hybrid A* algorithms in terms of path feasibility, smoothness, and computational efficiency. In these comparisons, A* and Hybrid A* search for the optimal grid among the eight neighbors based solely on travel cost and heuristic cost. The vehicle dimensions in the simulation were set to an overall length of 2 m, a wheelbase of 1.8 m, and a track width of 1.0 m. All scenarios start at an initial velocity of 1 m/s. The maximum steering angle was 36°, and the maximum heading angle was 45°.
Figure 7 shows the comparison between the baseline A* algorithm and the proposed algorithm in perpendicular and parallel parking scenarios. Blue and green markers denote the start and destination positions, dark cells represent obstacles, and the red lines indicate the selected paths. A* yields collision-free, piecewise-linear routes with abrupt heading changes, without guaranteeing curvature continuity or terminal-pose satisfaction. In other words, the A* path is geometrically valid but not executable for steering-constrained vehicles. The proposed method, on the other hand, enumerates kinematically feasible motion candidates, shown as black curves, and selects the minimum-cost trajectory at successive waypoints, with numeric labels indicating the evaluated costs. The resulting paths are curvature-bounded, maintain obstacle clearance, and smoothly align with the target pose in both scenarios. In the perpendicular case, the vehicle passes through the narrow entry with adequate clearance and performs an S-shaped heading transition that respects turning-radius limits, while the evaluated cost generally decreases as the vehicle approaches the goal. In the parallel case, the proposed planner first establishes proper lane alignment and then converges to the target pose without abrupt steering. Across both tasks, the proposed method improves kinematic feasibility, clearance, and terminal-pose satisfaction relative to the A* baseline.
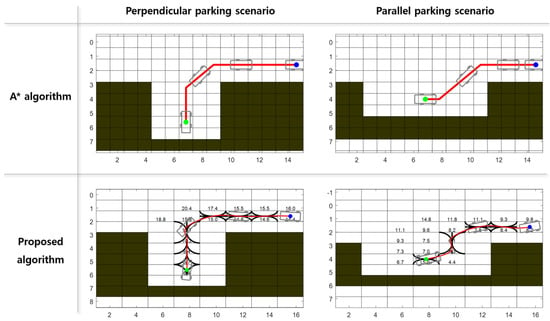
Figure 7.
Simulation results in perpendicular and parallel parking scenarios.
Figure 8 shows the results of A*, Hybrid A*, and the proposed algorithms in a structured parking-aisle environment. The A*-based path, shown in blue, is collision-free but involves frequent and unnecessary steering changes, which produce highly tortuous trajectories that skim obstacle boundaries and neglect curvature limits. The Hybrid A*-based path, depicted in green, enforces nonholonomic motion to some extent and smooths corners for feasibility, yet it still exhibits unnecessary weaving and lateral excursions, with portions running close to obstacles, thereby increasing collision risk.
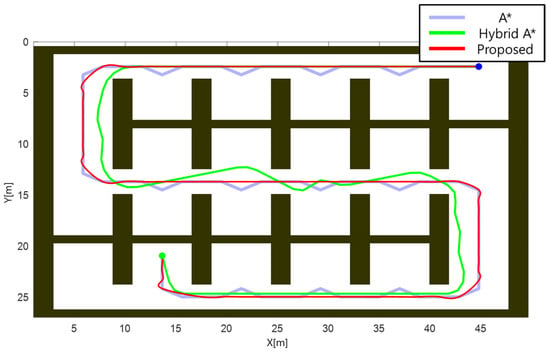
Figure 8.
Simulation results in a structured parking-aisle environment.
On the other hand, the path generated by the proposed method, depicted in red, yields a curvature-bounded trajectory that follows the corridor more consistently, maintains larger clearances near obstacles, and achieves better terminal alignment with the destination. In addition, compared with A* and Hybrid A*, the proposed method reduces path tortuosity and the number of steering reversals, producing a trajectory that can be directly executed by a steering-constrained vehicle. Qualitatively, the red path is shorter and involves fewer curvature extrema, which is advantageous for tracking accuracy, passenger comfort, and energy efficiency in narrow, cluttered aisles. In addition, Table 1 lists the average computing times of each algorithm for path planning. The proposed method achieved shorter computation times than both A* and Hybrid A*, even though the search space is larger. Therefore, the simulation results demonstrate that the proposed method achieves superior kinematic performance while maintaining computational efficiency comparable to A* and Hybrid A*.

Table 1.
Average planning time of path planning algorithms in a parking-aisle environment.
Figure 9 shows the results of real-world experiments conducted using a steering-constrained autonomous vehicle equipped with Camera-LiDAR-based simultaneous localization and mapping (SLAM) technique. The vehicle, representing approximately a 1/10-scale model of a real passenger car, has an overall length of 47 cm, a wheelbase of 22 cm, and a track width of 25 cm, with maximum steering and heading angles of 45° and 30°, respectively. The experimental parking lot was also scaled down by the same ratio, maintaining realistic geometric proportions between the vehicle and its environment. The vehicle was tasked with performing parking maneuvers in a structured parking lot while avoiding static obstacles and satisfying nonholonomic constraints under the assumption that the target parking position is known. Similar to the simulation results, A* produced a geometrically valid but kinematically infeasible path due to abrupt heading changes. Even A* yielded tortuous trajectories with redundant steering actions, increasing the risk of collisions. Hybrid A* achieved feasibility but resulted in unnecessary reversals, with lateral excursions. By contrast, the proposed method generated an S-shaped trajectory that smoothly aligned with the parking slot while respecting the minimum turning radius. In addition, the proposed method maintained larger obstacle clearance and minimized steering reversals, thereby improving safety and comfort.
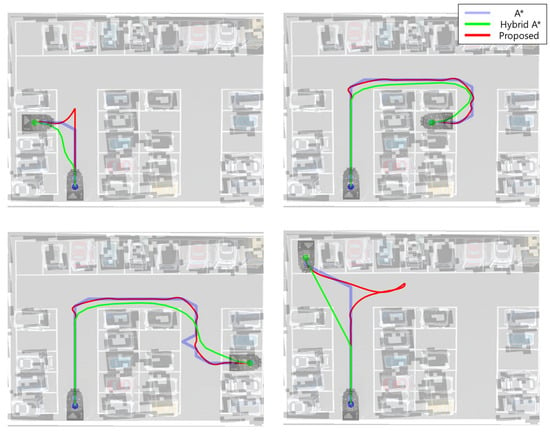
Figure 9.
Experimental validation results in a structured parking-aisle environment.
Figure 10 shows the experimental results in dynamic and non-standard parking environments. Figure 10a is for the case where another dynamic agent intermittently moves across the parking lane near Slot C and several non-standard parallel parking slots introduce irregular boundaries. Figure 10b presents the results in the same environment but with an increased initial velocity of 2 m/s. Figure 10c shows the case where the test vehicle has an extended wheelbase and a narrower track width, i.e., 71.3 cm and 31 cm, respectively, with an initial velocity of 1 m/s, resulting in more restrictive turning capability. In all experiments, the sixth parking slot was predetermined as the target. All three planners, including A*, Hybrid A*, and the proposed method, generated reversal-free trajectories toward Slot F, which had the minimum cost while avoiding the dynamic agent and maintaining sufficient clearance relative to the vehicle size. However, each planner produces a distinctly different trajectory shape.
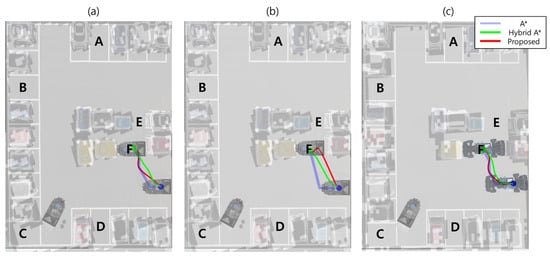
Figure 10.
Experimental validation results in dynamic and non-standard parking environments: (a) at 1 m/s; (b) at 2 m/s; and (c) with a vehicle requiring a more restrictive turning condition at 1 m/s.
All trajectories generated by the A* algorithm, depicted in blue, are geometrically valid but highly angular, showing abrupt heading changes near the target position due to the absence of kinematic constraints in its grid formulation. In scenarios requiring stricter kinematic feasibility, such as that in Figure 10c, A* fails to generate a curvature-feasible approach because of excessive turning demand. Therefore, these routes are only implementable for holonomic vehicles without steering constraints. The hybrid A* method generates smoother trajectories, depicted in green, by incorporating steering constraints, however, it still shows redundant lateral weaving with wide steering angles, leading to longer path lengths and reduced clearance. In addition, both A* and Hybrid A* show degraded terminal pose accuracy and require additional steering corrections near the goal when the initial velocity increases. In contrast, the proposed algorithm maintains curvature continuity, smooth steering transitions, and stable maneuvering even under irregular parking layouts, high initial velocities, and strict kinematic constraints, as demonstrated by the red trajectories. This performance is achieved through adaptive grid resolution and the switching-cost design, which enable kinematically feasible and dynamically robust motion generation.
Table 2 lists path length, peak curvature, minimum/average clearance, total curvature variation, and computing time for the three scenarios in Figure 10 to quantitatively substantiate the above observations. In terms of distance, the proposed method yields the shortest paths in Figure 10a,b, and remains comparable to Hybrid A* in Figure 10c. The minimum clearance is identical across planners due to the same safety buffer, whereas the proposed planner consistently achieves the largest average clearance, indicating safer margins near irregular boundaries and the dynamic agent. Regarding curvature, the proposed trajectories exhibit higher peak curvature and larger total curvature variation, reflecting tighter yet feasible maneuvers that shorten approach distance and improve terminal alignment while remaining within steering limits. In terms of computing time, the proposed planner demonstrates a remarkable improvement in computational efficiency across all scenarios. This consistent advantage suggests that the proposed approach effectively reduces unnecessary search operations and converges rapidly to a feasible trajectory. Consequently, the proposed method achieves both superior path quality and enhanced real-time performance, providing a favorable balance of distance, clearance, and computation while preserving kinematic feasibility in dynamic, non-standard parking environments.

Table 2.
Quantitative performance across Figure 10 scenarios.
Overall, the experimental validation confirms that the proposed algorithm consistently outperforms baseline methods by generating collision-free, curvature-bounded, and executable trajectories in real parking environments, even under varying vehicle configurations and velocity conditions. These results demonstrate the robustness of the kinematics-constrained grid formulation and the effectiveness of the enhanced cost function in achieving real-time, safe, and feasible parking maneuvers.
5. Conclusions
This paper proposes a kinematics-constrained grid-based path planning algorithm that overcomes the limitations of conventional A* and Hybrid A*. By embedding vehicle’s turning characteristics into the grid structure and incorporating switching and collision costs into the evaluation metric, the proposed algorithm successfully generates paths that are not only short but also smooth and executable by real vehicles. The addition of cubic spline interpolation further enhances path continuity and drivability. Validation results across diverse parking scenarios confirm that the proposed method improves kinematic feasibility, safety margins, and computational efficiency compared with benchmark algorithms. These findings suggest that the approach can serve as a practical foundation for autonomous parking systems, where both real-time performance and maneuverability are essential. Future work may extend the algorithm to dynamic environments and incorporate real vehicle testing for broader validation.
Author Contributions
Conceptualization, K.S. and J.G.; methodology, K.S.; software, J.K.; validation, K.S. and J.K.; formal analysis, J.K.; investigation, K.S.; resources, J.G.; data curation, K.S.; writing—original draft preparation, K.S.; writing—review and editing, J.G.; visualization, K.S.; supervision, J.G.; project administration, J.G.; funding acquisition, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Regional Innovation System & Education(RISE) program through the RISE Center, Gyeongsangnam-do, funded by the Ministry of Education(MOE) and the Gyeongsangnam-do Provincial Government, Republic of Korea.(2025-RISE-16-002); and funded by Global-Learning & Academic research institution for Master’s PhD students, and Postdocs(LAMP) Program of the National Research Foundation of Korea(NRF) grant funded by the Ministry of Education(No. RS2024-00444460).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors. The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kong, W.; Pojani, D.; Corcoran, J.; Sipe, N. Parking policies in six continents: Mixed outcomes and multifaceted barriers to reform. Policy Des. Pract. 2024, 7, 343–360. [Google Scholar] [CrossRef]
- Shoup, D.C. The High Cost of Free Parking. J. Plan. Educ. Res. 1997, 17, 3–20. [Google Scholar] [CrossRef]
- Olmos Medina, J.S.; Maradey Lázaro, J.G.; Rassõlkin, A.; González Acuña, H. An Overview of Autonomous Parking Systems: Strategies, Challenges, and Future Directions. Sensors 2025, 25, 4328. [Google Scholar] [CrossRef] [PubMed]
- Tscharaktschiew, S.; Reimann, F. Less workplace parking with fully autonomous vehicles? J. Intell. Connect. Veh. 2022, 5, 283–301. [Google Scholar] [CrossRef]
- Arasawa, K.; Hoshi, Y.; Oya, H. A Path Planning Method for Automated Parking Systems Based on Circular Arcs and Lines with Smoothly Curves. In Proceedings of the 2024 IEEE 3rd Industrial Electronics Society Annual On-Line Conference (ONCON), Online, 8–10 December 2024; pp. 1–7. [Google Scholar]
- Ma, J.; Qian, Y. Research on Vertical Parking Path Planning Based on Circular Arcs, Straight Lines, and Multi-Objective Evaluation Function. World Electr. Veh. J. 2025, 16, 152. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, F.; Wang, P. A Feasible Parking Algorithm in Form of Path Planning and Following. In Proceedings of the 2019 International Conference on Robotics, Intelligent Control and Artificial Intelligence, Shanghai, China, 20–22 September 2019; pp. 6–11. [Google Scholar] [CrossRef]
- Choi, M.; Kang, G.; Lee, S. Autonomous driving parking robot systems for urban environmental benefit evaluation. J. Clean. Prod. 2024, 469, 143215. [Google Scholar] [CrossRef]
- Hamad, L.; Khan, M.A.; Menouar, H.; Filali, F.; Mohamed, A. Haris: An advanced autonomous mobile robot for smart parking assistance. In Proceedings of the 2024 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 5–8 January 2024; pp. 1–6. [Google Scholar]
- Selmair, M.; Maurer, T.; Lai, C.-H.; Grant, D. Enhancing the efficiency of charging & parking processes for Autonomous Mobile Robot fleets: A simulative evaluation. J. Power Sources 2022, 521, 230894. [Google Scholar] [CrossRef]
- Alarabi, S.; Luo, C.; Santora, M. A PRM approach to path planning with obstacle avoidance of an autonomous robot. In Proceedings of the 2022 8th International Conference on Automation, Robotics and Applications (ICARA), Prague, Czech, 18–20 February 2022; pp. 76–80. [Google Scholar]
- Geemoon, N.; Jihoon, P.; Chanoh, M.; Daewoo, L. Parallelization of Probabilistic RoadMap for Generating UAV Path on a DTED Map. J. Korean Soc. Aeronaut. Space Sci. 2022, 50, 157–164. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Svestka, P.; Latombe, J.-C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 2002, 12, 566–580. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Y.; Bu, S.; Yang, J. Smart vehicle path planning based on modified PRM algorithm. Sensors 2022, 22, 6581. [Google Scholar] [CrossRef] [PubMed]
- Suh, H.J.; Deacon, J.; Wang, Q. A Fast PRM Planner for Car-like Vehicles. 2018. Available online: https://hjrobotics.net/wp-content/uploads/2018/10/A-Fast-PRM-Planner-for-Car-like-Vehicles.pdf (accessed on 21 July 2025).
- Chen, J.; Ma, R.; Lu, C.; Deng, Y. Autonomous Parking Path Planning Method for Intelligent Vehicles Based on Improved RRT Algorithm. World Electr. Veh. J. 2025, 16, 374. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-Exploring Random Trees: A New Tool for Path Planning. Res. Rep. 9811 1998. Available online: https://api.semanticscholar.org/CorpusID:14744621 (accessed on 21 July 2025).
- Solmaz, S.; Muminovic, R.; Civgin, A.; Stettinger, G. Development, analysis, and real-life benchmarking of rrt-based path planning algorithms for automated valet parking. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 621–628. [Google Scholar]
- Wang, Y.; Jha, D.K.; Akemi, Y. A two-stage RRT path planner for automated parking. In Proceedings of the 2017 13th IEEE conference on automation science and engineering (CASE), Xi’an, China, 20–23 August 2017; pp. 496–502. [Google Scholar]
- Zheng, K.; Liu, S. RRT based path planning for autonomous parking of vehicle. In Proceedings of the 2018 IEEE 7th Data Driven Control and Learning Systems Conference (DDCLS), Enshi, China, 25–27 May 2018; pp. 627–632. [Google Scholar]
- Vlasak, J.; Sojka, M.; Hanzálek, Z. Improving rapidly-exploring random trees algorithm for automated parking in real-world scenarios. J. Intell. Transp. Syst. 2025, in press. [Google Scholar] [CrossRef]
- Ata, K.; Soh, A.C.; Ishak, A.; Jaafar, H.; Khairuddin, N. Smart indoor parking system based on dijkstra’s algorithm. Int. J. Integr. Eng. 2020, 2, 13–20. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; Association for Computing Machinery: New York, NY, USA, 2022; pp. 287–290. ISBN 978-1-4503-9773-5. [Google Scholar]
- Junehong, P.; Hyewon, J.; Dongmahn, S.; Soobin, J. 3D LiDAR based Localization and Dijkstra’s Algorithm-Based Path Planning. In Proceedings of the 24th Korea Conference on Software Engineering (KCSE), Pyeongchang, Gangwon, Republic of Korea, 19–21 January 2022; pp. 481–483. [Google Scholar]
- Wang, H.; Zhang, F.; Cui, P. A parking lot induction method based on Dijkstra algorithm. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 5247–5251. [Google Scholar]
- Yu, L.; Jiang, H.; Hua, L. Anti-congestion route planning scheme based on Dijkstra algorithm for automatic valet parking system. Appl. Sci. 2019, 9, 5016. [Google Scholar] [CrossRef]
- Chen, K.Y. An improved A* search algorithm for road networks using new heuristic estimation. arXiv 2022. [Google Scholar] [CrossRef]
- Cho, S.H. A Pathfinding Algorithm Using Path Information. J. Korea Game Soc. 2013, 13, 31–40. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Kabir, R.; Watanobe, Y.; Islam, M.R.; Naruse, K. Enhanced robot motion block of a-star algorithm for robotic path planning. Sensors 2024, 24, 1422. [Google Scholar] [CrossRef] [PubMed]
- Yeong-Geun, R.; Yongjin, P. A Study on A* Algorithm Applying Reversed Direction Method for High Accuracy of the Shortest Path Searching. J. Korea Inst. Intell. Transp. Syst. 2013, 12, 1–9. [Google Scholar] [CrossRef]
- Zhao, Y. Automated Parking Planning with Vision-Based BEV Approach. arXiv 2024, arXiv:2406.15430. [Google Scholar]
- Daniel, K.; Nash, A.; Koenig, S.; Felner, A. Theta*: Any-angle path planning on grids. J. Artif. Intell. Res. 2010, 39, 533–579. [Google Scholar] [CrossRef]
- Harabor, D.; Grastien, A. Online graph pruning for pathfinding on grid maps. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011; Volume 25, pp. 1114–1119. [Google Scholar]
- Acernese, A.; Borrello, G.; Lorusso, L.; Basso, M. Informed Hybrid A Star-based Path Planning Algorithm in Unstructured Environments. In Proceedings of the 2024 European Control Conference (ECC), Stockholm, Sweden, 25–28 June 2024; pp. 1039–1044. [Google Scholar]
- Beomseong, C.; Seungwon, C.; Jaeun, R.; Kunsoo, H. Multi-Agent Path Planning Using Hybrid A* and Reinforcement Learning. In Proceedings of the KSAE 2022 Annual Autumn Conference & Exhibition, Jeju, Republic of Korea, 16–19 November 2022; pp. 851–854. [Google Scholar]
- Chang, T.; Tian, G. Hybrid A-Star path planning method based on hierarchical clustering and trichotomy. Appl. Sci. 2024, 14, 5582. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Practical search techniques in path planning for autonomous driving. In Proceedings of the First International Symposium on Search Techniques in Artificial Intelligence and Robotics (STAIR-08), Chicago, IL, USA, 13–14 July 2008. [Google Scholar]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path planning for autonomous vehicles in unknown semi-structured environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Sedighi, S.; Nguyen, D.-V.; Kuhnert, K.-D. Guided hybrid A-star path planning algorithm for valet parking applications. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 570–575. [Google Scholar]
- Xiong, L.; Gao, J.; Fu, Z.; Xiao, K. Path planning for automatic parking based on improved Hybrid A* algorithm. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence (CVCI), Tianjin, China, 29–31 October 2021; pp. 1–5. [Google Scholar]
- Hua, Y.; Li, Z.; Wu, H.; Zhang, M.; Sun, H. Parking path planning of autonomous vehicle based on B-spline curve. In Proceedings of the Ninth International Symposium on Sensors, Mechatronics, and Automation System (ISSMAS 2023), Xiamen, China, 6–8 January 2023; Volume 12981, pp. 1234–1240. [Google Scholar]
- Likhachev, M.; Gordon, G.J.; Thrun, S. ARA*: Anytime A* with provable bounds on sub-optimality. In Proceedings of the 17th International Conference on Neural Information Processing Systems, Whistler, BC, Canada, 9–11 December 2003; Volume 16, pp. 767–774. [Google Scholar]
- Liu, L.; Ye, Z.; Zhang, D.; Li, Y. Automated parking trajectory planning: A hybrid curve search and nonlinear optimisation approach. Cyber-Phys. Syst. 2025, 11, 297–324. [Google Scholar] [CrossRef]
- Veerapaneni, R.; Saleem, M.S.; Likhachev, M. Learning local heuristics for search-based navigation planning. In Proceedings of the International Conference on Automated Planning and Scheduling, Prague, Czech Republic, 8–13 July 2023; Volume 33, pp. 634–638. [Google Scholar]
- Wang, X.; Li, G.; Bian, Z. Research on the A* Algorithm Based on Adaptive Weights and Heuristic Reward Values. World Electr. Veh. J. 2025, 16, 144. [Google Scholar] [CrossRef]
- Takehara, R.; Gonsalves, T. Autonomous Car Parking System using Deep Reinforcement Learning. In Proceedings of the 2021 2nd International Conference on Innovative and Creative Information Technology (ICITech), Salatiga, Indonesia, 23–25 September 2021; pp. 85–89. [Google Scholar]
- Xu, X.; Xie, Y.; Li, R.; Zhao, Y.; Song, R.; Zhang, W. Hierarchical Reinforcement Learning for Autonomous Parking Based on Kinematic Constraints. In Proceedings of the 2024 IEEE International Conference on Robotics and Biomimetics (ROBIO), Bangkok, Thailand, 10–14 December 2024; pp. 274–279. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).