Abstract
In team collaboration environments, ensuring fair reward distribution is crucial for maintaining motivation and productivity. However, existing reward allocation methods often suffer from biases in self-assessment, leading to inequitable outcomes. In this study, we introduce a ranking mechanism that converts self-assessed contribution ratios into task orders based on the values of these ratios. Then we propose two methods using this mechanism: Method 1 uses quadratic optimization to adjust the contribution ratios, aligning them more closely with actual values, while Method 2 incorporates task reward differences to ensure fairer reward allotment. Experimental results show that the reward allotment method in the latest research reduces the loss by 25.31% compared to the conventional method, while our methods achieve a loss reduction of 53.28% for Method 1 and 64.4% for Method 2. Sensitivity analysis confirms the effectiveness of both methods under varying self-assessment errors, reward amounts, and task sizes, maintaining an average loss reduction of over 30%. These findings provide valuable insights for optimizing reward distribution, such as enhancing self-assessment accuracy and adjusting employee task assignments for improved fairness.
1. Introduction
In contemporary collaborative work environments, ensuring fair reward distribution among team members is essential for sustaining motivation, enhancing productivity, and promoting organizational justice [1,2]. Organizations that maintain fairness in reward distribution tend to experience higher employee satisfaction and reduced turnover, which in turn strengthens the overall competitiveness in the long run [3].
Conventional reward allotting methods frequently depend on employees’ self-assessed contribution ratios to tasks, which are susceptible to inherent biases such as overestimation driven by personal confidence or underestimation due to humility [4,5]. These distortions can result in misaligned allotments, where the employees’ received rewards do not accurately reflect their true efforts, leading to potential dissatisfaction and diminished team dynamics [6,7,8]. Although the state-of-the-art method introduces individual evaluation trend bias to correct personal assessment biases, it still suffers from biases due to personal comparisons with others, limiting the improvement in allocation fairness [9].
To tackle these challenges, this study proposes a ranking mechanism. In this mechanism, each employee’s contribution to tasks is ordered from highest to lowest based on their self-assessed contribution ratios across all tasks that they have participated in. This transforms self-assessed contribution ratios, which reflect comparisons with others, into rankings that allow for a self-to-self comparison across the tasks, thereby minimizing the biases introduced by external comparisons.
1.1. Literature Review
Studies on reward allotment in collaborative team contexts have extensively explored the challenges of achieving fairness. These studies focus on issues such as self-assessment biases, equity perceptions, incentive structures, and optimization techniques. Fuchs et al. [10] investigated biases in self-assessed contributions within innovation teams, using empirical data to demonstrate how identity-driven overconfidence led to inflated contribution estimates, which in turn skewed reward distributions. Karpen [11] examined the social psychology of self-assessment, employing qualitative methods to identify patterns of overestimation and underestimation that disrupted equitable reward allocation in collaborative settings. Froese and Roelle [9] demonstrated that without appropriate structural standards to guide self-assessment, individuals can have divergent interpretations of their contributions. These differences complicate the establishment of a consensus basis for resource allocation. Barana et al. [12] provided empirical evidence of systematic inaccuracies in self-assessments during team-based problem-solving. They found a prevalent tendency for individuals to underestimate their contributions. If this tendency is unaddressed, it can lead to inequitable outcomes for competent but self-critical members. Clayton Bernard and Kermarrec [13] further highlighted the affective complexities, showing that the emotional difficulties associated with peer and self-assessment can undermine the reliability of these mechanisms as tools for determining fair resource distribution. Woodcock [14] provided diagnostic tools to quantify team contributions objectively, offering a potential pathway to mitigate the biases inherent in subjective self-evaluations during reward allocation.
Research on team-based incentives has also highlighted their impact on fairness and performance. Li and Wu [15] conducted a cross-level study using multilevel modeling to assess how equitable reward distributions influenced innovative behaviors, finding that fair allocations strengthened team cohesion. Friebel et al. [16] implemented field experiments in a retail chain to evaluate team incentives, revealing that misaligned reward allotments led to increased free-riding and reduced productivity. Garbers and Konradt [17] performed a meta-analysis of financial incentives, synthesizing experimental and observational data to show that equitably distributed team rewards enhanced motivation, while unfair distributions led to dissatisfaction. Bredereck et al. [18] conducted a systematic review of reward systems in organizational contexts, analyzing 61 articles to identify how fair allocation influences employee behavior and suggesting future research directions on team dynamics. Danilov et al. [19] used laboratory experiments to study team incentives, finding that inequitable reward shares distorted advice quality and collaboration. Freeman et al. [20] demonstrated that equal sharing arrangements particularly enhance team output by motivating less skilled members to contribute more actively. Goette and Senn [21] found that well-designed team incentives significantly boost performance in settings requiring coordinated efforts on complex tasks. Francis et al. [22] emphasized that fair assessment and reward structures in educational teams minimize conflicts while maximizing participant engagement and satisfaction.
Optimization approaches have been developed to improve reward fairness. Tao et al. [23] proposed a quadratic programming model to achieve fairer resource allocation within the team. In this model, employees’ self-assessed contribution levels to the projects they have participated in are used to adjust the contribution ratios assigned by the company. Jiang et al. [24] introduced a data-driven optimization framework that accounts for deviations in self-assessments, adjusting these discrepancies to improve the accuracy of reward allocation. Li and Sun [25] introduced an allocation method employing data mining techniques to iteratively optimize how benefits or gains are distributed, providing a systematic approach to ensuring equitable returns. Similarly, Xin et al. [26] applied bi-level programming and inverse optimization models to ensure fairness in the distribution of profits among collaborators, emphasizing proportional allocation in achieving equity within collaborative settings. Qiao et al. [27] developed a fair incentive mechanism for collaborative causal inference, proposing a data valuation function to allocate rewards based on each party’s contribution. Tajabadi and Heider [28] proposed a framework for swarm learning, incorporating fair reward allocation to personalize models in collaborative environments. Saygın et al. [29] applied a game-theoretic approach to fair cost allocation in collaborative hub networks, comparing methods like the Shapley value, least core, and nucleolus to achieve stable and equitable distributions among partners. Herath et al. [30] developed a balanced scorecard model for team-based employee remuneration, using group target and weight selection to allocate bonuses fairly in collaborative settings, optimizing formulas tied to performance metrics. Ma et al. [31] proposed an optimum risk-sharing framework to incentivize integrated project delivery adoption, employing a novel method to optimize sharing incentives affected by risk allocation, ensuring fair distribution among project teams. Eissa et al. [32] utilized cooperative game theory combined with Monte Carlo simulations to determine fair and efficient risk-reward distribution plans in integrated project delivery, promoting equitable outcomes in construction team collaborations. Liu et al. [33] introduced a graph-theoretical approach for optimizing collaborative crowdsensing, using auction models from game theory to distribute earnings equitably among human contributors. Teng et al. [34] applied cooperative game theory, specifically the Shapley value, to develop a fair profit distribution model among participants in integrated project delivery systems, enhancing equity in collaborative construction projects. Emad et al. [35] employed cooperative game theory for team selection and cost deviation sharing in integrated project delivery systems, ensuring a fair distribution of savings and rewards based on contributions in emerging market team collaborations. Vander Schee and Birrittella [36] designed a hybrid peer assessment mechanism that maintains fairness in allocation while ensuring efficiency through standardized evaluation procedures. Tavoletti et al. [37] developed a machine learning-based technical solution to effectively identify and mitigate evaluation biases caused by nationality in global virtual teams, ensuring fairness in performance assessment. Peng [38] established a performance appraisal system using Key Performance Indicators (KPIs) for corporate management personnel, enhancing the objectivity and fairness of performance allocation through quantitative evaluation criteria. Resce et al. [39] proposed a collaboration prediction model based on network characteristics, providing data-driven support for the equitable allocation of research resources.
Despite these advancements, existing research has notable limitations. Firstly, many studies relied heavily on self-assessed contribution ratio values, which were susceptible to biases arising from individuals comparing themselves to others, such as overconfidence or social comparison effects [9,24,26]. While structured evaluation frameworks [38] and peer assessment systems [36] have improved objectivity and efficiency, and sophisticated mechanisms have been developed to counter systematic biases [37], these approaches collectively remain inadequate in addressing fundamental self-assessment biases and cognitive distortions. Secondly, game-theoretic approaches provided insights into allocation stability, but often failed to account for the uncertain perceptual biases in real-world collaborative settings [29,32,33,34,35]. Thirdly, various optimization and incentive allocation methods often neglect to account for self-assessment biases and the subjective nature of contribution evaluations. As a result, they may fail to accurately reflect individuals’ true contributions [27,30,31]. Furthermore, while Tao et al. [23] had incorporated a ranking mechanism to mitigate the subjective biases, their approach assumed uniform reward magnitudes across projects. This significantly reduces its effectiveness when bonus or resource disparities are substantial, thereby constraining its applicability in multi-project environments. Network-based collaboration models also lack sufficient consideration of how resource heterogeneity affects distribution fairness [39].
To address these gaps, this study introduces a novel approach that integrates a ranking mechanism with reward distribution, accounting for variations in task rewards. By transforming self-assessed contribution ratios into rankings, we mitigate biases from external comparisons, allowing for a more objective evaluation of individual contributions across tasks. This ranking mechanism reduces the subjectivity inherent in self-assessments, improving the accuracy of reward distribution. Additionally, unlike previous methods that assume uniform reward magnitudes, our approach incorporates differences in task rewards into the optimization process. This ensures that the rewards allocated to employees are more closely aligned with the actual contributions they made, even when there are significant disparities in the rewards across tasks. By combining these two elements—ranking and reward differentiation—our model offers a more robust and equitable solution for reward allocation in collaborative settings, particularly when working with diverse and multi-project environments.
1.2. Contributions and Organization
This study proposes two methods based on the ranking mechanism, which offer an order of tasks for each employee. The first method adjusts the self-assessment contribution ratios based on these orders, bringing them closer to the actual contribution ratios. By transforming subjective self-assessments into task rankings, this approach minimizes biases caused by external comparisons, leading to a more accurate reflection of individual contributions. The second method further incorporates the differences in rewards between tasks, ensuring that the reward distribution aligns more closely with what each employee truly deserves, rather than just making the adjusted contribution ratios more accurate. Unlike existing methods that assume uniform reward magnitudes across tasks, this method adapts to varying reward levels, ensuring fairness in multi-task environments where rewards differ significantly. Overall, this study makes several significant contributions to the field of reward allotment in collaborative environments:
- We introduce a ranking mechanism and propose two methods based on quadratic optimization: converting self-assessed contribution ratios into task ranking orders to reduce biases and improve the accuracy of reward distribution.
- We conduct extensive experiments, including sensitivity analyses, to validate the effectiveness of the proposed methods.
- We derive several managerial insights, providing actionable recommendations for improving reward distribution in collaborative settings.
The remainder of this paper is organized as follows: Section 2 presents the problem formulation and mathematical model. Section 3 details the computational experiments and sensitivity analyses conducted to assess the proposed methods. Section 4 concludes the paper and offers suggestions for future research.
2. Problem Formulation and Mathematical Model
In this section, we first present the problem formulation and introduce the two proposed methods along with the mathematical model in Section 2.1. Then, we discuss the evaluation metrics used to assess the effectiveness of the proposed methods in Section 2.2.
2.1. Mathematical Description
In a collaborative work environment, a set of employees completed several tasks. Each employee participated in at least two tasks, and each task involved at least two employees. Let (indexed by ) represent the set of tasks, and (indexed by ) represent the set of employees. For each task , the set of employees working on that task is denoted by . For each and , we denote the actual contribution ratio of to as . These actual contribution ratios are unobservable, intending to reflect the truly deserved contribution degrees of employees in the task. For each task , the sum of the actual contribution ratios of all employees involved in the task must equal 100%, i.e., , . Each task has a total monetary reward , which is to be distributed among the employees based on their contribution ratios. The actual reward that employee should receive for task , denoted by , is determined by the actual contribution ratio , which is calculated as:
Conventional Method. The conventional reward allocation method often requires employees to assess their own contribution ratios to the tasks that they have been involved in. In this case, the reward distribution is then based on each employee’s self-assessment of their contribution. In our study, we define this reward distribution approach as Conventional Method. Specifically, for each task and employee , the self-assessed contribution ratio of to is denoted as , where this value reflects the employee’s perception of their effort and input to the task. Then, the reward allotted to for in Conventional Method, denoted by , can be calculated as:
where represents the total sum of the self-assessed contribution ratios for all employees involved in task . This normalization ensures that the total of the self-assessed contribution ratios for all employees in each task equals 100%.
In Conventional Method, the reward distribution is based entirely on individual self-assessments of contributions. However, personal evaluations are inherently prone to biases, such as overestimating one’s own contribution ratios or underestimating one’s own efforts due to modesty. These biases can lead to inaccurate and unfair reward allotment, as the distribution depends solely on subjective judgment.
Method 0. To address the biases in self-assessment within collaborative settings, a state-of-the-art method introduces an evaluation trend bias [9]. In this method, which is referred to as Method 0 in our study, each employee is assigned a fixed evaluation trend bias , where indicates a tendency to underestimate their contributions, and reflects a tendency to overestimate their contributions. Then, in this method, the corrected contribution ratio for employee in task , denoted as , is adjusted by the evaluation trend bias as: . The objective of this method is to modify the self-assessed contribution ratios by accounting for each employee’s individual bias tendency, ensuring the total contribution ratios within each task align as closely with 100% as possible. This alignment is critical, as the sum of all contribution ratios for any given task is inherently required to equal 100%. Specifically, the quadratic optimization model in Method 0 is formulated as follows:
The objective function (3) aims to minimize the total squared difference between the sum of modified contribution ratios for all employees in each task and 100%. Constraint (4) ensures that each employee’s estimated trend for their contribution ratios remains consistent across all the tasks they are involved in. Constraints (5) and (6) are the domains of the decision variables.
After solving the quadratic optimization model, the allotment rewards in Method 0, denoted by , can be calculated based on the modified contribution ratios as follows:
Despite accounting for individual evaluation trend bias, Method 0 still relies on employees’ self-assessed contribution values, which cannot avoid comparisons between employees and may still significantly differ from actual contributions. To address this issue, it is necessary to adjust the existing award allotment methods of relying on personal evaluations.
In this study, we build upon the framework of Conventional Method by introducing a ranking mechanism to refine the reward distribution. In this framework, employees are asked to report their self-assessed contribution ratios across the different tasks they have participated in. These contribution ratios are then ordered by the employer to determine the order of each employee’s contribution ratio across all tasks that they have participated in, from highest to lowest. Specifically, based on the self-assessed contribution ratios , let represent the index of the task that employee considers to have the -th highest contribution ratio among all the tasks that they have participated in, e.g., corresponds to the task with the highest contribution ratio. The number of tasks that employee has participated in is denoted as ; then the ordered list for employee can be represented as . In this list, the indices in front correspond to tasks with contribution ratios greater than or equal to those behind. After ranking, only the ranking order is retained, and the specific self-assessed contribution ratio values provided by employees are discarded. This allows the employer to evaluate the employees’ relative contribution ratios across the tasks that they have participated in, rather than having the employees compare their performance to others, which helps reduce bias caused by external comparisons.
Specifically, we propose two methods, namely Method 1 and Method 2, which utilize the above ranking mechanism to adjust the self-assessed contribution ratios and improve the accuracy of reward distribution. To achieve this, we need to decide on modified contribution ratios for each employee in each task, which is denoted by in Method 1 and in Method 2. These ratios are modified to align with employees’ self-assessed task orders. Table 1 provides a summary of the employed notations.

Table 1.
Notations used in model formulation.
Method 1. The objective of this method is to modify the contribution ratios of employees for each task, ensuring that the total contribution ratios for each task sum as close as possible to 100%. We formulate the quadratic optimization model as follows:
The objective function (8) minimizes the total squared difference between the sum of modified contribution ratios for all employees in each task and 100%. Specifically, for each task, it calculates the squared difference between the sum of employees’ contribution ratios and 100%, and then sums these squared differences across all tasks. The goal is to minimize the total of these discrepancies, ensuring the total contribution ratios for each task are as close as possible to 100%. Constraints (9) ensure that the modified contribution ratios for each employee are consistent with their self-assessed rankings. Constraints (10) are the domains of the decision variables.
After solving the quadratic optimization model, the allotment rewards in Method 1, denoted by , can be calculated based on the modified contribution ratios as follows:
While Method 1 improves upon Method 0 by incorporating a ranking mechanism to modify self-assessed contribution ratios, it still has certain limitations, as Method 1 treats the deviation in contribution ratios uniformly across all tasks, regardless of the differences in the available rewards of each task. While this method does ensure that the overall deviation of contribution ratios is minimized, it does not account for the fact that tasks with larger rewards could disproportionately affect the overall fairness of the reward distribution. To address this issue, we introduce Method 2, which refines Method 1 by incorporating the reward of each task into the optimization process.
Method 2. We revise the objective function of optimization model for Method 1 by incorporating differences in total task rewards. Specifically, the refining quadratic optimization model is formulated as follows:
The objective function (12) minimizes the total squared difference between the sum of the allocated rewards and the total available rewards. Specifically, for each task, it calculates the squared difference between the sum of all employees’ modified contribution ratios, multiplied by the task’s reward, and the total reward for that task. After calculating this term for each task, the model sums these squared differences across all tasks. The goal is to minimize the total discrepancy, ensuring that the reward distribution aligns as closely as possible with the total available task rewards. Constraints (13) guarantee that each employee’s modified contribution ratios align with their self-assessed orders. Constraints (14) are the domains of the decision variables.
After solving the revised quadratic optimization model, the allotment rewards in Method 2, denoted by , can be calculated based on the new modified contribution ratios as follows:
Example 1.
An illustrative example of the mathematical difference between Method 1 and Method 2.
Consider a scenario with two tasks (,) and two employees (,): task has a reward of 1000 USD and task has a reward of 5000 USD, i.e., , . The actual contribution ratios are: , , , . Employees provide self-assessed contributions as follows: , , , . Then we can obtain the rankings from these self-assessed contribution ratios: , . For Method 1, We formulate the quadratic optimization model as follows:
For Method 2, We formulate the quadratic optimization model as follows:
It is notable that the constraints for both methods are the same. However, the objective functions are different. Method 1 focuses on adjusting the self-assessed contribution ratios to make both terms— and —approach 100%. In contrast, Method 2 takes into account the differences in rewards for each task. The two terms in Method 2’s objective function can be seen as weighted, where the model prioritizes aligning the higher reward task’s contribution ratio closer to 100%. Thus Method 2 tend to make the term approach 100%, while making deviate further from 100%.
2.2. Evaluation Metrics
To assess the effectiveness of the proposed methods and compare them against conventional approaches, we utilize the sum of squared errors (SSE). For comparison, we define the baseline loss values for Conventional Method, Method 0, Method 1, and Method 2 based on the total squared deviations of each employee’s allotted reward from their actual deserved reward across all tasks that they have participated in, denoted as , , , and , respectively. These losses are calculated as follows:
Then, compared to Conventional Method, we define the loss reduction percentage for each employee using Method 0, Method 1, and Method 2, denoted by , , and , respectively, which can be calculated as follows:
Positive values of , , or mean that, for employee , the reward allocations in Method 0, Method 1, or Method 2 are closer to the actual rewards compared to Conventional Method. To calculate the overall improvement, we average the loss reduction percentages across all employees. Specifically, the overall loss reduction for Method 0, Method 1, and Method 2, denoted as , , and , can be calculated as:
The Formulas (22)–(25) represent the sum of squared deviations between the rewards allotted to each employee and their actual deserved reward under each method. Squaring the differences amplifies larger misalignments, ensuring that significant discrepancies between the allocated and actual rewards are given more weight in the evaluation. In Formulas (26)–(28), we calculate the loss reduction percentage for each employee for Method 0, Method 1, and Method 2 compared to Conventional Method. This quantifies how much closer the reward allocation in the three methods is to the actual rewards. Larger values of , , and indicate more significant improvements in aligning the allocated rewards with the actual deserved rewards, meaning that the methods are more effective at minimizing the discrepancies. Finally, the overall loss reduction for Method 0, Method 1, and Method 2 is calculated by averaging the individual loss reductions across all employees, as shown in Formulas (29)–(31). This gives a comprehensive measure of the methods’ overall effectiveness in improving reward distribution fairness across the entire system.
3. Experiments
In this section, we first conduct computational experiments to assess the performance of Method 0, Method 1, and Method 2, followed by thorough sensitivity analyses to quantify how parameter variations affect the efficiency of our proposed methods.
3.1. Experiment Settings
In computational experiments, employees’ self-assessed contribution ratios are modeled to reflect biases inherent in personal evaluations. To ensure the reliability and realism of the simulation, we selected the parameters based on prior research and industry reports that reflect typical biases in real-world collaborative environments. Specifically, the self-assessed contribution ratios are assumed to follow a uniform distribution, with the error rate capturing the deviation from the true contribution due to subjective biases, i.e., . This distribution is suitable for modeling bounded errors in human judgment [10]. The value of is set to 20%, based on empirical studies indicating that employees typically overestimate or underestimate their contributions by 10–30% in collaborative settings, with 20% as a realistic midpoint for workplace scenarios [11]. Based on the study of organizational team sizes [40], our simulation environment includes 50 employees and 50 tasks, i.e., . According to Deloitte’s 2024 Global Human Capital Trends [41], the rewards for these 50 tasks and the number of employees assigned to each are summarized in Table 2, with larger-scale tasks involving more employees and having higher quantities of rewards available for distribution. Each employee participates in at least two tasks, with no upper limit on the number of tasks they can be involved in.

Table 2.
Rewards and the number of assigned employees for tasks.
After defining the parameter settings, we first calculate the basic results and then proceed with a sensitivity analysis to evaluate how variations in these parameters influence the outcomes. To account for the randomness in employee-task distribution (the assignment of employees to different tasks) and self-assessment biases, we randomly generate 10 distinct employee-task distribution scenarios. For each scenario, employees’ actual contribution ratios for tasks are determined, and 20 experiments are conducted, during which self-assessed contribution ratios are randomly generated. This multi-scenario, multi-experiment approach, which considers both task-employee distributions and the biases in self-assessed contributions, ensures the stability of the results. All models were solved using Gurobi Optimizer 10.0.1 via the Python 3.11.5 API.
3.2. Basic Results
The average values of , , , , and are calculated across the 20 experiments within each scenario. Table 3 shows the average values of , and for each of the 10 scenarios, along with the overall averages. The final evaluation metric is calculated by averaging the results from all 10 scenarios, which yields overall average values of , and as 25.39%, 53.28%, and 64.40%, respectively. And the results indicate that Method 1 significantly outperforms Method 0, and Method 2 further improves upon Method 1. All three methods demonstrate superior performance compared to Conventional Method.

Table 3.
Average values of , , and for each of the 10 scenarios and overall averages.
We further calculate the standard deviations and 95% confidence intervals for the average values of , and across the 10 scenarios. The standard deviations reflect the dispersion of values within each method across the different scenarios, which for Method 0, Method 1, and Method 2 are denoted as , and , respectively. These values are calculated based on the results in Table 3, yielding , , . The 95% confidence interval for Method 0 is then calculated for each method using the formula:
where is the sample size, and is the critical value for 95% confidence from a two-tailed t-test. Since we set 10 scenarios in each experiment, . Then with is approximately 2.262. Given the calculated standard deviations for Method 0, the corresponding confidence interval is [25.10%, 25.68%]. For Method 1 and Method 2, following the same procedure, we calculated the 95% confidence intervals: [52.31%, 54.25%] for Method 1 and [63.40%, 65.40%] for Method 2. From these results, we can observe that the outcomes obtained for all three methods are relatively stable.
To illustrate the improvement in reward allocation accuracy, we take Scenario 1 as an example and present the average results of all 20 experiments. For the 50 employees, the average values of in this scenario range from −36.73% to 65.19%, the values of range from −31.35% to 96.66%, the average values of in this scenario range from 13.17% to 98.90%. Table 4, Table 5 and Table 6 show the experimental results of the top and bottom six employees in terms of loss reduction percentage, including the baseline loss values and the corresponding loss reduction percentages.

Table 4.
The top and bottom six employees based on loss reduction percentage for Method 0.

Table 5.
The top and bottom six employees based on loss reduction percentage for Method 1.

Table 6.
The top and bottom six employees based on loss reduction percentage for Method 2.
Table 4 shows that, in this scenario, the bottom six loss reduction percentages for Method 0 are negative. This suggests that for these six employees, Method 0 performs worse than Conventional Method. However, the top six loss reduction percentages are significantly larger than 0. Table 5 shows that, in this scenario, the smallest average values are −31.35%. This suggests that for employee , Method 1 performs notably worse than Method 0. However, only four employees have values less than 0, indicating that, in most cases, reward allocation using Method 1 is better than using Conventional Method. In Table 6, we observe that for Method 2, all the average values are greater than 10%, indicating that Method 2 consistently outperforms Conventional Method across all employees.
In Scenario 1, the average loss values for each employee in Method 0, Method 1, and Method 2 are 25.31%, 56.21%, and 66.73%. The median loss values are 25.62%, 60.9%, and 68.58%. These results indicate that Method 2 consistently outperforms Method 1, which in turn outperforms Method 0, with Conventional Method performing the worst.
To provide a clearer comparison of the actual deserved rewards versus the rewards allocated by the three methods, we take employees – as examples and present the reward distributions of them in Table 7. This table directly compares the rewards allotted by each method to the actual deserved rewards, making it easy to assess how much the allotment differs for each employee under the three methods. Figure 1 further illustrates the reward distribution across the different methods for the ten selected employees.

Table 7.
Comparison of allotted and actual deserved rewards for employees –.
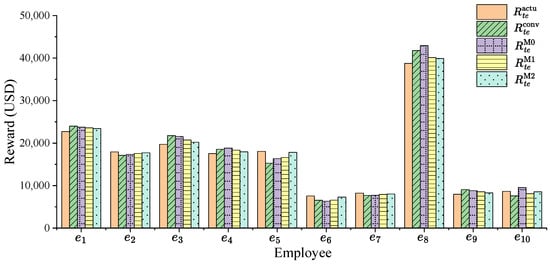
Figure 1.
Reward distribution comparison across methods for employees –.
Figure 1 clearly reveals that Conventional Method shows a significant discrepancy between the allotted rewards and the actual deserved rewards for the selected employees. In contrast, the rewards allotted using Method 1 show improved alignment with the actual deserved rewards, indicating that incorporating the ranking mechanism enhances the accuracy of the reward allotment. Overall, based on Method 2, the reward allotment is the closest to each employee’s actual deserved rewards. This demonstrates the advantage of Method 2, which not only includes the ranking mechanism but also accounts for the differences in total available reward across different tasks, improving the overall accuracy of the reward allotment. Method 0 consistently performs worse than Methods 1 and 2, although in most cases it is still better than Conventional Method. This demonstrates that the methods using the ranking mechanism we proposed are superior in terms of individual reward fairness compared to the method that introduces the self-assessment tendency.
3.3. Non-Parametric Hypothesis Test
This section presents a statistical significance test, aiming to further assess if the proposed methods utilizing the ranking mechanism can significantly enhance the fairness of reward distribution compared to Method 0.
We first perform a statistical significance test to assess whether the ranking mechanism significantly enhances the fairness of reward allotment by comparing Method 0 and Method 1. In an experiment, the average loss of all employees in Method 0 and Method 1 are denoted as and . We assume that is derived from an underlying population ; correspondingly, comes from another distinct population . These two populations are treated as mutually independent. Both populations have unknown distributions, with their means for and for are also unknown. Therefore, we turn to a non-parametric hypothesis testing approach that is well-suited for such scenarios: the Mann–Whitney U test [42]. This method allows us to evaluate whether there exists a significant difference in the medians of two independent samples drawn from these populations. Then we can further infer whether the means of the two populations differ significantly. The null hypothesis and alternative hypothesis are formulated as follows:
- The null hypothesis:
- The alternative hypothesis:
We acquire two collections of sample data based on the 10 distinct employee-task distribution scenarios. For each scenario, 20 experiments are conducted, then each collection holds 200 sample points, which are drawn from the two populations. We perform the Mann–Whitney U test on the hypotheses at a significance level of 0.05. The Mann–Whitney U test statistic yields a value of 22,466.7, and the corresponding p-value is , then we can reject the null hypothesis and infer that is significantly lower than . For Method 2 compared to Method 0, we follow the same experimental procedure as described for Method 1. After the 200 sets of experiments, the Mann–Whitney U test statistic yields a value of 24,045.6, and the corresponding p-value is . Then, we can conclude that Methods 1 and 2 significantly reduce the loss in reward allotment compared to Method 0, thereby enhancing the fairness of the allotting process.
3.4. Sensitivity Analysis
The selection of parameters and the simulated scenarios in this study may limit the generalizability of the results. Since the task-employee distributions in this study are simulated, they may not fully reflect the complexities of real-world collaborative environments. To address these limitations, we emphasize that modifications to the parameters and more extensive computational experiments are needed. Thus, conducting sensitivity analysis becomes essential to understand how variations in key input parameters can affect the outputs of the model.
Sensitivity analysis is a what-if analysis technique used to examine how changes in one or more input parameters affect the output of a model. It is commonly applied across various industries to understand the sensitivity of results to changes in assumptions, helping identify critical factors that significantly influence the model’s performance. This method is widely used, such as in power flow scheduling for microgrids with storage [43] and in optimizing robotic cells in manufacturing processes [44], as well as in many other sectors.
This section conducts sensitivity analyses to examine how the outputs of the models based on Method 1 and Method 2 respond to fluctuations in key input parameters, such as the employees’ self-assessed, the available reward of tasks, and the number of employees allocated to each task.
3.4.1. Sensitivity Analysis on Self-Assessed Error Rate
To investigate the impact of variations in the self-assessed error rate on the effectiveness of Method 1 and Method 2 compared to Conventional Method, we design instances by varying the error rate from 0.02 to 0.8 in steps of 0.02, while keeping the other parameters constant according to the settings detailed in Section 3.1. Figure 2 displays the results, where the x-axis represents , and the y-axis represents the overall average values of and across all scenarios and experiments.
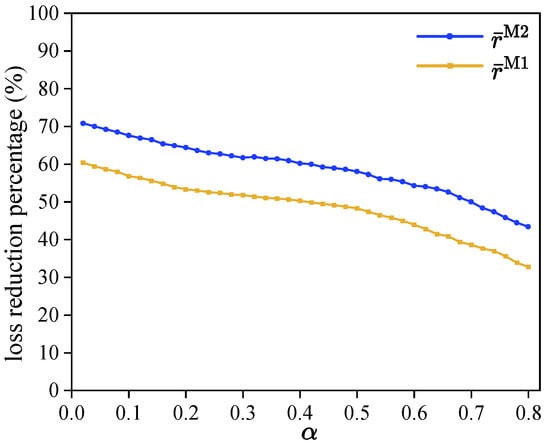
Figure 2.
and values with different self-assessed error rates.
As seen in Figure 2, the y-value of each data point represents the average and values across 10 distinct scenarios. The average values of both and decrease as increases, indicating that higher self-assessed error rates lead to a greater deviation between the allotted rewards and the actual deserved rewards. As rises, the advantage of Method 1 and Method 2 over Method 0 diminishes. This occurs because both Method 1 and Method 2 rely on task orders derived from employees’ self-assessed contribution ratios. When the self-assessments become less accurate, the order of tasks becomes increasingly unreliable, affecting the reward allocation. Despite this reduction in advantage, the average values of and remain above 30% in all experiments. Furthermore, Method 2 consistently outperforms Method 1, demonstrating its robustness even as the error rate varies.
3.4.2. Sensitivity Analysis on the Reward of Tasks
To investigate the impact of variations in the tasks’ available rewards on the effectiveness of Method 1 and Method 2 compared to Conventional Method, we design instances with different reward ratios, denoted as , where is the original reward of task and is the actual available reward for that task. These instances are generated with values ranging from 0.2 to 5.0 in steps of 0.1, while keeping the other parameters unchanged. Figure 3 shows the overall average values of and of these instances.
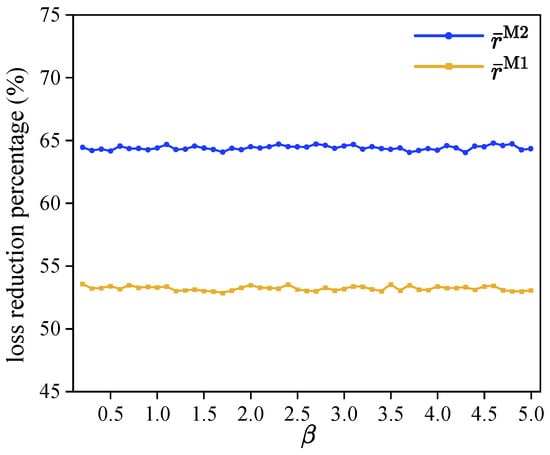
Figure 3.
and values with different reward ratios.
As seen in Figure 3, the y-value of each data point represents the average and values across 10 distinct scenarios. As increases, both Method 1 and Method 2 show relatively stable performance, with small fluctuations in the average values of and . This indicates that proportional changes in all task rewards do not significantly affect the accuracy of reward allotment for either Method 1 or Method 2. Both methods maintain a consistent advantage over Method 0 across the entire range of reward ratios.
3.4.3. Sensitivity Analysis on the Number of Employees to Tasks
To reflect the change in the number of employees assigned to each task, we define a parameter , which represents the additional number of employees assigned to a task. For each task , the new number of employees assigned to that task can be calculated as: . To investigate the impact of variations in the number of employees assigned to each task on the effectiveness of Method 1 and Method 2 compared to Conventional Method, we design instances by varying from 0 to 10 in steps of 1, while keeping the other parameters unchanged. Figure 4 displays the overall average values of and of these instances.
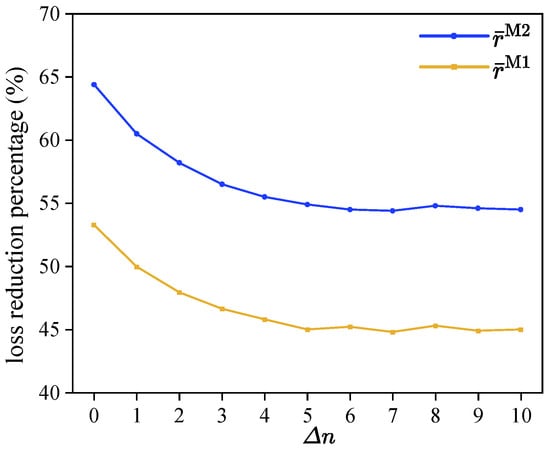
Figure 4.
and values with different assigned employee quantities.
The y-value of each data point represents the average and values across 10 distinct scenarios. As the number of employees assigned to each task increases, both Method 1 and Method 2 show a clear decline in performance. Initially, the average values of both and decrease significantly. As more employees are assigned to tasks, the task orders based on the self-assessed contribution ratios become increasingly distorted. However, after reaching a certain point, the decline in performance slows, and the methods’ effectiveness stabilizes. Since the ranking in such cases is already prone to inaccuracy due to the higher number of employees, further increases in the employee count do not worsen the situation considerably.
In summary, increasing the number of employees assigned to each task generally reduces the accuracy of the two ranking-based methods, especially when there are fewer employees in the tasks. However, across all experiments, and values remain above 40%, with Method 2 consistently outperforming Method 1. This demonstrates that the proposed methods are robust and effective, even with variations in the number of employees.
3.5. Discussion and Implications
In this section, we provide a detailed discussion of the key findings from the study, how they relate to prior research, and their theoretical and practical implications. Then we present the limitations of our approach and suggest directions for future work.
3.5.1. Key Findings and Relation to Prior Research
Through the sensitivity analyses presented, we investigate how different factors, such as self-assessed error rates, task reward differences, and the number of employees assigned to each task, impact the effectiveness of Method 1 and Method 2 in allotting rewards. The findings reveal that both Method 1 and Method 2 are sensitive to changes in the self-assessed error rate , with performance declining as the error rate increases. When task rewards change, both methods maintain stable performance. However, as the number of employees increases, the accuracy of reward allotment decreases for both methods, with performance eventually stabilizing after a certain point. Overall, Method 2 consistently outperforms Method 1. Both methods that introduce a ranking mechanism outperform the Conventional Method, which solely relies on self-assessed contribution ratios.
The sensitivity analyses reveal several insights that can help employers allocate rewards more fairly: (i) incorporating a ranking mechanism that accounts for varying task rewards can improve the fairness of reward distribution; (ii) improving the accuracy of employees’ self-assessed contribution ratios helps enhance the accuracy and effectiveness of the ranking-based allotment methods; (iii) reducing the number of employees allotted to each task can help improve the accuracy and fairness of reward distribution, particularly for tasks with fewer participants.
This research builds upon prior work that addresses inaccuracies in self-assessments in reward allocation models, a challenge commonly highlighted in the literature. However, our approach is distinguished by its introduction of a ranking mechanism that completely disregards original self-assessed values and relies solely on task orders to reflect employees’ contribution levels across different tasks. This contributes to refining the existing literature by offering a more effective way to model and address such issues in collaborative environments.
3.5.2. Theoretical and Practical Implications
The theoretical contribution of this study lies in the introduction of a ranking mechanism for reward allocation in collaborative settings, which improves upon conventional methods and the latest research methods built upon these approaches that rely on biased self-assessments. The insights gained from the sensitivity analysis further enhance the theoretical contribution by highlighting how factors such as self-assessment errors, task reward variations, and the number of employees per task influence the effectiveness of reward allocation models. These findings provide a deeper understanding of how biases in self-assessment and disparities in task rewards can undermine fairness in reward distribution.
In practical terms, this study offers valuable insights for improving reward allocation systems across various domains. The ranking mechanism can be applied in a variety of fields, such as academia, industry, and education, to ensure fairer evaluations. For example, in the peer review process, authors could rate their own submissions and rank them according to perceived quality, which can help reduce bias and provide a more objective basis for reviewer recommendations. Similarly, in project evaluation and funding distribution, where multiple contributions from different team members need to be assessed, this mechanism can offer a fairer way to evaluate individual input. For industry practitioners, the study provides practical insights into designing fairer reward systems by considering the varying task complexities and individual contributions. This approach ensures that rewards are more accurately distributed, even when tasks differ in scope or difficulty, improving employee motivation, satisfaction, and productivity. In educational settings, the ranking-based mechanism allows for more accurate and fair assessment of individual contributions in group projects, promoting transparent, equitable, and motivating assessments.
Overall, this study offers a practical framework for improving fairness in resource distribution, ensuring that rewards are better aligned with actual contributions rather than relying on biased self-assessments.
3.5.3. Limitations and Future Work
A limitation of this study is that, despite conducting multiple scenarios and experiments, the simulated data may not fully reflect the complexity of real-world collaborative environments. Specifically, the diversity and complexity of tasks, as well as the variation in reward amounts across tasks, were simplified. In future research, collecting more real-world data from various industries or teams would allow for better validation of the model and help assess its applicability to more diverse, real-world settings.
Additionally, employees may overestimate their contributions for tasks with higher rewards. This potential bias could distort the task rankings and thereby undermine the effectiveness of the proposed methods. Future research could incorporate psychological studies to address this issue, reducing the tendency for employees to overstate their contributions in high-reward tasks, and further refining the evaluation system.
4. Conclusions
In collaborative work environments, ensuring fair reward distribution is essential for motivation and organizational justice. Conventional methods often rely on biased self-assessments of contributions. While Method 0 introduces corrections for these biases through individual evaluation trend adjustments, it remains limited by the inherent biases stemming from personal comparisons with peers, which restricts its ability to achieve truly fair reward distribution. This study introduces two methods based on a task ranking mechanism to improve reward fairness by refining contribution ratios. Method 1 uses quadratic programming to align self-assessments with actual values, while Method 2 further incorporates task reward variations to ensure fairer reward allocation. Experimental results show that Method 0 reduces loss by 25.31%, while our proposed methods perform better, with Method 1 achieving a 53.28% reduction and Method 2 improving this further to 64.40%. A statistical significance test confirms that both Method 1 and Method 2 significantly outperform Method 0. Sensitivity analysis confirms that both methods outperform the baseline across varying self-assessment errors, reward amounts, and task sizes.
Through transforming external comparisons into self-rankings for each employee, the proposed methods address self-assessment biases in collaborative settings. Beyond reward allocation, this ranking mechanism can be extended to areas such as organizational management, team performance, and education, providing a foundation for designing fairer assessment systems and more transparent evaluations. Future research could test the model with larger datasets, explore scalability, and apply it to other domains.
Author Contributions
Conceptualization, S.W.; methodology, Y.T., B.J. and S.W.; software, Y.T.; validation, Y.T.; formal analysis, Y.T.; investigation, Y.T., B.J. and S.W.; resources, S.W.; data curation, Y.T. and B.J.; writing—original draft preparation, Y.T., B.J. and S.W.; writing—review and editing, Y.T., B.J. and S.W.; visualization, Y.T.; supervision, S.W.; project administration, S.W.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lane, I.M.; Messe, L.A. Equity and the distribution of rewards. J. Personal. Soc. Psychol. 1971, 20, 1–17. [Google Scholar] [CrossRef]
- Lee, H.W.; Rhee, D.Y. Effects of organizational justice on employee satisfaction: Integrating the exchange and the value-based perspectives. Sustainability 2023, 15, 5993. [Google Scholar] [CrossRef]
- Folger, R. Justice, motivation, and performance beyond role requirements. Empl. Responsib. Rights J. 1993, 6, 239–248. [Google Scholar] [CrossRef]
- Van Boven, L.; Epley, N. The unpacking effect in evaluative judgments: When the whole is less than the sum of its parts. J. Exp. Soc. Psychol. 2003, 39, 263–269. [Google Scholar] [CrossRef]
- Brown, J.L.; Farrington, S.; Sprinkle, G.B. Biased self-assessments, feedback, and employees’ compensation plan choices. Account. Organ. Soc. 2016, 54, 45–59. [Google Scholar] [CrossRef]
- Carrell, M.R.; Dittrich, J.E. Equity theory: The recent literature, methodological considerations, and new directions. Acad. Manag. Rev. 1978, 3, 202–210. [Google Scholar] [CrossRef]
- Scheel, T.E.; Otto, K.; Vahle-Hinz, T.; Holstad, T.; Rigotti, T. A fair share of work: Is fairness of task distribution a mediator between transformational leadership and follower emotional exhaustion? Front. Psychol. 2019, 10, 2690. [Google Scholar] [CrossRef]
- Haines, V.Y., III; Patient, D.; Guerrero, S. The fairness of human resource management practices: An assessment by the justice sensitive. Front. Psychol. 2024, 15, 1355378. [Google Scholar] [CrossRef]
- Froese, L.; Roelle, J. How to support self-assessment through standards in dissimilar-solution-tasks. Learn. Instr. 2024, 94, 101998. [Google Scholar] [CrossRef]
- Fuchs, C.; Sting, F.J.; Schlickel, M.; Alexy, O. The ideator’s bias: How identity-induced self-efficacy drives overestimation in employee-driven process innovation. Acad. Manag. J. 2019, 62, 1498–1522. [Google Scholar] [CrossRef]
- Karpen, S.C. The social psychology of biased self-assessment. Am. J. Pharm. Educ. 2018, 82, 6299. [Google Scholar] [CrossRef] [PubMed]
- Barana, A.; Boetti, G.; Marchisio, M. Self-assessment in the development of mathematical problem-solving skills. Educ. Sci. 2022, 12, 81. [Google Scholar] [CrossRef]
- Clayton Bernard, R.; Kermarrec, G. Peer-and self-assessment in collaborative online language-learning tasks: The role of modes and phases of regulation of learning. Eur. J. Psychol. Educ. 2025, 40, 7. [Google Scholar] [CrossRef]
- Woodcock, M. Team Metrics: Resources for Measuring and Improving Team Performance; Routledge: New York, NY, USA, 2024. [Google Scholar] [CrossRef]
- Li, T.; Wu, S. A cross-level study on the impact of team-based reward allocation on employees’ innovative behavior in manufacturing enterprises. Rev. Bus. Manag. 2024, 26, e20230195. [Google Scholar] [CrossRef]
- Friebel, G.; Heinz, M.; Krueger, M.; Zubanov, N. Team incentives and performance: Evidence from a retail chain. Am. Econ. Rev. 2017, 107, 2168–2203. [Google Scholar] [CrossRef]
- Garbers, Y.; Konradt, U. The effect of financial incentives on performance: A quantitative review of individual and team-based financial incentives. J. Occup. Organ. Psychol. 2014, 87, 102–137. [Google Scholar] [CrossRef]
- Bredereck, R.; Kaczmarczyk, A.; Niedermeier, R. Envy-free allocations respecting social networks. Artif. Intell. 2022, 305, 103664. [Google Scholar] [CrossRef]
- Danilov, A.; Biemann, T.; Kring, T.; Sliwka, D. The dark side of team incentives: Experimental evidence on advice quality from financial service professionals. J. Econ. Behav. Organ. 2013, 93, 266–272. [Google Scholar] [CrossRef]
- Freeman, R.B.; Pan, X.; Yang, X.; Ye, M. Team incentives and lower ability workers: A real-effort experiment. J. Econ. Behav. Organ. 2025, 233, 106986. [Google Scholar] [CrossRef]
- Goette, L.; Senn, J. Incentivizing interdependent tasks: Evidence from a real-effort experiment. J. Econ. Behav. Organ. 2024, 227, 106718. [Google Scholar] [CrossRef]
- Francis, N.; Pritchard, C.; Prytherch, Z.; Rutherford, S. Making teamwork work: Enhancing teamwork and assessment in higher education. FEBS Open Bio 2025, 15, 35–47. [Google Scholar] [CrossRef]
- Tao, Y.; Jiang, B.; Cheng, Q.; Wang, S. A quadratic programming model for fair resource allocation. Mathematics 2025, 13, 2635. [Google Scholar] [CrossRef]
- Jiang, B.; Tian, X.; Pang, K.W.; Cheng, Q.; Jin, Y.; Wang, S. Rightful rewards: Refining equity in team resource allocation through a data-driven optimization approach. Mathematics 2024, 12, 2095. [Google Scholar] [CrossRef]
- Li, J.; Sun, G. A rational resource allocation method for multimedia network teaching reform based on Bayesian partition data mining. Electron. Res. Arch. 2023, 31, 5959–5975. [Google Scholar] [CrossRef]
- Xin, X.; Wang, X.L.; Zhang, T.; Chen, H.C.; Guo, Q.; Zhou, S.R. Liner alliance shipping network design model with shippers’ choice inertia and empty container relocation. Electron. Res. Arch. 2023, 31, 5509–5540. [Google Scholar] [CrossRef]
- Qiao, R.; Xu, X.; Low, B.K.H. Collaborative causal inference with fair incentives. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 28300–28320. [Google Scholar]
- Tajabadi, M.; Heider, D. Fair swarm learning: Improving incentives for collaboration by a fair reward mechanism. Knowl.-Based Syst. 2024, 304, 112451. [Google Scholar] [CrossRef]
- Saygın, E.; Tekin, S.; Kuyzu, G. Fair cost allocation for collaborative hub networks. Oper. Res. 2025, 25, 55. [Google Scholar] [CrossRef]
- Herath, H.S.; Bremser, W.G.; Birnberg, J.G. Team-based employee remuneration: A balanced scorecard group target and weight selection-based bonus allocation. Account. Res. J. 2019, 32, 252–272. [Google Scholar] [CrossRef]
- Ma, Q.; Cheung, S.O.; Li, S. Optimum risk/reward sharing framework to incentivize integrated project delivery adoption. Constr. Manag. Econ. 2023, 41, 519–535. [Google Scholar] [CrossRef]
- Eissa, R.; Abdul Nabi, M.; El-Adaway, I.H. Risk–reward share allocation under different integrated project delivery relational structures: A Monte-Carlo simulation and cooperative game theoretic solutions approach. J. Constr. Eng. Manag. 2024, 150, 04024013. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, C.; Chen, X.; Tai, W. Optimizing collaborative crowdsensing: A graph theoretical approach to team recruitment and fair incentive distribution. Sensors 2024, 24, 2983. [Google Scholar] [CrossRef] [PubMed]
- Teng, Y.; Li, X.; Wu, P.; Wang, X. Using cooperative game theory to determine profit distribution in IPD projects. Int. J. Constr. Manag. 2019, 19, 32–45. [Google Scholar] [CrossRef]
- Emad, Y.; Eid, M.S.; Bassioni, H.A. Team selection and cost deviation sharing in IPD systems for emerging markets: A cooperative game theory approach. J. Leg. Aff. Disput. Resolut. Eng. Constr. 2025, 17, 04525005. [Google Scholar] [CrossRef]
- Vander Schee, B.A.; Birrittella, T.D. Hybrid and online peer group grading: Adding assessment efficiency while maintaining perceived fairness. Mark. Educ. Rev. 2021, 31, 275–283. [Google Scholar] [CrossRef]
- Tavoletti, E.; Stephens, R.D.; Taras, V.; Dong, L. Nationality biases in peer evaluations: The country-of-origin effect in global virtual teams. Int. Bus. Rev. 2022, 31, 101969. [Google Scholar] [CrossRef]
- Peng, J. Performance appraisal system and its optimization method for enterprise management employees based on the kpi index. Discret. Dyn. Nat. Soc. 2022, 2022, 1937083. [Google Scholar] [CrossRef]
- Resce, G.; Zinilli, A.; Cerulli, G. Machine learning prediction of academic collaboration networks. Sci. Rep. 2022, 12, 21993. [Google Scholar] [CrossRef]
- State of the Global Workplace. Available online: https://www.gallup.com/workplace/349484/state-of-the-global-workplace.aspx (accessed on 8 October 2025).
- 2024 Global Human Capital Trends. Available online: https://www.deloitte.com/us/en/insights/topics/talent/human-capital-trends/2024.html (accessed on 8 October 2025).
- Rubarth, K.; Sattler, P.; Zimmermann, H.G.; Konietschke, F. Estimation and testing of Wilcoxon–Mann–Whitney effects in factorialclustered data designs. Symmetry 2021, 14, 244. [Google Scholar] [CrossRef]
- Rigo-Mariani, R.; Sareni, B.; Roboam, X. Fast power flow scheduling and sensitivity analysis for sizing a microgrid with storage. Math. Comput. Simul. 2017, 131, 114–127. [Google Scholar] [CrossRef]
- Foumani, M.; Razeghi, A.; Smith-Miles, K. Stochastic optimization of two-machine flow shop robotic cells with controllable inspection times: From theory toward practice. Robot. Comput.-Integr. Manuf. 2020, 61, 101822. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).