The Effect of Degenerative Changes on the Stressed State of the Intervertebral Disc and Adjacent Tissues: A Finite Element Study

Featured Application

The results of this study, coupled with the modeling method outlined, could offer valuable insights in the realm of medical diagnosis, enabling a more comprehensive assessment of a patient’s health condition.

Abstract

The work presents a finite element analysis of the mechanical interaction of adjacent tissues in degenerative conditions of the intervertebral disc. To address this, we developed a three-dimensional finite element model that included the L1–L2 vertebrae, the intervertebral disc, and the hyaline endplate. Nonlinear elasticity theory was employed for the numerical computations, allowing for the consideration of hyperelastic properties of soft tissues. The research findings revealed significant trends associated with the increase in stiffness of the intervertebral disc: in the model with severe degeneration of annulus fibrosus and nucleus pulposus, the yield strength on the cortical bone is reached at a displacement of 3.2 mm, whereas with moderate stiffness of annulus fibrosus and nucleus pulposus, the bone’s strength reserve is significantly higher, and the maximum stresses under such loading conditions reach 50 MPa. In cases with a healthy intervertebral disc, the established stress values differed by almost 50 percent, the maximum value being 41 MPa.

1. Introduction

Numerical modeling effectively complements experimental studies of spinal biomechanics. The ability to parameterize models facilitates the assessment of interactions among objects possessing different mechanical behavior, a functionality not feasible in vitro. Additionally, this approach conserves both time and financial resources, providing opportunities to tackle various concerns, including the transmission of stiffness from the intervertebral disc (IVD) to the vertebra. Such tasks are especially relevant for studying intervertebral disc alterations induced by degenerative changes and confirming their impact on adjacent tissues.

Degenerative conditions of IVD can lead to structural alterations and biomechanical abnormalities within the disc [1]. These alterations not only compromise the disc’s ability to withstand mechanical loads but also affect its interaction with adjacent spinal structures, including bone tissue, vertebral surfaces and endplates [2].

Numerous studies in the field of numerical modeling have addressed this issue. For instance, authors [3] delved into the intricacies of intervertebral disc fractures and developed a finite element model predicting the mechanical behavior of the disc. Similar issues were addressed by authors [4], who derived an effective modulus of elasticity for the entire IVD. Authors [5] created a numerical model of the IVD reflecting the annulus fibrosus with complex multi-fiber networks. Their development allows for assessing complex deformation states under various types of loading. The influence of degeneration not only on mechanical characteristics but also on the transmission of electrical signals between the disc and vertebra was presented in the work of [6]. A poroelastic finite element investigation in the case of IVD arthroplasty was presented by [7], while [8] modeled and studied cases of disc fibrosis and collapse. A microstructure-based modeling approach aimed at assessing aging-sensitive mechanics was proposed by [9]. Their work considered the directions of tissue fibers. Stress analysis was performed in the work of [10]. The created model consisted of two lumbar vertebrae and the L4-5 disc. Various physiological activities accompanied by different types of loads were examined in the numerical experiment. The same segment of the spinal column was studied in [11], although this work focused primarily on annulus fibrosus interlamellar zones. An idealized model of the intervertebral disc for assessing its stress state was proposed by [12]. One of the strengths of this work is the consideration of fibrous layers. A macro model of the L4-L5 disc was proposed by [13]. Their work raises questions about the technical aspects of modeling, including possible convergence problems.

Despite the plethora of research dedicated to the mentioned problem, many questions remain unanswered. In most cases, authors agree that from a mechanical standpoint, degeneration primarily affects properties of the intervertebral disc, such as stiffness. However, trends in its changes with disease progression are often vaguely outlined. As a result, these studies lack specificity, particularly in the comparison of elastic constants with the patient’s clinical condition. Nevertheless, certain researchers have reported a decrease in segmental stiffness with low-grade degeneration [14,15], whereas other studies have noted an increase in stiffness with higher degeneration grades [16,17].

In our study, we address the impact of increased stiffness, induced by degenerative changes, on the stress state of the intervertebral disc and its surrounding tissues. Due to the lack of research where various degrees of intervertebral disc degeneration have been modeled, we recognize the need for a comprehensive investigation that examines different combinations of degenerative damage to the annulus fibrosus and nucleus pulposus. The results of this study, along with the proposed modeling method and calculations, could be valuable in medical diagnosis for evaluating a patient’s condition, thereby facilitating the physician’s choice of treatment strategy.

2. Materials and Methods

2.1. Geometry and Structure of the Model

The numerical model was developed based on scans of a sixty-year-old woman obtained using computer tomography. The DICOM (Digital Imaging and Communications in Medicine) files underwent several levels of processing. The CT (computed tomography) projections were first reconstructed into a 3D geometry using 3D Slicer (5.2.1 version) [18] and exported to STL format. Subsequently, using the MeshLab 2022.22 software package [19], the geometry underwent noise reduction and smoothing (Laplacian smoothing was applied). Then, the processed STL file was exported to the SolidWorks 2024 software package [20], where, using the 3D Scan module, the external geometry of the vertebrae underwent final cleaning, including removal of erroneous surfaces, additional smoothing, and was ultimately converted to solid geometry. Next, using the tools of the same SolidWorks 2024 software, an internal cavity for trabecular tissue was created in the geometry, and a thickness of 0.5 mm was assigned to the outer shell reflecting cortical bone. The intervertebral disc was added later using SolidWorks Features. At this stage of modeling, particular attention was paid to ensuring that the surfaces of the intervertebral disc were congruent with the endplates of the vertebrae. The final steps included adding the initially solid nucleus pulposus of the disc, as well as the hyaluronic endplate. Thus, the numerical model acquired its final form (Figure 1a).

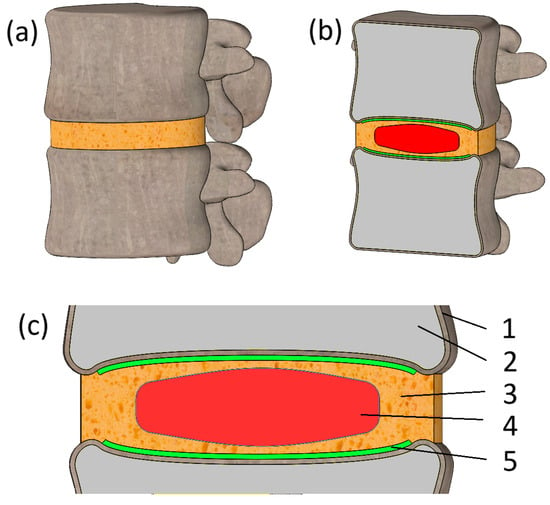
Figure 1. (a) General view of the model; (b) Section view of the model; (c) Section view of the IVD region: 1—cortical bone; 2—trabecular tissue; 3—annulus fibrosus; 4—nucleus pulposus; 5—endplate.

The initial geometry was processed three times, slightly altering its original shape and volume. Although the model reflects the bone’s characteristic curvature, errors in geometry are indeterminable due to the numerous refinements made to the initial file. Moreover, the model’s limitations include the absence of ligaments and paraspinal musculature. These structures play a significant role in stabilizing the vertebral column and redistributing mechanical loads. Their omission, while simplifying the analysis, may influence the magnitude and distribution of calculated stresses. Future models incorporating these elements would provide more physiologically accurate results. Geometry simplifications also include the component of the model reflecting trabecular tissue. It is presented here as a solid body, which can be seen in the model in cross-section (Figure 1b). This discrepancy with reality is partially compensated for by reducing the modulus of elasticity (more details on this in Section 2.2). Another significant geometry simplification is the perfectly flat surfaces of the model, namely the lower endplate of the L2 vertebra and the upper surface of the L1 vertebra. This is clearly visible in Figure 1b. This simplification is largely due to the fact that in this work, we are conducting a compression load test, and such surface shapes will securely fix the model and facilitate the application of the load. At the same time, the surfaces of vertebral endplates encompassing the intervertebral disc are modeled with utmost care, and we have made exceptional efforts to maintain their natural curvature intact, as we believe that the geometry in this area significantly influences the problem being solved. An enlarged image of the IVD region is shown in Figure 1c, where we can observe the arrangement of neighboring components—the cortical bone, trabecular tissue, hyaluronic plate, annulus fibrosus, and nucleus pulposus. Their stress state under compression load, depending on the degenerative condition of the disc, will be analyzed.

2.2. Mechanical Properties of Model Components

Both cortical and cancellous bone, as well as the endplates, were modeled as linear elastic continua. The mechanical properties of bone and endplates were set according to the values offered in [21,22,23]. They are presented in Table 1.

Table 1. Mechanical properties of bone and endplates.

Model Component	Young’s Modulus, MPa	Poisson’s Ratio	Yield Strength, MPa
Cortical bone	8000	0.3	64
Cancellous bone	100	0.3
Endplates	24	0.4

The annulus fibrosus and nucleus pulposus were modeled using the isotropic Mooney–Rivlin hyperelastic formulation. While this approach captures the nonlinear elastic behavior of soft tissues, it does not account for known anisotropies or time-dependent viscoelastic effects. Including such properties may alter the predicted stress distribution, particularly under dynamic or cyclic loading, and will be considered in future studies.

The Mooney–Rivlin strain energy density function is defined as a two-constant formulation [24]:

$$w=C_1\left(I_1-3\right)+C_2\left(I_2-3\right)+{\displaystyle \frac{1}{2}}K{(I_3-1)}^2,$$

(1)

where C₁ and C₂ are the first and second material constants, respectively, related to the response of distortion, and K is the material constant referred to the volumetric response. I₁, I₂, and I₃ are the reduced invariants of the Cauchy–Green deformation tensor and can be determined in terms of principal stretch ratios.

The material constant K can be expressed as:

$$K={\displaystyle \frac{6(C_1+C_2)}{3(1-2\upsilon )}};$$

(2)

The degradation degree of annulus fibrosus and nucleus pulposus is verified by varying the values of elastic constants. We assume that the more deteriorated tissue is reflected with higher stiffness. Although we refer to “stiffness“ for simplicity, these values represent changes in material behavior rather than structural stiffness. Thus, the term “stiffness“ should be understood as effective material stiffness, not geometry-dependent structural stiffness typically expressed in N/mm.

The range of cartilage elastic constants was reported by [25,26,27,28,29] and was involved in the study. The values of C₁ and C₂ constants are presented in Table 2, while Poisson’s ratio is assumed to be constant. It is set 0.45 for annulus fibrosus and 0.4995 for nucleus pulposus.

Table 2. Elastic constants of annulus fibrosus and nucleus pulposus accordingly to degeneration.

Stiffness	C1, MPa (Annulus Fibrosus)	C2, MPa (Annulus Fibrosus)	C1, MPa (Nucleus Pulposus)	C2, MPa (Nucleus Pulposus)
Mild	0.4	0.1	0.14	0.035
Moderate	0.6	0.15	0.17	0.041
Severe	0.9	0.23	0.19	0.045

2.3. Problem Formulation

To determine the mechanical behavior of the model, including the hyperelastic properties of annulus fibrosus and nucleus pulposus, the nonlinear theory of elasticity was applied [20]. In dynamic structural analysis, the equilibrium equations of the system at time step t + ∆t are:

$${\left. [M\right]}^{t+∆t}{\left\{U^{″}\right\}}^{\left(i\right)}+\left. [C\right]{{}_{}{}^{t+∆t}\left\{U^{\prime }\right\}}^{\left(i\right)}+{{}_{}{}^{t+∆t}\left. [K\right]}^{\left(i\right)}{{}_{}{}^{t+∆t}\left\{∆U\right\}}^{\left(i\right)}={}_{}{}^{t+∆t}\left\{R\right\}-{{}_{}{}^{t+∆t}\left\{F\right\}}^{\left(i-1\right)},$$

(3)

where [M] is the mass matrix, [C] is the damping matrix, t + ∆t[K](i) is the stiffness matrix, t + ∆t{R} is the vector of external loads, t + ∆t{F}(i − 1) is the vector of internal forces at iteration (i − 1), t + ∆t[∆U](i) is the vector of incremental displacements at iteration (i), t + ∆t{U′}(i) is the vector of total velocities at iteration (i), and [M]t + ∆t{U″}(i) is the vector of total accelerations at iteration (i), where damping matrix [C] was neglected, [C] = 0.

Employing the implicit time integration Newmark–Beta scheme and using Newton’s iterative method, the above equations are expressed in the form:

$${{}_{ }{}^{t+∆t}\left[K\right]}^{\left(i\right) } {\left\{∆U\right\}}^{\left(i\right)} = {{}_{ }{}^{t+∆t}\left\{R\right\}}^{\left(i\right)},$$

(4)

where t + ∆t{R}(i) represents the effective load vector, and t + ∆t[K](i) denotes the effective stiffness matrix. In order to perform calculations, the SolidWorks Simulation module is used.

To verify the stressed state of model components, the von Mises stress criterion was applied. It is depicted in Equation (5):

$${\sigma }_y=\sqrt{{\displaystyle \frac{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2}{2}}},$$

(5)

where σ₁, σ₂ and σ₃ are the maximum, intermediate, and minimum principal stresses, respectively. To assess the strength characteristics of the modeled bone structures, the calculated von Mises stress values were compared to the yield strength specified in Table 1.

2.4. Calculation Cases, Boundary Conditions and Mesh

To conduct a comprehensive study covering various combinations of degenerative conditions of the annulus fibrosus and nucleus pulposus, nine calculation cases are considered. They are listed in Table 3.

Table 3. Calculation cases.

No.	Annulus Fibrosus Stiffness	Nucleus Pulposus Stiffness
1	Mild	Mild
2	Mild	Moderate
3	Mild	Severe
4	Moderate	Mild
5	Moderate	Moderate
6	Moderate	Severe
7	Severe	Mild
8	Severe	Moderate
9	Severe	Severe

The loading scheme is depicted in Figure 2a. As we can see, the lower surface of the L2 vertebra is constrained from any motion, while the upper endplate of the L1 vertebra undergoes displacement loading.

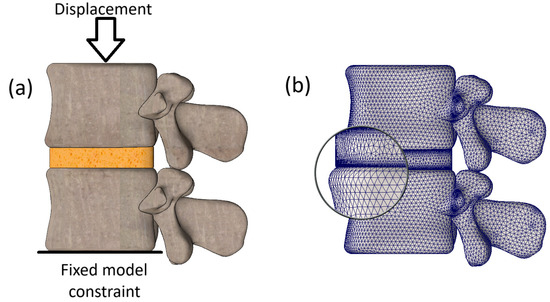
Figure 2. (a) Load schematization; (b) finite element mesh.

The model was loaded until the bone tissue of the model with the most severe properties of the intervertebral disc (IVD) reached yield strength (64 MPa). In other words, the displacement magnitude applied to the model was set according to calculation case No. 9 from Table 2. We justify this method of selecting displacement magnitude by aiming to establish the magnitude of the ultimate load on the most degenerated aspect of the model and then investigate how the same loads would affect a model with healthier properties. In our study, the magnitude of the ultimate displacement was determined to be 3.2 mm.

The model underwent meshing with tetrahedral finite elements, aligned with its curvature, as depicted in Figure 2b. It comprised 554,194 finite elements and 671,072 nodes, with a maximum element size of 1.359 mm and a minimum size of 0.067 mm, fitted to the complex geometry of the vertebral body. The entire model was characterized by 2,006,319 degrees of freedom. Equilibrium equations were solved using the Intel Direct Sparse solver.

While a formal mesh convergence study was not performed, a refined tetrahedral mesh (over 550,000 elements) was used to ensure accurate stress representation, particularly in regions with high geometric complexity. Mesh density was determined based on preliminary testing and prior experience with similar models.

Displacement-controlled loading was selected to ensure consistent deformation input across all cases, allowing comparative analysis of stress response under identical boundary displacements. While force control is physiologically relevant, displacement input helps estimate how degeneration affects mechanical capacity under the same external deformation.

3. Numerical Results and Discussion

The conducted calculations have shown that among all components of the model, the most diverse distribution of stresses depending on the degree of IVD degeneration was observed on the cortical bone. The stress state plots of all calculation cases are presented in Figure 3. As mentioned before, the displacement magnitude was determined using the model with the most degenerative annulus fibrosus and nucleus pulposus. It was found that in calculation case 9, the yield strength is reached at a displacement of 3.2 mm, and as seen from the provided scheme, zones with critical stress values spread across the outer shell of both vertebrae. The location of "red zones," as well as their visual size, indicates that failure is expected in the model under these conditions. It is worth noting that the primary interest in stress localization here is the vertebral body itself, and although areas with elevated stresses have appeared on the horizontal endplate, their emergence can be explained by the proximity of the applied load (Saint-Venant’s principle). Additionally, as seen from the stress diagram, the central part of the endplate is colored blue, indicating that the cortical shell primarily bears the load.

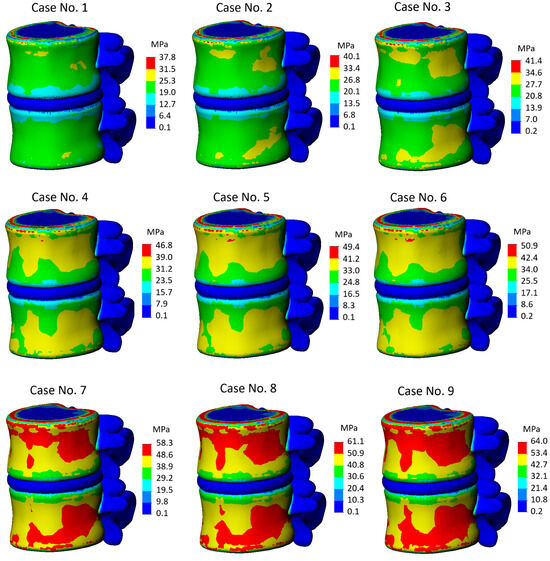
Figure 3. Von Mises stress plots on general view of the model.

For comparative analysis, we can juxtapose the results of Calculation Case no. 9 and Calculation Case no. 1, in which the healthiest model was tested. We observe a significant difference both in stress values and in the character of their distribution along the cortical shell. The maximum stress in Case no. 1 was 37.8 MPa, indicating that the model has a strength reserve exceeding 30 percent. Moreover, the distribution pattern can be considered uniform, with stress concentrators absent, except perhaps noticeable on the endplate, but as mentioned earlier, this is due to Saint-Venant’s principle.

In Cases 2 and 3, there is an increase in areas with elevated stress values; however, their magnitudes, compared to Calculation Case 9, are significantly lower. On the contrary, the stress values themselves do not differ greatly from those obtained with the healthiest model, even though the roughening of the nucleus pulposus was considered in the first three calculation cases.

In Cases 4, 5, and 6, the degenerative effect on the annulus fibrosus is taken into account, as reflected in the stress state schemes. With moderate annulus fibrosus and mild nucleus pulposus (Calculation Case no. 4), the maximum stress value was 46.8 MPa, almost a third higher than with a healthy annulus fibrosus and nucleus pulposus, and with further hardening of the nucleus pulposus, the stress values increase to 49.4 MPa and 50.9 MPa, respectively (Calculation Cases no. 5 and 6).

To summarize the results obtained at this stage, we compared the stress distribution pattern in the nine cases considered with the results presented in [30]. The main difference is that in the work of the mentioned authors, stress concentrators appear on the anterior wall of the cortical shell during vertebral compression, whereas in our work, the concentrators start their growth from the sides. This discrepancy can be explained by the following factors: firstly, the mentioned work did not account for the hyperelastic properties of the intervertebral disc, which makes the authors’ model stiffer; secondly, in the mentioned work, the endplate adjacent to the IVD was perfectly flat, without considering its natural curvature, which could also be a reason for the discrepancies in the results.

For a clearer understanding of the influence of degenerative effects, one can look at the graph of results presented in Figure 4. At first glance, it may seem that the properties of the annulus fibrosus have a greater impact on the stress state of the cortical tissue than the stiffness of the nucleus pulposus. And although judging by the provided stress values, this thesis holds true, we would like to emphasize that such a conclusion is premature and should not be misleading, as our computational model is limited by the absence of damping properties, and impact load was not considered in the study, and we believe that it is under such conditions that the component reflecting the nucleus pulposus would be much more influential.

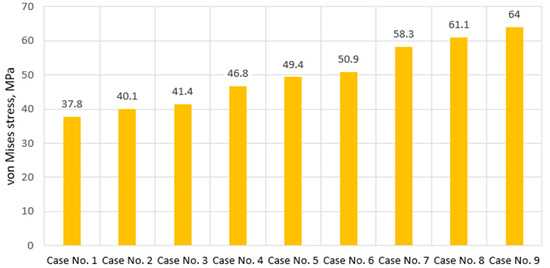
Figure 4. Maximum von Mises stress values on cortical bone in cases of various IVD degeneration.

As for the stress distribution on the component responsible for the trabecular tissue, no significant difference was found in all ten cases considered. Mostly, it was the stress values that differed rather than their localization. As seen from the stress state diagrams presented in Figure 5, with properties typical of a healthy IVD, the maximum stress identified on the trabecular component of the model was 2.3 MPa (calculation case no.1). This value increased by a third with moderate properties (calculation case no. 5) and reached 5.3 MPa with severe IVD. More detailed information on the obtained values can be found in Figure 6; however, it should be noted that no unexpected conclusions were drawn from the analysis of the trabecular component—the range of maximum values obtained varies from 2.3 to 5 MPa, and the trend of increasing stresses depending on the degree of IVD degeneration is similar to what we observed for the cortical tissue. It should be noted that due to the strong geometric simplification of the trabecular tissue (ignoring the influence of pores), the analysis of the trabecular component can hardly be considered primary, and its study was provided only to support the trends identified for the cortical shell.

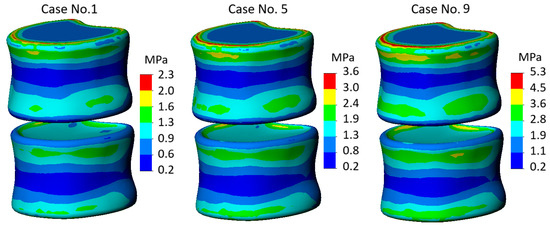
Figure 5. Von Mises stress plots on cancellous component of the model.

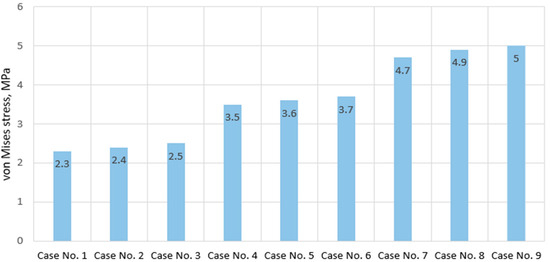
Figure 6. Maximum von Mises stress values on cancellous bone in cases of various IVD degeneration.

The most characteristic stress plots of the annulus fibrosus are shown in Figure 7. Here, we observe the stress distribution for calculation case no. 1 (mild-mild), for calculation case no. 5 (moderate-moderate), and no. 9 (severe-severe).

Figure 7. Von Mises stress plots on annulus fibrosus.

It is noteworthy that the difference between mild and severe differs almost twofold—1.309 MPa for mild, and 2.587 MPa in the case of severe. However, depending on the stiffness, there were no significant changes in stress localization—in all three cases, the most stressed areas of the component coincide with the region adjacent to the bone contact zone, while the region covered by the endplate experiences lower stress, which is clearly visible in the plot as it is colored blue. More detailed values of maximum stresses calculated on the annulus fibrosus component are presented in the graph (Figure 8).

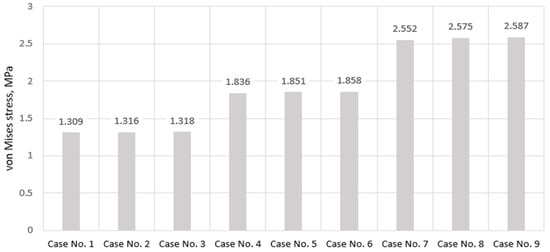
Figure 8. Maximum von Mises stress values on annulus pulposus in cases of various IVD degeneration.

As we can see, the primary factor influencing the stress magnitude of the annulus fibrosus in this study is directly its stiffness, while increasing the stiffness of the enclosed nucleus pulposus practically had no effect. This raises the question of whether this trend will work in reverse, i.e., whether the annulus fibrosus will affect the stress intensity of the nucleus pulposus, or whether their interaction in terms of stress growth will be insignificant. We will answer this question based on the results presented later, but first, let us examine the stressed plots of the endplate. They are presented in Figure 9.

Figure 9. Von Mises stress plots on endplates.

As seen from Figure 9, neither the difference in stress distribution nor the difference in their magnitudes is significant. However, it is on these plots that we can identify an interesting trend—as the degenerative effect of the disc increases and is accompanied by an increase in stiffness, stress values on the endplates do not increase; instead, they decrease. This phenomenon can only be explained by the fact that the increased stiffness of the annulus fibrosus, with other parameters remaining unchanged, gives it greater stability, thereby distorting the transmission of stiffness and resulting in this effect. It should be emphasized that the obtained result may be deceptive because, judging by the numbers, a more degenerative annulus fibrosus is more gentle to the endplates. However, this is not entirely true because if we pay attention to the distribution pattern of stresses (although similar, as noted earlier), we will notice that in general, in calculation case no. 3, stress concentrators practically do not appear, whereas in calculation case no. 6 and no. 9, they are already noticeable. And if we examine the obtained stress values when the nucleus pulposus roughens (graph in Figure 10, Calculation Cases 1–3, 4–6, 7–9), we will find that its degeneration contributes to increasing the values.

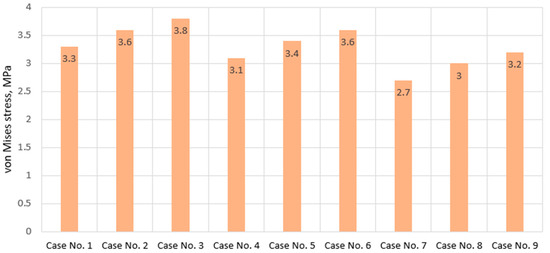
Figure 10. Maximum von Mises stress values on endplates in cases of various IVD degeneration.

The stress plots of the nucleus pulposus are shown in Figure 11. As with the endplate, the effect of annulus fibrosus roughening was unexpected—stress values decreased with an increase in annulus fibrosus stiffness, although, as seen from the values shown in the graph (Figure 12), roughening of the nucleus pulposus itself leads to their increase. With such contradictory results, it is advisable to look at the distribution pattern of stresses. As seen in Figure 11, at higher stress values (Calculation Case no. 3), the distribution pattern itself is more uniform, whereas at lower stress values (Calculation Case no. 6, and especially no. 9), stress concentrators appear. The obtained results can be interpreted as follows—the roughening of the annulus fibrosus itself does not pose a danger to the nucleus pulposus from a strength perspective, as the nucleus pulposus properties are similar to those of an incompressible fluid and cannot break; however, the stiffening of the annulus fibrosus can be hazardous for itself—compared to the nucleus pulposus, the annulus fibrosus is a stiffer material, and its stiffening may lead to the formation of micro-cracks. Stress concentrators (Figure 11, cases 6 and 9) contribute to this, and as a result, the risk of the nucleus pulposus being extruded increases. From this, it can be concluded that when studying the stress state of neighboring tissues, it is important to pay attention not only to stress values but also to the distribution pattern.

Figure 11. Von Mises stress plots on nucleus pulposus.

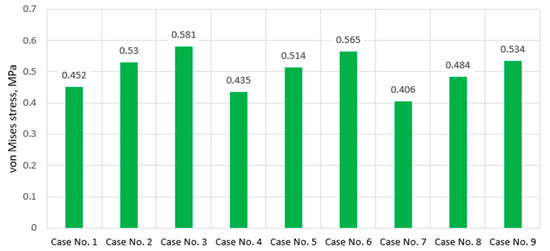
Figure 12. Maximum von Mises stress values on nucleus pulposus in cases of various IVD degeneration.

To validate the results of the present study, a comparative analysis was performed with recent finite element research focused on lumbar disc biomechanics [23,29]. Our results demonstrate a substantial increase in cortical bone stress (from 37.8 MPa to 64 MPa) and annulus fibrosus stress (from 1.3 MPa to 2.5 MPa) with increasing effective disc stiffness. These findings align with those of [29], who reported a comparable twofold rise in annular stress (0.4–2.6 MPa) and a decrease in intradiscal pressure with degeneration. Moreover, the increase in cancellous bone stress in our model (from 2.3 MPa to 5.3 MPa) closely matches the 43–73% rise observed by [23] in degenerated and osteoporotic spines. While our model incorporates only material property changes—excluding morphological alterations such as disc height loss—it replicates key biomechanical outcomes seen in both experimental and clinical studies, including load migration from the nucleus to the annulus and elevated stress in adjacent vertebral structures.

Summarizing the obtained results, several important points can be noted. One of the primary limitations of this study lies in the use of a single intervertebral disc geometry derived from a specific patient. Although this allowed for controlled parametric variation in degeneration severity, future work should include a broader range of individual geometries to validate and generalize the observed trends.

Some trends identified in this study were expected, particularly the increase in stresses in most model components with increasing stiffness of the disc’s constituent parts. However, despite the predictable outcome, the conducted calculations helped underscore the role of the annulus pulposus in transferring stiffness to neighboring tissues and revealed interesting trends in the mechanical interaction of parts of the spinal system. On the other hand, this work is unlikely to have answered all the questions of interest. For example, the tissue response to different types of loads remains unexplored. Furthermore, assigning constants to the degree of disc degeneration was based on general trends related to increased stiffness of affected tissues, without specific ties to a particular diagnosis. Such an approach to modeling is partly due to the lack of specific data in this area, and we hope that our efforts will serve as a catalyst for comprehensive experimental research, resulting in the expansion of knowledge in the field of mechanical behavior of biological tissues.

4. Conclusions

This study involved the development of a numerical model aimed at evaluating the stress distribution within the L1–L2 intervertebral disc region. The model took into consideration the hyperelastic properties of both the annulus fibrosus and nucleus pulposus, and their contribution to effective stiffness in cases of degenerative changes. The research conducted revealed certain patterns concerning the nonlinear behavior of soft tissues, notably the increase in bone stress due to the initial stiffness of cartilage, the emergence of stress concentrators on load-bearing bone surfaces, and the dislocation tendencies of stress on all components of the model.

This study demonstrated that increasing the effective stiffness of the annulus fibrosus due to degeneration significantly elevates stress levels in adjacent cortical bone, with the potential to reach yield strength under moderate displacement. In contrast, nucleus pulposus stiffening showed a more limited effect on stress transmission. Moreover, degeneration introduces stress concentrators at specific cortical regions, which could indicate early risk zones for failure.

Clinically, these findings of this study may inform risk assessment for vertebral compression fractures in patients with advanced disc degeneration. The observed stress concentration patterns suggest regions of mechanical vulnerability, which could be relevant for pre-operative planning, selection of therapeutic strategies, or rehabilitation protocols targeting load reduction.