Review of Approaches to Creating Control Systems for Solid-State Transformers in Hybrid Distribution Networks
Abstract
1. Introduction
2. The Main Features of Active Distribution Networks
- increase in the rate of electromechanical transient processes (up to 5–10 times) due to small mechanical inertia constants of distributed energy sources;
- overload of electric network equipment when integrating single distributed energy sources of high power or a large number of small-scale distributed energy sources;
- deviations in power quality indicators from standard values at the busbars of consumer electrical receivers;
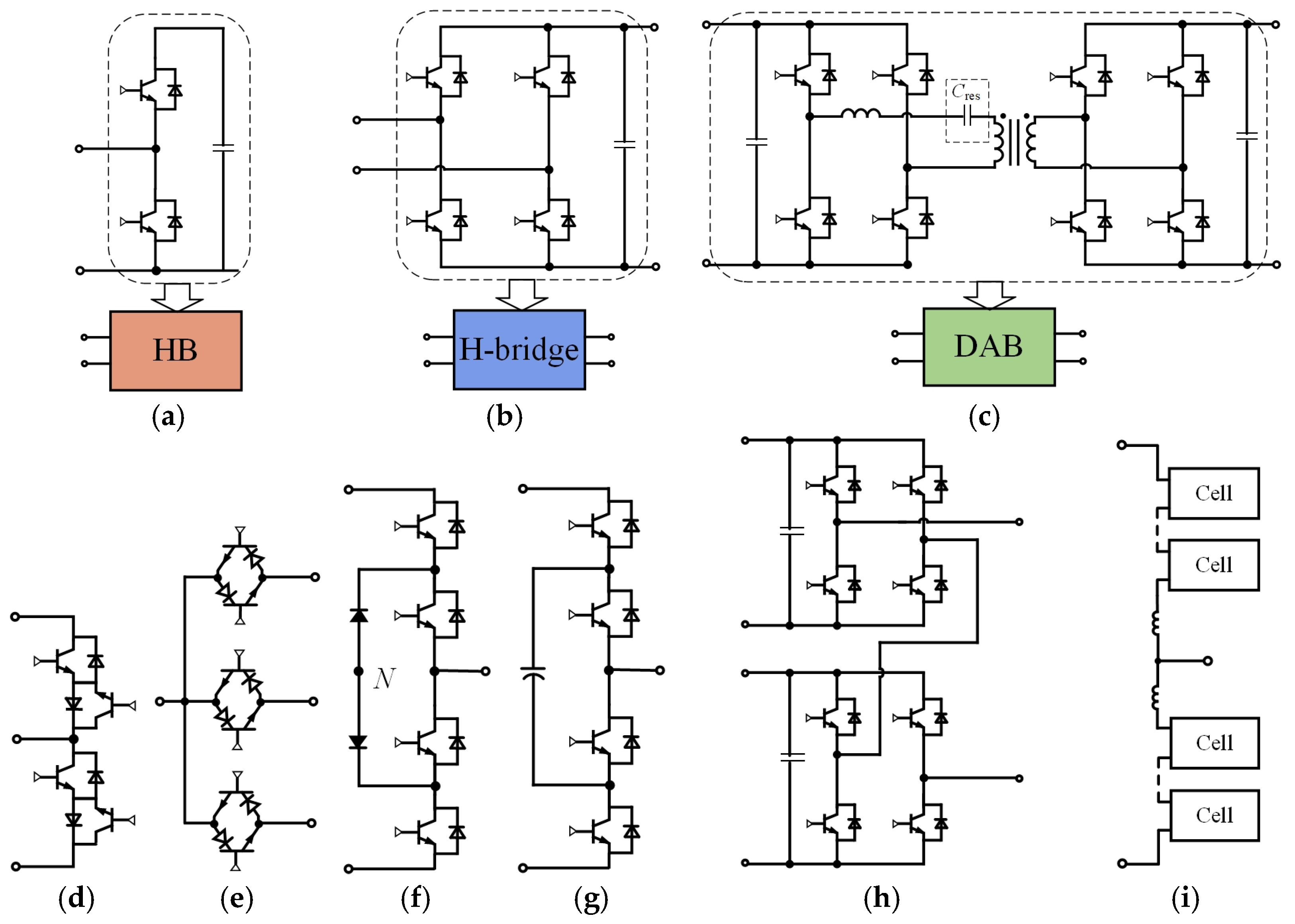
- by the number of AC conversion stages;
- by phase modularity;
- by circuit of connection to MV and LV networks.
- increasing the power of PEC with limited parameters of power semiconductor elements;
- backing up the PEC and its components without interrupting the output voltage and current;
- lowering the level of harmonic components in the input and output voltages and currents;
- coordinating the input and output values of voltage and current;
- unifying the applied set of components.
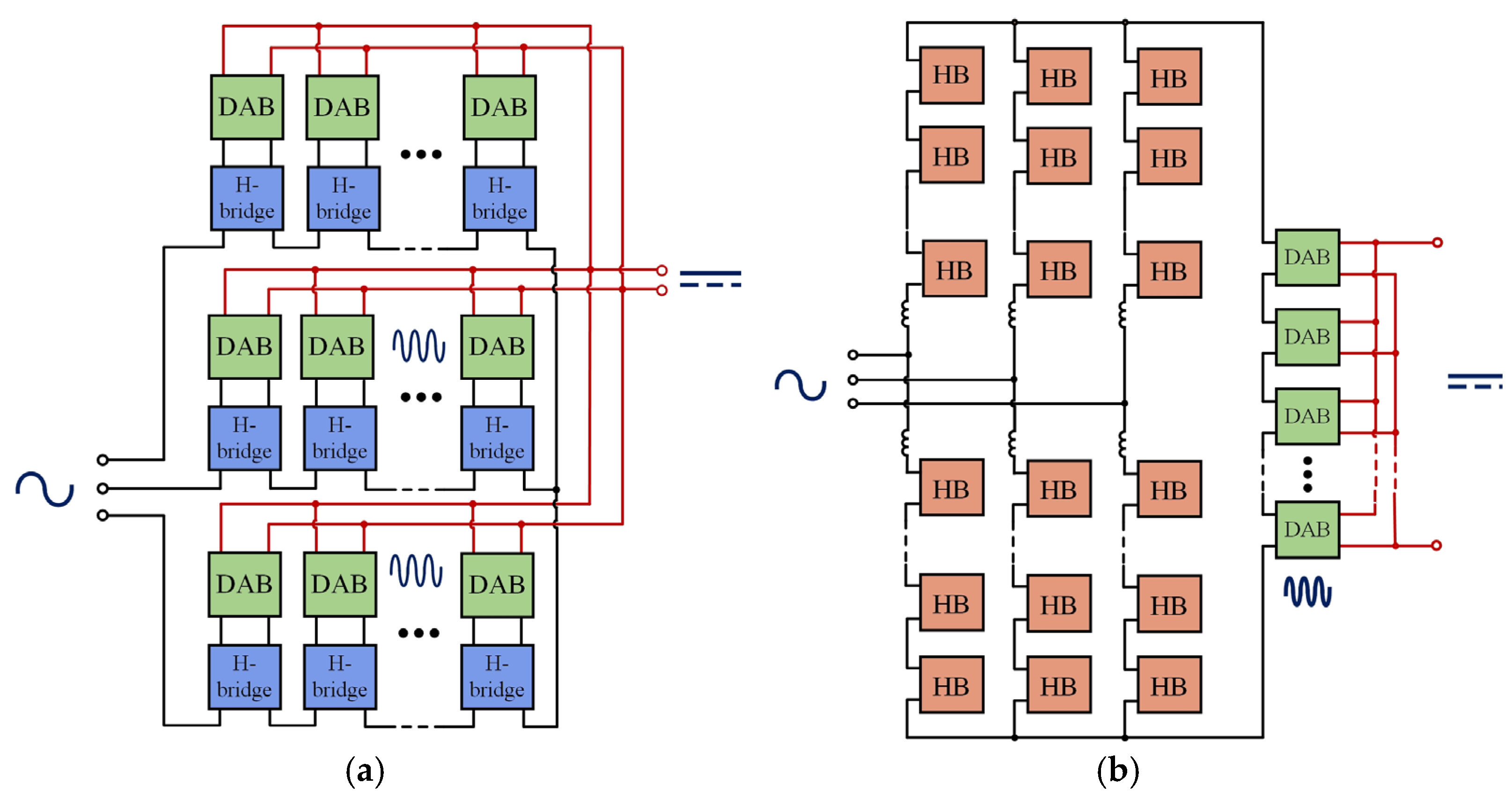
- parallel connection of PEC increases power, improves the quality of the input/output parameters, and boosts the PEC modulation frequency in DC-to-DC conversion;
- multi-module connection in rectifiers with capacitor-diode multiplication/division of the output voltage increases/decreases the output voltage;
- multi-level connection of PEC increases its operating voltage relative to the rated parameters of the electronic switches (in the case of their series connection) and reduces the level of harmonic distortion in the input and output voltages and currents;
- cascaded connection of PEC relies on single-phase bridge circuits made with various topologies, allowing multi-level inverters to be obtained.
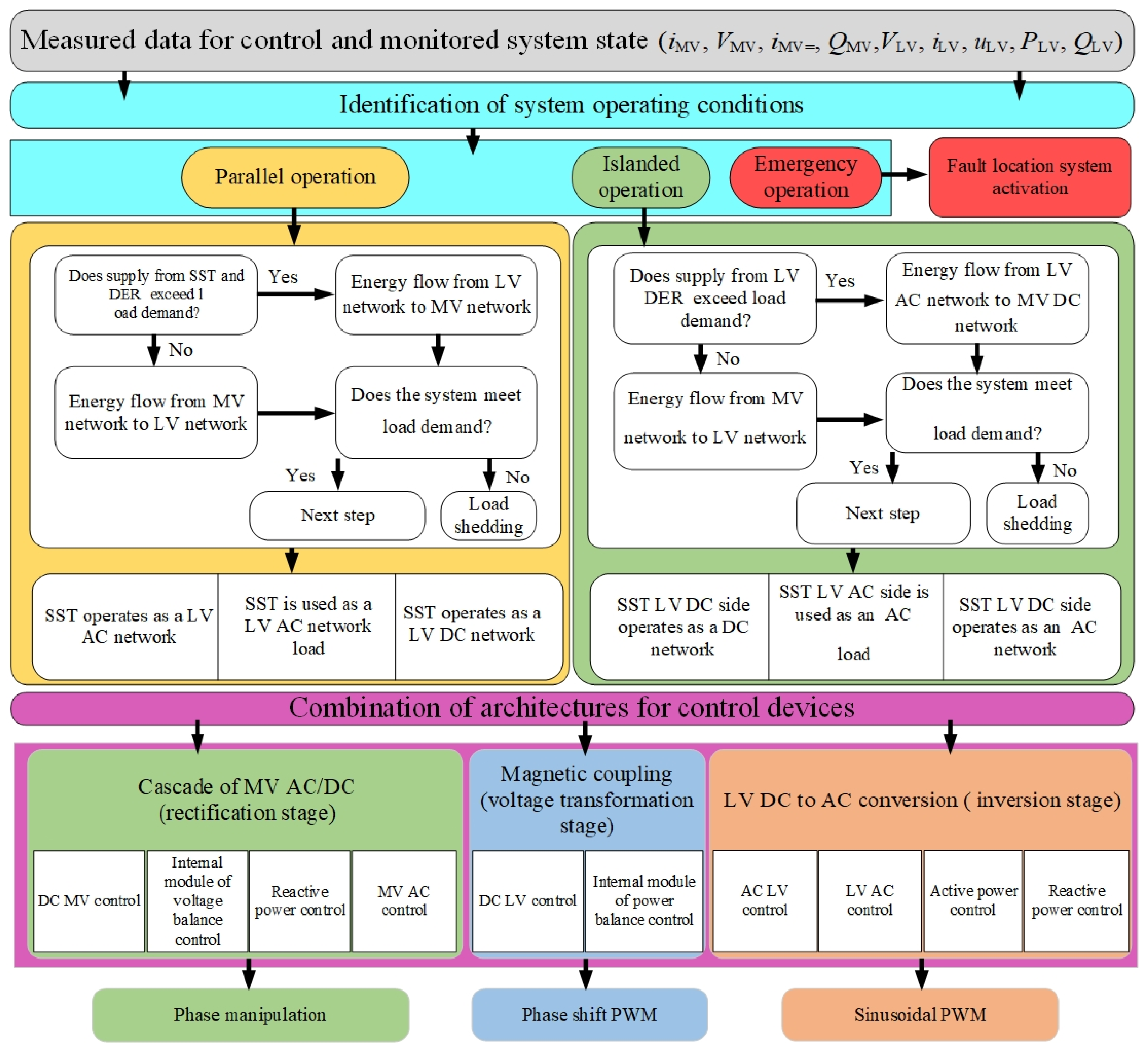
- controlling voltage, current, and frequency, as well as active and reactive power flows in active distribution networks;
- improving the quality of electric power due to the high switching frequency in PEC and filtering of harmonic components [59];
- switching on SSTs for parallel operation with power transformers of different rated powers due to the SST ability to fully control active and reactive power flow [60];
- developing electric charging infrastructure for electric vehicles due to the presence of LV DC output(s) for connecting electric charging stations to ensure fast charging of electric vehicles;
3. Main SST Topologies
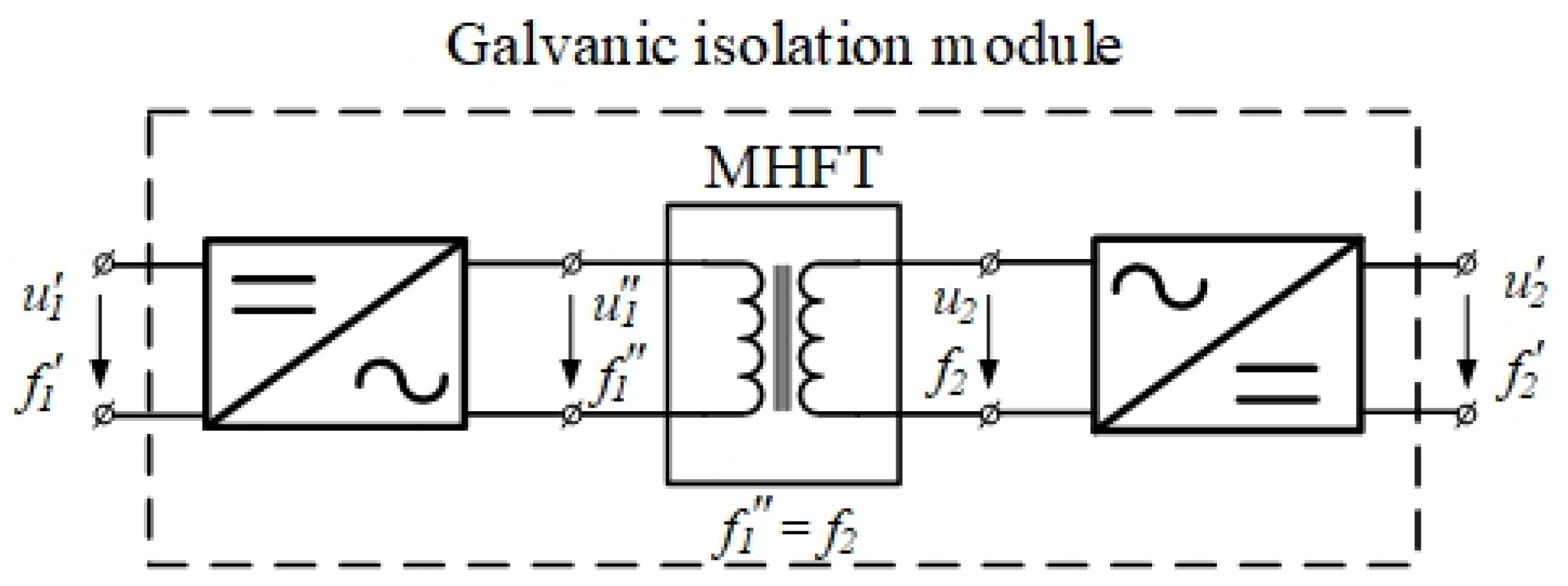
4. SST Control Principles
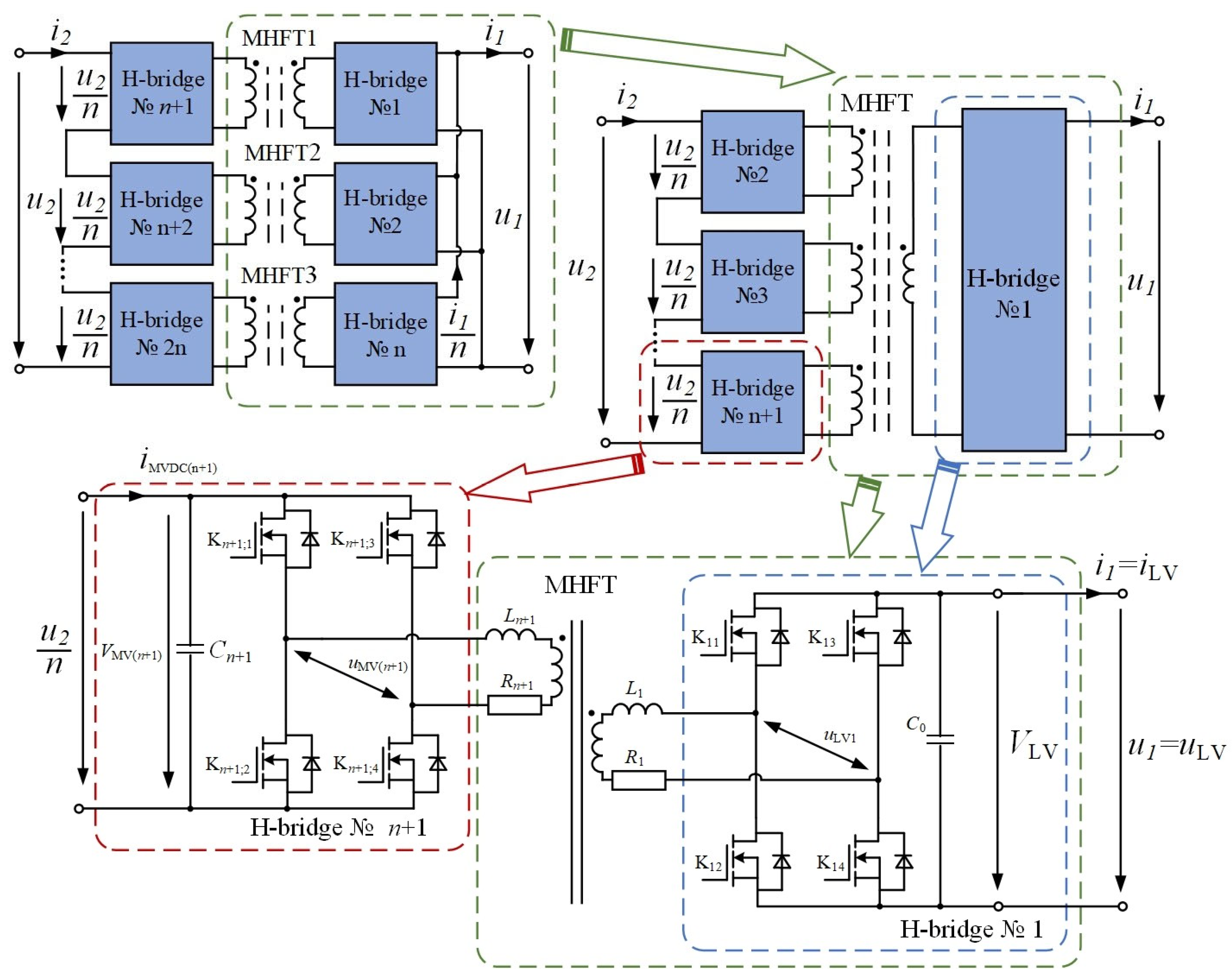
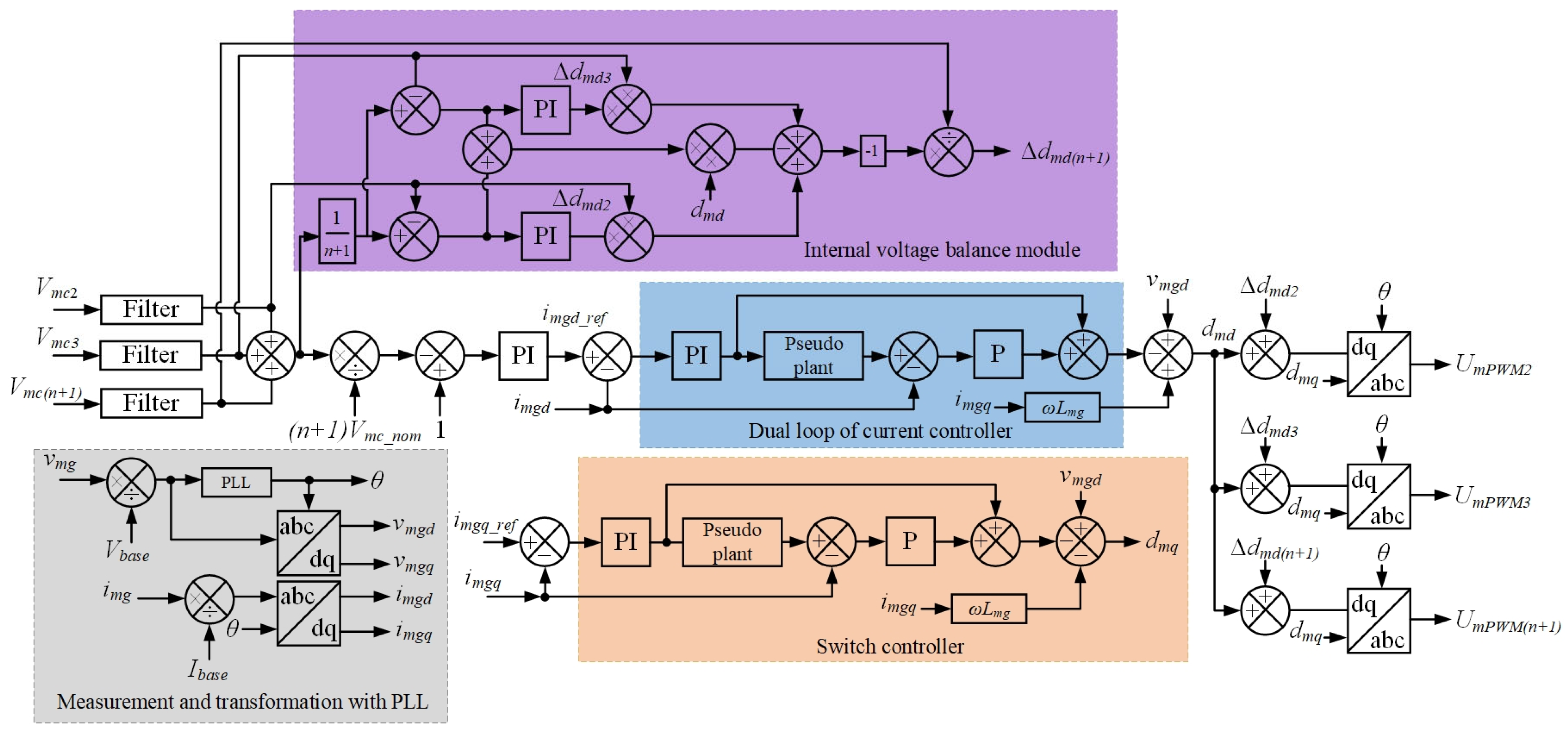
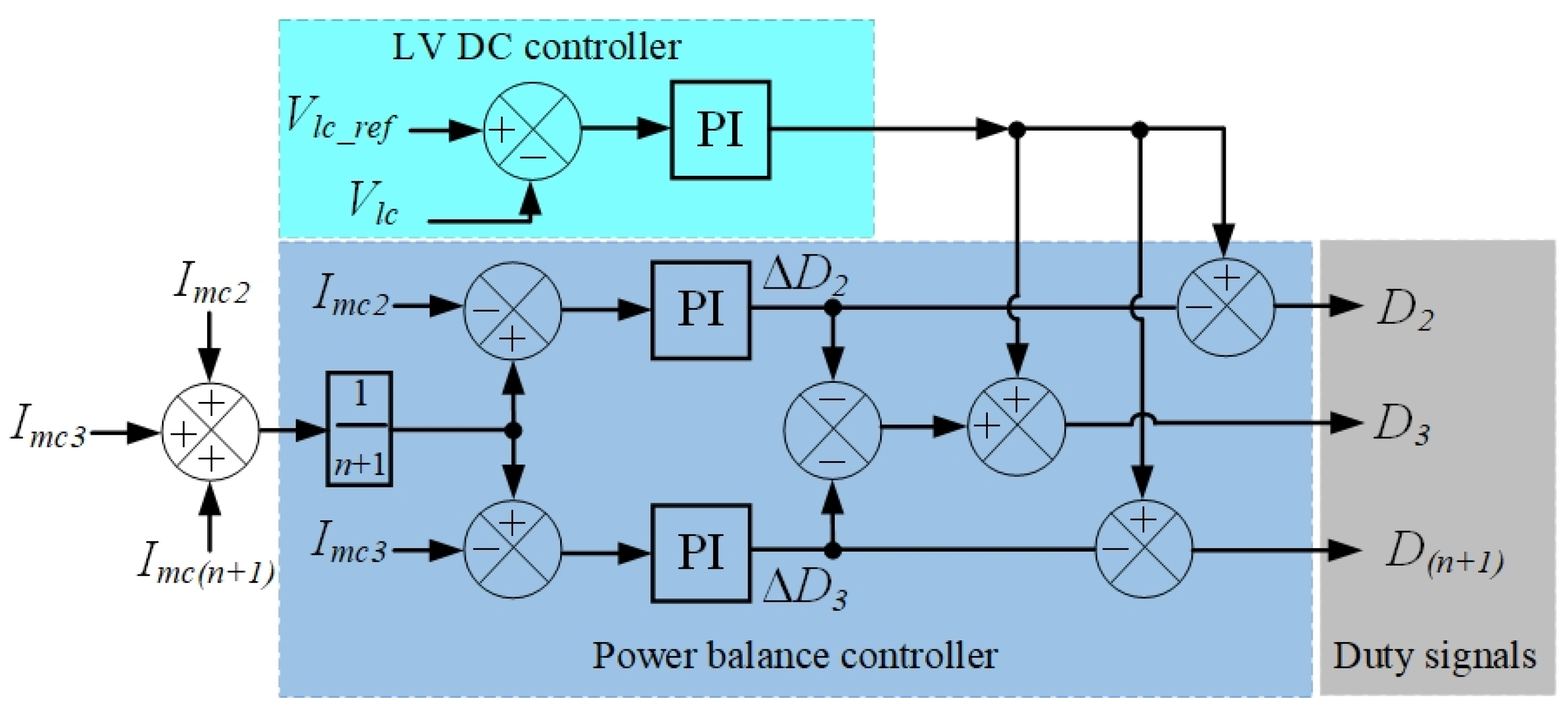
- the input module controller, which is responsible for the control of cascaded PECs with a dual-loop current control and the internal power balance module regulator during rectification (Figure 9);
- the galvanic isolation module controller, which controls electric power conversion, through the use of MHFT and PEC for DC-to-DC conversion (Figure 10);
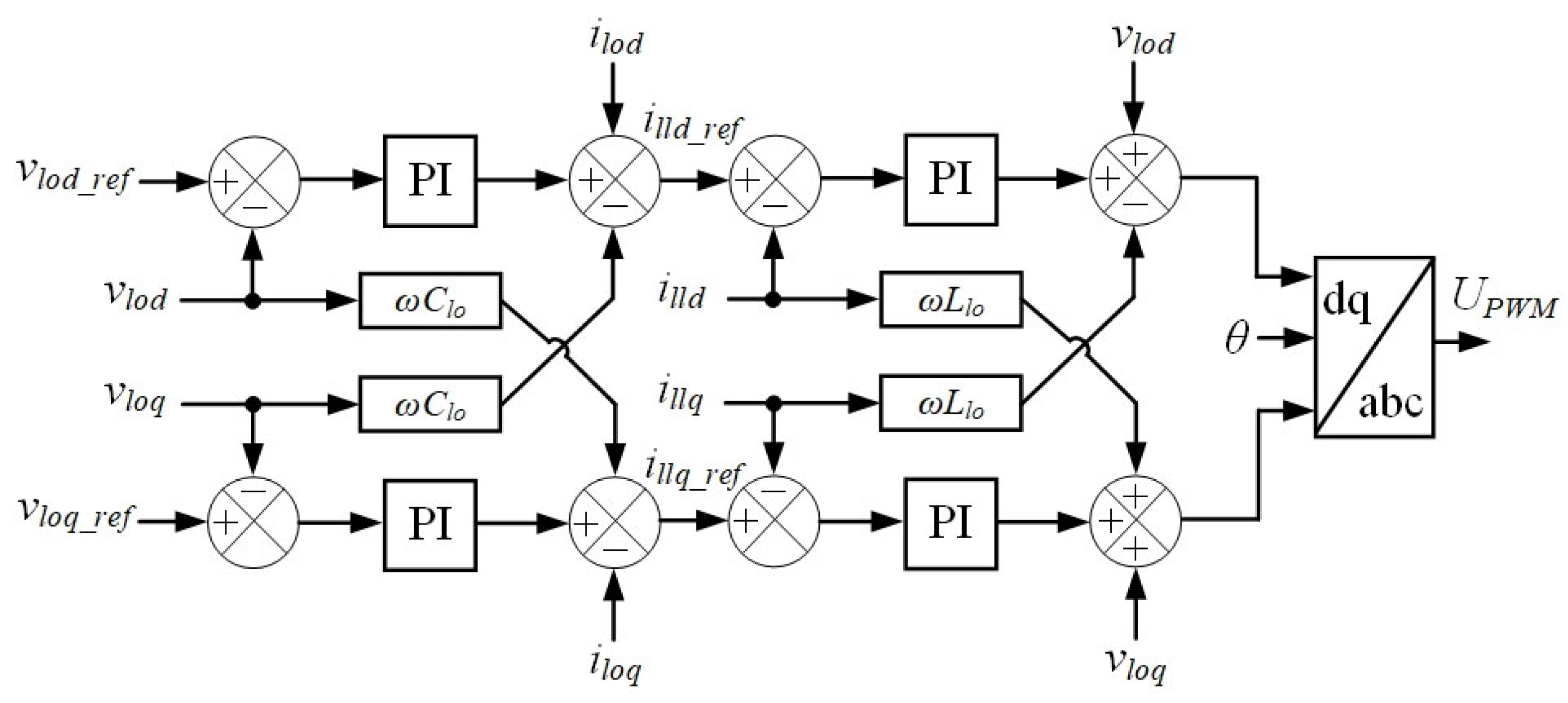
- the output module controller, which controls cascaded PECs for converting low-voltage DC into low-voltage AC (Figure 11).
- maintaining the voltage VLV at a given reference value on the LV side of the SST;
- balancing the cells for regulating the voltage on the DC bus of cascaded H-bridges, which allows the cells of the H-bridge to switch at the grid frequency without any additional voltage balance control;
- switching the cells of the cascaded H-bridges at the grid frequency with such switching angles of the H-bridge cells that the AC voltage inversion stages correspond to the input voltage of the SST (u1 or u2), and that the voltage conversion errors are minimal;
- switching in the galvanic isolation module at a high-frequency (40 kHz) to eliminate instantaneous voltage conversion errors introduced by the H-bridge cells and to yield a sinusoidal voltage waveform with a higher switching frequency on the SST MV side;
- using recirculating logic to minimize the unevenness of voltage and power distribution between the cells of the cascaded H-bridges to minimize losses in semiconductors arising due to switching on the SST MV side at a frequency of 50 Hz. In this case, switching at high frequencies is carried out only in the galvanic isolation module of the SST to increase its efficiency.
5. SST Control Methods
6. Discussion
Prospective Areas for Research and Development
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Di Silvestre, M.L.; Favuzza, S.; Sanseverino, E.R.; Zizzo, G. How Decarbonization, Digitalization, and Decentralization are changing key power infrastructures. Renew. Sustain. Energy Rev. 2018, 93, 483–498. [Google Scholar] [CrossRef]
- Muhanji, S.O.; Schoonenberg, W.C.H.; Farid, A.M. Transforming the Grid’s Architecture: Enterprise Control, the Energy In-ternet of Things, and Heterofunctional Graph Theory. IEEE Power Energy Mag. 2019, 17, 71–81. [Google Scholar] [CrossRef]
- Voropai, N. Electric Power System Transformations: A Review of Main Prospects and Challenges. Energies 2020, 13, 5639. [Google Scholar] [CrossRef]
- Florkowski, M.; Hayashi, H.; Matsuda, S.; Moribe, H.; Moriwaki, N.; Jones, D.; Pauska, J. Digitally Boosted Resilience: Digitalization to Enhance Resilience of Electric Power System. IEEE Power Energy Mag. 2024, 22, 100–109. [Google Scholar] [CrossRef]
- Boyko, E.; Byk, F.; Ilyushin, P.; Myshkina, L.; Suslov, K. Methods to Improve Reliability and Operational Flexibility by Inte-grating Hybrid Community Mini-Grids into Power Systems. Energy Rep. 2023, 9, 481–494. [Google Scholar] [CrossRef]
- Sidorov, D.; Panasetsky, D.; Tomin, N.; Karamov, D.; Zhukov, A.; Muftahov, I.; Dreglea, A.; Liu, F.; Li, Y. Toward Zero-Emission Hybrid AC/DC Power Systems with Renewable Energy Sources and Storages: A Case Study from Lake Baikal Region. Energies 2020, 13, 1226. [Google Scholar] [CrossRef]
- Burger, S.P.; Jenkins, J.D.; Huntington, C.S.; Pérez-Arriaga, I.J. Why Distributed?: A Critical Review of the Tradeoffs Between Centralized and Decentralized Resources. IEEE Power Energy Mag. 2019, 17, 16–24. [Google Scholar] [CrossRef]
- Ilyushin, P.; Filippov, S.; Kulikov, A.; Suslov, K.; Karamov, D. Intelligent Control of the Energy Storage System for Reliable Operation of Gas-Fired Reciprocating Engine Plants in Systems of Power Supply to Industrial Facilities. Energies 2022, 15, 6333. [Google Scholar] [CrossRef]
- Altamirano Flores, E.; Tinco Curi, V.; Tamayo Mattos, S.M.; Cáceres Cayllahua, E.; Quiroz Quezada, P.R. La Generación Distribuida como Complemento para la Confiabilidad del Suministro Eléctrico: Para el Desarrollo Económico Social Peruano. Cent. Sur 2025, 9, 15–26. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Filippov, S.P. Under-frequency load shedding strategies for power districts with distributed generation. In Proceedings of the 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 25–29 March 2019. [Google Scholar] [CrossRef]
- Čaušević, S.; Warnier, M.; Brazier, F.M. Self-determined distribution of local energy resources for ensuring power supply during outages. Energy Inform. 2019, 2, 6. [Google Scholar] [CrossRef]
- Blasi, T.M.; de Aquino, C.C.C.B.; Pinto, R.S.; de Lara Filho, M.O.; Fernandes, T.S.P.; Vila, C.U.; Aoki, A.R.; dos Santos, R.B.; Tabarro, F.H. Active Distribution Networks with Microgrid and Distributed Energy Resources Optimization Using Hierar-chical Model. Energies 2022, 15, 3992. [Google Scholar] [CrossRef]
- Jia, Q.; Jiao, W.; Chen, S.; Yan, Z.; Sun, H. A Trustworthy Cloud-Edge Collaboration Framework for Scheduling Distributed Energy Resources in Distribution Networks. IEEE Trans. Smart Grid 2025, 16, 2691–2694. [Google Scholar] [CrossRef]
- Zapparoli, L.; Oneto, A.; Parajeles Herrera, M.; Gjorgiev, B.; Hug, G.; Sansavini, G. Future Deployment and Flexibility of Distributed Energy Resources in the Distribution Grids of Switzerland. Sci. Data 2015, 12, 1491. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, S.; Chen, D. A Time- and Space-Integrated Expansion Planning Method for AC/DC Hybrid Distribution Networks. Sensors 2025, 25, 2276. [Google Scholar] [CrossRef]
- Cai, Y.; He, H.; Wen, Y.; Gao, Y.; Zhang, Q.; Zhang, S.; Lin, G. Optimal Scheduling Method of Medium and Low Voltage AC-DC Hybrid Distribution Network Based on Edge Cloud Cooperation. Recent Adv. Electr. Electron. Eng. 2025, 18, e23520965339482. [Google Scholar] [CrossRef]
- Mehdi, A.; Hassan, S.J.U.; Haider, Z.; Kim, H.-Y.; Hussain, A. Communication-Less Data-Driven Coordination Technique for Hybrid AC/DC Transmission Networks. Energies 2025, 18, 1416. [Google Scholar] [CrossRef]
- Mokgonyana, L.; Smith, K.; Galloway, S. Reconfigurable Low Voltage Direct Current Charging Networks for Plug-In Electric Vehicles. IEEE Trans. Smart Grid 2019, 10, 5458–5467. [Google Scholar] [CrossRef]
- Deng, M.; Zhao, J.; Huang, W.; Wang, B.; Liu, X.; Ou, Z. Optimal Layout Planning of Electric Vehicle Charging Stations Con-sidering Road–Electricity Coupling Effects. Electronics 2025, 14, 135. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J. Distributed Power, Energy Storage Planning, and Power Tracking Studies for Distribution Networks. Electronics 2025, 14, 2833. [Google Scholar] [CrossRef]
- Volnyi, V.; Ilyushin, P.; Suslov, K.; Filippov, S. Approaches to Building AC and AC–DC Microgrids on Top of Existing Passive Distribution Networks. Energies 2023, 16, 5799. [Google Scholar] [CrossRef]
- Garcia, I.; Santana, R. Unified Framework for the Analysis of the Effect of Control Strategies on On-Load Tap-Changer’s Automatic Voltage Controller. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1539–1548. [Google Scholar] [CrossRef]
- McGrath, A. Advances in MV voltage regulators. In Proceedings of the 2013 48th International Universities’ Power Engineering Conference (UPEC), Dublin, Ireland, 2–5 September 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Astashev, M.G.; Lunin, K.A.; Panfilov, D.I.; Petrov, M.I.; Rashitov, P.A. Semiconductor Voltage Regulators-Stabilizers for Distribution Networks. Power Technol. Eng. 2021, 55, 310–313. [Google Scholar] [CrossRef]
- Mishra, M.K. Power Electronics in Energy Systems: Enhancing Efficiency and Quality in Electrical Energy Conversion and Distribution. J. Data Sci. Inf. Technol. 2024, 1, 24–31. [Google Scholar] [CrossRef]
- Jarret, K.; Hedgecock, J.; Gregory, R.; Warham, T. Technical Guide to the Connexion of Generation to the Distribution Network; Department of Trade and Industry: London, UK, 2004. [Google Scholar]
- Schneider, L.; Pehnt, M. Embedding Micro Cogeneration in the Energy Supply System. In Micro Cogeneration; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Buchholz, B.M.; Styczynski, Z. Smart Grids—Fundamentals and Technologies in Electricity Networks; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2014; 396p. [Google Scholar]
- Electricity NIC Submission: SP Energy Networks—LV Engine, Nov 2017. Available online: https://www.ofgem.gov.uk/publications/electricity-nic-submission-sp-energy-networks-lv-engine (accessed on 26 August 2025).
- Syed, I.; Khadkikar, V.; Zeineldin, H.H. Loss Reduction in Radial Distribution Networks Using a Solid-State Transformer. IEEE Trans. Ind. Appl. 2018, 54, 5474–5482. [Google Scholar] [CrossRef]
- Kala, H.; Rawat, M.S.; Uniyal, A. Optimal allocation and technoeconomic analysis of solid state transformer in distribution network. Comput. Electr. Eng. 2025, 125, 110417. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Gan, J.; Ren, Q.; Yu, H.; Zhao, Y.; Zhang, H. A Cooperative Operation Optimization Method for Medium- and Low-Voltage Distribution Networks Considering Flexible Interconnected Distribution Substation Areas. Processes 2025, 13, 1123. [Google Scholar] [CrossRef]
- Xu, L.; Zeng, H.; Lin, N.; Yang, Y.; Guo, Q.; Poor, H.V. Risk-aware electricity dispatch with large-scale distributed renewable integration under climate extremes. Proc. Natl. Acad. Sci. USA 2025, 122, e2426620122. [Google Scholar] [CrossRef]
- Makanju, T.D.; Hasan, A.N.; Famoriji, O.J.; Shongwe, T. An Intelligent Technique for Coordination and Control of PV Energy and Voltage-Regulating Devices in Distribution Networks Under Uncertainties. Energies 2025, 18, 3481. [Google Scholar] [CrossRef]
- Ilyushin, P.V. Emergency and post-emergency control in the formation of micro-grids. E3S Web Conf. 2017, 25, 02002. [Google Scholar] [CrossRef]
- Kulikov, A.L.; Ilyushin, P.V.; Suslov, K.V.; Karamov, D.N. Coherence of Digital Processing of Current and Voltage Signals at Decimation for Power Systems with a Large Share of Renewable Power Stations. Energy Rep. 2022, 8, 1464–1478. [Google Scholar] [CrossRef]
- Aoun, A.; Adda, M.; Ilinca, A.; Ghandour, M.; Ibrahim, H.; Salloum, S. Efficient Modeling of Distributed Energy Resources’ Impact on Electric Grid Technical Losses: A Dynamic Regression Approach. Energies 2024, 17, 2053. [Google Scholar] [CrossRef]
- Iqbal, H.; Stevenson, A.; Sarwat, A.I. Impact Analysis and Optimal Placement of Distributed Energy Resources in Diverse Distribution Systems for Grid Congestion Mitigation and Performance Enhancement. Electronics 2025, 14, 1998. [Google Scholar] [CrossRef]
- Kulikov, A.L.; Shepovalova, O.V.; Ilyushin, P.V.; Filippov, S.P.; Chirkov, S.V. Control of Electric Power Quality Indicators in Distribution Networks Comprising a High Share of Solar Photovoltaic and Wind Power Stations. Energy Rep. 2022, 8, 1501–1514. [Google Scholar] [CrossRef]
- Kulikov, A.; Ilyushin, P.; Suslov, K.; Filippov, S. Organization of Control of the Generalized Power Quality Parameter Using Wald’s Sequential Analysis Procedure. Inventions 2023, 8, 17. [Google Scholar] [CrossRef]
- IEEE Std C57.12.00-2015 (Revision of IEEE Std C57.12.00-2010); IEEE Standard for General Requirements for Liquid-Immersed Distribution, Power, and Regulating Transformers. IEEE: New York, NY, USA, 2016; 74p.
- IEC 60076-1:2011; Power Transformer—Part 1: General. IEC: New York, NY, USA, 2011; 147p.
- GOST 30830-2002 (IEC 60076-1-93); Power Transformers. Part 1. General Provisions. IPK Publishing House of Standards: Moscow, Russia, 2003; 28p. (In Russian)
- Tenyenhuis, G. Reverse Power Flow Impacts for Legacy Power Transformers; CIGRE: Paris, France, 2022. [Google Scholar]
- Cipcigan, L.; Taylor, P.C. Investigation of the reverse power flow requirements of high penetrations of small-scale embedded generation. Renew. Power Gener. 2007, 1, 160–166. [Google Scholar] [CrossRef]
- Majeed, I.B.; Nwulu, N.I. Impact of Reverse Power Flow on Distributed Transformers in a Solar-Photovoltaic-Integrated Low-Voltage Network. Energies 2022, 15, 9238. [Google Scholar] [CrossRef]
- Cheng, D.; Mather, B.A.; Seguin, R.; Hambrick, J.; Broadwater, R.P. Photovoltaic (PV) Impact Assessment for Very High Penetration Levels. IEEE J. Photovolt. 2016, 6, 295–300. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhao, Z. Grid-connected photovoltaic power systems: Technical and potential problems—A review. Renew. Sustain. Energy Rev. 2010, 14, 112–129. [Google Scholar] [CrossRef]
- Huber, J.E.; Kolar, J.W. Solid-State Transformers: On the Origins and Evolution of Key Concepts. IEEE Ind. Electron. Mag. 2016, 10, 19–28. [Google Scholar] [CrossRef]
- Rehman, A.; Imran-Daud, M.; Haider, S.K.; Rehman, A.U.; Shafiq, M.; Eldin, E.T. Comprehensive Review of Solid State Transformers in the Distribution System: From High Voltage Power Components to the Field Application. Symmetry 2022, 14, 2027. [Google Scholar] [CrossRef]
- Bala, S.; Das, D.; Aeloiza, E.; Maitra, A.; Rajagopalan, S. Hybrid distribution transformer: Concept development and field demonstration. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 4061–4068. [Google Scholar] [CrossRef]
- Kopacz, R.; Menzi, D.; Krismer, F.; Rąbkowski, J.; Kolar, J.W.; Huber, J. New single-stage bidirectional three-phase ac-dc solid-state transformer. Electron. Lett. 2024, 60, e13084. [Google Scholar] [CrossRef]
- Brooks, J.L. Solid State Transformer Concept Development; Naval Construction Battalion Center: Port Hueneme, CA, USA, 1980; 51p. [Google Scholar]
- Adhikari, B.; Ghassemi, M. A Review of Electrical Insulation Challenges in Medium Voltage High-Frequency Transformers for Solid State Transformers. In Proceedings of the 2025 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 24–25 April 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Yi, Z.; Sun, K.; Liu, H.; Cao, G.; Lu, S. Design and Optimization of the Insulation of Medium-Voltage Medium-Frequency Transformers for Solid-State Transformers. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3561–3570. [Google Scholar] [CrossRef]
- Nirea, H.L.; Zhang, J.; Zhou, J.; Shi, G.; Luo, J.; Chen, G. A Novel Cascaded Multilevel Inverter and Modular Multilevel DC Transformer-Based Solid-State Transformer for Distribution Networks. In Proceedings of the 2025 IEEE 16th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Nanjing, China, 22–25 June 2025; pp. 73–78. [Google Scholar] [CrossRef]
- Chivenkov, A.I.; Sosnina, E.N.; Lipuzhin, I.A.; Trofimov, I.M.; Aleshin, D.A. Development and Research of Low-Voltage Solid-State Transformer. Russ. Electr. Engin. 2024, 95, 819–825. [Google Scholar] [CrossRef]
- Nila-Olmedo, N.; Mendoza-Mondragon, F.; Espinosa-Calderon, A.M. ARM+FPGA platform to manage solid-state-smart transformer in smart grid application. In Proceedings of the 2016 International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 30 November–2 December 2016; pp. 1–6. [Google Scholar]
- Avdeev, B.; Vyngra, A.; Chernyi, S. Improving the Electricity Quality by Means of a Single-Phase Solid-State Transformer. Designs 2020, 4, 35. [Google Scholar] [CrossRef]
- Manjrekar, M.D.; Kieferndorf, R.; Venkataramanan, G. Power electronic transformers for utility applications. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference. Thirty-Fifth IAS Annual Meeting and World Con-ference on Industrial Applications of Electrical Energy (Cat. No.00CH37129), Rome, Italy, 8–12 October 2000; Volume 4, pp. 2496–2502. [Google Scholar] [CrossRef]
- Eroshenko, S.A.; Ilyushin, P.V. Features of implementing multi-parameter islanding protection in power districts with dis-tributed generation units. In Proceedings of the 2018 IEEE 59th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–14 November 2018. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Pazderin, A.V. Requirements for power stations islanding automation an influence of power grid parameters and loads. In Proceedings of the 2018 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Moscow, Russia, 15–18 May 2018. [Google Scholar] [CrossRef]
- Al-Mahdawi, E.; Butler, A. Solid-State Transformers: A Game-Changer for Off- Grid and Emergency Power Systems. Int. J. Recent Technol. Eng. 2025, 14, 23–30. [Google Scholar] [CrossRef]
- Hang, M.; Xing, J.; Cheng, Y.; Yu, P. Multi-source Collaborative Optimal Scheduling Platform for Flexible Interconnected AC/DC Hybrid Distribution Networks. In Energy Power and Automation Engineering. ICEPAE 2023; Lecture Notes in Electrical Engineering; Yadav, S., Arya, Y., Muhamad, N.A., Sebaa, K., Eds.; Springer: Singapore, 2024; Volume 1118, pp. 353–362. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, L.; Tang, W.; Li, G.; Wang, C. Optimal Planning of Hybrid AC/DC Low-Voltage Distribution Networks Considering DC Conversion of Three-Phase Four-Wire Low-Voltage AC Systems. J. Mod. Power Syst. Clean Energy 2024, 12, 141–153. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Pazderin, A.V.; Seit, R.I. Photovoltaic power plants participation in frequency and voltage regulation. In Proceedings of the 17th International Ural Conference on AC Electric Drives (ACED), Ekaterinburg, Russia, 26–30 March 2018. [Google Scholar] [CrossRef]
- Chen, H.; Prasai, A.; Moghe, R.; Chintakrinda, K.; Divan, D. A 50-kVA Three-Phase Solid-State Transformer Based on the Minimal Topology: Dyna-C. IEEE Trans. Power Electron. 2016, 31, 8126–8137. [Google Scholar] [CrossRef]
- Valedsaravi, S.; El Aroudi, A.; Martínez-Salamero, L. Review of Solid-State Transformer Applications on Electric Vehicle DC Ultra-Fast Charging Station. Energies 2022, 15, 5602. [Google Scholar] [CrossRef]
- Kadandani, N.B.; Abubakar, I. On exploring the power quality enhancement capability and other ancillary functionalities of solid state transformer application in the distribution system. Bayero J. Eng. Technol. 2023, 18, 28–39. [Google Scholar]
- Abu-Siada, A.; Budiri, J.; Abdou, A.F. Solid State Transformers Topologies, Controllers, and Applications: State-of-the-Art Literature Review. Electronics 2018, 7, 298. [Google Scholar] [CrossRef]
- Faiad, A.A.; Hebala, O.M.; Hamad, M.S.; Abdel-Khalik, A.S. A Modular Multilevel Converter Based Solid State Transformer (MMC-SST) for High Power Wind Generators. In Proceedings of the 22nd International Middle East Power Systems Conference (MEPCON), Assiut, Egypt, 14–16 December 2021; pp. 631–636. [Google Scholar] [CrossRef]
- Predescu, D.-M.; Roșu, Ș.-G. Solid State Transformers: A Review—Part I: Stages of Conversion and Topologies. Technologies 2025, 13, 74. [Google Scholar] [CrossRef]
- Khan, S.; Rahman, K.; Tariq, M.; Hameed, S.; Alamri, B.; Babu, T.S. Solid-State Transformers: Fundamentals, Topologies, Applications, and Future Challenges. Sustainability 2022, 14, 319. [Google Scholar] [CrossRef]
- Huber, J.; Ortiz, G.; Krismer, F.; Widmer, N.; Kolar, J.W. η-ρ Pareto optimization of bidirectional half-cycle discontinu-ous-conduction-mode series-resonant DC/DC converter with fixed voltage transfer ratio. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 1413–1420. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Shao, S. A Three-Phase Modular Multilevel DC–DC Converter for Power Electronic Transformer Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 140–150. [Google Scholar] [CrossRef]
- Shadfar, H.; Pashakolaei, M.G.; Foroud, A.A. Solid-state transformers: An overview of the concept, topology, and its applications in the smart grid. Int. Trans. Electr. Energy Syst. 2021, 31, e12996. [Google Scholar] [CrossRef]
- Rahman, M.A.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Modeling and Control of SiC-Based High-Frequency Magnetic Linked Converter for Next Generation Solid State Transformers. IEEE Trans. Energy Convers. 2020, 35, 549–559. [Google Scholar] [CrossRef]
- Rahman, M.A.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Modeling, Design, and Control of Solid-State Transformer for Grid Integration of Renewable Sources. In Emerging Power Converters for Renewable Energy and Electric Vehicles; CRC Press: Boca Raton, FL, USA, 2021; 36p. [Google Scholar]
- Bhajana, V.V.S.K.; Jarzyna, W.; Fatyga, K.; Zielinski, D.; Kwaśny, L. Performance of a SiC mosfet based isolated dual active bridge DC-DC converter for electro-mobility applications. Rev. Roum. Des Sci. Tech. 2019, 64, 383–390. [Google Scholar]
- Chakraborty, S.S.; Bhawal, S.; Hatua, K. Minimization of Low Frequency Current Oscillation in Resonant Link of a Solid State Transformer by Passive Filters. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Pazderin, A.V. Approaches to Organization of Emergency Control at Isolated Operation of Energy Areas with Distributed Generation. In Proceedings of the 2018 International Ural Conference on Green Energy (UralCon), Chelyabinsk, Russia, 4–6 October 2018; pp. 149–155. [Google Scholar] [CrossRef]
- Coelho, S.; Dionizio, A.; Cunha, J.; Monteiro, V.; Afonso, J.L. Solid-state transformer: The catalyst for resilient and sustainable smart grids. Energy 2025, 327, 136321. [Google Scholar] [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme fast charging of electric vehicles: A technology overview. IEEE Transac. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Zentani, A.; Almaktoof, A.; Kahn, M.T. A Comprehensive Review of Developments in Electric Vehicles Fast Charging Technology. Appl. Sci. 2024, 14, 4728. [Google Scholar] [CrossRef]
- Rahman, M.A.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Data-Driven Coordinated Control of Converters in a Smart Solid-State Transformer for Reliable and Automated Distribution Grids. IEEE Trans. Ind. Appl. 2020, 56, 4532–4542. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, G.; Bhattacharya, S.; Huang, A.Q. Voltage and Power Balance Control for a Cascaded H-Bridge Converter-Based Solid-State Transformer. IEEE Trans. Power Electron. 2013, 28, 1523–1532. [Google Scholar] [CrossRef]
- Nie, J.; Yuan, L.; Wen, W.; Duan, R.; Shi, B.; Zhao, Z. Communication-independent power balance control for solid state transformer interfaced multiple power conversion systems. IEEE Trans. Power Electron. 2019, 35, 4256–4271. [Google Scholar] [CrossRef]
- Bhawal, S.; Patel, H.; Hatua, K.; Vasudevan, K.; Bhattacharya, S. Solid-State Transformer Based on Naturally Cell Balanced Series Resonant Converter with Cascaded H-Bridge Cells Switched at Grid Frequency. IEEE Trans. Power Electron. 2023, 38, 8208–8222. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Q.; Qin, D.; Cheng, K.; Li, Z. Power Control of a Modular Three-Port Solid-State Transformer with Three-Phase Unbalance Regulation Capabilities. IEEE Access 2020, 8, 72859–72869. [Google Scholar] [CrossRef]
- Cao, L.; Tang, Y.; Liu, W.; Wang, X.; Bai, Y.; Li, X.; Ding, J.; Tian, X.; Hao, J.; Liu, X. A novel four-terminal SiC MOSFET with improved single-event effect performance. Semicond. Sci. Technol. 2025, 40, 075008. [Google Scholar] [CrossRef]
- Madhusoodhanan, S.; Tripathi, A.; Patel, D.; Mainali, K.; Kadavelugu, A.; Hazra, S.; Bhattacharya, S.; Hatua, K. Solid State Transformer and MV grid tie applications enabled by 15 kV SiC IGBTs and 10 kV SiC MOSFETs based multilevel converters. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014—ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; pp. 1626–1633. [Google Scholar] [CrossRef]
- Zheng, L.; Han, X.; Kandula, R.P.; Kandasamy, K.; Saeedifard, M.; Divan, D. 7.2 kV Three-Port Single-Phase Single-Stage Modular Soft-Switching Solid-State Transformer with Active Power Decoupling and Reduced DC-Link. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 1575–1581. [Google Scholar] [CrossRef]
- Jakka, V.N.S.R.; Shukla, A.; Demetriades, G.D. Dual-Transformer-Based Asymmetrical Triple-Port Active Bridge (DT-ATAB) Isolated DC–DC Converter. IEEE Trans. Ind. Electron. 2017, 64, 4549–4560. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, D.; Wang, Y.; Wu, B.; Athab, H.S. Power and Voltage Balance Control of a Novel Three-Phase Solid-State Transformer Using Multilevel Cascaded H-Bridge Inverters for Microgrid Applications. IEEE Trans. Power Electron. 2016, 31, 3289–3301. [Google Scholar] [CrossRef]
- Ding, C.; Zhang, H.; Chen, Y.; Pu, G. Research on Control Strategy of Solid State Transformer Based on Improved MPC Method. IEEE Access 2023, 11, 9431–9440. [Google Scholar] [CrossRef]
- Ji, Z.; Sun, Y.; Jin, C.; Wang, J.; Zhao, J. A coordinated DC voltage control strategy for cascaded solid state transformer with star configuration. Turk. J. Electr. Eng. Comput. Sci. 2019, 27, 634–648. [Google Scholar] [CrossRef]
- Mao, X.; Falcones, S.; Ayyanar, R. Energy-based control design for a solid state transformer. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Ge, J.; Zhao, Z.; Yuan, L.; Lu, T. Energy Feed-Forward and Direct Feed-Forward Control for Solid-State Transformer. IEEE Trans. Power Electron. 2015, 30, 4042–4047. [Google Scholar] [CrossRef]
- Shamshuddin, M.A.; Rojas, F.; Cardenas, R.; Pereda, J.; Diaz, M.; Kennel, R. Solid State Transformers: Concepts, Classification, and Control. Energies 2020, 13, 2319. [Google Scholar] [CrossRef]
- Kadandani, N.B.; Hassan, S.; Abubakar, I. Solid State Transformer (SST) and the Challenges of the Future Grid. FUDMA J. Sci. 2023, 7, 330–335. [Google Scholar] [CrossRef]
- Nardoto, A.F.; Amorim, A.E.A.; Encarnação, L.F.; Santos, W.M.; Bueno, E.J.; Blanco, D.M. Model predictive control for solid state transformer. Electr. Power Syst. Res. 2023, 223, 109658. [Google Scholar] [CrossRef]
- Baier, C.R.; Ramirez, R.O.; Marciel, E.I.; Hernández, J.C.; Melín, P.E.; Espinosa, E.E. FCS-MPC Without Steady-State Error Applied to a Grid-Connected Cascaded H-Bridge Multilevel Inverter. IEEE Trans. Power Electron. 2021, 36, 11785–11799. [Google Scholar] [CrossRef]
- Li, Y.; Han, J.; Cao, Y.; Li, Y.; Xiong, J.; Sidorov, D.; Panasetsky, D. A modular multilevel converter type solid state transformer with internal model control method. Int. J. Electr. Power Energy Syst. 2017, 85, 153–163. [Google Scholar] [CrossRef]
- Disfani, V.R.; Fan, L.; Miao, Z.; Ma, Y. Fast model predictive control algorithms for fast-switching modular multilevel converters. Electr. Power Syst. Res. 2015, 129, 105–113. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Ouyang, S.; Xu, T.; Meng, F.; Song, S. Control and Experiment of an H-Bridge-Based Three-Phase Three-Stage Modular Power Electronic Transformer. IEEE Trans. Power Electron. 2016, 31, 2002–2011. [Google Scholar] [CrossRef]
- Song, W.; Hou, N.; Wu, M. Virtual Direct Power Control Scheme of Dual Active Bridge DC–DC Converters for Fast Dynamic Response. IEEE Trans. Power Electron. 2018, 33, 1750–1759. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, L.; Wang, J.; Gao, X.; Li, Z.; Zhang, Z. Robust Predictive Current Control of Permanent-Magnet Synchronous Motors with Newly Designed Cost Function. IEEE Trans. Power Electron. 2020, 35, 10778–10788. [Google Scholar] [CrossRef]
- Feng, G.; Zhao, Z.; Yuan, L.; Li, K. Combined DC voltage control scheme for three-port energy router based on instantaneous energy balance. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Fuentes, C.; Chavez, H.; Paternina, M.R.A. Predictive Control-Based NADIR-Minimizing Algorithm for Solid-State Trans-former. Energies 2022, 15, 73. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, H.; Li, D. A Fast and Fixed Switching Frequency Model Predictive Control with Delay Compensation for Three-Phase Inverters. IEEE Access 2017, 5, 17904–17913. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, W.; Li, Z.; Zhang, Y. Low-Complexity Model Predictive Power Control: Double-Vector-Based Approach. IEEE Trans. Ind. Electron. 2014, 61, 5871–5880. [Google Scholar] [CrossRef]
- Sun, Q.; Li, Y.; Ma, D.; Zhang, Y.; Qin, D. Model Predictive Direct Power Control of Three-Port Solid-State Transformer for Hybrid AC/DC Zonal Microgrid Applications. IEEE Trans. Power Deliv. 2022, 37, 528–538. [Google Scholar] [CrossRef]
- Lazanyuk, I.; Ratner, S.; Revinova, S.; Gomonov, K.; Modi, S. Diffusion of Renewable Microgeneration on the Side of End-User: Multiple Case Study. Energies 2023, 16, 2857. [Google Scholar] [CrossRef]
- Karamov, D.N.; Ilyushin, P.V.; Suslov, K.V. Electrification of Rural Remote Areas Using Renewable Energy Sources: Literature Review. Energies 2022, 15, 5881. [Google Scholar] [CrossRef]
- Wei, T.; Cervone, A.; Dujic, D. Active Power Decoupling for Single-Phase Input–Series–Output–Parallel Solid-State Trans-formers. IEEE Trans. Power Electron. 2024, 39, 5636–5648. [Google Scholar] [CrossRef]
- Ramírez, J.C.; Gómez-Luna, E.; Vasquez, J.C. Technical and Economic Feasibility Analysis to Implement a Solid-State Trans-former in Local Distribution Systems in Colombia. Energies 2025, 18, 3723. [Google Scholar] [CrossRef]


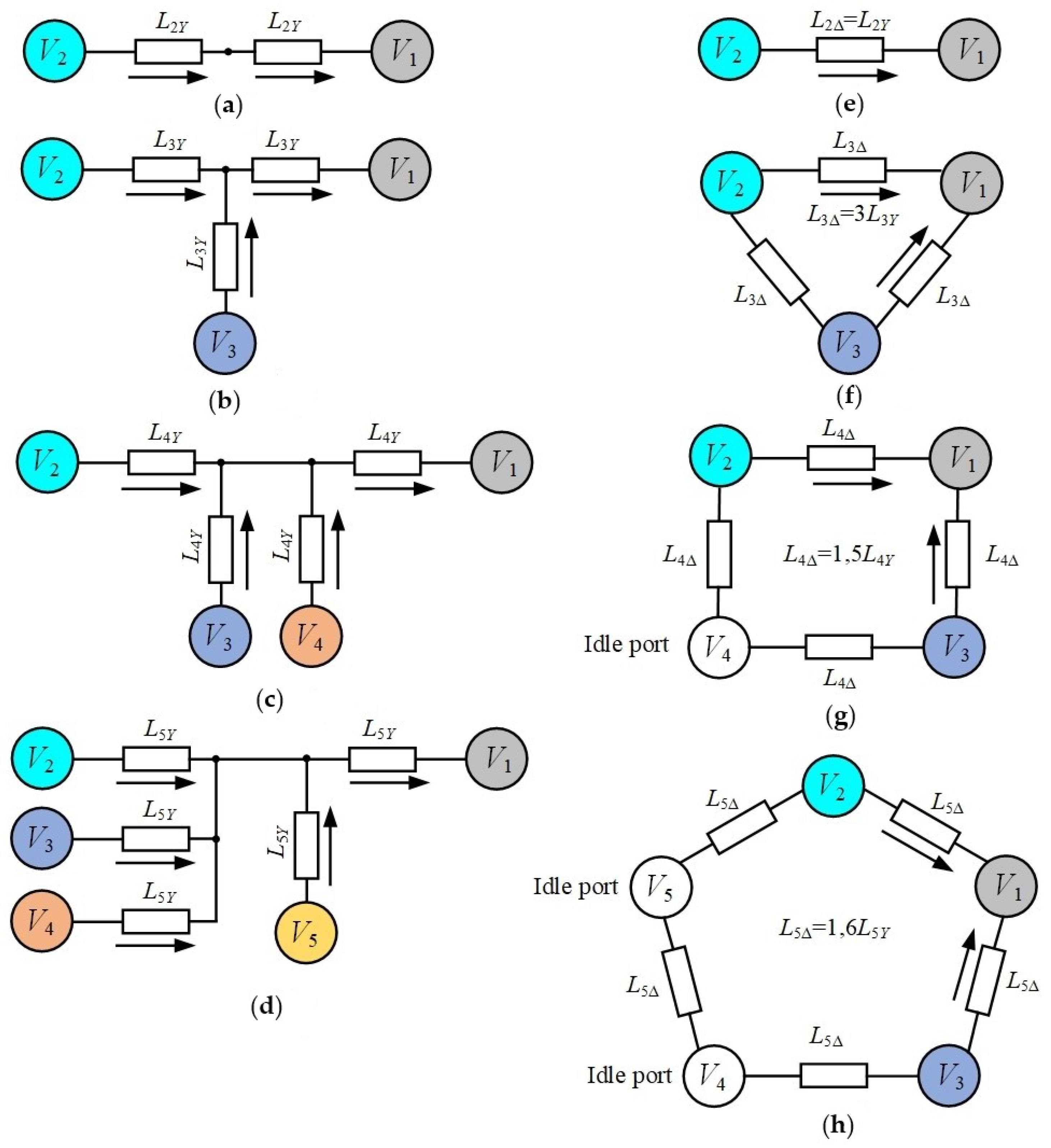

| PWM Control Method | Features | Advantages | Disadvantages | Application Areas |
|---|---|---|---|---|
| Single-phase shift | Phase shift between bridge arms | Simplicity and natural switching (zero voltage switching—ZVS) | Limited ZVS and high circulating currents | Basic and low-cost systems with a stable load |
| Extended shift | Additional shift | Flexibility and wider ZVS range | Increased control complexity | High-efficiency systems |
| Dual phase shift | Multi-level voltage (two shifts) | High efficiency, wide ZVS range, and low interference | High computational load | High-efficiency and high-dispersion systems |
| Phase shift keying | DC voltage level regulation | Clean RF waveform and simple inverter | Low efficiency and slow response | Systems with high requirements for voltage sinusoidality |
| Sinusoidal PWM | Formation of a 50/60 Hz sine wave | High output voltage quality | High losses and not suitable for RF applications | Output stage for generating line voltage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilyushin, P.; Volnyi, V.; Suslov, K. Review of Approaches to Creating Control Systems for Solid-State Transformers in Hybrid Distribution Networks. Appl. Sci. 2025, 15, 10970. https://doi.org/10.3390/app152010970
Ilyushin P, Volnyi V, Suslov K. Review of Approaches to Creating Control Systems for Solid-State Transformers in Hybrid Distribution Networks. Applied Sciences. 2025; 15(20):10970. https://doi.org/10.3390/app152010970
Chicago/Turabian StyleIlyushin, Pavel, Vladislav Volnyi, and Konstantin Suslov. 2025. "Review of Approaches to Creating Control Systems for Solid-State Transformers in Hybrid Distribution Networks" Applied Sciences 15, no. 20: 10970. https://doi.org/10.3390/app152010970
APA StyleIlyushin, P., Volnyi, V., & Suslov, K. (2025). Review of Approaches to Creating Control Systems for Solid-State Transformers in Hybrid Distribution Networks. Applied Sciences, 15(20), 10970. https://doi.org/10.3390/app152010970








