Bearing Semi-Supervised Anomaly Detection Using Only Normal Data

Abstract

Bearings are ubiquitous machinery parts. Monitoring and diagnosing their state is essential for reliable functioning. Machine learning techniques are now established tools for anomaly detection. We focus on a less used setup, although a very natural one: the data available for training come only from normal behavior, as the faults are various and cannot be all simulated. This setup belongs to semi-supervised learning, and the purpose is to obtain a method that is able to distinguish between normal and faulty data. We focus on the Case Western Reserve University (CWRU) dataset, since it is relevant for bearing behavior. We investigate several methods, among which one based on Dictionary Learning (DL) and another using graph total variation stand out; the former was less used for anomaly detection, and the latter is a new algorithm. We find that, together with Local Factor Outlier (LOF), these algorithms are able to identify anomalies nearly perfectly, in two scenarios: on the raw time-domain data and also on features extracted from them.

1. Introduction

Continuous machine health monitoring is essential for the rapid identification of faults and has been aided, in recent years, by anomaly detection techniques. It is also the case for rotating machinery, where bearing faults constitute a frequent and important cause of malfunctioning [1]. Vibrational signals, collected from accelerometers mounted on the machine, are often used for the task, since data acquisition does not interfere with machine functioning.

Goals. The purpose of our work is twofold. In terms of methodology, we argue that the most appropriate anomaly detection approach for bearing fault identification is a semi-supervised solution. It is unreasonable to assume, in most real-life applications involving operating machinery, that a recording of faulty functioning would be available and labeled beforehand, let alone with the same fault characteristics as the ones needing to be identified during machine monitoring. Normal operating data, on the other hand, are accessible and labeled as such. Process monitoring is expected to produce normal data as well as occasional faulty data, as defects occur. In the semi-supervised approach we argue for, training is performed on normal data only, and testing involves a mix of normal and faulty data, with the aim of distinguishing defects. Such an approach is called one-class anomaly detection, since labeled data belong to a single class, the normal one.

Our study shows that, despite the high number of existing anomaly detection algorithms for bearing fault identification, few proposals follow this setup. Moreover, we point out that the variety of machine learning setups present in the literature hinders benchmarking and a fair comparison of the results.

In what the methods are concerned, the aim of this study is to verify whether bearing faults can be identified using simple models, with low computational expenses. Although some authors [2] argue that nonlinear aspects of faulty bearing functioning are a burden for signal processing methods in identifying defects, recent results suggest near perfect detection is achievable with lightweight methods. We propose such a method and compare it to several others, both established and lesser known.

A substantial part of existing work, regardless of the type of methods used, relies on extracting features from the vibrational data. Since feature extraction adds numerical complexity, the present paper also considers the need for data processing and its influence on fault identification performance. While the effect varies with respect to the method, our study shows that, for some of the best performing methods, working with raw data may be in fact better.

Setup. Case Western Reserve University (CWRU) [3] is a dataset extensively used for testing machine learning techniques in the detection of bearing faults. Most recent methods, as discussed in Section 2, assume the availability of training data for all types of faults and attempt to identify those types. In such a scenario, there is no place for new types of faults. As previously stated, here, we assume the basic setup, where only normal data are available. Since, in most cases, the immediate repair solution is to replace the faulty bearing with a new one, such a setup is more realistic: the quick detection of a fault is important, not necessarily the type of fault, which can be determined later by a post-mortem analysis, after replacement.

Problem. The above setup defines a semi-supervised anomaly detection problem. We describe it here in its general form. We assume that a set of $N_{\mathrm{normal}}$ normal signals is available. A number of $N_{\mathrm{train}}$ of the normal signals are utilized for training, as described later in Section 4. The remaining ones, together with $N_{\mathrm{faulty}}$ faulty signals, are used for assessing the ability of a machine learning method to identify the faults. We denote $N_{\mathrm{test}}$ as the number of such signals.

Contribution. We provide a review of recent works on bearing fault identification using machine learning. We do not aim for an extensive review (several such works are referenced throughout the paper), rather we focus on exposing differences in methodology, as well as some relevant implementation details that put the results in context.

The central contribution of the paper consists in the proposal of a semi-supervised anomaly identification method, One-Class anomaly detection with regularized graph Total Variation (OC-TVreg). Minimizing the total variation of a graph whose nodes are the signals and edges are built based on a similarity distance was used when labels from two classes (normal/faulty) are available. We propose an optimization problem where it is enough to know a set of normal signals.

We tested the method, alongside other five solutions, among which dictionary learning (DL) is less used in anomaly detection, in two experimental conditions on the CWRU dataset. In the first, we assessed the influence of the motor load on the detection performance. Training was performed on each available motor load normal data, and we also tested separately for each load. The second experiment involved training on a mix of motor loads’ normal data.

Since we are also interested in determining the effect of data processing, in both the above experiments we performed two kinds of tests: on the raw time-series data and by applying a feature extraction technique.

Contents. We review existing solutions on bearing fault identification in semi-supervised, unsupervised, and supervised setups in Section 2. Section 3 presents the algorithms on which we perform the experiments. First, we briefly describe four commonly used anomaly detection methods and proceed with the less common dictionary learning approach. The section ends with the presentation of our proposed method, OC-TVreg.

In Section 4, we describe the CWRU bearing fault dataset, as well as all data treatment steps that we apply in the experiments.

The results are presented in Section 5, which starts with a description of the evaluation metrics and practical aspects concerning the parameters and heuristics of the tested methods. The performance on the two experimental setups (with training on either individual or all motor loads) is then presented, and the section ends with an analysis of execution times. Anticipating the results, we mention here that, in many test cases, the results provided by OC-TVreg, DL, and also LOF ensure perfect classification.

Concluding remarks follow in Section 6.

2. State of the Art

The CWRU dataset has attracted a lot of interest due to its realistic character, the diversity of measurement conditions, and the multitude of methods that can be applied. It has become a de facto benchmark for bearing fault analysis, surpassing other datasets like Paderborn University Bearing Dataset [4], Xi’an Jiaotong University Bearing Dataset [5], and others; see, for example, [6] and its bibliography.

In this section, we will give an overview of machine learning methods that have been used for analyzing the CWRU dataset. Such an endeavor is inherently partial. We will look especially at semi-supervised methods, since they are the most related to our approach. Then, we will present mostly recent results with unsupervised or supervised methods.

More bibliography can be found in review papers dedicated to CWRU: [7] (focusing on deep learning methods) and [8] (general machine learning methods).

2.1. Semi-Supervised Learning

In semi-supervised learning for anomaly detection problems, it is always assumed that knowledge of normal data is available. However, there are two main approaches regarding the faulty data. One either assumes that faulty data are unavailable for training (the case of interest to us) or that only few faulty data are available. In the latter case, there may be several types of faults, and so the classification may be no longer binary. A review of semi-supervised methods for industrial fault detection, including many applied to CWRU data, can be found in [9].

Of special interest to us are the works in which training is made only on normal data; all other data are not labeled. Despite the natural setup of the problem, there are only few papers in this category.

The method from [10] starts by computing 19 time and frequency domain features, further reduced to 6 by LDA; classification is performed with distance-preserving self-organizing maps; besides the normal data, it is assumed that the number and nature of classes are known. The resulting accuracy ranges from $0.958$ to $0.983$.

Although labeled as unsupervised, the domain adaptation method from [11] uses healthy samples to generate synthetic faults, a goal being also to balance the classes. The CWRU set is split into 4 classes; the classification accuracy is less than $0.85$. A similar domain adaptation setup was proposed in [12], but using adversarial training. The results were at about the same level, although with somewhat different premises. Unlike these works, we do not make any assumption about the anomalies.

In most of the papers on semi-supervised learning, training is made on data from all classes, although with some limitations, most commonly a (very) small number of labeled faulty signals.

Most methods from around a decade ago compute diverse features and then use standard or adapted classification methods. For example, in [13], 42 time, frequency, and wavelet features are extracted, then reduced to 3 by PCA; SVM is used for classification on a 10-class problem; the accuracy is of about $0.96$ with less than 10% labeled data, but not much larger with all data. In [14], time and wavelet features are the input of a manifold regularization method, followed by clustering, on a 4-class problem. Inference from one load to all loads is applied. In [15], Empirical Mode Decomposition and wavelet features are employed, and the method is weighted kernel clustering based on gravitational search; two 4-class problems are considered (one for fault position, other for fault size), and the accuracy ranges from $0.91$ to 1 (only for some particular subproblems). Other methods use label propagation [16], decision making [17], ensemble learning [18,19], and tensors [20]. In [21], an imbalanced 4-class problem is considered, with many normal signals and few anomalies in the training set, but with a balanced test set; over-sampling of faulty signals is used to increase the performance of standard classifiers like LS-SVM, thus obtaining better results (close to 1) than more complicated methods that use directly the imbalanced data. Over-sampling is also used in [19], with better results.

Dictionary learning is present among the semi-supervised classification methods for CWRU. In [22], label consistent DL with label adaptation is used. On a 10-class problem, an accuracy of $0.93$ is reached. A somewhat related solution is given in [23], where non-negative sparse coding and low-rank factorization are used to build a graph of relations between samples for semi-supervised learning. On a 10-class problem, with 10% labeled samples (same for each class), the obtained accuracy is $0.97$–$0.98$.

Graph methods are worth mentioning, especially since we propose one. In [24], an objective function representing error with respect to known labels, regularized with graph total variation, is minimized. The graph is built by connecting K-nearest neighbors, with $K=4$; time and frequency features or raw signals are used as input. On a 4-class problem (fault position), the obtained accuracy is 1 even for 1% labeled signals; however, the signals are long (at least 2048 samples) compared to ours (only 100). A related work is [25], where the graph is now directed, and so the Laplacian regularization is different. The length of signals is smaller (1200), and the accuracy is less than 1 even when 90% of the labels are known.

The most recent approaches use various forms of neural networks. Several types of architecture were employed, such as auto-encoders [26,27,28,29], graph NN [30,31] (the latter combined with adaptive feature fusion and giving better results than the former), dual graph NN [32], ARMA graph convolutional NN [33], convolutional NN [34,35,36], Generative Adversarial Network [37,38,39,40,41], adversarial network [42], meta-learning network [43], bidirectional gated recurrent unit (BiGRU) network [44], long short-term memory (LSTM) network [45], twin deep neural netorks for data with noisy labels [46], and Dual-Attention Fusion Transformer [47]. Some of the methods can achieve perfect accuracy if enough labeled signals are available. Thus, the border between semi-supervised and supervised learning is blurred.

2.2. Unsupervised Learning

In unsupervised learning, no information on the data is available. Training is made on all data, without labels. Ideally, after learning, clusters of data are revealed, and they are associated with classes.

In [48], time–frequency features are extracted from the spectrogram with an autoencoder and clustering is made with the K-means algorithms. Perfect accuracy is reported for the normal/faulty classification. The paper contains relatively few details, and it is not clear which faults are considered.

Many other approaches are based on neural networks, but the number of classes is larger, from 3 to 16. Sometimes, only abnormal signals are considered. Diverse tools are used for clustering. The classification accuracy is often quite large, although not equal to 1.

In [49] a sparsifying NN works in the spectral domain and produces features clustered with affinity propagation. Generative adversarial networks are used in [50,51], in both cases on a 16-class problem. Training is made on one load (speed) and testing on all loads. For some of the fault classes, the detection is perfect. Other notable works are [52,53], both employing auto-encoders, and [54].

2.3. Supervised Learning

In supervised learning, training is made on labeled data from all classes, normal and faulty. The number of faulty classes may range from 1 to 16 for the CWRU dataset, depending on the considered fault location, rotation speed, and fault size. The purpose is to identify the class of new signals. We give more details for papers where transfer learning is used in a form or another, and learning does not use samples from all classes.

In terms of methodology, some of the works provide interesting conclusions. In [55], where inference from one faulty dataset to another was examined, it was argued that prediction from one load (speed) to another, as performed in many papers, is much easier than prediction from one fault size to another. Of course, in our semi-supervised setup, we do not use at all faulty signals; hence, we are in the most difficult position. Similarly, in [56], data from a type of fault are used only in one of the training, validation, and testing datasets. In particular, binary classification (normal/faulty) is studied. For CWRU, the only method that gives an accuracy equal to 1 is Naive Bayes. Although the classification is perfect, faulty signals are used for training.

Among the approaches partially similar with ours, we can cite [57], where the problem is multiclass but with inference from some types of data (normal, inner race fault, outer race fault, all used for training) to other type (ball fault, not used for training). The recognition rate of unknown samples is $0.9966$.

In [58], where a neural network is used, only three classes are considered: normal, light damage, heavy damage. Training uses samples from all classes. Fault detection is made for each load separately, and the resulting accuracy nears 1.

Some of the methods from the previous decade do not use NNs but are interesting for employing features. Wavelets and SVM are used in [59] and time–frequency features in [60]. Neither of these works was applied to the CWRU dataset, but a comparison was made in [61] the advantage going to the NN approaches.

Currently, NN solutions are prevalent. Different architectures were used, like autoencoders [62,63], convolutional NN (CNN) [64], belief network [65], a combination of CNN and mixing layers [66], CNN having the input computed with multi-domain time-frequency transform [67], with Gram angle field transformation [68], with filtering using an optimized Maximum Correlated Kurtosis Deconvolution [69], with global and local feature extraction [70], or with augmented data via a diffusion model [71], fuzzy CNN [72], deep transfer reinforcement learning [73], self attention and CNN [74], transformer-based meta learning [75], an attention-based generative adversarial network (AttGAN), and dynamic perceptual convolutional neural network (DPCNN) [76]. A comparison of several deep learning methods was made in [77], where MixCNN [66] obtains the best results for the CWRU dataset, even when the training set is small.

In multiclass approaches (type of anomaly is also inferred), training and testing datasets are taken from all data. In neural networks methods:

Although not directly applied to CWRU data, there are some works where DL was used for rotating machinery diagnosis in a supervised manner. In [78], a dictionary was learned for each class, then classification was made by comparing representation errors, with examples for wind turbines. In [79], convolutional DL was used for qualitative analysis (feature extraction) after training separately for normal data and faulty data; the atoms of the dictionary were used for the analysis of vibration signals.

3. Methods

We use several methods to tackle the semi-supervised anomaly detection problem based on the CWRU data. Some of them are known and need only minimal or no tuning of hyper-parameters. We will describe them briefly in Section 3.1; they are: dictionary learning (DL) [80], Local Outlier Factor (LOF) [81], Isolation Forest (IF) [82], Robust Random Cut Forest (RRCF) [83], and One-class Support Vector Machine (OC-SVM) [84]. LOF, IF, RRCF, and OC-SVM are established methods and are part of state-of-the-art libraries like PyOD [85]. Although DL was used in anomaly detection, it is not as popular as the above methods; a goal of this paper is to prove its good performance on such problems. We also propose a new method, using the total variation of a neighborhood graph associated with the data; the method is the first of this kind using only training on normal data and is described in Section 3.3.

All methods assume only the knowledge of normal data, and their purpose is to classify new data into two categories: normal and faulty. They compute anomaly scores for each new signal; comparison with the scores of normal signals allows the classification. We denote $s\left({\mathit{y}}_i\right)$ the score associated with signal ${\mathit{y}}_i$. In most anomaly detection libraries, a higher score is more likely associated with an anomaly. In the description below, we give the natural value of the score for each method; if high scores are associated with normal signals, reversing the sign will give a score respecting the convention.

3.1. A Selection of Known Methods

3.1.1. Local Outlier Factor

LOF is a density-based method for identifying anomalies. The general assumption with density-based algorithms is that normal signals are similar to one another such that they cluster in dense regions of the signal space, whereas anomalies lie in lower-density ones. Since the actual structure of the data may not allow for an explicit assessment of the normal density, LOF considers a relative measure and computes the anomaly score of a signal (named the outlier factor), $s\left({\mathit{y}}_i\right)$, by comparing its local density to the local density of its neighbors. Locality refers to the K-nearest neighborhood of a signal. Data points that have similar local density to that of their neighbors, therefore a score that is close to 1, are considered normal.

3.1.2. Isolation Forest

IForest isolates signals by recursively choosing dimensions and splitting values at random. Intuitively, anomalies require fewer such decisions in order to be separated from the rest of the signals than normal ones do. The method constructs a forest of trees, where the interior nodes correspond to the decisions (or cuts), and the leaves correspond to data points. The trees are obtained by repeated subsampling of the dataset. The anomaly score, $s\left({\mathit{y}}_i\right)$, of a given signal is computed by passing the signal through the forest and returning its normalized mean height: a low height corresponds to anomalies and is translated into a high score.

3.1.3. Robust Random Cut Forest

RRCF views anomalies as responsible for an increase in model complexity when added to the dataset. The method constructs a forest of trees, where each tree corresponds to a random partitioning of the data. The anomaly score of a signal (termed the collusive displacement), $s\left({\mathit{y}}_i\right)$, is computed by considering the number of structural changes produced by its deletion from the trees: anomalies have a higher number of sibling displacements. This property is achieved by choosing the dimension to cut not at random, as with IForest, but proportional to its spread.

3.1.4. One-Class Support Vector Machine

OC-SVM also uses only normal signals in the training step. The method projects the signals to a feature space using a kernel function and computes a decision boundary that separates them from the origin, allowing for a maximum margin. In the testing phase, signals are passed to the binary decision function and labeled according to their position with respect to the boundary.

3.2. Dictionary Learning

Dictionary learning for sparse coding (DL) [80] is a signal processing technique used to learn sparse approximations of signals.

Given a signal ${\mathit{y}}_i\in {\mathbb{R}}^m$ and a basis (called the dictionary), $\mathit{D}\in {\mathbb{R}}^{m\times n}$, the aim of sparse coding is to compute a representation of ${\mathit{y}}_i$ that only has $\kappa$ nonzero entries. Here, n stands for the number of atoms (columns) in the dictionary and $\kappa \ll n$ for the (imposed) sparsity level. We call ${\mathit{x}}_i\in {\mathbb{R}}^n$ the sparse representation; the problem amounts to minimizing ${ϵ}_i={\parallel {\mathit{y}}_i-{\mathit{Dx}}_i\parallel }_2$, with ${\mathit{x}}_i$ having at most $\kappa$ nonzeros.

In the usual machine learning setup (and other signal processing tasks), the dictionary is not given but needs to be learned from the dataset $\mathit{Y}\in {\mathbb{R}}^{m\times N}$. The DL problem thus consists in minimizing ${\parallel \mathit{Y}-\mathit{DX}\parallel }_2$, jointly on $\mathit{D}$ and $\mathit{X}\in {\mathbb{R}}^{n\times N}$, with the constraint that $\mathit{X}$ has at most $\kappa$ nonzeros on each column. In other words, a dictionary is learned to represent all the signals in the dataset, but for each of them, only a few atoms are used for the approximation.

Note that in order to avoid multiplication ambiguity, the atoms of the dictionary are normalized. In the DL setting, the dictionary is said to be overcomplete, that is $n>m$, usually by at least a factor of 2.

Like many signal approximation methods, DL can be used to identify anomalies in semi-supervised or unsupervised scenarios by using the representation error ${ϵ}_i$ of a signal as anomaly score. Since anomalies are usually few and significantly different from the normal signals, the model is assumed to be better able to identify normal signals, hence producing a smaller error in their case.

Indeed, DL was used for anomaly detection, including fault detection tasks, such as structural diagnosis in solid media [86], vessel cracks in glass melting processes [87] or faults in other manufacturing processes [88]. These works, however, take a different approach than ours; the latter is a supervised solution, while the former ones build two different dictionaries, for representing normal and abnormal data features, respectively. While essentially they both rely on representation errors to compute anomaly scores or label estimates, the exact score computations are particular to each approach.

3.3. One-Class Anomaly Detection with Regularized Graph Total Variation

Several anomaly detection methods, notably [24], build an undirected graph based on distances between signals. Let $\mathcal{G}=(V,E)$ be the graph of distances. A node $i\in V$ represents a signal ${\mathit{y}}_i$; the weight $w_{ij}$ associated with an edge $(i,j)\in E$ can be constructed as follows, based on the K-nearest neighbors principle, where K is a given positive integer. If j is among the nearest K neighbors of i in terms of a distance $\delta ({\mathit{y}}_i,{\mathit{y}}_j)$, or i is among the K nearest neighbors of j, then $w_{ij}=\delta ({\mathit{y}}_i,{\mathit{y}}_j)$; otherwise, $w_{ij}=0$. We have used the cosine distance

$$\delta ({\mathit{y}}_i,{\mathit{y}}_j)=1-{\displaystyle \frac{{\mathit{y}}_i^T{\mathit{y}}_j}{\parallel {\mathit{y}}_i\parallel ·\parallel {\mathit{y}}_j\parallel }}$$

(1)

and the standard Euclidean distance, but any distance can be used, in principle.

Denoting $\mathit{W}$ as the matrix of weights and $\mathrm{\Phi }$ the diagonal degree matrix, with

$${\varphi }_{ii}=\sum _{j\in {\mathcal{N}}_i}{w}_{ij},$$

(2)

where ${\mathcal{N}}_i$ is the set of nodes that are immediate neighbors of i, the Laplacian matrix associated with the graph is

$$\mathit{L}=\mathrm{\Phi }-\mathit{W}.$$

(3)

The Laplacian is symmetric and positive semidefinite.

Given a graph signal $\mathit{f}$, which will be associated with an anomaly score in the sense that $s\left({\mathit{y}}_i\right)=f_i$, the total variation (TV) of the signal on the graph $\mathcal{G}$ is

$$\sum _i\sum _{j\in {\mathcal{N}}_i}{w}_{ij}{(f_i-f_j)}^2={\mathit{f}}^T\mathit{Lf}.$$

(4)

We would like to have $f_i=1$ for normal signals and $f_i=0$ for anomalies; this choice is not random as we will see immediately. Remind that we are in the setup where only some of the normal signals are labeled, while other normal signals and the anomalies are not labeled. In [24] and other papers, the ideal score values are 1 and $-1$, and the setup is different: some normal signals are labeled, but there are also some anomalies.

Minimizing the total variation of the graph makes sense in the context of computing an anomaly score. The TV is minimum when the signal is constant. Since distances should be small between normal signals and large between anomalies and normal signals, a small TV value reflects few changes between nodes, ideally those between some anomalies and some normal nodes; there should be no changes between normal nodes or between anomalies.

Since minimizing only the TV leads to a constant signal, we propose to minimize

$${\mathit{f}}^T\mathit{Lf}+\lambda {\parallel \mathit{f}\parallel }^2,$$

(5)

subject to the constraint that $f_i=1$ when the signal ${\mathit{y}}_i$ is known to be normal. The regularization term, weighted by a trade-off factor $\lambda >0$, tends to draw the signal towards zero. However, the TV term tends to minimize changes between neighbors, in the solution. The overall objective will thus combine these tendencies and distinguish between normal signals and anomalies: the former will have a larger value than the latter, although not necessarily 1.

Denoting

$$\mathit{Q}=\mathit{L}+\lambda \mathit{I}=\left[\begin{array}{cc}{\mathit{Q}}_{11}& {\mathit{Q}}_{12}\\ {\mathit{Q}}_{12}^T& {\mathit{Q}}_{22}\end{array}\right],$$

(6)

where ${\mathit{Q}}_{11}\in {\mathbb{R}}^{N_{\mathrm{train}}\times N_{\mathrm{train}}}$ and ${\mathit{Q}}_{22}\in {\mathbb{R}}^{N_{\mathrm{test}}\times N_{\mathrm{test}}}$ (without loss of generality, we order the signals such that the training ones come first, and taking into account that ${\mathit{f}}_1=\mathbf{1}$ (where ${\mathit{f}}_1\in {\mathbb{R}}^{N_{\mathrm{train}}}$ and $\mathbf{1}$ is a vector of ones), the solution of (5) is

$${\mathit{f}}_2=-{\mathit{Q}}_{22}^{-1}{\mathit{Q}}_{12}^T\mathbf{1}.$$

(7)

Since ${\mathit{Q}}_{22}$ is a positive definite matrix, the solution (7) can be computed via a Cholesky factorization or using adequate iterative solvers (e.g., conjugate gradient). Thus, the scores of the unlabeled signals are given by (7).

The resulting algorithm called OC-TVreg (One-Class anomaly detection with Total Variation regularization) is summarized as Algorithm 1.

Algorithm 1: OC-TVreg

Remark 1. 

In the ideal case, where the graph has two connected components, one for normal signals and the other for anomalies, it follows that the columns of ${\mathit{Q}}_{12}$ corresponding to anomalies are all zero and that ${\mathit{Q}}_{22}$ has a block diagonal structure, with separate blocks for anomalies and normal test signals; it results from (7) that the part of ${\mathit{f}}_2$ corresponding to anomalies is zero, and so OC-TVreg provides a nearly perfect score distribution: nearly 1 for normal signals and exactly 0 for anomalies. Similarly, all the anomaly nodes that form a connected component get a zero score through (7). Of course, this is less likely to happen in practice, but it suggests the soundness of the proposed heuristic.

Remark 2. 

The complexity of OC-TVreg is $O\left(N_{\mathrm{test}}^3\right)$, since (7) is in fact a system of linear equations. The most time-consuming operation is the Cholesky factorization of the matrix ${\mathit{Q}}_{22}$. So, the result can be obtained in reasonable time when $N_{\mathrm{test}}$ is at most a few thousand (which is the case in our experiments).

If the number of test signals is large, the test set can be split in several subsets, and the algorithm can be applied on each subset separately, with the same set of labeled normal signals.

Remark 3. 

The training and testing populations must be large enough, especially the testing one. The latter recommendation comes from a simple remark. If the testing set consists of only one signal, let us denote $i=N_{\mathrm{train}}+1$ and $w={\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}$. Then, the submatrix ${\mathit{Q}}_{22}$ is in fact a single element; due to (2), it has the expression ${\mathit{Q}}_{22}=q_{ii}={\varphi }_{ii}+\lambda =w+\lambda$. Additionally, ${\mathit{Q}}_{12}^T$ is a vector representing the last row of $\mathit{Q}$ without the diagonal; so, ${\mathit{Q}}_{12}^T\mathbf{1}=-w$. Hence, the solution (7) is

$$f_i={\displaystyle \frac{w}{w+\lambda }}.$$

This value, representing the score of the test signal, is smaller than 1, but it would be hard to decide whether it corresponds to a normal signal or to an anomaly. However, when many test signals are involved, the values of the solution are more likely to be smaller for anomalies than for normal signals.

Example 1. 

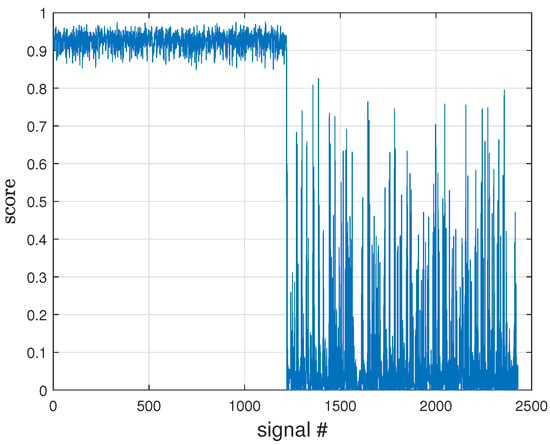
An example of a result, for one of the CWRU experiments to be described later, is shown in Figure 1. The sizes of the datasets are $N_{\mathrm{train}}=1220$ and $N_{\mathrm{test}}=2440$; half of the test signals are normal, and half are anomalies. The parameters are $K=20$, $\lambda =0.1$. The solution (7) has large values not far from 1 for the normal signals (first half of the figure) and smaller, although only some near zero, for the anomalies (second half). In this example, the classification is perfect: all the anomalies have lower scores than all normal signals.

Figure 1. An example of solution of (5).

4. The Data

In the CWRU test stand [3], two rolling bearings are placed at the drive and fan ends of the motor shaft. The motor operates at four four different loads: 0, 1, 2, 3 horse power (HP); the rotation speed is different for each load. Vibration data are collected with two accelerometers placed on the motor housing at the drive and fan ends. The experiments consist of both normal and faulty operations. Single-point faults are planted independently on the two bearings at five locations (inner race; ball; outer race orthogonal; centered; and opposite to the load zone). Three different fault depths (0.007, 0.014, and 0.021 inches) for each location are tested.

Note that although there would be 60 faulty scenarios, data are available only for 45 cases, as many outer race configurations were not tested.

Data are collected at 12 kHz (for both normal and faulty operation setups) and 48 kHz (for the drive-end faults). For the following experiments, we only used fan-end accelerometer data.

As shown in Section 2, the CWRU dataset was the test subject for many methods. Some of them give hints on which setups are easier and which are more difficult. The discussion in [89] is significant for the analysis of the CWRU data and the characterization of the difficulty; for example, it is argued that ball faults are the most difficult to diagnose.

4.1. Segmentation

We first segment the time series into $T=100$ samples windows without overlapping. We call the resulting windows, which are 8.33 miliseconds in length, signals or segments. For $\mathrm{HP}=0$, this corresponds to roughly a quarter of a motor rotation. The choice is motivated by the fact, ignored in many papers, that if superposing signals are one in the training set and the other in the testing set, the classification task may be easier, and an unfair advantage would be given to the evaluated method.

4.2. Training Methodology

We performed two types of experiments, both in a semi-supervised approach.

In the first experiment, we trained on normal data with a single motor load and tested on both normal and faulty data for each of the four motor loads separately. This allowed us to examine whether the fault detection was influenced by the motor load used in the training set.

In the second experiment, we verified whether training on multiple motor loads increased the performance. The training set is composed of an equal number of normal signals from each motor load. The testing set, as previously, consists of normal and faulty segments for each motor load.

All experiments were performed independently on each fault location and size.

4.3. Train–Test Split

In all the following experiments, regardless of training methodology, the testing set was roughly twice the size of the training set. Training was always performed on $N_{\mathrm{train}}=1220$ normal segments, corresponding to a time series of slightly over 10 s. The testing set contained the same number of normal signals and all available faulty segments for the respective fault location, size, and motor load. There were slight differences in the sizes of faulty datasets, ranging from $N_{\mathrm{faulty}}=1209$ to $N_{\mathrm{faulty}}=1223$ for inner roll faults, from $N_{\mathrm{faulty}}=1209$ to $N_{\mathrm{faulty}}=1223$ for ball faults, and from $N_{\mathrm{faulty}}=1207$ to $N_{\mathrm{faulty}}=1220$ for outer roll faults.

4.4. Feature Extraction

We performed two types of experiments: with raw time-series data and by extracting time and frequency features.

As stated earlier, in the case of time series data, the signals are non-overlapping windows of dimension $T=100$. Following the notation in Section 3.2, the signal dimension is $m=T=100$.

For extracting the features, we followed the indications in [24] and used 14 statistical time domain measures. Out of the 13 frequency domain measures in that work, however, we excluded the frequency features $F_4$ and $F_{10}$; both had very large values, and preliminary tests showed they negatively influenced the fault detection performance. In this case, the signal dimension is $m=25$.

4.5. Normalization

With both time-series and processed data, we performed z-score normalization on the training set and used the scaling and centering parameters to normalize the test set.

5. Results

In this Section, we present and discuss the results for both the proposed and existing methods detailed in Section 3.

We report the Area Under the Receiver Operating Characteristic Curve (ROC AUC) as a performance indicator, calculated as follows. The scores $s\left({\mathit{y}}_i\right)$ computed by a method are sorted decreasingly; the $N_{\mathrm{faulty}}$ signals with the largest scores are considered anomalies; the remaining signals are considered normal. The ROC curve has all possible false positive rates on the horizontal axis and the corresponding true positive rates on the vertical axis, both computed for the sorted signals. The ROC AUC is the area below this curve, with the ideal value being 1. All results correspond to the mean over five independent tests.

In discussing the results below, we start with the experiments where training is performed on a single motor load (Section 5.3) and follow with the ones where all motor loads are included in the training set (Section 5.4). In both cases, we first treat the raw time-series data and continue with time and frequency features.

5.1. Parameters

The DL model has three heuristics: sparsity of the representation, $\kappa$; dictionary overcompleteness, o; and number of training iterations (alternate minimization steps), $n_{iters}$. We report results on the following parameter values: $\kappa \in \left\{3,8,14,20\right\}$, $o\in \left\{2,3\right\}$, and $n_{iters}\in \left\{50,200\right\}$.

For OC-TVreg, we tested $K\in \left\{10,20,50,100\right\}$ and $\lambda \in \left\{0.01,0.1,0.5,1\right\}$. We will report the results for $K=20$ and $\lambda =0.1$, which are generally best or nearly best. A discussion on the robustness of this choice is presented in Section 5.5. We have used both the cosine (1) and Euclidean distances. For raw signals, the cosine distance gives much better results. For features, the Euclidean distance gives practically perfect results, and the cosine distance is only slightly behind. We will report the best results in each case.

When testing LOF, we used the default parameters: Euclidean distance metric and $K=20$ neighbors. We also tried the cosine distance, but the results were worse, and we do not report them.

For IF, we used the parameter values suggested by the authors of the method, 100 trees and 256 signals per tree. While empirical tests [90] suggest that the optimal number of samples in the tree depends on the properties of the dataset and in some cases might be larger than the default, we took into consideration the relatively small size of our dataset.

The same values were used for RRCF as well, where we set the collusive displacement method to ′maximal’.

Finally, for OC-SVM, we used the default parameters, with the exception of ′KernelScale’, which was set to ′auto’.

We used the MATLAB R2023a implementations of LOF, IF, RRCF, and OC-SVM.

The programs implementing OC-TVreg and the tests reported below can be found at https://asydil.upb.ro/software/ (accessed on 4 October 2025).

5.2. Summary of Results

Figure 2 shows a summary of the results obtained in the two motor load training setups and with both types of data: raw-time series and features. We discuss next the overall rank of the methods, in terms of the average ROC AUC over the entire experiment batch. The first position is contested by DL and OC-TVreg, with DL having a perfect identification score in experiments performed on time-series data (in both training scenarios) and OC-TVreg in those on time and frequency features, again with a mean ROC AUC of 1. LOF is always second, and in the last three positions, we have OC-SVM, IF, and RRCF, regardless of the experiment or data type. Features clearly give better results than raw signals for OC-TVreg, IF, RRCF, and OC-SVM; however, for the DL and LOF, the results are slightly worse.

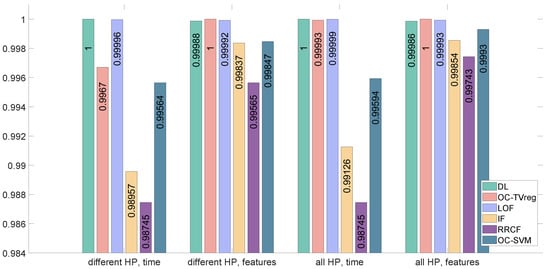
Figure 2. Summary of results: average ROC AUC on all combinations of training load (different/all) and signal type (raw/features).

Figure 3 shows the distribution of the ROC AUC values in each test case. The horizontal red line marks the median, the thick blue line corresponds to values between the 25th and 75th percentiles, the thin blue line covers extreme values not considered outliers, and the cross sign corresponds to outliers. For the methods obtaining perfect fault identification in all test cases, only the median is shown. Possible outliers are present for the methods with a mean ROC AUC close to 1.

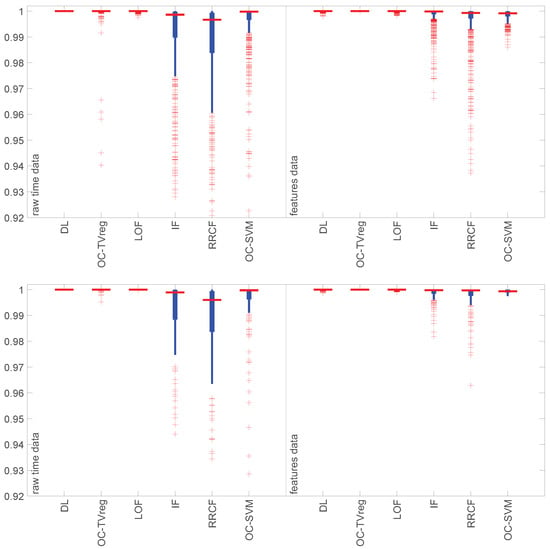
Figure 3. Summary of results: distribution of ROC AUC on all combinations of training load (different/all), signal type (raw/features), and independent test runs. Top: training on different motor loads. Bottom: training on all motor loads.

The figure thus shows that DL, OC-TVreg, and LOF are not only the best performing but also the most robust with respect to the experimental conditions: fault size, location, and motor load, and also to the train/test splits. Working with features instead of raw signals reduces the variance for the rest of the methods; among these, OC-SVM has the tightest distribution of results.

We continue by giving detailed results for each setup.

5.3. Training on Individual Motor Loads

Table 1 shows a summary of the results for all methods, when training is performed on raw data. Recall that each algorithm is trained separately on normal data for each motor load and tested on normal and faulty data for the different motor loads, independently. For brevity, we only present the average of four motor load test cases for each individual training set.

Table 1. Training on different motor loads, with raw time series data. Mean (over test loads and five independent runs) ROC AUC values.

Method	Train HP	Inner			Ball			Orth			Center			Opposite
		0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021
DL	0	1	1	1	1	1	1	1	1	1	1	1	1	1	-	-
	1	1	1	1	1	1	1	1	1	1	1	1	1	1	-	-
	2	1	1	1	1	1	1	1	1	1	1	1	1	1	-	-
	3	1	1	1	1	1	1	1	1	1	1	1	1	1	-	-
OC-TVreg (cosine)	0	0.9997	1	1	0.8553	1	1	1	0.9999	1	0.9996	1	1	1	-	-
	1	1.0	1	1	0.9987	1	1	1	1	1	1.0	1	1	1	-	-
	2	1.0	1	1	0.9991	1	1	1.0	1	1	1.0	1	1	1	-	-
	3	1.0	1	1	0.9992	1	1	1.0	1	1	1.0	1	1	1	-	-
LOF	0	1	0.9997	1	0.9995	1.0	1.0	1.0	1	1.0	1.0	1	1	1.0	-	-
	1	1	0.9999	1	0.9998	1.0	1.0	0.9998	1	1	1.0	1	1	1.0	-	-
	2	1	0.9999	1	0.9999	1.0	1.0	0.9999	1	1	1.0	1	1	1.0	-	-
	3	1	1.0	1	1.0	1.0	1.0	0.9999	1	1	1.0	1	1	1.0	-	-
IF	0	0.9998	0.9835	1.0	0.9787	0.9914	0.9971	0.9784	1.0	0.9979	0.9988	1	0.9999	0.9951	-	-
	1	0.9995	0.9781	1.0	0.9687	0.9860	0.9928	0.9601	0.9999	0.9968	0.9977	1	0.9996	0.9901	-	-
	2	0.9993	0.9756	0.9999	0.9639	0.9838	0.9905	0.9543	0.9998	0.9964	0.9970	1	0.9995	0.9875	-	-
	3	0.9997	0.9838	1.0	0.9737	0.9884	0.9935	0.9632	0.9999	0.9982	0.9984	1	0.9998	0.9911	-	-
RRCF	0	0.9993	0.9781	0.9998	0.9731	0.9867	0.9937	0.9708	0.9998	0.9955	0.9974	1.0	0.9996	0.9918	-	-
	1	0.9988	0.9763	0.9996	0.9649	0.9828	0.9907	0.9616	0.9997	0.9948	0.9966	1.0	0.9994	0.9878	-	-
	2	0.9986	0.9708	0.9995	0.9584	0.9797	0.9879	0.9526	0.9996	0.9931	0.9957	1.0	0.9991	0.9854	-	-
	3	0.9994	0.9788	0.9998	0.9695	0.9851	0.9925	0.9615	0.9998	0.9962	0.9975	1.0	0.9996	0.9899	-	-
OC-SVM	0	1.0	0.9903	1.0	0.9902	0.9958	0.9992	0.9880	1.0	0.9993	0.9996	1	1.0	0.9978	-	-
	1	1.0	0.9884	1.0	0.9871	0.9946	0.9984	0.9810	1.0	0.9991	0.9994	1	1.0	0.9964	-	-
	2	1.0	0.9936	1.0	0.9906	0.9963	0.9987	0.9854	1.0	0.9997	0.9996	1	1.0	0.9973	-	-
	3	1.0	0.9906	1.0	0.9865	0.9940	0.9976	0.9745	1.0	0.9995	0.9994	1	1.0	0.9954	-	-

The results, showing the ROC AUC values, are rounded up to four decimals; we reserve the integer notation 1 for perfect identification, while 1.0 corresponds to the rounded result. A value of 1 therefore indicates the situation where all anomalies are identified in all the four motor load test cases.

While the table only presents the results of the best performing DL parameter configuration for each test case, the experiments show that the DL algorithm is robust with respect to its heuristics. In most cases, several if not all the parameter configurations yield an ROC AUC of 1. Moreover, in $90\%$ of the tested scenarios, the $\kappa =3$, $o=2$, $n_{iters}=50$ configuration perfectly identifies the anomalies; for the remaining, an increase to $\kappa =8$ is sufficient to achieve this result. Since the DL heuristics impact speed, either directly (number of iterations) or indirectly (sparsity and dictionary overcompleteness determine model size), robustness also translates into the possibility of using the fastest model for identifying faults.

Note that, although in terms of overall rank, OC-TVreg is situated third, in terms of the individual test scenarios, it produces the second highest number of complete fault identifications. The blame for the poor general mean ROC AUC is due to the result for the 0.007 inch ball fault trained with no motor load. Without this case, the overall average of OC-TVreg is 0.99991, very close to that of the frontrunners, DL and LOF. Remind that the ball faults in CWRU are known [55] to be harder to identify than the other two locations.

Out of the four established anomaly detection methods we tested (LOF, IF, RRCF, OC-SVM), LOF is by far the best performing.

We now move to the experiments performed on time and frequency features data. Compared with results obtained on time-series data, DL and LOF perform worse, while all other methods see an improvement in the mean ROC AUC when working with data features.

Table 2 shows the detailed results for the experiments performed with time and frequency features. Aside from DL and, to a lower extent LOF, all methods benefit from using features. OC-TVreg produces near perfect detection in all cases; in particular, for ball faults, the improvement is high. We remind that the Euclidean distance was used for OC-TVreg. With the cosine distance, OC-TVreg has only a slightly lower performance, with the overall ROC AUC average being $0.99965$, which is still better than IF, RRCF, and OC-SVM. RRCF and OC-SVM have perfect detection in none of the fault configurations; however, the overall mean ROC AUC is better than in the raw time signals experiment, for both methods.

Table 2. Training on different motor loads, with features data. Mean (over test loads and five independent runs) ROC AUC values.

Method	Train HP	Inner			Ball			Orth			Center			Opposite
		0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021
DL	0	1.0	0.9999	1.0	0.9997	0.9999	0.9999	0.9996	1.0	1.0	1.0	1	1.0	0.9998	-	-
	1	1.0	1.0	1.0	0.9998	1.0	1.0	0.9998	1.0	1.0	1.0	1	1	0.9999	-	-
	2	1.0	1.0	1.0	0.9998	1.0	1.0	0.9999	1.0	1.0	1.0	1	1	1.0	-	-
	3	1.0	0.9998	1.0	0.9985	0.9999	0.9998	0.9992	1.0	0.9999	0.9999	1	1.0	0.9997	-	-
OC-TVreg (Euclidean)	0	1	1	1	1.0	1	1	1	1	1	1	1	1	1	-	-
	1	1	1	1	1	1	1	1	1	1	1	1	1	1	-	-
	2	1	1	1	1	1	1	1	1	1	1	1	1	1	-	-
	3	1	1	1	1.0	1	1	1	1	1	1	1	1	1	-	-
LOF	0	0.9999	0.9999	1.0	0.9999	0.9999	1.0	0.9996	1.0	1.0	0.9999	1	1	0.9998	-	-
	1	1.0	1.0	1.0	0.9999	1.0	1.0	0.9999	1.0	1.0	1.0	1	1	1.0	-	-
	2	1.0	0.9999	1.0	0.9999	1.0	1.0	0.9999	1.0	1.0	1.0	1	1	1.0	-	-
	3	1.0	0.9998	1.0	0.9997	0.9998	0.9998	0.9995	1.0	1.0	0.9999	1	1.0	0.9998	-	-
IF	0	1.0	0.9987	1.0	0.9957	0.9989	0.9988	0.9944	1.0	0.9995	0.9996	1	1.0	0.9990	-	-
	1	1.0	0.9987	0.9999	0.9974	0.9990	0.9994	0.9950	1.0	0.9999	0.9998	1	1.0	0.9989	-	-
	2	1.0	0.9993	0.9999	0.9983	0.9993	0.9997	0.9964	1.0	1.0	0.9999	1	1.0	0.9993	-	-
	3	1.0	0.9966	1.0	0.9890	0.9970	0.9979	0.9850	1.0	0.9989	0.9992	1	1.0	0.9978	-	-
RRCF	0	0.9996	0.9988	0.9997	0.9978	0.9989	0.9989	0.9968	0.9997	0.9993	0.9993	0.9996	0.9997	0.9990	-	-
	1	0.9991	0.9969	0.9991	0.9956	0.9969	0.9978	0.9944	0.9994	0.9986	0.9988	0.9988	0.9985	0.9976	-	-
	2	0.9994	0.9960	0.9997	0.9932	0.9965	0.9978	0.9896	0.9996	0.9991	0.9993	0.9995	0.9991	0.9973	-	-
	3	0.9940	0.9875	0.9955	0.9798	0.9896	0.9876	0.9762	0.9947	0.9887	0.9919	0.9964	0.9957	0.9890	-	-
OC-SVM	0	0.9988	0.9990	0.9991	0.9985	0.9989	0.9988	0.9987	0.9991	0.9988	0.9990	0.9991	0.9991	0.9987	-	-
	1	0.9986	0.9981	0.9986	0.9985	0.9985	0.9986	0.9980	0.9985	0.9994	0.9988	0.9967	0.9971	0.9984	-	-
	2	0.9989	0.9985	0.9987	0.9987	0.9987	0.9989	0.9988	0.9989	0.9994	0.9989	0.9964	0.9965	0.9987	-	-
	3	0.9983	0.9974	0.9978	0.9982	0.9974	0.9977	0.9978	0.9983	0.9974	0.9978	0.9987	0.9985	0.9977	-	-

Features seem to introduce more sensitivity to the training conditions, as shown by the results on $\mathrm{HP}=0$ and $\mathrm{HP}=3$ for the majority of methods.

5.4. Training on All Motor Loads

Training with raw data from all motor loads increases the performance on all methods (except for the RRCF, which has the same average ROC AUC) and does not change ranking.

Table 3 shows the detailed results for each test configuration. We provide a quick reminder as to why the structure of this table differs from the corresponding experiment on training with different motor loads, namely from Table 1. Indeed, data do not exist for all motor loads, fault locations, and size configurations; Table 3 reflects the dataset structure. In Table 1, however, the results are averaged on the training motor load, which means that if data from at least one fault configuration are available, a mean ROC AUC value is reported. Note also that the second column corresponds to Train HP and Test HP, respectively, in the two tables.

Table 3. Training on all motor loads, raw time series data. Mean (over five independent runs) ROC AUC values.

Method	Test HP	Inner			Ball			Orth			Center			Opposite
		0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021
DL	0	1	1	1	1	1	1	1	1	-	1	1	1	1	-	-
	1	1	1	1	1	1	1	1	1	1	1	-	-	1	-	-
	2	1	1	1	1	1	1	1	1	1	1	-	-	1	-	-
	3	1	1	1	1	1	1	1	1	1	1	-	-	1	-	-
OC-TVreg (cosine)	0	1.0	1	1	1	1	1	1.0	1	-	1.0	1	1	1	-	-
	1	1.0	1	1	0.9978	1	1	1	1	1	1.0	-	-	1	-	-
	2	1.0	1	1	0.9996	1	1	1	1	1	1.0	-	-	1	-	-
	3	1	1	1	0.9995	1	1	1	1	1	1	-	-	1	-	-
LOF	0	1	1	1	1.0	1.0	1.0	0.9998	1	-	1.0	1	1	1.0	-	-
	1	1	1	1	1.0	1	1	1.0	1	1	1	-	-	1	-	-
	2	1	1	1	1	1	1	1	1	1	1	-	-	1	-	-
	3	1	0.9999	1	0.9999	1.0	1	1.0	1	1	1.0	-	-	1.0	-	-
IF	0	0.9993	0.9963	1.0	0.9594	0.9863	0.9845	0.908	0.9999	-	0.9969	1	0.9999	0.9754	-	-
	1	0.9999	0.9895	1.0	0.9838	0.9871	0.9979	0.9795	1.0	0.9992	0.9993	-	-	0.9993	-	-
	2	1.0	0.9931	1	0.9931	0.9997	0.9998	0.9942	1.0	0.9994	0.9995	-	-	0.9998	-	-
	3	0.9999	0.9501	0.9999	0.9666	0.9853	0.9992	0.9953	1.0	0.9951	0.9982	-	-	0.9973	-	-
RRCF	0	0.9973	0.9914	0.9996	0.9487	0.9786	0.9725	0.9005	0.9995	-	0.9941	1.0	0.9995	0.9651	-	-
	1	0.9998	0.9846	0.9999	0.9769	0.9820	0.9951	0.9706	0.9999	0.9981	0.9987	-	-	0.9980	-	-
	2	0.9999	0.9864	1.0	0.9875	0.9990	0.9989	0.9879	0.9999	0.9972	0.9986	-	-	0.9989	-	-
	3	0.9994	0.9385	0.9996	0.9537	0.9756	0.9960	0.9894	0.9999	0.9890	0.9959	-	-	0.9938	-	-
OC-SVM	0	0.9999	0.9995	1.0	0.9801	0.9943	0.9958	0.9454	1.0	-	0.9990	1	1.0	0.9882	-	-
	1	1.0	0.9956	1.0	0.9928	0.9936	0.9994	0.9907	1.0	0.9998	0.9998	-	-	0.9998	-	-
	2	1	0.9976	1	0.9977	1.0	0.9999	0.9981	1	0.9999	0.9998	-	-	0.9999	-	-
	3	1	0.9724	1	0.9866	0.9949	0.9999	0.9987	1	0.9990	0.9997	-	-	0.9992	-	-

Returning now to Table 3, the average OC-TVreg result for the ball fault of size 0.007 on all test motor loads is now 0.9992. This value was only achieved when training on $\mathrm{HP}=3$ in the experiment with training on different loads (see again Table 1), all other values being lower. This as a significant improvement on what appears to be the most difficult defect in this dataset. Similar improvements can be seen for other methods and other fault configurations, which suggests training on all motor loads is, in general, beneficial.

Table 4 shows the detailed results for training on features data. The same general observations hold as made for Table 2, with respect to the overall performance of the methods, compared to the case of raw signals. The OC-TVreg results are again only slightly worse for the cosine distance, where the mean ROC AUC is 0.99992.

Table 4. Training on all motor loads, features data. Mean (over five independent runs) ROC AUC values.

Method	Test HP	Inner			Ball			Orth			Center			Opposite
		0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021	0.007	0.014	0.021
DL	0	1.0	1.0	1	0.9998	1.0	1.0	0.9997	1.0	-	1.0	1	1	0.9998	-	-
	1	1.0	0.9996	1.0	0.9993	0.9996	0.9995	0.9992	1.0	0.9998	0.9997	-	-	0.9995	-	-
	2	1	1	1	0.9997	1	1	0.9999	1	1	1.0	-	-	1.0	-	-
	3	1	1.0	1	1.0	1	1	1	1	1	1	-	-	1	-	-
OC-TVreg (Euclidean)	0	1	1	1	1	1	1	1	1	-	1	1	1	1	-	-
	1	1	1	1	1	1	1	1	1	1	1	-	-	1	-	-
	2	1	1	1	1	1	1	1	1	1	1	-	-	1	-	-
	3	1	1	1	1	1	1	1	1	1	1	-	-	1	-	-
LOF	0	1	1	1	1.0	1	1	1.0	1	-	1	1	1	1.0	-	-
	1	0.9999	0.9997	1.0	0.9994	0.9997	0.9996	0.9994	0.9999	0.9998	0.9998	-	-	0.9996	-	-
	2	1	1	1	1.0	1	1	1	1	1	1	-	-	1	-	-
	3	1	1	1	1	1	1	1	1	1	1	-	-	1	-	-
IF	0	0.9999	0.9996	1.0	0.994	0.9979	0.9979	0.9979	1.0	-	0.9996	1.0	1.0	0.9963	-	-
	1	0.9999	0.9974	0.9998	0.9934	0.9963	0.9982	0.9982	0.9999	0.9995	0.9995	-	-	0.9991	-	-
	2	1.0	0.9983	1.0	0.997	0.9998	0.9997	0.9997	1.0	0.9995	0.9997	-	-	0.9997	-	-
	3	1	0.9991	1	0.9989	0.9997	1.0	1.0	1	0.9999	1.0	-	-	0.9999	-	-
RRCF	0	0.9988	0.998	0.9994	0.9924	0.9963	0.9947	0.9859	0.9992	-	0.9984	0.9998	0.9992	0.9936	-	-
	1	0.9993	0.9952	0.9995	0.9918	0.995	0.9961	0.9889	0.9995	0.9984	0.9986	-	-	0.9979	-	-
	2	0.9997	0.9959	0.9998	0.9942	0.9992	0.9986	0.9935	0.9998	0.9978	0.9989	-	-	0.9989	-	-
	3	0.9999	0.998	1.0	0.9975	0.9989	0.9997	0.9993	0.9999	0.9993	0.9997	-	-	0.9996	-	-
OC-SVM	0	0.9990	0.9988	0.9990	0.9988	0.9990	0.9988	0.9989	0.9988	-	0.9989	0.9988	0.9989	0.9990	-	-
	1	0.9992	0.9986	0.9991	0.9989	0.9990	0.9988	0.9990	0.9988	0.9992	0.9990	-	-	0.9990	-	-
	2	0.9995	0.9991	0.9995	0.9993	0.9995	0.9994	0.9993	0.9994	0.9992	0.9994	-	-	0.9995	-	-
	3	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	-	-	1.0	-	-

In this case as well, algorithms are more sensitive to test conditions than when trained on raw data, this time with $\mathrm{HP}=1$ being the most affected case for DL and LOF.

5.5. OC-TVreg: Robustness to Parameter Choice

Our proposed method, OC-TVreg, has two parameters: the number of neighbors K in the graph and the regularization parameter $\lambda$ in (5). We present here an experiment, suggesting that OC-TVreg has a robust behavior with respect to the values of these parameters. Table 5 presents the average ROC AUC values given by OC-TVreg with Euclidean distance (like in Table 4) in the case where all motor loads were used for training on features. One can see that the optimal value of 1 is obtained for several combinations of parameters. In the other reported cases, the values are quite close to 1.

Table 5. Average ROC AUC of OC-TVreg, with Euclidean distance and training on features from all motor loads, for various values of the parameters K and $\lambda$.

$\mathit{\lambda }\setminus \mathit{K}$	5	10	20	50	100
$0.01$	1	1	1	$1.0$	1
$0.1$	1	1	1	$1.0$	1
1	$0.999995$	$0.999999$	$1.0$	$1.0$	1
10	$0.999981$	$0.999982$	$0.999982$	$0.999998$	1

Similar behavior is visible in Table 6, where OC-TVreg is run with the cosine distance on time signals from all motor loads (like in Table 3). Note that the maximum value is obtained for $K=10$, $\lambda =0.01$. Again, there are many parameter choices for which the obtained ROC AUC values are near to the best one.

Table 6. Average ROC AUC of OC-TVreg, with cosine distance and training on time signals from all motor loads, for various values of the parameters K and $\lambda$.

$\mathit{\lambda }\setminus \mathit{K}$	5	10	20	50	100
$0.01$	$0.999844$	$0.999945$	$0.999933$	$0.999687$	$0.999541$
$0.1$	$0.999774$	$0.999935$	$0.999929$	$0.999687$	$0.999541$
1	$0.998386$	$0.999528$	$0.999849$	$0.999685$	$0.999539$
10	$0.998528$	$0.999501$	$0.999373$	$0.998669$	$0.997549$

As a general rule, the number of neighbors K should be in the low tens. The value $K=20$ is a popular default choice for methods based on distance to neighbors, including LOF, COF, and SOD from PyOD [85]. Somewhat lower values are also frequently used. The regularization factor should be small compared to the norm of the Laplacian matrix $\mathit{L}$ in (5). Empirically, we noticed that $\lambda$ should be 100–1000 times smaller than ${\parallel \mathit{L}\parallel }_1$ (the 1-norm is chosen for ease of computation).

5.6. Execution Times

We now report the execution times for testing the methods on an Intel Core i9, 256 GB RAM machine. The results in Table 7 present the average execution times on 10 independent tests, in seconds. Since there is no significant difference in terms of data dimensions between the experiments (except, of course for raw vs. features cases), we only provide execution times for testing on inner roll faults of dimension $0.007$ and $\mathrm{HP}=0$.

Table 7. Execution times.

Method	Raw Data	Features
DL	0.5962	0.4220
DL parallel	0.0548	0.0496
OC-TVreg	0.3895	0.3829
LOF	0.0201	0.0071
IF	0.2211	0.1936
RRCF	0.2056	0.2104
OC-SVM	0.0449	0.0110

For DL, the training phase is significantly more computationally expensive then the test phase; however, in the semi-supervised approach proposed here, it does not constitute a drawback. In practice, it is feasible and preferable that the training phase, where the dictionary $\mathit{D}$ is learned on a normal functioning bearing, be performed offline, prior to the actual operative monitoring. In fact, this also holds for the rest of the methods.

Moreover, the testing in DL amounts to computing the sparse representations ${\mathit{x}}_i$ for each individual signal in the dataset and the corresponding error ${ϵ}_i$. These computations are independent for each signal; hence, parallelization can be employed. In Table 7, we also provide DL times using the MATLAB Parallel Computing Toolbox, version 2024a.

IF and RRCF can also benefit from a similar treatment, and MATLAB implementations allow this option. For IF, using parallel computations decreases the execution times by $48\%$ for raw data and $38\%$ for features. Surprisingly however, with RRCF, there is a $68\%$ increase in execution times when working with raw data and a $16\%$ increase for features. Due to this apparent inconsistency, in Table 7 we only report results on the default non-parallel implementations.

As expected, DL is faster with features, as the dictionary size is dependent on the signal size. Likewise, the heavy reliance on distance computations in LOF makes the algorithm slower on raw time-series data. Similarly, the execution time of OC-SVM grows with the dimensionality of the signal, albeit for different reasons, linked to the larger complexity of the quadratic optimization problem that is solved. While OC-TVreg also initially computes distances between signals (1), all subsequent operations, including the most computationally expensive (7), depend only on the total number of training and testing signals and not their dimension. Since, in theory, IF should also not be affected by the signal size, we attribute the differences between execution times in the two experiments to data validation and other support operations in the MATLAB implementation. For RRCF, the difference between the two experiments is within the standard deviation of the individual tests.

6. Conclusions

We have tested the behavior of several semi-supervised anomaly detection methods on the CWRU bearing dataset. Only normal data are assumed to be labeled and are used for training (in the methods that have an explicit training phase), unlike in most of other works with the CWRU data. The best results are obtained by three methods. One of them, OC-TVreg, is proposed in this paper and minimizes a regularized total variation of a neighborhood graph associated with the data. The second is based on Dictionary Learning, a versatile modeling tool, not often used in anomaly detection but quite natural in our semi-supervised setup. The third is a well established anomaly detection method, namely LOF. Training with data from one load or from all loads, using the raw vibration signals or derived features, the methods achieve a perfect ROC AUC for many of the faults types and loads and nearly perfect values in the remaining cases. One can thus argue that anomaly detection on the CWRU data, in the natural semi-supervised setup that we have studied, is not a difficult machine learning problem and also that the lightweight methods we employ are adequate.