Featured Application
The calibration method proposed in this paper is applicable to redundant robot arms with highly elastic joints. Such robot arms can be used in flexible product manufacturing scenarios, such as folding, packaging, and moving medical pads and diapers.
Abstract
This paper proposes a calibration method for redundant robot arms with highly elastic joints. The method uses the second-order Chebyshev polynomial to characterize the variation in the error with the poses of all joints. This error model is consistent with the variation in the gravitational torque on each joint and demonstrates good generalization. Based on this, the calibration model includes both kinematic errors and non-kinematic errors. For this high-dimensional model, an adaptive iterative identification algorithm is proposed for a large number of small error parameters of various types. The algorithm sets specific iteration rules for different types of error parameters and adjusts the convergence amplitude in each iteration, ensuring that the iterative algorithm converges to the global optimum. The simulation results show that for a redundant robot arm with 12 highly elastic joints, even with large linearization modeling errors, the new identification algorithm can gradually eliminate them during iteration, achieving an identification accuracy higher than 99.975% for all of the error parameters. The experimental results indicate that on a redundant robot arm with eight cable-driven elastic joints, the new model and identification algorithm reduce the 96.6% absolute positioning errors of the robot arm, enabling it to perform precise and flexible operations. It takes 40.534 s and 29.077 s to run the identification algorithm on MATLAB (R2023b, 2.10 GHz CPU) in the simulation and experiment, respectively.
1. Introduction
The absolute positioning accuracy is crucial to the working performance of robot arms [1]. For industrial robot arms, kinematic parameter errors are the main cause of absolute positioning errors, which mainly originate from the errors introduced during the manufacturing, assembly, and transmission processes of the links and joints [1,2]. Traditional calibration methods can effectively compensate for kinematic parameter errors and improve the absolute positioning accuracy of industrial robot arms, thus meeting the requirements of most tasks [1,2]. However, due to their strong rigidity, long links, and limited degrees of freedom, industrial robot arms are not suitable for some tasks in unstructured spaces that require flexible contact with soft workpieces, like diapers and medical pads [3]. As a result, redundant robot arms with highly elastic joints, short links, and a large number of joints have emerged [4,5,6].
Most conventional calibration methods fail to account for the influence of the robot arm’s self-weight and external payload on joint angle errors during calibration. For instance, the model presented by Jiang et al. [7,8,9] relies solely on fixed kinematic parameters. Likewise, Li et al. [10], Chen et al. [11], and Yang et al. [12] applied the product of exponentials (POE) theory to formulate a calibration framework; nevertheless, all kinematic parameters in their approach still remained constant.
Apart from the research previously discussed, other research has also been conducted on the compliance properties of robotic joints. A number of publications have introduced calibration methods for non-kinematic parameters using mass distribution information about the links. For instance, Klimchik et al. [13] and Nubiola et al. [14,15,16] proposed enhanced models incorporating both kinematic and non-kinematic parameters. Gong et al. [17] formulated non-kinematic parameters in terms of gravitational and center-of-mass variables—which are often impractical to measure directly—thereby eliminating the necessity of identifying these challenging quantities explicitly. Other efforts have targeted non-kinematic parameters resulting from external loads. Chen and Kao [18], for example, created a comprehensive stiffness model that translates joint space to Cartesian space, using techniques such as the conservative congruence transformation (CCT), to support calibration in the presence of external loads. Dumas et al. [19] refined the model into a more streamlined form, allowing for simplified stiffness calibration while largely preserving precision. Zhou et al. [20] broadened the framework to include both geometric inaccuracies and non-kinematic parameters. To enhance identifiability in real-world settings, Mamedov et al. [21] proposed a group of simplified models derived from parameter scaling and noise impact assessments. Theissen et al. [22] also presented an innovative calibration technique that integrates external loads with diverse directions and magnitudes. Assuming known gravitational and mass properties for each link, Nubiola and Bonev [23] suggested another stiffness model. Furthermore, Du et al. [24] and Chen et al. [25] established functional mappings relating two categories of non-kinematic parameters to end-effector positioning inaccuracies.
Based on the calibration models above, there are relatively few studies on parameter identification. The main method used is iterative identification without weight variation. That is, the error parameters identified in the previous round are compensated into the calibration model, and then the error parameters for the next round are solved. This process continues until the error parameters identified in a certain round are below the set threshold. Finally, the identification results of each round are accumulated to obtain the final error parameter results [11,23,26]. Some scholars have also proposed identification algorithms based on the Levenberg–Marquardt algorithm, which can adaptively adjust the damping factor in each iteration. This factor is multiplied by the identity matrix and then added to the Jacobian matrix of the least squares method to ensure that the matrix remains positive definite in each iteration [27].
These elasto-geometrical coupling modeling methods have the following four issues: (1) Calibration models are designed for industrial robot arms with high assembly precision, strong rigidity, and fewer degrees of freedom. The angular parameter errors and non-kinematic parameter values contained in these models are small, and the model dimensions are low. Therefore, the linearization errors introduced during modeling are small, and the models are well-conditioned. Simple iterative algorithms can achieve high-precision identification results. However, when dealing with large linearization errors and high-dimensional models, these methods are prone to divergence and are not suitable for redundant robot arms with lower assembly precision, higher flexibility, and more degrees of freedom. (2) Calibration models treat non-kinematic parameters and the influence of gravity as independent quantities to be identified and rely on simple geometric relationships to establish mappings from these parameters to joint angle errors. As a result, they are only applicable to typical industrial robot arms with two long links and two adjacent parallel joints. When applied to redundant robot arms with consistent link lengths, a large number of joints, and adjacent joints that are perpendicular to each other, the above mappings become highly nonlinear, making it difficult to linearize the calibration model. (3) The calibration models that adopted polynomials to model non-kinematic parameters only considered the pose impact of distal joints on the target joint, ignoring the impact of proximal ones. This strategy was effective on the industrial robot with only six joints but not applicable to the hyper-redundant one. In addition, most of these polynomials were constructed with high order or in a form (e.g., a series of trigonometric functions) that was difficult to map linearly, which probably resulted in ill-conditioned calibration models. (4) The identification algorithms currently used in robotic arm calibration are only suitable for low-dimensional calibration models. When facing high-dimensional ones, due to the large number and variety of error parameters, and the significant differences in linearization errors, the relatively simple and uniform iteration strategies of traditional identification algorithms find it difficult to converge the iterations to high-precision results. In summary, existing calibration methods are no longer sufficient for the calibration needs of elasto-geometrical coupling redundant robot arms. There is an urgent need for improvements in the completeness of parameter errors, the generalization of calibration models, and the convergence of identification algorithms.
To this end, this paper has three contributions: (1) The functional relationship between the joint angle errors and all joint angles is constructed based on Chebyshev polynomials during the modeling phase, thereby characterizing the flexible characteristics of the robot arm’s joints. (2) An elasto-geometrical coupling calibration model is established, which integrates kinematic parameter errors and non-kinematic errors, enhancing the completeness and generalization of the model. (3) With the aim of gradually reducing the impact of linearization errors, specific iteration rules are established for each type of parameter and integrated into a single iterative identification algorithm.
The remainder of this paper is organized as follows. Section 2 establishes the elasto-geometrical error model. Based on this, Section 3 establishes the calibration model. Section 4 proposes the iterative identification algorithm. Section 5 performs a simulation to validate the convergence of the identification algorithm and the accuracy of the identification results on an elastic robot arm with 12 joints. Section 6 performs an experiment on a cable-driven robot arm with eight joints to demonstrate the accuracy of this new calibration model and the effectiveness of the identification algorithm. Section 7 draws conclusions.
2. Bi-Directional Coupling Elasto-Geometrical Error Model
As shown in Figure 1, the coordinate systems of each joint of a serial redundant robot arm with k degrees of freedom (revolute joints) are established based on the Modified Denavit–Hartenberg (MDH) convention, namely the base coordinate system F0 of the redundant robot arm and the joint coordinate systems Fi (i = 1, 2, …, k).
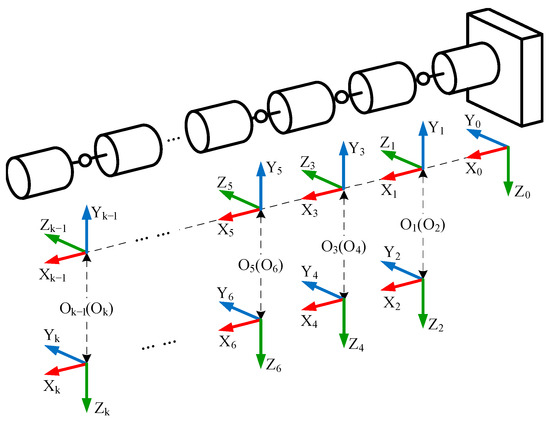
Figure 1.
Coordinate systems of a hyper-redundant robot arm with k joints.
Let i−1Ti denote the transformation matrix from the frame Fi−1 to Fi. Based on the MDH convention, the forward kinematic model of the i-th joint of the redundant robot arm is given by the following:
Let Rx(αi) and Rz(θi) denote the transformation matrices for rotations about the X-axis and Z-axis of the joint coordinate system, respectively. Let Dx(ai) and Dz(di) denote the transformation matrices for translations along the X-axis and Z-axis of the joint coordinate system, respectively. αi, ai, θi, and di are the nominal MDH parameters for joint i, where αi, ai, and di are fixed values related to the structure, and θi is the joint angle command corresponding to the i-th joint in the j-th measurement configuration. Then, i−1Ti in Equation (1) is calculated by
The MDH parameter errors for the i-th joint can be represented as Δui = [δαi, δai, δθi, δdi]T. Let Sθi and Cθi denote sin(θi) and cos(θi), respectively.
The redundant robot arm has a long and flexible arm structure, with a lower load-bearing capacity compared to industrial robot arms. It is not suitable for tasks such as machining that involve large loads and variable force directions. Instead, it is well-suited for tasks like detection, welding, and light-load assembly. Therefore, the primary source of flexibility errors is the additional bending of the elastic joints caused by the self-weight of the arm (including the end-effector), which affects the joint angle θi. First, the posture of the arm determines the lever arm of the gravitational moment acting on the axis of the target joint i. Thus, the joint angle error δθi caused by gravity should be represented as a function of all joint angles {θ1, …, θk}. Let (i = 1, 2, …, k) denote the normalized joint angle values and θi(min) and θi(max) represent the minimum and maximum values of θi, respectively, which are determined by the joint angle limits of the robot arm. Then, this yields
Let the set {iξ(0), iξ1(1), iξi(2), …, iξk(1), iξk(2)} (where i = 1, 2, …, k) represent the polynomial coefficients, defined as the non-kinematic parameters here. Based on this, a combination of second-order Chebyshev polynomials is used to represent δθi as
It should be noted that the second-order Chebyshev polynomial should originally include 0th-order, 1st-order, and 2nd-order terms. However, in Equation (4), all 0th-order terms are combined into iξ(0) to avoid parameter redundancy.
Let
and
Then, the total error parameter vector is established as
Let
Then, Jacobian can be constructed as
Based on the theory of differential transformations [25], the mapping matrix Ci from Δui to the pose error of Fi is
Further, by combining Equations (9) and (10), Jacobian Jk is constructed as
Let
Then, Chi can be constructed as
And CCheb can be obtained as
Now, in the j-th measurement configuration used for calibration, by combining Equations (13) and (14), the Jacobian which maps the parameter vector ΔU to the pose error vector Ej of the last joint can be constructed as
Finally, we obtain
3. Calibration Model
We assume that at the j-th measurement configuration, the actual transformation matrix of the end-effector coordinate system of the robot arm is represented as (0Tka)j
Based on the matrix elements in Equation (17), the corresponding actual pose vector pka(j) can be calculated using
where atan2(y, x) is a two-variable arctangent function.
Let i = k; then the nominal transformation matrix (0Tk)j for joint k at the j-th measurement configuration {θ1, …, θk}j can be obtained from Equation (1). Suppose that the elements of (0Tk)j are represented as
then the nominal pose vector pk(j) corresponding to (0Tk)j can be obtained as
From Equations (18) and (20), the pose error vector Ej for joint k at the measurement configuration {θ1, …, θk}j can be obtained as
If the calibration process uses n measurement configurations (where j = 1, 2, …, n), then Equation (6) can be expanded as
where
Finally, Equation (22) is transformed to Equation (24) to calculate ΔU
where J+ is the pseudo-inverse matrix of J and is a full-rank matrix as long as measurement configurations are properly selected.
4. Identification Algorithm
The calibration process is illustrated in Figure 2. The modeling procedure is detailed in Section 3, while the processes of the identification algorithm and the compensation algorithm are shown in the “adaptive iterative identification” and “classified compensation” modules in Figure 2, respectively.
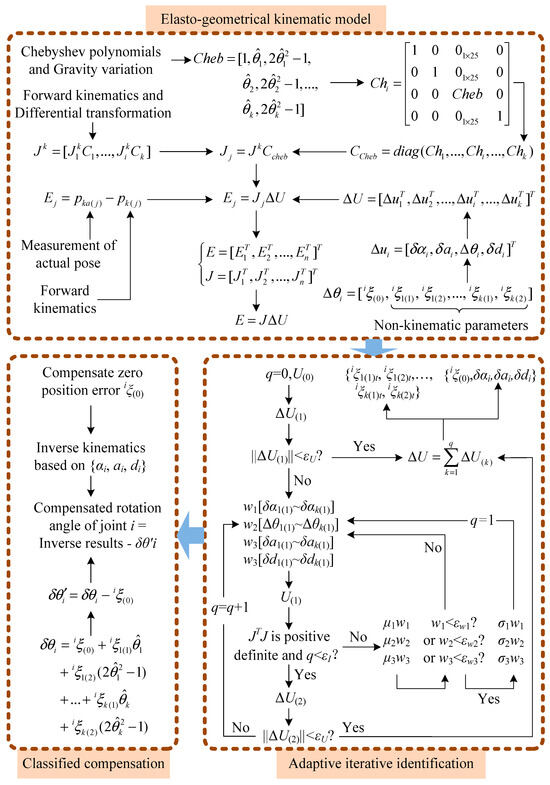
Figure 2.
The calibration process of the new method.
Step 1: Let the MDH parameters of the robot arm at the j-th measurement configuration obtained from the q-th iteration be denoted as U(q) = [α1(q), a1(q), θ1(q), d1(q), …, αi(q), ai(q), θi(q), di(q), …, αk(q), ak(q), θk(q), dk(q)]T. When q = 0, U(0) represents the nominal MDH parameters of the robot arm, where {θ1(0), θ2(0), …,θk(0)} are the joint angle commands at the j-th measurement configuration. Based on U(0), establish Equation (24). Define the result increment ΔU obtained from Equation (24) for the first time as the first identification result ΔU(1) = [δα1(1), δa1(1), Δθ1(1), δd1(1), …, δαi(1), δai(1), Δθi(1), δdi(1), …, δαk(1), δak(1), Δθk(1), δdk(1)]T, where q = 1. If ||ΔU(1)|| < εU, where εU is a predefined threshold, the iteration stops, and ΔU(1) is considered the final identification result. If ||ΔU(1)|| ≥ εU, proceed to the next step.
Step 2: Multiply the set {δα1(1), …, δαk(1)} in ΔU(1) by the weight w1 and then add them, respectively, to the set {α1(0), …, αk(0)} in U(0) to obtain {α1(1), …, αk(1)}. Multiply the set {Δθ1(1), …, Δθk(1)} by the weight w2 and substitute w2{Δθ1(1), …, Δθk(1)} and {θ1(0), …, θk(0) } into Equations (4) and (5) to obtain {δθ1(1), …, δθk(1)}, then add them, respectively, to {θ1(0), …, θk(0)} to get {θ1(1), …, θk(1)}. Multiply the sets {δa1(1), …, δak(1)} and {δd1(1), …, δdk(1)} by the weight w3 and then add them, respectively, to the sets {a1(0), …, ak(0)} and {d1(0), …, dk(0)} to obtain {d1(1), …, dk(1)}. The weights w1, w2, and w3 need to be manually set, and usually 0 < {w1, w2, w3} ≤ 1. Based on U(1) = [α1(1), a1(1), θ1(1), d1(1), …, αk(1), ak(1), θk(1), dk(1)]T, the calibration model of Equation (24) can be re-established.
Step 3: If the matrix JTJ is positive definite and the number of iterations is less than εI, then ΔU(2) can be directly obtained from Equation (24) and let q = q + 1. Here, εI is a threshold set manually. If the matrix JTJ is negative definite or semi-positive definite or the number of iterations reaches εI, then multiply w1, w2, and w3 by the reduction coefficients to get μ1w1, μ2w2, and μ3w3, respectively (μ1, μ2, and μ3 need to be set manually, and usually 0 < {μ1, μ2, μ3} < 1), and re-execute Step 1 to establish Equation (24) with q unchanged.
Step 4: Repeat Steps 1 to 3 until w1 < εw1, w2 < εw2, or w3 < εw3 still holds while ||ΔU(q)|| ≥ εU, at which point the iteration stops. Multiply w1, w2, and w3 by the reduction coefficients to get σ1w1, σ2w2, and σ3w3, respectively, then let q = 1 and execute Steps 1 to 3. Here, εw1, εw2, εw3, σ1, σ2, and σ3 need to be set manually, and usually 0 < {σ1, σ2, σ3} < 1. If ||ΔU(q)|| < εU, then the iteration stops. Now, ΔU can be obtained by
Step 5: In each load condition, the corresponding identification result ΔU can be obtained. If there are six sets of loads, then a total of six sets of ΔU will be obtained. Since iξ(0), δαi, δai, and δdi are independent of joint elasticity, they do not change with the load. Therefore, the average values of iξ(0), δαi, δai, and δdi from the six sets of ΔU are taken as the final identification results. However, {iξ1(1), iξ1(2), iξ2(1), iξ2(2), …, iξk(1), iξk(2)} represent joint elasticity and thus vary with the load. Therefore, their sample set is constructed as shown in Table 1.

Table 1.
Sample set of identification results of i-th non-kinematic parameters under multiple loads.
In Table 1, the subscripts “(mF2)” and “(mF3)” represent the identification results of the non-kinematic parameters {iξ1(1), iξ1(2), …, iξk(1), iξk(2)} under the loads mF2 and mF3, respectively. When a tool with a known weight mt is installed at the end of the robot arm, the sample interval where mt is located is first determined (here it is assumed that mt in [mF2, mF3]), and in actual implementation, it is determined according to the actual situation). Then, based on Table 1 and the following formula, linear interpolation can be performed to obtain the identification results of the non-kinematic parameters corresponding to the external load {iξ1(1)t, iξ1(2)t, …, iξk(1)t, iξk(2)t}.
Step 6: Based on the identification results obtained in Step 5, the compensation of ΔU is carried out in three sub-steps. First, for i = 1~k, take iξ(0) from ΔU at any measurement configuration as the zero-position error of the i-th joint, and then compensate all iξ(0) synchronously in the control system. Next, add {δαi, δai, δdi} from ΔU to {αi, ai, di} from U(0), respectively, to obtain the actual values {αi, ai, di} for the inverse kinematic solution (details are not repeated here). Finally, for i = 1~k, subtract δθ’i from the joint i rotation angle command obtained from the inverse solution to obtain the final compensated rotation angle commands for all joints. Here, δθ’i is
The δθi in Equation (27) is obtained by first performing linear interpolation as described in Step 5 to get {iξ1(1)t, iξ1(2)t, …, iξk(1)t, iξk(2)t} and then substituting these values into Equation (4) to perform calculations at the corresponding joint rotation angle commands obtained from the inverse solution.
5. Simulation
The simulation is performed on the MATLAB platform (R2023b, 2.10 GHz CPU). The procedure of the simulation is summarized in Figure 3.
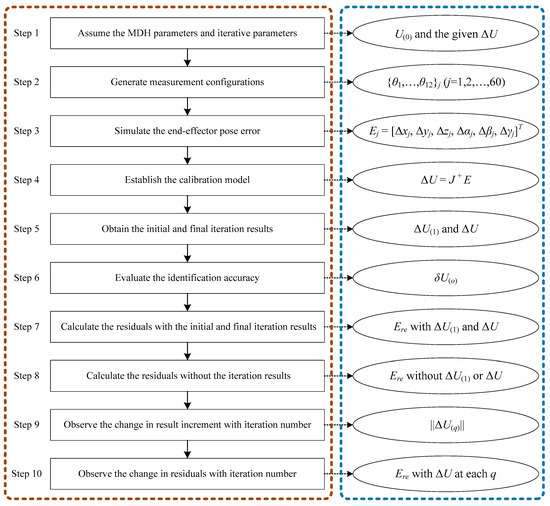
Figure 3.
The procedure of the simulation.
Step 1: According to the joint numbers adopted by most hyper-redundant robot arms, here, let k = 12, and assume that the nominal values of the MDH parameters of the redundant robot arm are as shown in Table 2, where the values are similar to those of our self-developed prototype. The MDH parameter error values and non-kinematic parameter values are as shown in Table 3, where iξ1(1)~iξ12(2) are set based on the elasticity of the material used for the joint drive cables in our prototype. The structural parameters {δαi, δai, iξ(0), δdi} are set according to the arm assembly error and zero position error, where the values are larger than those usually observed on industrial robots because the cable-driven robot arm is difficult to manufacture and assemble with very high precision. The error data obtained in previous studies [28,29,30] were also used as the basis for the assumed values. The iterative parameters are w1 = 1; w2 = w3 = 0.5; σ1 = σ2 = σ3 = 0.5; and μ1 = μ2 = μ3 = 0.5, where the values are set according to our experience that the initial results of δαi and iξ(0) are relatively accurate, while those of δai, δdi and iξ1(1)~iξ12(2) have large identification errors in most cases. The thresholds are εU = 0.00001; εI = 200; εw1 = 0.01; and εw2 = εw3 = 0.005.

Table 2.
Assumed nominal kinematic parameters in simulation.

Table 3.
Assumed nominal non-kinematic parameters in simulation.
Step 2: Use the DETMAX algorithm [7,8,9] to select the measurement configurations {θ1, …, θ12}j (j = 1, 2, …, 60).
Step 3: Simulate the end-effector pose error vector E. The elements of the pose error Ej = [Δxj, Δyj, Δzj, Δαj, Δβj, Δγj]T required in Equation (21) are obtained as follows
where 0T12a is obtained with the following equation in the case of {θ1, …, θ12}
In Equation (29), (i−1)aTia represents the actual (i−1)Ti affected by Δui, which is obtained by replacing {αi, ai, θi, di} in Equation (2) with {αi + δαi, ai + δai, θi + δθi, di + δdi}. Here, δαi, δai, and δdi are given in Table 3, and δθi is obtained from Equation (4), {θ1, …, θ12}j, and {iξ(0), iξ1(1), iξi(2), …, iξ12(1), iξ12(2)} in Table 3. In Equation (28), 0T12 is obtained from Equation (1) at i = 12 and the measured configuration {θ1, …, θ12}j. By combining Ej at the 60 measured configurations according to Equation (23), the complete pose error vector E can be established.
Step 4: Substitute the obtained E into Equation (24) to establish the calibration model.
Step 6: The identification accuracy of the o-th element in ΔU(1) and ΔU (where o represents the index of the error parameter in the ΔU vector) is denoted by δU(o) and is calculated using the following equation
where ΔUca(o) is the identification result corresponding to the assumed value ΔU(o), and the identification accuracy δU(o) of ΔU(1) and ΔU is shown in Figure 4.
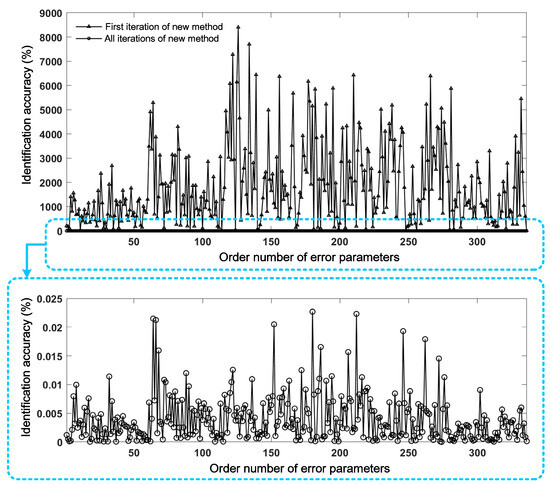
Figure 4.
A comparison of the accuracy between the first identification of the new method and the iterative identification of the new method.
Step 7: Randomly generate 1000 measurement points within the workspace of the robot arm, as shown in Figure 5.
Figure 5.
Distribution of test points.
Then, compensate for the identification results of ΔU(1) and ΔU, respectively, and calculate the absolute positioning residual Ere of the 12th joint of the robot arm after the first calibration iteration of the new method and after the complete calibration iteration of the new method at the test-th measurement point (where test = 1, 2, …, 1000), using the following formula.
The method for calculating the residuals after the first step of the new method’s iterative calibration and after the complete iterative calibration of the new method is similar to Equation (31). The differences are that the measurement configurations j are all replaced by the measurement point test, and the values of δαi, δai, δdi, and {iξ(0), iξ1(1), iξi(2), …, iξ12(1), iξ12(2)} are the corresponding identified values from ΔU(1) and ΔU. The statistical results of Ere for all measurement points are shown in Figure 6.
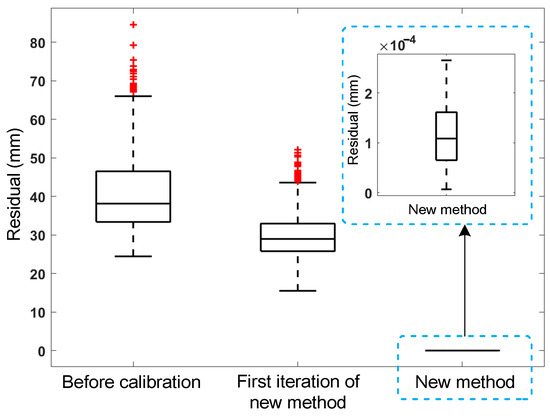
Figure 6.
Comparison of absolute positioning residuals for different stages of new method in simulation.
Step 8: Obtain the positioning error of the uncalibrated robot arm at measurement point test using a method similar to Equation (31), which serves as a control group for the two sets of residuals mentioned above. In Equation (31), Δxtest, Δytest, and Δztest are the corresponding components of E obtained in Step 3. The statistical results of the control group are also shown in Figure 6.
Step 9: Plot the values of ||ΔU(q)|| obtained from each iteration of the new method, as shown in Figure 7.
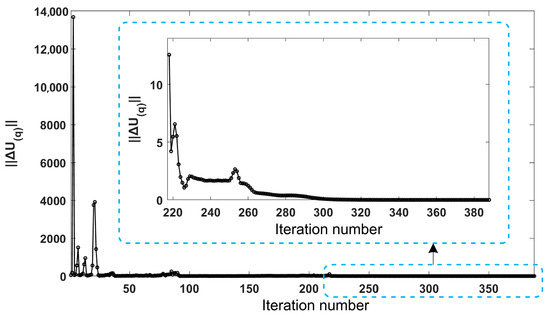
Figure 7.
Trend in ||ΔU(q)|| with iteration number in simulation.
Step 10: After compensating for the identification results from each iteration of the new method, calculate the positioning residual of the robot arm at the 1000 measurement points using Equation (30). The results are shown in Figure 8.
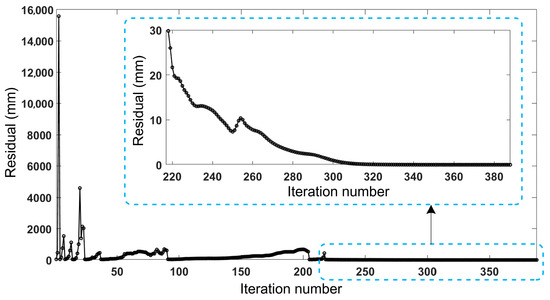
Figure 8.
Trend in absolute positioning residual with iteration number in simulation.
Figure 4 indicates that the identification accuracies δU(o) after the new method’s iterative convergence are all improved to be better than 0.025%, while some of those after the initial identification are extremely wrong (1 × 103%~9 × 103%). Figure 6 shows that the initial calibration and the iterative calibration using the new method can reduce the median residuals to 28.629 mm and 1.051 × 10−4 mm, respectively. Among them, the iterative calibration using the new method achieves the smallest residual, improving the calibration accuracy to about 99.975%. Figure 7 demonstrates that ||ΔU(q)|| gradually decreases with the increase in the number of iterations and eventually tends towards a stable and small value (smaller than 0.00001). Figure 8 shows that the positioning residuals gradually decrease with the increase in the number of iterations and finally stabilize. The curves in Figure 7 and Figure 8 exhibit several inflection points where the residuals do not decrease but increase before convergence. This occurs when the iteration encounters a situation where JTJ is not positive definite, leading to a tendency for the iteration to diverge. However, the adaptive weighting strategy of the identification algorithm enables ||ΔU(q)|| and the positioning residuals to quickly resume their downward trend and ultimately converge. The overall results show that the new method achieves a generalized representation of non-kinematic errors and enhances the completeness of the calibration model, more accurately representing the coupled characteristics of the robot arm’s rigidity and flexibility. Moreover, the new method overcomes the problem of the increased linearization errors caused by the dramatic increase in the dimensions of non-kinematic parameters through an iterative identification algorithm, ensuring the accuracy of parameter identification.
6. Experiment
6.1. Experiment Setup
A redundant robot arm with eight degrees of freedom (DOFs) is adopted here. Although this reduces the number of elastic joints compared with the 12 joints assumed in the simulation, this elastic robotic arm with 8 joints also has a high error model dimension (6n × 224), where the effectiveness of the new identification algorithm on the high-dimensional error model of highly elastic robotic arms can also be demonstrated. The experiment is conducted at room temperature of 25 °C (with air-conditioning on). The nominal kinematic parameters are listed in Table 4. The main specifications of the vision system are listed in Table 5.

Table 4.
Nominal kinematic parameters in experiment.

Table 5.
The main specifications of the vision system.
As shown in Figure 9, a marker (named marker-1) with a size of 50 mm × 50 mm is set close to the end of robot. The camera is located properly to ensure that the workspace of the robot can be entirely contained by the FOV (field of view).

Figure 9.
Installation of sensors and instruments for calibration.
Here, a laser tacker (API Radian PLUS with distance resolution of 0.5 μm and maximum permissible error of 15 μm + 5 μm/m) is also adopted to increase the accuracy of preparation. As shown in Figure 10a, due to the high precision in the manufacturing of the marker, touching the edge and surface of the marker with the laser tracker’s spherically mounted reflector (SMR) can fit the outer contour dimensions of marker-1 in the laser tracker coordinate system FL. This allows for the establishment of Fm1, as shown in the figure. By moving joint 8 of the robot arm to several rotation angles and performing the above operations at each angle, LTm1 at each angle can be obtained. Fitting the origins of this series of LTm1 into an arc yields the central axis of the arc, whose unit vector is the axis Z8 of joint 8. The same method is used to establish the axis Z7 of joint 7, and then F8 at each angle is established, as shown in the figure. Combining the corresponding Fm1 with it results in a constant 8Tm1.
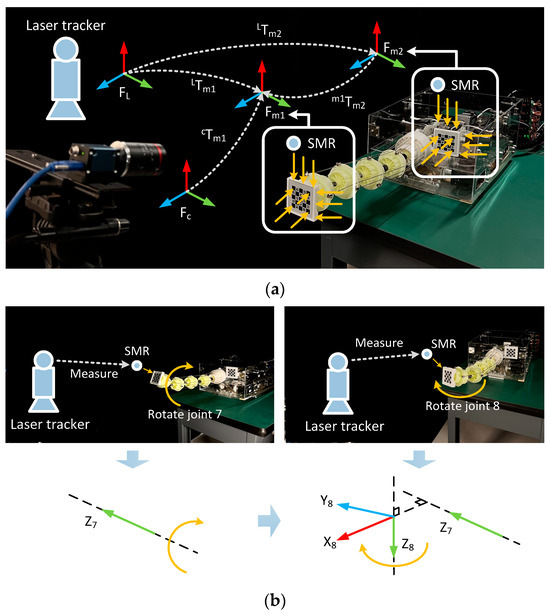
Figure 10.
Establishments of 8Tm1 and cT0 with hybrid measurement instruments: (a) Establishment of cT0. (b) Establishment of 8Tm1.
In addition, compared with traditional robot arms, flexible redundant robot arms have much higher flexibility and larger absolute positioning errors. Therefore, traditional hand–eye calibration methods cannot obtain an accurate transformation matrix cT0. To address this, as shown in Figure 10b, we adopted a dual-target pose transfer method to achieve hand–eye calibration for flexible redundant robot arms. Specifically, a target (marker-2) with the same size of marker-1 was set up next to the robot arm base, and it was precisely installed so that the transformation m2T0 from its coordinate system Fm2 to the base frame F0 is accurate. Similarly to LTm1, the SMR of the laser tracker was used to obtain LTm2. The robot arm was adjusted to a suitable posture so that the camera could accurately measure the pose of marker-1, i.e., accurately obtain cTm1. A method similar to that for LTm2 was used to obtain LTm1 at this time. Thus, cT0 = (cTm1)(m1TL)(LTm2)(m2T0)−1 can be obtained.
It should be noted that joint elasticity can cause obvious vibrations in the robotic arm. Therefore, after the robotic arm reaches each specified configuration, it is necessary to wait for about 5 s, that is, until the vibrations of the robotic arm stop, before carrying out the pose measurement. In addition, improper force control when the SMR touches marker-1 can also cause marker-1 to deviate from its correct position. Therefore, it is necessary to synchronously observe in real time whether there is a significant change in the pose of marker-1 on the camera at this time. The change in the position of marker-1 should be less than the camera’s repeatability measurement accuracy, which is 0.06 mm along both the Xc and Yc axes and 0.13 mm along the Zc axis, considering the camera’s characteristics in Table 5 and the measurement distance of 400 mm.
It should be explained that the measurement method described above, which employs a camera as the measuring instrument, allows for the use of lightweight markers as sensors. This method is suitable for the lightweight cable-driven robot arm used in this paper. When the measurement object is an elastic robot arm with a higher load-bearing capacity to move the SMRs, it is possible to consider using the commonly used laser tracker as the measuring device. In this way, not only can the series of preparations to improve the measurement accuracy of the vision system be avoided, but also a higher measurement accuracy can be achieved.
6.2. Pose Measurement and Parameter Identification
A total of 60 measurement configurations are selected according to the DETMAX algorithm and marker visibility, and some of them are presented in Figure 11. It is seen that the marker can be clearly seen by the camera at each pose. To minimize the influence of measurement noise, 50 pictures are taken for each marker at each measurement configuration. Marker-1 is considered one of the external loads described in Table 1. After collecting sufficient end-effector pose errors of the robot arm according to the above steps, the identification model can be established based on Section 2.
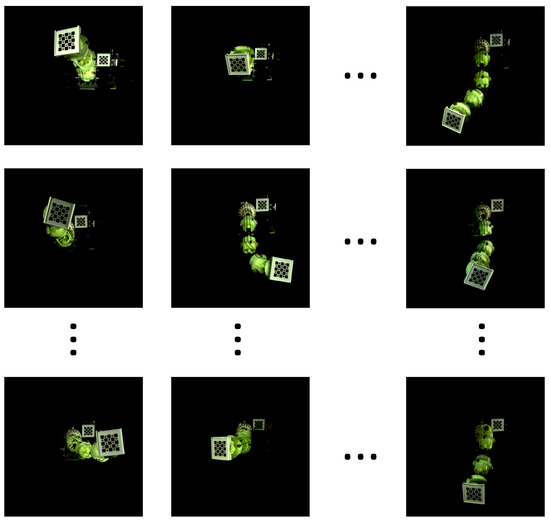
Figure 11.
Some of the visible optimized measurement configurations.
Then the proposed identification algorithm (the method is denoted by M1) can be executed. It should be noted that the iterative parameter values of the identification algorithm in the experiment are slightly different from those in the simulation. They are set as w1 = w2 = w3 = 1; σ1 = σ2 = σ3 = 0.5; μ1 = 0.8; and μ2 = μ3 = 0.5. It has to be explained that the joint number in the experiment is lower than that in the simulation, so the dimension of the error model is reduced. Accordingly, the initial identification errors of δai and δdi will also be reduced; thus, w2 and w3 increase from 0.5 to 1. In addition, the value of μ1 increases from 0.5 to 0.8 because the identification errors in each iteration of δαi and iξ(0) will also be reduced with the dimension of the error model. The thresholds εU, εI, εw1, εw2, and εw3 are the same as those in the simulation. Also, the identification algorithms proposed in Ref. [26] (the method is denoted by M2) and Ref. [27] (the method is denoted by M3) are adopted to the new calibration model for a comparison with the new adaptive iterative identification algorithm M1.
6.3. Experimental Results and Discussion
The changes in ||ΔU(q)|| with iteration number in the cases of the three identification algorithms are represented in Figure 12, Figure 13 and Figure 14, respectively. For M1, as shown in Figure 12, the identification stops at the 135th iteration, which takes 29.077 s. Similarly to the results in Figure 7, for ||ΔU(q)|| in Figure 12, as the number of iterations increases, the value gradually decreases and eventually stabilizes at a very small value (smaller than 0.00001). Before convergence, the curve exhibits several inflection points where it does not decrease but instead increases, indicating a tendency towards divergence at these points. However, the adaptive weighting strategy of the identification algorithm enables ||ΔU(q)|| and the positioning residual to quickly resume their downward trend and ultimately converge. For M2, as shown in Figure 13, the iteration does not converge and keeps oscillating within a very large range of ||ΔU(q)||, which indicates that algorithm M2 fails when facing the high-dimensional calibration model. For M3, as shown in Figure 14, the identification stops at the 135th iteration. Although M3 converges to the same high precision (smaller than 0.00001) as M1 and has the fewest iterations, the total time consumed by M3 is 124.905 s, which is much longer than that consumed by M1. The convergence in Figure 12 demonstrates that the modeling method and the corresponding adaptive identification algorithm proposed in this paper also have good applicability and convergence in practical use.
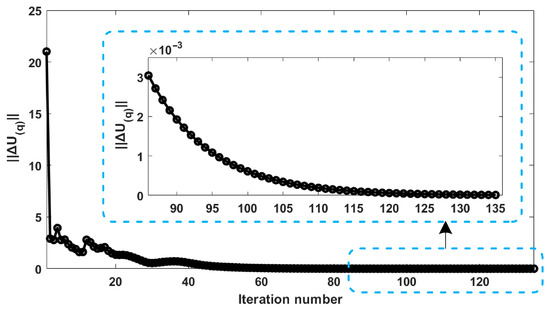
Figure 12.
Trend in ||ΔU(q)|| with iteration number of M1 in experiment.
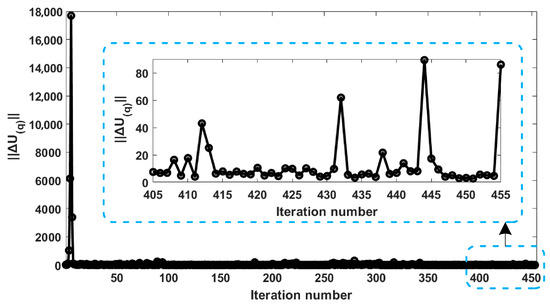
Figure 13.
Trend in ||ΔU(q)|| with iteration number of M2 in experiment.
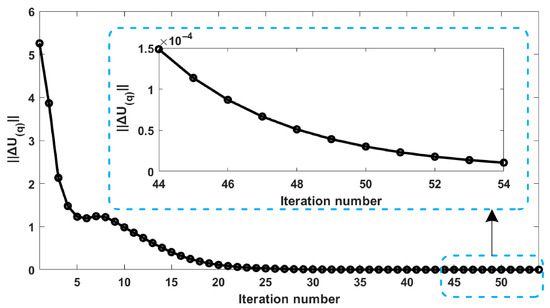
Figure 14.
Trend in ||ΔU(q)|| with iteration number of M3 in experiment.
Also, a comparison similar to that in Steps 7 and 8 in Section 5 is also performed here; that is, the absolute positioning residual of the robot arm before calibration, after one iteration of the algorithm, and after multiple iterations of the algorithm have converged is compared to evaluate the advantage of the new calibration method in the real world. It should be noted that the error compensation still follows the “classified compensation” module process shown in Figure 3. However, since the experiment uses a cable-driven flexible robot arm, after compensating for the joint angles of the arm, it is also necessary to additionally convert them into the extension and contraction amounts of the drive cables and instruct the drive motors to make corresponding output angle adjustments (the details of which are omitted here as they are not the focus of this paper). Here, we randomly generated another 100 measurable configurations for verifying the calibration accuracy and still used an industrial camera to measure the end-effector residual of the robot arm, the results of which are shown in Figure 15.
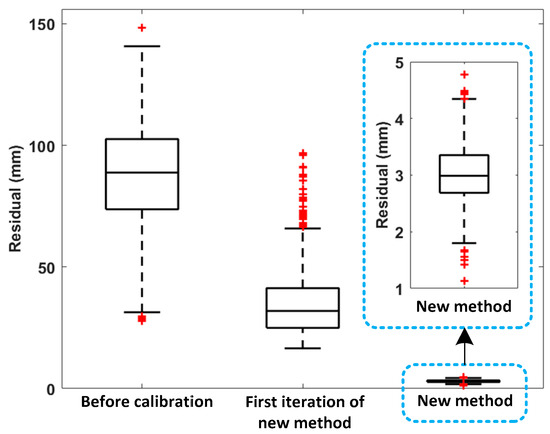
Figure 15.
Comparison of absolute positioning residuals for different stages of new method in experiment.
Similar conclusions to those in Figure 6 can be drawn from Figure 15, which shows that the initial calibration and the iterative calibration of the new method can reduce the median residuals to 31.929 mm and 2.988 mm, respectively. Among them, the iterative calibration of the new method achieves the smallest residual. It should be noted that by comparing the residual values shown in Figure 6 and Figure 13, it can be seen that even after optimization by the new calibration method, the absolute residual of the redundant robot arm in the experiment was reduced, but it is still much higher than that in the simulation. This indicates that there are many sources of error in the elastic redundant robot arm in practical applications. These errors are coupled with each other and mapped to the end-effector pose error, making it difficult for their identification and compensation to reach the accuracy level of those of traditional industrial robot arms. Specifically, as the pose of the arm changes, the pressure between the cable and the cable hole will change. This change will lead to a change in the friction force between the cable and the cable hole, and this friction force has a coupled effect on the end-effector pose with the joint elasticity. In addition, since the stiffness of the slender joint hinges of the self-developed cable-driven robotic arm is much lower than that of the robust joints of industrial robotic arms, the flexibility error of a certain joint’s hinge structure will be coupled with the flexibility error of the joint that is perpendicular to it. Even so, the new method proposed in this paper can already control the absolute positioning residual of the elastic redundant robot arm to a relatively low value, enabling it to be used in applications such as detection and grasping that have general working accuracy requirements.
It is worth mentioning that although the new modeling method and identification algorithm are proposed based on a highly elastic cable-driven robot arm, the method can be extended to other types of manipulators simply by adjusting the parameter values in the modeling and identification stages. For instance, in the case of the 6-DOF industrial robot, the order of Chebyshev polynomials in Equation (4) can be reduced to one or zero, since the joints are more rigid than those of the cable-driven ones. Also, all of the iterative parameters (except the thresholds) can be increased to be close to 1. The same strategy can be applied to the collaborative robot where the joints are more elastic than those of rigid industrial robots but more rigid than those of cable-driven ones.
The iterative identification algorithm proposed in this paper is specifically designed for the error parameters of the new model. Therefore, the adaptive adjustment strategy of this algorithm in the iteration has certain limitations; that is, it aims to gradually eliminate the identification errors caused by various kinematic and non-kinematic error parameters in each round of iteration. In fact, some researchers have proposed more widely applicable parameter identification algorithms. For instances, Sanin-Villa et al. tackled parameter estimation for thermoelectric generators using the Salps Search Algorithm, achieving impressively high consistency and accuracy [31]; they also compared metaheuristic algorithms for the inverted pendulum system, with the SSA delivering highly accurate and reliable results [32]. These algorithms have strong generalization ability and provide valuable references for our future optimization of the identification algorithm in this paper.
7. Conclusions
The calibration method for high-elastic redundant robot arms proposed in this paper, which couples rigidity and flexibility, demonstrated good model accuracy and identification accuracy in both simulations and experiments. In the experiments, we found that the base-fixed camera (which is also the installation form adopted by the vast majority of measuring devices) could hardly cover all the optimal measurement configurations of the redundant robot arm. Therefore, in the actual measurements, we used some measurable suboptimal configurations to replace the optimal measurement configurations that could not be measured. However, the pose data collected in this way could not fully cover the rotation space of each joint, and the calibration model established based on this was prone to ill-conditioning. In contrast, if the complete optimal measurement configurations could be captured, the coverage of the pose data would be more comprehensive, and the calibration model established would achieve the optimal condition level, with more accurate identified parameter values.
To address this issue, in the future, we plan to conduct research on our self-developed mobile-base measuring arm. We aim to make targeted pose adjustments for each optimal measurement configuration of the redundant robot arm before performing the measurements, thereby improving the flexibility and accuracy of the measurements.
Author Contributions
Conceptualization, B.W.; methodology, B.W. and Z.J.; software, B.W. and Z.J.; validation, B.W.; formal analysis, B.W. and Z.J.; investigation, B.W. and Z.J.; resources, B.W.; data curation, B.W.; writing—original draft preparation, B.W. and Z.J.; writing—review and editing, B.W.; visualization, Z.J.; supervision, Z.J.; project administration, Z.J.; funding acquisition, Z.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by General Program of National Natural Science Foundation of China, grant number 52175452.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within this article.
Acknowledgments
The authors would like to thank the factory survey opportunities and technical support provided by Beijing Beishute Maternity & Child Articles Co., Ltd.
Conflicts of Interest
Author Bin Wang is employed by the company Beijing Beishute Maternity & Child Articles Co., Ltd. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Baizid, K.; Cukovic, S.; Iqbal, J.; Yousnadj, A.; Chellali, R.; Meddahi, A.; Devedžić, G.; Ghionea, I. IRoSim: Industrial robotics simulation design planning and optimization platform based on cad and knowledgeware technologies. Robot. Comput. Integr. Manuf. 2016, 42, 121–134. [Google Scholar] [CrossRef]
- Gang, C.; Tong, L.; Ming, C.; Xuan, J.Q.; Xu, S.H. Review on Kinematics Calibration Technology of Serial Robots. Int. J. Precis. Eng. Manuf. 2014, 15, 1759–1774. [Google Scholar] [CrossRef]
- Khan, O.; Pervaiz, M.; Ahmad, E.; Iqbal, J. On the derivation of novel model and sophisticated control of flexible joint manipulator. Rev. Roum. Sci. Tech.—Ser. Électrotechnique Énergétique 2017, 62, 103–108. [Google Scholar]
- Bogue, R. Robots in the Nuclear Industry: A Review of Technologies and Applications. Ind. Robot Int. J. 2011, 38, 113–118. [Google Scholar] [CrossRef]
- Xu, W.; Liu, T.; Li, Y. Kinematics, Dynamics, and Control of a Cable-Driven Hyper-Redundant Manipulator. IEEE/ASME Trans. Mechatron. 2018, 23, 1693–1704. [Google Scholar] [CrossRef]
- Luo, M.; Li, E. A Bioinspired Coiled Cable-Driven Manipulator: Mechatronic Design and Kinematics Planning with Multiconstraints. IEEE/ASME Trans. Mechatron. 2023, 28, 3155–3166. [Google Scholar] [CrossRef]
- Jiang, Z.; Su, R.; Liu, Y.; Long, Z.; Song, B.; Tang, X. Accurate Relative Measurement of Multi-Target Poses by Monocular Vision for Nonmodel-Based Real-Time Calibration of Industrial Robot. Measurement 2024, 235, 114979. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, S.; Zhao, Y.; Long, Z.; Song, B.; Tang, X. Accurate Kinematic Calibration of a Six-DoF Serial Robot by Using Hybrid Models with Reduced Dimension and Minimized Linearization Errors. Ind. Robot Int. J. Robot. Res. Appl. 2024, 51, 772–788. [Google Scholar] [CrossRef]
- Jiang, Z.; Ding, R.; Liu, Y.; Long, Z.; Song, B. Vision-Based and Real-Time Calibration of Industrial Robot by Using Deep Learning and Dimension-Reduced Models. Precis. Eng. 2025, 96, 192–211. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.Q.; Lowe, H. POE-Based Robot Kinematic Calibration Using Axis Configuration Space and the Adjoint Error Model. IEEE Trans. Robot. 2016, 32, 1264–1279. [Google Scholar] [CrossRef]
- Chen, G.L.; Wang, H.; Lin, Z.Q. Determination of the Identifiable Parameters in Robot Calibration Based on the POE Formula. IEEE Trans. Robot. 2014, 30, 1066–1077. [Google Scholar] [CrossRef]
- Yang, X.D.; Wu, L.; Li, J.Q.; Chen, K. A Minimal Kinematic Model for Serial Robot Calibration Using POE Formula. Robot. Comput. Integr. Manuf. 2014, 30, 326–334. [Google Scholar] [CrossRef]
- Klimchik, A.; Furet, B.; Caro, S.; Pashkevich, A. Identification of the Manipulator Stiffness Model Parameters in Industrial Environment. Mech. Mach. Theory 2015, 90, 1–22. [Google Scholar] [CrossRef]
- Nubiola, A.; Slamani, M.; Bonev, I.A. A New Method for Measuring a Large Set of Poses with a Single Telescoping Ballbar. Precis. Eng. 2013, 37, 451–460. [Google Scholar] [CrossRef]
- Nubiola, A.; Bonev, I.A. Absolute Robot Calibration with a Single Telescoping Ballbar. Precis. Eng. 2014, 38, 472–480. [Google Scholar] [CrossRef]
- Nubiola, A.; Bonev, I.A. Non-Kinematic Calibration of a Six-Axis Serial Robot Using Planar Constraints. Precis. Eng. 2015, 40, 472–480. [Google Scholar]
- Gong, C.H.; Yuan, J.X.; Ni, J. Nongeometric Error Identification and Compensation for Robotic System by Inverse Calibration. Int. J. Mach. Tools Manuf. 2000, 40, 2119–2137. [Google Scholar] [CrossRef]
- Chen, S.F.; Kao, I. Conservative Congruence Transformation for Joint and Cartesian Stiffness Matrices of Robotic Hands and Fingers. Int. J. Robot. Res. 2000, 19, 835–847. [Google Scholar] [CrossRef]
- Dumas, C.; Caro, S.; Garnier, S.; Furet, B. Joint Stiffness Identification of Six-Revolute Industrial Serial Robots. Robot. Comput. Integr. Manuf. 2011, 27, 881–888. [Google Scholar] [CrossRef]
- Zhou, J.; Nguyen, H.N.; Kang, H.J. Simultaneous Identification of Joint Compliance and Kinematic Parameters of Industrial Robots. Int. J. Precis. Eng. Manuf. 2014, 15, 2257–2264. [Google Scholar] [CrossRef]
- Mamedov, S.; Popov, D.; Mikhel, S.; Klimchik, A. Compliance Error Compensation Based on Reduced Model for Industrial Robots. In Proceedings of the International Conference on Informatics in Control, Automation and Robotics (ICINCO), Porto, Portugal, 29–31 July 2018. [Google Scholar]
- Theissen, N.A.; Laspas, T.; Archenti, A. Closed-Force-Loop Elastostatic Calibration of Serial Articulated Robots. Robot. Comput. Integr. Manuf. 2019, 57, 86–91. [Google Scholar] [CrossRef]
- Nubiola, A.; Bonev, I.A. Absolute Calibration of an ABB IRB 1600 Robot Using a Laser Tracker. Robot. Comput. Integr. Manuf. 2013, 29, 236–245. [Google Scholar] [CrossRef]
- Du, L.; Zhang, T.; Dai, X.L. Compliance Error Calibration for Robot Based on Statistical Properties of Single Joint. J. Mech. Sci. Technol. 2019, 33, 1861–1868. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, Q.J.; Sun, Y.L. Non-Kinematic Calibration of Industrial Robots Using a Rigid-Flexible Coupling Error Model and a Full Pose Measurement Method. Robot. Comput. Integr. Manuf. 2019, 57, 46–58. [Google Scholar] [CrossRef]
- Sun, T.; Liu, C.; Lian, B.; Wang, P.; Song, Y. Calibration for Precision Kinematic Control of an Articulated Serial Robot. IEEE Trans. Ind. Electron. 2021, 68, 6000–6009. [Google Scholar] [CrossRef]
- Luo, G.; Zou, L.; Wang, Z.; Lv, C.; Ou, J.; Huang, Y. A novel kinematic parameters calibration method for industrial robot based on Levenberg-Marquardt and Differential Evolution hybrid algorithm. Robot. Comput. Integr. Manuf. 2021, 71, 102165. [Google Scholar] [CrossRef]
- Lou, Y.; Lin, H.; Quan, P.; Wei, D.; Di, S. Self-Calibration for the General Cable-Driven Serial Manipulator with Multi-Segment Cables. Electronics 2021, 10, 444. [Google Scholar] [CrossRef]
- Chen, Q.; Li, M.; Wu, H.; Liu, W.; Peng, J. Design, self-calibration and compliance control of modular cable-driven snake-like manipulators. Mech. Mach. Theory 2024, 193, 105562. [Google Scholar] [CrossRef]
- Yin, Y.; Gao, D.; Lu, Y.; Zhao, C.; Li, G.; Deng, K. In-situ robot joint stiffness identification using an eye-in-hand camera with optimal measurement pose selection. Measurement 2025, 253, 117579. [Google Scholar] [CrossRef]
- Sanin-Villa, D.; Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F.; Perea-Moreno, A.-J. Parameter Estimation of a Thermoelectric Generator by Using Salps Search Algorithm. Energies 2023, 16, 4304. [Google Scholar] [CrossRef]
- Sanin-Villa, D.; Rodriguez-Cabal, M.A.; Grisales-Noreña, L.F.; Ramirez-Neria, M.; Tejada, J.C. A Comparative Analysis of Metaheuristic Algorithms for Enhanced Parameter Estimation on Inverted Pendulum System Dynamics. Mathematics 2024, 12, 1625. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).