Abstract
Reusing cached data is a widely adopted technique for improving network and system performance. Future Internet architectures such as Named Data Networking (NDN) leverage intermediate nodes—such as proxy servers and routers—to cache and deliver data, reducing latency and alleviating load on original data sources. However, a fundamental challenge of this approach is the lack of trust in intermediate nodes, as users cannot reliably identify and verify them. To address this issue, many systems adopt data-oriented verification rather than sender authentication, using Merkle Hash Trees (MHTs) to enable users to verify both the integrity and authenticity of received data. Despite its advantages, MHT-based authentication incurs significant redundancy: identical hash values are often recomputed, and witness data are repeatedly transmitted for each segment. These redundancies lead to increased computational and communication overhead, particularly in large-scale data publishing scenarios. This paper proposes a novel scheme to reduce such inefficiencies by enabling the reuse of previously verified node values, especially transmitted witnesses. The proposed scheme improves both computational and transmission efficiency by eliminating redundant computation arising from repeated calculation of identical node values. To achieve this, it stores and reuses received witness values. As a result, when verifying 2n segments (n > 8), the proposed method achieves more than an 80% reduction in total hash operations compared to the standard MHT. Moreover, our method preserves the security guarantees of the MHT while significantly optimizing its performance in terms of both computation and transmission costs.
1. Introduction
In many data services, users are often required to verify multiple pieces of received data. For instance, future Internet architectures, such as Named Data Networking (NDN), treat each segment of requested content as an individual network packet. NDN assumes that intermediate network devices like routers can temporarily cache content segments and directly provide them to users [1,2,3]. If a router receives a request packet for a segment it has already cached, the router responds with the cached segment instead of forwarding the request to the original data source. While this in-network caching improves efficiency and reduces latency, it also means that users may receive segments from unidentified and potentially untrusted intermediate nodes. Since the authenticity of such network devices cannot be guaranteed, NDN mandates that users verify the integrity and authenticity of every received segment [4,5,6,7,8]. Similarly, in blockchain systems like Bitcoin, a block includes multiple transactions or contracts, and users must verify each individual component upon receiving the block [9,10,11]. In general, when data are composed of multiple subcomponents, users must verify not only the integrity of each subcomponent but also whether it is a valid part of the original dataset.
Traditionally, data verification relies on validating digital signatures or message authentication codes [12,13]. While these mechanisms ensure data integrity and authenticate the origin, they are less effective in determining whether a specific segment is a legitimate part of a larger dataset. Moreover, verifying numerous segments individually can cause significant latency. As the quality of digital content continues to improve, for instance, through high-resolution video, immersive media, and richer interactive applications, the required dataset size necessarily increases. In parallel, global digital data volumes are rapidly expanding. Analysts forecast that the world will enter the so-called “Zettabyte Era”, with up to 175 ZB of data generated annually by 2025 [14]. Similarly, mobile network traffic is projected to rise from approximately 120 EB per month in 2024 to about 280 EB per month by 2030 [15]. These trends clearly indicate that higher content quality directly translates into larger data volumes and, consequently, a greater number of segments that must be transmitted and verified in the network. In the context of NDN, this raises significant challenges for efficient segment verification. If a user must verify the digital signature of each segment of high-quality content, it can cause serious service delays, undermining the practical deployment of NDN for large-scale and latency-sensitive applications. Therefore, there is a strong need for an efficient verification scheme that can preserve security guarantees while minimizing computational and communication overheads.
Merkle Hash Tree (MHT) was proposed to efficiently verify large datasets composed of multiple segments [16,17,18,19]. MHT builds a binary tree consisting of hierarchically computed hash values: the hash value of each segment is sequentially placed at a leaf node, and each parent node’s value is calculated by hashing the concatenation of its two child nodes’ values. This tree structure ensures that any change in a leaf node (i.e., a segment) affects the root node value. Various studies have been conducted to improve the efficiency of MHT implementations: [20] proposed an optimized circuit design for SHA3-256-based MHT verification. By integrating the MHT with the Goldwasser–Kalai–Rothblum (GKR) protocol introduced in [21], the witness processing overhead can be reduced to . In [22], a technique was proposed that enhances witness verification by replacing traditional AND-based proofs with OR aggregation, thereby simplifying logical complexity. The authors in [23] introduced a deterministic authenticated data structure that combines the properties of binary search trees, heaps, and Merkle trees to support efficient and verifiable operations. These studies contribute to improving the performance of MHTs either through efficient hardware implementation or by enabling seamless integration with cryptographic protocols and authenticated data structures to support efficient and verifiable dataset operations.
To verify a segment using MHT, a user must recompute all node values along a path from the corresponding leaf node to the root node. This requires not only recursive hash computation but also access to sibling node values along the path. These sibling node values, provided by the publisher, are referred to as a witness. Thus, for partially overlapping paths across multiple segments, publishers and users perform redundant hash calculations and share redundant witnesses. This redundancy becomes more severe as the dataset grows and the MHT increases in size. With the increasing scale and volume of data, such inefficiencies could become a significant bottleneck. To address this, some studies have proposed using dynamic programming to store and reuse intermediate node values, thereby avoiding recalculation [24].
Contribution. This paper focuses on the fact that the witness generated by the original content publisher consists of a set of valid node values. Once a user verifies a segment, the corresponding witness is also validated. So, the user can obtain valid node values directly from the transmitted witnesses without recomputing them. Building on this observation, we propose an improved MHT-based data verification scheme that enhances computational efficiency by storing and reusing transmitted witnesses from previously verified segments. Since these witnesses have already been validated in earlier verifications, they can be safely reused without additional checks. By reusing valid witnesses, the proposed scheme achieves more than an 80% reduction in total hash operations compared to the standard MHT when verifying segments (). In addition, it significantly reduces witness transmission overhead. Finally, we present the proposed scheme in the context of NDN to demonstrate its practical applicability.
Organization. The remainder of this paper is organized as follows: Section 2 reviews the standard MHT structure and a previously proposed optimization [24], followed by performance analysis. Section 3 presents the proposed method. Section 4 provides evaluation results. Finally, Section 5 concludes this paper.
2. MHT-Based Data Authentication Overview
This section describes an MHT-based data authentication scheme and its computational inefficiency. Also, it introduces the improved scheme reusing the computed node values presented in [24].
2.1. Background: Merkle Hash Tree
Assume a scenario in which a user receives segments of a dataset over a distributed network. The user must validate each received segment based on the following three criteria:
- (1)
- The integrity of the segment is preserved.
- (2)
- The publisher of the segment is authenticated.
- (3)
- The segment is a valid component of the dataset requested by the user.
The first two requirements can be satisfied using traditional authentication mechanisms such as digital signatures and message authentication codes. However, these schemes are insufficient to fulfill the third requirement, verifying that a given segment is genuinely a part of the original dataset.
MHT enables efficient validation of both the integrity of each segment and its rightful inclusion within the original dataset. Furthermore, MHT offers a more efficient alternative for authenticating the data publisher than applying digital signatures to each segment individually [12].
In NDN, when a publisher distributes content, the content is first divided into small segments transmitted independently. Each segment forms the payload of a distinct network packet. One of the key features of NDN is that the user may retrieve these segments not only from the original publisher but also from nearby network nodes (e.g., switches, routers, or base stations) that have temporarily cached them. The caching behavior depends on each node’s cache management policy. When a network node caches a segment, subsequent requests for that segment may be served directly from the cache without forwarding the request to the original publisher. However, this decentralization means that the recipient cannot determine whether the segment originated from a trusted source, as the receiver cannot even identify its sender. Thus, because NDN lacks end-to-end authentication, users must verify the integrity and authenticity of each received segment for themselves.
To facilitate this, NDN leverages MHT-based segment and content verification. Figure 1 illustrates an example where a publisher generates content consisting of segments. A binary hash tree with leaf nodes is constructed, and each segment is assigned to one leaf node in order. Each node has a sequence number , where and a node level . The value of node of the tree is computed as follows:
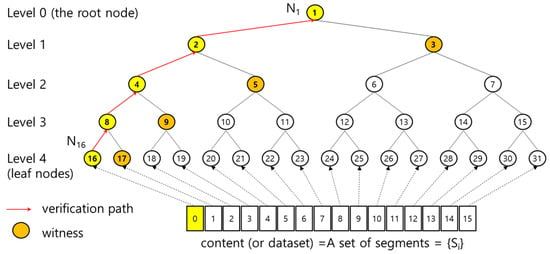
Figure 1.
A segment authentication using MHT.
- (1)
- If is a leaf node, , where is a segment having a sequence number , and .
- (2)
- Otherwise, , where and are the values of left and right child nodes of , respectively.
Once the root node value is calculated, the publisher signs it. Since is derived from all segments using a hash function, it represents the integrity of the entire dataset.
To verify a segment , a user must be able to reconstruct the root node value using along with a set of intermediate node values. For example, suppose the user receives the first segment . The user then computes , , , , and finally sequentially. While can be computed directly, calculating lower-level node values (e.g., ) requires access to sibling node values such as . This continues recursively up to the root node value . The sibling node values, which cannot be computed locally, are collectively referred as the witness of the segment. For MHT with leaf nodes, let denote the witness of a segment, where corresponds to the sibling node value at level along the path from the leaf node to the root. Accordingly, the publisher transmits a packet that includes the following:
- (1)
- A segment .
- (2)
- The witness corresponding to .
- (3)
- The digital signature of the root node value .
When a user receives the segment , the segment verification process is as follows:
- (1)
- Initial segment verification: When the user receives the first packet including , it computes a root node value using and its witness. The digital signature over is then verified using . If valid, the user accepts as a correct segment and stores as the trusted root value.
- (2)
- Subsequent segment verification: For any other segment where , the user computes using and its corresponding witness. The digital signature need not be verified again. Instead, the user simply checks whether , where has been stored during the initial verification process. If the values match, is accepted as valid.
By avoiding repeated signature verifications and limiting computation to hash operations, MHT significantly reduces overhead compared to traditional data authentication schemes. Moreover, MHT not only authenticates each segment of the content but also verifies that each segment is a legitimate part of the content. Therefore, by verifying all received segments, users can authenticate the entire content.
2.2. Reusing Computed Valid Node Values of MHT
As discussed in the previous section, when verifying segments, a content verification scheme that integrates digital signature technology with MHT can be more efficient than conventional schemes that rely solely on digital signature technology. MHT requires a user to compute the root node value every time segment is received. To verify , the user must compute all node values along the path from the corresponding leaf node to the root node . Many node values are computed repeatedly during the validation of all segments. If MHT consists of leaf nodes, the root node value is computed times, and is computed times. In general, each node value is repeatedly computed times. For example, in Figure 1, a user computes two times: one is to verify , and the other is to verify When verifying 16 segments, the user is required to compute four times, eight times, and sixteen times, respectively. Hence, when verifying large-size content consisting of many segments, the MHT-based scheme results in redundant computation due to repeated calculation of identical node values. Such redundant computation can still lead to inefficiencies in the verification process.
To address this problem, ref. [24] proposes a dynamic programming method that stores and reuses node values computed during the verification of earlier segments of content. For that, ref. [24] assumes that segments are received sequentially. If MHT has leaf nodes, the total number of nodes in the tree is . In this case, the total number of hash value computations required for verifying all segments is . This implies that a total of of the hash computations are redundant resulting from recalculations of the same intermediate node values.
If a segment is verified as valid, all computed node values along the node path from the corresponding leaf node to the root node can also be considered valid. For example, as shown in Figure 1, if the first segment is verified, it is also confirmed that the computed node values , , , , and are all valid. In [24], it is proposed that a user stores these valid node values except for the leaf node value. In Figure 1, after the first segment is verified, the user stores the computed , , , and . Hence, a user maintains stored node values when the MHT contains leaf nodes. While the standard MHT [16] requires the user to calculate whenever verifying each segment, ref. [24] proposed that a user use stored valid node values to avoid redundant node value calculations. For instance, in Figure 1, when a user verifies the third segment after the first segment has been verified, it suffices for the user to compute only , , and . If the newly computed matches the previously stored , then the yet-to-be-computed and can be regarded as being identical to the stored and , thus eliminating the need for further computation of and . Hence, if a user can store the valid node values obtained during the verification of each segment, it is not necessary to compute all node values along the full verification path for subsequent segments. Instead, when verifying a segment, the user only needs to identify an intermediate node on the full path corresponding to the segment that matches one of the nodes whose node values have been saved for the previous segment verification process. For example, in Figure 1, when verifying the third segment, the user does not need to consider the full path from to the root node . Instead, the user sufficiently considers a subpath from to because the user has stored the valid node value of . Hence, the user must only need to identify for verifying the third segment. If the computed node value of the matched node equals the corresponding saved node value, the remaining node values along the path—though not explicitly computed—can be considered to match their previously stored counterparts, thereby reducing redundant computations. Hence, the user can utilize a short subpath—from a leaf node corresponding to the segment to the matched node—to improve performance efficiency.
When utilizing the scheme proposed in [24], each internal node’s value is computed twice. Hence, if the MHT contains leaf nodes, the total number of internal node value computations is .
3. Minimizing Redundant Hash and Witness Operations
The scheme in [24] reuses valid node values computed locally by the user. However, it discards the received witness after segment verification even though the witness itself consists of valid node values. Considering all segments, the entries of witnesses are also significantly redundant. Practically, this repeated redundant witness transmission results in significant inefficiency. This paper focuses on the observation that a witness essentially consists of valid node values and that the same witness element values are often transmitted repeatedly. Based on this insight, this paper proposes a scheme that stores and reuses witnesses to additionally improve MHT: by selecting a shorter subpath than those employed in [24] and by reducing witness transmission, thereby enhancing overall efficiency. As in [24], this paper assumes that segments are received sequentially.
3.1. Analysis of Redundant Witness Transmission
When verifying segments, some transmitted witnesses contain overlapping node values. For instance, in Figure 1, is redundantly transmitted two times, as it is included in the witnesses for verifying two segments corresponding to and , respectively. Similarly, is transmitted four times when verifying four segments corresponding to , , , and . is transmitted eight times. As illustrated in Figure 1, the number of times a node value is transmitted as part of a witness varies depending on the location (i.e., depth) of the corresponding node in the MHT. This concept of a node’s depth is formally defined as follows:
Definition 1.
Node Level: Each node of MHT is assigned a unique sequence number in a top-down, left-to-right manner—from the root node to the leaf nodes. Suppose the MHT has leaf nodes. The root node is assigned sequence number , and the last leaf node is assigned sequence number . Let denote the node with sequence number . The node level of , denoted by , is defined as , indicating the depth of the within the binary tree. Let denote the node level .
The number of times a node value is repeatedly transmitted as a witness depends on the node level and the size of MHT. For example, the node has level . If the MHT contains leaf nodes, the value is transmitted eight times during all segment verifications. However, if the MHT has leaf nodes, is transmitted times. The repeated transmission count of a node value is defined as follows:
Property 1.
Repeated Transmission Count of a Witness Node Value: Assume the MHT has leaf nodes and let . The number of times that the node value is transmitted as a witness during the verification of all segments is given by the following:
where is the level of .
Property 2.
Total Transmission Count of Witness Values at Level : Assume the MHT has leaf nodes. Let denote a level in the MHT. There are nodes at level , and each node at this level is included as a witness in packet transmissions. Hence, the total number of node value transmissions for all witness values at level is the following:
Property 3.
Total Transmission Count of All Witness Values: Assume MHT has leaf nodes. The tree consists of -1 nodes. The total number of node value transmissions required as witnesses for verifying all segments is the following:
Figure 2 illustrates the number of packets that include a witness value at level . For example, the curve labeled represents the number of packets that contain for MHT with leaf nodes. As shown in Figure 2, if , and are transmitted more than 5000 times, respectively.
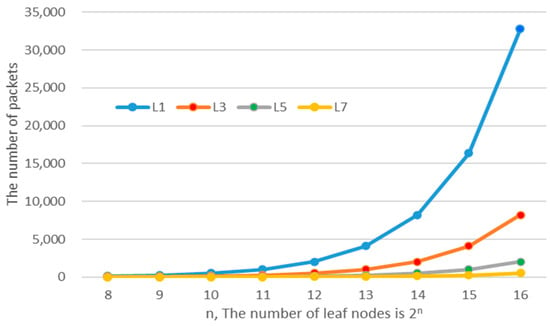
Figure 2.
Repeated transmission count of a witness value at level Lk.
3.2. Witness Reuse in MHT
A witness used to verify a segment consists of certain valid node values. Hence, when a user verifies a segment, the user effectively receives certain valid node values as part of the witness. Based on this observation, this paper proposes to reuse the transmitted, not computed by a user, valid node values. This section introduces a scheme that selectively stores valid node values contained in the received witness and then reuses them when verifying subsequent segments. As a result, the proposed scheme reduces the computation and transmission overheads associated with the MHT.
Definition 2.
The Verification Path of a Leaf Node: Let denote a path from a leaf node to an ancestor node . The verification path of the leaf node is defined as the shortest such subpath where has been verified as valid.
In Figure 1, suppose a user receives the first segment assigned to . At this point, the user has not yet verified any node values and therefore does not store any valid node values. As a result, the user must compute all node values along the full path, from to . In this case, the verification path of is . According to the scheme presented in [24], if the user stores the computed node values, , , , and after verifying the first segment, the verification path of a leaf node becomes , rather than .
Definition 3.
Level of the Verification Path of a Leaf Node: Assume MHT has leaf nodes. Let the given segment be assigned to a leaf node . If the verification path of the is , the level of verification path
is defined as the node level of the , that is, .
For example, the level of verification path of the leaf node assigned to the first segment is always . In Figure 1, if the user adopts the scheme in [24], the level of the verification path is .
Assume that a user receiving and verifying segments maintains a cache for transmitted witnesses. If segments are transmitted sequentially, the user can determine the verification path for each segment according to the following procedure: Let the size of MHT be 2n. The user maintains a set of internal caches , for storing the verified root node value and the received witness. Specifically, stores the verified root node value, while (for ) stores a witness entry corresponding to an internal node at level . Each cache entry is initialized to NULL.
- (1)
- Packet Reception: The user receives a packet containing a segment, its corresponding witness, and the digital signature. The segment has a sequence number , where .
- (2)
- Determining the Verification Path Level: The user computes the level of verification path of the leaf node corresponding to the received segment. If the packet contains the first segment, is . Otherwise, the user searches for the deepest-level node on the verification path that matches the node corresponding to one of the stored values in . The level is set to the level of this matched node. The user can predict the level prior to computing node values of the full verification path. To achieve this, the user refers to Algorithm 1, which defines how to determine based on the sequence number of the segment.
- (3)
- If , the user computes to verify the digital signature. If the signature is valid, the segment is considered valid. The user then stores the in the cache and the transmitted witness values into the cache , placing each value in the entry corresponding to its node level.
- (4)
- If , the user selects a verification path whose level is . The user then computes the value . If the computed value matches the one stored in , the segment is considered valid. The user then stores the witness values , which were used in the computation of , into the cache , indexed according to their corresponding levels.
| Algorithm 1 ComputeLevel(n, sn): Pseudo-Code for Calculating the level of verification path for a given segment | |
| Input | : The height of MHT, where the MHT has leaf nodes : The sequence number of a segment ) |
| Output | : The level of a verification path ) |
| 01: if sn is 0 then //the first segment 02: set 0 03: else if sn mod 2 is 1 then //odd-numbered segments 04: set n 05: else //even-numbered segments 06: set bit_mask 2 07: for Level, from n-1 down to 1 do 08: if (sn bit-AND-operation bit_mask) is not 0 then 09: break 10: else 11: set bit_mask bit_mask << 1 //<< operation: a left bit shift 12: end if 13: end for 14: end if 15: return | |
Algorithm 2 presents the pseudo-code of the above verification procedure for MHT with leaf nodes. For example, if and , the user has cached in after verifying . returns as the level of the verification path for . Then, the shortest verification path is , as shown in line 13 of Algorithm 2. Then, the user computes using both and witness , corresponding to line 15 in Algorithm 2. If the computed equals the cached value in , is verified as valid. Finally, the user caches according to their level, as described in line 18 of Algorithm 2.
3.3. Witness Generation for Reusing Witness
If a user stores and reuses transmitted witnesses, the publisher of segments may no longer need to repeatedly transmit the same witness values. To apply this idea in practical scenarios, assume that network and device conditions are stable enough for the user to successfully receive all segments sequentially. Under this assumption, the publisher can generate witnesses as follows: Assume that MHT has leaf nodes and the published content is fragmented into segments. The segment has a sequence number , where . Let denote the original witness of a segment.
- (1)
- For the First Segment: If , the publisher transmits the full original witness as is.
- (2)
- For Even-Numbered Segments: If is even, the witness for the segment is empty, that is, the publisher does not transmit the witness for it.
- (3)
- For Odd-Numbered Segments (After the First): If is odd, using Algorithm 1, the publisher computes the level of the verification path for the segment. Then, the publisher constructs a partial witness .
| Algorithm 2 VerifySeg(n,sn,Ssn,ω,σ,Ω): Pseudo-Code for Verifying a Segment using ComputeLevel(n, sn) | |
| Input | : The height of MHT, where the MHT has leaf nodes ) }: A transmitted packet : Caches for the root node value and witness |
| Output | : Segment Verification Result |
| 01: if is 0 then //the first segment verification 02: compute 03: verify 04: if is valid then 05: set //caching the valid root node value 06: store in order //caching valid witness 07: set 08: else 09: set 10: end if 11: else //the other segments verification 12: set //finding the shortest path 13: select 14: set //finding witness level 15: compute 16: compare //the node value verification 17: if then 18: store in order //caching witness 19: set 20: else 21: set 22: end if 23: end if 24: return vResult | |
4. Evaluation
4.1. Security Evaluation
When verifying segments, a user must check two properties:
- (1)
- The integrity of each segment: The verifier ensures that the segment has not been tampered with during transmission. In MHT, this is achieved by verifying the hash value of the segment using the full verification path associated with the segment.
- (2)
- The correctness of each segment: This ensures that the segment is an authentic part of the original content requested by the user. In MHT, the original content is represented by the root node value. If the user correctly recomputes the root node value using the segment, the segment is considered an authentic part of the content.
This paper considers a potential attack scenario to forge a segment. Let the number of leaf nodes of the MHT be , a dataset be , and a local cache be . We assume that a secure hash function is a collision-resistant (CRHF) and the second preimage-resistant, and it is optionally modeled as a random oracle (RO) for simpler proofs. The digital signature scheme is secure in the sense of existential unforgeability under chosen-message attacks (EUF-CMA). For segment (), assume that the user has already received and verified every segment , where . Security goals are as follows:
- (1)
- G1 (Cache-safety): It does not open new forgery avenues to reuse cached (previously verified) witness nodes.
- (2)
- G2 (Integrity): A probabilistic polynomial-time adversary () cannot cause node values to accept a modified segment as valid.
- (3)
- G3 (Correctness): The cannot cause acceptance of a segment not in the dataset.
Property 4.
Subtree commitment and valid verification path. Let be a node of the MHT over with node value . Under CRHF, the value uniquely commits to all node values in the subtree rooted at ; i.e., for fixed , there is a unique assignment of descendant values consistent with . Moreover, for any leaf node that lies in the subtree of (equivalently, whose index satisfies , where ), the path (, ) is a valid verification path: if the sibling values along this path are provided, one can recompute from .
Property 5.
Caching rule and stability of cached node values. Let be transmitted as a witness and be the node level of . Then, is the parent node of . The leftmost leaf node in the subtree rooted at is the node , where . When the segment (assigned to ) is verified, the verifier stores in the cache entry . Also, for the fixed dataset and under CRHF, the stored remains unchanged while verifying any other segment whose leaf node lies in the subtree of .
Theorem 1.
Cache safety (for G1): Let be a cached node value validated in previous verifications. If VerifySeg(,,,,,) selects the shortest verification path (, ), computes , and finally returns Success, accepting is as secure as a full path verification to the root node .
Proof.
We prove the theorem by induction on the segment index .
Base case (): When , VerifySeg verifies using the full path (,). Thus, acceptance of is identical to full-path verification, and the claim holds trivially.
Induction hypothesis: Assume that for all , if VerifySeg accepts , this acceptance is equivalent to full-path verification to . Consequently, the caches contain only valid node values that were previously received as witnesses.
Induction step (): Suppose, for contradiction, that VerifySeg returns Success for segment , yet this acceptance is not as secure as full-path verification to . This implies that the computed root node value differs from the valid stored root node value . Under CRHF, the root node value uniquely commits to all descendant node values along the path (,). Thus, if is computed, there must exist at least one mismatched intermediate value on the path. Let the shortest verification path chosen by VerifySeg be (,). One of the mismatched nodes must then occur at the computed value , i.e., , where is a valid node value. Since VerifySeg returns Success, it must have confirmed that . Since is a leaf node of subtree rooted at , it is a leaf node of subtree rooted at . By property 5, the cache entry was set to when the leftmost leaf node value of the subtree rooted at was first verified, and this cached value remains unchanged during the verification of all leaf nodes in that subtree. Hence, when is verified. Therefore, the condition cannot hold, leading to contradiction.
Conclusion: Thus, for segment , acceptance by VerifySeg is equivalent in security to full-path verification. By induction, the claim holds for all . □
Theorem 2.
Soundness Verification (for G2 and G3): An adversary has only negligible advantages in violating goals, G2 and G3, under CRHF and EUF-CMA.
Proof.
We consider two cases depending on the segment index . The first case is . For the first segment , the adversary must either forge corresponding signature or produce a different verification path leading to a forged root that still verifies under . Forging would directly break EUF-CMA security of the signature scheme, which is assumed to be infeasible. Producing the other path requires constructing a collision in the hash function along the path from the leaf node to the root node, contradicting the CRHF assumption. Thus, cannot forge with non-negligible advantage.
The second case is for subsequent segments , . The acceptance requires the recomputed intermediate node value to match the cached valid node value . The cache entries are witnesses that were previously verified against valid segments. To successfully forge a segment , the adversary must construct a fake witness corresponding to the such that the recomputed without using the legitimate . This reduces finding a second preimage under the hash function when computing . Such a second preimage attack contradicts the secure hash function assumption.
In both cases, forging an acceptable segment would either break EUF-CMA (by forging ) or break CRHF (by creating a collision or second preimage). Since both are assumed to be secure, the adversary has only a negligible advantage in violating G2–G3. □
4.2. Performance Evaluation
To implement the proposed scheme, if MHT has leaf nodes, a user needs to store at most witness values, one per tree level. This results in a storage overhead of , which is negligible compared to the dataset size . Therefore, the storage requirement grows only logarithmically with the number of segments. In the following subsection, we theoretically analyze the computation and transmission overheads.
4.2.1. Hash Computation Overhead
To evaluate the computation overhead of the proposed scheme, we analyzed the total number of hash computations required during segment verification process for segments of the content. In the standard MHT approach [16], each segment verification requires computing all hash values along the full path from the corresponding leaf node to the root node. Therefore, the total computation overhead is the following:
In the case of [24], only the hash values along a partial path—from the leaf node to the internal node having the highest node level whose node value has been computed, verified, and stored previously—must be calculated. Hence, ref. [24] reduces the number of hash computations needed for verifying all segments except the first one. Therefore, the total computation overhead is the following:
Similarly, our proposed scheme also computes hash values along a partial path. However, this path terminates at the internal node whose node value was previously received as a witness. In terms of path length, the partial path in our proposed scheme is typically 1 shorter than that in [24], except for the first segment. Therefore, the total computation overhead is as follows:
Figure 3 shows the total number of hash computations for various values of , where the number of segments is . As increases, the difference in computation overhead between the standard and the proposed methods becomes more pronounced. When , the proposed method achieves a reduction of more than 80% in total hash operations compared to the standard MHT. In comparison with [24], the proposed method yields an average reduction of approximately 33%. This reduction in computational cost is particularly advantageous for resource-constrained environments, such as IoT networks or edge devices, where minimizing CPU workload is essential.
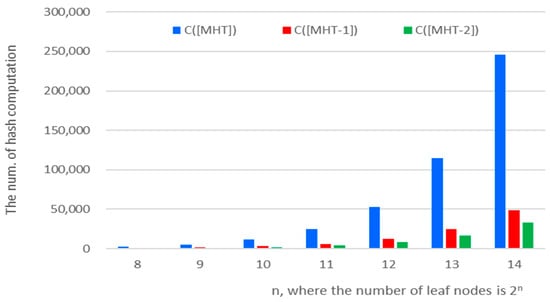
Figure 3.
Comparison of computation overheads for MHT-based verifications.
4.2.2. Witness Transmission Overhead
In the standard MHT, each segment requires a set of node values, referred to as a witness, to reconstruct the root node value. For a dataset consisting of segments, each witness contains node values. Therefore, the total witness transmission overhead is the following:
This means that many witness values are transmitted redundantly, resulting in significant communication overhead.
In the case of [24], a subtree of the full MHT is used to verify each segment. Although verification requires only the path within the subtree, the scheme still transmits the entire witness of the standard MHT for each segment. If [24] was modified to transmit only the partial witness corresponding to the subtree path, the transmission overhead could be reduced. Under this assumption, the total witness transmission overhead of [24] is given by the following:
In contrast, the proposed scheme enables users to store and reuse previously received witness values when verifying subsequent segments. As a result, redundant witness transmissions are eliminated: Each node value except for the root node value in the MHT is transmitted only once throughout the entire segment verification process. Therefore, the total witness transmission overhead of [24] is given by the following:
Figure 4 illustrates the total number of transmitted witness values for various values of , where the number of segments is . Here, T [16] represents the standard MHT, T [24] shows the result when [24] is improved as proposed in this paper, and T denotes the proposed scheme. As shown in Figure 4, when , the proposed method achieves a reduction of more than 90% in transmission overhead compared to the standard MHT. If [24] adopts a similar partial witness approach presented in this paper, the proposed method still yields a 50% reduction in transmission overhead. These results demonstrate that the proposed scheme significantly reduces transmission overhead compared to both the standard MHT and [24], particularly as the number of segments increases.
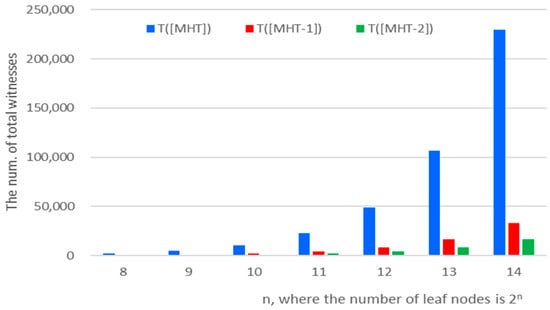
Figure 4.
Comparison of transmission overheads for MHT-based verifications.
5. Conclusions
MHT is widely used for efficiently verifying both individual segments of a dataset and the dataset as a whole. However, when applied to large-scale datasets, MHT-based verification still suffers from redundant hash computations and excessive witness transmissions, leading to performance inefficiencies. Previous studies have addressed the computation inefficiency for computing hash values by storing and reusing previously computed node values.
This paper proposed a method to improve both computational and transmission efficiency by storing and reusing received witness values. Since witnesses consist of valid node values, if a user caches them after verifying a segment and later reuses them to verify subsequent segments, the user can verify the subsequent segment via a subtree of the original MHT. In this case, the user only needs to compute the root node value of the subtree, thereby reducing the number of hash operations. Furthermore, since only a subset of the full witness is required for subtree verification, transmission overhead is also significantly reduced.
The proposed scheme enhances the practicality of MHT-based verification, especially in large-scale or latency-sensitive environments such as IoT and edge networks.
However, the proposed scheme and [24] assume that users receive every segment sequentially, without considering packet loss or network status. If a user receives the segment before receving the segment, the verification of the received segment must be delayed until the segment is obtained. Furthermore, neither scheme addresses the integrity of the local cache. For example, if the local cache is corrupted, segment verification will always fail regardless of the actual validity of the segment. Future work will focus on the scheme to enable verification of each segment independently of its sequence, as well as addressing local cache integrity issues. In addition, we plan to explore further optimizations using lightweight cryptographic techniques tailored for resource-constrained devices.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in this article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MHT | Merkle Hash Tree |
| NDN | Named Data Networking Architecture |
References
- Jacobson, V.; Smetters, D.; Thornton, J.; Plass, M.; Briggs, N.; Braynard, R. Networking Named Content. In Proceedings of the 5th International Conference on Emerging Networking Experiments and Technologies, Rome, Italy, 1–4 December 2009; pp. 1–12. [Google Scholar]
- Suwannasa, A.; Broadbent, M.; Mauthe, A. Impact of Content Popularity on Content Finding in NDN: Default NDN vs. Vicinity-based Enhanced NDN. In Proceedings of the 10th International Conference on Information Science and Technology (ICIST), Bath, London, Plymouth, UK, 9–15 September 2020. [Google Scholar]
- Mehrabi, M.; You, D.; Latzko, V.; Salah, H.; Reisslein, M.; Fitzek, F. Device-Enhanced MEC: Multi-Access Edge Computing (MEC) Aided by End Device Computation and Caching: A Survey. IEEE Access 2019, 7, 166079–166108. [Google Scholar] [CrossRef]
- Fei, Y.; Zhu, H. Modeling and verifying NDN access control using CSP. In Proceedings of the Formal Method and Software Engineering—20th International Conference on Formal Engineering Methods, Gold Coast, QLD, Australia, 12–16 November 2018; pp. 143–159. [Google Scholar]
- Fei, Y.; Yin, J.; Yan, L. Security verification framework for NDN access control. Nat. Sci. Rep. 2025, 15, 5479. [Google Scholar] [CrossRef] [PubMed]
- Anjum, A.; Agbaje, P.; Mitra, A.; Oseghale, E.; Nwafor, E.; Olufowobi, H. Towards named data networking technology: Emerging applications, use cases, and challenges for secure data communication. Future Gener. Comput. Syst. 2024, 151, 12–31. [Google Scholar] [CrossRef]
- Li, B.; Zheng, M.; Ma, M. A Novel Security Scheme Supported by Certificateless Digital Signature and Blockchain in Named Data Networking. IET Inf. Secur. 2024, 2024, 6616095. [Google Scholar] [CrossRef]
- Benmoussa, A.; Kerrache, C.; Calafate, C.; Lagraa, N. NDN-BDA: A Blockchain-Based Decentralized Data Authentication Mechanism for Vehicular Named Data Networking. Future Internet 2023, 15, 167. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 1 July 2025).
- Wood, G. Ethereum: A Secure Decentralized Generalized Transaction Ledger. Ethereum Yellow Pap. 2014, 151, 1–32. Available online: https://ethereum.github.io/yellowpaper/paper.pdf (accessed on 1 July 2025).
- Dahlberg, E.; Pulls, T.; Peeters, R. Efficient sparse Merkle trees: Caching strategies and secure updates. NordSec 2016, 199–215. Available online: https://www.bibsonomy.org/bibtex/2ad092077f775ca9122841b1a40cde2d1/dblp (accessed on 1 July 2025).
- Rivest, R.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Bellare, M.; Kilian, J.; Rogaway, P. The security of the cipher block chaining message authentication code. J. Comput. Syst. Sci. 1994, 61, 362–399. [Google Scholar] [CrossRef]
- Veronika, S. Scaling Up: How Increasing Inputs Has Made Artificial Intelligence More Capable. Our World in Data 2025. Available online: https://ourworldindata.org/scaling-up-ai (accessed on 1 July 2025).
- Mobile Data Usage: How Much Internet Do We Use Monthly? 2025. Available online: https://www.economyinsights.com/p/mobile-data-usage?utm_source=chatgpt.com (accessed on 1 July 2025).
- Merkle, R. Protocols for Public Key Cryptosystems. IEEE Symp. Secur. Priv. 1980, 73–104. [Google Scholar] [CrossRef]
- Merkle, R. A Digital Signature Based on a Conventional Encryption Function. In Proceedings of the Advances in Cryptology—CRYPTO ’87, Santa Barbara, CA, USA, 16–20 August 1987; pp. 369–378. [Google Scholar]
- Martel, C.; Nuckolls, G. An Efficient, Provably Secure Merkle Tree Commitment Scheme. In Proceedings of the ASIACRYPT, Jeju Island, Republic of Korea, 5–9 December 2004. [Google Scholar]
- Fan, L.; Cao, P.; Almeida, J.; Broder, A. Summary cache: A scalable wide-area web cache sharing protocol. IEEE/ACM Trans. Netw. 2000, 8, 281–293. [Google Scholar] [CrossRef]
- Ding, C.; Fu, Z. Efficient Layered Circuit for Verification of SHA3 Merkle Tree. IACR Cryptol. Eprint Arch. Rep. 2024. Available online: https://eprint.iacr.org/2024/1212 (accessed on 1 July 2025).
- Goldwasser, S.; Kalai, Y.; Rothblum, G. Delegating Computation: Interactive Proofs for Muggles. J. ACM (JACM) 2015, 62, 1–64. [Google Scholar] [CrossRef]
- Kuznetsov, O.; Rusnak, A.; Yezhov, A.; Kanonik, D.; Kuznetsova, K.; Domin, O. Efficient and Universal Merkle Tree Inclusion Proofs via OR Aggregation. Cryptography 2024, 8, 28. [Google Scholar] [CrossRef]
- Chystiakov, A.; Komendant, O.; Riabov, K. Cartesian Merkle Tree, Cryptography and Security. arXiv 2025, arXiv:2504.10944. Available online: https://arxiv.org/abs/2504.10944?utm_source=chatgpt.com (accessed on 1 July 2025).
- Lee, J.; Kim, D. The Shortest Verification Path of the MHT Scheme for Verifying Distributed Data. Appl. Sci. 2022, 12, 11194. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).