An Ease-Off Based Tooth Contact Analysis Method for Measured Face Gear Flanks

Abstract

To rapidly evaluate the meshing performance of manufactured face-gear drives, this study proposes an efficiency-optimized tooth contact analysis (TCA) method for measured gear flanks based on Ease-off surface. Initially, mathematical models of the pinion and face-gear tooth flanks are established. A TCA framework leveraging conjugate relationships and Ease-off surfaces is then developed. Subsequently, measured flank data are fitted into continuous error surfaces through Bicubic spline fitting, enabling full-tooth flank error mapping. These error distributions are integrated into the Ease-off surface model to simulate realistic meshing behavior, extracting critical performance metrics including contact paths and transmission errors. Validation through computational TCA, finite element analysis (FEA), and rolling tests confirm the method’s accuracy and computational efficiency.

1. Introduction

Face gear transmission generally consists of a face gear and a mating cylindrical gear (also called a pinion). When the pinion is a spur cylindrical gear, there is no axial force in the direction of the pinion’s rotation axis, and it is insensitive to axial installation errors of the pinion [1]. This can greatly reduce the weight of the support structure in the transmission system and the difficulty of assembly, thus being widely used in fields such as aerospace, automotive, and robotic joint transmission systems [2].

The tooth surface of a face gear is generated by the envelope of a shaper cutter with the same design parameter to its mating pinion, resulting in an extremely complex geometry, typically a hyperbolic envelope surface [3]. Therefore, the precision manufacturing of face gears, especially those with hardened tooth surfaces, has long been a major challenge in the industry. Claudio and José took the lead in proposing the use of a dish-shaped grinding wheel for face gear grinding [4]. This method offers advantages such as a simple tool structure and high precision but requires machining each tooth surface one by one, leading to low efficiency when the face gear has a large number of teeth. Based on the tooth surface generation process of face gears, Litvin et al. proposed using a worm that engages internally with the mating pinion and externally with the face gear’s tooth surface for continuous generating grinding of the face gear tooth surface [5]. This method significantly improves the machining efficiency of face gears; however, the worm, acting as a tool, requires complex dressing movements.

Despite the existence of numerous methods to improve the machining accuracy of face gears, such as milling [6], grinding [7,8], hobbing [9,10] and skiving [11,12], these approaches that pursue higher precision are accompanied by higher costs. However, in many application scenarios, such high machining precision is not required to meet the designed meshing performance indicators. Therefore, conducting TCA on the machined tooth surface is an effective method to evaluate whether the machining accuracy meets the meshing performance requirements and then reduce the production costs.

TCA technology aims to simulate the meshing process of two engaging gear pairs, thereby obtaining meshing performance indicators such as the contact path of contact points and transmission error during the meshing process. Litvin and Fuentes systematically outlined the mathematical method for contact analysis of two curved surfaces in space, which consists of five nonlinear equations with five unknowns [13,14]. The accuracy and stability of numerically solving these equations strongly depend on the selected algorithm and initial values. Mo et al. simplified these equations and reduced the variables to four [15]. Based on the meshing motion relationship of spatial gear pairs, Wang et al. reduced the number of nonlinear equations from five to three [16], and subsequently, Lu et al. further simplified them to two [17]. This method significantly improved the efficiency and stability of TCA technology; however, it still struggles to maintain computational stability when faced with tooth surface errors or assembly errors. Mu et al. introduced high-dimensional nonlinear equation systems in TCA using physics-informed neural network (PINN) technology, converting initial value problems in traditional iterative methods into physical boundary problems [18]. These systems were then applied to the TCA of point-contact conical envelope cylindrical worm-face worm gear drives. Wang et al. proposes a TCA model for gear tooth surfaces with waviness error by solving an innovative multiscale grid and a local iterative numerical algorithm, verifying its validity and discussing waviness parameters to reveal their meshing performance mechanism [19]. Ye et al. put forward a computer-based approach for loaded tooth contact analysis of high-contact-ratio spur gears—whether with or without flank modifications—taking into account tip corner contact and shaft misalignment [20]. This tradition method is applicable to the TCA of all point-contact gears, including the sphere-face gear pair [21] and the non-circular gears [22].

Different from the above methods, Sheveleva et al. proposed an Ease-off-based tooth contact analysis method in 2007 [23], which determines the contact situation by evaluating the distance between the tooth surface of gear and the conjugate surface of the pinion. This method only requires a one-dimensional search for the normal distance between each contact line on the conjugate surface and the gear’s tooth surface to calculate the contact points and contact path, enabling it to maintain good stability even in the presence of installation and manufacturing errors. Nevertheless, the solution accuracy depends on the step size of the one-dimensional search. Rong et al. improved this method by modifying the normal distance to the tangential direction where the two tooth surfaces approach each other and adopting a conforming discretization method to search for the distance of points on the contact line [24]. This improvement enhanced the accuracy of the method. However, when directly applying the Ease-off-based TCA method to measured face gear tooth surfaces (typically discrete point cloud data), significant challenges arise: it is difficult to efficiently obtain a high-precision continuous tooth surface model for contact analysis. Traditional methods rely on ideal tooth surfaces or small perturbation models, struggling to effectively handle complex spatial error distributions introduced by real manufacturing processes. Directly discretizing high-resolution measured point clouds for full tooth surface contact simulation incurs enormous computational load and low efficiency, severely limiting the application potential of this technology in actual manufacturing inspection. Therefore, there is an urgent need for an Ease-off based TCA method capable of efficiently processing measured tooth surface data and accurately integrating manufacturing errors.

To address this bottleneck, this study proposes an efficient Ease-off based TCA method for measured tooth surfaces. The core lies in: using bicubic spline surfaces to accurately fit discrete measured point clouds into continuous tooth surface error distribution maps, and seamlessly integrating them into the Ease-off model. This method significantly reduces the computational resources required to process measured data, and while maintaining the stability of the Ease-off method, enables efficient and accurate simulation of meshing behaviors (such as contact paths and transmission errors) of tooth surfaces with manufacturing errors.

The paper is structured as follows: Section 2 establishes the mathematical models of the theoretical tooth flanks for both cylindrical and face gears. Section 3 details the general Ease-off based TCA framework. Section 4 introduces the method of the measured tooth flanks processing and the error integration to the Ease-off surface. Finally, Section 5 gives the validation and discusses the proposed method.

2. Theoretical Tooth Flanks Models of Face Gear Drives

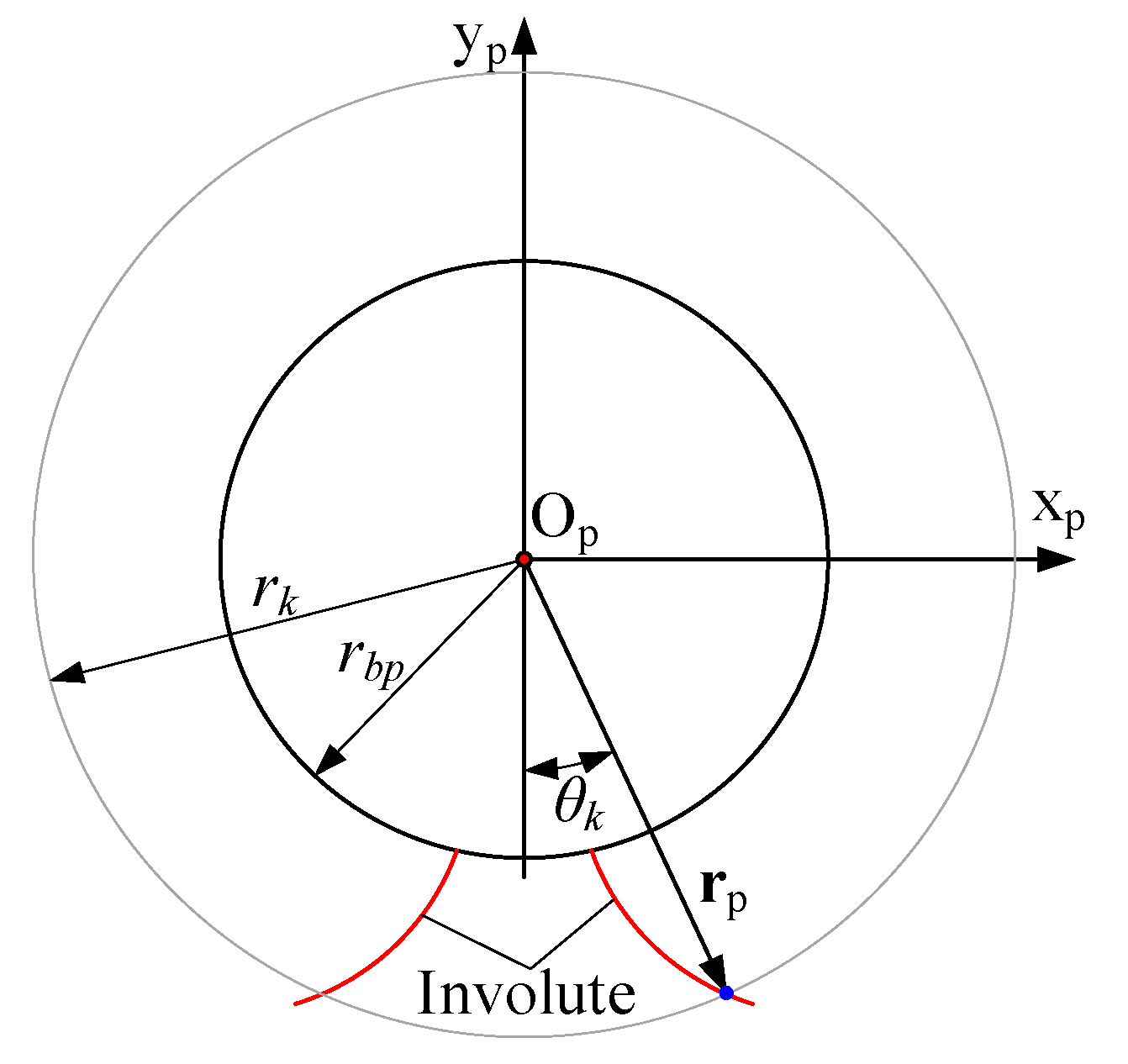
2.1. Tooth Flank of the Pinion

The pinion is an involute cylindrical gear, as shown in Figure 1, whose tooth flank vector can be defined as

$$\begin{array}{cc}\hfill r_p\left({\alpha }_k,u_k\right)& ={\left[\begin{array}{cccc}{r}_{px}\left({\alpha }_k,u_k\right)& r_{py}\left({\alpha }_k,u_k\right)& r_{pz}\left({\alpha }_k,u_k\right)& 1\end{array}\right]}^T\hfill \\ & ={\left[\begin{array}{cccc}\pm r_k\sin {\theta }_k& -r_k\cos {\theta }_k& u_k& 1\end{array}\right]}^T\hfill \end{array}$$

(1)

where “±” represents right and left tooth flanks of the pinion, and subscript “p” represent the element of the pinion. u_k is the parameter of the pinion in the direction of tooth width. r_k and θ_k are the radius and rolling angle of the involute, respectively, and they can be calculated by

$$r_k=r_{bp}/\cos {\alpha }_k$$

(2)

$${\theta }_k=\pi /2/N_p-inv{\alpha }_p+inv{\alpha }_k$$

(3)

where α_k is the pressure angle of the involute at the circle with radius r_k. N_p is the teeth number of the pinion. inv(x) is the involute function, and it can be expressed as

$$inv\left(x\right)=\tan \left(x\right)-x$$

(4)

2.2. Tooth Flank of the Face Gear

The tooth flank of the face gear is the envelope surface of the shaper cutter, as shown in Figure 2, which has same design parameters as the pinion [13]. Modifying “p” in Equation (1) to “s” can obtain the tooth flank equation of the shaper cutter, that is

$$r_s\left({\alpha }_s,u_s\right)={\left[\begin{array}{cccc}{r}_{sx}\left({\alpha }_s,u_s\right)& r_{sy}\left({\alpha }_s,u_s\right)& r_{sz}\left({\alpha }_s,u_s\right)& 1\end{array}\right]}^T$$

(5)

According to the envelope theory [13], the tooth flank of the face gear can be obtained as follows

$$\left\{\begin{array}{l}{r}_f\left({\alpha }_s,u_s,{\phi }_s\right)=M_{fs}\left({\phi }_s\right)r_s\left({\alpha }_s,u_s\right)\\ f\left({\alpha }_s,u_s,{\phi }_s\right)=n\cdot v=0\end{array}\right.$$

(6)

where M_fs(φ_s) is the homogeneous coordinate transform matrix (HCTM) from the coordinate system of the shaper cutter (S_r) to the face gear (S_f). According to the kinematics of the face gear generation, it can be written as

$$M_{fs}\left({\phi }_s\right)=\left[\begin{array}{cccc}\cos {\phi }_s\cos {\phi }_f& -\sin {\phi }_s& \cos {\phi }_s\sin {\phi }_f& 0\\ \cos {\phi }_f\sin {\phi }_s& \cos {\phi }_s& \sin {\phi }_f\sin {\phi }_s& 0\\ \sin {\phi }_f& 0& \cos {\phi }_f& -r_f\\ 0& 0& 0& 1\end{array}\right]$$

(7)

where r_f is the reference circle of the face gear, and it can be calculated by r_f = m*N_f/2. φ_s and φ_f are the rotation angle of the shaper cutter and face gear, respectively. They satisfy the following transition ratio

$${\phi }_s/{\phi }_f=N_f/N_s$$

(8)

N_f and N_s are the teeth number of the face gear and shaper cutter, respectively. The second formula of Equation (6) is the meshing equation [25], which is the dot product of the normal vector n of the contact point and the relative velocity v. Accordingly, one of the three parameters in Equation (6) can be expressed by other two, and then, the tooth flank equation of the face gear can be obtained

$$r_f\left({\alpha }_s,{\phi }_s\right)={\left[\begin{array}{cccc}{r}_{fx}\left({\alpha }_s,{\phi }_s\right)& r_{fy}\left({\alpha }_s,{\phi }_s\right)& r_{fz}\left({\alpha }_s,{\phi }_s\right)& 1\end{array}\right]}^T$$

(9)

The unit normal vector can be calculated as

$$n_f\left({\alpha }_s,{\phi }_s\right)={\displaystyle \frac{\partial r_f\left({\alpha }_s,{\phi }_s\right)}{\partial {\alpha }_s}}\times {\displaystyle \frac{\partial r_f\left({\alpha }_s,{\phi }_s\right)}{\partial {\phi }_s}}/\left|{\displaystyle \frac{\partial r_f\left({\alpha }_s,{\phi }_s\right)}{\partial {\alpha }_s}}\times {\displaystyle \frac{\partial r_f\left({\alpha }_s,{\phi }_s\right)}{\partial {\phi }_s}}\right|$$

(10)

3. Ease-Off Surface-Based TCA Framework

3.1. Conjugate Surface of the Pinion

The mating pinion of a face gear typically shares the same design parameters as its shaper gear to ensure continuous meshing with the face gear. Therefore, substituting r_s(α_s,u_s) in Equation (6) with Equation (1) allows the conjugate surface of the pinion to be calculated, whose equation is denoted as

$$\left\{\begin{array}{l}{r_f}^c\left({\alpha }_k,u_k,{\phi }_p\right)=M_{fs}\left({\phi }_p\right)r_p\left({\alpha }_k,u_k\right)\\ f\left({\alpha }_k,u_k,{\phi }_p\right)=n\cdot v=0\end{array}\right.$$

(11)

By solving the second equation in the above formula and eliminating the parameter u_k, the explicit equation of the conjugate surface can be obtained as follows:

$${r_f}^c\left({\alpha }_k,{\phi }_p\right)={\left[\begin{array}{cccc}{r_{fx}}^c\left({\alpha }_k,{\phi }_p\right)& {r_{fy}}^c\left({\alpha }_k,{\phi }_p\right)& {r_{fz}}^c\left({\alpha }_k,{\phi }_p\right)& 1\end{array}\right]}^T$$

(12)

3.2. Ease-Off Surface Construction

The generation process of the tooth flank of the conjugate face gear with the pinion is a single-parameter envelope of the pinion’s tooth flank under the action of the rotation angle φ_p. During the enveloping process, the two maintain a line contact, as shown in Figure 3. The unit normal vector at a point P on the contact line can be calculated as

$${n_f}^c\left({\alpha }_k,{\phi }_p\right)={\displaystyle \frac{\partial {r_f}^c\left({\alpha }_k,{\phi }_p\right)}{\partial {\alpha }_k}}\times {\displaystyle \frac{\partial {r_f}^c\left({\alpha }_k,{\phi }_p\right)}{\partial {\phi }_p}}/\left|{\displaystyle \frac{\partial {r_f}^c\left({\alpha }_k,{\phi }_p\right)}{\partial {\alpha }_k}}\times {\displaystyle \frac{\partial {r_f}^c\left({\alpha }_k,{\phi }_p\right)}{\partial {\phi }_p}}\right|$$

(13)

Its tangent vector v_t, oriented along the angular velocity direction around the face gear’s rotation axis, can be calculated with the following formula:

$$v_t\left({\alpha }_k,{\phi }_p\right)={r_f}^c\left({\alpha }_k,{\phi }_p\right)\times {a_f}^c/\left|{r_f}^c\left({\alpha }_k,{\phi }_p\right)\times {a_f}^c\right|$$

(14)

where $a_f^c$ represents the vector of rotation axis of the conjugate face gear.

According to the generation process of the face gear tooth flank mentioned in Section 2.2, the theoretical tooth flank of the face gear is the conjugate surface of the pinion, and the two maintain line contact. However, this contact condition will change when there is artificial modification or manufacturing error on the face gear’s tooth flank. It is assumed here that the normal deviation between the face gear and the conjugate surface of the pinion is $e_{i,j}^q$; this deviation can result from active modification designs by the designer or tooth flank errors caused by the manufacturing process. Then, the rotation angle q_i,j can be calculated as

$$q_{i,j}=e_{i,j}^q{n_f}^c\left({\alpha }_k,{\phi }_p\right)\cdot v_t\left({\alpha }_k,{\phi }_p\right)$$

(15)

By calculating the rotation angle values q_i,j corresponding to the points on the contact line at all moments during face gear meshing, the rotation angle matrix Q can be obtained. Using the radius and height of the contact line points as the X and Y values, and the rotation angle matrix Q as the Z value, the Ease-off surface can be constructed.

3.3. TCA Method Based on Ease-Off Surface

As shown in Figure 4, the face gear and the conjugate surface of the pinion are placed in the same coordinate system. At a certain moment, a point on the i-th contact line coincides with a point on the conjugate surface after rotating around the rotation axis of the face gear, and the rotated angle is denoted as q_i,j. The point with the smallest rotated angle on the contact line is the contact point at this moment, as shown in Figure 5a. By computing the minimum rotation angle value $q_i^{min}$ on each contact line, all contact points on the tooth flank can be determined; connecting these contact points yields the contact path, as shown in Figure 5b. Consequently, the transmission error (TE) can be obtained as follows:

$$TE\left(i\right)=q_i^{\min }=\min \left(q_{i,j}\right),j=1,2,\dots ,n$$

(16)

4. Measured Flank Processing and Error Integration

4.1. Flank Measurement Methodology

Accurate characterization of face-gear tooth flank geometry necessitates high-fidelity metrological techniques. This process typically employs Coordinate Measuring Machines (CMMs) equipped with tactile or optical probes (Figure 6a) to acquire dense point-cloud data across the topological surface, as shown in Figure 6b.

CMMs are currently the mainstream equipment for measuring complex tooth profiles, commonly used to measure the tooth flanks of gears with complex spatial three-dimensional geometries such as spiral bevel gears, face gears, and hypoid gears. The principle of their measurement is to gradually approach the given theoretical measurement point coordinates along the normal vector of the theoretical tooth surface, and calculate the tooth surface error at that point by comparing the distance between the actual measured point and the theoretical point in the normal direction, as shown in Figure 7. To avoid uncertain measurement errors caused by the probe touching the edge of the tooth flank, the boundary of the tooth flank measurement area is generally set at a certain distance from the tooth flank boundary, as shown in Figure 7. Therefore, only the tooth flank deviations within the measurement area can be obtained through tooth flank measurement.

The measurement area is divided into m × n points, and the coordinate vector and normal vector of each point can be calculated by the following equation:

$$\begin{array}{l}{R}_{i,j}=\sqrt{r_{fx}{\left({\alpha }_s,{\phi }_s\right)}^2+r_{fz}{\left({\alpha }_s,{\phi }_s\right)}^2}\\ H_{i,j}=r_{fy}\left({\alpha }_s,{\phi }_s\right)\end{array}$$

(17)

Here, R_i,j and H_i,j represent the corresponding radius and height at the (i, j)-th point, where i = 1, 2, …, m and j = 1, 2, …, n. By solving the above equation, the parameters of the point to be measured (α_s* and φ_s*) can be obtained. Substituting them into Equations (9) and (10), respectively, yields the coordinate point (r_f(α_s*,φ_s*)) and normal vector (n_f(α_s*,φ_s*)) of this point.

By using CMMs to approach the coordinate points on the theoretical tooth surface along the normal vector of each measurement point, the coordinate values of the points on the actual tooth surface can be obtained. The distance between the actual coordinates and the theoretical coordinates in the direction of the normal vector is the normal errors of the point to be measured, which can be calculated as

$$d_{i,j}=n_f\left({{\alpha }_s}^{*},{{\phi }_s}^{*}\right)\cdot \left({r_f}^m-r_f\left({{\alpha }_s}^{*},{{\phi }_s}^{*}\right)\right)$$

(18)

By iterating over all measurement points, the tooth surface error matrix D within the measurement area can be obtained.

4.2. Error Surface Reconstruction and Integration

As indicated in Section 4.1, during actual measurement, only a limited number of sample points within the measurement area are selected for inspection, without fully covering the entire tooth surface. According to AGMA-2009-B01 standard, the measurement area is defined as a region reduced by 10% in the face width direction and 5% in the tooth height direction. Within this region, 9 discrete points are distributed along the face width and 5 points along the tooth height, forming a 5 × 9 measurement grid [26]. The tooth surface errors are evaluated by measuring these 45 points in the specified area. This leads to two issues: (a) the error information of the tooth surface area between sample points is unknown; (b) the tooth surface error outside the measurement area is unknown. To address this issue, this section fits the error matrix D using a cubic B-spline function based on the error information at the known sample points within the measurement area, thereby obtaining the equation of the real tooth surface. The specific steps are described as follows:

• Step 1: Surface Parameterization

Since the tooth width coordinate values of face gears are often much larger than their tooth height coordinate values, direct use of these values in calculations may compromise the computational accuracy in the tooth height direction. Therefore, prior to calculations, it is necessary to normalize these coordinates to eliminate this adverse effect. The computational process initiates with domain normalization to establish a dimensionless parametric space. Physical coordinates (R_i,j,H_i,j) are transformed into unit-square parameters (u, v)∈[0,1]² through linear scaling:

$$u_i={\displaystyle \frac{R_i-\min \left(R\right)}{\max \left(R\right)-\min \left(R\right)}},v_i={\displaystyle \frac{H_j-\min \left(H\right)}{\max \left(H\right)-\min \left(H\right)}}$$

(19)

where R and H are the tooth radius and tooth height of the sample points on the measurement area. This parameterization eliminates dimensional heterogeneity and enhances numerical stability for subsequent operations. The resulting uniform grid enables consistent mathematical treatment across the entire domain while preserving topological relationships between data points.

• Step 2: Bicubic Spline Fitting

The errors of the measured discrete points can only represent the errors at the measurement locations, while the error information of the tooth surface outside these points is lost. Therefore, it is necessary to construct the distribution of errors across the entire tooth surface based on the known error data from the measured points. A bicubic B-spline surface S(u,v) is then fitted to approximate the Q matrix through regularized optimization. The surface function

$$S\left(u,v\right)={\displaystyle \sum _{k=0}^3{\displaystyle \sum _{l=0}^3{c}_{kl}{B}_k\left(u\right)}}{B}_l\left(v\right)$$

(20)

leverages cubic B-spline for local control and curvature continuity. Coefficients c_kl are determined by minimizing a penalized objective function:

$$\underset{c}{\min }{\sum _{i,j}\Vert S\left(u_i,v_j\right)-q_{i,j}\Vert }^2+\lambda {\displaystyle \iint {\left(\frac{{\partial }^{2}S}{\partial u^2}+2\frac{{\partial }^{2}S}{\partial u\partial v}+\frac{{\partial }^{2}S}{\partial v^2}\right)}^{2}dudv}$$

(21)

where the regularization term λ, calibrated via L-curve analysis, constrains surface curvature to prevent oscillatory artifacts. This yields a C²-continuous representation that balances fidelity to measured data with physical plausibility.

• Step 3: Prediction and Extrapolation

Based on the error distribution constructed above, the next step is to predict the error at any arbitrary point on the tooth surface. Prediction at points (R_i, H_j) involves parametric mapping followed by conditional evaluation. The coordinates are first normalized to (u_i, v_j) using the original scaling factors. For interior points ([0,1]²), $e_{i,j}^q$ = S(u_i, v_j) is directly computed. Extrapolation beyond the domain activates a gradient-based extension:

$$e_{i,j}^q=S\left(u_b,v_b\right)+{\left.\nabla S\right|}_{\left(u_b,v_b\right)}\cdot \left[\begin{array}{c}{u}_i-u_b\\ v_j-v_b\end{array}\right]$$

(22)

where (u_b,v_b) denotes the closest boundary projection point, and ∇S = [∂S/∂u,∂S/∂v]^T is the surface gradient.

• Step 4: Error Analysis

To evaluate the accuracy of surface fitting, it is necessary to assess the fitting errors. The fitting error is assessed via root-mean-square error

$$\zeta =\sqrt{{\displaystyle \frac{1}{\mathrm{mn}}}{\displaystyle \sum {\left(S\left(u_i,v_j\right)-q_{i,j}\right)}^2}}$$

(23)

Through the above steps, the error value corresponding to any (R, H) point can be calculated. Typically, this error value is restricted to within 1 × 10⁻⁴ to ensure favorable surface fitting performance and fidelity. Then, by integrating it into Equation (15), the rotation angle matrix Qa considering the measured tooth surface Ease-off can be obtained. Based on this matrix, the meshing performance indicators such as the contact path and transmission error of the measured face gear can be calculated in accordance with the TCA calculation process shown in Section 3.3.

5. Validation and Discussions

5.1. Numerical and Experimental Validation

5.1.1. Numerical Verification

The proposed method is applied to the contact analysis of the measured tooth surfaces of face gears after rough machining by gear skiving and finish machining by gear grinding, respectively. Its results are compared with those obtained by Litvin’s method [13] and the FEA method. The parameters of the face gear drives involved in the comparison are listed in

Table 1. The design parameters of the face gear drives.

Name	Sign	Value	Unit
Module	m	3.9	mm
Pressure angle	α	25	°
Teeth number of the shaper cutter	Ns	22	/
Teeth number of the face gear	Nf	142	/
Teeth number of the pinion	Np	21	/
Shaft angle	γ	90	°
Inner radius of the face gear	Ri	253.5	mm
Outer radius of the face gear	Ro	305	mm
Tooth addendum	ha	3.9	mm
Tooth dedendum	hf	4.875	mm
Tooth width of the pinion	B	55	mm

.

The measurement results of tooth surface errors of face gears after rough skiving and finish grinding are shown in Figure 8. The tooth surface of the face gear after rough skiving mainly exhibits errors in the form of pressure angle, as shown in Figure 8a, and the error distribution trends of the left and right tooth surfaces are basically the same. There is a residual phenomenon near the addendum and an over-cut phenomenon near the dedendum. The maximum over-cut and residual values occur near the dedendum on the inner diameter side and near the addendum on the outer diameter side of the tooth surface, respectively: for the left tooth surface, they are 53.1 μm and 26.0 μm; for the right tooth surface, they are 56.9 μm and 27.5 μm.

For the tooth surface after precision grinding, as shown in Figure 8b, the tooth surface error is significantly reduced, with all errors within 10 μm. Based on the measurement data processing in Section 4 and the integration method with the Ease-off surface, the calculated contact path on the face gear tooth surface is shown in

Table 2. The contact path on the skived face gear’s tooth flanks obtained by different methods.

Contact Path	Skived Face Gear
Traditional method
Proposed method
FEA method

. In addition, both the traditional method [13] solving five unknowns via five nonlinear equations and the Quasi-static FEA simulations are implemented. Their results of tooth surface contact path are also included in Table 2.

Table 2 and

Table 3. The contact path on the ground face gear’s tooth flanks obtained by different methods.

Contact Path	Ground Face Gear
Traditional method
Proposed method
FEA method

, respectively, present the tooth surface contact paths calculated by the traditional method, the proposed method, and the FEA method when the skived face gear and ground face gear mesh with the pinion, respectively. It can be seen from the table that for the skived face gear, contact paths predicted by all three methods exhibited strong agreement, and the contact paths are mainly entirely located on the addendum ridgeline of the face gear. This is because, as shown in Figure 8a, the tooth surface of the skived face gear exhibits an error distribution pattern of addendum residual and dedendum over-cut; thus, its contact paths are all located at the addendum ridgeline.

However, for the ground tooth surface, the traditional method is more sensitive to tooth surface errors, and there are differences between its calculation results and those of the other methods. This is because the traditional method is based on numerical solution methods, which have a high dependence on initial values and thus cannot well handle areas where the contact path has significant turns, as shown in Table 3. In contrast, the proposed Ease-off-based method can better handle this situation, and the calculated contact trajectories maintain a high consistency with those of the FEA method.

5.1.2. Experimental Validation

The ground face gear was mounted on a rolling test bench to detect the tooth surface contact path. Initially, the tooth surfaces of the face gear and pinion were evenly coated with red and blue coloring agents. When the gear pair rotated and meshed under a slight load, the extrusion and friction between the tooth surfaces caused the coloring agent to adhere to the tooth surface of the other gear, thereby forming a contact pattern on the tooth surface.

The contact patterns obtained by this method on the tooth surfaces of the ground cylindrical gear and face gear are shown in Figure 9. These patterns are located in the middle of the tooth surfaces, which are basically consistent with the positions of the contact marks in the calculation results based on the proposed method shown in Figure 6. The contact marks in the rolling test are slightly larger than the calculated results because the tooth surfaces deformed under the slight load during the rolling test, and the instantaneous contact points expanded into elliptical contact areas. In summary, this confirms the physical realism of contact mechanics simulated via error-integrated Ease-off.

5.2. Discussions

5.2.1. Method Advantages

• Simultaneously determine the edge contact and tooth surface contact states

The proposed method can simultaneously evaluate the contact states occurring both at the tooth surface edges and within the tooth surface area. In traditional methods [13], however, edge contact and surface contact of the tooth surface are often divided into the following two different sets of nonlinear equations. The contact discriminant on the tooth surface is

$$\left\{\begin{array}{l}{r_f}^{\left(1\right)}\left({\theta }_1,u_1,{\phi }_1\right)={r_f}^{\left(2\right)}\left({\theta }_2,u_2,{\phi }_2\right)\\ {N_f}^{\left(1\right)}\left({\theta }_1,u_1,{\phi }_1\right)={N_f}^{\left(2\right)}\left({\theta }_2,u_2,{\phi }_2\right)\end{array}\right.$$

(24)

The contact criterion for contacts occurring at the tooth surface edges is

$$\left\{\begin{array}{l}{r_f}^{\left(1\right)}\left({\theta }_1,u_1,{\phi }_1\right)={r_f}^{\left(2\right)}\left({\theta }_2,u_2,{\phi }_2\right)\\ {\displaystyle \frac{\partial {r_f}^{\left(1\right)}}{\partial {\theta }_1}}\cdot {N_f}^{\left(2\right)}=0\end{array}\right.$$

(25)

As shown in Figure 10, the proposed method can simultaneously calculate the contact points occurring both at the edges and on the tooth surfaces. Segments AB and CD correspond to the edge contact segments on the tooth surfaces of the face gear and the cylindrical gear, respectively, which are characterized by the edge ridgeline of one curved surface being tangent to the other curved surface. Segment BC is the set of contact points occurring on the tooth surfaces.

• Computational stability in different application scenarios

In addition, the proposed method determines contact points by evaluating the distance between the conjugate tooth surface of the pinion and the tooth surface of the face gear, thus avoiding the computational load caused by the numerical solution of a large number of nonlinear equations in traditional methods. It can not only evaluate the meshing performance of the actual tooth surface after manufacturing, but also provide tool support for evaluating the meshing performance of the tooth surface after modification and installation errors in the design stage.

Here, the face gear tooth surface adopts parabolic modification [13], and its modification parameters mainly include the parabolic coefficient a_r and vertex offset f_d. The pinion’s tooth surface adopts parabolic modification in both tooth profile and tooth width [27,28], with corresponding modification parameters including coefficients a_pr and a_lr, as well as vertex offsets f_pd and f_ld. The modification parameters are listed in

Table 4. The modification parameters of the face gear drives.

Cases	ar	fd	apr	alr	fpd	fld
1	0	0	0	0	0	0
2	0.0005	0	0	0	0	0
3	0.0005	−2	0	0	0	0
4	0.0005	−2	0.0010	0.0005	1	0
5	0.0005	−2	0.0010	0.0005	1	10
6	0	0	0.0010	0.0005	−1	−10

.

As shown in

Table 5. The contact paths of the face gear drive with different tooth flank modifications.

Cases	Contact Path on the Face Gear Tooth Flanks
1
2
3
4
5
6

, there are schematic diagrams of tooth contact paths under several different tooth flank modification methods.

Figure 11 presents the tooth contact paths on the face gear tooth flanks calculated by the proposed method under the given installation errors. Δq represents the installation error in the axial direction of the face gear, Δz denotes the error in the axial direction of the pinion, ΔE stands for the offset error between the axis of the pinion and that of the face gear, and Δγ indicates the shaft angle error between the two axes.

It can be seen from the figures that the proposed method has good calculation stability for different modification methods and installation errors.

• Computational efficiency

The comparison of calculation time between the proposed method, traditional methods, and the FEA method is shown in

Table 6. The calculation time of the proposed method, traditional methods, and the FEA method.

Methods	Time
Proposed method	2.66 s
Traditional method	1.98 s
FEA method	About 6 h

. The quasi-static analysis model established based on the FEA method includes the contact process of 3 tooth pairs, with 100 meshes in the tooth width direction, 70 meshes in the tooth height direction, and the mesh type is C3D8R, with 100 analysis steps. Three methods were executed on a laptop with the same configuration: 12th Gen Intel(R) Core (TM) i7-12700F @ 2.10 GHz, RAM: 32 GB DDR4. The software used was Abaqus 2018 and MATLAB 2022b, respectively. It can be found from the comparison that the calculation time of the proposed method is slightly longer than that of the traditional method (2.66 s vs. 1.98 s), but the calculation time of both methods is far shorter than that of the FEA method. Compared to the FEA method, the proposed method reduced computation time by 99% (2.66 s vs. About 6 h). This indicates that under the condition of achieving the same calculation accuracy, the proposed method can better balance calculation accuracy and efficiency.

5.2.2. Limitations and Outlook

Although the proposed method has certain advantages over existing methods in terms of stability and computational efficiency, it still has some limitations as follows:

• The current method only considers the entire process of a single tooth from meshing-in to meshing-out, without taking into account the load distribution among multiple teeth and the influence of contact ratio. This consideration mainly relies on the calculation of the meshing stiffness of face gear teeth. In future work, we should address this gap.
• In future research, the proposed method can be further combined with on-machine measurement technology to develop closed-loop manufacturing correction using real-time TCA feedback.

6. Conclusions

This paper proposes an Ease-off surface-based tooth contact analysis method for measured face gear tooth flanks, which can evaluate the meshing performance of face gear pairs based on the actual machined tooth flanks measurement data. The effectiveness of this method has been verified through numerical and experimental approaches.