Gaussian-UDSR: Real-Time Unbounded Dynamic Scene Reconstruction with 3D Gaussian Splatting
Abstract
1. Introduction
2. Related Work
3. Method
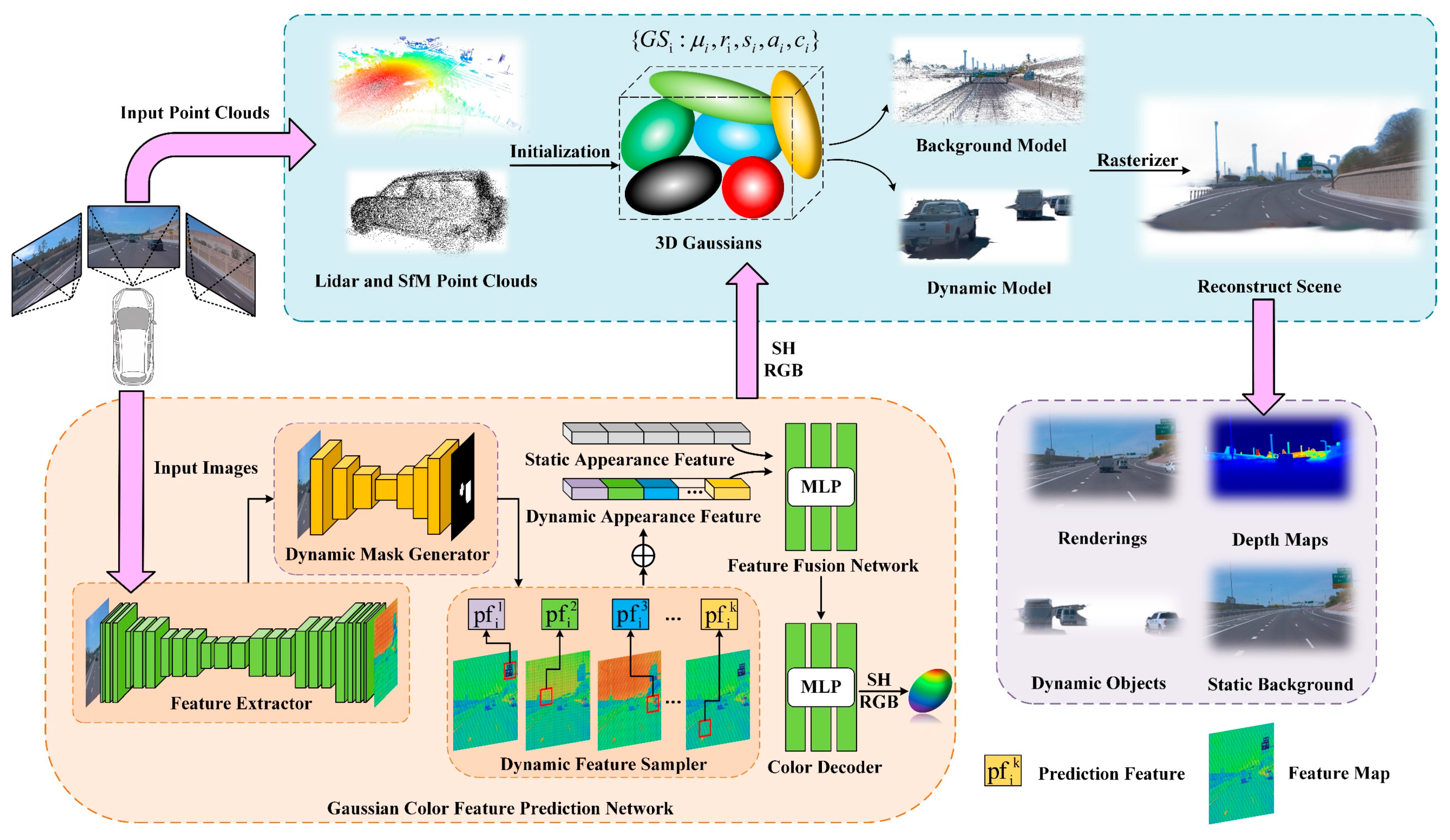
3.1. Overall Architecture
3.2. Gaussian Model
3.3. Gaussian Color Feature Prediction Network
3.4. Model Training
4. Experimental Evaluation
4.1. Experimental Setup
4.2. Reconstruction Evaluation
4.3. Ablation Experiment
4.4. Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tancik, M.; Casser, V.; Yan, X.; Pradhan, S.; Mildenhall, B.; Srinivasan, P.P.; Barron, J.T.; Kretzschmar, H. Block-nerf: Scalable large scene neural view synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8248–8258. [Google Scholar]
- Zhang, X.; Kundu, A.; Funkhouser, T.; Guibas, L.; Su, H.; Genova, K. Nerflets: Local radiance fields for efficient structure-aware 3d scene representation from 2d supervision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 8274–8284. [Google Scholar]
- Ost, J.; Laradji, I.; Newell, A.; Bahat, Y.; Heide, F. Neural point light fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18419–18429. [Google Scholar]
- Xie, Z.; Zhang, J.; Li, W.; Zhang, F.; Zhang, L. S-nerf: Neural radiance fields for street views. arXiv 2023. [Google Scholar] [CrossRef]
- Guo, J.; Deng, N.; Li, X.; Bai, Y.; Shi, B.; Wang, C.; Ding, C.; Wang, D.; Li, Y. Streetsurf: Extending multi-view implicit surface reconstruction to street views. arXiv 2023. [Google Scholar] [CrossRef]
- Lu, F.; Xu, Y.; Chen, G.; Li, H.; Lin, K.-Y.; Jiang, C. Urban radiance field representation with deformable neural mesh primitives. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 465–476. [Google Scholar]
- Rematas, K.; Liu, A.; Srinivasan, P.P.; Barron, J.T.; Tagliasacchi, A.; Funkhouser, T.; Ferrari, V. Urban radiance fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12932–12942. [Google Scholar]
- Wu, Z.; Liu, T.; Luo, L.; Zhong, Z.; Chen, J.; Xiao, H.; Hou, C.; Lou, H.; Chen, Y.; Yang, R.; et al. Mars: An instance-aware, modular and realistic simulator for autonomous driving. In Proceedings of the CAAI International Conference on Artificial Intelligence, Fuzhou, China, 22–23 July 2023; Springer: Singapore, 2023; pp. 3–15. [Google Scholar]
- Ost, J.; Mannan, F.; Thuerey, N.; Knodt, J.; Heide, F. Neural scene graphs for dynamic scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2856–2865. [Google Scholar]
- Kundu, A.; Genova, K.; Yin, X.; Fathi, A.; Pantofaru, C.; Guibas, L.J.; Tagliasacchi, A.; Dellaert, F.; Funkhouser, T. Panoptic neural fields: A semantic object-aware neural scene representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12871–12881. [Google Scholar]
- Yang, Z.; Chen, Y.; Wang, J.; Manivasagam, S.; Ma, W.-C.; Yang, A.J.; Urtasun, R. Unisim: A neural closed-loop sensor simulator. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1389–1399. [Google Scholar]
- Park, K.; Sinha, U.; Hedman, P.; Barron, J.T.; Bouaziz, S.; Goldman, D.B.; Martin-Brualla, R.; Seitz, S.M. Hypernerf: A higher-dimensional representation for topologically varying neural radiance fields. arXiv 2021. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, D.; Yan, F.; Zhao, T.; Zhang, F.; Ma, Y.; Wang, L.; Yang, R. Augmented LiDAR simulator for autonomous driving. arXiv 2020. [Google Scholar] [CrossRef]
- Wang, J.; Manivasagam, S.; Chen, Y.; Yang, Z.; Bârsan, I.A.; Yang, A.J.; Ma, W.-C.; Urtasun, R. Cadsim: Robust and scalable in-the-wild 3d reconstruction for controllable sensor simulation. arXiv 2023. [Google Scholar] [CrossRef]
- Chen, Y.; Rong, F.; Duggal, S.; Wang, S.; Yan, X.; Manivasagam, S.; Xue, S.; Yumer, E.; Urtasun, R. Geosim: Realistic video simulation via geometry-aware composition for self-driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7230–7240. [Google Scholar]
- Manivasagam, S.; Wang, S.; Wong, K.; Zeng, W.; Sazanovich, M.; Tan, S.; Yang, B.; Ma, W.-C.; Urtasun, R. Lidarsim: Realistic lidar simulation by leveraging the real world. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11167–11176. [Google Scholar]
- Yang, Z.; Manivasagam, S.; Chen, Y.; Wang, J.; Hu, R.; Urtasun, R. Reconstructing objects in-the-wild for realistic sensor simulation. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 11661–11668. [Google Scholar]
- Yang, Z.; Chai, Y.; Anguelov, D.; Zhou, Y.; Sun, P.; Erhan, D.; Rafferty, S.; Kretzschmar, H. Surfelgan: Synthesizing realistic sensor data for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11118–11127. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. Nerf: Representing scenes as neural radiance fields for view synthesis. arXiv 2021. [Google Scholar] [CrossRef]
- Garbin, S.J.; Kowalski, M.; Johnson, M.; Shotton, J.; Valentin, J. Fastnerf: High-fidelity neural rendering at 200fps. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 14346–14355. [Google Scholar]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. arXiv 2022. [Google Scholar] [CrossRef]
- Reiser, C.; Peng, S.; Liao, Y.; Geiger, A. Kilonerf: Speeding up neural radiance fields with thousands of tiny mlps. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 14335–14345. [Google Scholar]
- Yu, A.; Li, R.; Tancik, M.; Li, H.; Ng, R.; Kanazawa, A. Plenoctrees for real-time rendering of neural radiance fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 5752–5761. [Google Scholar]
- Fridovich-Keil, S.; Yu, A.; Tancik, M.; Chen, Q.; Recht, B.; Kanazawa, A. Plenoxels: Radiance fields without neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5501–5510. [Google Scholar]
- Deng, K.; Liu, A.; Zhu, J.-Y.; Ramanan, D. Depth-supervised nerf: Fewer views and faster training for free. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12882–12891. [Google Scholar]
- Yang, J.; Pavone, M.; Wang, Y. Freenerf: Improving few-shot neural rendering with free frequency regularization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 8254–8263. [Google Scholar]
- Barron, J.T.; Mildenhall, B.; Tancik, M.; Hedman, P.; Martin-Brualla, R.; Srinivasan, P.P. Mip-nerf: A multiscale representation for anti-aliasing neural radiance fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 5855–5864. [Google Scholar]
- Verbin, D.; Hedman, P.; Mildenhall, B.; Zickler, T.; Barron, J.T.; Srinivasan, P.P. Ref-nerf: Structured view-dependent appearance for neural radiance fields. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 5481–5490. [Google Scholar]
- Niemeyer, M.; Barron, J.T.; Mildenhall, B.; Sajjadi, M.S.; Geiger, A.; Radwan, N. Regnerf: Regularizing neural radiance fields for view synthesis from sparse inputs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5480–5490. [Google Scholar]
- Wang, G.; Chen, Z.; Loy, C.C.; Liu, Z. Sparsenerf: Distilling depth ranking for few-shot novel view synthesis. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 9065–9076. [Google Scholar]
- Kerbl, B.; Kopanas, G.; Leimkühler, T.; Drettakis, G. 3D Gaussian Splatting for Real-Time Radiance Field Rendering. arXiv 2023. [Google Scholar] [CrossRef]
- Wu, G.; Yi, T.; Fang, J.; Xie, L.; Zhang, X.; Wei, W.; Liu, W.; Tian, Q.; Wang, X. 4d gaussian splatting for real-time dynamic scene rendering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 20310–20320. [Google Scholar]
- Shao, R.; Sun, J.; Peng, C.; Zheng, Z.; Zhou, B.; Zhang, H.; Liu, Y. Control4d: Efficient 4d portrait editing with text. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 4556–4567. [Google Scholar]
- Chen, A.; Xu, Z.; Geiger, A.; Yu, J.; Su, H. Tensorf: Tensorial radiance fields. In Computer Vision—ECCV 2022, Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 333–350. [Google Scholar]
- Cao, A.; Johnson, J. Hexplane: A fast representation for dynamic scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 130–141. [Google Scholar]
- Yang, Z.; Gao, X.; Zhou, W.; Jiao, S.; Zhang, Y.; Jin, X. Deformable 3d gaussians for high-fidelity monocular dynamic scene reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 20331–20341. [Google Scholar]
- Liang, Y.; Khan, N.; Li, Z.; Nguyen-Phuoc, T.; Lanman, D.; Tompkin, J.; Xiao, L. Gaufre: Gaussian deformation fields for real-time dynamic novel view synthesis. arXiv 2023. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Sun, Y.-T.; Yang, Z.; Lyu, X.; Cao, Y.-P.; Qi, X. Sc-gs: Sparse-controlled gaussian splatting for editable dynamic scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 4220–4230. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5–9, 2015, Proceedings, Part III; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Advances in Neural Information Processing Systems 30, Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Neural Information Processing Systems Foundation, Inc. (NeurIPS): La Jolla, CA, USA, 2017. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Sun, P.; Kretzschmar, H.; Dotiwalla, X.; Chouard, A.; Patnaik, V.; Tsui, P.; Guo, J.; Zhou, Y.; Chai, Y.; Caine, B.; et al. Scalability in perception for autonomous driving: Waymo open dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2446–2454. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3354–3361. [Google Scholar] [CrossRef]
- Turki, H.; Zhang, J.Y.; Ferroni, F.; Ramanan, D. Suds: Scalable urban dynamic scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 12375–12385. [Google Scholar]
- Yang, J.; Ivanovic, B.; Litany, O.; Weng, X.; Kim, S.W.; Li, B.; Che, T.; Xu, D.; Fidler, S.; Pavone, M.; et al. Emernerf: Emergent spatial-temporal scene decomposition via self-supervision. arXiv 2023. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, C.; Jiang, J.; Zhu, X.; Zhang, L. Periodic vibration gaussian: Dynamic urban scene reconstruction and real-time rendering. arXiv 2023. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]









| Method | Input Modality | Scene Scale | Dynamic Modeling | Rendering Speed | Rendering Quality |
|---|---|---|---|---|---|
| D-NeRF [25] | RGB | Bounded (small) | MLP-based | Slow | Medium |
| 4DGS [32] | RGB + TriPlane | Bounded (small) | plane features | Medium | High |
| SC-GS [38] | RGB + Control Points | Bounded (small) | control points + KNN | Medium | Medium |
| GauFRe [37] | RGB + MLP | Bounded (small) | separated Gaussians | Medium | High |
| Ours | LiDAR + RGB + MLP | Unbounded (large) | motion separation | Real time (Fast) | High |
| Waymo Open Dataset | KITTI | |||||||
|---|---|---|---|---|---|---|---|---|
| Methods | FPS ↑ | PSNR ↑ | SSIM ↑ | LPIPS ↓ | FPS ↑ | PSNR ↑ | SSIM ↑ | LPIPS ↓ |
| StreetSurf [5] | 0.081 | 27.58 | 0.876 | 0.340 | 0.35 | 25.02 | 0.725 | 0.251 |
| Mars [8] | 0.027 | 22.36 | 0.675 | 0.399 | 0.032 | 27.16 | 0.864 | 0.227 |
| 3DGS [31] | 177 | 27.14 | 0.896 | 0.227 | 209 | 22.58 | 0.828 | 0.311 |
| SUDS [45] | 0.026 | 29.08 | 0.849 | 0.236 | 0.050 | 28.43 | 0.876 | 0.138 |
| EmerNeRF [46] | 0.037 | 28.92 | 0.830 | 0.355 | 0.094 | 26.74 | 0.753 | 0.206 |
| PVG [47] | 38.67 | 33.49 | 0.954 | 0.189 | 42.53 | 33.76 | 0.961 | 0.155 |
| Ours | 128 | 36.43 | 0.971 | 0.047 | 136 | 35.63 | 0.964 | 0.013 |
| Image Reconstruction | Novel View Synthesis | |||
|---|---|---|---|---|
| EmerNeRF | Ours | EmerNeRF | Ours | |
| Seq105887… | 28.96 | 35.52 | 28.73 | 32.58 |
| Seq106250… | 28.35 | 35.28 | 27.59 | 32.36 |
| Seq110170… | 28.79 | 35.46 | 28.89 | 33.65 |
| Seq119178… | 27.98 | 34.12 | 27.51 | 32.49 |
| Seq122514… | 28.37 | 35.31 | 28.45 | 32.89 |
| Seq123392… | 28.68 | 35.44 | 28.75 | 33.24 |
| Seq148106… | 29.02 | 36.19 | 28.09 | 34.81 |
| Average | 28.59 | 35.33 | 28.29 | 33.15 |
| Sequence | Image Reconstruction | |
|---|---|---|
| StreetSurf | Ours | |
| Seq100613… | 28.14 | 35.52 |
| Seq150623… | 28.58 | 35.28 |
| Seq158686… | 27.95 | 35.46 |
| Seq166085… | 27.68 | 34.12 |
| Seq322492… | 28.75 | 35.31 |
| Seq881121… | 28.62 | 35.44 |
| Seq938501… | 28.84 | 36.19 |
| Average | 28.59 | 35.33 |
| PSNR ↑ | SSIM ↑ | LPIPS ↓ | |
|---|---|---|---|
| w/o lidar depth | 36.22 | 0.970 | 0.050 |
| w/o SfM | 34.65 | 0.959 | 0.059 |
| w/o Feature prediction | 34.91 | 0.962 | 0.056 |
| w/o Pose tracking | 36.14 | 0.964 | 0.049 |
| Ours | 36.43 | 0.971 | 0.047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhou, Y.; Tian, B.; Wang, H.; Zhao, Y.; Wu, S. Gaussian-UDSR: Real-Time Unbounded Dynamic Scene Reconstruction with 3D Gaussian Splatting. Appl. Sci. 2025, 15, 6262. https://doi.org/10.3390/app15116262
Sun Y, Zhou Y, Tian B, Wang H, Zhao Y, Wu S. Gaussian-UDSR: Real-Time Unbounded Dynamic Scene Reconstruction with 3D Gaussian Splatting. Applied Sciences. 2025; 15(11):6262. https://doi.org/10.3390/app15116262
Chicago/Turabian StyleSun, Yang, Yue Zhou, Bin Tian, Haiyang Wang, Yongchao Zhao, and Songdi Wu. 2025. "Gaussian-UDSR: Real-Time Unbounded Dynamic Scene Reconstruction with 3D Gaussian Splatting" Applied Sciences 15, no. 11: 6262. https://doi.org/10.3390/app15116262
APA StyleSun, Y., Zhou, Y., Tian, B., Wang, H., Zhao, Y., & Wu, S. (2025). Gaussian-UDSR: Real-Time Unbounded Dynamic Scene Reconstruction with 3D Gaussian Splatting. Applied Sciences, 15(11), 6262. https://doi.org/10.3390/app15116262






