Enhancement of Low-Light Images Using Illumination Estimate and Local Steering Kernel

Abstract

Images acquired in low-light conditions often have poor visibility. These images considerably degrade the performance of algorithms when used in computer vision and multi-media systems. Several methods for low-light image enhancement have been proposed to address these issues; furthermore, various techniques have been used to restore close-to-normal light conditions or improve visibility. However, there are problems with the enhanced image, such as saturation of local light sources, color distortion, and amplified noise. In this study, we propose a low-light image enhancement technique using illumination component estimation and a local steering kernel to address this problem. The proposed method estimates the illumination components in low-light images and obtains the images with illumination enhancement based on Retinex theory. The resulting image is then color-corrected and denoised using a local steering kernel. To evaluate the performance of the proposed method, low-light images taken under various conditions are simulated using the proposed method, and it demonstrates visual and quantitative superiority to the existing methods.

1. Introduction

As artificial intelligence advances in modern society, automation and unmanned technologies are being introduced in various fields. In particular, intelligent CCTV systems, autonomous driving, and remote monitoring are composed of various computer vision algorithms. These systems require excellent visibility in the acquired images for high accuracy. However, objects may not be clearly identified under insufficient contrast in images acquired at night or due to environmental factors such as ambient light sources. Various low-light image enhancement algorithms have been proposed to address these issues.

A common approach for improving low-light images has been to enhance dark areas by expanding the dynamic range of the histogram in the image. However, in images with non-uniform lighting, this can lead to over-enhancement of bright areas, thereby corrupting data in bright areas [1,2]. Chiu et al. proposed an adaptive gamma correction method using a weight distribution to compensate low-light images, but it resulted in the over-enhancement of bright areas in the image [3].

Low-light image enhancement using the Retinex model divides an image into illumination and reflection components and uses these components to estimate or generate an illuminated image using various techniques [4,5]. For low-light footage enhancement to produce the best quality results, the lighting and reflections must be in ideal conditions [6]. Wang et al. applied a joint edge-preserving filter to the illumination to obtain improved images [7]. Guo et al. used a structure-aware smoothing technique to predict the illumination component in an image based on the Retinex model [8].

Traditional methods often fail to produce visually natural results. Some methods over-emphasize low-light areas, resulting in unnatural outcomes or even ruining the overall tonality of the input image. Moreover, incorrect estimates of illumination can lead to color mismatch issues in the resulting images, which can sometimes reduce visibility [9,10].

To address these issues, an algorithm has been proposed in this paper using illumination component estimation and a local steering kernel for low-light image enhancement. To maintain the naturalness of the image even when there are bright areas in the low-light image, the proposed algorithm estimates the illumination component by calculating the gamma value using the mean and distribution constant obtained from the histogram of the image. Then, the image with improved illumination is obtained using Retinex theory, and color correction is performed by comparing the pixel values of the RGB channels of the pixel to each other to emphasize the colors of the improved image. Finally, a local steering kernel is used for filtering to remove the co-amplified noise components during the low-light image enhancement process.

The paper is structured as follows. Section 2 introduces related research on low-light image enhancement, and Section 3 explains the process by which our proposed algorithm improves low-light images. Section 4 discusses the performance of our proposed low-light image enhancement algorithm based on simulation results, and finally, Section 5 presents the conclusions.

2. Related Research

2.1. Low-Light Image Enhancement Based on Deep Learning Technology

Recently, research utilizing deep learning has been taking place actively across various fields, with methods employing CNN (convolutional neural network) training gaining attention for improving low-light images. MSR-net [11] is a CNN-based learning model proposed to enhance low-light images and Retinex theory. MSR-net performs well compared with other traditional methods, but, due to the limited acceptance area of the network architecture, it can produce visually unnatural parts in the resulting images.

While these deep learning-based learning methods outperform classic manual low-light enhancement approaches, there are still some issues. Since most deep learning-based learning methods are based on supervised learning, they require large-scale training datasets consisting of low-light images and regular images captured under normal light conditions as input. The performance of a deep learning network is closely related to the dataset used to train it, but building large-scale training datasets that take into account real-world conditions is challenging. For example, while obtaining a pair of images with different exposures and generating an HDR (high dynamic range) image from them is relatively straightforward [12], this is feasible only when capturing still scenes under well-lit conditions during the daytime. Acquiring a large amount of clear normal light images in extremely low-light environments is difficult.

2.2. Low-Illumination Color Image Enhancement Based on Retinex Theory

Retinex theory is a model used to explain how the human visual system perceives brightness. The fundamental principle of Retinex theory is that an image can be separated into its illumination and reflection components. The original image $I\left(x,y\right)$ acquired by a camera or sensor can be represented using the following formula [13].

$$I\left(x,y\right)=S(x,y)L(x,y)$$

(1)

In the above formula, $S(x,y)$ and $L(x,y)$ represent the reflection and illumination components, respectively, and $x,y$ is the pixel coordinates of the image. In Retinex theory, $S(x,y)$ has a greater impact on $I\left(x,y\right)$ than $L(x,y)$ because it determines the unique characteristics of the image [14]. This reduces the effect of the illumination component on the reflection component, thus restoring clear image information [4]. Unlike traditional linear and non-linear methods that can only enhance certain types of image features, Retinex achieves a balance between dynamic range compression, edge enhancement, and color constancy, making it suitable for enhancing various types of images.

The process of improving low-light images using Retinex is as follows:

• The low-light image you want to improve is represented by Equation (1).
• To separate the illumination and reflection components, we take the logarithm as in the following formula [15].

$$\mathit{log}I\left(x,y\right)=log\left(S(x,y)L(x,y)\right)$$

(2)

3.

The illumination-enhanced image $\widehat{S}(x,y)$ can be obtained by subtracting the illumination estimate from the original image and taking the inverse logarithm, as shown below.

$$\mathit{log}\widehat{S}\left(x,y\right)=\mathit{log}I\left(x,y\right)-\mathit{log}\widehat{L}\left(x,y\right)$$

(3)

The methods based on Retinex theory such as SSR (single scale Retinex) [16] and MSRCR (multi-scale Retinex with color restoration) [17] estimate the illumination and reflectance of an image and adjust the dynamic range of illuminated pixels to improve the image. Wang et al. [18] improve upon existing Retinex-based image enhancement algorithms by incorporating Gabor filters and the Retinex theory. Wang et al.’s technique extracts the luminance component I in the HSI color space and applies the MSRCR technique to enhance the luminance component of low-light images. Additionally, they utilize the SSR algorithm based on Gabor filters in the RGB color space of low-light images to obtain images with improved texture and detail.

Ma et al. [19] propose an MSRCR image enhancement algorithm based on Gaussian filtering and guided filtering, using multiscale Gaussian filtering and guided filtering to estimate accurate illumination components in low-light images.

2.3. Low-Light Image Enhancement Based on RetinexNet

RetinexNet was proposed based on the Retinex theory to perform image enhancement by decomposing low-light images into reflection and illumination components. RetinexNet uses Decom-Net to decompose the input image into reflectance and illumination components in the decomposition stage, and trains by using pairs of low-light and normal images in the training stage. However, while RetinexNet’s results significantly enhance image brightness, they may introduce color distortion, and issues such as blurriness or noise amplification occur during the process of decomposing and combining images [20]. The improved network model proposed by Li et al. [21] uses the HSV color space model to address the color distortion and noise problems in RetinexNet. Advanced RetinxeNet [22] uses two subnets, DecomNet and EnhanceNet, to appropriately enhance the contrast and suppress noise in the resulting image.

However, existing low-light image enhancement methods can result in insufficient illumination improvement or color imbalance, and the process of amplifying low-light areas can also amplify noise components. Due to these issues, enhanced images may exhibit distortion and blurriness.

3. Proposed Method

Our proposed method aims to address the issues that arise during the enhancement of low-light images through the following approaches:

-

Estimating illumination components in low-light images using histogram smoothing and Retinex theory.

-

Color correction by selecting a correction channel among the RGB channels in an image with enhanced illumination.

-

Removal of noise from the resulting image with a non-local mean based on a local steering kernel.

The proposed method is specifically categorized into three parts based on the methods presented above. First, there is the illumination improvement part, which improves the illumination of low-light images. Secondly, there is the color correction part, which corrects distorted colors during the illumination improvement process. Finally, there is the noise removal part, which removes the noise amplified during the illumination improvement and color correction. Figure 1 shows a block diagram of the processing of the proposed algorithm.

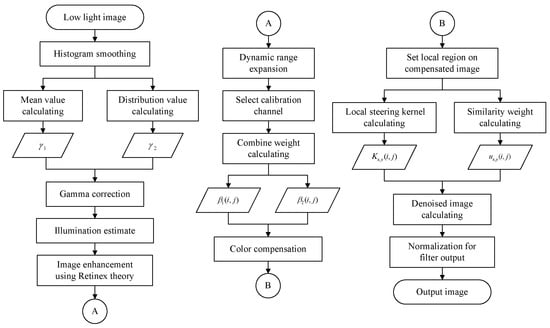
Figure 1. Block diagram of proposed method.

3.1. Illumination Estimate

Low-light footage may show areas in the image that are poorly lit or have an uneven brightness distribution. To accurately estimate the illumination components in these environments, we need information to determine the illumination environment of the low-light images. To determine the illumination environment, the proposed algorithm calculates the mean and distribution constants by obtaining the histogram of each channel in the RGB channel region of the low-light image. Here, the mean constant refers to the basis for judging the overall light level of the image, and the distribution constant refers to the frequency of local bright areas. In this case, a histogram smoothing technique is used to obtain a more natural result than the existing method. The smoothed histogram $\dot{H}\left(p\right)$ can be obtained as follows.

$$\dot{H}(p)=G \ast H_m(p)$$

(4)

$$G=\frac{1}{\sqrt{2\pi }{\sigma }_i}exp\left(-\frac{{\left(p-q\right)}^2}{{\sigma }_i^2}\right)$$

(5)

$$H_m\left(p\right)=\left\{H\left(q\right) | p-n\le q\le p+n\right\}$$

(6)

Here, $G$ refers to the Gaussian weight for histogram equalization, $H_m\left(p\right)$ represents the bin of the histogram $H\left(p\right)$ of the low-light image, $p$ represents pixel values, and $q$ represents pixel values that belong to a histogram bin, the range of which is determined by a constant $n$ that determines the width of the bin. If $q$ exceeds the range that can represent the pixel values in the image, the histogram $H\left(q\right)$ does not exist. Therefore, histogram smoothing is performed using the minimum histogram value. The mean constant $m$ of the image can be calculated from the smoothed histogram $\dot{H}\left(p\right)$ as follows.

$$m=\frac{1}{N}\left[\sum _{p=0}^{N}p\dot{H}\left(p\right)/\sum _{p=0}^N\dot{H}\left(p\right)\right]$$

(7)

Here, $N$ refers to the maximum number of pixel values that can be represented in an image. The proposed algorithm uses the following conversion formula to convert $m$ to a gamma value.

$${\gamma }_1=\frac{1}{1+exp\left(-2m\right)}$$

(8)

${\gamma }_1$ is given by Equation (8) as a range of $\left[0.5, 1\right]$, with darker images being closer to ${\gamma }_1=0.5$, indicating a lower illumination estimate.

The distribution constant is obtained from the smoothed histogram just like the mean constant, but the calculation is performed on only the low-light areas to emphasize the information about the values in the low-light areas. The proposed algorithm considers low-light areas as those with less than half of the pixel values that can be represented in the image, and obtains the distribution constant ${\gamma }_2$ as follows.

$${\gamma }_2=\frac{1}{RC}\sum _{p=0}^{N/2}\dot{H}\left(p\right)$$

(9)

Here, $R,C$ represents the horizontal and vertical dimensions of the video, respectively. Higher values of the distribution constant indicate images with more dark areas. The gamma value $\gamma$ for lighting estimation is calculated by weighting the mean and distribution constants as shown in the following formula.

$$\gamma =\frac{\tau }{1+exp\left(-2m\right)}+\frac{\left(1-\tau \right)}{RC}\sum _{p=0}^{N/2}\dot{H}\left(p\right)$$

(10)

Here, $\tau$ is the weighting constant to obtain the gamma value. $\tau$ is set to a range of $\left[0,1\right]$, with lower values improving low-light images more brightly. Conversely, a high value of $\tau$ will result in a more pronounced color contrast in the resulting image. The estimated illumination component $\widehat{L}(x,y)$ is obtained by applying the gamma value to the input image as follows, and then $\widehat{L}\left(x,y\right)$ is substituted into Equation (3) to obtain the enhanced image $\widehat{S}\left(x,y\right)$ as follows.

$$\widehat{L}\left(x,y\right)={I\left(x,y\right)}^{\gamma }$$

(11)

$$\widehat{S}\left(x,y\right)=exp\left(\mathit{log}I\left(x,y\right)-\mathit{log}\widehat{L}\left(x,y\right)\right)$$

(12)

Images with enhanced brightness may appear to have less contrast in the enhanced image because the pixel values in the low-light areas have been improved by a larger amount, concentrating them in the range of bright levels. To address these issues, we further extend the dynamic range for pixel values in low-light areas to naturally disperse concentrated pixel values in bright levels. The proposed algorithm extends the dynamic range by classifying the cases where the pixel values in the enhanced image are smaller than the median of the maximum pixel values that the image can represent as low-light regions, as shown in Equation (13).

$$S_p\left(x,y\right)=\left\{\begin{array}{l}\begin{array}{cc}\widehat{S}\left(x,y\right),& if 0.5<\widehat{S}(x,y)\end{array}\\ \\ \begin{array}{cc}2\widehat{S}{\left(x,y\right)}^2,& otherwise\end{array}\end{array}\right.$$

(13)

3.2. Color Compensation

For images with enhanced illumination, the rate at which pixel values are amplified may vary depending on differences in the mean and variance constants of the RGB channels. This can lead to color distortion or reduced contrast, which reduces the visibility of the resulting footage. The proposed algorithm uses color correction to make the contrast of colors more pronounced after image enhancement. The color correction step compares the pixel values of the RGB channels in the $x,y$ coordinates of the enhanced image $S_p\left(x,y\right)$ to each other, and the channel with the highest value is selected as the correction channel. Color correction applies different correction values to the correction channel and the remaining channels based on the difference between the pixel values of the correction channel and the pixel values of the other two channels. Here, if the pixel value of the RGB channel selected as the calibration channel is $t\left(x,y\right)$ and the pixel values of the other two channels are $d_1\left(x,y\right)$ and $d_2\left(x,y\right),$ respectively, the color correction values ${\widehat{t}}_1\left(x,y\right)$ and ${\widehat{t}}_2\left(x,y\right)$ for the two channels are obtained as follows.

$${\widehat{t}}_1\left(x,y\right)=t\left(x,y\right)+\alpha \left(t\left(x,y\right)-d_1\left(x,y\right)\right)\left(1-t\left(x,y\right)\right)d_1\left(x,y\right)$$

(14)

$${\widehat{t}}_2\left(x,y\right)=t\left(x,y\right)+\alpha \left(t\left(x,y\right)-d_2\left(x,y\right)\right)\left(1-t\left(x,y\right)\right)d_2\left(x,y\right)$$

(15)

Here, $\alpha$ refers to the color correction weight. The color correction value is calculated proportionally to the difference between $d_1\left(x,y\right)$ and $d_2\left(x,y\right),$ and the pixel value of the correction channel. In this case, if the pixel values of only one channel of $d_1\left(x,y\right)$ and $d_2\left(x,y\right)$ are significantly different, the color correction value may show a large value, so we set the weights for the color correction values ${\widehat{t}}_1\left(x,y\right)$ and ${\widehat{t}}_2\left(x,y\right)$ to minimize color distortion, maintain the naturalness of the image, and emphasize the color contrast. Taking this into account, the combined weights ${\beta }_1\left(x,y\right)$ and ${\beta }_2\left(x,y\right)$ can be calculated as follows.

$${\beta }_1\left(x,y\right)=\frac{d_1\left(x,y\right)}{d_1\left(x,y\right)+d_2\left(x,y\right)}$$

(16)

$${\beta }_2\left(x,y\right)=\frac{d_2\left(x,y\right)}{d_1\left(x,y\right)+d_2\left(x,y\right)}$$

(17)

The proposed algorithm sets $t\left(x,y\right)$ as the largest pixel value in the RGB channel for color correction, so the smaller $s_1\left(x,y\right)$ and $s_2\left(x,y\right)$ are calculated, the larger ${\widehat{t}}_1\left(x,y\right)$ and ${\widehat{t}}_2\left(x,y\right)$ are calculated. The sum of the two color correction values is obtained by applying the sum weight obtained in Equations (16) and (17) to the respective corrections ${\widehat{t}}_1\left(x,y\right)$ and ${\widehat{t}}_2\left(x,y\right)$. The combined color correction value $t_p\left(x,y\right)$ is calculated using the following formula.

$$t_p\left(x,y\right)={\beta }_1\left(x,y\right){\widehat{t}}_1\left(x,y\right)+{\beta }_2\left(x,y\right){\widehat{t}}_2\left(x,y\right)$$

(18)

3.3. Noise Removal Process

The proposed algorithm uses a non-local mean technique to remove the co-amplified noise during the enhancement process of low-light images. Unlike a typical local mean filter, the non-local mean technique uses an average of the pixels around the filter center to remove noise, weighted by how similar the surrounding pixels are to the center. This results in much better sharpness after filtering and less loss of detail in the image compared with the local mean filter. However, non-local mean techniques rely on similarity to set weights, which means that the structural features of the filtering region are not taken into account. To address these issues, this paper proposes a modified non-local mean algorithm based on a local steering kernel. Steering kernels are characterized by considering gradients and analyzing the radiosity of pixels in the local region, and typically take the following form [13].

$$\begin{array}{cc}{K}_{x,y}(i,j)=\frac{\sqrt{det\left(C_{x,y}\right)}}{2\pi h^2}exp\left(-\frac{{[i j]}^{T}C [i j]}{2h^2}\right),& -k\le i,j\le k\end{array}$$

(19)

Here, $C_{x,y}$ refers to the covariance matrix of size $2\times 2$ computed on a square local region centered at pixel $x,y$ [17]. $i,j$ refers to the relative coordinates away from the center of the steering kernel. $\left[i j\right]$ represents a matrix representation of the coordinates, and $k$ is a constant that determines the size of the steering kernel. $h$ is a smoothing constant to control the scope of the steering kernel [18]. The weights for denoising are calculated by comparing the similarity of the center and periphery regions to the steering kernel. The similarity comparison is calculated using Euclidean distance, and to convert this result to weights $u_{x,y}\left(i,j\right)$, we use the following formula.

$$u_{x,y}\left(i, j\right)=\frac{1}{z_{x,y}}exp\left(-\frac{{‖w\left(x,y\right)-w\left(x+i,y+j\right)‖}_2^2}{h^2}\right)$$

(20)

$$z_{x,y}=\sum _{i, j\in K_{x,y}}^{}exp\left(-\frac{{‖w\left(x,y\right)-w\left(x+i,y+j\right)‖}_2^2}{h^2}\right)$$

(21)

Here, $w\left(x,y\right)$ means the center window centered at $x,y,$ and $w\left(x+i,y+j\right)$ means the comparison window set at a distance of $i,j$ from the center window. $z_{x,y}$ is the normalization constant used to convert the results of the similarity comparison into weights. The denoising result $out\left(x,y\right)$ is calculated by convolving the pixel value with the steering kernel $K_{x,y}\left(i,j\right)$ and the weight $u_{x,y}\left(i,j\right)$, as shown in the following equation.

$$out\left(x,y\right)=M_{x,y}\left(i,j\right) \ast K_{x,y}\left(i,j\right) \ast u_{x,y}(i,j)$$

(22)

Here, $\ast$ refers to the convolution operator and $M_{x,y}\left(i,j\right)$ is the pixel value in the same region as the local steering kernel.

4. Simulation and Results

4.1. Experimental Setting

To evaluate the visual performance, the simulation compares the results of the existing low-light image enhancement technique and the low-light image processed by the proposed algorithm. The image used in the evaluation is a $600\times 400$-sized image from the LOL dataset, which is widely used in low-light image enhancement research [3]. To analyze the influence of the parameters of the proposed method on the resulting images, experiments are conducted under different conditions.

First, $\tau$, which is used in the low-light image enhancement process, is set to the range of $\left[0,1\right]$, and the closer the value is to 0, the brighter the illumination enhancement image is. Conversely, the closer $\tau$ is to 1, the more contrasting the colors in the resulting image. The proposed technique performs reasonably well for $\tau =0.45$ when the value of $\tau$ is varied in 0.05 increments from 0 to 1 in the simulation.

The color correction weight $\alpha$ used for color correction is the color correction weight, and the higher the value, the stronger the color correction effect. If the color correction weight is 0, an uncorrected image is output, and if it exceeds $\alpha =2$, the color distortion becomes severe. When the proposed algorithm is simulated by varying the value of the color correction weight $\alpha$ in increments of 0.1, the most natural color correction is achieved when the value is $\alpha =1$.

Since the steering kernel used in the denoising process is used to remove noise amplified during the enhancement of low-light images, it does not require strong denoising performance, so the small size of $15\times 15$ is sufficient. Also, due to the importance of preserving details such as edges and text, the best performance is achieved using a small window of $3\times 3$ for the similarity comparison.

For the other parameters, we select the values that show the best overall performance when running experiments under various conditions, and the results are shown in Table 1.

Table 1. Parameter set of proposed image enhancement method.

Parameter	Variable	Value
Gamma weight parameter	$\tau$	$0.45$
Color compensation weight	$\alpha$	$1$
Smoothing parameter	$h$	1.5
Steering kernel size	$K_{x,y}$	$15\times 15$
Window size	$w$	$3\times 3$

4.2. Experimental Result and Visual Compare

Figure 2, Figure 3, Figure 4 and Figure 5 show the low-light image and the enhanced and enlarged images, where (a) is the low-light image, (b–e) are the results of processing with existing techniques, namely, dark light [23], LIME [8], RBMP [24], and LIIEN [4], respectively, and (f) shows the result of processing with the proposed technique.

Figure 2. Enhancement result and enlarged image of low-light image (LOL493). (a) Low-light image, (b) dark light, (c) LIME, (d) RBMP, (e) LIIEN, and (f) proposed method.

Figure 3. Enhancement result and enlarged image of low-light image (LOL547). (a) Low-light image, (b) dark light, (c) LIME, (d) RBMP, (e) LIIEN, and (f) proposed method.

Figure 4. Enhancement result and enlarged image of low-light image (LOL665). (a) Low-light image, (b) dark light, (c) LIME, (d) RBMP, (e) LIIEN, and (f) proposed methods.

Figure 5. Enhancement result and enlarged image of low-light image (LOL780). (a) Low-light image, (b) dark light, (c) LIME, (d) RBMP, (e) LIIEN, and (f) proposed method.

In Figure 2, we compare object detection performance of very dark images. As a result, the detection performance of the images processed with dark light and LIME is insufficient. The RBMP-processed footage greatly improves the illumination of the footage, but when the dark areas are zoomed in, a significant presence of green light is noticed. The proposed technique sufficiently improves the illumination of the image, and the visibility of the dark areas is naturally enhanced.

In Figure 3, the dark light and LIME treatments do not improve the illumination of the background areas. RBMP’s enlargements are less visible due to the lack of contrast in the color tones, and LIIEN’s enlargements show relatively much noise. The proposed algorithm performs well in improving the overall illumination, and the color contrast of the enlarged image is clearly visible.

In Figure 4, the images processed with dark light and RBMP have low color contrast, resulting in blurry enlargements. The results of LIME and LIIEN show good overall visibility with sharp color contrast, but not enough illumination enhancement in dark areas. Overall, the proposed algorithm shows good visibility of objects in dark areas and clear color contrast.

In Figure 5, we zoom in on the areas where dark and light areas appear together, and the images processed with LIME and LIIEN appear darker in low-light areas and distorted in bright areas. The images processed with dark light and RBMP show a significant improvement in the dark areas, but the resulting images have a dull color contrast. The images processed by the proposed algorithm do not show any color distortion, and the overall result has vivid tones and good visibility.

Visual evaluation shows that the resulting images from existing methods have inadequate illumination enhancement or color distortion. On the other hand, the resulting image of the proposed algorithm exhibits sufficiently improved brightness, sharp contrast of colors, and natural texture of the image.

4.3. Objective Evaluation

To objectively evaluate the performance of the proposed method, a quantitative evaluation is conducted on the resulting images. The methods used for quantitative evaluation are LOE (lightness order error), peak signal-to-noise ratio (PSNR), and structural similarity (SSIM) [25]. LOE is proposed to objectively evaluate the naturalness of an image and evaluate the change in illumination of an image by assessing the sequential change in brightness of the image. Smaller LOE values indicate a more natural brightness transition in the resulting images. PSNR is the most commonly used video quality metric and is measured in (dB). PSNR evaluates the difference between two images, with higher values indicating greater similarity and less distortion between the images. SSIM compares the brightness, contrast, and structural similarity between two images, with values ranging from 0 to 1; values closer to 1 signify greater structural similarity. Table 2, Table 3 and Table 4 show the LOE, PSNR, and SSIM results for the processed videos in Section 4.2.

Table 2. LOE score comparison of test image.

Image	Dark Light	LIME	RBMP	LIIEN	PM
LOL493	162.072	94.739	88.600	80.840	72.030
LOL665	150.877	111.682	77.145	69.061	49.115
LOL669	194.140	143.954	61.474	86.141	123.681
LOL778	192.890	123.611	112.848	80.802	83.162
LOL780	248.520	133.832	190.140	121.238	124.381
Average	189.700	121.564	106.041	87.616	90.474

Table 3. PSNR comparison of test image.

Image	Dark Light	LIME	RBMP	LIIEN	PM
LOL493	17.019	16.434	16.366	15.744	20.030
LOL665	11.027	9.832	13.550	9.874	12.680
LOL669	11.606	11.437	24.817	11.980	18.750
LOL778	13.859	13.046	15.305	13.083	16.410
LOL780	20.725	20.086	24.305	20.227	23.820
Average	14.847	14.167	18.869	14.182	18.338

Table 4. SSIM comparison of test image.

Image	Dark Light	LIME	RBMP	LIIEN	PM
LOL493	0.504	0.408	0.541	0.409	0.576
LOL665	0.321	0.265	0.393	0.255	0.378
LOL669	0.445	0.489	0.621	0.457	0.613
LOL778	0.464	0.406	0.513	0.400	0.570
LOL780	0.708	0.645	0.786	0.611	0.742
Average	0.488	0.443	0.571	0.426	0.576

In the quantitative evaluation, dark light shows a poor performance overall, with a mean value of 189.700 for LOE and a mean of 14.847 and 0.488 for PSNR and SSIM, respectively. Overall, the quantitative evaluation is inadequate for the resulting videos from LIME; in particular, the PSNR average shows the lowest value at 14.167. While RBMP has superior PSNR and SSIM, the average LOE value is 106.041, which is slightly insufficient for the proposed algorithm. LIIEN has superior average LOE values, but PSNR and SSIM values show low average values. The quantitative evaluation of the proposed method shows that the average LOE value is 90.474, the average PSNR is 18.338 (dB), and the average SSIM is 0.576, which are generally superior to the existing methods. Table 5, Table 6 and Table 7 show the quantitative evaluation using 485 images from the LOL dataset, 100 images from the VE-LOL-L dataset, and 360 images from the SICE dataset for objective evaluation. Table 5, Table 6 and Table 7 show the average LOE, average PSNR, and average SSIM for each dataset.

Table 5. Comparison of average LOE score.

Datasets	Dark Light	LIME	RBMP	LIIEN	PM
LOL	226.942	138.152	75.430	91.237	110.961
VE-LOL-L	235.419	145.717	93.062	106.850	121.055
SICE	209.528	207.543	102.662	77.526	143.723

Table 6. Comparison of average PSNR score.

Datasets	Dark Light	LIME	RBMP	LIIEN	PM
LOL	12.472	12.464	16.957	12.085	15.986
VE-LOL-L	16.333	16.148	18.249	15.232	18.666
SICE	11.044	12.821	15.664	12.589	16.030

Table 7. Comparison of average SSIM score.

Datasets	Dark Light	LIME	RBMP	LIIEN	PM
LOL	0.437	0.393	0.487	0.318	0.472
VE-LOL-L	0.553	0.500	0.547	0.394	0.542
SICE	0.419	0.459	0.505	0.460	0.529

When comparing the LOE values for each datasheet in Table 5, the proposed algorithm has superior results compared with those of dark light and LIME, and it shows natural luminance changes in the resulting images. However, the results are similar to or slightly higher than the results of processing with RBMP and LIIEN.

The PSNR comparison results in Table 6 show that the best results are processed by the proposed algorithm. In particular, the VE-LOL-L dataset shows improvements of 2.333 (dB), 2.518 (dB), 0.417 (dB), and 3.434 (dB) over the existing method, respectively, and the most similar results are shown for the control image.

SSIM, the proposed method in Table 7, shows the highest value of 0.529 on the SICE dataset, with improvements of 0.100, 0.070, 0.024, and 0.069 over the existing methods, respectively. The SSIM results of the proposed method are superior to the existing methods in most cases, and they produce the most structurally similar results to the control image.

4.4. Discussion

The proposed method uses histogram smoothing and Retinex theory for natural illumination enhancement. It estimates the illumination component of low-light images based on mean and distribution constants. Color correction using compensating channel selection in the RGB channel reduces color distortion and sharpens contrast, and non-local averaging based on a local steering kernel minimizes noise in the resulting image. The resulting images of the proposed method show clear and natural images, unlike the existing methods in the visual evaluation, and the best results are achieved in quantitative evaluations.

5. Conclusions

In this paper, we propose a technique based on Retinex theory and local steering kernel to improve low-light images. To effectively improve the low-light images and address the color mismatch problem, the proposed technique estimates the illumination component of the low-light images by using the mean and distribution constants, and the improved images are obtained by using the Retinex theory. Then, color correction is used to highlight the hue of the improved image, and a denoising algorithm based on the local steering kernel is used to obtain the final image.

To evaluate the performance of the proposed algorithm, low-light images from the LOL dataset are used to compare it to existing methods. In terms of visual assessment, the existing method improves the overall illumination of the resulting image and amplifies the pixel values in dark areas, revealing hidden objects. The results are superior to those of existing methods, exhibiting sharper color contrast and less distortion. Additionally, during the process of enhancing low-light areas, the proposed method effectively suppresses the amplified noise signals. For quantitative evaluation, the LOE method is used to compare the naturalness of the resulting images, and the proposed method shows improved results with lower LOE values compared with existing techniques.