A Trusted Federated Incentive Mechanism Based on Blockchain for 6G Network Data Security

Abstract

The machine learning paradigms driven by the sixth-generation network (6G) facilitate an ultra-fast and low-latency communication environment. However, specific research and practical applications have revealed that there are still various issues regarding their applicability. A system named Incentivizing Secure Federated Learning Systems (ISFL-Sys) is proposed, consisting of a blockchain module and a federated learning module. A data-security-oriented trustworthy federated learning mechanism called Efficient Trustworthy Federated Learning (ETFL) is introduced in the system. Utilizing a directed acyclic graph as the ledger for edge nodes, an incentive mechanism has been devised through the use of smart contracts to encourage the involvement of edge nodes in federated learning. Experimental simulations have demonstrated the efficient security of the proposed federated learning mechanism. Furthermore, compared to benchmark algorithms, the mechanism showcases improved convergence and accuracy.

1. Introduction

The sixth-generation network (6G) is considered the forefront of next-generation mobile communication technology and is expected to bring revolutionary breakthroughs in data transmission rates, latency, connection density, and more. Sixth-generation networks still encounter various challenges, including complex network structures and diverse application scenarios [1], all of which require interdisciplinary collaboration to address. 6G will support an even greater number of Internet of Things (IoT) devices, which are often susceptible to security vulnerabilities. IoT devices that are not adequately protected can become entry points for network intrusions, posing a threat to the overall network security.

The immutable nature of blockchain technology has provided a novel avenue for enhancing data security. For example, in securities trading, the immutability of historical transaction records can be ensured because each block contains the hash value of the previous block, creating a continuously connected chain. Once transaction data are written to the blockchain, they are almost impossible to modify or delete [2]. Essentially, blockchain is a distinctive chain-like data structure where each block is interconnected through the hash value of its parent block. It can be regarded as a distributed ledger, with each node in the network locally storing a copy of the same ledger, containing an unalterable series of data operation records. The emergence of new applications like the IoT has led to the generation of substantial data by smart devices, driving the advancement of artificial intelligence methods in wireless networks and related applications [3,4]. Federated learning (FL), as a prominent distributed machine learning framework, enables the training of data analysis models using data from various sources without revealing user data, thereby mitigating certain security risks associated with data sharing [5].

Federated learning allows models to be trained on local devices without the need to transmit raw data to a central server, thus preserving the privacy of user-sensitive data. In contrast to centralized learning methods, federated learning transmits only the updates to model parameters rather than the entire dataset, reducing the demands on network bandwidth and communication costs. However, during the model parameter aggregation process, some federated learning solutions treat all participants as trusted entities [6,7], where multiple participants share model updates or hold the same key. This approach can reduce applicability in real-world scenarios and can lead to security issues and privacy breaches [8,9]. In traditional federated learning, the cloud serves as a parameter server and then parallel model updates based on client-local data and global model aggregation occur on the server side. It is important to note that the communication link between devices (such as smartphones or other terminal devices) and cloud servers is relatively long, resulting in increased data transmission time, which directly impacts the efficiency of model aggregation. Additionally, in relevant scenarios, to prevent malicious clients from affecting the aggregation of global model parameters, cosine similarity is used to measure the trustworthiness of client devices. However, the complex cosine similarity calculation process leads to relatively lower efficiency in model aggregation [10,11,12].

In addressing the aforementioned issues, this paper makes the following contributions:

a.

The system ISFL-Sys has been designed, incorporating an incentive mechanism based on blockchain smart contracts and a reliable federated learning mechanism. Encouraging device nodes to participate in the training of model parameters through incentive mechanisms and iteratively updating local model parameters using ETFL federated learning mechanisms to ultimately update global parameters.

b.

Designing a lightweight and efficient trust scoring method with improved optimized Euclidean distance similarity metric is included. After standardizing local model parameters, measuring the similarity between the server model and local model updates using Euclidean distance effectively reduces the resource consumption during the similarity measurement process.

c.

Building the simulation platform and comparing the ETFL framework with the Vanilla FL framework and the FedAvg framework, ETFL still maintains a prediction accuracy of over 97%.

The rest of this paper is structured as follows: Section 2 includes the related work of the study and analyzes the technical solutions of some of the reference. Section 3 describes the procedural model of the paper, in which the various research points are presented. Section 4 is the experimental part, which compares several solutions and verifies the effectiveness of our solution.

2. Related Work

The sixth generation network (6G) is expected to bring further evolution to networking, supporting more complex applications such as smart transportation and smart cities. The rapid development of smart industries has led to a data explosion, and transmitting a large number of data samples can result in significant transmission latency [13]. Additionally, standard machine learning methods cannot guarantee user privacy and low-latency transmission. This has led to the introduction of federated learning, a distributed machine learning framework that collaboratively constructs a unified model through local training.

The concept of blockchain was initially introduced in the Bitcoin white paper [14]. Fundamentally, a blockchain is a unique form of a linked data structure, where individual blocks are connected to each other through the hash value of the preceding block [15]. As illustrated in Figure 1, each block is composed of two main parts: the block header and the block body. The block header contains information such as the hash of the previous block (previous block Hash), timestamp of submission, mining difficulty (nonce), Merkle root, and the version number of the block. On the other hand, the block body consists of a sequence of transactions that have been sorted. Each transaction includes multiple queries and modification operations related to attributes of business objects [16]. The data among blocks are linked through a chain-like structure to maintain the stability of the blockchain, while the data within each block are connected through a tree-like structure to ensure that transaction data remains unaltered and secure from tampering. Consequently, any attempt to modify the content of the blockchain necessitates substantial computational costs [17].

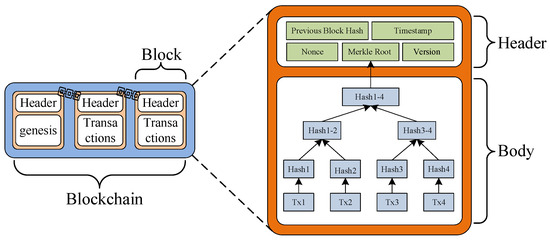
Figure 1. Schematic diagram of blockchain structure.

In the context of federated learning, the model parameter aggregation algorithm federated averaging (FedAvg) is mentioned in reference [18], and benefits from its simplicity and low communication cost, making it the preferred algorithm for federated learning (FL). However, experimental data demonstrate that certain specific distributions of device data can lead to the slow and unstable convergence of model parameters. In reference [5], the concept of distributing training data across mobile devices and learning a shared model through aggregating locally computed updates is introduced as a decentralized approach known as “federated learning” (FL). However, considering each client as a trusted entity in this approach leads to malicious participants uploading erroneous model parameters, thereby impacting the performance of the global model. Reference [19] introduces a three-tier collaborative FL architecture to support deep neural network (DNN) training. To address resource allocation issues among participating devices, the authors formulate a stochastic optimization problem to minimize FL evaluation loss. Nonetheless, due to the limited number of clients accessible by edge servers, inevitable training performance loss is encountered. In [20], the blockchain is integrated with FL to address data privacy concerns using blockchain’s trust and integrity guarantees. However, the trustworthiness of client devices is not adequately considered, leading to issues of abnormal devices affecting the accuracy of the global model. In another work, presented in reference [21], security and efficiency issues related to node participation in FL are addressed by proposing a blockchain-based secure incentive model. The detection of malicious nodes in this model employs a reputation-based node selection mechanism, which enhances security compared to the aforementioned approaches. Nevertheless, the computation resources required for calculating and verifying trust scores remain substantial.

Addressing the aforementioned issues, the proposed ISFL-Sys system establishes a distributed federated learning scenario based on blockchain. For the edge nodes within this scenario, they serve the dual roles of being both client nodes for federated learning training and nodes on the blockchain network. Leveraging the capabilities of blockchain technology, a distributed ledger is designed using a directed acyclic graph for local ledger storage of transactions in each edge node. Furthermore, ISFL-Sys integrates a novel incentive mechanism through blockchain’s smart contracts, specifically tailored for the federated learning context. This mechanism is designed to motivate device nodes to actively participate in the training process, resulting in increased training efficiency. During the model aggregation process, an innovative trust evaluation model is introduced. This model employs trust scores to effectively identify malicious clients, preventing intentional upload of erroneous model parameters by these malicious entities. This countermeasure safeguards the accuracy of the global model against potential degradation caused by malicious contributions. Within the trust evaluation model, a novel and optimized Euclidean distance evaluation method is proposed. This method reduces computational resource consumption while still providing relatively accurate trust assessment results. This optimized approach enhances the overall efficiency of the trust evaluation process. In conclusion, the ISFL-Sys system addresses the challenges posed by existing federated learning solutions by leveraging blockchain technology. It establishes a distributed learning environment, introduces an incentive mechanism, and employs a trust evaluation model to enhance security, efficiency, and accuracy in federated learning scenarios.

The detailed specifics of the ISFL-Sys system solution will be presented in the following sections.

3. Isfl-Sys Architecture

In this section, we will consider a distributed federated learning scenario that primarily involves several edge nodes. These nodes possess varying computational and storage resources, exhibiting significant heterogeneity. For each edge node, it serves not only as a participant in the federated learning process but also as a node in the blockchain. It assumes the responsibilities of model training in federated learning and transaction authentication, storage, and uploading in the blockchain context. In the aforementioned scenario, we introduce an asynchronous federated learning mechanism called ETFL. In the following sections of this section, we will elaborate on the overall architecture, incentive mechanism design, and the ETFL federated learning mechanism.

3.1. Overall Framework

As shown in Figure 2, a system named ISFL-Sys is designed. The overall architecture of the system consists mainly of the blockchain ledger module and the federated learning module within the edge nodes. In the following, we will provide a detailed explanation of the functionalities of each component.

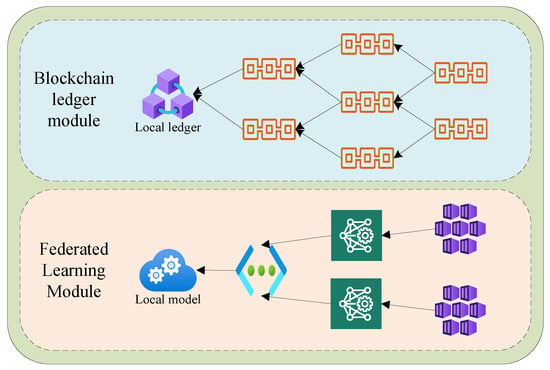
Figure 2. Architecture of the ISFL-Sys system.

The blockchain ledger module is primarily responsible for functions such as creating, authenticating, and publishing transactions within the system. Within each edge node, a ledger based on a local directed acyclic graph is maintained. This ledger is used to store transactions that the node can receive. The transactions store various pieces of information, including publishing nodes, authenticating nodes, and local models, among others, as shown in Figure 3. Within the system, different nodes can communicate with each other through wired or wireless networks, updating their local transaction information and broadcasting transactions to the rest of the nodes in the system.

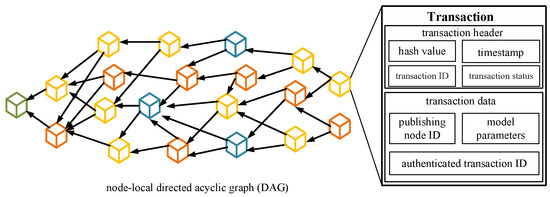
Figure 3. Node-local directed acyclic graph ledger and transaction structure.

Within the federated learning module, we introduce a novel and efficient trustworthy federated learning method named ETFL. This method incorporates a new federated learning aggregation rule. During the training iteration process, the security of client model parameters is validated by a trusted benchmark dataset model (server model) before being uploaded. After completing the training, the relevant information is packaged into transactions.

In this system, for the sake of managing the process of federated learning tasks, smart contracts in the blockchain can be utilized to control the system. By deploying smart contracts on the network, any node can act as an initiator for federated learning tasks, and by issuing rewards and other means, nodes actively participating in the training task can be incentivized, thus enhancing the enthusiasm of nodes within the network to engage in training, to prevent laziness and harmful nodes (engaging in poisoning attacks) from disrupting the learning task.

3.2. A Blockchain-Based Smart Contract Incentive Mechanism

In our proposed system, each edge node is required to invest its own computing and storage resources to participate in the learning process. However, this investment might not be cost-effective for edge nodes, potentially impacting their decision to engage in the learning process. To address this challenge, we introduce an incentive mechanism tailored for the current asynchronous federated learning scenario, aimed at enhancing the willingness of edge nodes to participate in the training.

3.2.1. Design of Smart Contracts

Unlike synchronous federated learning, where the parameter server can collect local models uploaded by each node in each iteration and distribute rewards based on global aggregation, asynchronous federated learning does not allow for global model aggregation or reward distribution. However, the incentive mechanism can achieve both model aggregation and reward distribution through smart contracts. In the ETFL architecture, a training task can be initiated by a specific node. Upon receiving the task initiation request, this node can bundle relevant information such as the initial model, reward distribution approach, task termination conditions, etc., into a smart contract. This smart contract will control the task process, including model submission for aggregation and reward distribution. Here, we primarily focus on reward distribution: During the training process, the smart contract constructs a directed acyclic graph ledger to collect transaction information published by nodes in the system. When the system’s iterations reach a certain point (e.g., after a specific time from the start of training), the smart contract will select transactions based on the local directed acyclic graph and distribute rewards accordingly. Once this reward distribution is completed, the currently selected transactions are cleared, and the process begins anew. The process of rewarding nodes can be determined based on the authentication status of transactions. In the case where transaction t is selected for reward distribution in this round and is allocated a reward of R, for this transaction, apart from the node that initiated the transaction contributing significantly to this particular transaction, nodes that authenticated the transaction will also have contributed to it. Consequently, the reward for this transaction will be divided into two parts: a reward for the transaction-initiating node and a reward for the authenticating nodes. These rewards are respectively assigned to the node that initiated the transaction and the nodes that authenticated it. This type of incentive mechanism not only encourages active participation of nodes in the federated learning training but also enables nodes to assist the system’s training process through authenticated transactions and earn rewards accordingly. This mechanism ensures that nodes with relatively limited computational power can also acquire substantial rewards from the system, enhancing their motivation to participate in learning and preventing training outcomes from being monopolized by nodes with higher computational power and larger datasets. The specific design of the smart contract process is as follows:

(1)

The node receiving the training task writes a smart contract within the system and broadcasts it to the network;

(2)

The smart contract periodically collects transactions within the system based on relevant configurations and selects a set of transactions with higher accuracy for this round of selection;

(3)

The models from the selected transactions are aggregated using federated aggregation algorithms, and the contribution of each node is assessed based on the transaction source and transaction validation;

(4)

Rewards are allocated to each node based on their contribution levels in accordance with their participation;

(5)

Upon achieving the preset expectations, the training is completed, and the smart contract concludes;

3.2.2. Reward Distribution

Transaction publishing nodes and authentication nodes each receive a portion of the reward for the transaction. Assuming that, after model aggregation by task-publishing node i, the training reward for this session is R, then for a certain transaction j containing models ${\omega }_j$, the reward that can be allocated to this transaction is calculated as follows:

$$R_j=\frac{F_i\left({\omega }_0\right)-F_i\left({\omega }_j\right)}{F_i\left({\omega }_0\right)-F_i\left({\omega }_i^t\right)}R,$$

(1)

where $F_i\left({\omega }_j\right)$ and $F_i\left({\omega }_i^t\right)$ are the loss function magnitudes of models ${\omega }_i$ and aggregated model ${\omega }_i^t$, respectively, contained in transaction j at task-publishing node i. For the initiating node of this transaction, it will be allocated a reward of $R_j/2$. As for the n transactions authenticated in this transaction, the publishing node k will receive rewards calculated as follows:

$$R_k=\frac{F_i\left({\omega }_0\right)-F_i\left({\omega }_k\right)}{2\left[F_i\left({\omega }_0\right)-\frac{1}{t}{\sum }_{t=0}^n{F}_i\left({\omega }_t\right)\right]}{R}_j,$$

(2)

where ${\omega }_k$ represents the model in the transaction submitted by node k, and ${\sum }_{t=0}^n{F}_i\left({\omega }_t\right)$ represents the sum of the loss functions of the selected and aggregated models in the transaction. The above reward distribution method takes into account both the cost of node participation in training and the cost of node authentication process. Furthermore, the reward allocation method is related to the node’s training results, encouraging nodes to publish higher-quality training results in order to obtain higher returns.

3.3. Etfl Federated Learning Mechanism

Prior to the ETFL training iteration, the server utilizes a benchmark dataset (an assuredly secure dataset) to maintain the server model. Throughout the training iteration, clients follow the procedure to carry out updates on their local model parameters, taking into consideration the contribution of their local model parameters using the server model. Existing FL methods focus solely on updating the global model through the local model updates from clients [22,23,24,25], excluding the process of assigning trust scores to client local models as in our approach. In contrast, ETFL simultaneously considers updates to the server model and client local models to update the global model.

In model attacks, malicious clients alter the direction and magnitude of model parameter updates, resulting in a detrimental impact on the global model in the opposite direction. Therefore, we arbitrarily define the magnitude of all model updates to be a fixed unit length, focusing solely on the differing directions of model updates. This mitigates the impact of local model attacks on amplitudes. ETFL utilizes the server model to evaluate the credibility of local models for allocating Trust Scores (TS), and ultimately updates the global model through a TS-weighted average. Specifically, ETFL iteratively follows the four steps outlined below, as depicted in Figure 4:

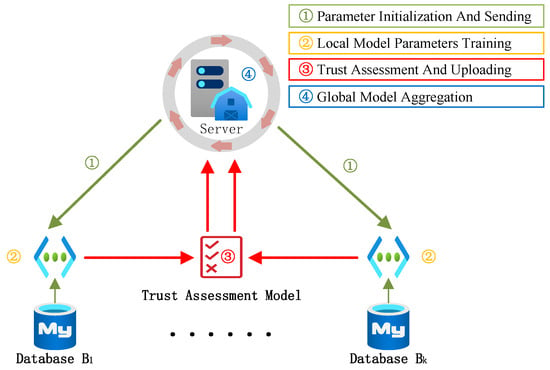
Figure 4. Iteration steps of ETFL.

(1)

Parameter Initialization and Sending: The server receives the initial model parameters ${\omega }_0$, such as weights and biases, and sends them to the client;

(2)

Local Model Parameters Training: In the t-th round of training, each node i trains the previous round’s model ${\omega }^{t-1}$ using its local dataset $D_i$ and calculates local model parameter updates ${\omega }_i^t$;

(3)

Trust Assessment and Uploading: Local model parameters are sent to the trust assessment model, and the model parameters that have undergone evaluation are uploaded to the server;

(4)

Global Model Aggregation: Based on trust assessment results, allocate aggregation weights to local model parameters, and maintain the global model.

3.3.1. Standardizing the Magnitude of Local Model Updates

In ETFL, we introduce a new aggregation rule for federated learning, where model updates can be seen as vectors containing both direction and scale. In this context, the Euclidean distance comprehensively measures the difference between vectors, accounting for both direction and magnitude. In our normalization approach, considering the limited computational resources of edge devices, we normalize and adjust the magnitude of each local model update. The specifics are as follows:

Artificially setting the magnitude of all model updates to a fixed unit length, focusing solely on differences in the direction of model updates, can effectively conserve significant computational resources. Therefore, our aggregation rule normalizes the magnitude of model updates when calculating the global model update, while also considering the direction of model updates. In a n-dimensional space, if there are vectors $x=\left(x_1,\cdots ,x_n\right)$ and $y=\left(y_1,\cdots ,y_n\right)$, then the Euclidean distance $d_{\left(x,y\right)}$ between these two vectors is defined as follows:

$$d_{\left(x,y\right)}=\sqrt{{\left(x_1-y_1\right)}^2+{\left(x_2-y_2\right)}^2+\cdots +{\left(x_n-y_n\right)}^2}=\sqrt{\sum _{i=1}^n{\left(x_i-y_i\right)}^2}.$$

(3)

The result’s range is not fixed and is influenced by the length, direction, and dimension of the vectors. In the above-mentioned approach, we use a fixed vector scale. Therefore, in the same dimension, the similarity between two vectors is only dependent on their direction.

3.3.2. Trust Scoring Method

(1) Cosine Similarity Evaluation Method: Common similarity measurement methods involve using cosine similarity between two gradients to quantify their directional similarity [26]. In an n-dimensional vector space, given two attribute vectors A and B, their cosine similarity is calculated based on their dot product and vector magnitudes, with the formula as follows:

$$similarity(A,B)=cos\left(\theta \right)=\frac{A·B}{∥A∥∥B∥}=\frac{{\sum }_{i=1}^n{A}_i\times B_i}{\sqrt{{\sum }_{i=1}^n{\left(A_i\right)}^2}\times \sqrt{{\sum }_{i=1}^n{\left(B_i\right)}^2}},$$

(4)

where the $A_i$,$B_i$ represent the respective components of vectors A and B. The resulting similarity ranges from −1 to 1, where −1 signifies that the two vectors point in completely opposite directions, 1 indicates that they point in exactly the same direction, 0 typically represents that they are independent (as in perpendicular), Values within the range of −1 to 1 represent the similarity or dissimilarity between the two entities.

To facilitate the understanding of the calculation method for two vectors in an n-dimensional vector space, Figure 5 illustrates the cosine similarity calculation method in two-dimensional and three-dimensional vector spaces.

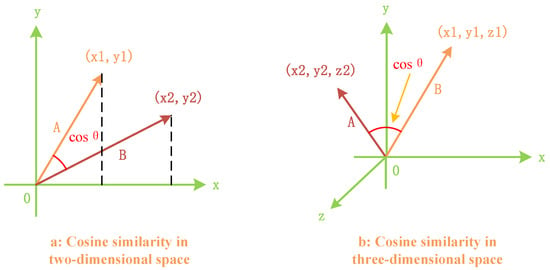
Figure 5. Cosine similarity evaluation method for vectors in two-dimensional and three-dimensional spaces.

As shown in the above figure, when the angle between two vectors is 0 degrees, indicating that their directions align perfectly, the cosine value is 1, signifying complete reliability. When the angle is 90 degrees, the cosine value is 0, implying no contribution to the global model aggregation and, hence, a lack of credibility. When the angle falls between 0 and 90 degrees, the cosine value is inversely proportional to the magnitude of the angle. Similarly, the obtained cosine value serves as a trust score.

To mitigate the negative impact of cosine similarity (resulting from reverse updates of model gradients), it is common practice to employ the Rectified Linear Unit ($ReLU$) function to clip the data range of cosine similarity. The final cosine similarity value obtained in this manner is referred to as the trust score. When the angle between the two vectors falls within the range of 0 to 90 degrees, the cosine value ranges from 0 to 1. Defined by the following formula,

$$T{S}_i=ReLU\left(c_i\right)=similarity(A,B),$$

(5)

$c_i$ represents the cosine similarity between the gradients of the two models in the i-th round, while $T{S}_i$ denotes the trust score for client updates of gradients in the i-th round. The cosine similarity values are constrained by the $ReLU$ function, as illustrated in Figure 6.

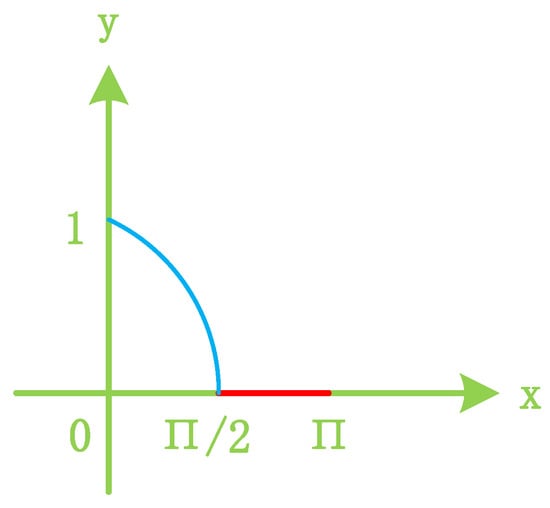
Figure 6. Clipping cosine similarity.

(2) Euclidean Distance Evaluation Method: A novel approach has been devised for assessing Euclidean distances, which measures the degree of similarity between two vectors. It is defined as follows: For two vectors with the same magnitude, the smaller the straight-line distance between their endpoints, the more similar the vectors are. In other words, upon standardizing the vectors’ magnitudes, the Euclidean distance becomes directly proportional to the size of the angle. Similarly to the previous explanation, our new Euclidean distance evaluation method is depicted in Figure 7.

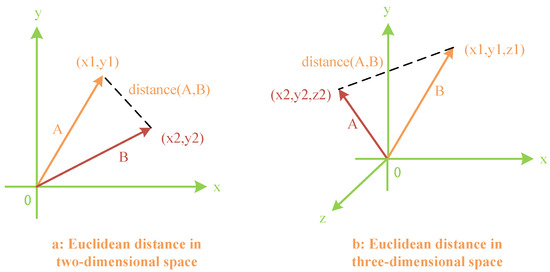
Figure 7. Euclidean distance evaluation method for vectors in two-dimensional and three-dimensional spaces.

Assuming that all normalized model gradient vectors involved in the evaluation have a magnitude of m, the maximum Euclidean distance between the server model and the client model is 2 m. To account for the potential malicious feedback caused by opposing model update trends, the same $ReLU$ function is used to clip the data range of the Euclidean distance. After removing the malicious models with reverse updates, the range of Euclidean distance values between the server model and the client model becomes $\left[0,\sqrt{2}m\right]$. The mapping relationship between Euclidean distance and model vector similarity is depicted in Figure 8.

Figure 8. Mapping relationship between Euclidean distance and model vector similarity.

Defining the actual Euclidean distance in the calculation as x and the maximum Euclidean distance as y, the trust score $TS\left(A,B\right)$ is calculated as follows:

$$TS\left(A,B\right)=distance\left(A,B\right)=1-\frac{x}{y}.$$

(6)

The trust score is when the Euclidean distance between the server model gradient vector and the client is 0 (minimum), i.e., the update direction is the same:

$$TS\left(A,B\right)=distance\left(A,B\right)=1-\frac{0}{\sqrt{2}m}=1.$$

(7)

The trust score for a Euclidean distance of $sqrt2m$ (maximum):

$$TS\left(A,B\right)=distance\left(A,B\right)=1-\frac{\sqrt{2}m}{\sqrt{2}m}=1-1=0.$$

(8)

In summary, when the Euclidean distance between the server model and the client model takes a range of $\left[0,\sqrt{2}m\right]$, the trust score $TS\left(A,B\right)$ takes a range of $\left[0,1\right]$.

3.3.3. Aggregate Local Model Updates

The server allocates trust scores for local model parameter updates based on the similarity with the direction of server model updates, where higher trust scores indicate higher similarity. After normalizing the model parameter update magnitudes, we employ our new method of Euclidean distance measurement to assess the consistency between the trends of two gradient updates. However, prior to these operations, we need to establish rules for the entire similarity evaluation, as when the angle between the vectors of the two model update gradients exceeds 90 degrees, it signifies malicious updates that could have a negative impact on the global model update. Thus, we further optimize the Euclidean distance similarity score and filter out malicious updates. The transformed Euclidean distance similarity becomes the required trust score. Finally, the global model is updated through a TS-weighted average. Defined by the following formula,

$$g=\frac{1}{{\sum }_{j=1}^{n}T{S}_j}\sum _{i=1}^{n}T{S}_i·{\overline{g}}_i=\frac{1}{{\sum }_{j=1}^{n}ReLU\left(c_j\right)}\sum _{i=1}^{n}ReLU\left(d\left(g_0,gi\right)\right)·K,$$

(9)

where g is the global model update, ${\overline{g}}_i$ is the standardized model parameters for the i-th client, and K is a constant parameter based on empirical common sense, depending on factors such as the speed of model convergence. Finally, we update the global model as follows, where $\alpha$ is the global learning rate:

$$\omega \leftarrow \omega +\alpha ·g.$$

(10)

3.3.4. Our ETFL Algorithm

The function ModelUpdate ($\omega$,D,b,$\beta$,R) in Algorithm 1 is utilized for computing model parameter updates through R iterations of stochastic gradient descent with a local learning rate $\beta$, as specifically referenced in Algorithm 2.

Algorithm 1 ModelUpdate($\omega$,D,b,$\beta$,R)

Output: Model update. 1: ${\omega }_0\leftarrow \omega$; 2: for  $r=1,2,\cdots ,R$  do 3:     Randomly sample a batch $D_b$ from D; 4:     ${\omega }_r\leftarrow {\omega }_{r-1}-\beta ▽Loss\left(D_b;\omega \right)$; 5: end for 6: end for 7: return ${\omega }_R-\omega$;

Algorithm 2 ETFL

Input: n clients with local training datasets $D_i$ , $i=1,2,\cdots ,n$; a server with root dataset $D_0$; global learning rate $\alpha$; number of global iterations $R_g$; number of clients $\tau$ sampled in each iteration; local learning rate $\beta$; number of local iterations $R_l$; and batch size b. Output: Global model $\omega$. 1: $\omega \leftarrow$ random initialization; 2: for  $r=1,2,\cdots ,R_g$  do 3:     // Step I: The server receives the initial model parameters and sends them to the client. 4:     The server randomly samples $\tau$ clients $C_1,C_1,\cdots ,C_{\tau }$ from $\left\{1,2,\cdots ,n\right\}$ and sends $\omega$ to them; 5:   6:     // Step II: Training client local models and server model. 7:     // (1)client local model. 8:     for $i=C_0,C_1,\cdots ,C_{\tau }$ do 9:         $g_i=ModelUpdate(\omega ,D_i,b,\beta ,R_l)$; 10:       Send $g_i$ to the server; 11:     end for 12:     // (2)server model. 13:     $g_0=ModelUpdate(\omega ,D_0,b,\beta ,R_l)$; 14:   15:     // Step III: Aggregating local model updates to update the global model. 16:     for $i=C_0,C_1,\cdots ,C_{\tau }$ do 17:         // A constant parameter based on empirical common sense. 18:         $\overline{g}$ = K; 19:         // Calculate the Euclidean distance. 20:         $T{S}_i=ReLU\left(d\left(g_0,gi\right)\right)$; 21:     end for 22:     $g=\frac{1}{{\sum }_{j=1}^{\tau }T{S}_{C_j}}{\sum }_{i=1}^{\tau }T{S}_{C_i}·{\overline{g}}_{C_i}$; 23:     $\omega \leftarrow \omega +\alpha ·g$; 24: end for 25: return $\omega$.

Algorithm 2 demonstrates our ETFL algorithm, divided into three steps over $R_g$ iterations:

I.

The server receives the initial global model parameters and sends them to the client;

II.

The client receives the global model parameters, trains its local model using local data, and uploads it to the server. Meanwhile, the server maintains server model updates based on the global model and reference dataset. Model updates are computed using the ModelUpdate($\omega$,D,b,$\beta$,R) function from Algorithm 1, combined with input parameters;

III.

The server maintains global model updates by aggregating local model updates and uses them to update the global model with a global learning rate $\alpha$.

4. Experimental Results and Analysis

4.1. Experimental Setup

The ETFL framework proposed in this paper is set up with the same experimental environment as the mainstream Vanilla FL framework and FedAvg framework, a simulation platform is built using PyTorch and based on which the effectiveness of our proposed federated learning mechanism as well as the incentive mechanism are verified. The experimental session uses FEMINIST, a benchmark dataset commonly used in federated learning, to implement an image classification task in a distributed environment.FEMINIST contains grayscale images of 62 different characters, with an image size of 28 × 28 pixels, and the number of samples is 805,263. The learning rate in the training of FL model is set to 0.01. The batch size (batch size) is set to 0.01, batch size is set to 10, and epoch is set to 5. In the following section, this paper will use the federated learning efficiency to evaluate the global model training efficiency of several different FL frameworks under the FEMINIST classification task, i.e., after a certain number of iterative rounds of training of the FL frameworks, the model exhibits the accuracy of the model after running the FEMINIST test set for one time, as well as the block generation efficiency and the block generation efficiency.

4.2. Global Model Training Efficiency

To evaluate the global model training efficiency of the proposed ETFL framework, in the following experiments, 0%, 5%, and 20% malicious nodes will be randomly set up in the ETFL framework along with the mainstream Vanilla FL framework and FedAvg framework, respectively, and the prediction accuracies of the global models under the FEMNIST dataset are recorded at the end of each iteration after 100 rounds of iterations.

As shown in Figure 9 and Figure 10, after 100 rounds of iterations, the prediction accuracy ACC of the global models of several FL frameworks under the FEMNIST dataset at the end of each iteration is recorded.

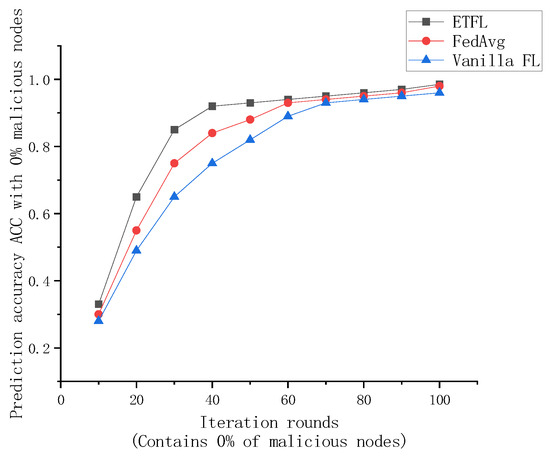
Figure 9. Comparison of global model accuracy in case of 0% malicious nodes.

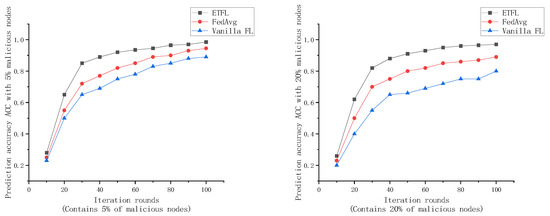
Figure 10. Comparison of global model accuracy for 5% and 20% malicious node cases.

As shown in Figure 9 and Figure 10, the global models trained by the three FL frameworks exhibit good prediction performance when all participating nodes are legitimate. At the end of the 70th iteration, the global models of all three frameworks achieve more than 95% prediction accuracy, but the three have different convergence efficiencies. For ETFL, since all nodes in the network participate in model training and the trust evaluation method used in this scheme consumes less arithmetic, it has the best learning performance in the absence of malicious nodes. However, for the case of containing 5% and 20% malicious nodes, ETFL’s scheme can still maintain higher security and accuracy in the presence of malicious nodes due to a trust scoring mechanism contained in the scheme. Thanks to the trust scoring mechanism, it can be observed from the above figure that as the number of training rounds increases, ETFL shows better stability because ETFL can effectively identify malicious nodes in the first 10–20 rounds as a way to reduce the negative impact of malicious nodes on the global model, and when the number of malicious nodes increases, the scheme’s trust scoring validation mechanism can be more effective in maintaining the global model’s training efficiency and robustness.

4.3. Training Effectiveness of the Global Model under the Incentive Mechanism

From Figure 11, it can be observed that when training for 100 rounds simultaneously, the scheme without the incentive mechanism involves edge nodes participating in the training process using a regular training mode, resulting in a slower convergence rate of the global model. On the other hand, the ETFL federated learning scheme with the incentive mechanism, as depicted in the graph, exhibits a faster convergence rate of the global model. The introduction of the incentive mechanism encourages edge nodes to participate in the training process more effectively, leading to better training results uploaded by the nodes. This enhancement improves the overall training performance of the system, and edge nodes also receive relatively better rewards, making them more willing to participate in subsequent training sessions.

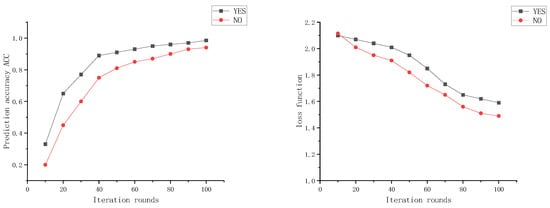
Figure 11. Incentive mechanism’s impact on model training results comparison.

4.4. Block Generation Efficiency

The 2nd task of evaluating the efficiency of federated learning is to analyze the efficiency of block generation in ETFL, which includes two parts: the efficiency of parameter validation and the efficiency of parameter aggregation. As shown in Figure 12, the validation time of ETFL is shorter than that of the other two FL schemes. This is because they do not optimize the validation mechanism. In contrast, ETFL is able to ignore part of the non-essential parameter evaluation process and achieve equivalent legitimacy verification. Thanks to the proof-of-contribution consensus mechanism, the verification time of ETFL will continue to decrease as the system continues to run.

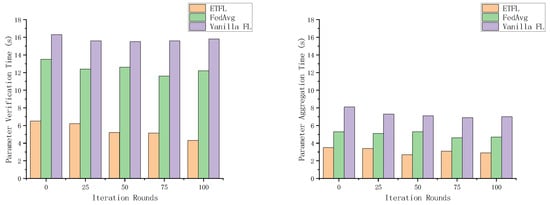
Figure 12. Parameter aggregation times for several scenarios for this.

As shown in Figure 12, in each iteration of the parameter aggregation process, ETFL adopts a contribution-based consensus mechanism to select the node with the highest contribution as the aggregator at the beginning of each iteration, which will greatly reduce the additional aggregation delay due to the mining competition during the block generation process, and exhibits a more excellent parameter aggregation efficiency compared to several other schemes.

4.5. Communication Complexity Assessment

The effectiveness of the incentive mechanism was tested by training on the FEMNIST dataset and the CIFAR-10 dataset. The results of comparing our proposed ETFL scheme with the Vanilla FL scheme, FedAvg scheme, and the FAIR scheme from reference [27] are shown in Figure 13. The iteration time of our ETFL scheme fluctuates around 22 s, significantly lower than the iteration times of FedAvg and the FAIR scheme. This is because of the effect of the incentive mechanism introduced in ETFL, which encourages nodes to participate in the training process, thereby reducing local training time and decreasing the time gap for local gradients to reach the server.

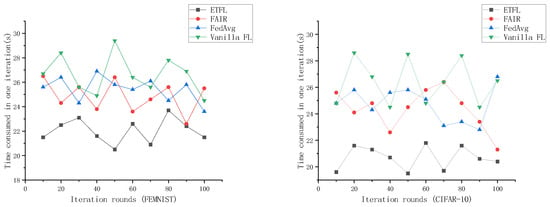
Figure 13. Comparison of one iteration time on FEMNIST Dataset and CIFAR-10 Dataset.

Simultaneously, we compared the training times for the ETFL scheme proposed in this paper, the Vanilla FL scheme, the FedAvg scheme, and the FAIR scheme when the model accuracy reached 95% on two different datasets, as illustrated in Figure 14. Due to the inclusion of an incentive mechanism in our approach, it facilitated node participation in the training process. Furthermore, the rewards provided to nodes encouraged them to upload more precise model parameters to the server, thereby reducing the time required for global model aggregation.

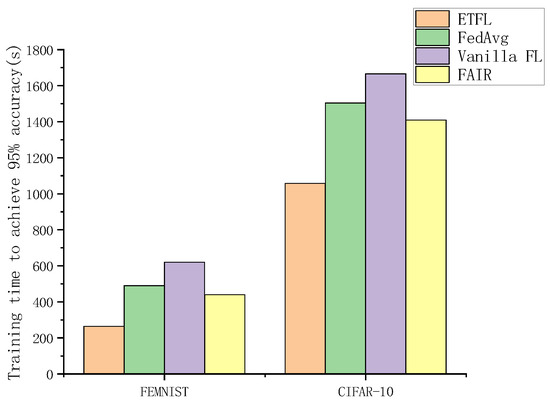
Figure 14. Training time to achieve 95% accuracy.

5. Conclusions and Future Work

In this paper, a system called ISFL-Sys is proposed, which comprises a blockchain module and a federated learning module. Within the blockchain module, an incentive mechanism based on smart contracts is introduced to boost the participation of edge nodes in training. A trusted federation learning mechanism for data security is designed in the federation learning module, which contains a new lightweight and efficient federation learning aggregation rule. Towards the end of the paper, a simulation platform is built using PyTorch. The results demonstrate that, in comparison with the Vanilla FL framework and the FedAvg framework, the predictive accuracy of ETFL continues to remain above 97%. In the future, further optimization of node selection schemes to reduce the workload of iterations will be explored. Privacy protection for model parameter gradients will be considered and more secure training strategies may be developed, possibly through the exploration of techniques such as homomorphic encryption and data augmentation algorithms.