Featured Application
The methodology presented in this paper can be applied to the design and evaluation of torque vectoring systems in hybrid electric vehicles. Comparison of different controllers is helpful in making design choices in these applications.
Abstract
In today’s automotive industry, electrification is a major trend. In-wheel electric motors are among the most promising technologies yet to be fully developed. Indeed, the presence of multiple in-wheel motors acting as independent actuators allows for the implementation of innovative active systems and control strategies. This paper analyzes different design possibilities for a torque vectoring system applied to an originally compact front-wheel drive hybrid electric vehicle with one internal combustion engine for the front axle and two added electric motors integrated in the wheels of the rear axle. A 14 degrees of freedom vehicle model is present o accurately reproduce the nonlinearities of vehicle dynamic phenomena and exploited to obtain high-fidelity numerical simulation results. Different control methods are compared, a PID, an LQR, and four different sliding mode control strategies. All controllers achieve sufficiently good results in terms of lateral dynamics compared with the basic hybrid version. The various aspects and features of the different strategies are analyzed and discussed. Chattering reduction strategies are developed to improve the performance of sliding mode controllers. For a complete overview, control systems are compared using a performance factor that weighs control accuracy and effort in different driving maneuvers, i.e., ramp and step steering maneuvers performed under quite different conditions ranging up to the limits.
1. Introduction
Electrification is a consolidated reality in the automotive sector. The use of electric motors (EMs) can have an impact on the energy efficiency of vehicles [1], but also create several interesting possibilities in terms of control. Especially when considering architectures with in-wheel motors (IWMs), the presence of EMs allows for the adoption of layouts with multiple power sources, a fact that would be unimaginable in vehicles with only internal combustion engines (ICEs). IWMs are widely discussed in the literature; however, owing to some important shortcomings, they are not yet an industry standard [2].
Direct yaw control (DYC) techniques such as torque vectoring (TV) are perfectly suited to electric vehicles’ (EVs) layouts with multiple motors, as they rely on the imbalance between the torques applied to the left and right sides of the vehicle.
The first technical applications based on this concept were implemented with the use of asymmetric brake action, actuated differentials, as well as rear axle steering systems; however, all these strategies have important limitations, which are in turn mitigated by the action of EMs. The TV system can guarantee improvements in terms of dynamic response. In particular, the control objectives in terms of lateral dynamics are to increase the maximum lateral acceleration of the vehicle, to extend the linear response region of the steering system, and to improve the responsiveness of the steering system [2].
Figure 1 shows the graph of the input steering angle () versus lateral acceleration () and how the curve is modified by the TV system action. The graph changes according to the achievement of the TV control goals.
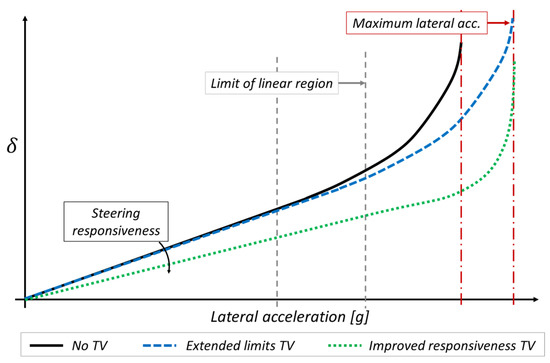
Figure 1.
Input steering angle () versus lateral acceleration ( ). The graph is changed by TV.
Some control strategies particularly suitable to tackle the TV systems issue are present in the relevant control literature, ranging from proportional, integral, derivative (PID) controllers [2,3] to model predictive control (MPC) [4,5,6] and sliding mode control (SMC) [7,8,9,10,11,12,13]. Although, in recent years, there has been a sharp increase in the number of new contributions that consider the TV control problem, there are still gaps in this area, particularly when considering hybrid electric vehicles (HEVs) for which torque allocation controllers usually address the issue of power management [1,14], instead of lateral dynamics. There are few examples of general comparison papers [15].
This paper considers as a case study an A-segment passenger vehicle containing an ICE in the front-wheel drive (FWD) layout, to which two independent EMs are added in each wheel of the rear axle, thus creating an all-wheel drive (AWD) architecture. The two EMs added to the rear axle are used to implement a DYC strategy. The P4 parallel hybrid vehicle (also called “parallel through the road”) is intended to both improve the handling and dynamic response of the HEV as well as give it better acceleration performance and enable better fuel efficiency management.
A first study on the subject was presented in [15], where a comparison between two controllers was performed, namely a PID strategy and a first-order sliding mode (FOSM). The two methods proved to be adequate for the set objectives in terms of overall handling; however, the FOSM exhibited pronounced chattering, which resulted in unacceptable vibrations that adversely affected the performance. In this paper, the PID control remains unchanged, while two different strategies are proposed to reduce the chattering in the FOSM, namely, the introduction of a low-pass filter and the replacement with a continuous approximation of the sign function are considered. To complete the discussion and comparison, a full-state linear-quadradic regulator (LQR) and two second-order sliding mode (SOSM) algorithms, the twisting algorithm [16,17] and the suboptimal algorithm [18], are also presented.
The 14 degrees of freedom (DoF) model of the vehicle is described in Section 2, while Section 3 presents the control strategies that have been considered. The main obtained results are discussed in Section 4. Finally, Section 5 provides some concluding remarks on the presented results and future developments.
2. Vehicle Modelling and Maneuvers
2.1. Vehicle Dynamics
The model used to represent the dynamic response of the vehicle is a 14 DoF model widely exploited and presented in the literature [19,20], an application of which can be found in [21].
The derivation of the 14 DoF model and its complete equations is beyond the scope of this paper. The 14 DoF of the model are briefly introduced below, corresponding to the scheme in Figure 2.
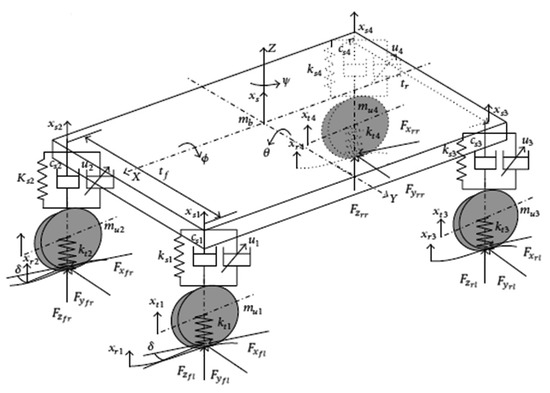
Figure 2.
Scheme and variables of the 14 DoF vehicle model.
- 6 DoF describe the free body motion of the vehicle sprung mass;
- 2 DoF for each of the four wheels represent the generalized position with respect to the body of the vehicle ζ (derived from the suspension kinematics) and the longitudinal slip of the tire.
The actual implementation of the model is performed using the CarRealTime software (CRT) from VI-Grade. CRT’s interface allows a complete description of the studied vehicle, including the characteristics of its many subsystems (steering, brakes, suspensions, body, powertrain, and so on). Being so, it is possible to analyze a fully non-linear response, especially when it comes to the limit driving conditions, with superior precision when compared with lower DoF mathematical models. The studied vehicle is based on the physical features of the Fiat 500, as shown in Table 1.

Table 1.
Parameters of the vehicle [15].
The vehicle model relies on custom damper, spring, and suspension curves; as far as tires are concerned, the appropriate Pacejka models are implemented, widely used in professional vehicle dynamics simulations [22]. The 14 DoF model, while suitable for the complete description of the vehicle’s motion and dynamics, is rather inconvenient during the implementation and theoretical calculations related to the control systems, owing to its complexity and inherent non-linearity. For that purpose, a simpler model is used in the preliminary phases of system setup, namely a 2 DoF bicycle model [19,20].
This widely known model considers the automobile as a single-track vehicle (collapsing the contribution of left–right wheels); Figure 3. It is valid under certain conditions such as small steering angles and linear range of the tires and it neglects some contributions such aerodynamic forces, suspension compliance, and load transfer.
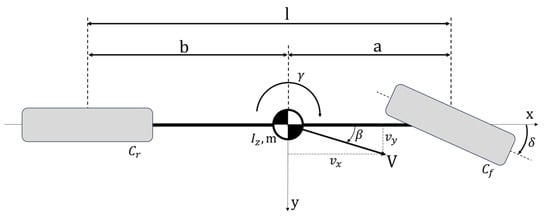
Figure 3.
Schematic representation of the 2 DoF bicycle model.
In the bicycle model, the 2 DoF used to describe the behavior of the vehicle are the side slip angle and yaw rate . By mild computations, which are not reported for the sake of brevity, the equations of motion can be written in a state-space representation as follows:
where the state vector x consists of the variables and , while the input vector u is made up of the steering angle at the wheels and the external yaw moment . The elements of the matrices A and B are calculated as functions of the physical parameters of the vehicle (as in Table 1) and of , which is the longitudinal velocity of the vehicle.
Notice that the used 2 DoF bicycle model has as one of the two inputs. This variable is not commonly present in the standard representation of the model. Its addition is particularly well suited for describing the effects of the TV, in which a yaw moment is generated as a consequence of left/right torque imbalance (dimension not present in the “mono-track” approach of the bicycle model).
2.2. Model and Torque Allocation of the Hybrid Powertrain
The components of the hybrid powertrain (PWT), as well as the control logic that defines the distribution between ICE and EMs, are shown in Figure 4, where each block represents a key element of the control system. This layout is presented in detail in [15], where a similar model is used for a preliminary analysis of the parallel hybrid P4 layout in the Fiat 500. The central idea of the system is that the imbalance between torques applied in the left and right wheel will create a yaw moment on the vehicle, which will be the main control action.
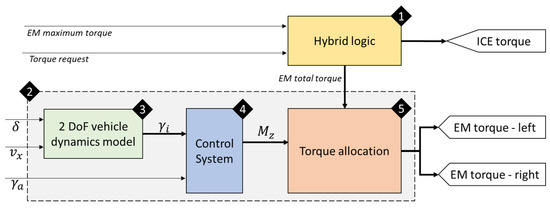
Figure 4.
Simulink model organized in different blocks and subsystems [15].
The interface chosen is a co-simulation environment between MATLAB/Simulink and VI-CRT. As displayed in Figure 4, the control system receives the torque request and EM limitations from the plant and, with the block “hybrid logic”, (1) decides on the best split between the front ICE and the rear EMs. The ICE torque request is directly sent to the plant again, while the overall EM torque request passes through the block “torque vectoring” (2), which will determine the split between left and right commands. Block (2) is then composed of three internal logic subsystems: the “bicycle model” block (3) calculates the ideal yaw rate using the 2 DoF handling model to estimate the yaw rate that a neutral vehicle would present in a given status of steering angle and velocity; then the block “control system” (4) obtains the reference yaw rate and compares it to the real yaw rate coming from the plant observation and, through the various proposed logics, defines the desired control action in terms of torque bias; finally, in the final “torque allocation” block (5), the total EM torque and the torque bias requests are combined to calculate the effective left and right torque requests for the EMs [15].
The ideal yaw rate is calculated by targeting the neutral understeer behavior characterized by an understeer coefficient with zero value. The ideal yaw rate can then be determined as follows:
The EM model is energetic, based on the maximum torque and power curves supplied by the manufacturer, as well as the efficiency map. Regarding the battery, a simple saturation strategy is put in place to restrain the current based on the series/parallel configuration of the cells and their maximum discharge rates and nominal voltage. The characteristics of the E-PWT are considered fixed for all values of state of charge and no thermal features are considered.
Some implementations of TV systems are based on the application of braking action. However, these strategies are less efficient because the braking power is dissipated (rather than regenerated). Being able to control each EM individually, this paper does not consider the actuation of the braking system as a control parameter.
After the definition of the individual torque requests, they are sent to CRT each with a timestep of 0.001 s, depicting all significant dynamic quantities. This timestep is also relevant to the dynamic response of the control system; all systems respond with the same overall frequency, even if, in a real application, some differences in refresh times and horizon would be expected.
2.3. Steering Maneuver
Let us now introduce the maneuvering conditions to which the vehicle is subjected to validate and compare the different control strategies under examination.
The first steering maneuver considered is ramp steering, in which the virtual driver linearly increases the steering wheel angle (SWA) at a slow rate and at the same time tries to keep the speed. Ramp steering requires a full range of lateral accelerations and limited throttle input to maintain the target speed, so it is suitable for TV validation and for assessing the quasi-static lateral behavior of vehicles.
The parameters used for ramp steering maneuver are shown in Table 2.

Table 2.
Ramp steering maneuver parameters.
At the start of the simulation and during the first 1 s, the steering is held at zero to allow the solver to stabilize. The final steering angle target is set above 1.0 g and above the expected road and tire grip limits; therefore, all configurations must be saturated and exhibit slip behavior by the end of the steering phase that occurs at 18 s. The simulation continues for another 2 s to fully show the nonlinear response of the vehicle.
Ramp steering shows a quasi-static lateral response; therefore, a more dynamic maneuver is chosen to highlight the transient behavior of the controlled vehicle, i.e., step steering. In this standard open loop maneuver, the driver quickly passes from a null steering condition to a fixed value, as described in Table 3. The step steering is repeated in two conditions: the first one far from the limit conditions with a steering angle of 50° (equivalent to a lateral acceleration of around 0.5 g) and the second one with a higher steering (80°) condition in which the actuators are saturated and the tires near the maximum grip.

Table 3.
Step steering maneuver parameters.
Figure 5 shows the imposed steering angle over time, in both the step steering and ramp steering maneuvers. The chosen maneuvers are open-loop, meaning that the driver inputs are predetermined and do not depend on the response of the system, which is particularly useful for a direct comparison of controllers.
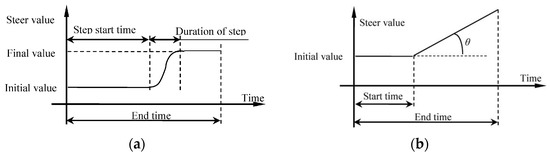
Figure 5.
Step steering (a) and ramp steering (b) maneuver definition.
The steering angle is used in (2) to compute the variation in the ideal yaw rate that serves as a reference for the control systems.
3. Control Systems and Performance Evaluation
The control strategies to be implemented and used to carry out the analysis and comparison are defined and briefly described below.
Four different control methodologies are considered, namely, PID, FOSM, LQR, and SOSM. The individual control strategies (apart from the LQR, which is a full-state control strategy) are implemented in a classic feedback control loop (Figure 6) based on the error between the actual and ideal yaw rate. The control action u in the specific case is the yaw moment induced by the torque bias between the left and right wheels.
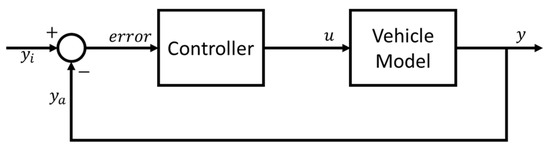
Figure 6.
Feedback control block diagram.
The HEV baseline corresponds to the system without torque bias, and it is obtained by setting the control signal to zero. The HEV baseline is without the TV active and is indicated as “OFF” in the following graphs. It is important to underline that, in the TV OFF condition, the rear motors are not idle, but are operated according to a P4 hybrid logic. In this case, the vehicle presents an AWD layout, with a 50% rear torque split for each side as in an open differential.
For all controllers, a minimum steering angle threshold of at the wheels is required to activate the TV system, to eliminate undesired oscillations in straight-line operation.
3.1. PID Controller
The PID strategy is a classic control, widely used in various sectors and applications, and represents the main control reference because its application on direct yaw control systems in the automotive sector is consolidated. The PID designs the control signal according to the following law (3):
where the PID parameters KP, KI, KD, and F are the gains of the proportional, integral, and derivative components, as well as the filtering frequency of the derivative term, respectively; γi is the ideal reference yaw rate; and γa is the actual yaw rate.
The used parameters values, established by a standard tuning phase evaluating the output performance in the different maneuvers to find an optimized performance, are presented in Table 4.

Table 4.
PID controller parameters.
As shown by [22], gain scheduling strategies are important during maneuvers with wide speed ranges; however, this is not the case of the proposed study. Furthermore, the work of [23] shows that adaptive PID controllers in DYC systems presents just marginal improvements with respect to fixed gain PID; therefore, a simpler fixed gain control is presented.
3.2. First-Order Sliding Mode (FOSM)
The FOSM controllers [24] are well suited to address the control of nonlinear uncertain systems [25]. In the design of an FOSM controller, a fundamental step is the definition of the sliding surface [24], S = 0, on which the trajectories of the controlled system must be steered in a finite time. For the considered TV control problem, the following sliding output (4) is defined:
The FOSM control law is then designed according to , where the control gain is a suitably chosen positive constant. The application of the FOSM control guarantees that the sliding surface is reached in a finite time.
Consider the 2 DoF system (1) [19,20]. Reaching the sliding surface in a finite time, i.e., S(t)→0 in a finite time, guarantees the stability according to Lyapunov’s theory as well as the achievement of the control objective for system (1).
The straightforward implementation of this SMC is presented in [15], performed by applying symmetric sign function. The work shows that, even though the simple FOSM can achieve the overall lateral performance for the system, it creates unacceptable vibrations to the system. The work also describes the effects of a delay and a hysteresis band, concluding that they are of small influence.
To attenuate the chattering effect and create suitable FOSM controllers for the proposed problem, two strategies were tested and are presented in this paper.
3.2.1. FOSM with a Low-Pass Filter
The first proposed technique is the inclusion of a low-pass filter after the sign function. As observed in [15], the output signal of the FOSM assumes a high-frequency oscillation behavior to maintain the steady-state control of the vehicle, thus the presence of a low-pass filter with a given dynamic response is expected to eliminate the discontinuity and improve stability and, on the other hand, to create a slower response owing to its inherent delay.
The implementation of the FOSM with the low-pass filter strategy is achieved through a relay function, imposing a zero-hysteresis system saturated at 100% of the maximum available torque bias. The sign function is placed in series with a low-pass filter with time constant equal to 1.2. The control law passing through the transfer function with an overall gain of 0.8 is given by (5):
3.2.2. FOSM with Continuous Approximation of the Sign Function
The second strategy studied to reduce the chattering and vibration problems created by the FOSM is the substitution of the sign function with an equivalent expression that is properly continuous. As proposed by [26] and implemented by [27] in relevant application, the following function (6) is used:
where S is the sliding output as in (4) and is a positive variable. Note that, as tends to zero, the function tends to the original sign function, while for high values of , the continuous function tends to zero, thus regulating the value of the constant can help improve the sharpness/smoothness of the control output.
It is also possible to consider an adaptive method for the definition of as in (7):
This strategy was tested in the studied system and no relevant advantage was observed, so the results refer to the simpler case with and no adaptive term.
3.3. Linear-Quadratic Regulator (LQR)
The linear quadratic regulator strategy is part of the optimal control theory, in which the control law is defined to minimize a cost function. This function is typically defined through a quadratic cost function as in (8):
where x is the state vector; u is the control vector; and Q, R, and N are the weight matrixes related to the system states, to the control inputs, and to the cross-contribution of x and u, respectively. The control law is defined by (9):
where K is the matrix that minimizes (8), defined by solving the continuous time Riccati differential equation.
The control law is like the pole-placement strategy, but instead of choosing the ideal poles of the system (not always a straightforward task), the challenge is to define relevant matrixes Q, R, and N to balance the state error and control effort. For the studied system, the used values of Q and R are as in (10), while no cross-contribution was included (N is null):
As the system state-space matrixes A and B are dependent on the vehicle’s speed, as defined in (1), so will be the results of K after the cost function minimization. Therefore, for the practical implementation of the LQR, the K matrix was calculated beforehand with a dedicated MATLAB script for a wide range of discrete velocities (from 1 to 100 m/s) and, during the simulations, the coefficients of the control were linearly interpolated from the closest neighbors of the actual vehicle’s velocity for each time step. This approach allowed for good precision of the control system without the requirement of excessive computational power.
Differently from the previous control systems PID and SMC, the LQR is a full-state control, meaning that the control gains and strategy use as input not a single error signal, but rather assume the availability of all of the relevant internal states of the plant. In the case of the DYC problem using the 2 DoF bicycle model, this means knowing not only the yaw rate as before, but in addition being able to observe the side-slip angle . The side-slip angle is a variable notoriously hard to directly measure, so its availability for an actual control system would depend on the estimation of the variable based on other output signals. This estimation is not the focus of this paper, so it will be assumed that is available with sufficiently high precision, as it is demonstrated to be achievable by some works present in the literature [28,29].
3.4. Second-Order Sliding Mode (SOSM)
The last control system category considered in this paper is the second-order sliding mode controllers. This kind of strategy follows similar principles to the FOSM, maintaining its typical features of robustness, but avoiding some of the main problems related to the chattering, which renders it suitable for evaluation in the case of DYC.
In the case of the SOSM, the definition of the sliding surface S can follow the same formulation as (4), being the difference between the real and target values of the yaw rate. However, in the second-order system, the proposed algorithms are such that not only the sliding output S tends to 0 in a finite time, but also its first time derivate [27]. Two algorithms are proposed to accomplish this condition.
3.4.1. SOSM Twisting Algorithm
The first algorithm proposed is the so-called twisting algorithm. This classical approach [16,17], implemented in relevant application [23], can effectively steer both S and to zero in a finite time.
The control law of the twisting algorithm [23], is defined by (11):
where and are control coefficients with .
To properly control the system, it is important to assure that and the ratio are sufficiently high.
In the present DYC, the values obtained are and after tuning the system. The fact that the control law (11) defines instead of u itself means that the typical discontinuities of the SMC systems are displaced to the derivative of the control input, not its direct value, theoretically reducing the issues related to the vibration induced by the FOSM.
3.4.2. SOSM Suboptimal Algorithm
The second algorithm that satisfies the conditions of the SOSM is the suboptimal algorithm [18]. In this version of the sliding mode, the control law is defined as (12):
where tMk is defined as the last moment in which . For the practical application of the simulation environment, in which the timesteps are small yet discrete, tMk is updated when there is a change of sign in the variation in S between two subsequent timesteps: S(t) − S(t − 1). The simulation begins with tMk = tM0 = 0, and thus S1(tM0) equals the initial value of .
The choice of the coefficient kr must be sufficiently high to guarantee stability [23]. In the studied application, the chosen value to satisfy such a condition is . To further reduce some of the residual chattering, known as the “ringing effect”, especially during the step steering maneuvers, the sign function was substituted with the continuous equivalent with a value of , as in (5).
3.5. Performance Evaluation
To properly compare the results of the control systems in an objective way, a performance indicator was applied. This performance factor (PF) is composed of three indexes:
- The control penalty (CP) is related to the effort of the controller in applying the control law, meaning that control systems that require more torque bias to stabilize the vehicle must be negatively evaluated.
- The error penalty (EP) directly evaluates the distance between the actual and target yaw rate during the maneuver, in such a way that less precise controllers are the most penalized.
- The timed error penalty (TEP) also takes into consideration the evolution of the error in time, meaning that controllers can afford a higher overshoot or initial displacement relative to the ideal behavior, if they are able to quickly eliminate the error. Steady-state error is heavily penalized in this indicator.
The three indicators are then normalized with respect to the reference value obtained by the original PID in the first step steering maneuver and combined through a weighted sum to compose a single performance indicator, as in (13):
4. Simulation Results
Simulations have been carried out for the case where no TV is applied and for all cases where the different control methods previously introduced and taken into consideration are applied, namely, PID, LQR, and the four versions of SMC strategies.
In the following section, the graphs of the obtained results are presented, which include control signals, vehicle state, and driver inputs labelled according to the following:
- The baseline HEV without TV (OFF);
- The PID controller (PID);
- The FOSM controller with the low-pass filter (FOSM lowpass);
- The FOSM controller with continuous function (FOSM continuous);
- The LQR (LQR);
- The SOSM controller with the twisting algorithm (SOSM twisting);
- The SOSM controller with the suboptimal algorithm (SOSM suboptimal).
The analysis of the graphic interface is useful for the interpretation of the results and for quick debugging and has been performed as the first step of the post processing. A pronounced understeering behavior of the baseline HEV could be found in all maneuvers; instead, all controlled versions are much closer together and can follow the desired yaw rate for much longer, confirming the overall good performance achieved by the control systems proposed. Let us now consider the main results of each maneuver.
4.1. 50° Step Steering
Figure 7 shows the graph of the right-side EM torque where it is possible to grasp the effect of the different control systems.
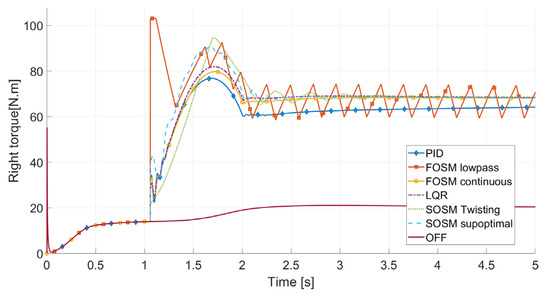
Figure 7.
The right-side EM torque during the 50° step steering.
The baseline plot shows the necessary torque requested to maintain the target speed during the maneuver, in this case applied in a balanced manner between left and right, while the other plots display the baseline contribution plus the bias.
FOSM lowpass shows the sharpest response after the threshold, quickly saturating the actuator at the beginning of the step and establishing a persistent oscillatory behavior, with a continuous signal but with a non-continuous derivative. This is an improvement with respect to the simple FOSM [15] with discontinuous control, but nonetheless it is expected to see a rough effect in terms of vibrations on the vehicle with such aggressive variations.
The actuation shape displayed by the PID, LQR, and FOSM continuous controllers are quite similar, with a first peak value followed by a stabilized steady-state contribution. The main difference between them is the intensity of the transient value, highest in the LQR and lowest in the PID. This difference is directly related to the optimized gains for each controller, which should balance promptness and stability.
The response of SOSM twisting is the slowest, achieving its peak only after 0.7 s, while SOSM suboptimal presents a prompt actuation after the beginning of the step. Both second-order SMC systems display sufficiently smooth and stable control outputs, as expected.
Regarding the main goal of the control systems, Figure 8 shows the yaw rate of the vehicle during the step steering and the error relative to the calculated ideal yaw rate.
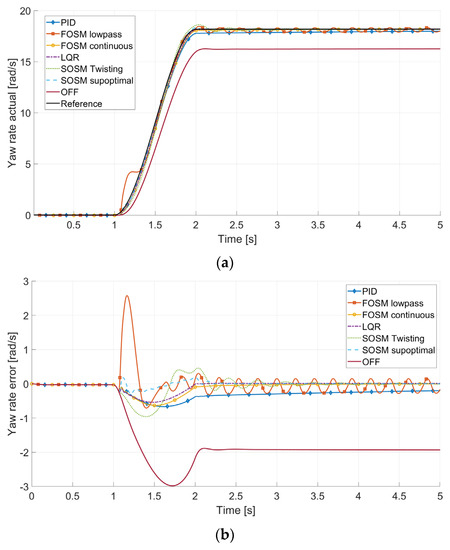
Figure 8.
Yaw rate (a) and yaw rate error (b) in the 50° step steering.
The relations between the control action and the yaw rate outcome are clear. FOSM lowpass presents a high overcontrol peak and a persistent vibration throughout the maneuver, while PID, FOSM continuous, and LQR display a similar shape of the response, even if it can be noted that the PID controller fails to guarantee a zero error in the 4 s after the step. SOSM twisting is relatively slow to respond and to stabilize while SOSM suboptimal is very precise, with the lowest maximum yaw error.
Figure 9 shows the lateral acceleration of the vehicle and its relation to the imposed steering angle, as in the goals presented in Figure 1.
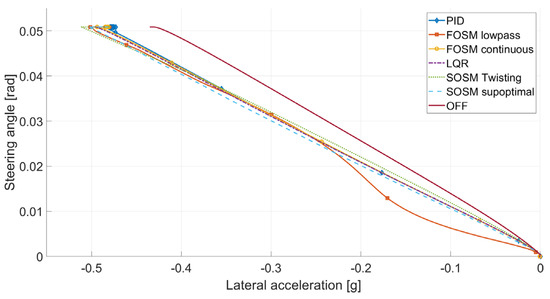
Figure 9.
Steering angle vs. lateral acceleration during the 50° step steering.
As expected, the baseline vehicle displays the lowest lateral acceleration in each steering condition. Apart from FOSM lowpass, all the other controllers create a similar outcome, with smooth and linear curves. The controller with the biggest impact on the understeering behavior is SOSM suboptimal, generating the most responsive dynamics; however, the difference between it and the second-best results (LQR) is of just shy of 3% lateral acceleration (at 0.04 rad/s steering) versus a 22% increase relative to the baseline.
4.2. 80° Step Steering
As opposed to the previous step steering where the controllers were able to achieve the yaw rate goal without (almost) never saturating the actuators, in a more challenging condition, this fact shall not hold any longer.
The equivalent results of torque and yaw rate can be observed in Figure 10 and Figure 11, respectively.
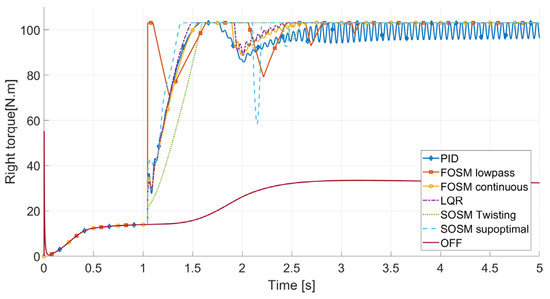
Figure 10.
Torque in the right-side EM during the 80° step steering.
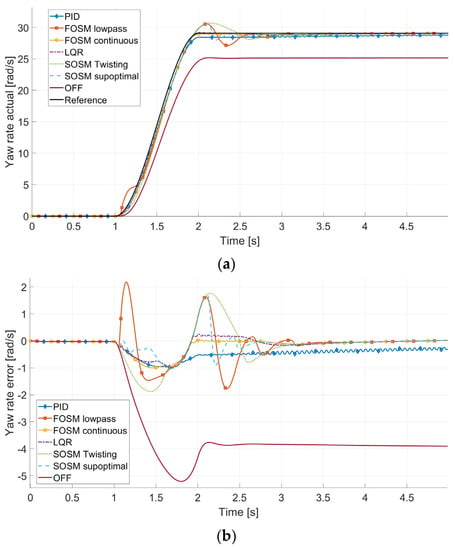
Figure 11.
Yaw rate (a) and yaw rate error (b) in the 80° step steering.
As predicted, the controllers take the right EM to its maximum torque value in all configurations around 1.5 s. Unlike the 50° case, in this condition, the most disturbed controller is the PID, displaying important oscillations after the completion of the steering action, most likely due to the integrative term combined with the saturated condition. FOSM lowpass instead reduced its vibrational behavior in the steady-state phase in the absence of the changing sign of the error signal. Once again, SOSM suboptimal is very responsive and quickly raises its torque level after the step input; however, this same promptness also affects its behavior after the saturation period, with a pronounced reduction around 2.2 s.
The best performing control systems in this case are LQR and the FOSM continuous, displaying a low maximum error and no significant overshoot or intense actuation vibrations.
All controllers except the PID successfully take the error to zero in the 5 s period. The PID controller continues to reduce the error very slowly, but the actuation vibrations jeopardize its performance.
4.3. Ramp Steering
The last maneuver studied is ramp steering, highlighting the steady-state response of the vehicle under a wide range of lateral accelerations.
As shown in Figure 12, the control systems present a first overshooting and slight vibrations (due to the initial threshold) followed by a linear ascending phase and a saturation around 12.5 s. Once again, the FOSM lowpass controller behaves poorly regarding the actuation smoothness, presenting quite accentuated vibrations before saturation.
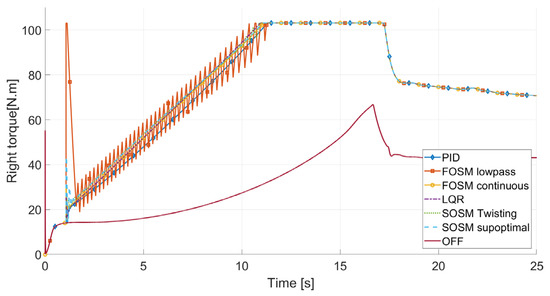
Figure 12.
Torque in the right-side EM during ramp steering.
Figure 13 displays the yaw rate and its error, while Figure 14 shows a zoomed-in section of the error plot between 0 and 14 s.
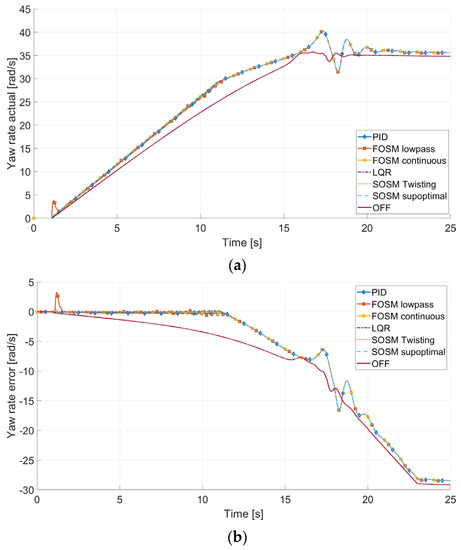
Figure 13.
Yaw rate (a) and yaw rate error (b) in ramp steering.
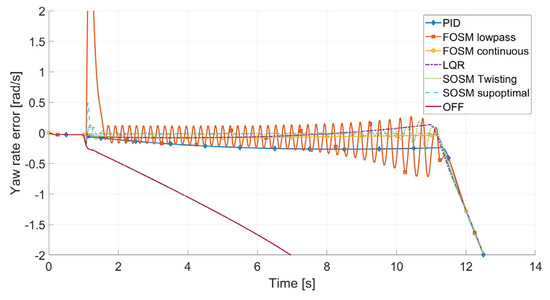
Figure 14.
Yaw rate error detail: zoomed-in region before saturation.
The controlled vehicles clearly change their behavior and follow quite well the yaw goal for the first part of the maneuver. After the saturation of the actuators, the controlled vehicles see their behavior move closer to the baseline version, as it is no longer possible to supply the required yaw moment to create a perfectly neutral vehicle.
At around 16 s, the baseline vehicle achieves its maximum lateral performance, as shown by the yaw rate peaking, corresponding to the reduction in the requested torque presented before. The same peak effect is displayed at around 17 s for all controlled systems, at a yaw rate of 40.3 rad/s vs. the 35.5 rad/s baseline.
After this peak, a highly non-linear response is observed, as expected, as the tires are no longer in their preferred working zone. It is hard to draw meaningful conclusions from the results after the tire saturation because the mechanical models tend to be much less precise.
A closer look at the first section of the maneuver allows for a more interesting discussion of the controller.
The plots confirm some previously stated conclusions, such as the high sensitivity and vibrational response of the FOSM lowpass controller; the quick settling time and prompt response of SOSM suboptimal; the PID controller with good transient behavior but finding it difficult to eliminate small steady-state error; the slower but smooth response of the SOSM twisting algorithm; and the similar smooth response of LQR and FOSM continuous.
Lastly, Figure 15 presents the lateral acceleration and steering angle.
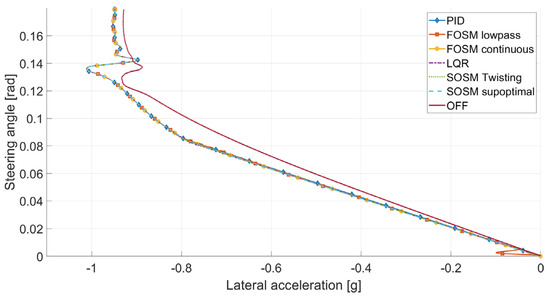
Figure 15.
Steering angle vs. lateral acceleration during ramp steering.
In Figure 9 and Figure 15, the advantage of all control systems over the baseline vehicle is clear. Higher maximum lateral acceleration and more responsive behavior can be observed in the plot. It is interesting to observe that the linearity goal is not completely achieved; in fact after the saturation of the EMs at 0.8 g, the slope of the plot changes significantly.
As can be noted in Figure 9, SOSM suboptimal exhibited more responsive behavior. In this case, the SOSM twisting and LQR controllers are much closer and have a higher lateral acceleration in several zones of the plot. This suggests that the SOSM suboptimal controller performs better in transient situations but gives no significant advantage in less dynamic conditions.
In [15], the constant radius corner condition was studied. In this paper, both of the presented maneuvers are open loop.
Finally, Table 5 shows, for comparison purposes, the numerical results obtained by the control systems considered in the three conditions studied and with reference to the proposed PF.

Table 5.
Numerical comparison of the control systems in the three conditions studied using the proposed PF.
The time considered for the step steering maneuvers is the total simulation time, while for ramp steering, the PF was calculated until 17 s of simulation, because, after that, the systems behave similarly, and the simulation precision is lower.
It is interesting to notice that the PID controller and FOSM lowpass generally display a lower level of performance than the other controllers, while SOSM twisting presents a good response in two simulations, but very poor performance in the 80° step. FOSM continuous, LQR, and SOSM suboptimal are the most consistent throughout the tested conditions.
5. Conclusions
In this paper, a comprehensive study of TV systems for an HEV based on different control methodologies was addressed. Analysis and comparison of the performances obtained were conducted using PID, LQR, and different SMC strategies for the TV applied to an FWD HEV with two electric motors integrated in the rear wheels. All the considered control architectures proved to be suitable for achieving the DYC objectives corresponding to increasing lateral acceleration and improving vehicle responsiveness. The extension of the steering linear region is conditioned by the saturation of the Ems, which generates the torque bias.
The chattering issue was encountered when plain FOSM was applied and it was successfully reduced by the proposed techniques, especially when the continuous FOSM algorithm was used. The best controllers with respect to the proposed PF were continuous FOSM, LQR, and suboptimal SOSM. Interestingly, the SMC with properly tuned control gains achieved performances very similar to those obtained by LQR, which theoretically should provide important advantages, being a full-state controller. The application of the SMC strategies with a continuous approximation of the sign proved to be particularly effective in terms of reducing the chattering as well as complexity of the controller, proving to be a valid option for the DYC.
Future work will be devoted to the development of TV systems for HEVs based on innovative and compliant SMC strategies, such as Simplex-based algorithms [25]. Attention will be paid to the inclusion of strategies based on MPC or machine learning, as well as to the experimental and DiL validation [30] of the obtained results.
Author Contributions
Conceptualization, H.d.C.P., M.C. and E.P.; methodology, H.d.C.P., M.C. and E.P.; software, H.d.C.P.; validation, H.d.C.P., M.C. and E.P.; formal analysis, H.d.C.P., M.C. and E.P.; investigation, H.d.C.P., M.C. and E.P.; resources, M.C. and E.P.; data curation, H.d.C.P.; writing—original draft preparation, H.d.C.P.; writing—review and editing, H.d.C.P., M.C. and E.P.; visualization, H.d.C.P.; supervision, M.C. and E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors want to acknowledge the support of the VI-Grade Italy team during the execution of the work and extend thanks for the availability of the simulation software used in its development.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carello, M.; Bonansea, P.; D’Auria, M. Driveline Optimization for a Hybrid Electric City Vehicle to Minimize Fuel Consumption. In Proceedings of the SAE 2014 World Congress & Exhibition, Detroit, MI, USA, 8–10 April 2014. SAE Technical Paper 2014-01-1090. [Google Scholar] [CrossRef]
- Pinheiro, H.D.C.; Messana, A.; Sisca, L.; Ferraris, A.; Airale, A.G.; Carello, M. Torque Vectoring in Electric Vehicles with In-wheel Motors. In Advances in Mechanism and Machine Science; Springer International Publishing: Cham, Switzerland, 2019; pp. 3127–3136. [Google Scholar] [CrossRef]
- Assadian, F.; Hancock, M. A comparison of yaw stability control strategies for the active differential. In Proceedings of the IEEE International Symposium on Industrial Electronics, Dubrovnik, Croatia, 20–23 June 2005; Volume 1, pp. 373–378. [Google Scholar] [CrossRef]
- Siampis, E.; Velenis, E.; Longo, S. Predictive rear wheel torque vectoring control with terminal understeer mitigation using nonlinear estimation. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 4302–4307. [Google Scholar] [CrossRef]
- Siampis, E.; Velenis, E.; Longo, S. Model Predictive torque vectoring control for electric vehicles near the limits of handling. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2553–2558. [Google Scholar] [CrossRef]
- Hu, X.; Chen, H.; Li, Z.; Wang, P. An Energy-Saving Torque Vectoring Control Strategy for Electric Vehicles Considering Handling Stability Under Extreme Conditions. IEEE Trans. Veh. Technol. 2020, 69, 10787–10796. [Google Scholar] [CrossRef]
- Goggia, T.; Sorniotti, A.; De Novellis, L.; Ferrara, A. Torque-vectoring control in fully electric vehicles via integral sliding modes. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3918–3923. [Google Scholar] [CrossRef]
- Canale, M.; Fagiano, L.; Ferrara, A.; Vecchio, C. Vehicle Yaw Control via Second-Order Sliding-Mode Technique. IEEE Trans. Ind. Electron. 2008, 55, 3908–3916. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Zhang, L.; Liu, M. Vehicle Stability Enhancement through Hierarchical Control for a Four-Wheel-Independently-Actuated Electric Vehicle. Energies 2017, 10, 947. [Google Scholar] [CrossRef]
- Xu, X.; Xiong, L.; Feng, Y. Torque Vectoring Control for Handling Improvement of 4WD EV. Adv. Mater. Res. 2013, 765–767, 1893–1898. [Google Scholar] [CrossRef]
- Chae, M.; Hyun, Y.; Yi, K.; Nam, K. Dynamic Handling Characteristics Control of an in-Wheel-Motor Driven Electric Vehicle Based on Multiple Sliding Mode Control Approach. IEEE Access 2019, 7, 132448–132458. [Google Scholar] [CrossRef]
- Tota, A.; Lenzo, B.; Lu, Q.; Sorniotti, A.; Gruber, P.; Fallah, S.; Velardocchia, M.; Galvagno, E.; De Smet, J. On the Experimental Analysis of Integral Sliding Modes for Yaw Rate and Sideslip Control of an Electric Vehicle with Multiple Motors. Int. J. Automot. Technol. 2018, 19, 811–823. [Google Scholar] [CrossRef]
- Zehetner, J.; Horn, M. Vehicle dynamics control with torque vectoring and active rear steering using sliding mode control. IFAC Proc. Vol. 2007, 40, 1–8. [Google Scholar] [CrossRef]
- Carello, M.; Pinheiro, H.D.C.; Longega, L.; Di Napoli, L. Design and Modelling of the Powertrain of a Hybrid Fuel Cell Electric Vehicle. SAE Tech. Pap. Ser. 2021, 3, 2878–2892. [Google Scholar] [CrossRef]
- de Carvalho Pinheiro, H.; Punta, E.; Carello, M.; Ferraris, A.; Airale, A.G. Torque Vectoring in Hybrid Vehicles with In-Wheel Electric Motors: Comparing SMC and PID control. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Levantovsky, L.V. Second order sliding algorithms: Their realization. In Dynamics of Heterogeneous Systems; Institute for System Studies Moscow: Moscow, Russia, 1985; pp. 32–43. [Google Scholar]
- Bartolini, G.; Ferrara, A.; Usai, E. Applications of a Sub-Optimal Discontinuous Control Algorithm for Uncertain Second Order Systems. Int. J. Robust Nonlinear Control 1997, 7, 299–319. [Google Scholar] [CrossRef]
- Milliken, W.F.; Milliken, D.L.; Metz, L.D. Race Car Vehicle Dynamics; Society of Automotive Engineers: Warrendale, PA, USA, 1995. [Google Scholar]
- Genta, G.; Morello, L. The Automotive Chassis: Volume 1–2; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Setiawan, J.D.; Safarudin, M.; Singh, A. Modeling, simulation and validation of 14 DOF full vehicle model. In Proceedings of the International Conference on Instrumentation, Communication, Information Technology, and Biomedical Engineering, Bandung, Indonesia, 23–25 November 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tyre and Vehicle Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2006. [Google Scholar]
- De Novellis, L.; Sorniotti, A.; Gruber, P.; Pennycott, A. Comparison of Feedback Control Techniques for Torque-Vectoring Control of Fully Electric Vehicles. IEEE Trans. Veh. Technol. 2014, 63, 3612–3623. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Bartolini, G.; Punta, E. Multi-Input Sliding Mode Control of Nonlinear Uncertain Non-Affine Systems with Mono-Directional Actuation. IEEE Trans. Autom. Control 2014, 60, 393–403. [Google Scholar] [CrossRef]
- Harashima, F.; Hashimoto, H.; Maruyama, K. Practical robust control of robot arm using variable structure system. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation Proceedings, San Francisco, CA, USA, 7–10 April 1986; pp. 532–539. [Google Scholar] [CrossRef]
- Menhour, L.; Lechner, D.; Charara, A. Sliding mode control to design a driver model for vehicle steering: Experimental validation and stability evaluation of sideslip motion. IFAC Proc. Vol. 2010, 43, 7–12. [Google Scholar] [CrossRef]
- De Martino, M.; Farroni, F.; Pasquino, N.; Sakhnevych, A.; Timpone, F. Real-time estimation of the vehicle sideslip angle through regression based on principal component analysis and neural networks. In Proceedings of the 2017 IEEE International Systems Engineering Symposium (ISSE), Vienna, Austria, 11–13 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Chindamo, D.; Gadola, M.; Bonera, E.; Magri, P. Experimental Comparison of The Two Most Used Vehicle Sideslip Angle Estimation Methods for Model-Based Design Approach. J. Phys. Conf. Ser. 2021, 1888, 012006. [Google Scholar] [CrossRef]
- de Carvalho Pinheiro, H.; Russo, F.; Sisca, L.; Messana, A.; De Cupis, D.; Ferraris, A.; Airale, A.G.; Carello, M. Active Aerodynamics through Active Body Control: Modelling and Static Simulator Validation. In Proceedings of the ASME 2020 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, 17–19 August 2020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).