Abstract
Trajectory planning is a crucial step in controlling robot motion. The efficiency and accuracy of trajectory planning directly impact the real-time control and accuracy of robot motion. The robot’s trajectory is mapped to the joint space, and a mathematical model of trajectory planning is established to meet physical constraints during motion and avoid joint coupling problems. To enhance convergence speed and avoid local optima, an improved quantum particle swarm optimization algorithm is proposed and applied to solve the mathematical model of robot trajectory planning. The trajectory planning in robot joint space is then tested based on the improved quantum particle swarm optimization algorithm. The results demonstrate that this method can replace the traditional trajectory planning algorithms and offers higher accuracy and efficiency.
1. Introduction
Efficient robotic trajectory planning is essential for the real-time control and operation of robots. It involves the generation of a robot’s trajectory in space, taking into account the initial and final motion states, such as position, velocity, acceleration, and jerk, while satisfying predetermined boundary conditions and constraints on velocity, acceleration, and jerk. There are different methods for trajectory planning, including Cartesian space and joint (driving limb) space [1]. In this paper, we focus on trajectory planning in joint (driving limb) space to avoid coupling problems that exist in Cartesian space trajectory planning. Trajectory planning can also be regarded as an optimization problem involving establishing a weighted objective function that considers motion energy consumption, actuator torque, jerk, and acceleration, and then employing corresponding optimization algorithms to solve it [1,2,3,4,5,6,7,8,9]. Many researchers have looked into the multi-objective hybrid criterion and proposed various multi-objective optimization methods for planning robot paths [10,11,12].
Typically, research on trajectory planning for robots involves optimizing a performance indicator that satisfies predefined constraints, such as time-optimal planning [13,14,15] and minimum jerk trajectory planning [16,17,18,19]. The common optimization method used is to construct a continuous acceleration change curve and optimize the selection of curve parameters to ensure boundary conditions and constraints on acceleration, velocity, and motion curve are met, and the optimal performance indicator is achieved. Some of the commonly used acceleration curve selections include a seven-segment step curve under zero initial and final acceleration condition, concatenated homogeneous polynomials, construction of conditional tree acceleration curve selection, cubic spline curve, and quintic B-spline curve [20,21].
However, the aforementioned optimization algorithms are limited by issues such as computing efficiency, which makes it impossible to achieve real-time planning of robot trajectories. As a result, there is a need for a highly efficient and accurate optimization algorithm. Quantum particle swarm optimization (QPSO) is an intelligent optimization algorithm that utilizes the principles of particle swarm optimization (PSO) and quantum computing theory [22]. The PSO algorithm has been applied to robot motion controller parameter optimization [23], and although it is highly effective in solving complex optimization problems, QPSO, like any other algorithm, has certain limitations. For instance, parameter selection, high algorithmic complexity, sensitivity to initial values, and the challenge of locally optimal solutions can be significant challenges. Consequently, many researchers have attempted to improve QPSO to overcome these shortcomings and develop more efficient and effective optimization algorithms that can meet the needs of various applications. As a result, many scholars have made corresponding improvements to QPSO in order to address these issues. These improvements have led to the development of more efficient and effective optimization algorithms that can better meet the needs of various applications. For example, QPSO, which dynamically adjusts the number of quantum bits and quantum rotation angles has been proposed to improve the algorithm’s convergence speed and global search capabilities [24]. Guoqiang Liu proposed a teamwork evolutionary particle swarm optimization algorithm (TEQPSO) that balances global search and local search. The TEQPSO algorithm can utilize the group information more effectively and improves the algorithm’s performance [25]. Jun Sun and Wei Fang proposed the quantum-behaved particle swarm optimization (QPSO) algorithm with the local attractor point subject to a Gaussian probability distribution (GAQPSO). The results show that the GAQPSO algorithm is an effective method that can greatly improve the performance of QPSO [26]. Baljeet Kaur presents an enhanced quantum-behaved particle swarm optimization (e-QPSO) algorithm, which improves the exploration and exploitation properties of the original QPSO for function optimization [27]. The self-organizing quantum-inspired particle swarm optimization algorithm (MMO_SO_QPSO) is another version of PSO for solving multimodal multi-objective optimization problems (MMOPs) [28]. Wang, Y et al. proposed a QPSO that adapts the number of quantum bits and quantum rotation angles to enhance the performance and robustness of the algorithm [29]. Liu et al. proposed a QPSO with dynamic parameter adjustment to enhance the algorithm’s global optimization capability [30]. Reference [31] proposes a quantum behavioral particle swarm optimization algorithm with adaptive parameter adjustment to improve the performance and robustness of the algorithm. Reference [32] proposes a quantum behavior particle swarm optimization algorithm with a dynamic learning strategy, aiming to improve the performance and adaptability of the algorithm. Jerzy Balicki conducted a many-objective quantum-inspired particle swarm optimization algorithm and confirmed that multi-objective quantum-inspired particle swarm optimization algorithms provide better solutions than other metaheuristics [33]. Arnaud Flori proposed a quantum particle swarm optimization (QUAPSO), which simplifies the setup of the algorithm by setting the velocity PSO parameter on top of the quantum superposition [34].
Based on previous research, the optimization degree of performance indicators in trajectory planning can be further improved by selecting Bernstein functions as the acceleration curve. In the actual application process, the order of the acceleration curve can be controlled according to the selection of Bernstein basis functions to ensure the smoothness of acceleration, velocity, and motion curves, thereby ensuring the smoothness of the robot motion process. Utilizing Bernstein functions can generate smoother motion trajectories, but the equations involve more parameters, thus increasing the difficulty of optimization. Therefore, the quantum particle swarm optimization algorithm (QPSO) has been improved to obtain the optimized parameters of the Bernstein function. The improved QPSO generates optimized acceleration, velocity, and motion curves to complete the robot trajectory planning process. This approach enhances the overall performance of the robot and improves its ability to execute complex tasks with precision and efficiency.
2. Improved Quantum Particle Swarm Optimization
2.1. Standard Particle Swarm Optimization Algorithm
Particle swarm optimization (PSO) is a heuristic group intelligence algorithm that iteratively evolves the entire population towards the position of the optimal solution with higher fitness. The location of the next generation of particle individuals is determined by their own information, such as the historical optimal location solution , social information, and the global optimal location solution .
In optimization problems, feasible solutions can be represented by the position of particles in n-dimensional space. Group X comprises m particles.
In the process of evolution, the position Xi(t) of particle i is:
Its velocity Vi is a vector with the same dimension:
At this time, the historical optimal position solution of particle is:
The global optimal location solution of the group is:
Then the particle’s speed and position update formula are:
In the above formula, represents the j-th dimension component of the parameters X, V, P, corresponding to the t-th iteration of particle i. and are the acceleration constant, used to adjust the length of learning step, and and are random number between [0, 1]. Xi,j is generally limited to range [Xmin, Xmax].
Based on the above iterative process of the PSO algorithm, inertia weight is introduced to improve the global or local convergence rate. The rewriting speed update formula is shown in Equation (8):
where the adjustment strategy of inertia weight is:
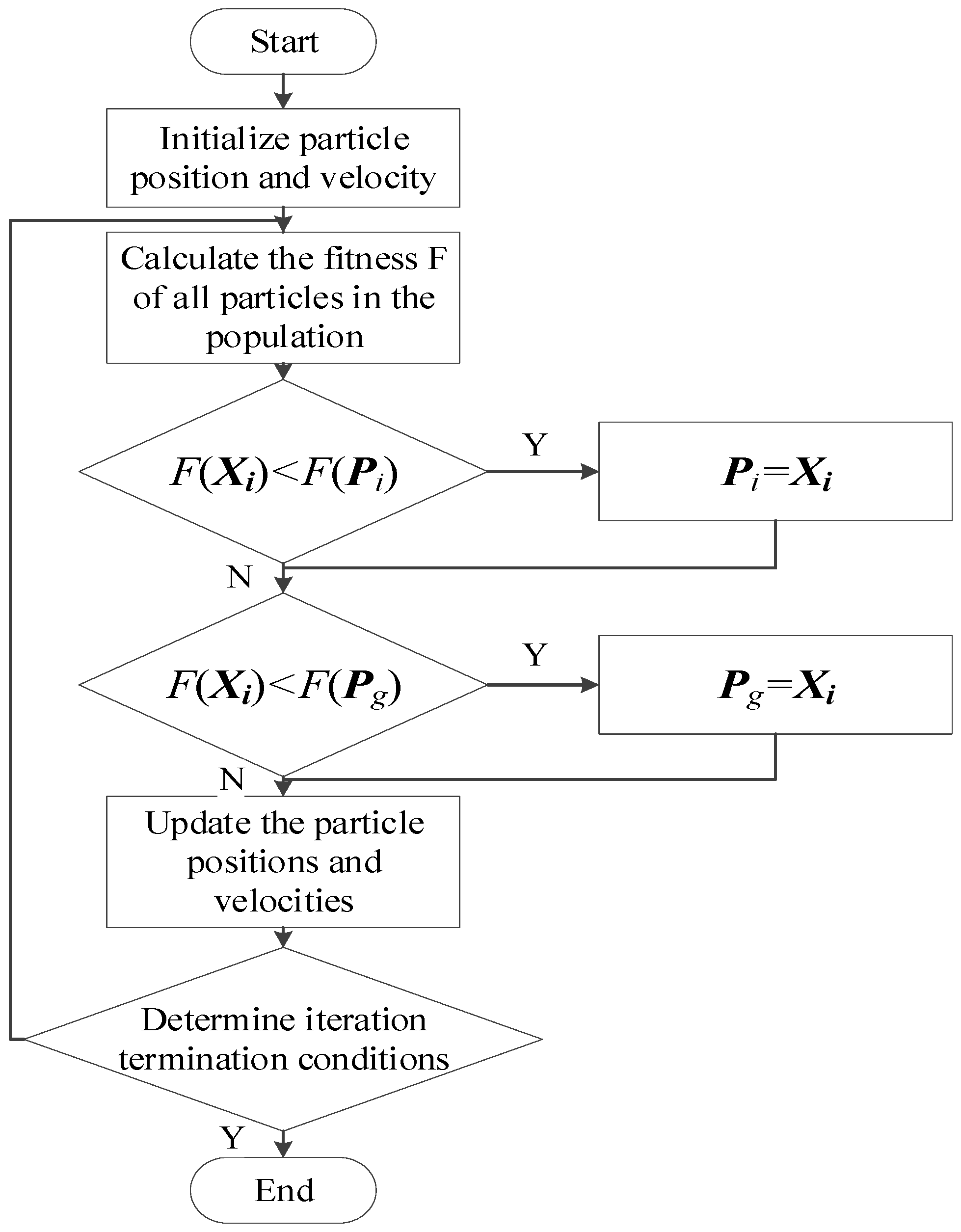
The iterative process as shown in Equations (7)–(9) is called the standard PSO algorithm flow, as shown in Figure 1.
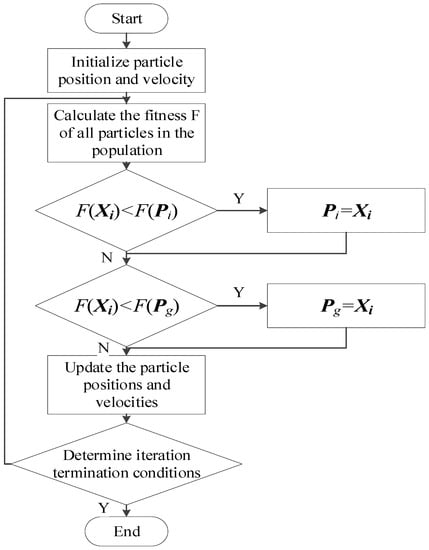
Figure 1.
Flow chart of the standard particle swarm optimization algorithm.
2.2. Quantum Particle Swarm Optimization
Let , and in the practical application of the algorithm, is generally taken, so that:
Then particle i is attracted by point during its iterative convergence. The parameter is a random value between and , and Equation (8) can be rewritten, as shown in Equation (11):
In the iterative process, the particles keep approaching and finally reach point p. This process can be regarded as the existence of attraction potential in the space where the particle swarm is located, which causes the particle to gravitate towards point p. Therefore, the random distribution of particles in space is avoided, and the convergence of the whole algorithm is guaranteed.
Under the mechanism of attraction potential, quantum particle swarm optimization (QPSO) is reconstructed based on the potential well in quantum theory to further improve the convergence and accuracy of the algorithm. According to Heisenberg’s principle, the observer cannot determine the position and velocity of particles at the same time. The velocity information and position information of particles are described by wave function and defined as the position of particles, as shown in Formulas (12) and (13).
where Q is the probability density function.
The position distribution of particles in quantum space satisfies the Schrödinger equation, as shown in Equation (14).
where is the Planck constant, is the Hamilton operator, is the potential field distribution in the space that the particle is located, and is the particle mass.
Generally speaking, the motion of a single particle in one-dimensional space is analyzed. The particle only has the degree of freedom in the x direction. Let the one-dimensional point of attraction be , , and define the potential field in the space where the particle is located, as shown in Equation (15).
where is the Dirac function.
Let , according to the spatial potential field distribution as shown in Equation (14), and rewrite the Hamilton operator as:
Set the particle in a steady state, and its probability density is independent of time, then:
The probability density function of the particle satisfies the Schrödinger equation as shown in Equation (18):
The wave function of a particle in one-dimensional space is:
Let , then the probability density function of the particle appearing at the designated point on the axis is:
Then its probability distribution function is:
Let obey the uniform distribution of .
Replace the probability density function with s, then:
By derivation, we can get
Therefore, the position renewal equation in the one-dimensional condition is shown in Equation (25):
Based on Equation (24), the position renewal equation is extended to a higher dimension, so the attractive point is rewritten as a vector form , and the potential well is constructed in each dimension. Then the wave function is shown in Equation (26):
The probability density function is shown in Equation (27):
Therefore, in the case of high dimension, the position update equation is as shown in Equation (28):
In the above iteration process, as the key parameter, can improve the efficiency of the algorithm and avoid falling into the local optimum by making it change adaptively with the number of iteration steps in the application. The general value is shown in Equation (29):
Among them, is the expansion–contraction factor.
In order to improve the efficiency and convergence of the algorithm, the center of all particle potential wells is used to replace the potential wells of a single particle . Therefore, the value of method is rewritten as:
It can be seen from Equation (11) that the position of the potential well is determined according to and , and Formulas (29) and (30) indicate that the updated example location is related to and . The further improvement of the algorithm focuses on the update process shown in Equations (11) and (30).
In the process of QPSO iteration, the parameter is set as inertia weight, and its value gradually decreases with the iteration process, which may lead to a premature fall into the local optimal value or affect the convergence speed. The adaptive method is introduced to improve Formula (11) and adjust the parameters dynamically. The group dispersion improved Formula (30) is introduced to ensure the diversity of the particle swarm, which can effectively solve the problem of local optimization or slow convergence.
2.3. Improvement for Quantum Particle Swarm Optimization
The evolution speed of individual particles is adjusted adaptively, and its definition is shown in Equation (32):
Equation (11) can be improved to
The evolution speed of an individual particle is determined by the ratio of the global historical optimal fitness to the individual’s historical optimal fitness, which changes dynamically in the iterative process. When the difference between individual optimal and global optimal is large, the ratio approaches 0. The updated attractive potential well is closer to the global historical optimal position, and the evolution speed is faster. While the difference is small, the ratio approaches to 1, and the evolution speed slows down.
The adaptive adjustment is made according to the group dispersion, and its definition is shown in Equation (34):
Then, Formula (30) is rewritten as:
The group dispersion also changes dynamically and tends to be 1 in the iterative process. Adding the adaptive variation of the group dispersion can ensure particle diversity and improve the algorithm’s convergence speed.
During the iteration, the position range of particles is limited according to the constraints. If the range of the updated particle position exceeds the limit, the particle position is reinitialized, and the value beyond the parameter range is set randomly within the limit. On the one hand, the algorithm avoids searching the invalid position and generating divergence; on the other hand, it resets the parameters randomly so that the population has a higher diversity, avoids the calculation falling into the local optimum, and improves the accuracy of the algorithm.
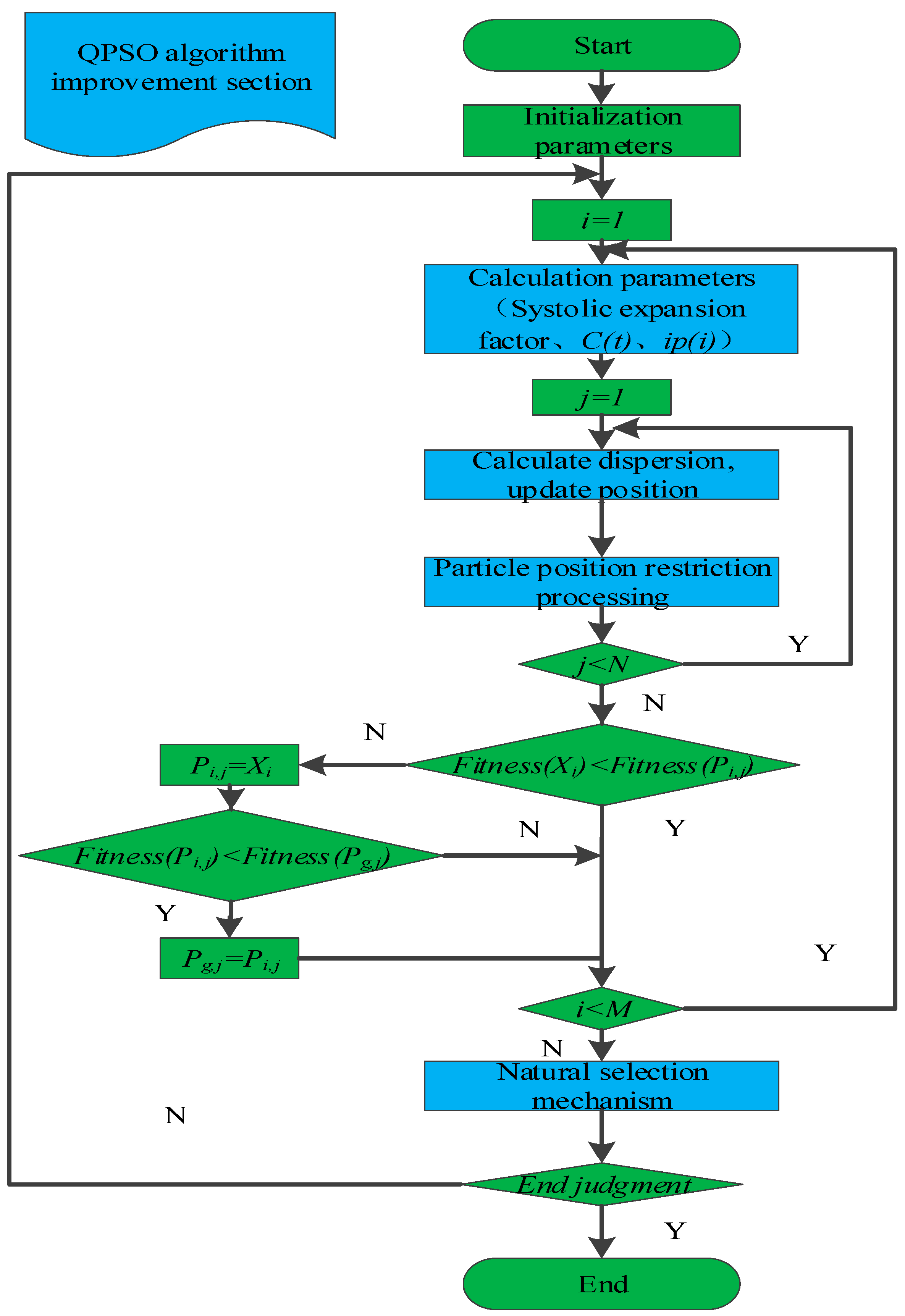
On this basis, a natural selection mechanism is added to the algorithm to eliminate the particles with the worst adaptability in the group and replace them with the particles with the best adaptability so as to improve the distribution of the whole particle swarm, improve the accuracy of the algorithm, and accelerate convergence. The improved QPSO algorithm flow is shown in Figure 2, the blue-filled part represents the QPSO algorithm improvement section.
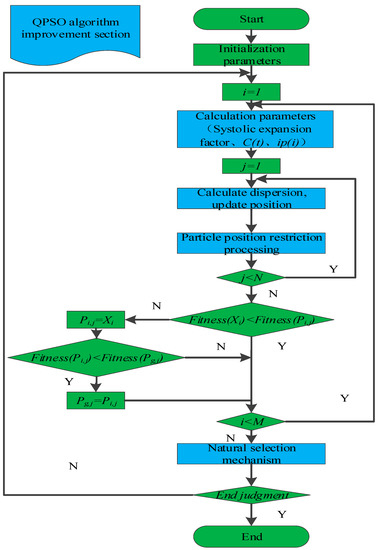
Figure 2.
Improved QPSO algorithm flow.
2.4. Example 1: Validation for Improved QPSO
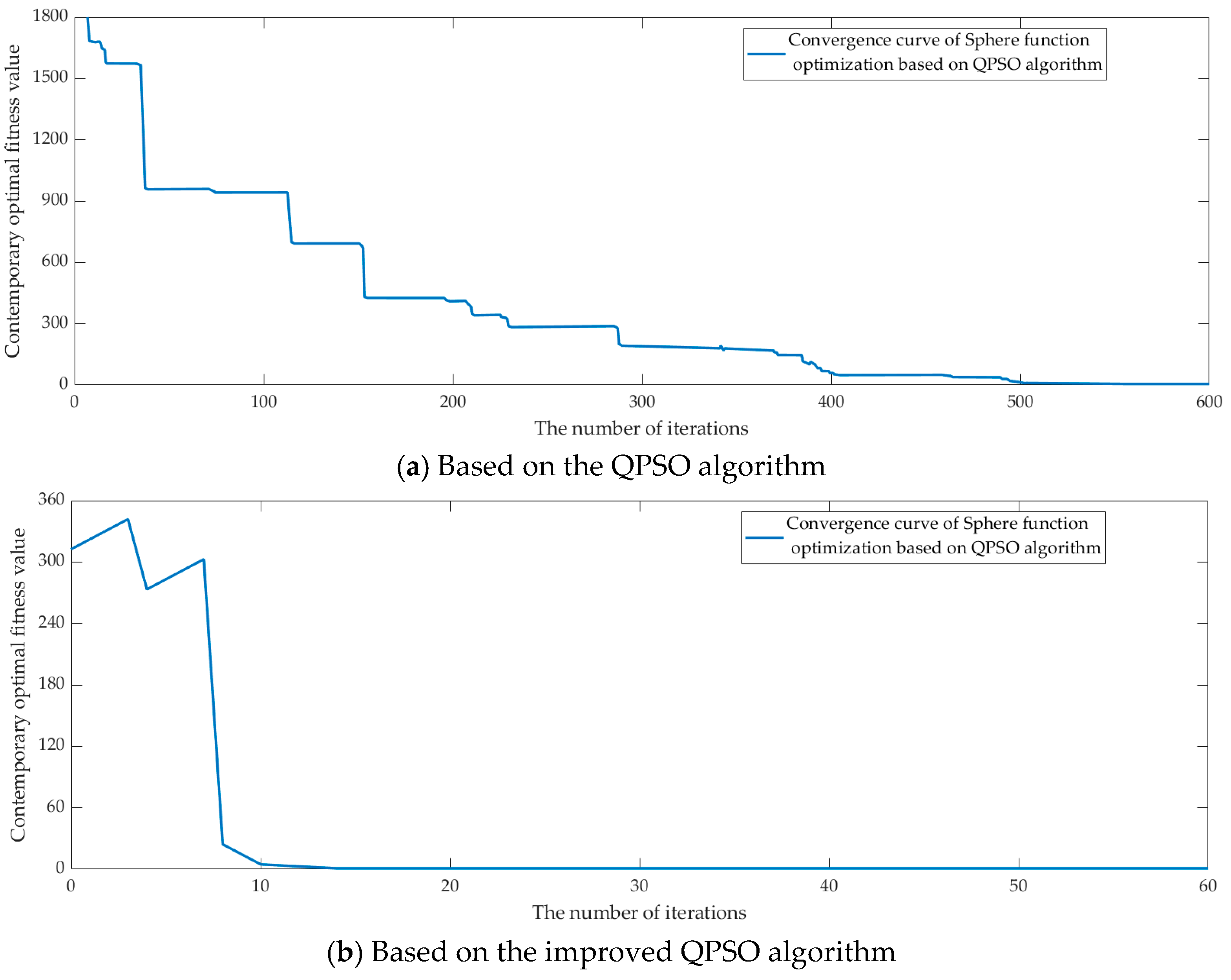
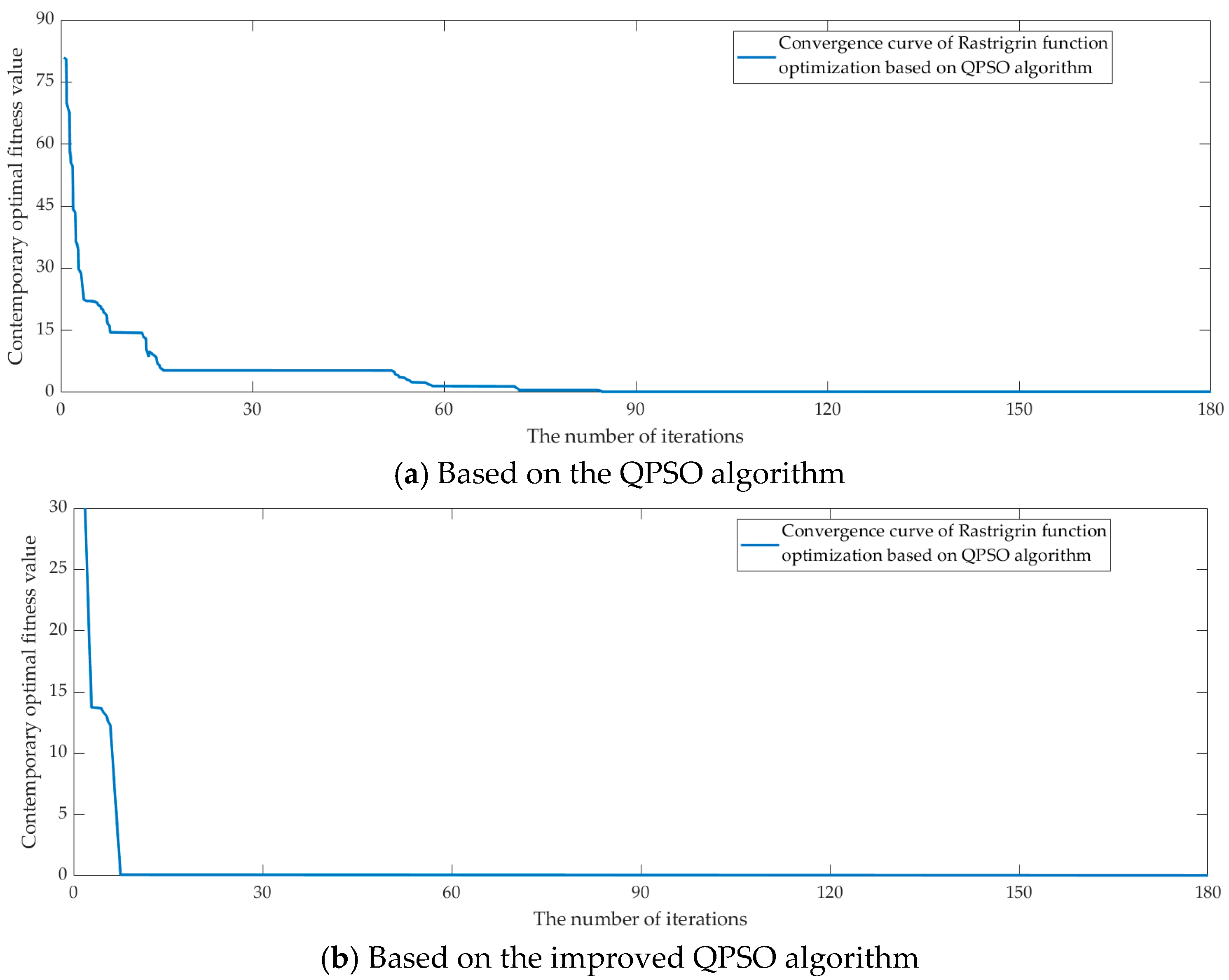
To evaluate the efficacy of the enhanced algorithm, experiments were conducted using the single-peak SPHERE function and multi-peak RASTRIGRIN function. The QPSO algorithm and improved QPSO algorithm were applied to optimize and solve these functions, and the convergence curves are presented in Figure 3 and Figure 4, respectively.
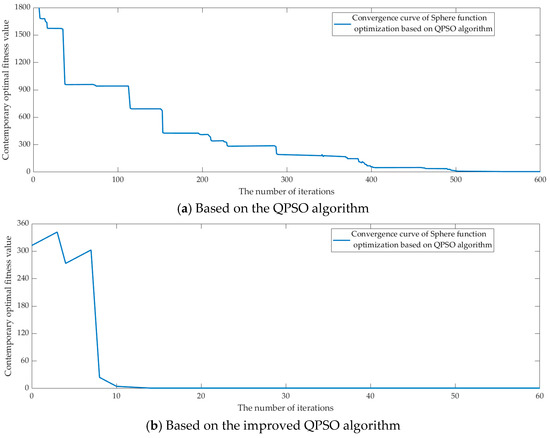
Figure 3.
Convergence curve of the sphere function optimization.
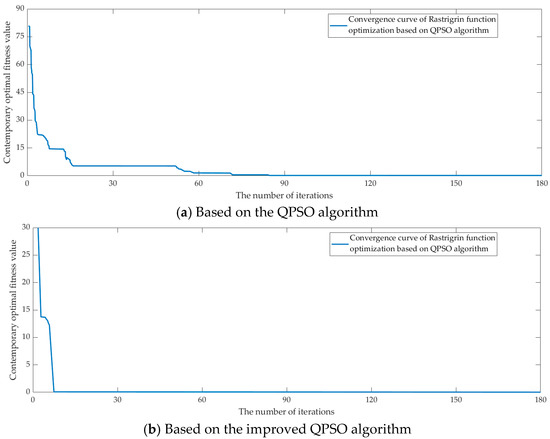
Figure 4.
Convergence curve of the RASTRIGRIN function optimization.
As illustrated by Figure 3 and Figure 4, the improved algorithm exhibits a noticeable improvement in convergence speed, reaching the optimal solution in fewer iterations. Moreover, it efficiently avoids becoming trapped in local optima for multi-peak function processing, highlighting the ability of the algorithm to maintain particle swarm diversity and avoid premature convergence.
3. Space Trajectory Planning of Robot Joint (Driving Limb)
The problem of the joint (driving limb) space trajectory planning pertains to the transition of a joint (driving limb) from an initial state to a target state within a specified movement time , while adhering to the speed , acceleration , and jerk constraints imposed by the robot joint (driving limb). For Point-to-Point (PTP) tasks, the trajectory planning parameters can be determined after the completion of joint (driving limb) space path planning, while for continuous path (CP) tasks, the parameters can be determined based on the corresponding processing parameters. As an optimization problem, the objective parameters of trajectory planning can include time and acceleration, among others, with the optimization goals being time-optimal trajectory optimization and minimum acceleration trajectory optimization.
In an in situ manufacturing processing system, the processing actuator is designed to be movable, which leads to dynamic coupling with the moving base. This can have consequential effects on the balance and stability of the actuator, ultimately impeding the processing effect of the entire system. To circumvent such undesirable effects, a reduction in the force between the actuator and moving base must be achieved, which can be accomplished by minimizing the acceleration in the process of joint (driving limb) movement, thus, making minimum acceleration trajectory planning the optimal goal of joint (driving limb) space trajectory planning in this domain.
Based on an analysis of a specific joint actuator, the preferred acceleration curve, which meets the desired conditions, is represented by a mathematical expression . The resulting mathematical model for joint actuator space minimum acceleration trajectory planning can be described using Equations (36)–(41):
The problem of trajectory planning is transformed into a function that conforms to the constraint Equations (37)–(41) to calculate the limit value of maximum . The corresponding speed and acceleration can be calculated by Equations (42) and (43):
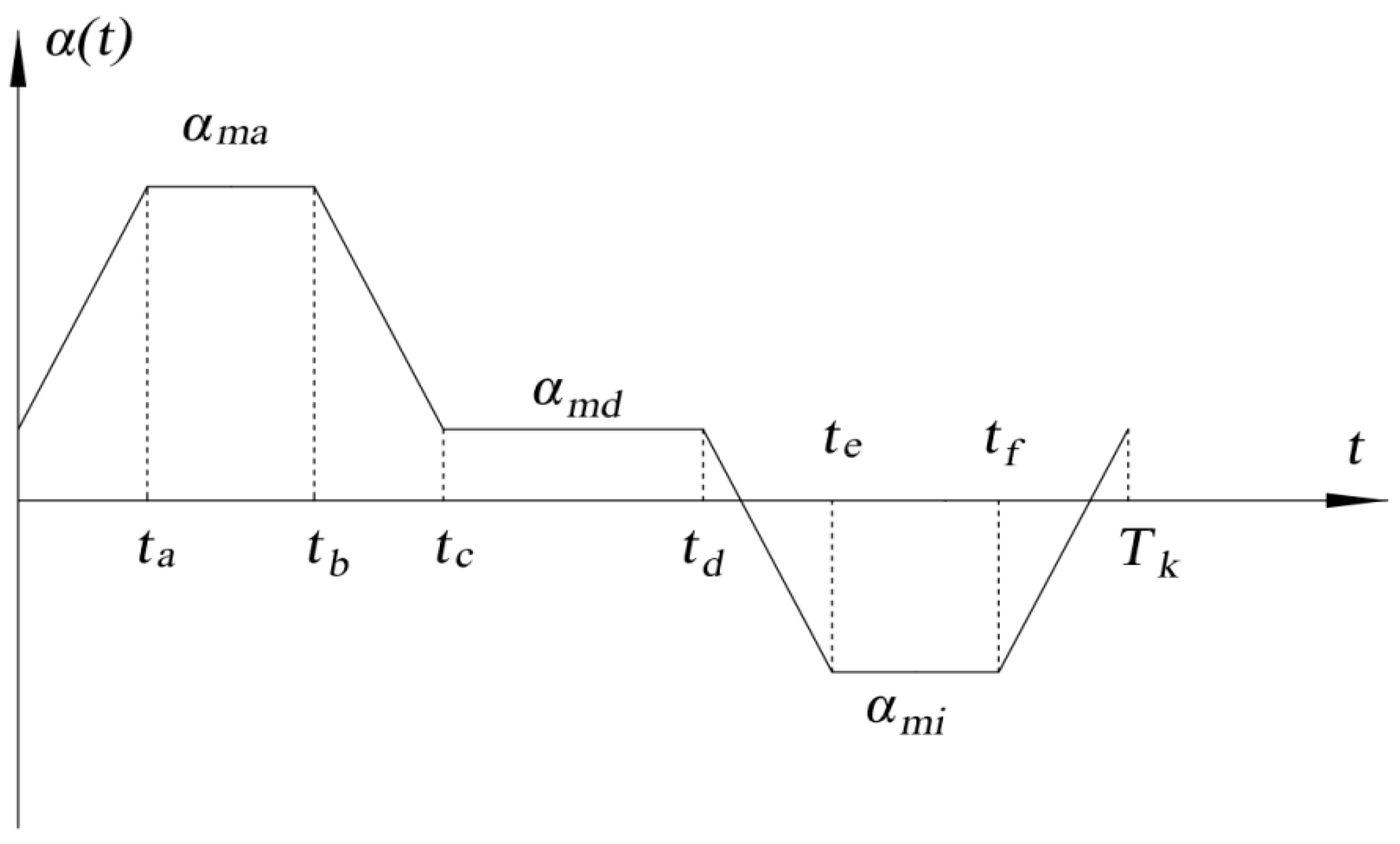
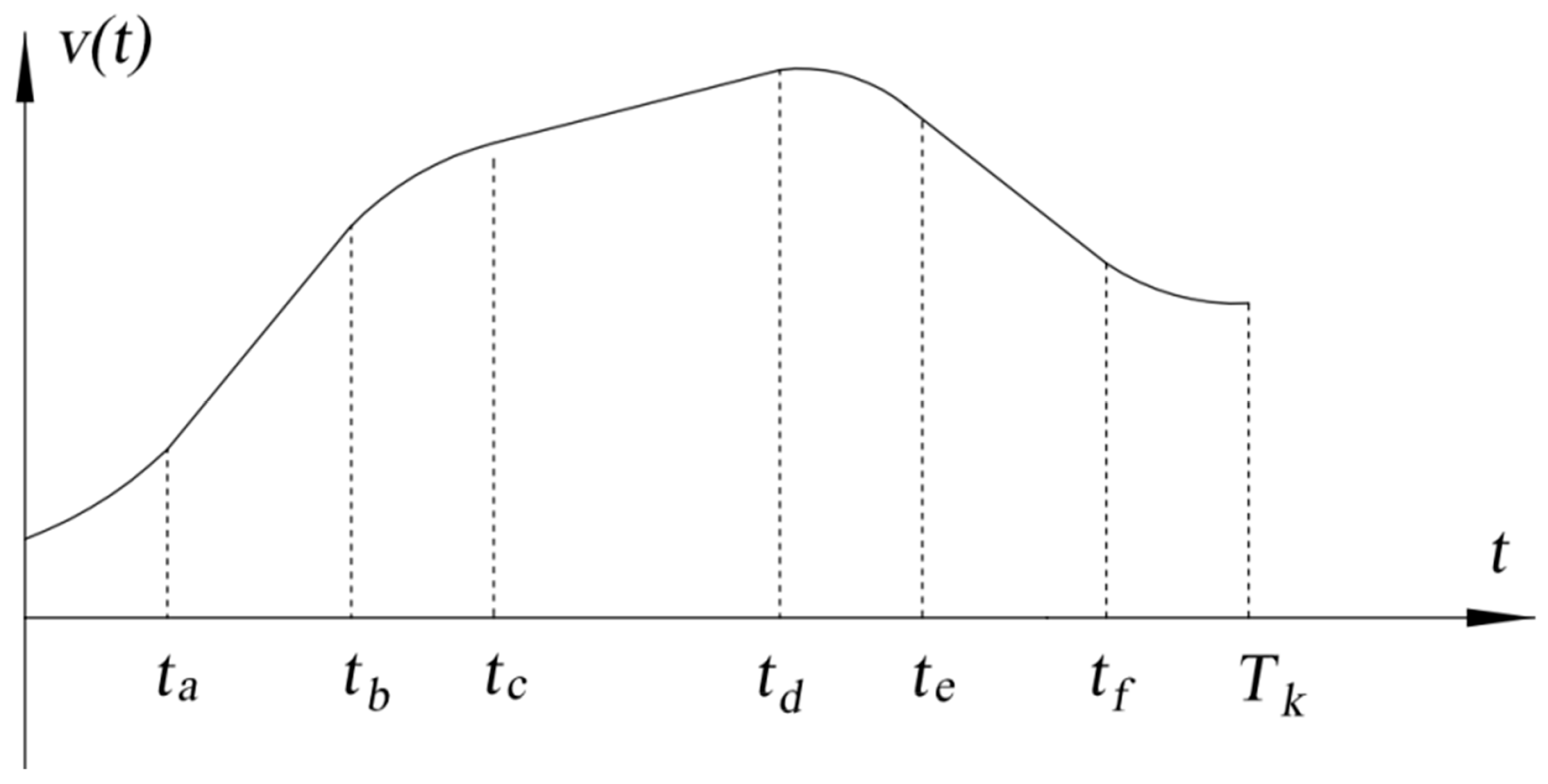
During planning, the acceleration curve is usually considered as a continuous piecewise linear function or continuous piecewise quadratic curve. To ensure the continuity and stability of the speed curve, the generated speed curve is generally or . Taking piecewise the linear function as an example, the acceleration curve is as shown in Figure 5, and the corresponding speed curve is shown in Figure 6.
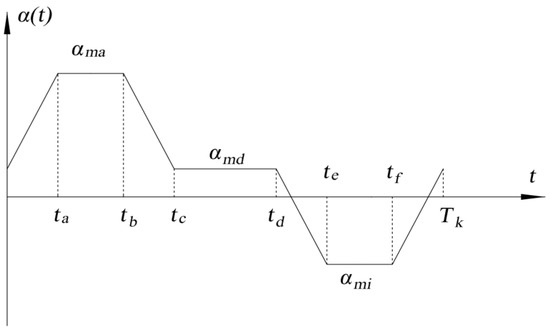
Figure 5.
Acceleration curve.
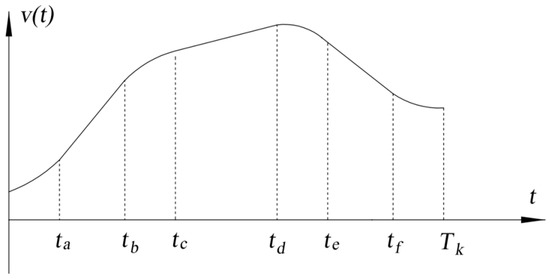
Figure 6.
Speed curve.
Here, , .
According to the above analysis, the acceleration curve can be made up of Bernstein function segments, and the piecewise linear interpolation is a special case, as shown in Equation (44):
where
is the normalized time variable; is the base function, and is the corresponding coefficient. Therefore, the trajectory planning problem of joint (driving limb) space, converts to the optimization problem with as the optimization object, Equation (36) as the objective function, and Equations (37)–(41) as the constraint condition.
4. Joint Space Trajectory Planning Based on Improved Quantum Particle Swarm Optimization
4.1. Example 2: Comparison between Improved QPSO and MATP
Reference [1] established the existence of the optimal solution within the feasible region for the mathematical model of the joint (driving limb) space trajectory planning presented in Equations (36)–(41). Therefore, the use of the improved QPSO algorithm in heuristic search within the feasible region is a viable optimization technique.
Table 1 specifies the target parameters required for planning the trajectory of a particular joint (driving limb) of the robot at a given time. The improved QPSO algorithm can be employed to optimize the trajectory under these conditions. Joint space trajectory planning is applicable to both series robots (joint type) and parallel robots (driving limb type). Thus, in Table 1, the unit of measurement used for each data field is not significant as long as unity is maintained.

Table 1.
Track planning parameter setting.
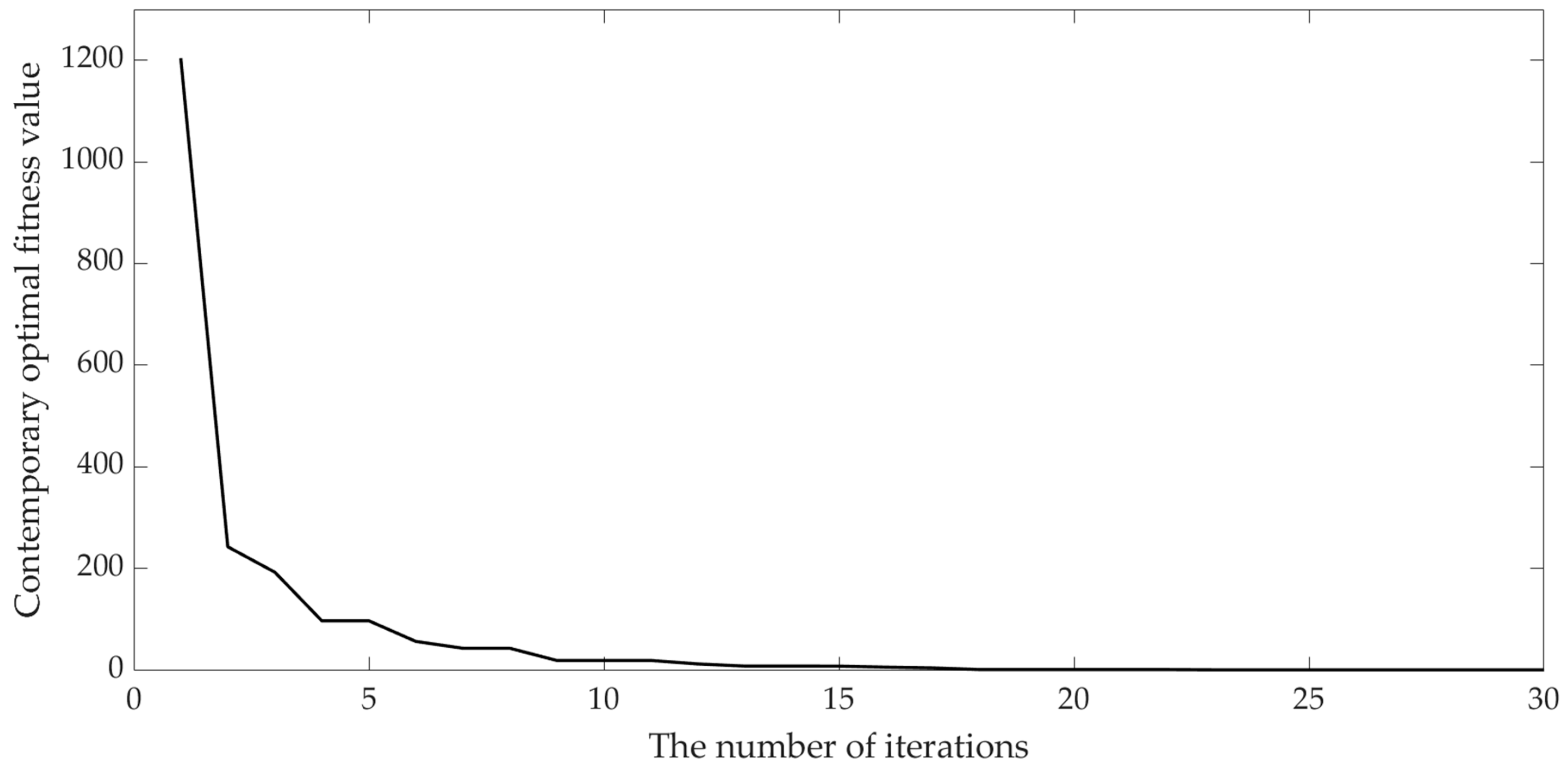
Using the parameters specified in Table 1, trajectory planning is performed using the improved QPSO algorithm, and the iterative convergence curve is depicted in Figure 7. It is evident from the figure that the algorithm converges rapidly during the iterative process, with the optimal value being attained after 20 iterations. The efficiency and accuracy of the improved QPSO algorithm have satisfied the demands of the engineering applications.
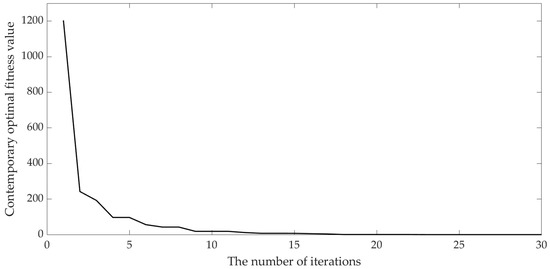
Figure 7.
Convergence curve of the improved QPSO joint space trajectory planning.
Reference [1] proposes a joint space trajectory planning method based on graph planning to achieve minimum acceleration trajectory planning (MATP) in joint space. By using the MATP method, a trajectory that satisfies the initial and final state conditions can be obtained, and the ultimate acceleration of the joint actuator can be minimized.
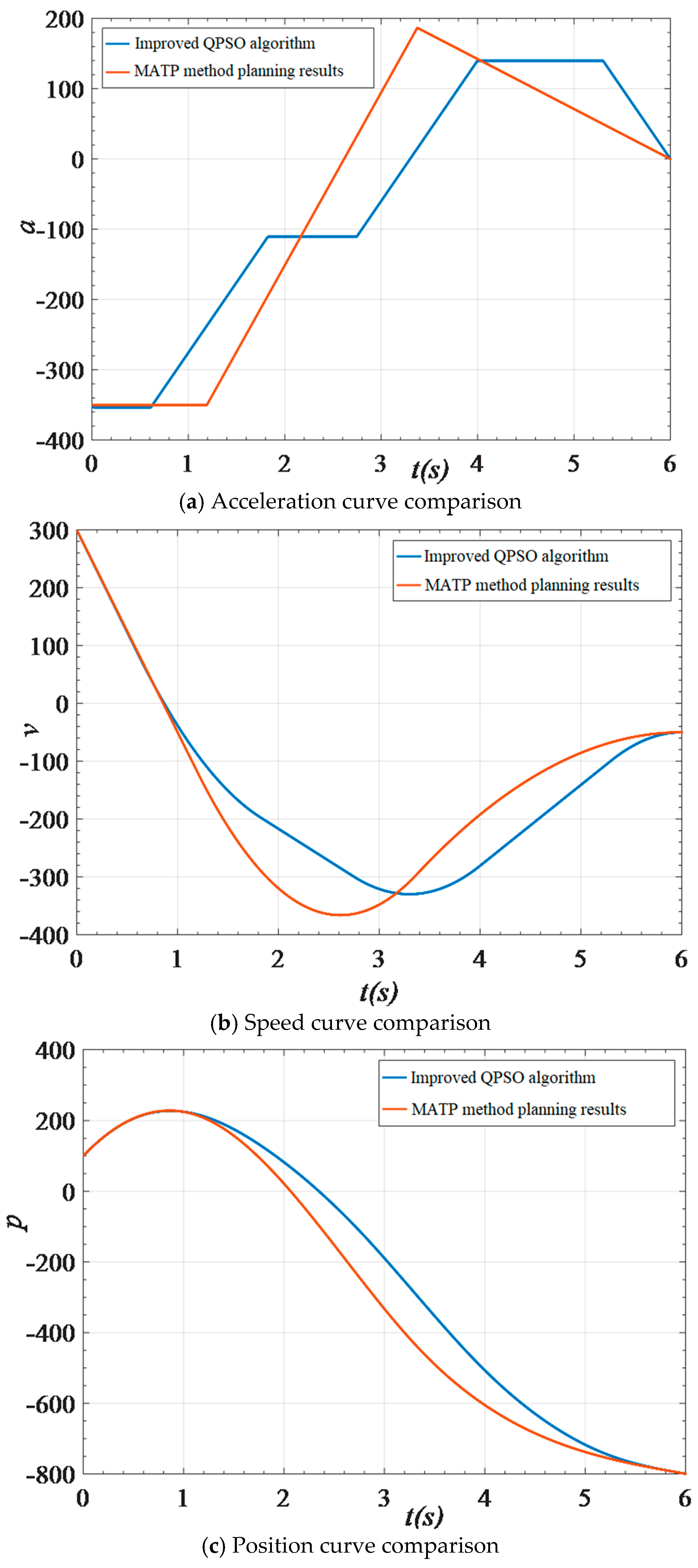
Using the same parameters, trajectory planning is performed using the MATP meth-od and compared with the results of the improved QPSO algorithm. The acceleration, speed, and position curves are compared in Figure 8. The results show that the acceleration, speed, and position obtained by both planning methods satisfy the initial and final state requirements, and the maximum acceleration limits of the two trajectories are identical. However, the forward maximum acceleration of the improved QPSO algorithm is smaller than that of MATP. From Figure 8a, it can be observed that the acceleration of the trajectory obtained by the improved QPSO planning is also smaller than that of the MATP method, indicating that the acceleration changes more smoothly.
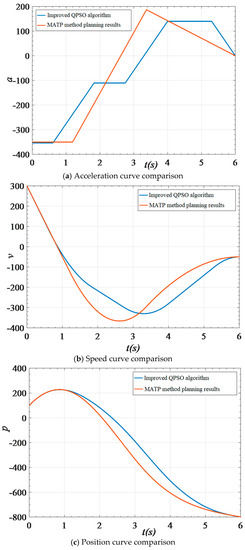
Figure 8.
Comparison of the track planning effects.
4.2. Example 3: Motion Planning for 4SPRR-SPR Parallel Robot
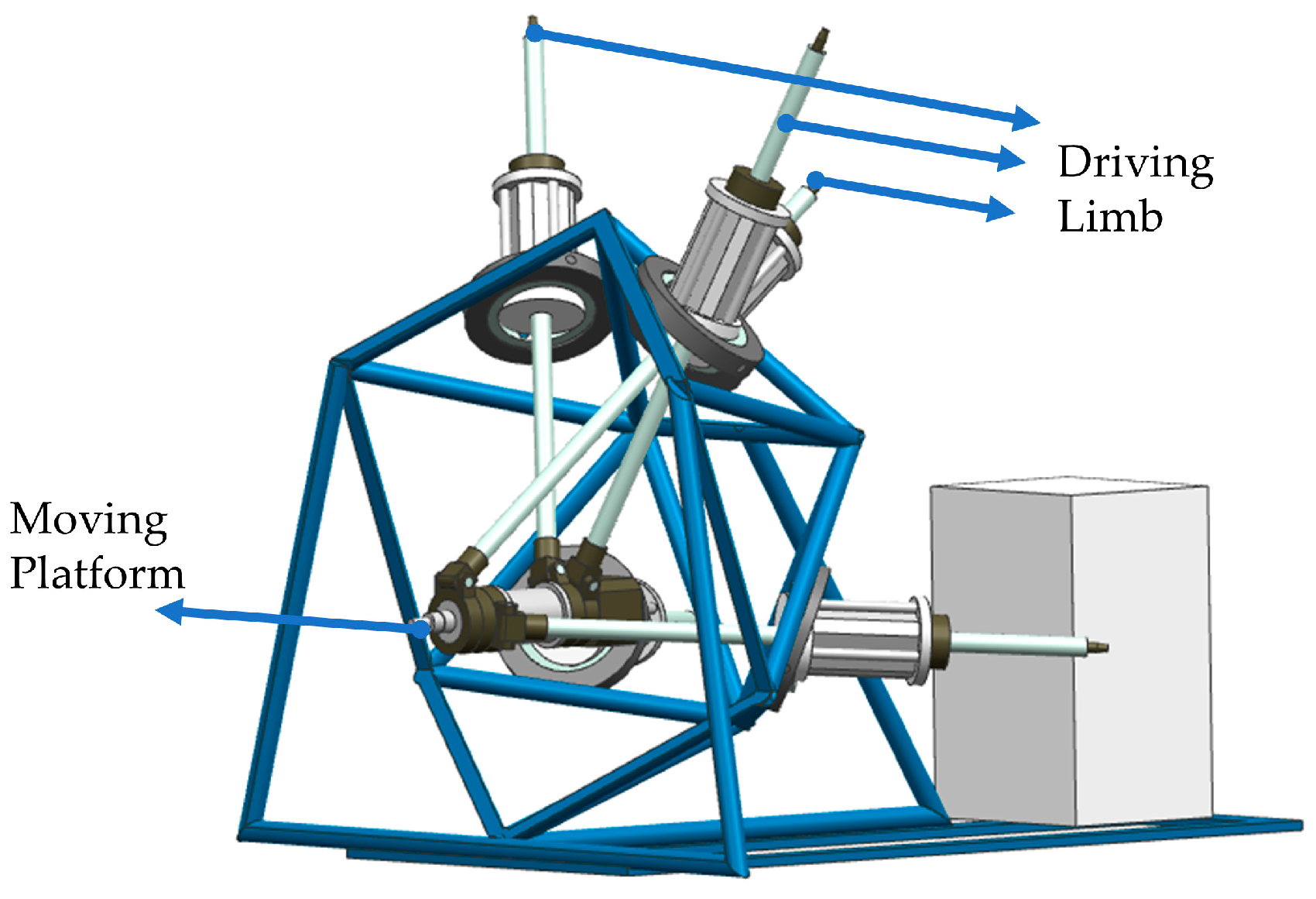
Figure 9 and Figure 10 illustrate the target motion path and the end actuator of a 4SPRR-SPR parallel robot, respectively. The motion planning approach in the driving limb space can enhance the stability of the driving limb motion while simultaneously achieving position and posture control of the robot. The improved QPSO algorithm is utilized to plan the spatial trajectory of the parallel robot driving limb. The position and posture of the target motion path are sampled based on the motion performance parameters of the robot, followed by the solution of inverse kinematics for the sampled position and posture. The acceleration, speed, and position of the driving limb obtained from the inverse kinematics planning are computed, and the motion of each driving limb is depicted in Figure 11 and Figure 12.
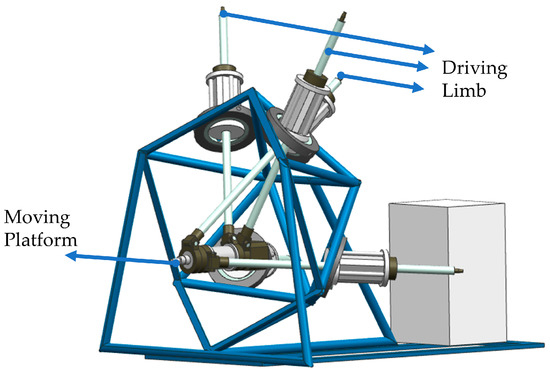
Figure 9.
The 4SPRR-SPR parallel robot.
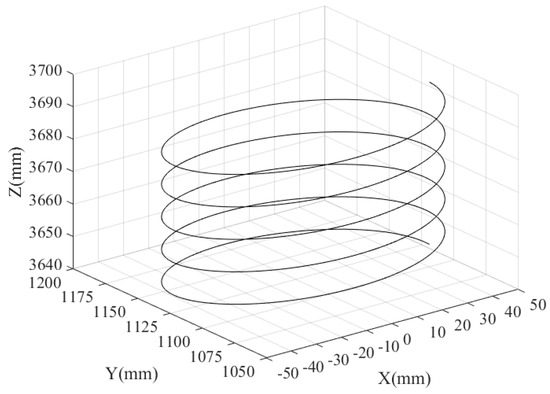
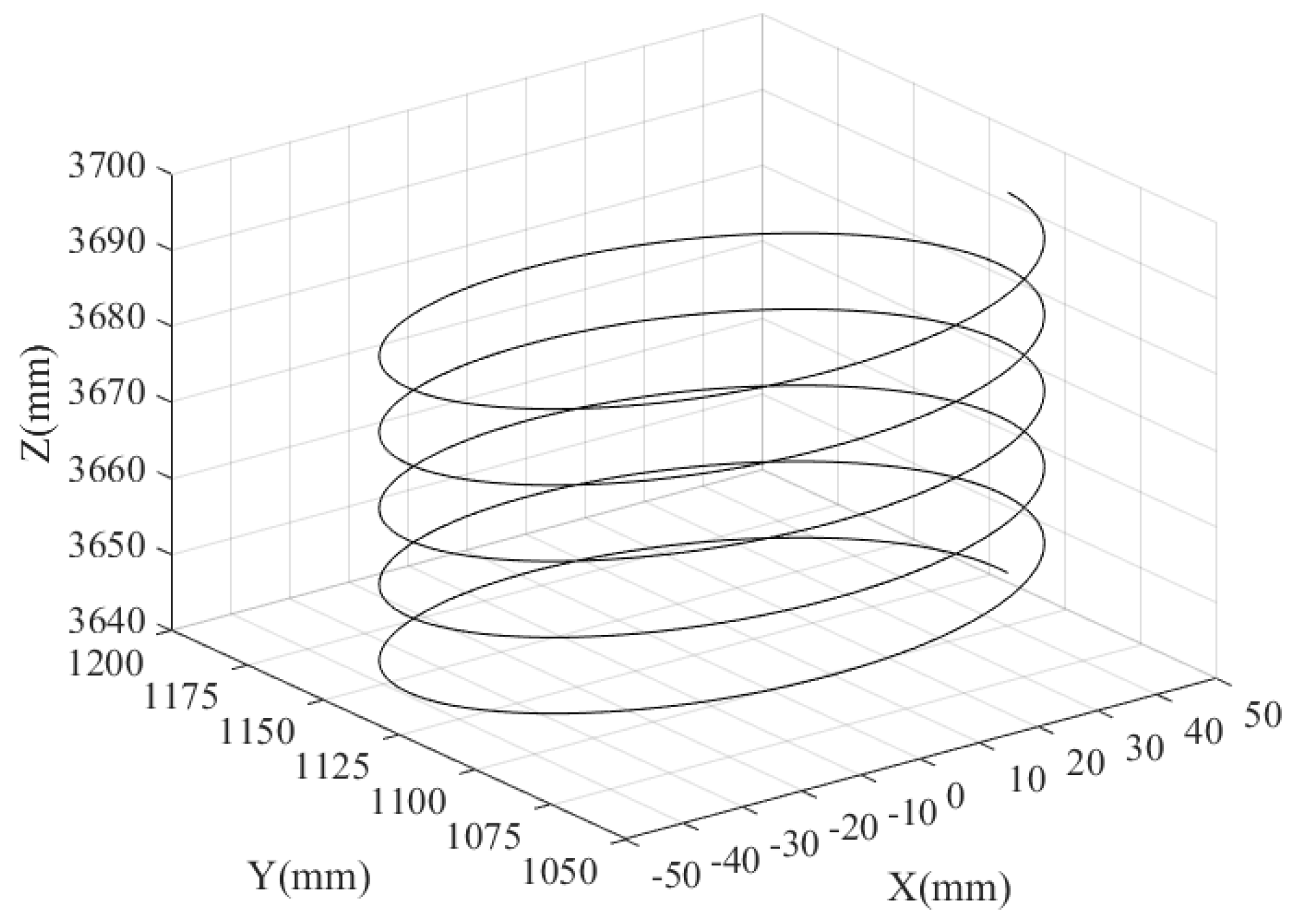
Figure 10.
Moving platform target trajectory.
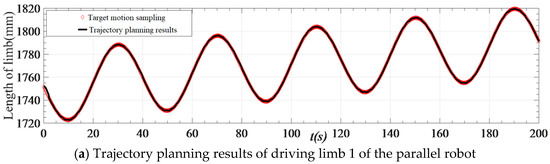
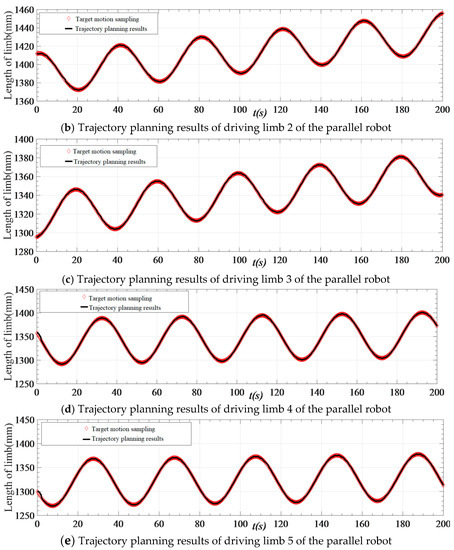
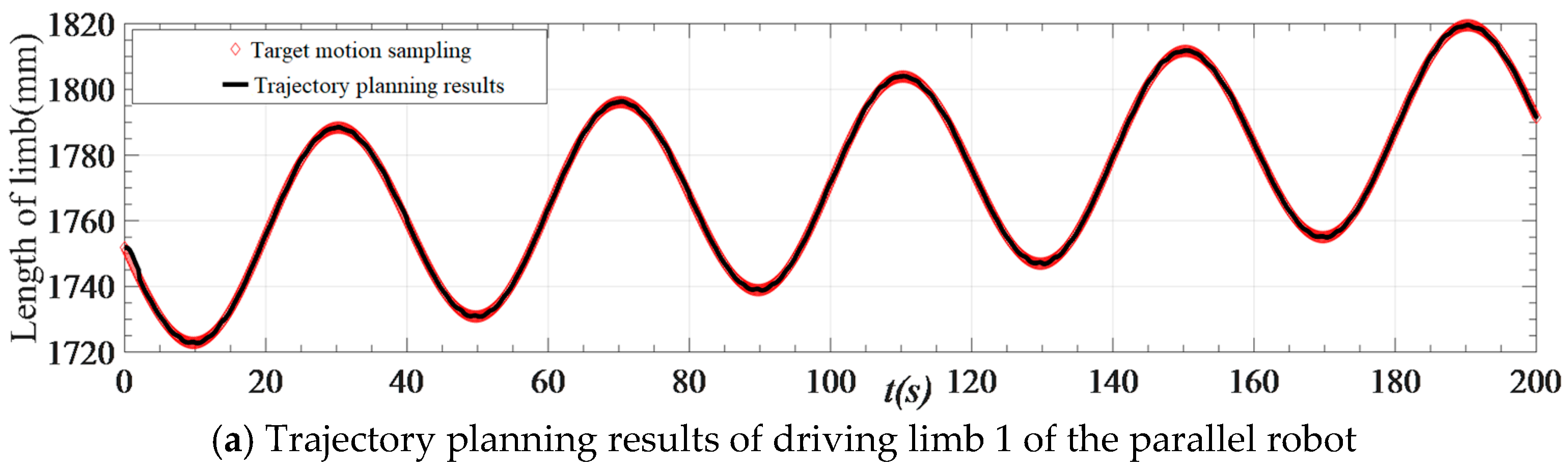
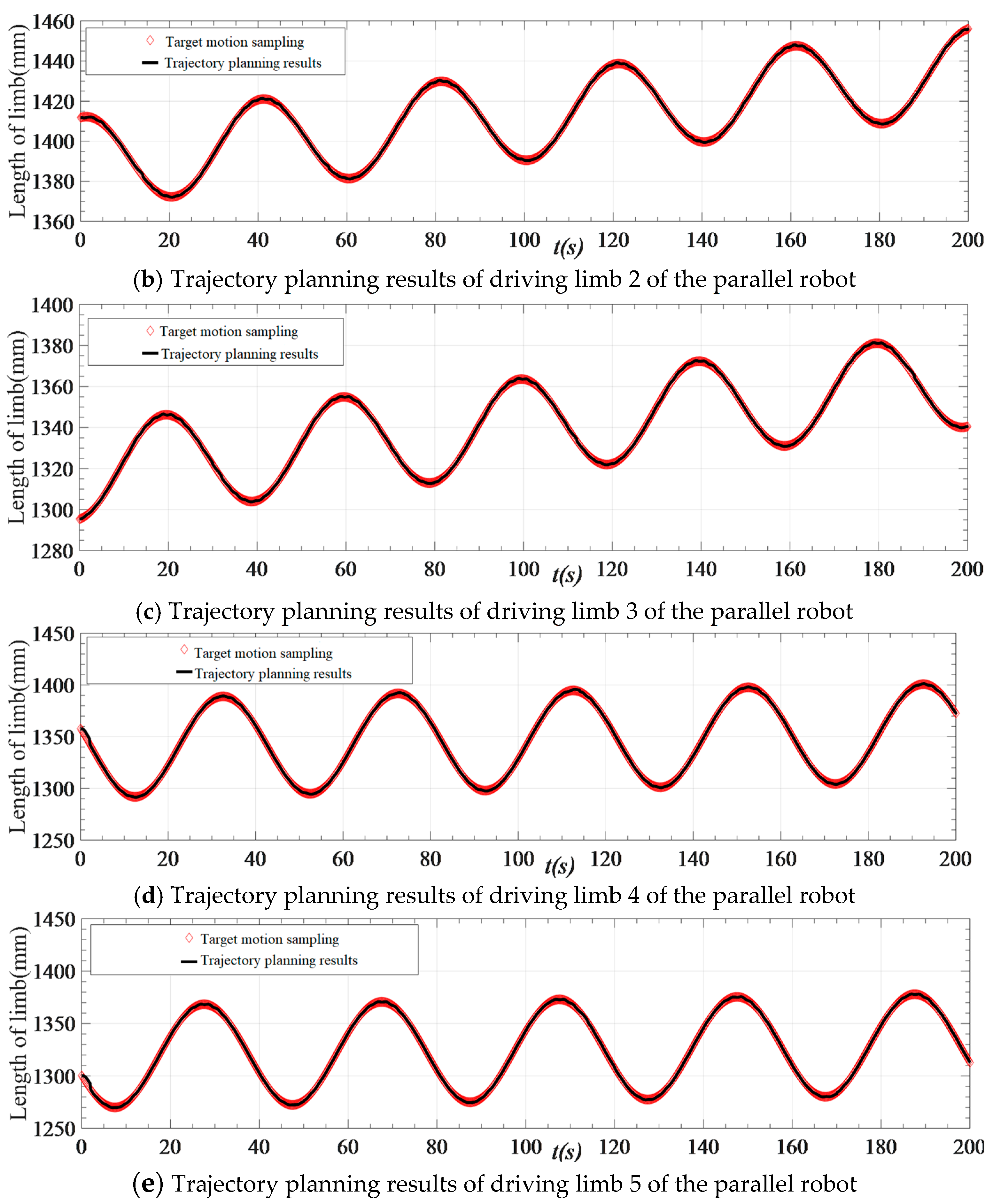
Figure 11.
Space trajectory planning results of the parallel robot driver.
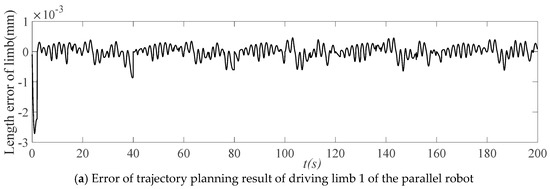
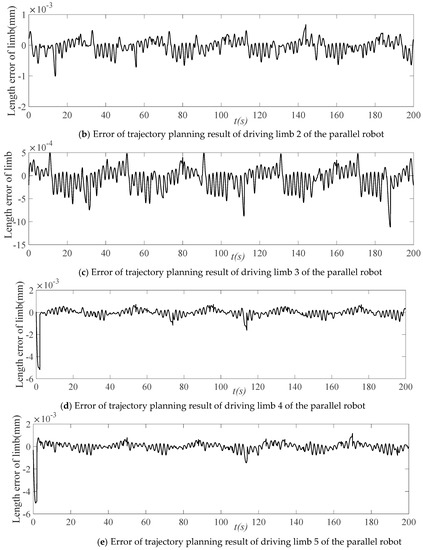
Figure 12.
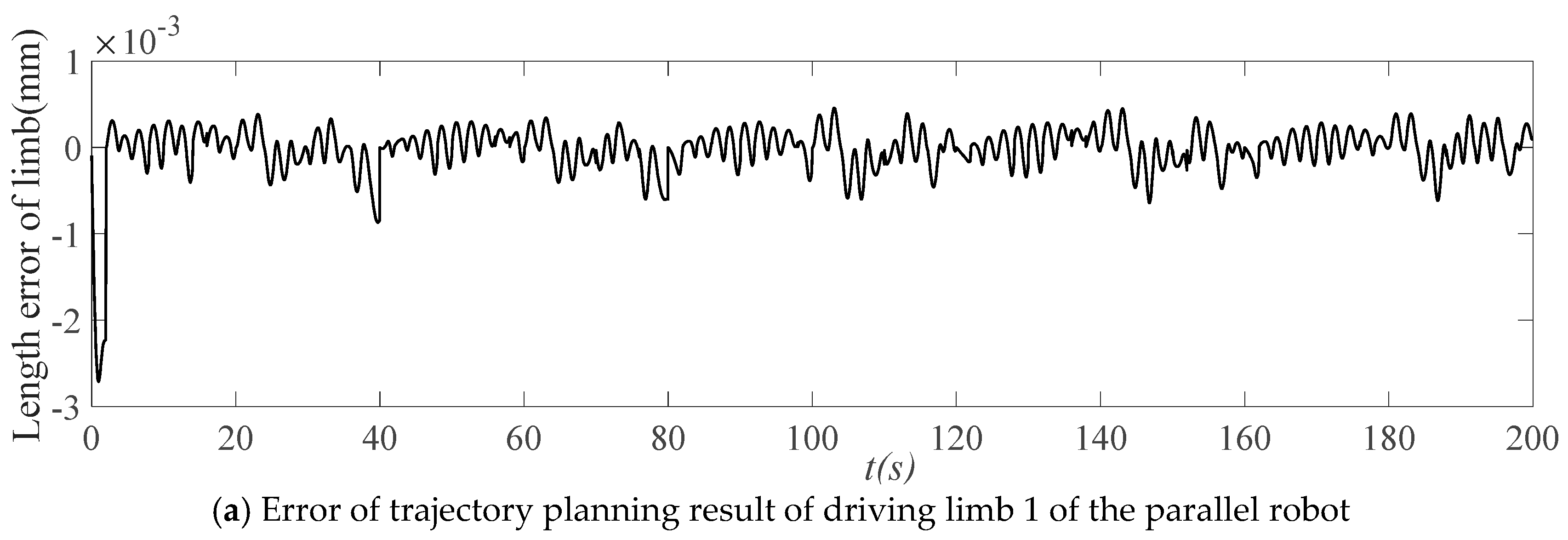
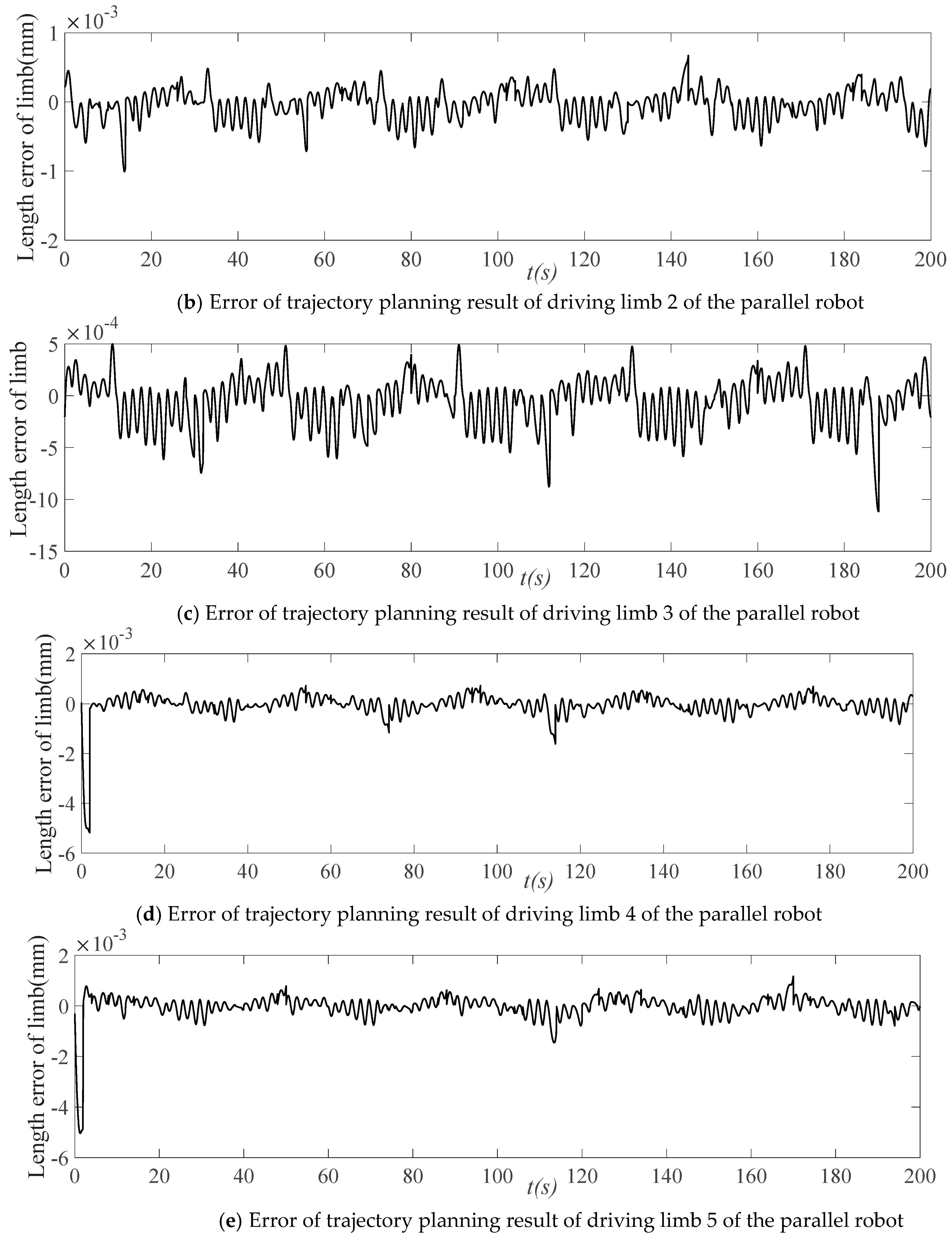
Space trajectory planning error of the parallel robot driver.
Figure 11 indicates that the motion of each driving limb is virtually identical to the target motion sampling results after planning, and the motion synchronization of each driving limb is ensured, thereby reducing the loss of motion accuracy of the robot end actuator caused by the asynchronization of the driving limb. Therefore, the efficacy of driving limb space trajectory planning utilizing the improved QPSO algorithm is validated.
By employing a smoothing spline to interpolate the sampling data of the driving limb and the corresponding time, the position of each driving limb at the same time as the trajectory planning outcome is calculated as the ideal trajectory of the driving limb at each time. The error of trajectory planning results is obtained, as illustrated in Figure 12. Through trajectory planning, the position error magnitude of each driving limb is 10−3 mm, which conforms with the actual requirements of the control process. As such, it is clear that the trajectory planning method based on the improved QPSO algorithm can guarantee the accuracy of the results.
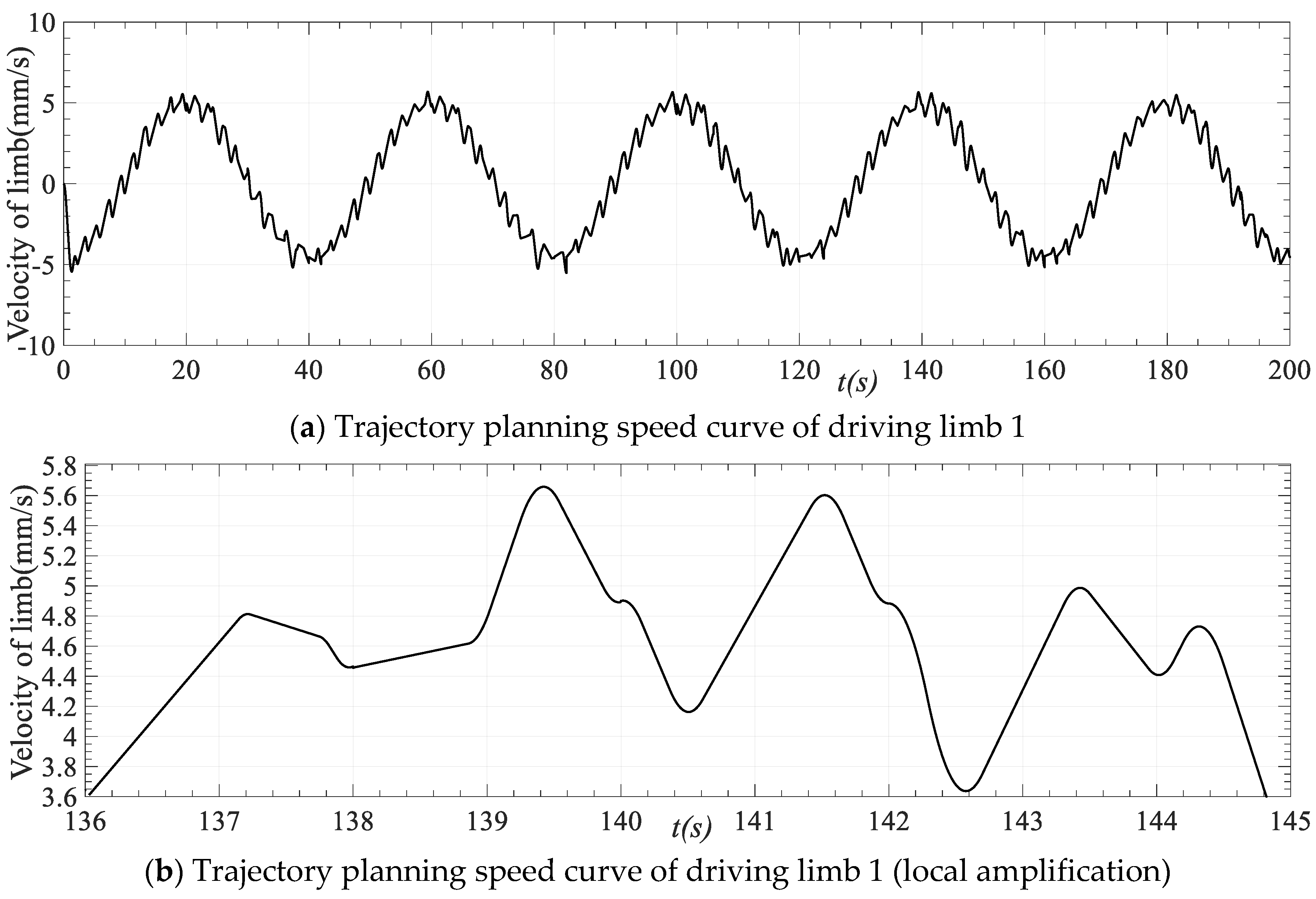
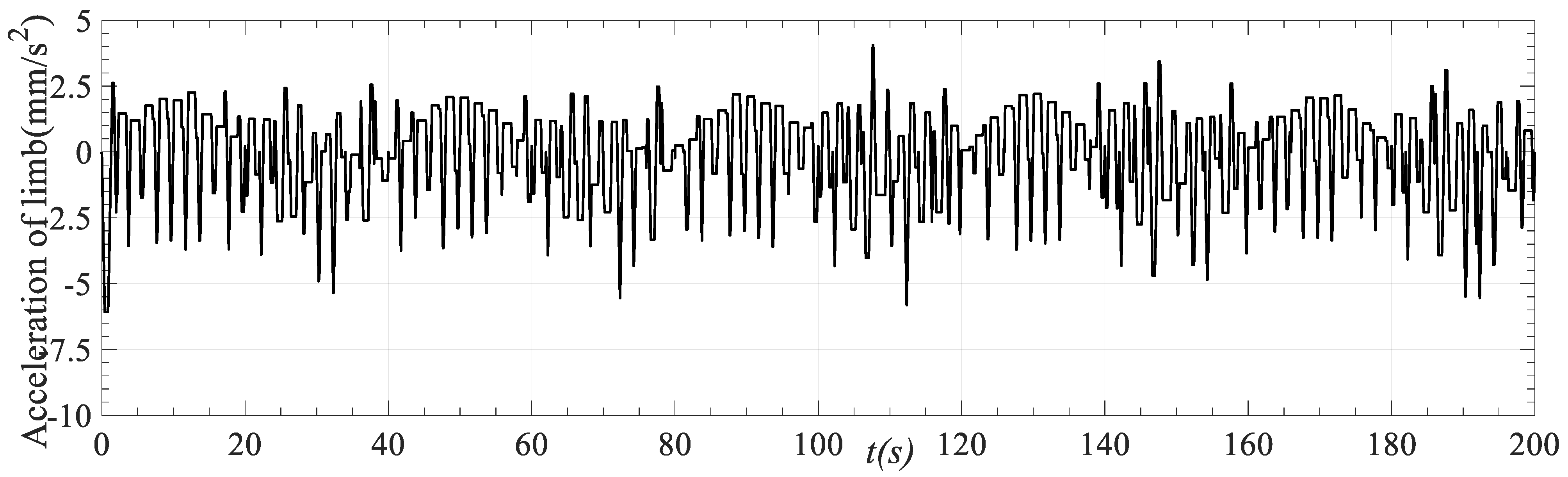
Taking driving limb 1 as an example, the speed, acceleration, and acceleration curves obtained after trajectory planning are shown in Figure 13, Figure 14 and Figure 15. It can be seen from Figure 13b that in the process of motion that during the motion process, the motion speed of the driving limb is relatively smooth, and the motion speed is continuous and derivable without noticeable mutation. As shown in Figure 13a and Figure 14, the limit speed value and the limit acceleration value of the whole motion process after planning fall within the allowable range of the motion performance of the parallel robot.
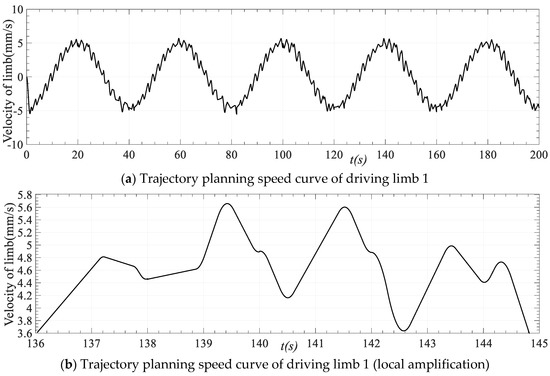
Figure 13.
Speed curve of driving limb 1 track planning.
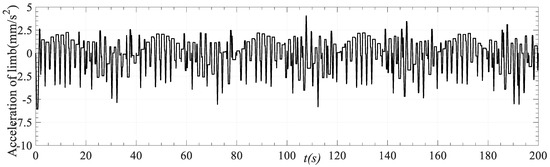
Figure 14.
Acceleration curve of driving limb 1 track planning.
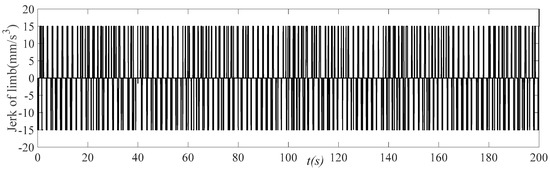
Figure 15.
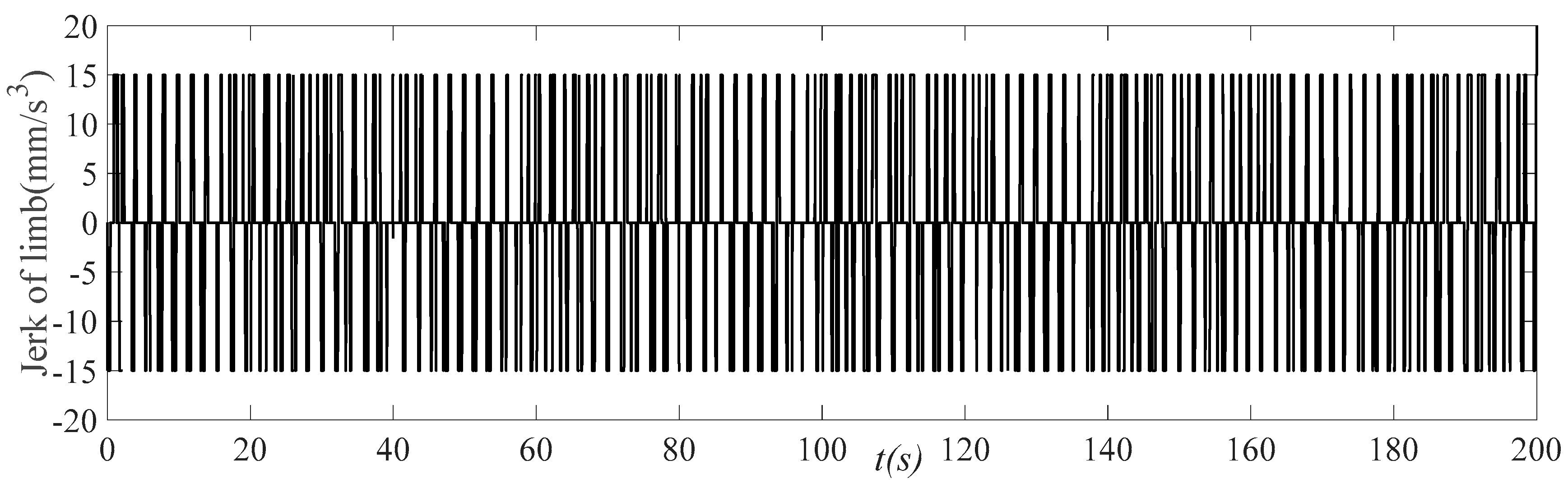
Jerk curve of trajectory planning of driving limb 1.
Figure 15 demonstrates that, while setting the allowable acceleration range, the planned acceleration speed is strictly limited within the range, and its limit value is precisely the upper and lower limit of the set range. This highlights that the optimization calculation process based on the improved QPSO algorithm ensures the reliability of the constraint conditions. In practical applications, to avoid extreme situations, a safety factor can be set, and the allowable range of the robot performance can be established to ensure the stability of the actual operation effect.
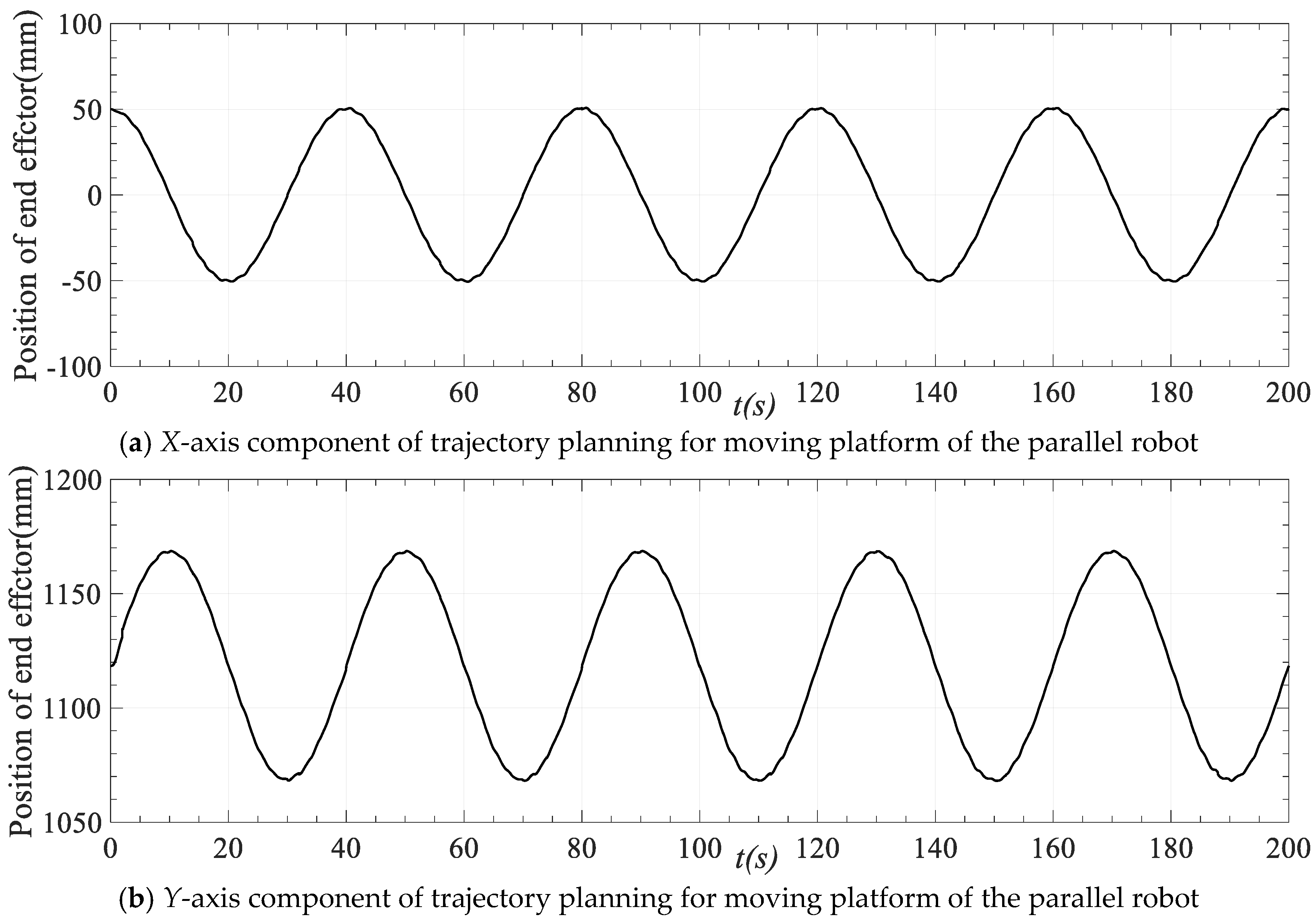
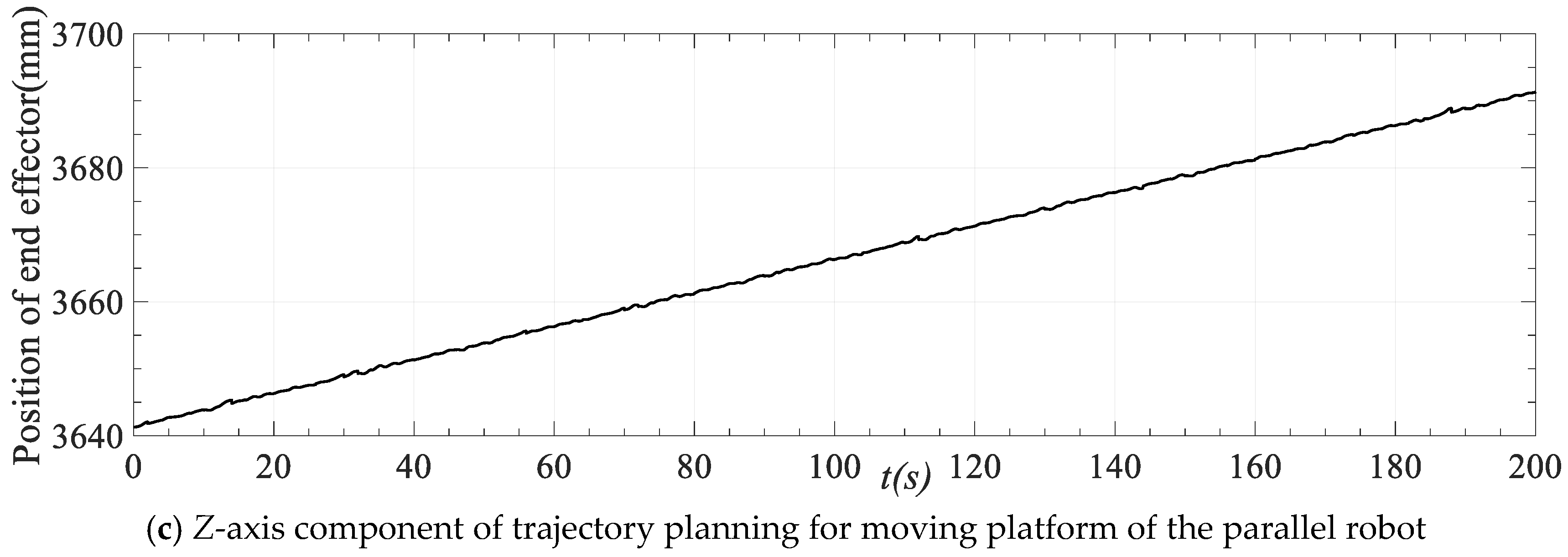
According to the trajectory planning results depicted in Figure 11, the position and posture of the moving platform of the robot at each time can be obtained based on the length of the driving limb of the parallel robot at each time. The position and posture change are the outcome of speed and acceleration planning for the motion path shown in Figure 10. Figure 16 displays the movement of each axis at different times of the end actuator in the trajectory planning results. If the spiral motion in Figure 10 is decomposed to each axis, the X-axis and Y-axis motions are sinusoidal, and the Z-axis motions are straight lines. It can be seen from Figure 15 that the trajectory of the moving platform is consistent with the ideal trajectory, which confirms the efficacy of trajectory planning based on the improved QPSO algorithm.
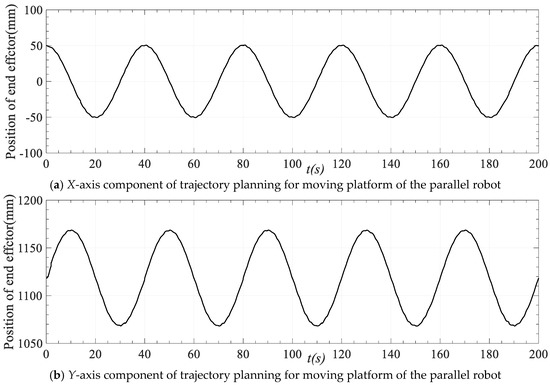
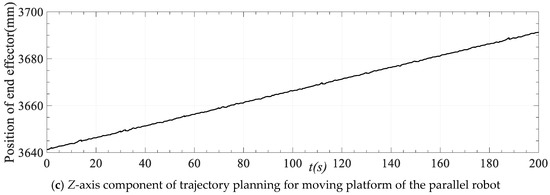
Figure 16.
Trajectory planning results of moving platform of the parallel robot.
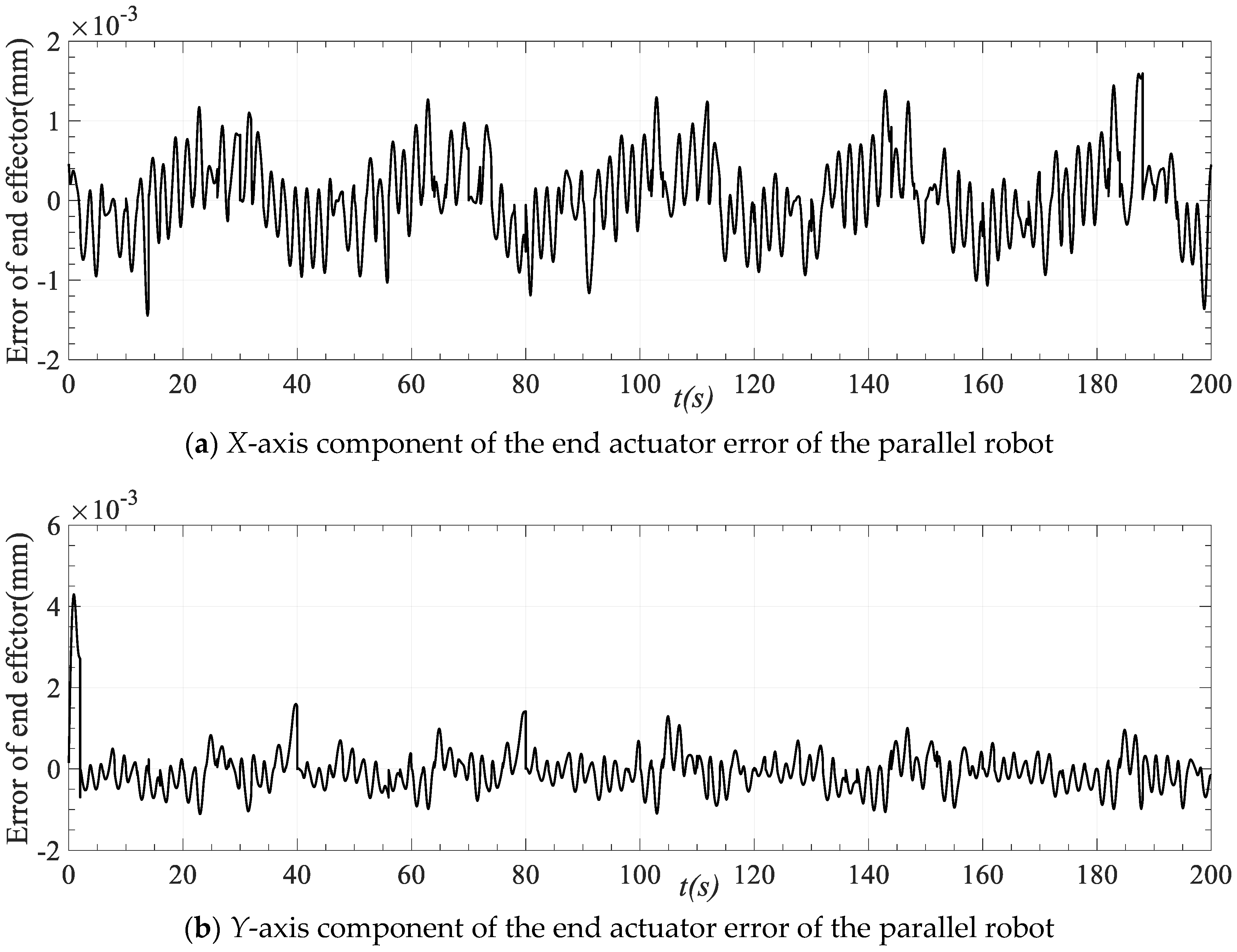
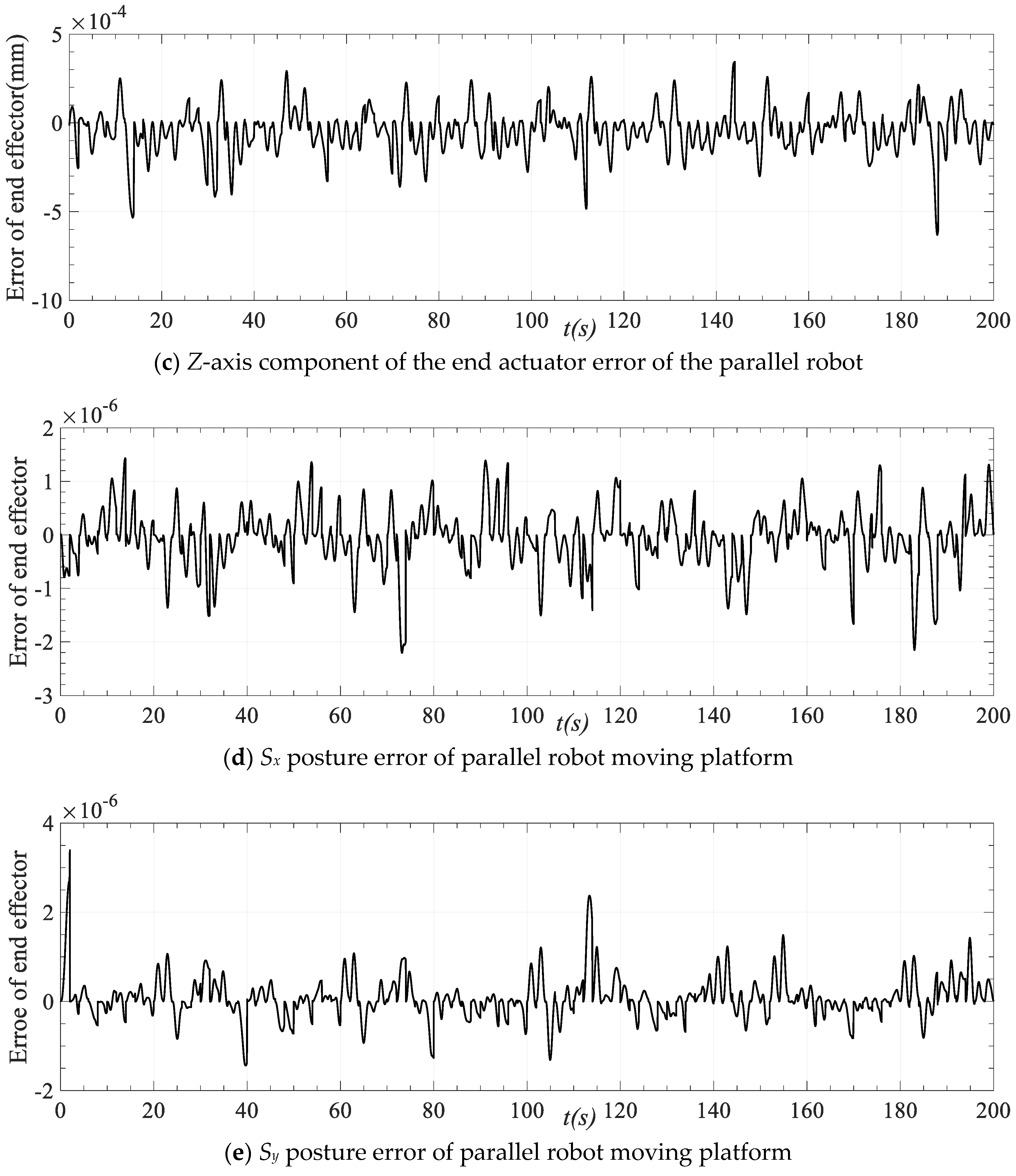
According to the ideal motion curve of each driving limb obtained by spline interpolation, the forward kinematics algorithm of the parallel robot is also used to solve the problem, and the ideal motion position and attitude change of the end actuator is obtained. By comparing with the actual trajectory planning results, the trajectory planning pose error change is presented in Figure 17. It can be observed from the figure that the position error magnitude of the trajectory planning result is about 10−3 mm, and the attitude error magnitude is about 10−6 mm, which fully meets the requirements of practical application for control. This highlights that the joint (driving limb) space trajectory planning can ensure the smoothness and stability of the driving limb motion, as well as the synchronization and motion position and posture accuracy of the multi-limb motion planning at the same time.
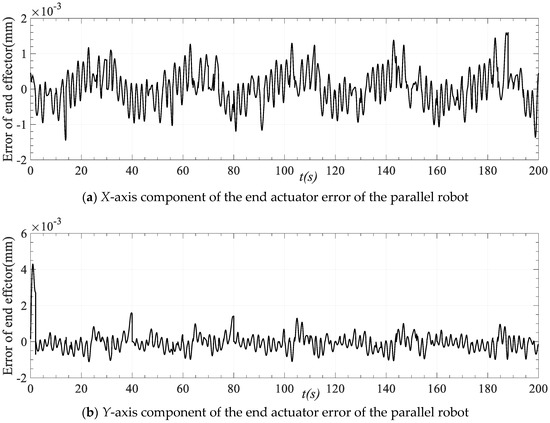
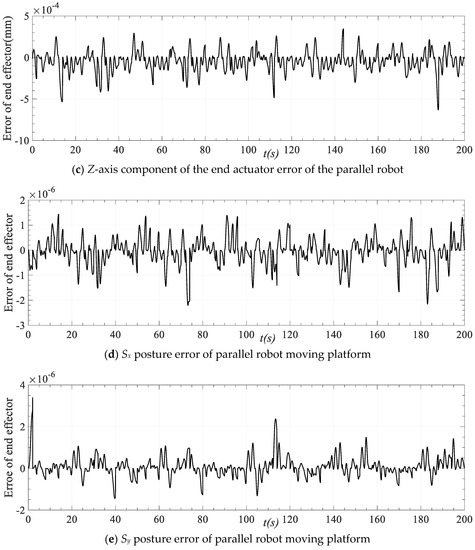
Figure 17.
Position and posture error of moving platform trajectory planning of the parallel robot.
5. Conclusions
1. The motion of the end-effector is mapped to the joint (driving limb) motion of the robot through kinematic analysis, and the path planning and trajectory planning are completed in the robot joint (driving limb) space, which effectively avoids the singularities and obstacle avoidance issues that may arise in Cartesian space trajectory planning. Planning in the robot’s joint (driving limb) space allows for better control of the robot’s motion and avoids situations where the robot is unable to move. Additionally, joint (driving limb) space planning can better consider the robot’s motion constraints and dynamic characteristics, improving the accuracy and reliability of trajectory planning.
2. An intelligent optimization algorithm suitable for trajectory planning is proposed: the improved quantum particle swarm algorithm, which effectively reduces computational complexity and search time by optimizing search strategies and parameter settings. Additionally, intelligent optimization algorithms can better adapt to different trajectory planning requirements by optimizing according to different objective functions and constraints, thereby improving the accuracy and reliability of trajectory planning.
3. After trajectory planning, the error level of each driving limb position is about 10−3 mm, which meets the actual requirements of the control process. After planning, the limit velocity and limit acceleration values of the whole motion process are within the allowable range of the parallel robot motion performance.
4. The key common problems of the industrial application of the robot system in the in situ manufacturing system are solved, which provides support for the concrete implementation and application of the in situ manufacturing system.
Author Contributions
L.L., K.C. and Q.Z. conceived the presented idea. L.L. and T.G. established an overall paper research framework and the model. L.L. and K.C. conducted data calculation for the overall paper. L.L. supervised the findings of this work. L.L., T.G. and Q.Z. collected and provided the model data. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Young Doctor Foundation Project of higher education institutions in Gansu Province (zz2022T50200004), the Science and Technology Project of the Gansu Province Natural Science Foundation (22JR5RA291), open Fund of Hubei Key Laboratory of Mechanical Transmission and Manufacturing Engineering, Wuhan University of Science and Technology (ZZ2023T50200002) and the Natural Science Foundation of Sichuan, China. (2022NSFSC1975).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yingshi, W. Study of Kinematics and Trajectory Planning of Redundant Robots. Ph.D. Thesis, Nankai University, Tianjin, China, 2014. [Google Scholar]
- Kröger, T. On-Line Trajectory Generation in Robotic Systems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kröger, T. Online Trajectory Generation: Straight-Line Trajectories. IEEE Trans. Robot. 2011, 27, 1010–1016. [Google Scholar] [CrossRef]
- Rubio, F.; Llopis-Aibert, C.; Valero, F. Assembly Line Productivity Assessment by Comparing Optimization-Simulation Algorithms of Trajectory Planning for Industrial Robots. Math. Probl. Eng. 2015, 2015, 10. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Rubio, F.; Valero, F. Modelling an Industrial Robot and Its Impact on Productivity. Mathematics 2021, 9, 769. [Google Scholar] [CrossRef]
- Rubio, F.; Llopis-Aibert, C.; Valero, F. Industrial robot efficient trajectory generation without collision through the evolution of the optimal trajectory. Robot. Auton. Syst. 2016, 86, 106–112. [Google Scholar] [CrossRef]
- Hongxin, Z.; Haoran, Q.; Xu, Z.; Ping, H. Recent Advances on Manipulator Trajectory Planning Methods. Recent Pat. Mech. Eng. 2020, 13, 303–327. [Google Scholar]
- Qidong, L.; Hehua, J.; Pengfei, X.; Feifei, C.; Fei, L. Optimal trajectory optimization of 7R robot for space maintenance operation. IEEE Access 2020, in press. [Google Scholar] [CrossRef]
- Davood, M.; Nabil, N. An improved volleyball premier league algorithm based on sine cosine algorithm for global optimization problem. Eng. Comput. 2021, 37, 2633–2662. [Google Scholar]
- Wichapong, K.; Pholdee, N.; Buraeerat, S. Trajectory Planning of a 6D Robot based on Meta Heuristic Algorithms. MATEC Web Conf. 2018, 220, 6004. [Google Scholar] [CrossRef]
- Liu, S. An on-line reference-trajectory generator for smooth motion of impulse-controlled industrial manipulators: International Workshop on Advanced Motion Control. In Proceedings of the 7th International Workshop on Advanced Motion Control, Maribor, Slovenia, 3–5 July 2002. [Google Scholar]
- Amruta, R.; Deepak, B.; Bibhuti, B.; Golak, B.M. Optimal trajectory planning of industrial robot for improving positional accuracy. Int. J. Robot. Res. Appl. 2021, 48, 71–83. [Google Scholar]
- Seyed, M.M.; Seyedeh, Z.M.; Shahrzad, S.; Seyedali, M. Sine Cosine Algorithm: Theory, Literature Review, and Application in Designing Bend Photonic Crystal Waveguides. Stud. Comput. Intell. 2019, 811, 201–217. [Google Scholar]
- Asma, B.G.; Yassine, M.; Seyedali, M. A comprehensive survey of sine cosine algorithm: Variants and applications. Artif. Intell. Rev. 2021, 54, 5469–5540. [Google Scholar]
- Gyorfi, J.S.; Wu, C.H. A Minimum-Jerk Speed-Planning Algorithm for Coordinated Planning and Control of Automated Assembly Manufacturing. IEEE Trans. Autom. Sci. Eng. 2006, 3, 454–462. [Google Scholar] [CrossRef]
- Gasparetto, A.; Zanotto, V. A new method for smooth trajectory planning of robot manipulators. Mech. Mach. Theory 2007, 42, 455–471. [Google Scholar] [CrossRef]
- Huang, P.; Chen, K.; Yuan, J. Motion Trajectory Planning of Space Manipulator for Joint Jerk Minimization. International Conference on Mechatronics & Automation. In Proceedings of the 2007 International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007. [Google Scholar]
- Amruta, R.; Golak, B.M.; Deepak, B.; Bibhuti, B.B. Kinematic and Dynamic Optimal Trajectory Planning of Industrial Robot Using Improved Multi-objective Ant Lion Optimizer. J. Inst. Eng. 2020, 101, 559–569. [Google Scholar]
- Borna, M.M.; Robin, C. On the guidance, navigation and control of in-orbit space robotic missions: A survey and prospective vision. Acta Astronaut. 2021, 184, 70–100. [Google Scholar]
- Macfarlane, S.; Croft, E.A. Jerk-bounded manipulator trajectory planning: Design for real-time applications. IEEE Trans. Robot. Autom. 2003, 19, 42–52. [Google Scholar] [CrossRef]
- Piazzi, A.; Visioli, A. Global minimum-jerk trajectory planning of robot manipulators. IEEE Trans. Ind. Electron. 2000, 47, 140–149. [Google Scholar] [CrossRef]
- Li, X.; Qin, Y.; Yang, S. A quantum-behaved particle swarm optimization algorithm for job shop scheduling problems. Eur. J. Oper. Res. 2008, 185, 312–326. [Google Scholar]
- Bingul, Z.; Karahan, O. Real-time trajectory tracking control of Stewart platform using fractional order fuzzy PID controller optimized by particle swarm algorithm. Ind. Robot. Int. J. Robot. Res. 2021, 49, 708–725. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Li, J. Quantum-behaved particle swarm optimization with dynamic adjustment of quantum bit number and quantum rotation angle. Inf. Sci. 2021, 567, 1–18. [Google Scholar] [CrossRef]
- Guoqiang, L.; Weiyi, C.; Huadong, C.; Jiahui, X. A Quantum Particle Swarm Optimization Algorithm with Teamwork Evolutionary Strategy. Math. Probl. Eng. 2019, 2019, 1805198. [Google Scholar]
- Jun, S.; Wei, F.; Vasile, P.; Xiaojun, W.; Wenbo, X. Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point. Appl. Math. Comput. 2021, 218, 3763–3775. [Google Scholar]
- Agrawal, R.K.; Kaur, B.; Agarwal, P. Quantum inspired Particle Swarm Optimization with guided exploration for function optimization. Appl. Soft Comput. J. 2021, 102, 107122. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Zhang, W.; You, W.; Wu, F.; Tu, H. Handling multimodal multi-objective problems through self-organizing quantum-inspired particle swarm optimization. Inf. Sci. 2021, 577, 510–540. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Zhang, Y. Quantum-behaved particle swarm optimization with adaptive quantum bit number and quantum rotation angle. Eng. Appl. Artif. Intell. 2021, 102, 104284. [Google Scholar]
- Liu, J.; Zhang, Y.; Li, J. Quantum-behaved particle swarm optimization with dynamic parameter adjustment for global optimization. Swarm Evol. Comput. 2021, 63, 100886. [Google Scholar]
- Xie, J.; Liu, X.; Zhou, Y. A novel quantum-behaved particle swarm optimization algorithm with adaptive parameters. Swarm Evol. Comput. 2021, 63, 100880. [Google Scholar]
- Li, X.; Zhang, X. A novel quantum-behaved particle swarm optimization algorithm with dynamic learning strategy. Swarm Evol. Comput. 2021, 62, 100864. [Google Scholar]
- Jerzy, B. Many-Objective Quantum-Inspired Particle Swarm Optimization Algorithm for Placement of Virtual Machines in Smart Computing Cloud. Entropy 2022, 24, 58. [Google Scholar]
- Arnaud, F.; Hamouche, O.; Patrick, S. QUAntum Particle Swarm Optimization: An auto-adaptive PSO for local and global optimization. Comput. Optim. Appl. 2022, 82, 525–559. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).