Experimentally Validated Analytical Solutions to Homogeneous Problems of Electrical Impedance Tomography (EIT) on Rectangular Cement-Based Materials

Abstract

Diagnostic technologies using X-rays and/or acoustic emissions for concrete infrastructures containing internal pores, defects, and cracks have attracted considerable interest. However, computerized tomography (CT) for concrete is challenging due to its radiation shielding characteristics. Electrical impedance tomography (EIT), initially developed for medical use, has recently shown a potential for developing a macro-CT technique for concrete structures. This study derived EIT analytical solutions for rectangular cement-based samples and validated them with experimental data obtained from cubic mortar samples. The experimental validation of the three mathematical functions (Dirac delta, Heaviside step, and Gaussian) used as current injection models, the Gaussian function produced the lowest relative absolute error (4.02%). This study also explored appropriate experimental setups for cement-based materials, such as Shunt model, current flow paths, and potential distribution.

1. Introduction

Cement-based materials have been widely used in the construction industry. Thus, many infrastructures consist of concrete. Early detection of internal damage to concrete structure is essential for structural longevity. However, since defects and damage inside concrete structures cannot be seen with the naked eye, it is difficult to detect them. To solve these problems, numerous studies have explored techniques for detecting the conditions inside concrete, such as half-cell and linear polarization resistance measurements, X-ray attenuation measurements, and acoustic emission sensors [1,2,3]. However, macro-scale tomography is essential for comprehensively visualizing the condition of concrete structures. Recent studies have explored electrical impedance tomography (EIT), a computerized tomography (CT) technology, for visualizing the internal conditions of concrete structures.

CT generates a two-dimensional (2D) image of the distribution of specific variables inside an object using data measured at the object’s boundary [4]. Medical CT has generally used X-rays as an incident source. However, due to the radiation-shielding characteristics of concrete, X-rays are not an ideal incident source for concrete structures. As another CT technique, EIT utilizes electric sources instead of X-rays. For medical purposes, EIT offers fast imaging with fewer side effect than X-ray-based CT [5]. Zhang et al. [6] demonstrated that the advantages of EIT over conventional CT in medical field. As such, EIT was initially developed for medical use.

Several studies have been conducted to obtain images of cement-based materials using EIT [7,8,9]. Because the electrical properties of concrete with cracks, moisture, or ion ingress differ from those of intact concrete, EIT can detect its defects and damage based on changes in these parameters [7,10,11]. However, the quality of reconstructions has not been sufficiently high for practical applications. This is because inverse ill-posed problems are extremely sensitive even to relatively small experimental and theoretical errors [7]. Such errors and uncertainties are mainly related to the object’s geometry and electrical boundary conditions. Thus, determining the effects of geometry and boundary conditions on the electric potential is key to improving the quality of EIT image reconstructions for concrete applications.

For medical applications, EIT analytical solutions of the disk (circular section) [12] and rectangular cross section using the Dirac delta function as a current injection model [13] have been investigated. On the other hand, the EIT boundary conditions and analytical solutions for cement-based materials and their representative geometry have not been systematically explored. Instead, the mathematical theories developed for medical use have been applied to cement-based materials. Therefore, fundamental research is necessary to explore analytical solutions for rectangular geometry, which is frequently used for concrete elements, and boundary conditions appropriate for cement-based materials.

In this study, analytical solutions were mathematically derived for the domain of the rectangular section frequently used in concrete structural elements. A main objective was to determine the appropriate boundary conditions using mathematical models that describe current injection: the Dirac delta function, the Heaviside step function, and the Gaussian function. To validate the analytical solutions and boundary conditions, voltages were measured using EIT and compared to theoretical voltages obtained from various boundary conditions and analytical solutions. A good match between EIT measurements and calculations indicates that the theoretical calculations accurately evaluate the electrical conductivity of cementitious materials. From these comparisons, this study presents appropriate experimental setups for cement-based materials and necessary values for the analytical solutions.

2. Theoretical Solutions

2.1. Shunt Model for the Boundary Conditions of Cement-Based Samples

The complete electrode model includes both the shunting effect and the contact impedance between the measuring electrodes and samples. Here, the shunting effect means that the electric potential on the electrodes is constant. Therefore, the intersectional governing equations and boundary conditions of the shunt and complete electrode models are as follows [14]:

$$0=\nabla \cdot \left(\sigma \nabla u\right)$$

(1)

$${\displaystyle \underset{e_l}{\int }\sigma \frac{\partial u}{\partial n}dS}=I_l,\hspace{1em}\mathrm{x} \in { \mathrm{e}}_l$$

(2)

$$\frac{\partial u}{\partial n}=0, \mathrm{x} \in \partial \Omega \mathrm{and} \notin { \mathrm{e}}_l$$

(3)

where, I_l is the current injected into the lth electrode, σ is the electrical conductivity of concrete, u is the electric potential, e_l is the location of the lth electrode, n is the normal vector, and S is the boundary area of domain Ω. The difference between the two models is as follows:

$$\begin{array}{l}\mathrm{Complete} \mathrm{electrode} \mathrm{model}: u+z\cdot \sigma \frac{\partial u}{\partial n}=U_l\hspace{1em}x\in e_l\\ \mathrm{Shunt} \mathrm{model}: u=U_l x\in e_l\end{array}$$

(4)

here, z is the contact impedance between the electrodes and sample, and U_l is the measured potential on the lth electrode.

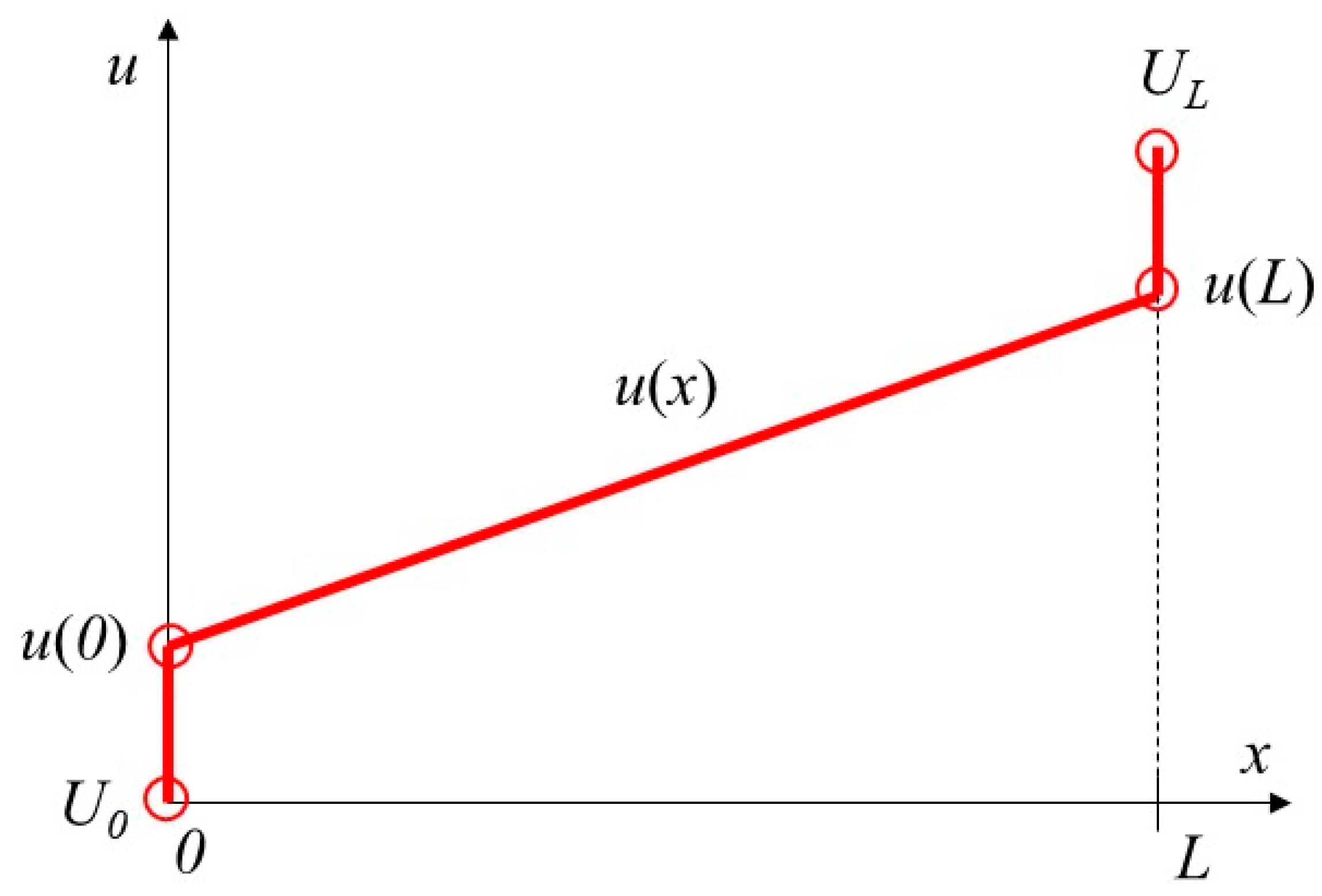
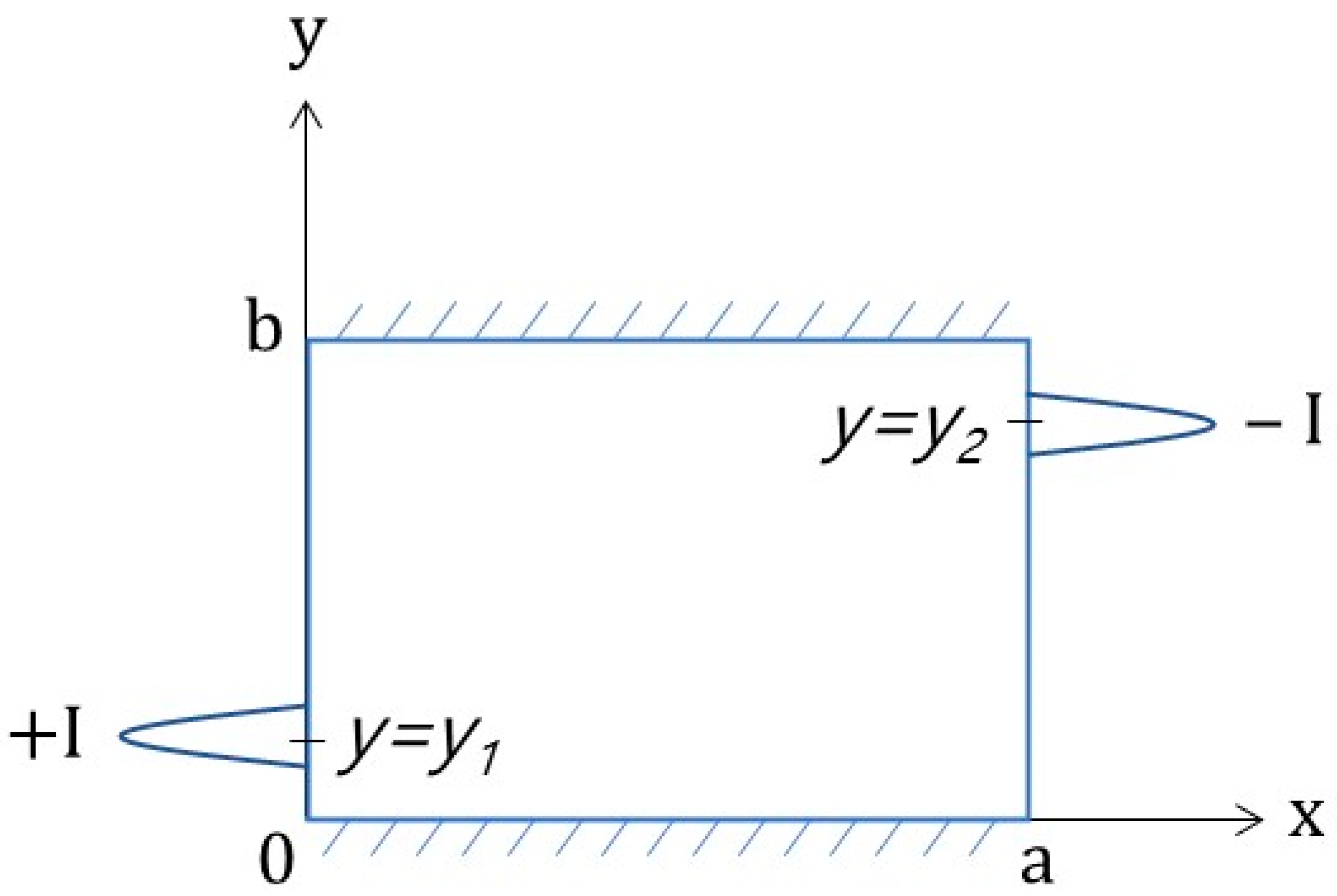
Considering a one-dimensional (1-D) problem of the complete electrode model, a typical electric potential is shown in Figure 1. The electrode distribution is similar to the temperature distribution. In this case, U₀ and U_L are fixed potentials at x = 0 and x = L, respectively, where they can be similarly considered fixed temperatures. The boundaries exhibit a potential drop from u(0) to U₀ and from U_L to u(L) at x = 0 and x = L, respectively, because of contact impedance (which can also be considered contact resistance). The governing equation and its solution are as follows:

$$0=\frac{d^{2}u}{d{x}^2}\Rightarrow u(x)=c_1\cdot x+c_0$$

(5)

$$\begin{array}{l}{\left.\sigma \frac{du}{dx}\right|}_{x=0}=\sigma \cdot c_1=\frac{1}{z}\left[u(0)-U_0\right]=\frac{1}{z}\left[c_0-U_0\right]\\ {\left.\sigma \frac{du}{dx}\right|}_{x=L}=\sigma \cdot c_1=\frac{1}{z}\left[U_L-u(L)\right]=\frac{1}{z}\left[U_L-c_{1}L-c_0\right]\end{array}$$

(6)

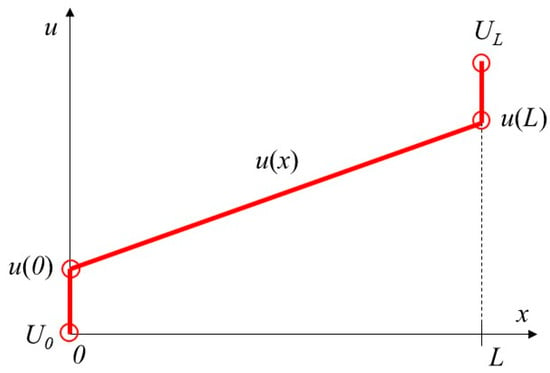
Figure 1. Typical plot of electric potential distribution for a 1-D case of the complete electrode model.

Here, the two unknows, c₀ and c₁, can be obtained from two equations (see Equation (6)), and current I can be expressed as follows:

$$I=\frac{V}{R}\Rightarrow I=\sigma \frac{du}{dx}=\sigma \cdot c_1=\frac{U_L-U_0}{\frac{L}{\sigma }+2z}=\frac{V}{\frac{L}{\sigma }+2z}$$

(7)

where, V is the voltage, and R is the resistance, and thus L/σ + 2z is equal to the resistance R. With low electrical conductivity and a long distance between the two electrodes (L/σ >> 2z), the voltages can be measured reliably by ignoring contact impedance (2z). The low electrical conductivity of concrete makes the influence of the surface resistivity on the electrical potential of concrete low. Base on Equation (7), if the electrical conductivity (σ) is 0.01 S·m⁻¹ (10 mS·m⁻¹) and the surface resistivity is 0.1~1 S⁻¹, the surface resistivity of concrete is neglectable because 1/σ is 100 and 2z is 0.2~2. This simplification, which is the Shunt model, is applicable to cement-based samples, because they have lower electrical conductivity and generally larger size than medical objects. The Wenner probe (also known as the four-point method) specified by AASHTO TP 95 [15] is a test for measuring electrical resistivity that also uses the Shunt model. Therefore, this study used the Shunt model because it is theoretically and practically appropriate for cement-based materials. However, it is noteworthy that the electrode measurements are sensitive to very low moisture contents and soluble salt on surface [16] so that this simplification can be applied to the cases of moderate moisture contents on concrete surface.

2.2. Derivation of Analytical Solutions

The governing equation for 2-D EIT problems is as follows:

$$0=\sigma \frac{{\partial }^{2}u}{\partial x^2}+\sigma \frac{{\partial }^{2}u}{\partial y^2}\Rightarrow 0=\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}$$

(8)

where, u is the electric potential. The boundary conditions for the Shunt model are as follows:

$$\begin{array}{l}{\displaystyle \underset{e_l}{\int }\sigma \frac{\partial u}{\partial n}dS}=I_l, (\mathrm{x}, \mathrm{y}) \in { \mathrm{e}}_l\\ \frac{\partial u}{\partial n}=0, (\mathrm{x}, \mathrm{y}) \in \partial \Omega \mathrm{and} \notin { \mathrm{e}}_l\\ u=U_l (\mathrm{x}, \mathrm{y})\in e_l\end{array}$$

(9)

where, I_l is the current injected into the lth electrode, σ is the electrical conductivity of concrete, e_l is the location of the lth electrode, n is a normal vector, and S is the boundary area of domain Ω. The following equation can be obtained from governing Equation (10):

$$\begin{array}{l}0=u_{xx}+u_{yy}=X^{″}(x)Y(y)+X(x)Y^{″}(y)\\ X^{″}(x)Y(y)=-X(x)Y^{″}(y)\end{array}$$

(10)

X(x) is an independent equation for the x variable in the partial derivative, and Y(y) is an independent expression for the y variable. By using variable separation, you can obtain general solutions for X(x) and Y(y) as follows.

$$\begin{array}{l}X(x)=A\cdot \cosh (\lambda x)+B\cdot \sinh (\lambda x)\\ Y(y)=C\cdot \cos (\lambda y)+D\cdot \sin (\lambda y)\end{array}$$

(11)

where, A, B, C, D and λ are the constant values of the general solution of the partial derivative.

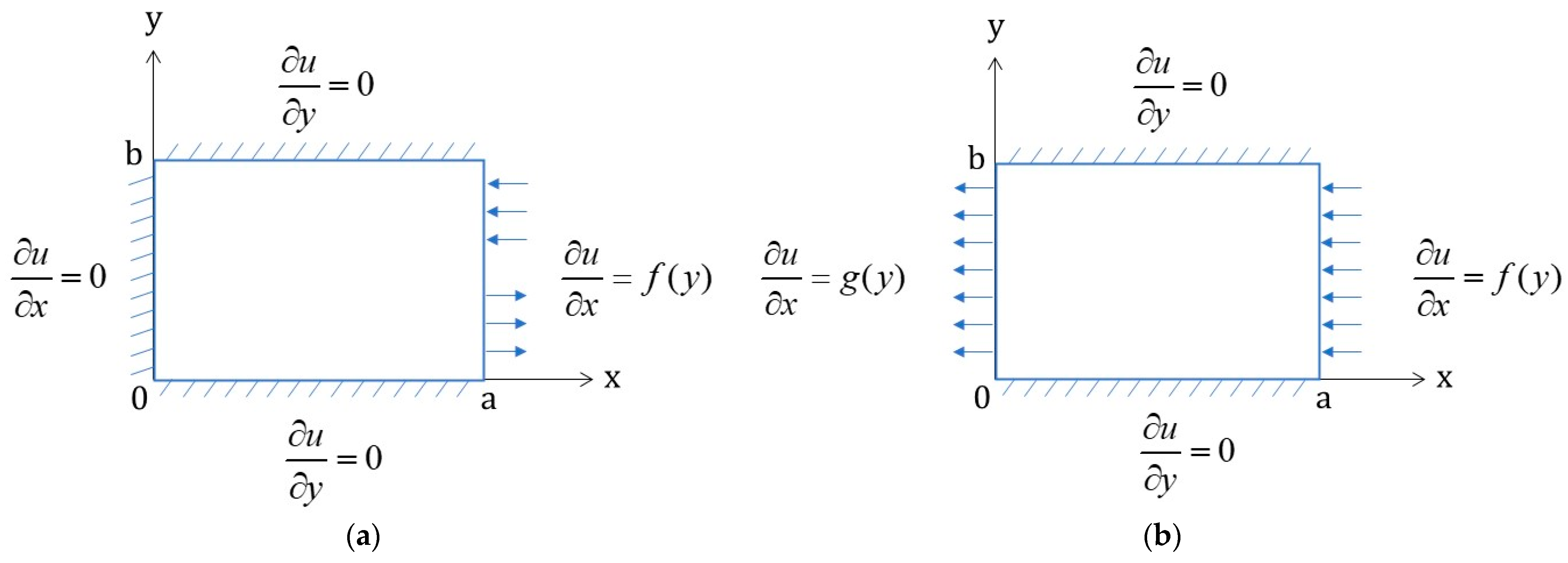
2.2.1. Case 1: Current Flows in and out of the Same Boundary

The configuration when a current is injected on and exits the same surface is illustrated in Figure 2a. Constant D becomes 0 by the boundary condition of Equation (12) at y = 0.

$${\left.0=\frac{\partial u}{\partial y}\right|}_{y=0} \Rightarrow 0=Y^{\prime }(0)=-C\lambda \sin (\lambda 0)+D\lambda \cos (\lambda 0)\Rightarrow \mathrm{D}=0$$

(12)

Figure 2. Illustration of the boundary conditions (a) where current flows in and out of the same surface (Case 1); (b) where current flows in from one boundary and out from the opposite boundary (Case 2).

The boundary condition at y = b derives λ using the following equation:

$${\left.0=\frac{\partial u}{\partial y}\right|}_{y=b} \Rightarrow 0=Y^{\prime }(b)=-C\lambda \sin (\lambda b)\Rightarrow \lambda ={\lambda }_n=\frac{n\pi }{b}$$

(13)

Constant B_n becomes 0 by the boundary condition of Equation (14) at y = 0.

$$0={\left.\frac{\partial u}{\partial x}\right|}_{x=0} \Rightarrow 0=X^{\prime }(0)=A_n{\lambda }_n\sinh ({\lambda }_{n}0)+B_n{\lambda }_n\cosh ({\lambda }_{n}0)\Rightarrow { \mathrm{B}}_n=0$$

(14)

Therefore, only A_n remains, and u(x, y) can be expressed as follows:

$$u(x, y)=X(x)\cdot Y(y)={\displaystyle \sum _{n=1}^{\infty }\left[A_n\cdot \cosh \left(\frac{n\pi x}{b}\right)\cdot \cos \left(\frac{n\pi y}{b}\right)\right]}$$

(15)

Now, the final boundary condition at x = a is applied, and A_n can be obtained using a Fourier transform as follows:

$$\begin{array}{l}{\left.f(y)=\frac{\partial u}{\partial x}\right|}_{x=a}={\displaystyle \sum _{n=1}^{\infty }\left[A_n\left(\frac{n\pi }{b}\right)\cdot \sinh \left(\frac{n\pi a}{b}\right)\cdot \cos \left(\frac{n\pi y}{b}\right)\right]}\\ A_n\left(\frac{n\pi }{b}\right)\cdot \sinh \left(\frac{n\pi a}{b}\right)=\frac{2}{b}{\displaystyle {\int }_0^{b}f(y)}\cdot \cos \left(\frac{n\pi y}{b}\right)dy\end{array}$$

(16)

The final solution is as follows:

$$\begin{array}{l}u(x, y)={\displaystyle \sum _{n=1}^{\infty }\left[A_n\cdot \cosh \left(\frac{n\pi x}{b}\right)\cdot \cos \left(\frac{n\pi y}{b}\right)\right]}\\ \mathrm{where}, A_n=\frac{2}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}{\displaystyle {\int }_0^{b}f(y)\cdot \cos \left(\frac{n\pi y}{b}\right)dy}\end{array}$$

(17)

2.2.2. Case 2: Current Flows in from one Boundary and out from the Opposite Boundary

Figure 2b illustrate a current injected through one boundary and exiting through the opposite boundary. Equation (19) can be derived from Equations (12)–(14) and (18).

$$u(x, y)=X(x)\cdot Y(y)+a_{0}x+b_0$$

(18)

$$u(x, y)={\displaystyle \sum _{n=1}^{\infty }\left[\left\{A_n\cosh \left(\frac{n\pi x}{b}\right)+B_n\sinh \left(\frac{n\pi x}{b}\right)\right\}\cdot \cos \left(\frac{n\pi y}{b}\right)\right]+a_{0}x+b_0}$$

(19)

The remaining boundary conditions are as follows:

$$f(y)={\left.\frac{\partial u}{\partial x}\right|}_{x=0},\hspace{1em}g(y)={\left.\frac{\partial u}{\partial x}\right|}_{x=a}$$

(20)

Using Fourier transforms, Equations (21) and (22) provide all remaining constants, which are A_n, B_n, a₀, and b₀.

$$\left[\begin{array}{cc}0& \frac{n\pi }{b}\\ \frac{n\pi }{b}\sinh \left(\frac{n\pi a}{b}\right)& \frac{n\pi }{b}\cosh \left(\frac{n\pi a}{b}\right)\end{array}\right]\cdot \left[\begin{array}{c}{A}_n\\ B_n\end{array}\right]=\left[\begin{array}{c}-\frac{2}{b}{\displaystyle {\int }_0^{b}f(y)\cdot \cos \left(\frac{n\pi y}{b}\right)dy}\\ \frac{2}{b}{\displaystyle {\int }_0^{b}g(y)\cdot \cos \left(\frac{n\pi y}{b}\right)dy}\end{array}\right]$$

(21)

$$a_0=-\frac{1}{b}{\displaystyle {\int }_0^{b}f(y)dy}=\frac{1}{b}{\displaystyle {\int }_0^{b}g(y)dy}, b_0=-\frac{a_0}{2}$$

(22)

Therefore, the final solution can be obtained by substituting A_n, B_n, a₀, and b₀ in Equation (19).

3. Experiments

3.1. Materials and Sample Preparation

The composition of the mortar matrix used in this study is summarized in Table 1. The mortar consisted of Portland cement type 1, silica sand, silica fume, silica powder, and fine steel slag aggregates (FSSAs). The average diameter of silica sand was 0.2 mm, while the maximum diameter of the FSSAs was 0.39 mm. The properties of FSSAs are listed in Table 2. Additionally, super-plasticizer with a 30% solid content was used to ensure the workability of the mortar mixture.

Table 1. Composition of the cement-based samples by weight ratio (FSSA: fine steel slag aggregate, weight ratios based on the cement weight as 1).

Cement (Type I)	Silica Sand	FSSAs	Silica Fume	Silica Power	Water	Super-Plasticizer
1.0	0.50	0.50	0.15	0.25	0.20	0.042

Table 2. FSSA properties.

Diameter (μm)	Density (g/cm3)	Electrical Conductivity (106 Sm−1)
<390	3.56	11.2

A Hobart type laboratory mixer with a capacity of 20 L was used for mixing. The matrix components were first dry mixed for 5 min. Then, water was added to the mixture, which was then mixed for another 5 min. The superplasticizer was then gradually added to the mixture while mixing for another 5 min. The mixture was subsequently poured into cubic molds. Light vibration was then applied to reduce the air bubbles in the samples. After casting, all samples were covered with plastic sheets and placed in a laboratory at room temperature (25 °C) and 60% relative humidity for two days prior to demolding. After demolding, the samples were cured with hot water at a temperature of 90 °C for 3 days.

3.2. EIT Measurements

The sample size was cubic 50 × 50 × 50 mm in the form of a cube. A layer of silver paste was applied to the surface of the hardened samples, and then copper tape electrodes were attached to the silver paste. The silver paste was supplied by Ted Pella Inc. as Prod No. 16031. Eight copper tapes were placed on two opposite sides (four on each side) of the samples, as shown in Figure 3. Electrodes were mounted at 1, 2, 3, and 4 cm positions on one side of the sample, and the other side was installed in the identical manner. The width of the electrodes was 5 mm, and the distance between the centers of the electrodes was 10 mm. The EIT measurements were performed using an experimental setup and a Sciospec EIT device (Figure 4). The EIT data were obtained from the eight electrodes (Figure 4a). The amplitude and frequency of the electrical current were 10 mA and 80 kHz, respectively. The voltages were measured from electrode pairs in a series. The uncertainty of the measurement is the variation in humidity of the sample and the possibility of sample inhomogeneity.

Figure 3. Setup of sample electrodes.

Figure 4. (a) Experimental EIT setup of the samples, (b) Sciospec EIT device.

4. Results and Discussion

4.1. Cutoff of Infinite Series Solutions

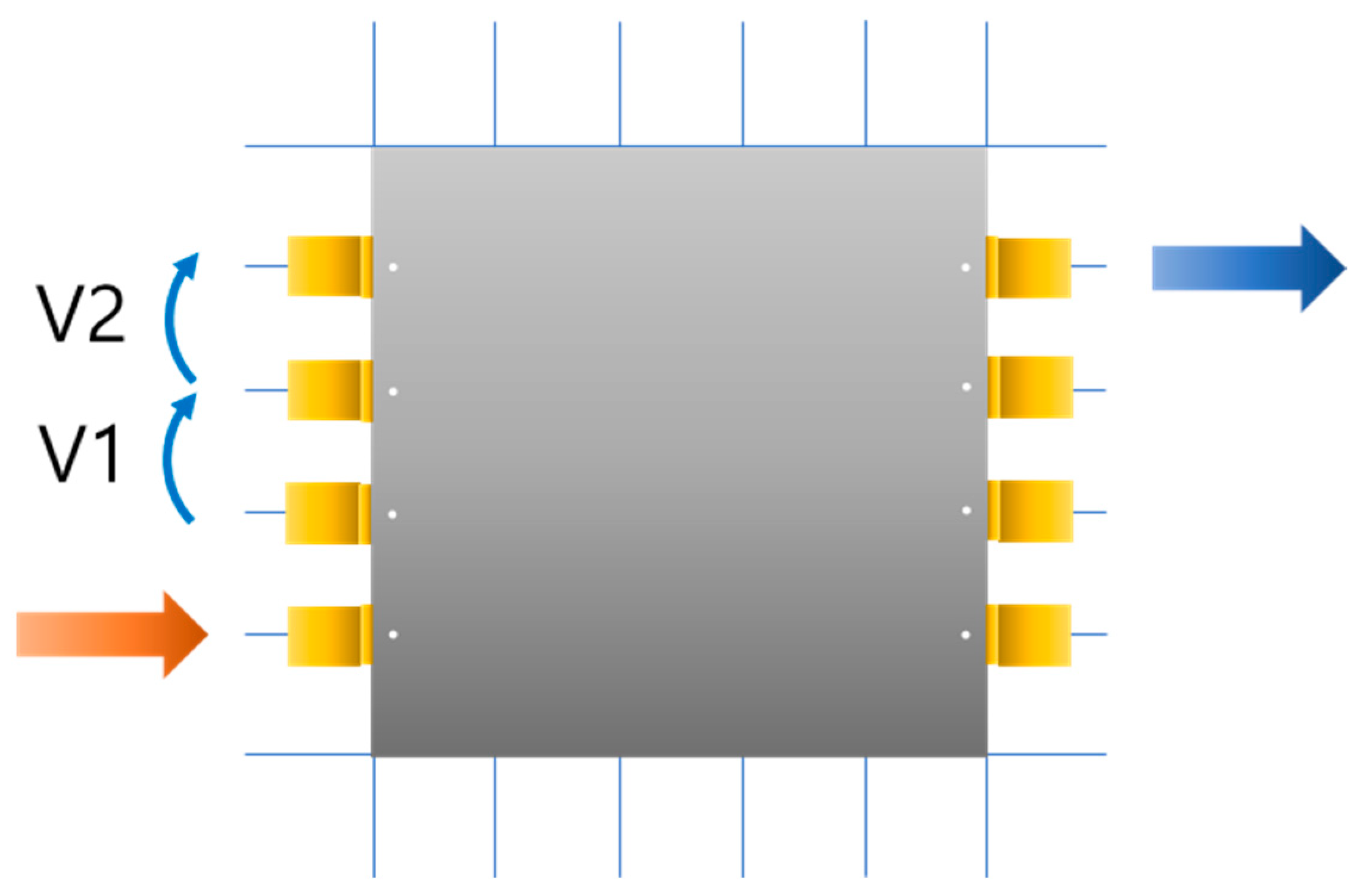
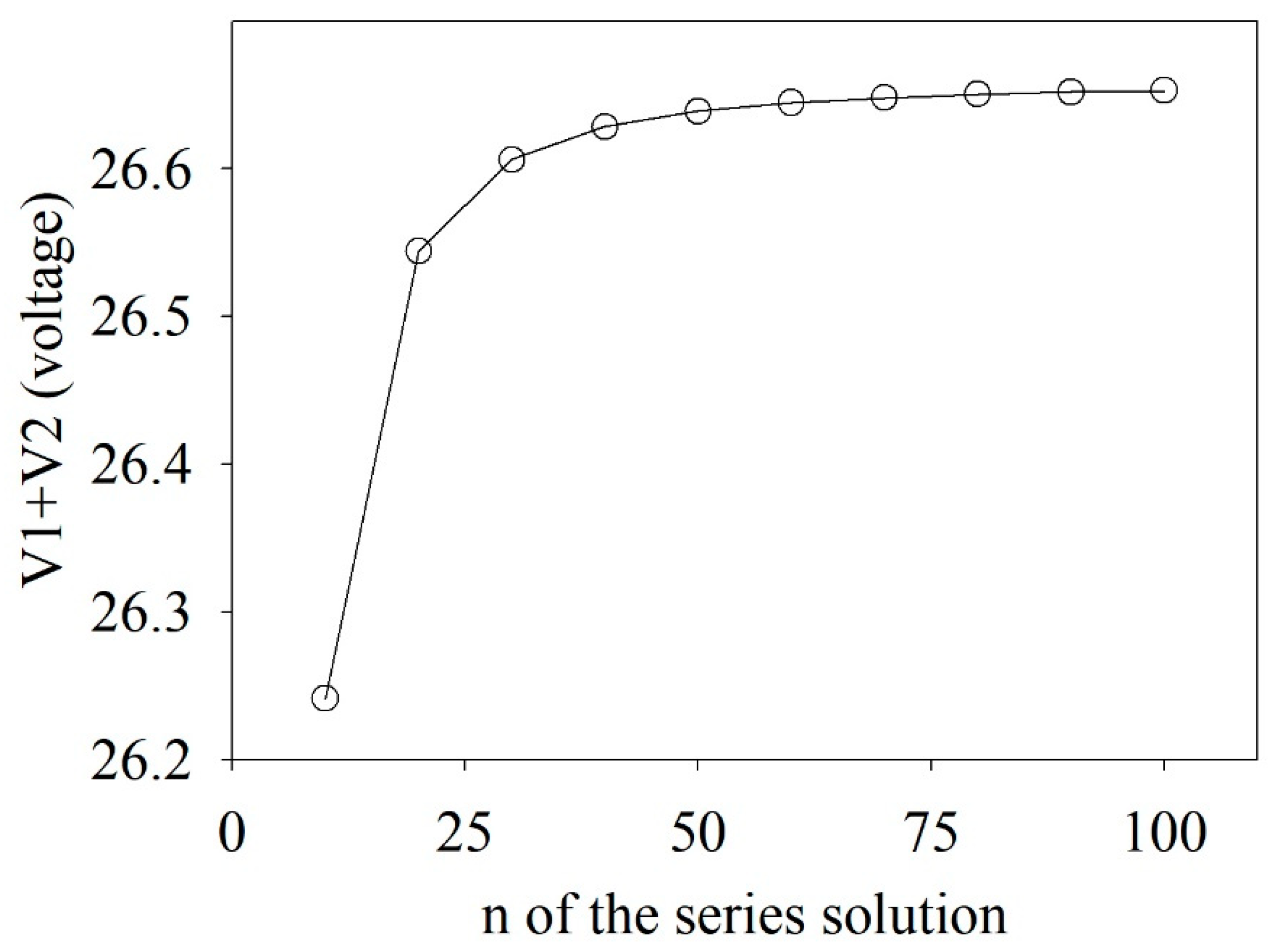
As EIT analytical solutions have the form of an infinite series, it is necessary to determine the number of terms required for computations. To the end, the configuration shown in Figure 5 was chosen, and the sum of voltage V1 and V2 voltages was calculated to determine the point where the difference in voltage did not change significantly as the number of terms increased. As shown in Figure 6, the voltage change stabilized after adding the 50th term of the series (n = 50). Therefore, the analytical solutions of the infinite series were changed to a finite series that added up to the 50th term. However, it is noteworthy that the cutoff of infinite series depends on the size and the composition of the samples.

$$\mathrm{Case} 1: u(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(A_n\cdot \cosh \left(\frac{n\pi x}{b}\right)\cdot \cos \left(\frac{n\pi y}{b}\right)\right)}\simeq {\displaystyle \sum _{n=1}^{50}\left(A_n\cdot \cosh \left(\frac{n\pi x}{b}\right)\cdot \cos \left(\frac{n\pi y}{b}\right)\right)}$$

(23)

$$\begin{array}{l}\mathrm{Case} 2: u(x,y)={\displaystyle \sum _{n=1}^{\infty }\left[\left\{A_n\cosh \left(\frac{n\pi }{b}x\right)+B_n\sinh \left(\frac{n\pi }{b}x\right)\right\}\cos \left(\frac{n\pi }{b}y\right)\right]}+a_{0}x+b_0\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \simeq {\displaystyle \sum _{n=1}^{50}\left[\left\{A_n\cosh \left(\frac{n\pi }{b}x\right)+B_n\sinh \left(\frac{n\pi }{b}x\right)\right\}\cos \left(\frac{n\pi }{b}y\right)\right]}+a_{0}x+b_0\end{array}$$

(24)

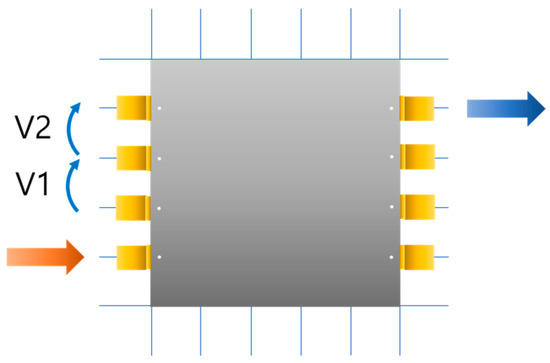
Figure 5. Theoretical setup for determining the cutoff of infinite series solutions (V1 and V2 were measured simultaneously).

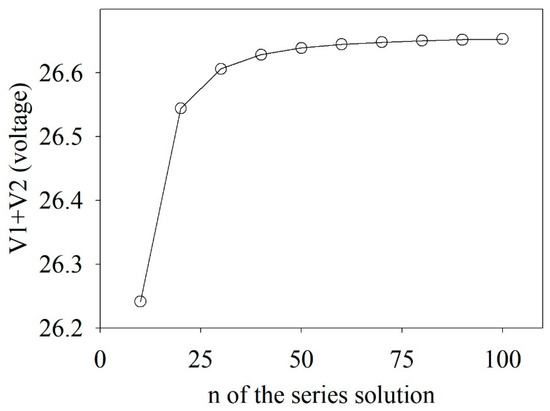
Figure 6. Sum of voltages V1 and V2 as a function of series n.

4.2. Experimental Validation of Current Injection Models

Current injection models indicate the functions of f(y) and g(y) in Equation (25), which are derived from the boundary conditions on the current-injected surface. Therefore, they describe how current inflow and outflow occur.

$$\sigma \frac{\partial u}{\partial n}=I \mathrm{on} \partial {\Omega }_I\Rightarrow u_x(0,y)=g(y) \mathrm{and} u_x(a,y)=f(y)$$

(25)

Three models were investigated: Dirac delta function, Heaviside step function, and Gaussian function (also known as the normal distribution function). The Dirac delta function was used in a previous study [13]. However, since the electrodes where the current goes in and out have a certain width, the Heaviside step function might better represent the current inflow and outflow than the Dirac delta function. Nevertheless, the Gaussian function might better describe the current density than the Heaviside step function. This is because it can better describe common physical phenomena, such as stress density and heat density, even though the ideal density for calculations is the Heaviside step function.

4.2.1. Dirac Delta Function

Case 1: Current Flows in and out of the Same Boundary

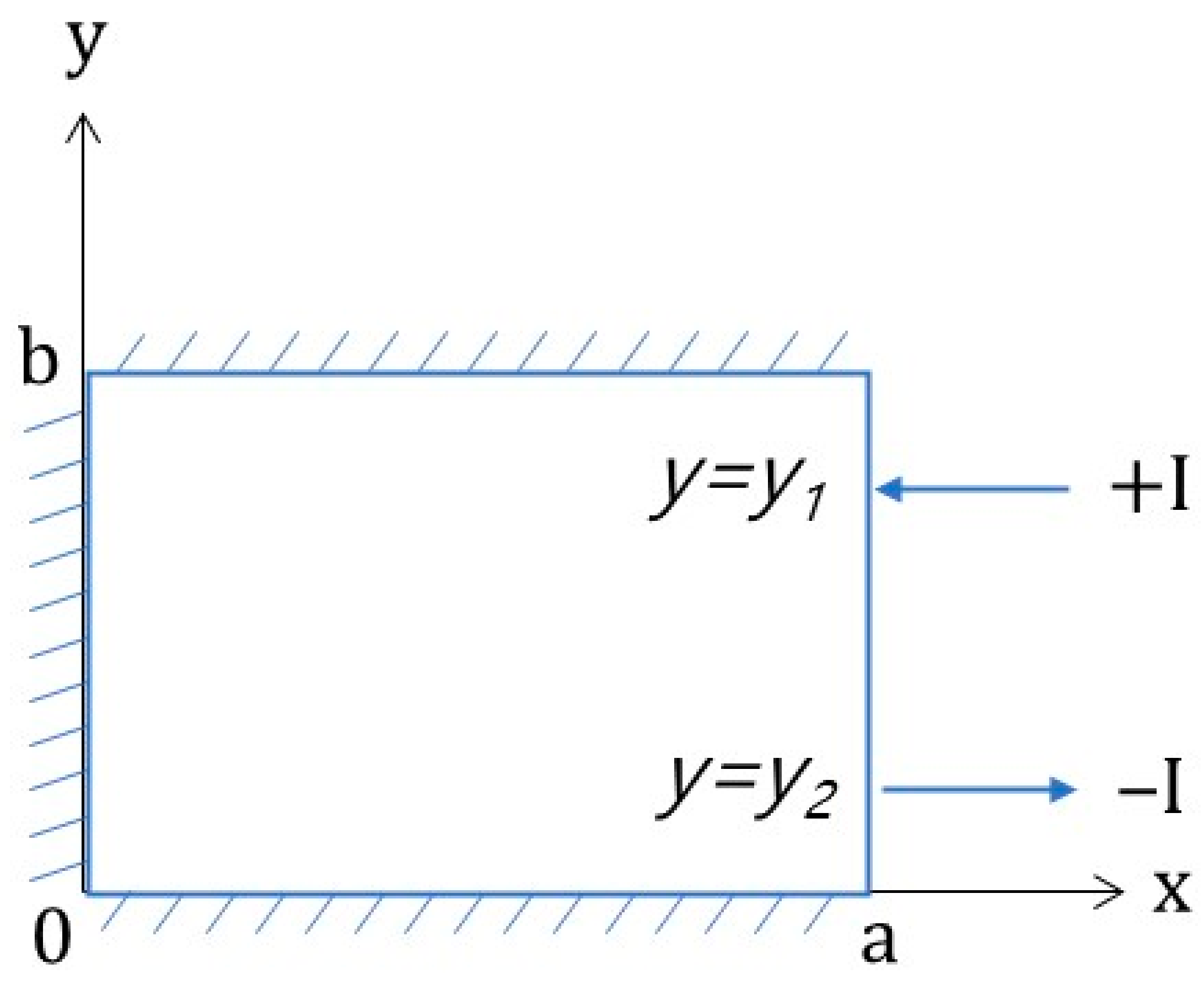
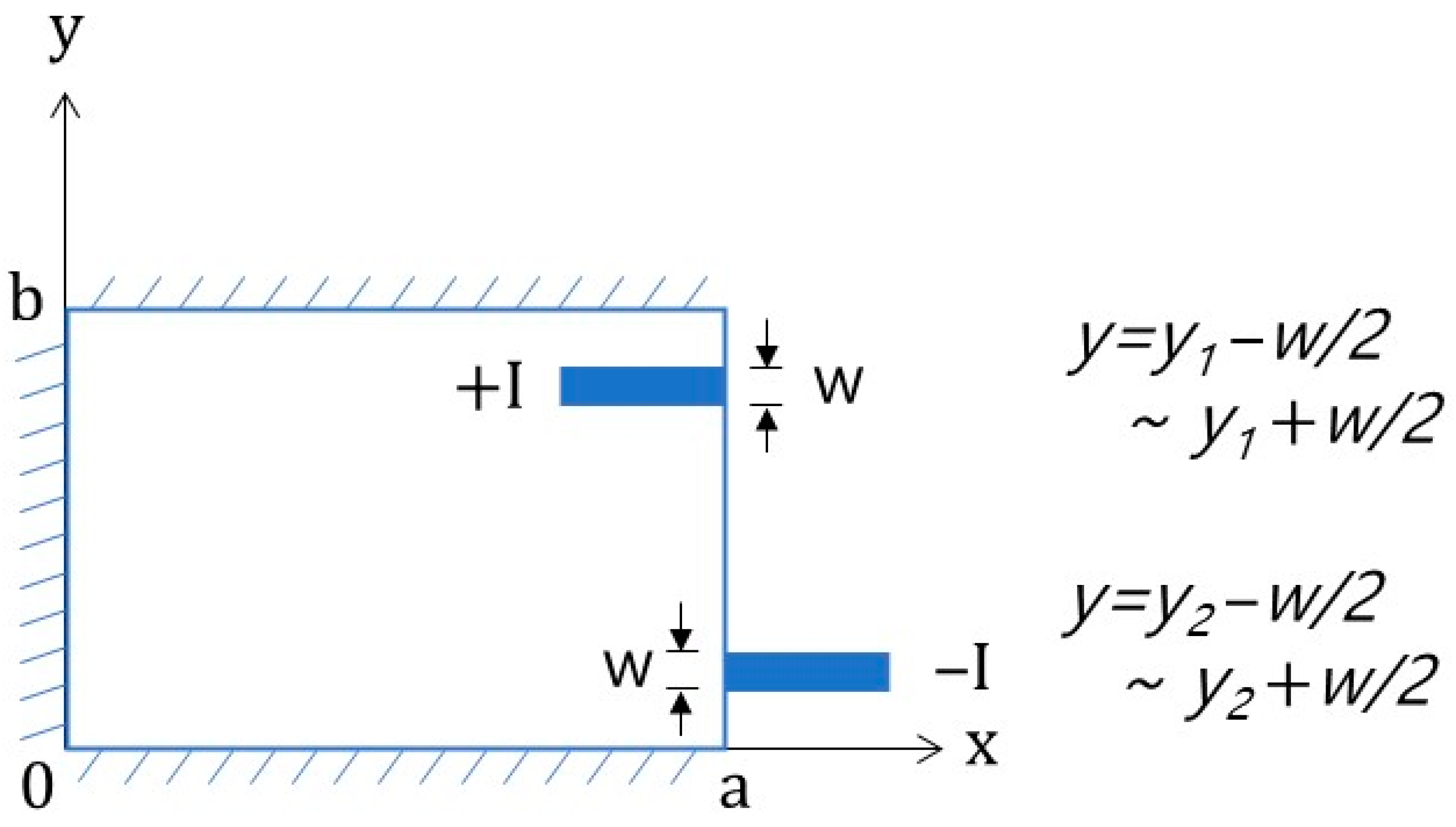
As shown in Figure 7, if current I is injected from the right boundary point (x = a, y = y₁) of the rectangular object to point x = a, y = y₂, the function of the boundary condition at x = a can be expressed by the Dirac delta function.

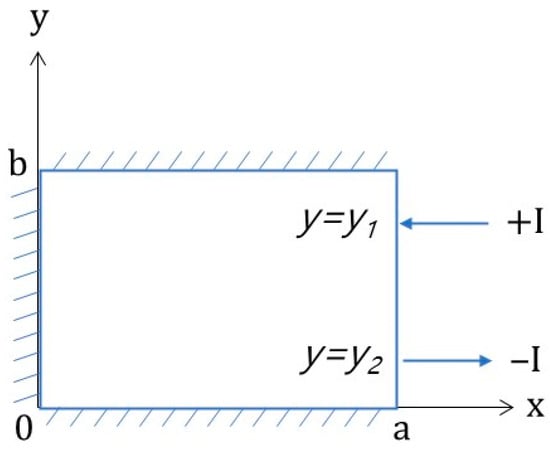
Figure 7. Boundary illustration of the current injection model using the Dirac delta function for Case 1.

The Dirac delta function is written as δ(y − y_k), which is δ(y − y_k) = ∞ at y = y_k and δ(y − y_k) = 0 otherwise. Using the Dirac delta function, Equation (25) becomes g(y) = 0 and f(y) = (I/σ)∙{δ(y − y₁) − δ(y − y₂)}, and A_n in Equation (17) is calculated as follows:

$$\begin{array}{l}{A}_n=\frac{2\cdot (I/\sigma )}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}\cdot \left({\displaystyle {\int }_0^b\left(\delta (y-y_1)-\delta (y-y_2)\right)\cdot \cos \left(\frac{n\pi y}{b}\right)dy}\right)\\ \hspace{1em} =\frac{2\cdot (I/\sigma )}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}\cdot \left(\cos \left(\frac{n\pi y_1}{b}\right)-\cos \left(\frac{n\pi y_2}{b}\right)\right)\end{array}$$

(26)

where, I is the injected current, σ is the electrical conductivity of concrete, and a and b are the lengths of the concrete sample along the x- and y-axes, respectively. As A_n is applied to Equation (27), the electric potential u(x, y) can be calculated, and thus the potential difference between two electrodes corresponds to the measured voltages.

$$u(x,y)={\displaystyle \sum _{n=1}^{50}\left(A_n\cdot \cosh \left(\frac{n\pi x}{b}\right)\cdot \cos \left(\frac{n\pi y}{b}\right)\right)}$$

(27)

Using nonlinear regression [17], the voltages calculated by Equation (27) are fitted to the measured voltages. Table 3 shows the nonlinear regression results. The fitted electrical conductivity was 16.077 mS∙m⁻¹, the rate of relative absolute error (RAE) was 22.009%:

$$\mathrm{Rate} \mathrm{of} \mathrm{Relative} \mathrm{Absolute} \mathrm{Error} (\mathrm{RAE} \mathrm{rate})=\frac{{\displaystyle \sum \left|\mathrm{Residuals}\right|}}{{\displaystyle \sum \left|\mathrm{Caculation}\right|}}$$

(28)

Table 3. Comparisons between the measured and calculated voltages using the Dirac delta function for Case 1 (unit: 10⁻³ Volt).

Experimental Configuration			Measured	Calculated	Residual (Mea.-Cal.)	|Res.|/Cal. (%)
Set #1	V1		0.384	0.950	−0.566	59.579
	V2		0.964	1.058	−0.094	8.885
	V3		0.964	0.765	0.199	26.013
Set #2	V1		1.269	2.008	−0.739	36.803
	V2		2.433	2.373	0.059	2.486
	V3		2.561	1.823	0.738	40.483
Set #3	V1		2.011	2.773	−0.762	27.479
	V2		3.738	3.431	0.307	8.948
	V3		3.127	2.773	0.354	12.766
Set #4	V1		0.872	1.058	−0.186	17.580
	V2		1.367	1.315	0.052	3.954
	V3		1.708	1.058	0.650	61.437

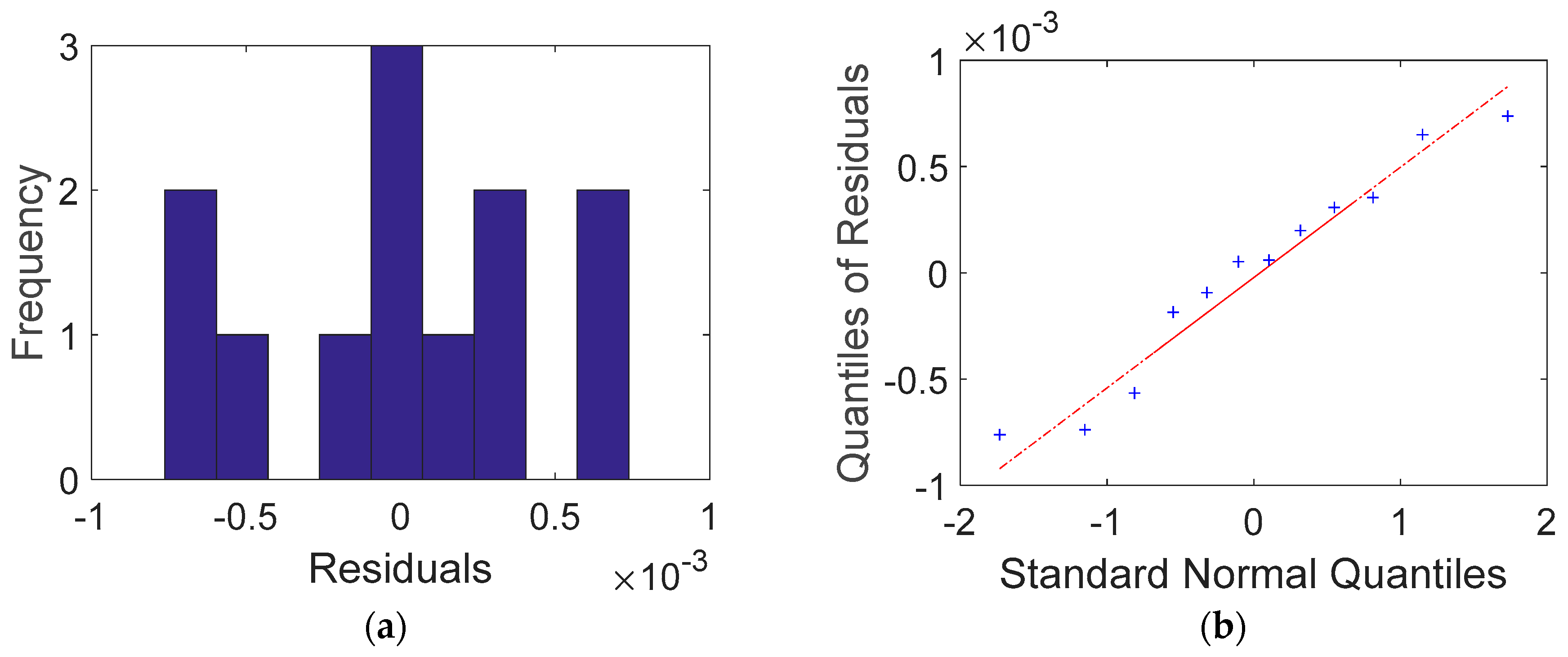
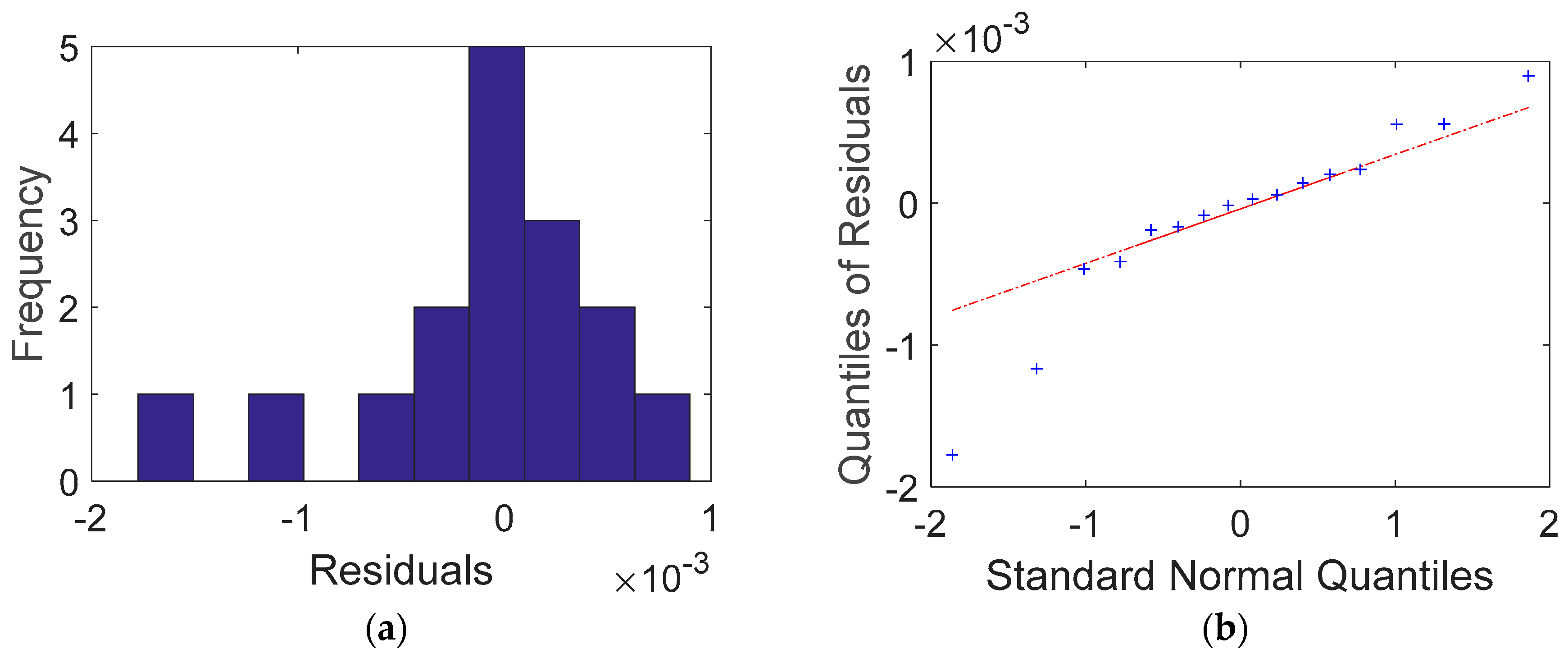
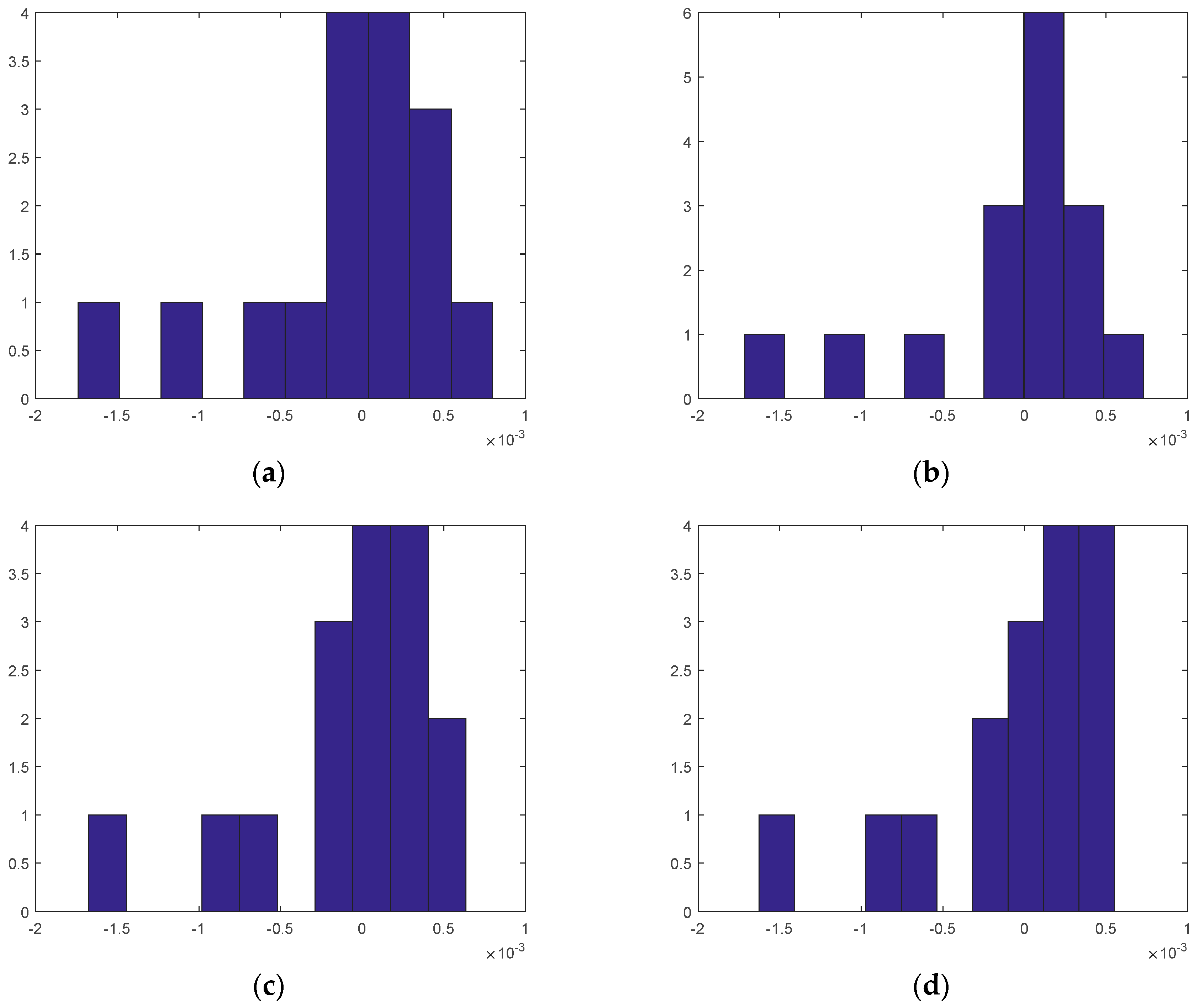
As shown in Table 3, V1 and V3 resulted in higher residuals between the calculated and measured voltages than V2 in all experimental sets (Sets #1–#4). Regardless of the path of electric current flow, the inner areas of the cement-based samples provided more stable measurements than the corner areas. This was likely due to the higher volatility of the electric potential in the corner areas. To better understand the residuals, a histogram and Q-Q (quantile-quantile) plot were drawn. The histogram shown in Figure 8a was similar to a normal distribution, except for its tail bounds induced from V1 and V3 in the corner areas. Nevertheless, the Q-Q plot in Figure 8b shows that the residuals closely followed the normal distribution.

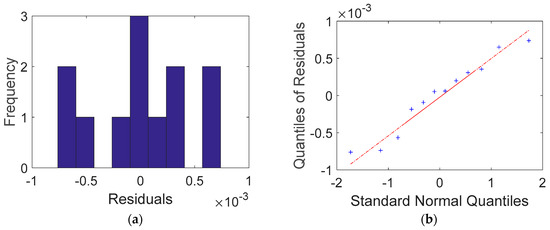
Figure 8. Comparison between a normal distribution and residuals obtained from the Dirac delta function for Case 1: (a) histogram of residuals and (the label of x axe: residuals (differences) between calculations and measurements in 10⁻³ volt unit, the label of y axe: the number of residuals in frequency) (b) Q-Q plot.

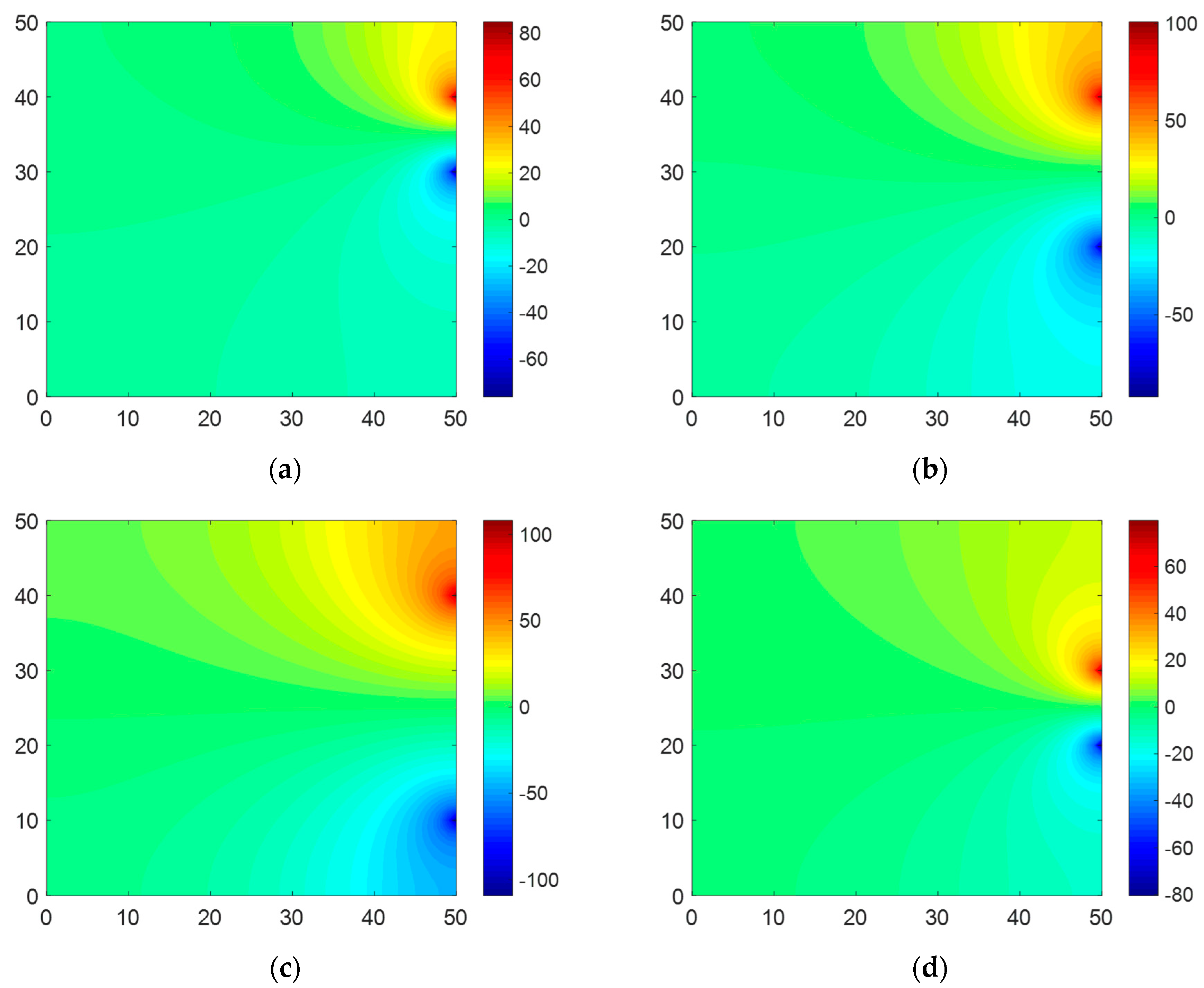
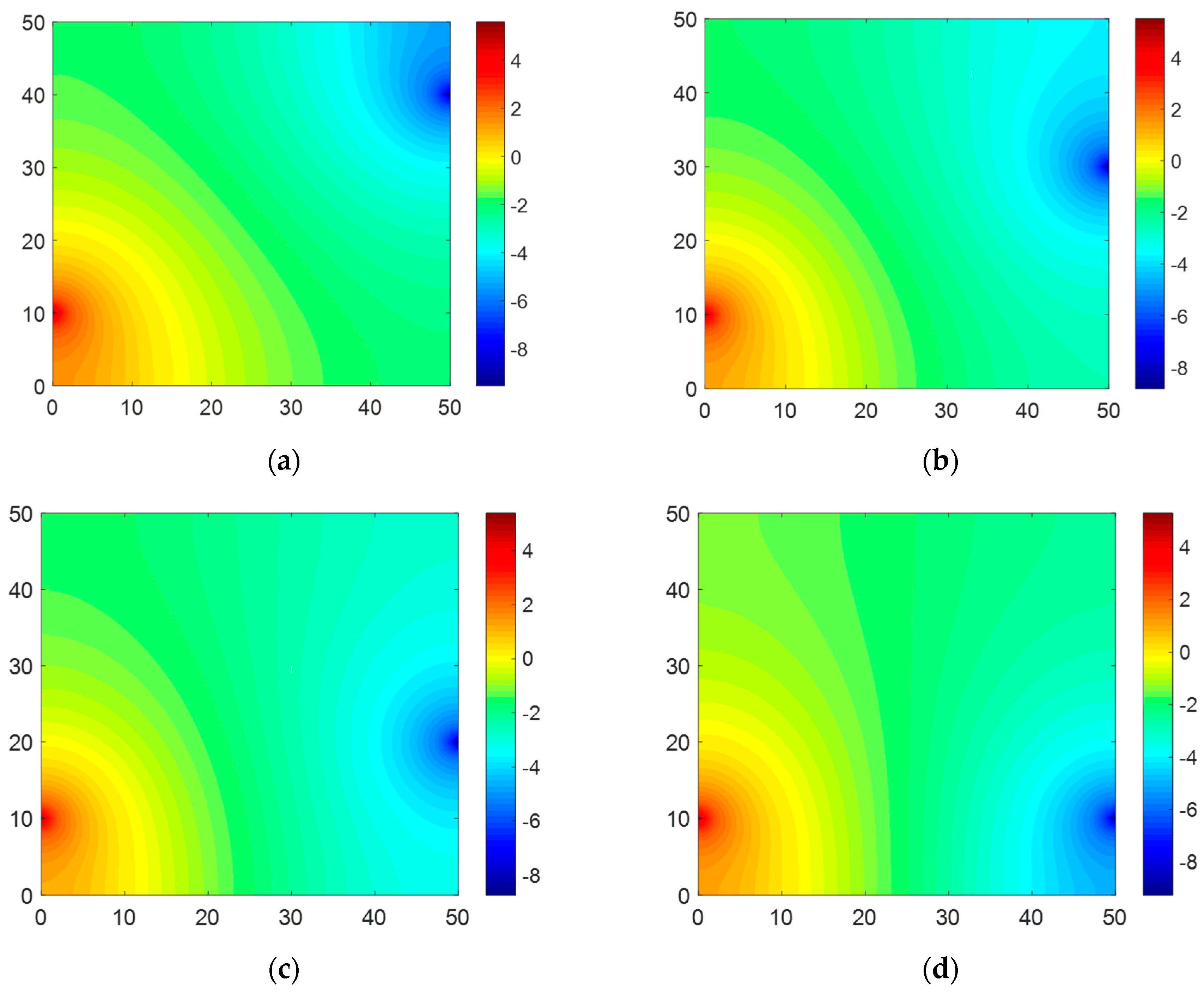
Electric potential maps were created based on the calculations from Equations (26) and (27). As shown in Figure 9, when the current-injected point was located at an inner area, the potential distribution was concentrated at that point, whereas when the point was in a corner area, the potential was distributed over a wide area. Furthermore, a significant variation in the potential field mostly occurred near the electrodes where the current flowed in and out. For other boundary interfaces, the potential change was gradual, and the potential variation was substantially smaller at the boundary interface where the voltages were measured. This might be the reason for the high RAE (22.009%) as the sensitivity to the measurement increased.

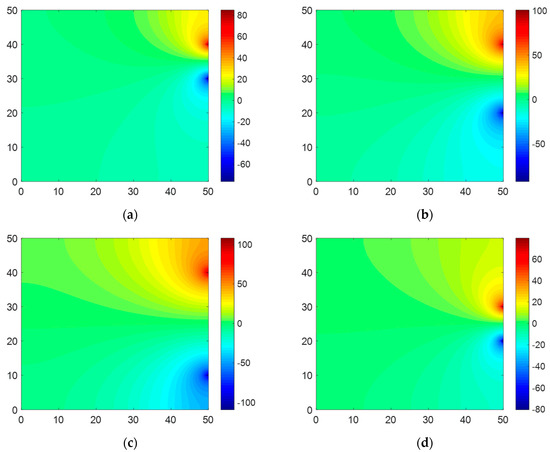
Figure 9. Electric potential maps created based on calculation from the Dirac delta function for Case 1: (a) Set #1, (b) Set #2, (c) Set #3, and (d) Set #4 (x and y axes indicate 50 × 50 mm corresponding to the size of the sample; the red and blue colors mean positive and negative voltage, respectively).

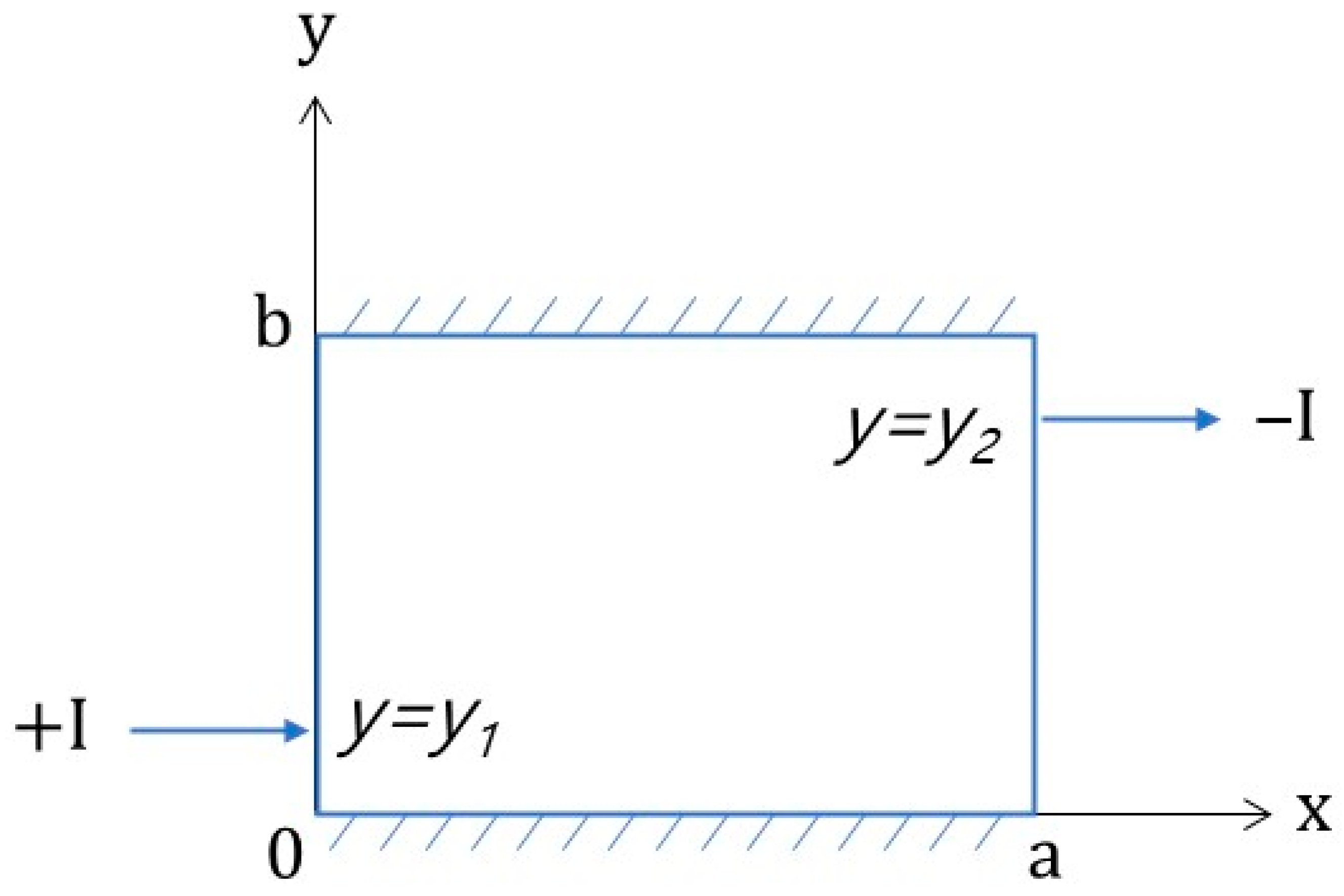
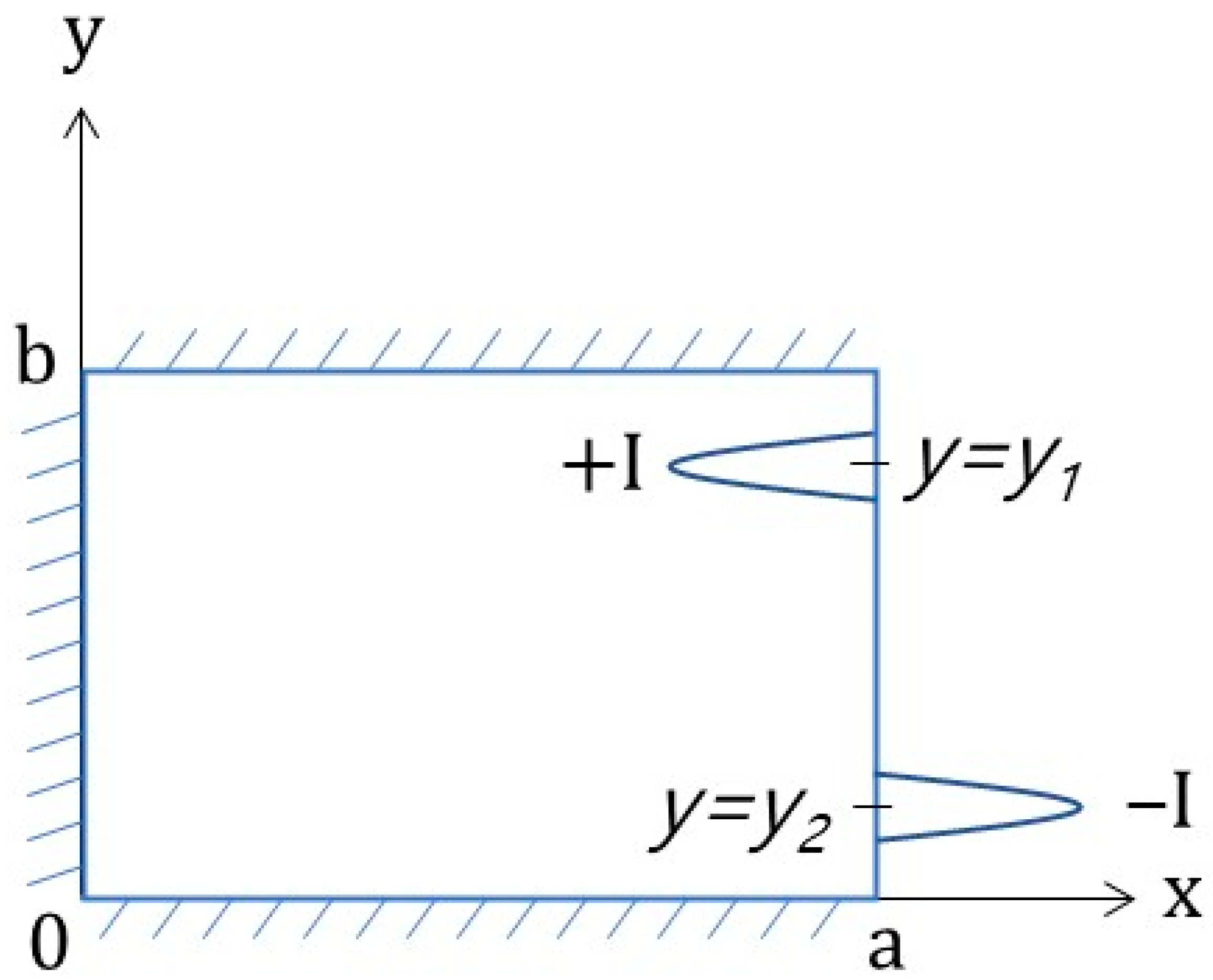
Case 2: Current Flows in from one Boundary and out from the Opposite Boundary

As shown in Figure 10, the current was injected at y = y₁ on the left boundary (x = 0) of the rectangular area and flowed out at y = y₂ on the right boundary (x = a). Using the Dirac delta function, the functions of boundary conditions f(y) and g(y) can be expressed as follows:

$$g(y)=\frac{I}{\sigma }\cdot \delta (y-y_1) \mathrm{and} f(y)=-\frac{I}{\sigma }\cdot \delta (y-y_2)$$

(29)

where, δ is the Dirac delta function, I is the current, and σ is the electrical conductivity.

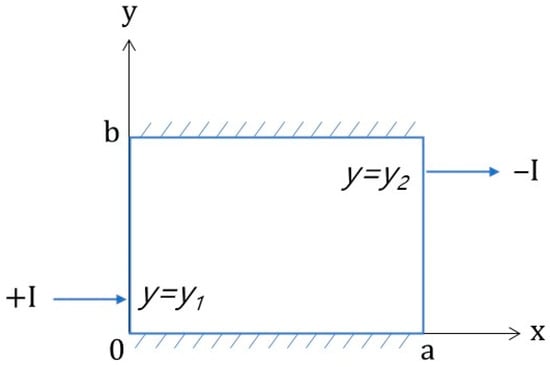
Figure 10. Boundary illustration of the current injection model using the Dirac delta function for Case 2.

Using Equation (29), Equation (21) is converted to the following equation:

$$\left[\begin{array}{cc}0& \frac{n\pi }{b}\\ \frac{n\pi }{b}\sinh \left(\frac{n\pi a}{b}\right)& \frac{n\pi }{b}\cosh \left(\frac{n\pi a}{b}\right)\end{array}\right]\cdot \left[\begin{array}{c}{A}_n\\ B_n\end{array}\right]=\left[\begin{array}{c}-\frac{2}{b}\left(\frac{I}{\sigma }\right)\cos \left(\frac{n\pi y_1}{b}\right)\\ \frac{2}{b}\left(-\frac{I}{\sigma }\right)\cos \left(\frac{n\pi y_2}{b}\right)\end{array}\right]$$

(30)

By going through the inverse matrix process, A_n and B_n in Equation (30) can be expressed as follows:

$$\begin{array}{l}{A}_n=\frac{2\left(\raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.\right)}{n\pi \tanh \left(\frac{n\pi a}{b}\right)}\cos \left(\frac{n\pi y_1}{b}\right)+\frac{2\left(-\raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.\right)}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}\cos \left(\frac{n\pi y_2}{b}\right)\\ B_n=-\frac{2\left(\raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.\right)}{n\pi }\cos \left(\frac{n\pi y_1}{b}\right)\end{array}$$

(31)

The part, a₀∙x + b₀, of Equation (22) is solved as follows:

$$\begin{array}{l}{a}_0=\frac{1}{b}{\displaystyle {\int }_0^b-f(y)dy}=-\frac{1}{b}\cdot \left(\frac{I}{\sigma }\right){\displaystyle {\int }_0^b\delta (y-y_1)dy=}-\frac{1}{b}\cdot \left(\frac{I}{\sigma }\right)\\ b_0=-\frac{a_0}{2}\end{array}$$

(32)

The completed series solution of u(x, y) is as follows:

$$u(x,y)={\displaystyle \sum _{n=1}^{50}\left[\left\{A_n\cosh \left(\frac{n\pi }{b}x\right)+B_n\sinh \left(\frac{n\pi }{b}x\right)\right\}\cos \left(\frac{n\pi }{b}y\right)\right]}+a_{0}x+b_0$$

(33)

Equation (33) was fitted to the measured voltages. The fitted electrical conductivity was 15.907 mS∙m⁻¹ and the RAE was 4.372%. Thus, Case 2 had a considerably low RAE than Case 1 (22.009%). In contrast to conventional medical uses, the application of EIT to cement-based materials, which have electricity insulation characteristics, requires the electric current to pass through the sample thoroughly. This might be because Case 2 had higher voltage value than Case 1, reflecting a significant difference in the electric potential field. A comparison of the calculated potential fields is presented below.

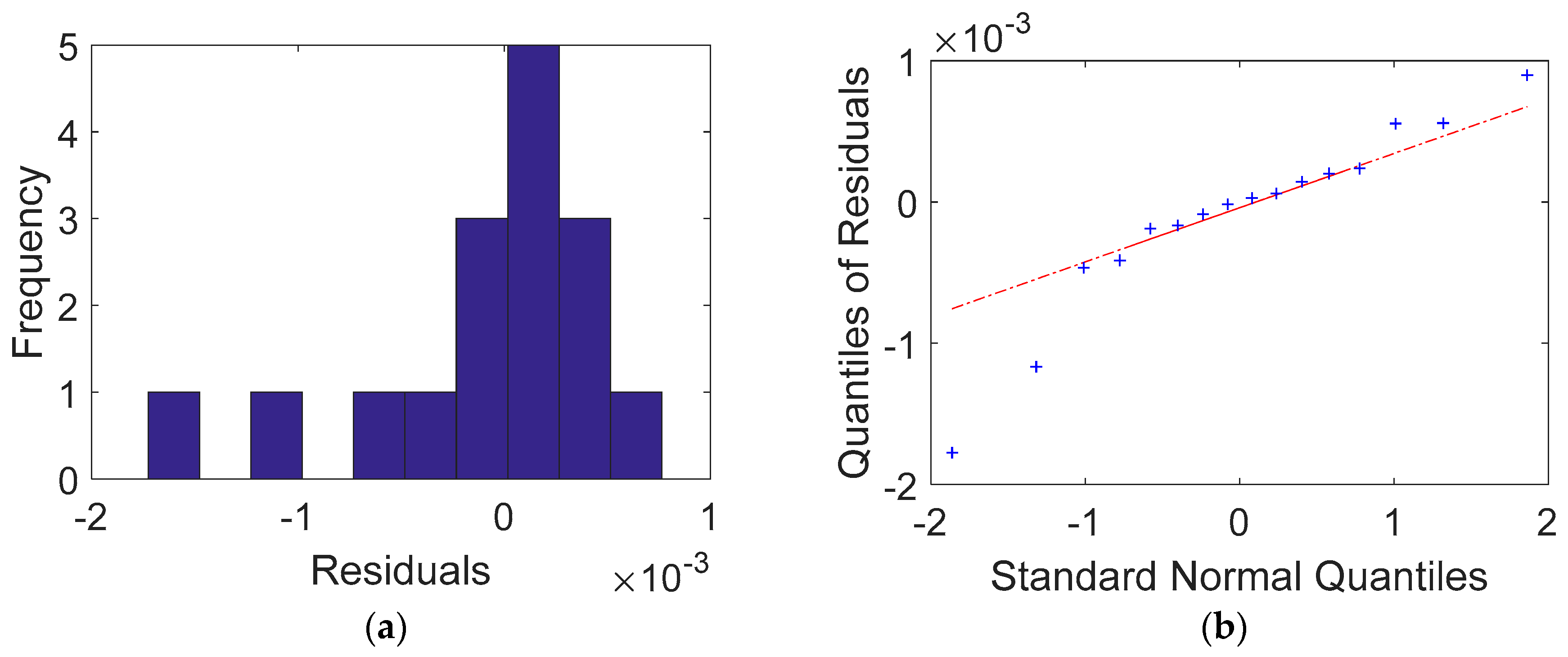
Table 4 shows the measured and calculated voltages. Large errors occurred in V1 in Sets #5 to #8. These values were potential differences between two electrodes that had a current-injected electrode between them. Therefore, for voltage measurements, selecting two electrodes that have a current-injected electrode between them should be avoided because the electric field around the current-injected electrode changes so dramatically that the voltage measurement is considerably less accurate. Figure 11 shows the histogram and Q-Q plot of residuals. The residuals exhibited a well-defined normal distribution, except for two outliers toward the minus direction obtained from V1 of Sets # 6 and # 7. As previously noted, these voltages were measured from two electrodes with a current-injected electrode between them. The Q-Q plot also shows that the residuals followed the normal distribution, except for a heavy tail toward the negative values. Generally, residuals that follow a well-defined normal distribution function indicate a reliable validation between a theoretical solution and a well-controlled measurement [15].

Table 4. Comparisons between the measured and calculated voltages using the Dirac delta function for Case 2 (unit: 10⁻³ Volt).

Experimental Configuration		Measured	Calculated	Residual (Mea.−Cal.)	|Res.|/Cal. (%)
Set #1	V1	17.923	17.896	0.027	0.151
	V2	8.716	8.882	−0.166	1.869
Set #2	V1	16.638	16.826	−0.188	1.117
	V2	7.981	7.921	0.060	0.757
Set #3	V1	15.412	15.497	−0.085	0.548
	V2	7.090	6.852	0.238	3.473
Set #4	V1	14.015	14.428	−0.413	2.862
	V2	6.064	6.079	−0.015	0.247
Set #5	V1	6.936	7.401	−0.464	6.269
	V2	13.440	13.298	0.143	1.075
Set #6	V1	4.392	5.558	−1.167	20.997
	V2	12.895	12.337	0.558	4.523
Set #7	V1	1.386	3.160	−1.774	56.139
	V2	12.166	11.268	0.898	7.969
Set #8	V1	1.332	1.130	0.202	17.876
	V2	11.050	10.495	0.555	5.288

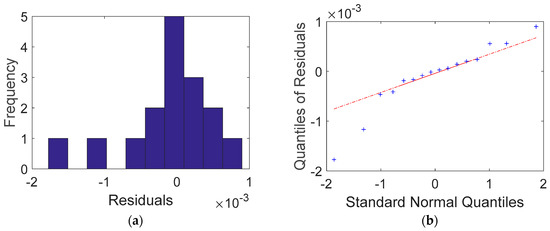
Figure 11. Comparison between a normal distribution and residuals obtained from the Dirac delta function for Case 2: (a) histogram of residuals (the label of x axe: residuals (differences) between calculations and measurements in 10⁻³ volt unit, the label of y axe: the number of residuals in frequency) (b) Q-Q plot.

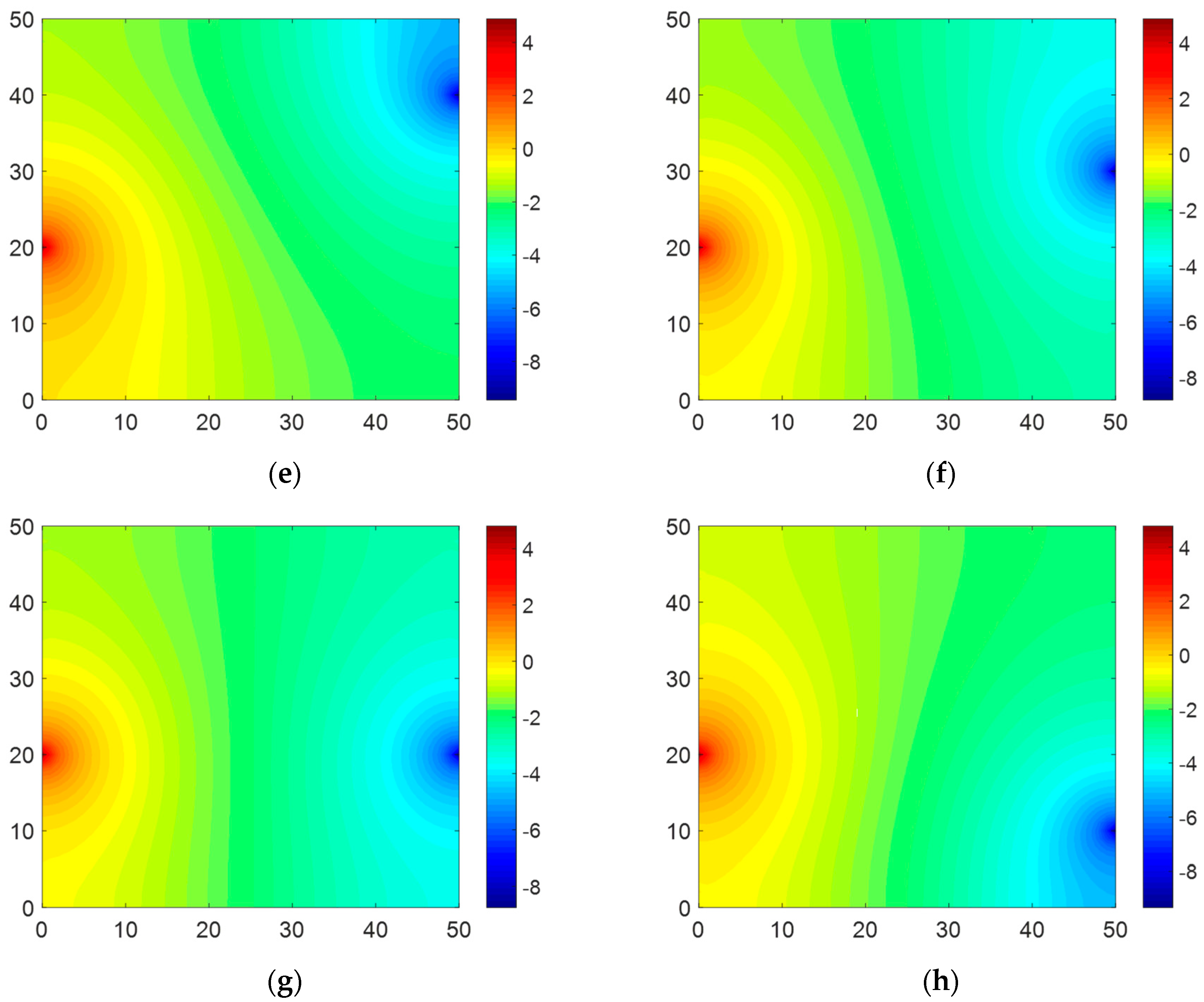
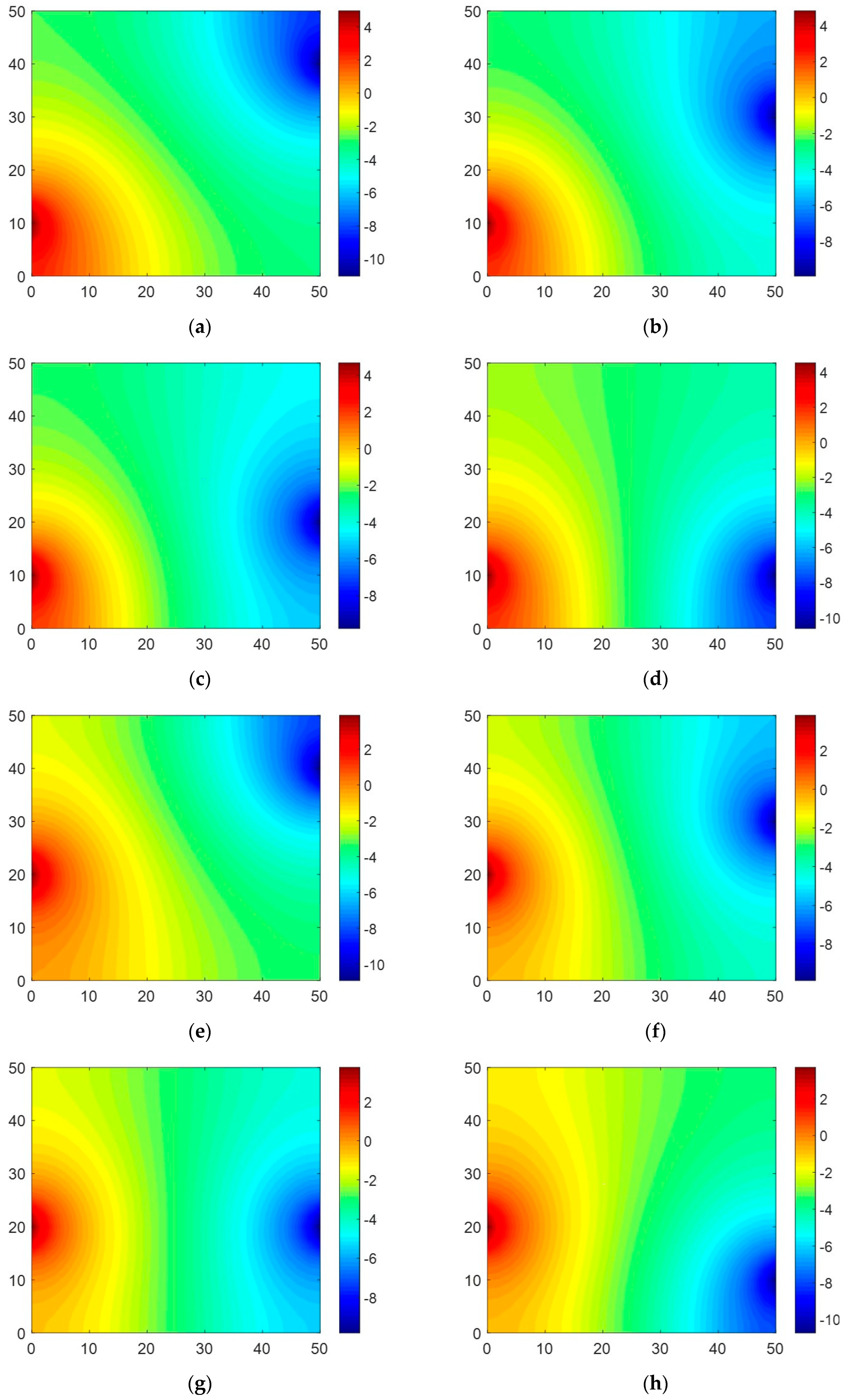
Figure 12 shows the electric potential field obtained from Equations (31)–(33). Compared to Case 1 (Figure 9), the change in potential difference in Case 2 occurred in a wider area. A similar phenomenon was in fact observed in Sets #3 and #4 in Case 1 (Figure 9c,d). When the two electrodes where the current flowed in and out were sufficiently far apart, a change in potential difference occurred over a large area of the domain. This clear potential difference caused higher voltage values in Case 2, making it less sensitive to voltage measurements. For this reason, the RAE in Case 2 was considerably lower than that in Case 1 (Table 3 and Table 4).

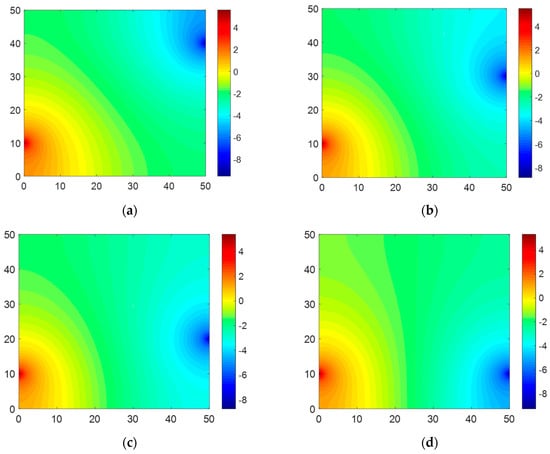
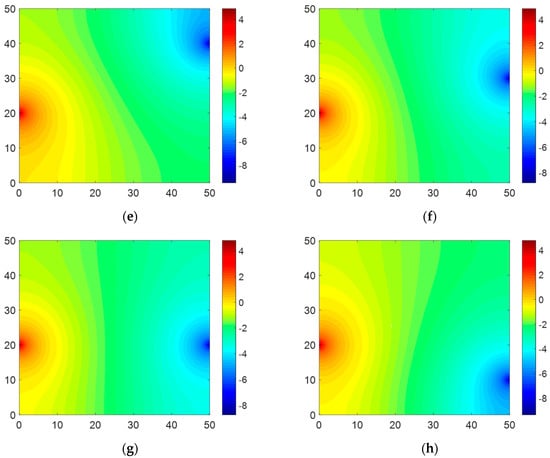
Figure 12. Electric potential maps created based on calculation from the Dirac delta function for Case 2: (a) Set #1, (b) Set #2, (c) Set #3, (d) Set #4, (e) Set #5, (f) Set #6, (g) Set #7, and (h) Set #8 (x and y axes indicate 50 × 50 mm corresponding to the size of the sample; the red and blue colors mean positive and negative voltage, respectively).

4.2.2. Heaviside Step Function

Case 1: Current Flows in and out of the Same Boundary Surface

Figure 13 illustrates the boundary conditions of Case 1 for the model using the Heaviside step function. Since current I enters and exits through electrodes of a certain width w, the height of the Heaviside step function becomes I/w. Therefore, the integral function containing f(y) is as follows:

$${\displaystyle {\int }_0^{b}f(y)\cdot \cos \left(\frac{n\pi y}{b}\right)}dy={\displaystyle {\int }_{y_1-w/2}^{y_1+w/2}\frac{1}{\sigma }\cdot \frac{I}{w}\cdot \cos \left(\frac{n\pi y}{b}\right)}dy-{\displaystyle {\int }_{y_2-w/2}^{y_2+w/2}\frac{1}{\sigma }\cdot \frac{I}{w}\cdot \cos \left(\frac{n\pi y}{b}\right)}dy$$

(34)

where, I is the injected current, σ is the electrical conductivity of concrete, w is the electrode width, y₁ and y₂ are the electrode positions where current flows in and out, and a and b are the lengths of the concrete sample along the x- and y-axes, respectively.

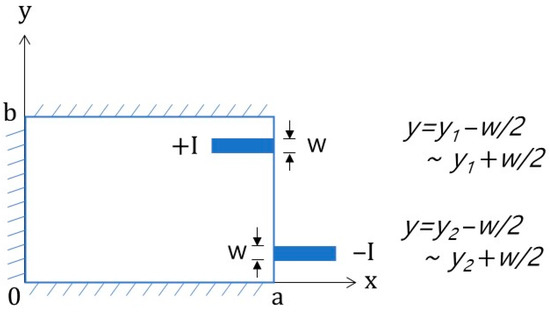
Figure 13. Boundary illustration of the current injection model using the Heaviside step function for Case 1 (w: electrode width).

The coefficients of the series A_n for the electric potential field equation can be determined by deriving Equation (35) from Equation (34). Here, A_n of Equation (27) is calculated by Equation (35), so that u(x, y) contains the injected current flow described by the Heaviside step function.

$$\begin{array}{l}{A}_n=\frac{2}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}\cdot \left({\displaystyle {\int }_0^{b}f(y)\cdot \cos \left(\frac{n\pi y}{b}\right)dy}\right)\\ \hspace{1em}\hspace{1em} \frac{2\cdot (I/\sigma )}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}\cdot \left({\displaystyle {\int }_{y_1-w/2}^{y_1+w/2}\frac{1}{w}\cdot \cos \left(\frac{n\pi y}{b}\right)}dy-{\displaystyle {\int }_{y_2-w/2}^{y_2+w/2}\frac{1}{w}\cdot \cos \left(\frac{n\pi y}{b}\right)}dy\right)\end{array}$$

(35)

Table 5 shows a comparison of the measured and calculated voltages. The fitted electrical conductivity was 16.010 mS∙m⁻¹, and the RAE rate was 21.987%. Compared to the Dirac delta function, the Heaviside step function marginally reduced the RAE. This reduction came from V1 and V3 of Sets #1 and #2, which had high residuals. Since the results obtained from the Dirac delta and the Heaviside step functions were similar, their histograms and Q-Q plots were also similar.

Table 5. Comparisons between the measured and calculated voltages using the Heaviside step function for Case 1 (unit: 10⁻³ Volt).

Experimental Configuration		Measured	Calculated	Residuals (Mea.−Cal.)	|Res.|/Cal. (%)
Set #1	V1	0.384	0.949	−0.565	59.536
	V2	0.964	1.058	−0.094	8.885
	V3	0.964	0.766	0.198	25.849
Set #2	V1	1.269	2.007	−0.738	36.771
	V2	2.433	2.373	0.059	2.486
	V3	2.561	1.824	0.737	40.406
Set #3	V1	2.011	2.773	−0.762	27.479
	V2	3.738	3.431	0.307	8.948
	V3	3.127	2.773	0.354	12.766
Set #4	V1	0.872	1.058	−0.186	17.580
	V2	1.367	1.315	0.052	3.954
	V3	1.708	1.058	0.650	61.437

Case 2: Current Flows in from one Boundary and out from the Opposite Boundary

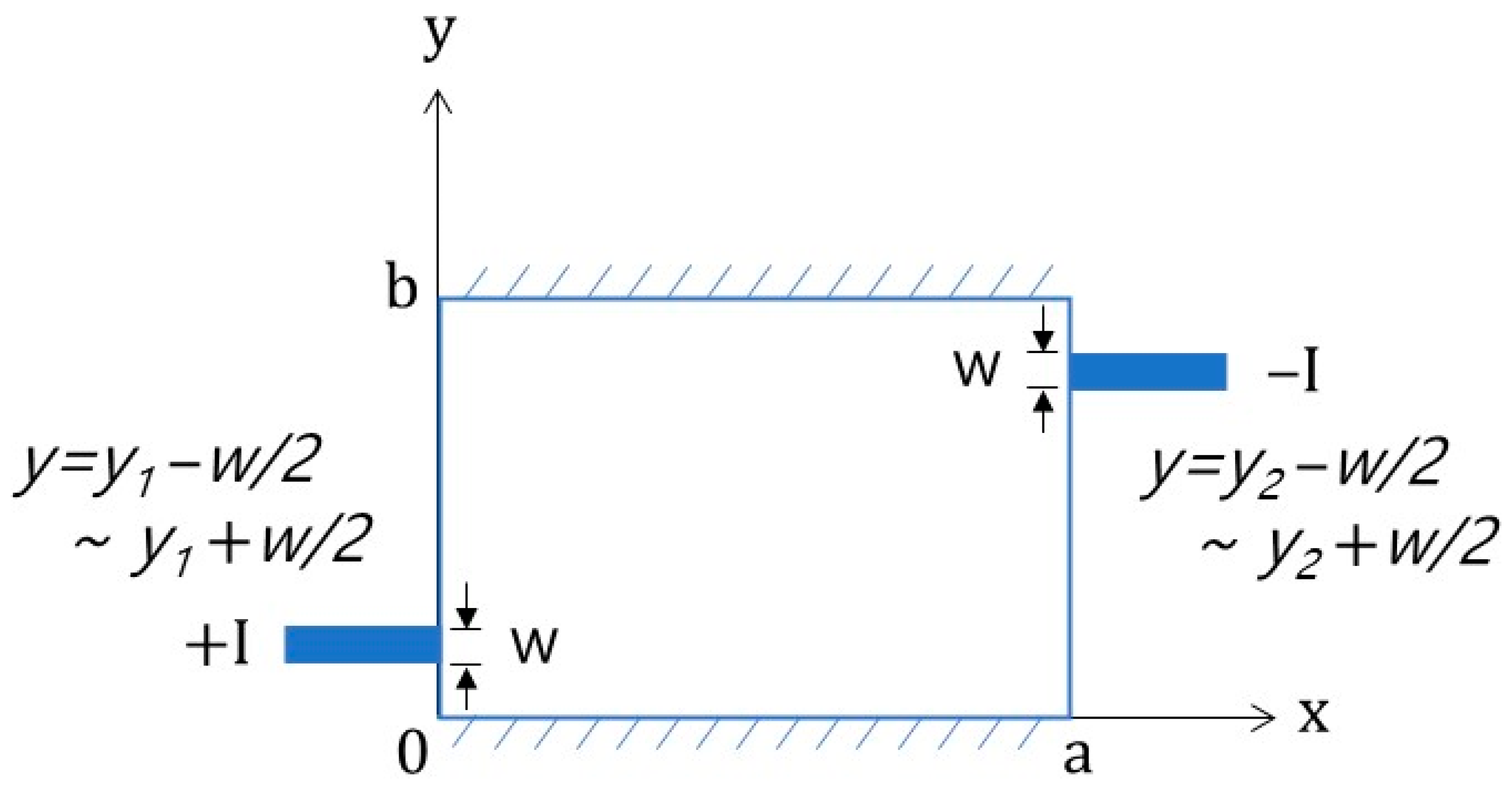
Assuming that an equally distributed current flows in and out through electrodes of width w, the configuration can be expressed as shown in Figure 14. If the current is injected into the electrode of width w at y = y₁ on the left boundary of the rectangular area and flows to another electrode at y = y₂ on the right boundary, g(y) and f(y) of the boundary condition can be expressed as follows:

$$\begin{array}{l}g(y)=\left\{\begin{array}{c}\frac{1}{\sigma }\cdot \frac{I}{w}{, \mathrm{y}}_1-\frac{w}{2}\le y\le {\mathrm{y}}_1+\frac{w}{2}\\ 0, \mathrm{otherwise}\end{array}\right.\\ f(y)=\left\{\begin{array}{c}-\frac{1}{\sigma }\cdot \frac{I}{w}{, \mathrm{y}}_2-\frac{w}{2}\le y\le {\mathrm{y}}_2+\frac{w}{2}\\ 0, \mathrm{otherwise}\end{array}\right.\end{array}$$

(36)

where, I is the injected current, σ is the electrical conductivity of concrete, w is the electrode width, and y₁ and y₂ are the electrode positions where the current flows in and out, respectively. Functions f(y) and g(y) are applied to obtain A_n and B_n as follows:

$$\left[\begin{array}{cc}0& \frac{n\pi }{b}\\ \frac{n\pi }{b}\sinh \left(\frac{n\pi a}{b}\right)& \frac{n\pi }{b}\cosh \left(\frac{n\pi a}{b}\right)\end{array}\right]\cdot \left[\begin{array}{c}{A}_n\\ B_n\end{array}\right]=\left[\begin{array}{c}-\frac{2}{b}{\displaystyle {\int }_{y_1-\frac{w}{2}}^{y_1+\frac{w}{2}}\frac{1}{\sigma }\cdot \frac{I}{w}\cos \left(\frac{n\pi y}{b}\right)dy}\\ \frac{2}{b}{\displaystyle {\int }_{y_2-\frac{w}{2}}^{y_2+\frac{w}{2}}-\frac{1}{\sigma }\cdot \frac{I}{w}\cos \left(\frac{n\pi y}{b}\right)dy}\end{array}\right]$$

(37)

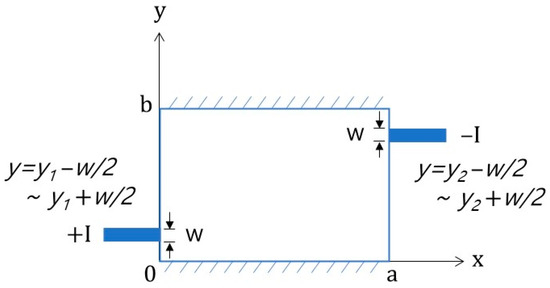
Figure 14. Boundary illustration of the current injection model using the Heaviside step function for Case 2 (w: electrode width).

As a result, A_n and B_n can be obtained as follows:

$$\begin{array}{l}{A}_n=\frac{2\cdot \raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$(\sigma \cdot w)$}\right.}{n\pi \tanh \left(\frac{n\pi a}{b}\right)}{\displaystyle {\int }_{y_1-\frac{w}{2}}^{y_1+\frac{w}{2}}\cos \left(\frac{n\pi y}{b}\right)dy}+\frac{2\left(-\raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$(\sigma \cdot w)$}\right.\right)}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}{\displaystyle {\int }_{y_2-\frac{w}{2}}^{y_2+\frac{w}{2}}\cos \left(\frac{n\pi y}{b}\right)dy}\\ B_n=-\frac{2\cdot \raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$(\sigma \cdot w)$}\right.}{n\pi }{\displaystyle {\int }_{y_1-\frac{w}{2}}^{y_1+\frac{w}{2}}\cos \left(\frac{n\pi y}{b}\right)dy}\end{array}$$

(38)

Furthermore, a₀ and b₀ are calculated as follows:

$$\begin{array}{l}{a}_0=\frac{1}{b}{\displaystyle {\int }_0^b-f(y)dy}=-\frac{1}{b}{\displaystyle {\int }_{y_1-\frac{w}{2}}^{y_1+\frac{w}{2}}\left(\frac{I}{\sigma \cdot w}\right)dy=}-\frac{1}{b}\cdot \left(\frac{I}{\sigma }\right)\\ b_0=-\frac{a_0}{2}\end{array}$$

(39)

When all coefficients (A_n, B_n, a₀, and b₀) are applied to Equation (33), function u(x, y) is the electric potential field over the rectangular domain.

Table 6 shows a comparison between the measured and calculated voltages using the Heaviside step function. Throughout the fitted values, the electrical conductivity was 16.073 mS∙m⁻¹, and the RAE was 4.218%. Compared to the Dirac delta function, the RAE decreased from 4.372% to 4.218%. This reduction was evenly distributed across all data. This is clearly shown in the histogram and Q-Q plot of Figure 15. The asymmetry in the normal distribution was lower than that in the Dirac delta function. Although a heavy tail was also observed in the Q-Q plot of Case 2, the data were evenly distributed above and below the reference line of the plot in the −1 to 1 interval of the standard normal quantiles.

Table 6. Comparisons between the measured and calculated voltages using the Heaviside step function for Case 2 (unit: 10⁻³ Volt).

Experimental Configuration		Measured	Calculated	Residual (Mea.−Cal.)	|Res.|/Cal. (%)
Set #1	V1	17.923	17.881	0.041	0.229
	V2	8.716	8.816	−0.101	1.146
Set #2	V1	16.638	16.828	−0.189	1.123
	V2	7.981	7.871	0.110	1.398
Set #3	V1	15.412	15.518	−0.106	0.683
	V2	7.090	6.817	0.273	4.005
Set #4	V1	14.015	14.464	−0.449	3.104
	V2	6.064	6.053	0.010	0.165
Set #5	V1	6.936	7.324	−0.387	5.284
	V2	13.440	13.320	0.120	0.901
Set #6	V1	4.392	5.506	−1.115	20.251
	V2	12.895	12.375	0.520	4.202
Set #7	V1	1.386	3.143	−1.757	55.902
	V2	12.166	11.321	0.845	7.464
Set #8	V1	1.332	1.143	0.189	16.535
	V2	11.050	10.558	0.492	4.660

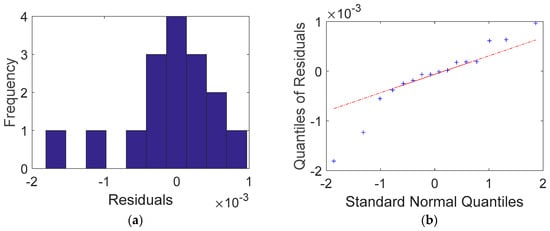
Figure 15. Comparison between a normal distribution and residuals obtained from the Heaviside step function for Case 2: (a) histogram of residuals (the label of x axe: residuals (differences) between calculations and measurements in 10⁻³ volt unit, the label of y axe: the number of residuals in frequency) (b) Q-Q plot.

4.2.3. Gaussian Function

Case 1: Current Flows in and out of the Same Boundary Surface

Figure 16 illustrates the boundary conditions when the Gaussian function was applied to the current injection model. Here, boundary condition function g(y) = 0 because the boundary surface at x = 0 has no current flow, while f(y) can be expressed as follows:

$$f(y)=\left(\frac{I}{\sigma }\right)\cdot \left(\frac{1}{{\sigma }_s\sqrt{2\pi }}\right)\left[e^{-0.5{\left(\frac{y-y_1}{{\sigma }_s}\right)}^2}-e^{-0.5{\left(\frac{y-y_2}{{\sigma }_s}\right)}^2}\right]$$

(40)

where, I is the injected current, σ is the electrical conductivity of concrete, σ_s is a standard deviation for the Gaussian function, and y₁ and y₂ are the electrode positions where the current flows in and out, respectively. Standard deviation σ_s is an important constant. The electric potential field function corresponding to the Gaussian function has not yet been derived, but constant σ_s will first discussed using the electric potential function, which will be derived later.

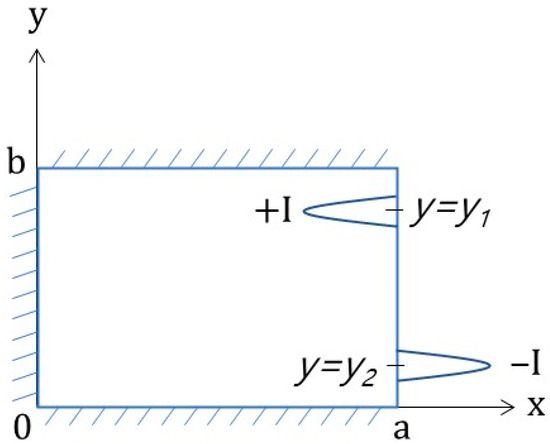
Figure 16. Boundary illustration of the current injection model using Gaussian function for Case 1.

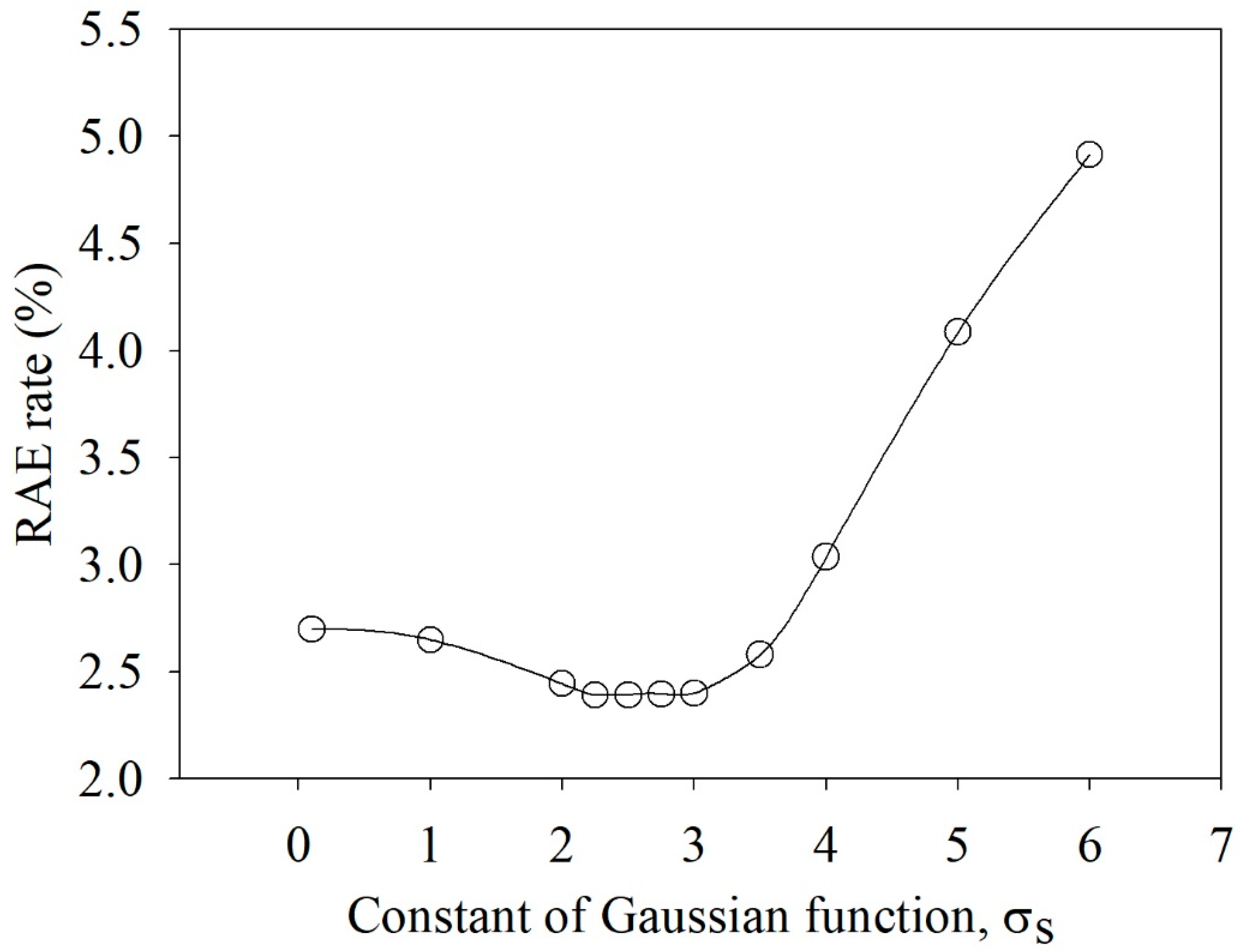
Figure 17 shows the plot of the RAE as a function of σ_s using Gaussian function in Case 2, which had in a low RAE. In this case, the voltage data from V1 of Sets #6 to #8 were excluded as outliers because the fitting process was mainly dominated by these three sets, whose residual values were much higher than those of the others. Figure 18 shows histograms with various σ_s values. As shown in Figure 17, a σ_s value between 2 and 3 had the lowest RAE. Figure 18 shows that the histogram of residuals followed the normal distribution most closely with σ_s = 2.5. Therefore, considering that the electrode width was 5 mm, half that width is the best selection for constant σ_s.

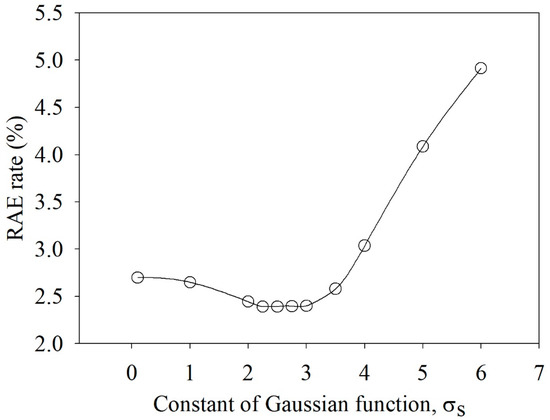
Figure 17. Relative absolute error as a function of constant σ_s of the Gaussian function for Case 2.

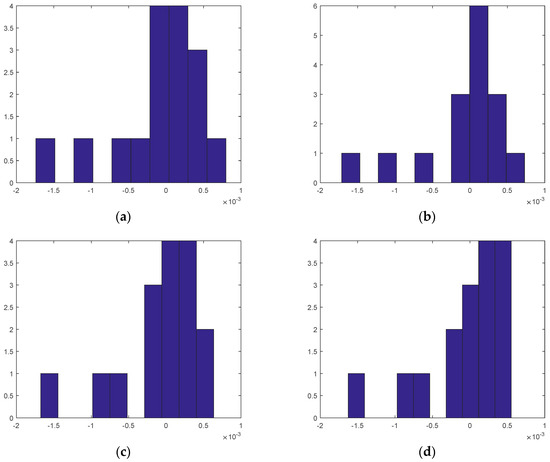
Figure 18. Histograms of residuals at different σ_s values: (a) σ_s = 2.0, (b) σ_s = 2.5, (c) σ_s = 3.0, and (d) σ_s = 3.5 (the label of x axe: residuals (differences) between calculations and measurements in 10⁻³ volt unit, the label of y axe: the number of residuals in frequency).

Equation (41) provides the coefficients of series A_n using Equation (40). By applying Equation (41) to Equation (27), it is possible to obtain the electric potential equation u(x, y) for Case 1.

$$\begin{array}{l}{A}_n=\frac{2}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}\cdot \left({\displaystyle {\int }_0^{b}f(y)\cdot \cos \left(\frac{n\pi y}{b}\right)dy}\right)\\ \hspace{1em}=\frac{2\cdot (I/\sigma )}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}\cdot \left(\frac{1}{{\sigma }_s\sqrt{2\pi }}\right){\displaystyle {\int }_0^b\left[e^{-0.5{\left(\frac{y-y_1}{{\sigma }_s}\right)}^2}-e^{-0.5{\left(\frac{y-y_2}{{\sigma }_s}\right)}^2}\right]\cdot \cos \left(\frac{n\pi y}{b}\right)dy}\end{array}$$

(41)

Table 7 shows a comparison between the measured and calculated voltages. The fitted electrical conductivity was 15.915 mS∙m⁻¹, and the RAE was 21.955%. The RAE was marginally reduced compared to the Heaviside step function. Since the residual rates of the Gaussian function shown in Table 7 were similar to those of the Heaviside step function, the histograms and Q-Q plots of two functions were also strikingly similar. For this reason, the histogram and Q-Q plot of the Gaussian function are not displayed here.

Table 7. Comparisons between the measured and calculated voltages using the Gaussian function for Case 1 (unit: 10⁻³ Volt).

Experimental Configuration		Measured	Calculated	Residual (Mea.−Cal.)	|Res.|/Cal. (%)
Set #1	V1	0.384	0.948	−0.564	59.494
	V2	0.964	1.058	−0.094	8.885
	V3	0.964	0.768	0.196	25.521
Set #2	V1	1.269	2.006	−0.737	36.740
	V2	2.433	2.373	0.059	2.486
	V3	2.561	1.826	0.735	40.252
Set #3	V1	2.011	2.774	−0.763	27.505
	V2	3.738	3.431	0.307	8.948
	V3	3.127	2.774	0.353	12.725
Set #4	V1	0.872	1.058	−0.186	17.580
	V2	1.367	1.315	0.052	3.954
	V3	1.708	1.058	0.650	61.437

Case 2: Current Flows in from one Boundary and out from the Opposite Boundary

Assuming that the current in the electrode follows a normal distribution, its distribution can be illustrated as shown in Figure 19. The current flows in from the right boundary and out from the left boundary. Therefore, g(y) and f(y), which represent the right and left boundaries, respectively, can be expressed by Equation (42).

$$\begin{array}{l}g(y)=\left(\frac{I}{\sigma }\right)\cdot \left(\frac{1}{{\sigma }_s\sqrt{2\pi }}\right)\cdot e^{-0.5{\left(\frac{y-y_1}{{\sigma }_s}\right)}^2}\\ f(y)=-\left(\frac{I}{\sigma }\right)\cdot \left(\frac{1}{{\sigma }_s\sqrt{2\pi }}\right)\cdot e^{-0.5{\left(\frac{y-y_2}{{\sigma }_s}\right)}^2}\end{array}$$

(42)

where, I is the injected current, σ is the electrical conductivity of concrete, σ_s is a standard deviation for the Gaussian function, and y₁ and y₂ are the electrode positions where the current flows in and out, respectively. Using g(y) and f(y), A_n and B_n are obtained from a matrix inverse of Equation (43).

$$\left[\begin{array}{cc}0& \frac{n\pi }{b}\\ \frac{n\pi }{b}\sinh \left(\frac{n\pi a}{b}\right)& \frac{n\pi }{b}\cosh \left(\frac{n\pi a}{b}\right)\end{array}\right]\cdot \left[\begin{array}{c}{A}_n\\ B_n\end{array}\right]=\left[\begin{array}{c}-\frac{2}{b}\left(\frac{I}{\sigma }\right)\cdot \left(\frac{1}{{\sigma }_s\sqrt{2\pi }}\right){\displaystyle {\int }_0^b{e}^{-0.5{\left(\frac{y-y_1}{{\sigma }_s}\right)}^2}\cos \left(\frac{n\pi y}{b}\right)dy}\\ \frac{2}{b}\left(\frac{I}{\sigma }\right)\cdot \left(\frac{1}{{\sigma }_s\sqrt{2\pi }}\right){\displaystyle {\int }_0^b-e^{-0.5{\left(\frac{y-y_2}{{\sigma }_s}\right)}^2}\cos \left(\frac{n\pi y}{b}\right)dy}\end{array}\right]$$

(43)

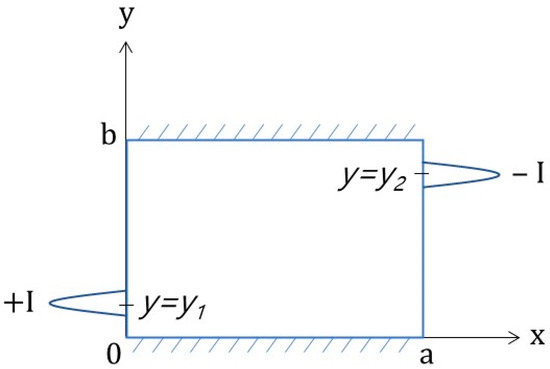
Figure 19. Boundary illustration of the current injection model using the Gaussian function for Case 2.

Consequently, the necessary coefficients (A_n, B_n, a₀, and b₀) of Equation (33), are derived by Equations (44) and (45).

$$\begin{array}{l}{A}_n=\frac{2\cdot \raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.}{{\sigma }_s\sqrt{2\pi }}\cdot \left\{\frac{1}{n\pi \tanh \left(\frac{n\pi a}{b}\right)}{\displaystyle {\int }_0^b{e}^{-0.5{\left(\frac{y-y_1}{{\sigma }_s}\right)}^2}\cos \left(\frac{n\pi y}{b}\right)dy}+\frac{-1}{n\pi \sinh \left(\frac{n\pi a}{b}\right)}{\displaystyle {\int }_0^b{e}^{-0.5{\left(\frac{y-y_2}{{\sigma }_s}\right)}^2}\cos \left(\frac{n\pi y}{b}\right)dy}\right\}\\ B_n=-\frac{2}{n\pi }\cdot \frac{\raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.}{{\sigma }_s\sqrt{2\pi }}{\displaystyle {\int }_0^b{e}^{-0.5{\left(\frac{y-y_1}{{\sigma }_s}\right)}^2}\cos \left(\frac{n\pi y}{b}\right)dy}\end{array}$$

(44)

$$\begin{array}{l}{a}_0=\frac{1}{b}{\displaystyle {\int }_0^b-f(y)dy}=-\frac{1}{b}\cdot \frac{I}{\sigma }\cdot \frac{1}{{\sigma }_s\sqrt{2\pi }}{\displaystyle {\int }_0^b{e}^{-0.5{\left(\frac{y-y_1}{{\sigma }_s}\right)}^2}dy=}-\frac{1}{b}\cdot \left(\frac{I}{\sigma }\right)\\ b_0=-\frac{a_0}{2}\end{array}$$

(45)

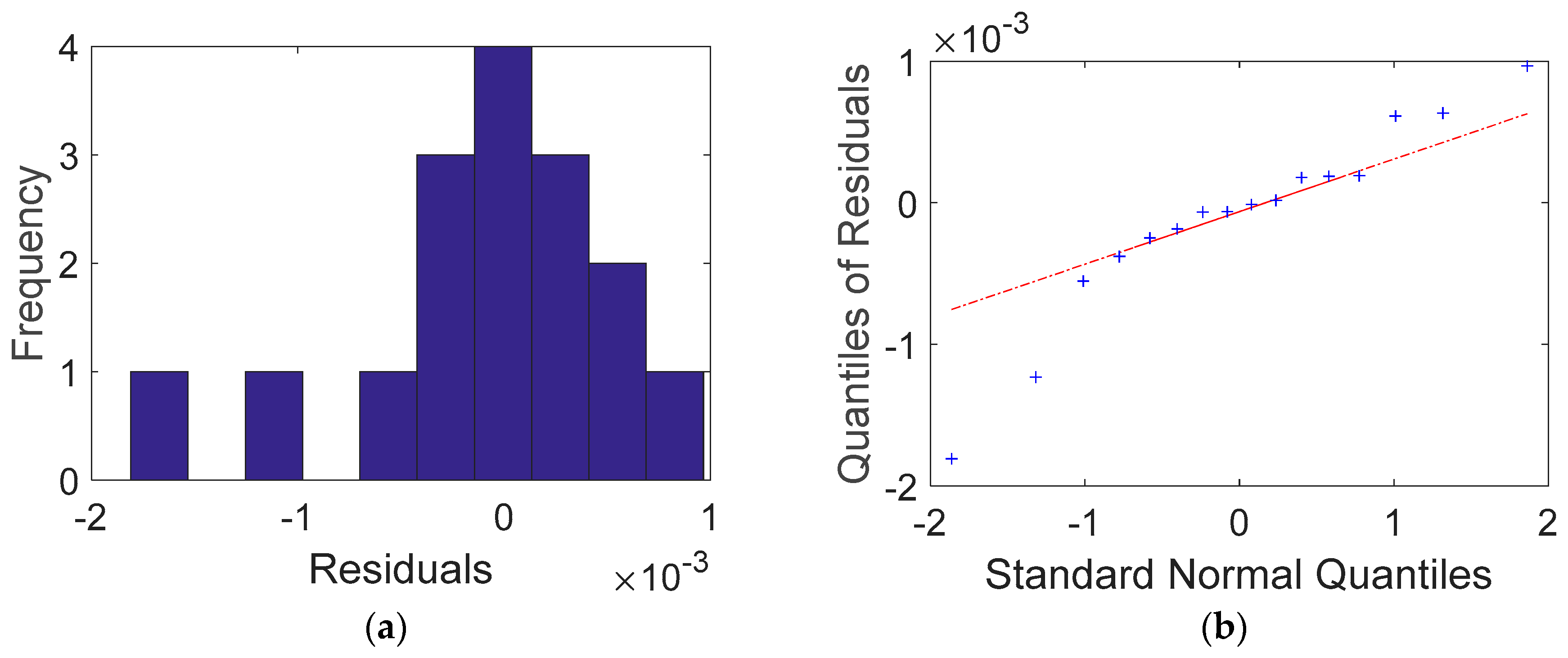
The electric potential equation u(x, y) obtained from Equations (33), (44) and (45) can be used to calculate the potential field in the rectangular domain. The fitted results showed that the electrical conductivity was 16.337 mS∙m⁻¹ and the RAE was 4.023%. The RAE rate was thus improved compared to the Dirac delta and Heaviside step functions. The improvement over the Dirac delta function was 8.0%. Table 8 shows a comparison between the measured and calculated voltages. An improvement was observed in all voltage data. The trend is better illustrated in the histogram of Figure 20. Except for two data sets corresponding to the negative heavy tail of the standard normal quantiles, the histogram shows a better-fitted normal distribution, which is more clearly shown in the Q-Q plot of Figure 20. Furthermore, Figure 21 shows the electric potential field using the Gaussian function. Compared to the Dirac delta function, the potential changed more gradually around the electrodes. This gradual variation was more similar to the real potential distribution, as revealed by the comparison between the measured and calculated voltages.

Table 8. Comparisons between the measured and calculated voltages using the Gaussian function for Case 2 (unit: 10⁻³ Volt).

Experimental Configuration		Measured	Calculated	Residual (Mea.−Cal.)	|Res.|/Cal. (%)
Set #1	V1	17.923	17.857	0.066	0.370
	V2	8.716	8.709	0.006	0.069
Set #2	V1	16.638	16.826	−0.188	1.117
	V2	7.981	7.786	0.195	2.504
Set #3	V1	15.412	15.545	−0.133	0.856
	V2	7.090	6.755	0.334	4.944
Set #4	V1	14.015	14.514	−0.499	3.438
	V2	6.064	6.007	0.056	0.932
Set #5	V1	6.936	7.203	−0.267	3.707
	V2	13.440	13.356	0.085	0.636
Set #6	V1	4.392	5.424	−1.033	19.045
	V2	12.895	12.432	0.463	3.724
Set #7	V1	1.386	3.113	−1.727	55.477
	V2	12.166	11.402	0.764	6.701
Set #8	V1	1.332	1.159	0.173	14.927
	V2	11.050	10.653	0.396	3.717

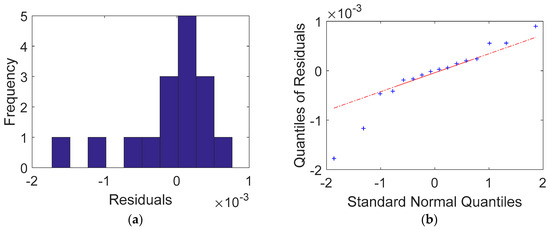
Figure 20. Comparison between a normal distribution and residuals obtained from the Gaussian function for Case 2: (a) histogram of residuals and (the label of x axe: residuals (differences) between calculations and measurements in 10⁻³ volt unit, the label of y axe: the number of residuals in frequency) (b) Q-Q plot.

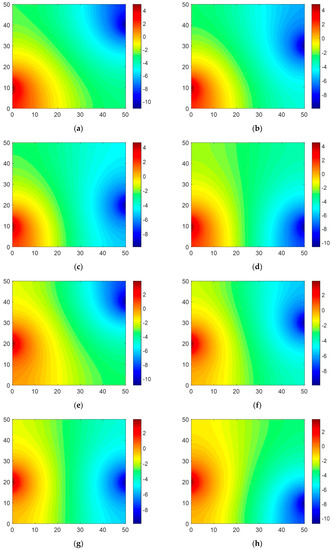
Figure 21. Electric potential maps created based on calculations using the Gaussian function for Case 2: (a) Set #1, (b) Set #2, (c) Set #3, (d) Set #4, (e) Set #5, (f) Set #6, (g) Set #7, and (h) Set #8 (x and y axes indicate 50 × 50 mm corresponding to the size of the sample; the red and blue colors mean positive and negative voltage, respectively).

5. Conclusions

This study aimed to derive EIT analytical solutions to homogeneous problems of rectangular cement-based materials and validate them experimentally. The following conclusions can be drawn from the results:

• The Shunt model can generally describe the boundary conditions of cement-based materials, which have low electrical conductivity. This was shown by both theoretical and experimental approaches. However, there are a few data having a significant discrepancy between some the calculated and measured voltages. Therefore, it is necessary to consider uncertainties such as the inhomogeneity of the sample and the humidity of the surface electrode.
• The analytical solutions were derived in the form of infinite series. A cutoff up to the 50th was effective in comparing the theoretical to the measured voltages.
• For cement-based elements, the convergence between theoretical and experimental voltages is higher when the current flows from one boundary to the opposite boundary of a sample than in and out of the same boundary.
• In comparisons between theoretical and experimental voltages, the Gaussian function shows the lowest RAE, which suggests that it describes current injection more accurately than the Dirac delta and Heaviside step functions. Especially, when σs corresponding to the necessary constant of the Gaussian function is approximately half of the electrode width, the Gaussian function provides the lowest RAE.