Uncertainty Analysis and Improvement of Propellant Gauging System Applied in Space

Abstract

Propellant Gauging is of vital importance to a spacecraft at the end of its life. Based on the Monte Carlo Method, uncertainty analysis and the improvement of propellant gauging using gas injection have been studied. As a result of the analysis, the gauging uncertainty has weak relation to the uncertainties of the volumes of the injection room and tank, the uncertainties of the pressure, and the temperature in the injection room. Relatively, the uncertainties of the temperature and pressure in the tank have a great effect on the gauging uncertainty. By improving the uncertainties of the tank pressure and temperature within 0.04% and 0.4%, the final gauging uncertainty can be obtained within 0.4%. Ground tests have been conducted and the results came out with approximately 0.4% error, well within the theoretical analysis.

1. Introduction

The measurement accuracy of residual propellant during the end-of-life state shows great value for spacecraft [1,2,3]. Based on the measured results, a detailed transferring strategy for the grave orbit can be formulated [4]. Usually, the cost of one commercial communication satellite reaches several billion dollars. It is a valuable cost-saving method to improve the measuring accuracy of the residual propellant at the end-of-life state. In this way, the satellite can be used until the very end of its service life. Researchers focusing on the ultrahigh precision method for propellant gauging have been studying this for decades [1,5].

Since the 1960s, major countries, including the United States of America and Europe, have investigated the residual propellant mass gauge (MG) [1]. There are several main MG methods. The bookkeeping (BK) method is based on the accumulation of the engine’s work time in space. The measurement uncertainty of the used propellant increases as time lapses. The BK method is primarily used in the short time measurement when the engine is working. The Pressure–Volume–Temperature method (PVT) [6,7,8,9] is often chosen as a long-duration measurement method as it is an absolute error method. The uncertainty of PVT is decided by the uncertainty of the precision of the gas law to real gas as well as the precision of the temperature and pressure sensors applied in the measurement. The PVT method is based on the gas law of pressure, temperature, and volume for a certain amount of gas. Usually, the gas law is applied with real gas modification. The Compression Mass Gauge (CMG) is a modified PVT method, which uses a bellow to change the total gas volume with the tank volume [5,10,11,12]. For instance, the changed volume is 0.01% of the tank volume. The CMG method is a promising way to obtain ultrahigh precision as well as a relatively heavy weight. The use of the CMG method also requires ultrahigh precision of the real gas law. Fu [12,13,14,15] conducted a series of ground tests using the CMG method. From their theoretical analysis, the measuring uncertainty of CMG can be within 1%, which maintains the application requirement. Tang [16,17] accomplished the residual propellant mass gauge with a modified propellant gauge system in an FY-4 satellite from the HS601. The measuring uncertainty was approximately 1.65%. The Propellant Gauge System (PGS) method is another improved PVT method, which uses a certain amount of gas to inject into the tank. From the pressure and temperature before and after the gas injection, the amount of gas in the tank can be calculated. The PGS method is usually applied in a large satellite that contains a rather large tank. In order to improve its use, the right theoretical model, such as isothermal or adiabatic process assumption, is firstly discussed. The obvious shortcoming of the PGS method is the limit of the injected gas amount. The Optical Mass Gauge (OMG) [2,18,19,20] method is based on the energy loss law during the process where the light is passed from liquid to gas. It uses the Beer–Lambert Law. The OMG method is promising for use in large tanks. However, the inner surface of the tank is required to be smooth, and the optical fiber is settled in certain locations. Cyrille [18] manufactured a theoretical machine of the OMG method by building an optical measuring setup. The uncertainty of liquid Oxygen on the ground is approximately 3%. The Thermal Mass Gauge (TMG) method [21,22,23] is applied according to the thermal response to a given thermal signal. When it comes to the end of a satellite, there remains little propellant. The thermal response can be distinguished easily as the temperature varies to a certain amount of given heat. The uncertainty of TMG is unacceptable at the early age of a satellite as there is too much propellant. In recent years, TMG has been growing to become a new research hot point [22,23,24], and it shows high measuring precision at a rather low propellant fulfillment. The Radio Frequency Mass Gauge (RFMG) method has shown rapid progress during recent years and the proven uncertainty in space is approximately 0.5~2%. The RFMG method [25,26,27,28,29] is based on the frequency response of the tank to certain incentives given at different propellant fulfillments. The tank should be reconstructed before the RFMG method is used. Ding [30] introduced the advantages and disadvantages of the RFMG method via theoretical analysis. From a recent report, the RFMG method has been verified in the SHIIVER project, and the reported uncertainties were approximately 0.5%.

Though many attempts have been made, the vital problem of MG has still not been solved completely. Among the above methods, NASA listed four promising solution methods for future study: CMG, TMG, PGS, and RFMG.

The PGS method is one of the traditional residual propellant mass gauge methods [31,32,33,34,35,36,37,38], which has the advantages of high accuracy, high success rate, and no need for engine maintenance. Tang [16,17] has applied the PGS method in China’s satellites’ residual propellant mass gauge by advancing the propellant pipes in the FY-4 satellite.

This paper will discuss the effect factor of the PGS method and the measuring uncertainty in applications. Some suggestions on the modification of precision will be proposed, and the results of the ground tests are given.

2. Theoretical Model of the PGS Method

The basic process of the PGS method is to inject gas into the propellant tank, which will improve the inner gas pressure. Then, the initial gas volume is calculated by comparing the start and end pressure in the propellant tank before and after the gas injection. As the total volume is assumed to be unchanged, the propellant volume can be obtained by taking away the gas volume.

Figure 1 shows the process of the PGS method. P, V, and T represent the pressure, volume, and temperature and the subscript $P$ and $T$ represents the gas in the injection room and in the tank.

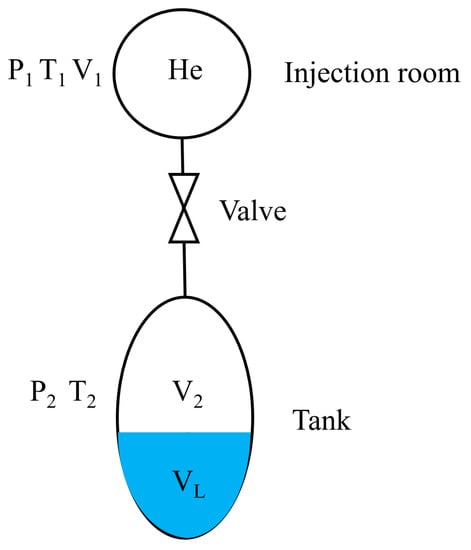
Figure 1. Schematic of the PGS method.

The gas is regarded as ideal, and then we can obtain:

$$PV=nRT$$

(1)

According to the mass conversion, the gas mass injected into the tank is equal to the gas from the bottle:

$$n_{1i}+n_{2i}=n_{1f}+n_{2f}$$

(2)

where the subscript 1, 2, i, and f represent the injection room, tank, before injection, and after injection.

Combining Equations (1) and (2), one can obtain:

$$\frac{P_{1i}{V}_{1i}}{T_{1i}}+\frac{P_{2i}{V}_{2i}}{T_{2i}}=\frac{P_{1f}{V}_{1f}}{T_{1f}}+\frac{P_{2f}{V}_{2f}}{T_{2f}}$$

(3)

The volume of the injection room and tank are suspected to be solid before and after gas injection and the propellant in the tank is non-compressible, so one can obtain:

$$V_{2i}=V_{2f}=V_2$$

(4)

$$V_{1i}=V_{1f}=V_1$$

(5)

Then comes:

$$V_2=V_1\left(\frac{P_{1i}}{T_{1i}}-\frac{P_{1f}}{T_{1f}}\right)/\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)$$

(6)

$$V_L=V_0-V_2$$

(7)

where $V_0$ represents the total volume of the tank and remains unchanged before and after gas injection.

Consequently, the residual propellant mass in the tank can be calculated as:

$$V_L=V_0-V_2=V_0-V_1\left(\frac{P_{1i}}{T_{1i}}-\frac{P_{1f}}{T_{1f}}\right)/\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)$$

(8)

3. Measuring Uncertainty Analysis and the Modified Model

3.1. Measuring Uncertainty Analysis

Based on Equation (1), the measuring uncertainty can be transferred from the effect factor as:

$$S_{V_L}=\sqrt{{\left(\frac{\partial V_L}{\partial V_0}\right)}^2{S}_{V_0}^2+{\left(\frac{\partial V_L}{\partial V_1}\right)}^2{S}_{V_1}^2+{\left(\frac{\partial V_L}{\partial P_{1i}}\right)}^2{S}_{P_{1i}}^2+{\left(\frac{\partial V_L}{\partial P_{1f}}\right)}^2{S}_{P_{1f}}^2+{\left(\frac{\partial V_L}{\partial P_{2i}}\right)}^2{S}_{P_2{}_i}^2+{\left(\frac{\partial V_L}{\partial P_{2f}}\right)}^2{S}_{P_{2f}}^2+{\left(\frac{\partial V_L}{\partial T_{1i}}\right)}^2{S}_{T_{1i}}^2+{\left(\frac{\partial V_L}{\partial T_{1f}}\right)}^2{S}_{T_{1f}}^2+{\left(\frac{\partial V_L}{\partial T_{2i}}\right)}^2{S}_{T_2{}_i}^2+{\left(\frac{\partial V_L}{\partial T_{2f}}\right)}^2{S}_{T_{2f}}^2}$$

(9)

where $S$ stands for the standard error.

From Equation (8), one can obtain:

$$\begin{array}{l}\frac{\partial V_L}{\partial V_0}=1\\ \frac{\partial V_L}{\partial V_1}=-\left(\frac{P_{1i}}{T_{1i}}-\frac{P_{1f}}{T_{1f}}\right)/\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)\\ \frac{\partial V_L}{\partial P_{1i}}=-\frac{V_1}{T_{1i}}/\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)\\ \frac{\partial V_L}{\partial P_{1f}}=\frac{V_1}{T_{1f}}/\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)\\ \frac{\partial V_L}{\partial P_{2i}}=-\frac{V_1}{T_{2i}}\left(\frac{P_{1i}}{T_{1i}}-\frac{P_{1f}}{T_{1f}}\right)/{\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)}^2\\ \frac{\partial V_L}{\partial P_{2f}}=\frac{V_1}{T_{2f}}\left(\frac{P_{1i}}{T_{1i}}-\frac{P_{1f}}{T_{1f}}\right)/{\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)}^2\\ \frac{\partial V_L}{\partial T_{1i}}=\frac{V_1{P}_{1i}}{T_{1i}^2}/\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)\\ \frac{\partial V_L}{\partial T_{1f}}=-\frac{V_1{P}_{1f}}{T_{1f}^2}/\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)\\ \frac{\partial V_L}{\partial T_{2i}}=\frac{V_1}{T_{2i}^2}\left(\frac{P_{1i}}{T_{1i}}-\frac{P_{1f}}{T_{1f}}\right)/{\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)}^2\\ \frac{\partial V_L}{\partial T_{2f}}=-\frac{V_1}{T_{2f}^2}\left(\frac{P_{1i}}{T_{1i}}-\frac{P_{1f}}{T_{1f}}\right)/{\left(\frac{P_{2f}}{T_{2f}}-\frac{P_{2i}}{T_{2i}}\right)}^2\end{array}$$

(10)

Now we take the orbit condition of the FY-4 satellite as an example. The influence on the final propellant mass gauge of each effect factor listed above will be researched.

Using a side-pipe design, the FY-4 satellite applies a high-pressure helium gas bottle to inject gas into the propellant tank. The pressure and temperature in the high-pressure helium gas bottle and tank are listed in Table 1 before and after gas injection (from the reference).

Table 1. Working conditions of PGS in FY-4.

Vessel	Before Gas Injection		After Gas Injection
	P (MPa)	T (°C)	P (MPa)	T (°C)
High-pressure gas bottle 1	10.15	/	9.30	/
High-pressure gas bottle 2	10.25	/	9.40	/
Tank 1 (Fuel)	1.45	9.5	1.57	11.5
Tank 2 (Oxygen)	1.48	13.3	1.60	14.8
Tank 3 (Fuel)	1.45	11.8	1.56	14.0
Tank 4 (Oxygen)	1.48	11	1.59	12.5

From Table 1 of the PGS method working conditions, the tank pressure before the gas injection is approximately 1.45 MPa, and then becomes 1.60 MPa after gas injection, while the temperature ranges from 10–15 °C. According to reference [39], the pressure of the injection room before injection remains approximately 5 MPa, the temperature is 15 °C (before injection), −45 °C (just after injection), and −15 °C (long after injection). The volume of high pressure is 50 L, the volume of the injection room is 7.3 L, and the tank volume is 720 L.

Considering the reference, the valve shut down when the pressure of the injection room and tank were equal. Then, the temperature reached a new balance after a period. Focusing on the time response, the pressure balance is reached within a few minutes but the temperature changes slowly. Consequently, the heat exchange of the gas in the injection room and tank with the outside environment can be neglected when the pressure becomes equal. The gas in the injection room and tank has no heat exchange.

The re-model work of the FY-4 satellite can be performed according to the analysis above.

Firstly, the gas was injected into the injection room from the 50 L high-pressure bottle. Injection valve 1 shut down the pressure of the injection room reached 5 MPa. Secondly, we waited for the temperature of the injection room and the environment to become equal. Thirdly, we applied the gas in the tank from the injection room and shut down injection valve 2 when the pressure of the injection room and the tank became equal. The gas injection process from the injection room into the tank is suspected to be isothermal. The initial temperature of the injection room is 10 °C, the initial pressure is 5 MPa, and the volume of the injection room is 7.3 L. The initial temperature of the tank is 10 °C, the initial pressure is 1.6 MPa, and the volume of the tank is 720 L. The initial fulfillment of the liquid propellant is set to 20%.

Regarding the isothermal model,

$$P{V}^{\gamma }=C$$

(11)

where $\gamma$ = 1.667, which is the process coefficient of helium.

3.1.1. Monte Carlo Method

This section mainly introduces the detailed application of the Monte Carlo Method to the error analysis. All the effect factors are well considered in the measurement uncertainty of the propellant volume.

The total volume of the tank is assumed to be $V_0$, and 10⁶ values of $V_0$ are obtained by a random normal distribution ($V_{01},V_{02},V_{03,}\cdots ,V_{0n};n={10}^6$), the mean value of which is $V_0$, and the standard error is set according to the error. The uncertainty of other effect factors is set to be 0 when the uncertainty of the tank total volume is discussed. The $V_{Ln}$ can be calculated according to Equation (7) when the uncertainty of all the effect factors equals 0.

The accuracy of each independent factor should first be settled when calculating the propellant volume. A normal distribution is applied to each factor, and the mean value of the uncertainty is 0. Then, the Monte Carlo Method can be used to calculate the uncertainty after each independent factor has its own uncertainty model.

3.1.2. Calculation Input

In the experiments applied in aerospace research, the experimental conditions are usually distinguished as degreed and over-degreed. Considering the safety of high pressure and the cost, the degreed experimental conditions are chosen in this research. In this paper, the experimental degreed factor is approximately 20 times the base pressure and 1 times the injected pressure. The tank volume of 600 L used in the theoretical analysis is a certain value of a future spacecraft.

The total tank volume is set to be 600 L, the fulfillment is 50%, and the gas volume in the tank is then 300 L. The initial pressure and temperature are 0.5 MPa and 20 °C. The initial pressure and temperature in the injection room are 0.9 MPa and 20 °C. The uncertainties of the tested pressure and temperature are set to approximately 1% FS. The liquid propellant is uncompressible. All the uncertainties are defined in full scale. We assumed that there is no heat exchange between the gas in the injection room and the tank. The whole process of the gas injection is isothermal.

$$P{V}^{\gamma }=C$$

(12)

where $C$ is a constant and the process coefficient $\gamma =1.667$.

The pressure in the injection room and in the tank is calculated as 0.50245 MPa from the isothermal assumption after the pressure reached a balanced state after gas injection. In the same process, the temperatures in the tank and injection room are 20.6 °C and −166.8 °C. A few moments later, the temperature in the injection room and tank reached the same as the environment and was 20 °C. The tank pressure became 0.50408 MPa and the injection room pressure reached 0.69605 MPa.

3.1.3. Uncertainty Analysis of Each Factor

The Monte Carlo Method is used in the uncertainty analysis above. The effect of each factor in the uncertainty is obtained. Then, the main factors are chosen to be improved.

The analysis results of Equations (6) and (7) are given in Figure 2. The effect of $V_0$, $V_P$, $P_{P_i}$, $T_{P_i}$, $P_{P_f}$, and $T_{P_f}$ on the measuring uncertainty is within 0.03% FS. The effect of $P_{T_f}$, $T_{T_f}$, $P_{T_i}$, and $T_{T_i}$ on the measuring uncertainty can reach approximately 4% FS.

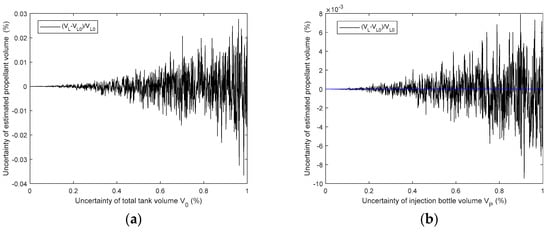
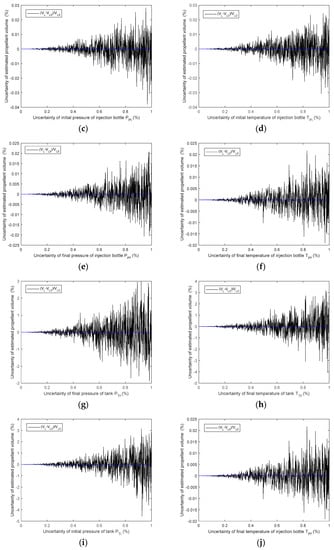
Figure 2. Effect of each factor on the final mass gauge uncertainty ((a) is of the total volume of the tank, (b) is of the injection bottle volume, (c) is of the initial pressure of the injection bottle, (d) is of the initial temperature of the injection bottle, (e) is of the final pressure of the injection bottle, (f) is of the final temperature of the injection bottle, (g) is of the final pressure of the tank, (h) is of the final temperature of the tank, (i) is of the initial pressure of the tank, and (j) is of the final tenperature of the injection bottle).

It can be easily understood that there is little effect on the measuring uncertainty of the total tank volume, propellant volume, and the temperature and pressure of the injection room before and after gas injection. However, the effect of the temperature and pressure in the tank has a great effect on the measuring uncertainty. In order to improve the final measuring uncertainty, it is necessary to improve the uncertainty of the temperature measurement and pressure gauge.

3.2. Modified Model

According to the results in Figure 2, the temperature and pressure measurement in the tank showed an important effect on the final gauge uncertainty. There seems to be a great need to improve the precision of the sensors. Then, the final measuring uncertainty can be reduced by adjusting the measuring precision in the tank. An adjustment schematic was created, and the measuring precision of the pressure and temperature was 0.04% FS and 0.35% FS.

The final mass gauge uncertainties of the adjustment schematic are shown in Figure 3.

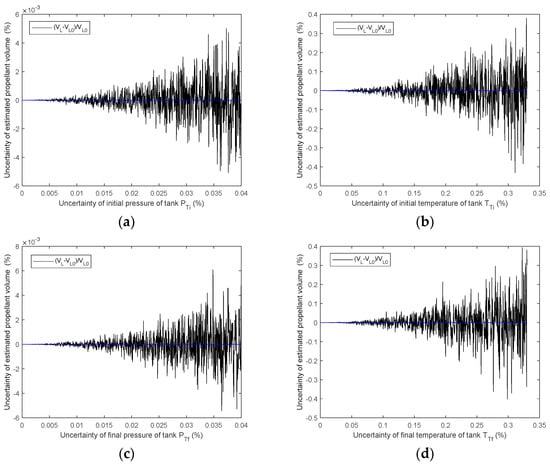
Figure 3. Effect of the improved measuring uncertainties in the tank on the final measuring uncertainty((a) is of the initial pressure of the tank, (b) is of the initial temperature of the tank, (c) is of the final pressure of the tank, and (d) is of the final temperature of the tank).

The measuring uncertainty is improved by using better temperature and pressure measurements, as shown in Figure 3. When the temperature measuring accuracy in the tank is within 0.4% FS, the final measuring uncertainty can reach 0.4% FS. When the pressure measuring accuracy in the tank is within 0.04% FS, the final measuring uncertainty can be improved to 0.008% FS. If the temperature accuracy is improved to 0.14% FS, the final uncertainty can be controlled to be within 0.1% FS. The results of the simulated calculation can be seen in Figure 4.

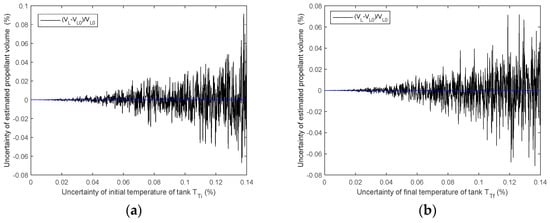
Figure 4. Effect of the temperature accuracy in the tank on the final measuring uncertainty ((a) is of the initial temperature of the tank, and (b) is of the initial temperature of the tank).

Based on the temperature and pressure range in the application of the PGS method, the pressure range is suggested to be 0–1 MPa, with an uncertainty of 0.4 kPa. The temperature range is suggested to be 18–23 °C, with an uncertainty of 0.4 K.

4. Ground Tests

Experiment Setup

Figure 5 gives the schematic of the experimental setup of the ground test.

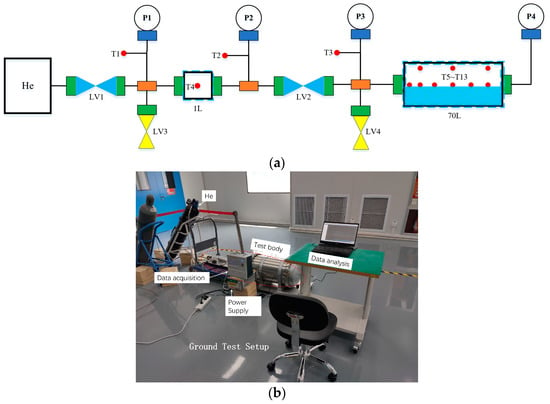
Figure 5. Experimental setup of the ground test ((a) is the schematic, and (b) is the real setup).

From Figure 5a,b, one can see the ground test setup. There is a helium gas source of approximately 13~15 MPa, an injection bottle of approximately 1 L, a propellant tank of approximately 70 L, some valves, and pressure and temperature sensors. The volume in the ground test is chosen to be small to reduce the danger as well as reduce the cost, which is approximately 10 times smaller than the theoretical model. LV1 and LV2 are valves used in the high pressure and LV2 and LV4 are valves used in the middle pressure. Temperature sensors T1 and T2 are set in the tube at the injection bottle inlet and outlet and T4 is inside the injection bottle to monitor the injection bottle temperature. Temperature sensors T3 and T5~T13 are installed in the tank inlet tube as well as on the shelf, which is built into the tank to monitor the inner gas temperature. All the test data are analyzed with a PC. When the gas injection test was conducted, the gas injected into the injection bottle and tank is released from LV3 and LV4, which will cause the pressure to be equal to the environment.

It should be mentioned that the pressure sensors are selected with ultrahigh precision at 0.04% FS and the temperature sensors are selected with a precision of 0.4% FS, while its response time to the temperature change around is 0.1 s.

The initial pressure before infusion in the injection bottle is set at 0.4, 0.5, and 0.6 MPa. Correspondingly, the initial pressure in the tank is set at 0.1 MPa.

Figure 6 shows the process of the gas injection method during which the pressure and temperature are recorded. Based on the pressure and temperature and the true value of the tank liquid, the liquid mass gauge uncertainty is calculated. The calculated results fit well with the true value of the liquid mass in the tank, with uncertainty within 0.3% FS after gas injection (t = 0 s in Figure 6c) into the tank for approximately 330 s.

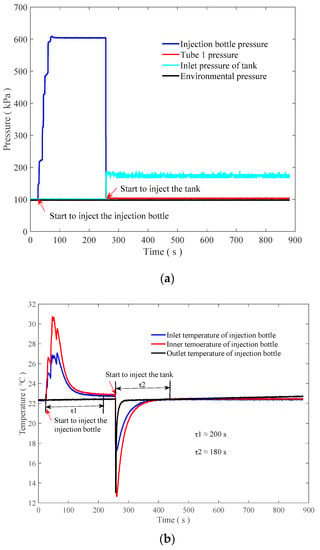
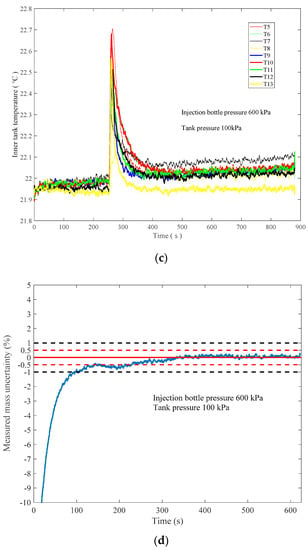
Figure 6. Mass gauge process: (a) pressure, (b,c) temperature, and (d) calculated uncertainty.

From the Monte Carlo simulations, the theoretical uncertainty can be 0.4% FS and the test result on the ground came to 0.4% FS. The test result and the theoretical analysis fit rather well. The reason for the slightly higher accuracy of the ground test than the theoretical result may be that the accuracy of the sensors is larger than the real accuracy sensors can obtain. For example, the pressure sensor with 0.04% FS can likely obtain 0.3% FS or less, which can reduce the final measurement uncertainty. The uncertainty is the ratio of the difference between the calculated volume and the weighed volume to the total tank volume of 70 L.

Table 2 gives the results of the calculated uncertainties of the gas injection method with different working conditions. From the ground test results, the pressure precision improved to 0.04% FS and the temperature precision improved to 0.4% FS, which can help to improve the mass gauge uncertainties to within 0.4% FS under the injection bottle pressure at 0.37 MPa~0.62 MPa.

Table 2. Measured mass uncertainties.

No.	Injection Bottle Pressure (kPa)	Tank Pressure (kPa)	Uncertainty (% FS)
1	374.326	102.536	−0.383
2	377.676	101.296	−0.270
3	390.306	101.976	0.120
4	399.426	98.900	−0.360
5	402.406	103.986	0.210
6	487.956	108.896	0.163
7	488.506	108.616	0.024
8	506.286	109.976	−0.199
9	503.276	105.176	−0.305
10	519.114	100.386	−0.014
11	608.356	112.156	−0.110
12	617.566	116.446	−0.220
13	603.996	114.396	0.120
14	611.216	115.656	−0.167
15	595.316	114.986	0.204

From the authors’ knowledge, the usual uncertainty of traditional PVT is approximately 2~3% FS. The reported PGS method is approximately 1.6% FS applied in an FY-4 satellite. The newest uncertainty of the RFMG method applied in SHIIVER ranges from 0.5~2% FS [28]. The uncertainty of the TMG method can reach approximately 1% FS according to the ground test [22]. The 0.4% FS uncertainty of the tested adjusted PGS method is relatively high. Compared with the other methods, the adjusted PGS method can reach an ultrahigh precision for a given time. The setup of the adjusted PGS method is relatively simple.

The improvement of the uncertainties of the temperature and pressure sensors in the tank can help to reduce the measurement uncertainty a great deal, from 1.6% FS [16,17] to 0.4% FS. This study can help to prove that an adjusted PGS method can be used in future propellant measurement that requires ultrahigh accuracy within 0.5% FS.

5. Conclusions

The effect of each factor on the final measuring uncertainty of the Propellant Gauging System Method was analyzed by applying the Monte Carlo Method. From the analyzed results, the temperature and pressure in the tank have a great effect on the measuring uncertainty. Using the suggested pressure sensor and temperature sensor with an uncertainty of 0.04% FS and 0.4% FS, the final measuring uncertainty of the Propellant Gauging System Method can reach 0.4% FS. By building a ground experimental setup, the adjusted PGS method was tested, and the inspired measurement uncertainty came to 0.4% FS, which is very high compared to the commonly used method in space.

The future work of this research should lie in the ultrahigh real gas law, which can help to calculate the exact amount of gas in each vessel. Another suggestion for further research is an applied construction for high pressure that is equal to the real working conditions in space for engine tanks.