Abstract
The ornamental stone industry has always played an important role in the world economy. Polishing the slabs to increase their gloss is important to enhance the beauty and richness of these natural materials. Many industrial polishing machines rely on a rotating head’s movement along zigzag trajectories (controlled by belt, transverse and rotational speeds), to erode the surface as stochastically as possible (to avoid scratches and other visual defects caused by paths that are too symmetrical). Optimizing (and automatizing) these three speeds together therefore represents a significant gain for the industry, in time, energy, and quality of product. In this work we show that this optimization can be accomplished by fulfilling these conditions: (1) the displacement of the polishing head after a single zigzag movement should be smaller than its diameter; and (2) the displacement of the polishing head after a single rotation should be smaller than its radius. To assess the validity of these two conditions, we studied the polishing activity using experiments based on gloss measurements of the polished stone and computer simulations based on the geometric contacts between the tool and the stone. We concluded that: (i) a clear correlation can be established between experimental and simulation data; (ii) the two displacement parameters represent an effective way to control the quality and efficiency of the polishing process; and (iii) there is a limit to the gloss acquired through polishing processes, thus polishing above a given threshold decreases the efficiency without increasing the quality. The correspondence between experimental and modelling results opens the door to further optimizations of these polishing processes in the future.
1. Introduction
Polishing is an important processing stage in several industries, particularly in ornamental stone processing. Whenever possible, polishing is performed in the industry using machines with several rotating heads that polish the stone slabs positioned over a moving belt (complex pieces are still polished by hand and large surfaces may be polished by robots following some stochastic algorithm). However, the tribological events involved in polishing are still largely unknown and need to be studied further. It is known that, in all types of materials (including metals), polishing operations may be time-consuming and expensive; and, thus, the prediction of polished surface quality is a key issue to reduce the cost of these operations [1]. Polishing of porcelain tiles has been analyzed and the kinematics involved in the polishing process were simulated by Sousa et al. [2,3].
Concerning stone materials (marbles, granites, limestones, etc.), models for predicting the surface roughness and the material removal depth of the workpiece surface are available in the literature, e.g., [4,5]. However, since the commercial applications of ornamental stones have progressively focused on the surface aspect, the study of the polishing parameters and development of the tool’s characteristics envisaging the improvement of the surface gloss have gained an increasing industrial importance, that must be paired with the scientific interest of better understanding the roughness and optical mechanisms that determine these surface phenomena.
Polishing is a finishing process aiming to achieve a high level of surface gloss, through the application of a sequence of abrasives (with decreasing grit sizes) [6,7,8,9,10]. Studying the output produced by an industrial linear polishing machine (typically with 12–26 polishing heads, each one with 4–6 polishing elements, see Figure 1) on the stone surface allows us to gain insight into the influence of the various velocities controlling a linear polishing machine: the conveyor belt velocity, VL, the transverse head velocity, VT, and the rotational velocity, ω. These studies were carried out by measuring the surface gloss (as roughness measurements proved ineffective for the highly polished surfaces that were analyzed) and comparing it with computer simulations of the same polishing procedures, to better understand the geometrical and kinematic issues determining the final results.

Figure 1.
Aspects of a linear polishing machine with rotating heads (example from PEDRINI).
2. Theoretical Background and Adopted Polishing Cycle
It has been shown [11,12] that the quality and efficiency of a stone polishing process in a linear polishing machine, with one or more rotating heads moving along zigzag trajectories, as indicated in Figure 2, is controlled by a geometric condition relating the two linear velocities, VL and VT. Condition 1 states that after a complete zigzag movement (with two linear segments), the tool center should be closer to its initial position than the tool diameter [1]: l < d, with d = 2r = tool diameter. Otherwise, there will be gaps of size l − d where the polishing head does not interact with the surface.
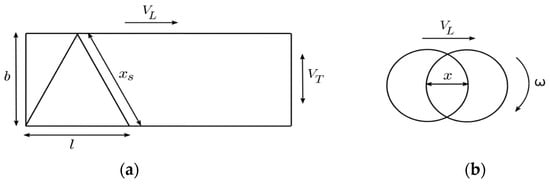
Figure 2.
The two polishing conditions. (a) l ≤ d; (b) x ≤ r.
In this work we suggest that a second condition should be considered, relating the linear and rotating tool speeds, thus including all the most relevant kinematic parameters involved in the process. Condition 2 states that after a complete rotation, the tool center should be closer to its initial position than the tool radius [11]: x < r. Otherwise each point of the surface only interacts with a small angular fraction of the circular polishing head, and in some circumstances it may not be touched at all.
The combination of these two conditions determines the relations that must exist between the three velocities involved in this polishing process: the conveyor belt velocity, VL, the transverse head velocity, VT, and the rotational head velocity, ω.
Defining b as the width of the conveyor belt, the time needed for the tool to move across the belt is given by tT = b/VT and the belt shift after a zigzag becomes l = 2bVL/VT ≤ d (limited by condition 1).
The distance xS moved by the polishing head in one linear segment (half of a complete zigzag) is given by:
Defining nS = ωtT as the number of rotations executed during the time tT by the tool head rotating at ω rotations per unit of time, the distance x that the tool head moves in a single rotation is given by (limited by condition 2):
To assess the validity of condition 2 and its combination with condition 1, we acquired experimental data and compared them with equivalent simulated results.
The polishing operations used in this work involved the last three stages of the polishing sequence (320, 400, and 5 Extra grit [13] sequence—see Figure 3). This sequence was selected to achieve a mirrored surface, with a significant gloss.

Figure 3.
Sequence of the polishing cycle abrasives used in this work: (a) 320 grit; (b) 400 grit; (c) Frankfurt 5 Extra grit.
The quantitative effectiveness of the surface polishing was then assessed experimentally measuring the gloss [14] with a TQC GL0030 glossmeter (TQC Sheen B.V., Capelle aan den Ijssel, The Netherlands)—depicted in Figure 4—at 20°, 60°, and 85° to the normal surface (the standard angles usually supported by this type of equipment). A wired grid positioned over the stone was used to define each square section where gloss was measured.

Figure 4.
The TQC GL0030 glossmeter.
The light reflected (the gloss) for a given angle can be compared with a standard scale going from 100 gloss units (GU) for a highly reflective black glass, to 0 gloss units for a perfectly matt surface [15]. Therefore, the measuring head of a glossmeter must be calibrated previously. Highly reflective materials, such as mirrors, may achieve gloss values as high as 1000, when measured at 20°. The measuring angle is selected according to the expected gloss: (1) 20° for high gloss, above 70 GU; (2) 60° for medium gloss, between 10 and 60 GU; and (3) 85° for low gloss, below 10 GU. For example, when the gloss measured at 60° is above 70 GU, the measurement should be repeated at 20° to optimize precision [16].
To quantitatively assess the polishing results, roughness measurements were also attempted, but surface fluctuations are too small for common roughness meters. Roughness measurements should be considered in tests involving much coarser surfaces where gloss is too small to be determined with standard equipment.
3. Computational Details
A few computer modelling studies have previously been reported [17,18,19] to analyze mechanical and chemical aspects related to the polishing process, but these studies do not aim to simulate the overall macroscopic result of a polishing treatment. To simulate the polishing process, we used PAM: Polishing Analysis Modelling, a new modelling tool developed to simulate the polishing processes occurring in the industry, namely, in ornamental stone processing. Users are expected to supply information describing the polishing tools, the operational parameters, and the trajectories to follow. In return, PAM simulates the polishing process and returns graphical and statistical data allowing users to investigate the results and its causes.
This two-dimensional simulator moves and rotates a tool representation (see Figure 5) over the stone surface, both represented by lattices of small cells (henceforth designated by pixels, typically with one mm size), and accumulates the contacts between them (henceforth designated by abrasion) for each cell. Each contact of a surface cell (a pixel) with the polishing tool is accumulated giving the total abrasion. Abrasion can take any value from 0 (black cells) onward, with more white regions representing progressively more eroded cells. Figure 6 represents the abrasion produced in two simulations of a tool with 320 grit elements, rotating at 600 rpm, for time steps of 100 and 1000 per second, corresponding to increment angles of 36 and 3.6 degrees, respectively. Figure 6a shows that, at this rotation speed, a time step of 0.01 s (second) is clearly insufficient to properly describe the fast movement of the tool over the stone. Decreasing the time step to 0.001 s, as shown in Figure 6b, the simulator is already able to account for the finer details of the movement, producing an essentially continuous pattern that seems to emulate a real polishing tool rotating at high speed over a fixed stone well.
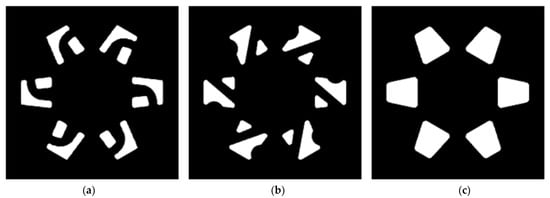
Figure 5.
Simulated tool heads used in this work, containing six abrasive elements of: (a) 320 grit; (b) 400 grit; (c) 5 Extra grit.
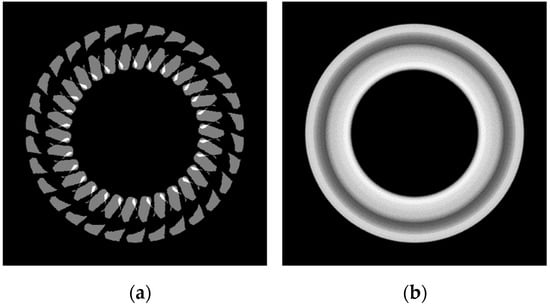
Figure 6.
Tool head with six 320 grit elements rotating at 10 rotations per second, simulated with: (a) a time step of 0.01 s, corresponding to an increment angle of 36° per step; (b) a time step of 0.001 s, corresponding to an increment angle of 3.6° per step.
The detailed data that can subsequently be acquired for more realistic simulations, involving complex paths, with straight and curved trajectories, with simultaneous translations and rotations, allow users to obtain detailed insight into the various aspects governing a stone polishing process.
When the simulation ends, the quality of the polished surface is analyzed through a range of parameters that includes, for each pixel, the total abrasion, the x and y average polishing shifts (measured from the pixel to the tool center), the average distance, and the distance standard deviation of the pixel (again, relative to the tool center). The detailed data thus acquired for each simulation allow users to obtain detailed insight into the various aspects governing a stone polishing process.
4. Experimental Procedure
As in previous works [6,11,12], we used a linear polishing machine with a single head, specifically built for polishing research (by PIRRA—Máquinas Ferramentas Lda, Estremoz, Portugal), with the following working ranges: belt speed (500–2000 mm/min), transverse speed (50–200 mm/s), rotational speed (500–1000 rpm), head pressure (1–8 bar), and water flow (10–40 L/min). Results are automatically sampled at a 10 Hz frequency and stored in a database.
The polishing head of the machine was equipped with six Frankfurt tools. The diameter of the polishing head was d = 435 mm and the cross distance on a transverse movement was b = 240 mm. We used constant values, previously optimized, for the conveyor belt speed VL = 600 mm/min, the head pressure P = 2 bar, and the water flow Q = 30 litter/min. These values were chosen to maximize quality and reproducibility of the results, and to emulate industrial data. For example, a minimum coefficient of variation (standard variation/mean value) of 6% in gloss measurements was achieved for a head pressure P = 2 bar. Six slabs of limestone, as equal as possible, were selected for these tests due to the high homogeneity of its surface. This is required to simplify the comparison between experimental and simulation data, as the simulator assumes a perfect, two dimensional, stone surface. After applying the sequence of abrasives, the surface gloss is measured and compared with the abrasion predicted in the same conditions by the polishing simulator (see Figure 7 and Figure 8). To make the measurements more precise, we used a physical grid made of wire to precisely define the sections where gloss was measured for comparison with simulated values. Throughout this work, sections with homogeneous simulated abrasion values were identified as green cells (see Figure 7) while sections with simulated abrasion values too different were marked red and discarded in the subsequent analysis and comparison with experimental results. The gloss values reported represent average values over the various green cells (typically 10, depending of each experimental pattern). After each experiment, the slab surface was reset, using the more abrasive tool head (320 grit), thus slabs were only discarded after significant wear.
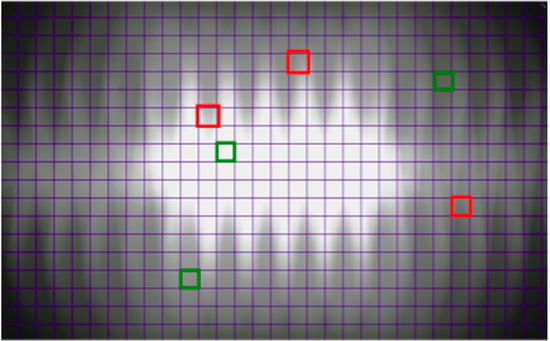
Figure 7.
Output image showing the simulated abrasion with homogeneous (green) cells and heterogeneous (red) cells.

Figure 8.
Experimental setup used to measure gloss data, using a wired grid with cells of 30 × 30 mm2, where each gloss measurement takes place.
To obey condition 1 (l < d), with VL = 600 mm/min as stated above, the transverse speed VT must be VT ≥ 20 mm/s. To obey condition 2 (x < r), with VL = 600 mm/min and VT ≥ 20 mm/s, the head rotation speed must be ω ≥ 10 rpm. Table 1 shows the various operational conditions tested in this work, whereas l values are determined by condition 1 and ω values are determined by condition 2. Clearly, setting conditions 1 and 2 leads to an increase of the transverse velocity (to decrease l) and an increase of the rotational velocity (to decrease x). The simulated linear velocity (V) matches the vectorial combination of both cross and conveyor belt velocities from the polishing machine, according to the following equation:

Table 1.
Twenty-four polishing conditions used in experimental and modelling work, obeying conditions 1 and 2.
5. Results and Discussion
Given the typical conveyor belt speed used throughout this work (VL = 600 mm/min = 1 cm/s) and the relatively large tool head diameter (d = 435 mm), condition 1 is easily obeyed, even for small transverse speeds (see Table 1). As expected, increasing the transverse speed requires larger rotational speeds to fulfil condition 2. Decreasing x, from x = r to x = r/8, to further obey condition 2, requires even larger rotational speeds.
Experimental results (see Figure 9) for surface gloss as a function of transverse velocity VT, for x = r, x = r/2, x = r/4, and x = r/8 conditions, show a significant increase in gloss from 40 to 200 mm/s for all four x conditions. For higher transverse velocities, gloss remains essentially constant, showing that a maximum threshold has been attained and further increasing the energy spent in the polishing process (by increasing the transverse and rotational speeds) does not lead to a refinement of the surface quality.
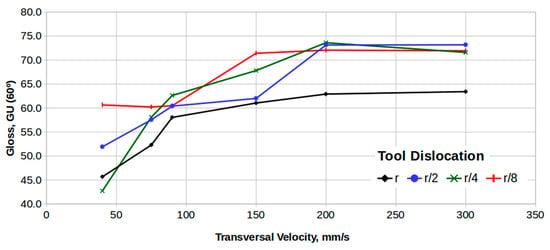
Figure 9.
Gloss as a function of transverse velocity VT, for x = r, x = r/2, x = r/4, and x = r/8.
The results clearly show that a better surface quality is obtained for smaller x values when the rotating action is more effective. For x = r, the maximum attainable gloss is below 65 GU while for x = r/2, x = r/4, and x = r/8 the maximum gloss is above 70 GU; essentially the same value in the three cases. However, for x = r/8, this limit is reached sooner for lower transverse (and rotational) speeds.
Simulation results (see Figure 10) for the same conditions show the same general trends, although the flat region for higher transverse velocities is not observed because the simulator simply adds abrasion contacts between the tool and the stone in a linear way, without considering any asymptotic effects.
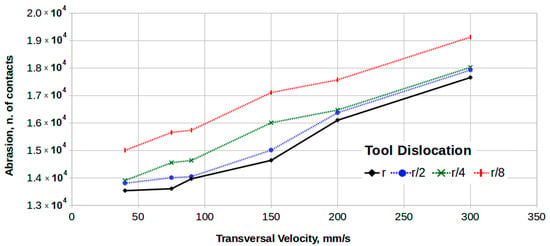
Figure 10.
Abrasion as a function of transverse velocity VT, for x = r, x = r/2, x = r/4, and x = r/8.
Clearly, gloss increases with transverse velocity and rotation velocity (which increases from x = r to x = r/8), with a slope that essentially matches the values obtained from the experimental curves. Figure 11 shows, for three different transverse velocities (for the curve for x = r/8), that as the zigzag trajectories become more parallel (when the transverse velocity increases), the polishing intensity and surface homogeneity should also increase, as indicated by experimental and simulation results.

Figure 11.
Abrasion images from polishing simulation, for three transverse velocities VT: (a) 40 mm/s; (b) 90 mm/s; (c) 200 mm/s, with x = r/8.
Figure 12 compares experimental gloss with simulation abrasion, as a function of transverse velocity, for x = r/8. While the simulated abrasion increases linearly with transverse velocity, experimental gloss shows a less predictable evolution, although the overall trends are similar for both types of data. In both cases the polishing quality increases substantially when the transverse speed increases (and rotational speed, to obey condition 2).
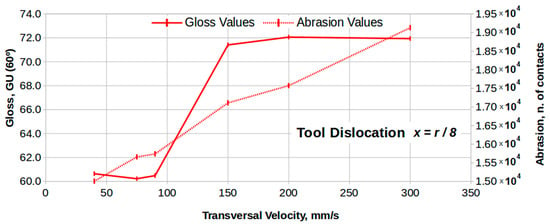
Figure 12.
Comparison of abrasion and gloss results, both as functions of transverse velocity VT, for x = r/8.
However, the data in Figure 9 and Table 1 clearly show that increasing these two speed parameters separately is not sufficient to achieve a good polished surface. Decreasing x from x = r to x = r/2 is crucial to achieve a good polished surface. Decreasing x even further to x = r/8 permits obtaining the same results at lower transverse speeds. In our case, working at x = r/8 with VT = 150 mm/s (w = 330 rpm, from Table 1) provides essentially the same final quality (Figure 10) as working at x = r/2 with VT = 200 mm/s (w = 110 rpm). On the other hand, working at low VT speeds, such as 90 mm/s, a good polished surface is never attained, even for x = r/8 and high rotational speeds (ω = 200 rpm). Transverse and rotational speeds must be expertly combined to achieve adequate levels of polishing at low energy consumption.
6. Conclusions
In this work we used experimental measurements (gloss on limestone slabs) and (abrasion) computer simulations to test the validity of two suggested conditions, l < d and x < r, to obtain the best stone polishing results with linear polishing machines with rotating heads. The results obtained for both experimental and modelling analyses indeed confirm that these two conditions must be applied to optimize polishing. These conditions are useful because they provide mathematical relations between the three velocities (conveyor belt, transverse, and rotational) involved in these industry machines.
As expected for a linear polishing machine, the polishing quality increases with transverse and rotational velocities, until a maximum surface quality is achieved. Increasing the transverse or rotational velocities even more does not lead to further refinements in surface quality. In this work we found that values for transverse velocities below 150 mm/s are insufficient to achieve the maximum surface quality and values above 250 mm/s just waste energy.
Transverse and rotational speeds must be expertly combined to obtain optimal results. Independently increasing transverse and rotational velocities does not necessarily lead to surfaces with maximum quality (industrial empirical evidence shows that surface quality can even be reduced).
Further experiments will be needed to confirm these conclusions for other types of stone materials and linear polishing machines.
Author Contributions
A.C., conceptualization, data curation, writing—original draft preparation; J.C.G.P., methodology, software, validation, data curation, visualization, writing—review and editing; P.M.A., methodology, data curation, visualization, formal analysis; L.G.R., formal analysis, resources, project administration, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The results presented in this paper were obtained in the frame of the project 24535 INOVSTONE 4.0, funded by the European Regional Development Fund (FEDER) through the Alentejo Regional Operational Programme (PO Alentejo). This research was also supported by the Portuguese Foundation for Science and Technology (FCT), through IDMEC, under LAETA, project UIDB/50022/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roman, A.L.P.D.; Chaves-Jacob, J.; Linares, J.M.; Arrazola, P.J. Analytical-method for polishing-surface prediction considering tool flexibility and grain-material interaction. J. Mater. Process. Technol. 2021, 295, 117208. [Google Scholar] [CrossRef]
- Sousa, F.J.P.; Weingaertner, W.L.; Alarcon, O.E. Computational simulation of the polishing process of stoneware tiles. In Proceedings of the World Congress of Quality in Ceramic Tiles, QUALICER 2008, Castellón, Spain, 10–13 February 2008; pp. 359–367. Available online: https://www.qualicer.org/recopilatorio/ponencias/pdfs/0833103e.pdf (accessed on 12 July 2022).
- Sousa, F.J.P.; Aurich, J.C.; Weingaertner, W.L.; Alarcon, O.E. Optimization of the kinematics available in the polishing process of ceramic tiles by computational simulations. J. Am. Ceram. Soc. 2009, 92, 41–48. [Google Scholar] [CrossRef]
- Xi, F.; Zhou, D. Modeling surface roughness in the stone polishing process. Int. J. Mach. Tools Manuf. 2005, 45, 365–372. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Xu, Z. Modeling and analysis of the material removal depth for stone polishing. J. Mater. Process. Technol. 2009, 209, 2453–2463. [Google Scholar] [CrossRef]
- Amaral, P.M.; Rosa, L.G.; Pinto, S.; Pozo, D. New line of diamond tools raise productivity in polishing stone. IDR Ind. Diamond Rev. 2004, 3, 33–37. Available online: https://scholar.tecnico.ulisboa.pt/records/3f3e886c-472e-4261-9cf7-b6938a6dff86 (accessed on 12 July 2022).
- Yang, H.D.; Li, H.C.; Zhu, C.J.; Fang, H.; Li, J. A process parameters selection approach for trade-off between energy consumption and polishing quality. Int. J. Comput. Integr. Manuf. 2018, 31, 380–395. [Google Scholar] [CrossRef]
- Soares, J.E.; Aurich, J.C.; Sousa, F.J.P.; Nascimento, R.M.; Paskocimas, C.A. Estimation of the minimum material removal thickness during the polishing process of ceramic tiles by laser triangulation. Ceram. Int. 2018, 44, 4646–4652. [Google Scholar] [CrossRef]
- Sani, A.S.A.; Sousa, F.J.P.; Hamedon, Z.; Azhari, A. Contact pressure distribution during the polishing process of ceramic tiles: A laboratory investigation. IOP Conf. Ser. Mater. Sci. Eng. 2016, 114, 012008. [Google Scholar] [CrossRef]
- Nascimento, A.S.B.D.; Sousa, F.J.P. Distribution of contact pressure over the surface of ceramic floor tiles during the polishing process. J. Eur. Ceram. Soc. 2014, 34, 3209–3215. [Google Scholar] [CrossRef]
- Barbosa, A.R.J. Validação Experimental de Simulador de Polimento em Rocha Ornamental. Master’s Thesis, Instituto Superior Tecnico, Technical University of Lisbon, Lisbon, Portugal, 15 December 2014. Available online: https://fenix.tecnico.ulisboa.pt/cursos/memat/dissertacao/846778572210523 (accessed on 8 July 2022).
- Barbosa, A.R.; Coelho, A.; Fernandes, J.C.; Amaral, P.M.; Rosa, L.G.; Pereira, J.C. A contribution for an optimization of the polishing quality of stone slabs: Simulation and experimental study using a single-head polishing machine. In Proceedings of the International Conference on Stone and Concrete Machining (ICSCM), Bochum, Germany, 2–3 November 2015; Volume 3, pp. 178–187. [Google Scholar] [CrossRef]
- Frankfurt 5 Extra for Marble. Difa Stonetech Co., Ltd. Available online: http://www.difastone.com/e_productshow/?44-Frankfurt-5-Extra-for-Marble-44.html (accessed on 8 July 2022).
- Hanson, A.R. Good Practice Guide for the Measurement of Gloss; Measurement Good Practice Guide, No. 94; National Physical Laboratory: Teddington, UK, 2006; Available online: https://www.npl.co.uk/special-pages/guides/gpg94_gloss.aspx (accessed on 12 July 2022).
- Carvalho, D.L.S. Determinação de Parâmetros do Polimento, em Três Tipos de Rochas Graníticas. Master’s Thesis, Escola de Engenharia de São Carlos, Universidade de São Paulo, Campus USP de São Carlos, São Carlos, Brazil, 17 August 2014. Available online: https://teses.usp.br/teses/disponiveis/18/18132/tde-02122011-154618/fr.php (accessed on 8 July 2022).
- Yavuz, H.; Ozkahraman, T.; Demirdag, S. Polishing experiments on surface quality of building stones tiles. Constr. Build. Mater. 2011, 25, 1707–1711. [Google Scholar] [CrossRef]
- Ranjan, P.; Balasubramaniam, R.; Jain, V.K. Molecular dynamics simulation of mechanical polishing on stainless steel using diamond nanoparticles. J. Manuf. Sci. Eng. 2019, 141, 014504. [Google Scholar] [CrossRef]
- Maekawa, K.; Itoh, A. Friction and tool wear in nano-scale machining—a molecular dynamics approach. Wear 1995, 188, 115–122. [Google Scholar] [CrossRef]
- Qin, K.; Moudgil, B.; Park, C.-W. A chemical mechanical polishing model incorporating both the chemical and mechanical effects. Thin Solid Films 2004, 446, 277–286. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).