You are currently on the new version of our website. Access the old version .
MDPIMDPI
Search all articles
Applied SciencesApplied Sciences
Download PDF
  • Article
  • Open Access

14 May 2022

The Effectiveness of Rubber Bumpers in Reducing the Effects of Earthquake-Induced Pounding between Base-Isolated Buildings

,
,
,
,
and
1
Center of Semnan Municipality, University of Applied Science and Technology, Semnan 13114-16846, Iran
2
Faculty of Civil Engineering, Semnan University, Semnan 35131-19111, Iran
3
Seismic Geotechnical and High Performance Concrete Research Centre, Civil Engineering Department, Semnan Branch, Islamic Azad University, Semnan 61349-37333, Iran
4
Faculty of Civil and Environmental Engineering, Gdańsk University of Technology, 80-283 Gdańsk, Poland
Appl. Sci.2022, 12(10), 4971;https://doi.org/10.3390/app12104971
This article belongs to the Topic Advances in Dynamics of Building Structures
Version Notes
Order Reprints

Abstract

The methods for preventing earthquake-induced structural pounding between two adjacent buildings include ensuring a sufficient separation distance between them or decreasing their relative displacement during seismic excitation. Some equations or even specific values of such gap sizes between two buildings have been introduced so as to avoid collisions. Increasing the stiffness of buildings, using tuned mass dampers, applying liquid dampers, or decreasing the mass of the structures may reduce lateral displacements, and therefore pounding can be prevented. On the other hand, the application of base isolation systems may result in the elongation of the natural period of the building, thus increasing the probability of structural pounding. The aim of the present paper is to verify the effectiveness of using rubber bumpers to reduce the negative effects of earthquake-induced pounding between base-isolated buildings. The analysis was conducted for different gap sizes between buildings, as well as for various values of the thickness, number and stiffness of rubber bumpers. The results of the study show that the peak impact force decreases with increasing thickness, stiffness, and number of bumpers. Moreover, the peak impact forces are reduced with increasing gap size. The results of the investigation clearly indicate that the use of additional rubber bumpers can be considered an effective method for reducing the negative effects of earthquake-induced pounding between base-isolated buildings.

1. Introduction

The phenomenon of earthquake-induced structural pounding is described on the basis of impacts between bridge segments, or buildings, when they are located close to each other without any critical distance [1,2,3,4,5,6]. The presence of large relative displacements between neighboring structures during ground motions may result in dangerous collisions leading to serious damage [7,8,9,10,11]. To avoid such situations, consideration should be directed towards ensuring an appropriate minimum distance between adjacent structures as well as to adjusting the properties of the buildings. The most natural approach (the easiest from an engineering point of view) is to increase the size of the gap between the buildings, or to fill it using viscoelastic materials (see [12,13]). Several studies have focused on different methods for estimating gap sizes that will be sufficient to prevent earthquake-induced structural pounding [14,15,16]. However, providing a sufficient separation distance is not always possible due to the cost of land, which results in the use of the maximum possible area in metropolitan cities. Therefore, methods for controlling structural displacement are often considered as an alternative solution for preventing collisions between buildings during earthquakes. However, from the engineering point of view, these methods can be difficult to be implemented in practice. Anagnostopolos and Karamaneas [17] and Barros and Khatami [18] considered the effectiveness of concrete shear walls for increasing the stiffness of the structures, thereby minimizing the gap size between adjacent buildings. Zhang and Xu [19] and Matsagar and Jangid [20] studied different types of links between neighboring buildings by using spring and dashpot elements in order to improve the structural dynamic behavior. Connections between adjacent structures with the use of stiff additional beams were also considered by Westermo [21]. He used a special link element that was able to dissipate energy and prevent collisions during ground motions. Kasai et al. [22] eliminated pounding effects by applying viscoelastic dampers installed between two adjacent buildings. Another work in which the application of viscoelastic dampers was analyzed was performed by Kazemi et al. [23]. The effect of rubber bumpers was also studied by Panayiotis et al. [24], Polycarpou et al. [25] and Abdel Raheem [26]. Sołtysik et al. [27] used polymer elements to reduce negative pounding effects during earthquakes. Dogrul [28], Braz and Barros [29], and Garcia [30,31] investigated the nonlinear behavior of structures with the aim of decreasing lateral structural displacements using passive dampers.
On the other hand, the application of base isolation systems, which are considered to be a very effective seismic protection method (see, for example, Kelly [32] and Falborski et al. [33,34]), results in elongation of the natural period of the building and an increase in subsequent structural displacements during earthquakes, thus increasing the probability of structural pounding. Therefore, Khatami et al. [35] and Naji et al. [36] investigated methods for reducing the lateral displacement of isolated buildings using tuned mass dampers.
The aim of the present paper is to verify the effectiveness of the application of rubber bumpers in reducing the negative effects of earthquake-induced pounding between base-isolated buildings. To meet this challenge, two three-story structures with different configurations (one isolated and one non-isolated) were considered, and their dynamic response under seismic excitation was determined. In further considerations, one of the buildings was equipped with four bumpers that were square in shape, applied at the base level of each side of the model. Then, the dynamic response of the two three-story models of buildings was determined under four different seismic excitations. The analysis was conducted for various values of gap size and for various values of thickness, number and stiffness of the rubber bumpers. The effectiveness of the application of rubber bumpers for reducing the negative effects of earthquake-induced pounding between base-isolated buildings was verified.

2. Numerical Study

The numerical study was focused on the dynamic response of two three-story models of concrete adjacent buildings in various configurations under seismic excitation. Each building model, with lumped mass in each story, possessed the following properties: story mass of 26,500 kg, story stiffness of 350 MN/m, and building vibration period equal to 1.22 s. Damping coefficient equal to 6.82 × 104 kg/s and damping ratio of 5% were assumed in the numerical study. Three different configurations of neighboring buildings were analyzed. In the first one, two three-story models of non-isolated buildings with the same properties were considered, while in the second arrangement, two isolated structures were taken into account (see Figure 1a,b). In the third situation, isolated and non-isolated buildings were analyzed (see Figure 1c). The initial stiffness and post yield stiffness of the isolation system was taken to be equal to 40 MN/m and 5 MN/m, which confirmed the bilinear characteristics of the isolation system. In this model, the structural vibration period of the base-isolated building was calculated to be 1.57 s.
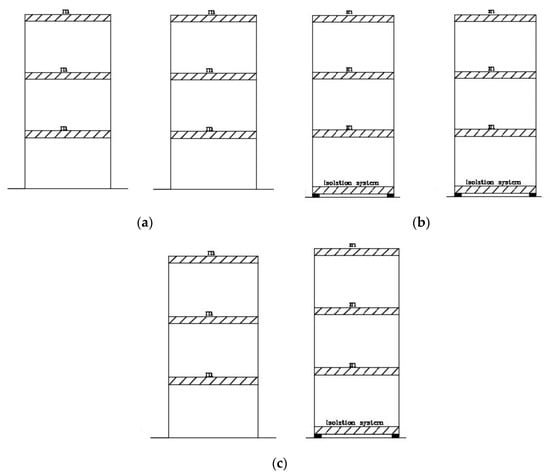
Figure 1. Arrangement scheme of two three-story models investigated in the numerical study (where m is a story mass): (a) two non-isolated; (b) two isolated; (c) one non-isolated and one isolated.
Linear elastic structural behavior was considered in the analysis in the case of fixed-base building. On the other hand, the base-isolated building was modeled as a nonlinear structure by defining the initial stiffness and post yield stiffness of the isolation system. The geometric and material parameters of the presented models were selected in such a way that they describe the parameters of the real building. Parameters such as building natural vibration period and damping coefficient, which depend significantly on the mass and stiffness of the stories, were confirmed numerically, allowing us to verify the accuracy of the models created (compare [37]). Other assumptions were obtained based on previously conducted studies (see [35,36,38]).
The CRVK (Coefficient of Restitution, Velocity and Stiffness) program was used to perform dynamic analyses and solve impact problems (see [39] for details). The CRVK program is a computer program based on MATLAB software that was written by Khatami et al. at the FEUP in order to solve different mathematical relations focusing on dynamic modeling during seismic excitations. Parameters such as number of stories, lumped masses, story stiffness, damping, building vibration period, height of building and also characteristics of earthquake records are generally defined as input values. CRVK is able to collect all of these data, analyze them, and also test them so as to obtain optimal outputs. It is mainly focused on calculating the lateral displacements, velocities, and accelerations of pounding-involved responses of buildings, energy absorption and impact force. CRVK can also suggest the best outputs based on the requested data as optimum responses in different fields such as the critical distance between adjacent buildings, damping ratio, and also the number of collisions recorded during earthquakes.
Several different earthquake records (difference in frequency contents and peak ground acceleration values) were used in the study to investigate the dynamic response of two three-story adjacent buildings. In the first part of the paper, the most representative results are presented, which were those obtained for the El Centro earthquake, characterized by a peak ground acceleration of 307 cm/s2.

2.1. Two Three-Story Non-Isolated Models of Buildings

In the first considered situation, two three-story non-isolated buildings were analyzed. As the two models considered had the same dynamic properties, their behavior in the zone of lateral displacement, when earthquake record was naturally activated, was the same (see Figure 2). Consequently, no collision took place even without any distance between them. In fact, one of the methods preventing impacts during seismic excitation is to design and erect buildings with similar dynamic properties so as to induce their in-phase vibrations. However, it has to be underlined that such situations only take place when the spatial variability of ground motion is ignored. If the ground excitations for the two buildings have a slight difference, a collision might happen. As presented in Figure 2, the peak lateral displacement of each model was equal to 23.9 cm.
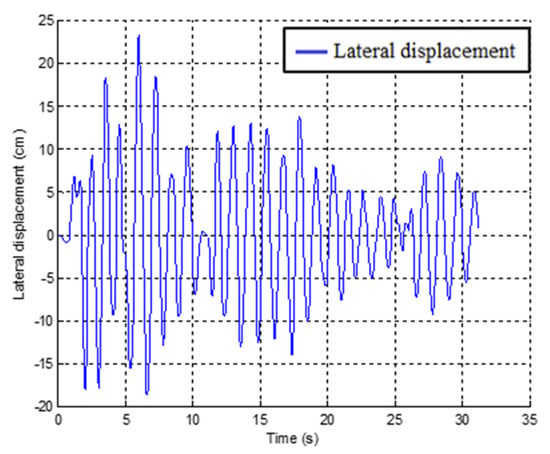
Figure 2. Top lateral displacement time histories of both non-isolated buildings.

2.2. Two Three-Story Models of Buildings: Non-Isolated and Isolated (Gap Size = 10 cm)

In the next stage of the investigation, the dynamic response of two models of buildings (non-isolated and isolated) was investigated. The results of the analysis are graphically presented in Figure 3 in the form of time history displacements. As can be seen from the figure, providing the isolation system in the base level of one of the buildings resulted in an increase in displacements, and some collisions could be observed. The value of the peak lateral displacement of the top of the isolated building strictly depends on the value of the base lateral displacement during seismic excitation. The peak value of lateral displacement for the isolated building was estimated to be equal to 17.14 cm, which represents a difference between the top and base levels of the model equal to 6.76 cm.
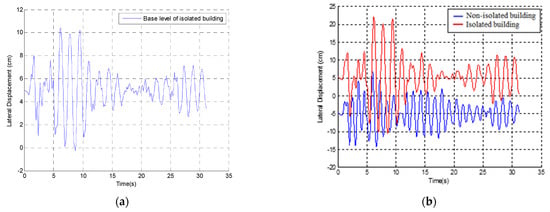
Figure 3. Lateral displacement time histories of a non-isolated building and an isolated one: (a) base level; (b) top level.

2.3. Two Three-Story Isolated Models of Buildings

In the third part of the numerical study, two three-story isolated models of buildings were considered. Since they were characterized by the same properties, their behavior was the same, and no collision between them was observed—the results of the numerical study are shown in Figure 4. As can be seen from the figure, the peak lateral displacement of each model was equal to 34.2 cm.
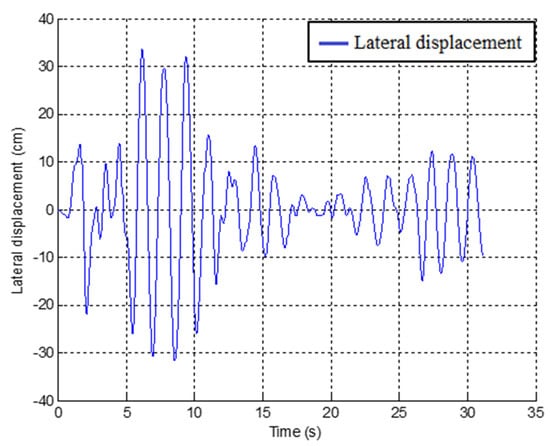
Figure 4. Top lateral displacement time histories of both isolated buildings.
The results obtained from the first and the third configuration of two three-story models of buildings show that the gap size between them can even be equal to 0, since the dynamic properties of building models are the same and they vibrate in phase during the whole duration of the earthquake. On the other hand, in the case where one of the buildings is a base-isolated one (the second situation) some collisions between the two models are to be expected.
In further considerations, a seismic gap between the two isolated models of three-story building was increased to 19 cm.

2.4. Two Three-Story Models of Buildings: Non-Isolated and Isolated (Gap Size = 19 cm)

To avoid collisions between two adjacent buildings (one non-isolated and one isolated), it was calculated that the seismic gap size should be increased to 19 cm so as to prevent collisions. The results of such a configuration are presented in Figure 5.
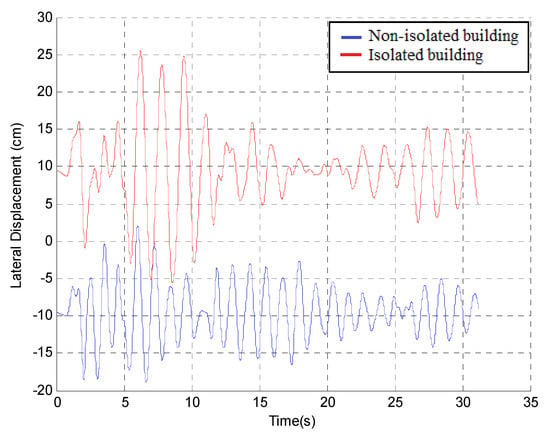
Figure 5. Lateral displacement time histories of non-isolated and isolated building with a 19 cm gap.
However, it should be underlined that a gap size of 19 cm cannot be justified due to economic considerations (i.e., the high price of land) and cannot be implemented in reality. For this reason, in the next step of the investigation, this distance was reduced to 8 cm, and one of the buildings (the isolated one) was equipped with four bumpers that were square in shape.

2.5. Two Three-Story Models of Buildings: Non-Isolated and Isolated with Rubber Bumpers

In this analysis, an isolated building was equipped with four bumpers that were square in shape. Rubber bumpers were modeled as elements with a square cross-section with dimensions of 40 × 40 cm, and their arrangement is presented in Figure 6. The stiffness of the bumpers was assumed to be 0.12 kN/mm, while the post yield impact stiffness was equal to 500 kN/mm.
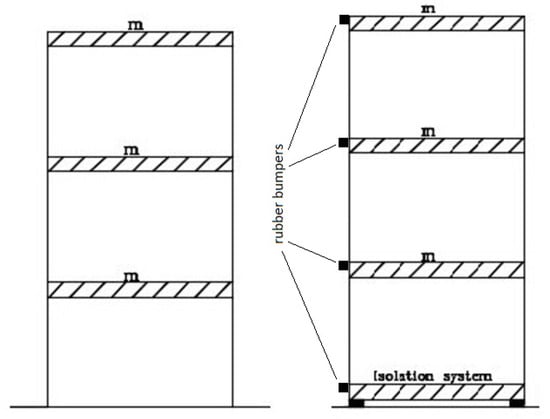
Figure 6. Schematic diagram of two three-story isolated models and the locations of rubber bumpers.
The dynamic response of the three-story non-isolated and the isolated buildings was determined, and the effectiveness of the application of rubber bumpers in reducing the negative effects of earthquake-induced pounding between base-isolated buildings was verified.
As can be seen from Figure 7, some collisions between the two models during seismic excitation were observed. Moreover, the rubber bumpers were activated after impact. Figure 7 indicates that the first story exhibited an overlap of 1.62 cm, the second story an overlap of 4.78 cm, and the third story one of 6.52 cm.
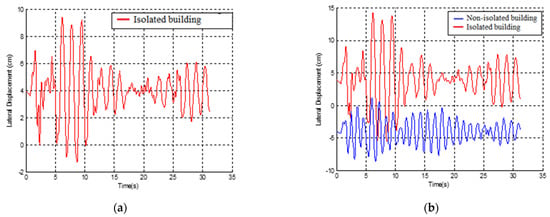
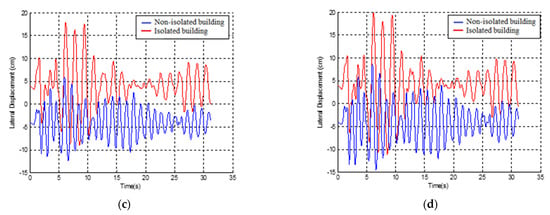
Figure 7. Lateral displacement time histories of non-isolated and the isolated buildings with an 8 cm size gap: (a) base level; (b) first story; (c) second story; (d) third story.
The maximum impact forces in each story were calculated to be 2.38 × 105 kN, 6.9 × 105 kN and 10.05 × 105 kN for the first, second and the third story, respectively (see Figure 8). Moreover, time histories for the impact forces are presented in Figure 9.
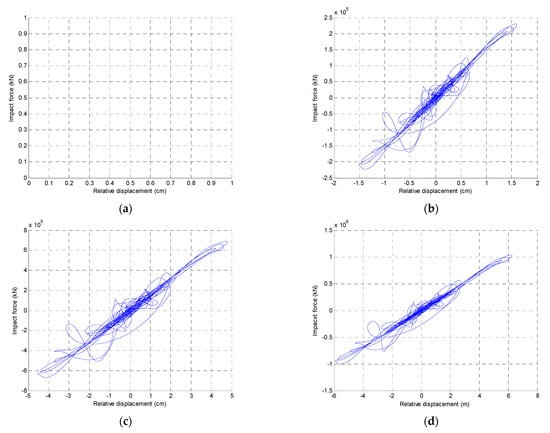
Figure 8. Hysteresis loops of rubber bumpers during impact: (a) base level; (b) first story; (c) second story; (d) third story.
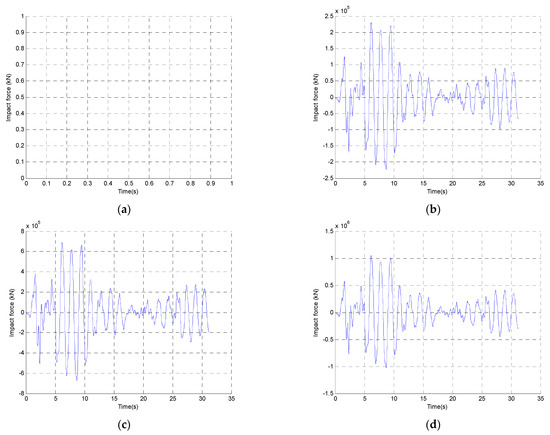
Figure 9. Impact force time histories obtained for each story: (a) base level; (b) first story; (c) second story; (d) third story.
Another case was analyzed in which the gap size between the two adjacent buildings was reduced to 5 cm.

2.6. Two Three-Story Models of Buildings: Non-Isolated and Isolated (Gap Size = 5 cm) Exposed to Different Earthquakes

To investigate the effectiveness of rubber bumpers during seismic excitation more intensively, four different earthquake records were considered: Kobe (1995), Parkfield (1966), San Fernando (1971) and Tabas (1978). Their peak ground accelerations were 817 cm/s2, 462 cm/s2, 1202 cm/s2 and 344 cm/s2, respectively. A model of three-story buildings with a seismic gap of 5 cm was used in the analysis. The lateral displacement time histories for each story of the buildings during seismic excitation are presented in Figure 10. As can be seen from Figure 10, the peak values of the lateral displacements of buildings were equal to 20.99 cm for the Parkfield earthquake, 10.19 cm for the Kobe earthquake, 20.00 cm for the San Fernando earthquake and 37.00 cm for the Tabas earthquake. Moreover, the peak drifts of all models were calculated to be 0.606 cm, 0.257 cm, 0.577 cm and 0.345 cm for the Parkfield, Kobe, San Fernando and Tabas earthquakes, respectively.
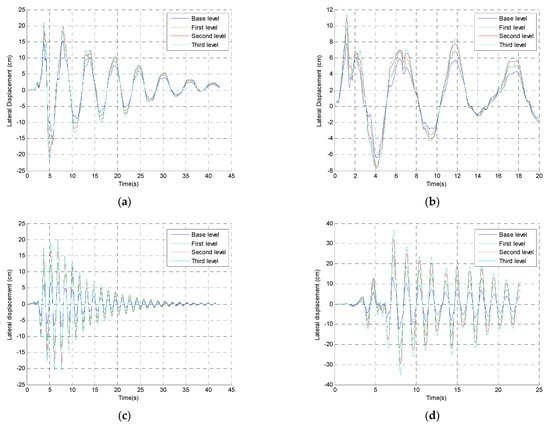
Figure 10. Lateral displacement time histories of each story in the non-isolated model of a building during seismic excitation: (a) Parkfield; (b) Kobe; (c) San Fernando; (d) Tabas.
The hysteresis loops of the rubber bumpers during impact, when the base level exceeds a relative displacement of 5 cm, are shown in Figure 11. The results indicate that the energy was absorbed by bumpers in order to control the lateral displacement of all stories. The peak values of the forces induced in bumpers were equal to: 15.55 × 103 kN, 8.15 × 103 kN, 4.85 × 103 kN and 10.40 × 103 kN for the Parkfield, Kobe, San Fernando and Tabas earthquakes, respectively. As can be clearly seen, impact occurred after the critical distance (5 cm) and energy had dissipated, as depicted by the hysteresis loops in Figure 11.
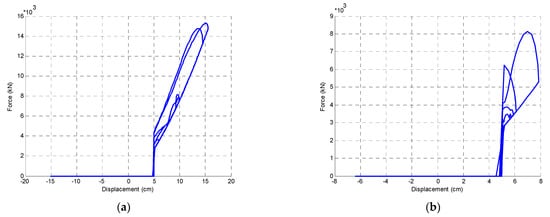
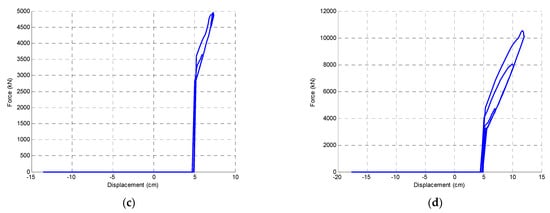
Figure 11. Hysteresis loops determined for the model under different earthquake excitations: (a) Parkfield; (b) Kobe; (c) San Fernando; (d) Tabas.

3. The Effect of Changes in Rubber Bumper Properties

3.1. Changes in Bumper Thickness

The next stage of the numerical investigation was focused on the effect of different thicknesses of the rubber bumpers. The analysis was conducted for two different seismic excitations (the Parkfield, Kobe, San Fernando and Tabas earthquakes) and with various gap sizes between the buildings. Four different thickness values were analyzed (from 1 cm to 4 cm), and the corresponding peak impact forces were calculated for four different earthquake records (see Figure 12). As can be seen from Figure 12, the peak impact force observed during the Parkfield earthquake was equal to 16.05 × 103 kN, while in the case of the Kobe earthquake, a value of 9.45 × 103 kN was obtained. In the case of the San Fernando earthquake, the peak impact force was equal to 5.17 × 103 kN, while in the case of the Tabas earthquake, this value was 10.86 × 103 kN. The results of the analysis indicate that the peak impact force decreased with increasing bumper thickness, and also with increasing gap size. For instance, considering the Parkfield earthquake, the peak impact forces were equal to: 4.95 × 103 kN, 4.68 × 103 kN, 4.42 × 103 kN and 3.97 × 103 kN for bumper thicknesses of 1 cm, 2 cm, 3 cm and 4 cm when the gap size was 15 cm. On the other hand, for the Kobe earthquake, the peak impact forces were shown to be 6.90 × 103 kN, 6.10 × 103 kN, 5.95 × 103 kN and 4.85 × 103 kN for bumper thicknesses of 1 cm, 2 cm, 3 cm and 4 cm when the gap size was 4 cm. In the case of the San Fernando earthquake, the peak impact forces were equal to 5.17 × 103 kN, 5.14 × 103 kN, 5.14 × 103 kN and 5.13 × 103 kN for bumper thicknesses of 1 cm, 2 cm, 3 cm and 4 cm when the gap size was 5 cm. On the other hand, for the Tabas earthquake, the peak impact forces were shown to be 10.86 × 103 kN, 10.68 × 103 kN, 10.35 × 103 kN and 10.11 × 103 kN for bumper thicknesses of 1 cm, 2 cm, 3 cm and 4 cm when the gap size was 5 cm.
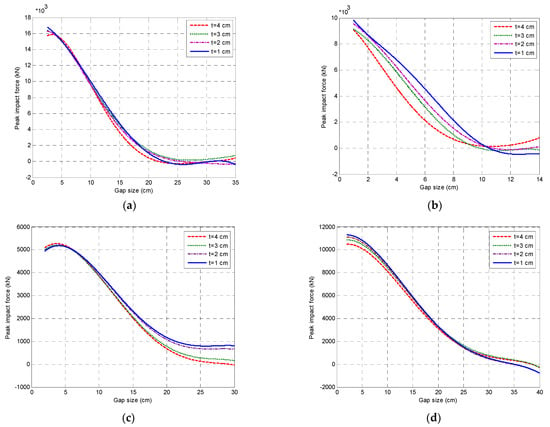
Figure 12. Peak values of impact force for different gap sizes and rubber bumper thicknesses under different seismic excitations: (a) Parkfield; (b) Kobe; (c) San Fernando; (d) Tabas.

3.2. Changes in the Number of Bumpers

In the next stage of the study, the influence of the number of bumpers was numerically evaluated. For this purpose, different cases were analyzed considering different gap sizes (4 cm, 8 cm and 12 cm) and various numbers of bumpers (from one to eight). The results of the investigation are presented in Figure 13. As can be seen from the figure, the peak impact forces decreased with increasing number of bumpers as well as stiffness. For example, the peak impact force in the case of the Parkfield earthquake was calculated to be equal to 8.15 kN when the gap size was 4 cm and six bumpers were used. The results show that increasing the number of bumpers and the gap size between structures increases the effectiveness of the maximum compressive strain of the bumpers, thus resulting in a slow decrease in the peak impact forces.
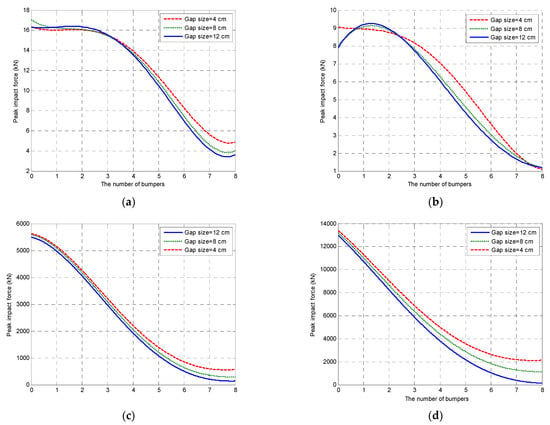
Figure 13. Peak values of impact force for different numbers of rubber bumpers and gap sizes under different seismic excitations: (a) Parkfield; (b) Kobe; (c) San Fernando; (d) Tabas.

3.3. Changes in Bumper Stiffness

Finally, the effect of bumper stiffness was numerically evaluated using different values of stiffness (from 0.08 kN/mm to 2 kN/mm). The results of the analysis for different gap sizes are presented in Figure 14. As can be seen from the figure, increasing the bumper stiffness leads to a decrease in the peak impact forces. For instance, using a gap size of 5 cm, the peak impact forces for the Parkfield earthquake were equal to 15.2 × 103 kN, 15.55 × 103 kN, 16.75 × 103 kN and 17.65 × 103 kN for bumper stiffnesses of 0.08 kN/mm, 1.2 kN/mm, 1.6 kN/mm and 2 kN/mm. At the same time, the values of the peak impact forces for the Kobe earthquake were equal to 4.35 × 103 kN, 4.55 × 103 kN, 4.65 × 103 kN and 5.85 × 103 kN for the corresponding values of bumper stiffness. Considering a 20 cm gap size, the peak impact forces for the San Fernando earthquake were equal to 6.45 × 102 kN, 7.20 × 102 kN, 7.90 × 102 kN and 8.10 × 102 kN for bumper stiffnesses of 0.08 kN/mm, 1.2 kN/mm, 1.6 kN/mm and 2 kN/mm. At the same time, the values of the peak impact forces for the Tabas earthquake were equal to 3.98 × 103 kN, 4.65 × 103 kN, 4.98 × 103 kN and 5.05 × 103 kN for the corresponding values of bumper stiffness.
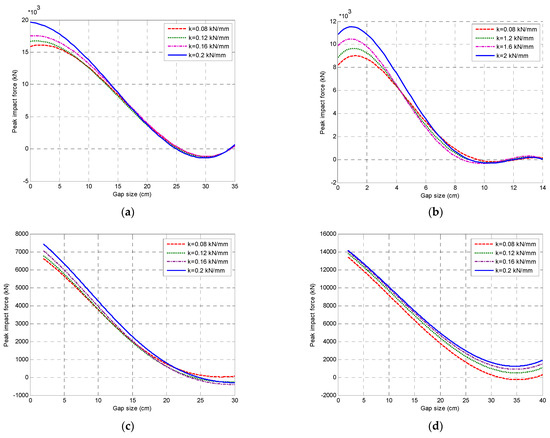
Figure 14. Peak values of impact force for different rubber bumper stiffnesses and gap sizes under different seismic excitations: (a) Parkfield; (b) Kobe; (c) San Fernando; (d) Tabas.

4. Conclusions

In this paper, the effectiveness of using rubber bumpers in order to reduce the negative effects of earthquake-induced pounding between base-isolated buildings was investigated. The analysis was conducted for different gap sizes between buildings as well as for various values for the thickness, number and stiffness of the rubber bumpers.
The results of the study show that the peak impact force decreases with increasing thickness, stiffness, and number of bumpers. Moreover, the peak impact forces decrease with increasing gap size.
The results of the investigation clearly indicate that the use of additional rubber bumpers can be considered an effective method for improving the behavior of closely spaced base-isolated buildings. It can be successfully applied in practice to reduce the negative effects of earthquake-induced pounding between structures. Therefore, the method can be recommended to designers of pounding-prone base-isolated buildings exposed to ground motions.

Author Contributions

Conceptualization, S.M.K., H.N. and A.S.; methodology, S.M.K., H.N., A.S., A.M., N.L. and R.J.; software, S.M.K. and A.S.; validation, S.M.K., H.N., A.S., A.M., N.L. and R.J.; formal analysis, S.M.K. and A.S.; investigation, S.M.K. and A.S.; writing—original draft preparation, S.M.K., H.N., A.S. and A.M.; writing—review and editing, N.L. and R.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Anagnostopoulos, S.A. Pounding of buildings in series during earthquakes. Earthq. Eng. Struct. Dyn. 1988, 16, 443–456. [Google Scholar] [CrossRef]
  2. Mavronicola, E.A.; Polycarpou, P.C.; Komodromos, P. Effect of ground motion directionality on the seismic response of base isolated buildings pounding against adjacent structures. Eng. Struct. 2020, 207, 110202. [Google Scholar] [CrossRef]
  3. Rezaei, H.; Moayyedi, S.A.; Jankowski, R. Probabilistic seismic assessment of RC box-girder highway bridges with unequal-height piers subjected to earthquake-induced pounding. Bull. Earthq. Eng. 2020, 18, 1547–1578. [Google Scholar] [CrossRef]
  4. Flenga, M.G.; Favvata, M.J. Probabilistic seismic assessment of the pounding risk based on the local demands of a multistory RC frame structure. Eng. Struct. 2021, 245, 112789. [Google Scholar] [CrossRef]
  5. Miari, M.; Choong, K.K.; Jankowski, R. Seismic pounding between bridge segments: A state-of-the-art review. Arch. Comput. Methods Eng. 2021, 28, 495–504. [Google Scholar] [CrossRef]
  6. Kazemi, F.; Miari, M.; Jankowski, R. Investigating the effects of structural pounding on the seismic performance of adjacent RC and steel MRFs. Bull. Earthq. Eng. 2021, 19, 317–343. [Google Scholar] [CrossRef]
  7. Al-Fahdawi, O.A.; Barroso, L.R. Adaptive neuro-fuzzy and simple adaptive control methods for full three-dimensional coupled buildings subjected to bi-directional seismic excitations. Eng. Struct. 2021, 232, 111798. [Google Scholar] [CrossRef]
  8. Al-Fahdawi, O.A.; Barroso, L.R.; Soares, R.W. Adaptive neuro-fuzzy and simple adaptive control methods for attenuating the seismic responses of coupled buildings with semi-active devices: Comparative study. J. Soft Comput. Civ. Eng. 2019, 3, 1–21. [Google Scholar]
  9. Al-Fahdawi, O.A.; Barroso, L.R.; Soares, R.W. Utilizing the adaptive control in mitigating the seismic response of adjacent buildings connected with MR dampers. In Proceedings of the Annual American Control Conference 2018 (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 912–917. [Google Scholar]
  10. Al-Fahdawi, O.A.; Barroso, L.R.; Soares, R.W. Semi-active adaptive control for enhancing the seismic performance of nonlinear coupled buildings with smooth hysteretic behavior. Eng. Struct. 2019, 191, 536–548. [Google Scholar] [CrossRef]
  11. Al-Fahdawi, O.A.; Barroso, L.R.; Soares, R.W. Simple adaptive control method for mitigating the seismic responses of coupled adjacent buildings considering parameter variations. Eng. Struct. 2019, 186, 369–381. [Google Scholar] [CrossRef]
  12. Lasowicz, N.; Kwiecień, A.; Jankowski, R. Experimental study on the effectiveness of polyurethane flexible adhesive in reduction of structural vibrations. Polymers 2020, 12, 2364. [Google Scholar] [CrossRef] [PubMed]
  13. Kwiecień, A.; Gams, M.; Rousakis, T.; Viskovic, A.; Korelc, J. Validation of a new hyperviscoelastic model for deformable polymers used for joints between RC frames and masonry infills. Eng. Trans. 2017, 65, 113–121. [Google Scholar]
  14. Jia, H.Y.; Lan, X.L.; Zheng, S.X.; Li, L.P.; Liu, C.Q. Assessment on required separation length between adjacent bridge segments to avoid pounding. Soil Dyn. Earthq. Eng. 2019, 120, 398–407. [Google Scholar] [CrossRef]
  15. Elwardany, H.; Seleemah, A.; Jankowski, R.; El-Khoriby, S. Influence of soil-structure interaction on seismic pounding between steel frame buildings considering the effect of infill panels. Bull. Earthq. Eng. 2019, 17, 6165–6202. [Google Scholar] [CrossRef] [Green Version]
  16. Khatami, S.M.; Naderpour, H.; Mortezaei, A.; Nazem Razavi, S.M.; Lasowicz, N.; Jankowski, R. Effective Gap Size Index for Determination of Optimum Separation Distance Preventing Pounding between Buildings during Earthquakes. Appl. Sci. 2021, 11, 2322. [Google Scholar] [CrossRef]
  17. Anagnostopoulos, S.A.; Karamaneas, C.E. Use of collision shear walls to minimize seismic separation and to protect adjacent buildings from collapse due to earthquake-induced pounding. Earthq. Eng. Struct. Dyn. 2008, 37, 1371–1388. [Google Scholar] [CrossRef]
  18. Barros, R.C.; Khatami, S.M. Damping ratios for pounding of adjacent building and their consequence on the evaluation of impact forces by numerical and experimental models. Rev. Da Assoc. Port. De Análise Exp. De Tensões 2013, 22, 119–131. [Google Scholar]
  19. Zhang, W.S.; Xu, Y.L. Dynamic characteristics and seismic response of adjacent buildings linked by discrete dampers. Earthq. Eng. Struct. Dyn. 1999, 28, 1163–1185. [Google Scholar] [CrossRef]
  20. Matsagar, V.A.; Jangid, R.S. Viscoelastic damper connected to adjacent structures involving seismic isolation. J. Civ. Eng. Manag. 2005, 11, 309–322. [Google Scholar] [CrossRef]
  21. Westermo, B.D. The dynamics of interstructural connection to prevent pounding. Earthq. Eng. Struct. Dyn. 1989, 18, 687–699. [Google Scholar] [CrossRef]
  22. Kasai, K.; Jeng, V.; Patel, P.C.; Munshi, J.A.; Maison, B.F. Seismic pounding effects—Survey and analysis. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992; pp. 3893–3898. [Google Scholar]
  23. Kazemi, F.; Mohebi, B.; Jankowski, R. Predicting the seismic collapse capacity of adjacent SMRFs retrofitted with fluid viscous dampers in pounding condition. Mech. Syst. Signal Process. 2021, 161, 107939. [Google Scholar] [CrossRef]
  24. Panayiotis, C.; Polycarpou, P.; Komodromos, P. Numerical investigation of potential mitigation measures for pounding of seismically isolated building. Earthq. Struct. 2011, 2, 1–24. [Google Scholar]
  25. Polycarpou, P.C.; Komodromos, P.; Polycarpou, A.C. A nonlinear impact model for simulating the use of rubber shock absorbers for mitigating the effects of structural pounding during earthquakes. Earthq. Eng. Struct. Dyn. 2013, 42, 81–100. [Google Scholar] [CrossRef]
  26. Abdel Raheem, S.E. Mitigation measures for earthquake induced pounding effects on seismic performance of adjacent buildings. Bull. Earthq. Eng. 2014, 12, 1705–1724. [Google Scholar] [CrossRef]
  27. Sołtysik, B.; Falborski, T.; Jankowski, R. Preventing of earthquake-induced pounding between steel structures by using polymer elements—Experimental study. Procedia Eng. 2017, 199, 278–283. [Google Scholar] [CrossRef]
  28. Dogruel, S. Application of Genetic Algorithms for Optimal Aseismic Design of Passively Damped Adjacent Structures; Individual Study; State University of New York at Buffalo: Buffalo, NY, USA, 2005. [Google Scholar]
  29. Braz, C.; Barros, R.C. Semi-active vibration control of buildings using MR dampers: Numerical and experimental verification. In Proceedings of the 14th European Conference on Earthquake Engineering, Ohrid, Macedonia, 30 August–3 September 2010. [Google Scholar]
  30. Garcia, D.L.; Soong, T.T. Evaluation of current criteria in predicting the separation necessary to prevent seismic pounding between nonlinear hysteretic structural systems. Eng. Struct. 2009, 31, 1217–1229. [Google Scholar] [CrossRef]
  31. Garcia, D.L. Separation between adjacent non-linear structures for prevention of seismic pounding. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–4 August 2004. [Google Scholar]
  32. Kelly, J.M. Earthquake-Resistant Design with Rubber; Springer: London, UK, 1993. [Google Scholar]
  33. Falborski, T.; Jankowski, R. Polymeric bearings—A new base isolation system to reduce structural damage during earthquakes. Key Eng. Mater. 2013, 569–570, 143–150. [Google Scholar] [CrossRef]
  34. Falborski, T.; Jankowski, R. Experimental study on effectiveness of a prototype seismic isolation system made of polymeric bearings. Appl. Sci. 2017, 7, 808. [Google Scholar] [CrossRef]
  35. Khatami, S.M.; Naderpour, H.; Nazem Razavi, S.M.; Barros, R.C.; Jakubczyk, A.; Jankowski, R. Study on Methods to Control Interstory Deflection. Geoscience 2020, 10, 75. [Google Scholar] [CrossRef] [Green Version]
  36. Naderpour, H.; Naji, N.; Burkacki, D.; Jankowski, R. Seismic response of high-rise buildings equipped with base isolation and non-traditional tuned mass dampers. Appl. Sci. 2019, 9, 1201. [Google Scholar] [CrossRef] [Green Version]
  37. Jankowski, R. Non-linear FEM analysis of earthquake-induced pounding between the main building and the stairway tower of the Olive View Hospital. Eng. Struct. 2009, 31, 1851–1864. [Google Scholar] [CrossRef]
  38. Mahmoud, S.; Jankowski, R. Elastic and inelastic multi-storey buildings under earthquake excitation with the effect of pounding. J. Appl. Sci. 2009, 9, 3250–3262. [Google Scholar] [CrossRef]
  39. Naderpour, H.; Barros, R.C.; Khatami, S.M.; Jankowski, R. Numerical Study on Pounding between Two Adjacent Buildings under Earthquake Excitation. Shock Vib. 2016, 2016, 1504783. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Temporomandibular Disorders and Bruxism in Patients Attending a Tinnitus Clinic
Previous
Railway Bridge Condition Monitoring Using Numerically Calculated Responses from Batches of Trains
Next