Abstract
The article addresses the issue of clustering of multidimensional data arrays with a noise using the methods of discrete mathematical analysis (DMA clustering). The theory of DMA clustering through the logical densities calculus is detailed, and the new algorithm Linear Discrete Perfect Sets (LDPS) is described. The main objective of the LDPS algorithm is to identify linearly stretched anomalies in a multidimensional array of geo-spatial data (geophysical fields, geochemistry, satellite images, local topography, maps of recent crustal movements, seismic monitoring data, etc.). These types of anomalies are associated with tectonic structures in the upper part of the Earth’s crust and pose the biggest threat for integrity of the isolation properties of the geological environment, including in regions of high-level radioactive waste disposal. The main advantage of the LDPS algorithm as compared to other cluster analysis algorithms that may be used in arrays with a noise is that it is more focused on searching for clusters that are linear. The LDPS algorithm can apply not only in the analysis of spatial natural objects and fields but also to elongated lineament structures.
Keywords:
finite metric space; density; solidity; clusters; discrete perfect sets; linear structures 1. Introduction
In 2019, the construction of an underground research laboratory (URL) was started in granitic gneiss rocks of the Nizhne–Kansky rock mass (Russia, Krasnoyarsk Territory) to justify the safety of disposal of high-level radioactive waste (HLRW). The safety of HLRW underground insulation for a period of ten thousand years or more is guaranteed due to a geological barrier. The main threat of disturbance of the isolation properties of the geological environment where HLRW are disposed is associated with large-scale geodynamic processes and phenomena.
Therefore, a priority task in the field of geo-sciences includes the analysis of multidimensional geological and geophysical data as well as the creation of a geodynamic model based on such data, which provides a forecast of the safety of the rock isolation properties over the whole period of time when the radiobiological danger of a radioactive nucleus persists [1].
In order to resolve this task, we must determine linearly stretched anomalies in a multidimensional array of geo-spatial data (geophysical fields, geochemistry, satellite images, local topography, maps of recent movements, seismic monitoring data, etc.). As is known, these types of anomalies are associated with tectonic structures in the upper part of the earth crust—faults, the boundaries of large blocks, linear structures, potential zones of possible earthquakes, etc.
These are geodynamic zones that pose the biggest threat to the isolation properties of the greatest [2]. Their search is mandatorily regulated by the statutory documents applicable in the field of HLRW disposal.
It should be emphasized that the developed methodology is very versatile and can be applied to a wide range of practical tasks of the earth sciences—in geology, geodynamics, mineral exploration, etc. Thus, this methodology is used where there is a problem in identifying linear extended anomalies from spatially referenced data of field observations. A specific link to the problem of HLRW burial in geological formations is due to the fact that these algorithms were developed in the framework of the project on this problem.
The available geospatial data arrays are almost always insufficient, uncertain and distorted due to the noise, which dictates the need for developing effective analysis and interpretation algorithms [3,4,5]. This issue is resolved in the article within the framework of discrete mathematical analysis (DMA), an original data analysis approach developed at the Geophysical Center of the Russian Academy of Sciences.
One of the development areas of discrete data analysis and discrete math is substantially related to modeling the researcher’s data analyzing skills. An experienced researcher will—better than any formal technique—distinguish any anomalies within physical fields with a small number of dimensions, move from their local level to the global one for holistic interpretation, find signals of the required form (morphology) on records of small length and many other things.
However, the researcher is helpless if faced with a large number of dimensions and volumes; therefore, a task teaching the computer in date analysis to act like a human being becomes ever more topical. When solving this task, it was considered that when the researcher thinks and operates not with numbers, but with fuzzy concepts; therefore, a technical framework for modeling includes fuzzy math and fuzzy logic along with classical math [6,7].
The advantage that researcher has in the analysis of discrete data over formal techniques is due to his or her more flexible, adaptive and stable attitude to real discrete-stochastic manifestations of fundamental mathematical properties (proximity, limitation, continuity, connectivity, trend, etc.) as compared with formal techniques, since the data analysis algorithms are built precisely on this basis as from a constructor. Hence, the plan for computer learning in the researcher’s skills is as follows: building fuzzy models for discrete counterparts of fundamental math properties and then using them according to classical math scenarios to create data analysis algorithms.
The said tasks were implemented as a researcher-oriented data analysis approach, which takes an intermediate position between hard math methods and soft combinatoric methods. This is called discrete mathematical analysis (DMA) [8,9,10,11].
This paper addresses the study of stationary data arrays representing the sets in multidimensional spaces, using the DMA methods by means of clustering. The initial concept in DMA clustering is a fuzzy model of fundamental mathematical properties, such as “limitations”. This is called density in DMA and represents a non-negative relationship between an arbitrary subset and any point in the initial finite space where the clustering is assumed to be carried out.
The value of density should be understood as a binding force between the subset and the point and interpreted as the degree of effect from the subset on the point, or, ambiguously, as the degree of limitation of the point for the subset. This view of density automatically requires that is shall be monotone over a subset: the larger the subset, the stronger its effect on the point, and it is more limiting for such subset.
Recording the density level and understanding it as an ideality level, we can define any topological concept in the initial space, in particular, discrete perfection with level : a subset is called discrete-perfect with the level of limitation (density) if it is comprised precisely of all points of the initial space that are of limiting kind for such a subset.
Taking into account what was said about density above, we give an equivalent formulation of the concept of discrete-perfectness: a subset is discrete-perfect with level , if the strength of its connection with each of its points is not less than , and with any point outside the subset is strictly less than . Precisely this understanding of clustering formed the basis of the article and became the subject of this study. DMA has a strict theory of discrete perfect (DPS-) sets [12,13]. This serves as a methodological framework for DMA clustering and is summarized in Section 3. DMA clustering algorithms and their operation examples are shown in Section 4.
2. Review
Although there is no unified understanding of cluster, Everitt’s empirical definition of cluster is one of the largest known and most convincing definitions in cluster analysis with the following wording: “Clusters are ‘continuous’ areas of a (certain) space with a relative higher density of points, separated from other similar areas by the areas with a relatively low density of points” [14]. Subsequently, this interpretation of the cluster is referred to as empirical. It has an advantage as it does not reduce the concept of cluster to a simple form.
One possible approach to formalizing an empirical cluster is as follows: first, we introduce the idea of a dense subset against the background of the entire source space, and then a maximum subset is distinguished inside of such space, which, in turn, is broken down into connected components. The latter will be dense, isolated regions in the original space, i.e., clusters.
It is precisely this scenario that underlies the SDPS DMA-clustering algorithm, which came into the spotlight due to its effective applications in seismology [15]. The space where it operates is assumed to be a finite metric space (FMS), and the density of a subset at a point is equal to the number of points at its intersection with its spherical neighborhood. We will call this “sets” and designate its value by S. The concept of density relative to a set is explained in Figure 1.
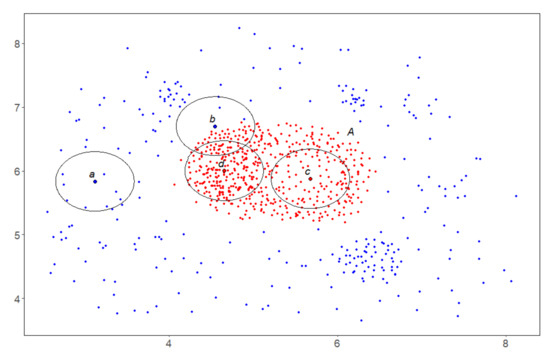
Figure 1.
The concept of density relative to a set. A—a set of red dots, in which four points a, b, c and d are highlighted. The density S of the subset A at the selected points is equal to the number of red points included in the balls described around them. The densest point relative to A will be point c, followed by points b, d and a.
With the density S and setting its level to , the most natural answer to the question about the density against the general background seems to be an answer in the form of a level solution, i.e., the subset of all points in the original space where the density level S is not lower than . However, this is only a first approximation, and it may not be sufficient: a dense point may be isolated because space is dense here and not in its neighbors. Therefore, density against the general background requires more, i.e., that each dense point has a sufficient number of dense neighbors capable of ensuring the desired level of density on its own here (using its own resources).
The discrete -perfection of the density of “Sets” is exactly a formal expression of the above. The DMA theory of -perfect sets guarantees that there is such a maximum subset available within the original space and that -perfection will retain its property when passing to its connected components. The SDPS algorithm finds this subset and splits it into connected components. The fuzzy comparisons developed within DMA [8] allow us to effectively choose the level of limitation so that the SDPS results are indeed internally indiscrete and externally dense, thus, embodying an empirical understanding of the cluster.
The application of the SDPS algorithm is illustrated in Figure 2. With the viewing radius for the density S and its level , the SDPS algorithm begins its work on the array X (Figure 2a). SDPS acts on X iteratively, sequentially in four steps (Figure 2b–e) carving out of it the desired result—a local -perfect subset ) in X (Figure 2e). The green points in Figure 2b–d show the points that did not pass the next iteration in SDPS. SDPS further splits ) into connected components (Figure 2f, yellow and black subsets).
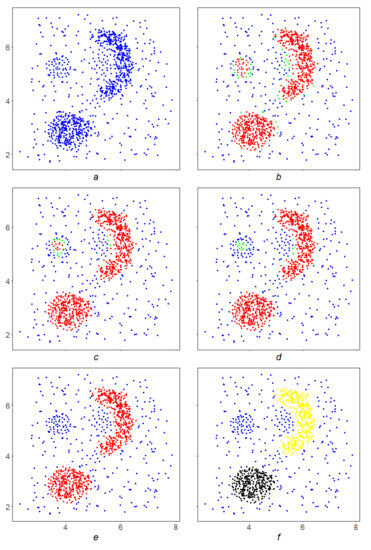
Figure 2.
Application of the SDPS algorithm to the array X (a). Four iterations are shown in figures (b–e). The result is a local -perfect subset of in X (e). The green points in figures (b–d) show the points that did not pass the next iteration in SDPS. SDPS further splits into connected components ((f), yellow and black subsets).
Let us detail the SDPS algorithm within the framework of classical cluster analysis: SDPS-density algorithm of direct, free, parameter-dependent classification that does not require human involvement and does not depend on the order of space scanning [16,17]. The SDPS algorithm, like the well-known modern algorithms DBSCAN, OPTICS, and RSC [18,19,20], represents a new stage in cluster analysis, since it not only breaks the original space into homogeneous parts but also pre-clears it of noise (filters), passing to the maximum -perfect subset.
The use of the construction of -perfect sets is an essential difference of the SDPS algorithm. For example, the SDPS and DBSCAN algorithms have the same initial parameters: the radius r of the view and the density level (the minimum number of points that must be in a ball of radius r). Then, they act in different ways. As mentioned above, SDPS cuts out the maximum -perfect set from the original space, parses it into connected components and considers them to be clusters. The DBSCAN algorithm uses an asymmetric reachability ratio, searches for regions of such reachability with centers at dense points, combines under the condition of r-proximity and considers them to be clusters.
Figure 3 shows examples of clustering a complex array (Figure 3a) using algorithms: MDPS (Figure 3b), DBSCAN (Figure 3c) and OPTICS (Figure 3d). Removing noise from space and then partitioning the balance part into connected components is possible based on a large and most important class of local monotone densities. This scenario is called a DPS-scheme, and its specific implementations at a particular density are called DPS-series algorithms (DPS-algorithms). They represent the state-of-the-art DMA clustering.
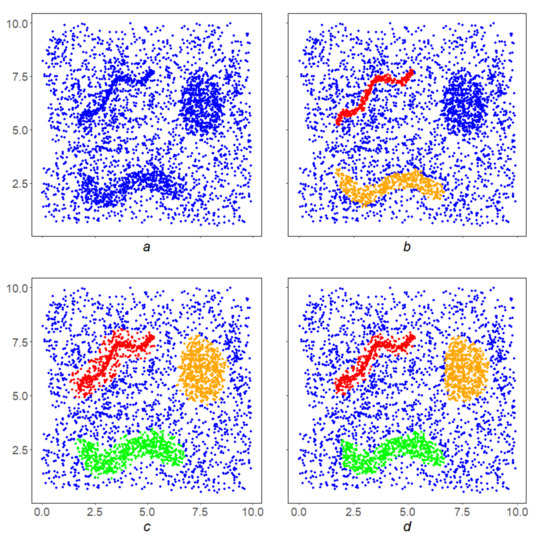
Figure 3.
Examples of clustering a complex array (a) using algorithms: MDPS (b), DBSCAN (c) and OPTICS (d).
Previous DMA clustering algorithms Rodin, Crystal and Monolith [21,22,23] were based on non-monotone densities, and, despite successful applications, theoretically, they had drawbacks that are characteristic of density-based cluster analysis algorithms: dependence on the order of space scanning and, as a consequence, ambiguity of results, issues with convergence, etc.
In conclusion of the general description of DMA clustering, we note that the DPS-series algorithms are extremely versatile: they are capable of working with any kind of similarity in cluster analysis (distance, correlation and associativity factors). The point is that DMA has effective procedures in place that construct monotone densities.
Let us go back to the SDPS algorithm. The resulting clusters do not have any special geometry: they are simply “continuous” and contain “much space” locally. It seems that the natural extension of research should be the search for clusters with a particular geometry. Doubtless, the first step in that process is deemed to be linear structures.
3. Materials and Methods
As mentioned in the Introduction, by clustering in the initial finite space, we mean discrete perfection with respect to the density set on it. Density is an expression in the language of fuzzy mathematics of the “limit” property. By fixing the level of the selected density in the original study, it is possible to define the reference through the normal topology. Thus, in the original dimension, there is an indexed by non-negative numbers and an ascending family of topologies. It starts at zero with the minimal inseparable topology of concatenated points and ending with the separable maximal topology of all subsets.
On an arbitrary finite metric space, one can define densities that reflect various fuzzy interpretations of the “limit” property, and some of them are used in present paper. Thus, each density on a finite metric space sets its own view of it and the corresponding research program. Density, which expresses a fuzzy interpretation of the “limit” property in a finite space, is a new concept that is not reducible to the concepts of classical mathematics, for which finite metric spaces are topologically arranged in the same way–zero-dimensional, separable.
Within the framework of this work, in the family of topologies generated on the basis of density, the property of “perfection” is of interest. We will provide a brief summary of the theory of discrete perfect sets. Its complete proof can be found in [12].
3.1. Discrete Perfect Sets
Suppose X is a finite set, and and are its subsets and points, respectively.
Definition 1.
Let us call a mapping of the product ofinto non-negative numbersin the set X, increasing by the first argument and trivial-on-zero inputs as the density P:
For a density P set on X and a level , we make a sequence of hulls of A in X by P:
Induction on n, using the increasing monotonicity of P, establishes the following
Statment 1.
Due to the finiteness of the set X, in the non-decreasing and bounded sequence of hulls, starting from some number , stabilization occurs:
Definition 2.
Let us call the sethull of the set A and represent it by.
The set demonstrates semi-invariance: its first density hull does not fall beyond the set.
Statment 2.
contains its first-hull by the density:
Hence, it immediately follows that for a set a series (2) of its hulls is constant.
Consequence 1.
Let us designate hull for through . Therefore:
Sequentially plotting the hulls based on the density P, we obtain the following scheme:
Due to the X finiteness in a non-increasing sequence
starting with some number , stabilization occurs:
Let us designate the set by . The process of constructing has a stage of increasing from to and a stage of decreasing from to :
Statement 3.
matches its first-hull.
Remark 1.
Statement 3 means that the setis comprised exactly of those points x of space X where its density is more than α or equal to it:
Let us treat the densityas a limiting measure of the point x for the set A. The point x with sufficiently large densityis considered to be the limiting one for A. Thus, the first hull ofrepresents the set of all limiting points for A in X in that sense. The points from the second hullwill, in general, be limiting points for A in X through—that is, of the second order, etc. Statement 2 means thatis a closed set as it contains all its α-limiting points in X. Moving insideleads to the already α-perfect set, for restated Statement 3 means thatconsists exactly of all finite points to it in X, i.e., it is a perfect one.
Definition 3.
The set A consisting of exactly all α-limiting with regard to this set points of the initial space X is called an α-discrete perfect (simply perfect, DPS-) set in X:
Numerous studies and the examples below show that DPS-sets are condensations in X and are closely related to clustering therein. We have a way of generating them in X, i.e., construction. It depends on four parameters: the initial space X, set A, density P and level :
Statement 4.
Dependencies for A, P and X are increasing dependencies, and dependence forare decreasing dependence:
- 1.
- If, then.
- 2.
- If P, Q densities on X and, then.
- 3.
- If, then.
- 4.
- Ifand measure P are set to Y, then.
3.2. Complete : Scheme and Algorithms
Definition 4.
The construction process for the set A in the universe X based on the density P of its hullis called the complete Discrete Perfect Sets algorithm and is designated through
Remark 2.
On a fixed space X, thealgorithm depends on two parameters, the major one being the density P. In order to emphasize this fact, we will write, omitting the level α, though keeping it in mind. Furthermore, we will need a broader understanding ofas a correspondencebetween densities and algorithms on X. In this case, we will speak ofas a scheme on X.
Generally, the DPS algorithm has two stages (3):
- increasing
- and decreasing
There are situations when it works “faster” and has no more than one stage. The trivial “zero stages” case takes place for -perfect A.
The algorithm constructs for each its perfect hull . Given that is of a non-trivial kind, we consider it as a promising set in X, playing a reference role and most naturally related to A. Hull answers the question of the role and effect of A in X. By substituting A, through the set , we obtain the information about the structure of X at the selected level of limitation .
Therefore, the algorithm is required for a thorough study of the space X through perfect hulls of its subsets, and for cluster analysis in X is too redundant and unnecessarily clumsy. Further research will show that clusters should be considered “connected pieces” of the X-maximal perfect subset . They will be searched using a simplified version of the algorithm DPS.
3.3. Simple DPS: Scheme and Algorithms
Throughout the entire space X, the algorithm has only a decreasing stage, iteratively carving from X its maximum -perfect subset , playing a major role, and therefore it has a separate name “simple Discrete Perfect Sets” algorithm and designation .
The algorithm is antagonistic by its nature to the algorithm to a certain extent: a simple algorithm is of global kind, intercepts the maximum perfect subset from X, whereas full is largely of local king, passing from A to by “auto-critical crystallization”.
Remark 3.
As in Remark 2, the correspondenceis called a DPS scheme.algorithms are resulted from matching the densities P and a DPS scheme, and therefore they are of the same nature (DPS scheme), independent of P. There will be five such matching instances, e.g.,, , , and their complex LDPS-combination.
In this context, we are talking about them as DPS-algorithms, DPS-set algorithms.
If there is a d-metric on X space and the density P (5) is consistent with it, the -perfection property is inherited by “connected” components . They are those that most accurately correspond to the idea of empirical clusters.
Subsequently, a metric d is set on X; therefore, is a FMS. For we designate a full-sphere in A with the center in x radius r:
Definition 5.
Given that P is the density on X (1),is the proximity radius. We assume that P has r-local influence (r-local) if
Based on equivalence and normalization on P, it follows that
Statement 5.
If the density P is r-local, then the implication is valid
3.3.1. Topological Retreat
Two points x and y in A are called r-connected if there is a chain of r-close points in A– with the starting point and terminus . The ratio of r-connectivity is an equivalence splitting the set A into components of r-connectivity , :
Algorithmically, the split (4) is achieved as follows: let a point be in A and component of r-connectivity that contains it. Then,
where
By virtue of finiteness A everything is balanced and makes sense. Let us consider as the first component in (4). If it is not the last one, the same reasoning applies to . As a result, we have the second component and so on.
Statement 6.
If the density P is r-local, then every r-link component of the setis-perfect.
In the event of r-local density, we will understand the algorithm through a broader lens.
Definition 6.
The process of construction for the finite metric spacebased on the r-local density P of the α-hullwith its subsequent splitting into r-connected components is called a “simple DPS algorithm”:
Let us summarize our conversation about with its flow charts and comments to it (Figure 4).
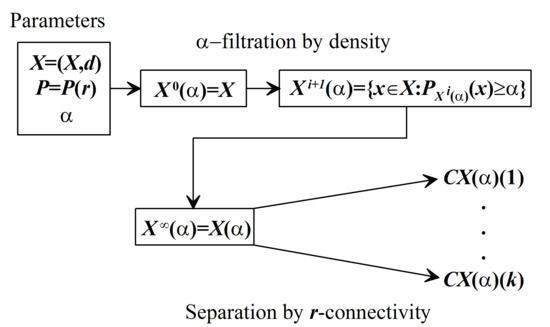
Figure 4.
Block diagram of the DPS.
The first stage of DPS intercepts the maximal subset , dense against the general background, from the initial space X. The second DPS stage splits into components . Each component combines density against the background and connectivity, that is, it formally expresses empirical clustering.
3.3.2. Parameter Selection: Localization Radius r
Suppose that be the set of all non-trivial distances in X:
The localization radius r is defined as a power mean with a negative exponent d of all distances from :
3.3.3. Parameter Selection: Density Level α
The selection of level greatly affects the result of the DPS algorithm. A convenient means for selecting the level is fuzzy comparisons [8]. They allow us to effectively construct the limitation level so that the DPS results are really dense against the general background, that is, they are empirical clusters.
The fuzzy comparison of two non-negative numbers a and b is a measure of the superiority of number b over number a, expressed as a scale of segment :
A fuzzy comparison of a number a and a finite set B can be defined as the mean of fuzzy comparisons a with all numbers from B:
and understood as a measure of minimality and a measure of maximality of the number a against the background B:
The measure of maximality enables formulating the necessary requirement for the DPS algorithm results: its density at each of its points must be significant (maximum enough) against the background X.
To do this, it is necessary first to calculate the density of the entire space X at all its points
This is a background of X. If is the required level of density extremeness P against the background of X, then the immediate level for P is uniquely determined by from equation
since the relation is of continuous and monotone kind. Equation (6) can be solved by dividing the segment at halves.
Therefore, the DPS algorithm must find a subset in X, that is -extremely P-dense against the general background X at each of its points:
and split it by the components of the r-connectivity for r from (5).
3.3.4. Quality Criterion
The DMA methods allow us to evaluate the quality of the algorithm in a different way, as an advantage of the result over complement .
One of the options for the quality criterion will be discussed in Example 6.
3.4. Density
If, in comparison (6) is replaced by with arbitrary and , then we obtain a variable density alternating in sign on X with values on the scale .
Definition 7.
Density
is called the extreme density generated by P (extreme P-density).
The value of does not clearly answer the following question: “To what extent is the subset of A dense at the point x against the general background of space X?”
It is convenient for us to consider the segment , rather than the segment , as the base scale in fuzzy mathematics and fuzzy logic, and given (7), all densities are normalized to the scale . Following these assumptions, the density at fixed A is a fuzzy structure on X. Therefore, with the help of fuzzy logic operations, as well as some others, it is possible to obtain new densities on the basis of the existing ones. This extends the capabilities of the and DPS algorithms in space X.
Statement 7.
- 1.
- If P and Q are densities on X andnondecreasing mapping, then superpositionwill be the density on X.
- 2.
- If ¬ fuzzy negation on, then the superpositionwill be the density on X.
- 3.
- If n is a fuzzy comparison on, then the superpositionwill be the density on X.
Consequence 2.
- 1.
- R-connection P andwill be the density on X
- 2.
- If ⊤ (⊥, ) is t-norm (t-co-norm, generalized averaging operator) [7], then superpositions , , will be densities on X.
- 3.
- If, then-connectionwill be density on X.
- 4.
- A “fuzzy comparison”will be the density on X:
3.4.1. The Logical Densities Calculus
Suppose that properties of elements of space X, which clusters can be obtained by the DPS algorithm with respect to densities .
If is a complex property obtained from properties using the fuzzy logic formula Φ containing only monotone operations: then clusters for in X can be obtained using DPS algorithm with density .
Remark 4.
The schemesand DPS depend on parameters, the main of which is the density P. Connecting with it, they become algorithmsandwith a subordinate parameter α.
Therefore, and DPS induce relations and , that to a certain extent resemble “functors” from the “category of densities” to the “category of algorithms”. This enables correct understanding (“through functors”) of the results of Statement 7–Section 3.4.1: the operations described therein can be considered “functors” on densities. Their superpositions with and DPS provide new mappings of densities into algorithms, that is, new algorithmic schemes that depend on density.
Example 1.
- 1.
- Scheme
- 2.
- Scheme
- 3.
- Scheme
Algorithms representing implementations of these schemes on specific densities play an important role in the FMS analysis and will be discussed below.
Remark 5.
Combination of fuzzy logic with densities gives great expressive power at the local level in studying of FMS X. On the other hand, the DPS scheme is very effective in connecting local data. These two circumstances make the DPS algorithms a powerful tool in studying of FMS X at the global scale.
The final part of the article will address the empirical evidences of this scheme by giving examples of DPS with different densities thus describing versions of DPS.
4. Results
4.1. SDPS Algorithm
Historically, the set-theoretical SDPS was the first in a series of DPS-algorithms. It is based on the density S with the name “Number of points” (“Number of space”) [12,13] and conveying the degree of concentration of space X round each of its points x (the most natural understanding of density X in x).
The density depends on the localization radius (5) and the non-negative parameter p, considering the distance to x in the full-sphere :
When , we have the usual number of points, explaining the name S:
The S density is r-local, and the SDPS algorithm is the implementation of the DPS scheme based on S, described in Definition 6–Section 3.3.3: . The result of SDPS is condensations in X ≡ sets locally containing “many X”. They correspond to empirical clusters in terms of the most formal criteria. By varying the SDPS parameters, it is possible to obtain a fairly complete picture of the hierarchy of clusters in X.
Example 2.
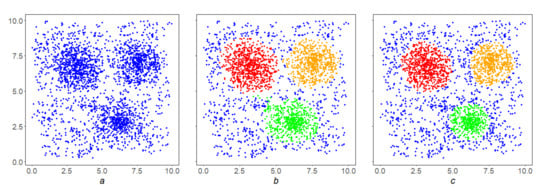
Figure 5b shows the result of selection by levelfor density S on the initial array X (Figure 5a), that is, the first iterationof the SDPS algorithm. It contains isolated points that needs to be removed, and in this sense is inferior to the final resultof the SDPS algorithm on X (Figure 5c.)

Figure 5.
Application of the SDPS algorithm (, , ): (a) the original array; (b) the result of the first iteration containing isolated points; and (c) the final result of applying SDPS.
Example 3.
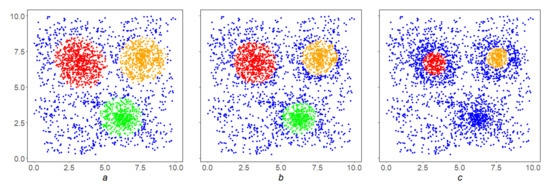
In the conditions of the Example 2, the inverse correlation of the SDPS algorithm performance with the parameter β is shown. By increasing it, we go inside the condensation, finding dense nuclei inside them (Figure 6a–c).

Figure 6.
Inverse dependence of the result of the SDPS algorithm on the parameter : (a) the result of the SDPS algorithm at ; (b) the result of work at ; and (c) the result of work at . (In all cases , ).
Example 4.
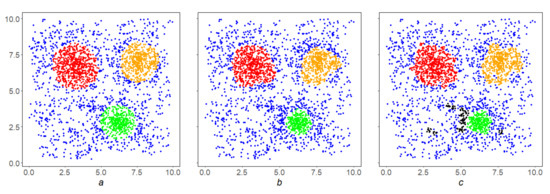
In the conditions of Example 2 the direct correlation of the SDPS algorithm performance with the parameter q is shown. By lowering it, we make the SDPS algorithm more local, focusses on finding smaller condensations (Figure 7a–c). All small condensations in Figure 7c are shown in black.

Figure 7.
Dependence of the result of the SDPS algorithm on the parameter q: (a) the result of the SDPS algorithm at ; (b) the result of work at ; and (c) the result of work for (in all cases , ).
Example 5.
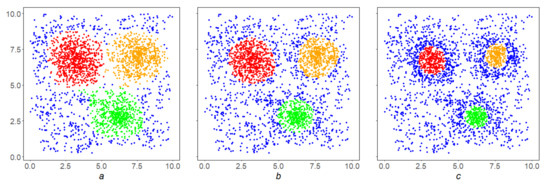
In the conditions of the Example 2, the inverse correlation of the SDPS algorithm performance with the parameter p is shown. By increasing it, we make the SDPS algorithm more stringent (Figure 8a–c).

Figure 8.
The inverse nature of the dependence of the SDPS algorithm on the parameter p: (a) the result of the SDPS algorithm at ; (b) the result of work at ; and (c) the result of work for (in all cases , ).
The above examples illustrate the general property of SDPS algorithm dependence on parameters: the stronger the localization and the density level is, the stricter the SDPS algorithm is, and its results are denser and finer.
Example 6.
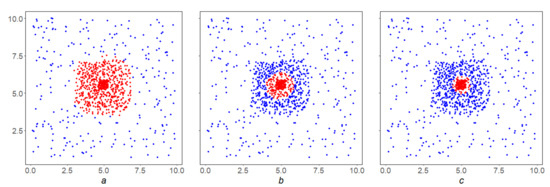
Let us illustrate the clustering qualityintroduced in Section 3.3.4 on the SDPS work in the array shown in Figure 9. Let us designate byandthe mean densities of the setsandat their points, then the result of their fuzzy comparisoncan be considered a version of the quality of thealgorithm on the space X. From left to right it is equal to, , respectively. This is true: the clustering in Figure 9a is clearly better, and Figure 9b,c are fairly the same.

Figure 9.
Illustration from left to right of the quality of the SDPS algorithm at ; ; . Clustering in figure (a) is clearly better, and in figures (b,c) is approximately the same. (As a fuzzy comparison, we used .
4.2. MDPS Algorithm
The SDPS algorithm is especially effective in heterogeneous, irregular spaces, where the property “density against the background” is strongly pronounced. If it is weakly expressed, there may be disadvantages in the work of SDPS caused by the density S.
Example 7.
- 1.
- Suppose that X is a uniform finite grid. The nodes at the edge X have a lower density S than the central nodes, although space X looks equally homogenous in both cases.
- 2.
- If in a full-sphereall points other than x, are concentrated on the circleand there are many of them, then the densityis significant, regardless ther-isolation x.
Another construct of the density M, which is also expressing the concentration of space X at the point x does not have such disadvantages, It is called solidity and is part of the main DMA-clustering algorithm with the correspondent name [21]. Let us talk about it.
Fix natural number and construct a uniform grid of nodes , in the interval . Then, we define a concentric in x semi-open ring for each :
For each , we assign the relevant weight . Solidity is defined as the ratio of the sum of the weights of non-empty rings to the sum of the weights of all rings:
The solidity M is r-local, and the MDPS algorithm is the implementation of the M-based DPS scheme described in Definition 6–Section 3.3.3: .
Remark 6.
Constructs S and M express the density of X in x in a different way, and this difference is shown in their names: construct S is focused on the “quantity”, is concentrated around x, while construct M is focused on “uniformity”, around x, expressed through the presence in rings.
Example 8.
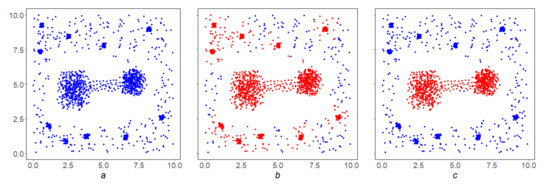
The dumb-bell shaped in Figure 10a has a monolithic but weak handle, so MDPS highlights it cleanly (Figure 10c), while SDPS cannot do so (Figure 10b). This example illustrates the independence of the MDPS and SDPS algorithms.

Figure 10.
An illustration of the independence of the MDPS and SDPS algorithms: the “dumbbell” in the original array (a) has a sparse handle, which MDPS highlights cleanly (c); SDPS cannot do this (b).
4.3. FDPS Algorithm
The functional version of the DPS algorithm is related to a special r-local density , based on function weighting :
The FDPS algorithm is the operation of the DPS circuit on F, as described in Definition 6–Section 3.3.3: [24]. It aims at finding subsets in X with r-local high weights , and is capable to work on regular spaces and successfully complements the SDPS and MDPS algorithms.
Remark 7.
Weight ν can be thought of as a non-negative relief on X. The FDPS algorithm efficiently searches for the bases of these elevations, which is fundamental in data analysis, in particular in time series analysis (DRAS, FC ARS algorithms etc.) [25].
Example 9.
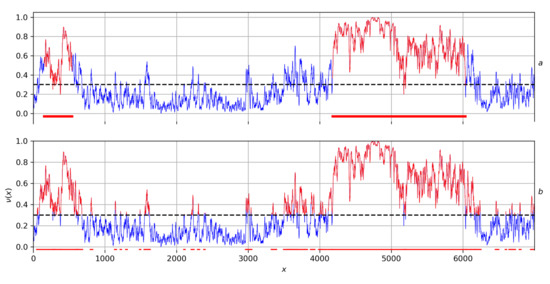
Figure 11a shows how the FDPS algorithm works: space X in this case is a regular grid on the horizontal axis, where the weight ν of each pointis plotted vertically. The result of the FDPS algorithm will be two red bars on the horizontal axis, serving as the bases of the two most significant stochastic ν-elevations on X.

Figure 11.
Operation of the FDPS algorithm on a regular grid (a). The FDPS algorithm results in two red lines on the horizontal axis, which serve as the bases of the two most significant stochastic heights. Figure (b) shows a classic choice with respect to a given level, highlighting many weak heights.
As can be seen from this figure, the FDPS algorithm is stable: it disregards to insignificant drops of contour ν below the set level, as well as to insignificant rises of ν above it. This property of the FDPS explains the solidity of its highlighted elevations and is essential in decision-making issues: the selected areas must be massive and resistant to minor disturbances within them.
To compare, Figure 11b shows a classical selection on grid X with respect to a given level for relief ν. As we can see from the figure, it is unstable, it gives a lot of weak elevations.
4.4. GDPS Gluing: Scheme and Algorithms
Suppose the local property of space X at each of its points x, its quantification, a is a subset in the full-sphere , where it is reached. In other words, is the subset in where the property is most clearly pronounced. It does not necessarily coincide with .
Task 1.
For a fixed level ofproperty, find the subsetin X, whose each full-spherewould have the propertyat each pointto the power.
If the quantification of property function P is the density on X Definition 1, then the result of the algorithm can be taken as A. Otherwise, we consider a set of local data in X
and try to comprehensively fit into the global subset . Let us formulate the requirements for A:
Under the natural assumption of “continuity” of the property we can expect its level of occurrence on to be close to .
The mismatch with in (8) can be understood differently. Some variants of it make it possible to find a solution of (8) using the DPS scheme (Definition 6–Section 3.3.3) with respect to densities specifically constructed by covering . Let us focus on one of them.
The initial space Y will carry the covering :
The density G is normalized: , and its level is the proximity index in (9).
The dependence (9), connecting with the DPS scheme (Definition 6–Section 3.3.3), leads to another dependence , which we designate as GDPS and will be understood like Remark 2 and DPS Remark 3 ambiguously:
- as a schema if we are talking about a dependency given above;
- as the GDPS algorithm when it comes to the operation of the DPS scheme (Definition 6–Section 3.3.3) on density with parameter : . Its result solves problem Task 1 by “gluing” local data in a certain way. This explains the name of the algorithm (gluing).
If the quantification of P property is the density on X, then the space Y is the first -hull of space X. The first solution Task 1 (let us call it “a strong one”) is the operation of SDPS on X with respect to P with level . It may differ from the second solution Task 1 (let us call it “a weak one”), which represents the operation of GDPS.
The point is that the SDPS algorithm in its interception on is guided primarily by preserving the density level , while the GDPS algorithm seeks to preserve the proximity level on . The weak version is more versatile, since the quantification of P property shall not be necessarily the density on X and it is also more “save” when carving. Therefore, it is the GDPS algorithm that will be part of the DPS-scheme Definition 6–Section 3.3.3 operation when the property represents a local linearity in X.
Let us explain the above on two examples relating to the density . In this case, the property will be the r-local “space count”, and S will be its formal expression. Since S is a density Definition 1, this Task 1 has two possible solutions: a strong and weak one. The basis for these is the space —the first iteration of the initial space X of relative density S for the level of extremeness .
The strong solution is the result of the SDPS algorithm on X with parameter (a subset of in Y. The weak solution is the result of the GDPS algorithm in this setting, i.e., the result of a DPS-scheme with density constructed on the basis of local data :
and a given level of proximity (a subset of ).
4.5. LDPS Algorithm
We believe that the initial FMS lies in the Euclidean plane. It is convenient to designate it by Q rather than X for reasons that will be clear below. In this paragraph we implement in detail the previous scenario for the local linearity property in Q. The result of this work done will be the LDPS algorithm from the series of DPS-algorithms, aimed at finding global linear structures in Q.
4.5.1. Initial Data and Designations
is the universe plane
- —fixed orthogonal coordinate system on ,
- —loose orthogonal coordinate system on , obtained by moving coordinate origin O to point and turning the axes by the angle ,
- Relation of coordinates
- Q is a finite-state array in : ,
- , (5),
- —the property of local linearity in Q.
4.5.2. Quantification
Let be an arbitrary fixed point in Q, arbitrary angle in . Let us move to the coordinates and we denote the “square” neighborhood Q in of radius r:
The additional parameter “height” enables defining the corridor in
Using and we define a measure of local linearity of space Q at point to the direction as the density against the background of by serial relation:
Maximum value
will be considered a quantitative expression of the property for Q in , and the neighborhood of is the best corridor where this maximum is reached.
For geometrical reasons, the relation must be considered as satisfied.
4.5.3. Search for Global Linear Structures
A quantification L of the property is made. Hence, it is possible to involve a GDPS scheme based on L for the weak solution of Task 1 in this case, which leads to the algorithm, where is the expression level of property L and is its representativity degree.
Research shows that in the generic case its result Z on space needs additional filtering, which is done by the MDPS algorithm with a solidity level . Its result is considered final in the search for linear structures within the space.
The LDPS algorithm is the described superposition of GDPS and MDPS:
Its parameters will be (parameters L) + (parameters M) + , and the result is the global linear structures in Q relative to them.
The LDPS algorithm has four stages:
- the first of them with the selected parameters of local linearity r and h constructs its quantification at each point q of space Q, and the best corridor , where the estimate is reached;
- the second stage includes constructing the basis for application of the GDPS scheme, namely coverage for a given level of local linearity ;
- the third stage is GDPS scheme working on data. Its result will represent linear structures in Q. On spacea measure is constructed (9)The result will represent the raw linear structures on Q;
- the fourth stage is their filtering by solidity using the MDPS algorithm with a level of .
In conclusion, we will address the operation of the LDPS algorithm on two arrays, while the operation in the first instance will be explained in detail, and in the second instance only the result is shown.
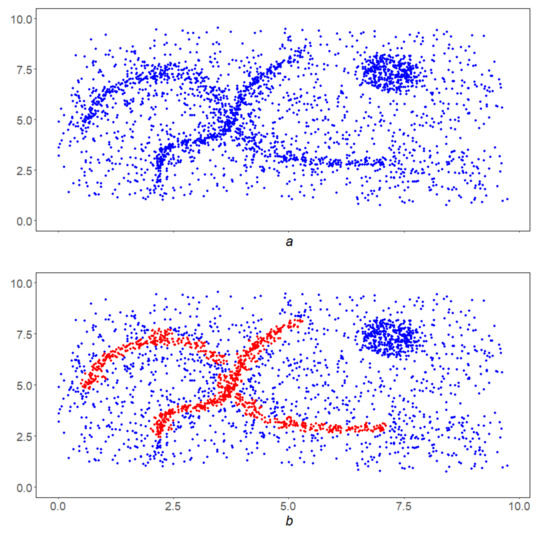
Example 10.
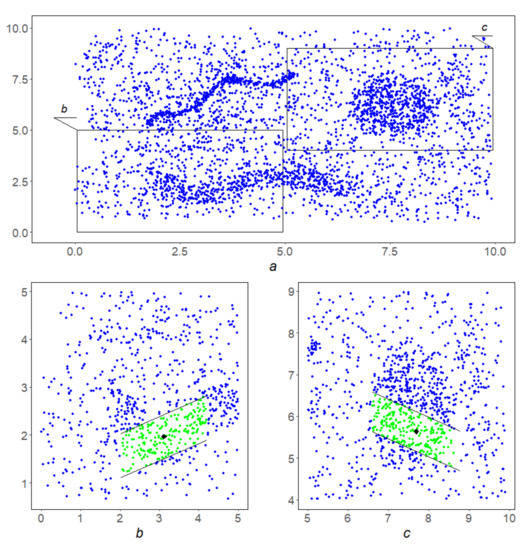
The initial array Q is shown in Figure 12a

Figure 12.
The first stage of the LDPS algorithm. (a) original array; (b) a corridor with a separability equal to ; and (c) a corridor with a separation of 0.5. The position of the fragments of the original array shown in figures (b,c) is indicated by the leaders in figure (a).
- At the first stage with the chosen parameters at each blue point q a linear corridoris constructed with parametersand, then its separabilityis calculated. Figure 12b,c show corridors in green with centers at black points. Their separability equals to and , respectively. In the second instance, it proves to be insufficient to overcome the second stage.
- Second stage. The separability level α is assumed to be. Figure 13a shows the points y in red, that passed this selection and formed the basis Y—the first half for application of the GDPS scheme. The second half GDPS scheme: corridorsare shown for the already familiar point on the left (Figure 13b) and at some point on the right (Figure 13c). It can be seen from the figures that the relative density of red dots in the left corridor is higher than in the right one. This circumstance will help the left point overcome the third stage and move into the lower linear structure, while the right point will not stand the test with GDPS operation and will not be included in the final result.
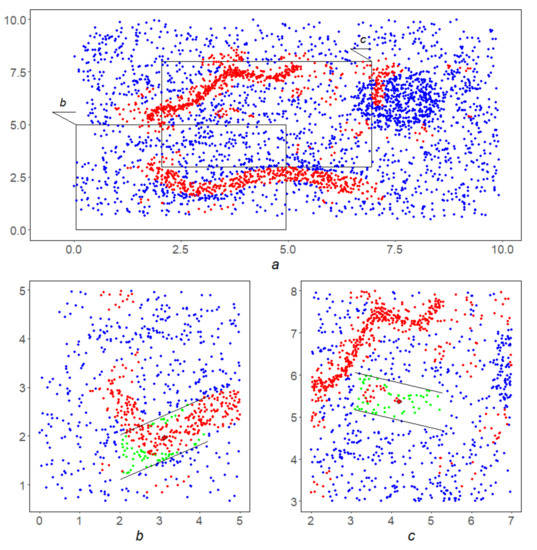 Figure 13. The second stage of the algorithm. (a) The original array with the selected base (red dots); (b) points from in the corridor from Figure 12b; and (c) points from in the corridor from Figure 12c. The position of the fragments of the original array shown in figures (b), (c) is indicated by the leaders in figure (a).
Figure 13. The second stage of the algorithm. (a) The original array with the selected base (red dots); (b) points from in the corridor from Figure 12b; and (c) points from in the corridor from Figure 12c. The position of the fragments of the original array shown in figures (b), (c) is indicated by the leaders in figure (a). - Third scheme. The GDPS scheme operation on the red points from the Y. Its result Z is shown in Figure 14a. It needs to be filtered.
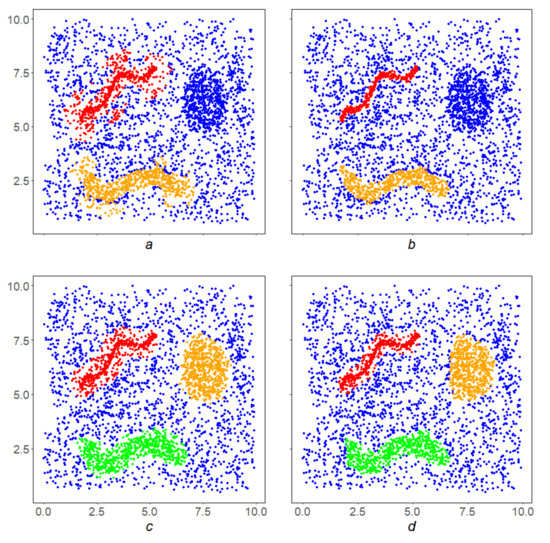 Figure 14. Result of the third and fourth stages of the LDPS algorithm. (a) The result of the third stage–the work of the GDPS algorithm; (b) the result of the fourth stage–the work of the MDPS algorithm; (c) the result of the DBSCAN algorithm; and (d) the result of the OPTICS algorithm.
Figure 14. Result of the third and fourth stages of the LDPS algorithm. (a) The result of the third stage–the work of the GDPS algorithm; (b) the result of the fourth stage–the work of the MDPS algorithm; (c) the result of the DBSCAN algorithm; and (d) the result of the OPTICS algorithm.
5. Discussion
This paper addressees the study of stationary data arrays, which are finite sets in multidimensional spaces, using the DMA methods by means of clustering.
A complex local condition is a conjunction of the conditions of local linearity and local representativeness. Local linearity: each point L has a linear corridor containing it that is dense against the background of Q, i.e., each point on the plane has a rectangle centered at q, which is a local corridor for L, and the intersection is dense against the background Q. Local representativeness: the intersection L is dense in .
The global condition for L consists of the requirement that L has no isolated points, i.e., in its discrete perfection. The detection of local linearity in the implementation of LDPS consists of a direct check for all points of the original space Q of this property. Analytical procedures are available to reduce routine calculations. In addition, in the future, we propose to modify the algorithm so that the dimensions of the corridors generally change from point to point.
The points in Q that pass the local linearity test form a subset of Y—the first approximation in Q to linear structures. We checked the linear representativity on Y in the LDPS algorithm as an implementation of the DPS scheme with respect to the special density G (clause 4.5.3). In the future, we plan to implement other variants of the LDPS algorithm based on a change in the interpretation of linear representativeness.
Studies have shown that, among the subset of points that have passed the local test for representativeness, there may be isolated points. The global condition in LDPS eliminates this drawback: its check for Z is also organized as an implementation of the DPS scheme with respect to the density “monolithicity” (MDPS algorithm). The points that pass the global test will be the result of applying the LDPS—that is, the union of all linear structures in Q.
In the general case, the set of linear structures L is divided into connected components. For example, in the examples given in Figure 14b and Figure 15b, two connectivity components are obtained. In the first example, the components of connectivity should be considered independent linear structures, and in the second example, as part of a single whole. In the future, we plan to introduce an additional procedure for joining the results of applying the LDPS algorithm in order to obtain global linear structures in the original space Q.
Comparison of the LDPS algorithm with the well-known new generation cluster analysis algorithms DBSCAN and OPTICS, as well as with the previously created DMA clustering algorithms, shows that the LDPS algorithm is not inferior to them in detecting clumps; however, at the same time, it is more focused on recognizing clumps with a linear structure.
The implementation of the formal approach as shown in the article can be very effective in various fields of Earth sciences where linear structures play a special role in the investigation of spatial patterns of geographical location and geometric configuration of natural objects. This is vital when solving the issue of predicting the isolation properties of the geological environment for the preparation of a rationale for the geodynamic stability over long periods of time (ten to one hundred thousand years), arising in the selection of HLRW disposal sites. Further to this task, the algorithm can apply to the analysis of elongated artificial structures, such as road networks, etc.
Author Contributions
All authors contributed to the study conception and design. Conceptualization, original draft preparation: S.A., S.B. and V.T.; conceptualization, methodology, review and editing and validation: D.K. and V.K.; material preparation, formal analysis, data curation, algorithm development: S.B. and M.O. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by Russian Science Foundation No 18-17-00241 “Study of the rock massifs stability by system analysis of geodynamic processes for geoecologically safe underground of radioactive waste isolation”.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| URL | Underground research laboratory |
| HLRW | High-level radioactive waste |
| DMA | Discrete mathematical analysis |
| DPS | Discrete perfect sets |
| FMS | Finite metric space |
References
- Gvishiani, A.D.; Kaftan, V.I.; Krasnoperov, R.I.; Tatarinov, V.N.; Vavilin, E.V. Geoinformatics and systems analysis in geophysics and geodynamics. Phys. Earth 2019, 1, 42–60. [Google Scholar] [CrossRef]
- Laverov, N.P.; Omelyanenko, B.I.; Velichkin, V.I. Geological aspects of the problem of radioactive waste disposal. Geoecology 1994, 6, 3–20. (In Russian) [Google Scholar]
- Dzeboev, B.A.; Karapetyan, J.K.; Aronov, G.A.; Dzeranov, B.V.; Kudin, D.V.; Karapetyan, R.K.; Vavilin, E.V. FCAZ-recognition based on declustered earthquake catalogs. Russ. J. Earth. Sci. 2020, 20, ES6010. [Google Scholar] [CrossRef]
- Gorshkov, A.I.; Soloviev, A.A. Recognition of earthquake-prone areas in the Altai-Sayan-Baikal region based on the morphostructural zoning. Russ. J. Earth. Sci. 2021, 21, ES1005. [Google Scholar] [CrossRef]
- Belov, S.V.; Gvishiani, A.D.; Kamnev, E.N.; Morozov, V.N.; Tatarinov, V.N. Development of complex model of evolution of structural-tectonic blocks of the Earth’s crust for choosing storage sites of high level radioactive waste. Russ. J. Earth. Sci. 2008, 10, ES4004. [Google Scholar] [CrossRef][Green Version]
- Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Averkin, A.N.; Batyrshin, I.Z.; Blishun, A.F.; Silov, V.B.; Tarasov, V.B. Fuzzy Sets in Models of Control and Artificial Intelligence; Publ. Nauka: Moscow, Russia, 1986; 312p. (In Russian) [Google Scholar]
- Agayan, S.M.; Bogoutdinov, S.R.; Krasnoperov, R.I. Short introduction into DMA. Russ. J. Earth Sci. 2018, 18, ES2001. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Dzeboev, B.A.; Agayan, S.M. FCAZm intelligent recognition system for locating areas prone to strong earthquakes in the Andean and Caucasian mountain belts. Izv. Phys. Solid Earth 2016, 52, 461–491. [Google Scholar] [CrossRef]
- Widiwijayanti, C.; Mikhailov, V.; Diament, M.; Deplus, C.; Louat, R.; Tikhotsky, S.; Gvishiani, A. Structure and evolution of the Molucca Sea area: Constraints based on interpretation of a combined sea-surface and satellite gravity dataset. Earth Planet. Sci. Lett. 2003, 215, 135–150. [Google Scholar] [CrossRef]
- Gvishiani, A.; Soloviev, A.; Krasnoperov, R.; Lukianova, R. Automated Hardware and Software System for Monitoring the Earth’s Magnetic Environment. Data Sci. J. 2016, 15, 18. [Google Scholar] [CrossRef]
- Agayan, S.M.; Bogoutdinov, S.R.; Dobrovolsky, M.N. On one algorithm for searching the dense areas and its geophysical applications. In Proceedings of the Materials of 15th Russian National Workshop “Mathematical Methods of Pattern Recognition, MMRO-15”, Petrozavodsk, Russia, 11–17 September 2011; Maks Press: Moscow, Russia, 2011; pp. 543–546. (In Russian). [Google Scholar]
- Agayan, S.M.; Bogoutdinov, S.R.; Dobrovolsky, M.N. Discrete Perfect Sets and Their Application in Cluster Analysis. Cybern. Syst. Anal. 2014, 50, 176–190. [Google Scholar] [CrossRef]
- Everitt, B.S. Cluster Analysis; Halsted-Heinemann: London, UK, 1980; 170p. [Google Scholar]
- Dzeboev, B.A.; Gvishiani, A.D.; Agayan, S.M.; Belov, I.O.; Karapetyan, J.K.; Dzeranov, B.V.; Barykina, Y.V. System-Analytical Method of Earthquake-Prone Areas Recognition. Appl. Sci. 2021, 11, 7972. [Google Scholar] [CrossRef]
- Mandel, I.D. Cluster Analysis; Publ. Finansy i Statistika: Moscow, Russia, 1988; 176p. (In Russian) [Google Scholar]
- Mark, S.A.; Roger, K.B. Cluster Analysis (Quantitative Applications in the Social Sciences); SAGE Publications, Inc.: Newbury Park, CA, USA, 1984; 88p. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; Simoudis, E., Han, J., Fayyad, U.M., Eds.; AAAI Press: Palo Alto, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.; Kriegel, H.-P.; Sander, J. OPTICS: Ordering Points To Identify the Clustering Structure. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 31 May–3 June 1999; ACM Press: New York, NY, USA, 1999; pp. 49–60. [Google Scholar] [CrossRef]
- Bojchevski, A.; Matkov, Y.; Günnemann, S. Robust Spectral Clustering for Noisy Data: Modeling Sparse Corruptions Improves Latent Embeddings. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD-17), Halifax, NS, Canada, 13–17 August 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 737–746. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Agayan, S.M.; Bogoutdinov, S.R.; Soloviev, A.A. Discrete mathematical analysis and geological and geophysical applications. Bull. Earth Sci. 2010, 2, 109–125. (In Russian) [Google Scholar]
- Mikhailov, V.; Galdeano, A.; Diament, M.; Gvishiani, A.; Agayan, S.; Bogoutdinov, S.; Graeva, E.; Sailhac, P. Application of artificial intelligence for Euler solutions clustering. Geophysics 2003, 68, 168–180. [Google Scholar] [CrossRef]
- Agayan, S.M.; Soloviev, A.A. Highlight dense areas in metric spaces based on crystallization. Syst. Res. Inf. Technol. 2004, 2, 7–23. (In Russian) [Google Scholar]
- Agayan, S.M.; Tatarinov, V.N.; Gvishiani, A.D.; Bogoutdinov, S.R.; Belov, I.O. Strong-Earthquake-Prone Areas FDPS algorithm in stability assessment of the Earth’s crust structural tectonic blocks. Russ. J. Earth Sci. 2020, 20, ES1005. [Google Scholar] [CrossRef]
- Agayan, S.; Bogoutdinov, S.; Soloviev, A.; Sidorov, R. The Study of Time Series Using the DMA Methods and Geophysical Applications. Data Sci. J. 2016, 15, 16. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).