Sentence Compression Using BERT and Graph Convolutional Networks

Abstract

Sentence compression is a natural language-processing task that produces a short paraphrase of an input sentence by deleting words from the input sentence while ensuring grammatical correctness and preserving meaningful core information. This study introduces a graph convolutional network (GCN) into a sentence compression task to encode syntactic information, such as dependency trees. As we upgrade the GCN to activate a directed edge, the compression model with the GCN layers can distinguish between parent and child nodes in a dependency tree when aggregating adjacent nodes. Furthermore, by increasing the number of GCN layers, the model can gradually collect high-order information of a dependency tree when propagating node information through the layers. We implement a sentence compression model for Korean and English, respectively. This model consists of three components: pre-trained BERT model, GCN layers, and a scoring layer. The scoring layer can determine whether a word should remain in a compressed sentence by relying on the word vector containing contextual and syntactic information encoded by BERT and GCN layers. To train and evaluate the proposed model, we used the Google sentence compression dataset for English and a Korean sentence compression corpus containing about 140,000 sentence pairs for Korean. The experimental results demonstrate that the proposed model achieves state-of-the-art performance for English. To the best of our knowledge, this sentence compression model based on the deep learning model trained with a large-scale corpus is the first attempt for Korean.

1. Introduction

Sentence compression is a natural language-processing (NLP) task where the primary objective is to generate a short paraphrase of an input sentence [1]. Deletion-based compression is the most common approach to sentence compression—it is a sequence-labeling problem that determines whether each word should be retained or deleted from a source sentence to form a compressed sentence [2]. With this approach, only the remaining words are used to compose a compressed sentence. Syntactic information, such as a syntactic tree, has been adopted as a feature in many sentence compression systems to maintain the grammaticality of a compressed sentence.

A graph neural network (GNN) is a powerful architecture for modeling structural data such as trees or graphs [3]. The GNN has recently gained popularity in the dependency parsing research domain because it can appropriately represent a node of a dependency tree by aggregating its parent and child nodes and by gradually incorporating higher-order information of a dependency tree by collecting neighboring nodes.

We adopt a deletion-based approach to sentence compression that performs word-based deletion from a source sentence. Thus, representing a word with as much information as possible is critical in a sentence compression model. In this study, we introduce a graph convolutional network (GCN) [4] to obtain structural information of words in a dependency tree. The GCN is one of the most common GNNs because it operates using the same convolution used in conventional convolutional neural networks. The GCN can support node representation in a dependency tree, allowing neighboring nodes to be integrated with shared weights. Furthermore, we use pre-trained Bidirectional Encoder Representations from Transformers (BERT) [5] to obtain contextualized information of words in a sentence.

In this study, we upgrade GCNs to activate directed edges; therefore, the proposed GCNs can distinguish between parent and child nodes when aggregating adjacent nodes. In addition, as the number of layers in GCNs increases, the GCNs gradually collect high-order information of a dependency tree by propagating information through the layers. The sentence compression model equipped with the upgraded GCN can glean information within nodes two hops away from a given node by differentiating ancestors and descendants when the GCN has two layers. We implement a sentence compression model for Korean and English in this study. The model has three components: a BERT pre-trained model, GCN layers, and a scoring layer. First, a sequence of word vectors of an input sentence can be obtained using the BERT pre-trained model. The word vectors contain contextualized information of a sentence. Syntactic information—such as parent and child nodes of a dependency tree—is then embedded into the word vectors using the GCN aggregation operation. Finally, the scoring layer decides whether a word should remain in a compressed sentence based on information on the word vector.

To train the proposed sentence compression model, we require a parallel corpus consisting of pairs of original and corresponding compressed sentences. We use the Google sentence compression dataset for English. For Korean, we use the Korean sentence compression corpus [6], which contains approximately 140,000 sentence pairs. We evaluate the proposed model on the Korean and English corpora. To the best of our knowledge, this proposed deletion-based sentence compression is the first attempt for Korean. For English, the proposed model can achieve state-of-the-art performance.

Our contributions to sentence compression are as follows:

(1)

We introduce GCNs to sentence compression tasks to efficiently exploit a dependency tree when representing words.

(2)

This study is the first to build a sentence compression model for Korean based on deep neural networks and to evaluate sentence compression on a large-scale Korean corpus.

(3)

The proposed model achieves state-of-the-art performance in English sentence compression.

The rest of the paper is organized as follows. We first explore related studies in Section 2. In Section 3, we present a sentence compression model based on BERT and GCNs. The experimental results are presented in Section 4, and the conclusion is presented in Section 5.

2. Related Studies

Sentence compression performed in [7] focused on enhancing robustness across domains and tasks. The basic architecture used in [7] was a three-layered bidirectional long short-term memory (bi-LSTM) model that uses the embeddings of words, parts of speeches, and dependency relations as inputs. Furthermore, the researchers adopted an integer linear programming (ILP) technique to incorporate constraints based on syntactic relationships between words and to adjust the expected lengths of compressed sentences. The evaluation results demonstrated that their model outperformed the basic model with layered bi-LSTMs both within and across domains. They asserted that the syntactic features in bi-LSTMs and syntactic constraints in ILP help to improve the model’s domain adaptability.

The basic compression model in [8] is a bi-LSTM that uses embeddings of words, parts of speeches, and dependency relations as inputs. As the researchers adopted reinforcement learning approaches to compress sentences, the basic compression model operates as a policy network. The policy network continues to sample the actions of removing or retaining words until an entire compressed sentence is yielded. A reward function is an essential component in reinforcement learning. In [8], a syntax-based evaluator that assesses the grammaticality of a compressed sentence was proposed as a reward function. The syntax-based evaluator is implemented as a syntax-based language model that can predict the next word token given previous words and part-of-speech tags and dependency relationship labels. Another reward function using a compression rate is used to generate a compressed sentence with a similar compression rate.

A deletion-based compression model with a sequence-to-sequence architecture can unidirectionally compress a source sentence. Thus, the model cannot capture the relationship between decoded and unseen words decoded in future time steps, potentially resulting in compressed sentences with grammatical errors or relevant words dropped. Kamigaito & Okumura [9] proposed the Syntactically Look-A-Head Attention Network (SLAHAN), which can traverse both parent and child words recursively in a dependency tree during the decoding time. SLAHAN encodes a dependency tree as a graph representation and traverses the dependency tree recursively by calculating attention scores. In human evaluations, SLAHAN improved the informative performance without losing readability. Furthermore, the researchers found that looking ahead for important words by traversing a dependency tree can improve compression accuracies.

For Korean sentence compression, Choi et al. [10] proposed an abstractive sentence compression model with an event attention. The model they adopted is a combination of a sequence-to-sequence model and a pointer generator. As they focused on compressing news articles in which event words play a key role, they adopted an event attention to concentrate on important eventual content in a source sentence. Although their dataset consisting of only 3117 Korean sentences is not sufficient to train a deep learning model, the proposed model with the event attention achieved a better performance than the base model without the event attention.

3. Sentence Compression Using BERT and GCNs

This section describes a baseline model and then introduces GCNs to the baseline model. Next, we propose directed GCNs representing a dependency structure to improve the aforementioned models.

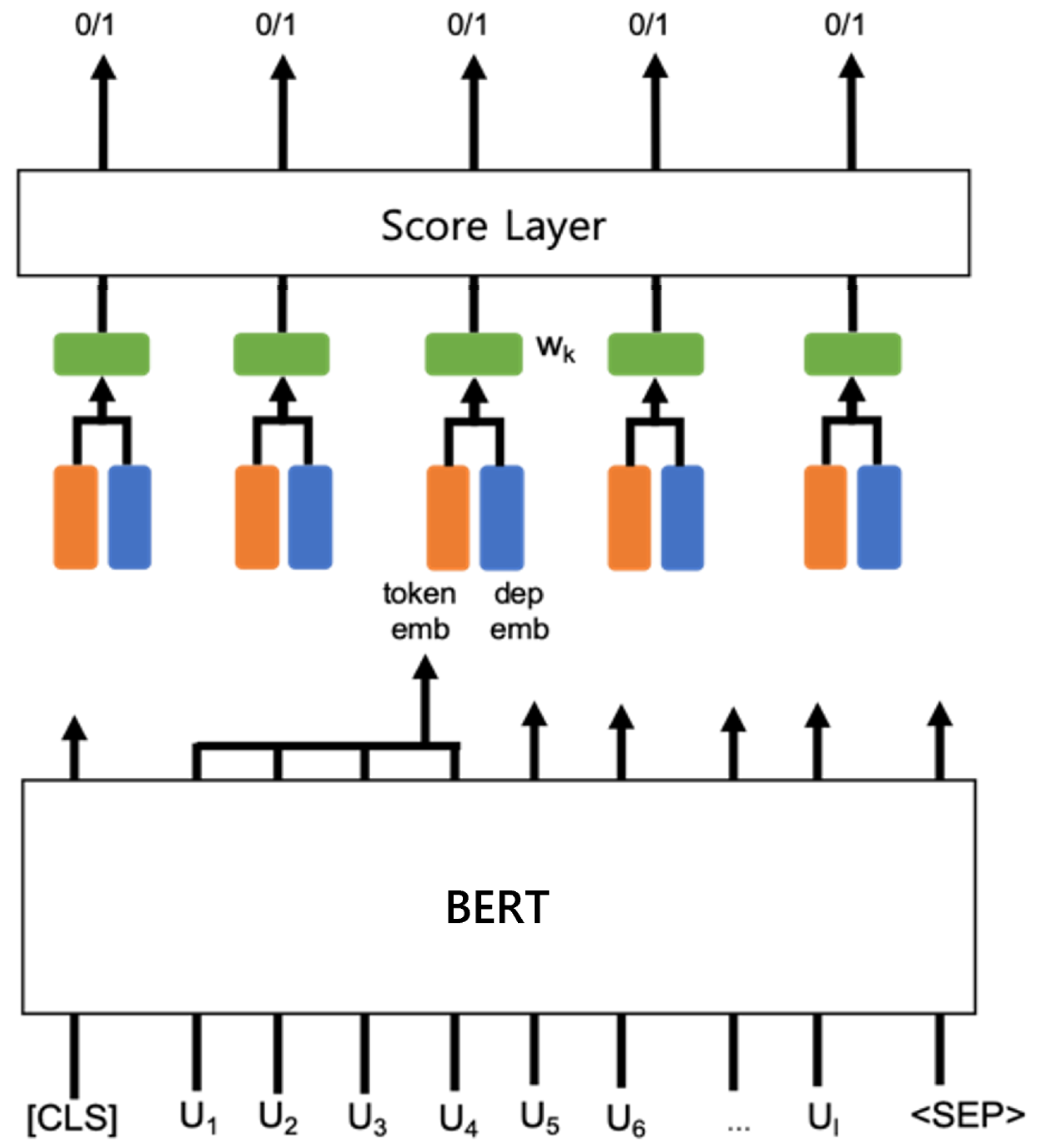
Given a sentence consisting of n words, $s=\{w_1,w_2,\dots ,w_n\}$ is a sequence of word representations of a sentence. A score layer uses the word representation $w_k$ as an input and computes a final score to predict if the k-th word corresponding to $w_k$ remains in a compressed sentence. Therefore, if the score is less than 0.5, the k-th word is deleted (“0” indicates deletion in Figure 1); otherwise, the word remains (“1”). In this study, the score layer consists of two linear layers and a logistic sigmoidal function in the final layer, as described in Equation (1).

$$ScoreLayer\left(w_k\right)=\sigma (W_s\ast relu(W_i{w}_k+b_i)+b_s)$$

(1)

where $w_k$ is a vector representation of the k-th word and can be obtained by concatenating a token embedding ($toke{n}_{-}em{b}_k$) and a dependency label embedding ($de{p}_{-}em{b}_k$) according to Equation (2). The dependency label indicates a syntactic role between the k-th word and its parent word in a dependency tree.

$$w_k=relu(W_w\ast [toke{n}_{-}em{b}_k\left|\right|de{p}_{-}em{b}_k\left]\right)$$

(2)

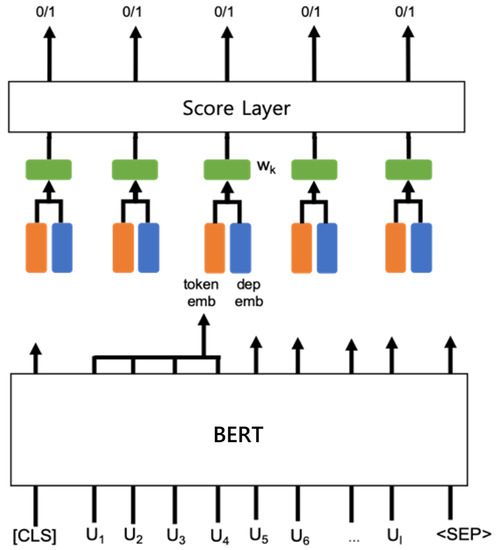
Figure 1. Baseline model representing sentence compression.

3.1. Baseline Model

Figure 1 illustrates a basic sentence compression model [11] with BERT and a score layer.

BERT, a well-known pre-trained model, can provide a sequence of contextualized word embeddings for an input sentence. As BERT adopts sub-word tokenization (a word may be split up into multiple tokens), a sentence compression model using word-based deletion must combine multiple tokens from BERT outputs into a word. A token embedding $toke{n}_{-}em{b}_k$ for the k-th word consisting of m sub-word tokens can be obtained by concatenating two final hidden states of bi-LSTMs, as in Equation (3).

$$\begin{array}{c}\hfill toke{n}_{-}em{b}_k=[\overrightarrow{LSTM}\left(t_{k_m}\right|t_{k_1},t_{k_2},\dots ,t_{k_{m-1}})\left|\right|\\ \hfill \overleftarrow{LSTM}\left(t_{k_1}\right|t_{k_2},t_{k_3},\dots ,t_{k_m})],\end{array}$$

(3)

where $t_{k_i}$ is an output of BERT for the i-th sub-word token of the k-th word.

3.2. Sentence Compression Using GCNs

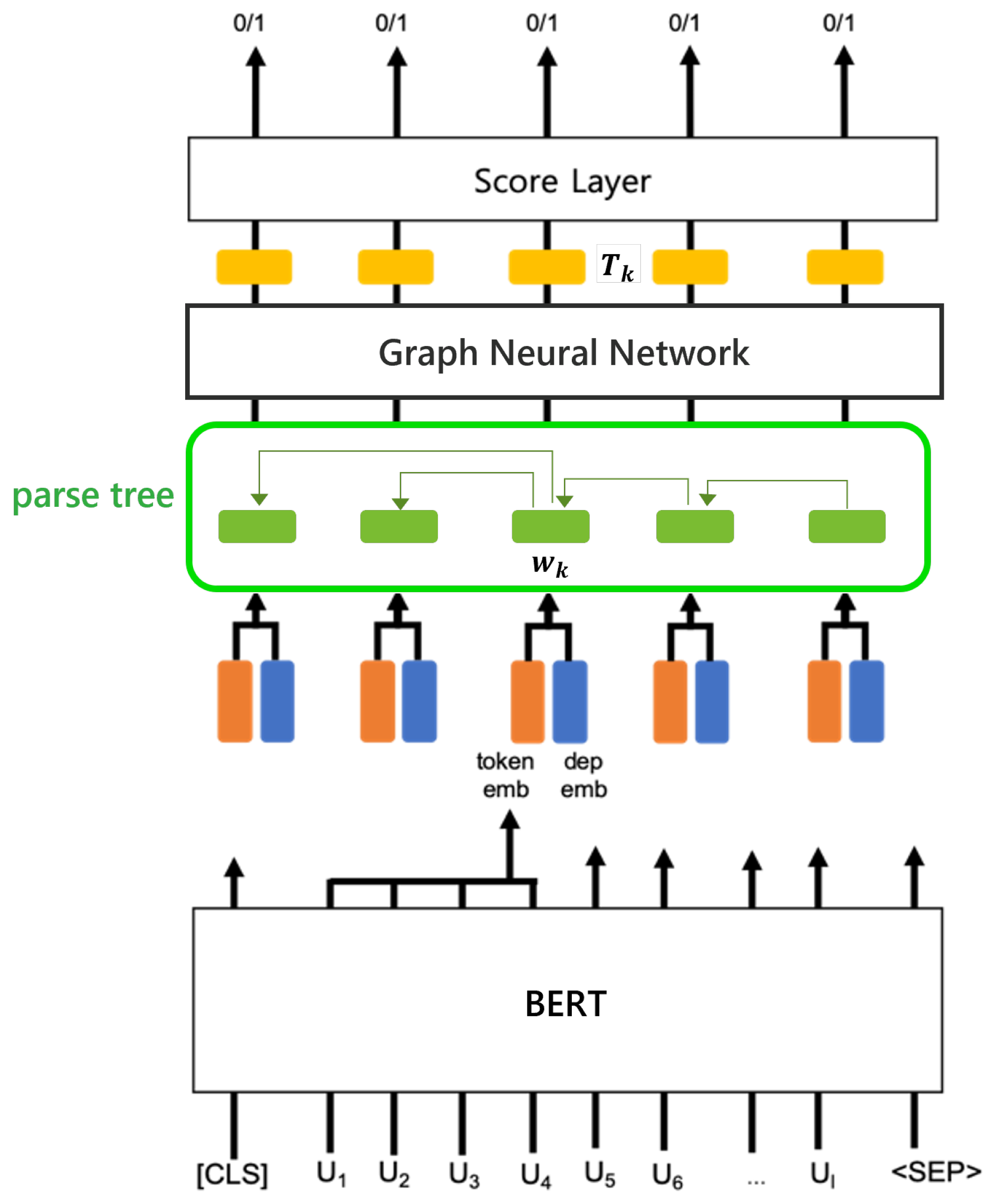
Figure 2 depicts a basic architecture representing sentence compression using a GNN to process syntactic information. An input sequence $s=\{w_1,w_2,\dots ,w_n\}$ is re-calculated by the GNN and its syntactic parse tree. Node $T_k$, the output of the GNN layer for the k-th word, becomes an input for the score layer.

Figure 2. Sentence compression model with a GNN.

In a graph, each node is naturally defined by its features and related nodes. The objective of GNNs is to learn a node embedding that contains the neighbors’ information of the node. From a parsing perspective, the node embedding of a syntactic dependency tree is represented by aggregating with its parent and child nodes.

A GCN is one of the most commonly used GNNs. A basic aggregator in GCNs is a convolution operation that shares all the weights within the same layer. GCNs, similar to GNNs, can consider multi-hop neighboring nodes when they have multiple layers. In this study, we introduce two types of GCNs to obtain a node’s embeddings: (1) GCNs with undirected edges and (2) directed GCNs where all edges have directions.

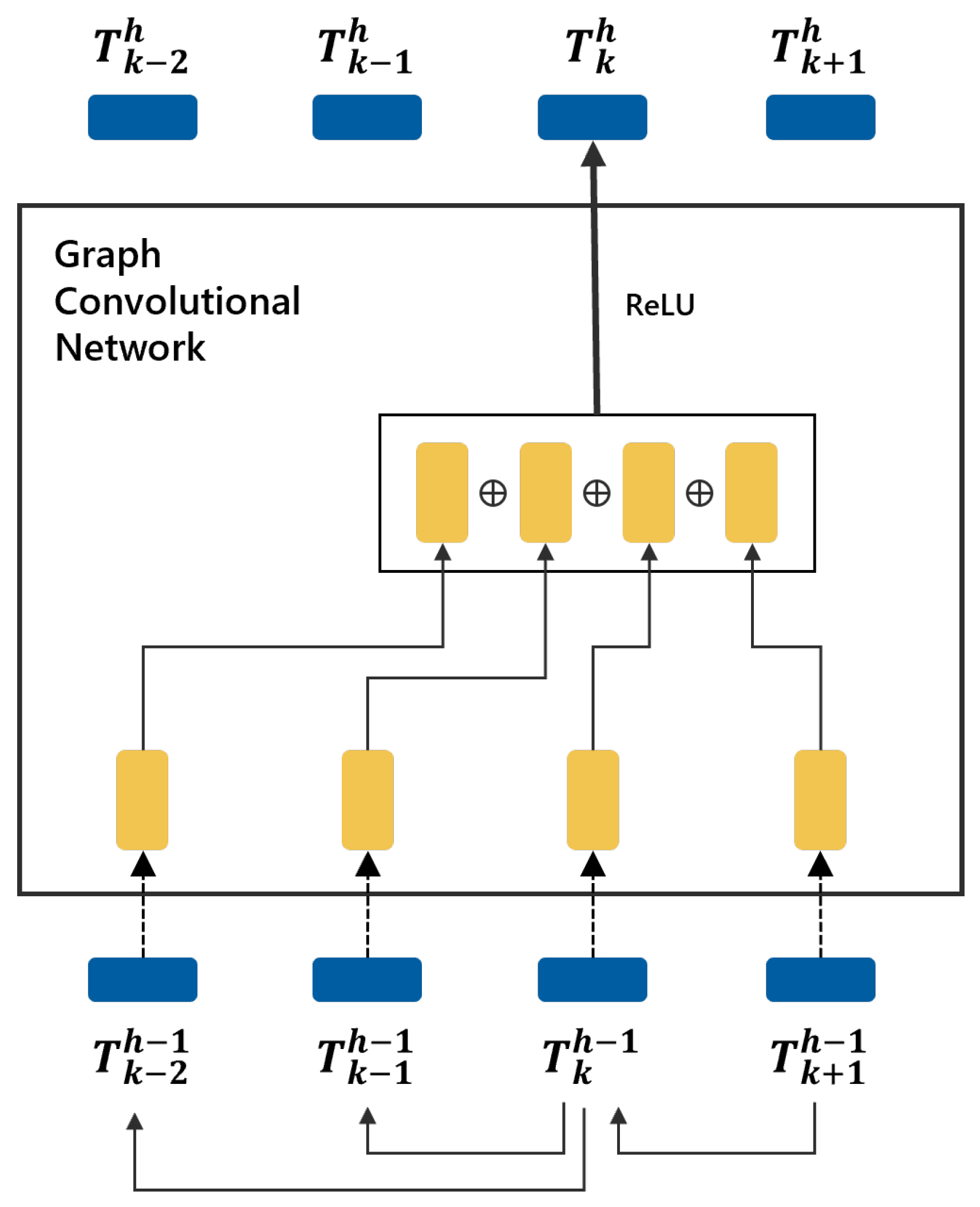
In GCNs, a node can be propagated to the next layer by aggregating the neighbors’ information using a convolutional operation. Equation (4) is a layer-wise propagation rule in a multi-layer GCN [4]:

$$T^h=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{T}^{h-1}{W}_g^h\right),$$

(4)

where $\tilde{A}=A+I_N$ is an adjacency matrix of an undirected graph with self-connections added. $I_N$ is the identity matrix, ${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$, and $W_g^h$ is a layer-specific learnable weight matrix. $\sigma$ is an activation function, and the rectified linear unit (ReLU) was used in this study. The adjacency matrix was normalized by ${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$. $T_k^{h-1}$ is an input matrix to the h-th layer of a GCN that is propagated to $T^h$ by Equation (4) and $T^0={[w_1,w_2,\dots ,w_n]}^T$.

Figure 3 illustrates an example of how to propagate a node $T_k^{h-1}$ with two child nodes and a parent node (indicated by arrows at the bottom) to $T_k^h$ in the h-th layer. As all edges in a GCN have no direction, the adjacency matrix for this example is symmetric. In the h-th GCN layer, the node $T_k^{h-1}$ itself, its parent, and two child nodes are all aggregated by a convolutional operation and applied by the ReLU function for propagation to a new $T_k^h$ in the next layer.

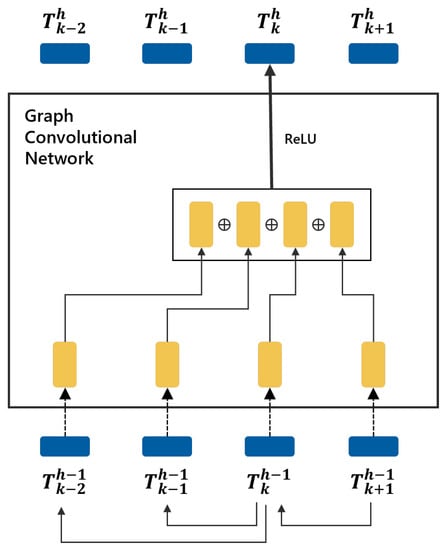
Figure 3. Example of node propagation in the h-th GCN layer.

3.3. Sentence Compression Using Directed GCNs

As a dependency tree inherently has directional information between a node and its parent, GCNs with undirected edges cannot fully represent syntactic tree information. We addressed this shortcoming by extending the GCNs to include directional information on edges—referred to as directed GCNs(d-GCNs) in this study.

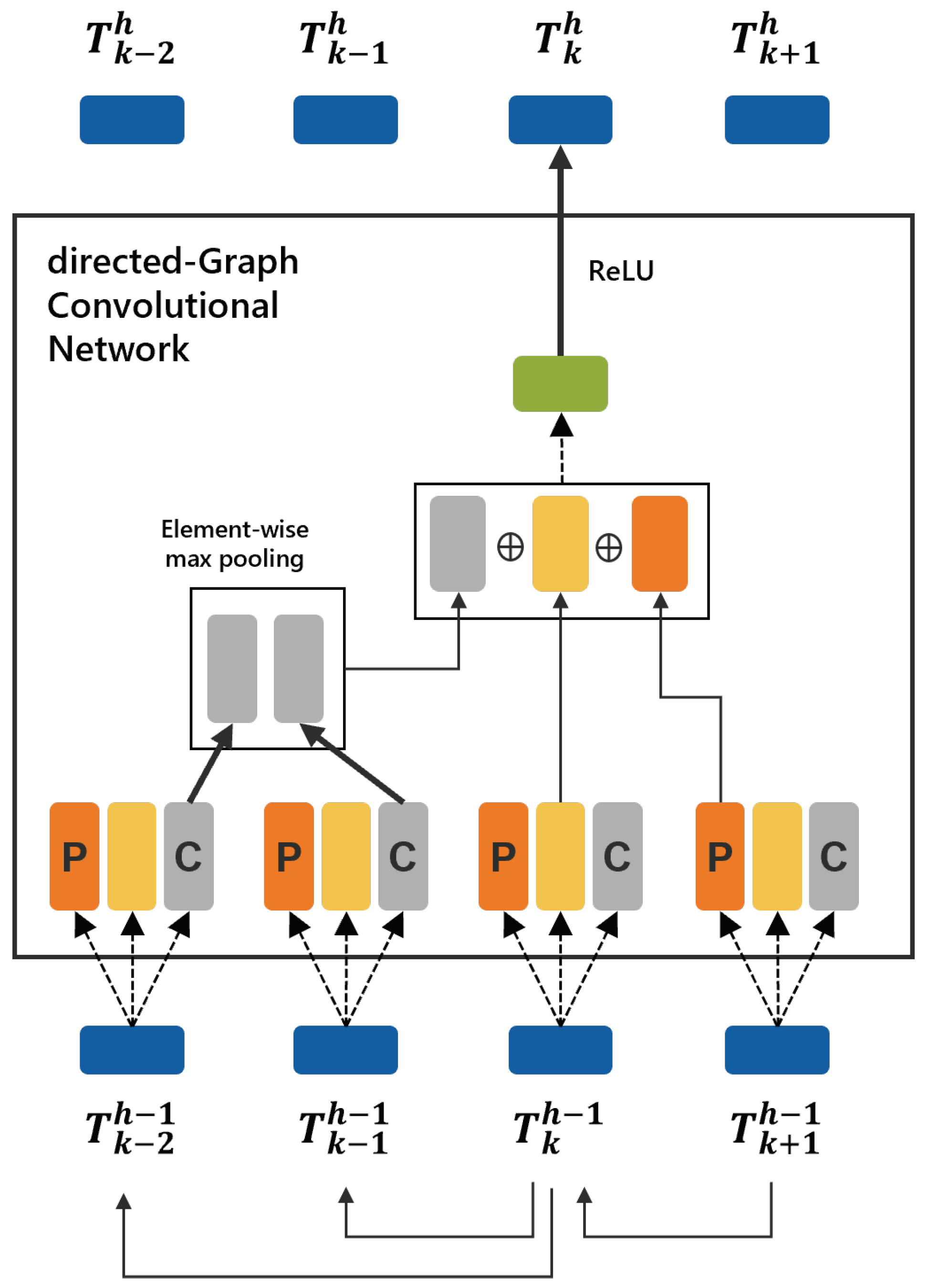
To fully utilize the directed edges in a directed graph, the propagation steps of parent and child nodes should be treated differently. Therefore, two types of weight matrixes are incorporated in Equation (5) to glean more precise structural information [12]:

$$T^h=\sigma \left(D_p^{-1}{A}_p\sigma \left(D_c^{-1}{A}_c{T}^{h-1}{\theta }_c^h\right){\theta }_p^h\right),$$

(5)

where $D_p^{-1}{A}_p$ and $D_c^{-1}{A}_c$ are the normalized adjacency matrixes for the parent and child nodes, respectively, and ${\theta }_p^h$ and ${\theta }_c^h$ are learnable weight matrixes at the h-th layer to linearly transform parent and child nodes, respectively.

We modify the propagation rule in Equation (5) slightly for this study. Equation (6) is a node propagation rule of the d-GCN proposed in this study. Figure 4 further explains Equation (6). The k-th input node $T_k^{h-1}$ to the layer h can be propagated to $T_k^h$ by Equation (6):

$$\begin{array}{cc}\hfill T_k^h=\sigma \left(\right(& \sigma \left(T_k^{h-1}{\theta }_I^h\right)\hfill \\ \hfill & \oplus \sigma \left(T_{P\left(k\right)}^{h-1}{\theta }_p^h\right)\hfill \\ \hfill & \oplus maxpoolin{g}_{\forall c\in C\left(k\right)}\left(\left\{\sigma \left(T_c^{h-1}{\theta }_c^h\right)\right\}\right)\left){\theta }_l^h\right),\hfill \end{array}$$

(6)

where the functions $P\left(k\right)$ and $C\left(k\right)$ return a parent index and child indexes of the k-th word in a dependency tree.

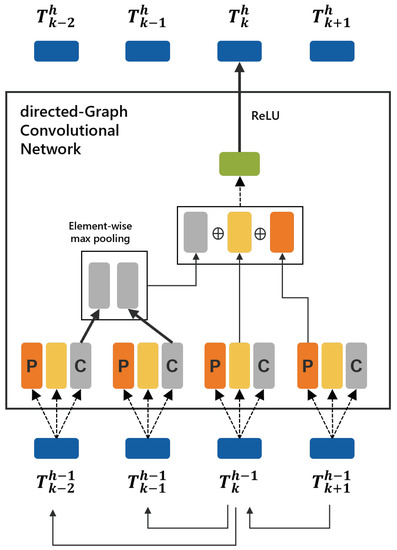
Figure 4. Example of node propagation in the h-th d-GCN layer.

As a node can have several child nodes in a dependency tree, an aggregator is necessary to combine all child nodes’ information. In Equation (5), all child nodes are aggregated by a simple element-wise mean. In this study, we adopt an element-wise max-pooling aggregator to combine child information because not all child nodes are equally important to their parent. In the final step of node propagation, another linear transformation is performed by multiplying the weight matrix ${\theta }_l^h$. This step is then followed by the non-linearity ReLU function.

4. Experiments

In this section, we first describe the details of datasets and experimental enviroments and then present experimental results of the performance of the compression models. Some examples of compressed sentences are also provided at the end of this section.

4.1. Datasets and Experimental Setup

Training a sentence compression model based on deep learning requires a parallel corpus consisting of pairs of original and compressed sentences.

We use the Korean sentence compression corpus [6] consisting of 144,987 pairs, of which 117,252 are part of the training set, 13,130 are used as the validation set, and 14,605 are used as a testing set. This corpus was built by a sentence compression algorithm that deletes nodes from a syntactic dependency tree of an original sentence while preserving the grammaticality of a compressed sentence. The algorithm chooses nodes to be deleted using the structural constraints and semantically required information on a sentence. The Korean sentence compression corpus was successfully built by applying the algorithm to headlines and the first sentences of news articles. The average number of words in source sentences is 16.5, and that of words in compressed sentences is 12.0. The average compression ratio (CR) for word-based is about 72.5, and that for character-based is about 75.5.

This study used the Google sentence compression dataset for English (https://github.com/google-research-datasets/sentence-compression, accessed on 16 September 2021). The first 1000 pairs of “comp-data.eval.json” were used as a testing set, and the last 1000 pairs were used as a validation set. Of the 200,000 pairs in sent-com.train*.json, 199,915 pairs in which the original sentence lengths were less than 512 tokens were used as a training set. The average CR for the dataset is 42.3.

The hyperparameters used in the experiments are depicted in Table 1. The version of BERT we used is BERT-BASE (https://huggingface.co/bert-base-uncased, accessed on 16 September 2021) for English and KorBERT (http://aiopen.etri.re.kr, accessed on 16 September 2021) for Korean.

Table 1. Hyperparameters used in experiments.

Hyperparameters	Values
Number of LSTM layers	2
Hidden dimension of LSTM	768
Dimension of dependency label embedding	768
Number of layers in GCN and d-GCN	2
Hidden dimension of GCN and d-GCN	1536
Optimizer	Adam
Learning rate of BERT	5 × 10${}^{-5}$
Learning rate of other deep learning models	1 × 10${}^{-3}$

4.2. Results and Evaluation

As this study is the first attempt to compress Korean sentences using a deep learning model, the experimental results cannot be compared with those of previous studies. Therefore, we establish a pruning model for an initial comparison model that compresses a sentence by pruning its dependency tree at a specified depth. The experimental results for Korean sentence compression are described in Table 2. The CR is the average number of characters of a compressed sentence divided by that of an original sentence, and Δ$C$ is the CR of sentences compressed by a model minus the CR of a training set. We set the depth of the pruning model to 5 to generate compressed sentences as close as possible to the CR of the training set.

Table 2. Evaluation results for Korean sentence compression. ^† indicates that the difference of the F1 score from the BASELINE is statistically significant with 0.95 confidence. We used paired-bootstrap-resampling [13] with 14,605,000 random samples.

Models	ALL				LONG (43.7%) (Length ≥ 16.34)
	F1	CR	Δ$\mathit{C}$	# of Sub-Trees	F1	CR	Δ$\mathit{C}$	# of Sub-Trees
PRUNING (depth = 5)	80.16	82.37	6.9	1	76.14	71.75	−1.2	1.0
BASELINE	90.33	75.51	0.6	1.18	89.32	73.31	0.3	1.29
BASELINE + GCN	90.34	76.74	1.2	1.16	89.27	72.97	0.8	1.25
BASELINE + d-GCN	$\mathbf{90.98}{}^{†}$	78.00	2.5	1.04	$\mathbf{90.12}{}^{†}$	74.79	1.8	1.07

The baseline model with only BERT and the score layer achieved a high F1 score of 90.33. This result implies that contextualized information of a sentence calculated by self-attention operations in BERT is helpful for deciding which words should remain in compressed Korean sentences.

When the model was equipped with the GCN, its F1 score was similar to the baseline model, but the CR increased. The model that adopted the d-GCN achieved a higher F1 score, but the CR became higher than the comparison models.

We reason that the d-GCN layers were well-trained in choosing appropriate nodes for compressing a sentence while preserving the grammaticality of the compressed sentences. Although the model with d-GCN produced the longest compressed sentences, the number of sub-trees in the compressed sentences was the smallest among the comparison models besides the pruning model. The model with the d-GCN tends to generate a longer compressed sentence in which all words are connected in a valid syntactic tree. “LONG” is the evaluation result only for the sentences in which the average lengths exceeded those in the testing set. The percentage of the “LONG” sentences in the testing set is also presented in the table.

The experimental results for English sentence compression are described in Table 3. The compression model with GCN had a similar F1 score as the baseline model and the previous studies. However, the model with d-GCN achieved state-of-the-art performance. The gap in the F1 scores of the models with d-GCN and without d-GCN widened more for “LONG” sentences than for “ALL”. The performance improvements are attributed to the propagation rules in the d-GCN layers that differentiate parent and child nodes and aggregate child nodes with a max-pooling operation.

Table 3. Evaluation results for English sentence compression. ^† indicates that the difference of the F1 score from the baseline is statistically significant with 0.95 confidence. We used paired-bootstrap-resampling [13] with 1,000,000 random samples.

Models	ALL				LONG (41.7%) (Length ≥ 27.04)
	F1	CR	Δ$\mathit{C}$	# of Sub-Trees	F1	CR	Δ$\mathit{C}$	# of Sub-Trees
Evaluator-LM [8]	85.5	39.0	−2.7	-	-	-	-	-
SLAHAN [9]	85.5	40.7	−1.5	-	83.3	28.4	−1.9	-
BASELINE	85.2	40.1	−2.3	1.70	82.9	29.6	−1.3	1.91
BASELINE + GCN	85.5	40.3	−2.1	1.65	82.4	30.0	−0.9	1.88
BASELINE + d-GCN	$\mathbf{86.2}{}^{†}$	40.9	−1.4	1.55	$\mathbf{84.2}{}^{†}$	31.3	0.4	1.72

In order to conduct human evaluation of the three compression models, we collected 100 sentences each from the Korean and English testing sets. The compression ratio strongly correlates with human judgments of informativeness and grammaticality [14]. Therefore, only sentences with a compression ratio difference of less than 10.0% were collected and evaluated. All sentence–compression pairs were assessed by three human raters who were asked to rate them on a five-point Likert scale from one to five. These pairs were evaluated for both readability and informativeness. Table 4 summarizes the human evaluation results. In Korean and English, the system with d-GCN outperformed the other models under both metrics. The performance of the compression model using GCN is not as good as we would expect, and the readability score of English is even lower than that of the baseline. However, the model adopting d-GCN has shown significant improvements in both metrics.

Table 4. Results of human evaluation of Korean and English sentence compression. ^† indicates that the difference of the score from the BASELINE is statistically significant with 0.95 confidence. We used the same method as in Table 2 and Table 3 with 100,000 random samples.

Models		Readability	Informativeness
Korean	BASELINE	3.55	3.64
	BASELINE + GCN	3.68	$3.79{}^{†}$
	BASELINE + d-GCN	$\mathbf{3.84}{}^{†}$	$\mathbf{3.99}{}^{†}$
English	BASELINE	3.72	3.57
	BASELINE + GCN	3.59	3.57
	BASELINE + d-GCN	$\mathbf{3.89}{}^{†}$	$\mathbf{3.91}{}^{†}$

Examples of the compressed sentences are listed in Table 5.

Table 5. Examples of compressed sentences.

Models	Sentences
Input	British mobile phone giant Vodafone said Tuesday it was seeking regulatory approval to take full control of its Indian unit for $1.65 billion, after New Delhi relaxed foreign ownership rules in the sector.
Gold	Vodafone said it was seeking regulatory approval to take full control of its Indian unit.
BASELINE	it was seeking approval to take control of its Indian unit.
BASELINE + GCN	said it was seeking approval to take control of its Indian unit.
BASELINE + d-GCN	Vodafone said it was seeking regulatory approval to take full control of its Indian unit.
SLAHAN w/syn [9]	Vodafone said it was seeking regulatory approval to take full control of its Indian unit.
Input	Broadway’s original Dreamgirl Jennifer Holliday is coming to the Atlanta Botanical Garden for a concert benefiting Actor’s Express.
Gold	Broadway’s Jennifer Holliday is coming to the Atlanta Botanical Garden.
BASELINE	Jennifer Holliday is coming to the Atlanta Botanical Garden.
BASELINE + GCN	Broadway Jennifer Holliday is coming to the Atlanta Botanical Garden.
BASELINE + d-GCN	Broadway’s Jennifer Holliday is coming to the Atlanta Botanical Garden.
SLAHAN w/syn [9]	Broadway’s Jennifer Holliday is coming to the Atlanta Botanical Garden.
Input	Robert Levinson, an American who disappeared in Iran in 2007, was in the country working for the CIA, according to a report from the Associated Press’s Matt Apuzzo and Adam Goldman.
Gold	Robert Levinson who disappeared in Iran in 2007 was in the country working for the CIA.
BASELINE	Robert Levinson an American who disappeared in Iran was.
BASELINE + GCN	Robert Levinson was in the country working for the CIA.
BASELINE + d-GCN	Robert Levinson who disappeared in Iran was in the country working for the CIA.
Input	Tamil cinema star Kamal Haasan, who had last year threatened to leave India in the light of controversies surrounding his film Vishwaroopam, on Monday pledged his ‘commitment’ to the country and expressed hope he would not leave it.
Gold	Kamal Haasan threatened pledged his commitment to the country.
BASELINE	Kamal Haasan pledged his commitment the.
BASELINE + GCN	Haasan threatened and expressed hope he would not leave.
BASELINE + d-GCN	Kamal Haasan pledged his commitment he would not leave.
Input	British mobile phone giant Vodafone said Tuesday it was seeking regulatory approval to take full control of its Indian unit for $1.65 billion, after New Delhi relaxed foreign ownership rules in the sector.
Gold	Vodafone said it was seeking regulatory approval to take full control of its Indian unit.
BASELINE	it was seeking approval to take control of its Indian unit.
BASELINE + GCN	said it was seeking regulatory approval to take control of its Indian unit.
BASELINE + d-GCN	Vodafone said it was seeking regulatory approval to take full control of its Indian unit.

5. Conclusions

This study introduced d-GCN into a sentence compression task to represent a word with a dependency tree. As the d-GCNs can handle directed edges and can be stacked with multiple layers, the compression model with the d-GCNs could distinguish between descendants and ancestors when aggregating neighbors and could gradually collect high-order information by propagating across the layers.

The proposed sentence compression model consists of a BERT pre-trained model, d-GCN layers, and a scoring layer. The scoring layer of the model determines whether a word should remain in a compressed sentence by judging the word vector containing contextual and syntactic information encoded by BERT and the d-GCN layers.

The proposed model achieved state-of-the-art performance for English sentence compression. As this is the first attempt to use GCNs for Korean sentence compression, the current experimental results are a cornerstone for future studies.