The Vehicle Routing Problem: State-of-the-Art Classification and Review

Abstract

Transportation planning has been established as a key topic in the literature and social production practices. An increasing number of researchers are studying vehicle routing problems (VRPs) and their variants considering real-life applications and scenarios. Furthermore, with the rapid growth in the processing speed and memory capacity of computers, various algorithms can be used to solve increasingly complex instances of VRPs. In this study, we analyzed recent literature published between 2019 and August of 2021 using a taxonomic framework. We reviewed recent research according to models and solutions, and divided models into three categories of customer-related, vehicle-related, and depot-related models. We classified solution algorithms into exact, heuristic, and meta-heuristic algorithms. The main contribution of our study is a classification table that is available online as Appendix A. This classification table should enable future researchers to find relevant literature easily and provide readers with recent trends and solution methodologies in the field of VRPs and some well-known variants.

1. Introduction

Problems related to the distribution of goods between warehouses and customers are generally considered as vehicle routing problems (VRPs). The VRP was first proposed by Dantzig and Ramser [1] in 1959 to model how a fleet of homogeneous trucks could serve the demand for oil from a number of gas stations from a central hub with a minimum travel distance. Five years later, Clarke and Wright [2] added more practical restrictions to VRPs in which the delivery of goods to each customer must occur within a set of bounds. This type of problem model became known as the VRP with time windows (VRPTW), which is one of the most widely studied topics in the field of operations research [3].

However, current VRP models differ significantly from those introduced by Dantzig and Ramser [1] and Clarke and Wright [2], because they aim to incorporate real-world complexities. Because VRPs are some of the most critical challenges faced by logistics companies, an increasing amount of research is focusing on VRPs. Several surveys and taxonomies for VRPs can be found in [3,4,5,6] ((Eksioglu et al. (2009); Braekers et al. (2016); Elshaer and Awad (2020); Konstantakopoulos et al. (2020)) and in many other books or book chapters [7,8,9,10] ((Cordeau et al. (2007); Golden et al. (2008); Toth and Vigo (2014)); Nalepa (2019)).

Solving VRPs is computationally expensive and categorized as NP-hard [11], because real-world problems involve complex constraints such as time windows, time-dependent travel times (reflecting traffic congestion), multiple depots, and heterogeneous fleets. These features introduce significant complexity and have dramatically evolved the VRP research landscape.

The processing speed and memory capacity of computers has grown rapidly, enabling the processing of increasingly complex instances of VRPs and widespread application of logistics distribution scenarios. The number of VRP solution methods introduced in the academic literature has grown rapidly over the past few decades. According to Eksioglu et al. [4], the VRP represents an evolving field of operations research that has been growing exponentially at a rate of 6% per year, which makes it difficult to keep track of developments in the field and obtain a clear overview of which variants and solution methods are relatively novel.

The VRP family can be considered as two combinatorial senses: (1) the number of possible solutions, which grow exponentially with computer science and algorithm design; and (2) the number of conceivable problem variants, which also grow exponentially with a variety of problem attributes [12]. This survey classifies the academic literature on VRPs from the perspective of solution methodologies, as well as the detailed characteristics of VRPs. Because we base our classification on the taxonomy presented in [4], we restrict our analysis to articles published between 2019 and August of 2021. Therefore, we do not intend to provide an exhaustive overview of VRP literature. To the best of our knowledge, this article provides the first structured classification of recent VRP literature based on solution and problem attributes.

The main contribution of our paper is a classification table that is available online as Appendix A. This classification table should enable future researchers to find relevant literature easily by eliminating or selecting characteristics in the taxonomy, leaving only articles tailored to their interests. The main objective of this work is to provide readers with recent trends and solution methodologies in the field of VRPs and some well-known variants. This survey is expected to help future researchers identify a problem domain and promising topics for research.

Section 2 defines the scope of this survey and Section 3 introduces the VRP and its variants. A comprehensive survey of state-of-the-art strategies currently used for solving VRPs is presented in Section 4. Section 5 summarizes our observations and conclusions.

2. Scope of the Survey

We analyzed recent literature published between 2019 and August of 2021 using a taxonomic framework. Classification is followed by a survey that uses the taxonomy to evaluate trends in the field and identify which articles contribute to these trends. We restricted the reviewed literature to the following features: only relevant articles published in English-language journals were considered, meaning books, conference proceedings, and dissertations were excluded.

To extract the most relevant literature and keep the number of articles manageable, the following search strategy was applied. First, only articles containing ‘‘vehicle routing” as title words or keywords were selected. Second, the search was limited to articles that were extended by highly cited articles published in any ranked journal (Google Scholar top 20), excluding review papers. For papers published in 2021, which are too recent to have cite ranking, we selected the top five pages from Google Scholar, each of which had 10 cited articles, as well as two review papers written by Moghdani et al. [13] and Asghari and Al-e (2021). Third, the abstracts of selected articles were read to determine their relevance to the subject.

This search strategy resulted in a final set of 88 articles. Although this selection is not exhaustive, it contains the majority of recent articles on VRPs and can be considered as representative of the field.

3. VRP and Its Variants

3.1. VRP

In addition to the classical VRP, several variants have also been studied. Capacitated VRP (CVRP), VRPTW, VRP with heterogeneous fleets (HFVRP), time-dependent VRP (TDVRP), and multi-depot VRP (MDVRP) are some of these variants. The classical VRP can be described as follows. Let $\mathrm{G}=\left(V, A\right)$ be a graph, where $V=\left\{v_0,v_1, v_2, \dots , v_N\right\}$, where $\left\{v_1, v_2, \dots , v_N\right\}$ is the node set representing customers to be served and $v_0$ is the depot. Each customer is characterized by a demand $D_i$. $A=\left\{\left(v_i, v_j\right): v_i, v_j\in V\right\}$ is the arc set (subscript indicates sequence) linking nodes i and j with a distance $d_{ij}$. Let ${\mathrm{M}}_m=\left\{m_1,m_2,m_3,\dots ,m_m\right\}$ denote the vehicle set, where each vehicle has a maximum load capacity $ca{p}_m$, meaning the total load of vehicle m cannot exceed the maximum load capacity $ca{p}_m$. To reflect a real distribution scenario accurately, different features are considered according to the settings of heterogeneous models. The goal of the VRP is to derive optimal vehicle routes such that each customer is visited exactly once by one vehicle and each vehicle starts and ends its route at the depot. The following assumptions are adopted:

• The depot has a demand equal to zero.
• Each customer location is serviced by only one vehicle.
• Each customer’s demand is indivisible.
• Each vehicle shall not exceed its maximum load capacity cap_m.
• Each vehicle starts and ends its route at the depot.
• Customer demand, distribution distances between customers, and delivery costs are known.

The notations used for problem definition are summarized as Table 1, Table 2 and Table 3.

Table 1. Sets and indices of VRP.

V	Node set, where $v_0$ is the depot and {v1, v2, …, vN} are customers
i,j	Subscripts of the customer nodes, $i,j=1,2,\dots N$
A	$A=\left\{\left(v_i, v_j\right): v_i, v_j\in V\right\}$ is arcs set linking nodes i and j
Mm	The set of vehicles with m types

Table 2. Parameters of VRP.

Di	Demand of customer i
dij	Distance between nodes i and j
vehm	Maximum available number of each vehicle type
capm	Maximum load capacity of vehicle type m
fcm	Fixed cost of vehicle type m
vcm	Variable cost of vehicle type m
Dmij,m	Amount carried using vehicle type m from i to j

Table 3. Decision variable of VRP.

Xij,m

Value of one if vehicle type m travels from node i to j. Otherwise, value of zero

Traditional logistics models focus on minimizing the total cost of a network. This is where the concept of the VRP is best applied. We follow this concept and add the fixed cost $f{c}_m$ of a vehicle, which represents rent cost or operating costs, to the total cost to minimize the total number of vehicles. We also include the variable cost $v{c}_m$ of delivery using each type of vehicle to optimize vehicle scheduling. Additional constraints appear in the target calculation in the form of penalty functions to enforce vehicle limit constraints. The objective of minimizing the total cost is defined as follows:

$$\mathrm{Minimize} {\displaystyle \sum }_{m=1}^M{\displaystyle \sum }_{i=0}^N{\displaystyle \sum }_{j=0}^N{X}_{ij,m}f{c}_m+{\displaystyle \sum }_{m=1}^M{\displaystyle \sum }_{i=0}^N{\displaystyle \sum }_{j=0}^N{d}_{ij}D{m}_{ij,m}v{c}_m$$

(1)

subject to the following constraints:

Routing:

$${{\displaystyle \sum }}_{i=1}^N{X}_{i0,m}=1 \forall m \in {\mathrm{M}}_m$$

(2)

$${\displaystyle \sum }_{m=1}^M{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^N{X}_{ij,m}=1 \forall \left(i,j\right)\in \mathrm{A} \forall m \in {\mathrm{M}}_m$$

(3)

$${\displaystyle \sum }_{m=1}^M{\displaystyle \sum }_{i=1}^N{X}_{ip,m}={\displaystyle \sum }_{m=1}^M{\displaystyle \sum }_{i=1}^N{X}_{pi,m} \forall p \in V$$

(4)

Demand and capacities:

$${\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^N{X}_{ij,m}{D}_j=D{m}_{ij,m} \forall \left(i,j\right)\in \mathrm{A} \forall m \in {\mathrm{M}}_m$$

(5)

$${\displaystyle \sum }_{i=1}^{N}D{m}_{0i,m}\le ca{p}_m \forall m \in {\mathrm{M}}_m$$

(6)

$${\displaystyle \sum }_{m=1}^M{X}_{ij,m}\le ve{h}_m \forall m \in {\mathrm{M}}_m$$

(7)

The objective function in Equation (1) is the total cost, which includes the fixed cost and variable cost. Constraint (2) states that each vehicle should return to the depot, where the subscript is zero. Constraint (3) ensures that each node can only be visited once in a route. Constraint (4) states that, if a vehicle arrives at a node, it must leave that node, thereby ensuring route continuity. Constraints (5) and (6) impose restrictions on the amounts of demand and capacity. Constraint (7) defines the maximum number of available vehicles veh_m.

3.2. VRP Variants

Practical requirements and new challenges require extensive definitions and formulations of the VRP. For example, distance, driver working hours, time windows, traffic conditions, and so on can all arise in real-world VRPs and enrich the definition and applications of VRPs. This chapter provides an overview of recent research on different models for vehicle routing. The main goal of this chapter is to present an overview of vehicle routing and scheduling areas while discussing several real-world applications.

Some features of VRPs are summarized in Table 4 based on the research by Eksioglu et al. [4]. Other variants have also been studied beyond the classical VRP. These variants include the influence of time factors, time windows of customers, maximum operating time of vehicles, differing delivery times caused by varying traffic conditions, varying characteristics of vehicles, varying capacities, varying speeds, and new types of electric vehicles. By referring to the taxonomy of [4], we divided models into three main categories: customer-related, vehicle-related, and depot-related models, which is the most important issue to represent the difference in real delivery problems. These categories have representative model features that are sorted in the tables below according to the year as shown in Table 5, Table 6 and Table 7.

Table 4. Taxonomy of VRP literature (adapted from [4]).

1. Type of Study	3.4. Number of Points of Origin
1.1. theory	3.4.1 single origin
1.2. applied methods	3.4.2 multiple origins
1.2.1 exact methods	3.5. number of points of loading/unloading facilities (depot)
1.2.2 heuristics	3.5.1 single depot
1.2.3 simulation	3.5.2 multiple depots
1.2.4 real-time solution methods	3.6. time window type
1.3. implementation documented	3.6.1 restriction on customers
1.4. survey, review of meta-research	3.6.2 restriction on roads
2. scenario characteristics	3.6.3 restriction on depot/hubs
2.1. number of stops on rout	3.6.4 restriction on drivers/vehicle
2.1.1 known (deterministic)	3.7. number of vehicles
2.1.2 partially known, partially probabilistic	3.7.1 exactly n vehicles
2.2. load splitting constraint	3.7.2 up to n vehicles
2.2.1 splitting allowed	3.7.3 restriction on drivers/vehicle
2.2.2 splitting not allowed	3.8. capacity consideration
2.3. customer service demand quantity	3.8.1 limited capacity
2.3.1 deterministic	3.8.2 unlimited capacity
2.3.2 stochastic	3.9. vehicle homogeneity (capacity)
2.3.3 unknown	3.9.1 similar vehicles
2.4. request times of new customers	3.9.2 load-specific vehicles
2.4.1 deterministic	3.9.3 heterogeneous vehicles
2.4.2 stochastic	3.9.4 customer-specific vehicles
2.4.3 unknown	3.10. travel time
2.5. on-site service/waiting times	3.10.1 deterministic
2.5.1 deterministic	3.10.2 function dependent
2.5.2 time dependent	3.10.3 stochastic
2.5.3 vehicle type dependent	3.10.4 unknown
2.5.4 stochastic	3.11. transportation cost
2.5.5 unknown	3.11.1 travel time dependent
2.6. time window structure	3.11.2 distance dependent
2.6.1 soft time windows	3.11.3 vehicle dependent
2.6.2 strict time windows	3.11.4 operation dependent
2.6.3 mixture of both	3.11.5 function of lateness
2.7. time horizon	3.11.6 implied hazard/risk related
2.7.1 single period	4. information characteristics
2.7.2 multiple periods	4.1. evolution of information
2.8. backhauls	4.1.1 static
2.8.1. nodes request simultaneous pickups and deliveries	4.1.2 partially dynamic
2.8.2. nodes request either linehaul or backhaul service, but not both	4.2 quality of information
2.9. node/arc covering constraints	4.2.1 known (deterministic)
2.9.1 precedence and coupling constraints	4.2.2 stochastic
2.9.2 subset covering constraints	4.2.3 forecasted
2.9.3 recourse allowed	4.2.4 unknown (real-time)
3. problem physical characteristics	4.3. availability of information
3.1. transportation network design	4.3.1 local
3.1.1 directed network	4.3.2 global
3.1.2 undirected network	4.4. processing of information
3.2 locations of addresses (customers)	4.4.1 centralized
3.2.1 customers on nodes	4.4.2 decentralized
3.2.2 arc routing instances	5. data characteristics
3.3 geographical locations of customers	5.1 data used
3.3.1 urban (scattered with a pattern)	5.1.1 real-world data
3.3.2 rural (randomly scattered)	5.1.2 synthetic data
3.3.3 mixed	5.1.3 both real and synthetic data
	5.2 no data used

Table 5. Model categories of VRPs published in 2021.

No.	Authors	Model Features
		Customer-Related Aspects	Vehicle-Related Aspects	Depot-Related Aspects
1	(Mojtahedi, Fathollahi-Fard, Tavakkoli-Moghaddam, & Newton [14])	time windows	heterogeneous vehicles	single depot
2	(Nguyen, Dang, & Tran [15])	classical	truck and drone	single depot
3	(Basso, Kulcsár, & Sanchez-Diaz [16])	classical	electric vehicles	single depot
4	(Pan, Zhang, & Lim [17])	time windows	homogeneous vehicles	loading at the depot simultaneously
5	(Keskin, Çatay, & Laporte [18])	time window	electric vehicles	time window
6	(Wang, Liu, & Wang [19])	time window	heterogeneous vehicles	single depot
7	(Behnke, Kirschstein, & Bierwirth [20])	time window	heterogeneous vehicles	single depot
8	(Anderluh, Nolz, Hemmelmayr, & Crainic [21])	“grey zone” customers	vehicle synchronization	single depot
9	(Dewi & Utama [22])	classical	green vehicle	single depot
10	(Martins, Hirsch, & Juan [23])	classical	homogeneous vehicles	single depot
11	(Gmira, Gendreau, Lodi, & Potvin [24])	time windows	travel speeds are associated with road segments in the road network	single depot
12	(Archetti, Guerriero, & Macrina [25])	static and online customers	heterogeneous vehicles	single depot
13	(Abdirad, Krishnan, & Gupta [26])	time windows, dynamic, demands from customers at different locations that arrive in the system at different times	heterogeneous vehicles	single depot
14	(Latorre-Biel, Ferone, Juan, & Faulin [27])	customer demands are not only stochastic, but also correlated	heterogeneous vehicles	single depot
15	(Srivastava, Singh, & Mallipeddi [28])	soft time windows	heterogeneous vehicles	single depot
16	(Altabeeb, Mohsen, Abualigah, & Ghallab [29])	time windows	heterogeneous vehicles	single depot
17	(Sadati & Çatay [30])	classical	homogenous vehicles	multiple depots
18	(İLHAN [31])	classical	homogenous vehicles	single depot
19	(Euchi & Sadok [32])	classical	homogenous vehicles	single depot
20	(Florio, Hartl, Minner, & Salazar-González [33])	time window, stochastic	homogenous vehicles	single depot
21	(Chaabane, Montecinos, Ouhimmou, & Khabou [34])	time window	end-of-life vehicles	single depot
22	(Park, Son, Koo, & Jeong [35])	time windows	heterogeneous vehicles	single depot
23	(Chen, Demir, & Huang [36])	time windows	after the emergence of delivery assistants, each van can be equipped with several delivery robots while performing last-mile parcel delivery tasks in populated areas	single depot
24	(Abdullahi, Reyes-Rubiano, Ouelhadj, Faulin, & Juan [37])	time windows	green vehicle	single depot
25	(Pan, Zhang, & Lim [38])	time windows, time-dependent	heterogeneous vehicles	single depot
26	(Lee [39])	time window	electric vehicles	single depot
27	(Li, Wang, Chen, & Bai [40])	time windows	with satellite bi-synchronization	single depot
28	(Fan, Zhang, Tian, Lv, & Fan [41])	time windows	green vehicle	multiple depots
29	(Quirion-Blais & Chen [42])	time windows	heterogeneous vehicles	single depot
30	(Mühlbauer & Fontaine [43])	classical	cross-docking from vans to cargo bicycles at so-called satellites	single depot
31	(Lin, Ghaddar, & Nathwani [44])	time windows	electric vehicle	single depot
32	(Wang, Xu, & Wang [45])	time windows	heterogeneous vehicles	multi-depot
33	(Mendes, Lush, Wanner, Martins, Sarubbi, & Deb [46])	passengers are transported from their origin to their destination sharing the same vehicle	heterogeneous vehicles	single depot
34	(Aerts, Cornelissens, & Sörensen [47])	classical	heterogeneous vehicles	single depot
35	(Niu, Wen, Cao, & Xiao [48])	stochastic demandtime window	heterogeneous vehicles	single depot
36	(Jia, Mei, & Zhang [49])	classical	homogeneous electric vehicle	single depot
37	(Sitek, Wikarek, Rutczyńska-Wdowiak, Bocewicz, & Banaszak [50])	time windows	homogenous vehicles	single depot
38	(Niu, Cao, Gao, Xiao, Song, & Zhang [51])	time windows, stochastic demands	heterogeneous vehicles	single depot
39	(Casazza, Ceselli, & Wolfler Calvo [52])	time windows	heterogeneous vehicles	single depot
40	(Grabenschweiger, Doerner, Hartl, & Savelsbergh [53])	classical	heterogeneous vehicles	single depot
41	(Afsar, Afsar, & Palacios [54])	accept the service if the zone prices are below individual thresholds	homogenous vehicles	single depot
42	(Olgun, Koç, & Altıparmak [55])	classical	green vehicle	vehicles departing from a certain depot must return to the same depot
43	(Stellingwerf, Groeneveld, Laporte, Kanellopoulos, Bloemhof, & Behdani [56])	time and temperature dependent	heterogeneous vehicles	single depot
44	(Wang, Liao, Li, Yan, & Chen. [57])	time window	heterogeneous vehicles	single depot
45	(Zhang, Li, Sun, & Hou [58])	the probability that customers are served before their (uncertain) deadlines must be higher than a predetermined target	heterogeneous vehicles	single depot
46	(Haixiang, Fang, Wenwen, & Mingyun [59])	an unknown number of customer requests that dynamically appear during route execution	heterogeneous vehicles	single depot
47	(Dalmeijer & Desaulniers [60])	time window	heterogeneous vehicles	single depot
48	(Guo, Huang, & Huang [61])	time window	heterogeneous vehicles	single depot

Table 6. Model categories of VRPs published in 2020.

No.	Authors	Model Features
		Customer-Related Aspects	Vehicle-Related Aspects	Depot-Related Aspects
1	(Pasha, Dulebenets, Kavoosi, Abioye, Wang, & Guo [62])	time window	two vehicles are expected to serve one customer each, while one vehicle is expected to serve two customers after visiting the required supplier and manufacturer nodes	after completing the service for the last customer, each vehicle returns to the dummy depot, travel costs from each customer location to the dummy depot are assumed to be zero
2	(Abbasi, Rafiee, Khosravi, Jolfaei, Menon, & Koushyar [63])	classical	homogenous vehicles	single depot
3	(Kitjacharoenchai, Min, & Lee [64])	classical	drone truck	multiple drones are not allowed to be launched or retrieved at the same node at any given time
4	(Raeesi & Zografos [65])	time windows	electric commercial vehicles (ECVs), battery-swapping vans (BSVs)	ECVs and BSVs in the fleet to operate routes that start and finish at the depot
5	(Zhang, Chen, Zhang, & Zhuang [66])	time windows	electric vehicle	single depot
6	(Song, Li, Han, Han, Liu, & Sun [67])	time windows, adopt a rating method to determine customer satisfaction	vehicles with different energy consumption indexes are considered	single depot
7	(Giallanza & Puma [68])	classical	green vehicle with a defined capacity	single depot
8	(Zhang, Chen, Zhang, Wang, Yang, & Cai [69])	classical	homogenous vehicles	shared carriers and depots (multiple depots)
9	(Brandão [70])	classical	homogenous vehicles	multiple depots, vehicles do not return to the depot after delivering goods to customers
10	(Eshtehadi, Demir, & Huang [71])	time windows	multi-compartment vehicles	single depot
11	(Zhen, Ma, Wang, Xiao, & Zhang [72])	time windows and release dates	multi-trip vehicle	multiple depots
12	(Kancharla & Ramadurai [73])	classical	electric vehicle	allow multiple visits to a charging station without duplicating nodes
13	(Molina, Salmeron, Eguia et al. [74])	time windows	heterogeneous vehicle	single depot
14	(Mao, Shi, Zhou, & Zhang [75])	time windows	homogeneous electric vehicles	single depot
15	(Lu, Chen, Hao, & He [76])	time windows	homogeneous fleet of k electric vehicles	single depot
16	(Fachini & Armentano [77])	time windows	heterogeneous fixed fleet	single depot
17	(Shi, Zhou, Ye, & Zhao [78])	time windows	classical	single depot
18	(Trachanatzi, Rigakis, Marinaki, & Marinakis [79])	classical	homogenous vehicles	single depot
19	(Li, Wang, Chen, & Bai [80])	time windows	mobile satellites	single depot
20	(Sethanan & Jamrus [81])	classical	heterogeneous fixed fleet	single depot

Table 7. Model categories of VRPs published in 2019.

No.	Authors	Model Features
		Customer-Related Aspects	Vehicle-Related Aspects	Depot-Related Aspects
1	(Wang & Sheu [82])	arc-based	with drones	single depot
2	(Pelletier, Jabali, & Laporte [83])	classical	electric freight vehicles	single depot
3	(Schermer, Moeini, & Wendt [84])	classical	homogenous vehicles	single depot
4	(Bruglieri, Mancini, Pezzella, & Pisacane [85])	classical	green vehicle	single depot
5	(Li, Soleimani, & Zohal [86])	classical	green vehicle	multiple depots
6	(Basso, Kulcsár, Egardt, Lindroth, & Sanchez-Diaz [87])	classical	electric commercial vehicles	single depot
7	(Breunig, Baldacci, Hartl, & Vidal [88])	classical	electric two-echelon vehicle	single depot
8	(Zhen, Li, Laporte, & Wang [89])	classical	unmanned aerial vehicles	single depot
9	(Stavropoulou, Repoussis, & Tarantilis [90])	classical	consistent vehicle	single depot
10	(Keskin, Laporte, & Çatay [91])	time windows	electric vehicle	single depot
11	(Huang, Blazquez, Huang, Paredes-Belmar, & Latorre-Nuñez [92])	classical	feed vehicle	single depot
12	(Arnold & Sörensen [93])	classical	homogenous vehicles	single depot
13	(Long et al. [94])	classical	prize-collecting vehicle	single depot
14	(Sacramento, Pisinger, & Ropke [95])	classical	unmanned aerial vehicles	single depot
15	(Schermer, Moeini, & Wendt [96])	classical	homogenous vehicles	single depot
16	(Zhao, Luo, & Han [97])	time window	homogenous vehicles	single depot
17	(Froger, Mendoza, Jabali, & Laporte [98])	classical	electric vehicle	single depot
18	(Yu, Wang, Wang, & Huang [99])	time window	homogenous vehicles	single depot
19	(Marinakis, Marinaki, & Migdalas [100])	time window	homogenous vehicles	single depot
20	(Altabeeb, Mohsen, & Ghallab [101])	classical	homogenous vehicles	single depot

The objectives of VRPs can also be diversified according to different stakeholder requirements. The traditional objective of the standard VRP is to minimize a cost function, which is considered to be the total distance traveled by all vehicles. However, recent studies have focused on various negative externalities of transportation, including carbon emissions and duration. For an objective discussion, we classified single and multiple objectives according to the diversity of objectives and then listed the objectives used in different studies. The papers with the same numbers as those in Table 2, Table 3 and Table 4 are listed in Table 8, Table 9 and Table 10. Additionally, we discussed the test instances used in different studies.

Table 8. Model objectives of VRPs published in 2021.

No.	Multi-Object	Single-Object	Dataset	Max Nodes	Other Settings
1	cost, green emissions		self-generation	72
2		minimize the operational cost	self-generation	400	driving and flight times of trucks and drones are assumed to be deterministic
3		energy consumption	real data	map
4		minimize the total travel distance	based on the TDVRPTW instances proposed in [102]	100	multiple trips per vehicle, time-dependent travel times
5		tune constant waiting times	100 customer EVRPTW-SP instances from [103]	108	stochastic waiting times at recharging stations
6	minimize costs, service waiting times, and number of vehicles in multiple service periods		VRPTW-SP instances from [103]	41
7		reduce greenhouse gas (GHG) emissions	instances for emission-oriented vehicle routing on a multigraph (uni-halle.de)	100	different vehicle–load combinations
8	minimize cost consisting of total GHG emissions		adapted Solomon instances introduced in [104]	100
9	time-related and distance-related variable costs		adapted Solomon instances introduced in [104]	100
10		minimize the total duration of delivery routes (cost)	test instances proposed in [105]	150
11		minimize the total duration of routes	exact branch-and-price (BP) method reported in [106]	200
12		minimize the distribution cost	from the well-known Solomon VRPTW instances presented in [107] and described in [108]	200
13		minimize transportation cost	self-generation	100
14		stochastic and correlated customer demands	instance A-n32-k5 (available from https://bit.ly/3eGxGx9 accessed on 31 August 2020)	31
15	minimize number of vehicles, total travel distance, makespan, total waiting time, and total delay time incurred by late arrivals		same testing datasets used in [109,110]	250
16		minimize the total distance	02 instances from seven standard benchmarks in [111,112,113,114]	200
17		minimize the total distance	GVRP instances generated in [115]	483
18		minimize the total distance	benchmarks instances proposed in [111]	199
19		minimize the total travel time of vehicles and drones	benchmarks instances from [95]	200
20	VRPSD-PDC (reduce traveling costs and the number of required vehicles)		self-generation	60	optimal restocking
21		minimize the total cost	self-generation	20
22		minimize the total distance	self-generation	20
23		minimize the sum of route completion times	https://data.mendeley.com/datasets/kxfcwkwdb9/draft?a=edb5ce79-b4c7-4121-93ca-317e82328b1c accessed on 23 January 2020	200	delivery robots
24	minimize distance, economic dimension cost, and environmental dimension cost		five instances from [116]	43
25		duration minimizing	test instances adopted from [102] and newly generated instances	100
26	total travel and charging time		adapted Solomon instances	36
27		minimize the total cost	test instances adopted from [116]	120
28		reduce distribution costs	self-generation	144	time-varying road network
29	maximize the number of lengthy historical customer chains in the solution and minimize the total cost		random generated instances	105
30		minimize the total cost	self-generation	300
31		minimize the total distance	self-generation	100
32		minimize logistics operating costs	real data	180
33		reduce operating and riding costs	https://doi.org/10.1016/j.eswa.2020.114467 accessed on 16 August 2020	250
34		minimize the order picking travel distance	Henn & Wäscher [117] originally included 5760 instances	100
35	minimize travel distance, drivers, remuneration, and number of vehicles		self-generation	200
36		minimize total traveling distance	EEE WCCI2020 competition on EC for the EVRP is adopted [118]	1000
37		minimize the distances travelled by vehicles and the penalties for delivering items (shipments) to alternative points	self-generation	6	alternative delivery and pickup
38	minimize total cost and customer dissatisfaction		self-generation	120
39		minimize the total cost	test instances adopted from [119]	30
40		minimize the total cost	available instance set from [120]	75	heterogeneous locker boxes
41		maximize the total profit	classical CVRP instances from [121]	50
42		minimize fuel consumption costs	generated randomly from [122]	199
43	minimize product decay, CO2 emissions, cost, and maximum decay		real data obtained from seven supermarket chains	80
44	minimize the total route distance and total customer waiting time for the improvement of customer satisfaction		test instances adopted from [123]	30
45		minimize the total cost	self-generation	-
46		minimize the total cost	self-generation	60
47		minimize the expected cost of distribution	instances for the TWAVRP introduced in [124] and extended in [125]; these instances are available in the VRP repository VRP-REP [126]	50
48		minimize the total cost	P-n-k” instances are from [111], “RY” instances are from the “RY ATT48” in [127], and “Tai” instances are from [128] with the number of nodes ranging from 75 to 150.	150

Table 9. Model objectives of VRPs published in 2020.

No.	Multi-Object	Single-Object	Dataset	Max Nodes	Other Settings
1		minimize the total supply chain cost	self-generation	75	factory will be assembled at each customer location to meet existing demand
2		minimize the total cost	self-generation	-
3		minimize the total truck arrival time of trucks at the depot	benchmarks from [111] (sets A, B, and P) and [112]	75	multiple drones are not allowed to be launched or retrieved at the same node at any given time, meaning the times of both trucks and drones at customer locations must be adjusted to be the same
4		minimize the total cost	VRPTW instances proposed in [129]	100	battery swapping service begins before or after customer service
5		minimize the total travel distances of all EVs	fuzzy optimization model for EVRPTW and recharging stations (https://figshare.com accessed on 25 June 2019) [66]	200	recharging stations studied in an uncertain environment
6		minimize the total cost	test instances adopted from [107]	100	cold chain logistic system
7	total costs and carbon emissions are minimized		test instances adopted from [130]	based on dataset
8	operating quality, operating reliability, operating cost, operating time		test instances adopted from [131]	(depots) 30
9		minimize the distance travelled	test instances adopted from [121,132,133,134]	288
10		minimize fixed and variable vehicle costs	self-generation	200	each compartment requires energy to maintain the temperature for the total number of delivery crates inside a compartment
11		minimize the total traveling time of all vehicles	test instances adopted from [107]	200
12		minimize the total time (travel times plus charging times)	test instances adopted from [135]	320	the number of such duplications is not known a priori and the size of the problem increases
13	maximize the total number of served customers and minimize the total travel cost		test instances adopted from [136,137]	based on dataset	limited number of resources
14		minimize the total cost	test instances adopted from [129]	100
15		minimize the total cost	self-generation	200
16		minimize fixed and variable vehicle costs	test instances adopted from [107,138,139,140]	100
17		minimize the total cost	test instances adopted from [141]	based on dataset
18		minimize the total cost	test instances adopted from [107]	200
19		minimize the total cost	test instances adopted from [107]	100	one DC in which a homogeneous fleet of van–UAV combinations are available
20		minimize the total cost	test instances adopted from [138,142]	100

Table 10. Model objectives of VRPs published in 2019.

No.	Multi-Object	Single-Object	Dataset	Max Nodes	Other Settings
1		minimize total cost	self-generation	13	1
2		minimize total cost	test instances adopted from [135]	320	2
3		minimize the makespan through constraints	test instances adopted from [143]	100	3
4		minimize the total travel distance	test instances adopted from [115,144]	100	4
5	revenue maximization, and travel time, emission, and cost minimization		self-generation	35	5
6	stage one: path minimization; stage two: route minimization for total energy consumption		self-generation	20	6
7		minimize total cost	sets two and three from [145], set five from [146], and set six from [147]; charging stations follow the guidelines from [129] (instances of the electric VRP with time windows and recharging stations) and [103]	200	7
8		minimize the total time required to complete monitoring tasks	self-generation	724	8
9		maximize the net acquired profit	from the traditional VRP instances in [112]	199	9
10		minimize total cost	VRPTW instances presented by Schneider et al. [129]	100	10
11		minimize total cost	self-generation	200	11
12		minimize the number of routes	instance set from [148], MDVRP experiments using the benchmark set from [134]	1000	12
13	minimize the total traveling cost, maximize the prizes collected by all vehicles		http://www.coin-or.org/SYMPHONY/branchandcut/VRP/data/index.htm.old accessed on 14 June 2018	32	13
14		minimize the operational cost when visiting customers	self-generation	200	14
15		minimize the makespan	test instances adopted from [105]	50	15
16	minimize transportation and time cost		test instances adopted from [107]	100	16
17	minimize total driving and charging time		Montoya et al.’s [139] testbed (publicly available at http://vrp-rep.org accessed on 18 June 2018).	20	17
18		minimize carbon emission	test instances adopted from [107]	100	18
19		minimize the number of vehicles	test instances adopted from [107], includes 56 instances divided into six sets with 100 nodes; includes 300 instances of different sizes from [108]	1000	19
20		minimize the total distance travelled by vehicles	self-generation	80	20

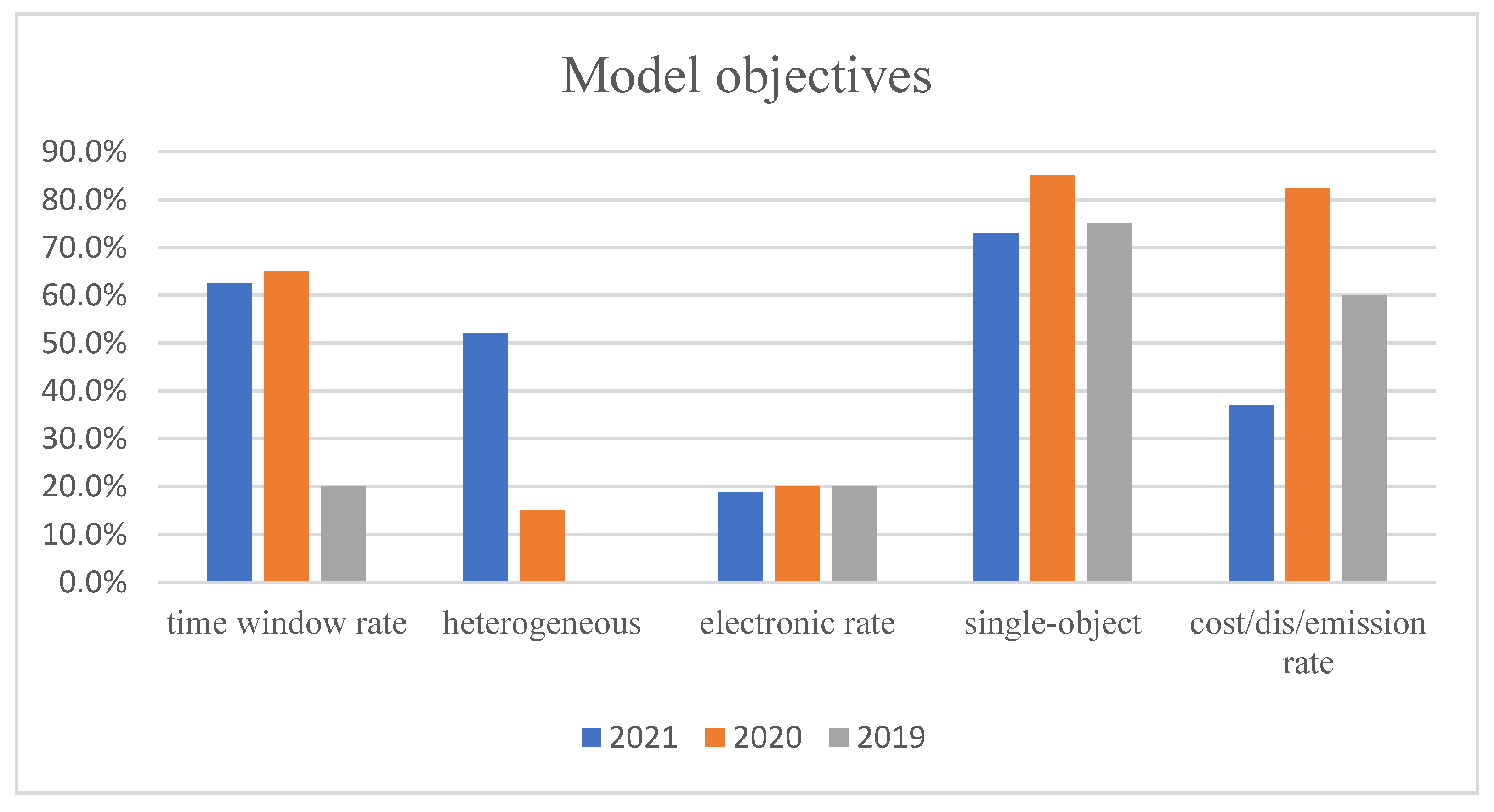
As shown in the tables above, there are different main model objectives for different years. The results are summarized in Figure 1.

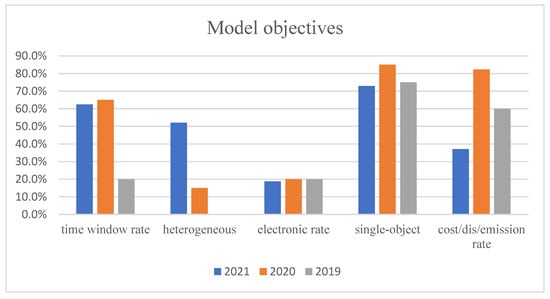
Figure 1. Different model objectives in different years.

One can see that the time window still occupies a large proportion of model objectives and is the mainstream of current research on the VRP and its variants. This trend is closely related to the concept of the “to C” distribution, where customers focus on service satisfaction. There have been various extensions of the VRP, including the VRPTW and time-dependent problems such as those discussed in [17,24,41,75,89]. Additional research has focused on heterogeneous vehicle problems that are closely related to real-life vehicle applications. With the increasing focus on environmental protection, electric vehicle distribution has also gradually become a mainstream research topic. Relevant research can be found in [49,72,81,89,116]. Single-objective models still occupy a certain research space, where the objective value setting is still largely based on cost metrics (e.g., cost, distance, and CO₂ emission). However, unlike cost metrics in past research, the costs in the current single-objective problem research tend to be compound costs representing actual delivery costs.

4. Solutions for VRPs

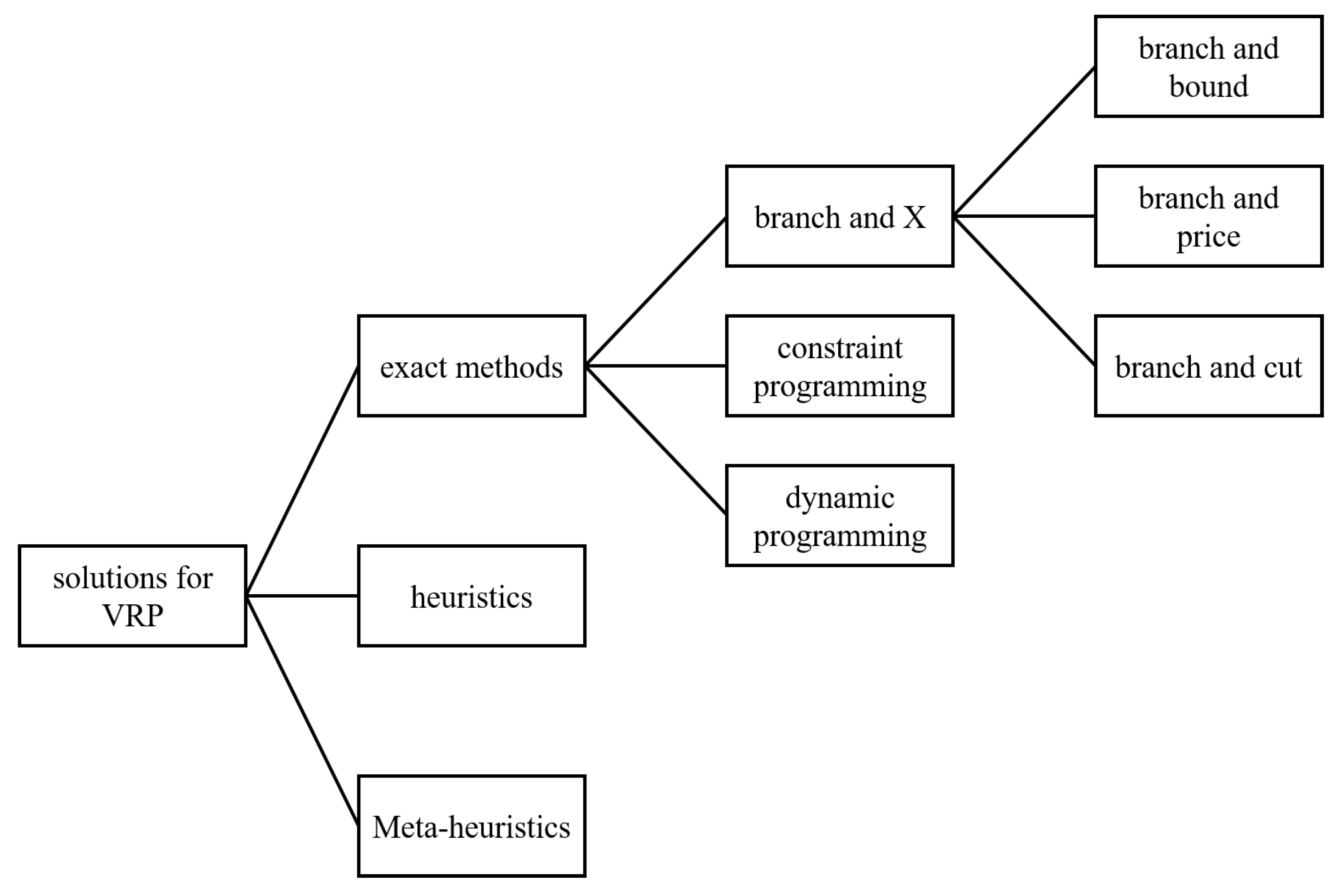
Because real-world problems involve complex constraints, advanced algorithms are required to solve VRPs in complicated and constantly changing environments. The number of customers and vehicle types is increasing and the use of optimization algorithms is a key component of effective customer service and efficient operations. A large variety of VRP solution strategies have been presented in the literature. These strategies range from exact methods to heuristics and meta-heuristics. Exact methods provide optimal solutions, whereas heuristics and meta-heuristics generally yield near-optimal solutions. Exact methods are typically only suitable for small-scale problems (up to 200 customers). Because the VRP and its variants are known to have NP-hard complexity, solving larger instances optimally is very time-consuming. However, there are no bounds on problem size when solving problems using heuristics and meta-heuristics that can efficiently handle large numbers of constraints and still output near-optimal solutions. Figure 2 presents various approaches to solving the VRPs and was adapted from content in [6,149].

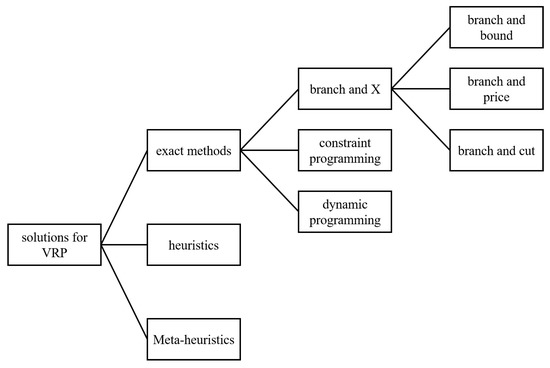
Figure 2. Solutions for VRPs.

Exact methods include a variety of approaches, mainly branch and X (X: cut, bound, price, and so on) approaches, as well as dynamic programming and column generation methods. In recent years, significant advances in the exact solution of VRPs have been achieved. A major milestone was the branch-and-price algorithm proposed by Pecin et al. [150]. The branch-and-bound (BB) method was developed to explore solution spaces implicitly. Because the performance of BB algorithms depends on the quality of bounds obtained throughout a tree, BB algorithms can be combined with the generation of cutting planes, forming so-called branch-and-cut algorithms, or with column generation, resulting in BAP algorithms [151]. Branch and X remain the dominant VRP approaches [150,152]. While branch and X approaches treat VRPs as integer linear programming (ILP) or mixed ILP (MILP), dynamic programming breaks complex problems into a number of simpler sub-problems. Constraint programming is a model that interrelates different variables using constraints. When the search space is reduced, relatively simple problems can be solved by various search algorithms [149].

Approximate methods called heuristics are designed to solve specific problems. Heuristics focus on systematically finding an acceptable solution within a limited number of iterations. A heuristic yields solutions faster than an exact method. A meta-heuristic may be referred to as an intelligent strategy combining subordinate heuristics for exploration and exploitation.

For solution discussion, we classified exact methods, heuristic algorithms, and meta-heuristic algorithms in papers with the same numbers as those in Table 11, Table 12 and Table 13. The results are presented in the tables below.

Table 11. Solutions to VRPs published in 2021.

No.	Solution			Operating Environment
	Exact Methods	Heuristic Algorithms	Meta-Heuristic Algorithms
1			Simulated annealing (SA)	/
2		Slack induction through string and sweep removals		C++ compiled with GCC 9.3.0. Use CPLEX 12.10 to solve MILPs. All tests run on a desktop operating Xubuntu 20.04 with an AMD Ryzen 3700X @4.0 GHz CPU, 16 GB RAM.
3		Paths first, routes second		/
4		Hybrid ALNS–variable neighborhood descent (VND) algorithm		Java and the MIP model is solved by IBM ILOG CPLEX 12.8.0 (IBM CPLEX, 2017). All experiments run on an Ubuntu 18.04.3 LTS server with an Intel(R) Xeon(R) Silver 4216 CPU of 2.10 GHz
5		Deterministic greedy insertion, probabilistic greedy insertion, probabilistic greedy insertion with confidence		Coded in Java programming language and all experiments conducted on an Intel Core i7-8700 CPU 3.2 GHz processor with 16 GB RAM
6			Hybrid heuristic algorithm with three-dimensional k-means clustering	/
7	1. Solve the shortest-path problem using a backward labelling algorithm, 2. Use the column generation technique to set up a fast heuristic and a branch-and-price (BAP) algorithm			C++ with Visual Studio 2017, single core of an Intel i7-2600 CPU with 8 GB RAM
8		Large neighborhood search (LNS)		C/C++ and tested under Linux Ubuntu 16.04 LTS running on a virtual machine (using two processors and 2 GB RAM) on a host Intel(R) Core(TM) i5-3320 M CPU @2.60 GHz and 4 GB RAM
9			HWOA algorithm based on the whale optimization algorithm	Linux Ubuntu 16.04 LTS running on a virtual machine
10		Agile optimization (refers to the massive parallelization of BR algorithms)		p2 GB RAM with a host Intel(R) Core(TM) i5 CPU
11		The initial solution is generated by a greedy insertion heuristic and the neighborhood of the current solution is generated using CROSS exchanges		3320 M CPU @2.60 GHz with 4 GB RAM
12		Using an iterative insertion algorithm to construct an initial solution and re-optimize using the 2-O re-optimization algorithm		Coded in Java, while the offline problem was solved using Cplex 12.5. All experiments run on an Intel(R) Core(TM) i7-16700HQ CPU with two cores operating @2.60 GHz with 16 GB RAM.
13		Construction algorithms: path cheapest arc, savings, and global cheapest arc are applied to the construction phase of a route		Algorithm was implemented in Python. Experiments performed on a personal PC with an Intel® Core™ i7- 4790S CPU @3.20 GHz with four cores and 8 GB RAM
14			Petri net predictor
15			Non-dominated sorting genetic algorithm II (NSGA-II)	C language and Linux based. 2.50 GHz Intel Core i7 CPU system with 8 GB RAM
16			Firefly algorithm (FA)	Coded in Java and executed on an Intel i5 CPU @3.2 GHz with 4 GB RAM on a 32-bit Windows 7 OS
17		General variable neighborhood search method (GVNS) with tabu search (TS)		Intel Core i7-8700 @3.2 GHzand 32 GB RAM
18			SA algorithm with a crossover operator	Intel Core i7 @2.40 GHz and 8 GB RAM
19			modified hybrid genetic algorithm (nearest-neighbor heuristic and modified savings heuristic)	Visual Studio C++ application, 64 bits (win64), Intel® Core ™ i5-2450M @ 2.5 GHz and 4 GB RAM
20	novel BAP algorithm			Single thread of an Intel® CoreTM i7-4790 @3.60 GHz 32 GB RAM. Linear programs were solved using IBM® CPLEX® version 12.6.1
21		first phase focuses on “routes’ construction using dealers” characteristics, second phase of “routes’ assignment” assigns the most interesting routes to internal carrier trucks, and the cheapest carrier brokers get the remaining dealers		Computational experiments were conducted on a workstation with an Intel Core i7-2600 @3.4 GHz, 16 GB RAM, and Windows 7 Enterprise 2009 (64 bits). For VRP mathematical model validation, the LINGO solver V.15. For heuristic development, Python 2.7.13 with CPXOPT was used
22			genetic algorithm (GA)	/
23		adaptive large neighborhood search (ALNS) algorithm		MS Windows with MATLAB R2020a (Math Works, 2020) on a laptop computer with an Intel i5-3610QM CPU @2.30 GHZ with 4 GB RAM. The mathematical model was solved using the IBM CPLEX 12.10.0 solver (IBM, 2019)
24		BRIG-LS generic framework combining a biased-randomized technique with an iterative greedy technique		Java application on an Intel QuadCore i5 CPU @3.2 GHz with 4 GB RAM
25		ALNS with TS algorithm		/
26	BAP			3.2 GHz Intel Xeon W CPU with 32 GBof RAM
27	CPLEX 12.4, a modified ALNS heuristic			/
28			hybrid GA with VNS	MATLAB2018b on the Windows 10 OS, 4 GB RAM, Intel(R) Core(TM) i7-7700 @3.60 GHz
29		Case base reasoning (CBR)
30		Greedy insertion, repack insertion, regret insertion		C++11 compiled with GCC version 5.1.0. All runs were performed on a computer with 8 GB RAM and an Intel i5-6200 CPU @2.40 GHz
31			policy gradient algorithm	Macbook Pro (2018) running Mac OS 10.13.6 with 4 CPU processors @2.3 GHZ and 16 GB RAM. The RL model was realized using Tensorflow 2.2.0. The code was implemented in Python
32			hybrid GA with TS	/
33	cluster algorithm			/
34		Adapted Hausdorff-based batching heuristic		C++ Visual Studio 17. All experiments carried out on an Intel(R) Core i7-6820HQ CPU @2.7 GHz with 16 GB RAM
35		chromosome representation, decision tree		Python 3 on a machine with an Intel Core i5-8600K
36			Bi-level ant colony optimization (ACO) algorithm	C++ and executed on an Intel i7-6700 @3.40 GHz on the Arch Linux system
37		Construction heuristic (nearest neighbor)		Intel(R) Celeron(R) CPU 1005 M 2 @1.90 GHz, 8 GB RAM, Windows 10 64-bit
38			CLP and MP, CLP and GA	Python, Windows 10 with an AMD Rayzen7 1700x processor
39	check which integrality constraints are not satisfied and enforce them by exploring a search tree through branching rules			C++ using the SCIP framework version 4.0.0. LP sub-problems were solved using the simplex algorithm implemented in CPLEX 12.6 (CPLEX development team, 2011)
40		ALNS, iterative first-fit decreasing algorithm		C++ programming language. CPLEX 12.9 used for solving exact models (MIP). Multithreading deactivated. All programs run on an Intel Xeon Processor E5-2670 v2 (25 MB Cache, 2.50 GHz) with 3 GB RAM. The operating system was Linux
41	BAP			/
42		develop an HH-ILS algorithm based on ILS and VND heuristics, nearest neighborhood search heuristic for initial solution		Intel Core i7-4720HQ CPU @2.6 GHz computer with Windows 10 OS and 16 GB RAM. Metaheuristic was implemented in C++. Code compiled in Visual Studio Professional 16.7.1 with MSC compiler version 1927 with default settings. Commercial solver IBM ILOG CPLEX 10.2.0 with its default settings used as an optimizer to solve the MIP formulation
43	new two-index-based mathematical formulation			/
44			NSGA-II as a static optimizer when the environment does not change	16 GB RAM, Intel Core i7-10700 @2.9 GHz.
45	First is the difficulty of obtaining exact moment measures for the ambiguity set Pi and second is when the distribution function is continuous			/
46			improved differential evolution (DE) algorithm	MATLAB R2014a, Windows 7 (x32)
47		heuristic dynamic programming		Coded in C and C++, IntelXeon E3-1226 v3 @3.30 GHz and 16 GB RAM
48			MCWS-LS heuristic, S-ALNS algorithm with SA	Coded in JAVA, computations executed on a Dell XPS PC with a 2.80 GHz Intel Xeon CPU (E5-2680-V2) and 32 GB RAM

Table 12. Solutions to VRPs published in 2020.

No.	Solution			Operating Environment
	Exact Methods	Heuristic Algorithms	Meta-Heuristic Algorithms
1		Evolutionary algorithm		MATLAB (2016a), Intel(R) CoreTMi7-7700K CPU and 32 GB RAM, Windows 10 OS
2			GA	Intel (R) Core i5-7600 @3.50 GHz with 8 GB RAM equipped with an NVIDIA GeForce GTX 1060 graphics card. This GPU has 1280 cores and its base and boost clocks are 1506 MHz and 1708 MHz, respectively, C++ CUDA 8.0 (V8.0.61)
3		DTRC, LNS
4		Dynamic programming algorithm and integer program, ILNS algorithm		Intel CoreTM i5 @3.40 GHz CPU with 8 GB RAM. The branch-and-bound solver of CPLEXTM 12.9.0 was used as the exact solver and all other algorithms were coded in MATLAB. When necessary, CPLEXTM is called from MATLAB.
5		ALNS algorithm, VND algorithm		3.60 GHz AMD Ryzen 7 3700X CPU with 32 GB RAM, Windows 10 OS
6		Improved artificial fish swarm algorithm, push forward insertion heuristic (PFIH)		/
7			NSGA-II	/
8			Proposed EVNS algorithm	/
9		Nearest-neighbor heuristic, insertion heuristic		C language, desktop PC with an Intel Core i7-3820 CPU @3.6 GHz and 32 GB RAM
10		ALNS algorithm
11			Particle swarm optimization (PSO), GA	Intel Core i7 @2.80 GHz, 8 GB RAM, model implemented in CPLEX (version 12.6.2) with C# (VS2015)
12		ALNS algorithm		Coded in GAMS 23.9 and solved using the Gurobi 7.5 solver hosted on the NEOS server. The server runs on an Intel XeonE5-2430 @2.2 GHz with 3 GB RAM. ALNS algorithm coded in Python and tested on a PC running a 3.6 GHz Intel Core-i7-7700 CPU with 16 GB RAM
13		VND tabu search algorithm with holding list		Algorithm coded in C++ and run on a 3.30 GHz Intel® Core(TM) i5-2400 CPU
14			improved ant colony optimization (ACO) algorithm	Coded in Visual C++ and implemented on an Intel Core i5 CPU @3 GHz with 8 GB RAM
15		IVNS algorithm, VND procedure		Coded in C++ and run on a Linux cluster system with an AMD Opteron 4184 CPU (2.8 GHz and 2 GB RAM) running Ubuntu 12.04. For the general CPLEX solver, the latest version of 12.6 was used
16			constructive heuristic based on LNS meta-heuristic	Programmed in C# and run on an Intel® Core™ i7-6500U CPU @2.5 GHz with 16 GB RAM
17		PFIH method, neighborhood search, tabu search
18			FA based on coordinates	Gurobi 4.5.1 with Python 3.0 on an Intel(R) Core(TM) i7-7700HQ CPU @2.80GHz with 8 GB RAM.
19		ALNS algorithm		CPLEX 12.9, coded in C++. The code for the heuristic and exact method was executed on a Windows 8 computer configured with an Intel(R) Core(TM) 3.2 GHz CPU with 8 GB RAM
20			GA	MatLab on a 2.10 GHz PC, with 8 GBytes of RAM

Table 13. Solutions to VRPs published in 2019.

No.	Solution			Operating Environment
	Exact Methods	Heuristic Algorithms	Meta-Heuristic Algorithms
1	BAP			C# on a computer with an Intel I7 CPU @2.69 GHz and 16 GB RAM. Gurobi 8.0.0 chosen as an MIP solver
2		LNS with cutting-plane method		C++, executed on a cluster of 27 machines, each with two Intel(R) Xeon(R) X5675 CPUs @3.07 GHz with 96 GB RAM running on Linux. Each machine had 12 cores and each instance was executed using a single thread
3		DASP		Intel® Xeon® Gold 6126 CPUs and 16 GB RAM, algorithms in Java SE 8 and Gurobi Optimizer 8.1.0 for solving MILPs
4	Path-based exact solution			Intel i7-5500U @2.4 GHz with 16 GB RAM, coded in Java
5			improved ACO algorithm	/
6		Bellman–Ford algorithm		/
7		LNS		Coded in Fortran 77 and run on a single thread of a 3.6 GHz Intel i7-4790 CPU with 32 GB RAM. Relies on CPLEX 12.5.1 for the resolution of linear programs and some integer sub-problems. Metaheuristic was coded in Java (JRE 1.8.0-151), and run on a single thread of a 3.4 GHz Intel i7-3770 CPU
8			tabu search metaheuristic	IBM ILOG CPLEX Optimization Studio 12.6.1 (Visual Studio 2015, C#) on a DELL Precision 7600 workstation with two Xeon E5-2643 V3 CPUs (24 cores) @3.4 GHz with 128 GB RAM
9		Adaptive tabu search		C++ and all computational experiments were performed on a 3.30 GHz Intel Core i5 CPU on a single thread
10		ALNS algorithm		Intel Xeon E5 2.10 GHz CPU virtual machine with 16 GB RAM
11			ACO algorithm	JAVA computer language, executed using a computer with an Intel (R) Core (TM) i7 CPU @3.40 GHz and 4 GB RAM
12		Knowledge-guided local search		AMD Ryzen 3 1300X CPU @3.5 GHz on Windows 10
13		Genetic local search algorithm		C++ language and all 120 instances run independently five times on a PC with two Intel i7-7820 CPUs @2.9 GHz and 32 GB RAM on the Windows 10 OS (64-bit)
14		ALNS algorithm		Java, run on a Huawei XH620 V3 computer with an Intel Xeon 2660v3 CPU @2.60 GHz
15		Hybrid VNS/tabu search algorithm		Intel® Xeon® Gold 6126 cluster, where each node operated at 2.6 GHz with 16 GB RAM (hyper-threading disabled). Algorithms implemented in Java SE 8 and Gurobi Optimizer 8.1.0 used for solving MILPs (Gurobi Optimization, 2018).
16			NSGA-II	MATLAB R2017a
17		Exact heuristic algorithm		Gurobi 7.5.0, 12 GB RAM and on a cluster of 27 computers, each with 12 cores and two Intel(R) Xeon X5675 @3.07 GHz CPUs
18	Improved BAP algorithm			C# and CPLEX with a 3.10 GHz Intel Core TM i5-2400 CPU using the Microsoft Windows 7 OS with 8 GB RAM
19			Multi-adaptive PSO algorithm	Intel Core i5 2430M @2.40 GHz with 4 GB RAM on the Windows 7 Home Premium 64-bit OS
20			improved hybrid FA	Coded in Java and run on 12 computers with Intel i-5 @3.2 GHz CPUs and 4 GB RAM with 32-bit Windows 7

As shown in the tables above. Heuristic algorithms and meta-heuristic algorithms are still the mainstream solution methods, although branch and X methods will continue to increase in popularity in 2021. As mentioned previously, with the rapid growth in the processing speed and memory capacity of computers (i.e., operating environments), more complex instances of the VRP can be solved.

5. Observations and Conclusions

Based on the practical importance of VRPs in real life, such problems have attracted significant research attention in recent years. Most work has been devoted to classical cost objectives such as total cost, total travel distance, and CO₂ emission. Some studies have considered multiple objectives. In order to solve the problem of greenhouse gas emission, the discussion of trolley distribution has become a research trend. Time windows still account for a large proportion of modern papers and are mainstream in current research on the VRP and its variants. Time windows are closely related to the current mode of “to C” distribution, where customers focus on service satisfaction.

Regarding datasets, different studies make various adjustments to data and many use generated datasets in addition to real data, which makes it difficult to compare algorithms using a unified standard. There is still scope for significant further work in the field. Therefore, researchers should be motivated to develop publicly available datasets, and effective and efficient methods for dealing with VRPs. The gaps in the available literature mentioned above may motivate further work in these directions for researchers in this field.

For solving algorithms, with the development of the processing speed and memory capacity of computers, using the exact way such as branch and X to solve VRPs is rapid growth. However, heuristic algorithms and meta-heuristic algorithms are still the mainstream solution methods, such as SA [14], GA [35,41,45], NSG [28,47], SSO [153], and so on. It is hoped that more exact algorithms can be applied to solve VRPs in the future, and the number of nodes in the dataset that can be solved can be increased as much as possible.

Our research protocol was well defined because it aims at an efficient and thorough review of multiple VRP variants. The main goal of this study was to identify the trends of VRP variants and the algorithms applied to solve them. Additionally, papers that are considered to represent pioneering efforts from the research community were presented. The papers with the most citations were considered to be the most significant and they were discussed in detail in this review.