Abstract
In this work, substrate control of a biological process with unknown varying control gain, input saturation, and uncertain reaction rate is addressed. A novel adaptive controller is proposed, which tackles the combined effect of input saturation and unknown varying control gain with unknown upper and lower bounds. The design is based on dead zone radially unbounded Lyapunov-like functions, with the state backstepping as control framework. The convergence of the modified tracking error and the boundedness of the updated parameters are ensured by means of the Barbalat’s lemma. As the first distinctive feature, a new second-order auxiliary system is proposed that tackles the effect of saturated input and the unknown varying control gain with unknown upper and lower bounds. As the second distinctive feature, the modified tracking error converges to a compact set whose width is user-defined, so that it does not depend on bounds of either external disturbances, model terms, or model coefficients. The convergence region of the current tracking error is determined for the closed loop system subject to the formulated controller and the proposed auxiliary system. Finally, numerical simulation illustrates the performance of the proposed controller.
1. Introduction
Automatic control of biological processes based on non-adaptive schemes is commonly affected by model uncertainty: (i) uncertain time varying coefficients of the reaction rates, (ii) uncertain time varying reaction yields, (iii) uncertain concentrations, and (iv) varying and uncertain or noisily measured inflow substrate concentration [1,2,3]. Adaptive control can achieve output stabilization despite these model uncertainties. Indeed, it can guarantee asymptotic convergence of the tracking error and boundedness of its updated parameters [4,5,6,7].
In addition to the effects of model uncertainty, control of biological process can be affected by actuator saturation in the case that integral action is used, for instance, the case with update laws [8,9]. Indeed, in adaptive control design, updated parameters may change excessively [10]. One strategy for tackling the effect of input saturation in control design of nonlinear systems is the augmented error signal (AES). In adaptive controllers with AES strategy, it is ensured that (i) closed loop signals are bounded and excessive increase of updated parameters is avoided and (ii) the modified tracking error asymptotically converges to a compact set of small size [10,11,12]. An early incorporation of the AES strategy to Lyapunov-based adaptive control is presented in [10]. The tracking error signal is substituted by the modified tracking error, which is the sum of the tracking error and a filter in terms of the input error , which is the difference between the constrained and unconstrained input signals [10,11,12]. In the case of high order nonlinear systems, the backstepping strategy is commonly used, and the auxiliary system is defined as a nth order filter in terms of [11,12,13].
In adaptive backstepping control design, the input saturation is usually tackled by using the AES strategy [12,14]. However, accounting for unknown varying control gain is not common in these designs. In [12], a general nonlinear time-delay system of nth order is considered, and an output feedback backstepping is designed. Moreover, the model of a two-stage chemical reactor with recirculation is considered as a second-order particular case. However, the controller design assumes the control gain as constant and perfectly known. In [15], a CSTRconsisting of a second-order SISO model is considered, in which only the output is known. The used anti-windup compensator amounts to the auxiliary system of the AES strategy. However, the controller design assumes that the control gain is perfectly known. In [14], a nth order system with unknown nonlinear control gain is considered. The unknown nonlinear nature of the control gain is tackled by using the Nussbaum gain strategy. However, the width of the convergence region of the modified tracking error depends on unknown model coefficients and terms. In summary, in the aforementioned AES-based robust adaptive backstepping control designs, the modified tracking error converges to a compact set whose width depends on the bounds of either external disturbances, model terms or model parameters [11,12,14]. This implies that such bounds must be known to achieve a user-defined magnitude of the steady value of the modified tracking error.
In this study, a modified/new robust adaptive backstepping controller is developed for a second-order SISO nonlinear system, tackling the effect of input saturation and unknown varying control gain with unknown upper and lower bounds. The design is based on dead zone radially unbounded forms, and a new auxiliary system is proposed. The asymptotic convergence of the modified tracking error is proved by using the Barbalat’s lemma, accounting for the unknown varying control gain, the saturated input, and the formulated controller. It is ensured that the regular tracking error converges to a residual set of user-defined width, for the case that the input saturation eventually ceases. The main contributions of this study with respect to adaptive backstepping control designs for systems with input saturation are listed below.
- The proposed auxiliary system is robust against varying and unknown control gain with unknown upper and lower bounds. This is in contrast to common adaptive backstepping control designs (see in [12,15]) where the auxiliary system considers the control gain as constant and unknown.
- The modified tracking error converges to a compact set whose width is user-defined, so that it does not depend on the bounds of either external disturbances, model terms, system states, or model parameters. This is in contrast to common adaptive backstepping control designs (see in [12,15]) and also those that use the Nussbaum gain strategy (see in [14]) where the width of the convergence region of the modified tracking error depends on such kind of bounds.
- The convergence region of the tracking error is determined for the closed loop system under the formulated controller with the proposed auxiliary system.
The work is organized as follows. In Section 2, the model of the biological process, the reference model, and the statement of the control goal are presented. In Section 3, the controller is designed and the stability properties of the closed loop states are determined. In Section 4, a simulation example is presented. In Section 5, the conclusions are drawn.
2. Model Description, Reference Model and Control Goal
2.1. Model Description
is the nutrient concentration in the upper CSTR, is the nutrient concentration in the lower CSTR, is the volume of the lower CSTR, is the volume of the upper CSTR, and is the flow that leaves the upper CSTR and enters the lower CSTR; is the flow that leaves the lower CSTR and enters the upper CSTR; is the flow of addition of fresh nutrient solution to the mixing tank; and is the nutrient concentration of the flow. The state is the output to be controlled, whereas the inlet flowrate is chosen as control input, it is non-negative and its upper bound is determined by the operational limit of the pump. Therefore, the relationship between the constrained control signal (denoted as v) and the unconstrained control signal (denoted as u) is
The following assumptions are considered:
Assumption 1.
The state variables and , are bounded for v bounded, and satisfy , , .
Assumption 2.
, , , are constant, , , are unknown whereas is known.
Assumption 3.
The reaction rate satisfies one of the following: (i) it is unknown, non-negative, and , where is unknown, positive, constant, whereas is a known continuous function of with well-defined ; (ii) it is a known continuous function of , with well-defined ; in this case, with , holds true.
Assumption 4.
The values of , are known, whereas is noisily measured: , where is the noisy measurement and is the measurement noise.
Assumption 5.
There is lack of knowledge on the control gain b according to one of the following conditions: (i) , where is known, and possibly varying, and bounded for , , bounded, whereas is unknown, varying, and satisfies: , where , are constant, positive and unknown; (ii) b is unknown, varying, and satisfies , where , are unknown positive constants; in this case, b can be expressed as , , , so that is unknown, varying and satisfies . In both conditions, , where is known, whereas is unknown, varying and satisfies ; so that .
2.2. Reference Model
The use of a reference model allows to obtain the expected transient plant response (rise time, settling time, overshoot). The reference model is defined as [16,17]
where is the desired output; is the command signal, which is user-defined and bounded; is a positive constants defined by the user, which determine the speed of convergence of the signal towards ; and is the differential operator. Due to the above characteristics, the signals , , are bounded and known. The reference model (5) can be rewritten as
or, equivalently,
2.3. Control Goal
Consider (i) the plant model (1) to (3), subject to input constraint (4) and Assumptions 1 to 5; (ii) the tracking error , where is the output, and is the desired output, whose characteristics are mentioned in Section 2.2; (iii) the residual set , whose width is positive, constant and user-defined. The goal of the controller design is to formulate a control law for v such that (Gi) the tracking error e converges asymptotically to the residual set , (Gii) the control law and the update laws are bounded under closed loop operation, so that excessive parameter increase is avoided; (Giii) the control law, the update law and the auxiliary system involve no discontinuous signals.
Remark 1.
The condition Giii is stated because the presence of discontinuous signals in the control law may lead to input chattering, and problems of existence and uniqueness of closed loop trajectories, and consequently, Filippov theory is needed, as discussed in [18,19].
3. Control Design and Stability Analysis
In this section, the proposed robust adaptive controller is developed for the model described in Section 2, which involves input constraint, unknown varying control gain, and unknown model parameters.
3.1. Controller Design
The controller design uses Lyapunov theory, with the adaptive backstepping strategy as framework. New states and are defined as function of , , and updated parameters. Furthermore, an overall Lyapunov function V is defined as the sum of , the dead zone Lyapunov function for ; , the dead zone Lyapunov function for ; and a Lyapunov function for each parameter updating error. Differential equations are defined for the new states, and the time derivatives of the Lyapunov functions are defined. The mechanisms for the updated parameters and the control input u are chosen such that is negative semi-definite, thus implying the asymptotic convergence of . Other important features of the developed procedure are
- a new auxiliary system of second order is proposed, whose input includes the control signal error , which is the difference between the constrained and the unconstrained control signals;
- a modified tracking error is defined as the sum of the regular tracking error and the state of the auxiliary system;
- the definition the states is based on the adaptive state backstepping method;
- dead zone radially unbounded quadratic forms are used instead of current quadratic forms; and
- a new treatment of the term is proposed, including a new parameterization of the unknown model parameters, and the formulation of a new auxiliary system.
In a basic adaptive backstepping control design, the state would be defined as the tracking error, . In contrast, we define by adding to the tracking error:
where the state is the output of a stable second order linear filter whose input contains the input error , the difference between the non-saturated and the saturated input signals. The controller design is aimed at driving to , . The advantages of the definition of (6) and the controller design based on instead of the tracking error e are (i) excessive increase of the updated parameters is avoided and (ii) the convergence region of the tracking error in presence of input saturation can be determined. The time derivative of Equation (6) is
Incorporating the expression (1) yields
Let
This truncated Lyapunov function is inspired on that of [20,21]. Early versions of dead zone Lyapunov functions are presented in [17,22,23]; versions for backstepping-based controllers in [21,24], and other versions in [20,25,26]. The use of the dead zone Lyapunov function (9) allows designing the adaptive controller, tackling the presence of unknown varying terms or parameters, and avoiding the use of discontinuous signals. The main properties of (9) are
The above properties and a stable dynamics of imply the convergence of to , , as is shown in the convergence theorem in Section 3.2.
Incorporating the expression for (8) into Equation (10) and arranging yields
where was incorporated in order to provide robustness and was expressed as , which would imply the presence of the signal in the definition of and would hamper the determination of . Thus, notice that from the definition of (11) it follows that
To obtain the required right hand side of , the effect of the term should be tackled by adequate definition of the new state . However, is unknown and is unknown, and its upper bound comprises and unknown constant . Therefore, the term should be expressed in terms of updated parameters and parameter estimation error. Recall from Assumption 3 that or , therefore
As the parameter vector is unknown, we express it in terms of an updated parameter vector and a parameter updating error as follows. Let , where , are the parameter estimation error and the updated parameter, being provided by an updating mechanism defined later. Thus, can be expressed as . Substituting into Equation (18) yields . Substituting this into Equation (16) yields
The dynamics of is affected by the following terms: (i) the term is negative and it provides stability; (ii) the term , which is later tackled by defining a quadratic form for , as can be noticed in the boundedness and convergence theorems in Section 3.2; and (iii) the term , which is later tackled by adequate definition of the new state , so that this term equals and (20) yields
The effect of the term can be tackled by adequate dynamics of and , such that involves the term , being a saturation function of and a quadratic function of . To this end, the required dynamics of is generated next.
Differentiating (22) with respect to time yields
The auxiliary state and its time derivatives are provided by the auxiliary system, whose general structure consists of a second order linear filter whose input involves the input error :
where the term , which will be defined later, is used to cancel the effect of the term, which is the difference between the saturated and non-saturated input signals. From (24), (25) it follows that . Substituting this expression and the expressions for (7), (1) and (3) into Equation (23) and arranging yields
where
and is defined in Equation (15). Let
The main properties of are
The above properties and a stable dynamics of imply the convergence of to , , as shown in the convergence theorem in Section 3.2.
Differentiating with respect to time yields
Differentiating in (29) with respect to time yields . Substituting the expressions for (21) and (33) yields
To obtain the required right hand side of , the terms
should be rewritten and tackled by means of proper definition of and the control law.
In the term, the signal must be expressed in terms of , because the controller design is based on the dead zone functions and rather than and . From definition (32), it follows that ,
therefore, and . Therefore, . Substituting into Equation (34) yields
so that the error term leads to the undesired uncertainty term in Equation (35). The property implies that , which is canceled by the already existing term , so that , and Equation (35) yields
Therefore, the term incorporated in Equation (12) is necessary for counteracting the effect of the error term resulting from .
In order to facilitate the design of the control law for u, the constrained input signal v is expressed in terms of the unconstrained input signal u and the input error , and the effect of is later canceled by the input of the auxiliary system, . Let
The effect of the term should be canceled by an adequate choice of , but this is hampered by the uncertainty on the control gain b. To this end, b is expressed in terms of an updated parameter and a parameter updating error. Recall from assumption 5 that . Therefore,
As the upper bound is unknown, it is expressed in terms of updated parameter and parameter updating error. Let , where , are a parameter estimation error and an updated parameter, and is provided by an updating mechanism defined later. From the above definition it follows that . Substituting into Equation (40) and arranging, yields
Substituting into Equation (39), yields
Thus, the right hand side of is affected by the following terms: (i) the term , which is later tackled by properly choosing , and (ii) the term , which is later tackled by defining the quadratic form for . To this end, if is expressed as , the resulting expression of would contain the signal, so that chattering might occur. Therefore, we notice from definition (32) that
Therefore, (41) leads to
we choose
substituting into Equation (24), (25) gives the auxiliary system
where is defined in (44). Substituting (46) into Equation (45) yields . Substituting this into (42) gives
The term
should be canceled by the input signal u appearing in the term , but this is hampered by the lack of knowledge on (i) , , , and (ii) the control gain term and its lower bound . Therefore, we need to express these terms as function of , updated parameters and parameter updating errors. To begin, the term comprising can be expressed as
Let , where and are a parameter updating error and an updated parameter, respectively, and is provided by an updating mechanism defined later. From the above definition it follows that can be expressed as . Substituting into Equation (49) and using property from Assumption 5, yields
In a similar way
Notice that the expressions (50)–(54) contain . If it is expressed as , the resulting control law would contain the signal, so that input chattering might occur. Thus, we use the expression (43), so that
Thus, the right hand side of is affected by the following terms: (i) the term which leads to convergence of and to zero, as shown in the convergence theorem in Section 3.2; (ii) the terms involving , , , , , , , which are later tackled by properly defining their quadratic forms and the update laws, what is shown later in the analysis of ; and (iii) the remaining term
which is tackled by properly defining the control law, so that the u signal cancels it:
Remark 2.
From the control law (58), it follows that the value of the control signal u depends on (i) the nutrient concentration in the upper CSTR, that is, ; (ii) the nutrient concentration in the lower CSTR, that is, , (iii) the measurement of the liquid volume in the lower CSTR, that is, ; (iv) the reaction rate term and , which are functions of ; and (v) the desired output and its time derivative , provided by Equation (5). Therefore, the input signal v also depends on , , , , as it is a saturation function of u according to expression (4).
Remark 3.
Remark 4.
In order to tackle the effect of the parameter updating errors in , the overall Lyapunov function is defined as
where is the sum of the quadratic forms for the parameter updating errors, and it is defined as
The vector of closed loop state variables is . Differentiating (60) with respect to time yields
Differentiating (61) with respect to time yields
In order to cancel the effect of the term
the update laws are chosen as
where is diagonal matrix whose diagonal entries are user-defined, positive, and constant, whereas , , , , , and are user-defined positive constants.
Remark 5.
The formulated controller comprises (i) the control law (58); (ii) the update laws (65) to (71); and (iii) the auxiliary system (47a), (47b). The signals involved therein are (i) (6), (11), (14), (22), (32), (44), (19), (27), (28); (ii) the desired output , provided by model (5), according to subSection 2.2; (iii) the input error (37), which involves u (58) and v (4), (iv) the constants , , , , which are user-defined and positive; (v) the user-defined positive constant , which is the width of the residual set defined in Section 2.3; and (vi) the constant .
Remark 6.
In the controller development, a new treatment of the term is proposed, and the main tasks of this treatment are (i) the term is expressed in terms of its upper bound (40); (ii) as such upper bound is unknown, it is expressed in terms of parameter updating error and update parameter (41); and (iii) the update law (69) is defined so as to obtain adequate time derivative of the overall Lyapunov-like function.
Remark 7.
Remark 8.
The modified tracking error asymptotically converges to the compact set , whose width is user-defined, so that it does not depend on the bonds of external disturbances, model coefficients, or model terms. Consequently, the convergence of is achieved without requiring knowledge on these bounds. This is in contrast to common robust adaptive backstepping designs (see [11,12,14]), where the convergence region depends on such kind of bounds, so that the convergence of the modified error to a compact set of user-defined size requires the knowledge on such bounds.
Remark 9.
Some remarkable features of the formulated controller are (i) the control law, the update laws and the auxiliary system are function of modified error instead of the regular tracking error , and (ii) saturation functions of the tracking error are used instead of discontinuous functions, in order to avoid undesired chattering.
3.2. Boundedness and Convergence Analysis
Theorem 1
(Boundedness of the closed loop signals). Consider the model (1) to (3), subject to input constraint (4) and Assumptions 1 to 5. If the control law (58), update laws (65) to (71) and auxiliary system (47a), (47b) are applied, then (Ti) the signals , , , , , , , , are bounded; (Tii) the signals , are bounded.
Proof.
Arranging and integrating Equation (72), yields
Theorem 2
(Convergence of signals , and e). Consider the model (1) to (3), subject to input constraint (4) and Assumptions 1–5. If the control law (58), update laws (65) to (71) and auxiliary system (47a), (47b) are applied, then (Ti) the signal converges asymptotically to , ; (Tii) the signal converges asymptotically to , ; (Tiii) if vanishes, then converges asymptotically to , ; (Tiv) converges asymptotically to ,
where , are constants that satisfy .
Proof.
From Equation (73) it follows that
so that . Applying the Barbalat’s lemma [27], yields . Furthermore, considering the definition of (11), it follows that converges asymptotically to . This completes the proof of Ti. From Equation (76) if follows that . Applying the Barbalat’s lemma [27], yields . Furthermore, considering the definition of (32), it follows that converges asymptotically to . This completes the proof of Tii.
From the definition of (6), it follows that can be expressed as
From Equations (47a) and (47b), it follows that if vanishes, then and converge to zero. From (77), accounting for the convergence of to , it follows that e converges asymptotically to . This completes the proof of Tiii.
We choose the quadratic form
Differentiating with respect to time, yields . Substituting the auxiliary system (47a), (47b) and arranging, yields . Factorizing, yields
Using the definition of (78), we get
From this it follows that converges asymptotically to ,
Remark 10.
The parameter updating errors are bounded despite input saturation, so that excessive increase of updated parameters is avoided.
Remark 11.
From result Tiv of Theorem 2, it can be observed that the bound of the steady tracking error can be made small by choosing large values of , .
4. Simulation Example
Consider the aeroponic system described in Appendix A whose model is given by Equations (1)–(3), with input constraint (4), Assumptions 1–5, and control goal and desired output stated in Section 2.2 and Section 2.3. The control law, the update laws, the auxiliary system, and their parameters and signals are stated in Remark 5. At what follows, the values of , and are generated through the model (1) to (3) with specific parameter values. These values of , and are used by the controller, but the model parameters and upper or lower bounds are not.
The input saturation values are and
The input value is used until reaches the value 70 mg/L, so that the controller is started at days. The parameters of the reference model (5) are chosen as and
whereas the desired width of the convergence region is chosen to be . The user-defined parameters of the control law, update laws and auxiliary system are chosen as
, , , , , , , , , .
We consider the measurement noise for in the control gain b, such that b satisfies the first condition of assumption 2.5, with
Due to the controller starting at days and the change of at days, the system behavior is separated in the time intervals and days. For days:
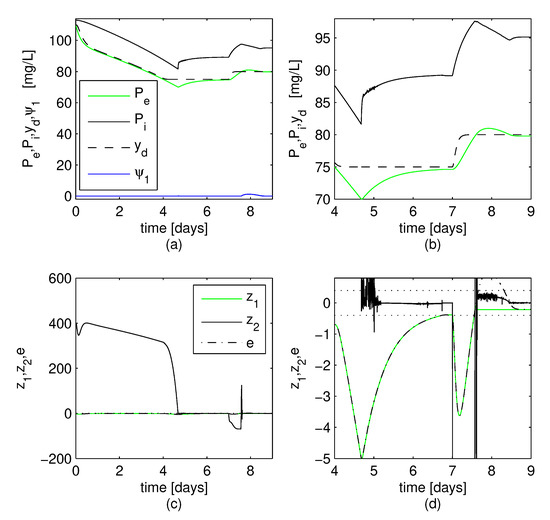 Figure 1. Simulation results for the system signals under the formulated controller. (a) Time course of the states , , desired output , and auxiliary signal . (b) Detail of the time course of , , and . (c) Time course of the modified tracking error , signal and tracking error e. (d) Detail of the signals , , and e; the horizontal dotted lines represent and .
Figure 1. Simulation results for the system signals under the formulated controller. (a) Time course of the states , , desired output , and auxiliary signal . (b) Detail of the time course of , , and . (c) Time course of the modified tracking error , signal and tracking error e. (d) Detail of the signals , , and e; the horizontal dotted lines represent and .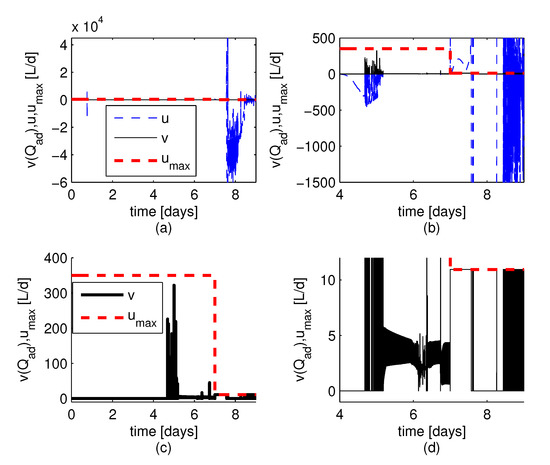 Figure 2. Simulation results for the system signals under the formulated controller. (a) Time course of the non-saturated input u and the saturated input v. (b) Detail of the time course of signals u and v. (c) Time course of the saturated input v. (d) Detail of the signal v.
Figure 2. Simulation results for the system signals under the formulated controller. (a) Time course of the non-saturated input u and the saturated input v. (b) Detail of the time course of signals u and v. (c) Time course of the saturated input v. (d) Detail of the signal v.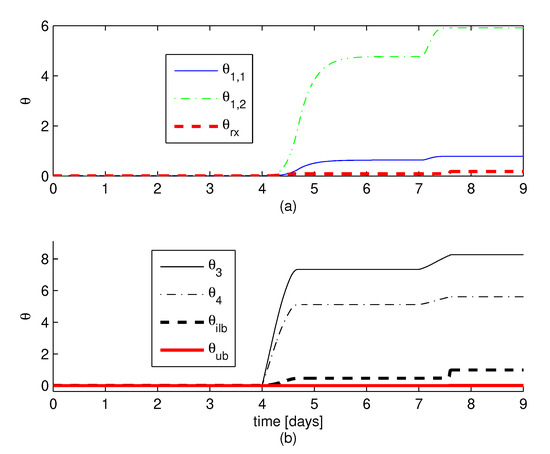 Figure 3. Simulation results for the system signals under the formulated controller. (a) Time course of the updated parameters , , . (b) Time course of the updated parameters , , , .
Figure 3. Simulation results for the system signals under the formulated controller. (a) Time course of the updated parameters , , . (b) Time course of the updated parameters , , , .- the signal is near at initial time , it enters at days and it remains inside until days (Figure 1d).
- the updated parameters remain bounded, and its change is not excessive; , change when , and remain constant otherwise (Figure 3).
- input signal v: for days it exhibits reiterated saturation at its lower bound, with only one moment of saturation at its upper bound (at days approx); during other moments it exhibits changing behavior (Figure 2c,d).
For days:
- the signal is inside at days , it leaves, it enters at days approx. and it remains inside afterwards (Figure 1d).
- the updated parameters remain bounded, , are constant when , and the other updated parameters are constant when (Figure 3).
- input signal v: for days, it remains saturated at its upper bound; for days, it exhibits saturation at its lower bound with some few saturation at its upper bounds; for days, it exhibits reiterated saturation at both its upper and lower bounds (Figure 2c,d).
5. Conclusions
In this paper, an adaptive backstepping controller was developed for a second order plant model subject to unknown model parameters, unknown reaction rate, unknown varying control gain, and input saturation. The controller provides important contributions to adaptive control design for second-order models with input saturation:
- It tackles the combined effect of constrained control input and unknown varying control gain with unknown bounds. To this end, a new auxiliary system is proposed.
- The modified tracking error asymptotically converges to a compact set whose width is user-defined and it does not depend on bounds of either external disturbances, model terms or parameters. Recall that in common robust backstepping designs, the tracking error converges to a compact set whose width depends on such kind of bounds, so that these bounds are required in order to obtain the expected width.
Other important features of the controller and closed loop system are
- the model coefficients, and upper and lower bounds of model terms are not required to be known, except ;
- the exact value of the reaction rate term is not required to be known;
- the control gain b is varying and unknown, although it can be expressed as , where is known and is unknown;
- discontinuous functions are not used in the control law, update laws and auxiliary system; instead, saturation type functions are used; and
- the boundedness of the updated parameters is ensured in the presence of input saturation, so that excessive parameter increase is avoided.
Significant improvements were made to the control design in order to tackle the unknown varying nature of the control gain b and the input saturation. Dead zone radially unbounded functions were used. As the gain b appears in the term, the design of the auxiliary system must be modified.
The developed controller design can be applied to other second order nonlinear systems as the mathematical manipulations are provided.
Author Contributions
Conceptualization, A.R.; methodology, A.R.; validation, F.E.H. and J.E.C.-B.; formal analysis, A.R., F.E.H., and J.E.C.-B.; investigation, A.R.; writing—original draft preparation, A.R.; writing–review and editing, A.R., F.E.H., and J.E.C.-B.; visualization, F.E.H. and J.E.C.-B. All authors have read and agreed to the published version of the manuscript.
Funding
The work of A. Rincón was supported by Universidad Católica de Manizales. The work of F.E. Hoyos and J.E. Candelo-Becerra was supported by Universidad Nacional de Colombia—Sede Medellín.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Hydroponic System and Formulation of the Mass Balance Model
The hydroponic system of the work in [28] comprises three vertical cultivation beds with grown tomatoes, a nutrient solution tank (mixing tank), a closed nutrient solution circulation system, and a lighting system. An electric pump drives a fraction of the nutrient solution from the mixing tank to the cultivation beds, and the drainage solution is conveyed back to the mixing tank. The mixing tank is eventually replenished with new nutrient solution in order to maintain a high EC, near mS/cm. The nutrient solution in the mixing tank exhibits decrease of electrical conductivity (EC) and concentration of major ions during time periods with no addition of fresh nutrient solution, whereas there is an increase of EC during addition of nutrient solution [28].
We consider the control of concentration of some major ion in the cultivation bed, by manipulation of the flow of fresh nutrient solution to the mixing tank , considering constant flows and . To this end, the mass balance model is developed for the concentration of some general nutrient ion, but in the simulation example the ion is considered, because its behavior is quite similar to that of the electrical conductivity (EC). We consider the mixing tank, the cultivation beds with plants, the flow of addition of fresh nutrient solution to the mixing tank, and the flows of nutrient solution between the mixing tank and the cultivation beds. We assume that the system can be represented by two linked continuous stirred tank reactors (CSTR), see Figure A1:
- The upper CSTR corresponds to the nutrient solution in the cultivation beds. The nutrient concentration is denoted as , the water volume is denoted as , the rate of nutrient removal is denoted as , and the evapotranspiration rate is denoted as . Nutrient removal occurs via sorption and plant uptake. We assume that the water volume is constant.
- The lower CSTR corresponds to the nutrient solution in the mixing tank. The nutrient concentration is denoted as and the water volume is denoted as . The nutrient solution mixes with the incoming flow, which is in turn the flow leaving the upper CSTR. We assume that is varying because of water evaporation losses and varying nature of flow .
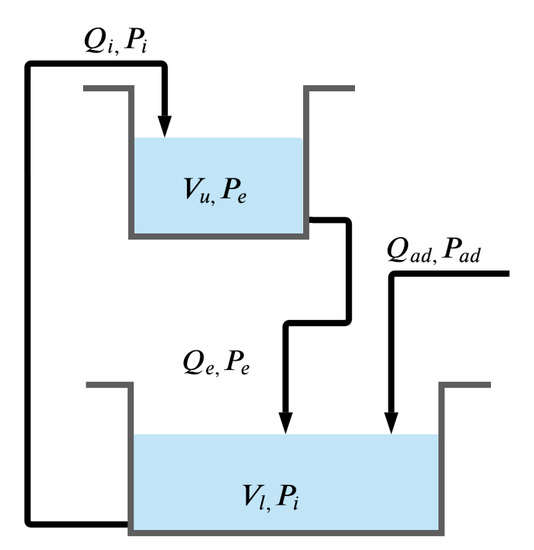
Figure A1.
Schematic diagram of the CSTR-based model for the hydroponic system.
In addition, is the flowrate that leaves the lower CSTR and enters the upper CSTR, and is the flowrate that leaves the upper CSTR and enters the lower CSTR. The outflow is lower than the inflow , due to evapotranspiration and constant nature of volume . We assume that flows and are constant. The development of the mass balance model gives as result the model (1) to (3).
This model with the reaction rate expression
was fitted to the experimental data of shown in [28], time interval 20–33 days, which corresponds to stage II (adaptation). This was performed by minimization of the squares of the errors between experimental and simulated values of [29]. The obtained model parameters are , , L/day, L/day, mg/L, mg/(Ld), mg/L, and mg/(Ld).
References
- Schaum, A.; Alvarez, J.; Garcia-Sandoval, J.P.; Gonzalez-Alvarez, V.M. On the dynamics and control of a class of continuous digesters. J. Process Control 2015, 34, 82–96. [Google Scholar] [CrossRef]
- Battista, H.D.; Jamilis, M.; Garelli, F. Global stabilisation of continuous bioreactors: Tools for analysis and design of feeding laws. Automatica 2018, 89, 340–348. [Google Scholar] [CrossRef]
- Battista, H.D.; Picó, J.; Picó-Marco, E. Nonlinear PI control of fed-batch processes for growth rate regulation. J. Process Control 2012, 22, 789–797. [Google Scholar] [CrossRef]
- Dalal, P.; Roy, S.; Chopda, V.; Gomes, J.; Rathore, A.S. Comparison and implementation of different control strategies for improving production of rHSA using Pichia pastoris. J. Biotechnol. 2019, 290, 33–43. [Google Scholar]
- Lara-Cisneros, G.; Femat, R.; Dochain, D. An extremum seeking approach via variable-structure control for fed-batch bioreactors with uncertain growth rate. J. Process Control 2014, 24, 663–671. [Google Scholar] [CrossRef]
- Nuñez, S.; Garelli, F.; Battista, H.D. Closed-loop growth-rate regulation in fed-batch dual-substrate processes with additive kinetics based on biomass concentration measurement. J. Process Control 2016, 44, 14–22. [Google Scholar] [CrossRef]
- Petre, E.; Selisteanu, D.; Sendrescu, D. Adaptive and robust-adaptive control strategies for anaerobic wastewater treatment bioprocesses. Chem. Eng. J. 2013, 217, 363–378. [Google Scholar] [CrossRef]
- Bastin, G.; Dochain, D. On-Line Estimation and Adaptive Control of Bioreactors; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Méndez-Acosta, H.O.; Campos-Delgado, D.U.; Femat, R.; González-Alvarez, V. A robust feedforward/feedback control for an anaerobic digester. Comput. Chem. Eng. 2005, 29, 1613–1623. [Google Scholar] [CrossRef]
- Polycarpou, M.; Farrell, J.; Sharma, M. On-line approximation control of uncertain nonlinear systems: Issues with control input saturation. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 543–548. [Google Scholar]
- Gao, S.; Ning, B.; Dong, H. Fuzzy dynamic surface control for uncertain nonlinear systems under input saturation via truncated adaptation approach. Fuzzy Set. Syst. 2016, 290, 100–117. [Google Scholar] [CrossRef]
- Min, H.; Xu, S.; Ma, Q.; Zhang, B.; Zhang, Z. Composite-observer-based output-feedback control for nonlinear time-delay systems with input saturation and its application. IEEE Trans. Ind. Electron. 2018, 65, 5856–5863. [Google Scholar] [CrossRef]
- Lin, D.; Wang, X.; Yao, Y. Fuzzy neural adaptive tracking control of unknown chaotic systems with input saturation. Nonlinear Dynam. 2012, 67, 2889–2897. [Google Scholar] [CrossRef]
- Askari, M.R.; Shahrokhi, M.; Talkhoncheh, M.K. Observer-based adaptive fuzzy controller for nonlinear systems with unknown control directions and input saturation. Fuzzy Set. Syst. 2017, 314, 24–45. [Google Scholar] [CrossRef]
- Nassira, Z.; Mohamed, C.; Essounbouli, N. Adaptive neural-network output feedback control design for uncertain CSTR system with input saturation. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies, CISTEM, Algiers, Algeria, 29–31 October 2019. [Google Scholar]
- Astrom, K.J.; Wittenmark, B. Adaptive Control; Addison-Wesley Publising Company: Reading, MA, USA, 1995. [Google Scholar]
- Slotine, J.; Li, W. Applied Nonlinear Control; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Polycarpou, M.M.; Ioannou, P.A. On the existence and uniqueness of solutions in adaptive control systems. IEEE Trans. Automat. Control 1993, 38, 474–479. [Google Scholar] [CrossRef]
- Polycarpou, M.M.; Ioannou, P.A. A robust adaptive nonlinear control design. Automatica 1996, 32, 423–427. [Google Scholar] [CrossRef]
- Rincon, A.; Piarpuzán, D.; Angulo, F. A new adaptive controller for bio-reactors with unknown kinetics and biomass concentration: Guarantees for the boundedness and convergence properties. Math. Comput. Simulat. 2015, 112, 1–13. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, C.; Wen, C. Robust adaptive output control of uncertain nonlinear plants with unknown backlash nonlinearity. IEEE T. Automat. Control 2007, 52, 503–509. [Google Scholar] [CrossRef]
- Koo, K. Stable adaptive fuzzy controller with time-varying dead-zone. Fuzzy Set. Syst. 2001, 121, 161–168. [Google Scholar] [CrossRef]
- Wang, X.; Su, C.; Hong, H. Robust adaptive control of a class of nonlinear systems with unknown dead-zone. Automatica 2004, 40, 407–413. [Google Scholar] [CrossRef]
- Su, C.; Feng, Y.; Hong, H.; Chen, X. Adaptive control of system involving complex hysteretic nonlinearities: A generalised Prandtl–Ishlinskii modelling approach. Int. J. Control 2009, 82, 1786–1793. [Google Scholar] [CrossRef]
- Wang, Q.; Su, C. Robust adaptive control of a class of nonlinear systems including actuator hysteresis with Prandtl–Ishlinskii presentations. Automatica 2006, 42, 859–867. [Google Scholar] [CrossRef]
- Ranjbar, E.; Yaghubi, M.; Suratgar, A.A. Robust adaptive sliding mode control of a MEMS tunable capacitor based on dead-zone method. Automatika 2020, 61, 587–601. [Google Scholar] [CrossRef]
- Ioannou, P.; Sun, J. Robust Adaptive Control; Prentice-Hall PTR: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Lee, J.Y.; Rahman, A.; Azam, H.; Kim, H.S.; Kwon, M.J. Characterizing nutrient uptake kinetics for efficient crop production during Solanum lycopersicum var. cerasiforme Alef. growth in a closed indoor hydroponic system. PLoS ONE 2017, 12, e0177041. [Google Scholar] [CrossRef] [PubMed]
- Mutolsky, H.; Christopoulos, A. Fitting Models to Biological Data Using Linear and Nonlinear Regression; GraphPad Software: San Diego, CA, USA, 2003. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).