Abstract
Reluctance coil guns are electromagnetic launchers having a good ratio of energy transmitted to actuator volume, making them a good choice for propelling objects with a limited actuator space. In this paper, we focus on an application, which is launching real size soccer balls with a size constrained robot. As the size of the actuator cannot be increased, kicking strength can only be improved by enhancing electrical to mechanical energy conversion, compared to existing systems. For this, we propose to modify its inner structure, splitting the coil and the energy storage capacitor into several ones, and triggering the coils successively for propagating the magnetic force in order to improve efficiency. This article first presents a model of reluctance electromagnetic coil guns using a coupled electromagnetic, electrical and mechanical models. Four different coil gun structures are then simulated, concluding that splitting the kicking coil into two half size ones is the best trade-off for optimizing energy transfer, while maintaining an acceptable system complexity and controllability. This optimization results in robust enhancement and leads to an increase by of the energy conversion compared to a reference launcher used. This result has been validated experimentally on our RoboCup robots. This paper also proves that splitting the coil into a higher number of coils is not an interesting trade-off. Beyond results on the chosen case study, this paper presents an optimization technique based on mixed mechanic, electric and electromagnetic modelling that can be applied to any reluctance coil gun.
Keywords:
coil gun; reluctance; electromagnetic launcher; mechatronics; electronics; mechanics; simulation; RoboCup 1. Introduction
Propelling projectiles with a controlled speed and trajectory is a technological challenge having lots of applications ranging from kicking soccer balls to launching rockets or satellites, including testing military ammunitions. In this introduction, we focus on propulsion techniques having strong accelerations, so that an important speed can be obtained in a short distance. Common propulsion techniques of this type are among the following ones:
- Chemical propulsion: mainly used for propelling weapons or rockets; chemical propulsion uses the product of a chemical explosive or expanding reaction to push out a projectile [1]. The benefit of this propulsion is to have a high density of energy stored in a small size as a chemical product leading to strong accelerations, without the need of being connected to a power supply. Its drawback is that the propulsion is a single shot one due to the chemical reaction.
- Mechanical propulsion: there are many types of mechanical propulsion systems. Among the solutions allowing a strong acceleration of the payload are the inertial launchers. They are mostly using an energy storage in heavy high speed rotating mechanical parts such as iron cylinders. These parts are accelerated slowly by a standard motor and part of the stored energy is transferred in a very short amount of type to a projectile by friction. These systems are very simple but their size is much more important than the size of chemical or electromagnetic launchers for a given propelling strength. An example is presented later in this paper.
- Rail Gun propulsion: a rail gun is composed of a pair of conductive parallel rails connected to a direct current (DC) power supply. The electrical circuit is a closed sliding conductor where a payload is placed. Once current flows through the rails, a Lorentz force is created, accelerating the payload to launch it. This propulsion technique is very efficient, and output speed can be higher than using a conventional chemical propulsion as shown in [1], for a launching structure having the same overall size. Compared with chemical propulsion, this solution can be far less expensive than chemical propulsion for launching limited size payloads such as small satellites [2]. However, the presence of a mechanical contact between the rails and the payload propeller can lead to several issues reducing the energy transfer, such as friction losses [3] and plasma phenomena at very high speeds [2,4].
- Coil Gun propulsion: a coil gun is an electromagnetic launcher (EML) converting electricity into kinetic energy using coils [5,6]. There are two types of coil guns. The first one is based on induction to accelerate a conductive non-magnetic projectile using eddy currents induced in a conductive/non-magnetic moving rod inside a magnetic field created by a fixed coil [7]. This solution has an important drawback due to magnetic losses leading to heat generation and controllability loss. The second one is based on accelerating a magnetic projectile by minimizing the reluctance between the projectile and a magnetic field generated by a current flowing through a fixed coil [8]. This type of coil gun, also named reluctance accelerator is simpler to drive than induction coil guns and is very compact.
1.1. Comparison of Existing Soccer Ball Launching Systems
In this article, we focus on a case study having strong constraints: a real size soccer ball kicking system embedded in robots participating in the RoboCup (the autonomous robot soccer World Cup) in Middle Size League (Figure 1). This competition puts strong constraints on the robot size and weight, requiring to choose the launcher having the highest ratio of energy transmitted to launcher volume (Figure 2).

Figure 1.
RoboCup 2019—Sydney—Australia.

Figure 2.
RoboCup RCT robot 2020.
The balls used for the competition are real soccer balls (diameter 22 cm) having a weight equal to 450 g. Size constraints on the robots are a maximum width and length cm and a maximum height cm. Considering these robots are all using omnidirectional propulsion with 3 or 4 wheels, the space for embedding the kicking system is very small and cannot exceed a length of 30 cm and a width of 20 cm, as shown in Figure 3. Moreover, its height must be limited because the mass centre of the robot must be as low as possible in order to allow high accelerations.
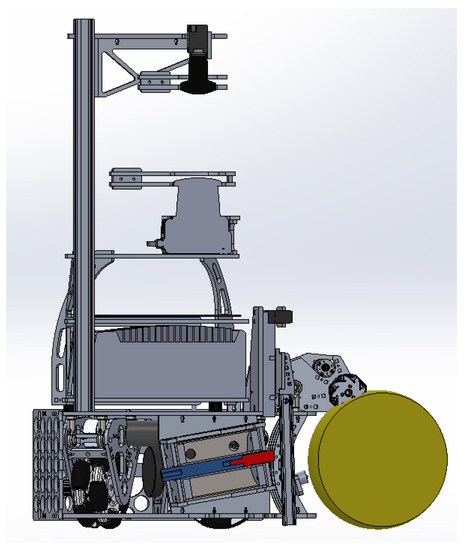
Figure 3.
Cut view of RCT robot 2020.
A comparison of existing soccer ball launchers is first proposed in this section. Chemical propulsion has not been considered because they are dangerous and not reusable. Moreover, Ref. [1] shows that the size of a chemical launching system is equivalent to an electromagnetic one. The only advantage is that it does not need any power supply, but it is not a problem in our case considering that the robot has one.
The reference for understanding ball kicking systems is the human. Professional soccer players shots can reach 130 km·h = 36 m·s, corresponding to an kinetic energy equal to J. As shown in Figure 4, the surface swept by the leg during a kick is important and approximately equal to one third of the surface of a circle having a radius cm. The mass of a soccer player leg is approximately equal to kg.
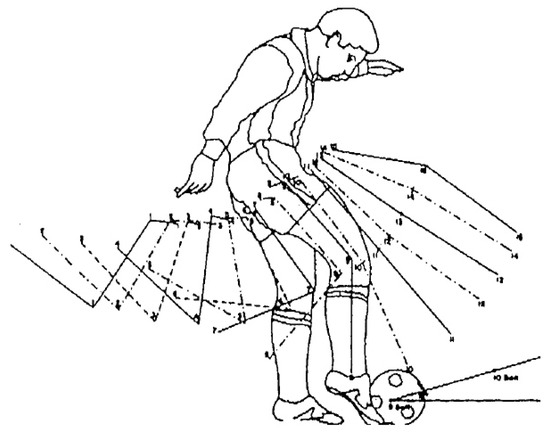
Figure 4.
Human kicking sequence.
Mechanical propulsion is also one of the most commonly used methods for propelling a soccer ball. A commercial system, shown in Figure 5, is able to launch soccer balls at a maximum speed of 105 km·h = 29 m·s corresponding to an kinetic energy equal to J, using two 10 kg cylinders coated with rubber. The propulsion part (cylinders and motors) of the system weighs 15 kg and its dimensions are cm and cm and cm.

Figure 5.
Mechanical inertial rotating launcher.
Another mechanical system that can be used for propelling a soccer ball is a robotic leg powered by a motor as shown in the kicking from Adidas [9] or as described in [10]. These solutions, using a robotic arm, have multiple degrees of freedom [10] or a set of rotary and linear spring-loaded actuators [9]. The Adidas solution shown in Figure 6 is composed of a m robotic thigh rotating at 85 RPM and m shank rotating at a maximum speed of 165 RPM, leading to a maximum ball speed of 21 m·s corresponding to an kinetic energy equal to J. However, the whole system is heavy (more than 50 kg) and its dimensions are important as it sweeps a m radius cylinder.

Figure 6.
Mechanical robot leg.
These mechanical systems are interesting for simulating a football player leg [9,10] and for training humans in real conditions. However, embedding them in a RoboCup robot is very difficult. This is probably the reason why the RoboCup research community is mainly focused on electromagnetic launchers, and more especially on variable reluctance coil guns. Authors in [11] introduced a design of a variable reluctance coil gun (Figure 7) that is used in the RoboCup robots of the 2019 World Champion team. This actuator’s dimensions are cm, cm and cm, its weight is kg and ball maximum speed can reach m·s, corresponding to a kinetic energy equal to J. Output speed is smaller than mechanical design, but volume has been divided by factor 20 compared with an inertial rotating launcher.

Figure 7.
Tech United Reluctance Coil Gun.
Table 1 shows a comparison between existing ball launchers, including humans. These solutions are very different. This comparison is done considering the weight and size for each system, as it is a strong constraint in our case study. It is important to note that the energy transferred to the ball is close to the maximum value for all systems, except for the robot leg. This one is based on an industrial actuator able to carry heavy loads, and largely oversized for launching a soccer balls in terms of torque and power. Because it is not used at full power, its ratio of energy transmitted to launcher volume is very low compared to other solutions. However, this solution takes too much space due to the rotation of the leg and is not relevant for a small size launcher.

Table 1.
Existing ball launchers comparison.
In conclusion of this section, the most relevant launching systems in terms of energy transferred to the ball for a given actuator volume are reluctance coil guns, with a ratio of energy transmitted to launcher volume better than rotating inertial launchers by a factor , and better than most humans by a factor 5.
Since these electromagnetic coil guns seem to be the most promising solution for launching balls, this paper will only focus on improving that solution in order to maximize this energy transfer without changing the volume and the weight of the actuator.
1.2. Reluctance Coil Guns: A Ball Launcher That Can Be Optimized
Even if reluctance coil guns are a relevant solution for kicking soccer balls efficiently, it is important to note that they are not very efficient in terms of energy conversion. In [11], electrical energy for the coil gun is stored in a capacitor having a capacitance value C = 4700 F under 425 V. Stored electrical energy is equal to:
Consequently, the ratio of ball kinetic energy to the input electrical one is only , and the ratio of the overall mechanical transmitted energy (including the kinetic energies of the iron rod, the lever and the ball as explained later) to the input electrical one is . However, the energy necessary for kicking like human soccer players is already stored in the capacitor. This means that if a robot’s kick is 10 times less powerful than a human one, it is not an issue related to available energy, but it is a problem of inefficiency of energy transfer in reluctance coil guns.
Optimizing this energy transfer can be done in two main ways without changing the size and the weight of the launcher. The first one is to adjust the initial position of the plunger, and the length of its non-magnetic extension. [12] shows that energy transmission can be increased by using this technique compared to the reference case presented in [11]. This optimization is interesting because nothing is changed on the coil gun structure and size; it is only an optimization of initial conditions and a plunger parameter adjustment.
A second way of improving the energy transfer of a coil gun is to modify its inner structure by splitting the coil and the energy storage capacitor into several ones [7,13], without changing the overall quantity of coil copper and the overall capacitance value. Instead of sending an energy pulse to a single coil, a sequence of smaller energy pulses will be sent to the different coils propagating the magnetic force along the coil as the plunger enters it. The number of coils and the triggering sequence are the parameters to be optimized.
This paper focuses on this second method for optimizing the energy transfer in a reluctance coil gun. It is divided into three sections:
- Section 2 recalls the principles of coil guns.
- Section 3 describes 4 mechatronic coupled models of reluctance coil guns. All these coil guns use the same coil copper quantity and have the same overall electrical energy storage capacitance, but they have, respectively, one, two, three and four coils. The electromagnetic part of each model has been implemented using FEMM 4.1, a finite element electromagnetic simulation tool, and Matlab Simulink is used for modelling the electrical and mechanical parts.
- Section 4 presents results, which are discussed in order to conclude on the most relevant coil structure for maximizing the ball speed and the energy transfer of the reluctance coil gun, while maintaining a high level of robustness.
2. Principles of Coil Guns
2.1. Physical Concept
Magnetic field in a looped circuit composed of magnetic material and air gap tends to be maximized when a current is applied. Hopkinson law used in magnetic circuits tells that: , with:
- I: current in the coil (A)
- N: number of turns of the coil
- : flux (Wb)
- R: reluctance (H)
Increasing the magnetic field is similar to an increase of . For a given current and number of coil turns, this increase can be done by reducing the reluctance R of the magnetic circuit. Its expression is R, with:
- H·m: permeability of vacuum
- : relative magnetic permeability
- S: cross-sectional area of the circuit (m)
- l: length of the magnetic circuit (m)
The way to reduce reluctance is to minimize the air gap in the magnetic circuit, replacing it by a portion of the iron plunger (having a relative magnetic permeability equal to 5000 or more). Thus, under a strong coil current, the plunger will be propelled in order to reduce the air gap, with an important force dependent on the coil current and the number of coil turns. Figure 8 shows a three-stage coil gun. In this case, coil 1 is powered first, then coil 2, then coil 3. This is the principle of a multi-stage variable reluctance actuator.
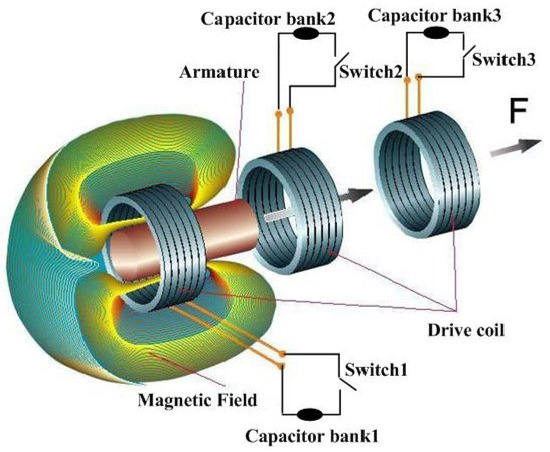
Figure 8.
Three Coils Electromagnetic Launcher Principle [14].
Our case study focuses on coil gun implementations having one, two, three or four coils, with a fixed overall size and quantity of copper, as shown in Figure 9. It is important to note that between each coil, an iron plate has been placed in order to close the magnetic circuit around each coil.
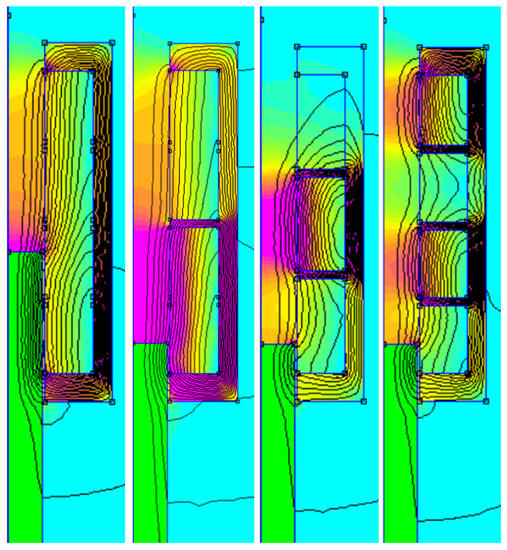
Figure 9.
Coil gun configurations with 1, 2, 3 and 4 coils sharing the same quantity of copper.
In our case study, each coil is powered by an identical capacitor. These capacitors have an global overall capacitance equal to (4700 F). This capacitance is split into n smaller equal ones, where n is the number of coils. Each capacitor can be discharged, one at a time, in its corresponding coil producing a strong current which generates a magnetic force. The iron rod, mobile part of the magnetic circuit slides in a stainless steel tube in order to reduce the air gap of the magnetic circuit. This iron rod is attracted and accelerated as long as the air gap can be minimized. It is slowed down if the plunger goes to far and the air gap increases again. To avoid that, the duration of the current pulse in each coil has to be limited in time.
Discharge from the capacitor to the coil inductor can be described by a second order differential equation. This equation has non-constant coefficients because the value of the inductor highly depends on the value of the current in the coil and on the plunger position in the sliding tube. This mixed non-linear model combining electrical and mechanical inputs will be presented in the following sections.
2.2. Electromagnetic Theory and Simulation Software
The model of an electromagnetic actuator has to take into account many non-linearities such as:
- The saturation of magnetic materials under high currents [15] as shown in Figure 10.
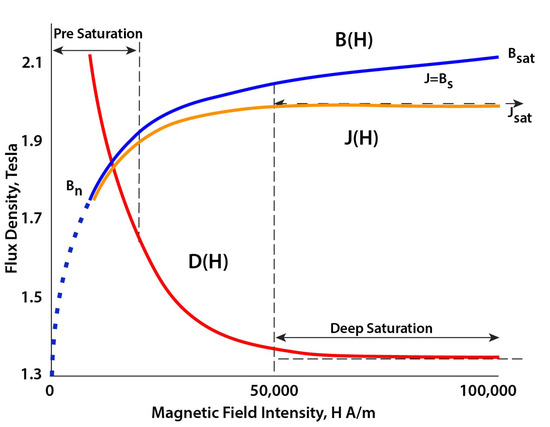 Figure 10. Example of magnetic field saturation [15].
Figure 10. Example of magnetic field saturation [15]. - The impact of the plunger position leading to change locally the relative magnetic permittivity by a factor 5000 or more.
Considering this, it is diffficult to find a theoretical solution to calculate the strength of the force applied to the rod. For taking non-linearities into account, the model used is a finite elements one obtained using an open-source simulation tool called FEMM 4.2. It has been developed by D.C. Meeker. This tool calculates force and inductance values under different conditions [16]. More precisely, magnetic field and potential vector are calculated everywhere using a successive approximation finite element solver on an axisymmetric model with a spherical boundary as shown in Figure 11.
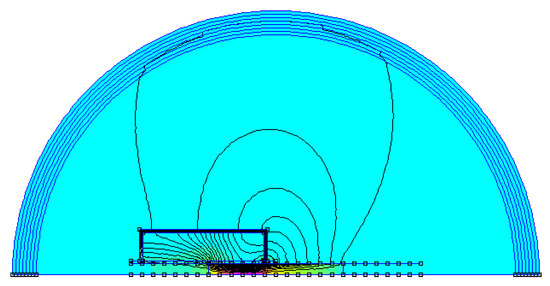
Figure 11.
FEMM 4.2 model: flux density.
The mesh used for this computation is determined using an heuristic approach having the following characteristics: a maximum allowable mesh size is then computed as of the length of the diagonal of the bounding box of any region, leading to generate a default mesh with about 4200 elements in an empty square region as shown in Figure 12. Fine meshing is also forced in all corners and a five-degree default discretization is used for arc segments.
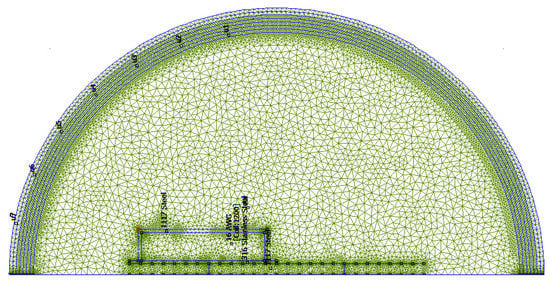
Figure 12.
FEMM 4.2 mesh with its boundary.
Evaluating force and inductance value which are integral values on the mesh is also done by FEMM 4.2 on pre-defined specific parts of the system such as the iron plunger or the inductance of the coil. Computation needs approximately 5 s on a standard Intel Core I7 processor.
In order to compute force and inductance for all combinations of currents and plunger position, a LUA script is used in FEMM 4.2. Simulations have been done for 30 different positions of the plunger and 6 different currents for each coil: 0 A, 40 A, 80 A, 120 A, 160 A and 200 A. Simulation times are as follows:
- One coil: 180 combinations—15 min
- Two coils: 1080 combinations—90 min
- Three coils: 6480 combinations—9 h
- Four coils: 38,880 combinations—54 h
Considering the high computational cost of the electromagnetic simulations, our study has been limited to four coils, but we will show later that it is not necessary to go further.
2.3. Electrical Model
At each stage of the coil gun, a F, 450 V capacitor C is discharged in the inductance L using a controlled switch based on a MOSFET Transistor as shown in Figure 13. In this LC circuit, resistor R must be considered because its value is not negligible at all due to the important number of loops in the coil. can be evaluated or measured, where is the resistivity of copper, L the total length of the coil wire and S the surface of a wire section. This leads to the differential Equation (1) where L is not constant, but depends on the plunger position and on the coil current. Considering that, Equation (1) must be solved by numerical simulation.
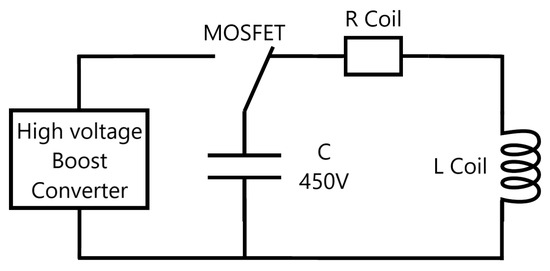
Figure 13.
Electric circuit.
As shown in Figure 14, FEMM 4.2 simulations shows that L inductance varies by a factor 20 from mH to mH in a 1 coil kicking system.
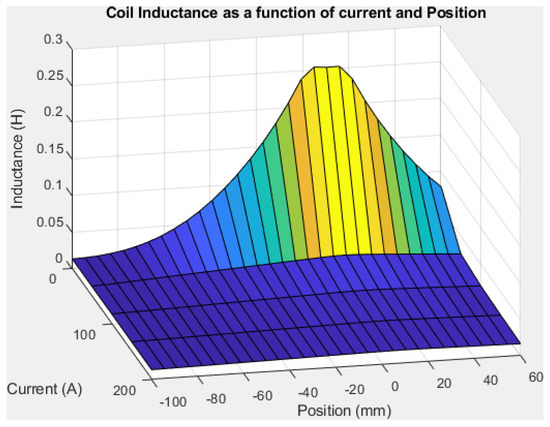
Figure 14.
Variation of the inductance value depending on the plunger position and the coil current.
The inductance value depends on the plunger position and the saturation of the magnetic circuit due to the current in the coils. In Figure 14, discrete values of the inductance are calculated for positions of the plunger (Figure 15) varying from mm to 60 mm by increment of 5 mm, and for coil currents varying from 1 A to 200 A by increment of 50 A.
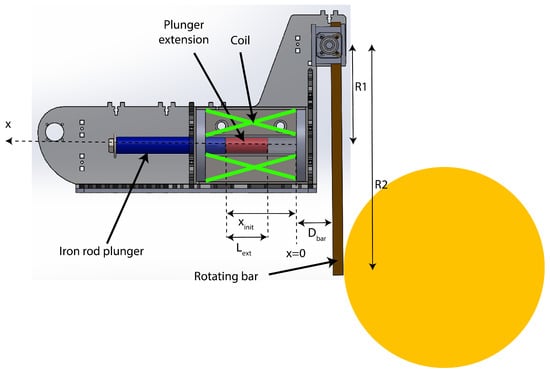
Figure 15.
RoboCup reluctance coil gun kicking system.
It is important to note that:
- Inductance value L increases as the plunger enters the coil, is maximized when the plunger centre is aligned with the coil centre, and decreases after that. This is because the magnetic field is well guided when the plunger is inside the coil with a low air gap.
- The inductance value is highly dependent on the coil current. For a current A, L varies, depending on plunger position, from mH to mH whereas for a current A, L varies only from mH to mH. There is an important difference between maximal values because at a low current, magnetic material is not saturated, leading to a high inductance value. In contrast, there is no difference between minimal values because when the plunger is outside the coil, the air gap is so important that it leads to a huge reluctance in the air gap part which prevents saturation of the magnetic circuit.
2.4. Mechanical Model
The mechanical model has been defined following the coil gun structure described in [11]. However, our kicking system is very similar in terms of dimensions and weight to that one which serves as a reference design for most RoboCup teams. Consequently, this model will be reusable for other teams, and can be adapted for other use cases by changing the content of some blocks according to the chosen mechanical design. However, changing parameters of the coil requires to simulate again the electromagnetic part, as force depends on coil gun geometry, current and plunger position.
As for the electrical model, an analytical calculation of the force is not possible. The finite elements model using FEMM 4.2 shows that force varies in our case study from −1900 N to 19,000 N for the same coil depending on the plunger position and on the coil current (Figure 16). Discrete values of the force are calculated for positions of the plunger (Figure 15) varying from mm to 60 mm by increment of 5 mm, and for coil currents varying from 1 A to 200 A by increments of 50 A.
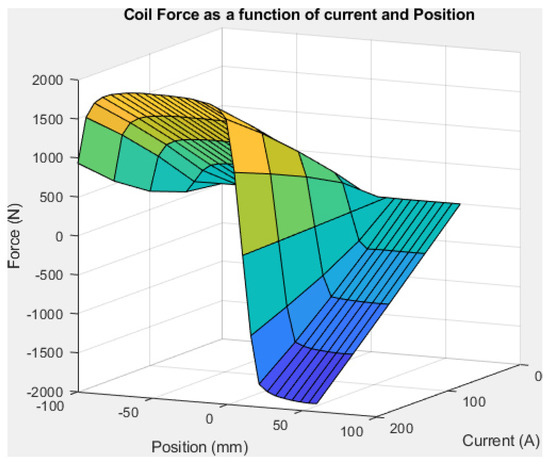
Figure 16.
Variation of the force on the plunger depending on its position and the coil current.
It is important to note that:
- Force F is almost linear with coil current in any situation.
- Force F is highly dependent on the plunger position. For a current A, F varies, depending on plunger position, from N to N, with N when the plunger is exactly aligned with the centre of the coil. This is because magnetic flux tends to be maximized in a magnetic circuit, leading to reduce the air gap. Consequently, as shown in Figure 16, the magnetic force on the plunger is symmetrical around the point where the centre of the plunger is aligned with the centre of the coil. Thus, it is important to stop powering the coil as soon as the plunger has crossed the coil.
- Force is very small if the plunger is outside the coil. This is normal considering the important length of the air gap replacing the plunger for looping back the magnetic circuit. We can also note that when the plunger is at the centre of the coil, force is null for any value of the current because magnetic flux can not be maximized.
3. Mixed Electrical and Mechanical Model of the Reluctance Coil Gun
Implementation has been done using Matlab Simulink for this mechatronic model. Simulated inductance and magnetic force values using FEMM 4.2 are implemented in look-up tables interpolating data in order to have a force and inductance value for any position of the plunger and any coil current. Figure 17 shows the model of a single coil electromagnetic launcher used for simulations. Figure 18 shows the model of a four-coil electromagnetic launcher used for simulations. The mechanical simulation part is unique in both models, whereas the electrical part is replicated by the number of coils present in the electromagnetic launcher.
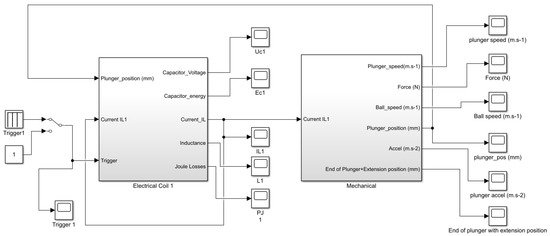
Figure 17.
Mechatronic model of a 1 coil electromagnetic launcher.
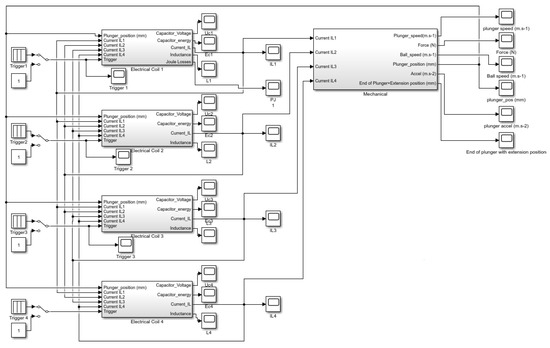
Figure 18.
Mechatronic model of a 4 coils electromagnetic launcher.
3.1. Electrical Model
A model of the electrical part of the first coil of the electromagnetic launcher is described in Figure 19 in the case of a single coil launcher, and in Figure 20 in the case of a four-coil launcher. Electrical differential Equations (1) are implemented using discrete blocks because coefficients of the equation are not constant due to the dependence of inductance L on the current and position of the plunger.
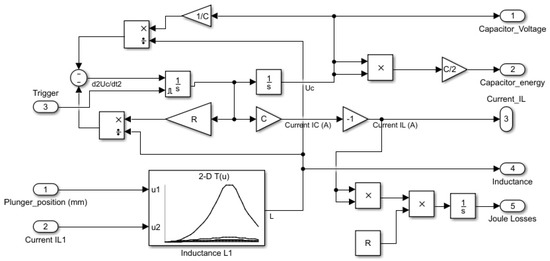
Figure 19.
Electrical model of the first coil of an electromagnetic launcher with 1 coil.
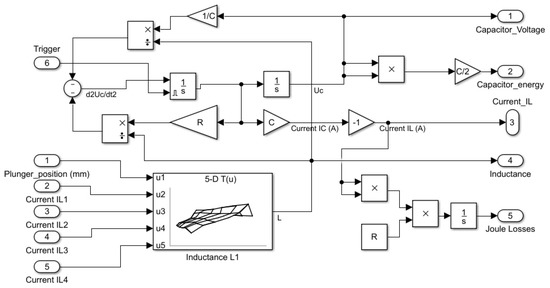
Figure 20.
Electrical model of the first coil of an electromagnetic launcher with 4 coils.
As shown in Figure 19 and Figure 20, the only difference between both models is the number of inputs of the inductance look-up table (LUT) block interpolating linearly the value of L using the simulations performed with FEMM 4.2. In the case of a four-coil EML, there are five inputs: plunger position, and the currents on each of the four coils.
It is important to note that there is a trigger input in each block. This input corresponds to an electronic trigger supplied by a pilot board and used for piloting the MOS transistor commutating the capacitor on the coil. There is one trigger input per coil, so that it is possible to drive them independently.
3.2. Mechanical Model
The reluctance coil gun mechanical system shown in Figure 15 has been described in a former work [12]. This model takes into account the transmission of the movement from the plunger to the ball through an aluminium lever. Movement can be split into three phases as shown in Figure 21:
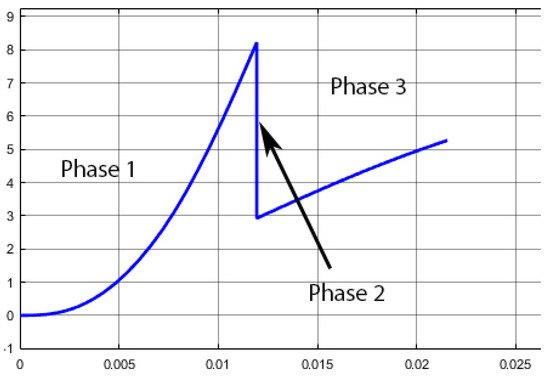
Figure 21.
Plunger speed in m·s over the time in s.
- Phase 1: Acceleration of the plunger without contact on the lever, due to the magnetic force as shown in Equation (2) without contact on the lever. Force depends non-linearly on plunger position and current I. A look-up table (LUT) interpolates linearly the value of F using the simulations performed with FEMM 4.2.
- Phase 2: Impact on the lever corresponding to an elastic shock when plunger hits it at a distance from its rotation centre. Kinetic energy is conserved as described in Equation (3).where is the inertial moment of the lever, and the distances between the lever axis and respectively the plunger impact point and the ball impact point as shown in Figure 15. This leads to a plunger speed just after the shock equal to the given in Equation (4).
- Phase 3: the plunger is accelerated in contact with the lever, which is also in contact with the ball. This means that the lever applies a force on the plunger in subtraction of the magnetic force as shown in Equation (5). This force is an inertial one due to the acceleration of the ball and the lever as shown in Equation (6). It is important to note that theoretically, the speeds of the ball, lever and plunger are not equal after the shock, but in reality they are due to the elastic deformation of the ball as shown in the slow motion picture in Figure 22.wherewith:For small angles, , this leads to:
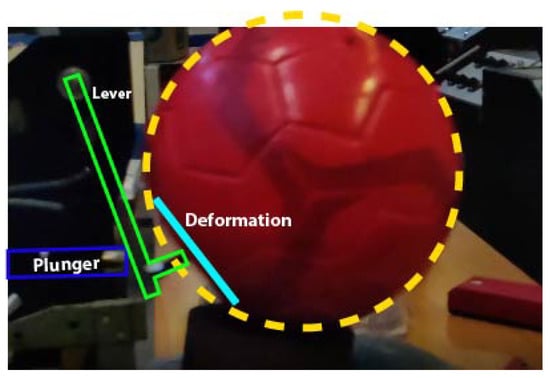
Figure 22.
Ball deformation after phase 2.
Implementation of this three-phase mechanical model has been done using Matlab Simulink. Figure 23 shows the mechanical part model of a 1 coil electromagnetic launcher, whereas Figure 24 shows the mechanical part model of a 4 coils electromagnetic launcher. It is important to note that, as shown in Figure 22, plunger, lever and ball are in contact after the shock. This is due to the softness of the ball, and because the ball is close to be in contact with the lever before the impact. Thus, the hypothesis of a perfect elastic shock is almost verified except for a transitional short period of less than one millisecond after the shock of the rod on the lever.
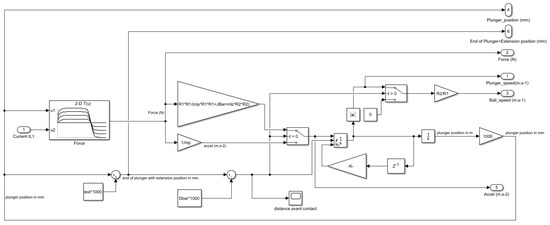
Figure 23.
Mechanical part model of a 1 coil electromagnetic launcher.
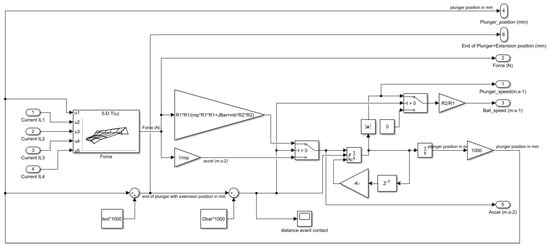
Figure 24.
Mechanical part model of a 4 coils electromagnetic launcher.
However, in order to understand more accurately what is going on during this transition, impact of the plunger on the lever and impact of the lever on the soft ball will be modelled in another work (for example using MSC ADAMS software), but this is out of the scope of this paper.
As shown in Figure 23 and Figure 24, the only difference between both models is the number of inputs of the force look-up table (LUT) block interpolating linearly the value of F using the simulations performed with FEMM 4.2. In the case of a four-coil EML, there are five inputs: plunger position, and the currents on each of the four coils.
4. Reluctance Coil Gun Simulations
4.1. Hypothesis
The reluctance coil gun previously described and used in robots at the RoboCup has been simulated using Matlab Simulink. In this study, we focus on optimizing the inner structure of the coil gun and especially we aim at finding the optimal number of coils and the optimal instant and duration of triggering for each coil in a sequence.
Optimality is not only focused on the ball speed which must be as important as possible, but also on the reliability and robustness of the triggering system, which can be very sensitive to a small change in the triggering delay when several coils (especially 3 or 4) are used.
This last point is important because we have decided of not adding an observer of the plunger position in the system such as a set of infrared light barriers. This choice has been done considering the mechanical difficulties for inserting sensors inside the coil gun structure, and the issues about robustness it can raise due to the huge impacts and vibrations on the EML structure. Instead of that, a simple and robust open loop driving has been chosen, each coil being commutated during a fixed time and with a fixed delay from the start of the sequence. Considering that the initial conditions of the plunger position are always the same ones (this is true because the plunger is returned to its initial position by an elastic restoring force), the ball speed has been measured to be almost the same at each shooting sequence.
This paper does not focus on optimizing the initial position of the plunger, and the length of the non-magnetic extension of the plunger, as done in [12]. In this study, we started using the results presented in [12]. However, in a final step, a fine optimization has been done for getting the best possible solution on both parameters.
4.2. Model Parameters
In order to compare results with other previous studies, the kicking system simulated is identical to the Tech United Team one described in [11]. However, geometry of our coil gun is very similar to this reference design. Parameters of the model are as follows:
- Distance from lever axis to plunger touch point: cm
- Distance from lever axis to ball touch point: cm
- Coils number (each coil as been chosen identical):
- Coils length (for each coil): cm
- Coils number of turns (for each coil): turns
- Coils resistance (for each coil):
- Capacitors number:
- Capacitors value (for each capacitor): 4700 F/
- Capacitors charge voltage: 425 V
- Plunger iron rod diameter: mm
- Plunger iron rod length: cm
- Plunger iron rod mass: g
- Plunger extension diameter: mm
- Plunger extension length: cm
- Plunger extension mass: (in m)
- Distance from coil to lever: cm
- Vertical lever mass: g
- Ball mass: g
4.3. Simulations
Simulations have been done using coil guns having one, two, three and four coils. As explained before, the overall quantity of copper and the global number of coil turns is a constant, as is the sum of the capacitors value. Delays and durations of each trigger pulses for each coil have been optimized manually in order to maximize the ball speed.
Results of simulation for an EML having one coil are presented in Figure 25. is triggered during 25 ms. Optimal initial position of the plunger is mm. Ball speed reaches m·s.
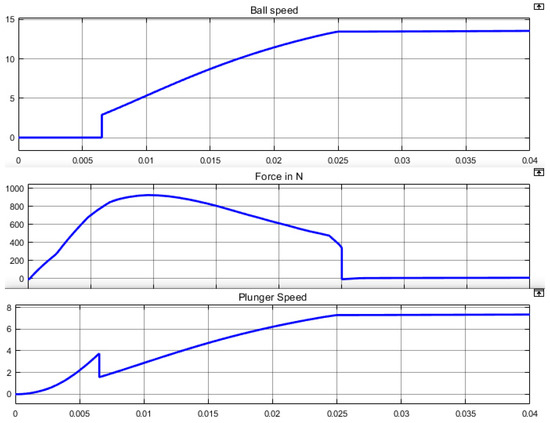
Figure 25.
Simulation of one coil EML used in an optimal way.
Results of simulation for an EML having two coils are presented in Figure 26. is triggered during 15 ms, is triggered during 14 ms with a delay of 10 ms. Optimal initial position of the plunger is mm and optimal plunger extension length is 104 mm. Ball speed reaches 16 m·s.
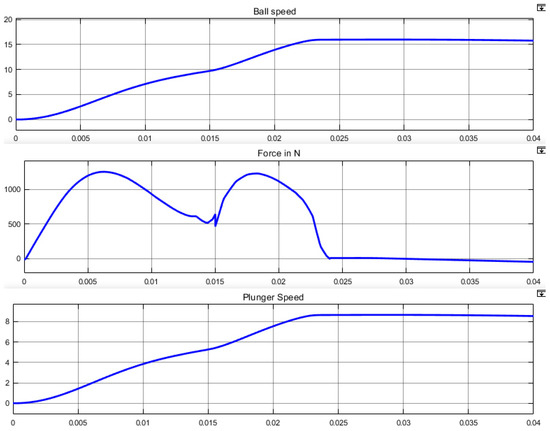
Figure 26.
Simulation of a two-coil EML used in an optimal way.
Results of simulation for an EML having three coils are presented in Figure 27. is triggered during 10 ms, is triggered during 15 ms with a delay of 7 ms, is triggered during 12 ms with a delay of 11 ms. Optimal initial position of the plunger is mm and optimal plunger extension length is 90 mm. Ball speed reaches m·s.
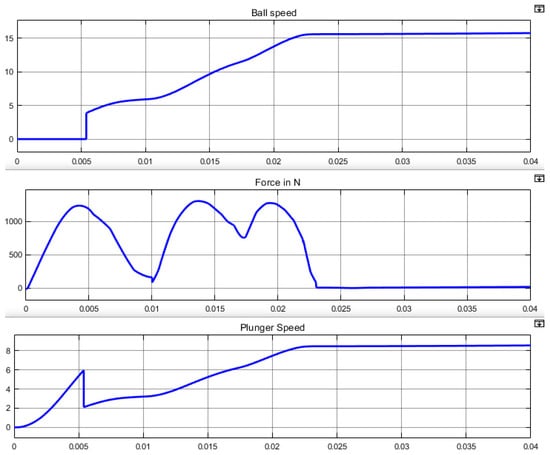
Figure 27.
Simulation of a two-coil EML used in an optimal way.
Results of simulation for an EML having 4 coils are presented in Figure 28. is triggered during 10 ms, is triggered during 10 ms with a delay of 7 ms, is triggered during 12 ms with a delay of 11 ms, is triggered during 14 ms with a delay of ms. Optimal initial position of the plunger is mm and optimal plunger extension length is 104 mm. Ball speed reaches m·s.
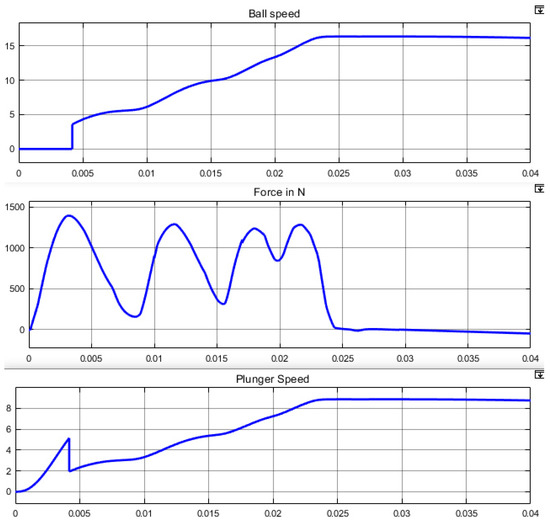
Figure 28.
Simulation of a four-coil EML used in an optimal way.
5. Results and Discussion
5.1. Discussion on Simulation Results
5.1.1. Impact of the Coil Gun Structure
As presented in the results section, increasing the number of coils allows to transfer more power to the ball as shown in Table 2:

Table 2.
Optimal ball speed depending on the number of coils in the EML.
Increasing the number of coils from one to two allows to increase the speed by , corresponding to an energy transfer optimization of . However, increasing the number of coils from two to three or four allows to increase the speed by only respectively and , corresponding to an energy transfer optimization of respectively and . This result is not intuitive and is important. Consequently, considering the impact of adding a coil to the EML in terms of mechanical and electrical integration, the two-coil EML seems to be the best configuration in our case.
5.1.2. Comparison between the Reference Case and the Chosen Configuration
Comparing the reference situation described in [11], optimization of the number of coils of the EML, the initial position and the extension length leads to increase the ball speed by , from m·s to 16 m·s. This corresponds to an energy transfer improved by compared to the reference situation, without complicating the coil gun structure too much.
Shooting range, which is defined as the distance of the first rebound in case of a kick, without considering air friction, increases from m in the reference situation described in [11] to 26 m in the optimal configuration.
5.1.3. Impact of a Variation of the Coil Triggering Instants
Having a powerful coil gun is important, but its behaviour robustness is also a key factor. This is especially true for the triggering instants which are important parameters for optimizing power transmission and have to be tuned carefully.
In the case of a two-coil EML, simulations show that the second coil optimal triggering instant is 10 ms after the first coil. Table 3 shows that a variation of this triggering instant of ms has a very limited impact on the ball speed, which is only reduced by less than , leading to a good robustness of this system.

Table 3.
Impact of a variation of the second coil triggering instant in the case of a 2 coils EML.
In the case of a four-coil EML, the fourth coil optimal triggering instant is ms after the first coil. Table 4 shows that a variation of this triggering instant of ms has an important impact on the ball speed which is reduced by or more. Consequently, the EML using four coils is far less robust than the EML using two coils in terms of sensitivity to the coil-triggering instants.

Table 4.
Impact of a variation of the fourth coil triggering instant in the case of a four-coil EML.
5.2. Experimental Results
In order to validate the simulation results, experiments have been done using a two-coil reluctance coil gun corresponding to the optimal configuration (as explained in Section 5.1). This launcher is shown in Figure 29. It is part of our new RoboCup robot presented in Figure 30.

Figure 29.
2 coils optimized reluctance coil gun.

Figure 30.
RoboCup robot for testing the optimized coil gun.
A custom four-channel coil gun driver has been designed but is not in the scope of this paper. It includes four MOSFET for capacitor commutation with a 160 A current peak under 450 V on each coil. A safety system for dissipating energy stored in the capacitors when the system is switched off or stopped has been implemented in this driver, justifying the aluminium ventilated power heat sink that can be seen on the right board of Figure 31. For triggering the coils in a very accurate time sequence (and for controlling DC motors and low level sensors), a micro-controller board has been designed and can be seen on the left side of Figure 31. In our test corresponding to the chosen optimal case, the second coil has been triggered exactly 10 ms after the first one.

Figure 31.
Four-channel reluctance coil gun driver (on the right).
Ball speed measurements have been done using a high speed camera on 20 successive tests. Average measured ball velocity is equal to m·s. This is consistent with the theoretical value (16 m·s). Error is only and dispersion is low ( m·s). These results show that the simulation model used in this paper is accurate, despite many strongly non-linear effects, and that the structure of a reluctance coil gun can be optimized very efficiently without changing the amount of copper used and the size of the actuator.
6. Conclusions
In this paper, a method for optimizing the structure of a reluctance coil gun has been proposed. Kicking real soccer balls used at the RoboCup in the Middle Size League has been chosen as a case study. After having presented the principles of coil guns, a mechatronic model coupling mechanic, electromagnetic and electric ones has been proposed and implemented. Simulation results have been explained and discussed so that this optimization method can be easily reproduced in another application.
Results show that the output speed of the non-magnetic object propelled by the EML highly depends on the structure of the coil gun, the sequence for triggering it, the initial position of the iron plunger and the size of its non-magnetic extension. Among the results of this paper, we show that
- Using a two-coil EML is energetically more efficient than the reference situation of an existing coil gun [11], without adding too much mechanical, electrical and algorithmic complexity to the EML. As shown in Table 5, it is also ten times more efficient than a human considering the ball energy to launcher volume ratio.
 Table 5. Ball launchers comparison including optimized launcher.
Table 5. Ball launchers comparison including optimized launcher. - Having a high number of coils is not necessary for optimizing the energy transfer. In our case, having two coils in the EML is an excellent trade-off between energy transfer optimization and system complexity.
- Robustness in terms of sensitivity to the coil triggering instants decreases with the number of coils.
Author Contributions
Writing—original draft preparation, V.G.; writing—review and editing, T.S., S.M., H.G. and V.H.; visualization, V.B. and H.B. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by [the Conseil Départemental du Var, France].
Acknowledgments
The authors would like to thank Pôle INPS of Toulon University and the Embedded Electronics Technology Platform of Toulon University named SMIoT (Scientific Microsystems for Internet of Things) [17] for its support in the achievement of this work, and the Conseil Départemental du Var, France, for funding this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tzeng, J.T.; Schmidt, E.M. Comparison of Electromagnetic and Conventional Launchers Based on Mauser 30-mm MK 30-2 Barrels. IEEE Trans. Plasma Sci. 2011, 39, 149–152. [Google Scholar] [CrossRef]
- McNab, I. Progress on Hypervelocity Railgun Research for Launch to Space. IEEE Trans. Magn. 2009, 45, 381–388. [Google Scholar] [CrossRef]
- Cao, B.; Guo, W.; Ge, X.; Sun, X.; Li, M.; Su, Z.; Fan, W.; Li, J. Analysis of Rail Erosion Damage during Electromagnetic Launch. IEEE Trans. Plasma Sci. 2017, 45, 1263–1268. [Google Scholar] [CrossRef]
- Wetz, D.; Stefani, F.; McNab, I. Experimental Results on a 7-m-Long Plasma-Driven Electromagnetic Launcher. IEEE Trans. Plasma Sci. 2011, 39, 180–185. [Google Scholar] [CrossRef]
- Orbach, Y.; Oren, M.; Golan, A.; Einat, M. Reluctance Launcher Coil-Gun Simulations and Experiment. IEEE Trans. Plasma Sci. 2019, 47, 1358–1363. [Google Scholar] [CrossRef]
- Meessen, K.J.; Paulides, J.J.H.; Lomonova, E.A. Analysis and design of a slotless tubular permanent magnet actuator for high acceleration applications. J. Appl. Phys. 2009, 105, 07F110. [Google Scholar] [CrossRef]
- Bencheikh, Y.; Ouazir, Y.; Ibtiouen, R. Analysis of capacitively driven electromagnetic coil guns. In Proceedings of the XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–5. [Google Scholar]
- Abdo, T.M.; Elrefai, A.L.; Adly, A.A.; Mahgoub, O.A. Performance analysis of coil gun electromagnetic launcher using a finite element coupled model. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 506–511. [Google Scholar] [CrossRef]
- Schempf, H.; Kraeuter, C.; Blackwell, M. Roboleg: A robotic soccer-ball kicking leg. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 2, pp. 1314–1318. [Google Scholar] [CrossRef]
- Vahidi, M.; Moosavian, S. Dynamics of a 9-DoF robotic leg for a football simulator. In Proceedings of the 2015 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015; pp. 314–319. [Google Scholar] [CrossRef]
- Meessen, K.J.; Paulides, J.J.H.; Lomonova, E.A. A football kicking high speed actuator for a mobile robotic application. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 1659–1664. [Google Scholar] [CrossRef]
- Gies, V.; Soriano, T. Modeling and Optimization of an Indirect Coil Gun for Launching Non-Magnetic Projectiles. Actuators 2019, 8, 39. [Google Scholar] [CrossRef]
- Williamson, S.; Horne, C.D.; Haugh, D.C. Design of pulsed coil guns. IEEE Trans. Magn. 1995, 31, 516–521. [Google Scholar] [CrossRef]
- Kang, Y. A high power-density, high efficiency front-end converter for capacitor charging applications. In Proceedings of the Applied Power Electronics Conference and Exposition (APEC 2005), Austin, TX, USA, 6–10 March 2005; Volume 2, pp. 1258–1264. [Google Scholar] [CrossRef]
- Rao, D.K.; Kuptsov, V. Effective Use of Magnetization Data in the Design of Electric Machines with Overfluxed Regions. IEEE Trans. Magn. 2015, 51, 1–9. [Google Scholar] [CrossRef]
- Lequesne, B.P. Finite-element analysis of a constant-force solenoid for fluid flow control. IEEE Trans. Ind. Appl. 1988, 24, 574–581. [Google Scholar] [CrossRef]
- SMIOT: Scientific Microsystems for the Internet of Things. 2019. Available online: http://www.smiot.fr (accessed on 2 March 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).