Bending by Concentrated Force of a Cantilever Strip Having a Through-thickness Crack Perpendicular to Its Axis

Abstract

The article focuses on the bending problem for a cantilever beam with a straight through-thickness crack, perpendicular to its axis under bending by concentrated force. Depending on the crack location in relation to the axis, crack faces may be in three states: perfect contact, particular contact, or noncontact. Using the theory of functions of complex variable and complex potentials, the considered problem was reduced to a linear conjunction one. An analytical solution of the problem was obtained. In the case of particular contact, the length of the contact area and stress intensity factors were determined. The ultimate force that causes beam destruction was determined. Numerical analyses of the problem were also performed.

1. Introduction

Beam elements of structures are widely used in engineering practices. They may contain cracks that are powerful stress concentrators, decreasing the reliability and durability of such structures.

Under external load, crack faces may be in contact. Many researchers have studied plane contact problems in crack theory of homogeneous bodies and developed methods for solving this problem. They are: Mosakovskyy V.I., Zagubizhenko P.A. [1,2], Bojko L.T., Berkovych P.E. [3], Grylitskyy N.D., Kit G.S. [4], Grylitskyy D.V., Lytsyshyn R.M. [5], Kryvcun M.G., Grylitskyy N.D. [6], Lozovyy B.L., Panasjyk V.V. [7,8], Savruk M.P. [9], Filshtynskyy L.A., Hvorost V.F. [10], Bowie O.L., Freese C.E. [11], and Guz A.N., Zozulya [12].

There are lots of various fracture criteria for cracked bodies in scientific literature. Several of them are of significant interest [13,14,15,16,17,18,19].

The problem of bending of a cantilever-cracked beam by concentrated force applied at its end, perpendicular to its axes, is investigated in the papers [7,8]. It was assumed that the crack is straight, through-thickness, perpendicular to beam axis, and its faces are particularly contacting. Using the theory of complex variable functions and complex potentials, the considered problem was reduced to a linear conjunction problem, and to a singular integral equation in unknown contact stresses. The complex potentials of the problem, the length of the contact area of crack faces, and the ultimate value of the force responsible for beginning of crack propagation were determined.

A similar problem for nonsymmetrical cracks was studied in this paper. Depending on the location of a crack, its faces may be in perfect contact, particular contact, or have no contact.

On the base of energy [15,16] and improved [17,18,19] criteria, an ultimate value causing beam fracture was derived.

Mark meaning are listed in Table 1 to improve understanding article by reader’s.

Table 1. Mark meaning.

Mark	Mark meaning
$L_3$	the distance from the left edge of the strip to the crack line
$2h$	crack width
$2\tilde{b}$	crack thickness
$А(d_1,0)$ and $B(d_2,0).$	crack tips
$2l$	crack length
$L_1$	unloaded zone $АC$ of the crack
$L$	crack faces are smooth closed in area $CB$
${\sigma }_{yy}$ and $y_{хy}$	components of stress tensor
$\nu$	the second component of displacement vector of the beam point
$\Phi \left(z\right)$, $\Omega \left(z\right)$	complex potentials
$\mu$	shear modulus
$к$	Mushelishvili’s constant
$u$	the first component of displacement vector of the beam point
${\Phi }_0\left(z\right)$, ${\Omega }_0\left(z\right),$	crack potentials
$b_1$ and $b_0$	unknown constants
$\lambda$	length of non-contacted zone of the crack
$c_j(j=\overline{0,3})$	unknown coefficients
$K_1^{\pm },$$K_2^{\pm }$	stress intensity factors
$Q^{\ast \pm }$	the ultimate value of the force causing beam fracture for contacted crack tip, where sign “+” corresponds to tip $A$ and “–“ to tip $B$.
$K_{1C},$$K_{2C}$	constants responsible for fracture strength of material
${\tilde{Q}}^{\ast \pm }$	the ultimate force causing beam fracture for non-contacted crack tip, where sign “+” corresponds to tip $A$ and “–“ to tip $B$.

2. Materials and Methods

We considered an isotropic cantilever strip of $2L_3$ length that was rigidly fixed at left end. Its width and thickness were designated $2h$ and $2\tilde{b}$, respectively.

A Cartesian coordinate system was placed in symmetry axes of the strip as shown in Figure 1. The strip was weakened by a through crack of $2l$ length, non-symmetrically placed on the $Ox$- axis about the $Oy$- axis. Parameter d denotes the distance from the left edge of the strip to the crack line ($d<L_3$). It was assumed that the crack length was essentially less than the width of the strip. The strip was loaded by a concentrated force $Q,$ applied at its end, perpendicularly to the $Oy$- axis. Crack tips were in the points $А(d_1,0)$ and $B(d_2,0)$ ($\left|d_i\right|<1$).

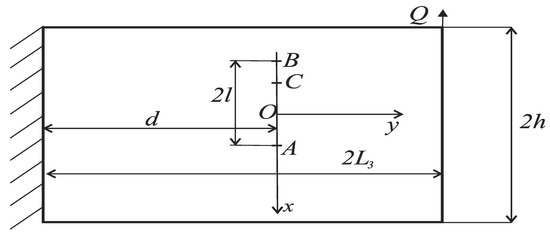
Figure 1. Scheme of loading of the cracked beam.

We considered three possible cases of stress-strain state of the cracked beam.

Case 1. Crack with particularly contacting faces.

We assume that under external load, crack faces are smooth and enclosed in area $CB$, denoted by $L.$ Point C has coordinates $C(\lambda ,0)$, where $\lambda$ is unknown parameter, responsible for length of contact zone. The unloaded zone $АC$ of the crack is denoted by $L_1.$

According to the problem statement, there are the following boundary conditions at the crack faces

$${\sigma }_{yy}^{+}={\sigma }_{yy}^{-},v^{+}-v^{-}=0,x\in L;{\sigma }_{yy}^{\pm }=0,x\in L_1;$$

(1)

$${\sigma }_{хy}^{\pm }=0,x\in L+L_1,$$

(2)

where ${\sigma }_{yy}$ and $y_{хy}$ are components of stress tensor; signs “+” and “−” stand for limit values of appropriate magnitude as $\sigma \to \pm 0$; $\nu$ is the second component of displacement vector of the beam point.

Stresses and displacements may be expressed in terms of complex potentials $\Phi \left(z\right)$, $\Omega \left(z\right)$ according to [13]

$${\sigma }_{yy}-i{\sigma }_{xy}=\Phi \left(z\right)+\Omega \left(\overline{z}\right)+\left(z-\overline{z}\right)\overline{{\Phi }^{\prime }\left(z\right)},$$

(3)

$$2\mu {\left(u+iv\right)}^{\prime }{}_{х}=\kappa \Phi \left(z\right)-\Omega \left(\overline{z}\right)-\left(z-\overline{z}\right)\overline{{\Phi }^{\prime }\left(z\right)},$$

(4)

where $\mu$ is shear modulus; $к-$ Mushelishvili’s constant; $f^{\prime }=\frac{\partial f}{\partial x};$ $u$ is the first component of displacement vector of the beam point, $z=x+iy$, $i=\sqrt{-1}$.

Next, we introduce complex potentials ${\Phi }_0\left(z\right)$ and ${\Omega }_0\left(z\right)$ [7,8] that describe the stress-strain state in the cantilever-uncracked strip, under the same load. For large values of $\left|z\right|$ they are

$${\Phi }_0\left(z\right)=-ia{z}^2+bz,{\Omega }_0\left(z\right)=5ia{z}^2+3bz-i4a{h}^2,$$

(5)

where

$$a=Q/8I, І=\frac{4}{3}\tilde{b}{h}^3, b=-2a(2L_3-d).$$

(6)

We determine the stress-strain state of cantilever-cracked strip by satisfying boundary conditions (1), (2) at the crack and by demanding that in the considerable distance from the crack potentials ${\Phi }_0\left(z\right)$ and ${\Omega }_0\left(z\right)$ have the form

$$\Phi \left(z\right)={\Phi }_0\left(z\right)+O\left(1/z^2\right), \Omega \left(z\right)={\Omega }_0\left(z\right)+O\left(1/z^2\right).$$

(7)

Boundary conditions (1) and (2) may be rewritten as

$${({\sigma }_{yy}-і{\sigma }_{хy})}^{+}-{({\sigma }_{yy}-і{\sigma }_{хy})}^{-}=0,x\in L+L_1.$$

(8)

Substitution (3) into (8) leads to the following linear conjunction problem

$${\left(\Phi (x)-\Omega (x)\right)}^{+}-{\left(\Phi (x)-\Omega (x)\right)}^{-}=0, x\in L+L_1$$

(9)

with the solution [13]

$$\Phi \left(z\right)-\Omega \left(z\right)=D_1{z}^2+D_{2}z+D_3=D\left(z\right),$$

(10)

where

$$D_1=-6ai,D_2=-2b,D_3=4ai{h}^2.$$

From (10) we express the function $\Omega \left(z\right)$ in terms of $\Phi \left(z\right)$:

$$\Omega \left(z\right)=\Phi \left(z\right)-D\left(z\right).$$

(11)

Next, we introduce a new function

$$F\left(z\right)=\Phi \left(z\right)-\frac{1}{2}D\left(z\right)$$

(12)

and rewrite the boundary conditions (1) as

$$v^{+}-v^{-}=0,x\in L,{\sigma }_{yy}^{+}+{\sigma }_{yy}^{-}=0 x\in L_1.$$

(13)

Using (3), (4), (11), and (12), the boundary conditions (13) are reduced to the linear conjunction problem

$$\begin{array}{l}{\left(F\left(х\right)+\overline{F}\left(х\right)\right)}^{+}-{\left(F\left(х\right)+\overline{F}\left(х\right)\right)}^{-}=0,x\in L,\\ {\left(F\left(х\right)+\overline{F}\left(х\right)\right)}^{+}+{\left(F\left(х\right)+\overline{F}\left(х\right)\right)}^{-}=0,x\in L_1.\end{array}$$

(14)

Solving this problem we obtain the connection

$$F\left(z\right)+\overline{F}\left(z\right)=(b_{1}z+b_0)\tilde{X}(z),$$

(15)

where $b_1$ and $b_0$ are unknown constants and

$$\tilde{X}(z)=\sqrt{\frac{z-\lambda }{z-d_1}}.$$

(16)

For large $\left|z\right|$, this function allows series expansion

$$\tilde{X}(z)=1+\frac{d_1-\lambda }{2z}+\frac{3d_1^2-2\lambda d_1-{\lambda }^2}{8z^2}+\mathrm{\dots }$$

(17)

In order to determine coefficients $b_1$ and $b_0$ we present the function $F\left(z\right)=\Phi \left(z\right)-\frac{1}{2}D\left(z\right)$ in form of power series, using formulas (5), (7), and (12). Then, taking into account (17), we equate coefficients at the same degrees of $z$ in (15). In such a way, we have

$$b_1=4b,b_0=-2b(d_1-\lambda ),$$

(18)

$$\lambda =-\frac{1}{3}{d}_1.$$

(19)

Parameter $\lambda$ is length of the non-contacted zone of the crack. Since point $B$ lies at a greater distance from origin O than $\lambda$ (see Figure 1), it is follows from (19) that the crack faces are in particular contact if $d_2<-\frac{1}{3}{d}_1.$

In such a way, we have one equation (15) in two functions $F\left(z\right)+\overline{F}\left(z\right)=(b_{1}z+b_0)\tilde{X}(z).$

In order to obtain missing the equation, we consider the following boundary condition

$${\sigma }_y^{+}+{\sigma }_y^{-}=0,x\in L+L_1.$$

Taking into account the relations (3), (11), and (12), we obtain the linear conjunction problem

$${\left(F\left(х\right)-\overline{F}\left(х\right)\right)}^{+}+{\left(F\left(х\right)-\overline{F}\left(х\right)\right)}^{-}=0,x\in L+L_1.$$

Its solution is

$$F\left(z\right)-\overline{F}\left(z\right)=\frac{c_3{z}^3+c_2{z}^2+c_{1}z+c_0}{X(z)},$$

(20)

where $c_j(j=\overline{0,3})$ are unknown coefficients and

$$X(z)=\sqrt{(z-d_1)(z-d_2)}.$$

(21)

Then, the function $X^{-1}(z)$ for large values of $\left|z\right|$ has a series expansion

$$\frac{1}{X(z)}=\frac{1}{z}+\frac{d_1+d_2}{2z^2}+\frac{3(d_1^2+d_2^2)+2d_1{d}_2}{8z^3}+\frac{5(d_1^3+d_2^3)+3d_1{d}_2(d_1+d_2)}{16z^4}+\mathrm{\dots }$$

(22)

Taking into account (5), (7), (12), and (22), by expanding both sides (20) into a series at large $\left|z\right|$ and equating the coefficients at the same degrees of $z$ after some transformations, we obtain formulas for the unknown coefficients $c_j(j=\overline{0,3})$

$$c_3 = 4ia,c_2 = - 2ia(d_1+d_2), c_1 = -ia\left[4h^2 +\frac{1}{2}{(d_1-d_2)}^2\right], c_0 =ia(d_1+d_2) \left[2h^2 -\frac{1}{4}{(d_1 -d_2)}^2\right].$$

(23)

Adding (20) and (15), we find the function

$$F\left(z\right)=\frac{1}{2}\left[(b_{1}z+b_0)\tilde{X}(z)+\frac{c_3{z}^3+c_2{z}^2+c_{1}z+c_0}{X(z)}\right].$$

(24)

Function $\Phi \left(z\right)$ is found from (12) using (16), (21) and (24)

$$\Phi \left(z\right)=\frac{1}{2}\left[D(z)+\sqrt{\frac{z-\lambda }{z-d_1}}(b_{1}z+b_0)+\frac{c_3{z}^3+c_2{z}^2+c_{1}z+c_0}{\sqrt{(z-d_1)(z-d_2)}}\right].$$

(25)

Stress intensity factors are determined on the base of formula [14]

$$\begin{array}{l}{K}_1^{+}-i{K}_2^{+}=2\underset{x\to d_1+0}{\lim }\left[\sqrt{2(x-d_1)}\Phi (x)\right],\\ K_1^{-}-i{K}_2^{-}=2\underset{x\to d_2-0}{\lim }\left[\sqrt{2(d_2-x)}\Phi (x)\right].\end{array}$$

(26)

Replacing the function $\Phi \left(x\right)$ by expression (25) in (26) we obtain

$$\begin{array}{l}{K}_1^{+}=\sqrt{2(d_1-\lambda )}(b_1{d}_1+b_0),K_2^{+}=-\frac{\sqrt{2}}{\sqrt{d_1-d_2}}{\displaystyle \sum _{j=0}^3{\tilde{c}}_j}{d}_1^j,\\ K_1^{-}=0,K_2^{-}=\frac{\sqrt{2}}{\sqrt{d_1-d_2}}{\displaystyle \sum _{j=0}{\tilde{c}}_j{d}_1^j},c_j=i{\tilde{c}}_j.\end{array}$$

(27)

According to (18), (23), Formula (27) can be expressed as

$$K_j^{\pm }=q{\tilde{K}}_j^{\pm }.$$

(28)

In (28) we use the following notifications

$$\begin{gathered} q=\frac{Q}{I}{h}^{5/2},{\tilde{K}}_1^{+}={\left(\frac{2}{3}{\tilde{d}}_1\right)}^{3/2}\left(2{\tilde{L}}_3-\tilde{d}\right),{\tilde{d}}_1=d_1/h,{\tilde{L}}_3=L_3/h,\tilde{d}=d/h, \\ {\tilde{K}}_1^{-}=0,{\tilde{K}}_2^{+}=\frac{\sqrt{\tilde{l}}}{4}\left[{({\tilde{d}}_1-\tilde{l})}^2+{\tilde{d}}_1^2-2\right],\tilde{l}=l/h, \\ {\tilde{K}}_2^{-}=\frac{\sqrt{\tilde{l}}}{4}\left[2{({\tilde{d}}_1-\tilde{l})}^2-2{\tilde{d}}_1\tilde{l}+3{\tilde{l}}^2-2\right], \end{gathered}$$

(29)

where sign “+” corresponds to tip $A$ and “–“ to tip $B$. In order to determine the ultimate value of force $Q^{\ast }$ causing the crack propagation, we use the energy fracture criterion [15,16,17]

$${\gamma }^{*}=\frac{\pi }{8{\tilde{b}}^{2}E}\left(K_1^2+K_2^2\right),$$

(30)

where $E$ is Young’s modulus, ${\gamma }^{\ast }-$ the effective density of surface energy of the crack for beam material.

Using (28) dependence (30) can be rewritten as

$$Q^{\ast \pm }=\frac{Q}{{\tilde{b}}^2\sqrt{E{\gamma }^{*}{h}^3}}=\frac{8\sqrt{2}}{3\sqrt{\pi }}\frac{1}{\sqrt{{\left({\tilde{K}}_1^{\pm }\right)}^2+{\left({\tilde{K}}_2^{\pm }\right)}^2}}.$$

(31)

Case 2. Crack with non-contacting faces.

Now we consider the case when crack faces are not contacting. This means that the crack is completely located in the tensile zone and its faces are unloaded. In this case, $d_2>-\frac{1}{3}{d}_1$ must be fulfilled. The part of the axis containing the crack is denoted by $L_1.$ On $L_1$, the following boundary conditions take place

$${\sigma }_{yy}^{\pm }=0,{\sigma }_{хy}^{\pm }=0,x\in L_1,$$

(32)

and they also may be written in form (9). Repeating the appropriate transformations we obtain dependence (11). The boundary condition (32) can be rewritten as

$${\left({\sigma }_{yy}-i{\sigma }_{xy}\right)}^{+}+{\left({\sigma }_{yy}-i{\sigma }_{xy}\right)}^{-}=0,x\in L_1.$$

Taking into account (3) and (11), we come to the linear conjunction problem

$${\left[\Phi (x)-\frac{1}{2}D(x)\right]}^{+}+{\left[\Phi (x)-\frac{1}{2}D(x)\right]}^{-}=0,x\in L_1.$$

Solving this problem and taking into account the behavior of function $\Phi (z)$ for large values of $\left|z\right|$ (5) we have

$$\Phi (z)=\frac{1}{2}D(z)+{\displaystyle \sum _{j=0}^3{\alpha }_j{z}^j}/X(z),$$

(33)

where

$$\begin{array}{l}{\alpha }_3=2ia,{\alpha }_2=2b-ia(d_1-d_2),{\alpha }_1=-ia\left[2h^2+\frac{{(d_1-d_2)}^2}{4}\right]-b(d_1+d_2),\\ {\alpha }_0=ia(d_1+d_2)\left[h^2-\frac{1}{8}{(d_1-d_2)}^2\right]-b\frac{{(d_1-d_2)}^2}{4}.\end{array}$$

(34)

In this case, we find the stress intensity factor using Formulas (26) and (33)

$$K_1^{\pm }=q{\tilde{K}}_j^{\pm },$$

(35)

where

$${\tilde{K}}_1^{+}=\frac{\sqrt{\tilde{l}}}{2}\left(2{\tilde{L}}_3-\tilde{d}\right)\left(2{\tilde{d}}_1-\tilde{l}\right),{\tilde{K}}_1^{-}=\frac{\sqrt{\tilde{l}}}{2}\left(2{\tilde{L}}_3-\tilde{d}\right)\left(2{\tilde{d}}_1-3\tilde{l}\right).$$

The coefficients $q$ and ${\tilde{K}}_2^{\pm }$ are expressed by Formulas (29) at $\tilde{l}<\frac{2}{3}{\tilde{d}}_1.$

The ultimate value of force we obtain from formula

$$Q^{\ast \pm }=\frac{8\sqrt{2}}{3\sqrt{\pi }}\frac{1}{\sqrt{{\left({\tilde{K}}_1^{\pm }\right)}^2+{\left({\tilde{K}}_2^{\pm }\right)}^2}}.$$

(36)

Case 3. Crack with perfectly contacting faces.

Now we consider the case when crack faces were in perfect contact $(d_1<0).$ The part of the $Ox-$ axis where the contact take place is denoted by $L$. In this case, we have the following boundary conditions

$${\sigma }_{yy}^{+}={\sigma }_{yy}^{-},{\sigma }_{xy}^{\pm }=0,v^{+}-v^{-}=0,x\in L.$$

(37)

Similarly to the previous case, we write boundary conditions at $L$ in form (6) and come to the linear conjunction problem (9). Solution of this problem has the form (11). Then, from the boundary condition

$${(v^{+}-v^{-}{)}^{\prime }}_x=0,x\in L,$$

taking into account (4) and (11), we obtain another linear conjunction problem

$${\left[F\left(х\right)+\overline{F}\left(х\right)\right]}^{+}-{\left[F\left(х\right)+\overline{F}\left(х\right)\right]}^{-}=0, x\in L.$$

By solving this problem, we get

$$F\left(z\right)+\overline{F}\left(z\right)=4bz.$$

(38)

Next, using Formulas (3), (11), and (12), and satisfying the boundary condition

$${\sigma }_{xy}^{+}+{\sigma }_{xy}^{-}=0, x\in L,$$

we come to the linear conjunction problem. Its solution is given by (20).

Adding (38) and (20), we find the function

$$F(z)=2bz+\frac{1}{2X(z)}{\displaystyle \sum _{j=0}^3{c}_j{z}^j}.$$

(39)

Substituting (39) into (12) gives

$$\Phi (z)=2bz+\frac{1}{2}D(z)+\frac{1}{2X(z)}{\displaystyle \sum _{j=0}^3{c}_j{z}^j}.$$

(40)

Considering (40) and (26), we find the stress intensity factors

$$K_1^{\pm }=0,K_2^{\pm }=q{\tilde{K}}_2^{\pm },$$

where $q,$ ${\tilde{K}}_2^{\pm }$ are determined according to the Formula (29).

The ultimate value of the force causing beam failure is obtained from the formula

$$Q^{\ast \pm }=\frac{8\sqrt{2}}{3\sqrt{\pi }}\frac{1}{\left|{\tilde{K}}_2^{\pm }\right|}.$$

(41)

It is known from scientific literature that the energy criteria of the fracture of cracked bodies do not always give satisfactory results. Therefore, we use an improved energy fracture criterion presented in [20].

$${\left(\frac{K_1}{K_{1C}}\right)}^2+{\left(\frac{K_2}{K_{2C}}\right)}^2=1$$

(42)

where $K_{1C}$ and $K_{2C}$ are constants responsible for the fracture strength of the material and

$$\frac{3}{4}<\left(\frac{K_{2C}}{K_{1C}}=\alpha \right)<\sqrt{\frac{2}{3}}$$

(43)

Using (43) and (44), the ultimate force causing beam fracture for a non-contacted crack tip is determined as

$${\tilde{Q}}^{\ast \pm }=\frac{2\sqrt{2}Q}{h^{3/2}\tilde{b}\sqrt{\pi }{K}_{1C}}=\frac{8\sqrt{2}}{3\sqrt{\pi }}\frac{1}{\sqrt{{\left({\tilde{K}}_1^{\pm }\right)}^2+{\left({\tilde{K}}_2^{\pm }/\alpha \right)}^2}}.$$

(44)

and for contacted crack tip as

$${\tilde{Q}}^{\ast \pm }=\frac{2\sqrt{2}Q}{h^{3/2}\tilde{b}\sqrt{\pi }{K}_{2C}}=\frac{8\sqrt{2}}{3\sqrt{\pi }}\frac{1}{\left|{\tilde{K}}_2^{\pm }\right|}.$$

(45)

3. Results and Discussion

Graphical dependences of ultimate force $Q^{\ast \pm }$ on relative crack length $\tilde{l}=l/h$ at various problem parameters are presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, and Figure 7. Calculations were performed at ${\tilde{L}}_3=L_3/h=2,$ $\tilde{d}=d/h=1$. In Figure 2 and Figure 3 dependences are presented for the case of a crack with non-contacting faces.

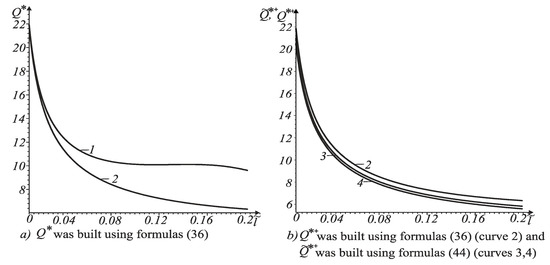
Figure 2. Dependence of ultimate force $Q^{\ast }$ on relative length $\tilde{l}$ for the crack with non-contacting faces at ${\tilde{d}}_1=0,3$.

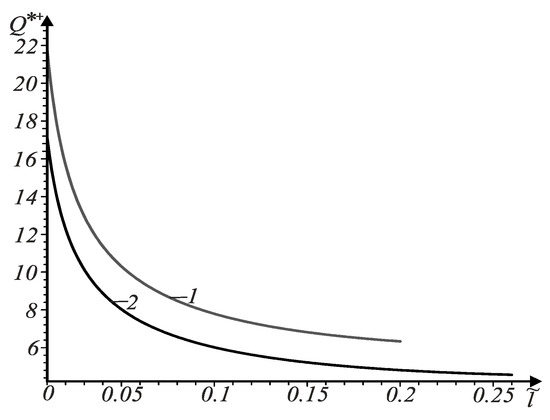
Figure 3. Dependences of the ultimate force $Q^{\ast +}$ on the relative length $\tilde{l}$ for a crack with non-contacting faces at the tip $B$ at various values ${\tilde{d}}_1$.

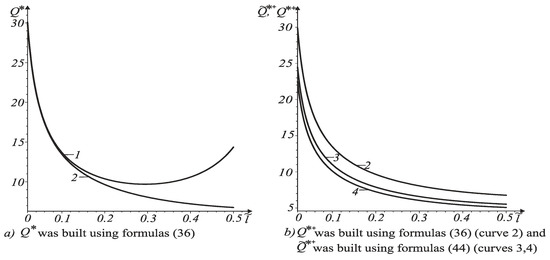
Figure 4. Dependence of ultimate force $Q^{\ast }$ on relative length $\tilde{l}$ of crack with particularly contacting faces at ${\tilde{d}}_1=0.03$.

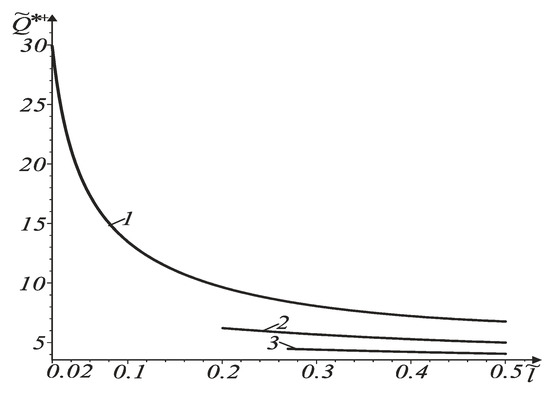
Figure 5. Dependences of ultimate force ${\tilde{Q}}^{\ast +}$ on relative length $\tilde{l}$ for crack with particularly contacting faces.

Figure 6. Dependences of the ultimate force ${\tilde{Q}}^{\ast +}$ on relative length $\tilde{l}$ for cracks with perfectly contacting faces at ${\tilde{d}}_1=-0,05$.

Figure 7. Dependences of ultimate force ${\tilde{Q}}^{\ast }$ on relative length for cracks with perfectly contacting faces at various values of ${\tilde{d}}_1$.

In Figure 2, curve 1 corresponds to the crack tip $B$, and curve 2 to the opposite one. These curves were built using Formula (36). Curves 3 and 4 were built using Formula (44). Curve 3 corresponds to $\alpha =\sqrt{\frac{2}{3}}$ and curve 4 – to $\alpha =\frac{3}{4}$. From analysis of these curves it follows that failure of the beam begins from crack tip $A$ where the ultimate value $Q^{\ast }$ is lesser.

In Figure 3, curve 1 corresponds to coordinate ${\tilde{d}}_1=d/h=0,3,$ while curve 2 corresponds to coordinate ${\tilde{d}}_1=0,4.$ It is seen that for a fixed crack length, the ultimate force $Q^{\ast }$ decreases with increasing distance between the crack center and the beam axis.

Dependences in Figure 4 and Figure 5 stand for cracks with particularly contacting faces at $\tilde{l}>(2{\tilde{d}}_1)/3.$ In Figure 4, curve 1 corresponds to contacting tip $B$ and curve 2 – to non-contacting crack tip $A$. These curves were built using Formula (36). Curves 3 and 4 were built using Formula (44). Curve 3 corresponds to $\alpha =\sqrt{\frac{2}{3}}$ and curve 4 – to $\alpha =\frac{3}{4}$. It is clear that beam failure begins from a non-contacting tip.

As shown in Figure 2b and Figure 4b, the energy criterion for the fracture of cracked bodies gives an overestimated value of the force, in comparison with improved fracture criterion (42). In addition, with increasing crack length, the ultimate force decreases.

The curves in Figure 5 were constructed for non-contacting crack tip, $A.$ Curve 1 corresponds to ${\tilde{d}}_1=0,03,$ curve 2 – to ${\tilde{d}}_1=0,3,$ curve 3 – to ${\tilde{d}}_1=0,4.$ We can conclude that with distancing of the tip $A$ from the beam axis, the ultimate force increases.

The dependences of the ultimate force $Q^{\ast }$ on relative length $\tilde{l}$ of cracks with perfectly contacting faces at various values of $A$ are presented in Figure 6 and Figure 7.

In Figure 6, curve 1 corresponds to crack tip $A$ that is closer to the beam axis, while curve 2 corresponds to remote tip $B$. It is clear that beam failure begins simultaneously at both tips.

These curves are built for constant crack length. Curve 1 corresponds to ${\tilde{d}}_1=-0,05$, while curve 2 corresponds to ${\tilde{d}}_1=-0,1$. It follows that with distancing of the crack tip $A$ from the beam axis, the ultimate force decreases for a fixed relative length of the crack.

4. Conclusions

(1) Without regard to the location of a crack with contacting faces in the beam, expressions of stress intensity factor $K_2^{\pm }$ are the same; and of $K_1^{\pm }-$ are different in all considered cases.

(2) For cracks with non-contacting or particularly contacting faces, beam failure begins distanced from the beam axis crack tip located in the tensile zone. However, in the case of perfect crack closure, this process begins closer to the tip.

(3) With increasing crack length, the ultimate force of failure of the beam decreases.

(4) For cracks with non-contacting faces, increasing the distance between the center and beam axis leads to the ultimate force decreasing, but for cracks with perfectly contacting faces, the ultimate force increases.

(5) For cracks with particularly contacting faces, the ultimate force decreases with the distance of the non-contacting tip from the beam axis.

(6) The action of concentrated force on a cantilever beam weakened by cracks with perfectly contacting faces leads to different stress-strain states, in contrast to the pure bending of the same beam with the same crack.

(7) With increasing crack length, the ultimate force always decreases.

(8) In calculating the ultimate force for cantilever beams, it is desirable to use the improved fracture criterion, without regard to location of crack and interaction between its faces.