Abstract
In general, the demand for delivery cannot be fulfilled efficiently due to the excessive traffic in dense urban areas. Therefore, many innovative concepts for intelligent transportation of freight have recently been developed. One of these concepts relies on drone-based parcel delivery using rooftops of city buildings. To apply drone logistics system in cities, the operation design should be adequately prepared. In this regard, a mixed integer programming model for drone operation planning and a heuristic based on block stacking are newly proposed to provide solutions. Additionally, numerical experiments with three different problem sizes are conducted to check the feasibility of the proposed model and to assess the performance of the proposed heuristic. The experimental results show that the proposed model seems to be viable and that the developed heuristic provides very good operation plans in terms of the optimality gap and the computation time.
1. Introduction
Cities all over the world are leveraging state-of-the-art digital technologies to build open and intelligent control systems for their smart city initiatives using real-time information for public traffic, emergency management, and public security. Empowered by new tools and recently developed technologies, cities are now far more designable than ever before. Among many new technologies, drones and small unmanned aerial vehicles (UAVs) can play vital roles in the smart city environment from the viewpoint of parcel delivery. Drones can help to deliver small parcels to destinations without any traffic congestion, which would otherwise delay delivery and affect the customer service level. Logistical drones (i.e., drones designed for parcel delivery services) are typically small battery-powered rotary-blade copters with a payload capacity of approximately 2 kg. Amazon, DHL, UPS, and Google have already announced various plans to use drones to deliver parcels from their distribution centers (warehouses) directly to end-customers in urban areas [1,2,3,4]. Domino’s Pizza delivered its pizza to actual customers using drones in the town of Whangaparaoa in New Zealand [5]. Other successful applications include hybrid truck-drone delivery by UPS in Florida, USA [6] and drone-based package delivery to islands by the Chinese e-commerce company Alibaba [7].
Drone delivery could offer several advantages over traditional parcel delivery, such as shorter delivery times, lower maintenance costs, and environmental friendliness [8,9]. Industrial and commercial applications of drones have strongly increased in the last few years, which we will review in Section 2. Especially with the help of the recent growth of e-commerce, the importance of the rapid delivery of ordered products (i.e., last-mile delivery) to consumers has increased. Increasing delivery speed has become a major challenge in urban areas. Thus, as a new element of urban logistics, we need to determine the feasibility of drone-based delivery. In addition, proper places for unloading the parcels should be prepared to implement drone-based parcel delivery, and the rooftops of buildings can be a suitable candidate.
In this research, we first propose a mixed-integer linear programming (MILP) model for generating a schedule for drone-based parcel delivery using the rooftops of buildings in cities. Even if there are several regulatory and technological barriers to overcome before the widespread adoption of drones for urban logistics, it appears that drone-based delivery will be viable in the near future. Drone-based delivery could overcome any accessibility restrictions associated with residential/commercial locations in dense urban areas. Cities are already packed with buildings and people, and any increase in the number of delivery vehicles in urban areas results in more traffic congestion, air and noise pollution, and traffic accidents [10]. However, drones are powered by electric batteries, which means that they are more eco-friendly, and they move efficiently and quickly because they are not constrained by road conditions and traffic congestion.
Next is the validation of the proposed model by conducting numerical experiments with random data settings that mimic plausible situations in the cities. In addition, we develop a heuristic that can generate solutions (i.e., schedules) very quickly regardless of problem size. Although any commercial optimization software can generate solutions using a sophisticated algorithm for small- and medium-sized MILP problems, it is very difficult to provide solutions for large problems that have many decision variables and constraints in a reasonable amount of time [11]. This issue will be discussed again when we illustrate the experimental results in Section 4.
The remainder of this paper is organized as follows. Section 2 introduces the related literature. The mathematical model for our problem is proposed in Section 3. Section 4 provides a heuristic-based solution to cope with large delivery networks that can frequently occur in cities. Finally, concluding remarks on how our research can be extended are discussed in Section 5.
2. Related Works
2.1. Urban Logistics
There are many definitions of urban logistics, but common to each of them is finding efficient and effective ways to transport goods in urban areas while taking into account the negative effects on congestion, safety, and environment. As mentioned above, the trends of growing e-commerce and urbanization have led to an increasing number of transport activities in cities. To make our approach more relevant for practical urban applications, concentration is shifted on the optimization and operational perspective of last-mile delivery. Within the supply chain of goods, the last mile represents the final and most expensive section of the transport chain [12]. Today, trucks and light commercial vehicles perform the majority of urban logistic activities. However, different strategies and concepts are likely to be needed to improve the efficiency and effectiveness of last-mile delivery in general. It is believed that the problem of last-mile delivery can be addressed in innovative ways thanks to the development of information and communication technologies (ICTs) and environmentally-friendly vehicles. Therefore, many studies with several approaches for urban logistics (e.g., parcel lockers, crowdsourcing, food delivery, and electric vehicles) have been published. Lemke et al. [13] focused on the analysis of the usability and efficiency of parcel locker logistics in a case study of a Polish company. They showed that the most important factor for efficiency in this kind of solution is the location of the machines. Then, Deutsch and Golany [14] considered designing a parcel locker network as a solution to the last-mile problem in logistics. They formulated a 0–1 integer linear program to solve the problem and applied it to an industrial-sized network. In their model, the optimal number of locations and the optimal size of the parcel lockers were addressed. Devari et al. [15] investigated peoples’ motivation to participate in crowdsourced delivery. It was found that using friends in a social network to assist in last-mile delivery greatly reduced delivery costs and total emissions while ensuring fast and reliable delivery. Kafle et al. [16] considered urban parcel deliveries where trucks serve a network of transshipment points and crowdshippers perform the last-mile deliveries from those points to the customers. Here, crowdshippers are neither restricted by existing trips nor by an upper bound on detouring. Instead, they place bids on delivery jobs. The authors developed a tailored tabu search-based algorithm to solve the system design problem. Tarantilis and Kiranoudis [17] addressed an open multidepot vehicle routing problem (VRP) for distributing fresh meat from depots to customers located in an area of the city of Athens. To solve the problem, a new stochastic meta-heuristic search algorithm termed the list-based threshold accepting algorithm was proposed. Song and Ko [18] also solved the food delivery problem in metropolitan cities. Generally, the problems of last-mile route planning for cold-chain distribution can be modeled as a VRP with time windows, which considers the costs involved in cold-chain logistics and the characteristics of temperature-sensitive products. The authors developed a nonlinear mathematical model and a heuristic algorithm to generate efficient vehicle routings with the objective of maximizing the total level of customer satisfaction, which is dependent on the freshness of delivered food products. In addition, there have been some studies that considered adopting electric vehicles to urban logistics and assessed the environmental effects. Jovanovic et al. [19] proposed green vehicle distribution in a public transportation network. The problem was defined as one of nonlinear optimization requiring neuro-fuzzy logic. They tested their solution on a part of the public transport system in central Belgrade, Serbia. Desaulniers et al. [20] presented effective branch-price-and-cut algorithms for four variants of the electric VRP with time windows (EVRPTW), which were defined according to the maximum number of recharges per route (single versus multiple) and the type of recharge (partial versus full). Therefore, the vehicles could be employed to meet the emission targets of delivery fleets or to serve restricted inner-city areas with noise and emission limits. More recently, Lee et al. [21] focused on developing a truck-bike mixture model to reduce operating costs for an existing truck-only service by replacing some of the trucks with bicycles and exploring the resulting effects in terms of reducing overall carbon emissions. The results showed that an almost 10% reduction in carbon emissions could be achieved. However, reducing the distance traveled by trucks and increasing the distance traveled by bikes resulted in a small decrease in fuel costs but a much greater increase in labor costs.
Although urban logistics has been investigated in academia as described above, the subject is still evolving because of the continuous changes in urban environments and citizens’ lifestyles. In particular, the increase in mobile shopping and improvements in technological developments might lead to another delivery mode, such as drone-based parcel delivery using the rooftops of buildings in urban areas.
2.2. Drone-Based Parcel Delivery
In recent years, drones have shown great potential for parcel delivery. Drone delivery is thought to be faster, less expensive, and more eco-friendly than traditional delivery modes such as trucks. Commercial drones require small batteries. According to the existing prototypes, logistical drones (i.e., for parcel delivery services) tend to be small battery-powered rotary-blade copters with a payload capacity of 2 kg [22]. In academia, many studies related to drone-based delivery have been conducted. Murray and Chu [23] studied the flying sidekick traveling salesman problem for UAV-based cargo delivery. They designed heuristic algorithms for two UAV delivery VRP problems. Ferrandez et al. [24] first found optimal launch locations by clustering and then determined vehicle routes by using genetic algorithms. In their model, all demands are known in advance, and the drone is launched from the vehicle, which follows a traveling salesman problem (TSP) route. Each drone can carry at most one package and therefore must traverse large distances of ingress and egress from the vehicle to the delivery location and back to the vehicle. The solution approach used K-means clustering to find the vehicle stops and a genetic algorithm for finding the vehicle route. Dorling et al. [25] studied the optimal routing of delivery drones. They approached the problem of UAV trajectory optimization for the drone delivery of material goods by minimizing the total energy cost under a delivery time limit constraint, as well as by minimizing the overall delivery time under an energy budget constraint. Campbell et al. [26] examined drone deliveries using small payload-capacity drones (e.g., 5 lbs.) from fixed depots in conjunction with hybrid vehicle-drone routes and vehicle-only delivery. Agatz et al. [27] investigated a flying sidekick TSP. An integer programming formulation was proposed, and several heuristics based on local search and dynamic programming were developed. These heuristics begin by forming a delivery and then partitioning the route into locations delivered by truck and locations delivered by drone. Ha et al. [28] proposed a TSP with drones in which the objective is to minimize the total transportation cost, comprising vehicle and drone costs. Jeong et al. [29] proposed a mathematical model for the operation of a truck-drone hybrid delivery system using the truck as a station for drones and considered the effect of both parcel weight on drone energy and restricted flying areas. More recently, Torabbeigi et al. [30] designed a drone-based parcel delivery system considering the impact of payload-induced drone battery consumption rates (BCRs). First, they showed the linear relationship between the BCR and the payload amount. Based on a linear regression model, they proposed strategic and operational planning for a given region. The results showed that 3 out of 5 flight paths were not feasible if the BCR was not considered.
Although relevant topics on urban logistics and drone-based parcel delivery have been surveyed or studied in recent years, to the best of our knowledge, there is a lack of studies regarding drone operation planning using the rooftops of buildings within cities. Most of the studies have focused on truck-drone hybrid delivery systems, which seem to be much more difficult than rooftop-based drone delivery systems in terms of operability and adaptability. A truck-drone hybrid delivery system might require both an expert who can drive and operate drones together and appropriate spaces for truck parking and drone operation in the center of cities that are full of buildings.
The unique contributions of this paper are as follows.
- The optimal operation planning of a drone-based parcel delivery using the rooftops of city buildings is suggested.
- A heuristic to quickly and effectively generate solutions (i.e., delivery schedules) is proposed, even for large problems that can commonly occur in dense urban areas.
- Our proposed optimization model and heuristic are validated by conducting experiments with realistic settings.
3. Model Development
3.1. Parcel Delivery Issues in Cities
As we previously mentioned, freight shipment activities within urban areas are critical because emissions from parcel-delivery trucks comprise a large share of toxic air pollutants and greenhouse gases in most metropolitan areas worldwide. In addition to the environmental impact, freight shipment activities also lead to traffic congestion and traffic accidents within cities. It seems that one of the most prominent factors for the increase in freight shipment activities is the growth of online shopping. In a recent study, eMarketer estimated that worldwide retail e-commerce sales will increase from $2.3 trillion in 2017 to $4.5 trillion by the end of 2021, representing approximately 16.1% of total retail sales [31].
Before the proliferation of online shopping, people would visit local stores to purchase products that they needed in their daily lives. In addition, they tended to visit large warehouse stores usually located far from their home to purchase their daily necessities on weekends. However, following the development of ICTs, people started to purchase their daily necessities not only from local shopping stores but also from online shopping stores through the internet. In this environment, customers can obtain their items within several hours during the working day, providing customers with a notable sense of convenience [18]. However, the explosive growth of online shopping has placed unprecedented pressure on the logistics industry, especially for last-mile parcel delivery [32].
Logistics and distribution channels are attempting to overcome such issues by optimizing their logistics and transport activities with the help of advanced technologies and information systems in urban areas. Better forecasting and planning can be conducted by adopting machine learning and big data analytics. Additionally, from the viewpoint of transport modes, drones are widely considered as support for conventional delivery modes. As the importance of last-mile delivery increases and the online shopping market grows, parcel delivery issues within cities will become one of the top priorities for improving the convenience and quality of city life. In line with this trend, drone-based parcel delivery using the rooftops of city buildings could be considered a good alternative to resolve such issues.
3.2. Assumptions and Problem Description
Rooftop-based drone operations have the following potential advantages over other drone operations in terms of operability. It would be much easier for drones to find, follow, and land on the rooftops of buildings than to perform those actions with moving destinations such as delivery vans. In other words, the rooftops of buildings, particularly flat rooftops, can provide safe landing zones for drones. Real-time identification and selection of safe landing zones on rooftops based on light detection and ranging and camera sensor feedback have already been developed. Additionally, some trials to check the accuracy of rooftop-based drone operation have been conducted using a downward-facing camera to implement vision-guided rooftop landing [33].
In line with the abovementioned progress in the related technologies, we develop a MILP-based mathematical model for drone scheduling for parcel delivery using rooftops. To formulate the model, the following general assumptions are needed.
- There are several buildings, each of which has a rooftop with sufficient space.
- One of the rooftops of any building or the rooftop of a delivery center (e.g., post office building) is designated a drone operation center.
- Drones are operated on a hub-and-spoke network, and each drone can carry at most one package due to their fixed payloads; thus, they can move between the drone operation center to one of the delivery locations only [24].
- Multiple drones are used, and the number of drones for parcel delivery is given.
- Drones are not used to replace conventional delivery modes but to supplement them.
- The demand is represented as the number of parcels, which is known and given for each building.
- The delivery location for each building is set to the center of the rooftop, and the delivery distance can be calculated by checking the straight-line distance between each destination and the drone operation center.
In addition to the above assumptions, because the weight of the loadable item is limited to approximately 2 kg, it is difficult for most commercial parcel delivery drones to complete a delivery route with multiple parcels. The available moving distance of a drone is only approximately 10–15 km when there are weak winds and a clear line of sight. The battery can be recharged at any time when the battery is not fully charged. The general specifications of the drones manufactured for parcel delivery are summarized in Table 1. If such specifications are altered in accordance with improvements in the related technologies, they can be considered in our proposed model without modifying any of the model’s constraints.

Table 1.
Delivery drone specifications in the case study.
Among the various specifications of the drones in Table 1, the worst-case battery consumption scenario was calculated using the equation proposed by D’Andrea [34]. Since battery consumption is critical to the safe flight of drones, we use the worst-case battery consumption to avoid any battery problems during the flight.
The drone operating hours are set from 9:00 am to 6:00 pm (9 h) given the visibility condition of the drones. The take-off and landing of the drones and the loading/unloading of the goods are regarded as additional work, and we assume that this additional work takes approximately 15 min (0.25 h). Finally, the effects of weather, such as strong winds, are not taken into consideration because drones will not be operated for delivery in such conditions. In the beginning, drones start to deliver parcels to one target destination (i.e., rooftop) with a full battery capacity. Drones must choose either delivery or battery recharging as the next operation whenever they finish their previous operation. Additionally, drones need to recharge their batteries to amounts greater than the minimum recharging ratio to prevent full discharge, up to its full capacity. The accumulated operation time after the final operation should be less than the available hours (i.e., the drone operating hours).
Figure 1 depicts a conceptual diagram of drone-based parcel delivery using the rooftops of buildings in cities.
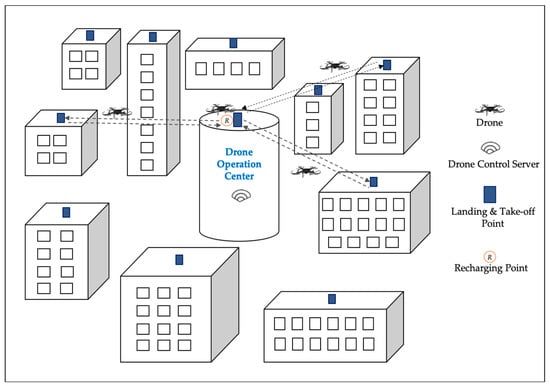
Figure 1.
Drone-based parcel delivery using the rooftops of buildings.
3.3. Mathematical Model
Considering the above assumptions and the current drone technologies, we propose a new drone operation planning model for effectively delivering parcels in urban areas. The proposed model is based on MILP.
To formulate the model, the following parameters and variables are required.
Indices
- drone index ().
- destination (rooftops) index ().
- drone operation index (). The upper bound of the drone operation index, , can be set by adding the estimated number of recharging operations and the estimated number of delivery operations. Of course, can be adjusted during the pre-experiments.
Parameters
- demand at destination (unit: number of parcels).
- distance between the drone operation center and rooftop (unit: ).
- worst-case battery consumption (unit: ).
- battery capacity of the drone (unit: kWh).
- average speed of the drone (unit: km/h).
- required time to load, unload, take-off, and land the drone (unit: hour).
- daily available hours for drone operations (unit: hour).
- minimum recharging ratio to prevent full discharge. The battery capacity of the drone should not fall below this ratio.
- battery recharging time from the minimum charging ratio () to full charge (unit: hour).
Decision Variables
- 1 if drone delivers a parcel to destination as the th operation, and0 otherwise.
- 1 if drone recharges its battery as the th operation, and0 otherwise.
- battery recharging ratio (%) when drone recharges its battery as the th operation. . If is 0.5, then the recharge amount of the battery capacity is 0.5.
- the battery charge after drone finishes its th operation. The initial battery charge is set to .
- time after drone finishes its th operation. The initial time is set to zero, and it increases as the operations are performed.
Using the parameters and the decision variables defined above, the drone operation planning model can be formulated as follows.
Drone Operation Planning Model (DROP-Model)
Subject to:
The objective function in Equation (1) works to maximize the number of parcels delivered. In many past related studies, the authors pursued the minimization of the total transportation cost. However, it is impossible for drones to take all the portion of delivery demand in any building because drones are not used to replace the conventional transport modes but to supplement them, as mentioned in the assumptions. Thus, in this study, drones need to be operated continuously during the operating hours. In short, drones are required to deliver as many parcels as possible during the given hours. Additionally, the related costs (mainly battery recharging) to operate several drones are not high and can be disregarded in comparison with delivery van operations, which require relatively substantial fuel costs.
The constraint in Equation (2) indicates that the number of deliveries to any rooftop should not be more than its demand. The constraint in Equation (3) ensures that drone conducts either delivery or recharging, but it is not allowed to do both concurrently. The constraint in Equation (4) guarantees that drone delivers a parcel as the next task if the current task is recharging the battery. The constraint in Equation (5) ensures that the mission of the drone is terminated when both tasks (delivery and recharging) are not assigned and conducted in the previous step. This constraint prohibits any unnecessary breaks for drones during operating hours. The constraint in Equation (6) guarantees that the recharging percentage can be determined when the mission of the drone is to recharge its battery. However, the constraint in Equation (7) also guarantees that the drone recharges its battery to an amount greater than the minimum recharging ratio to prevent full discharge. In this study, we set this minimum recharging ratio to 0.1. Thus, the battery needs to be recharged to at least 10% of the battery capacity once recharging is selected. The constraint in Equation (8) is a flow conservation equation for the battery charge. This explains that the current battery charge is determined by either subtracting the consumed charge for delivery from the battery charge remaining after the previous task or by adding the recharged amount to the battery charge remaining after the previous task. The constraint in Equation (9) limits the battery recharging amount. For example, if the battery charge after the previous task () is 0.3 , the upper bound of is set to 0.7. In other words, when is 0.3 (i.e., the current battery charge is 30% of the full capacity), the battery can be recharged by up to 70% of its full capacity. The constraint in Equation (10) sums the operating times of either delivery or recharging to check the duration of each operation. The constraint in Equation (11) guarantees that the accumulated operation time after the final task is less than the available hours. The constraint in Equation (12) requires that the decision variables for the battery charge, time, and battery recharging ratio are nonnegative. Finally, the constraint in Equations (13) and (14) show the binary decision variables that are relevant to delivery and recharging.
In the above DROP-Model, we can replace the constraint in Equation (9) with Equation (15) below to make the drone fully recharge its battery when it is assigned to recharge. In other words, the battery recharging ratio () is set to make the battery capacity full.
After preparing all the required data, we can obtain the optimized drone operation plan by running the proposed DROP-Model.
4. Heuristic-Based Solution
As mentioned in Section 1, commercial optimization software has difficulty in providing optimized planning for large MILP problems in a reasonable time. This problem also occurred in our case, which will be summarized in a later section. Thus, to address the computational tractability of the proposed problem, we developed an efficient heuristic that can quickly generate optimal or near-optimal solutions in terms of the objective value of the DROP-Model for various problem instances.
The proposed heuristic is based on two basic steps: 1) building a solution by stacking blocks and 2) improving the solution by making space and inserting blocks. Each step can be explained as follows.
• Step 1: Building a solution by stacking blocks.
First, we need to define a block. A block is assigned to each destination (e.g., rooftop) and includes the time information (i.e., block time) for delivery and charging. For example, block ‘1′ has 0.68 h, 0.29 h for any drone to deliver a parcel to destination ‘1′ and 0.39 h for any drone to charge the battery for this delivery only. Once the blocks for all destinations are defined, we can start to stack the blocks for each drone to generate a solution (i.e., schedule).
- Step 1.1: Initially, adopt a simple assignment rule for block stacking. Shorter deliveries and charging times are assigned first. Among the blocks, the shorter blocks are assigned to the drones first, as shown in Figure 2a. Each line represents a schedule or delivery work allocation for each drone. However, since our schedule should not exceed the operating hours (i.e., 9 h), we cannot assign blocks that go over the given operating hours. Thus, we need to rearrange the blocks to avoid violating the operating hours.
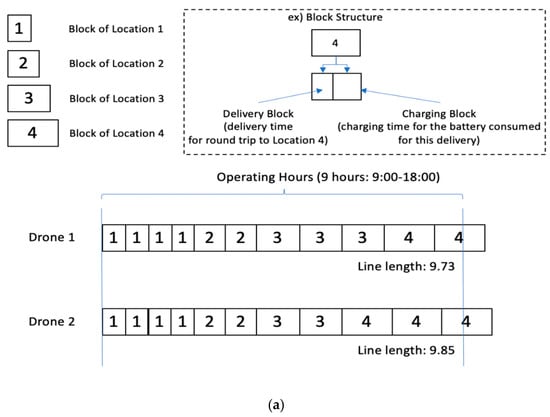
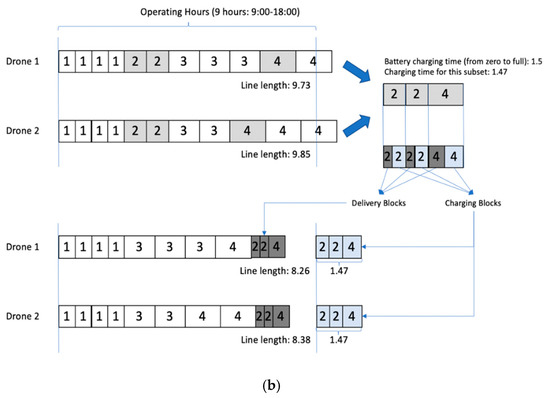 Figure 2. Building a solution by stacking blocks. (a) Initial block stacking; (b) grouping and relocation.
Figure 2. Building a solution by stacking blocks. (a) Initial block stacking; (b) grouping and relocation. - Step 1.2: Whenever trying to stack any block to a line, create a power set from the line to pick up the blocks with summed charging times that are most similar to the time for a battery to be fully charged. For example, if the summed charging time from blocks ‘2′, ‘2′, and ‘4′ is 1.47, then there is only a 0.03 gap to the battery charging time (from zero to full) of 1.5. This grouping can be easily made by checking the summed charging time of each combination in the power set. The reason why we pick up those blocks as a group is that we want to allocate them at the end of the line. Because charging is no longer required after operating hours (i.e., zero battery will be okay at the end of operating hours), those blocks need to be allocated at the end of the line, as shown in Figure 2b. However, if the allocation of such a block group for any drone exceeds the operating hours, we cancel the allocation of the block group for that drone.
• Step 2: Improving the solution by making space and inserting blocks.
After Step 1, we can obtain the lines of blocks for the drones that do not exceed the operating hours. Next, we have to improve the current solution (i.e., lines) by inserting more blocks because the objective function of the DROP-Model maximizes the number of delivered parcels.
- Step 2.1: Try to make a space to add a new block that has a shorter block time among the remaining blocks (not inserted in the lines yet). To do this, the lines for the drones need be sorted in descending order of their remaining time. If any line’s length (i.e., the sum of the block times of the line) is 8.26, the remaining time of this line would be 0.74 (= 9.0–8.26).
- Step 2.2: Choose the first and the second lines from the sorted list and then find the common destinations (i.e., intersection) that exist among both lines. From those common destinations, we need to generate combinations whose elements are two destinations only. For example, if there are three destinations 1, 2, and 3 that compose the intersections of the two lines, we can generate three combinations: {1, 2}, {1, 3}, and {2, 3}.
- Step 2.3: From the combinations, choose the one that has the largest gap of block time between two elements, as shown in Figure 3a. However, this gap should be less than the remaining time of the second line (the reason will be explained in Step 2.4).
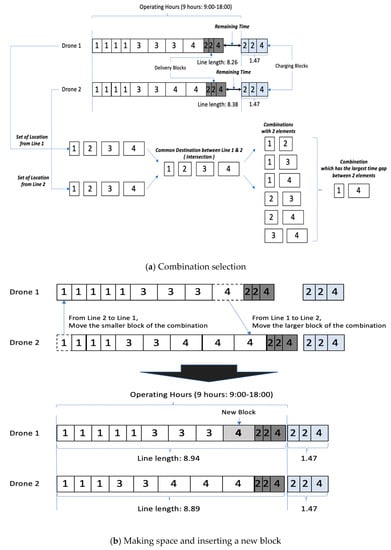 Figure 3. Improving the solution by making space and inserting blocks.
Figure 3. Improving the solution by making space and inserting blocks. - Step 2.4: Remove the smaller block of the chosen combination from the second line and stack the larger block of the chosen combination on the second line instead. If the gap between two blocks exceeds the remaining space of the second line, the larger block of the combination cannot be inserted into the second line. Repeat Step 1.2 for the modified second line. If the length of the modified second line exceeds the operating hours, return to Step 2.3 and choose another combination that has the next largest gap of block time between two elements. Otherwise, (if the length of the modified second line does not exceed the operating hours), remove the larger block of the combination from the first line and then stack the smaller block of the combination to the first line. At this moment, the modified second line becomes fixed, while the modified first line can generate a space for a new insertion, as shown in Figure 3b.
- Step 2.5: If there is no combination to consider between the first and second lines, return to Step 2.2 but choose the first line and the next line (e.g., third, fourth, fifth, etc.) with the next longest remaining times.
- Step 2.6: If there is enough space in the modified first line, stack a new block and check the feasibility of the line using Step 1.2. Repeat Steps 2.1–2.6 until the sum of the remaining time of all the lines is less than the length of any remaining block. If there is no appropriate combination to try further, it is terminated.
After obtaining the final lines from the proposed heuristic, we can convert them to the final schedule for drone delivery. Figure 4 shows an example of how the generated line can be converted to the final schedule.
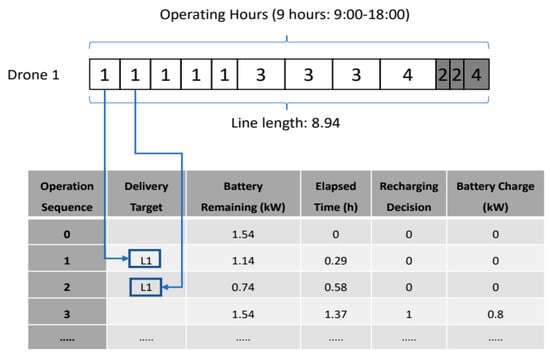
Figure 4.
Final schedule generation.
Since any blocks in the line can be processed (delivered) regardless of the current sequence in the line, various schedules that generate the same objective value (i.e., the number of parcels) can be obtained. In other words, because the blocks in the line are already set to not exceed the operating hours, the sequence of the blocks can be changed inside the line except for the final group of blocks, which are intentionally allocated at the end of the line.
The overall flow of the proposed heuristic can be seen in Figure 5. Additionally, the pseudocodes of the proposed heuristic are attached in the Appendix A.
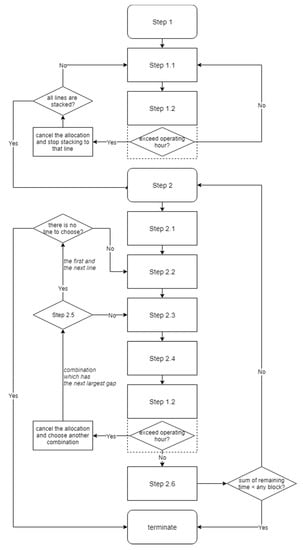
Figure 5.
Overall flow of the proposed heuristic.
5. Experiments
5.1. Experimental Design
To check the feasibility of the proposed DROP-model and evaluate the performance of the proposed heuristic-based solution, we create various problem instances by considering a real situation in one of the districts of Seoul (the capital city), South Korea. The Gangnam District is one of the 25 local government districts that make up the city of Seoul, and it is the third-largest district in Seoul, with an area of 39.5 . As of the 2017 census, Gangnam District had a population of approximately 560 thousand. Residential and commercial areas are located together in this district, and thus, there is a great demand for parcel delivery every day. Along with several private delivery companies, Korea Post is also responsible for the delivery demand in this district. Korea Post, a government organization, usually accounts for approximately 10% of the domestic market share (ranked 4th) for parcel delivery in South Korea. The Gangnam Post Office (GPO) is one of several post offices in Seoul operated by Korea Post and is located in the northeastern part of the Gangnam District. There are many residential and business buildings within a 6–8 km radius of the GPO, and some of their demand needs to be fulfilled by the GPO. Thus, for our experiments, we constructed a delivery network using the rooftops of the GPO and several nearby buildings, as shown in Figure 6.
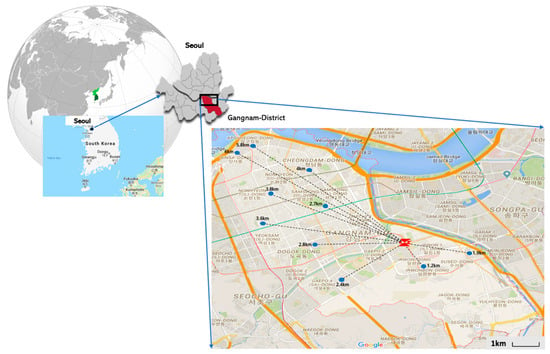
Figure 6.
Experimental delivery network in the Gangnam district of Seoul.
For the experimental delivery network, we create three different problem instances: small (2 drones and 10 destinations), medium (4 drones and 20 destinations), and large problem (10 drones and 50 destinations) instances. For each problem size, 20 different problem instances were randomly generated for testing. The distance and daily demand for each location, used in creating the problem instances, are randomly chosen from real values between 1 and 10 for distance, and integer values between 1 and 5 for daily demand, respectively.
All experiments were implemented on a personal computer with an Intel® Core™ i5 3.10 GHz CPU and 8.00 GB RAM. We used GUROBI Optimizer 8.1 (http://www.gurobi.com), a commercial optimization tool, to run the DROP-Model to obtain the optimal solution. Additionally, we implemented the proposed heuristic using Python 3.7.1 and Conda 4.7.5.
5.2. Experimental Results
Table 2 shows the experimental results for the comparison of the objective values between GUROBI and the proposed heuristic. The average computational times are also summarized.

Table 2.
Experimental results.
As expected, the computational time of GUROBI drastically increases as the number of drones and delivery destinations increases due to the curse of dimensionality. The computational times of GUROBI for the small- and medium-sized problems are 0.14 s and 7.21 s on average, respectively. For the large problems, GUROBI cannot find optimal solutions for 18 out of 20 problem instances within 12 h. We set 12 h as the computation time limit of GUROBI because the drone schedules should be prepared immediately before opening the operation center the next day. A better computing environment might be able to shorten the computational time of the commercial optimization software. However, if the problem size grows, the same dilemma will arise. In contrast, the proposed heuristic requires only 0.3 s (for small), 1.12 s (for medium), and 7.51 s (for large) on average to derive the optimal solutions for each problem size. For the problem instances that can be solved using GUROBI, the proposed heuristic gives 0% optimality losses with respect to the GUROBI solutions for all small (20 problem instances), medium (20 problem instances), and large-sized problems (2 problem instances) as shown in Table 2. The optimality gap is calculated using Equation (16).
As shown in Table 2, the computational time of the MILP increases rapidly as the number of variables (i.e., number of drones, number of destinations) increases. According to the IBM Knowledge Center [35], the out-of-memory or too many calculations issue almost always occurs when the branch & cut tree of commercial optimization software such as CPLEX and GUROBI becomes so large that insufficient memory remains to solve any subproblem. In such a situation, it terminates the process with an error message. Of course, a better computing environment might be able to handle this issue. However, if the problem size grows, say 20 drones and 100 destinations, the same dilemma will arise [11]. Whereas the proposed heuristic could find solutions for all the 20 large problem instances under 8 s on average. In short, it is expected that the proposed heuristic could generate a feasible schedule much faster than commercial optimization software.
6. Conclusions
In this research, we proposed the MILP model for drone operation planning to maximize the number of deliveries on the assumption that drone-based parcel delivery using the rooftops of buildings will soon become a reality. Next, a block-stacking-based heuristic was newly proposed to provide quick and effective solutions. For conducting experiments, three different problem settings were made up: small (2 drones and 10 destinations), medium (4 drones and 20 destinations), and large (10 drones and 50 destinations). The results of the experiment showed that the proposed heuristic can generate a very good solution (i.e., 0% optimality gap) in a short time for all problem sizes. Moreover, the solutions were all found even in the large size problem setting, in which GUROBI, commercial optimization software, cannot find optimal solutions for 18 out of 20 problem instances within 12 h. It is hoped that modeling and algorithmic contributions in this paper will facilitate the impending implementation of drone-based parcel delivery using the rooftops of city buildings as drone technologies continue to evolve in the future.
7. Future Research
For future research, various uncertainties, such as the weather conditions (e.g., wind direction and speed, temperature), need to be further considered when formulating a planning model. More realistic data should be collected and used for model parameters when the real validation work of the proposed delivery system starts later. Because the location of the drone operation center might affect drone operation planning, the location problem needs to be assessed. Additionally, multiple drone operation centers can be considered for drone-based parcel delivery. Under multiple drone operation center environments, drones could freely move to each center for battery charging, which might improve the utilization rates of the drones. As for the performance of the proposed heuristic, it needs to be compared with that of metaheuristics such as genetic algorithms.
Finally, we will be able to apply the proposed heuristic to other application areas, such as electric car recharging and operating problems.
Author Contributions
Conceptualization, J.K. and H.J.; methodology, H.M. and H.J.; software, H.M. and J.K.; validation, J.K., H.M., and H.J.; formal analysis, J.K. and H.J.; writing—original draft preparation, J.K.; writing—review and editing, H.J.; supervision, H.J.; funding acquisition, H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea, funded by the Ministry of Education (NRF-2017R1D1A1B03032560). This work was also supported by the Inha University Research Grant (60630–1).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
| Algorithm A1: Pseudo Codes of the Proposed Heuristic. |
| 1: Enumerate all demand and distance information of each destination. Calculate delivery time, charging time, and battery consumption after delivering a parcel to each destination. Create a destination block for each building, which consists of delivery and charging blocks. |
| 2: Enumerate drones and consider each drone to be a container to stack blocks. |
| # Stack blocks (Step 1) |
| 3: while all containers are closed do |
| 4: Stack the smallest destination block to an open container which has the largest space. |
| 5: Create a power set made out of delivery blocks in the container, and select a subset whose summed battery consumption is most similar to the battery amount. |
| 6: Move destination blocks in the selected subset to the end of the container. Divide the moved destination blocks into delivery blocks and charging blocks, and remove charging blocks. |
| 7: L = blocks’ total length |
| 8: If L > operation time do |
| 9: Withdraw lines 4, 5, 6, and 7 |
| 10: Close the container |
| # Organize blocks to make space to stack a new block (Step 2) |
| 11: while the total remaining space of containers >= the size of the new block to stack do |
| 12: Sort containers in descending order of the total remaining space of the container. |
| 13: Select a container that has the largest remaining space (1st) and a container that has the second-largest remaining space (2nd). |
| 14: Make combinations that have 2 elements, made out of the intersection between the destinations of two selected containers. |
| 15: Select combination which has the largest gap between 2 elements on condition that this gap does not exceed the remaining space of the 2nd container. |
| 16: Remove a smaller destination block of the selected combination from the 2nd container, and stack a larger destination block of the selected combination to the 2nd container. |
| 17: With the 2nd container, implement lines 5, 6, and 7. |
| 18: If L > operating hours do |
| 19: Withdraw lines 15, 16, and 17. |
| 20: Return to line 15, and select combination which has the next largest gap. |
| 21: Else do |
| 22: Remove a larger destination block of the selected combination from the 1st container, and stack a smaller destination block of the selected combination to the 1st container. |
| 23: If there is no appropriate combination between the 1st and the 2nd containers do |
| 24: Return to line 13, and select the 1st container and a container that has the next largest space (3rd, 4th, 5th…). |
| 25: If there is enough space to stack new block do |
| 26: Stack the new block. |
| 27: Implement lines 5, 6, and 7. |
| 28: If L > operation time do |
| 29: Withdraw lines 26 and 27. |
| 30: If there is no appropriate combination among all containers do |
| 31: break |
| 32: Get schedules |
References
- Bryan, V. Drone Delivery: DHL “parcelcopter” Flies to German Isle. 2014. Available online: https://www.reuters.com/article/us-deutsche-post-drones/drone-delivery-dhl-parcelcopter-flies-to-german-isle-idUSKCN0HJ1ED20140924 (accessed on 25 May 2020).
- Madrigal, A.C. Inside Google’s Secret Drone-Delivery Program. 2014. Available online: http://www.theatlantic.com/technology/archive/2014/08/inside-googles-secret-drone-delivery-program/379306/ (accessed on 25 May 2020).
- Rose, C. Amazon’s Jeff Bezos Looks to the Future. 2013. Available online: http://www.cbsnews.com/news/amazons-jeff-bezos-looks-to-the-future (accessed on 25 May 2020).
- Stern, J. Like Amazon, UPS Also Considering Using Unmanned Flying Vehicles. 2013. Available online: http://abcnews.go.com/Technology/amazon-ups-drone-delivery-options/story?id=21086160 (accessed on 25 May 2020).
- Murphy, M. The Future is Here: Drones are Delivering Domino’s Pizzas to Customers. 2016. Available online: https://qz.com/838254/dominos-is-delivering-pizza-with-autonomous-drones-to-customers-in-new-zealand/ (accessed on 25 May 2020).
- Stewart, J. A drone-slinging UPS van delivers the Future. 2017. Available online: https://www.wired.com/2017/02/drone-slinging-ups-van-delivers-future/ (accessed on 25 May 2020).
- Xinhua. Chinese E-Commerce Giant Alibaba’s Drones Deliver Packages to Islands. 2017. Available online: http://www.xinhuanet.com//english/2017-11/08/c_136735278_3.htm (accessed on 25 May 2020).
- Lee, H.L.; Chen, Y.; Gillai, B.; Rammohan, S.; Technological Disruption and Innovation in Last-Mile Delivery. Retrieved from Stanford Graduate School of Business. 2016. Available online: https://www.gsb.stanford.edu/faculty-research/publications/technological-disruption-innovation-last-mile-delivery (accessed on 25 May 2020).
- Lim, J.; Jung, H. Drone delivery scheduling simulations focusing on charging speed, weight, and battery capacity: Case of remote islands in South Korea. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 4550–4551. [Google Scholar]
- Demir, E.; Huang, Y.; Scholts, S.; Woensel, T.V. A selected review on the negative externalities of the freight transportation: Modeling and pricing. Transp. Res. E Logist. 2015, 77, 95–114. [Google Scholar] [CrossRef]
- Song, B.D.; Park, K.; Kim, J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic. Comput. Ind. Eng. 2018, 120, 418–428. [Google Scholar] [CrossRef]
- Gevaers, R.; Van de Voorde, E.; Vanelslander, T. Characteristics of innovations in last mile logistics using best practices, case studies and making the link with green and sustainable logistics. In Proceedings of the European Transport Conference, Leiden, The Netherlands, 5–7 October 2009; pp. 1–21. [Google Scholar]
- Lemke, J.; Iwan, S.; Korczak, J. Usability of the parcel lockers from the customer perspective–The research in Polish Cities. Transp. Res. Proc. 2016, 16, 272–287. [Google Scholar] [CrossRef]
- Deutsch, Y.; Golany, B. A parcel locker network as a solution to the logistics last mile problem. Int. J. Prod. 2017, 56, 251–261. [Google Scholar] [CrossRef]
- Devari, A.; Nikolaev, A.G.; He, Q. Crowdsourcing the last mile delivery of online orders by exploiting the social networks of retail store customers. Transp. Res. E Logist. 2017, 105, 105–122. [Google Scholar] [CrossRef]
- Kafle, N.; Zou, B.; Lin, J. Design and modeling of a crowdsource-enabled system for urban parcel relay and delivery. Transp. Res. B Meth. 2017, 99, 62–82. [Google Scholar] [CrossRef]
- Tarantilis, C.D.; Kiranoudis, C.T. Distribution of fresh meat. J. Food Eng. 2002, 51, 85–91. [Google Scholar] [CrossRef]
- Song, B.D.; Ko, Y.D. A vehicle routing problem of both refrigerated and general type vehicles for perishable food products delivery. J. Food Eng. 2016, 169, 61–71. [Google Scholar] [CrossRef]
- Jovanovic, A.D.; Pamucar, D.S.; Pejcic-Tarle, S. Green vehicle routing in urban zones: A neuro-fuzzy approach. Expert Syst. Appl. 2014, 41, 3189–3203. [Google Scholar] [CrossRef]
- Desaulniers, G.; Errico, F.; Irnich, S.; Schneider, M. Exact algorithms for electric vehicle routing problems with time windows. Oper. Res. 2016, 64, 1388–1405. [Google Scholar] [CrossRef]
- Lee, K.; Chae, J.; Kim, J. A courier service with electric bicycles in an Urban Area: The case in Seoul. Sustainability 2019, 11, 1255. [Google Scholar] [CrossRef]
- Clarke, R. Understanding the drone epidemic. Comput. Law Secur. Rev. 2014, 30, 230–246. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Ferrandez, S.M.; Harbison, T.; Weber, T.; Sturges, R.; Rich, R. Optimization of a truck-drone in tandem delivery network using k-means and genetic algorithm. Int. J. Ind. 2016, 9, 374–388. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle routing problems for drone delivery. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef]
- Campbell, J.F.; Sweeney, D.C.; Zhang, J. Strategic design for delivery with trucks and drones. Supply Chain Anal. Rep. SCMA. 2017, 04(1), 1–38. [Google Scholar]
- Agatz, N.; Bouman, P.; Schmidt, M.; Optimization approaches for the traveling salesman problem with drone. ERIM Report Series in Management. 2018. Reference No. ERS-2015-011-LIS. Available online: http://ssrn.com/abstract=2639672 (accessed on 25 May 2020).
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Ha, M.H. On the min-cost traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Song, B.D.; Lee, S. Truck-drone hybrid delivery routing: Payload-energy dependency and No-Fly zones. Int. J. Prod. Econ. 2019, 214, 220–233. [Google Scholar] [CrossRef]
- Torabbeigi, M.; Lim, G.J.; Kim, S.J. Drone delivery scheduling optimization considering payload-induced battery consumption rates. J. Intell. Robot. Syst. 2020, 97, 471–487. [Google Scholar] [CrossRef]
- eMarketer. A Brief Overview of the Global Ecommerce Market. eMarketer Retail, 2019. Available online: https://retail.emarketer.com/article/brief-overview-of-global-ecommerce-market/59690010ebd40005284d5cc5 (accessed on 25 May 2020).
- Wang, F.; Zhu, Y.; Wang, F.; Liu, J.; Ma, X.; Fan, X. Car4Pac: Last mile parcel delivery through intelligent car trip sharing. IEEE Trans. Intell. Transp. Syst. 2019, Early Access. 1–15. [Google Scholar] [CrossRef]
- Castagno, J.; Yao, Y.; Atkins, E. Realtime Rooftop Landing Site Identification and Selection in City Simulation. 2019. Available online: https://arxiv.org/abs/1903.03829 (accessed on 9 June 2020).
- D’Andrea, R. Can drones deliver? IEEE Trans. Autom. Sci. Eng. 2014, 11, 647–648. [Google Scholar] [CrossRef]
- IBM Knowledge Center. Running out of Memory. 2017. Available online: https://www.ibm.com/support/knowledgecenter/en/SSSA5P_12.10.0/ilog.odms.cplex.help/CPLEX/UsrMan/topics/discr_optim/mip/troubleshoot/61_mem_gone.html (accessed on 15 June 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).