Abstract
Honeycomb weathering is a common phenomenon found on various rock surfaces all around the world. However, honeycomb formation mechanisms are still poorly understood. In this study, we propose a model describing moisture transport within the sandstone and erosion resulting from salt deposition during evaporation of moisture off the rock surface. The moisture transport model is based on the non-linear diffusion equation, where the volumetric moisture content is a combined parameter accounting for the moisture and gas (vapor) content. The moisture transport model accounts for the several-orders-of-magnitude decrease in moisture diffusivity, observed during drying. It was assumed that erosion occurs when the evaporation front is located close to the rock surface. The depth of erosion is proportional to the moisture flow rate through the drying surface. The ABAQUS finite-element software suite was used for numerical solution of the non-linear diffusion equation. The iterative scheme of erosion simulation for different drying cycles was implemented using the Python programming language. Computations were conducted in the 2D setting for the square model with dimensions of 50 mm × 50 mm. Simulation results demonstrate the possibility of obtaining various landform shapes (honeycombs, tafoni) by varying only the value of the distribution of moisture content at the bottom side, simulating the rate of internal wetting of rock.
Keywords:
cavernous weathering; moisture; salt; rock honeycombs; tafoni; model; sandstone; rocks; salt weathering 1. Introduction
Honeycombs are a common phenomenon observed on various rock surfaces in various environmental conditions [1,2,3,4,5,6,7]. Honeycombs can be found in coastal areas [2,8,9], hot and cold deserts [10,11,12,13], wet areas [4], and on surfaces of historical buildings [14,15,16,17]. Honeycombs may also be observed on the surface of other planets [18,19]. Honeycombs represent rock surface with a dense cellular structure consisting of multiple closely adjacent pits with the size of several centimeters, separated from its neighbors by thin lips (Figure 1).

Figure 1.
Honeycombs: (a) Apolena Rock City, CZ; (b) Bukhta Desantnaya, Ussuri Bay, Primorsky Krai, RU.
In spite of intensive studies conducted over a last hundred years, honeycomb formation mechanisms still remain one of the most puzzling and confusing phenomena in geology [3]. Various processes were proposed to explain honeycomb origin, such as chemical weathering, frost weathering, thermal shock, biological weathering, case hardening, salt weathering [2,20,21,22,23,24]. Many researchers consider salt weathering the most probable cause of honeycomb formation; however, the actual mechanisms are still poorly understood. Why are thin lips formed between pits preserved [21]? Why do similar structures form on different rock types under considerably different environmental conditions [25]? Why, on the other hand, can we observe different structures, sometimes at a different stage of honeycomb formation, present on the same rock [8]? Why do honeycombs tend to form in the areas with perfect balance between wetting and drying [26]?
Finding the mechanisms of honeycomb formation is a complex problem due to a very long duration of occurring processes and scale issues [27]. For example, sandstone erosion rate constitutes several dozen millimeters per 1000 years [23]. There are successful laboratory experiments substantiating the formation of spectacular sandstone landforms such as arches, alcoves, pedestal rocks, pillars [28,29], and arcades [5] as a result of erosion. However, successful laboratory experiments illustrating the whole cycle of honeycomb formation are yet to be conducted. Computer simulation may be of a help in substantiating the erosion mechanisms of sandstone landform formation. Thus, several studies simulated the formation of arches, pedestal rocks, pillars, and arcades [30,31,32,33] based on the principal idea of negative feedback between stress and erosion. In [34], the growth of tafoni was modeled by salt weathering during a sequence of wetting/drying cycles. However, no studies have yet been conducted on simulation of honeycomb formation.
In this study, the authors propose the description of various stages of honeycomb development, based on the mathematical model of moisture transport within rock and of moisture evaporation off the rock surfaces, where erosion occurs as the result of salt deposition.
2. Methods
The proposed physical model describes moisture transport in the rock, and is based on the non-linear diffusion equation, where the volumetric moisture content is a combined parameter accounting for the moisture and gas (vapor) content; and is the moisture diffusivity depending on the actual moisture content [35,36,37,38]:
where is the time, and is the gradient. The moisture flow model accounts for the several-orders-of-magnitude decrease in moisture diffusivity, observed during drying. In addition, as a function of moisture content, the moisture diffusivity has a clear and deep minimum at moisture content, which is commonly considered to be the marker of the evaporation front location. The intensity of moisture evaporation off the rock surface decreases with the drying and goes to zero at the moisture content of , equal to the humidity of the air at the external surface. To describe moisture evaporation, the flux condition at the rock surface is set as follows:
where is the mass transfer coefficient, is the relative humidity of the blown air, is the relative humidity of the surface material, and is the normal to the surface .
Typical values of model parameters are given in Table 1. In this study, for D(θ) and , we used linear approximation between values. Figure 2 shows the plot for .

Table 1.
Typical parameters values [37].
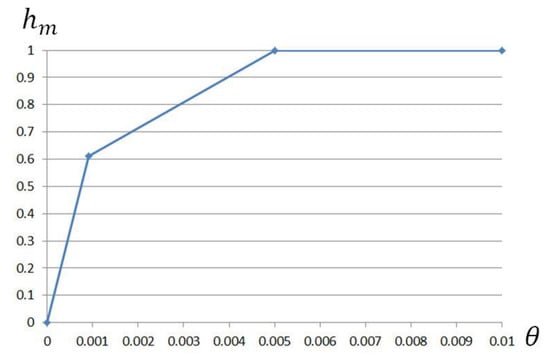
Figure 2.
Relationship between the relative humidity, , of the surface material and moisture content .
The ABAQUS finite-element software suite (version 6.14) was used for numerical solution of the non-linear diffusion Equation (1) [39]. ABAQUS allows a researcher to obtain realistic solutions for non-linear mechanical problems quickly [40,41,42,43,44,45]. In addition, its user subroutines mechanism makes it possible to locally change the material properties and distribution of loads during computations. In this study, the USDFLD, DFLUX, and UEXTERNALDB user subroutines were used: USDFLD—to account for changes in material properties in finite elements during the erosion process; DFLUX—to assign the flux condition (2) at each iteration step; and UEXTERNALDB—to assign algorithm parameters before modeling and to register results of computing the moisture flow rate through the drying surface after each iteration. The user subroutines were implemented in Fortran programming language.
All computations were conducted in the 2D setting for the square model with dimensions of 50 mm × 50 mm (see Figure 3). To imitate moisture content inside the rock, the constant value for moisture content, , is assigned at the bottom surface. For symmetry imitation, the no-penetration condition is set at the side surfaces. To imitate moisture evaporation at the rock surface, the flux conditions are set at the upper side of the model. The DC3D8 linear hexahedral elements were used in all computations discussed here.
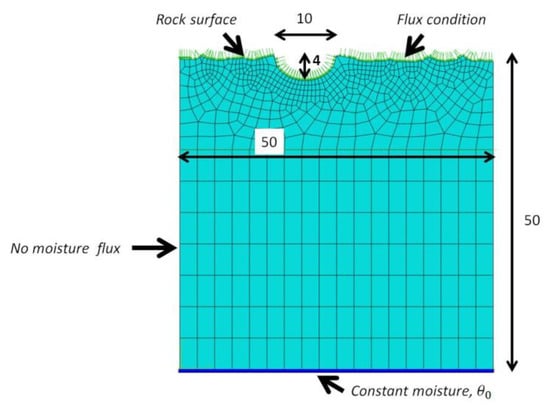
Figure 3.
Finite element computational model and boundary conditions.
Here, the sandstone erosion caused by salt deposition is considered to be the essential mechanism influencing formation of honeycomb [4,34,46,47,48,49,50]. The process of rock erosion is only affected by salt depositions leading to formation of subflorescence [51,52]. Authors believe that erosion occurs when the evaporation front is located close to the rock surface:
At the same time, the depth of erosion is proportional to the moisture flow rate through the drying surface q. For computations, repeating cycles of air humidity changes are modeled by changing the parameter of the relative humidity, . The following parameter values were considered: 0.78; 0.76; 0.74. Figure 4 shows the modeling algorithm for rock surface erosion. The upper part of the model (see Figure 3) simulating the rock surface is built with the polyline consisting of line segments. When building the model, the size of each segment should be at least 0.3 mm and should not exceed 1.0 mm. After the finite element mesh is built automatically, the boundary conditions are set, including flux conditions with the current values for parameters and . A steady state solution is found when solving the diffusion equation. The values of the relative rate of evaporation are computed for each segment, using the following equation . Then, for each segment, we determine its displacement into the rock region as the result of erosion. The displacement is proportional to the magnitude of q. The height of the model is maintained constant and equal to 50. If necessary, the upper surface is shifted upwards. The cycle consists of k calculations for various combinations of the parameter, … . The cycle repeats the specified number of times, N. The scheme described here is implemented in Python programming language.
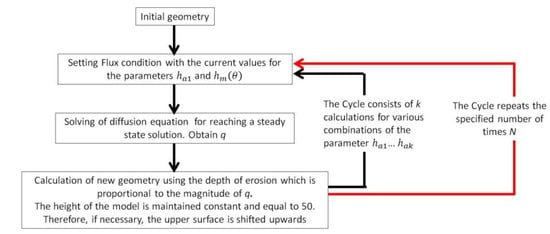
Figure 4.
Numerical implementation of erosion simulation.
3. Results and Discussion
In order to analyze the influence of boundary conditions and rock surface morphology on moisture transport, position of the evaporation front, and the rate of evaporation (see Figure 5), simulations were performed with the rectangular 2D object. At the bottom side, we set conditions of constant distribution of moisture content to simulate the rate of internal wetting of rock. At the upper side we set flux condition to describe moisture evaporation off the rock surface. At the left and right sides, the conditions of zero moisture transport are set. During simulations, we analyzed the data on hydraulic field distribution obtained after reaching the steady state condition. First, we consider the rectilinear upper edge simulating the smooth surface of the rock (see Figure 5a, Supplementary Figure S1) at different levels of rock saturation, i.e., the moisture content (Supplementary Figure S1). The results show that the rate of moisture evaporation off the rock surface, q, is maximal for and, in certain cases, constitutes 1.0. Within the range of , the rate of evaporation, q, decreases sharply and reaches 0.37, and then, at , a smooth fall-off to zero can be observed (see Figure 5b). The evaporation front appears at ; the distance between the evaporation front and the upper edge increases with a decrease in ; i.e., the depth of the vapor zone increases (Supplementary Figure S1). Then, the single 15 mm-wide pit is added at the center of the upper edge. The depth of the pit, H, is varied, while keeping constant at (Figure 5e, Supplementary Figure S2). Thus, we can see that the increase in H results in the tenfold reduction in the rate of evaporation, q, at the vertex, A, of the pit from 0.6 (H = 0.0 mm) to 0.06 (H = 7.5 mm) (Figure 5f). At the same time, at point B, located in the center at the bottom of the pit, the rate of evaporation, q, increases sharply with the increase in H, reaching q = 0.99 at H = 4 mm (Figure 5f). Additionally, at H ≥ 6 mm, the evaporation front is almost absent in the point B area (Supplementary Figure S2); i.e., the values of moisture content exceed , indicating that only a capillary zone is present in this area. In the next simulations, we add two symmetrically positioned 15 mm-wide and 4 mm-deep pits (H = 4.0 mm). The distance between pits, L, is varied while keeping constant at (Figure 5i, Supplementary Figure S3). The reduction in L from 25 mm to 15 mm results in the decrease in the rate of evaporation, q, at the vertex A located between two pits, from 0.20 to 0.03, while the minimum value of q = 0.03 is observed in the case of immediately adjacent pits with L = 15.0 mm (Figure 5j). With a further reduction in L, a sharp increase in the rate of evaporation, q, can be observed at the vertex A (Figure 5j).
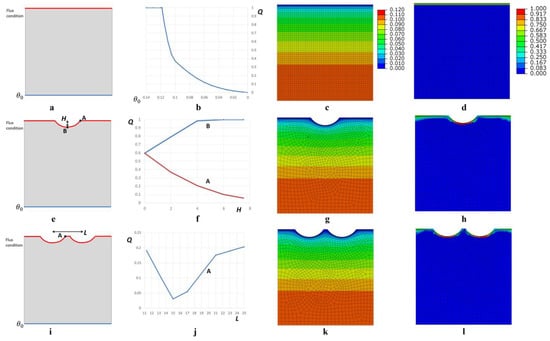
Figure 5.
Influence of boundary conditions on the hydraulic field. (a–d) Smooth surface of rock at various levels of saturation, . (a) Computational model. (b) Rate of evaporation, q, as the function of . (c) Moisture content distribution at . (d) Distribution of evaporation rate, q, at . (e–h) Single 15 mm-wide pit located at the center of the right edge, at various values of H, with constant . I Computational model. (f) Rate of evaporation, q, as the function of . (g) Moisture content distribution at H = 4.0 mm. (h) Distribution of evaporation rate, q, at H = 4.0 mm. (i–l) Two adjacent 15 mm-wide and 4.0 mm-deep pits with various center-to-center distances, L, at constant . (i) Computational model. (j) Rate of evaporation, q, as the function of L. (g) Moisture content distribution at L = 17.0 mm. (h) Distribution of evaporation rate, q, at L = 17.0 mm.
In order to model honeycomb weathering during erosion in accordance with the proposed method, the square computational model is used, where the upper side imitates the surface of rock and has a random structure with 10 mm-wide and 4 mm-deep pits (see Figure 3). During simulations, only the value of constant distribution of moisture content at the bottom side was changed, simulating the rate of internal wetting of rock. Figure 6 shows simulation results for constant distribution of moisture content at the bottom side set to = 0.115. Moisture content over the whole volume exceeds , showing that the model is fully wet, and no erosion takes place (3). Figure 7 shows simulation results after 40 iterations with the constant distribution of moisture content at the bottom side set to = 0.110. A virtually flat surface can be observed here. This can be explained that only protruding parts dry out below , and hence, only protruding parts undergo erosion. The evolution of a pitted surface into a virtually flat one is shown in Supplementary Video S1.
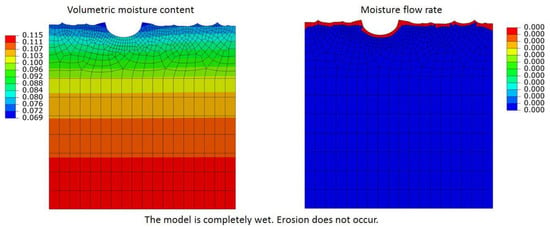
Figure 6.
Erosion process simulation. The value of constant distribution of moisture content at the bottom side is set to . Moisture content over the whole volume exceeds , indicating that the model is fully wet, and no erosion takes place (3).
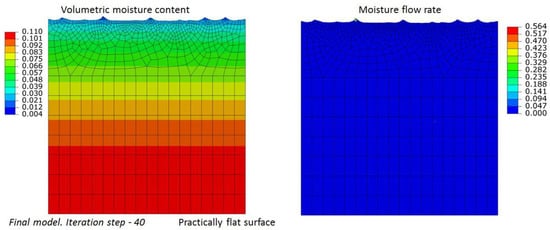
Figure 7.
Erosion process simulation. The value of constant distribution of moisture content at the bottom side is set to . The virtually flat surface can be observed. This can be explained that only the protruding parts dry out below , and the erosion occurs only in protruding parts.
Figure 8 shows simulation results after 40 iterations; the constant distribution of moisture content at the bottom side is set to = 0.109. The formation of the isolated single lip can be observed where the protruding part undergoes significant drying, resulting in a considerable reduction in the evaporation rate. Simultaneously, a more intense evaporation takes place at other regions. Thus, the lip forms from the initially protruding part that undergoes significant drying as compared to other rock surface. The formation of the lip corresponds to the formation of honeycombs. The evolution of the initial surface with pits into a virtually flat surface with a single isolated lip is shown in Supplementary Video S2. We can see that the lip stays dry all the time, as the evaporation front is located at the foundation of the lip. Thus, no erosion occurs, and the lip retains its shape. At the lesser value of = 0.108 the number of lips increases due to a larger number of protruding parts that undergo drying, resulting in a significant reduction in the evaporation rate (see Figure 9). The evolution of the initial surface with pits into a virtually flat surface with several isolated lips is shown in Supplementary Video S3.
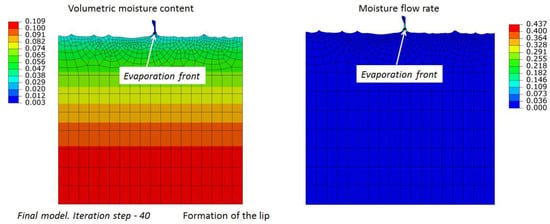
Figure 8.
Erosion process simulation. The value of the constant distribution of moisture content at the bottom side is set to . The formation of the single isolated lip can be observed.
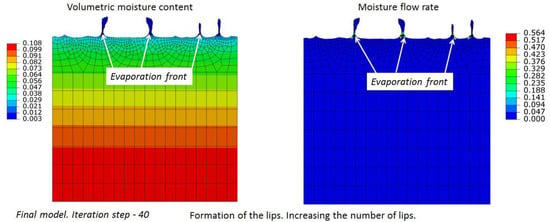
Figure 9.
Erosion process simulation. The value of the constant distribution of moisture content at the bottom side is set to . Formation of several isolated lips can be observed.
Figure 10 shows simulation results after 40 iterations; constant distribution of moisture content at the bottom side is set to = 0.106. We can observe the increasing number and thickness of lips. The evolution of the initial surface into a virtually flat one with several isolated thicker lips is shown in Supplementary Video S4. Further reduction in the value of constant distribution of moisture content at the bottom side to = 0.100 results in a growing thickness of lips and merging of some adjacent lips (see Figure 11 and Supplementary Video S5).
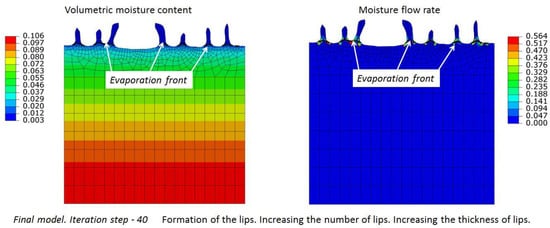
Figure 10.
Erosion process simulation. The constant distribution of moisture content at the bottom side is set to . The increase in number and thickness of lips can be observed.
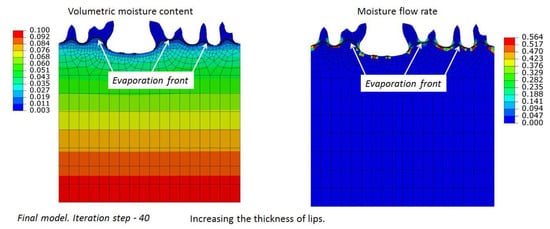
Figure 11.
Erosion process simulation. The constant distribution of moisture content at the bottom side is set to . The further increase in lips thickness and merging of several adjacent lips can be observed.
Figure 12 shows simulation results after 67 iterations; the constant distribution of moisture content at the bottom side is set to = 0.06. The evaporation front is located closer to the bottom of the pit than in other regions. That is why the erosion actively develops at the bottom of the pit. Here, one can observe the formation of the deep isolated pit (tafoni) from the initial pit. In other regions, the erosion process is less pronounced because the evaporation front is removed from the surface. The formation of the deep isolated pit (tafoni) from the initial pit is shown in Supplementary Video S6. At = 0.03, the evaporation front is located at a significant distance from the surface (see Figure 13), and no erosion takes place (3).
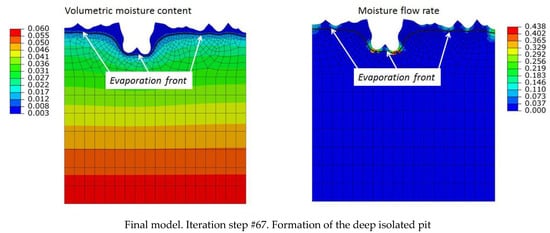
Figure 12.
Erosion process simulation. The constant distribution of moisture content at the bottom side is set to = 0.060. Formation of the deep isolated pit (tafoni) from the initial pit can be observed. In other regions, the erosion process is less pronounced because the evaporation front is removed from the surface.
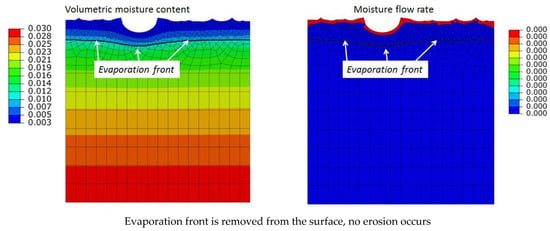
Figure 13.
Erosion process simulation. The constant distribution of moisture content at the bottom side is set to . Evaporation front is far away from the surface, and no erosion occurs.
The simulation results shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 and in Table 2 demonstrate the possibility of obtaining various landform shapes (honeycombs, tafoni) by varying only the value of constant distribution of moisture content at the bottom side, simulating the rate of internal wetting of rock. At high values of , the evaporation front is close to the surface, and thus, almost the entire surface remains wet, and erosion occurs only on the protruding surfaces. This results in smoothing of the surface. However, at low values of , the evaporation front moves away from the surface, and a more intense flow takes place at the bottom of the pits, leading to their deepening. Thus, at different values of , two opposite phenomena can be observed—smoothing of the surface and deepening of the pits. At intermediate values of , the interaction of these opposing phenomena results, accordingly, in the formation of lips and honeycombs.

Table 2.
Simulation results of various landform shapes.
To illustrate the simulation results, Figure 14 shows the photographs of the edge of the rock located in Apolena Rock City, CZ, where various landform shapes are represented. The lower right part of the rock is close to the earth and is, presumably, very wet. Hence, no erosion occurs there (see Figure 6). Higher up, the internal wetting of rock decreases. First, we can see the flat surface of rock (see Figure 7). Further on, as the height increases, we can observe the region with honeycombs (see Figure 9). Closer to the edge of the rock, the intense drying of the rock can be observed, resulting in the formation of tafoni (see Figure 12). At the very edge of the rock, the material is presumably very dry, and no erosion occurs (see Figure 13).

Figure 14.
The example of various shapes formed at the same rock under the same environmental conditions. It is assumed that formation of various shapes is related to height variations in moisture content inside the rock. The object is located in Apolena Rock City, CZ.
The results presented in this study are the first attempt to describe the process of honeycomb formation via numerical simulation. The results obtained here can provide answers to some questions formulated in the Introduction section. Thin lips formed between pits are retained because the evaporation front is located at the foundation of lips, and no intensive evaporation takes place inside the pits. This phenomenon is not inherent in specific types of rocks, but is determined by the physical processes of liquids evaporation. Taking into account that the simulations were conducted with typical properties of the rock and its environment, we can expect that the formation of structures on different rock types takes place under considerably different environmental conditions. The formation of honeycombs is related to the following physical phenomena: decrease in moisture diffusivity of the rock by several orders of magnitude under drying and decrease in evaporation rate during drying. Rock erosion is only affected by salt depositions leading to the formation of subflorescence that occurs when the evaporation front is close to the surface. That is why the formation of honeycombs can be expected in the presence of physical phenomena described earlier and under specific moisture content in the rock. We also proposed the example describing the formation of various shapes at the same rock, where the differences in surface structures are explained by the non-uniform distribution of moisture inside the rock. Simulation results demonstrate that honeycombs tend to form in the areas having perfect balance between wetting and drying.
Additionally, it is necessary to note and comment on certain features of the proposed numerical algorithm. There is no specific time in the calculations. We can say that equal time intervals are allocated for each case. The distinctive feature of this simulation is that we assume a constant value of the moisture content on the lower part of the model (the inner part of the rock). During computations of each case, a steady state solution is sought. In real time, the steady state can be achieved in 5–20 h, depending on the air humidity. Each case can be interpreted as a season lasting several months; i.e., different time scales are used in computations. As there is a separate calculation for each case, the humidity changes occur instantly. The computations are based on the assumption of a stationary condition for the moisture content on the lower surface. Therefore, after reaching a stationary solution, the position of the drying front does not change. The amount of subflorescence precipitated is calculated simply by multiplying local distribution of the moisture flow rate over a period of time. Thus, the variable length of wetting and drying periods can be easily taken into account.
The results presented here are qualitative. In order to quantitatively describe the formation of various shapes for concurrent rocks and to predict erosion in, for example, structures of building materials [53,54], it is necessary to measure material properties, such as moisture diffusivity and the relative humidity of the surface material , as functions of moisture content [55,56,57,58]. It is also necessary to validate the proposed physical and numerical model based on specific objects [59], by measuring seasonal changes in evaporation rate [60,61], the distribution of moisture and salts in the rock [62], and the position of the evaporation front [63]. It is also necessary to identify the influence of other factors that affect rock decay (chemical weathering [23], frost weathering [64], thermal shock [65], biological weathering [8], case hardening [4], erosion caused by the wind pressure [21], etc.). Additionally, the decay rate model needs to be improved by taking into account the petrography, mineralogy, and structural heterogeneity of the stone. The authors also intend to adapt the proposed model for the simulation of 3D structures, since this work does not describe the modeling of the formation of a regular honeycomb structure. These questions will be addressed in further studies.
This mathematical model can be applied in the forecasting of salt weathering of porous building materials, prediction of the life span of building structures, and developing methods for the conservation of historical monuments and our cultural heritage [53,66,67]. In addition, the developed algorithm for solving the non-linear diffusion equation with the evolution of the solution domain and boundary conditions can be applied to a wide range of natural and biological processes including neural networks, vascular networks, slime mold, plant routes, fungi mycelium, bone remodeling, bacterial biofilms [68] and colony patterns [69,70], the formation of the skeletons of microorganisms [71,72], fulgurites [73], and snowflakes [74], etc.
4. Conclusions
The proposed model demonstrates the formation of various landform shapes (honeycombs, tafoni) through the variation of moisture content, simulating the rate of internal wetting of the rock. At high values of moisture content in the rock, the evaporation front is located close to the surface, and thus, almost the entire surface remains wet, and erosion occurs only on the protruding parts of the surface. This results in smoothing of the surface. However, at low moisture content, the evaporation front moves away from the surface, and a more intense flow is observed at the bottom of the pits, leading to their deepening. Thus, at different values of moisture content inside the rock, two opposite phenomena can be observed—smoothing of the surface and deepening of the pits. At intermediate values of moisture content, the interaction of these opposite phenomena results, accordingly, in the formation of lips and honeycombs.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/geosciences13060161/s1, Supplementary Figure S1: Hydraulic field under various . (a) . (b) . (c) . (d) . (e) . (f) . (g) . (h) . (i) ; Supplementary Figure S2: Hydraulic field under various pit depths H. Width of pit is , . (a,c,e,g,i) The distribution of moisture content. (b,d,f,h,j) The distribution of the intensity of evaporation q. (a,b) H = 0 mm. (c,d) H = 2.0 mm. (e,f) H = 4.0 mm. (g,h) H = 6.0 mm. (i,j) H = 7.5 mm; Supplementary Figure S3: Hydraulic field with two adjacent pits. Width of pits is , pits depth is H = 4.0 mm, . (a,c,e,g,i) The distribution of moisture content. (b,d,f,h,j). The distribution of the intensity of evaporation q. (a,b) L = 25.0 mm. (c,d) L = 21.0 mm. (e,f) L = 17.0 mm. (g,h) L = 15.0 mm. (i,j) L = 11.3 mm; Video S1: Erosion process simulation. The value of constant distribution of moisture content at the bottom side is set to ; Video S2: Erosion process simulation. The value of constant distribution of moisture content at the bottom side is set to ; Video S3: Erosion process simulation. The value of constant distribution of moisture content at the bottom side is set to ; Video S4: Erosion process simulation. The value of constant distribution of moisture content at the bottom side is set to ; Video S5: Erosion process simulation. The value of constant distribution of moisture content at the bottom side is set to ; Video S6: Erosion process simulation. The value of constant distribution of moisture content at the bottom side is set to .
Author Contributions
Conceptualization, A.S.; methodology, A.S.; software, A.S. and K.M.; validation, A.S. and K.M.; formal analysis, A.S.; investigation, A.S.; resources, A.S.; data curation, A.S.; writing—original draft preparation, A.S.; writing—review and editing, A.S. and K.M.; visualization, K.M. and A.S.; supervision, A.S.; project administration, A.S.; funding acquisition, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors greatly appreciate the suggestions of the anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, P.J. Why honeycomb weathering? Nature 1982, 298, 121–122. [Google Scholar] [CrossRef]
- Mustoe, G.E. The origin of honeycomb weathering. Geol. Soc. Am. Bull. 1982, 93, 108–115. [Google Scholar] [CrossRef]
- Groom, K.M.; Allen, C.D.; Mol, L.; Paradise, T.R.; Hall, K. Defining tafoni: Re-examining terminological ambiguity for cavernous rock decay phenomena. Prog. Phys. Geogr. 2015, 39, 775–793. [Google Scholar] [CrossRef]
- Bruthans, J.; Filippi, M.; Slavík, M.; Svobodová, E. Origin of honeycombs: Testing the hydraulic and case hardening hypotheses. Geomorphology 2018, 303, 68–83. [Google Scholar] [CrossRef]
- Filippi, M.; Bruthans, J.; Řihošek, J.; Slavík, M.; Adamovič, J.; Mašín, D. Arcades: Products of stress-controlled and discontinuity-related weathering. Earth-Sci. Rev. 2018, 180, 159–184. [Google Scholar] [CrossRef]
- Evelpidou, N.; Karkani, A.; Tzouxanioti, M.; Spyrou, E.; Petropoulos, A.; Lakidi, L. Inventory and Assessment of the Geomorphosites in Central Cyclades, Greece: The Case of Paros and Naxos Islands. Geosciences 2021, 11, 512. [Google Scholar] [CrossRef]
- Migoń, P. Sandstone geomorphology—Recent advances. Geomorphology 2021, 373, 107484. [Google Scholar] [CrossRef]
- Mustoe, G.E. Biogenic origin of coastal honeycomb weathering. Earth Surf. Process. Landf. 2010, 35, 424–434. [Google Scholar] [CrossRef]
- McBride, E.F.; Picard, M.D. Origin of honeycombs and related weathering forms in Oligocene Macigno Sandstone, Tuscan coast near Livorno, Italy. Earth Surf. Process. Landf. 2004, 29, 713–735. [Google Scholar] [CrossRef]
- Prebble, M.M. Cavernous weathering in the taylor dry Valley, Victoria Land, Antarctica. Nature 1967, 216, 1194–1195. [Google Scholar] [CrossRef]
- André, M.F.; Hall, K. Honeycomb development on Alexander Island, glacial history of George VI Sound and palaeoclimatic implications (Two Step Cliffs/Mars Oasis, W Antarctica). Geomorphology 2005, 65, 117–138. [Google Scholar] [CrossRef]
- Inkpen, R.; Hall, K. Universal shapes? Analysis of the shape of antarctic tafoni. Geosciences 2019, 9, 154. [Google Scholar] [CrossRef]
- Strini, A.; Guglielmin, M.; Hall, K. Tafoni development in a cryotic environment: An example from Northern Victoria Land, Antarctica. Earth Surf. Process. Landf. 2008, 33, 1502–1519. [Google Scholar] [CrossRef]
- Dragovich, D. Building Stone and Its Use in Rock Weathering Studies. J. Geol. Educ. 1979, 27, 21–25. [Google Scholar] [CrossRef]
- Siedel, H. Alveolar weathering of Cretaceous building sandstones on monuments in Saxony, Germany. Geol. Soc. Spec. Publ. 2010, 333, 11–23. [Google Scholar] [CrossRef]
- Oguchi, C.T.; Yu, S. A review of theoretical salt weathering studies for stone heritage. Prog. Earth Planet. Sci. 2021, 8, 32. [Google Scholar] [CrossRef]
- Pötzl, C.; Siegesmund, S.; Dohrmann, R.; Koning, J.M.; Wedekind, W. Deterioration of volcanic tuff rocks from Armenia: Constraints on salt crystallization and hydric expansion. Environ. Earth Sci. 2018, 77, 660. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C. Evidence of honeycomb weathering on Mars. Geophys. Res. Lett. 1998, 25, 3249–3252. [Google Scholar] [CrossRef]
- Smith, P.J. Can honeycomb weathering be ET? Nature 1983, 301. [Google Scholar] [CrossRef]
- Schnepfleitner, H.; Sass, O.; Fruhmann, S.; Viles, H.; Goudie, A. A multi-method investigation of temperature, moisture and salt dynamics in tafoni (Tafraoute, Morocco). Earth Surf. Process. Landf. 2016, 41, 473–485. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C.; Doehne, E.; Sebastian, E. Origins of honeycomb weathering: The role of salts and wind. Bull. Geol. Soc. Am. 1999, 111, 1250–1255. [Google Scholar] [CrossRef]
- Conca, J.L.; Rossman, G.R. Case hardening of sandstone. Geology 1982, 10, 520–523. [Google Scholar] [CrossRef]
- Turkington, A.V.; Paradise, T.R. Sandstone weathering: A century of research and innovation. Geomorphology 2005, 67, 229–253. [Google Scholar] [CrossRef]
- Zwalińska, K.; Dąbski, M. Cavernous weathering forms in SW Iceland: A case study on weathering of basalts in a cold temperate maritime climate. Misc. Geogr. 2012, 16, 11–16. [Google Scholar] [CrossRef]
- Klimchouk, A. Tafoni and honeycomb structures as indicators of ascending fluid flow and hypogene karstification. Geol. Soc. Lond. Spec. Publ. 2018, 466, 79–105. [Google Scholar] [CrossRef]
- Paradise, T.R. Tafoni and Other Rock Basins. In Treatise on Geomorphology; Academic Press: San Diego, CA, USA, 2013; Volume 4. [Google Scholar]
- Viles, H.A. Scale issues in weathering studies. Geomorphology 2001, 41, 63–72. [Google Scholar] [CrossRef]
- Bruthans, J.; Soukup, J.; Vaculikova, J.; Filippi, M.; Schweigstillova, J.; Mayo, A.L.; Masin, D.; Kletetschka, G.; Rihosek, J. Sandstone landforms shaped by negative feedback between stress and erosion. Nat. Geosci. 2014, 7, 597–601. [Google Scholar] [CrossRef]
- Řihošek, J.; Slavík, M.; Bruthans, J.; Filippi, M. Evolution of natural rock arches: A realistic small-scale experiment. Geology 2019, 47, 71–74. [Google Scholar] [CrossRef]
- Ostanin, I.; Safonov, A.; Oseledets, I. Natural Erosion of Sandstone as Shape Optimisation. Sci. Rep. 2017, 7, 17301. [Google Scholar] [CrossRef]
- Moore, J.R.; Geimer, P.R.; Finnegan, R.; Bodtker, J. Between a beam and catenary: Influence of geometry on gravitational stresses and stability of natural rock arches. Geomorphology 2020, 364, 107244. [Google Scholar] [CrossRef]
- Safonov, A.A. Computing via natural erosion of sandstone. Int. J. Parallel Emergent Distrib. Syst. 2018, 33, 742–751. [Google Scholar] [CrossRef]
- Safonov, A.; Filippi, M.; Mašín, D.; Bruthans, J. Numerical modeling of the evolution of arcades and rock pillars. Geomorphology 2020, 365, 107260. [Google Scholar] [CrossRef]
- Huinink, H.P.; Pel, L.; Kopinga, K. Simulating the growth of tafoni. Earth Surf. Process. Landforms 2004, 29, 1225–1233. [Google Scholar] [CrossRef]
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Pel, L.; Kopinga, K.; Brocken, H. Moisture transport in porous building materials. Heron 1996, 41, 95–105. [Google Scholar]
- Landman, K.A.; Pel, L.; Kaasschieter, E.F. Analytic modelling of drying of porous materials. Math. Eng. Ind. 2001, 8, 89–122. [Google Scholar] [CrossRef]
- Pel, L.; Landman, K.A. A Sharp Drying Front Model. Dry. Technol. 2004, 22, 637–647. [Google Scholar] [CrossRef]
- Abaqus/CAE, Simulia. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/abaquscae/ (accessed on 25 May 2023).
- Safonov, A.A. 3D topology optimization of continuous fiber-reinforced structures via natural evolution method. Compos. Struct. 2019, 215, 289–297. [Google Scholar] [CrossRef]
- Safonov, A.; Chugunov, S.; Tikhonov, A.; Gusev, M.; Akhatov, I. Numerical simulation of sintering for 3D-printed ceramics via SOVS model. Ceram. Int. 2019, 45, 19027–19035. [Google Scholar] [CrossRef]
- Vedernikov, A.; Safonov, A.; Tucci, F.; Carlone, P.; Akhatov, I. Modeling spring-in of l-shaped structural profiles pultruded at different pulling speeds. Polymers 2021, 13, 2748. [Google Scholar] [CrossRef]
- Safonov, A.; Jones, J. Physarum computing and topology optimisation. Int. J. Parallel Emergent Distrib. Syst. 2017, 32, 448–465. [Google Scholar] [CrossRef]
- Moskaleva, A.; Gusev, S.; Konev, S.; Sergeichev, I.; Safonov, A.; Hernandez-Montes, E. Composite freeform shell structures: Design, construction and testing. Compos. Struct. 2023, 306, 116603. [Google Scholar] [CrossRef]
- Safonov, A.; Adamatzky, A. Computing via material topology optimisation. Appl. Math. Comput. 2018, 318, 109–120. [Google Scholar] [CrossRef]
- Wellman, H.W.; Wilson, A.T. Salt weathering, a neglected geological erosive agent in coastal and arid environments. Nature 1965, 205, 1097–1098. [Google Scholar] [CrossRef]
- Flatt, R.J.; Caruso, F.; Sanchez, A.M.A.; Scherer, G.W. Chemo-mechanics of salt damage in stone. Nat. Commun. 2014, 5, 4823. [Google Scholar] [CrossRef]
- Schiro, M.; Ruiz-Agudo, E.; Rodriguez-Navarro, C. Damage mechanisms of porous materials due to in-pore salt crystallization. Phys. Rev. Lett. 2012, 109, 265503. [Google Scholar] [CrossRef]
- Rijniers, L.A.; Huinink, H.P.; Pel, L.; Kopinga, K. Experimental evidence of crystallization pressure inside porous media. Phys. Rev. Lett. 2005, 94, 075503. [Google Scholar] [CrossRef] [PubMed]
- Flatt, R.J. Salt damage in porous materials: How high supersaturations are generated. J. Cryst. Growth 2002, 242, 435–454. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C.; Doehne, E. Salt weathering: Influence of evaporation rate, supersaturation and crystallization pattern. Earth Surf. Process. Landf. 1999, 24, 191–209. [Google Scholar] [CrossRef]
- Scherer, G.W. Stress from crystallization of salt. Cem. Concr. Res. 2004, 34, 1613–1624. [Google Scholar] [CrossRef]
- Charola, A.E. Salts in the Deterioration of Porous Materials: An Overview. J. Am. Inst. Conserv. 2000, 39, 327–343. [Google Scholar] [CrossRef]
- D’Altri, A.M.; de Miranda, S.; Beck, K.; De Kock, T.; Derluyn, H. Towards a more effective and reliable salt crystallisation test for porous building materials: Predictive modelling of sodium chloride salt distribution. Constr. Build. Mater. 2021, 304, 124436. [Google Scholar] [CrossRef]
- Gupta, S.; Huinink, H.P.; Prat, M.; Pel, L.; Kopinga, K. Paradoxical drying of a fired-clay brick due to salt crystallization. Chem. Eng. Sci. 2014, 109, 204–211. [Google Scholar] [CrossRef]
- Gonçalves, T.D.; Brito, V.; Pel, L. Water Vapor Emission From Rigid Mesoporous Materials during the Constant Drying Rate Period. Dry. Technol. 2012, 30, 462–474. [Google Scholar] [CrossRef]
- Ketelaars, A.A.J.; Pel, L.; Coumans, W.J.; Kerkhof, P.J.A.M. Drying kinetics: A comparison of diffusion coefficients from moisture concentration profiles and drying curves. Chem. Eng. Sci. 1995, 50, 1187–1191. [Google Scholar] [CrossRef]
- Pel, L.; Pishkari, R.; Casti, M. A simplified model for the combined wicking and evaporation of a NaCl solution in limestone. Mater. Struct. 2018, 51, 66. [Google Scholar] [CrossRef]
- Mareš, J.; Bruthans, J.; Weiss, T.; Filippi, M. Coastal honeycombs (Tuscany, Italy): Moisture distribution, evaporation rate, tensile strength, and origin. Earth Surf. Process. Landf. 2022, 47, 1653–1667. [Google Scholar] [CrossRef]
- Slavík, M.; Bruthans, J.; Weiss, T.; Schweigstillová, J. Measurements and calculations of seasonal evaporation rate from bare sandstone surfaces: Implications for rock weathering. Earth Surf. Process. Landf. 2020, 45, 2965–2981. [Google Scholar] [CrossRef]
- Slavík, M.; Bruthans, J.; Schweigstillová, J. Evaporation rate from surfaces of various granular rocks: Comparison of measured and calculated values. Sci. Total Environ. 2023, 856, 159114. [Google Scholar] [CrossRef]
- Karatas, T.; Bruthans, J.; Filippi, M.; Mazancová, A.; Weiss, T.; Mareš, J. Depth distribution and chemistry of salts as factors controlling tafoni and honeycombs development. Geomorphology 2022, 414, 108374. [Google Scholar] [CrossRef]
- Weiss, T.; Mareš, J.; Slavík, M.; Bruthans, J. A microdestructive method using dye-coated-probe to visualize capillary, diffusion and evaporation zones in porous materials. Sci. Total Environ. 2020, 704, 135339. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.B.G.; Robinson, D.A. Weathering of sandstone by the combined action of frost and salt. Earth Surf. Process. Landf. 1981, 6, 1–9. [Google Scholar] [CrossRef]
- McGreevy, J.P. Thermal properties as controls on rock surface temperature maxima, and possible implications for rock weathering. Earth Surf. Process. Landf. 1985, 10, 125–136. [Google Scholar] [CrossRef]
- Filho, F.F.M.; Morillas, H.; Derluyn, H.; Maguregui, M.; Grégoire, D. In-situ versus laboratory characterization of historical site in marine environment using X-ray fluorescence and Raman spectroscopy. Microchem. J. 2019, 147, 905–913. [Google Scholar] [CrossRef]
- D’Altri, A.M.; de Miranda, S. Environmentally-induced loss of performance in FRP strengthening systems bonded to full-scale masonry structures. Constr. Build. Mater. 2020, 249, 118757. [Google Scholar] [CrossRef]
- Fei, C.; Mao, S.; Yan, J.; Alert, R.; Stone, H.A.; Bassler, B.L.; Wingreen, N.S.; Košmrlj, A. Nonuniform growth and surface friction determine bacterial biofilm morphology on soft substrates. Proc. Natl. Acad. Sci. USA 2020, 117, 7622–7632. [Google Scholar] [CrossRef] [PubMed]
- Wakano, J.Y.; Maenosono, S.; Komoto, A.; Eiha, N.; Yamaguchi, Y. Self-Organized Pattern Formation of a Bacteria Colony Modeled by a Reaction Diffusion System and Nucleation Theory. Phys. Rev. Lett. 2003, 90, 258102. [Google Scholar] [CrossRef] [PubMed]
- Mimura, M.; Sakaguchi, H.; Matsushita, M. Reaction-diffusion modelling of bacterial colony patterns. Phys. A Stat. Mech. Its Appl. 2000, 282, 283–303. [Google Scholar] [CrossRef]
- Hildebrand, M. Diatoms, biomineralization processes, and genomics. Chem. Rev. 2008, 108, 4855–4874. [Google Scholar] [CrossRef]
- Cox, E.J.; Willis, L.; Bentley, K. Integrated simulation with experimentation is a powerful tool for understanding diatom valve morphogenesis. Biosystems 2012, 109, 450–459. [Google Scholar] [CrossRef]
- Pasek, M.A.; Hurst, M. A Fossilized Energy Distribution of Lightning. Sci. Rep. 2016, 6, 30586. [Google Scholar] [CrossRef] [PubMed]
- Libbrecht, K.G. The physics of snow crystals. Rep. Prog. Phys. 2005, 68, 855. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).