Abstract
The evaluation of natural periods and related mode shapes of earth dams represents a critical issue when performing structure-specific probabilistic seismic hazard analyses (PSHA). The identification of critical scenario events, using techniques such as disaggregation of the seismic hazard, and the calculation of a suitable target spectrum for ground motion selection and scaling procedures (e.g., the conditional mean spectrum), require at least the knowledge of the fundamental period of the system. This problem can be solved using analytical, numerical, and/or empirical techniques. We present several linear elastic modal analyses for an earth dam located in Southern Italy, using a numerical solution of the generalized eigenvalue problem obtained by the finite element method (FEM). Our numerical experiments are performed, testing various assumptions on boundary conditions, degree of saturation, and the distribution of geotechnical characteristics of the dam’s materials. We then compare our results against existing analytical solutions. We show that ignoring soil–structure interaction effects due to the flexibility of the dam foundation (i.e., under the assumption of fixed base) can lead to a substantial underestimation of the fundamental period of the dam. This effect should be carefully addressed when modal analysis results are used in PSHA-related applications.
1. Introduction
Earth dams are critical infrastructure systems playing an important role for the global economy. Most earth dams in Western countries were built during the second half of the 20th century [1] and are in their old-age stage [2]. Many of them were designed based on older building codes, without considering seismic actions, or using superseded simplified methods. As a result, there is an urgent need to perform seismic analyses and/or re-evaluations of such important structures. Such analyses are typically performed using response history analyses by means of numerical simulations. This approach is currently required to assess the performance of Italian dams during earthquakes [3,4,5]. Selecting an appropriate suite of input motions for use in response history analyses is an important step of this process. Acceleration time series are typically selected and scaled to be consistent, over a given period range, with a uniform hazard spectrum (UHS) and/or a scenario conditional mean spectrum (CMS [6,7]). Such target spectra and associated scenarios are generally derived from probabilistic seismic hazard analysis (PSHA) outcomes and the results of disaggregation of the seismic hazard. To perform such analyses, it is important to define important periods of the dam-foundation system (i.e., the fundamental period of vibration of the system and higher-mode periods) and their associated mode shapes.
Various methods can be used to identify the fundamental period and higher-mode periods of dams: (1) analytical solutions, such as the shear beam method [8], (2) empirical data analyses, using ambient noise methods or analyzing ground motions recorded at the dam site during earthquake events [9,10] (such methods can also involve operational modal analysis approaches; e.g., [11,12]), and/or (3) numerical simulations, such as the solution of the generalized eigenvalue problem or free-vibration analysis, using finite difference or finite element methods (FEM) [13,14,15]. This study focuses on method (3). Such analyses can be performed at different levels of complexity, ranging from the simple approach of a homogeneous dam on rigid foundation, to the most complex analysis of a zoned earth dam with variable stiffness characteristics with depth on a flexible foundation. Additional hypotheses can be made on the effect of the impounded reservoir and related groundwater flow conditions on the vibrational characteristics of the dam.
In this study, we present results of a numerical solution of the generalized eigenvalue problem obtained using the FEM for the Farneto del Principe earth dam in Calabria, an active seismic region in Southern Italy. Figure 1 shows the location of the Farneto del Principe dam, along with active seismogenic structures (i.e., shallow crustal faults, and the Calabrian Arc subduction zone) compiled and used for site-specific PSHA applications by Zimmaro and Stewart [16]. Figure 2 shows a representative cross-section of the Farneto del Principe dam and its monitoring instrumentation [2]. We perform various numerical experiments testing a number of assumptions on boundary conditions, degree of saturation, and the distribution of geotechnical characteristics of the dam’s materials. We also compare our results against available analytical solutions. We then describe the impact of each simplifying assumption on the correct identification of the important periods of earth dams and associated mode shapes. Through the lens of a case study, we provide conclusions that we believe can be generally applied.
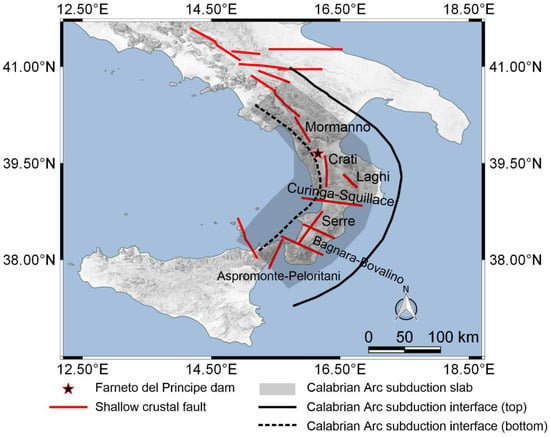
Figure 1.
Location of the Farneto del Principe dam (Southern Italy), shallow crustal seismogenic faults, and Calabrian Arc subduction zone.
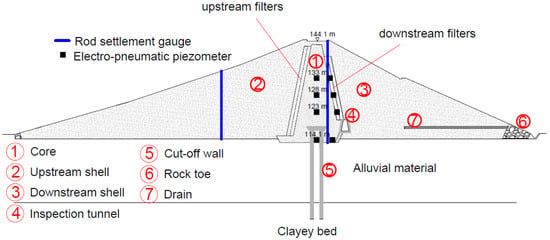
Figure 2.
Representative cross-section and location of the monitoring instrumentation of the Farneto del Principe dam (adapted from [2]).
2. Methodology and Data
Our analysis is based on the numerical solution of the generalized eigenvalue problem obtained using the FEM through the software Sap2000 Research Ultimate V17 [17] for the Farneto del Principe dam. The undamped free-vibration mode shapes and frequencies for this study were calculated, solving the generalized eigenvalue problem (Equation (1)):
where K is the stiffness matrix, M is the diagonal mass matrix, is the diagonal matrix of eigenvalues, and is the matrix of corresponding eigenvectors (mode shapes). Each eigenvalue–eigenvector pair is called natural vibration mode of the dam. The modes are identified by numbers from 1 to n in the order in which the modes are found by the program. The eigenvalue is the square of the circular frequency, ω, for that mode. The cyclic frequency (f) is related to ω by Equation (2), while the period (T) is the inverse of f (Equation (3)):
The numerical model was set up specifying a maximum number of modes to be found equal to 100 and a convergence tolerance of 10−9.
One of the variables in the numerical experiment presented in this paper is the variation of the shear wave velocity, VS (and of the shear modulus, G), of soil with depth. Over the last few decades, several authors investigated this effect for different boundary conditions and soil types [8,18,19,20,21,22,23,24,25]. The scheme used by Dakoulas and Gazetas [8] considers the dependency of the variability with depth of the shear modulus in dams and embankments on an inhomogeneity factor, m, varying from 0 to 1 (Equation (4)):
where Gb is the shear modulus at the base of the dam, z is the depth starting from the top of the model, and H is the total height of the dam. Similarly, it is possible to calculate the variation of VS with depth using the well-known Equation (5):
where VH is the shear wave velocity at the base of the model, n is the inhomogeneity factor that accounts for the variation of VS with depth (notice that n differs than the inhomogeneity factor used in Equation (4), m—the latter is defined as the inhomogeneity factor relative to the shear modulus profile), and b is defined by Equation (6):
where V0 is the initial shear wave velocity at the top of the model (crest of the dam), as shown in the geometrical scheme presented in Figure 3.
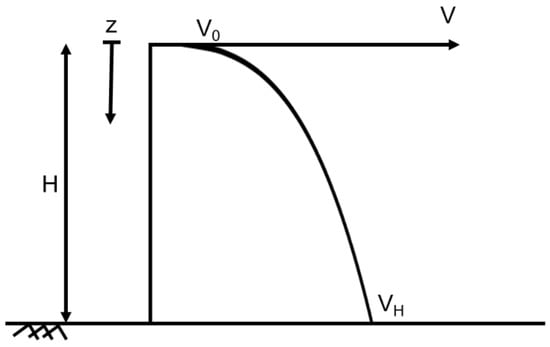
Figure 3.
Shear wave velocity profile scheme.
Another important variable considered in this study is the saturation effect when considering the presence of a water table within the embankment. This effect can be considered using a simplified approach where the Poisson’s ratio for the materials below the phreatic surface is set as equal to 0.49 [26]. Neither groundwater nor hydrodynamic pressure effects were considered in this analysis.
Our analyses are presented for five models of the Farneto del Principe dam, using different levels of sophistication: (1) dam on a rigid base without reservoir, and constant material characteristics with depth, (2) dam on a rigid base and constant material characteristics with depth, considering groundwater flow effects on the degree of saturation of the dam’s material, (3) dam on a rigid base without reservoir, and variable material characteristics with depth, (4) dam on a rigid base and variable material characteristics with depth, considering groundwater flow effects on the degree of saturation of the dam’s material, and (5) dam on a flexible base, and variable material characteristics with depth, considering groundwater flow effects on the degree of saturation of the dam’s material. A summary of the model characteristics is provided in Table 1. In models 2, 4, and 5 a phreatic surface correspondent to the maximum allowable level of the reservoir was considered.

Table 1.
Parameters used for the modal analyses of the Farneto del Principe dam 1.
The main input parameters in the FEM model are: (1) material density, (2) Poisson’s ratio, and (3) shear wave velocity (or shear modulus). Some field and laboratory test results are available for the Farneto del Principe dam [27]. Unit weight (γ) and corresponding density values were derived from the available laboratory data. Shear modulus values were derived using a combination of site-specific data for the Farneto del Principe dam, and data from similar Italian dams. Such additional non structure-specific data were necessary to complement the available field data for the Farneto del Principe dam [2]. Based on this dataset, we estimated an inhomogeneity factor, n = 0.25, with VH = 550 m/s and V0 = 250 m/s, for the shells of Farneto del Principe dam. For the core, we decided to use a constant, VS = 250 m/s (inhomogeneity factor n = 0, according to previous studies for overconsolidated clays [28,29]). These values are in good agreement with available measurements at the Farneto del Principe, San Valentino, Camastra, and Bilancino dam cores [2,30,31]. Input parameters for models 1–5 are summarized in Table 2.

Table 2.
Input parameters used for the modal analyses of the Farneto del Principe dam.
Several analytical methods are available in the literature to estimate natural mode periods of earth dams and similar structures. In this study, we analyze three methods: (1) the homogeneous shear beam solution [8], (2) the inhomogeneous shear beam solution [8], and (3) the classical solution for free undamped vibrations in a single homogeneous layer over rigid base [32]. The latter is not a dam-specific solution, rather, a general solution that can be used for one-dimensional profiles. Equation (7) shows the classical homogeneous shear beam solution commonly used for earth dams [6]:
where βi is a parameter that depends on the geometry of the dam (provided by the authors for several modes). For the case of i = 1 (fundamental period of the dam, T1), Equation (7) becomes the well-known Equation (8):
Equations (9)–(11) present the inhomogeneous shear beam solution by Dakoulas and Gazetas [8]. This solution differs from the approach described by Equation (7), because it accounts for the inhomogeneity of the dam materials and the shear wave velocity variation with depth within the dam body.
where i is the ith mode, m is the inhomogeneity factor (m = 0 corresponds to the homogeneous case—i.e., ai ≡ βi —in this case, Equation (9) can be reduced to Equation (7)) that is provided by the authors for different dam geometries (m = 0.57 for the Farneto del Principe dam), ai is dependent on the inhomogeneity factor m and soil properties (stiffness, geometry, etc.), and is the average shear wave velocity of the dam, calculated using Equation (10):
where Cb is the shear wave velocity at the base of the dam and λ is the so-called truncation ratio of the dam, equal to 0.05 for the case study, that can be calculated using Equation (11):
where h is the vertical distance between the crest of the dam and the top of a triangle having the same slopes of the upstream and downstream shells of the dam (i.e., λ is equal to 0 in the limit case of a triangular dam).
The analytical solution for free undamped vibrations in a single homogeneous layer over rigid base [32] is reported in Equation (12):
3. Results
In this section, we summarize all outcomes of the FEM numerical experiments we performed on the five models of the Farneto del Principe dam, shown in Table 1. Modal analysis results can provide important information on the range of important periods for the dam. Such a period range can be then used for selecting and scaling ground motions to match the horizontal component of a target spectrum (UHS and/or CMS). As a result, the most important translational horizontal modes are shown and discussed in this section. The level of importance of each mode is defined based on modal participating mass ratio (MPMR) values (i.e., the percentage of total structural masses involved in each mode).
Figure 4a shows the mesh used to build Model 1 (dam on a rigid base without reservoir, and constant material characteristics with depth), while Figure 4b,c show the first and the second mode shape, respectively. Figure 5a–c show the mesh of Model 2 (dam on a rigid base and constant material characteristics with depth, considering groundwater flow effects on the degree of saturation of the dam’s material), its first and second mode shape, respectively. The difference between Models 1 and 2 is that in Model 1, all soils are dry, while in Model 2, the upstream shell and core materials are considered saturated below the phreatic surface. In both models, the shear modulus is constant with depth. Figure 6a–c show the mesh of Model 3 (dam on a rigid base without reservoir, and variable material characteristics with depth); first and second mode shapes, respectively. The shear modulus of the shells of Model 3 is variable with depth with the law shown in Equations (5) and (6). Model 3 does not consider the effect of water within the dam body. Model 4 considers both the effect of saturation within the dam body and the shear modulus of the shells variable with depth. Model 4’s first and second mode shapes are shown in Figure 7a–c. Model 5 is similar to Model 4, but it includes the effect of the flexibility of the dam’s foundation. Thus, Model 5 accounts for the impact of soil structure interaction (SSI) effects on the modal analysis. The foundation material is 17 m deep below the base of the dam, it comprises sand and gravel, and it was modelled as a continuous, homogeneous layer with a shear wave velocity of 650 m/s. On the lateral boundaries the vertical displacements are restrained, while the base is fixed in both directions. Figure 8a–c show the mesh used for Model 5; its first and second mode shapes.
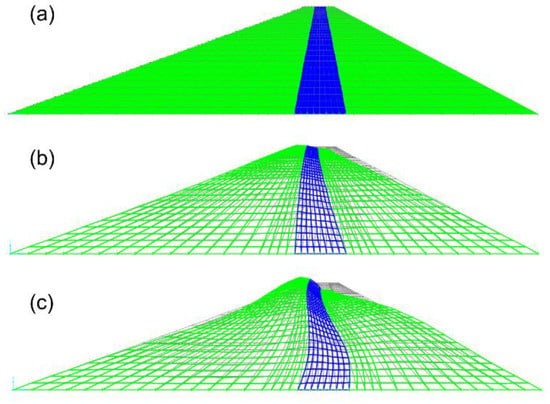
Figure 4.
Finite element method (FEM) Model 1: (a) undeformed mesh, (b) first mode shape, and (c) second mode shape.
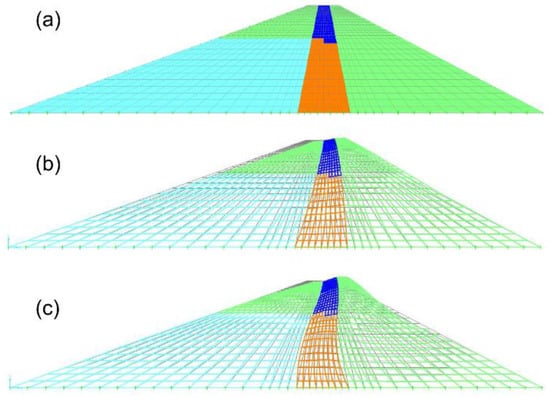
Figure 5.
FEM Model 2: (a) undeformed mesh, (b) first mode shape, and (c) second mode shape.
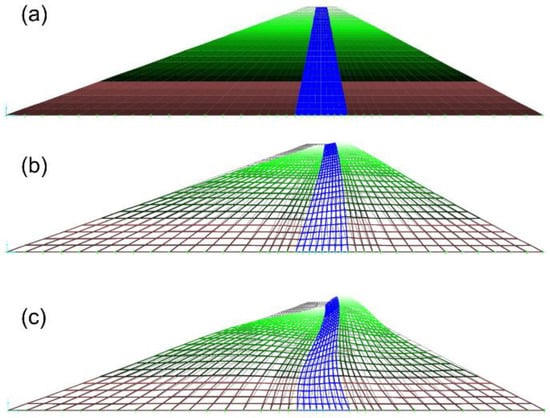
Figure 6.
FEM Model 3: (a) undeformed mesh, (b) first mode shape, and (c) second mode shape.
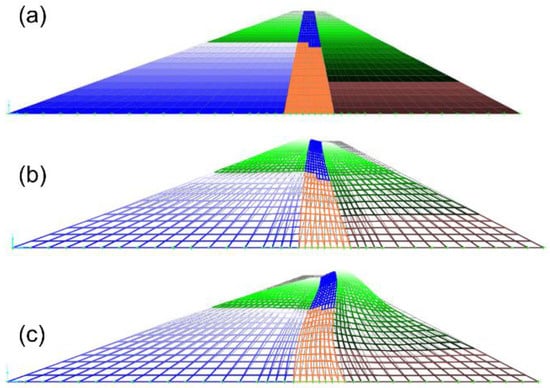
Figure 7.
FEM Model 4: (a) undeformed mesh, (b) first mode shape, and (c) second mode shape.
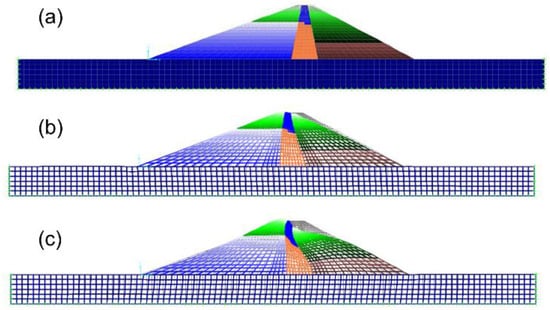
Figure 8.
FEM Model 5: (a) undeformed mesh, (b) first mode shape, and (c) second mode shape.
Table 3 shows, for all fixed base models (Models 1–4), natural periods and MPMRs for the four most important modes. The analysis of Table 3 shows that modal periods and MPMR are similar for all four models. This outcome suggests that even a simplified FEM model can provide useful information on the vibrational characteristics of earth dams. It should be noted that MPMRs in Table 3 do not sum up to 100%. This effect is due to a “dispersion” of contribution in spurious and predominantly vertical modes that were excluded from the analysis.

Table 3.
Modal periods and MPMRs for Models 1–4 (fixed base models).
Table 4 shows a direct comparison for the two most important modes of Models 4 and 5. This comparison illustrates the impact of SSI effects on the natural periods of the dam. To add the foundation below the dam body, the boundary conditions of the FEM model needed to be modified, and the model itself extended laterally. This modification of the model’s geometry has an influence on the MPMR values. As a result, a formal comparison of MPMR values between Models 4 and 5 cannot be performed. Table 5 shows that the deformability of the foundation has an important impact on the natural periods of the dam. The elongation of the fundamental period (ΔT1) is equal to 22%. Such elongation is also evident, looking at the second modal period, where ΔT2 = 29%. These results highlight the importance of considering the dam foundation when performing modal analyses. SSI effects due to the flexibility of the foundation have a strong impact on all important modes of earth dams. This finding is consistent with other studies on the vibrational characteristics of earth dams [33]. Such effect is much more important than that of the degree of saturation within the dam and the variability of shear modulus values in the dam core.

Table 4.
Comparison between Model 4 (fixed base) and 5 (flexible base).

Table 5.
Modal periods for three analytical solutions used in this study and complete fixed-base FEM solution (Model 4).
From the analysis of Table 3 and Table 4, it is evident that the Farneto del Principe dam, regardless of the boundary conditions and assumptions made to build the model, is a first-mode dominated structure (i.e., the MPMR of the first mode is significantly higher than those of higher modes). Furthermore, the MPMR of the first two modes, for all models, is higher than 70%. This outcome is expected for an earth dam. For such structures, the target CMS should be constructed using a single anchoring period, or it can be broadened over a relatively narrow conditioning period range [34].
Table 5 shows the four most important periods obtained using the homogeneous shear beam solution, the inhomogeneous shear beam solution, and the solution for free undamped vibrations in a single homogeneous layer over rigid base. These models all assume rigid base conditions. As a result, all periods reported in Table 5 should be compared with results from FEM models with the same boundary conditions (i.e., Models 1–4). To facilitate such comparison, Table 5 also shows the four most important periods for Model 4. Both shear beam solutions underestimate period values for the most important modes of vibration of the dam, if compared with the numerical solution obtained using Model 4. This effect mainly depends on the ratio of the average shear wave velocity between core and shells. The simplified solution for free undamped vibrations in a single homogeneous layer over rigid base overestimates the first mode period and underestimates higher-mode periods. Given the big differences between this method and the FEM models, we argue that this simple solution should not be used to estimate natural mode periods of earth dams.
4. Discussion and Conclusions
The identification of the vibrational characteristics of earth dams is extremely useful when analyzing the seismic performance of such structures. Such information is even more important in PSHA contexts, and when performing numerical response history analysis for which the definition of target spectra (UHS or CMS) is necessary. The identification of natural periods of earth dams can be performed using analytical, numerical, and/or empirical techniques. In this paper, we presented several linear elastic modal analyses for the Farneto del Principe dam in Southern Italy, using a numerical solution of the generalized eigenvalue problem obtained by the FEM. Our study solely focuses on numerical approaches. The goal of the study is twofold: (1) test and verify the validity of various typical simplifying assumptions on the outcomes of numerical solutions of the eigenvalue problem, and (2) provide guidance on how to use such results in a PSHA context. We recognize that empirical data can be used in combination with numerical solutions to identify important frequencies of such structures. In this connection, modelling choices could be validated using operational modal analysis approaches (e.g., [11,12]).
We investigate the effect of various assumptions on boundary conditions and material characteristics of the model by means of various numerical experiments. Our analysis shows that the influence of material saturation and the variation of the shear modulus with depth in the dam shells is negligible. We also show that SSI effects due to the presence of a flexible foundation beneath the dam body produce substantial period elongations for all main vibration modes of the dam. As a result, such effects should always be modelled when numerical simulations are used to derive modal periods. By comparing results from our FEM solutions and available analytical models, we demonstrated that analytical shear beam solutions are appropriate to identify important periods of the dams on fixed base. Such analytical models should not be used when a flexible foundation is present. Simplified one-dimensional analytical solutions overestimate the natural period of the Farneto del Principe dam by large amounts. As a result, it should not be used to estimate natural periods of earth dams.
Our analysis clearly shows that earth dams are first-mode dominated structures. As a result, the use of CMS based on a single conditioning period or a narrow range of conditioning periods is appropriate when deriving scenario target spectra for dam-specific applications. Although this conclusion is drawn using results from a single structure, it can be generalized as the vibrational characteristics of earth dams (as other large infrastructure systems) are typically dominated by the first mode of vibration. However, care should be used when defining important period ranges, as the relative importance of the first and higher-mode periods is a highly structure-dependent property.
Author Contributions
Conceptualization, P.Z. and E.A.; methodology, P.Z. and E.A.; software, P.Z. and E.A.; validation, P.Z. and E.A.; formal analysis, P.Z. and E.A.; resources, P.Z. and E.A.; writing—original draft preparation, P.Z. and E.A.; writing—review and editing, P.Z. and E.A.; visualization, P.Z. and E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ernesto Ausilio’s research funds of University of Calabria.
Acknowledgments
The Authors are deeply indebted and would like to dedicate this paper to Massimo Mancuso (Dipartimento di Ingegneria “Enzo Ferrari”, Università di Modena e Reggio Emilia, Italy), who developed, together with the Authors, the concept of this paper and the numerical experiments presented herein.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Penman, A.D.M. On the embankment dam. Geotechnique 1986, 36, 301–348. [Google Scholar] [CrossRef]
- Zimmaro, P. Seismic Response of the Farneto del Principe Dam in Italy Using Hazard-consistent and Site-specific Ground Motions. Ph.D. Thesis, University Mediterranea, Reggio Calabria, Italy, March 2015. [Google Scholar]
- Norme Tecniche per la Progettazione e la Costruzione Degli Sbarramenti di Ritenuta (Dighe e Traverse); Ministry of Infrastructures and Transport of Italy: Rome, Italy, 14 June 2014. (In Italian)
- Aggiornamento delle Norme Tecniche per le Costruzioni; Ministry of Infrastructures and Transport of Italy: Rome, Italy, 17 January 2018. (In Italian)
- Verifiche Sismiche delle Grandi dighe, degli Scarichi e delle opere Complementari e Accessorie; Ministry of Infrastructures and Transport of Italy: Rome, Italy, 3 July 2019. (In Italian)
- Baker, J.W. Conditional Mean Spectrum: Tool for ground motion selection. J. Struct. Eng. 2011, 137, 322–331. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C.A. Spectral shape, epsilon and record selection. Earthq. Eng. Struct. Dyn. 2006, 35, 1077–1095. [Google Scholar] [CrossRef]
- Dakoulas, P.; Gazetas, G. A class of inhomogeneous shear models for seismic response of dams and embankments. Soil Dyn. Earthq. Eng. 1985, 4, 166–182. [Google Scholar] [CrossRef]
- Watanabe, H.; Kikuchi, K.; Cao, Z. Vibration Modes of Rockfill Dam Based on the Observations of Microtremors and an Earthquake; Research report; Thammasat Univ. Rangsit Campus: Pathum Thani, Thailand, 1995. [Google Scholar]
- Castro, R.R.; Mucciarelli, M.; Pacor, F.; Federici, P.; Zaninetti, A. Determination of the characteristic frequency of two dams located in the region of Calabria. Bull. Seismol. Soc. Am. 1998, 88, 503–511. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014. [Google Scholar]
- Aloisio, A.; Di Pasquale, A.; Alaggio, R.; Fragiacomo, M. Assessment of seismic retrofitting interventions of a masonry palace using operational modal analysis. Int. J. Archit. Herit. 2020, 1–13. [Google Scholar] [CrossRef]
- Chugh, A.K. Natural vibration characteristics of gravity structures. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 607–648. [Google Scholar] [CrossRef]
- Chakraborty, S.; Das, J.T.; Puppala, A.J.; Banerjee, A. Natural frequency of earthen dams at different induced strain levels. Eng. Geol. 2019, 248, 330–345. [Google Scholar] [CrossRef]
- Yaseri, A.; Konrad, J.M. Estimation of natural periods of earth dam-flexible canyon systems with 3D coupled FEM-SBFEM. Comput. Geotech. 2020, 123, 103546. [Google Scholar] [CrossRef]
- Zimmaro, P.; Stewart, J.P. Site-specific seismic hazard analysis for Calabrian dam site using regionally customized seismic source and ground motion models. Soil Dyn. Earthq. Eng. 2017, 94, 179–192. [Google Scholar] [CrossRef]
- CSI Analysis Reference Manual for SAP2000, ETABS and SAFE; Computers and Structures, Inc.: Berkeley, CA, USA, 2013.
- Ambraseys, N.N. A note on the response of an elastic overburden of varying rigidity to an arbitrary ground motion. Bull. Seismol. Soc. Am. 1959, 49, 211–220. [Google Scholar]
- Seed, H.B.; Idriss, I.M. The influence of ground conditions on ground motions during earthquakes. J. Soil Mech. Found. Div. 1969, 94, 93–137. [Google Scholar]
- Dobry, R.; Whitman, R.; Roesset, J.M. Soil Properties and the One-dimensional Theory of Earthquake Amplification; Research Report R71-18; M.I.T.: Cambridge, MA, USA, May 1971. [Google Scholar]
- Schreyer, H. One-dimensional elastic waves in inhomogeneous media. J. Eng. Mech. Div. 1977, 103, 979–990. [Google Scholar]
- Gazetas, G. Vibrational characteristics of soil deposits with variable wave velocity. Int. J. Numer. Anal. Methods Geomech. 1982, 6, 1–20. [Google Scholar] [CrossRef]
- Towhata, I. Seismic wave propagation in elastic soil with continuous variation of shear modulus in the vertical direction. Soil. Found. 1996, 36, 61–72. [Google Scholar] [CrossRef]
- Rovithis, E.; Parashakis, C.; Mylonakis, G. 1D harmonic response of layered inhomogeneous soil: Analytical investigation. Soil Dyn. Earthq. Eng. 2011, 31, 879–890. [Google Scholar] [CrossRef]
- Durante, M.G.; Karamitros, D.; Di Sarno, L.; Sica, S.; Taylor, C.A. Characterisation of shear wave velocity profiles of non-uniform bi-layer soil deposits: Analytical evaluation and experimental validation. Soil Dyn. Earthq. Eng. 2015, 75, 44–54. [Google Scholar] [CrossRef]
- Bishop, A.W.; Height, D.W. The value of Poisson’s ratio in saturated soils and rocks stressed under undrained conditions. Geotechnique 1977, 27, 369–384. [Google Scholar] [CrossRef]
- Ausilio, E.; Dente, G.; Zimmaro, P. Geotechnical Investigation and Field Performance of a Zoned Earth Dam in Italy. In Proceedings of the 1st IMEKO TC4 International Workshop on Metrology for Geotechnics, Benevento, Italy, 16–18 March 2016. [Google Scholar]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundations; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1970. [Google Scholar]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Measurement and parameter effects, Terzaghi Lecture. J. Soil Mech. Found. Div. 1972, 98, 603–624. [Google Scholar]
- Mancuso, C. Aspetti Metodologici ed Applicazione della Tecnica Sperimentale SASW. Riv. Ital. Geotec. 1995, 4, 271–288. [Google Scholar]
- Pagano, L.; Mancuso, C.; Sica, S. Prove in sito sulla diga del Camastra: Tecniche sperimentali e risultati. Riv. Ital. Geotec. 2008, 3, 11–28. [Google Scholar]
- Jacobsen, L.S. Motion of a soil subjected to a simple harmonic ground vibration. Bull. Seismol. Soc. Am. 1930, 20, 160–195. [Google Scholar]
- Idriss, I.M.; Mathr, J.M.; Seed, H.B. Earth Dam-foundation interaction during earthquakes. Earthq. Eng. Struct. Dyn. 1973, 2, 313–323. [Google Scholar] [CrossRef]
- Carlton, B.; Abrahamson, N. Issues and approaches for implementing conditional mean spectra in practice. Bull. Seismol. Soc. Am. 2014, 104, 503–512. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).