Abstract
Autonomous surgery involves surgical tasks performed by a robot with minimal or no human involvement. Thanks to its precise automation, surgical robotics offers significant benefits in enhancing the consistency, safety, and quality of procedures, driving its growing popularity. However, ensuring the safety of autonomous surgical robotic systems remains a significant challenge. To address this, we propose a simulation-based validation method to detect potential safety issues in the software of surgical robotic systems, complemented by a digital twin to estimate the gap between simulation and reality. The validation framework consists of a test case generator and a monitor for validating properties and evaluating the performance of the robotic system during test execution. Using a robotic arm for needle insertion as a case study, we present a systematic test case generation method that ensures effective coverage measurement for a three-dimensional, irregular model. Since no simulation can perfectly replicate reality due to differences in sensing and actuation, the digital twin bridges the gap between simulation and the physical robotic arm. This integration enables us to assess the discrepancy between virtual simulations and real-world operations by verifying whether the data from the simulation accurately predicts real-world outcomes. Through extensive experimentation, we identified several flaws in the robotic software. Co-simulation within the digital twin framework has highlighted these discrepancies that should be considered.
1. Introduction
Autonomous systems are typically designed to operate in real-time, using multiple cooperating modules to pursue specific goals within complex, dynamic environments while satisfying global constraints. Progress in robot autonomy is enabling robots to perform a wider range of tasks in more environments, such as autonomous delivery systems, precision manufacturing, and exploratory drones for environmental monitoring.
Robotic systems are increasingly being incorporated into surgical procedures [1,2]. Robot-assisted surgeries have demonstrated many benefits over the traditional approach including lower risk of infection, shorter recovery, and a safer procedure for patients. The da Vinci system [3] is one of the successful applications in robotic-assisted surgery. The surgical console provides surgeons with direct control over the instruments used in operations. Meanwhile, the success of AI in image recognition and decision-making is advancing autonomous robotic surgery, with these techniques being integrated into existing systems to increase their level of autonomy [4,5]. For example, trajectory tracking can adopt reinforcement learning techniques to achieve higher accuracy [6], and deep learning techniques can assist in medical imaging [7]. However, most AI-based techniques lack interpretability and failures in the autonomous system could lead to serious consequences.
The combination of these characteristics makes system-level verification extremely challenging and often infeasible [8]. A potential solution is simulation-based validation [9], which simulates system operation and evaluates its performance based on the simulated results. Simulation is generally more cost-effective and safer for collecting experimental data and can be executed during the system design phase rather than through real-world operation. Therefore, simulation-based testing is widely adopted to validate robotic and autonomous systems.
However, the system’s inherent complexity and the black-box nature of its AI components make it challenging to assess test adequacy and generate cases that reveal system defects [10,11].
Industrial players and academic partners have made significant efforts to evaluate and validate simulation-based systems. For example, numerous studies focus on testing autonomous driving systems [12,13,14,15]. However, there is comparatively little research on robotic systems. Given the large volume of potential test cases for autonomous systems, evaluating the adequacy of tests—an essential and challenging task—remains difficult. This challenge is particularly exacerbated in the simulation-based validation of robotic systems used in surgical procedures.
Furthermore, no simulation can perfectly replicate reality [16]. The idealized environment within a simulator does not fully reflect its real-world counterpart, and the control and motion of a virtual robot differ from those of a physical one. As a result, accurately predicting the gap between simulated and physical operations becomes a significant challenge.
The robotic systems literature currently lacks standardized testing methodologies and robust evaluation metrics for assessing system-level quality [9]. To explore feasible solutions for ensuring test coverage and effectiveness, we consider a robotic arm capable of autonomously performing a needle insertion task as our case study. Robotic arms, with functions similar to human arms, are widely used in manufacturing, healthcare, and home service applications.
To systematically validate the robotic arm’s safety and control performance in task execution and obstacle avoidance, we propose a discretization method for measuring test sufficiency. For performance comparison between virtual and real worlds, we built a validation framework that combines a physical robotic arm with an existing simulator equipped with an identical model to the physical counterpart. To drive the simulation and validate the simulated system against given properties or key performance indicators (KPIs), the framework also includes a test case generator and a runtime monitor. The monitor extracts the global states from the simulator or the physical robotic arm and evaluates deviations from the requirements. The test case generator systematically generates test cases based on the given target model. These generated test cases are fed into the simulator to detect any abnormalities in the simulation. Meanwhile, the framework can also feed the test cases into the physical robotic arm to compare the trajectory differences between the virtual and the real world.
The contributions of the paper are multi-fold:
- We have proposed a general test case generation method for robotic arms to facilitate coverage measurement. It discretizes the input domain, specifically a three-dimensional (3D) irregular model of the target, as the basis of coverage metrics for the test inputs and the guidance of the effective validation process.
- We have developed a validation framework for robotics using a digital twin that links a simulator and a physical robotic arm. The simulator and the physical robotic arm can synchronize through the real-time trajectory data of the robotic arm. The functionality of the robotic arm can be validated in a simulated interplay during the design phase. By using a digital twin, we can assess whether simulation results accurately predict real-world behavior. Furthermore, this approach enables us to quantify the gap between simulated outcomes and actual performance in the real world.
- We have conducted extensive experimentation on a needle insertion case study. The gradual refinement of the discretization granularity helps identify the defect of the system efficiently and highlights the advantages of our method over the random method.
The organization of this paper is as follows. Section 2 provides an overview of the framework. In Section 3, we describe the problems addressed in the paper. We propose the testing and validation method for autonomous surgical robotic systems in Section 4. The detailed comparison with the randomized test case generation, and the comparison between virtual and physical simulation are demonstrated in Section 5. After the discussion of the related work in Section 6 and threats to the validity of the work in Section 7, we conclude in Section 8.
2. An Overview of the Framework
In Figure 1, we present an overview of the proposed framework which utilizes an existing robotic simulator (CoppeliaSim Simulator [17] in this work) and integrates it with a test case generator and a monitor for the validation of the robotic system. The framework is also equipped with interfaces to connect a physical robotic arm in the validation process. The idea of the framework is to leverage a publicly available simulator to validate autonomous robotic arms against given properties and KPIs.
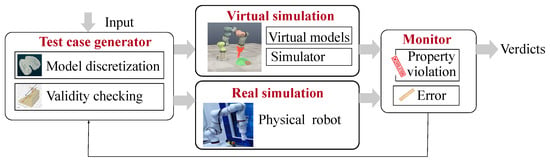
Figure 1.
The digital twin validation framework.
The test case generator drives both the simulation and physical operation process with a predefined strategy. Given the models and their positions, as well as the initial configuration of the robotic arm, it generates test cases that require the robotic arm, whether in a physical or virtual platform, to execute a sequence of actions to complete. In this paper, we consider an autonomous robotic arm for needle insertion as the case study. The source (the original position) of the robotic arm is relatively fixed. The target points (in the lung model) play the role of test cases intended to drive the simulated system towards specific configurations, for example, to meet specific coverage criteria.
The simulator executes a cyclic process on a system model comprising the robotic arm, a target lung model, and obstacle models for collision avoidance (e.g., the heart and blood vessels). In each cycle, the simulator provides coordinate information to each of the arm’s joints, whose state is defined by its kinematics and position. The resulting global behavior must satisfy all specified safety properties and performance requirements.
The monitor checks the extracted runs (trajectories) of the simulated system from the simulator against given criteria and reports any system performance issues and property violations.
3. Problem Statement
A robotic system can implement various functionalities. In the case study, we consider a 7-DOF (degree of freedom) robotic system for autonomous needle insertion surgery. The 7-DOF robotic arm features a 360-degree rotating base and six subsequent joints, each driven by an individual servo motor with integrated sensors for precise angular positioning. Rigid links connect the axes and house internal components like cabling. The arm terminates in a versatile mounting point for attaching application-specific end-effectors. The arm is controlled by specifying a 7-dimensional vector of joint angles, which fully defines its configuration. However, not all vectors represent valid states. Invalid states fall into two categories: those exceeding the mechanical limits of a joint’s angular range, and those resulting in self-collision. The end-effector’s position for a given joint vector is computed via forward kinematics. Conversely, inverse kinematics calculates the joint angles required to achieve a desired end-effector position.
The goal of the needle insertion procedure for the robotic system is twofold: first, to reach a specified target point in the lung, and second, to do so without causing injury to adjacent organs or self-collision between the robot’s components.
The needle insertion process consists of five stages:
- 1.
- Initialization stage: moving the needle from the default position to the source position specified in the test input.
- 2.
- Approaching stage: moving the needle from the source position to the point on the skin for needle insertion.
- 3.
- Injection stage: injecting from the point on the skin to the target point in the lung.
- 4.
- Extraction stage: pulling out the needle from the target point out of the skin.
- 5.
- Reset stage: returning the needle to the source position.
Among these five stages, the third and the fourth stages are the most important, for they are internal operations, and any misoperation may lead to physical injury to patients.
In the case study, the target point in the lung must be located outside of any bronchial passages or blood vessels. At the same time, the needle must not collide or penetrate these structures.
The lung model is simplified by neglecting deformation, respiratory motion, and internal structures such as bronchi and blood vessels.
During the needle insertion process, targeting errors (needle misplacement) can occur. Clinical studies have identified several causes for these errors, including imaging limitations, image misalignments, target uncertainty, tissue deformation-induced target movement, and needle deflection. It is crucial to minimize the targeting error, ensuring that it remains within the specified bounds. Aside from the constraints on targeting error, during the injection stage, the needle must maintain a consistent angle to avoid enlarging the penetration area. In addition, the trajectory during the injection stage should align with that of the extraction stage.
For a given pair of source and target points, the system autonomously plans a trajectory and executes the procedure while avoiding collisions between its own joints and surrounding organs. Consequently, this operational domain is formally represented by the lung model and a set of obstacle models. A test case within this environment specifies a source point outside the lung and a target point within it. A successful test requires the arm to reach the target within a tolerable error while ensuring no collisions occur throughout the motion.
To validate the robotic system against the specified criteria, it is essential to design effective test generation methods and metrics for the validation process and assess the consistency between virtual simulations and physical operations.
4. Proposed Method
In the simulation-based needle injection process, users first select a target point. The system then autonomously generates a path—a sequence of coordinates and joint angles—for the robotic arm’s movement, based on the specified obstacles and target model in the input. As we focus on the validation method for autonomous robotic systems, we regard the robotic system as a black box and check whether the system satisfies the requirement. Therefore, the test generation method does not consider the mechanisms of the robotic arm. The validation process tests whether the needle, attached to the robotic arm, can reach the target point without violating safety constraints and KPIs.
4.1. Coverage-Oriented Automatic Test Case Generation
Unlike the operational design domain of autonomous driving systems, which involves a wide range of input parameters, the robotic arm system operates with a relatively smaller set of input parameters. For a test case, the source point is the starting point of the robotic arm, which is outside any models. However, the domain of targeting points is a continuous and irregular three-dimensional space—a 3D lung model that can be sampled during needle injection surgery. Consequently, the generation of valid test cases and the evaluation of coverage present a significant challenge.
Random sampling cannot guarantee uniform coverage across the entire model. To effectively measure the coverage of a set of test cases, we propose to divide the 3D model into multiple cubes. The number of cubes is countable, whereas the number of points within each cube is uncountable. We adopt the number of explored cubes to measure the coverage of the test suite. For example, Figure 2a,b present the three-dimensional models of the left and right lungs. This geometry was discretized into a finite number of cubes (Figure 2c), where a smaller cube size yields a finer granularity.
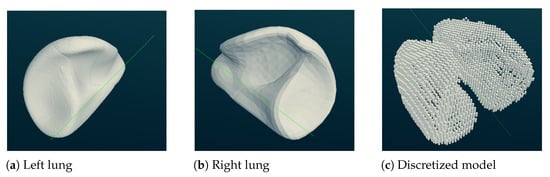
Figure 2.
The lung model and its discretization.
Because the lung model has an irregular shape, not all cubes in the discretized grid are fully occupied. As shown in Figure 3a, a cube may intersect with the model, resulting in a partially filled volume like the one highlighted in yellow. Consequently, discretization yields two cube types: fully filled and partially filled. For partially filled cubes, a selected target point may lie outside the lung model, which would make the test case invalid.
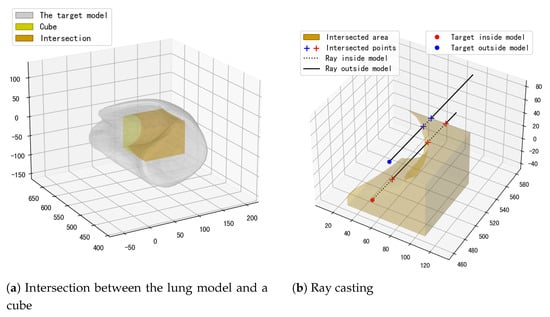
Figure 3.
Ray casting method.
To generate valid test cases, we use the ray casting algorithm [18] to determine whether a selected point lies within the target model. According to the algorithm, if the number of intersections between the model and a ray originating from a given point is odd, the point is inside the model. For example, in the partially filled cube of Figure 3b, the red point lies inside the model, as the number of intersections between the model and the ray is odd. In contrast, the blue point lies outside the model, since the number of intersections is even. Because the lung model is non-convex, validity checking is required for each generated test case.
To improve the efficiency of test case generation, we mark the fully filled cubes during the model discretization process. Consequently, validity checks are performed only for the partially filled cubes.
4.2. Assessment Metrics
The validation of the robotic system takes into account the motion trajectory of the robotic arm, which is represented as a sequence of states. For an n-DOF robotic arm, a state is defined as the vector of coordinates and angles of n joints, denoted by . Each joint is represented by its 3D Cartesian coordinates and the direction of the vector, characterized by its azimuth and altitude . When the robotic arm is in state s, the state of the needle attached to the end-effector, denoted by , which includes the position and the angular orientation of the needle tip, can be computed based on state s.
In the operating process, we assume that the states of joints in a robotic arm are updated periodically at intervals of time units. During the motion of the robotic arm from a source to a target point, the run of the system within the time interval is then denoted by a sequence of states , where is the state of the joints when the robotic arm is at the source. The sequence of states for the needle tip is denoted by , representing its trajectory, with a total length of . In the autonomous robotic arm system, the planned trajectory of the needle for a given test input is denoted by .
By abuse of notation, we define the following functions to represent the distance between two components, x and y:
- : the Euclidean distance between two points x and y in Cartesian coordinates.
- : the distance between a point x and a trajectory y. If the point is inside the trajectory, it returns 0. Otherwise, it returns the minimal distance between the point and the trajectory.
- : the minimal distance between a point x and the surface of model y. If the point is inside the model, it returns 0.
- : the distance between two trajectories x and y.
Let M be the target model and be a set of obstacles. We require that for any joint of state s and any obstacle with , {p2mdis, p2mdis, where {p2mdis is the minimal distance between the joints to the surface of the model , and is the tolerable constant. That is, all the joints of the robotic arm should keep a safe distance from the obstacles. Meanwhile, at any state s, the joints of the robotic arm should not collide with each other, which is denoted by , where .
During simulation, the needle tip’s trajectory is extracted by periodically sampling the robotic arm’s state. However, sampling variations can cause the same test case to yield trajectories with different numbers of states across simulation runs. Therefore, pairwise distance between states is an unreliable metric for measuring trajectory similarity.
We adopt Fréchet distance [19] in function t2tdis() as the measure of similarity between two trajectories. As a trajectory consists of a sequence of points, we utilize the discrete Fréchet distance.
Let and be two given trajectories. Trajectory has n points , and has m points .
A coupling L between the two trajectories is a sequence
where , and , and for every step i, or , and or .
Let be the set of coupling sequences. The discrete Fréchet distance between trajectories and is
In other words, the discrete Fréchet distance is the smallest maximum pairwise distance between corresponding points on two trajectories. More formally, it measures the similarity between two trajectories by identifying the smallest maximum distance between any pair of corresponding points along the trajectories. This approach ensures that overall similarity is captured, even if the trajectories have a different number of points or were sampled at varying rates.
4.3. Considered Properties
Our simulation-based validation framework assesses both safety properties, to ensure reliability, and key performance indicators (KPIs), to quantify system performance.
In this section, we formalize safety properties as formulas in linear temporal logic. We consider first-order linear temporal logic using temporal modalities with their usual meanings. For example, let be a property to be satisfied by the robot; the following formula specifies that for any run of the system with n joints and a set of k obstacles , formula should always hold on a system run:
In addition to the quantitative metrics of system performance defined in Section 4.2, we introduce the following predicates for the property specification.
- safediff, if the difference between two values and is less than a given bound , i.e., .
- safebound, if the Euclidean distance of two points x and y is less than some given bound, i.e., .
- safedis, if the Euclidean distance of the two points x and y is greater than zero, i.e., .
- nocollision, if the point x is out of the model M, i.e., p2mdis.
We list the properties and KPIs of the robotic arm considered in the case study in Table 1. The first category considers the avoidance of collisions between the components of the robotic arm and obstacles. The second category focuses on KPIs for the precision of the operation.

Table 1.
Typical properties of the robotic arm and the specification in linear temporal logic.
5. Implementation and Experimentation
5.1. Implementation
We have implemented the proposed method to validate the robotic arm system within the framework. The test case generator systematically produces valid test cases with the given target and obstacle models. The test cases drive the virtual simulation in the simulator or the physical robotic arm. The monitor extracts trajectories from the virtual or physically simulated system, evaluates the KPIs, and checks the satisfiability of the properties considered. The test case generator and the monitor are both implemented in Python 3.8.10.
Figure 4 illustrates the digital twin environment, which integrates multiple modules to operate physical and virtual robots in parallel. Data flow between these modules is indicated by their connecting edges. It provides versatile programming APIs to switch between virtual and physical robotic systems and extract the necessary information in the simulation. We have also developed interfaces to feed the test cases into the digital twin and to synchronize the virtual simulation with the physical robotic system.
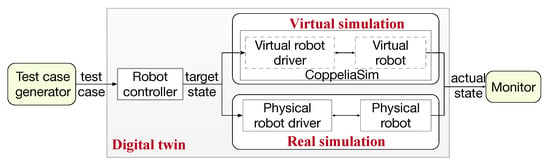
Figure 4.
Implementation of the digital twin.
The system under test is the robot controller software, which communicates via TCP with a kinematic module implemented in C++ using ROS and MoveIt 1.1.11. This module is configured with custom kinematics for the robot. Upon receiving a target state from the controller for a given test case, the robot driver commands the robot to reach that state. Execution is handled by either a manufacturer-provided driver for the physical robot or an integrated driver for the virtual robot in the simulator.
We adopt the CoppeliaSim Simulator [17] to simulate the robotic system, which provides multi-physics engine support and well-maintained documents to develop the custom components. In the simulator, each model can be controlled individually in various ways, such as an embedded script, a plugin, a remote API client, or a custom solution.
Both virtual and physical elements share a common test case generator, robot controller, and monitor. However, they are driven by separate, platform-specific drivers. The controller receives a task from the test case generator and computes the target state for each timestep. This target state is dispatched to the respective driver, which commands the robotic arm to achieve it.
The actual state of each robot is continuously sampled and sent to a unified monitor. The monitor subsequently analyzes the functional and performance data from both systems for comparison.
5.2. Experimentation
We consider the following research questions in the experimentation.
- : Is the discretization effective in ensuring the coverage for test case generation?
- : Is the simulation-based validation effective in revealing the deficiencies of the software system in the robotic arm?
- : Is performance evaluation from a virtual simulation predictive of real-world performance?
To answer the first research question, we carry out experiments with different discretization granularities and compare the coverage and error-triggering rates against those obtained using the random method. Coverage is measured by the percentage of the discretized areas covered by the generated test cases, while the error-triggering rate is the percentage of those test cases that violate a specified property.
To answer the second research question, we employ simulation-based testing to validate the properties and evaluate the KPIs. The resulting property violations and KPI measurements demonstrate the effectiveness of our test case generation method.
To answer the third research question, we compare the deviations from the expected trajectories in both the virtual simulation and physical operation using a common set of test cases, in order to assess whether the deviations are similar.
5.2.1. Setup
To evaluate the effectiveness of our discretization method in ensuring coverage and revealing system deficiencies, we use random test case generation as a baseline. This random method is a widely adopted standard in software and system testing due to its simplicity and minimal assumptions. Since a proper discretization granularity cannot be determined theoretically, we refine it incrementally and assess its impact experimentally.
The framework uses a sampling frequency of 10 Hz (i.e., a 100-ms interval). The physical robot is an ER3 Pro-M manufactured by ROKAE (https://www.rokae.com/en/ (accessed on 29 August 2025)), supporting a maximum load of 3 kg. The virtual robot is simulated with the model of ER3 Pro-M in the CoppeliaSim simulator. The physical robotic system and its virtual counterpart are configured with identical parameters.
In the experimentation, the joints can always avoid collision with each other. However, the needle cannot maintain the same angle during the injecting and extracting stages. Therefore, we focus solely on the safety property that the needle must avoid collision with the heart model. Meanwhile, for KPIs, we consider the difference between the expected and the actual targets or traces.
5.2.2. : Effectiveness of Discretization in Coverage Assurance
In this experiment, we use the left lung model with three levels of coarse granularity and focus on the safety property that the needle must avoid collision with the heart model. For each granularity level, we randomly select three points as targets within each discretized area during the experiment, ensuring full coverage of the model and diversity in the test cases.
We first compare the performance of our method with the random generation method in terms of coverage and error-triggering rate. An example of a violation of safety properties is illustrated in Figure 5. The green zones represent the patient’s lungs, which are accessible for puncture. The red zone represents the heart, which is a forbidden zone. The needle is permitted to puncture the green zone but must never enter the red zone. In this example, a flaw in the robot’s controller caused it to mistakenly enter the forbidden zone.

Figure 5.
An example of a safety issue.
The comparison is summarized in Table 2, where # denotes a numeric value. The first column presents the number of discretized areas and the total number of valid test cases included in this comparison. The second column specifies the granularity level under consideration. The third column reports the total number of generated points required by the discretization method to pass validity checks. Columns four and five detail the number and percentage of test cases generated using the discretization method that violate the safety property. Column six provides the number of generated points needed by the random method to pass validity checks. Column seven indicates the coverage of discretized areas achieved by the randomly generated test cases, while the eighth column highlights the maximum number of test cases present in any single discretized area. Finally, the remaining columns outline the number and percentage of property violations triggered by the random generation method.

Table 2.
Comparison with random method in coarser granularity for the left lung.
In Table 2, the experimental results reveal that the coverage of the random method is low, particularly at coarser granularities. Despite an increase in the number of test cases, the random method fails to achieve full coverage. Furthermore, the distribution of test cases generated by the random method is non-uniform. For example, among the 69 test cases, 17 are located in the same discretized area. This non-uniform distribution may lead to a smaller number of totally generated points if they are centralized in certain areas of the lung model. Meanwhile, the non-uniform distribution may also result in a higher error-triggering rate, since error-prone targets are not evenly spread across the model.
When the granularity is coarse, the total number of test cases generated by the discretization method exceeds that of the random method, which leads to increased time consumption in the validity checking of test cases. This is because the discretization method must cover every cube to ensure full coverage. Even when the overlap of a cube with the lung model is minimal, the discretization method still requires finding valid test cases. Additionally, the discretization method demonstrates a lower error-triggering rate compared to the random method. As the granularity of the discretization becomes finer, the error-triggering rate of our method tends to increase. This is because finer granularity provides a more detailed representation of the input space, making it easier to detect potential defects in the system.
To further check the selection of discretized granularity on the effectiveness of the test, we analyze the diversity of trajectories between different test cases in each discretized area, which is evaluated with the distance between various trajectories. We calculate the minimum, average, and maximum Fréchet distances between the trajectories of various test cases within each discretized area. These results are presented for different granularities in Figure 6. In the figure, the distance between the trajectories from the source to various targets within a discretized area is generally smaller than the length of the cube, indicating that the shapes of the trajectories may not differ significantly. Since the points are randomly selected, the corresponding trajectories in the same area vary. As the granularity decreases, the distance between the trajectories decreases. The minimal distance reveals that none of the trajectories is identical. However, the difference in maximum distances between the first two granularities is not significant, indicating that the number of test cases considered in coarse granularity is not enough to ensure diversity.
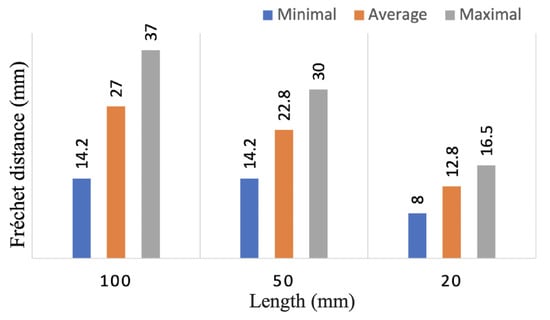
Figure 6.
Variation in trajectory distance.
In the experimentation, we observe that while some discretized areas exhibit no property violations, other areas consistently trigger property violations, indicating that certain regions are more prone to safety issues than others.
To identify the locations of error-triggering cases, we provide a visualization of both error-triggering and normal cases in the left lung for a granularity with a cube length of 20 mm. The spatial distribution in Figure 7 shows a clear concentration of error-triggering cases (red) near the heart, contrasting with the spread of normal cases (green). This clustering suggests a direct link between proximity to the heart and the occurrence of property violations.
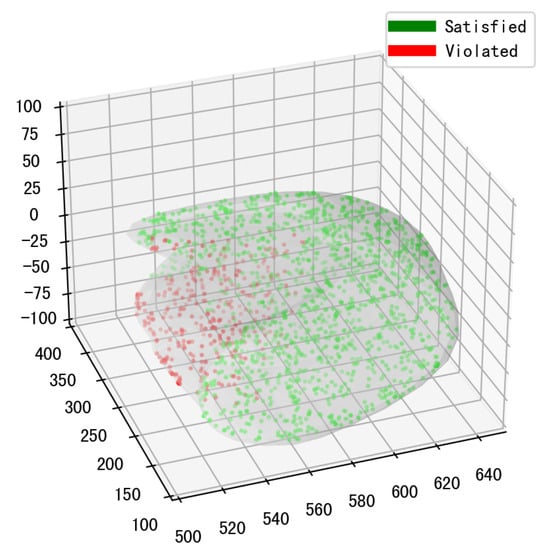
Figure 7.
Distribution of error-triggering test cases.
5.2.3. RQ2: Effectiveness of the Simulation-Based Validation Method
To answer this research question, we consider the experiments on both property validation and performance evaluation.
Comparison with Random Method on Triggering Property Violations
The experimental results in Section 5.2.2 indicate that certain areas are more likely to trigger property violations. Therefore, we focus on a specific part of the left lung model, i.e., the sub-model that is 7% of its total volume for this experimentation. We evaluate four different granularities in the experimentation, i.e., 20, 10, 5, and 2 mm. In this experimentation, we also consider the safety property that the needle should avoid collision with the heart model.
For different granularities, we provide the comparison of coverage and error-triggering efficiency with the random method in Table 3. The legends of the columns are similar to those in Table 2.

Table 3.
Comparison with random method for a part of the left lung.
In Table 3, we first observe that the total number of test cases generated by the random method is significantly higher than that of the discretization method. This is because the sub-model is relatively small, making it more likely for the random method to generate invalid points. In contrast, our method achieves a higher proportion of fully filled cubes, reducing the effort required for validity checking. Second, the random generation method cannot ensure full coverage, even with a large number of test cases, due to the non-uniform distribution of generated points. Third, since the selected sub-model is located near the heart, the rate of property violations is relatively high. As the number of test cases increases, the violation rates for the random generation method remain relatively consistent. In contrast, our method not only ensures full coverage of the model but also increases the rate of violations detected.
Figure 8 provides a visualization of all 88,554 test cases at the finest granularity, with green and red points denoting cases from the random and our discretization methods, respectively. The random method results in a significantly less dense distribution near the model’s boundaries compared to our proposed approach.
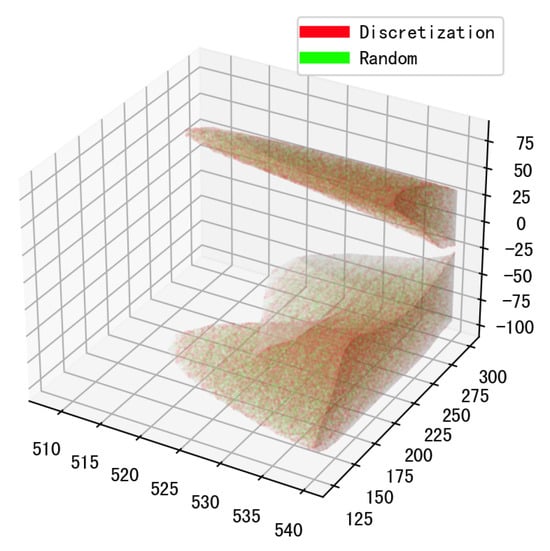
Figure 8.
Distribution of the test cases.
To investigate the correlation between target depth and safety property violations, we compared the distance-to-boundary distributions of error-triggering and normal cases. Figure 9 presents this comparison, with red bars indicating violations and green bars indicating normal cases. Our analysis shows that error-triggering cases generated by the discretization method are located significantly closer to the model boundary. This spatial correlation is explained by the proximity to the heart, a primary source of property violations. Unlike the random method, our approach ensures a fixed sampling rate per discretized area, which guarantees a higher density of test cases—and consequently, a higher detection rate of errors—in these critical boundary zones near the heart.
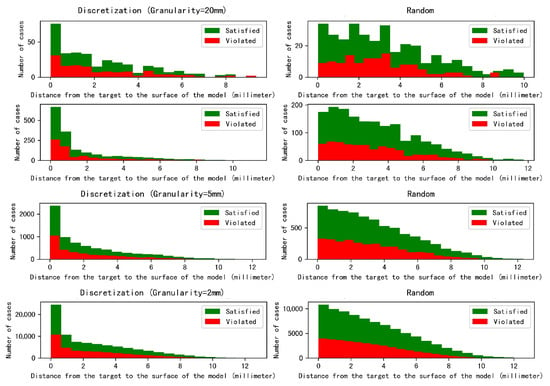
Figure 9.
Distance distribution of error-triggering test cases.
Discussion for the Comparison with the Random Method
From Table 2 and Table 3, we observe that when the granularity is coarse, the random method outperforms the discretization method in terms of both test generation and error-triggering efficiency. This is because the random method does not guarantee full coverage, and the error-triggering points in the lung model are not uniformly distributed. However, as the granularity becomes finer, the discretization method shows improved test generation and error-triggering efficiency. In contrast, the random method requires checking a larger number of points to generate the specified number of valid test cases. Although the number of error-triggering cases is comparable between the two methods, the error-triggering rates for the random method do not increase significantly and remain relatively consistent across all granularities.
The Deviation Between the Needle Tip’s Actual and Expected Positions
We further evaluate system performance in simulation using the generated test cases. Figure 10 compares the deviation of the needle tip from its expected position for both the partial and whole left lung models. The deviation for the sub-model is consistently below 2 mm (Figure 10a), while certain cases in the whole model exceed 3 mm (Figure 10b). Notably, the largest deviations occur for test cases located on the right side of the model.
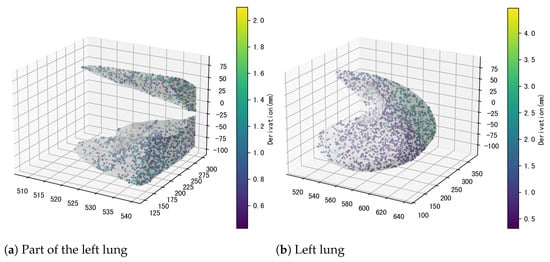
Figure 10.
Derivation of the actual end position.
5.2.4. : Consistency Checking Between Simulation and Physical Operation
In this experiment, we adopt the identical route planning code in both the simulator and the physical robotic arm. Meanwhile, we maintain the same sampling frequency between the simulator and the robotic arm. As a result, the planning algorithm generates the same set of expected trajectories from the source to the target for the robotic arm in both the virtual and the physical environments.
To check the consistency between simulation and physical operation, we ignored the test cases with property violations. As physical operation is all-consuming, we randomly selected more than fifty test cases without collision with the heart model. In the physical operation, the test cases did not trigger any safety issues. We conduct a comparative analysis of trajectory deviations in virtual versus physical operations. The state of the robot is defined by its seven joint angles. However, as this 7-dimensional data is difficult to visualize, we instead calculate the position of the robot’s end-effector. Figure 11 illustrates the discrepancy between the expected trajectory (blue) and the actual trajectories for both the real and virtual robots (red and green, respectively). The states of the expected trajectory are generated by the robot controller, which both the real and virtual robots then attempt to reach. Trajectories are sampled and extracted from both the simulator and the physical robotic arm during operation. The difference between expected and actual trajectories demonstrates the precision which each robot can achieve. As the figure shows, the real trajectory deviates more significantly from the expected than the virtual robot’s state.
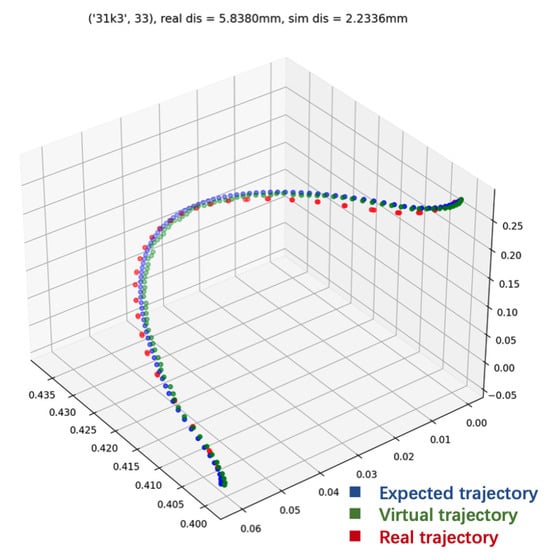
Figure 11.
Accuracy difference comparison between actual and expected trajectories.
We calculate the accuracy difference between the expected and the actual for both joint angles and end positions. The corresponding statistics for deviations between actual and expected performance are provided in Table 4. The third row of the table lists the angle differences between the actual and expected in terms of joint coordinates. The fourth row provides the distance differences for the needle tip between the actual and expected in terms of Cartesian coordinates.

Table 4.
Accuracy difference comparison between the actual and the expected trajectories.
In the table, the errors of joint coordinates are smaller than those of the end positions. The fact shows that though the errors of the joint coordinates are small, the accumulated errors in the seven joints lead to larger errors in the end positions. Meanwhile, the errors from the simulator are smaller than those from the physical arm. This phenomenon indicates that the motion of the physical robot arm may be affected by its environment and the interference between various joints. Such differences should be considered in the physical operation to avoid unexpected consequences. Furthermore, from the statistics, we can infer the quantitative error range between the physical robot and its digital twin. Specifically, the worst-case accuracy difference is the sum of the errors from the virtual simulation and the physical operation.
6. Related Work
Robotic systems require rigorous assurance of both functional and extra-functional properties [20], such as safety [21], reliability, security [22], and performance. Verification and validation of robotic and autonomous systems have attracted a lot of attention from both the research and industrial communities [9,23]. However, the complexity of autonomous systems makes system verification less feasible. Verification is typically applied at the component level. For example, Bresolin et al. applied reachability analysis of hybrid automata for the puncturing action in the surgery planned with a sequence of sub-tasks [24]. The Lagrange method has been used for the dynamic analysis of a spherical parallel manipulator used in brain surgery applications [25]. During surgeries, to prevent inadvertent damage and complications for patients, runtime verification techniques are utilized to monitor the actions performed by surgeons [26,27].
Due to the scalability limits of verification methods, simulation-based validation has become a major solution for evaluating the performance and improving the reliability of autonomous robotic systems. For example, mutation testing is applied to test industrial robotic systems in simulated environments [28]. Ortega et al. proposed the concept of composable and executable scenarios and tool support for simulation-based testing of mobile robots [29].
Nowadays, simulators are increasingly being adopted for both validation and training purposes in surgical operations. For example, the SmartArm system [30] provides control algorithms for robotic arms, allowing untrained users to operate the robot to complete given tasks in a master–slave setup. Kawashima et al. provide a systematic review on the adoption of virtual reality simulations for robotic surgery training [31]. Our focus is on validating autonomous robotic systems using simulators.
Prior work, such as that by Lee et al., has utilized deep reinforcement learning for path planning in automated surgical needle insertion, with performance validation conducted in simulation [32]. Validation in a simulator for the Da Vinci Research Kit primarily focuses on tracking problems for kinematic models [33]. Our approach differentiates itself from existing methods by incorporating systematic validation that evaluates both KPIs and safety properties, an aspect seldom explored in the literature of robotic systems. Adaptive learning strategies are also being developed to mitigate the discrepancy between simulation and real-world performance [34].
In addition to simulation of software systems, researchers have also focused on studying the performance gap between simulation and reality. For example, in experiments conducted with visual navigation models [16], the authors found that the configuration of simulation parameters can lead to a low correlation in performance between simulation and real-world scenarios.
In recent years, the concept of digital twin has gained increasing attention due to its ability to create a software representation of a physical object, allowing the physical and virtual entities to co-exist. This approach is particularly powerful for describing, controlling, and visualizing the behavior of real objects in robotic systems. The development of a robotic arm digital twin was explored using multiple simulation platforms [35]. A large-scale digital twin facility is developed with high-fidelity simulation and comprehensive data capture to evaluate and optimize mobile robotic systems in a lab environment, reducing real-world testing costs and risks [36]. Among the various efforts in this field, MATLAB is one of the most frequently adopted platforms for connecting real robotic arms with visualization tools [37]. An application of digital twins is in the automated remote health monitoring of patients, which incorporates various sensors and AI-driven algorithms [4]. Szybicki et al. demonstrated the advantages of using a digital twin for designing safety components in robotic stations [38]. Corral-Acero et al. introduced the concept of a digital twin in cardiology [39] by building the virtual model of patients to improve clinical decisions. They highlighted that mechanistic and statistical models are the two pillars of the digital twin. Hein et al. presented a proof of concept for creating a surgical digital twin of an ex vivo spinal surgery by using multiple cameras and a laser scanner to dynamically capture the geometry and appearance of the entire surgical scene [40]. In our work, we construct the digital twin by integrating the robotic arm model into the CoppeliaSim Simulator and establishing connections between the physical and virtual models. Within this framework, we observe that the physical robotic arm requires strict settings to avoid reaching joint limitations. In addition, there is a precision discrepancy between the simulation and the real-world performance.
7. Threats to Validity
In this section, we discuss the internal and external validity of our method.
7.1. Internal Validity
The discretization granularity significantly influences the performance of our test case generation method. With coarse granularity, the number of test cases is limited, and the uniform distribution of these test cases may result in fewer detected defects. As a result, its performance is not as effective as the random method, which, although not ensuring full coverage, generates more diverse test cases. However, coarse granularity is unsuitable for testing safety-critical robotic systems due to insufficient coverage.
As the granularity becomes finer, the effort required to generate valid test points decreases. Additionally, since the sub-model is error-prone, the rate of error-triggering cases increases relative to the total number of generated points.
Although implemented for needle insertion surgery, the test generation method is general and independent of both the simulator and the target model.
7.2. External Validity
We simplified the lung model by ignoring bronchial and vascular tissues. For a lung model that includes these tissues, the test generation method should be able to distinguish them within the discretized cubes and select valid points. Once the model is provided, the positions of these tissues are fixed, allowing them to be separated. Therefore, we assume that the lung model does not involve other tissues and only handles its irregular shape.
For other irregular models except for the lung model, the discretization method is still applicable to measure the test coverage.
The digital twin framework is specifically developed for needle insertion surgery, detailing the models in the simulator and the interfaces to their real-world counterparts. However, the concept is broadly applicable to other types of autonomous robotic systems.
Our experimental results are highly repeatable and robust. Despite using different granularities, the studies consistently identified similar violating zones and yielded closely matched quantitative data. The sample sizes varied from 69 to 88,554, determined by the specific experimental settings for granularity and target area selection. This large range of samples effectively minimizes random noise and reinforces the reliability of our conclusions.
8. Conclusions
In this work, we present a simulation-based validation framework for autonomous needle insertion surgeries. The framework comprises a test case generator, a physical robotic system, a virtual simulator, and a monitor. The idea is to systematically generate test cases that can drive both virtual and physical simulations, thereby validating the safety properties and performance of the robotic system. To measure the coverage of the test cases, we propose a discretization method that decomposes a 3D model into countable areas. Our results confirm the framework’s superiority over random methods, achieving full coverage and high error-triggering rates (up to 39.4%) using significantly fewer test cases (20.2% to 53.2% of the test cases needed by the random method), while enabling critical performance comparisons. In addition, the framework facilitates the comparison between virtual and physical simulations, enabling more accurate predictions of real-world performance.
The framework provides a general simulation-based validation method for specific surgical applications. The current implementation uses a simplified lung model and considers only the heart as an obstacle for avoidance. Nevertheless, the test case generation and validation methods are not relevant to the implementation details. Future work will focus on integrating complex physiological models and expanding the property specifications, thereby enhancing the framework’s comprehensiveness and solidifying its role as an essential tool for the safe deployment of autonomous surgical systems. Meanwhile, we will also investigate the simulation-based validation of autonomous robotic systems for other types of surgical applications.
Author Contributions
Conceptualization, J.L. (Jun Lin) and K.H.; methodology, T.S., R.S. and R.Y.; software, T.S. and R.S.; validation, T.S. and R.S.; formal analysis, R.Y.; investigation, D.Z.; resources, J.L. (Jun Lin) and R.S.; data curation, T.S. and R.S.; writing—original draft preparation, R.Y.; writing—review and editing, K.H., L.L. and J.L. (Jiewu Leng); visualization, T.S.; supervision, J.L. (Jun Lin) and K.H.; project administration, J.L. (Jun Lin) and D.Z.; funding acquisition, R.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by Major Project of ISCAS (ISCAS-ZD-202302) and Basic Research Project of ISCAS (ISCAS-JCZD-202403).
Data Availability Statement
The experimental data and the simulation results are available in https://github.com/system-test-2025/robot-test (accessed on 29 August 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Moglia, A.; Georgiou, K.; Georgiou, E.; Satava, R.M.; Cuschieri, A. A systematic review on artificial intelligence in robot-assisted surgery. Int. J. Surg. 2021, 95, 106151. [Google Scholar] [CrossRef]
- Fiorini, P.; Goldberg, K.Y.; Liu, Y.; Taylor, R.H. Concepts and trends in autonomy for robot-assisted surgery. Proc. IEEE 2022, 110, 993–1011. [Google Scholar] [CrossRef]
- Surgical, I. da Vinci. Surgical System. 2013. Available online: https://www.intuitive.com/en-us/products-and-services/da-vinci (accessed on 29 August 2025).
- Wang, Q.; Jiao, W.; Wang, P.; Zhang, Y. Digital twin for human-robot interactive welding and welder behavior analysis. IEEE/CAA J. Autom. Sin. 2020, 8, 334–343. [Google Scholar] [CrossRef]
- Rivero-Moreno, Y.; Rodriguez, M.; Losada-Muñoz, P.; Redden, S.; Lopez-Lezama, S.; Vidal-Gallardo, A.; Machado-Paled, D.; Guilarte, J.C.; Teran-Quintero, S. Autonomous Robotic Surgery: Has the Future Arrived? Cureus 2024, 16, e52243. [Google Scholar] [CrossRef] [PubMed]
- Ji, G.; Yan, J.; Du, J.; Yan, W.; Chen, J.; Lu, Y.; Rojas, J.; Cheng, S.S. Towards safe control of continuum manipulator using shielded multiagent reinforcement learning. IEEE Robot. Autom. Lett. 2021, 6, 7461–7468. [Google Scholar] [CrossRef]
- Zhou, S.K.; Le, H.N.; Luu, K.; Nguyen, H.V.; Ayache, N. Deep reinforcement learning in medical imaging: A literature review. Med. Image Anal. 2021, 73, 102193. [Google Scholar] [CrossRef]
- Redfield, S.A.; Seto, M.L. Verification challenges for autonomous systems. In Autonomy and Artificial Intelligence: A Threat or Savior? Springer: Berlin/Heidelberg, Germany, 2017; pp. 103–127. [Google Scholar]
- Araujo, H.; Mousavi, M.R.; Varshosaz, M. Testing, validation, and verification of robotic and autonomous systems: A systematic review. ACM Trans. Softw. Eng. Methodol. 2023, 32, 1–61. [Google Scholar] [CrossRef]
- Afzal, A.; Le Goues, C.; Hilton, M.; Timperley, C.S. A study on challenges of testing robotic systems. In Proceedings of the 2020 IEEE 13th International Conference on Software Testing, Validation and Verification (ICST), Porto, Portugal, 24–28 October 2020; IEEE: Porto, Portugal, 2020; pp. 96–107. [Google Scholar]
- Zhou, Y.; Sun, Y.; Tang, Y.; Chen, Y.; Sun, J.; Poskitt, C.M.; Liu, Y.; Yang, Z. Specification-based autonomous driving system testing. IEEE Trans. Softw. Eng. 2023, 49, 3391–3410. [Google Scholar] [CrossRef]
- Koopman, P.; Wagner, M. Challenges in autonomous vehicle testing and validation. SAE Int. J. Transp. Saf. 2016, 4, 15–24. [Google Scholar] [CrossRef]
- Zhong, Z.; Tang, Y.; Zhou, Y.; Neves, V.d.O.; Liu, Y.; Ray, B. A survey on scenario-based testing for automated driving systems in high-fidelity simulation. arXiv 2021, arXiv:2112.00964. [Google Scholar]
- Lou, G.; Deng, Y.; Zheng, X.; Zhang, M.; Zhang, T. Testing of autonomous driving systems: Where are we and where should we go? In Proceedings of the 30th ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Singapore, 14–18 November 2022; pp. 31–43. [Google Scholar]
- Tang, S.; Zhang, Z.; Zhang, Y.; Zhou, J.; Guo, Y.; Liu, S.; Guo, S.; Li, Y.F.; Ma, L.; Xue, Y.; et al. A survey on automated driving system testing: Landscapes and trends. ACM Trans. Softw. Eng. Methodol. 2023, 32, 1–62. [Google Scholar] [CrossRef]
- Kadian, A.; Truong, J.; Gokaslan, A.; Clegg, A.; Wijmans, E.; Lee, S.; Savva, M.; Chernova, S.; Batra, D. Sim2real predictivity: Does evaluation in simulation predict real-world performance? IEEE Robot. Autom. Lett. 2020, 5, 6670–6677. [Google Scholar] [CrossRef]
- Bogaerts, B.; Sels, S.; Vanlanduit, S.; Penne, R. Connecting the CoppeliaSim robotics simulator to virtual reality. SoftwareX 2020, 11, 100426. [Google Scholar] [CrossRef]
- Freud, N.; Duvauchelle, P.; Létang, J.M.; Babot, D. Fast and robust ray casting algorithms for virtual X-ray imaging. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms. 2006, 248, 175–180. [Google Scholar] [CrossRef]
- Eiter, T.; Mannila, H. Computing Discrete Fréchet Distance; CD-TR 94/64; Technical University of Vienna: Vienna, Austria, 1994. [Google Scholar]
- Gupta, B.B.; Nedjah, N. Safety, Security, and Reliability of Robotic Systems: Algorithms, Applications, and Technologies; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Adesiji, A.D.; Ibitoye, S.E.; Mahamood, R.M.; Olayemi, O.A.; Omoniyi, P.O.; Jen, T.C.; Akinlabi, E.T. Safety Considerations in Deployment of Robotic Systems–A Systematic Review. J. Field Robot. 2025. [CrossRef]
- Alonso, R.; Haber, R.E.; Castaño, F.; Recupero, D.R. Interoperable software platforms for introducing artificial intelligence components in manufacturing: A meta-framework for security and privacy. Heliyon 2024, 10, e26446. [Google Scholar] [CrossRef]
- Ebert, C.; Weyrich, M. Validation of autonomous systems. IEEE Softw. 2019, 36, 15–23. [Google Scholar] [CrossRef]
- Bresolin, D.; Geretti, L.; Muradore, R.; Fiorini, P.; Villa, T. Formal verification of robotic surgery tasks by reachability analysis. Microprocess. Microsyst. 2015, 39, 836–842. [Google Scholar] [CrossRef]
- Güzin, D.; Gezgin, E. Development of a spherical parallel manipulator for brain surgery applications: Preliminary study on the dynamic analysis and verification. Robotica 2022, 40, 3726–3750. [Google Scholar] [CrossRef]
- Gupta, G.; Shankar, S.; Pinisetty, S. Automated Surgical Procedure Assistance Framework Using Deep Learning and Formal Runtime Monitoring. In Proceedings of the International Conference on Runtime Verification, Tbilisi, Georgia, 28–30 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 25–44. [Google Scholar]
- Li, Z.; Hutchinson, K.; Alemzadeh, H. Runtime detection of executional errors in robot-assisted surgery. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Philadelphia, PA, USA, 2022; pp. 3850–3856. [Google Scholar]
- Dos Santos, M.G.; Hallé, S.; Petrillo, F.; Guéhéneuc, Y.G. AAT4IRS: Automated acceptance testing for industrial robotic systems. Front. Robot. AI 2024, 11, 1346580. [Google Scholar] [CrossRef]
- Ortega, A.; Parra, S.; Schneider, S.; Hochgeschwender, N. Composable and executable scenarios for simulation-based testing of mobile robots. Front. Robot. AI 2024, 11, 1363281. [Google Scholar] [CrossRef]
- Marinho, M.M.; Harada, K.; Morita, A.; Mitsuishi, M. SmartArm: Integration and validation of a versatile surgical robotic system for constrained workspaces. Int. J. Med. Robot. Comput. Assist. Surg. 2020, 16, e2053. [Google Scholar] [CrossRef]
- Kawashima, K.; Nader, F.; Collins, J.W.; Esmaeili, A. Virtual reality simulations in robotic surgery training: A systematic review and meta-analysis. J. Robot. Surg. 2024, 19, 29. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Tan, X.; Chng, C.B.; Chui, C.K. Simulation of robot-assisted flexible needle insertion using deep Q-network. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; IEEE: Bari, Italy, 2019; pp. 342–346. [Google Scholar]
- Ferro, M.; Mirante, A.; Ficuciello, F.; Vendittelli, M. A CoppeliaSim dynamic simulator for the da Vinci Research Kit. IEEE Robot. Autom. Lett. 2022, 8, 129–136. [Google Scholar] [CrossRef]
- Chukwurah, N.; Adebayo, A.S.; Ajayi, O.O. Sim-to-real transfer in robotics: Addressing the gap between simulation and real-world performance. Int. J. Robot. Simul. 2024, 6, 89–102. [Google Scholar] [CrossRef]
- Singh, M.; Kapukotuwa, J.; Gouveia, E.L.S.; Fuenmayor, E.; Qiao, Y.; Murray, N.; Devine, D. Comparative Study of Digital Twin Developed in Unity and Gazebo. Electronics 2025, 14, 276. [Google Scholar] [CrossRef]
- Martins, J.G.; Nutonen, K.; Costa, P.; Kuts, V.; Otto, T.; Sousa, A.; Petry, M.R. AR/VR Digital Twin for Simulation and Data Collection of Robotic Environments. In Proceedings of the 2025 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Funchal, Portugal, 2–3 April 2025; IEEE: Funchal, Portugal, 2025; pp. 198–203. [Google Scholar]
- Yenorkar, R.; Chaskar, U. GUI based pick and place robotic arm for multipurpose industrial applications. In Proceedings of the 2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 14–15 June 2018; IEEE: Madurai, India, 2018; pp. 200–203. [Google Scholar]
- Szybicki, D.; Pietruś, P.; Burghardt, A.; Kurc, K.; Muszyńska, M. Application of Digital Twins in Designing Safety Systems for Robotic Stations. Electronics 2024, 13, 4179. [Google Scholar] [CrossRef]
- Corral-Acero, J.; Margara, F.; Marciniak, M.; Rodero, C.; Loncaric, F.; Feng, Y.; Gilbert, A.; Fernandes, J.F.; Bukhari, H.A.; Wajdan, A.; et al. The ‘Digital Twin’ to enable the vision of precision cardiology. Eur. Heart J. 2020, 41, 4556–4564. [Google Scholar] [CrossRef]
- Hein, J.; Giraud, F.; Calvet, L.; Schwarz, A.; Cavalcanti, N.A.; Prokudin, S.; Farshad, M.; Tang, S.; Pollefeys, M.; Carrillo, F.; et al. Creating a digital twin of spinal surgery: A proof of concept. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2355–2364. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).