Abstract
A general high-order linear consensus protocol is proposed for coupling topologies defined by directed graphs with partial relative state information and a reference model with lobal/local gains. Necessary and sufficient second-order stability bounds for the cases of relative position feedback with reference velocity and relative position and velocity feedback are then reviewed. Next, new necessary and sufficient stability bounds are obtained for third-order consensus for three cases of feedback of full and partial relative state information. The stability bounds obtained, unlike in prior studies, allow for the gains to be conveniently selected in a sequential manner and are shown to utilize those for second-order consensus. Comparisons with conservative stability bounds from previous studies are shown, and illustrative examples of the proposed consensus protocols and the obtained stability bounds are provided.
1. Introduction
Decentralized control of multi-agent systems has been one of the fastest growing fields in control systems during the past few decades due to recent developments in actuator and sensor technologies, communication networks, and computing science, as well as the wide range of practical applications. In particular, multi-agent consensus problems, in which the states of the agents (or other quantities of interest) converge to a common set of values, have attracted increasing attention in recent years. Such control problems are addressed with various strategies, including leaderless protocols, leader–follower protocols with or without a reference model, and multi-agent containment protocols, among others, for both undirected and directed communication networks that account for cooperative as well as antagonistic interactions in some cases. While the initial results in this area applied linear protocols to homogeneous single integrator dynamics, the methodology has been extended to account for nonlinear protocols, high-order and/or heterogeneous dynamics, switching network topologies, communication and input delays, and other important properties [1].
In particular, consensus protocols for double integrator systems, in which the positions and velocities converge to a common set of values, have received significant attention due to their applications in mechanical systems and robotics [2,3,4,5,6]. Such protocols typically include feedback of the relative positions and velocities between connected neighbors in the network, although the lack of relative velocity information can also be accommodated. In [5,6] a group reference velocity (or a second-order reference model) is used in lieu of relative velocities while [4] treats the general case. While any positive set of position and velocity gains produce consensus for connected undirected graphs, for the case of directed graphs that contain a spanning tree, a lower bound exists on the velocity gain, which is a function of the position gain and the network structure, in order for consensus to be successfully achieved. In this case, the eigenvalues of the closed loop matrix have negative real part (aside from a number of zeros) and the consensus manifold is stable.
High-order consensus protocols (i.e., where the dynamics are third-order or higher) have been previously studied in [7,8,9,10,11], including the case where only the lowest-order position-like relative states are used, along with higher-order reference states (which can be zero) obtained from a reference model. Such protocols have immediate application to problems in unmanned quadcopters and UAVs [12], mobile robots [13,14], and PID consensus control of double integrator mechanical systems in which the relative positions, velocities, and integrated position states are used for feedback [11]. High-order cluster consensus on directed graphs that contain a spanning tree was studied in [10] in terms of the feedback gains and the graph Laplacian. However, the format of the obtained necessary and sufficient conditions (which apply to a single consensus as well as multiple consensus clusters), consisting of coupled polynomial equations obtained from the Hurwitz criteria, is not convenient for gain selection while a sufficient condition shown for the third-order case is overly conservative. In [11] a stability condition for fractional-order PID consensus of double integrator systems was proposed, although errors were present. Some works require LMI solutions to guarantee consensus stability and thus are not convenient to implement in real time. In [9] a constructive method for choosing the gains for high-order consensus was proposed. However, except for the double integrator case, necessary and sufficient stability bounds on the gains for stability of the consensus subspace were not shown. In [15] a fully distributed consensus algorithm for high-order consensus is proposed that does not utilize global information for gain selection. Nevertheless, the obtained sufficient stability criteria are conservative, while having necessary and sufficient stability bounds in terms of the graph Laplacian is convenient for evaluating the stability margins using the conservative criteria.
In this paper, a high-order multi-agent linear consensus protocol is proposed for multi-agent systems that communicate via networks represented by directed graphs with cooperative interactions, full or partial relative state information, and a reference model with both global and local gains. The proposed protocol is shown to be equivalent to previously shown protocols under certain assumptions such as no local gains or reference model, both of which help to widen its applicability to a broader set of problems. Next, the necessary and sufficient stability bounds for second-order protocols with either full relative state information or only relative positions with a reference model are obtained and shown to be equivalent to those obtained previously. This serves as a necessary introduction to the main contribution of this paper, namely the derivation of new necessary and sufficient stability bounds for third-order consensus in terms of the global/local feedback gains and graph Laplacian where the gains can be selected sequentially. Three cases of full and partial relative state feedback (with and without a reference model) are considered, and the stability bounds obtained are shown to depend on those for the second-order problems reviewed earlier. Next, comparisons with conservative stability bounds from the previous literature are shown, and finally a set of illustrative examples on both small and large directed network topologies are provided which confirm the validity of the third-order stability bounds obtained previously.
In summary, the primary advances of this paper are as follows:
- A new high-order linear consensus protocol is proposed for coupling topologies defined by directed graphs with partial relative state information and a reference model with global/local gains.
- New necessary and sufficient stability bounds for a third-order consensus are obtained for three cases of feedback of full and partial relative state information with and without a reference model.
- The obtained stability bounds are compared with previously obtained conservative stability bounds in the literature.
- Illustrative examples are presented that leverage both small and large directed networks and verify the third-order stability bounds presented earlier for cases of only global gains and both global/local gains.
The remainder of the paper is as follows. In Section 2 the problem addressed in this paper is defined, the new consensus protocol leveraging global/local gains is proposed, and a new theorem addressing consensus stability in terms of the spectrum of the closed loop matrix is presented. In Section 3 the previously obtained stability bounds for second-order consensus are reviewed, and in Section 4 the main results for three cases of third-order consensus are presented and rigorously proved. Section 5 reviews alternative sufficient stability criteria appearing previously (which is more conservative), and Section 6 then presents the aforementioned illustrative examples that verify the third-order stability bounds obtained in Section 4. Finally, some conclusions are offered.
2. High-Order Consensus Protocol with Global/Local Gains
Assume there are N agents that share information according to a network defined by directed graph with vertex set , edge set , adjacency matrix , and Laplacian where and . The edge weights are positive if agent i receives information from agent j. While the eigenvalues of are generally complex, they are real for the cases of an undirected graph or a spanning tree. Before introducing the agent dynamics and consensus protocol, the following well-known Lemma is briefly reviewed.
Lemma 1
([1]). has a simple zero eigenvalue with corresponding right and left eigenvectors and , respectively, while the remaining eigenvalues have positive real part if and only if contains a spanning tree. For a connected undirected graph .
Now, define the local state of agent i as , the global state in terms of , and assume the N agents obey the nth-order dynamics
where . Suppose only the s lowest-order relative states are available for where , all agents can access a reference state defined by reference model , and consider a consensus protocol given by
where the scalars are global and local gains, respectively. The protocol in Equation (2) is a generalization of the one proposed in [9] which corresponds to , s = 1, and in Equation (2). If , then the consensus protocol depends on the ith agent’s own states, its neighbors’ partial state information, and the reference states. If , then it depends on its neighbors’ full state information.
Define matrix and note the property indicates that is a Laplacian matrix of , which has a spanning tree if and only if has a spanning tree. Defining the error state as the closed loop of Equations (1) and (2) is given by where
where and is the jth natural basis expressed as a row matrix, e.g., . The characteristic equation for is
Matrix has Nn eigenvalues, and at least s are zero, since there is at least one zero eigenvalue of , i.e., . The following states the necessary and sufficient condition for which the dynamics in Equation (1) achieve consensus with the protocol in Equation (2).
Theorem 1.
Consensus defined by is achieved asymptotically in Equations (1) and (2) if, and only if, has exactly s zero eigenvalues with a single Jordan block and the rest have negative real part.
Proof.
(Sufficiency) Assume has exactly s zero eigenvalues with a single Jordan block and the rest have negative real part. Then, Equation (4) implies that has a single zero eigenvalue with right and left eigenvectors satisfying and . Since has only one right eigenvector associated with zero, this eigenvalue has geometric multiplicity of one. Therefore, is expressed as where the Jordan matrix distinguishes the Jordan block with s zero eigenvalues and the block containing the remaining Nn-s nonzero eigenvalues with negative real part, while matrices and contain the right and left eigenvectors and generalized eigenvectors of with the first s of each corresponding to the Jordan block J. Hence. □
(Necessity) If has more than s zero eigenvalues or any with non-negative real part, then the rank of is at least s + 1 for large t. However, since and requires that has rank s for large t, which results in a contradiction.
In the following sections, we first review the established stability bounds for case of n = 2 before showing new necessary and sufficient stability conditions for the third-order case.
3. Stability Bounds for Second-Order Consensus
3.1. Relative Position Feedback with Reference Velocity
For the case of n = 2 in Equations (1) and (2), we relabel the states as and (positions and velocities). Assume s = 1, i.e., the relative velocities are unavailable although a reference velocity is available. Then, the consensus protocol in Equation (2) becomes
Equation (6) is an extension of the protocols in [5,6] to allow for local gains and of the protocol in [9] to allow for a nonzero reference velocity. Defining the error state as , the closed loop matrix in Equation (3) has the characteristic equation
A necessary and sufficient condition for consensus in (1) and (6) is that has exactly one zero eigenvalue and the rest have negative real part. Let be the jth eigenvalue of the modified Laplacian of . The consensus state given by and is reached asymptotically where if contains a spanning tree, and [9]
This result, which is easily verified using Routh–Hurwitz on the real polynomial
was shown in [5] and [9] and is less conservative than the sufficient condition in [6]. If is undirected or a spanning tree, Equation (8) results in .
3.2. Relative Position and Velocity Feedback
For the case where s = 2, i.e., both the relative positions and velocities are available, consider the protocol [1,2,3]
The closed loop matrix in (3) has the characteristic equation
A necessary and sufficient condition for consensus in Equations (1) and (10) is that has exactly two zero eigenvalues and the rest have negative real part [4]. The consensus state given by and where is reached asymptotically if contains a spanning tree, and
This result, which is easily verified using Routh–Hurwitz on the real polynomial
was obtained in [3,4,5,10] and is less conservative than the sufficient condition given in [1,2]. If is undirected or a spanning tree, (12) results in .
4. Stability Bounds for Third-Order Consensus
4.1. Relative Position-like Feedback with Reference Model
For the case of n = 3 in Equations (1) and (2), we first assume s = 1, i.e., that only the relative position-like states are available as in [9]. The consensus protocol in Equation (2) becomes
Equation (14) is an extension of the protocol in [7] to allow for local gains and of the protocol in [9] to allow for a nonzero reference. Then, the closed loop matrix
in Equation (3) has the characteristic equation
The matrix has 3N eigenvalues, and at least one is zero.
Corollary 1.
Consensus with and is achieved asymptotically in Equations (1) and (14) if and only if in Equation (15) has exactly one zero eigenvalue and the rest have negative real part. In addition, if consensus is reached then
where .
Proof.
This follows from Theorem 1 with s = 1 and Equation (5). □
Theorem 2.
Asymptotic consensus with , is achieved in Equations (1) and (14) if contains a spanning tree, , , , and where
Proof.
Setting and in Equation (16) yields. □
Eliminating yields
Substituting into the real part of Equation (19) yields the stability bound for in Equation (18). The fact this is an upper bound can be verified from using Routh–Hurwitz in real polynomial where from Equation (16) while noting that factor is Hurwitz for , . Note if is undirected and connected, Equation (18) is equivalent to .
4.2. Relative Position-like and Velocity-like Feedback with Reference Model
Now, assume s = 2, i.e., that only the relative position-like states and velocity-like states are available. Consider the consensus protocol given by
Then the closed loop matrix
in (3) has the characteristic equation
with at least two zero eigenvalues.
Corollary 2.
Consensus with is achieved asymptotically in Equations (1) and (21) if and only if in Equation (22) has exactly two zero eigenvalues with a single Jordan block and the rest have negative real part. In addition, if consensus is reached, then
where .
Proof.
This follows from Theorem 1 with s = 2 and Equation (5). □
Theorem 3.
Asymptotic consensus with is achieved in Equations (1) and (21) if contains a spanning tree, , , in Equation (8), and
Proof.
Setting and in Equation (23) yields. □
Eliminating yields
Substituting into the real part of Equation (26) yields the stability bound for in Equation (25). The fact this is an upper bound can be verified from using Routh–Hurwitz in real polynomial where from Equation (23) while noting that factor is Hurwitz for . Note if is undirected and connected Equations (8) and (25) are equivalent to . Furthermore, for a positive , must satisfy the lower bound in Equation (8). Therefore, , Equation (8) and in Equation (25) guarantee that the remaining eigenvalues of have negative real part.
4.3. Relative Feedback of All States
Now, assume s = 3, i.e., that all relative states are available, and consider the linear consensus protocol given by [7]
Equation (28) is an extension of the protocols in [8,10] to allow for local gains . Then, the closed loop matrix
in Equation (3) has the characteristic equation
with at least three zero eigenvalues.
Corollary 3.
Consensus is achieved asymptotically in Equations (1) and (28) if and only if in Equation (29) has exactly three zero eigenvalues with a single Jordan block and the rest have negative real part. In addition, if consensus is reached then
where .
Proof.
This follows from Theorem 1 with s = 3 and Equation (5). □
Theorem 4.
Asymptotic consensus is achieved in Equations (1) and (28) if contains a spanning tree, , , in Equation (12), and
Proof.
Setting and in Equation (30) yields. □
Eliminating and yields . Substituting into the real part of Equation (33) yields the stability bound in Equation (32). The fact this is an upper bound can be verified from using Routh–Hurwitz in real polynomial where from Equation (30). Note if is undirected and connected with , Equations (12) and (32) are equivalent to the conditions . Furthermore, for a positive this results in the same lower bound for given by Equation (12). Therefore, Equation (12) and in Equation (32) guarantee the remaining eigenvalues of have negative real part. Note that Equations (12) and (32) are equivalent to conditions in [10] for third-order consensus, but are more convenient for gain selection, while Equation (32) corrects the sign error in [11].
5. Stability Condition Comparisons
In [12] a sufficient stability constraint for s = 1 is obtained for nth-order consensus in Equation (2). Converting to the current notation, for n = 3 this requires and real negative roots of for agents with in-degree . By simultaneously solving and , this is seen to be equivalent to
In [10] a necessary and sufficient stability constraint for n = s = 3 (relative feedback of all states) is obtained from the Hurwitz criteria as the coupled polynomial equations
In addition to being less practical for gain selection than Theorem 4, Equation (35) is strictly speaking not sufficient. In addition, a sufficient condition was also provided in [10] for third-order consensus as
although Equation (36) is unnecessarily conservative as will be shown in the next section.
6. Examples
In this section, the performance of the proposed consensus protocols is studied for the case of a multi-agent system of third-order integrators and compared with the analytical stability bounds in Section 4 as well as the previously obtained conservative bounds in Section 5. The first three examples utilize the three protocols in Equations (14), (21), and (28) on a directed ring network with 4 nodes, while the final example considers Equation (28) for a large scale directed network with 24 nodes.
Example 1.
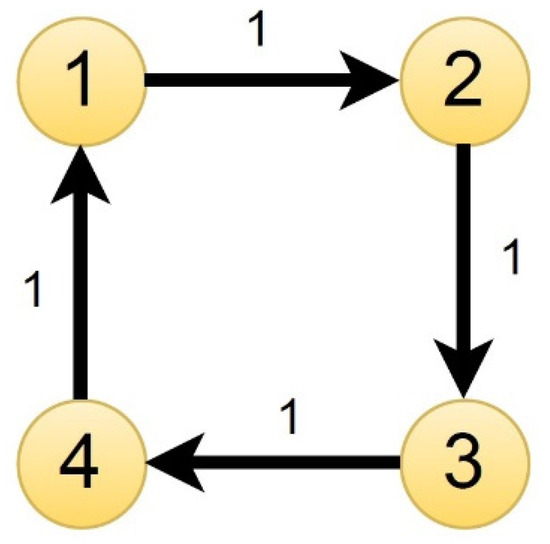
Consider N = 4 agents sharing states via the four-node directed ring graph with unity edge weights of Figure 1, for which the Laplacian matrix is
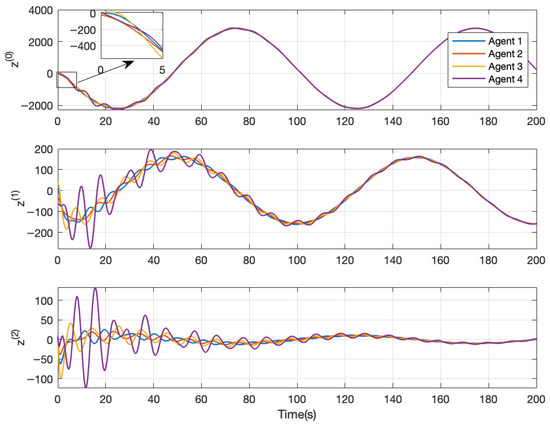
where . Assume only the relative position-like states are available. Using Equation (1) with n = 3 along with the protocol in Equation (14), , , and yields from Equation (18). However, now we choose to alternate with . For , Equation (18) yields , thus increasing the upper bound for consensus stability. Choosing the gains and yields and , respectively. Figure 2 shows the case of = 0.75 for reference control . For this example the second condition in Equation (34) with is obtained as , for which the conservative upper bound is 43% of the true value, while the alternate yields a more conservative lower value.

Figure 1.
Directed ring graph on four nodes with unity edge weights.

Figure 2.
Consensus simulation for Equations (1) (n = 3) and (14) on the network in Figure 1, with , , , , and reference control .
Example 2.
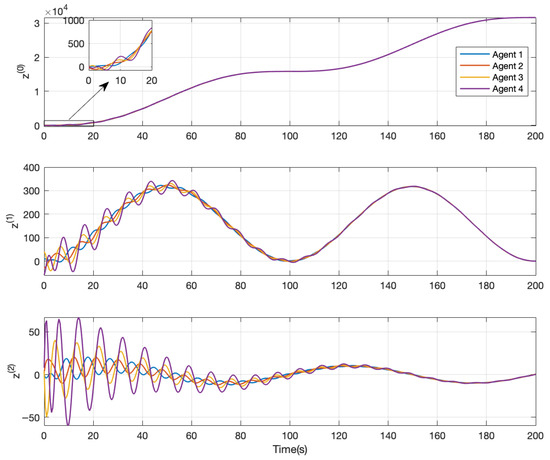
Now, assume only the relative position-like and velocity-like states are available. Using Equation (1) with n = 3 along with the protocol in Equation (21), , and yields from Equation (8). Then, choosing yields from Equation (25). Now, using the alternate yields from Equation (25), thus increasing the upper bound for consensus stability. Choosing the gains and yields and , respectively. Figure 3 shows the stable case of = 0.65 for the same reference control as in Figure 2. However, for and the consensus state is unstable with .

Figure 3.
Consensus simulation for Equations (1) (n = 3) and (21) on the network in Figure 1, with , , , , and reference control .
Example 3.
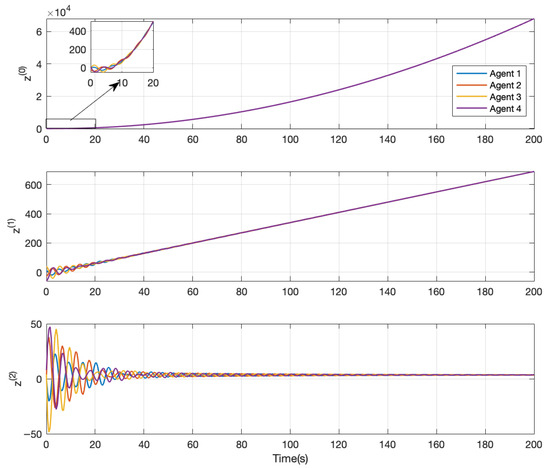
Now, assume all relative states are available. Using Equation (1) with n = 3 along with the protocol in Equation (28), , and yields from Equation (12). Then, choosing yields from Equation (32). Choosing the gains and yields and , respectively. Figure 4 shows the stable case of = 2.5. Using in this case is not advantageous. For the set , , , the conditions in Equation (35) are seen to be satisfied; however, the consensus state is unstable with . The additional constraint that is needed, which in turn requires in Equation (12) as stated in Theorem 4. Assuming , then Equation (36) requires (twice the true lower bound) while the constraint implies that (27.4% of the true upper bound ), while with Equation (36) yields . This illustrates the large stability margin implied in Equation (36), while the necessary and sufficient stability bounds in Theorem 4 are just as straightforward to apply for selection of a stable set of gains.

Figure 4.
Consensus simulation for Equations (1) (n = 3) and (28) on the network in Figure 1, with , , , and .
Example 4.
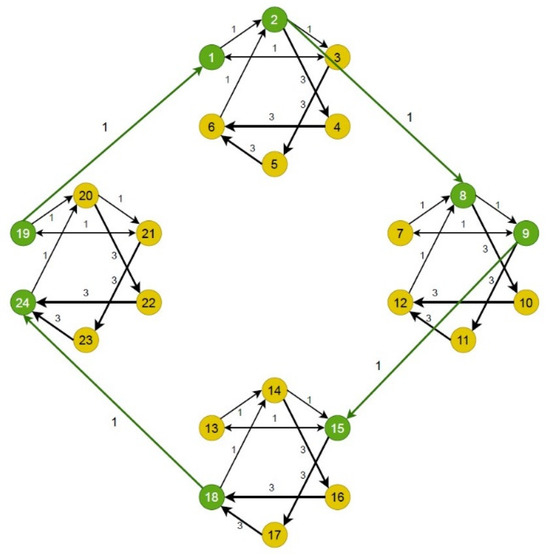
Consider N = 24 agents sharing states via the directed ring graph of Figure 5, where the green nodes in each subgraph transmit/receive information to/from other subgraphs and the Laplacian has the eigenvalue spectrum

Figure 5.
Directed network on N = 24 nodes.
Again, assume all relative states are available for feedback. Using Equation (1) with n = 3 along with the protocol in Equation (28), , and yields from Equation (12). Then, choosing yields from Equation (32). Choosing the gains and yields and , respectively. Figure 6 and Figure 7 show successful (i.e., stable) and unsuccessful (i.e., unstable) consensus simulations for these two cases.
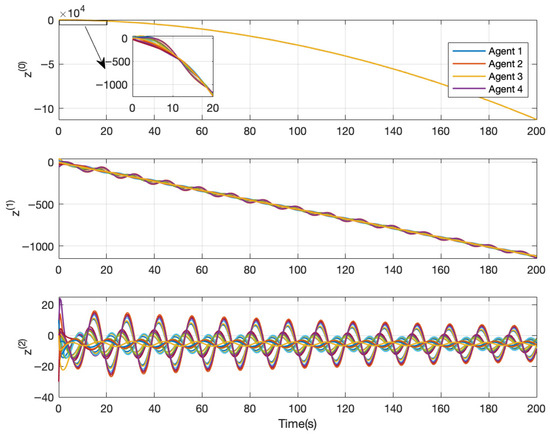
Figure 6.
Consensus simulation for Equations (1) (n = 3) and (28) on the network in Figure 5, with , , , and .
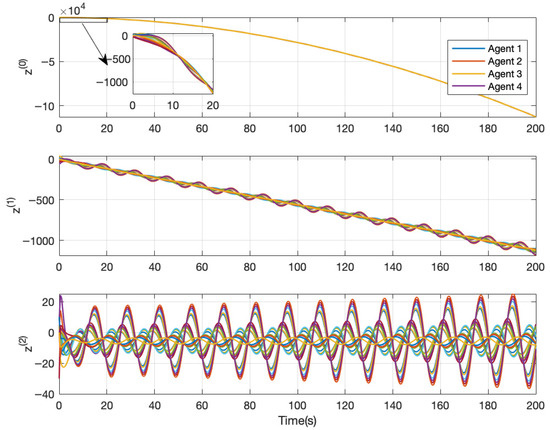
Figure 7.
Simulation for Equations (1) (n = 3) and (28) on the network in Figure 5, with , , , and . The system is unstable and does not reach consensus.
7. Conclusions
A linear consensus protocol was proposed for high-order integrators on directed graph topologies, in which feedback of full or partial relative state information is employed, along with a reference model and both global gains, which are common to all the agents, and local gains, which can vary with the agents. The main contribution of this work has been in the new necessary and sufficient stability bounds on the gains for third-order consensus for feedback with full relative state information or partial relative state information along with a reference model. The stability bounds obtained, which were shown to utilize those previously obtained for second-order consensus, are not overly conservative and allow for the gains to be conveniently selected in a sequential manner. This has direct application to PID consensus control in second-order mechanical systems, multi-agent mobile robots, and unmanned helicopters and UAVs, for example. The illustrative examples served to verify the obtained stability bounds and illustrate the use of the third-order protocol, in particular, while comparisons with other stability conditions were shown. Although they are not pursued in this paper, in the future it is suggested to extend the investigation to nonlinear agent dynamics and/or consensus protocols, switching network topologies, time delays in communication and actuation, heterogeneous agents, and to include uncertainties and disturbances [14], properties which are relevant to real world networked control systems. Finally, the results presented here, in addition to their importance for decentralized control and coordination of multi-agent systems, may also be relevant to distributed filtering and decision-making in information aggregation in multi-agent systems and real-time decision processes [16].
Author Contributions
Conceptualization, E.A.B.; methodology, E.A.B. and M.M.; software, E.A.B. and M.M.; validation, E.A.B. and M.M.; formal analysis, E.A.B.; investigation, E.A.B. and M.M.; resources, E.A.B. and M.M.; writing—original draft preparation, E.A.B.; writing—review and editing, E.A.B. and M.M.; visualization, E.A.B. and M.M.; supervision, E.A.B.; project administration, E.A.B.; funding acquisition, E.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
Research was sponsored by the Army Research Office and was accomplished under Grant Number W911NF-23-1-0155. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-Vehicle Cooperative Control; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ren, W.; Atkins, E. Distributed multi-vehicle coordinated control via local information exchange. Int. J. Robust Nonlinear Control 2007, 17, 1002–1033. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M. Some necessary and sufficient conditions for second-order consensus in multi-agent dynamical systems. Automatica 2010, 46, 1089–1095. [Google Scholar] [CrossRef]
- Zhu, J.; Tian, Y.-P.; Kuang, J. On the general consensus protocol of multi-agent systems with double-integrator dynamics. Linear Algebra Appl. 2009, 431, 701–715. [Google Scholar] [CrossRef]
- Mei, J.; Ren, W.; Chen, J. Distributed consensus of second-order multi-agent systems with heterogeneous unknown inertias and control gains under a directed graph. IEEE Trans. Autom. Control 2016, 61, 2019–2034. [Google Scholar] [CrossRef]
- Ren, W. On consensus algorithms for double-integrator dynamics. IEEE Trans. Autom. Control 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Ren, W.; Moore, K.L.; Chen, Y. High-order and model reference consensus algorithms in cooperative control of multivehicle systems. ASME J. Dyn. Syst. Meas. Control 2007, 129, 678–688. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. Average consensus over high-order multi-agent systems. IEEE Trans. Autom. Control 2015, 60, 3047–3052. [Google Scholar] [CrossRef]
- Jiang, F.; Wang, L. Consensus seeking of high-order dynamic multi-agent systems with fixed and switching topologies. Int. J. Control 2010, 83, 404–420. [Google Scholar] [CrossRef]
- Develer, U.; Akar, M. Higher-order cluster consensus of a multi-agent network with continuous-time dynamics. Trans. Inst. Meas. Control 2021, 43, 1734–1744. [Google Scholar] [CrossRef]
- Yaylali, D.; Butcher, E.A.; Dabiri, A. Fractional PID consensus control protocols for second-order multiagent systems. In Proceedings of the AIAA SciTech, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Rastgoftar, H.; Kolmanovsky, I.V. Safe affine transformation-based guidance of a large-scale multiquadcopter system. IEEE Trans. Control Networked Syst. 2021, 8, 640–653. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Cai, X. Distributed control algorithms for nonholonomic mobile robots with time-varying position constraints and event-triggered communication. IEEE Access 2025, 13, 94658–94666. [Google Scholar] [CrossRef]
- Sha, H.; Guo, R.-W.; Zhu, X.; Miao, Z. Cooperative adaptive consensus tracking control for multiple wheeled mobile robot systems with model uncertainties and external disturbances. Int. J. Robust Nonlinear Control 2025, 35, 3533–3544. [Google Scholar] [CrossRef]
- Abdessameud, A.; Tayebi, A. Distributed consensus algorithms for a class of high-order multi-agent systems on directed graphs. IEEE Trans. Autom. Control 2018, 63, 3464–3470. [Google Scholar] [CrossRef]
- Talebi, S.; Mandic, D. On the dynamics of multiagent nonlinear filtering and learning. In Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, London, UK, 22–25 September 2024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).