Neural Network Disturbance Observer-Based Adaptive Fault-Tolerant Attitude Tracking Control for UAVs with Actuator Faults, Input Saturation, and External Disturbances
Abstract
1. Introduction
- (1)
- An NDI controller based on NNDO technique is proposed for the high precision attitude tracking of UAVs. It is clear from [1,10] that the typical NDI control law relies on the system model. The presence of uncertainties such as actuator faults, external disturbances, and input saturation can degrade the control performance. In this paper, introducing the estimation of NNDO in NDI control law can effectively enhance the disturbance immunity and robustness.
- (2)
- Unlike fault-tolerant control strategies based on fault detection or estimation in [1,4,5,6,8,22,23], the L1 adaptive fault-tolerant controller in this paper provides online estimation of a lumped uncertainty consisting of system uncertainties, actuator faults, external disturbances, and approximation errors, and designs a control law with a low-pass filter to counteract the negative effects. This proposed adaptive fault-tolerant controller has the advantage of simple algorithms and easy implementation because it does not require precise estimates of faults and disturbances.
- (3)
- Compared to the monotonous stability analysis of closed-loop systems in most of the existing research works, both the stability and performance bounds are rigorously derived in this paper by Lyapunov stability theorem and an L1 reference system, which provide strong guarantees for controller design and performance improvement.
2. System Modeling
2.1. Attitude Control Systems for UAVs
2.2. Actuator Fault
- (1)
- and , no faults;
- (2)
- and , LOE (i.e., multiplicative fault);
- (3)
- and , additive fault;
- (4)
- and , composite fault.
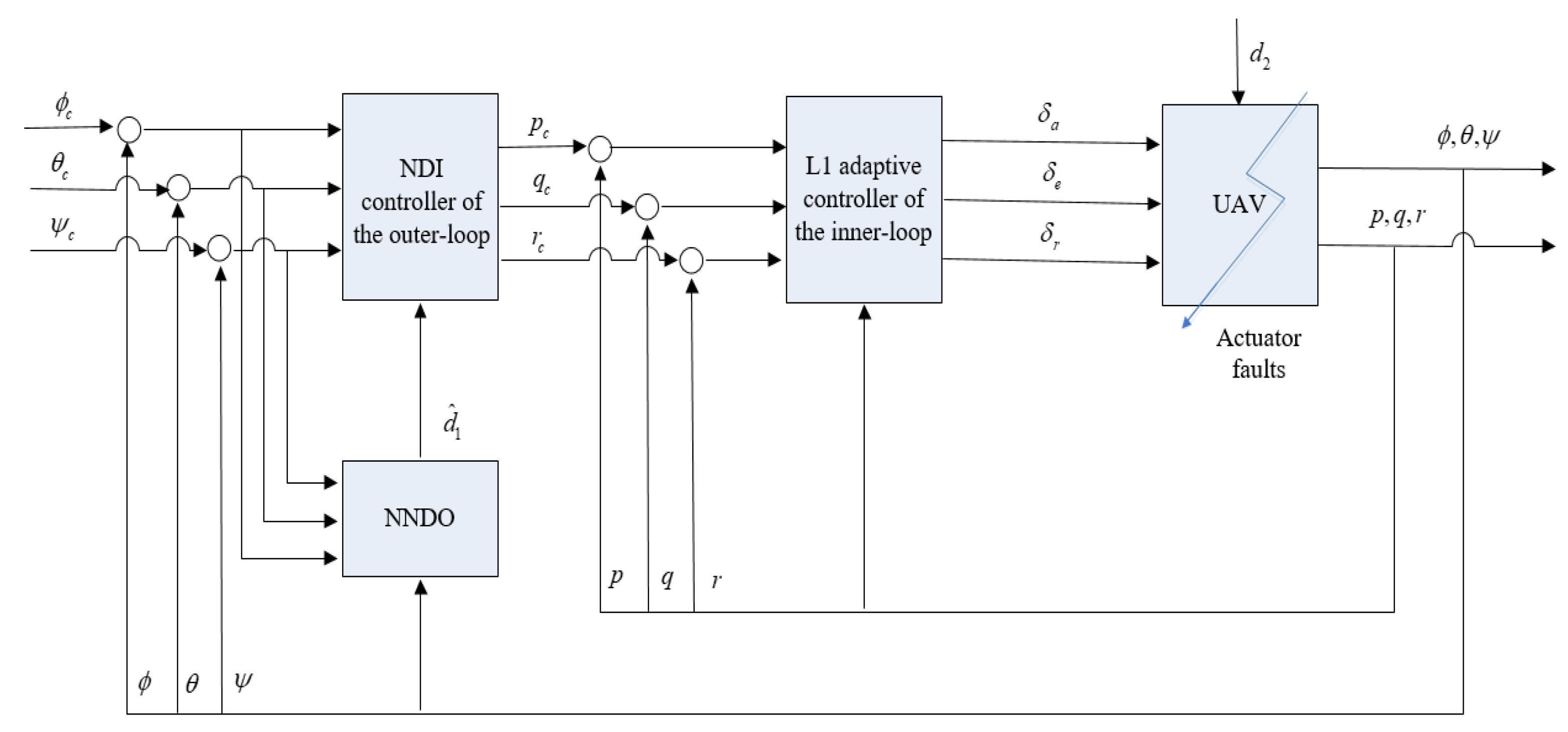
3. Design and Analysis of a Fault-Tolerant Controller for UAV Attitude Control System
3.1. Design of the Outer-Loop Attitude Angle Controller
3.2. Design and Analysis of the Inner-Loop Attitude Angular Velocity Controller
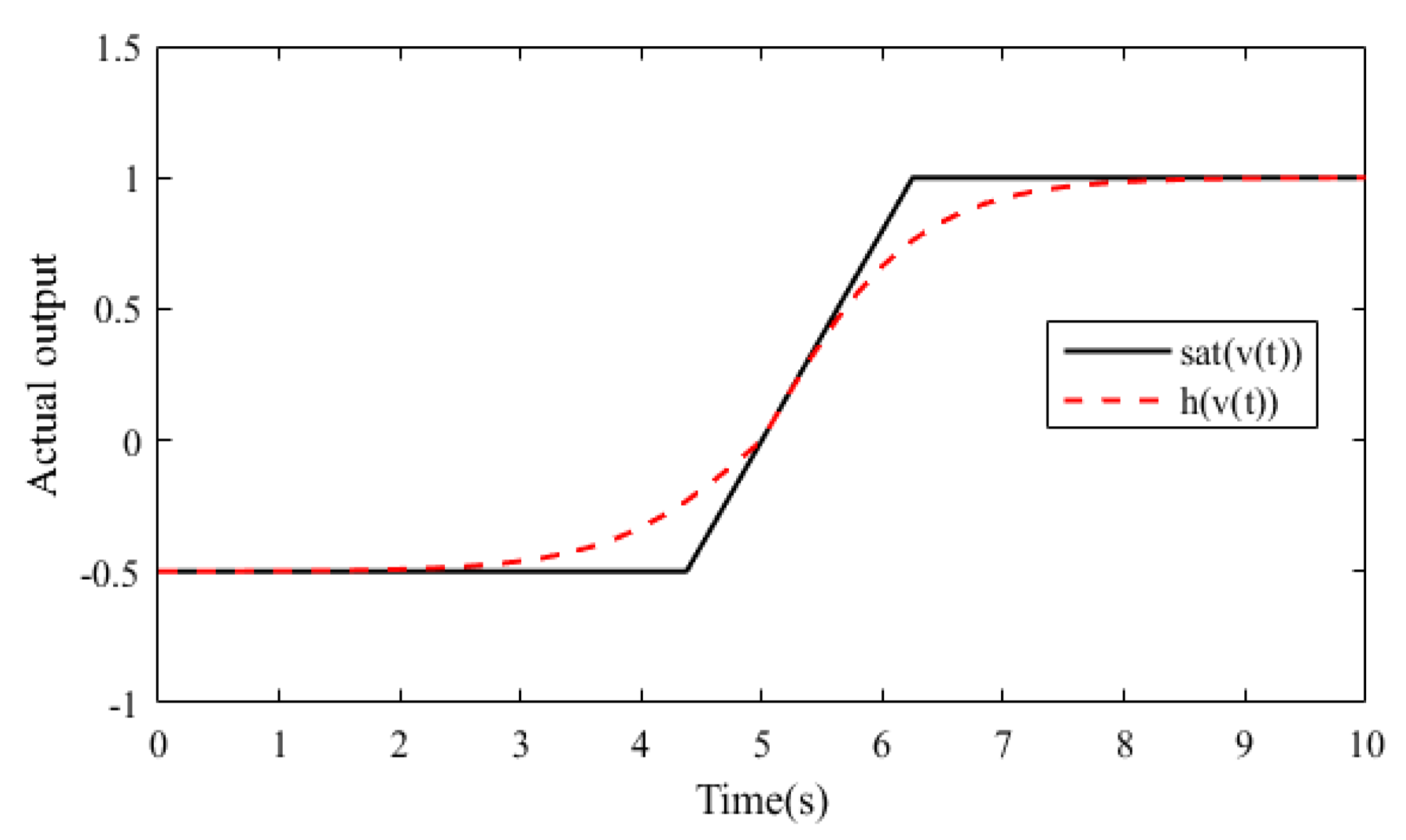
3.2.1. Conversion of the Input Saturation Function
3.2.2. Design of the L1 Adaptive Fault-Tolerant Controller
3.2.3. Performance Analysis of the L1 Adaptive Fault-Tolerant Controller
- Stability analysis
- 2.
- Performance boundaries analysis
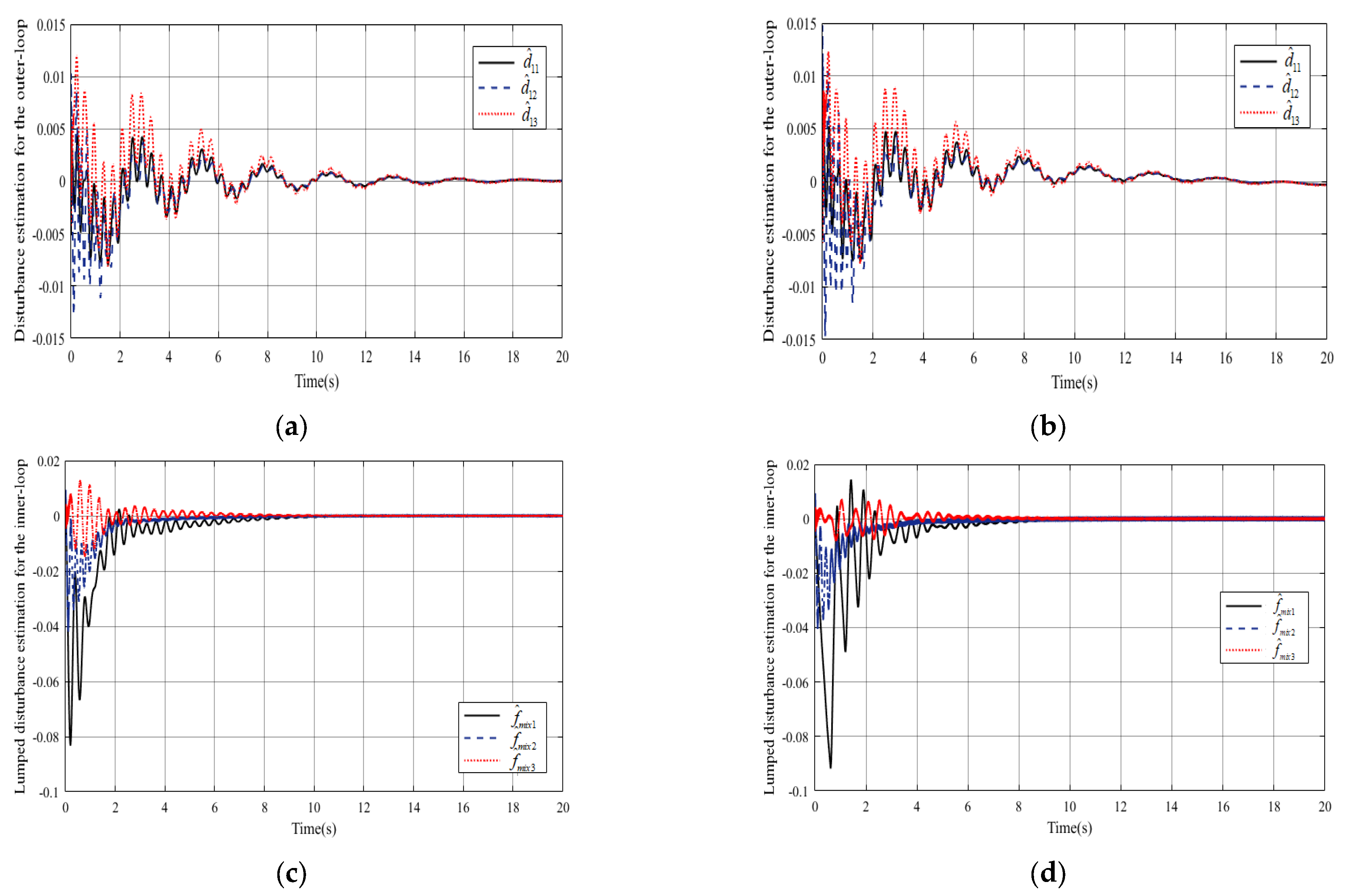
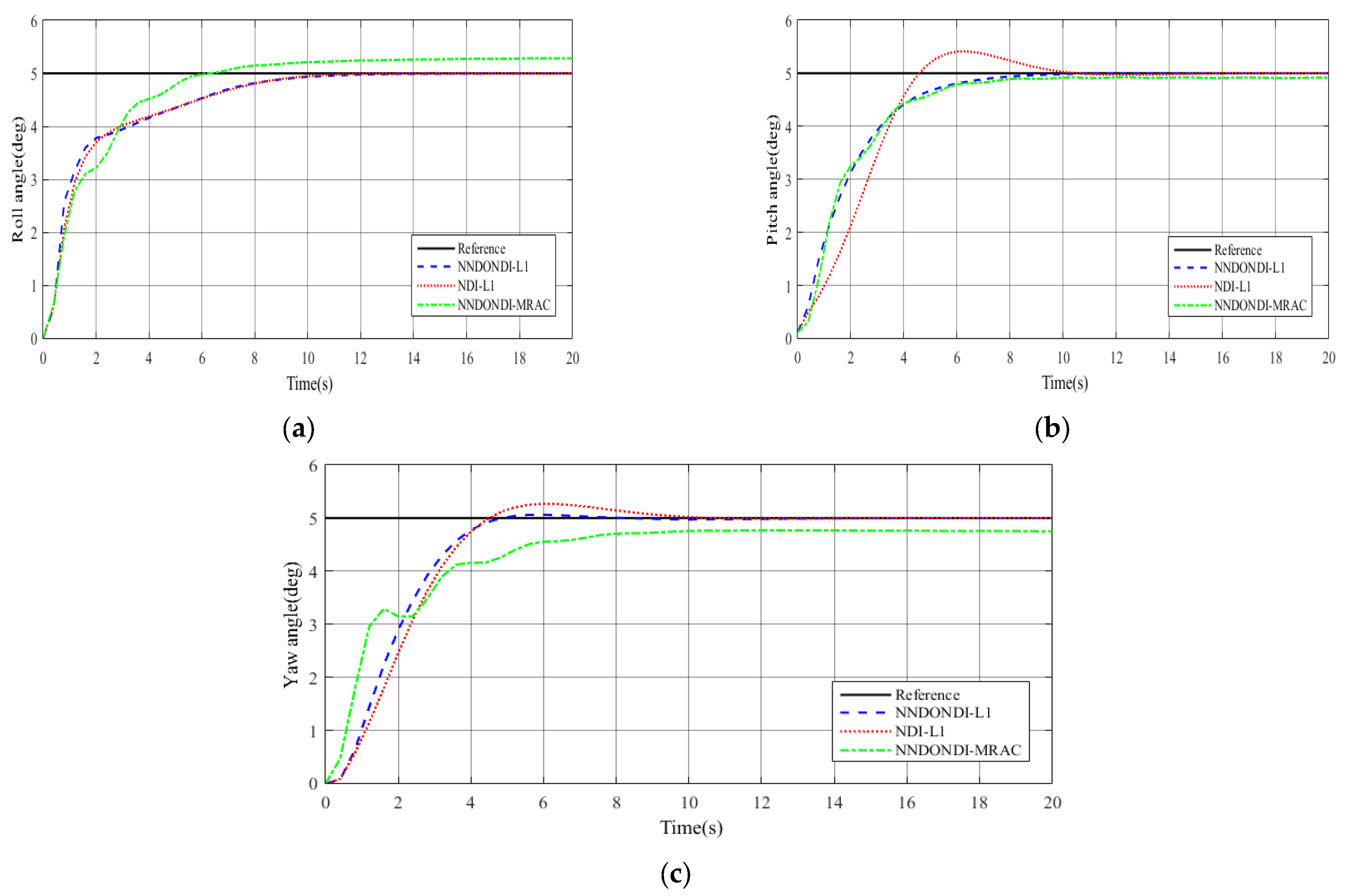
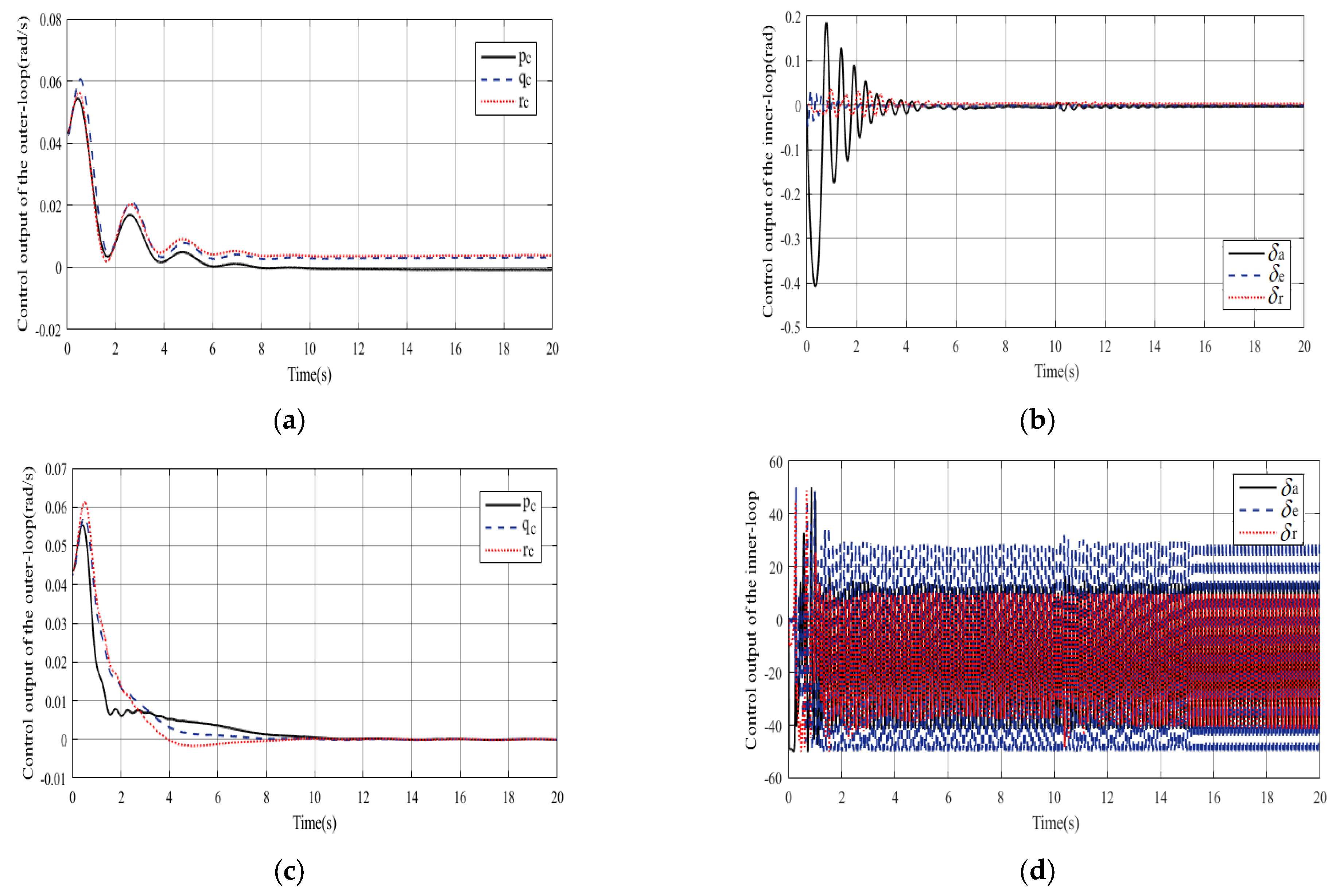
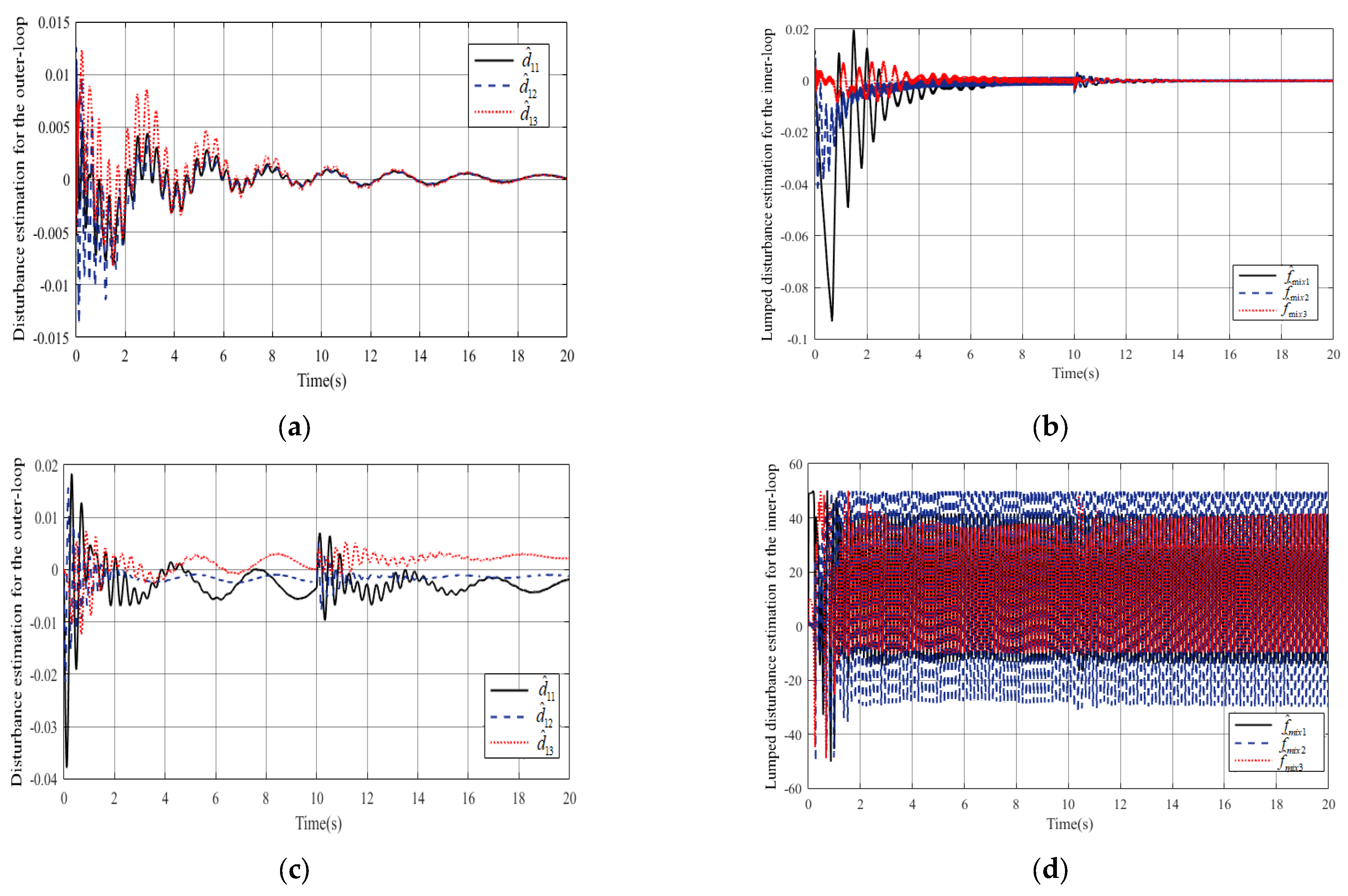
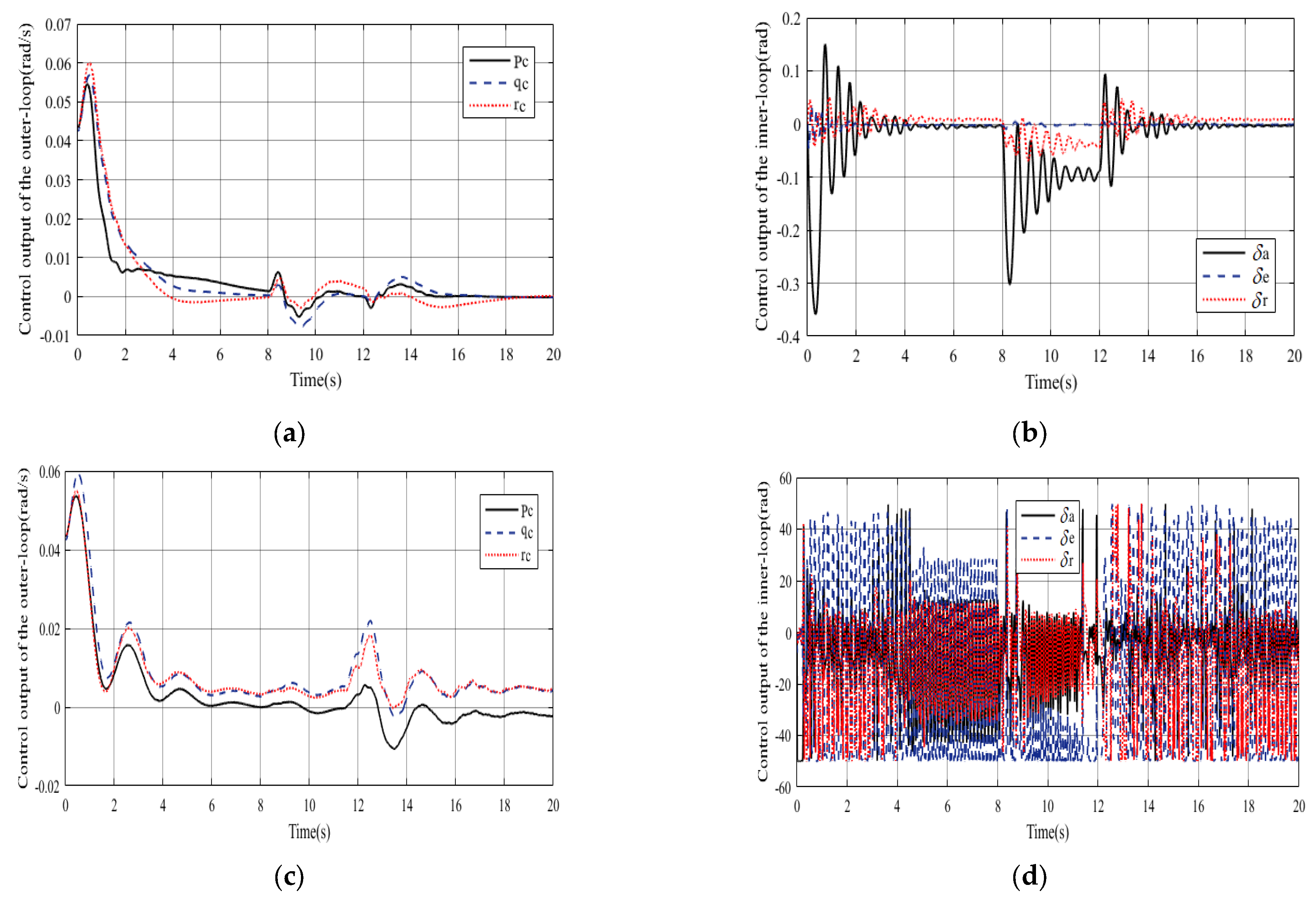
4. Simulation Experiments
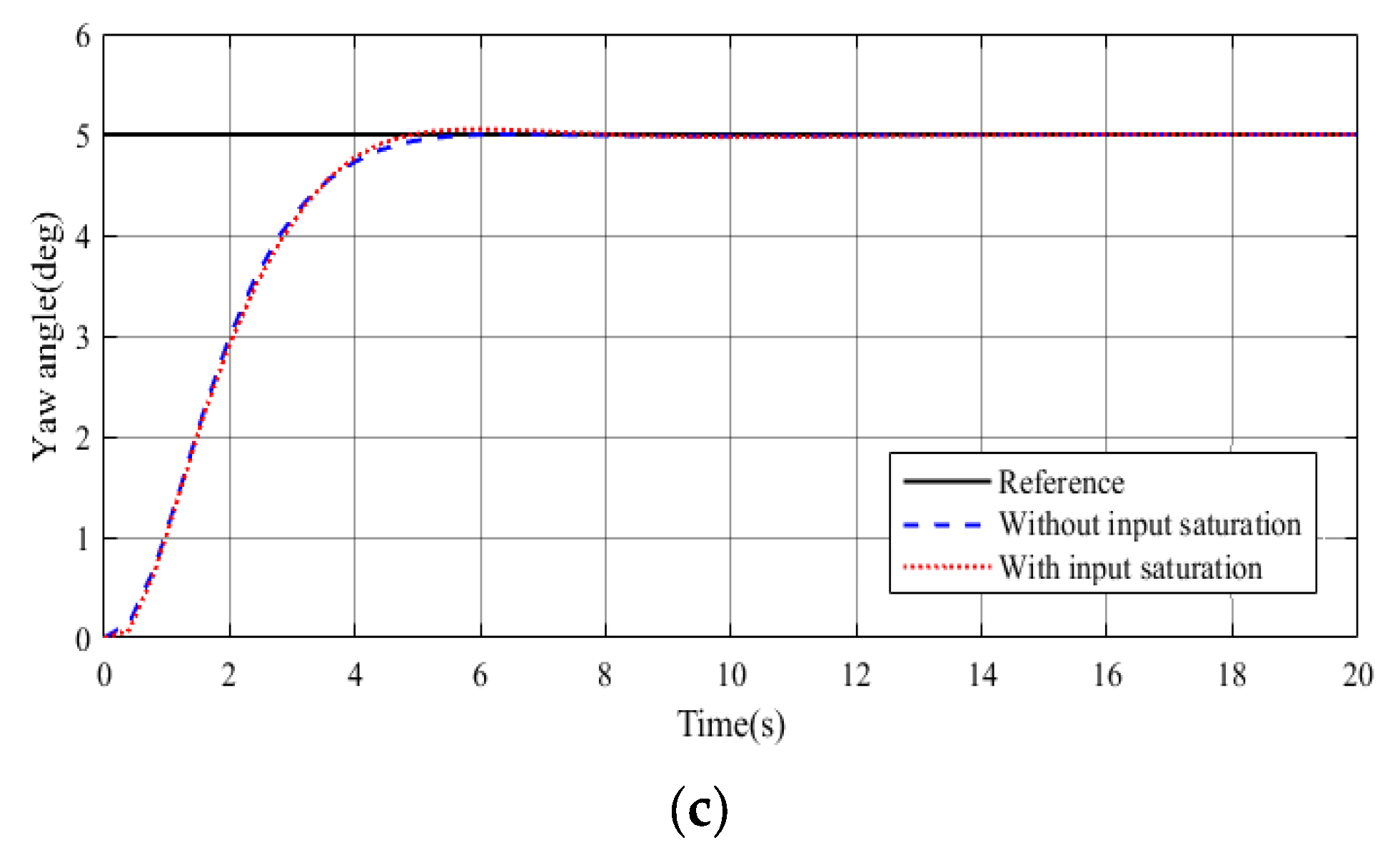
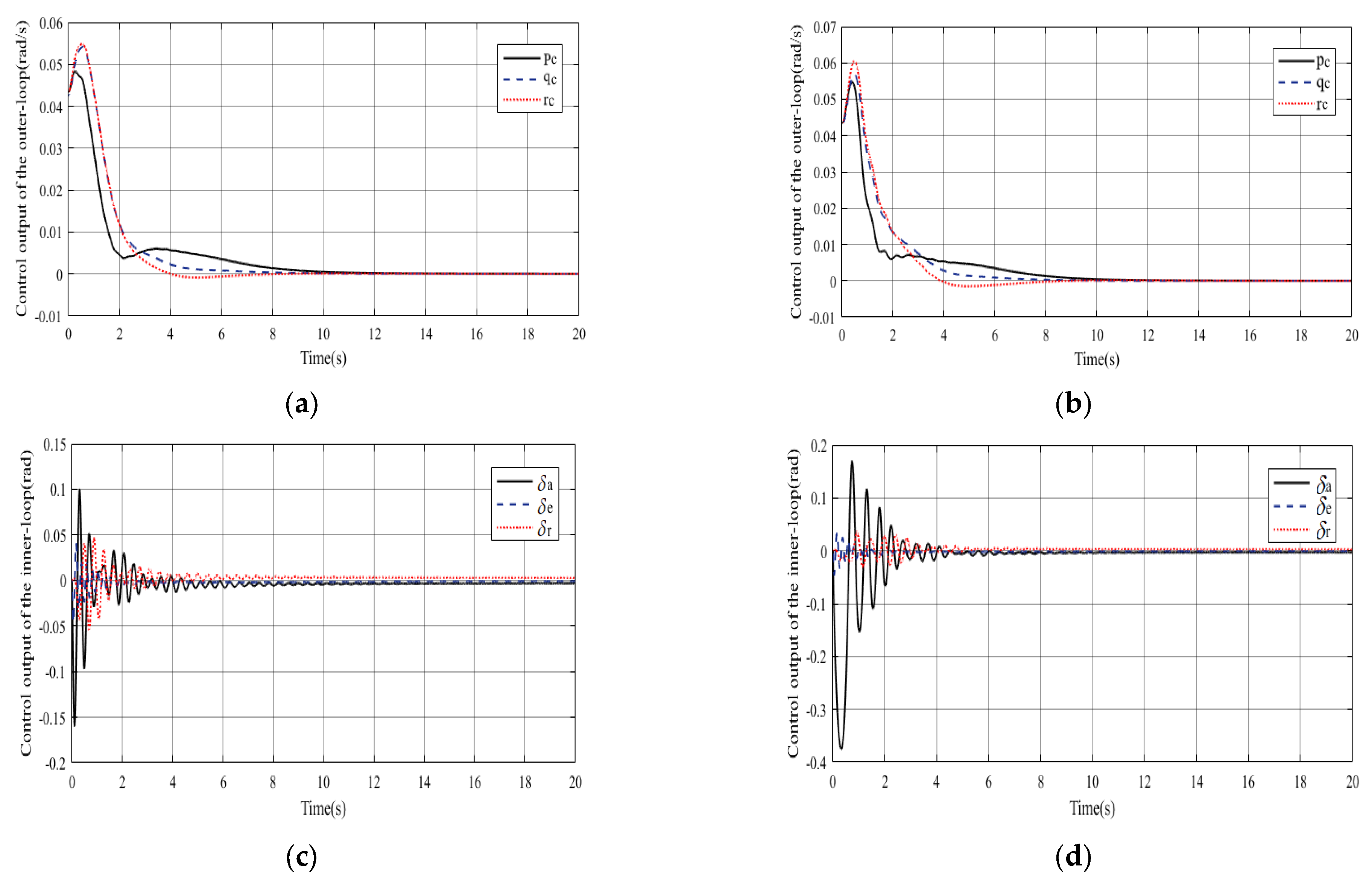
- Scenario 1. System only subject to input saturation.
- Scenario 2. System subject to input saturation and external disturbances.
- Scenario 3. System subject to input saturation, external disturbances, and actuator faults.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbaspour, A.; Yen, K.K.; Forouzannezhad, P.; Sargolzaei, A. A neural adaptive approach for active fault-tolerant control design in UAV. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3401–3411. [Google Scholar] [CrossRef]
- Mallavalli, S.; Fekih, A. A fault tolerant tracking control for a quadrotor UAV subject to simultaneous actuator faults and exogenous disturbances. Int. J. Control 2020, 93, 655–668. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Pitakwachara, P. Integral terminal sliding mode fault tolerant control of quadcopter UAV systems. Sci. Rep. 2024, 14, 10786. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Yan, J.; Pan, X.H.; Tan, S.L.; Cao, H.W.; Song, Y.D. Fault-tolerant attitude tracking control with practical finite time convergence for unmanned aerial vehicles under actuation faults. Int. J. Robust Nonlinear Control 2022, 32, 3737–3753. [Google Scholar] [CrossRef]
- Li, W.; Yang, P.; Geng, K.K.; Zhu, X.Y. Fault-tolerant attitude tracking control of tandem rotor helicopter considering internal actuator saturation and external wind gust. Int. J. Adapt. Control Signal Process. 2023, 37, 1671–1692. [Google Scholar] [CrossRef]
- Duan, H.B.; Yuan, Y.; Zeng, Z.G. Distributed cooperative control of multiple UAVs in the presence of actuator faults and input constraints. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4463–4467. [Google Scholar] [CrossRef]
- Yu, Z.L.; Li, Y.H.; Lv, M.L.; Pei, B.B.; Fu, A.Q. Event-triggered adaptive fuzzy fault-tolerant attitude control for tailless flying-wing UAV with fixed-time convergence. IEEE Trans. Veh. Technol. 2024, 73, 4858–4869. [Google Scholar] [CrossRef]
- Shen, Q.; Yue, C.F.; Goh, C.H.; Wang, D.W. Active fault-tolerant control system design for spacecraft attitude maneuvers with actuator saturation and faults. IEEE Trans. Ind. Electron. 2019, 66, 3763–3772. [Google Scholar] [CrossRef]
- Wang, X.H.; Tan, C.P.; Wu, F.; Wang, J.D. Fault-tolerant attitude control for rigid spacecraft without angular velocity measurements. IEEE Trans. Cybern. 2021, 51, 1216–1229. [Google Scholar] [CrossRef]
- Zhang, S.J.; Han, W.H.; Zhang, Y.M. Finite time convergence incremental nonlinear dynamic inversion-based attitude control for flying-wing aircraft with actuator faults. Actuators 2020, 9, 70. [Google Scholar] [CrossRef]
- Zhu, G.B.; Ma, Y.; Li, Z.X.; Malekian, R.; Sotelo, M. Event-triggered adaptive neural fault-tolerant control of underactuated MSVs with input saturation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7045–7057. [Google Scholar] [CrossRef]
- Liang, H.J.; Liu, G.L.; Huang, T.W.; Lam, H.K.; Wang, B.H. Cooperative fault-tolerant control for networks of stochastic nonlinear systems with nondifferential saturation nonlinearity. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1362–1372. [Google Scholar] [CrossRef]
- Meng, Y.Z.; Liu, C.; Liu, Y.L. Adaptive attitude angle constrained fault-tolerant control of hypersonic vehicle with unknown centroid shift. Aerosp. Sci. Technol. 2023, 140, 108475. [Google Scholar] [CrossRef]
- Chen, M.; Yan, K.; Wu, Q.X. Multiapproximator-based fault-tolerant tracking control for unmanned autonomous helicopter with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5710–5722. [Google Scholar] [CrossRef]
- Yu, Z.Q.; Liu, Z.X.; Zhang, Y.M.; Qu, Y.H.; Su, C.Y. Distributed finite-time fault-tolerant containment control for multiple unmanned aerial vehicles. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2077–2091. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.Q.; Yang, Y.S.; Xiao, B.; Ran, D.C. Appointed fixed time observer-based sliding mode control for a quadrotor UAV under external disturbances. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 290–303. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Cao, D.; Yang, J.; Wang, H.M. High-order sliding mode observer-based trajectory tracking control for a quadrotor UAV with uncertain dynamics. Nonlinear Dynam 2020, 102, 2583–2596. [Google Scholar] [CrossRef]
- Hu, Y.P.; Guo, J.; Ying, P.; Zeng, G.N.; Chen, N.Y. Nonlinear control of a single tail tilt servomotor tri-rotor ducted VTOL-UAV. Aerospace 2022, 9, 296. [Google Scholar] [CrossRef]
- Emami, S.A.; Banazadeh, A.; Hajipourzadeh, P.; Castaldi, P.; Fazelzadeh, S.A. Disturbance observer-based adaptive neural guidance and control of an aircraft using composite learning. Control Eng. Pract. 2023, 134, 105463. [Google Scholar] [CrossRef]
- Lungu, M. Auto-landing of UAVs with variable centre of mass using the backstepping and dynamic inversion control. Aerosp. Sci. Technol. 2020, 103, 105912. [Google Scholar] [CrossRef]
- Lv, J.X.; Wang, C.H.; Kao, Y.G. Adaptive fixed-time quantized fault-tolerant attitude control for hypersonic reentry vehicle. Neurocomputing 2023, 520, 386–399. [Google Scholar] [CrossRef]
- Liu, S.Q.; Whidborne, J.F. Observer-based incremental backstepping sliding-mode fault-tolerant control for blended-wing-body aircrafts. Neurocomputing 2021, 464, 546–561. [Google Scholar] [CrossRef]
- Rong, Y.F.; Chou, W.S.; Jiao, R. Robust fault-tolerant motion/force control of a fully-actuated hexarotor using adaptive sliding mode impedance control. Int. J. Robust Nonlinear Control 2022, 32, 4149–4172. [Google Scholar] [CrossRef]
- Kong, C.Y.; Zhao, D.J.; Dai, M.Z.; Liang, B.G. ESO-based event-triggered attitude control of spacecraft with unknown actuator faults. Adv. Space Res. 2023, 71, 768–784. [Google Scholar] [CrossRef]
- Cai, X.; Zhu, X.Z.; Yao, W. FTESO-adaptive neural network based safety control for a quadrotor UAV under multiple disturbances: Algorithm and experiments. Ind. Robot. 2024, 51, 20–33. [Google Scholar] [CrossRef]
- Xu, X.F.; Chen, M.; Li, T.; Wu, Q.X. Composite fault tolerant attitude control for flexible satellite system under disturbance and input delay. Appl. Math. Comput. 2021, 409, 126419. [Google Scholar] [CrossRef]
- Shen, Y.X.; Zhou, D.J.; Wu, Y.D.; Huang, D.W. Anti-disturbance control for HVs system subject to nonlinear actuator characteristics with extended state observer. J. Frankl. Inst. 2023, 360, 14676–14695. [Google Scholar] [CrossRef]
- Mazare, M. Reconfigurable tolerant control of nonlinear Euler-Lagrange systems under actuator fault: A reinforcement learning-based fixed-time approach. Aerosp. Sci. Technol. 2023, 142, 108631. [Google Scholar] [CrossRef]
- Sanwale, J.; Dahiya, S.; Trivedi, P.; Kothari, M. Robust fault-tolerant adaptive integral dynamic sliding mode control using finite-time disturbance observer for coaxial octorotor UAVs. Control Eng. Pract. 2023, 135, 105495. [Google Scholar] [CrossRef]
- Cao, C.Y.; Hovakimyan, N. Design and analysis of a novel L1 adaptive controller, part I: Control signal and asymptotic stability. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 3397–3402. [Google Scholar] [CrossRef]
- Meng, X.F.; Zhang, G.C.; Han, B. Fault-tolerant control of underactuated MSVs based on neural finite-time disturbance observer: An Event-triggered Mechanism. J. Frankl. Inst. 2024, 361, 106603. [Google Scholar] [CrossRef]
- Hazem, Z.B.; Saidi, F.; Guler, N.; Altaif, A.H. Reinforcement learning-based intelligent trajectory tracking for a 5-DOF Mitsubishi robotic arm: Comparative evaluation of DDPG, LC-DDPG, and TD3-ADX. Int. J. Intell. Robot. Appl. 2025. [Google Scholar] [CrossRef]
- Liu, H.; Li, B.; Xiao, B.; Ran, D.C.; Zhang, C.X. Reinforcement learning-based tracking control for a quadrotor unmanned aerial vehicle under external disturbances. Int. J. Robust Nonlinear Control 2023, 33, 10360–10377. [Google Scholar] [CrossRef]
- Durham, W.C.; Lutze, F.H. Perfect explicit model-following control solution to imperfect model-following control-problems. J. Guid. Control Dynam 1991, 14, 391–397. [Google Scholar] [CrossRef]
- Pomet, J.B.; Praly, L. Adaptive nonlinear regulation: Estimation from Lyapunov equation. IEEE Trans. Autom. Control. 1992, 37, 729–740. [Google Scholar] [CrossRef]
- Yousef, H.A.; Hamdy, M.; Nashed, K. L1 adaptive fuzzy controller for a class of nonlinear systems with unknown backlash-like hysteresis. Int. J. Syst. Sci. 2017, 48, 2522–2533. [Google Scholar] [CrossRef]
- Li, Z.Y.; Shi, S.; Liu, H. Trajectory tracking of tail-sitter aircraft by adaptive fault tolerant control. J. Syst. Eng. Electron. 2021, 32, 1477–1489. [Google Scholar] [CrossRef]



| System Parameters | Descriptions |
|---|---|
| attitude angles of roll, pitch, and yaw | |
| attitude angle velocities of roll, pitch, and yaw | |
| moments of roll, pitch, and yaw | |
| coefficients | |
| dynamic pressure | |
| reference area of the wing | |
| span of the wing | |
| mean geometric chord length of the wing | |
| angle of attack | |
| angle of sideslip | |
| aerodynamic coefficients | |
| deflection angles of aileron, elevator, and rudder |
| Attitude Angles | Indicators | Without Input Saturation | With Input Saturation |
|---|---|---|---|
| Roll angle | steady-state error | 0.0005 | 0.0006 |
| convergence time | 9.1525 | 9.153 | |
| IAE | 0.1685 | 0.1684 | |
| ISE | 0.0063 | 0.0064 | |
| ITAE | 0.426 | 0.4203 | |
| ITSE | 0.0064 | 0.0064 | |
| Pitch angle | steady-state error | 0.0001 | 0.0001 |
| convergence time | 6.9308 | 7.1491 | |
| IAE | 0.1717 | 0.1719 | |
| ISE | 0.0082 | 0.0082 | |
| ITAE | 0.2925 | 0.3047 | |
| ITSE | 0.0075 | 0.0076 | |
| Yaw angle | steady-state error | 0.0004 | 0.0002 |
| convergence time | 4.6711 | 4.3802 | |
| IAE | 0.169 | 0.1726 | |
| ISE | 0.0103 | 0.0103 | |
| ITAE | 0.2288 | 0.2416 | |
| ITSE | 0.0089 | 0.0089 |
| Attitude Angles | Indicators | NNDONDI-L1 | NDI-L1 | NNDONDI-MRAC |
|---|---|---|---|---|
| Roll angle | steady-state error | 0.0006 | 0.0009 | 0.2853 |
| convergence time | 10.6281 | 12.1248 | — | |
| IAE | 0.1683 | 0.1708 | 0.2014 | |
| ISE | 0.0064 | 0.0077 | 0.0072 | |
| ITAE | 0.4193 | 0.4248 | 0.9848 | |
| ITSE | 0.0064 | 0.0073 | 0.0093 | |
| Pitch angle | steady-state error | 0.0001 | 0.0011 | 0.0181 |
| convergence time | 9.787 | 11.1028 | 8.8169 | |
| IAE | 0.172 | 0.2679 | 0.1948 | |
| ISE | 0.0081 | 0.0149 | 0.0087 | |
| ITAE | 0.3073 | 0.6748 | 0.5653 | |
| ITSE | 0.0076 | 0.0206 | 0.0083 | |
| Yaw angle | steady-state error | 0.0001 | 0.0014 | 0.248 |
| convergence time | 10.0135 | 10.8314 | — | |
| IAE | 0.1736 | 0.2029 | 0.2389 | |
| ISE | 0.0103 | 0.0116 | 0.0112 | |
| ITAE | 0.2461 | 0.3724 | 1.129 | |
| ITSE | 0.0089 | 0.0116 | 0.0119 |
| Attitude Angles | Indicators | Analysis |
|---|---|---|
| Roll angle | IAE | Minimum IAE: 0.1683(NNDONDI-L1), 1.5% lower than NDI-L1, 16.4% lower than NNDONDI-MRAC |
| ISE | Minimum ISE: 0.0064(NNDONDI-L1), 16.9% lower than NDI-L1, 11.1% lower than NNDONDI-MRAC | |
| ITAE | Minimum ITAE: 0.4193(NNDONDI-L1), 1.3% lower than NDI-L1, 57.4% lower than NNDONDI-MRAC | |
| ITSE | Minimum ITSE: 0.0064(NNDONDI-L1), 12.3% lower than NDI-L1, 31.2% lower than NNDONDI-MRAC | |
| Pitch angle | IAE | Minimum IAE: 0.172(NNDONDI-L1), 35.8% lower than NDI-L1, 11.7% lower than NNDONDI-MRAC |
| ISE | Minimum ISE: 0.0081(NNDONDI-L1), 45.6% lower than NDI-L1, 6.9% lower than NNDONDI-MRAC | |
| ITAE | Minimum ITAE: 0.3073(NNDONDI-L1), 54.5% lower than NDI-L1, 45.6% lower than NNDONDI-MRAC | |
| ITSE | Minimum ITSE: 0.0076(NNDONDI-L1), 63.1% lower than NDI-L1, 8.4% lower than NNDONDI-MRAC | |
| Yaw angle | IAE | Minimum IAE: 0.1736(NNDONDI-L1), 14.4% lower than NDI-L1, 27.3% lower than NNDONDI-MRAC |
| ISE | Minimum ISE: 0.0103(NNDONDI-L1), 11.2% lower than NDI-L1, 8% lower than NNDONDI-MRAC | |
| ITAE | Minimum ITAE: 0.2461(NNDONDI-L1), 33.9% lower than NDI-L1, 78.2% lower than NNDONDI-MRAC | |
| ITSE | Minimum ITSE: 0.0089(NNDONDI-L1), 23.3% lower than NDI-L1, 25.2% lower than NNDONDI-MRAC |
| Attitude Angles | Indicators | NNDONDI-L1 | NDI-L1 | NNDONDI-MRAC |
|---|---|---|---|---|
| Roll angle | steady-state error | 0.0013 | 0.0014 | 0.2974 |
| convergence time | 10.6102 | 10.6123 | — | |
| IAE | 0.1722 | 0.1855 | 0.23 | |
| ISE | 0.0064 | 0.008 | 0.0071 | |
| ITAE | 0.4674 | 0.5634 | 1.338 | |
| ITSE | 0.0065 | 0.0104 | 0.0185 | |
| Pitch angle | steady-state error | 0.0065 | 0.0068 | 0.089 |
| convergence time | 15.9374 | 15.942 | — | |
| IAE | 0.1926 | 0.2791 | 0.2135 | |
| ISE | 0.0081 | 0.0153 | 0.0087 | |
| ITAE | 0.5685 | 0.7201 | 0.779 | |
| ITSE | 0.0083 | 0.0256 | 0.0282 | |
| Yaw angle | steady-state error | 0.0186 | 0.0218 | 0.253 |
| convergence time | 17.2399 | 18.3102 | — | |
| IAE | 0.2083 | 0.2432 | 0.2509 | |
| ISE | 0.0105 | 0.0118 | 0.0181 | |
| ITAE | 0.6893 | 0.8826 | 1.276 | |
| ITSE | 0.0109 | 0.0145 | 0.0212 |
| Attitude Angles | Indicators | Analysis |
|---|---|---|
| Roll angle | IAE | Minimum IAE: 0.1722(NNDONDI-L1), 7.2% lower than NDI-L1, 25.1% lower than NNDONDI-MRAC |
| ISE | Minimum ISE: 0.0064(NNDONDI-L1), 20% lower than NDI-L1, 9.9% lower than NNDONDI-MRAC | |
| ITAE | Minimum ITAE: 0.4674(NNDONDI-L1), 17% lower than NDI-L1, 65.1% lower than NNDONDI-MRAC | |
| ITSE | Minimum ITSE: 0.0065(NNDONDI-L1), 37.5% lower than NDI-L1, 64.9% lower than NNDONDI-MRAC | |
| Pitch angle | IAE | Minimum IAE: 0.1926(NNDONDI-L1), 30.1% lower than NDI-L1, 9.8% lower than NNDONDI-MRAC |
| ISE | Minimum ISE: 0.0081(NNDONDI-L1), 47.1% lower than NDI-L1, 6.9% lower than NNDONDI-MRAC | |
| ITAE | Minimum ITAE: 0.5685(NNDONDI-L1), 21.1% lower than NDI-L1, 27% lower than NNDONDI-MRAC | |
| ITSE | Minimum ITSE: 0.0083(NNDONDI-L1), 67.6% lower than NDI-L1, 70.6% lower than NNDONDI-MRAC | |
| Yaw angle | IAE | Minimum IAE: 0.2083(NNDONDI-L1), 14.4% lower than NDI-L1, 17% lower than NNDONDI-MRAC |
| ISE | Minimum ISE: 0.0105(NNDONDI-L1), 11% lower than NDI-L1, 42% lower than NNDONDI-MRAC | |
| ITAE | Minimum ITAE: 0.6893(NNDONDI-L1), 21.9% lower than NDI-L1, 46% lower than NNDONDI-MRAC | |
| ITSE | Minimum ITSE: 0.0109(NNDONDI-L1), 24.8% lower than NDI-L1, 48.6% lower than NNDONDI-MRAC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Liu, Y.; Li, J.; Liu, H. Neural Network Disturbance Observer-Based Adaptive Fault-Tolerant Attitude Tracking Control for UAVs with Actuator Faults, Input Saturation, and External Disturbances. Actuators 2025, 14, 437. https://doi.org/10.3390/act14090437
Zhou Y, Liu Y, Li J, Liu H. Neural Network Disturbance Observer-Based Adaptive Fault-Tolerant Attitude Tracking Control for UAVs with Actuator Faults, Input Saturation, and External Disturbances. Actuators. 2025; 14(9):437. https://doi.org/10.3390/act14090437
Chicago/Turabian StyleZhou, Yan, Ye Liu, Jiaze Li, and Huiying Liu. 2025. "Neural Network Disturbance Observer-Based Adaptive Fault-Tolerant Attitude Tracking Control for UAVs with Actuator Faults, Input Saturation, and External Disturbances" Actuators 14, no. 9: 437. https://doi.org/10.3390/act14090437
APA StyleZhou, Y., Liu, Y., Li, J., & Liu, H. (2025). Neural Network Disturbance Observer-Based Adaptive Fault-Tolerant Attitude Tracking Control for UAVs with Actuator Faults, Input Saturation, and External Disturbances. Actuators, 14(9), 437. https://doi.org/10.3390/act14090437






