Stability Assessment of Operation Tunnels Considering Long-Term Interaction Between the Lining and Surrounding Rock

Abstract

Operational tunnels are generally accompanied by time-dependent deformation and structural failures due to delayed behaviors, e.g., loading effects from surrounding rock and degradation of the concrete lining. This paper presents an analytical approach to investigate the long-term stability of tunnels considering those delayed behaviors. To quantitatively characterize the degradation process of concrete lining, specific degradation models are adopted according to the identified obstacles in service environments. The viscoelastic Burgers model is selected to recognize the long-term creep properties of the surrounding rock. The time-varying solutions for tunnel deformation and lining stress can be obtained using the displacement compatibility condition between the concrete lining and the surrounding rock. The results find that the long-term stability of tunnels is governed by the interaction between the concrete lining and the surrounding rock. Different degradation models and rates significantly influence mechanical response, with thinner linings showing greater susceptibility. Viscoelastic rock properties further affect system behavior. The amplified effect of degradation under long-term rock loading underscores the necessity of understanding these coupled mechanisms for accurate life predictions. On account of the findings, a long-term performance maintenance method for operation tunnels is proposed and illustrated by a rehabilitation project for tunnel damage. Remediation of structural damage in operation tunnels should consider the surrounding rock condition and support structure performance, significantly improving long-term safety and reducing remediation costs. Overall, the present work provides some insight into the long-term stability assessment of operation tunnels.

1. Introduction

The complex, practical nature of tunnel engineering, the experience dependence on tunnel design, and the variability of the service environment have led to a lack of reliable guidance for the safety control of tunnel structures [1,2,3,4,5], creating a vast potential danger to tunnel operation [6,7,8]. Tunnel structure, as a complex system, is subject to various types and degrees of damage after being put into operation or service, and related safety accidents are frequent. In general, tunnel structural damage results from the long-term undesirable interaction between the support and the surrounding rock, and its essence is the variation in stress condition caused by the change in the surrounding rock and the support state [9,10,11,12], as shown in Figure 1. For tunnel engineering, the surrounding rock often exhibits significant time-lapse characteristics, and the resulting long-term loading effect is one of the leading causes of tunnel structural failure [13,14,15,16]; in addition, the continuous deterioration of the support in the service environment also negatively impacts the long-term stability of the tunnel structures [17,18,19,20]. As a result, cases of structural failure during the service life of tunnels, like the ones in Figure 2, are common. Nevertheless, existing research and design concepts have not paid enough attention to the impact of these factors on the service safety of tunnel engineering, resulting in a lack of systematic and scientific theoretical guidance for structural design and long-term stability assessment of tunnels.

Figure 1. Tunnel safety is dependent on the behavior of the surrounding rock and support structure.

As a natural material, rock often exhibits significant aging properties due to geo-stress [21,22,23] and the external environment [24,25,26]. Although some tunnels can maintain their short-term stability, the load effect caused by rock creep may disrupt short-term stability over time, thereby threatening the long-term service safety of tunnel engineering. Numerical simulations and theoretical approaches have yielded rich results in studying the long-term loading effects from the surrounding rock of operation tunnels. In the numerical simulation, Liu et al. [10] established numerical models of tunnel structure in inclined and weak strata, and they explored the cracking mechanism of the lining structure during the operation period under the rheological loading effect of the surrounding rock. In addition, the theoretical approach is also highly respected in analyzing the interaction mechanism between support and rheological rock to reveal the intrinsic mechanism of the research problem. Yang et al. [27] established a coupled mechanical model considering surrounding rock rheology and prestressed anchor support to analyze the creep displacement and the long-term stress of prestressed anchor anchorage. Wu et al. [28], Chang Liu et al. [29], and Chu et al. [30] established analytical mechanical models to explore the mechanism of the creep effect of surrounding rock on the long-term mechanical state of the tunnel structure. The literature consistently identifies the understanding of long-term loading effects as a fundamental prerequisite for analyzing the safety of tunnel structures. Unfortunately, tunnel design that inadequately considers the long-term loading effects of the surrounding rock is the leading cause of in-service failure of tunnel structures.

Figure 2. Lining failure due to long-term load from the surrounding rock for operational tunnels, as shown (a) by Liu et al. [31], (b) by Wang et al. [32], (c) by Zhao et al. [14], (d) by Sui et al. [33], (e) by Ma et al. [8], (f) by Xu et al. [34], (g) by Liu et al. [10], (h) by Wang et al. [35], (i) by Xu and Gutierrez [36], (j) by Zhao et al. [14], (k,l) were taken by authors.

On the other hand, concrete linings in the tunnel operation stage can be affected by aging and show a reduction in stiffness and strength (Figure 3). Moreover, lining degradation is one of the leading causes of tunnel structural damage. The following surveys can reinforce this statement: the service status of 6705 Japanese road tunnels was investigated in 1990, and 24% of tunnels suffered from degradation [37]. A survey of more than 2000 operation tunnels in Chengdu, China, Feng et al. [38] found that lining concrete degradation is prevalent and is the main culprit behind the reduction in structural load-bearing capacity. In addition, Wang et al. [39] systematically investigated the distribution characteristics of railroad tunnel damage, where they identified the degradation of lining concrete materials and external environmental factors as one of the main causes of tunnel damage, which accounted for 27% and 23% of the total, respectively. It is well known that various factors, such as humidity, temperature, and corrosive groundwater, accelerate concrete linings’ degradation [40,41]. Therefore, empirical models have been proposed to describe the degradation characteristics of concrete material. In some instances, their predictive power suffers from a significant degree of uncertainty, and specific models may be applied to study a particularly critical section of a specific structure. Therefore, degradation models have been put forward by diminishing Young’s modulus and compressive strength with time. For example, Mori and Ellingwood [42] proposed three degradation models (i.e., linear, parabolic, and square root models) to assess the reliability of aging concrete structures. Also, two degradation models (i.e., exponential and parabolic functions of time) were adopted to describe the decreasing concrete compressive strength by Chan and Melchers [43], and the failure probability of structural systems was discussed. In general, previous research has shown that these idealized or simplified degradation models are suitable for analyzing the degradation characteristics of concrete during the operation stage.

Figure 3. Degradation of concrete lining [17,44].

It can be seen that the two components of the tunnel system, surrounding rock and support, show significant time characteristics in the service period, undoubtedly disturbing the dynamic relationship between the support-surrounding rock and even breaking the equilibrium of the tunnel structural system. Accordingly, this issue has been emphasized; for example, Ma et al. [8] proposed a numerical modeling method to simulate the spatial variability and stochastic process of lining reinforcement corrosion, and the evolution law of lining structure reliability under the coupling effect of surrounding rock rheology and steel corrosion degradation is revealed. The modified Burgers model was proposed by Yin et al. [45] to simulate the long-term degradation effect of the grouted reinforcement zone for the surrounding rock, and then the mechanical behavior of the lining structure was investigated by numerical simulation. Xu and Gutierrez [36] employed numerical methods to study the long-term evolution law of internal force and damage characteristics of secondary lining under anchor corrosion and creep loading of surrounding rock. Andreotti and Lai [46] investigated the long-term safety of tunnels by considering the degradation process of the surrounding rock and support structures during the tunnels’ service life by the parameter discounting method. In the theoretical approach, Zhang et al. [47] introduced an exponential decay model to characterize the degradation of lining structure stiffness, on which an analytical model was established to analyze the effect of lining degradation on the service mechanical behavior of an undersea tunnel. Du et al. [48] established a mechanical model considering the degradation of surrounding rock and lining to explore the service performance of tunnel structures. In addition, Liu et al. [7] established a coupled analytical model considering lining degradation characteristics and surrounding rock rheological effects; after that, the mechanical response of the tunnel structure was examined. It can be found that the classical element model is mainly used to describe the creep behavior of the surrounding rock, whereas the degradation characteristics of the support structure are generally characterized by the empirical model. In summary, the concrete lining and rheological rock during the service life of tunnels could show significant time-dependent characteristics, thus rendering the long-term mechanical response of the tunnel support structure system intricate.

As seen above the safety control of operation tunnels has become a high-interest and challenging issue, but existing research has failed to systematically explore the influence mechanism of lining degradation characteristics and surrounding rock rheological characteristics on the long-term safety of the structure system because tunnel equilibrium depends critically on the interaction between the concrete lining and the surrounding rock. Considering that the theoretical approach has an advantage on the intrinsic mechanism of the research problem [28], the theoretical analytical method is particularly advantageous for elucidating fundamental mechanisms in tunnel engineering, especially when performing parametric studies relative to numerical models. An analytical model considering the long-term loading effects of the surrounding rock and the degradation process of the concrete lining is expected to be developed in this paper to assess the stability evolution over time. Moreover, the degradation of the concrete lining can be quantitatively characterized by the put-forward empirical models, where the classical element model is adopted to describe the long-term delayed behaviors of the surrounding rock. Hereby, time-varying solutions for tunnel deformation and lining stress can be obtained using the displacement coordination relationship between surrounding rock and concrete lining for specific initial conditions. The analytical model is employed to illustrate the impacts of the main degradation processes of concrete lining and creep features of surrounding rock on the tunnel long-term stability. The safety of the tunnel structure is further investigated by establishing a service life prediction model based on the relationship between support loads and the bearing capacity of concrete lining. Upon this basis, a method for long-term performance maintenance of tunnel structures is proposed and guides the damage rehabilitation of an operational tunnel.

2. Time-Dependent Characteristics of Tunnel Structures

2.1. Degradation Process of Concrete Lining

Erosion and corrosion occur within the concrete lining under the long-term action of the service environment, causing damage to the microstructure of the concrete [3,8,19,49], eventually leading to the reduction in compressive strength and elastic modulus of the concrete lining [49,50,51,52]. Time-dependent influences on the in situ mechanical performance should be considered when assessing the impact of aging and structural degradation of concrete linings. Therefore, empirical models have been proposed to quantitatively characterize the evolution of mechanical properties of concrete structures during the degradation process [37,40,42,47,48]. Based on existing studies, the degradation of the strength or stiffness of concrete R(t) at time t (years) can be defined by:

$$R\left(t\right)=R_0\cdot g\left(t\right)$$

(1)

where R₀ is the component strength or stiffness at the initial state, and g(t) is the time-dependent degradation model, which defines the fraction of the initial strength or stiffness remaining at time t. Conceptually, a function g(t) is associated with each environmental component, but their impact on the time-dependent stability of tunnels has not been examined to date [42].

Based on existing research, the effect of the degradation of strength and stiffness of concrete is illustrated using three typical parametric representation models, as shown in Figure 4. The square root function represents a diffusion-controlled degradation process and concrete carbonation with a decreasing degradation rate over time [53,54], and the linear function has a constant degradation rate in strength and stiffness [55,56]. In addition, concrete is subjected to an accelerated degradation process because of sulfate attack, defined by a parabolic function [57]. As data to quantify the variability in degradation rate is insufficient, each function is assumed to be deterministic. Alternatively, the degradation rate may vary inside the concrete lining; after that, it is necessary to investigate the effects of degradation rates and different degradation models on the long-term stability of tunnels. For example, different degradation models for various degradation rates are shown in Figure 4. In Figure 4b, the parameter a is the degradation coefficient, and the units of different degradation models are different.

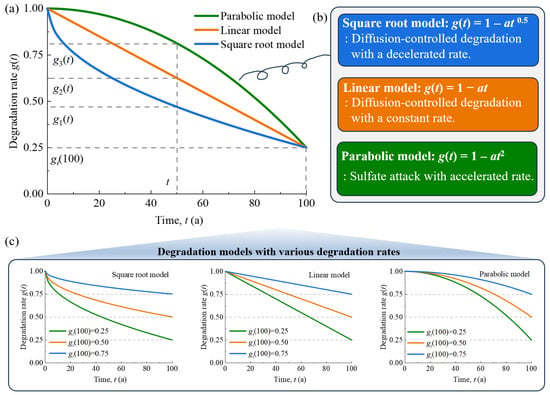
Figure 4. Degradation models of concrete lining: (a) Different degradation models, (b) Function of degradation models, (c) Different degradation models with various degradation rates.

Based on the above analysis, long-term degradation of the concrete lining is represented by reductions in Young’s modulus and compressive strength over time, while the Poisson ratio μ_s remains constant. The lining consists of elastic material and is assumed to be installed instantaneously at t = t₀. The stiffness and strength of concrete lining at time t are given as follows [47,49,50,52]:

$$\left\{\begin{array}{c}{E}_s\left(t\right)=E_0\cdot g\left(t\right)\\ {\sigma }_s\left(t\right)={\sigma }_0\cdot g\left(t\right)\end{array}\right.$$

(2)

where E₀ and σ₀ are the initial Young’s modulus and strength of the concrete lining, respectively. Here, the degradation constitutive model of concrete at each incremental Δt is given by [58]

$$\Delta \epsilon (t)={\displaystyle \frac{\Delta \sigma \left(t\right)}{E_s\left(t\right)}}$$

(3)

The following expression can be obtained after the integral operation of Equation (3):

$$\epsilon \left(t\right)={\displaystyle \frac{\sigma \left(t\right)}{E_s\left(t\right)}}+{\int }_0^t\sigma \left(t\right){\left[{\displaystyle \frac{-1}{E_s\left(t\right)}}\right]}^{\prime }dt$$

(4)

Equation (4) is the classical integral expression, where the first term on the right side of Equation (4) is the instantaneous strain under the present load at time t and the second is the strain due to the delayed behavior.

2.2. Time-Dependent Behavior of Surrounding Rock

Various formulations and constitutive laws have been put forward and developed to capture the time-dependent behavior of rock materials. The most commonly used formulation of time-dependent behavior proposed in the literature is the rheological model [58,59,60]. They are based on constitutive relationships between stress and strain. Elastic springs, viscous dashpots, and plastic sliders are usually coupled in series or parallel to simulate the time-dependent viscous behavior. It is then possible to reproduce elastoplastic, visco-elastic, visco-plastic, elastic-viscoplastic, etc., mechanical behaviors [59,61,62]. Some typical models have been proposed to simulate creep behavior, where σ and ε are stress and strain, G, K, and η are shear modulus, bulk modulus, and viscosity, subscript m and k refer to the Maxwell model and Kelvin model, q and p are deviatoric stress and mean stress.

Creep tests have found that linear viscoelastic models provide a good description of the time-dependent behavior of various rocks before failure [7,59,63,64,65]. Moreover, the present study focuses on the long-term creep properties of the surrounding rock with the support of the concrete lining. For simplicity here, no plastic yield is considered in this work. It should be stated that there is no simple model that can describe all the creep stages satisfactorily and can be used for all rock types and all in situ conditions without limitations [7,64,65]. However, the Burgers model is preferable for practical applications and has a suitable role in the long-term behavior of tunnels [59,61,66]. The Burgers model consists of transient and stationary creep stages and can be degenerate to the Maxwell model, Kelvin model, Generalized Maxwell model, and Generalized Kelvin model. Therefore, the Burgers models are selected to describe the time-dependent behaviors of surrounding rock.

For viscoelastic models, time-dependent deformation is determined by deviatoric stress, while the hydrostatic component only contributes to elastic dilation. Therefore, the integral constitutive of linear rheological models can be expressed as [67]

$$\left.\begin{array}{c}{e}_{ij}=J(t) \ast d{s}_{ij}(t)\\ {\epsilon }_m={\sigma }_m/3K\end{array}\right\}$$

(5)

where J(t) and K are creep compliance and bulk modulus of surrounding rock, and K is assumed to be constant. e_ij and s_ij are the deviatoric components of strain and stress, respectively. ε_m and σ_m are the mean strain and mean stress, respectively. The mean stress and mean strain are assumed to remain constant, with the primary variation occurring in the deviatoric strain. The deviatoric strain and stress are written as

$$e_{ij}={\epsilon }_{ij}-{\epsilon }_m,s_{ij}={\sigma }_{ij}-{\sigma }_m$$

(6)

The asterisk (∗) in Equation (5) represents the convolution integral, which is defined as [67]

$$f_1(t) \ast d{f}_2(t)=f_1(t)f_2(0)+{\int }_o^t{f}_1(t-\xi ){\displaystyle \frac{\partial f_2(\xi )}{\partial \xi }}d\xi$$

(7)

As mentioned above, the Burgers model is suitable for representing the long-term viscoelastic behavior of surrounding rock formed by a Maxwell and a Kelvin element in series. The creep compliance of the Burgers model is given as [59]

$$J(t)={\displaystyle \frac{1}{2G_m}}+{\displaystyle \frac{t}{2{\eta }_m}}+{\displaystyle \frac{1}{2G_k}}(1-e^{-{\displaystyle \frac{G_{k}t}{{\eta }_k}}})$$

(8)

where G_m and η_m are the shear modulus and viscosity of the Maxwell model, respectively, while G_k and η_k are those of the Kelvin model.

3. Long-Term Interaction Between the Lining and Surrounding Rock Considering Delayed Processes

3.1. Modeling and Derivation of Coupled Analytical Models

The time-dependent behavior of surrounding rock and the degradation process of concrete lining both affect the long-term stability of tunnels. Because the tunnel stability strongly depends on the interaction between the lining and surrounding rock. Herein, an analytical model is developed to explore the long-term mechanical response of tunnel structures. As such, a circular tunnel is assumed to be embedded in a homogenous infinite viscoelastic Burger rock medium subject to a hydrostatic pressure field p₀. The tunnel has a circular form and is supported by concrete lining, and the support pressure between the surrounding rock and concrete lining is q(t). Due to its simplicity, although it is limited by basic assumptions (plane strain and axisymmetric conditions), this approach method has proved to be an intrinsic mechanism of the research problem; it is also widespread and well-developed for investigating the interaction between the lining and surrounding rock [1,7,28,58,62]. Based on these considerations, an analytical model that considers the surrounding rock’s time-dependent behavior and the degradation process of the concrete lining can be developed. To describe the mechanical response of the tunnel structure more comprehensively, the whole interaction process (before and after installation of concrete lining) between support and surrounding rock is analyzed.

3.1.1. First Stage: Free Convergence of an Unlined Tunnel

Excavation advancement during the tunnel construction stage is considered to assess the actual mechanical performance of the tunnel. At this stage, the tunnel’s excavation is accomplished immediately (i.e., at time t = 0). The fictitious support pressure p₁(t) is applied to the excavation face, and the expression can be defined as p₀ = p₁(t)[1 − λ(t)]. Also, the dimensionless parameter λ(t) can be expressed as: λ(t) = 1 − αexp(−mt) [2,58], where parameters α and m can be determined by in situ measurement or numerical simulations. And m = v/r₀, where v is the excavation speed.

The excavation rate in the longitudinal direction is assumed to be small enough that the dynamic effect can be neglected [64,65]. Therefore, the stress boundary conditions of the surrounding rock after excavation are listed as

$$\left\{\begin{array}{c}{\sigma }_r(r=r_0,t)=p_1(t)\\ {\sigma }_r(r\to \infty ,t)=p_0\end{array}\right.$$

(9)

Combined with the boundary conditions in Equation (9), the radial and tangential stresses of the surrounding rock are given as follows:

$$\left\{\begin{array}{c}{\sigma }_r(t)=\left[1-\lambda (t){\displaystyle \frac{r_0^1}{r^2}}\right]p_0\\ {\sigma }_{\theta }(t)=\left[1+\lambda (t){\displaystyle \frac{r_0^1}{r^2}}\right]p_0\end{array}\right.$$

(10)

where r₀ is the tunnel radius. The longitudinal strain is zero for the plane strain problem. Therefore, the stress in the longitudinal direction can be written as

$${\sigma }_z\left(t\right)={\nu }_r\left[{\sigma }_r\left(t\right)+{\sigma }_{\theta }\left(t\right)\right]$$

(11)

where v_r is the Poisson’s ratio of surrounding rock, then the mean stress σ_m of surrounding rock can be calculated by

$${\sigma }_m={\displaystyle \frac{{\sigma }_r\left(t\right)+{\sigma }_{\theta }\left(t\right)+{\sigma }_z\left(t\right)}{3}}={\displaystyle \frac{2\left(1+{\nu }_r\right)}{3}}{p}_0$$

(12)

Combined with Equation (6), the increment tangential deviatoric stresses caused by excavation are given by

$$\Delta s_{\theta }(t)=\left[1+\lambda (t){\displaystyle \frac{r_0^1}{r^2}}\right]p_0-p_0=\lambda (t){\displaystyle \frac{r_0^1}{r^2}}{p}_0$$

(13)

Based on the strain-displacement relationship, the radial displacement $u_{r\_1}\left(t\right)$, caused by tunnel excavation, is

$$\Delta {\epsilon }_{\theta }(r,t)={\displaystyle \frac{u_{r\_1}\left(t\right)}{r}}$$

(14)

Therefore, the time-dependent radial displacement of surrounding rock at the tunnel boundary can be calculated by

$$u_{r\_1}(t)=r_0\left[J(t)\Delta s_{\theta }(0)+{\int }_0^{t}J(t-\xi ){\left[\Delta s_{\theta }\left(\xi \right)\right]}^{\prime }d\xi \right]$$

(15)

By substituting Equations (8) and (14) into Equation (15), the solution of $u_{r\_1}\left(t\right)$ can be calculated as

$$u_{r\_1}(t)={\displaystyle \frac{r_0{p}_0}{2}}\left[{\displaystyle \frac{1}{G_m}}+{\displaystyle \frac{t}{{\eta }_m}}+{\displaystyle \frac{1}{G_k}}\left(1-e^{{\displaystyle \frac{-t}{T_k}}}\right)\right]-{\displaystyle \frac{\alpha r_0{p}_0}{2}}\left[{\displaystyle \frac{1}{m{\eta }_m}}-({\displaystyle \frac{1}{m{\eta }_m}}-{\displaystyle \frac{1}{G_m}})e^{-mt}+{\displaystyle \frac{\left(e^{-mt}-e^{\frac{-t}{T_k}}\right)}{G_k\left(1-m{T}_k\right)}}\right]$$

(16)

where T_k= η_k/G_k.

3.1.2. Second Stage: Operation of the Tunnel

The concrete lining is installed at time t = t₀, where the inside radius of the lining is r₁. For convenience, the parameter τ = t − t₀ is introduced. As mentioned above, the elastic modulus of concrete decreases with time. Combining with Equations (3) and (4), the constitutive Equation of the concrete lining at each incremental time ∆τ is given by the following expression:

$$\left\{\begin{array}{c}\Delta {\epsilon }_r\left({\tau }_i\right)={\displaystyle \frac{1-{\mu }_s^2}{E\left({\tau }_i\right)}}\left[\Delta {\sigma }_r\left({\tau }_i\right)-{\displaystyle \frac{{\mu }_s}{1-{\mu }_s}}\Delta {\sigma }_{\theta }\left({\tau }_i\right)\right]\\ \Delta {\epsilon }_{\theta }\left({\tau }_i\right)={\displaystyle \frac{1-{\mu }_s^2}{E\left({\tau }_i\right)}}\left[\Delta {\sigma }_{\theta }\left({\tau }_i\right)-{\displaystyle \frac{{\mu }_s}{1-{\mu }_s}}\Delta {\sigma }_r\left({\tau }_i\right)\right]\end{array}\right.$$

(17)

Combined with the stress boundary conditions of concrete lining σ_r(r₀, τ) = q(τ) and σ_r(r₁, τ) = 0, the stress components of the concrete lining can be deduced:

$$\left\{\begin{array}{c}{\sigma }_r(r,\tau )={\displaystyle \frac{r_0^2{r}_1^{2}q\left(\tau \right)}{r^2\left(r_1^2-r_0^2\right)}}-{\displaystyle \frac{r_0^{2}q(\tau )}{r_1^2-r_0^2}}\\ {\sigma }_{\theta }(r,\tau )=-{\displaystyle \frac{r_0^2{r}_1^{2}q\left(\tau \right)}{r^2\left(r_1^2-r_0^2\right)}}-{\displaystyle \frac{r_0^{2}q\left(\tau \right)}{r_1^2-r_0^2}}\end{array}\right.$$

(18)

Substituting Equation (18) into Equation (17), we have

$$\Delta {\epsilon }_{\theta }\left({\tau }_i\right)={\displaystyle \frac{1}{E\left({\tau }_i\right)}}{\displaystyle \frac{r_0^2\left(1+{\mu }_s\right)}{r_1^2-r_0^2}}\left({\displaystyle \frac{r_1^2}{r^2}}+2{\mu }_s-1\right)\Delta q\left({\tau }_i\right)$$

(19)

By integrating both sides of the above Equation, we can obtain

$$\Delta {\epsilon }_{\theta }\left({\tau }_i\right)={\displaystyle \frac{r_0^2\left(1+{\mu }_s\right)}{r_1^2-r_0^2}}\left({\displaystyle \frac{r_1^2}{r^2}}+2{\mu }_s-1\right){\int }_0^{\tau }{\displaystyle \frac{1}{E\left(\tau \right)}}{\displaystyle \frac{dq\left(\tau \right)}{d\tau }}d\tau$$

(20)

Based on the strain-displacement relationship ε_θ(τ) = u_s(r,τ)/r, radial displacement is expressed as

$$u_s(r,\tau )={\displaystyle \frac{r\left(1+{\mu }_s\right)}{\frac{r_1^2}{r_0^2}-1}}\left({\displaystyle \frac{r_1^2}{r^2}}+2{\mu }_s-1\right){\int }_0^{\tau }{\displaystyle \frac{1}{E\left(\tau \right)}}{\displaystyle \frac{dq\left(\tau \right)}{d\tau }}d\tau$$

(21)

Therefore, the radial displacement is obtained by substituting r = r₀ into the above equation and simplifying the result in the following form:

$$u_s(r_0,\tau )={\displaystyle \frac{r_0}{K_s}}\left[{\displaystyle \frac{q\left(\tau \right)}{g\left(\tau \right)}}+{\int }_0^{\tau }{\displaystyle \frac{g^{\prime }(\tau )}{g^2\left(\tau \right)}}q(\tau )d\tau \right]$$

(22)

where

$$K_s={\displaystyle \frac{E_0\left(1-{r_1}^2/{r_0}^2\right)}{\left(1+{\mu }_s\right)(1-2{\mu }_s+{r_1}^2/{r_0}^2)}}$$

(23)

Similarly to the above analysis, the radial displacement $u_{r\_2}\left(t\right)$ of surrounding rock induced by q(τ) can be obtained:

$$u_{r\_2}(\tau )=r_0\left[q(\tau )J(0)+{\int }_0^{\tau }q(\xi ){\displaystyle \frac{dJ(\tau -\xi )}{d(\tau -\xi )}}d\xi \right]$$

(24)

The radial displacement of surrounding rock induced by tunnel excavation at t ≥ t₀ is given as

$$u_{r\_1}(t_0+\tau )-u_{r\_1}\left(t_0\right)=h\left(\tau \right)r_0$$

(25)

where h(τ) is an undetermined function. Combining with Equation (16), the expression of h(τ) can be derived as follows:

$$h(\tau )={\displaystyle \frac{p_0}{2}}\left\{{\displaystyle \frac{\tau }{{\eta }_m}}+{\displaystyle \frac{e^{-t_0/T_k}}{G_k}}\left(1-{\displaystyle \frac{\alpha }{1-m{T}_k}}\right)\left(1-e^{-\tau /T_k}\right)+\alpha e^{-m{t}_0}\left({\displaystyle \frac{1}{G_k\left(1-m{T}_k\right)}}-{\displaystyle \frac{1}{m{\eta }_m}}+{\displaystyle \frac{1}{G_m}}\right)\left(1-e^{-m\tau }\right)\right\}$$

(26)

After the installation of the concrete lining, the compatibility condition between the concrete lining and the surrounding rock at the tunnel boundary is

$$h\left(\tau \right)r_0-u_{r_{-}2}\left(\tau \right)=u_s\left(\tau \right)$$

(27)

Inserting Equations (24) and (26) into Equation (27) yields

$$h(\tau )-\left[q(\tau )J(0)+{\int }_0^{\tau }q(\xi ){\displaystyle \frac{dJ(\tau -\xi )}{d(\tau -\xi )}}d\xi \right]={\displaystyle \frac{1}{K_L}}\left[{\displaystyle \frac{q(\tau )}{g\left(t\right)}}+{\int }_0^{\tau }q(\tau ){\displaystyle \frac{g^{\prime }\left(\tau \right)}{g^2\left(\tau \right)}}d\tau \right]$$

(28)

Substituting Equation (8) into Equation (28), the Equation about the support pressure q(τ) is obtained as

$$h(\tau )-{\displaystyle \frac{1}{2{\eta }_m}}{\int }_0^{\tau }q(\xi )d\xi -{\displaystyle \frac{1}{2{\eta }_k}}{e}^{{\displaystyle \frac{G_k}{{\eta }_k}}\tau }{\int }_0^{\tau }{e}^{{\displaystyle \frac{G_k}{{\eta }_k}}}q(\xi )d\xi -{\displaystyle \frac{1}{K_L}}{\int }_0^{\tau }{\displaystyle \frac{g^{\prime }(\tau )}{g^2(\tau )}}q(\tau )d\tau =q(\tau )\left[{\displaystyle \frac{1}{K_L\cdot g\left(\tau \right)}}+J(0)\right]$$

(29)

Then, by deriving the two sides of Equation (29) and rearrangement, a second-order differential equation is obtained for q(τ) with the following expression:

$$C_1{\displaystyle \frac{d^{2}q\left(\tau \right)}{d{\tau }^2}}+C_2{\displaystyle \frac{dq\left(\tau \right)}{d\tau }}+C_{3}q(\tau )=C_4$$

(30)

where C₁, C₂, C₃, and C₄ are listed as follows:

$$\left\{\begin{array}{c}{C}_1={\displaystyle \frac{1}{K_L\cdot g\left(\tau \right)}}+{\displaystyle \frac{1}{2G_m}}\\ C_2={\displaystyle \frac{G_k}{{\eta }_k}}\left[{\displaystyle \frac{1}{K_L\cdot g\left(\tau \right)}}+{\displaystyle \frac{1}{2G_m}}\right]+{\displaystyle \frac{1}{2{\eta }_k}}+{\displaystyle \frac{1}{2{\eta }_m}}-{\displaystyle \frac{g^{\prime }\left(\tau \right)}{K_L\cdot g(\tau {)}^2}}\\ C_3={\displaystyle \frac{G_k}{2{\eta }_m{\eta }_k}}, C_4={\displaystyle \frac{G_k}{{\eta }_k}}{h}^{\prime }(\tau )+h^{″}(\tau )\end{array}\right.$$

(31)

The detailed derivation is provided in the Appendix A. Considering Equation (26), the expressions of h’(τ) and h″(τ) can be deduced. As mentioned in Section 2.2, the expression of g′(τ) for different shapes of the degradation functions can be written as

$$\left\{\begin{array}{c} \mathrm{Square} \mathrm{root}: g\left(t\right)=1-a{t}^{0.5},g^{\prime }\left(t\right)=-0.5a{t}^{-0.5}\\ \mathrm{Linear} : g\left(t\right)=1-at,g^{\prime }\left(t\right)=-a\\ \mathrm{Parabolic} : g\left(t\right)=1-a{t}^2,g^{\prime }\left(t\right)=-2at\end{array}\right.$$

(32)

Hence, the support pressure q(τ) can be obtained by solving a second-order differential equation requiring two initial conditions. The first initial condition is support pressure at time τ = 0 given by q(0) = 0. The second condition is the support pressure rate at τ = 0⁺ from Equation (29). This yields

$$q^{\prime }(0)=h^{\prime }(0){\left({\displaystyle \frac{1}{K_L\cdot g\left(0\right)}}+{\displaystyle \frac{1}{2G_m}}\right)}^{-1}$$

(33)

Combining the two initial conditions, the solution of q(τ) can be obtained by The Runge–Kutta method. Then, the radial displacement u_s(τ) can be solved from Equation (21).

3.2. Verification of Coupled Mechanics Models

This section compares existing solutions and numerical simulations to verify the solutions of the coupled mechanics model proposed in the previous section. The solutions derived in this paper could be seen as an expansion of the research of Chu et al. [61], who proposed a solution for a circular tunnel in Burgers viscoelastic rock. As shown in Figure 5a, the solutions presented in the present study are identical to those of Chu et al. [61] for cases where degradation of concrete lining is not considered, i.e., g(t) = 1. Therefore, specific comparisons should be executed to preliminarily invalid solutions in this study, where the parameters employed are listed in Table 1 [61,62,64,65]. Chu et al. [61] focused on the support forces during the construction stage under rock rheology; our research investigates the long-term mechanical response of the tunnel structure during its entire service life, considering the coupled effects of surrounding rock rheology and support system degradation. Therefore, our model incorporates a broader and more complex set of factors, leading to a significantly distinct scope and findings.

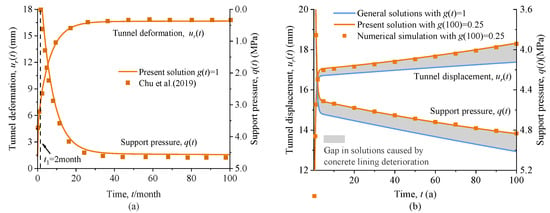
Figure 5. Comparison between the analytical solution with (a) existing solution [61] and (b) numerical simulation.

Table 1. Parameters employed for verification.

Surrounding rock	Gm = 3.45 GPa, ηm = 160 GPa∙month, Gk = 0.35 GPa, ηk = 7.98 GPa∙month
Lining	r0 = 4.57 m, r1 = 3.96 m, E0 = 16.55 GPa, vs = 0.2
Other parameters	p0 = 6.90 MPa, t0 = 2 month, α = 0.7, m = 0.5, v = 2.28 m/day

Moreover, this section also adopts numerical simulations conducted by FLAC3D to verify the proposed solutions. A quarter plane strain model of size 20r₀ × 20r₀ is established, and the model’s right and top boundaries are applied with hydrostatic pressure. The symmetric boundary conditions are fixed at the left and bottom of the model. In the numerical simulation, the Burgers model is adopted to represent the rheological effect of the surrounding rock, where the support structure is simulated by the elastic model. And the deterioration of the concrete lining is characterized by a gradually decrease in the modulus of elasticity with time, which is achieved by programming the FISH, where the parameters employed are also the same as in Table 1. The tunnel deformation and support pressure calculated by the proposed analytical model and numerical simulation are presented in Figure 5b, utilizing the square root degradation model of concrete lining. A fair agreement between the analytical and numerical simulation solutions for g(100) = 0.25 is observed. The long-term rheological effect of the surrounding rock leads to an increase in structural load, which is an established behavior. Although the lining undergoes degradation, resulting in a redistribution of loads, the single-layer support structure continues to bear these loads, and thus the overall load continues to rise over time. However, compared to an undegraded lining at the same time point, the load acting on the degraded lining is lower. This indicates that the load effect in a degraded lining is influenced by the coupled behavior of both the surrounding rock and the support structure.

4. Analysis of Long-Term Coupling Mechanism Between Lining Structure and Surrounding Rock

A coupled mechanical analytical model is established to account for the long-term load effects of surrounding rock and the deterioration process of lining concrete. With the primary objective of revealing the evolution of the tunnel’s service performance, this model will be employed to systematically analyze the impact of three key factors: the time-dependent degradation of the lining, the surrounding rock load, and the interfacial contact state between the lining and the rock.

4.1. Mechanical Response of Tunnel Structure Considering Delayed Processes

A parametric study is performed to investigate the effect of different parameters on the mechanical response of the tunnel structure. This section focused on the degradation rate and degradation model of the concrete lining, as well as the viscoelastic properties of the surrounding rock (represented by four parameters of the Burger model). The parameters employed in the parametric investigation are the same as those presented in the previous section. In this parametric study, these properties correspond to mean values. Furthermore, the focus parameter varies during the parametric study, while all other parameters are kept constant.

4.1.1. Influence of Degradation Model of Concrete Lining

The degradation rate of the concrete lining can be represented by g(100), as mentioned in Section 2, where a smaller value of g(100) corresponds to a more considerable ultimate degradation degree, and g(t) = 1 indicates that the concrete lining does not deteriorate. Figure 6 shows the tunnel displacement and normalized support pressure according to the different degradation rates of the three degradation models. It can be seen that both tunnel deformation and support pressure grow with time under the long-term rheological loading effect of the surrounding rock. Meanwhile, the degradation of the concrete lining alters the dynamic interaction between the support and the surrounding rock. As the degradation of lining concrete reduces its ability to resist deformation, the tunnel deformation increases when the lining deteriorates. Also, the higher the degree of lining deterioration, the greater the growth rate of tunnel deformation and the lower the growth rate of support pressure. Additional accumulation of tunnel deformation is observed when the concrete lining has a larger degradation rate. Thus, a minor g(100) corresponds to a higher growth rate of the tunnel deformation, while the reduction in the concrete lining’s bearing capacity slows down the growth rate of the support pressure. The concrete degradation is minor when the degradation coefficient g(100) = 0.75; thus, the tunnel deformation and support pressure are close to the evolution law of the undeteriorated case. Both the degradation rate and degree increase with g(100) = 0.5, so there is a significant increase in the tunnel deformation at the exact moment compared to the case of g(100) = 0.75, while there is a specific reduction in the support pressure. This finding is due to the reduced stiffness of the concrete lining diminishing the ability to carry loads, resulting in a gradual slowing of the rate of load increase. As the degradation rate and the degree of concrete lining increase further, the tunnel deformation significantly increases with g(100) = 0.25 compared to g(100) = 0.5, while the support pressure decreases further. It can be seen that the stiffness of the deteriorated concrete lining decreases, tunnel deformation increases significantly, and support pressure shows an unloading effect compared to the non-deteriorated case.

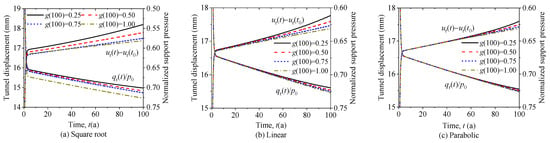
Figure 6. Tunnel deformation and support pressure for various concrete degradation rates: (a) Square root model; (b) Linear model; (c) Parabolic model.

To identify the influence of degradation models of concrete lining on tunnel deformation and support pressure, the degradation rate g(100) should be kept constant. Herein, the time-dependence curves of tunnel deformation and support pressure for g(100) = 0.25, 0.5, and 0.75 are presented in Figure 7. As mentioned in Section 2, the Square root model has a gradually decreasing degradation rate over time, the Linear model has a uniform degradation rate, and the Parabolic model has an increasing degradation rate over time. The order of the concrete lining’s degradation rate at the identical moment is Square root model > Linear model > Parabolic model. Due to the significant rheological loading effects on the surrounding rock in the early stages of tunnel service, the dynamic interaction between the lining and the surrounding rock is most significantly affected when the concrete matches the degradation pattern of the Square root model because of its higher degradation rate in the early stages. As shown in Figure 7, the tunnel deformation under different degradation models is the Square root model > Linear model > Parabolic model; otherwise, the support force is the Square root model < Linear model < Parabolic model. Moreover, the larger the concrete degradation rate is, the more significant the difference between the tunnel deformation and the support pressure under different degradation models. From the analysis, it can be seen that the degradation rate of the lining concrete and the degradation model have a significant effect on the long-term mechanical response of the tunnel structure, so it is of great significance to grasp the actual service state of the lining concrete to clarify the evolution law of the long-term mechanical characteristics of the tunnel structure in operation. Under the Square Root, Linear, and Parabolic models, the surrounding rock displacements are 18.19 mm, 17.77 mm, and 17.60 mm at t = 100 years, respectively. This indicates that the displacement in the Square Root Model is 3.4% higher than that in the Parabolic Model. Meanwhile, the corresponding normalized support pressure are 0.701, 0.719, and 0.723, respectively, showing that the support force under the Square Root Model is 3.2% lower than that under the Parabolic Model.

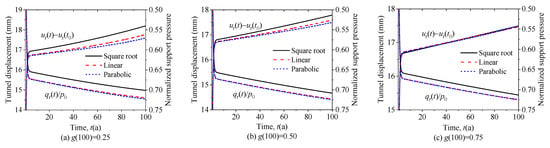
Figure 7. Tunnel deformation and support pressure for different degradation models.

4.1.2. Influence of Thickness of Concrete Lining

Assuming that the degradation process of the concrete lining follows the Square root model, the influence of the concrete lining’s thickness on the long-term mechanical response of tunnel structures is investigated. Evolution curves of tunnel deformation and support pressure with the thickness of d/r₁=0.05, 0.10, and 0.15 are presented in Figure 8. As the lining thickness is minor, the less its ability to resist deformation; thus, the growth rate of tunnel deformation and support pressure under load effect of surrounding rock increases and decreases, respectively. Upon continued degradation of the lining concrete, the reduction in lining stiffness increases the tunnel deformation, while the supporting pressure tends to decrease. In particular, the higher the degradation of the concrete lining, the higher the perimeter tunnel deformation and the lower the support pressure simultaneously. In addition, the thinner concrete lining induces a significant tunnel deformation for the same degradation condition. It can be seen that the degradation of thinner lining has a higher impact on the long-term coupling effect on the surrounding rock-support system than the thicker lining, which may be one of the reasons for the generally thicker linings designed so far. As such, selecting an appropriate thickness of the lining structure is not only the basis for ensuring the long-term safety of the tunnel structures. Still, it is also of great significance in saving the project cost.

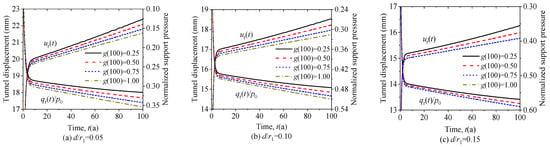
Figure 8. Tunnel deformation and support pressure for the thickness of concrete lining.

4.1.3. Influence of Rheological Properties of Surrounding Rock

The mechanical characteristics of the surrounding rock are not only related to its physical properties but also closely related to the tunnel service environment, leading to the complexity and uncertainty of the long-term loading effect of the surrounding rock. Herein, the influence of the surrounding rock’s time-dependent characteristics on the lining structure’s long-term loading effect is investigated by altering four parameters of the Burgers model. Figure 9 shows that four parameters exert different impacts on the long-term stability of tunnel structures. The value of parameters ${\eta }_{\mathrm{m}}^{\mathrm{mean}}$, ${\eta }_{\mathrm{k}}^{\mathrm{mean}}$, $G_{\mathrm{m}}^{\mathrm{mean}}$ and $G_{\mathrm{k}}^{\mathrm{mean}}$ are the same in Table 1, where the degradation rate g(100) is set as 0.5. As presented in Figure 9a, the variation of η_m dramatically influences interaction performance between the surrounding rock and concrete lining. The growth rates of both the tunnel deformation and the support pressure are more significant when ${\eta }_m=0.1{\eta }_m^{\mathrm{mean}}$, and the variability of the tunnel deformation between the three degradation models gradually increases with time. In addition, the long-term growth rate of tunnel deformation and support pressure decreases as the parameter η_m increases, and the variability of tunnel deformation decreases among the three degradation models, whereas the variability of support pressure increases among different degradation models. It can be seen that a smaller value of η_m results in a more extensive tunnel deformation and support pressure. These findings are consistent with the results presented by Do et al. (2020) [64]. Because of the more significant long-term effect of smaller values of η_m, a more pronounced difference in rock displacement can be expected among the three degradation models.

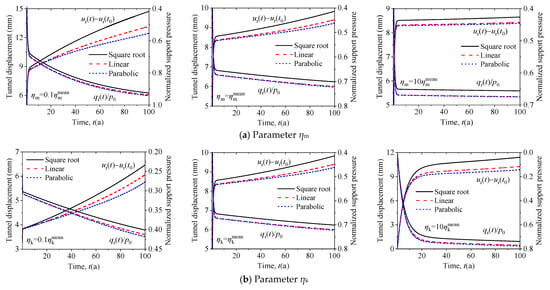
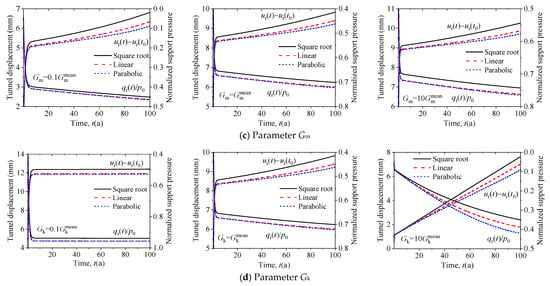
Figure 9. Influence of the viscoelastic parameters of the Burger rock on the tunnel deformation and normalized support pressure: (a) η_m; (b) η_k; (c) G_m; (d) G_k.

Figure 9b shows that the dashpot of the Kelvin element (η_k) exerts a remarkable effect on the long-term responses of rock displacement and support pressure. A smaller value of η_k results in a shorter transient stage, which yields more significant initial deformation and less long-term displacement. A more prolonged rock attenuation creep stage as the parameter η_k increases is associated with a more considerable tunnel deformation and support pressure. Therefore, it leads to a gradual decrease in the incremental share of the total amount of tunnel deformation and support pressure induced by long-term loading effects. Figure 9c presents the effect of parameter G_m variation on the long-term evolution of the tunnel deformation and support pressure. It can be seen that the parameter G_m controls the short-term deformation characteristics of the surrounding rock, but its influence on the long-term rheological effect of the surrounding rock is not significant. However, the smaller value of G_m results in a more significant difference in tunnel deformation among the three degradation models. In the diagrams shown in Figure 9d, the variation of G_k plays a prominent role in the long-term effect. Decreasing the value of G_k results in a faster accumulation and a more immense final value of the pressure on lining structures. Moreover, a higher value of G_k leads to an effective growth rate of rock displacement and support pressure after ten years. Therefore, the higher the value of G_k, the more significant the difference in tunnel deformation among the three degradation models.

The above analysis shows that the parameters η_m, η_k, and G_k of the Burgers model significantly influence the long-term rheological effect of the surrounding rock. Among them, the smaller the viscosity coefficient η_m and η_k are, the more prominent the long-term rheological effect of surrounding rock is, while a larger shear modulus G_k corresponds to a more significant long-term rheological effect of surrounding rock. For surrounding rock with significant long-term rheological effects, the tunnel deformation and the support pressure increase significantly during the tunnel service stage, disturbing the interaction between the lining structure and the surrounding rock. On the other hand, increased degradation of the lining concrete results in a continuous reduction in strength. Therefore, the equilibrium status between the lining structure and the surrounding rock is expected to be disrupted when the internal force of the lining structure exceeds its ultimate load-bearing capacity, thereby allowing failure of the lining structure. What can be attained is that the long-term loading effect of the surrounding rock amplifies the impact of lining degradation on the long-term safety of the tunnel structure. In summary, rheological parameters significantly impact the tunnel’s long-term load effect, and suitable rock parameters should be selected in conjunction with the actual project when analyzing the long-term safety of the tunnel structure. It has been pointed out in Section 2.2 that the Burgers model can be simplified to other commonly used rheological models, such as generalized Kelvin, Kelvin, Maxwell, etc. Therefore, the analysis in this chapter can also provide a reference for the long-term analysis of tunnel structure under the condition that the surrounding rock meets different types of rheological impact.

4.2. Long-Term Stability Assessment of Operation Tunnels

It can be concluded that the pressure imposed on the concrete lining is an increasing function of time; otherwise, the compressive strength of the concrete lining decreases over time. The concrete lining could fail when the maximum principal stress exceeds the compressive strength. When the bearing capacity of the concrete lining is lower than its stress level, the equilibrium of the tunnel system is interrupted. Therefore, yields occurring in the lining concrete for its failure have been judged as follows: σ_θ(r, t) − σ_r(r, t) ≤ σ₀ [7,29,64,65]. The stress in the concrete lining can be calculated by Equation (18), and the bearing capacity of the concrete lining can be obtained from Equation (2). It is known that yielding could occur first at the intrados of the concrete lining (the minimum principal stress is nil at the intrados). Based on the above analysis, the example below exhibits how the stability of operation tunnels can be predicted. In the application example, Young’s modulus and uniaxial compressive strength of concrete are chosen from Do et al. [64], where the elastic modulus and uniaxial compressive strength of the concrete lining are 39.1 GPa and 50 MPa, respectively.

Figure 10 compares the principal stress and uniaxial compressive strength of concrete lining with three degradation models, where the degradation rate is set as 0.75. It can be seen that maximum principal stress is an increasing function over time, but the uniaxial compressive strength of concrete lining is a decreasing function over time. The estimated time until lining failure is 38.6 years, 57.7 years, and 73.7 years for the Square root, Linear, and Parabolic models, respectively. Figure 11 shows the influence of the surrounding rock’s viscoelastic parameters on the tunnel structure’s failure time. Also, the parameter η_m is taken as an example to illustrate it. It can be seen that the failure time of the tunnel structure is 14.5 years, 38.6 years, and 50 years when parameter η_m equals to $0.1{\eta }_m^{\mathrm{mean}}$, ${\eta }_m^{\mathrm{mean}}$, and $10{\eta }_m^{\mathrm{mean}}$, respectively. It indicates that increasing stresses in the concrete lining induced by the surrounding rock’s loading effect could accelerate the tunnel structure’s yielding.

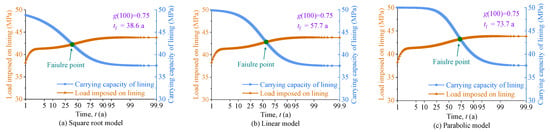
Figure 10. Predicted service life of tunnel structure with different degradation models.

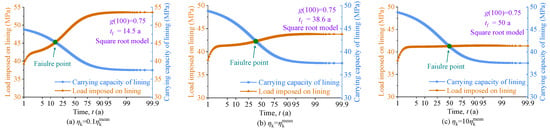
Figure 11. Predicted service life of tunnel structure with different viscoelastic parameters of surrounding rock.

The above analyses have pointed out that the lining degradation and the surrounding rock’s rheological characteristics significantly affect the long-term interaction between the surrounding rock and the support. Herein, the service life of the tunnel structure is predicted under the influence of the surrounding rock’s rheological parameters (taking parameter η_m as an example) and the concrete lining’s degradation degree. Figure 12 illustrates the predictions of the service life of concrete lining structures under three degradation models. A small value of η_m has a strong negative impact on the long-term coupling relationship between the surrounding rock and the support, leading to a shorter service life of the lining structure. Thus, considerable attention should be paid to the long-term rheological effects of the surrounding rock during the design and construction stages of tunnel engineering. It can also be found that the service life of the concrete lining structure meeting the Square root degradation model is significantly smaller than that of the Linear degradation model when the surrounding rock rheological parameters are the same. Moreover, since the degradation rate of the Parabolic degradation model is the lowest among the three models at the exact moment, the service life of the lining structure is significantly longer than that of the previous two degradation models when concrete meets the Parabolic degradation model. In addition, when the degradation law of the concrete lining is consistent with the Square root model, the concrete degradation has a significantly higher impact on the tunnel’s long-term safety than the surrounding rock rheological characteristics. In contrast, the opposite is observed for the Parabolic degradation model. Consequently, understanding the long-term load evolution process of the surrounding rock and the mechanical response of the lining structure is the prerequisite and basis for accurately predicting the service life of the lining structure.

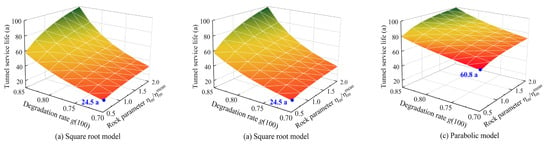
Figure 12. Influence of degradation models on predicted service life of tunnel structure.

5. Discussion

Design methods for tunnel structures do not consider the reduction in structural resistance over time, which is an essential consequence of insufficient durability of the structural performance. In addition, it is vital to pay attention to the structure’s mechanical response induced by the surrounding rock’s long-term delayed behaviors when characterizing the structural safety of tunnels. Thus, the long-term safety of tunnels should start from the aspect of the tunnel system, and then combine the surrounding rock’s status and the supporting structure’s performance to investigate structural resistance and the loading on the support structure. The bearing capacity of the support structures of tunnels decreases with time, as shown by the R₁(t), R₂(t), and R_i(t) curves in Figure 13. In particular, evolutionary characteristics of the bearing capacity are related to the tunnel service environment, i.e., the rate of concrete deterioration. On the other hand, the load on the support structure increases with time, such as the curves represented by S₁(t), S₂(t), and S_i(t). It can be seen that different geological conditions and service environments lead to different mechanical responses and service states of the tunnel structure. Hence, the additional load from the surrounding rock and the support’s degradation process must be considered when examining the tunnel structure’s long-term safety, where F₁, F₂, …, and F_i represent the predicted service lives corresponding to the different degradation and loading scenarios.

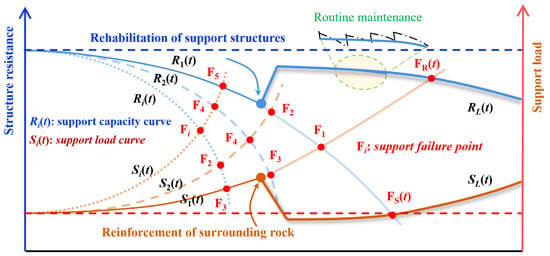
Figure 13. Long-term performance maintenance technology for tunnel structures: R_i(t) is the support capacity curve, S_i(t) is the support load curve, F_i is the support failure point.

A growing number of operational tunnels are suffering from lining damage, for which measures such as the reconstruction of concrete lining, newly added shotcrete lining, bonding fibrous composite, bonding steel plate, and bonding steel arch framework have been applied to rehabilitate structural damage in tunnels. However, it is not enough to improve the bearing performance of the support structure alone during the structural remediation for complex tunnels, which is the cause why some tunnels are frequently damaged after rehabilitation [3,68]. If the load response caused by the delayed effect of the surrounding rock is not considered during remediation, the rock-support interaction cannot be adequately improved. This omission can lead to subsequent failure of the repaired support. As a result, structure damage in operational tunnels should be rehabilitated by considering both the reinforcement of surrounding rocks and the improvement of structural performance, as shown by the R_L(t) and S_L(t) curves in Figure 13. On the one hand, the support is repaired to increase the structural resistance, and on the other hand, the surrounding rock is reinforced to reduce the support loads. This combined measure could maintain the tunnel structural system’s long-term stability and maximize the tunnel’s service life.

Figure 13 depicts the evolving loads and support capacity in tunnels. Since failure often arises from the coupling of these two factors, both must be considered in safety evaluation. Current practices, which often treat the support and rock mass separately, fail to address their interactive nature—a key reason behind frequent tunnel damage. As shown in Figure 14, two treatment measures for lining damage are adopted for an operation tunnel in Zhejiang Province [9]. In scheme A, hollow grouting bolts with a 4 m length were employed to reinforce the surrounding rock in the tunnel arch, where a layer of shotcrete structure was applied to the lining surface to enhance the integrity of the lining in this part. Moreover, the pressure between the shotcrete layer and the original lining indicates that the newly added layer bears little rock load. In addition, grouting reinforcement steel pipes of 4 m in length were adopted to enhance the integrity of the surrounding rock in scheme B, as shown in Figure 14b. Considering the severe cracking of the lining structure in this zone, a new lining structure was constructed to replace the old one. We also found that the stresses in the secondary lining stabilized 15 days after installation, and the pressure at different locations remained low.

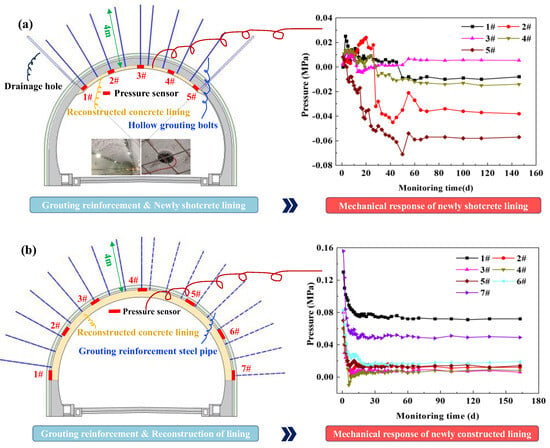
Figure 14. Treatment measures for lining damage of an operation tunnel: (a) Scheme A: grouting reinforcement of the surrounding rock and newly added shotcrete lining; (b) Scheme B: Grouting reinforcement of the surrounding rock and reconstruction of the secondary lining.

It can be seen that the long-term load of the supporting structure can not significantly increase after the reinforcement of the surrounding rock during the remediation of the operation tunnel. In this case, the purpose of repairing the supporting structure is to improve the long-term safety of the tunnel, i.e., the safety reserve factor is increased. This case also demonstrates the effectiveness of the proposed concept of structural damage treatment for operation tunnels. The treatment of lining damage is essential to improve service performance and extend the service life of the operation tunnels. The rehabilitative measure should be selected considering the applicability, cost of repair, time required, and impact on traffic. From the perspective of the treatment effectiveness of tunnel damage, reinforcement of the surrounding rock can significantly improve its stability and reduce the load on supports, where the repair of the support structure enhances the bearing capacity and safety reserve of the supports. Therefore, remediation of structural damage in operation tunnels should consider the surrounding rock condition and support structure performance, significantly improving long-term safety and reducing remediation costs.

6. Conclusions

In this paper, a coupled analytical model is established to examine the long-term stability of tunnels considering both the degradation of concrete linings and the creep effect of surrounding rock. Using the proposed model, influences imposed by the degradation model, degradation rate of concrete linings, and viscoelastic constants of the surrounding rock on the mechanical response of the tunnel are assessed. In addition, the service life of operation tunnels is predicted by an application example. Based on this, long-term performance maintenance techniques for operation tunnels are proposed and illustrated by a case study. The main findings are presented as follows:

(1)

The long-term stability of tunnels is governed by the interaction between the concrete lining and the surrounding rock. Under sustained rheological effects, tunnel deformation and support pressure increase over time, while lining degradation reduces structural stiffness, slowing pressure growth but accelerating deformation. Different degradation models and rates significantly influence mechanical response, with thinner linings showing greater susceptibility. Viscoelastic rock properties further affect system behavior. By analyzing the evolution of structure stress and bearing capacity, this study evaluates how rock rheology and lining deterioration collectively impact service life. The amplified effect of degradation under long-term rock loading underscores the necessity of understanding these coupled mechanisms for accurate life predictions.

(2)

Remediation of structural damage in operation tunnels should consider the surrounding rock condition and support structure performance, significantly improving long-term safety and reducing remediation costs. A long-term performance maintenance method for operation tunnels is proposed and illustrated by a tunnel rehabilitation project, and the reliability of the proposed method has been verified through long-term field monitoring. The presented approach for assessing the long-term stability of tunnels, although valid for some simplified conditions, allows us to estimate the influence of significantly delayed behaviors that affect the support structure and surrounding rock.

(3)

This study employs theoretical analytical methods to investigate the mechanical behavior of tunnel structures during service. Given the complexity of the derivation, certain necessary assumptions were introduced. The interaction between tunnel support and surrounding rock is fundamentally a multi-body contact behavior, involving interfaces between the support and the rock, as well as among different support components. In long-term service, the contact patterns and load transfer mechanisms among these bodies may evolve. Therefore, future research should focus on the evolution of contact relationships and the corresponding mechanical behavior between the support and surrounding rock throughout the tunnel’s service life.