Machine Learning Prediction on Progressive Collapse Resistance of Purely Welded Steel Frames Considering Weld Defects
Abstract
1. Introduction
2. Experiment Program and Establishment of FEM
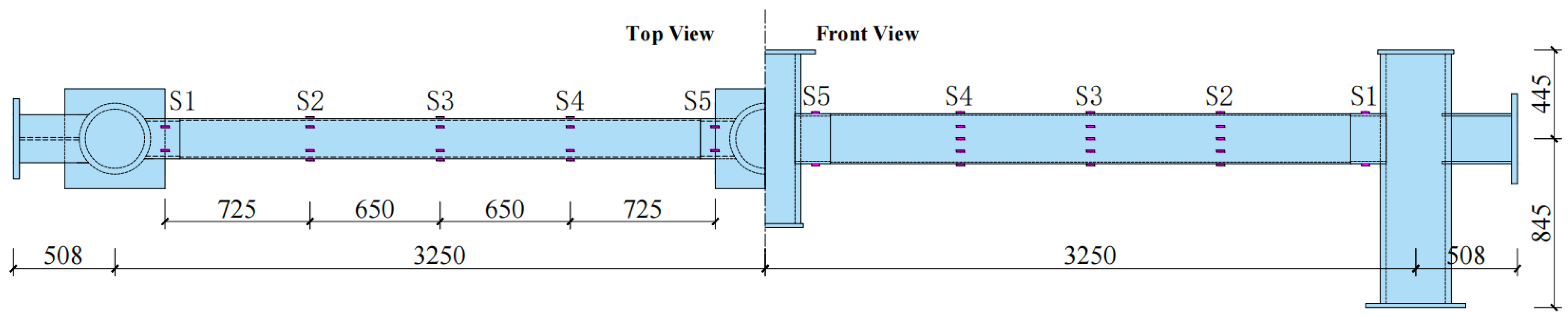
2.1. Specimen Design and Test Setup
2.2. Establishment of FEM
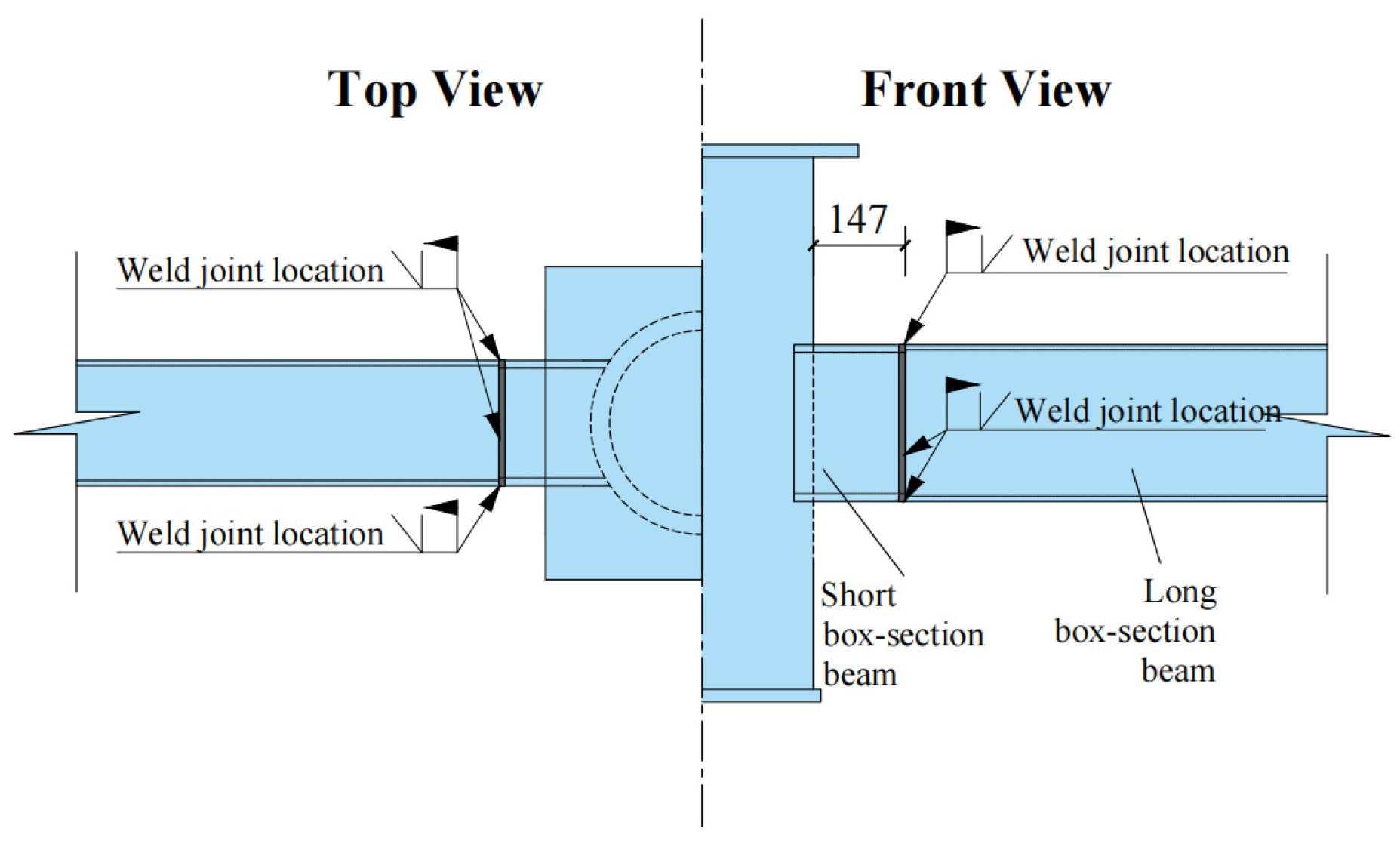
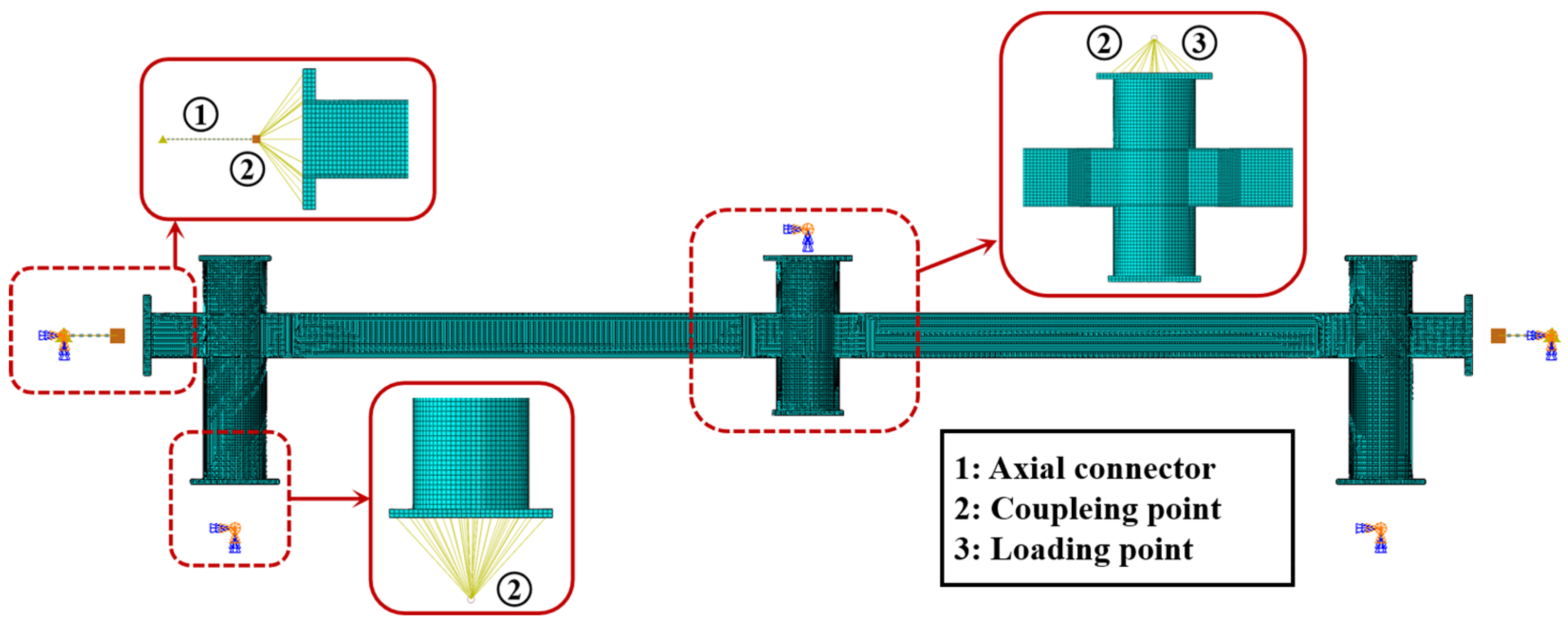
2.2.1. Model Overview
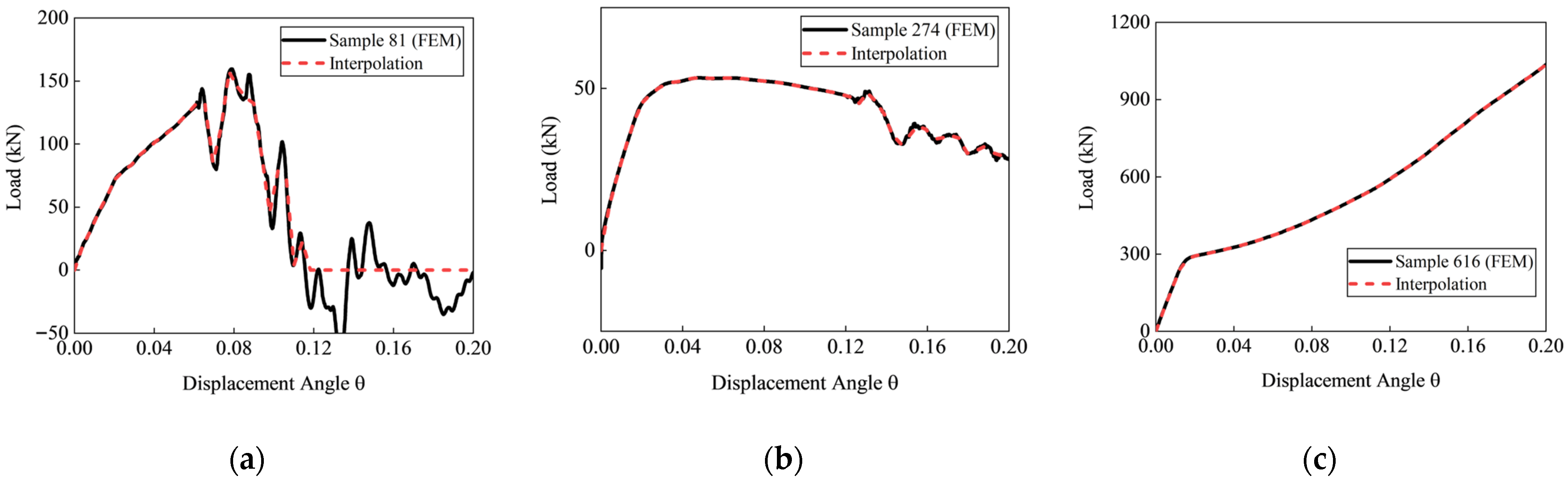
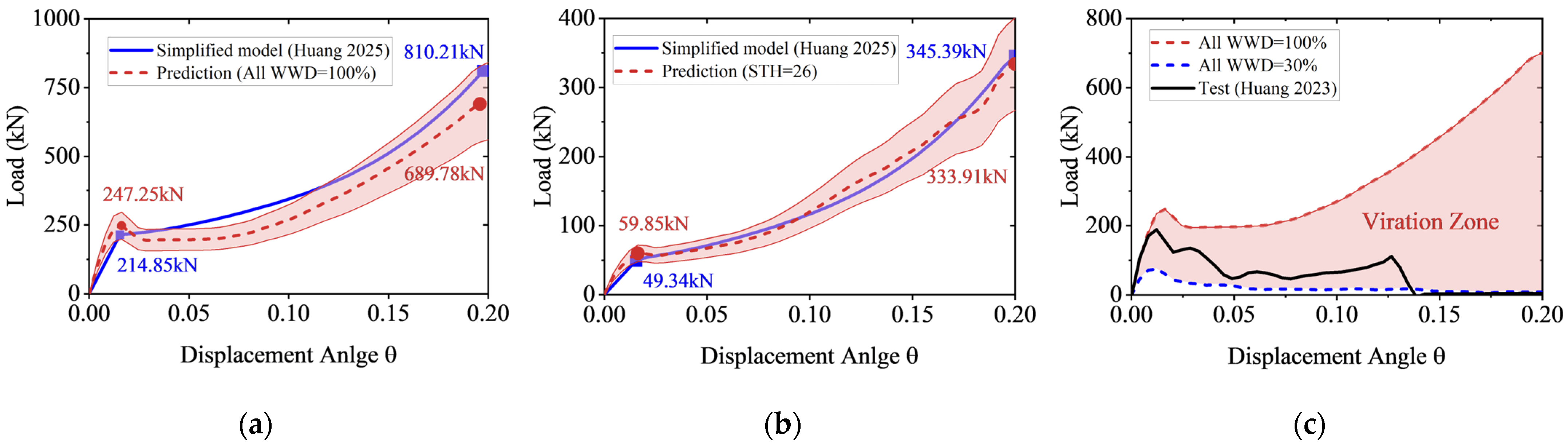
2.2.2. Model Validation
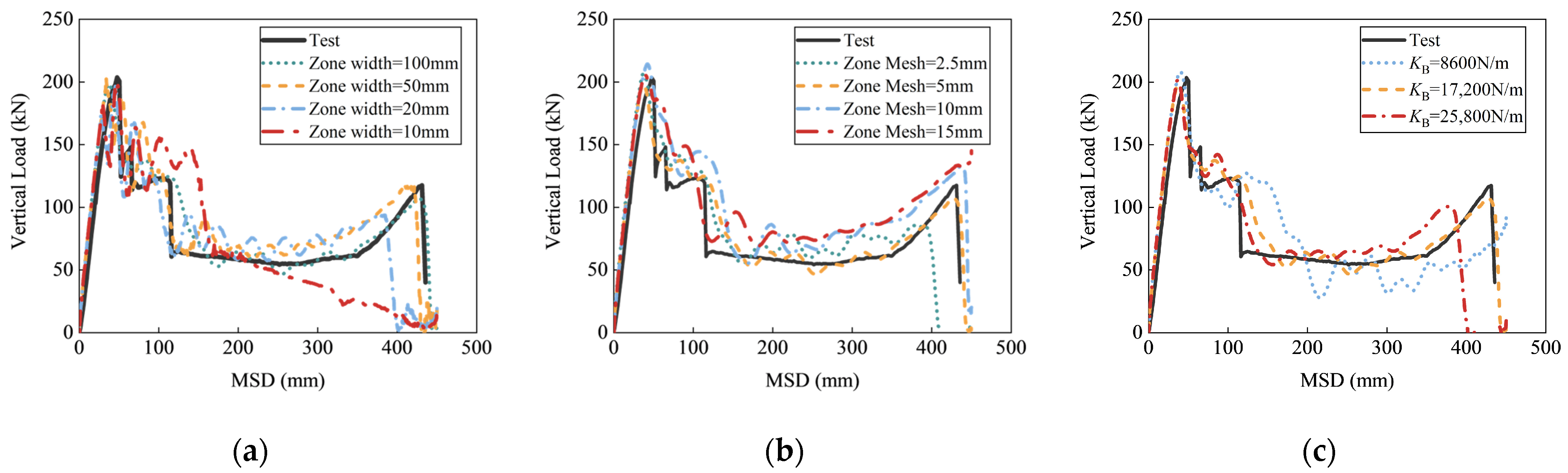
2.2.3. Sensitivity Analysis
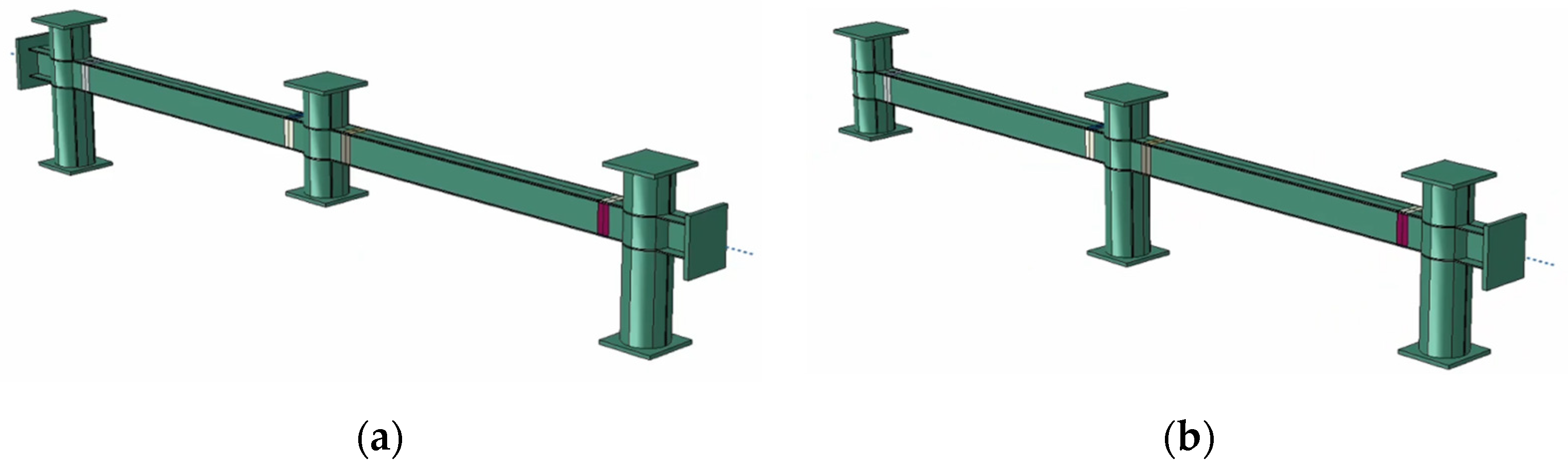
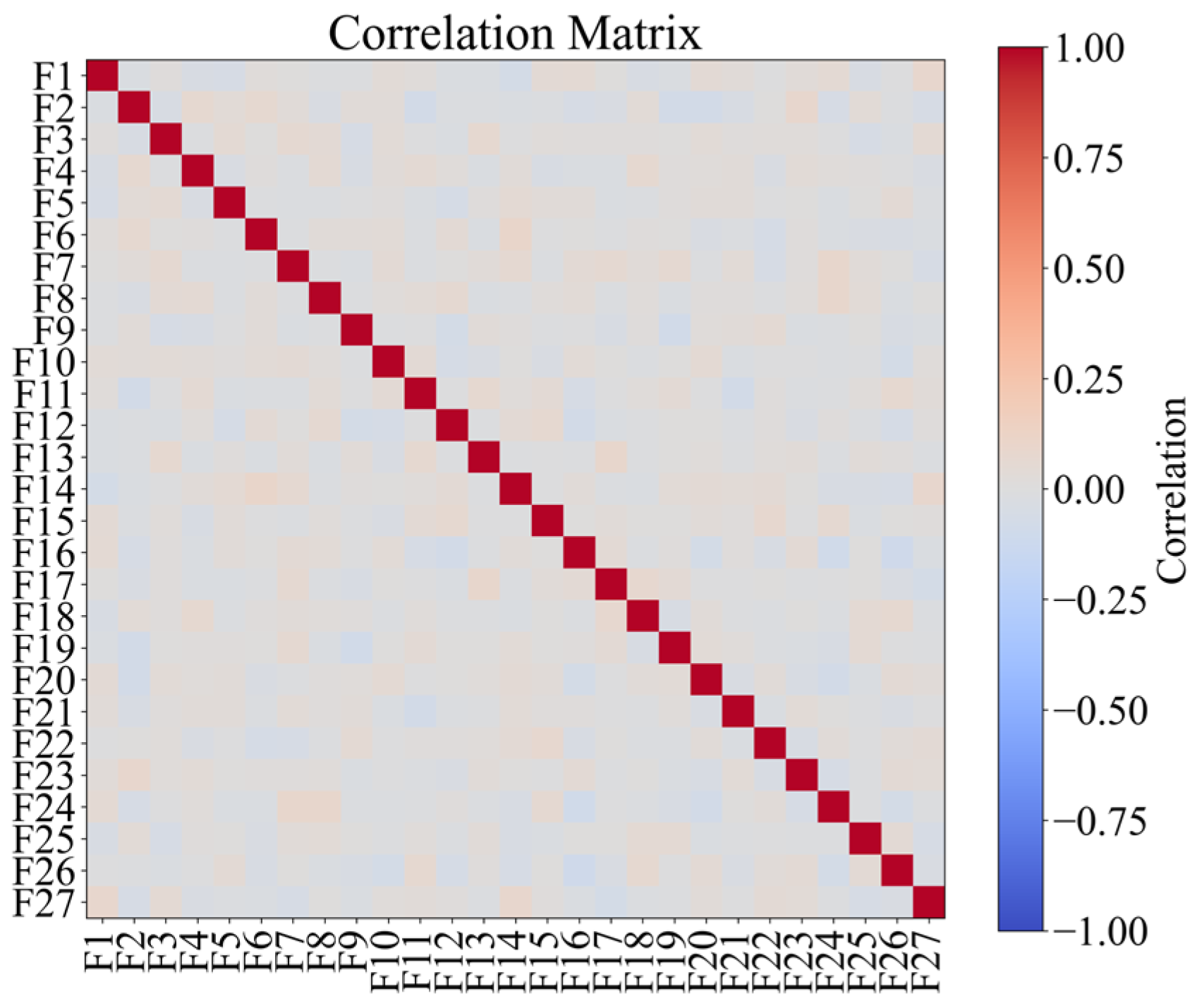
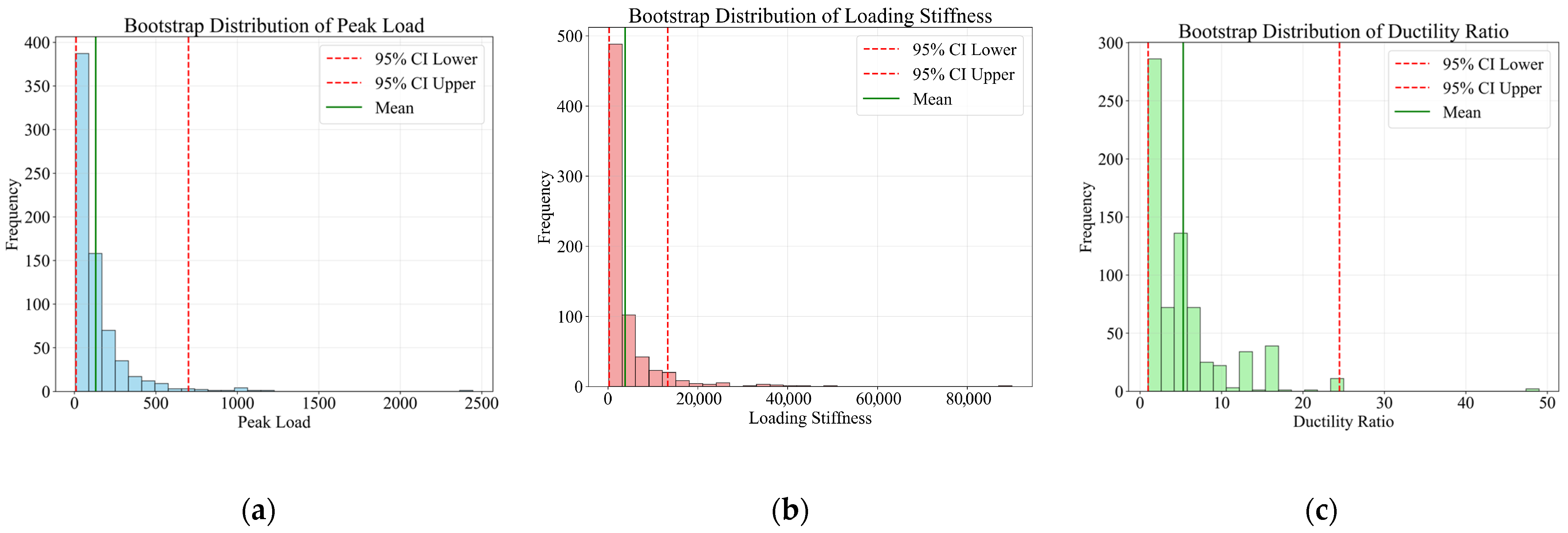
3. Progressive Collapse Database Creation
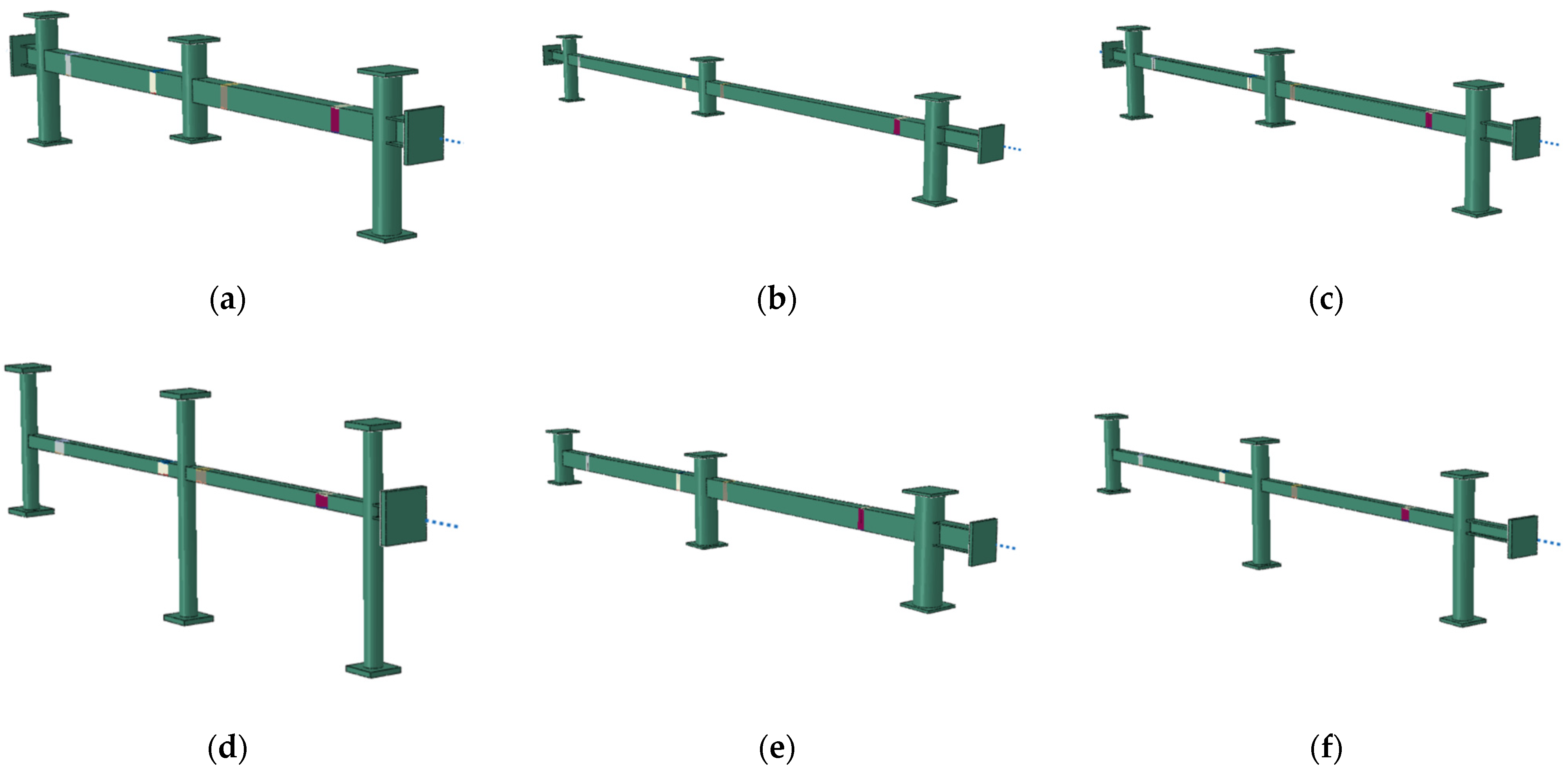
3.1. Parametric Modelling Program
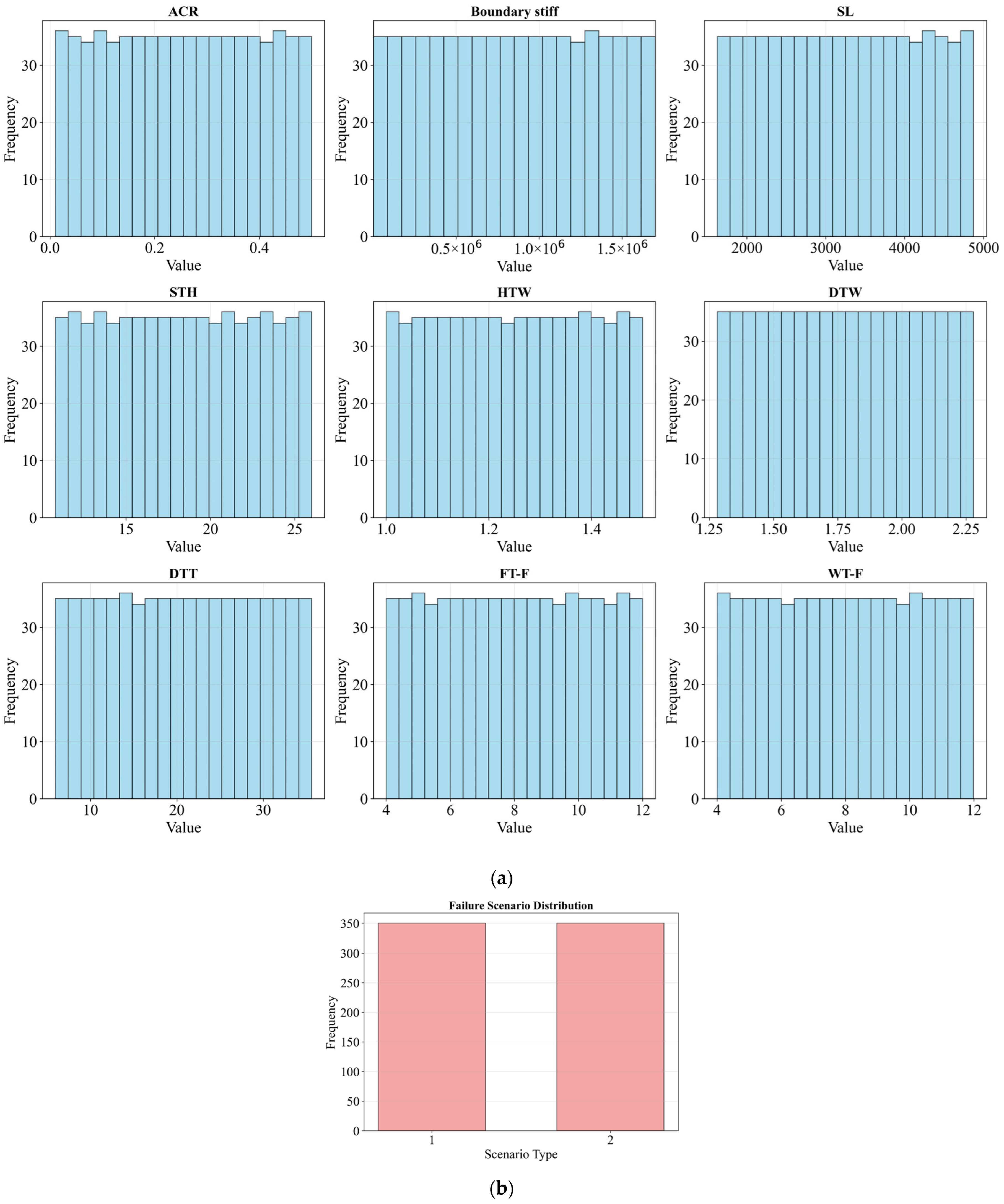
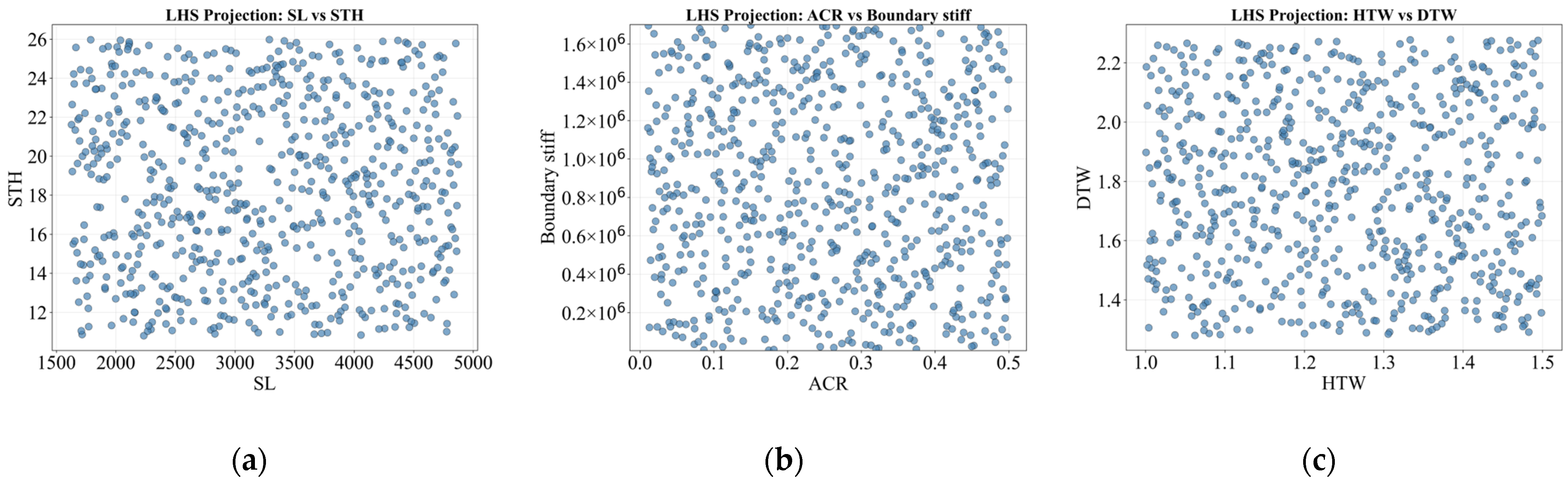
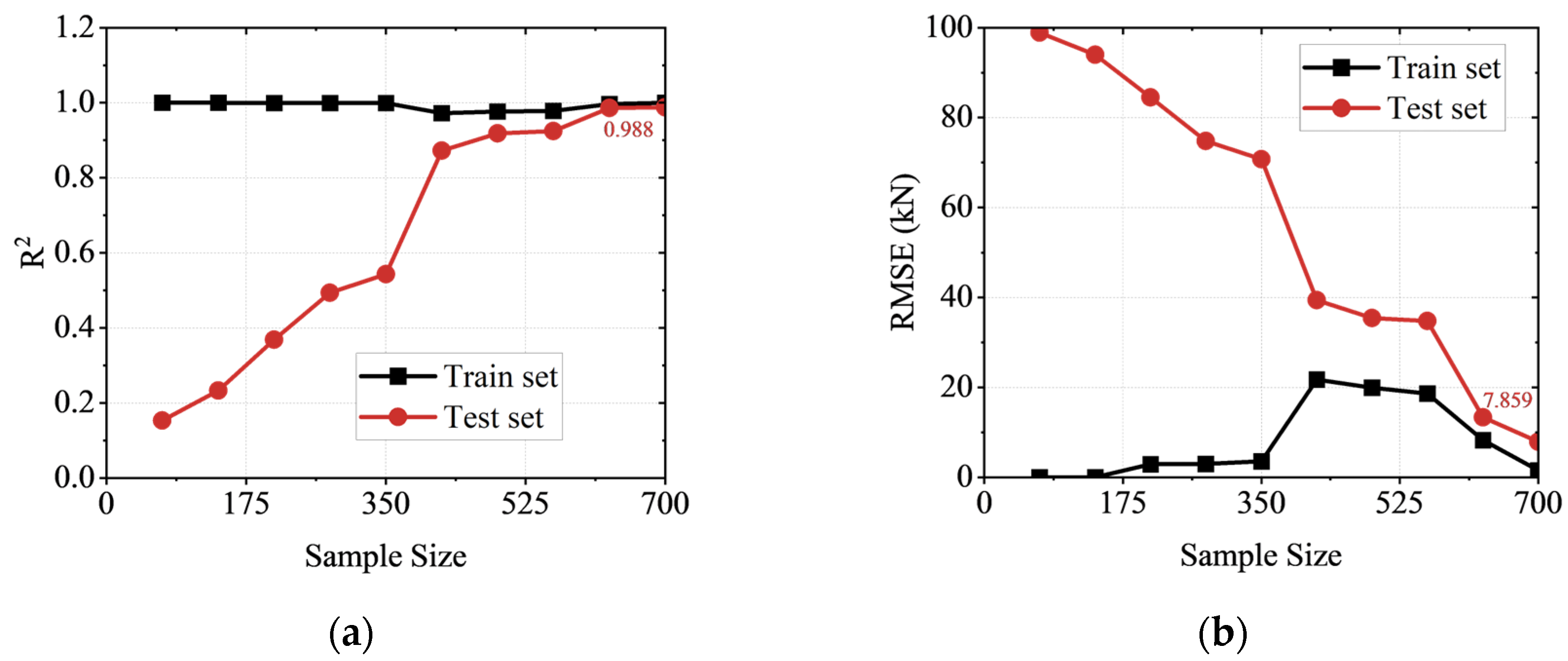
3.2. LHS Hypercube Sampling
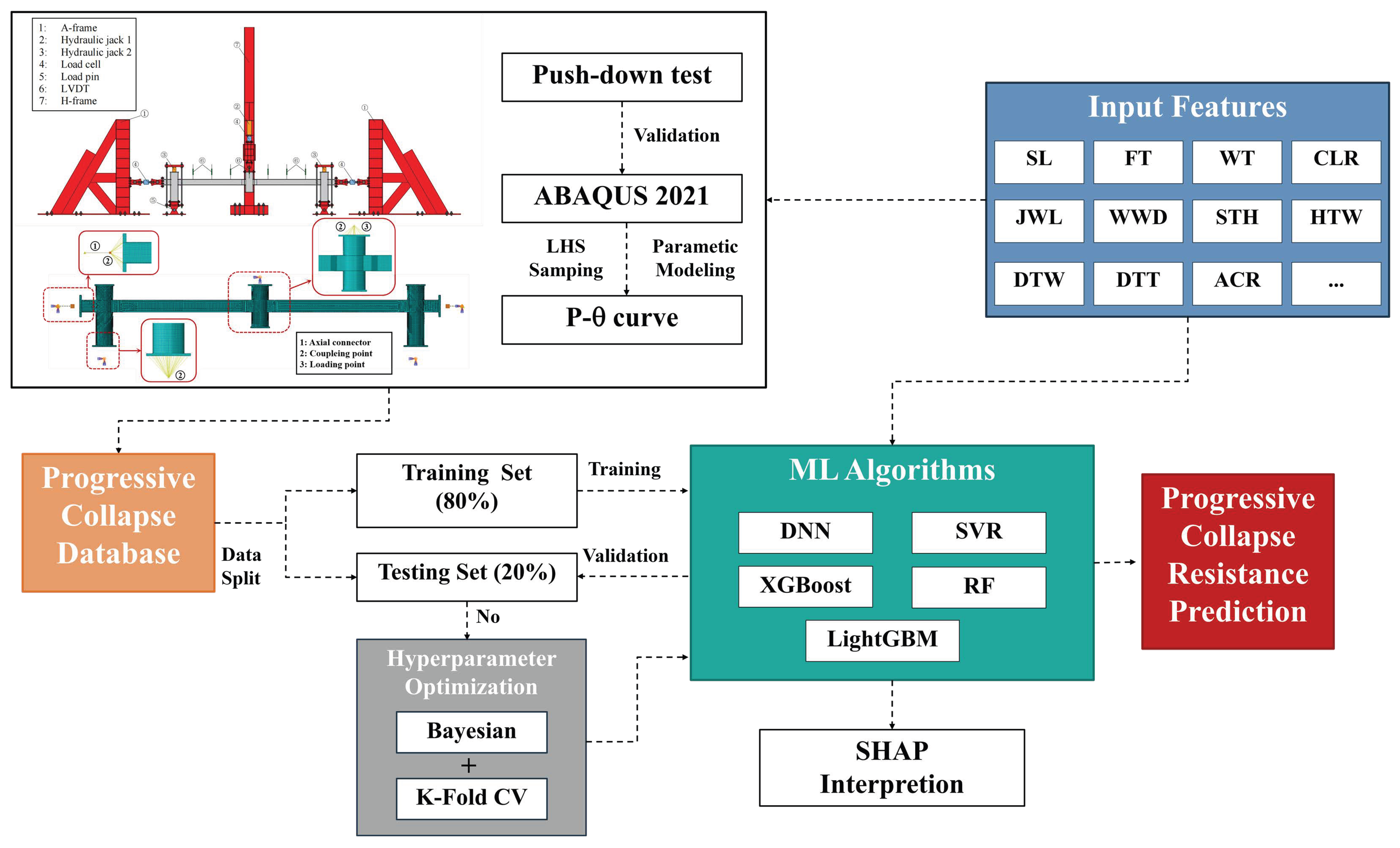
4. Machine Learning Prediction for Progressive Collapse Resistance
4.1. Machine Learning Frame
4.2. Machine Learning Algorithms
4.2.1. Deep Neutral Network (DNN)
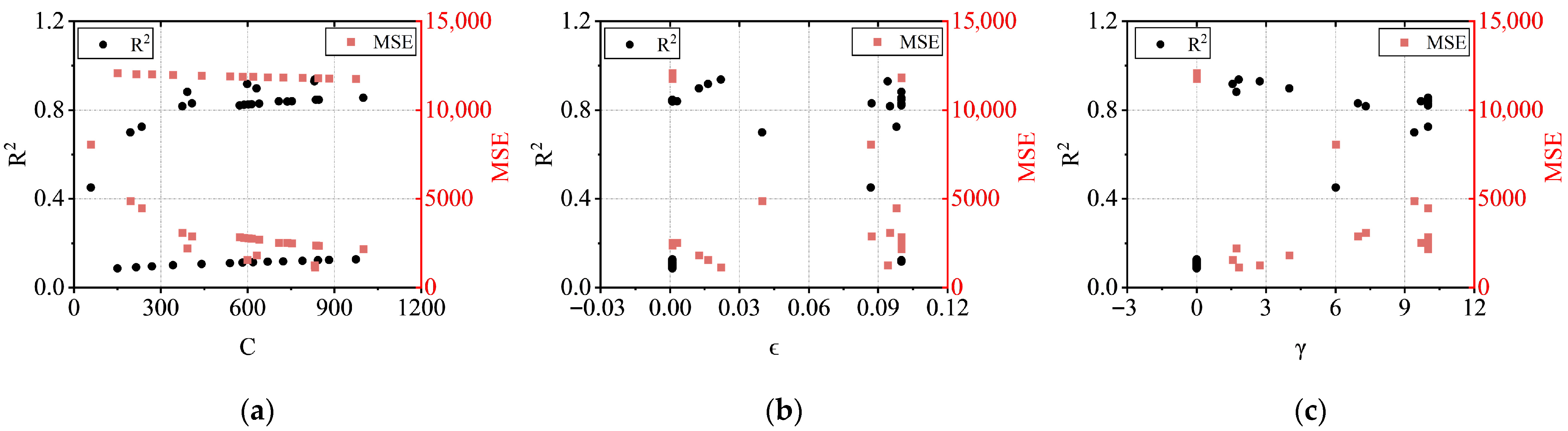
4.2.2. Support Vector Regression (SVR)
4.2.3. Random Forest
4.2.4. eXtreme Gradient Boosting (XGBoost)
4.2.5. Light Gradient Boosting Machnie (LightGBM)
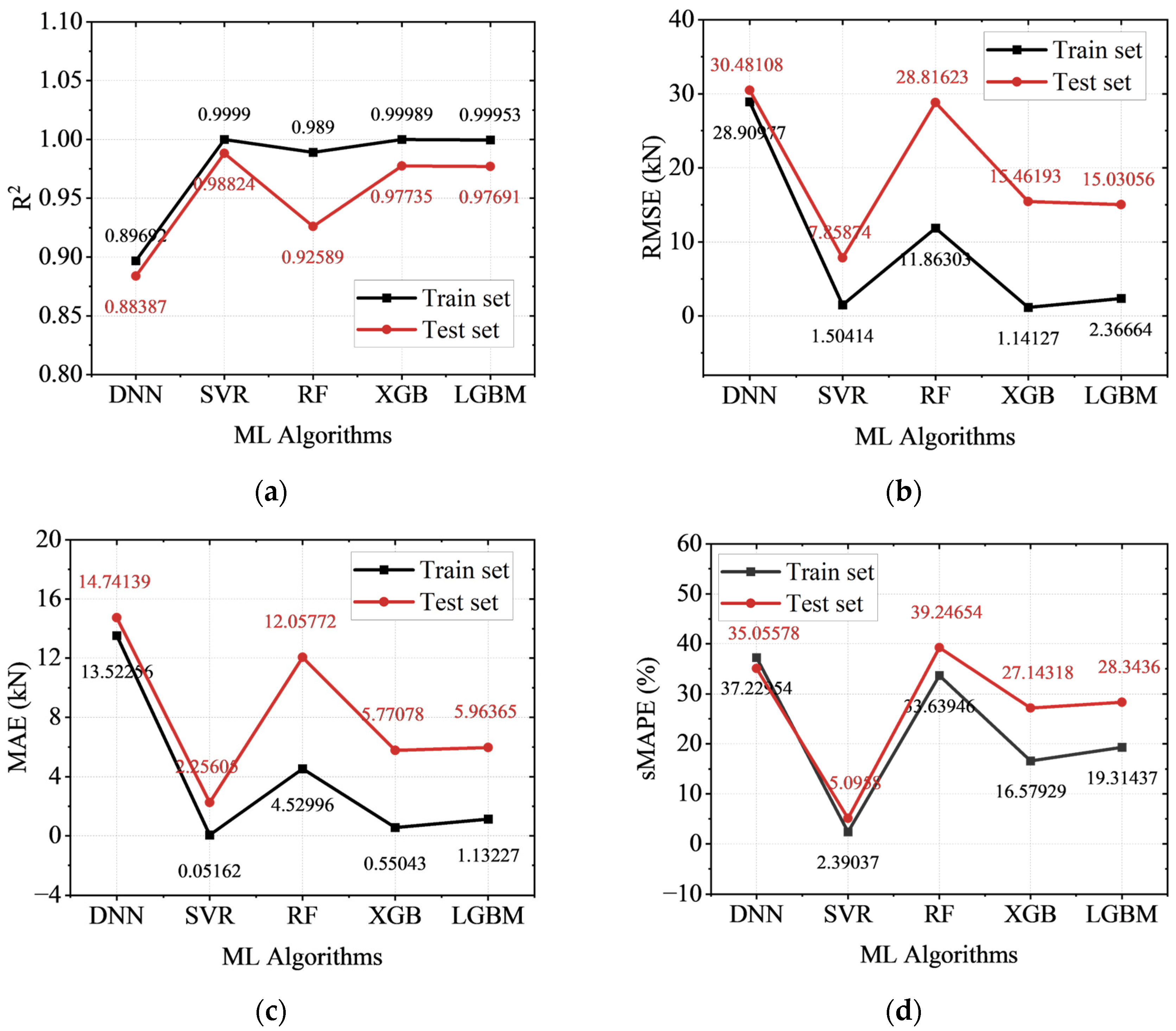
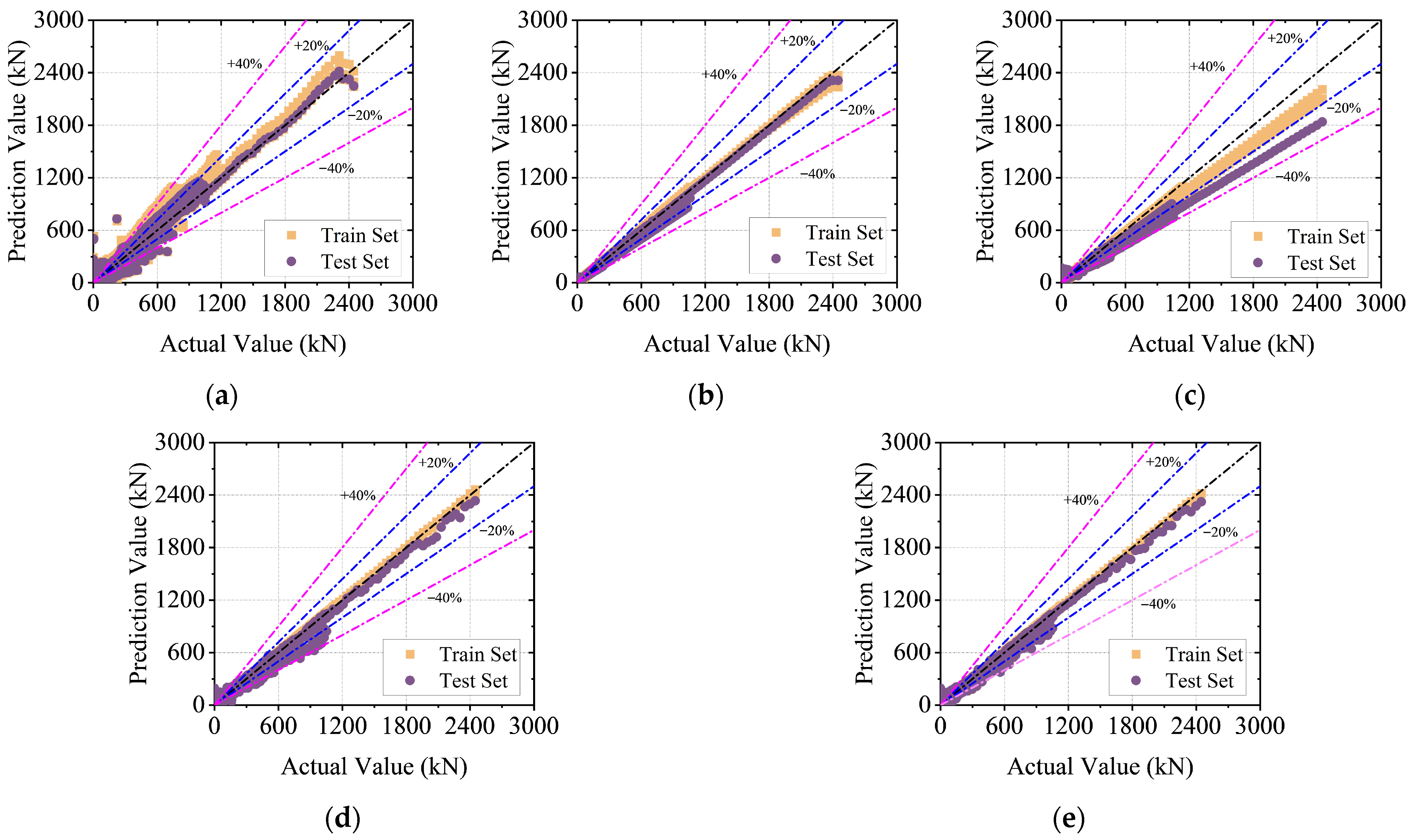
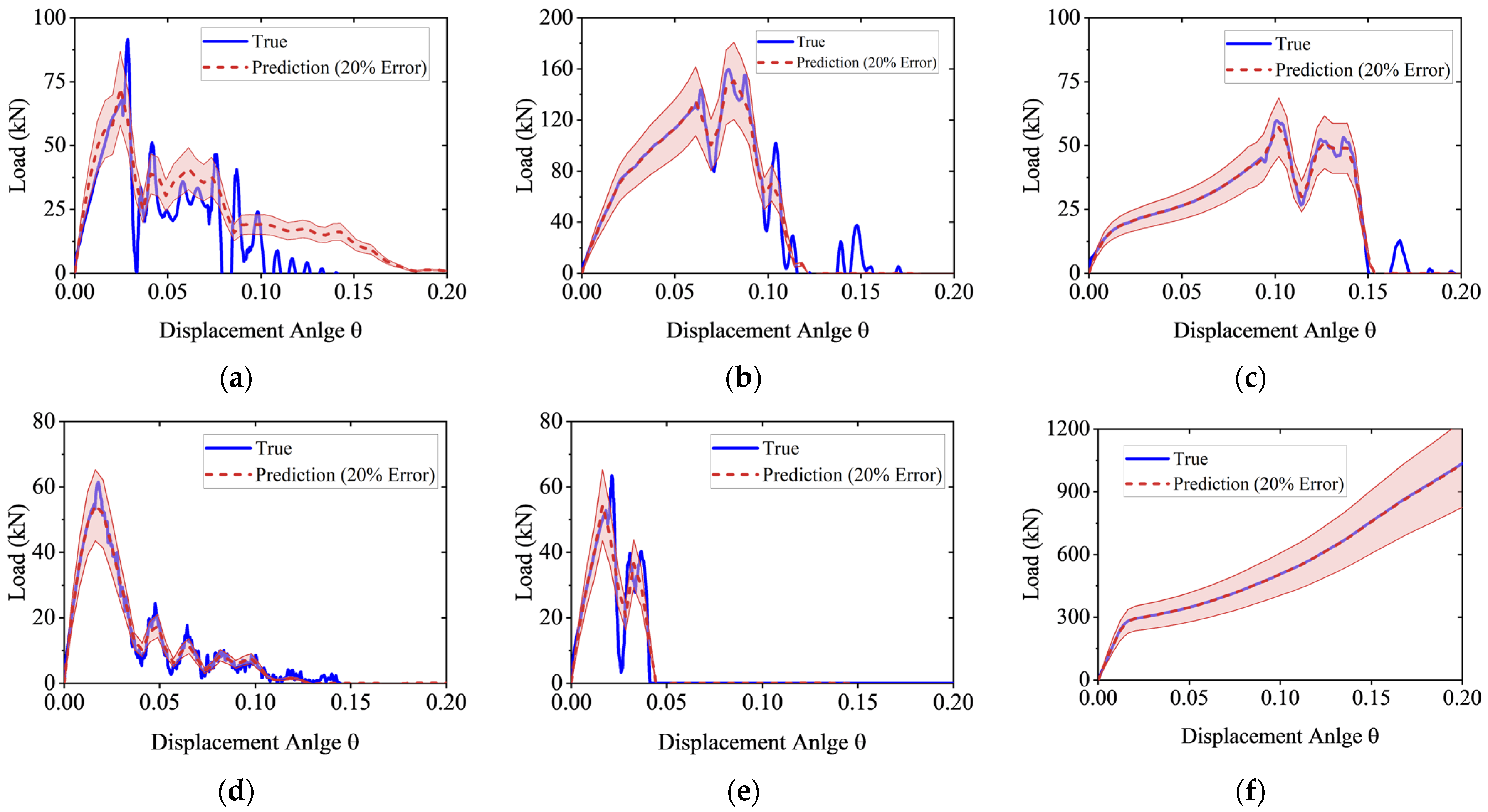
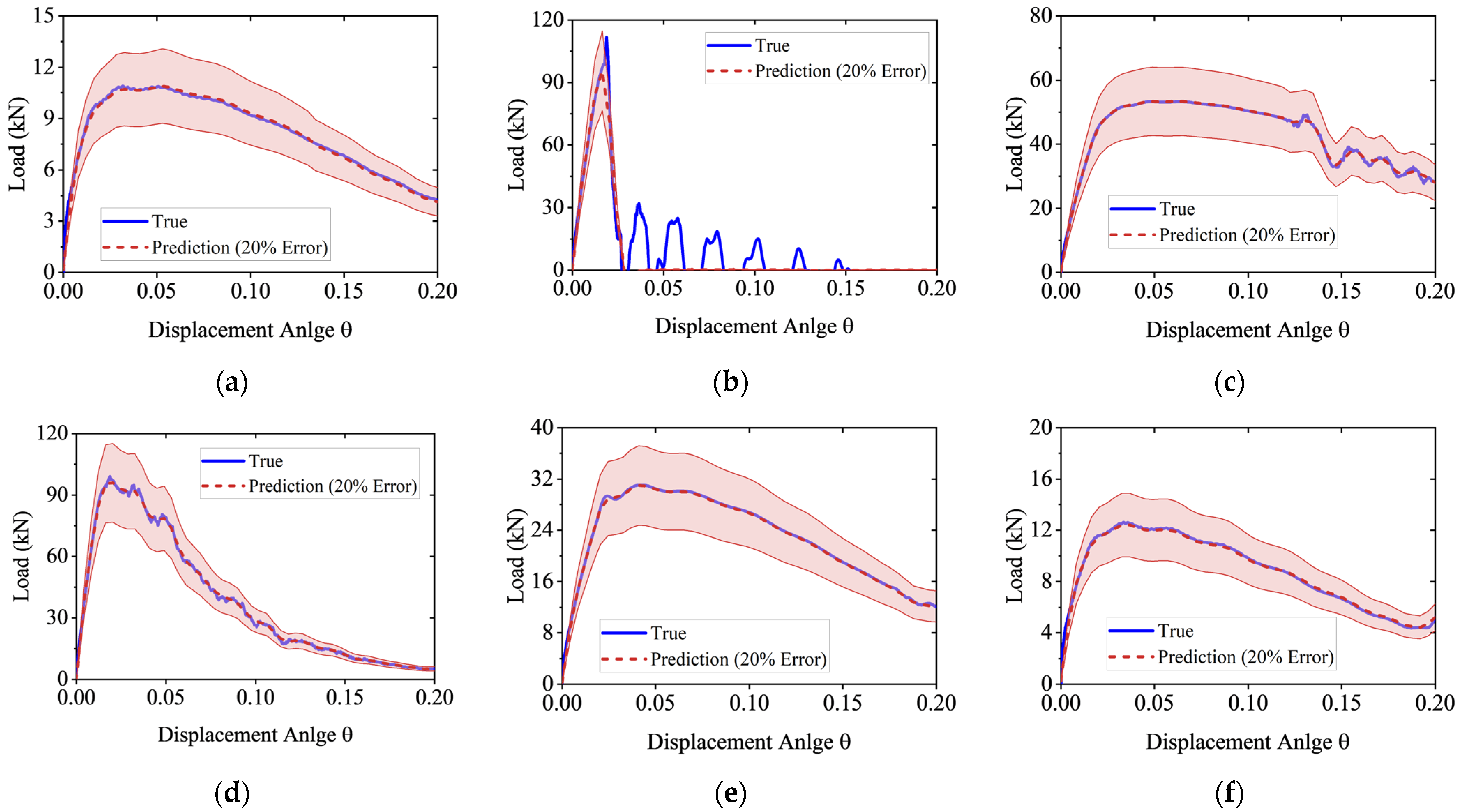
4.3. Model Predictions
5. Machine Learning Interpretations
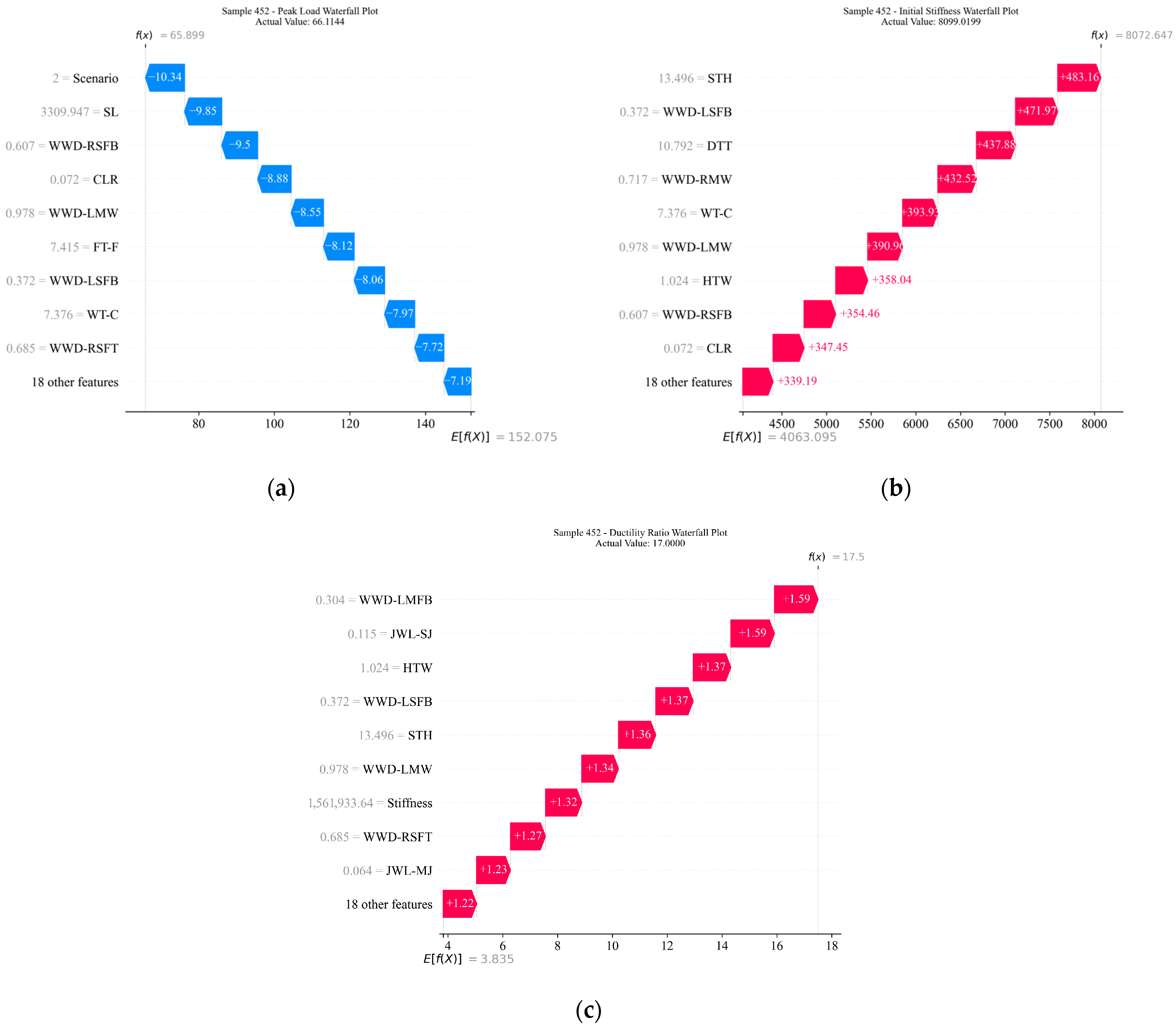
5.1. Individual Interpretation
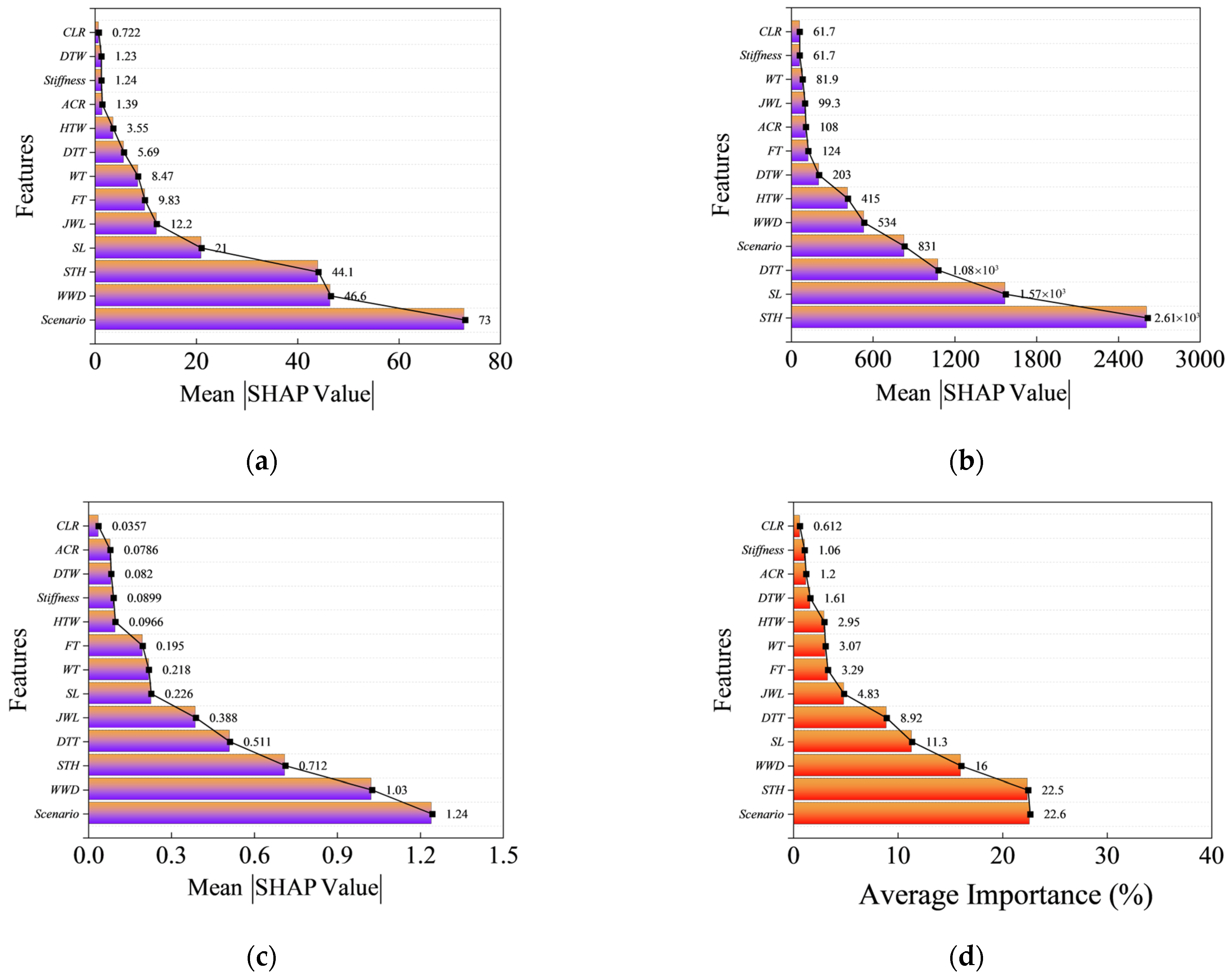
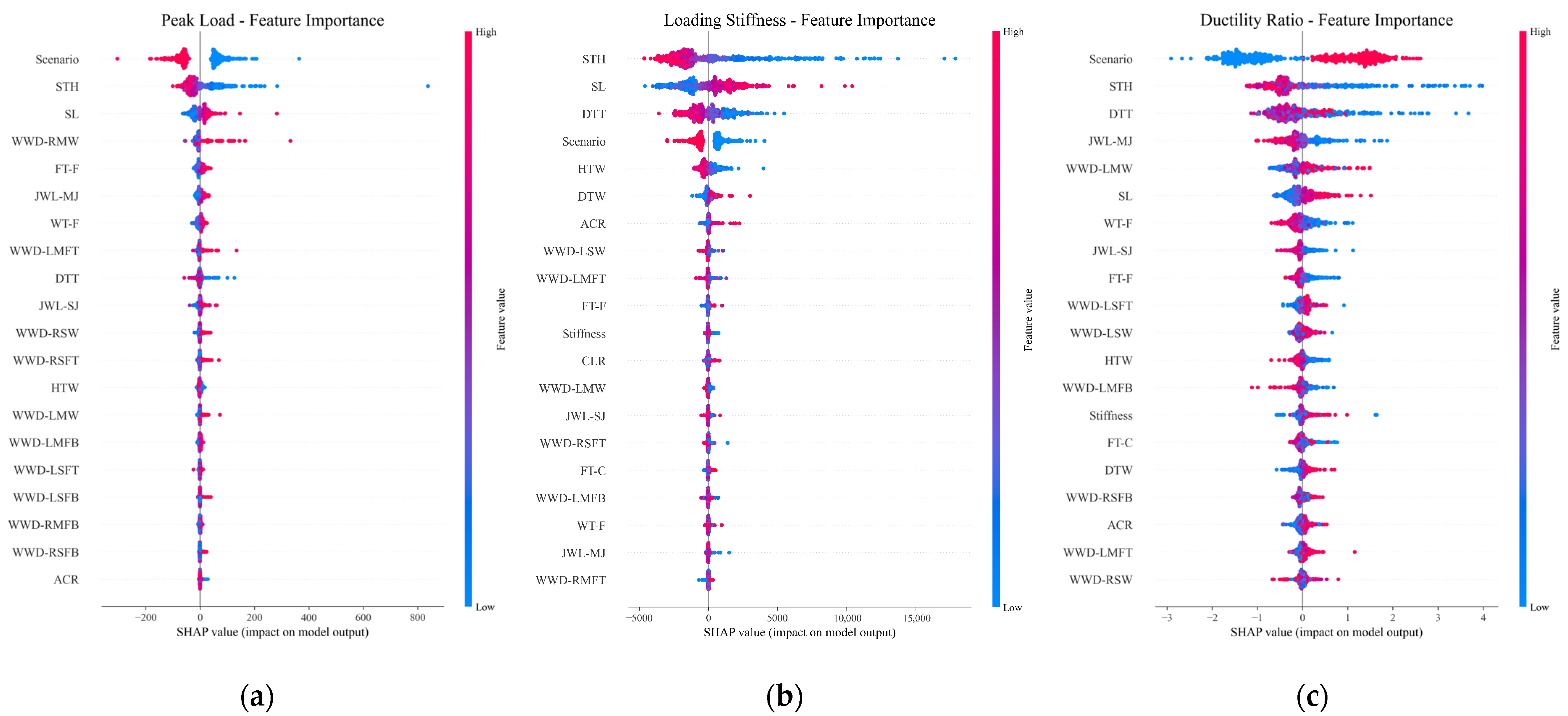
5.2. Global Interpretation
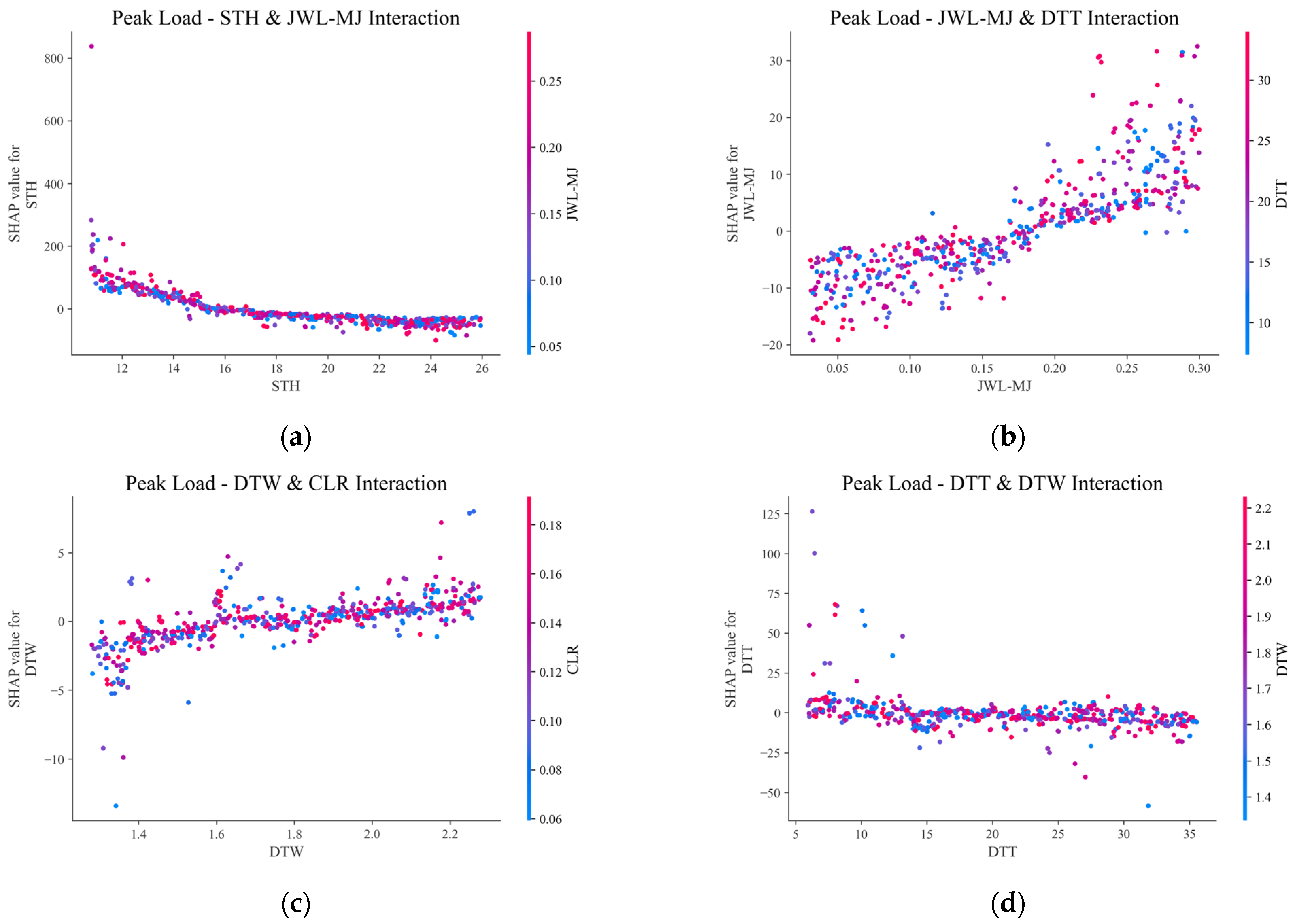
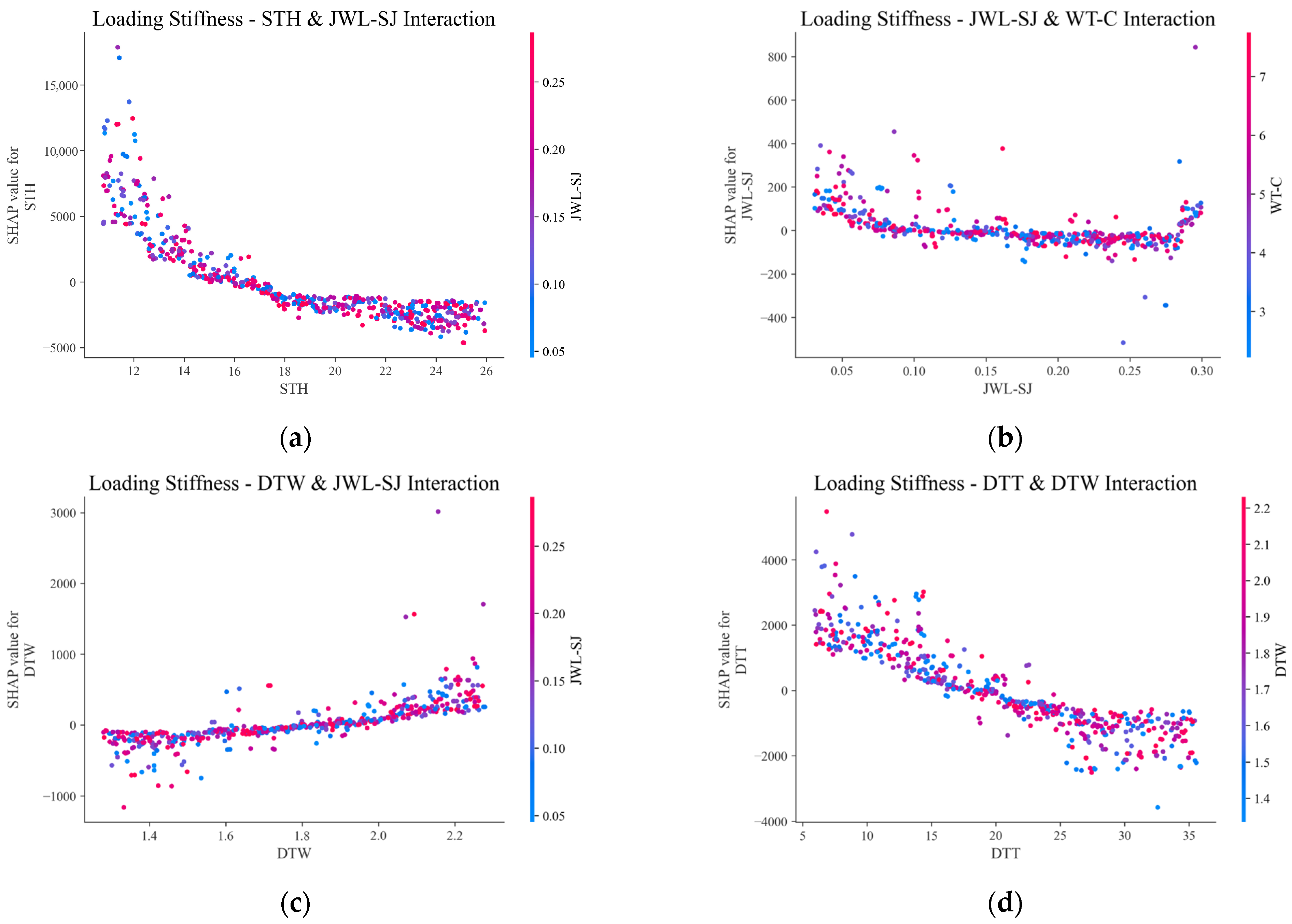
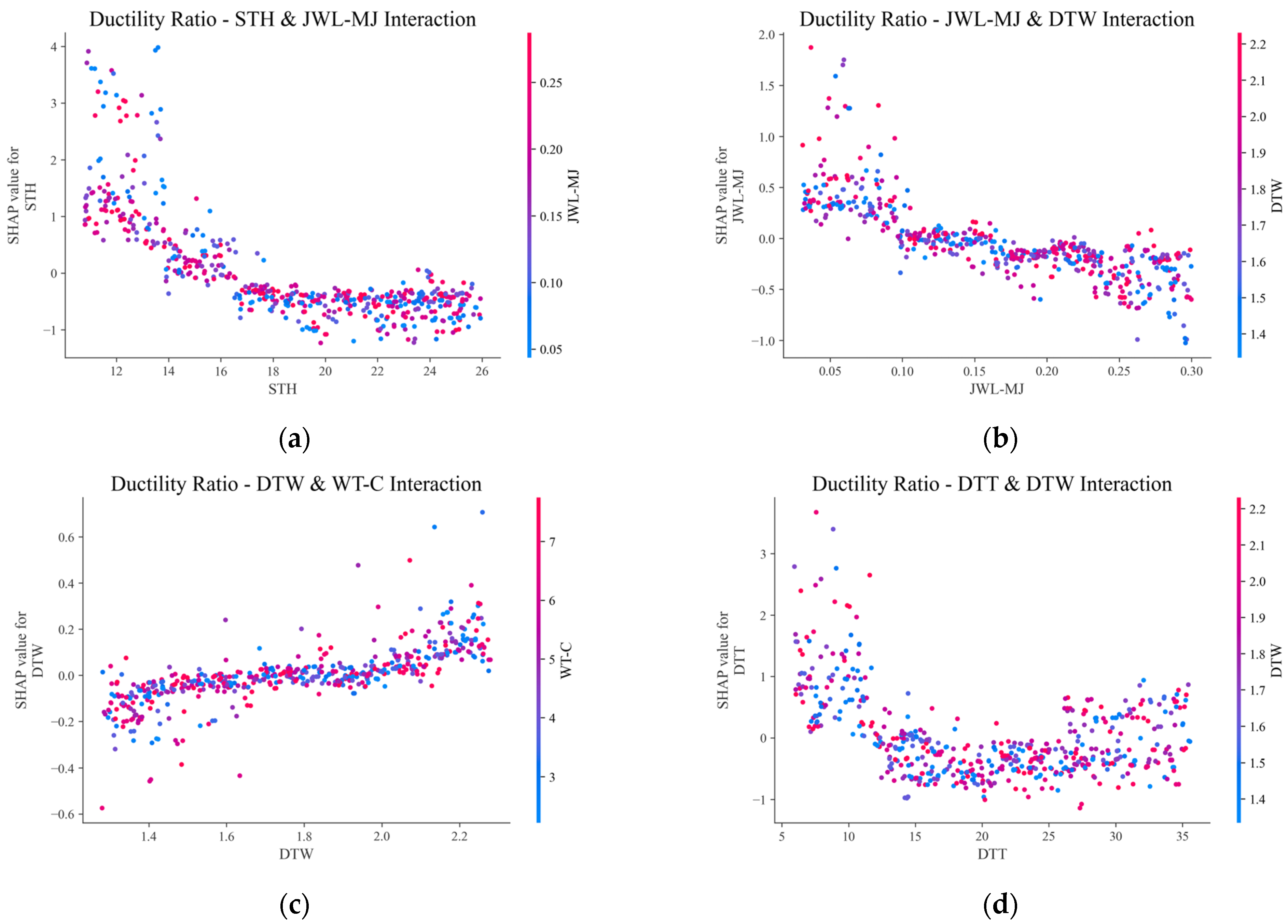
5.3. Feature Interaction
6. Conclusions
- An FEM of a steel frame substructure considering weld defects was established and validated by comparing with test results. Subsequently, a parametric modeling program was developed, which employed Latin Hypercube Sampling (LHS) to generate 700 feature combinations from 27 features and to create the corresponding numerical models. Based on the load–displacement angle (P–θ) results from all 700 models, a progressive collapse database was constructed to facilitate machine learning.
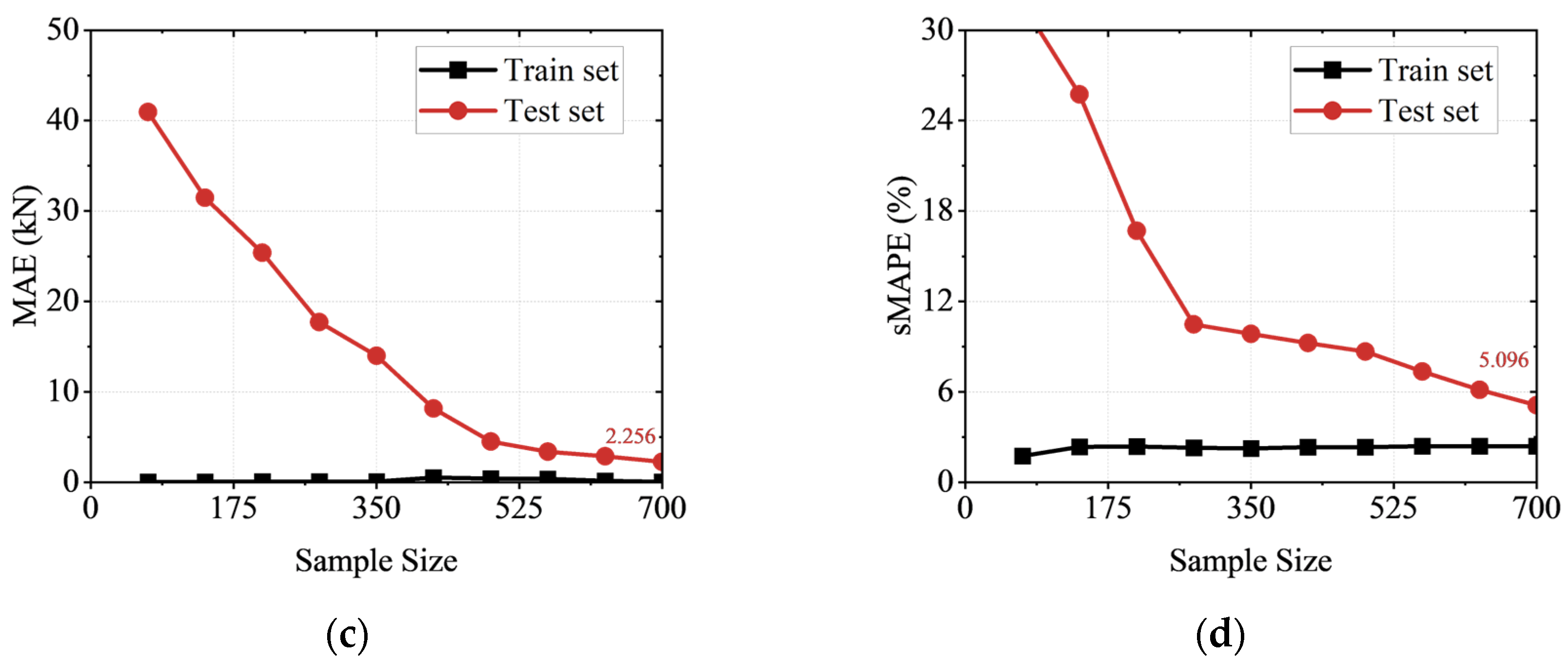
- Five machine learning algorithms—DNN, SVR, RF, XGBoost, and LightGBM—were trained on the multi-output database. The SVR algorithm, optimized via Bayesian hyperparameter tuning combined with 5-fold cross-validation, demonstrated the best performance. It achieved an R2 of 0.988 and an sMAPE of 5.096% for the full-process load prediction on the test set, indicating high accuracy and strong generalization capability. Compared to theoretical models, the machine learning method can account for the complex effects of weld uncertainty on progressive collapse resistance while enabling efficient prediction, which offers broader applicability.
- SHAP was employed for both single sample and global interpretation to analyze the contribution of each feature to the progressive collapse resistance of substructures. The results revealed that the failure scenario, span-to-height ratio, and weld quality are the three most critical factors, accounting for 22.6%, 22.5%, and 16% of the average importance.
- Engineering practice should prioritize ensuring the weld quality of pure welded steel frames. Considering both cost and progressive collapse resistance performance, this study suggests that a beam span-to-height ratio of approximately 15, stub diameter-to-width of beam ratio of about 1.8, stub diameter-to-thickness ratio of around 13, and weld joint relative position ratio set within 0.15 to 0.18 are suitable for engineering practice.
- Although this study established a mapping between ISO weld quality acceptance grades and the approximate ranges of property weakened degree, it is recommended to directly measure the performance degradation of welding material through tests under identical conditions to ensure accuracy. The proposed machine learning framework is developed for predicting the progressive collapse resistance of purely welded steel frames with box-section beam, with its predictive scope confined to the defined feature domain. However, this framework remains applicable to steel frame structures with bolted or hybrid connections, provided that a representative dataset is available. Additionally, this study does not yet consider the synergistic optimization between structural performance and economic benefits, which could serve as a direction for future research. Finally, while this study focuses on static scenarios based on the alternative load path method, the framework requires further validation and development for dynamic scenarios, such as sudden column loss or blasts and impacts. Such future work should incorporate the effects of material strain rate and structural dynamic response.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine learning |
| FEM | Finite element model |
| SHAP | Shapley additive explanations |
| LHS | Latin hypercube sampling |
| DNN | Deep neutral network |
| SVR | Support vector regression |
| SVM | Support vector machine |
| RF | Random forest |
| XGBoost | Extreme gradient boosting |
| GOSS | Gradient-based one-sided sampling |
| LightGBM | Light gradient boosting machine |
| KNN | K-nearest neighbors |
| DCN | Deep convolutional neutral network |
| K Fold CV | K fold cross-validation |
| CA | Catenary action |
| FA | Flexural action |
| DAF | Dynamic amplification factor |
| RC | Reinforced concrete |
| CWP | Cover plate flange connection |
| EPH | End plate bolted connection |
| RBS | Reduced beam section welded connection |
| ACR | Axial compressive ratio |
| MSD | Middle stub displacement |
| SL | Beam span length |
| FT | Beam flange thickness |
| WT | Beam web thickness |
| CLR | Ratio of cantilever beam length to main beam span |
| JWL | Relative position ratio of the weld-weakened area center |
| WWD | Weld-weakened degree in the joint region |
| STH | Ratio of beam span to height |
| HTW | Ratio of beam height to width |
| DTW | Ratio of stub diameter to beam width |
| DTT | Ratio of stub diameter to stub thickness |
| RMSE | Root mean square error |
| R2 | Coefficient of determination |
| MAE | Mean absolute error |
| sMAPE | Symmetric mean absolute percentage error |
References
- Marjanishvili, S.M. Progressive Analysis Procedure for Progressive Collapse. J. Perform. Constr. Facil. 2004, 18, 79–85. [Google Scholar] [CrossRef]
- Shalva, M. Agnew Elizabeth Comparison of Various Procedures for Progressive Collapse Analysis. J. Perform. Constr. Facil. 2006, 20, 365–374. [Google Scholar]
- Sasani, M.; Sagiroglu, S. Progressive Collapse Resistance of Hotel San Diego. J. Struct. Eng. 2008, 134, 478–488. [Google Scholar] [CrossRef]
- General Services Administration (GSA). GSA 2016: Alternate Path Analysis & Design Guidelines for Progressive Collapse Resistance; General Services Administration: Washington, DC, USA, 2016.
- Qian, K.; Liu, Y.; Yang, T.; Li, B. Progressive Collapse Resistance of Posttensioned Concrete Beam-Column Subassemblages with Unbonded Posttensioning Strands. J. Struct. Eng. 2018, 144, 04017182. [Google Scholar] [CrossRef]
- Qian, K.; Li, B. Performance of Precast Concrete Substructures with Dry Connections to Resist Progressive Collapse. J. Perform. Constr. Facil. 2018, 32, 04018005. [Google Scholar] [CrossRef]
- Yang, B.; Tan, K.H. Robustness of Bolted-Angle Connections against Progressive Collapse: Mechanical Modelling of Bolted-Angle Connections under Tension. Eng. Struct. 2013, 57, 153–168. [Google Scholar] [CrossRef]
- Oosterhof, S.A.; Driver, R.G. Behavior of Steel Shear Connections under Column-Removal Demands. J. Struct. Eng. 2015, 141, 04014126. [Google Scholar] [CrossRef]
- Weigand, J.M.; Berman, J.W. Integrity of Bolted Angle Connections Subjected to Simulated Column Removal. J. Struct. Eng. 2016, 142, 04015165. [Google Scholar] [CrossRef]
- Dinu, F.; Marginean, I.; Dubina, D. Experimental Testing and Numerical Modelling of Steel Moment-Frame Connections under Column Loss. Eng. Struct. 2017, 151, 861–878. [Google Scholar] [CrossRef]
- Zhong, W.; Tan, Z.; Tian, L.; Meng, B.; Song, X.; Zheng, Y. Collapse Resistance of Composite Beam-Column Assemblies with Unequal Spans under an Internal Column-Removal Scenario. Eng. Struct. 2020, 206, 110143. [Google Scholar] [CrossRef]
- Zhong, W.; Song, X.; Ma, B. Analysis of Anti-Collapse Performance of Beam–Column Substructure with Welded Flange-Bolted Web Connection in Minor-Axis Direction Under Different Span Ratios. Int. J. Struct. Stab. Dyn. 2018, 19, 1940005. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, J.; Xu, S.; Wang, Z. An Investigation of the Effect of Semi-Rigid Connections on Sudden Column Removal in Steel Frames. Structures 2018, 13, 166–177. [Google Scholar] [CrossRef]
- Qian, K.; Lan, X.; Li, Z.; Li, Y.; Fu, F. Progressive Collapse Resistance of Two-Storey Seismic Configured Steel Sub-Frames Using Welded Connections. J. Constr. Steel Res. 2020, 170, 106117. [Google Scholar] [CrossRef]
- Qian, K.; Lan, X.; Li, Z.; Fu, F. Behavior of Steel Moment Frames Using Top-and-Seat Angle Connections under Various Column-Removal Scenarios. J. Struct. Eng. 2021, 147, 04021144. [Google Scholar] [CrossRef]
- Yu, P.; Huang, X.; Li, H.; Nie, Y.; He, S. Progressive Collapse Resistance of Unsymmetrical Steel Sub-Structure under a Middle Column-Removal Scenario. J. Build. Eng. 2023, 69, 105994. [Google Scholar] [CrossRef]
- Huang, X.; Elchalakani, M.; Yu, P.; Lin, R.; Nie, Y.; He, S. Progressive Collapse Resistance of Steel Frame with Beam to Column Transfer Structure under a Middle Column-Removal Scenario. Structures 2023, 51, 1–12. [Google Scholar] [CrossRef]
- Yang, B.; Tan, K.H. Behavior of Composite Beam-Column Joints in a Middle-Column-Removal Scenario: Experimental Tests. J. Struct. Eng. 2014, 140, 04013045. [Google Scholar] [CrossRef]
- Yang, B.; Tan, K.H. Experimental Tests of Different Types of Bolted Steel Beam–Column Joints under a Central-Column-Removal Scenario. Eng. Struct. 2013, 54, 112–130. [Google Scholar] [CrossRef]
- Wang, F.; Yang, J.; Pan, Z. Progressive Collapse Behaviour of Steel Framed Substructures with Various Beam-Column Connections. Eng. Fail. Anal. 2020, 109, 104399. [Google Scholar] [CrossRef]
- Huang, X.; Yu, P.; He, S.; Zhang, C. Effects of RWS and Horizontal Restraint on Progressive Collapse of Steel Sub-Structure with Box-Beams. J. Build. Eng. 2025, 104, 112389. [Google Scholar] [CrossRef]
- Shariati, M.; Raeispour, M.; Naghipour, M.; Kamyab, H.; Memarzadeh, A.; Nematzadeh, M.; Toghroli, A. Flexural Behavior Analysis of Double Honeycomb Steel Composite Encased Concrete Beams: An Integrated Experimental and Finite Element Study. Case Stud. Constr. Mat. 2024, 20, e03299. [Google Scholar] [CrossRef]
- Davoodnabi, S.M.; Mirhosseini, S.M.; Shariati, M. Analyzing Shear Strength of Steel-Concrete Composite Beam with Angle Connectors at Elevated Temperature Using Finite Element Method. Steel Compos. Struct. 2021, 40, 853–868. [Google Scholar]
- Yu, P.; Guo, Z.; Yun, W.; Guo, X. Investigation on the New Bolt-Welded Joint of Concrete-Encased CFST under Eccentric Compression. Structures 2025, 72, 108183. [Google Scholar] [CrossRef]
- Guo, Z.; Yu, P.; Huang, X.; Chen, X.; Yao, Y. Numerical Investigation on Dynamic Behaviour of Unbonded Post-Tensioned Precast Concrete Beam Column Sub-Assemblages under Drop Impact Loading. J. Build. Eng. 2025, 113, 113954. [Google Scholar] [CrossRef]
- Kazemi, F.; Shafighfard, T.; Yoo, D.-Y. Data-Driven Modeling of Mechanical Properties of Fiber-Reinforced Concrete: A Critical Review. Arch. Comput. Methods Eng. 2024, 31, 2049–2078. [Google Scholar] [CrossRef]
- Lu, X.-G.; He, Y.; Zheng, W. Design of Advanced Steels by Integrated Computational Materials Engineering. Mater. Genome Eng. Adv. 2024, 2, e36. [Google Scholar] [CrossRef]
- Geng, X.; Wang, F.; Wu, H.-H.; Wang, S.; Wu, G.; Gao, J.; Zhao, H.; Zhang, C.; Mao, X. Data-Driven and Artificial Intelligence Accelerated Steel Material Research and Intelligent Manufacturing Technology. Mater. Genome Eng. Adv. 2023, 1, e10. [Google Scholar] [CrossRef]
- Zhu, Y.F.; Yao, Y.; Huang, Y.; Chen, C.H.; Zhang, H.Y.; Huang, Z. Machine Learning Applications for Assessment of Dynamic Progressive Collapse of Steel Moment Frames. Structures 2022, 36, 927–934. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, B.; Alqawzai, S.; Chen, K.; Kong, D. Machine Learning-Based and Interpretable Models for Predicting the Resistance and Probability of Progressive Collapse of Steel Frame-Composite Floor Structures. Eng. Struct. 2025, 332, 120089. [Google Scholar] [CrossRef]
- Elkady, N.; Augusthus Nelson, L.; Weekes, L.; Makoond, N.; Buitrago, M. Progressive Collapse: Past, Present, Future and Beyond. Structures 2024, 62, 106131. [Google Scholar] [CrossRef]
- Fu, F. Fire Induced Progressive Collapse Potential Assessment of Steel Framed Buildings Using Machine Learning. J. Constr. Steel Res. 2020, 166, 105918. [Google Scholar] [CrossRef]
- Esfandiari, M.; Haghighi, H.; Urgessa, G. Machine Learning-Based Optimum Reinforced Concrete Design for Progressive Collapse. Electron. J. Struct. Eng. 2023, 23, 1–8. [Google Scholar] [CrossRef]
- Esfandiari, M.J.; Urgessa, G.S. Progressive Collapse Design of Reinforced Concrete Frames Using Structural Optimization and Machine Learning. Structures 2020, 28, 1252–1264. [Google Scholar] [CrossRef]
- Hwang, S.-H.; Mangalathu, S.; Shin, J.; Jeon, J.-S. Machine Learning-Based Approaches for Seismic Demand and Collapse of Ductile Reinforced Concrete Building Frames. J. Build. Eng. 2021, 34, 101905. [Google Scholar] [CrossRef]
- Wang, S.; Cheng, X.; Li, Y.; Song, X.; Guo, R.; Zhang, H.; Liang, Z. Rapid Visual Simulation of the Progressive Collapse of Regular Reinforced Concrete Frame Structures Based on Machine Learning and Physics Engine. Eng. Struct. 2023, 286, 116129. [Google Scholar] [CrossRef]
- Gan, Y.; Chen, J.; Li, Y.; Xu, Z. Prediction of Progressive Collapse Resistance of RC Frames Using Deep and Cross Network Model. Structures 2023, 51, 800–813. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, B.; Zhou, Z.; Yao, J.; Lu, Y. Machine Learning-Based Models for Predicting the Progressive Collapse Resistance of Truss String Structures. Eng. Struct. 2024, 307, 117946. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin Hypercube Sampling for Structural Reliability Analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Mostafaei, H.; Behnamfar, F.; Alembagheri, M. Reliability and Sensitivity Analysis of Wedge Stability in the Abutments of an Arch Dam Using Artificial Neural Network. Earthq. Eng. Eng. Vib. 2022, 21, 1019–1033. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
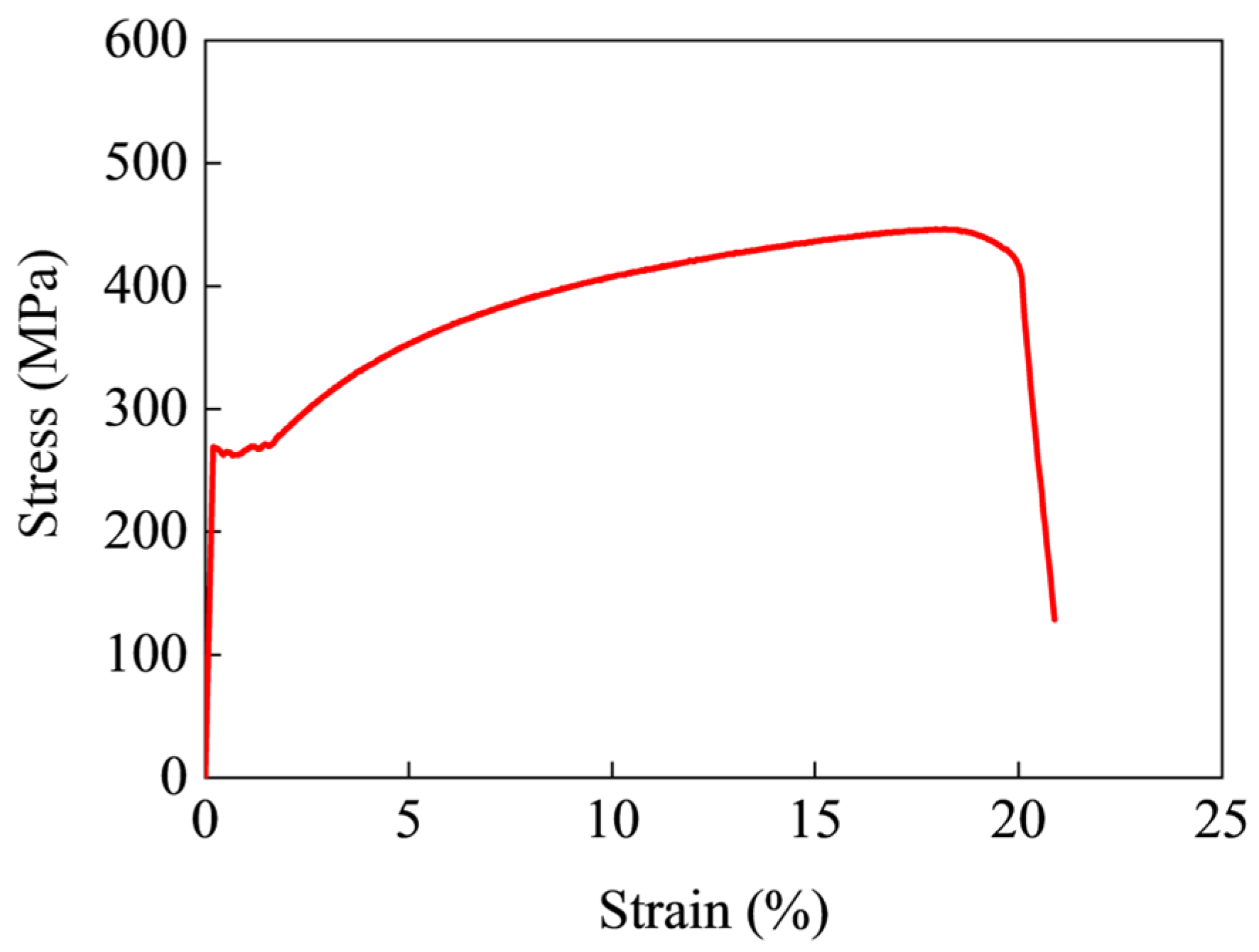
- Eroğlu, M.; Aksoy, M.; Orhan, N. Effect of Coarse Initial Grain Size on Microstructure and Mechanical Properties of Weld Metal and HAZ of a Low Carbon Steel. Mater. Sci. Eng. A 1999, 269, 59–66. [Google Scholar] [CrossRef]
- Jia, Z. Experimental Study on Mechanical Properties of Butt Welded Connection at High Temperature. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2019. (In Chinese). [Google Scholar]
- Kuwamura, H. Classification of Material and Welding in Fracture Consideration of Seismic Steel Frames. Eng. Struct. 2003, 25, 547–563. [Google Scholar] [CrossRef]
- Palanci, M. Fuzzy Rule Based Seismic Risk Assessment of One-Story Precast Industrial Buildings. Earthq. Eng. Eng. Vib. 2019, 18, 631–648. [Google Scholar] [CrossRef]
- Yuan, C.; He, C.; Xu, J.; Liao, L.; Kong, Q. Bayesian Optimization for Selecting Efficient Machine Learning Regressors to Determine Bond-Slip Model of FRP-to-Concrete Interface. Structures 2022, 39, 351–364. [Google Scholar] [CrossRef]
- Ling, H.; Qian, C.; Kang, W.; Liang, C.; Chen, H. Combination of Support Vector Machine and K-Fold Cross Validation to Predict Compressive Strength of Concrete in Marine Environment. Constr. Build. Mater. 2019, 206, 355–363. [Google Scholar] [CrossRef]
- ISO 5817; Welding—Fusion-Welded Joints in Steel, Nickel, Titanium and Their Alloys (Beam Welding Excluded)—Quality Levels for Imperfections. International Organization for Standardization: Geneva, Switzerland, 2023.

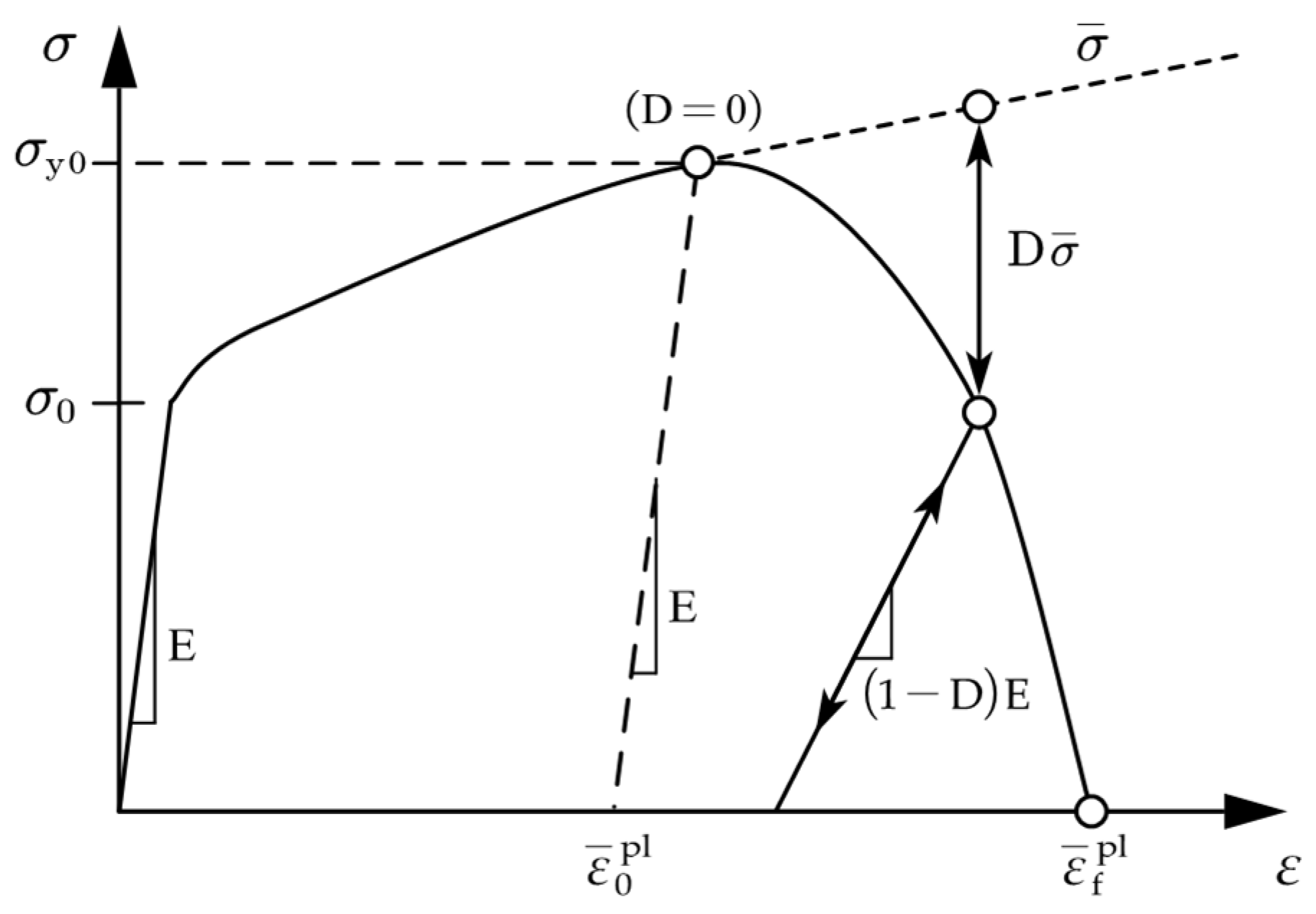
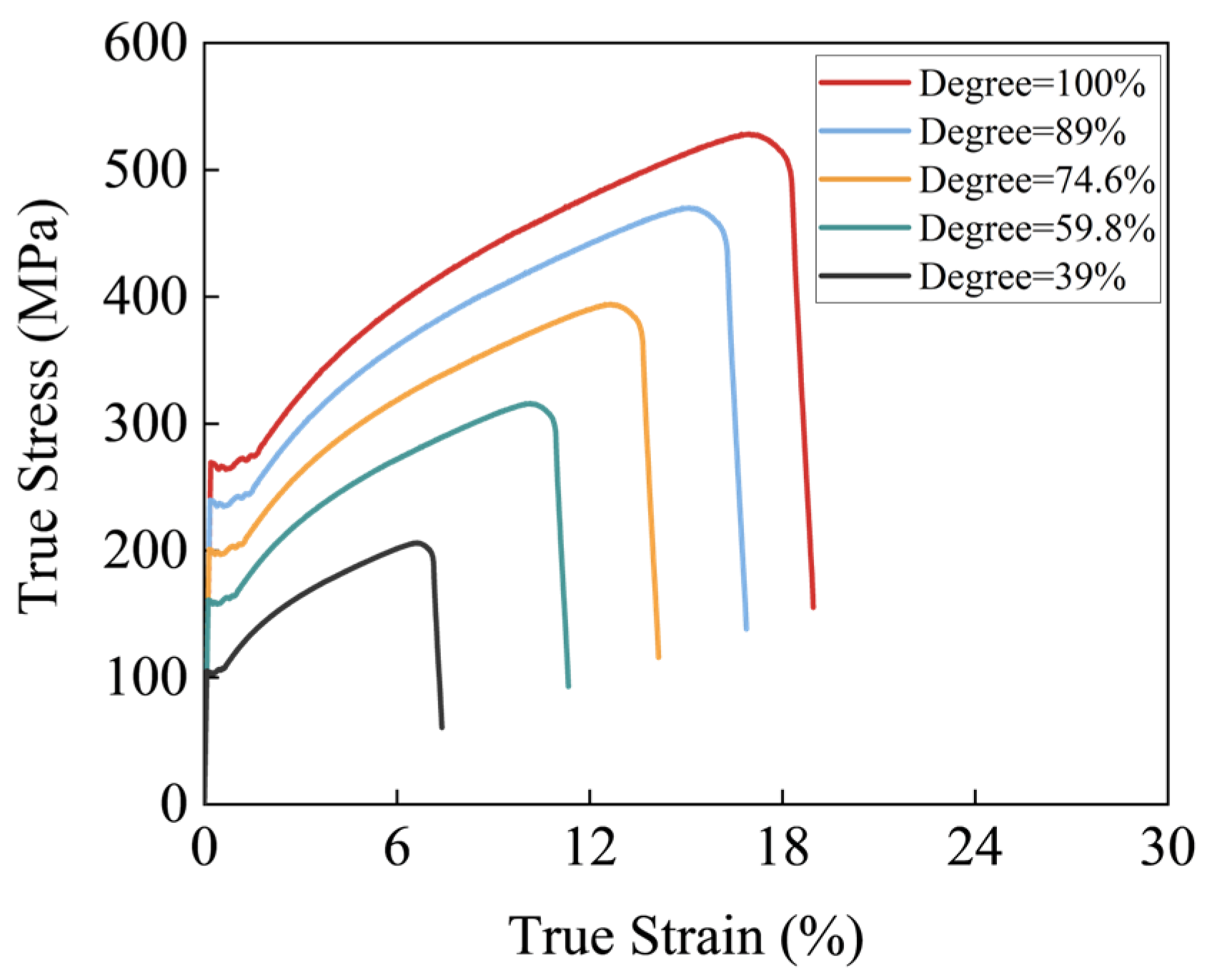
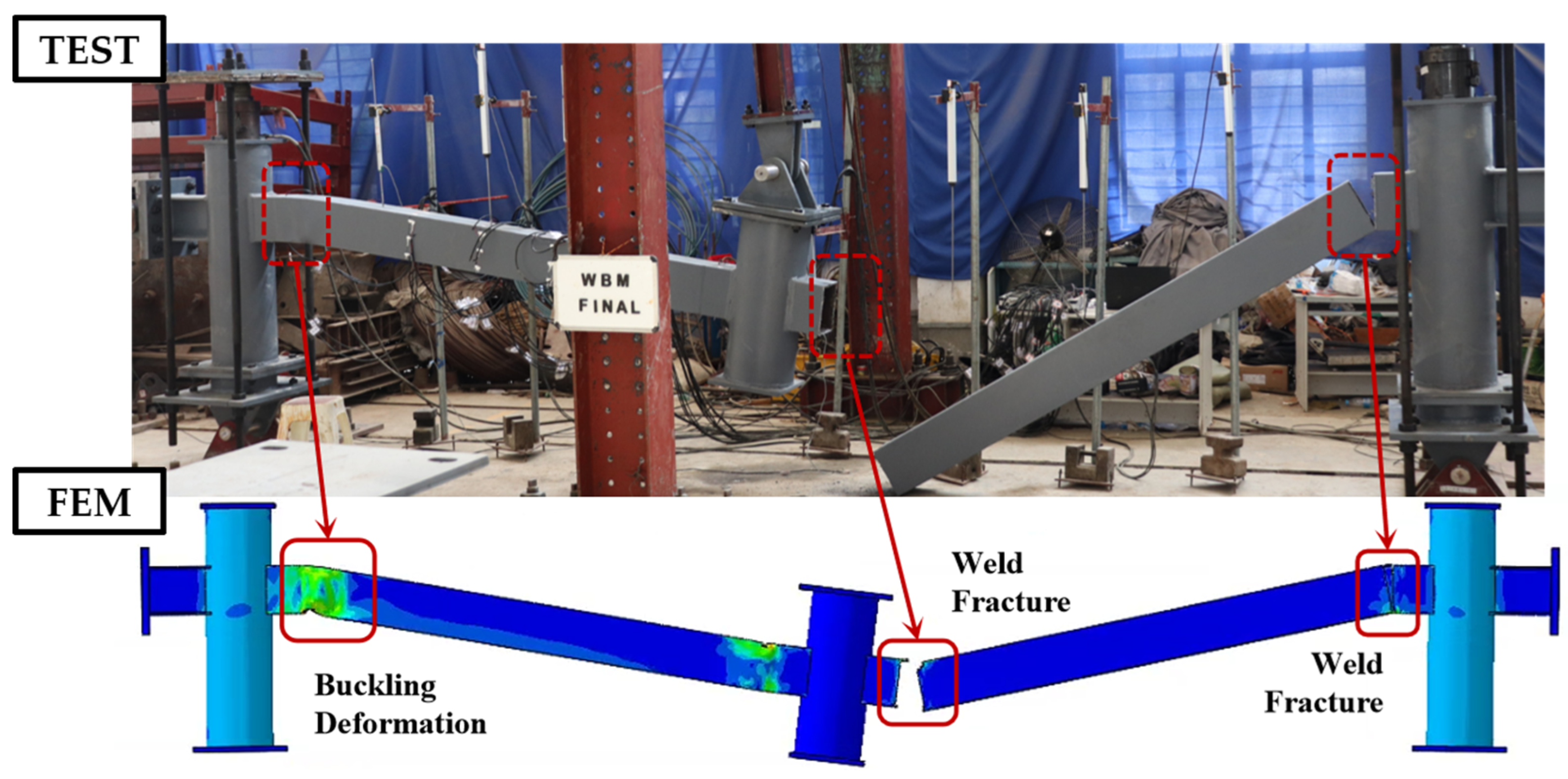
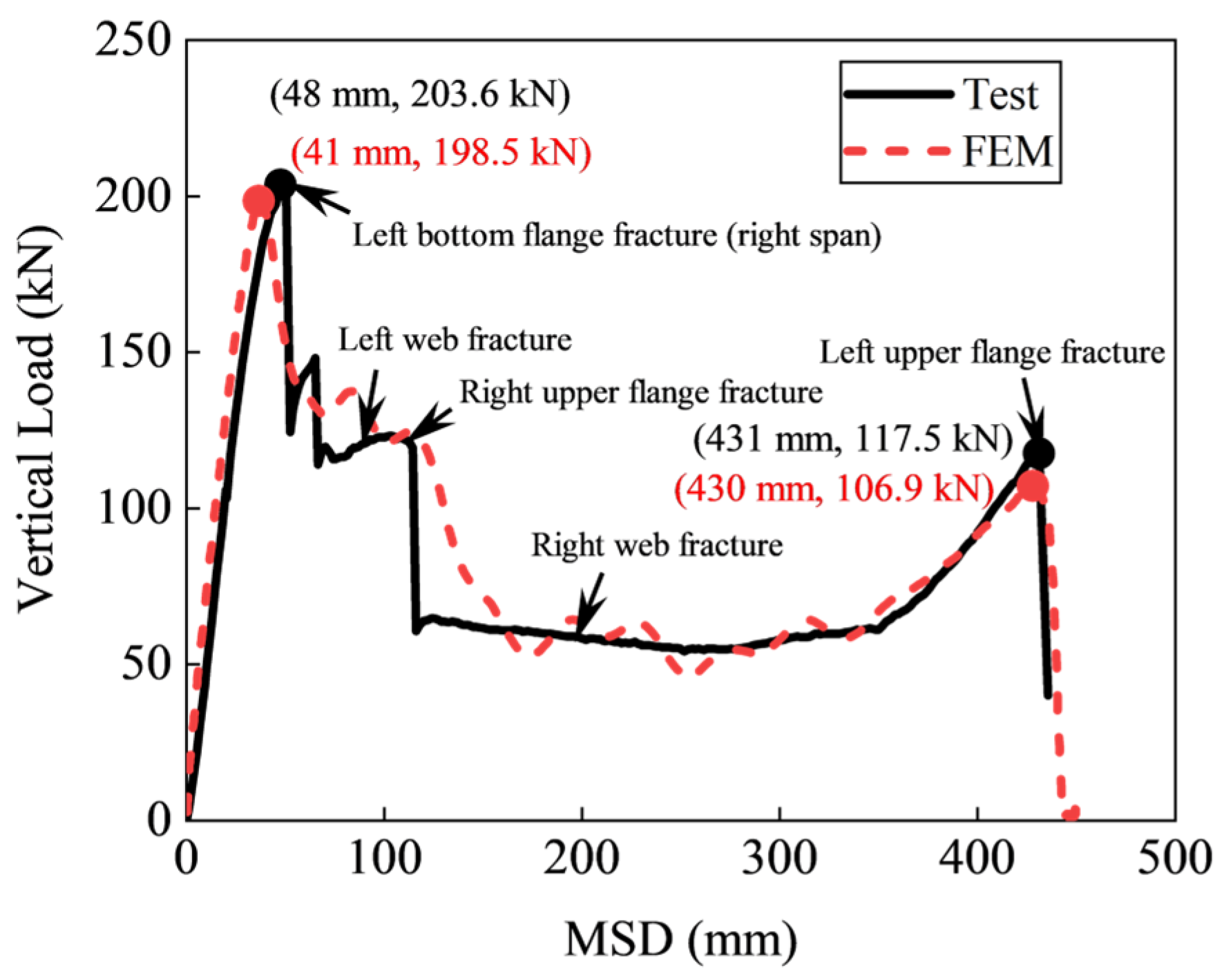
| Degree (%) | Fracture Strain (%) | Stress Triaxiality | Strain Rate (s−1) | Fracture Energy (N/mm2) |
|---|---|---|---|---|
| 100 | 19 | 1/3 | 0 | 0.001 |
| 89 | 16.9 | 1/3 | 0 | 0.001 |
| 74.6 | 14.1 | 1/3 | 0 | 0.001 |
| 59.8 | 11.3 | 1/3 | 0 | 0.001 |
| 39 | 7.4 | 1/3 | 0 | 0.001 |
| Feature Category | Unit | Maximum | Minimum |
|---|---|---|---|
| SL | mm | 1625 | 4875 |
| FT | mm | 4 | 20 |
| WT | mm | 4 | 20 |
| CLR | % | 0.05 | 0.2 |
| JWL | % | 0.03 | 0.3 |
| WWD | % | 0.3 | 1 |
| STH | % | 10.8 | 26 |
| HTW | % | 1 | 1.5 |
| DTW | % | 1.28 | 2.28 |
| DTT | % | 5.93 | 35.6 |
| ACR | % | 0 | 0.5 |
| Stiffness | kN/m | 1720 | 1,720,000 |
| Scenario | - | Middle Stub | Side Stub |
| Algorithm | Hyperparameters Optimization |
|---|---|
| DNN | Activation: ReLu; Hidden layers: 5 (3~8); Units: 439 (128~512); Dropout_rate: 0.1713 (0.15~0.4); Learning_rate: 0.0026 (0.0005~0.005); Batch_size: 31 (16~32); Epochs: 46 (16~500) |
| SVR | C: 832.4594 (0.1~1000); Epsilon: 0.0221 (0.001~0.1); Gamma: 1.8191 (0.001~10); Kernel: RBF |
| RF | N_estimators: 245 (50~500); Max_depth: 31 (5~50); Min_samples_split: 2 (2~20); Min_samples_leaf: 1 (1~10); Max_features: 0.1 (0.1~1) |
| XGBoost | N_estimators: 498 (100~500); Max_depth: 9 (3~10); Learning_rate: 0.0889 (0.01~0.1); Subsample: 0.7732 (0.7~0.9); Colsample_bytree: 0.8623 (0.7~0.9); Reg_alpha: 0.2368 (0.1~1); Reg_lambda: 0.9742 (0.1~1); Min_child_weight: 9 (1~10) |
| LightGBM | N_estimators: 328 (100~500); Max_depth: 10 (3~10); Learning_rate: 0.1 (0.01~0.1); Num_leaves: 28 (20~100); Subsample: 0.7 (0.7~0.9); Colsample_bytree: 0.9 (0.7~0.9); Reg_alpha: 0.1 (0.1~1); Reg_lambda: 1 (0.1~1); Min_child_sample: 12 (5~20) |
| ISO 5817 Quality Levels | Defect Characteristics | Suggested Weakening Degree | Explanation |
|---|---|---|---|
| Level B (Stringent) | Permits only minimal defects. (e.g., undercut depth ≤ 0.5 mm). | 100–85% | This level represents high-quality welds. The performance is close to that of the base metal. |
| Level C (Intermediate) | Allows for defects of certain dimensions. (e.g., undercut depth ≤ 1 mm). | 85–60% | This is the common standard for most static structures. A reduction within this range is sufficient to significantly affect structural ductility and collapse resistance. |
| Level D (Basic)/ Non-Compliant | Permits significant defects or the presence of individual, excessively large defects. (e.g., undercut depth > 1.5 mm). | 65–30% | This level corresponds to poor-quality or non-compliant welds. Such welds should be deemed unacceptable on critical load paths for progressive collapse resistance. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Yu, P.; Huang, X.; Yao, Y.; Zhang, C. Machine Learning Prediction on Progressive Collapse Resistance of Purely Welded Steel Frames Considering Weld Defects. Buildings 2025, 15, 4174. https://doi.org/10.3390/buildings15224174
Guo Z, Yu P, Huang X, Yao Y, Zhang C. Machine Learning Prediction on Progressive Collapse Resistance of Purely Welded Steel Frames Considering Weld Defects. Buildings. 2025; 15(22):4174. https://doi.org/10.3390/buildings15224174
Chicago/Turabian StyleGuo, Zikang, Peng Yu, Xinheng Huang, Yingkang Yao, and Chunwei Zhang. 2025. "Machine Learning Prediction on Progressive Collapse Resistance of Purely Welded Steel Frames Considering Weld Defects" Buildings 15, no. 22: 4174. https://doi.org/10.3390/buildings15224174
APA StyleGuo, Z., Yu, P., Huang, X., Yao, Y., & Zhang, C. (2025). Machine Learning Prediction on Progressive Collapse Resistance of Purely Welded Steel Frames Considering Weld Defects. Buildings, 15(22), 4174. https://doi.org/10.3390/buildings15224174







