Ground-Motion Modification by Soil, Structures, and Topography: A Review of Soil Structure Interaction (SSI) and Its Multi-Scale Extensions

Abstract

The effect of an earthquake on any structure is primarily determined by both its inherent properties and the surrounding environmental conditions. When seismic waves pass through different media, their characteristics and properties, such as amplitude, frequency content, and duration can change, thereby changing the seismic response of both soil and structures. The intensity and distribution of seismic waves can be influenced by several of key factors, including the local geology and stratigraphy, irregular topography, existence of man-made structures, and others. Relevant researches and studies have consistently emphasized the significance of the surrounding environment in seismic wave modification. Historical data also shows that similar types of earthquakes can result in varying degrees of damage depending on geographic location. Hence, a thorough understanding of the interaction between seismic waves and the surrounding environment is necessary for achieving precision in seismic design, risk assessment, and proper seismic mitigation strategies. An overview of contemporary research on seismic wave modification and the resulting interaction effects, presenting significant findings and analytical techniques related to phenomena such as soil-structure interaction (SSI) and its extended forms, including structure–soil–structure interaction (SSSI), soil–structure–cluster interaction (SSCI), and site–city interaction (SCI), is presented in this review article. The underlying mechanisms of these interactions are explored in this study and a detailed assessment of fundamental concepts, practical challenges, and methodologies for preventing and mitigating their effects in site-dependent settings is provided. Further, Topographic soil–structure interaction (TSSI) and topographic–structure–soil–structure interaction (TSSSI) are also discussed within a unified framework that considers the combined influence of topography and SSI extensions. This study focuses on the importance of the surrounding environment in influencing ground motion during earthquakes by identifying the complex interactions that affect the seismic response of both surface and underground structures. Some illustrative figures were generated with Microsoft Copilot and subsequently edited and validated by the authors.

1. Introduction

A seismic wave is a vibration that propagates through the Earth, transmitting energy that results from earthquakes, volcanic activity, or any other sudden ground movements [1,2]. These waves are the principal carriers of earthquake energy, which determines the ground motion patterns. Seismic waves can be classified according to their propagation characteristics, such as wave movement patterns, particle motion, and the medium they traverse. The two primary types of seismic waves are body waves and surface waves, and each has a distinct influence on ground motion [3]. Body waves move within the subsurface, while surface waves are confined to the ground surface. Structural damage can be dominated by surface waves, especially in soft sedimentary basins and at longer periods, but near-source damage is often controlled by S waves and rupture directivity [3,4]. Primary P waves are compressional body waves with particle motion parallel to the direction of propagation in an isotropic elastic medium [5]. Secondary S waves are shear body waves with particle motion perpendicular to propagation [5]. The principal free-surface waves are Rayleigh waves and Love waves [6]. In the ideal layered model, Love waves are horizontally polarized with negligible vertical displacement. They are guided by layering and are supported when a slower near-surface shear-wave layer overlies a faster half-space [4,5,6]. For a homogeneous half-space, Rayleigh waves cause retrograde elliptical motion at the surface. The vertical and horizontal components decay with depth. Stratification can alter the ellipse and the direction of rotation [5,6].

The study on modifications of seismic wave properties caused by the surrounding environment is an important topic in the fields of seismology and earthquake engineering. When seismic waves propagate through a region, they dynamically interact with numerous natural features and constructed infrastructure within their surroundings [7,8]. These include geological formations such as hills, slopes, valleys, and gorges [9,10,11], as well as human-made structures like buildings, underground facilities, dams, and retaining walls [12,13]. These elements can collectively or individually influence the propagation of seismic waves, causing variations in intensity and amplification, thereby influencing the vulnerability of structures to seismic forces. Seismic waves’ behavior can also be altered by the properties of the soil they pass through, making the interaction more complex and site-dependent [14,15,16,17]. Hence, Seismic wave behavior in a specific area is governed by a combination of topography, built infrastructure, and subsurface conditions. Several past earthquakes and field investigation results have shown that similar seismic events can result in varying levels of ground shaking and structural damage across different regions and location [18,19,20,21,22]. These variations are primarily due to the site-specific responses resulting from the interaction between seismic waves and local environmental conditions, which may either amplify or attenuate the ground motions. Therefore, for precise seismic hazard assessment and effective earthquake-resistant design, it is important to comprehend the structural response to seismic waves and the resulting stress at specific locations [23,24]. Understanding the importance of the surrounding environment in the propagation of seismic waves is fundamental for precisely evaluating seismic hazards and constructing the earthquake-resistant structures. Structural designers must incorporate these complicated interaction mechanisms into their structural designs to ensure structural safety and resilience. A detailed comprehension of these phenomena facilitates the optimization of structural performance and the enhancement of safety and resilience in seismic-prone areas. Further, this understanding also contributes to the development of effective mitigation strategies that can reduce the potential earthquake-induced damage.

The fundamental concepts presented in this article provide a basis for forecasting and estimating seismic wave effects at specific sites, including coupled responses such as soil–structure interaction (SSI), structure–soil–structure interaction (SSSI), soil–structure–cluster interaction (SSCI), and site–city interaction (SCI) in the study area. The study also includes topographic effects and amplification, topographic–soil structure interaction (TSSI), and topographic–structure–soil–structure interaction (TSSSI).

2. Seismic Wave Modification Mechanisms and Site Effects

The release of energy and the resulting seismic wavefield are primarily determined by the magnitude and depth of the earthquake [2]. Seismic wave propagation is further influenced by interactions with the geological and environmental composition, local site conditions, and epicentral distance, all of which significantly affect wave behavior [see Figure 1]. Seismic waves propagating through heterogeneous media undergo reflection, refraction, diffraction, scattering, and mode conversion, which modify their characteristics. These effects are more significant at material boundaries and discontinuities such as faults, fractures, sedimentary layers, and topographic variations [25,26,27]. At these interfaces, incident energy is partially reflected and transmitted. The transmitted energy refracts and may undergo mode conversion between P and S waves, depending on the impedance contrast and angle of incidence. Additionally, edges and terminations cause diffraction, leading to the spreading of waves around obstacles. These wave–environment interactions can significantly alter the direction, intensity, and duration of seismic waves, with the effects being strongly influenced by the physical and mechanical properties of the subsurface [25,27]. Material heterogeneity also causes dispersion and scattering, further modifying wave amplitude, phase, and apparent direction [25,26,27]. Wave dynamics are further influenced by secondary processes such as attenuation, site effects, and amplification [15,28,29]. Attenuation is the reduction in seismic wave energy due to absorption, dispersion, and geometric spreading during propagation. Sedimentary basins and topographic features such as ridges and slopes can trap or amplify seismic energy, prolonging shaking and influencing slope stability [11,15,29]. In contrast, fault zone discontinuities and intersecting structural planes tend to disperse seismic energy, creating complex wave fields [25,26,27]. Topographic effects on slopes can amplify seismic acceleration when excitation frequencies align with local site resonance. This amplification increases dynamic stresses in the slope, potentially causing cracking and reducing stability during an earthquake [9,10].

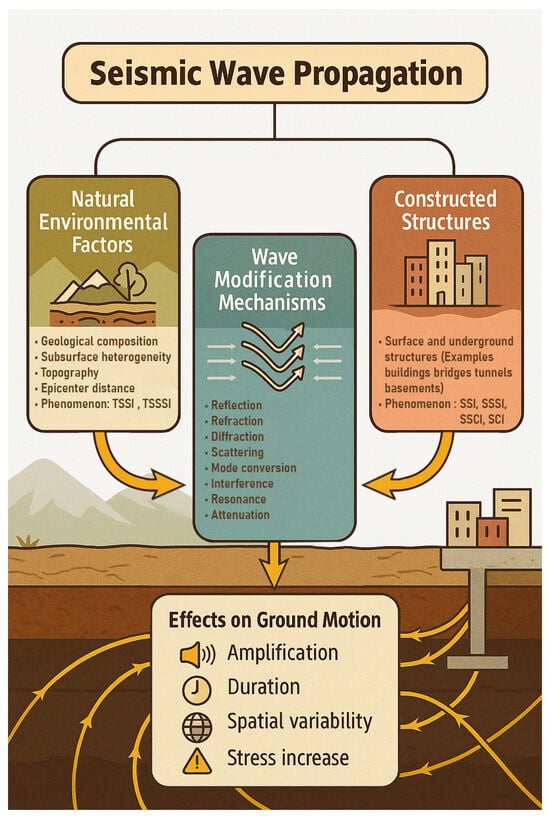
Figure 1. Seismic wave propagation and ground-motion modification.

Site effects further modify ground motion through the interaction of seismic waves with local soils and stratigraphy [30]. Seismic wave propagation and attenuation vary depending on soil stiffness, density, and water content. Higher water content can increase energy dissipation, while lower stiffness and density decrease wave speed [7,16,26]. Soft soils amplify motion at low frequencies, whereas stiffer soils and rocks transmit seismic energy with less distortion [19,23]. Resonance occurs when the natural frequency of soil layers coincides with the dominant frequency of incoming seismic waves, causing strong amplification and prolonged shaking [19,22,31]. Scattering within fissures and heterogeneous strata redistributes seismic energy, generating irregular ground motion patterns that complicate predictions [25,32]. In addition to these geological factors, man-made structures can also influence seismic wave propagation. Depending on the geometry and material properties of these structures, they can amplify, scatter, or focus seismic energy, thus altering the local seismic response [13,15]. The interaction between underground structures and surrounding soils can further redistribute seismic energy and modify the overall motion field [7,12,13]. Resonance effects are particularly pronounced for flexible high-rise buildings on soft soils when the structural period is close to the dominant site or basin period, leading to amplified displacement and drift, especially with sustained long-period energy in the input motion [3,19,20]. Major large earthquakes are typically dominated by low-frequency energy, while high peak ground acceleration (PGA) events increase high-frequency components [33], intensifying dynamic stresses in slopes, foundations, and structural systems [19,23,28,34].

Strong shaking can cause nonlinear behavior in soils, altering the amplitude and frequency content of ground motion through mechanisms such as stiffness degradation and increased damping [24,35]. These phenomena combine to create complex wave patterns that have a significant impact on seismic response, making it essential to consider them in hazard assessments, structural design, and mitigation strategies. The resulting wave fields can notably alter ground motion. Therefore, understanding these interactions is fundamental for accurately assessing the effects of earthquakes on structures and for developing effective seismic hazard assessments, earthquake-resistant designs, and mitigation plans in seismically active regions.

3. Interconnected Seismic Interaction Mechanisms

The seismic responses can only be precisely assessed when the coupled interactions of seismic waves, soil, and structural systems are fully considered. This comprehensive approach requires the integration of multiple scales, from single-building SSI to city-scale SCI, with intermediate levels like SSSI and SSCI. A consistent scale language is used in which multi-scale SSI extends from single-building SSI to city-scale SCI, including SSSI and SSCI [see Figure 2]. Cross-scale coupling denotes transfer of effects upward and downward across these scales. Hierarchical interaction describes sequential solution strategies that pass state variables across scales. Multi-scale SSI serves as the umbrella term and cross-scale coupling and hierarchical schemes are mentioned only as needed for the methodology. Soil–structure interaction (SSI) is a significant phenomenon linked to the transfer of seismic forces between soil and structure [36,37]. Structure–soil–structure interaction (SSSI), soil–structure cluster interaction (SSCI), site–city interaction (SCI) are the sophisticated frameworks that serve as specialized extensions of the broader topic of SSI [38,39,40] [Table 1]. Topographic soil–structure interaction (TSSI) and topographic–structure–soil–structure interaction (TSSSI) integrates topographic effects with SSI and its extensions [41,42]. These terms provide a framework for analyzing the interplay between topography, soil, and structural systems. An in-depth understanding of SSI and its extensions is required to represent the complex dynamics in seismic response analysis. Detailed analyses and assessments of seismic behavior in a specific region require the understanding of all these terminologies. Individually or collectively, these phenomena can significantly influence the modification of seismic waves during propagation and the resulting structural dynamics, hence they must be included for valid analysis to simulate the realistic seismic condition and to determine the seismic behavior of the structure and its overall safety.

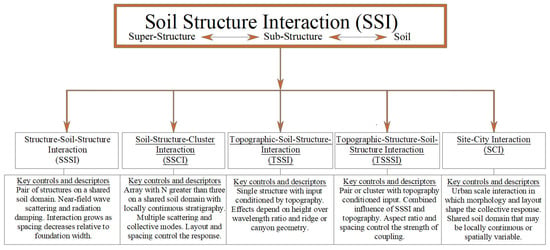
Figure 2. Multi-scale SSI framework and classification.

Table 1. Seismic Interaction Mechanisms and Primary Effects.

Interaction Mechanism	Definition/Scope	Key Influences	Typical Triggers	Dominant Seismic Effects
SSI (Soil–Structure Interaction)	Dynamic interaction between a structure and surrounding soil	Soil stiffness, damping, foundation type	Soft deposits; tall/flexible structure	Reflection, amplification, resonance, attenuation
SSSI (Structure–Soil–Structure Interaction)	Mutual interaction of adjacent structures via shared soil	Building spacing, soil type, structural frequency	Close spacing; similar frequencies	Scattering, focusing/shadowing, resonance
SSCI (Soil–Structure Cluster Interaction)	Collective response of multiple structures in clusters	Building density, arrangement, soil stratification	High density; repeated typologies	Wave scattering, energy redistribution, resonance
SCI (Site–City Interaction)	City-scale effects of built environment on seismic waves	Urban density, geometry, underground infrastructure	Dense cores; soil-building frequency match	Reflection, amplification, prolonged shaking
TSSI (Topographic–Soil–Structure Interaction)	Influence of terrain (ridges, slopes, valleys) on SSI	Relief height, slope angle, H/λ ratio	Steep slopes, ridges, canyons, oblique SV	Amplification at crests, shadowing on lee slopes, resonance
TSSSI (Topographic–Structure–Soil–Structure Interaction)	Combined effect of topography, soil, and multiple structures	Terrain geometry, soil conditions, clustered buildings	Dense hillsides; oblique incidence	Wave focusing, resonance, attenuation

4. Criteria for Considering Soil–Structure Interaction: Site Classification and Soil-Foundation Flexibility Effects

The soil–foundation flexibility effect is caused by the natural deformability of both the soil and the foundation, which allows for displacement and rotation of the foundation [43]. This flexibility modifies the dynamic properties of the soil–structure system and introduces radiation damping, which may reduce base shear under certain conditions but can also increase displacement and drift demands, depending on the frequency content of the ground motion [36]. The effects of soil–structure interaction (SSI) is typically negligible for very stiff foundations on hard rock, where the system response is comparable to that of a fixed-base condition [44]. However, because soft soils are more deformable, they can substantially affect structural response, resulting in pronounced SSI effects [36]. Soil stiffness is usually quantified through shear-wave velocity (Vs) [26,45], with the small-strain shear modulus defined as

$$G=\rho V{s}^2$$

(1)

where $\rho$ is the bulk density of the soil, which generally is in the range of 1.6–2.0 Mg/m³ (1600–2000 kg/m³). Since the density varies only within a narrow band, Vs is the primary controlling parameter for soil stiffness.

International seismic design codes classify sites primarily based on Vs,30 (the average shear-wave velocity in the upper 30 m). For example, ASCE/SEI 7-22 specifies classes A–F by Vs,30 with A ≳ 1500 m/s (>5000 ft/s) and class F of problematic soils requiring site-specific evaluation [46]. Eurocode 8 (EN 1998-1) classifies sites by Vs,30 into ground types A–E and designates special soils S1 and S2 that require specific studies [47]. Highway-bridge code (JRA, Specifications for Highway Bridges) of Japan distinguishes ground categories I–III, and prescribes type-specific design spectra and coefficients. The scheme is category-based rather than a Vs,30 table, and it requires evaluation of deep alluvial deposits and liquefaction where applicable [48]. Building code of China, GB 50011 [49] assigns site Classes I–IV (Class I subdivided into I₀ and I₁ using equivalent shear wave velocity (Vse) to a specified depth together with cover layer thickness. Recent research work establishes Vs,30 based mappings that relates these categories to internationally used Vs,30 system [50]. Table 2 compares site classifications across major international codes.

Table 2. Comparison of site classifications across different international codes.

Criterion	ASCE/SEI 7-16 (USA) A	IBC (USA) B	Eurocode 8 (Europe) C	China GB 50011-2010 D	Japan (AIJ/MLIT) E	India (IS 1893) F
Site Class	Site Classes A–F by Vs,30 (Table 20.3-1)	Same as ASCE 7	Ground types A–E by Vs,30, special S1 & S2	Site Classes I–IV (Class I subdivided into I0 and I1) Using Vse and cover thickness	Ground Type I–III, Category based	Site Types I–III (rock/hard, medium, soft) by SPT N
Primary velocity/ Index parameter	Vs,30 primary; alternatives via profiles and testing where permitted	Same as ASCE	Vs,30 primary; N-SPT and Cu alternatives allowed by Table 3.1 notes	Equivalent shear-wave velocity Vse to a specified depth with overburden thickness	Category assignment by soil profile and ground period (TG); No Vs,30 table. Types I–III with type-specific spectra	SPT-N based types with Vs correlations used in practice
Problematic/special soils that trigger special studies	Site Class F (e.g., liquefiable soils, sensitive clays, peat, very high PI clays, collapsible soils) requires site-specific procedures	Same triggers as ASCE	S1 and S2 require special studies	Soft-soil or deep alluvial sites and liquefiable deposits are flagged for special evaluation and mitigation under GB 50011	Liquefiable soils, lateral-spreading or large-deformation sites, and deep alluvium (Type III) require site-specific evaluation	Soft or deep deposits, liquefiable or filled ground, and important structures require site-specific evaluation
Site-Specific Analysis Required	Class F always, Sometimes C–E per Ch. 21	Same as ASCE via reference	Required for S1/S2; otherwise as justified by local conditions	Required where code thresholds indicate (e.g., soft/deep deposits, liquefaction)	Required for flagged soils (deep alluvium, liquefiable)	Required for important facilities; recommended for problematic soils
Connection to Seismic Design	Site class selects Fa and Fv; informs SSI checks and design spectra	IBC refers to ASCE spectra and coefficient	Ground type sets elastic design spectrum; S1/S2 handled by special provisions	Site class affects group, spectra, drift, detailing	Type-specific design spectra and coefficients are prescribed	Soil type governs spectra and detailing
Notes	Vs,30 bands: A: >1500, B: 760–1500, C: 360–760, D: 180–360, E: <180; F: Special soils		Vs,30 bands: A: >800, B: 360–800, C: 180–360, D: < 180, E = 5–20 m C/D layer over much stiffer material Special: S1 &S2	Classes I–IV defined by Vse and thickness criteria	Category-based scheme; spectra differ for Types I–III	Site Types I–III broadly correspond to rock/hard, medium, soft soils

Standards cited A. ASCE/SEI 7-22; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2022. B. 2021 International Building Code (IBC). International Code Council: Country Club Hills, IL, USA, 2020. C. EN 1998-1:2004; Eurocode 8 Design of Structures for Earthquake Resistance—Part 1 General Rules, Seismic Actions and Rules for Buildings. CEN: Brussels, Belgium, 2004. D. GB 50011-2010 (2016 Edition); Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2016. E. Japan Road Association; Specifications for Highway Bridges, Part V: Seismic Design. Japan Road Association: Tokyo, Japan, 2017. F. IS 1893 (Part 1):2016; Criteria for Earthquake Resistant Design of Structures—Part 1 General Provisions and Buildings. Bureau of Indian Standards: New Delhi, India, 2016.

In practice, when Vs is near hard rock values around 1100 m/s and shear strains are about 10⁻⁶ to 10⁻⁵, SSI effects are often minor, and this should be used only as a screening guideline [51]. Site-specific investigations are mandatory for problematic soil categories in all major codes (e.g., ASCE Class F, Eurocode S1/S2, Chinese soft-soil categories under GB 50011, and Japan’s soft soil classifications) [46,47,48,49]. These site classes critically influence seismic design: stiffer soils typically result in higher accelerations and inertial demands, whereas softer soils tend to prolong shaking and amplify displacements and drifts.

5. Soil–Structure Interaction (SSI)

The soil–structure interaction (SSI) describes the mutual response between a structure and the supporting soil during dynamic events such as earthquakes. It is the process by which a structure, rather than acting independently, interacts with the surrounding soil when subjected to external loads [37,52]. This reflects the multifaceted relationship between soil and structure, wherein the response of soil affects the motion of the structure, and in turn, the structure influences the soil. Although the system is coupled, soil and structural motions are not identical. Kinematic interaction alters the foundation input relative to the free field, and inertial feedback from the superstructure changes the near-foundation soil through compliance, rocking, and radiation damping, so relative displacement can occur at the interface [36,37,52]. Figure 3 can be introduced to illustrate the interaction between the seismic waves and the structure as described. Seismic soil–structure interaction observes the direct influence of earthquake forces on the coupled soil–structure system, where resonance, damping, and natural frequency are significantly modified [36,37,52,53,54]. It represents the dynamic interaction between a structure and the surrounding soil during seismic events, as seismic waves propagate through the ground and affect the structural response, while the structure simultaneously alters the stress and motion within the soil. The interaction between the substructure, superstructure, and underlying soil determines the overall response of structures during an earthquake [37,52,53]. SSI analysis assesses the collective response of these components to a specified ground motion. For reinforced-concrete frames, SSI alters effective period, base shear, and drift demands, with implications for stability and sustainability [55,56].

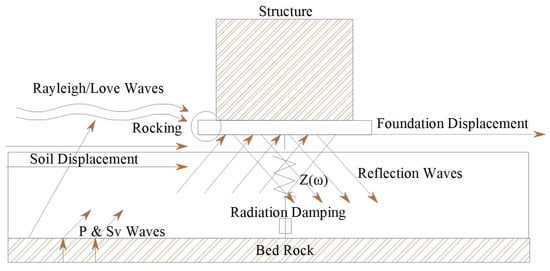
Figure 3. Soil structure interaction.

The seismic response of a structure primarily depends on the properties of the supporting soil, influencing the amplification or damping of earthquake vibrations [23,24]. SSI impacts structures in two main ways: it can alter propagating seismic waves, thereby changing the motion applied to a structure, and it can affect the structural response through re-distribution of forces and displacements depending on soil flexibility and damping [36,52,57]. Relative to free-field conditions, SSI can modify the dynamic response of the structure, affecting its natural frequency, damping characteristics, and the ground motion at the foundation level [36,52,58,59]. Softer soil may reduce structural stiffness and natural frequency, compared to the hard rock [37,52]. When ground motion amplitude increases as a result of soil characteristics and geological conditions, amplification occurs. Soft soils such as clay or loose sands, with low stiffness and high pore-water pressure, tend to amplify seismic waves, whereas hard soils like rock or dense sands can absorb and reduce amplitudes [16,19,23,60]. Foundation flexibility and soil properties are key parameters that govern the structural response to ground motion [37,52,53]. The energy dissipation, deformation, and force distribution of the system all depend on SSI. The primary mechanism through which SSI enhances structural damping is radiation damping, where energy is transferred from the structure into the surrounding soil and dissipated as seismic waves [26,36,52]. This effect is most noticeable in soft soils or flexible foundations [52,61,62], and it also further depends on factors such as soil composition, material characteristics, seismic input, and structural frequency [23,24,30,63,64]. In rigid-base structures, shear walls provide greater resistance to seismic forces [64,65], which generally limits frame damage to minor cracking. However, in flexible-base systems, deformation and rotation of the shear walls can induce larger frame distortions and more pronounced cracking, even though the overall force demand on the shear walls may be reduced compared with rigid bases [52,61,64,66].

Early investigations by Veletsos and Meek [61], Wolf [66], and Gazetas and Mylonakis [62] demonstrated that neglecting SSI can result in unsafe designs for critical infrastructure, including buildings and bridges. These findings are further substantiated by historical events, which clearly highlight the significant risks associated with neglecting SSI [19,67]. Observations from several past earthquakes have reinforced this conclusion. For example, in the 1995 Kobe (Hyogoken Nanbu) earthquake, the collapse of the 18-span Hanshin Expressway at Fukae was mainly caused by the inadequate shear capacity of the reinforced concrete piers under a strong near-fault velocity pulse [67,68]. Soil–foundation–structure interaction played a secondary role in the failure [69]. Additionally, liquefaction-induced ground deformation and lateral spreading were the primary contributors to the damage observed at waterfront facilities on reclaimed ground. Similarly, during the 1985 Mexico City earthquake, extensive structural damage in soft lacustrine clays was linked to wave amplification associated with SSI [19.69]. During the 1989 Loma Prieta earthquake, liquefaction-induced ground movement and lateral spreading along waterfronts and artificial fills caused significant damage to bridge approaches and pile-supported waterfront facilities. SSI played a key role in transmitting these deformations through foundation systems [70].

The performance of structures during earthquakes can be significantly affected by the dynamic characteristics of soil, such as stiffness, damping, and shear-wave velocity [64,69]. These properties influence the transmission of seismic forces and vibrations to structures, thereby affecting their behavior. SSI can significantly modify the dynamic response of a structure, at times amplifying stresses and deformations and emphasizing the need to consider it in seismic design [52,65]. Studies show that analyses incorporating SSI often closely match observed behavior in earthquakes [54,67].

5.1. Effects of SSI on Seismic Behavior and Structural Performance

Soil–structure interaction (SSI) significantly influences seismic behavior and structural performance. Therefore, identifying the conditions under which SSI critically impacts structural performance is fundamental to effective seismic design and assessment [36,37,52]. SSI generally increases the natural period of a structure and may enhance its effective damping [56,61,66,71]. It modifies the dynamic characteristics of a soil–foundation–structure system, often resulting in a longer fundamental period compared with the fixed-base assumption [52,61,64,66]. For estimating the modified natural period under SSI effects, the following formula is adopted, considering the influence of soil flexibility on structural dynamics [52,61,62].

$${\displaystyle \frac{\tilde{T}}{T}}=\sqrt{1+{\displaystyle \frac{k}{k_{h0}}}}$$

(2)

where k is the lateral stiffness of superstructure, kₕ₀ is the horizontal stiffness of the soil or foundation system, $\tilde{T}$ is the modified natural period of the structure considering SSI effect, and T is the natural period of the structure with a fixed-base assumption.

These parameters are interrelated because SSI effects may increase the natural period of the structure, which might not always lead to a lower spectral acceleration response and could potentially result in a hazardous structural response [52,61,64,66]. Stiffness degradation and damping changes can lengthen the period and shift the demand, often reducing high-frequency accelerations while increasing drift, rocking, and rotation [52,63,64,66,71,72,73]. In liquefiable deposits, pore pressure buildup and cyclic mobility filter high-frequency base input but can increase residual settlement, tilt, and lateral spreading [74,75,76]. Taller buildings on soft soils may encounter resonance and amplified vibrations if their fundamental frequency matches the natural frequency of the underlying soil [64,77,78]. In these systems, SSI lengthens the fundamental period and increases effective damping through radiation into the half-space and nonlinear soil hysteresis [52,61,64,66]. These changes arise from foundation compliance (flexibility and rocking), energy dissipation into the half-space, and nonlinear hysteretic soil behavior, while kinematic filtering at the base modifies the transmitted motion [52,59,61,66]. The result is often lower base shear demand but larger inter-storey drift and residual displacement, with increased sensitivity to second-order P-delta effects [52,64,72,79]. In very soft deposits or with deep embedment, the expected base shear reduction may be limited or reversed at specific storeys [52,79]. Recent three-dimensional SSI studies show that models combining frequency dependent, impedance-based radiation damping with strain compatible nonlinear soil hysteresis reproduce observed responses more reliably than two mode Rayleigh damping models calibrated at limited frequencies [73,79,80]. Frequency appropriate impedance functions and strain compatible G(γ)-ξ(γ) relationships should be used in design, while ensuring drift amplification and P-delta stability is checked in tall buildings and critical structures [52,56,64,73]. SSI can also increase ductility demands [37] and may lead to permanent soil deformations or even soil failures [52,64,75,76,80]. Seismic forces transmitted to structures are modified by the dynamic interaction between soil and structure, which is frequency dependent, as seismic waves exhibit different responses at various frequencies [32,52,64]. The incident wave is a primary determinant of SSI effects. Surface waves commonly control near surface demands, S-waves dominate shear response, and P-waves rarely govern except at sharp impedance contrasts [32,81]. For ground motion within shallow depths (approximately 0.1 to 0.3 of the dominant wavelengths), surface waves typically control deformation demand [32]. Oblique SV input couples with transverse soil flexibility and induces racking and ovaling in various structural elements [64,76]. SH and Love waves can control along long, continuous underground structures, while P waves rarely control unless at stiff or strongly layered sites with sharp impedance contrasts or nearly vertical incidence [32,82]. Saturation increases Rayleigh participation by lowering shear-wave velocity, enhancing dispersion and near surface amplitudes [32]. Topography and shallow layering can focus surface wave energy, intensifying SSI effects at crests and soft caps [31,83]. Together with the incoming wave field, the natural frequencies of the soil structure system and the stiffness and damping characteristics of the soil govern the overall response [52,64]. High-frequency seismic waves are attenuated in soils with higher damping, while low-frequency waves may amplify in soft deposits due to resonance effects [23,32,64]. SSI effects are critical for tall and slender structures, as well as those where the P-delta effect is significant [52,64,84]. Taller buildings and stronger earthquakes tend to amplify SSI effects on structural responses, posing challenges to meeting performance standards in soft soil regions [52,85,86]. The interaction between soil and structure during earthquakes can also increase shear forces in the lowermost story, reducing structural stiffness [52,65,72] and increasing lateral displacement parameters, including inter-storey drift and roof displacements. For mid and high-rise structures on soft soils, SSI effects must be considered [52,64]. Farghaly and Ahmed [87] suggest that flexible foundations can mitigate adverse SSI impacts by allowing deformation, dissipating seismic energy, and reducing force transmission to upper stories. Performance based seismic design methodologies explicitly incorporating SSI will be crucial for enhancing structural resilience in soft soil regions [52,84]. The post-earthquake functionality, particularly on soft soils, is significantly affected by permanent soil deformation beneath combined piled raft foundations. Bagheri et al. [79] model these effects using a performance-based SSI framework that applies effective-stress cyclic soil models to capture residual strain and explicitly treats gap/slip at raft soil and pile soil interfaces. The analysis also includes raft rocking and potential uplift, along with neutral plane migration. Calibration uses site-specific shear-wave velocity and CPT data and is validated against centrifuge tests and three-dimensional simulations. Design checks cover residual settlement, rotation, drift, and combined axial–shear demands. Additionally, mitigation strategies such as added raft stiffness, local thickening, and targeted ground improvement are recommended. Furthermore, probabilistic fragility analysis demonstrates that the moment frame shear wall (MFSW) system shows 1.4–1.6 times higher peak ground acceleration (PGA) capacity across different damage states than the conventional moment frame (MF) system [79].

5.2. Components of SSI: Kinematic and Inertial Interaction

The effects of SSI can be primarily classified into three categories: kinematic interaction, inertial interaction, and soil–foundation flexibility effect [52,61,62,66]. Several studies show that kinematic and inertial interaction factors cause the ground motion at a point to vary from free-field motion [52,59,61,66,88]. Kinematic interaction is caused due to the difference in stiffness values between the soil and the structure, whereas the inertia force of the structure results in inertia interaction [61,66,89]. When the foundation cannot exactly replicate the free-field ground motion, discrepancies arise between the free-field motion and the foundation input motion (FIM). This difference is termed kinematic interaction. It occurs primarily due to wave scattering, diffraction, and filtering effects introduced by the embedment and geometry of the foundation, and the stiffness variations between the foundation system and the surrounding soil [52,59,66,88]. Likewise, the inertia forces generated by the mass of the structure and its foundation are transmitted to the supporting soil during the earthquake. These forces induce displacements and rotations at the soil foundation interface, with their magnitude governed by the stiffness ratio of soil and structure. As the vibrating structural mass generates stress waves within the soil, the resulting soil deformation modifies both the foundation motion and the structural response. This feedback mechanism, in which structural inertia influences the supporting soil and alters the overall system behavior, is known as inertial interaction [61,66,89]. Softer soil together with flexible foundation also modifies the seismic response, as the deformable soil alters the effective boundary conditions at the base of the structure, leading to longer natural periods with increased damping [52,64,66,90]. These effects of flexibility are particularly important in soft soils, where the structural performance can be significantly impacted by foundation compliance [52]. Since kinematic interaction enhances radiation damping and extends the vibration period, it becomes particularly significant during low-intensity ground shaking [59,66,88]. However, when there is severe ground shaking, the radiation damping significantly decreases due to the deterioration of soil modulus in the near field. This leads to a significant increase in inertial interaction and large displacement close to the ground surface [64,66,73,91]. Therefore, kinematic interaction is prominent during lower-level shaking, while inertial interaction is prominent during strong shaking [59,64,88,89].

5.3. Linking Soil-Structure Interaction (SSI) to Design-Level Engineering Demand Parameters (EDPs)

Soil–structure interaction (SSI) significantly influences key engineering demand parameters (EDPs) such as base shear, inter-storey drift ratio, and residual drift [52,64,90]. SSI is a combination of kinematic and inertial interactions where kinematic interaction can modify the foundation input motion, which differs from the free-field motion by de-amplifying high frequency content [52,59,66,88]. Similarly, inertial interaction, represented by frequency dependent impedances, modifies the stiffness and damping of the system. This results in period elongation (referred to as the effective period) and increased damping (referred to as effective damping), with radiation and soil hysteretic damping contributing to the increase in effective damping [61,64,66,90].

These changes in effective period and effective damping can directly affect the design-level EDPs. While base shear typically decreases with period elongation and increased damping, amplification of foundation input motion in certain configurations (such as deep basins or asymmetric structures) may counteract this reduction [29,52,59,64]. Similarly, while the reduction in base shear might suggest a decrease in inter-storey drift ratio, the larger spectral displacements due to period elongation, along with foundation rocking, can lead to unchanged or even increased inter-storey drift ratio, as demonstrated in shaking table tests [64,92]. Bridge column shake table tests show that foundation rocking can result in large drift ratios even when intended to limit damage [93]. Regarding residual drift, though SSI may reduce forces, it can increase permanent foundation deformations such as settlement and gapping, particularly in soft or liquefiable soils [76,94,95]. These deformations may result in significant residual displacements after an earthquake, emphasizing the need for site-specific foundation input motion and nonlinear SSI analyses to assess residual drift and ensure compliance with drift limits [52,59,64].

5.4. Experimental and Numerical Studies on SSI

SSI significantly influences the seismic response of a wide range of systems, as demonstrated by numerous numerical analyses, experimental studies, and field evidence [37,64]. Farghaly and Ahmed [87] observed that incorporating SSI in numerical models can occasionally lead to conservative design outcomes, as they found that SSI tends to overestimate top-floor displacements. Huseynli et al. [96] found that SSI can improve seismic performance by increasing the median capacity of substandard RC frames, indicating that its effects are context dependent rather than uniformly negative. However, more recent studies emphasize that SSI should not be neglected, as it exerts a substantial influence on structural response [37,97]. Different experimental work also shows that SSI changes system frequencies, redistributes modal energy, and alters demands relative to the free field [98]. EuroMASS conducted full-scale tests at the Piana di Toppo site in northeast Italy, using a semi-dense array to record the structure, foundation, and surrounding soil. The tests enabled analysis of wave propagation from a single-degree-of-freedom oscillator and the corresponding soil response. Key findings included outward wave radiation, soil-structure feedback, frequency-dependent attenuation, and transfer functions for estimating foundation impedances and validating SSI models [99]. Multi-array shaking table systems are advanced testing tools designed to reproduce complex seismic input patterns, including uniform and non-uniform excitations, and simulate traveling wave effects. Wang et al. [100] demonstrated that these systems effectively minimize boundary effects and prevent resonance, which is crucial for testing large underground structures. This improves the accuracy of simulating real seismic responses, providing reliable data for analyzing the seismic behavior of complex underground facilities. Shaking table tests on tunnel soil piled-structure models reveal direction-dependent proximity effects. Crown motions tend to amplify, inverted motions reduce, and the lining may ovalize, indicating that underground SSI modifies local demands compared to free-field conditions [101]. These results emphasize the need to consider SSI in seismic design, particularly for critical structures. Advanced SSI studies and tests on nuclear-type shield buildings show that fixed-base assumptions are often unreliable for such structures. Incorporating foundation compliance and soil coupling results in frequency reductions and shifts in mode participation [102]. In large one caisson tests, soil caisson dynamic interactions were isolated, showing frequency dependent trade-offs, where horizontal acceleration decreases as induced rotation increases with stronger seismic input [103]. These studies collectively show that SSI increases effective periods, redistributes modal energy, and changes spectral peaks and shaking duration. They also highlight the need for precise modeling of radiation damping, traveling-wave input, and soil nonlinearity to ensure reliable seismic analysis and design. They also highlight the necessity of precise modeling of radiation damping, traveling-wave input, and soil nonlinearity to ensure reliable seismic analysis and design [73,99,102,103].

5.5. Soil-Structure Interaction (SSI) Analysis Techniques and Their Importance

Soil–structure interaction (SSI) analysis involves different techniques, from simple models to advanced methods, each essential for accurately assessing the interaction between soil and structures. While simpler methods can provide initial estimates, advanced modeling and realistic boundary conditions are required for more detailed and accurate analyses. Two broad approaches are used. Direct methods model soil and structure in a single coupled domain (e.g., finite element (FEM), boundary element (BEM), and calibrated macro elements), allowing nonlinear soil and structural response [37,66,90]. Indirect methods consider soil and structure as subsystems coupled through impedance functions [52,66,90]. In the substructure/superposition approach, free-field motion is computed, translated to foundation input through transfer functions, and coupled with springs and dashpots for stiffness and damping. This method can reduce computational cost but can oversimplify key effects if not validated [52,104]. In linear SSI, the system may be formulated as a single combined linear model or as two linear subsystems with compatible boundaries [105]. However, nonlinear SSI incorporates plasticity, gapping or slip, liquefaction, and strain-dependent stiffness and damping, with direct nonlinear models applying global boundaries and allowing nonlinearity in both soil and structure, while substructure nonlinear models assign nonlinear properties to components and then couple them [106,107]. Neglecting these effects leads to biased predictions and significantly underestimates the potential risks.

Simplified tools such as Winkler springs, p-y curves, and elastic-continuum idealizations provide first estimates of stresses, rotations, and lateral deflections. In Winkler idealizations, the modulus of subgrade reaction (ks) is the ratio of ground pressure (p) to ground deformation (δ). This can be useful for the screening, but it does not capture full spatial variability or strong nonlinearity [52,64,90]. Finite element method (FEM) can address heterogeneous, nonlinear media with implicit or explicit dynamics [106,108]. Series solutions, such as Fourier methods, remain valuable for solving selected canonical SSI problems [109]. The macro-elements method simplifies essential SSI behavior into reduced-order models, enabling rapid studies when properly calibrated. Computational fluid dynamics with fluid–structure interaction (CFD–FSI) is used when fluid effects dominate, such as groundwater around underground structures, by solving both the fluid and structural fields together, including the soil as required [110].

Recent advancements in hybrid and probabilistic SSI techniques have enhanced the modeling of radiation and layered half-space representation, while maintaining efficiency in SSSI applications. In Hybrid FEM-BEM, the enhancement of radiation modeling and layered half-space representation ensures efficiency in SSSI applications, supported by implementable formulations and validation benchmarks [111,112,113,114]. Probabilistic SSI considers spatial soil variability, incoherent ground motion, and elasto-plastic soil behavior, transferring these factors to engineering demand parameters using stochastic FEM and related methods. Field identification and model updating further refine the calibration [115,116,117,118]. Together, these developments reduce bias in model form and boundary representation, making hybrid-stochastic workflows practical for complex sites and clusters [111,112,113,114,115,116,117,118,119].

With advances in hybrid and probabilistic SSI, recent analytical developments have refined foundation impedance modeling, enhancing the understanding of foundation behavior across various conditions. These advancements provide improved understanding of foundation performance in applications such as helical pipe piles, torsional vibration in layered soils, and pile-bucket foundations. Key innovations include

• Helical pipe piles: Recent work extends the impedance transfer method to helical pipe piles, introducing helix-modified vertical, lateral, and torsional impedances. The closed form, frequency dependent stiffness and damping capture helix geometry (pitch and diameter), embedment, and layering, providing calibration targets for macro-elements and performance-based foundation models [120].
• Torsional vibration in layered saturated soils: For pipe piles in layered saturated soils, additional mass formulations yield torsional impedance and rotation torque frequency functions that include saturation-dependent added mass and radiation damping. These relationships enable layer-wise impedance assembly and improve 3D PSSI calibration for rotation-controlled checks [121].
• Pile-bucket foundations: For pile-bucket foundations in saturated soils, analytical solutions for lateral and rocking behavior provide frequency dependent impedances and cross coupling terms, including seepage induced damping. The ratio of bucket diameter to embedment controls low frequency stiffness, while saturation enhances effective damping, supporting design screening and macro-element calibration for vertical force, moment, and rotational displacement behavior [122].

Advancements in computational tools, such as the machine learning-based approach presented by Asgarkhani Et Al. [123], are pivotal in enhancing the accuracy of SSI analysis, enabling more reliable seismic response predictions and improving structural resilience in complex environments.

5.6. Soil–Structure Interfaces: Models and Simulation Challenges

Interfaces between soil and structure control the stability and functionality of the soil–foundation–structure system. These interfaces include joints and contact surfaces, shaped by mechanical and physical interaction, and their behavior must be characterized for both safe, resilient design and precise simulation. The mechanical behavior involves load transfer, stress redistribution, stick and slip, gapping, dilation, and possible crushing, all dependent on normal stress, loading history, and material properties [104,124]. A range of constitutive models is used for soil–structure interfaces, including linear elastic, viscoelastic, elastoplastic models such as Mohr–Coulomb or Drucker–Prager with tension cut-off, hypoplastic, and time-dependent (creep or viscoplastic) formulations. Interface laws primarily employ Coulomb friction with cohesion, dilation rules, and cyclic degradation, with parameters calibrated from direct shear and cyclic tests or back analysis of pile and foundation experiments [52,124]. Modeling remains challenging due to nonlinearity, heterogeneity, boundary condition sensitivity, and the need for calibration [52,105]. In saturated soils, rate effects and pore pressure evolution add complexity to the modeling process [125]. Available methods include zero-thickness interface elements for explicit slip and separation, thin-layer or Winkler-type elements for screening studies, calibrated thin continuum layers, and contact formulations using penalty or Lagrange methods [126]. The selected method should align with the specific characteristics of the problem and the available data, balancing accuracy with computational efficiency [124,126,127].

6. Extensions of Soil Structure Interaction: From Structures to Clusters and Cities

While soil–structure Interaction (SSI) is adequate for assessing the seismic response of isolated structures, a broader analysis that includes nearby structures, varying soil conditions, and topographical variations introduces significant challenges. A comprehensive analytical framework for these complex scenarios should integrate SSI, structure–soil–structure interaction (SSSI), soil–structure–cluster interaction (SSCI), topographic–soil–structure interaction (TSSI), and topographic–structure–soil–structure interaction (TSSSI), considering their combined effects on seismic performance. As the complexity of the system increases, it is important to evaluate the interactions between adjacent structures, topography, and soil conditions and how these factors influence the seismic response of each other. SSI describes the interaction between a single structure and its foundation soil influencing its seismic response [52,64]. The dynamic interaction between adjacent structures through the underlying soil is known as structure–soil–structure interaction (SSSI) [128], where the motion of one structure alters soil stresses, affecting nearby buildings and changing their natural periods and seismic responses [129,130]. SSCI focuses on the collective dynamics of structures grouped in clusters [130,131], while SCI extends this analysis to the city level, incorporating the effects of site features and urban infrastructure on wave propagation [15,132]. Topography also significantly influences seismic behavior, with the interaction between terrain features, soils, and structures addressed by TSSI [133]. TSSSI considers the combined effects of terrain, soil conditions, and adjacent buildings [41,134]. In densely built areas or regions with significant topographic variation, extended SSI mechanisms, including TSSI and TSSSI, can significantly alter ground motion, structural response, and seismic resilience. These interactions are particularly important in tall urban structures, where multiple building systems, soil conditions, and topographic features coexist [135]. The dynamic interactions between these systems can significantly influence ground motion and structural behavior, emphasizing the need for a comprehensive framework that incorporates all types of interactions. The primary parameters for such a framework include soil properties (e.g., stiffness, damping, nonlinearity), with soil type being especially critical for many of these factors, structural characteristics (e.g., mass, damping, stiffness matrices), interface properties (e.g., friction coefficients, cohesion), and topographic features (e.g., slope angles, layering effects) [52,64]. Historically, these interactions were often overlooked in favor of single-structure analysis. However, recent research has shown that such analysis is insufficient, as the seismic response of multiple interacting structures differs significantly from that of an isolated system [15,136]. Understanding these mechanisms is essential for accurate seismic assessment, developing reliable surface models, and improving design practices in urban regions.

6.1. Structure Soil Structure Interaction (SSSI)

Structure–soil–structure interaction (SSSI) is the dynamic interaction between ad-jacent structures, mediated by the shared soil medium and induced by dynamic loads such as earthquakes [38,128]. It describes nearby structures being dynamically coupled through the underlying soil, significantly impacting their seismic responses. when structures are in close proximity, Seismic waves and vibrations generated by one structure can propagate through the soil and affect the dynamic responses of others [75,137]. Hence, the seismic response of structures in densely constructed areas depends not only on their own structural and foundation characteristics but is also significantly influenced by these shared-soil interactions [37,129,132]. See Figure 4 for a schematic of soil-mediated coupling and wave exchange between adjacent foundations. This phenomenon can modify ground motion, structural accelerations, displacements, and rotations, depending on variables such as foundation type, soil properties, inter-building spacing, and dynamic characteristics [137,138,139]. SSSI influences the response spectrum, leading to either amplification or attenuation [37,38]. When seismic waves approach at an inclined angle instead of vertically, the influence of structure–soil–structure interaction (SSSI) increases and spreads over longer distances between buildings [137,138,139,140]. As a result, SSSI can generate prominent variations in seismic demands, including inter-story drift ratios and base shear forces, particularly where building proximity, height, stiffness contrast, and soil conditions are critical [39,76,141]. Numerous studies have examined the detailed dynamics between adjacent buildings, stressing the importance of including SSSI in seismic analysis and design. For example, heavier or stiffer structures may intensify seismic demands on adjacent lighter buildings, increasing their peak accelerations [136,139,142]. However, under certain soil and spacing conditions, interaction may redistribute seismic energy and reduce demands. These findings stress the importance of explicitly incorporating SSSI into seismic assessment and design. To mitigate adverse effects, it can be effective to integrate structural and geotechnical measures, such as retrofitting with shear walls and soil-cement columns [143,144]. Numerous experimental and analytical studies show sizable drift reductions from retrofits with dampers and rocking systems, often on the order of a few tens of percent, depending on device capacity and placement [145,146]. Several Japanese projects, including those in Tokyo, demonstrated that these treatments reduced inter-building or inter-story drift by approximately 25–50% [147,148]. These findings emphasize that SSSI must be regarded as an essential aspect of seismic design for urban environments rather than a secondary effect [38,130].

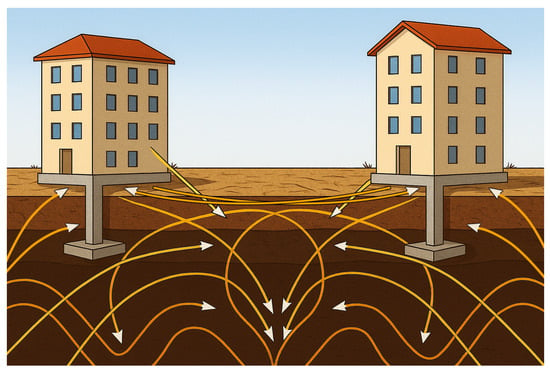
Figure 4. Conceptual illustration of Structure–soil–structure interaction.

6.1.1. Factors Influencing SSSI

The influence of SSSI depends on a combination of soil conditions, structural characteristics, proximity, and seismic excitation.

Soil Conditions

Soil properties, including stiffness, damping, and nonlinear behavior, strongly shape the extent of SSSI [37,38,64]. These parameters determine whether waves are amplified or attenuated, thereby controlling the seismic demands imposed on neighboring structures. [149]. Soft soils with low shear-wave velocities tend to magnify interaction effects, whereas stiffer deposits with velocities above about 760 m/s usually reduce them [150]. In general, soft layers filter out high-frequency motions but strengthen long-period waves, thereby increasing the interaction between neighboring structures [24,29,64]. As a result, variations in soil type and stratification produce different seismic demands, influencing base shear, drift, and acceleration. For instance, high-rise buildings founded on soft clay can exhibit inter-story drift increases of nearly 20% due to vibration mismatches, while soft deposits overlying rigid bedrock may reflect seismic waves and intensify SSSI within building clusters [39,65,129,130].

Nonlinear soil behavior further complicates the interaction process. Plastic deformation, stiffness degradation, and damping variation can change interaction effects, with inelastic soil response often increasing energy dissipation and reducing seismic demands [24,73]. Numerical studies confirm that nonlinear soil modeling is essential. Vicencio et al. [38] showed that accounting for nonlinearity mitigates exaggerated SSSI effects observed in linear models, while Alfach [151] demonstrated that mass ratio variations combined with nonlinear behavior can significantly alter structural accelerations and pile forces, with bending moments and shear forces varying by up to 290%. In liquefiable deposits, coupled hydro-mechanical SSSI using PM4Sand, validated by centrifuge tests, shows that the effects are influenced by spacing and mass ratio [75,76,94]. Rotations can increase even when settlements decrease, which indicates that elastic half-space assumptions may mislead for adjacent buildings on sand, as shown by Kassas et al. [75] and by combined centrifuge-numerical evaluations [76].

Structural Characteristics and Proximity

Structural characteristics such as height, mass, stiffness, and natural period strongly influence SSSI [38,137,152]. Resonance between adjacent buildings with similar dynamic properties can significantly amplify seismic demands, particularly inter-story drifts [128,137,152]. When properties differ, the interaction may either mitigate or intensify demands, depending on the frequency content of the ground motion [130,152]. Mass ratio is another critical factor, with heavier buildings often imposing greater demands on lighter neighbors, increasing their accelerations and base shear [76,152]. Stiffness ratio also affects vulnerability, with softer structures on flexible soils generally more susceptible to amplified interaction effects [38]. Proximity strongly modulates interaction intensity. When the spacing-to-width ratio (S/B) is below 0.5, seismic demands such as base shear and drift ratios increase significantly, whereas larger separations (S/B > 1) tend to resemble isolated SSI behavior [131,137,153]. SSSI occurs when the waves radiated by one foundation and the compliance of the shared soil field modify the input to an adjacent structure [130,154]. When the spacing-to-width ratio is small, coupling is most pronounced, particularly when neighboring structures have mismatched stiffness or periods, and this effect is further intensified in soft or liquefiable soils [94,130,154]. In shallow foundations, the more flexible building commonly develops larger drifts and rocking, while the presence of deep foundations introduces kinematic filtering along piles, shifting phases and redistributing base shear [75,137,140,155]. When the spacing increases to several times the width, the structures behave almost as if they were isolated. These behaviors are commonly observed in studies of neighboring and clustered structures and are consistent with findings on depth-dependent soil–foundation–structure interaction (SFSI) [94,130,153,154,155]. Interference can modulate demands, with numerical studies reporting reductions of ~40–55% at certain frequency–spacing combinations, while other configurations lead to amplification [137,140]. However, such reductions are not universal; in soft soils or when adjacent buildings have mismatched dynamics, the interaction can intensify demands [15]. In liquefiable soils, SSSI increases rotational demands (θ) while reducing settlement (w) [75,76]. Adjacent buildings with spacing greater than 0.5 times the foundation width (S > 0.5 W) may experience reduced settlement, with shallow layers (Dₗ/B = 1) causing outward rotations and deeper layers (Dₗ/B = 2) causing inward rotations [75]. When considering SSI and SSSI effects, structural pounding between nearby buildings can significantly increase seismic demand. The impact forces and accelerations caused by pounding amplify lateral forces on both structures, leading to higher foundation demands, increased shear forces in the soil, and potential residual displacements. To accurately model these effects, it is important to consider the gap spacing between buildings, nonlinear contact forces, foundation stiffness, and soil flexibility, all of which influence the seismic response [156,157,158].

Building configuration plays a decisive role in SSSI outcomes. Smaller, low-rise structures positioned beside or between taller neighbors often undergo amplified responses, as seismic energy transmitted through the soil tends to concentrate disproportionately on the shorter buildings [159]. According to Ngo et al. [160], SSSI response is significantly impacted by the height and mass ratios of nearby buildings, with smaller structures responding more strongly to seismic activity when situated close to taller ones. Padrón et al. [137] found that SSSI also has a significant effect on the seismic response of closely spaced pile foundation high-rise buildings under seismic excitation. Resonant amplification is most severe when the spacing between structures equals half the soil wavelength. When a short-period building is flanked by more flexible long-period neighbors at close spacing, inter-building coupling can amplify its response by on the order of 10–30%, depending on spacing-to-wavelength and period ratios [132,161].

Foundation Systems

Foundation systems in SSSI play an important role in determining the seismic response, as their configuration and characteristics directly influence the dynamic interactions between adjacent structures, soil, and surrounding infrastructure during seismic events [38,52,64]. The type and depth of the foundation significantly affect the SSSI, with mixed foundation depths altering the interaction spectrum by filtering high-frequency content and transmitting more low-frequency energy to adjacent structures. This modification occurs as piles filter high-frequency content and allow more low-frequency energy to pass through to neighboring structures [52,59,88]. In addition, shallow footings are more prone to drift and rocking when placed in close proximity [92,162]. In 3D pile–soil–structure interaction (PSSI), pile-group configuration and soil conditions jointly affect the seismic response of mid to high rise steel buildings [137,140,163]. Closer pile spacing and dense groups enhance pile-to-pile interaction and modify radiation damping, while soft or degrading soils increase periods and amplify drift and base rotation. Adjusting the layout or using mixed pile lengths can redistribute these demands [137,140,164]. Deep pile foundations can reduce amplification but often increase rotational demands, while shallow foundations are more susceptible to shaking and settlement [64,162,165,166]. Liquefiable soils can intensify interaction effects, leading to rotations, differential settlements, and even overturning moments in tall, slender structures. Research on liquefiable deposits indicates that SSSI often raises rotational demands while reducing net settlement [76,94]. The seismic resilience of pile groups in liquefiable soils can be assessed using 3D parallel finite element modeling, which couples soil–pile–structure interaction with effective stress soil models. This approach simulates shear-wave propagation, pore-pressure buildup, and lateral spreading effects [94,163]. In sandy soils with low shear modulus, uneven settlement of adjacent foundations is common, with amplified rotational vibrations dominating the response [167]. Basement structures and foundation geometry also significantly influence SSSI. Deep basements can stiffen nearby shallow footings, reducing rotations and permanent displacements, which limits damage [162]. Additionally, SSSI amplifies shear forces at pile heads, altering the distribution of loads within the foundation system [94,140,168]. When rotation or lateral rocking coupling dominates, the frequency-dependent foundation impedances outlined in Section 5.5 should be applied, including specialized forms for helical piles, torsional behavior in layered saturated soils, and bucket foundations, prior to evaluating interaction effects at close spacing [120,121,122].

6.2. Soil–Structure–Cluster Interaction (SSCI)

The dynamic interaction between clusters of structures and the underlying soil is known as soil–structure–cluster interaction (SSCI). It describes the interactive dynamics among multiple adjacent structures, whether on the surface, underground, or both, through a shared soil medium subjected to dynamic loads, particularly seismic forces [131,153]. SSCI is an extension of SSI that influences both ground motion and structural response during earthquakes by analyzing the dynamic interactions within structure clusters, between clusters, and between clusters and the underlying soil [130,153]. Seismic wave propagation and site response are altered by the collective presence of multiple structures, which are treated by SSCI as an interacting system at the cluster scale [see Figure 5]. Compared to soil–structure interaction (SSI) in isolated structures, SSCI induces more pronounced changes in seismic response due to wave scattering, energy redistribution, and displacement compatibility among multiple interacting structures [129,130,161]. While the primary focus of structure–soil–structure interaction (SSSI) investigations is on pairwise interactions, SSCI broadens this by modeling multi-body coupling [38,129]. SSCI considers building clusters as interacting systems that modify seismic wave propagation and site response. It complicates seismic wave behavior through interference, diffraction, and scattering, particularly when structures are closely spaced. Numerous studies have shown that this multi-level interaction of SSCI can alter natural frequencies, modify seismic wave propagation, and redistribute dynamic demands across structural foundations [130,153]. SSCI incorporates factors such as building density, soil stratification, cluster arrangement, and geometry to assess collective resonance, wave scattering, and energy redistribution effects [129,131]. The seismic response of clustered buildings is significantly influenced by kinematic and inertial interactions, resulting in dynamic behaviors that are different from those of isolated structures [90,129,130]. SSCI can amplify or de-amplify ground motion beneath individual structures depending on structural arrangement and soil conditions. Consequently, it can cause notable variations in displacements, accelerations, and velocities among clustered buildings during seismic events [15,153,169]. Overall, SSCI has a substantial impact on seismic ground motion and structural performance, influencing both site soil behavior and structural response during earthquakes. Understanding SSCI is increasingly important with the rise in dense building clusters from rapid urbanization and site expansion. In dense clusters, SSCI can modify the local wavefield through scattering, interference, and resonance. Central buildings commonly exhibit lower acceleration and displacement than isolation because surrounding mass and stiffness draw energy and shift system frequencies, while peripheral buildings often experience higher response due to weaker shielding and edge effects [131,170]. The outcome depends on density, spacing and arrangement [129,161]. Staggered layouts or mixed heights can break coherence and reduce resonance, whereas uniform closely spaced arrays can raise demands. The following subsections synthesize experimental and numerical results and quantify the influence of density, spacing, and arrangement [15,38,130,131,153,169].

Figure 5. Dense building clusters on variable terrain.

6.2.1. Experimental and Numerical Studies on SSCI

Recent studies on soil structure cluster interactions (SSCI) combine numerical simulations and experimental methods to investigate the seismic response of building clusters and characterize the feedback between soil and structures [131,153,169,171]. These studies, which include shaking table and centrifuge tests, show that SSCI influences ground motion propagation within clusters and alters seismic demand [153,172,173]. The findings reveal that the SSCI effect can either amplify or reduce seismic responses depending on the specific conditions of the cluster [130,131,169]. The shifts in spectral peaks, shaking duration, and response amplitudes vary, with effects influenced by the spacing ratio and period alignment between structures [131,153,169]. As cluster density increases, free-field vibrations are often reduced, and soil-induced motions may weaken, indicating density dependent SSCI effects [130,153]. Additionally, experimental studies demonstrate that closely spaced building clusters can alter ground motion characteristics, affect soil liquefaction behavior, and modify dynamic energy transfer between adjacent structures [76,94,153,172].

To investigate the effects of SSCI on seismic response, Wang et al. [153] conducted shaking table experiments involving multiple structures and verified their numerical models. They found that increasing the number of structures in a dense cluster amplifies the SSCI effect, resulting in significant reductions in the seismic response of individual structures, especially in the central building. Compared to the isolated case, the maximum reductions in roof acceleration and displacement of the central building reached approximately 23% and 18%, respectively. The experiments also showed that relative deformation of individual structures decreases with larger cluster sizes, with the middle storeys experiencing the largest deformation [131,153]. These results indicate that dynamic coupling through shared soil media can amplify displacements several times beyond those in isolated structures. The denser the layout of buildings, the more pronounced the SSCI effect, significantly impacting both soil and structural responses. In a separate parametric analysis, Du et al. [169] found that SSCI can either reduce or amplify seismic demand compared to isolated SSI, with changes in superstructure peak acceleration ranging from −40% to +27%. The response is primarily influenced by the structural spacing ratio and period alignment between neighboring buildings, with additional sensitivity to site stratigraphy, structural configuration, and the frequency content of the input motion. These findings suggest that the layout of clusters and their dynamic interactions play an important role in ground-motion modification and structural response in urban environments, emphasizing the importance of incorporating SSCI effects into performance evaluations.

SSCI also influences displacement patterns, where central buildings generally exhibit reduced displacements, while surrounding structures, particularly those on the outermost edges, experience increased displacements [38,131,171]. Different shaking table studies demonstrate that non-central buildings experience larger displacements along the excitation direction, with velocity demands potentially increasing or decreasing depending on the position of the building within the cluster and the characteristics of the input motion [38,153,171]. The SSCI effects are most pronounced in densely arranged clusters with buildings of similar dynamic properties, located on flexible soils and subjected to strong shaking. Increased seismic intensity enhances inertial coupling and activates soil nonlinearity, while clusters with similar height or stiffness are more susceptible to resonance and demand amplification [15,171]. Qi Ge et al. [131] observed that when the spacing between buildings exceeds 1.32 times the foundation size, cluster interactions diminish, and the responses become similar to those of isolated structures. Their study emphasized the significant influence of soil conditions, structure spacing, and the number of structures on seismic behavior, with interactions potentially increasing displacements by up to 770%. SSCI was found to reduce spectral amplification, shift fundamental frequencies, and alter wave propagation, showing the significance of these effects in seismic design for densely built, soft-soil urban environments. In another study, Qi Ge et al. [170] found that SSCI significantly reduces spectral amplification and fundamental resonance frequencies, with the acceleration response decreasing significantly when multiple structures interact. These effects were found to be more pronounced with smaller spacing and taller structures. Numerical simulations using a Davidenkov foundation model confirmed these findings, closely matching laboratory shaking table experiments, which validate the role of SSCI in altering ground motion. SSCI can also shift the effective frequencies of building arrays, modify wave propagation through interference and scattering, and redistribute seismic demands across foundations. Torsional effects are particularly significant in asymmetric arrangements, emphasizing the importance of considering these interactions in seismic design [130]. Y. Isbiliroglu et al. [130] found that torsional effects are more pronounced in asymmetric structural models, where uneven interaction forces in clusters containing asymmetrical structures result in significant torsional responses. These findings show the importance of incorporating SSCI effects into performance-based seismic design and urban resilience assessments, considering the substantial potential for structural interactions to amplify seismic responses in densely populated urban environments.

6.2.2. Factors Influencing SSCI

The impact of SSCI is determined by various factors such as soil conditions, the soil–structure stiffness ratio, urban density, the spatial distribution of structures, and the dynamic characteristics of the structures [38]. These factors are significant in determining the extent of interaction among structures within the cluster. The type and mechanical properties of the soil are key determinants of seismic wave propagation and soil–structure interactions, as the structures are embedded within the soil. Soft soils in particular tend to amplify seismic waves more than rigid soils, which may result in more significant displacements and higher levels of damage in building clusters with similar foundation conditions [23,131,174]. Furthermore, the seismic behavior of a structural cluster is significantly influenced by the soil–structure stiffness ratio. Lower ratios enhance energy absorption and minimize damage, whereas higher ratios increase inertial forces and amplify the seismic response [153]. During earthquakes, heterogeneous systems often perform better than homogeneous ones [38], with soil stiffness, foundation depth, and mass distribution among buildings all having a significant impact on cluster behavior. These factors often result in multiple structures exhibiting more dynamic seismic responses than isolated buildings, primarily due to the multifaceted interactions caused by the reflection and scattering of seismic waves at the foundations within the cluster [25,129].

During the earthquake, the performance of the structural clusters also varies significantly depending on the urban density. In high-density urban environments, SSCI may induce compounded interaction effects that cause damage patterns distinct from those typically observed in isolated structural systems [129,130,175]. Additionally, other key variables such as structure height, distribution patterns, number of structures, structural type (e.g., frame or high-rise buildings), layout configuration (periodic or aperiodic), inter-structure spacing, and the amplitude and type of seismic input also significantly affect SSCI responses [131,153,169]. The layout and spacing of buildings within a cluster affect the seismic response, with clustered structures frequently experiencing lower responses than single, isolated buildings [131,153]. The location, arrangement, and proximity of structures within a cluster significantly influence seismic wave propagation and their interaction with the built environment. These interactions can either increase or decrease the overall seismic response [129,153,169]. Gubo et al. [153] examined the effect of altering building arrangements from linear to cross configurations on structural behavior, finding that even slight layout adjustments significantly impact inter-story drift. These results indicate that structural arrangement is a key factor in seismic response, shaping the drift characteristics of individual buildings within a cluster.

SSCI can reduce the acceleration, displacement, and relative deformation of central buildings compared to isolated structures [129,153,169]. The cluster effect of SSCI refers to the differential seismic responses of structures within a cluster that result from their varying locations. It is also critical to determine which locations inside the cluster could be more critical and require more examination [131]. The location of buildings within a cluster impacts their seismic response; central structures benefit from the combined mass and stiffness of surrounding buildings, which reduces their seismic response, while peripheral structures experience larger displacements due to reduced stabilizing effects from neighboring buildings [153]. According to Qi Ge et al. [131], displacement tends to grow with distance from the center; buildings in the periphery may experience displacements up to 8.7 times larger than those of structures in the center. Influence coefficients for displacement due to SSCI can reach up to 770%, demonstrating the critical need for considering inter-structural interactions into account in seismic design and analysis. These variables contribute to increased spatial variability in ground motion and a reduction in high-frequency base excitations, primarily due to energy redistribution and enhanced damping.

6.2.3. Integrating SSCI into Seismic Design and Urban Planning

SSCI has a significant impact on ground motion characteristics and structural responses during earthquakes [130]. Hence, Integrating SSCI into seismic analysis and design is essential for predicting structural performance in densely built urban areas. The dynamic interactions between clustered buildings and the underlying soil can cause significant variations in the amplitude, duration, and frequency content of ground motion, as measured by observed beat oscillations and prolonged vibration periods [171,174]. It has been evidenced by various post-disaster investigations, including the 1985 Mexico City earthquake [19,22,176]. The impact of clustered structures may either increase or decrease seismic demands depending on soil type, spacing, and layout [130,131,153]. Incorporating SSCI into performance-based design frameworks can enhance the reliability of seismic risk mitigation strategies and emergency response planning by enabling more accurate predictions of damage distribution. The effect of building clusters on wave propagation, energy redistribution, and seismic demand needs to be further investigated by field observations, large shaking table testing, and sophisticated numerical modeling [100,172]. Integrating SSCI principles into construction standards and urban planning is essential for seismic risk reduction in rapidly urbanizing regions worldwide.

6.3. Site City Interaction (SCI)

The dynamic interaction between the underlying soil and the urban built environment during earthquakes is known as site–city Interaction (SCI). Building density, geometric distribution, foundation conditions, and soil characteristics can significantly alter free-field ground motion and structural response at the city scale [129,177,178]. SCI is also an extension of soil–structure Interaction (SSI) which strongly influences structural behavior and ground motion in the dense urban settings, particularly where heterogeneous soils are present [132,177]. The seismic response in urban areas is further complicated by tunnels, underground utilities, and transit systems, as shown schematically in Figure 6 [14,15,179]. The layout and density of buildings can modify seismic response, as structures act as barriers or waveguides that alter wave propagation and redistribute ground motion [129,154]. Tall buildings can reflect and refract seismic waves, affecting nearby infrastructure, while local site effects from soil conditions and underground structures may amplify or attenuate motion, producing spatial variability [15,180]. Seismic wave propagation in urban environments results from the combined influence of natural terrain, human-induced modifications, and continued urban development [177,178].

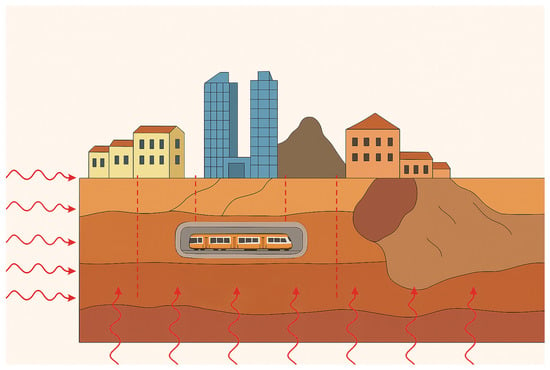
Figure 6. Schematic of site–city interaction with incident waves, layered soils, topography, urban structures, and a metro tunnel.

Studies have repeatedly shown that buildings clustered on soft soils can alter nearby ground motion and, in some cases, amplify the shaking through their own vibrations [177,181]. The 1985 Mexico City earthquake provides a well-documented example, in which soft lacustrine clays and closely spaced mid- to high-rise buildings induced resonance and prolonged shaking [19,22,176]. Records show that spectral accelerations were amplified for approximately two seconds, corresponding to the resonance between the soil and the buildings [19,22]. In contrast, numerical modeling of SCI in Nice, France, has shown that urban geometry and soft alluvial basins, such as the Paillon Valley, can further amplify seismic effects [182]. The contrast between observed data from Mexico and simulations in Nice shows that soil conditions, urban morphology, and seismic source characteristics must be incorporated into SCI risk assessments [132,177].

In cities with irregular layouts, SCI can affect seismic wave propagation in more complex ways [8,154]. The uneven distribution of buildings and varying soil conditions cause seismic waves to scatter in unpredictable patterns, resulting in areas where ground motion is either amplified or diminished. The varying distances between buildings, along with differences in building heights and foundation types, can result in complex interactions that affect both the intensity and duration of seismic shaking. To better quantify these effects, indices like Plan Coverage Ratio (φ), Normalized Spacing (η), and Frequency Shift Index (FSI) can be utilized [38,96]. These indices can provide a method for evaluating the impact of irregularities in urban layouts, supporting the assessment of seismic risks and contributing to the design of more resilient urban planning strategies.

Simulations strongly validate the complexity of SCI in irregular layouts, confirming its significant role in amplifying response levels, prolonging shaking, and redistributing peak motions. Two- and three-dimensional boundary element simulations confirm that SCI can amplify response levels, prolong shaking, shift frequencies, and redistribute peak motions [15,178]. These impacts are primarily driven by heterogeneous subsurface profiles and dense structural configurations, which intensify wave scattering, reflection, and resonance [15,129,154]. As urban areas expand horizontally with complex underground infrastructure and vertically with high-rise development, SCI becomes increasingly critical. Comprehensive seismic hazard assessments and careful design strategies are essential to account for SCI in order to ensure the resilience and safety of urban infrastructure [177,183].

6.3.1. Factors Influencing Site City Interaction

The study of site–city interaction (SCI) includes a broader spatial domain, involving multiple structures and more extensive subsurface conditions compared to traditional studies of SSI and SSSI [38,129,177]. Recent research has shown that SCI effects can emerge even with as few as five surrounding structures [154]. There are several key parameters that have been identified as primary contributors to SCI effects. Among them, the most influential variables include the type and heterogeneity of the ground on which structures are founded (i.e., local site conditions); the spatial configuration, distribution pattern, and proximity of adjacent structures; the dynamic characteristics of the structures themselves (such as height, mass, stiffness, and foundation type); urban density; the soil–structure eigenfrequency ratio; and the characteristics of incident seismic waves (including frequency content, amplitude, direction of propagation, and duration) [15,38,129,130,177]. Recent research has further identified other contributing parameters, such as topographic features, basin geometry, nonlinear soil behavior, and the combined effects of wave scattering and multiple reflections in densely built environments [15,129,133,154,161,177,182,184,185].

Urban Density

Soil urban density, often referred to as the plan coverage ratio and denoted by φ, is a key parameter in SCI. As building density increases, separations decrease, which enhances soil coupling and promotes multiple scattering [161]. At the scale of entire urban areas, these processes give rise to site–city interaction (SCI), where collective building layouts alter free-field ground motion and structural response [129,130,132,177]. Numerical simulations as well as field studies show that SCI effects, including modifications to ground motion and shifts in response spectra, become more pronounced with higher densities [130,132,177]. For a complete geometric characterization, urban density should be expressed with the floor area ratio and a normalized spacing, capturing both plan occupation and proximity [129,154,175,178,186].

$$\mathsf{\phi }={\displaystyle \frac{\sum {\mathrm{A}}_{\mathrm{f}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{t},\mathrm{i}}}{{\mathrm{A}}_{\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{a}\mathrm{n}}}}$$

(3)

$$FAR={\displaystyle \frac{\sum {\mathrm{A}}_{\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{o}\mathrm{r},\mathrm{i}}}{{\mathrm{A}}_{\mathrm{u}\mathrm{r}\mathrm{b}\mathrm{a}\mathrm{n}}}}$$

(4)

$$\mathsf{\eta }={\displaystyle \frac{\mathrm{s}}{\mathrm{B}}}$$

(5)

Here, A_footprint,i denotes the ground footprint area of building i, A_floor,i is the total floor area of building i, and A_urban is the mapped urban ground area. The parameter s represents the mean center-to-center spacing between adjacent buildings, while B is a characteristic building width. The ratios φ (plan coverage ratio), FAR (floor area ratio), and η (normalized spacing) are all dimensionless.

Higher plan density and tighter spacing strengthen building–wave coupling, which can cause SCI to amplify or de-amplify response spectra and shift peak frequencies.

Structural Distribution Pattern

The effects of SCI are greatly influenced by the spatial arrangement of structures. Factors such as variations in building height, layout regularity, spacing between buildings, alignment with seismic waves, and the presence of city-edge conditions contribute to changes in seismic wave scattering, resonance, and amplification patterns [15,129,175,178]. Due to their significant impact on localized seismic responses, these distribution-related parameters must be carefully considered when evaluating the effects of SCI [15,175]. Urban regions can be classified into two categories: in periodic cities, structures are uniform and spaced at regular intervals, while in non-periodic cities, the structures and scattering patterns are more diverse [175,178,187]. Although studying the seismic response of an ideal periodic city provides a useful foundation for examining more complex distributions, most real cities are non-periodic and exhibit irregular spacing and heterogeneous building heights [175,177,187]. Research shows that such non-periodic configurations can increase localized seismic responses by up to 50%, particularly near city edges, due to chaotic wave scattering, disrupted energy dissipation, and the absence of coherent site-city resonance [15,188]. Bard et al. [177] showed that non-periodic urban layouts result in spatially variable seismic responses through two-dimensional experiments and numerical simulations of irregularly spaced, non-uniform blocks on soft soil. They found that random wave scattering and disrupted resonance result in local amplifications that are up to 35% higher than those in periodic layouts. All of these results show that SCI is significantly impacted by structural type, spacing, and orientation, indicating that building distribution patterns and urban layout are important factors in seismic analysis and design [15,129,175].

Soil–Structure Eigenfrequency Ratio

The soil–structure eigenfrequency ratio is defined as the ratio between the fundamental frequency of the soil layer and that of the structure. When the frequency ratio is nearly unity, or when the natural frequency of the structure almost matches that of the soil deposit, SCI effects typically occur at the maximum [161,177,189]. Such resonance conditions result in strong soil–structure coupling, which significantly amplifies ground and structural responses [175,177]. Therefore, the soil–structure eigenfrequency ratio plays a critical role in determining seismic response. Numerous studies have demonstrated that due to SCI effects, the frequency of a structure in a building cluster is lower than that of an isolated structure [189,190]. The inertial effect of superstructures can also alter the fundamental frequency of the ground. Urban buildings have a broad range of eigenfrequencies due to differences in mass, height, and structural features, while ground conditions are typically complex and heterogeneous. The primary challenge in analyzing SCI is the precise determination of representative eigenfrequencies for both soil and structures. Various methods are used to calculate dominant frequencies, including simplified site-response models and statistical analyses of building typologies [30,191]. However, these approaches often fail to capture the full spatial variability and nonlinear behaviors present in urban areas.

Site Condition

The extent and magnitude of SCI effects in densely built urban areas, can be significantly influenced by the specific site conditions. Key factors include soil type, stratification, and dynamic characteristics. These parameters affect the intensity of resonance, the level of ground-motion amplification, and the spatial distribution of seismic responses [15,129]. When the natural frequency of the soil aligns with that of the overlying structures, soft, deep deposits with low shear-wave velocity can prolong ground shaking and substantially amplify seismic waves [15,176]. Case studies of cities founded on clay and alluvial soils have confirmed this resonance effect [132]. Groups of structures further modify seismic wave propagation by altering their direction, amplitude, and frequency content, which can either intensify or reduce localized ground motion depending on soil properties and layering [15]. In soft deposits, strong energy exchange between the soil and buildings can generate collective behaviors such as frequency-dependent amplification or attenuation, beat phenomena, and wavefield depolarization [161]. The heterogeneity and geometry of the underlying soil layers have a significant impact on the spatial impact of SCI. It is found that the seismic amplification in the central areas of dense urban blocks is typically higher due to wave trapping and constructive interference, while the seismic responses in edges or corners are lower due to energy scattering and leakage [15,192]. However, depending on the urban layout, building characteristics, and local soil conditions, these patterns may change. Research has demonstrated that cities situated on heterogeneous site conditions exhibit weaker seismic wave coherence compared to those located on homogeneous ground [177]. Moreover, in areas with basins, reflected waves from buildings may be trapped, thereby intensifying ground motion [193]. Therefore, differed site conditions can result in varied SCI and site effects. Site condition effects can be categorized into several types, including basin effect, stratification effect, lateral heterogeneity effect, and topographic effect etc. [64].

Characteristic of Seismic Waves

The influence of SCI depends strongly on the frequency content, amplitude, duration, and direction of seismic waves [175,177]. Low-frequency waves (around 1–3 Hz) couple with entire building clusters, producing collective effects such as resonance, wave trapping, and long-period amplification across urban blocks [161,175]. In contrast, high-frequency waves (>5 Hz) are more strongly scattered and attenuated by individual buildings, foundations, and small-scale heterogeneities, resulting in localized rather than city-scale effects [130,175]. Wave type and incidence also affect SCI. Numerical and experimental studies show that SV waves can produce stronger soil–structure coupling in dense urban areas compared with SH waves [191]. While oblique incidence causes dispersion, polarization shifts, and more irregular amplification, vertical incidence of seismic waves tends to enhance resonance in symmetrical layouts [175]. Surface waves (Rayleigh and Love waves) dominate in soft soils and they interact strongly with urban clusters, amplifying ground motion and prolonging shaking [13,194]. However, although less dominant at the surface, body waves (P and S) also contribute to inertial coupling between soil and structures, thereby influencing the redistribution of seismic energy across urban areas [177,194]. Phase coherence and wave direction determine whether interference amplifies or weakens motion, influencing the spatial variability of SCI effects. When resonance occurs, shaking is prolonged and energy transfer between soil and structures increases, which can intensify cumulative damage. Hence, SCI is governed by the characteristics of seismic waves, which influence amplification, resonance, scattering, interference, and the redistribution of energy within urban environments [175,177].

6.3.2. SCI Screening: Density and Spacing Predictors

The screening of site–city interaction (SCI) involves several key factors that influence the interaction between clusters [136]. Plan density, defined as the ratio of the built-up area of structures to total block area, plays a significant role in strengthening SCI effects [129,175]. As plan density increases, the interactions between structures become more pronounced, leading to enhanced SCI effects. Normalized spacing, which refers to the center-to-center distance between buildings relative to a representative building width, indicates that smaller spacing increases the coupling between buildings, thereby enhancing SCI effects [129,161,178]. Similarly, the frequency ratio compares the fundamental frequency of the building to the frequency of the site. It indicates that the risk of resonance increases as the frequency ratio approaches 1. This resonance amplifies SCI effects, making them more pronounced [175,176,191]. The height-to-surface wave-wavelength ratio, which divides the building height by the near-surface shear-wave wavelength, indicates that larger ratios lead to stronger interactions, potentially shifting spectral peaks and further altering ground motion behavior [161,175]. Impedance contrast, which compares the shear-wave velocity of soft soil to that of stiff soil, combined with the soft-cap depth, demonstrates that greater impedance contrasts promote wave trapping, resulting in larger modifications to spectral responses [83,195]. Finally, layout irregularities, such as variations in building spacing or height, tend to disrupt re-radiation and reduce coherent amplification, ultimately diminishing the overall SCI effects [129,154,178]. Table 3 summarizes these parameters for practical SCI screening.

Table 3. SCI screening.

Predictor	Definition	Units	Typical Range (Indicative)	Amplification Trend
ρb (Plan density)	ρb$={\displaystyle \frac{{\mathrm{A}}_{\mathrm{b}\mathrm{u}\mathrm{i}\mathrm{l}\mathrm{t}}}{{\mathrm{A}}_{\mathrm{b}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{k}}}}$	–	0.2–0.7 (districts)	Higher plan density generally increases SCI modification
s/B (Normalized spacing)	Center to center spacing (s)/building width(B)	–	1–6	Smaller normalized spacing increases coupling.
rf (Frequency ratio)	rf$={\displaystyle \frac{{\mathrm{f}}_{\mathrm{b}\mathrm{u}\mathrm{i}\mathrm{l}\mathrm{d}}}{{\mathrm{f}}_{\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{e}}}}$	–	0.5–1.5	Frequency ratio near 1 generally produces peak SCI effects
H/λs	Building height/Near surface shear-wave wavelength	–	0.1–0.6	Higher height-to-wavelength ratio generally gives stronger interaction
VS contrast	${\displaystyle \frac{{\mathrm{V}\mathrm{s}}_{\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}}{{\mathrm{V}\mathrm{s}}_{\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{f}\mathrm{f}}}}$ with soft-cap depth	m/s ratio	0.3–0.7	Larger impedance (Vs) contrast generally enhances wave trapping

Note: Ranges are indicative and should be calibrated to local building stock and site wavelengths. Notation for SCI screening parameters. ρ_b: Plan density (plan coverage ratio), defined as the ratio of total built-up footprint area A_built to the block area A_block. s: Mean center-to-center spacing between adjacent buildings. B: Representative building width in plan. r_f: Frequency ratio, defined as the ratio of the fundamental building frequency f_build to the site fundamental frequency f_site. H: Characteristic building height. λs: Near surface shear-wave wavelength associated with the predominant surface-wave or site frequency. Vs_soft: Shear-wave velocity of the softer near-surface layer (soft-cap). Vs_stiff: Shear-wave velocity of the underlying stiffer stratum.

6.3.3. Reduced-Order Modeling for City-Scale SCI

Reduced order models offer a practical approach based on physics to assess site–city interactions across entire districts, all while ensuring compatibility with design timelines [40,154]. These models represent building blocks with a few dynamic degrees of freedom, while soil coupling is incorporated through calibrated springs and dashpots that account for foundation compliance and inter-building interaction [139,175,178]. They effectively represent the amplification and reamplification across frequencies, shifts in dominant peaks, and changes in duration influenced by factors such as plan density, spacing, and the tuning between building and site frequencies [129,136,175,177,178,191]. They have been validated against finite-element analyses (FEA) and laboratory data for macro-scale screening, mapping, and prioritization in dense districts [154,172]. By using projection-based model order reduction, such as proper orthogonal decomposition or reduced bases, these models achieve significant speed improvements and enable rapid sensitivity studies. These studies cover variables like plan density, normalized spacing, frequency ratio, and height to wavelength, and can even support near real-time evaluations for multiple ground motions [40,129,175,178,191]. However, their effectiveness may be limited when strong soil nonlinearity, liquefaction, complex three-dimensional basin effects, or spatially varying input dominate the response [21,52,76,196]. The recommended approach is to calibrate the reduced model against a small set of high-fidelity simulations or data, use it for city or district-level screening, and then revert to full models for design-level checks in flagged areas [40,52,136,154,177].

6.4. Topographic Effects in Soil–Structure and Structure–Soil–Structure Interaction (TSSI and TSSSI)

In seismic engineering, the topographic effect refers to the influence of terrain features such as ridges, hills, and slopes on seismic wave propagation. These features can amplify or reduce seismic wave amplitudes, focus or disperse seismic energy, generate edge-induced surface waves, and affect the phase and duration of shaking [133,197,198,199]. The specific pattern and intensity of these effects are influenced by various geometric and physical factors, including the relief height to wavelength ratio (H/λ), three-dimensional curvature, and the characteristics of incoming seismic waves, such as their incidence (the angle at which waves strike the surface) and polarization (the direction of wave oscillation) [184,199,200]. The relief height is defined as the vertical distance from the toe (the base of the slope) to the crest (the highest point) [199,201]. Topographic amplification can be assessed using the topographic amplification factor (η), which is the ratio of relief height (H) to the seismic wavelength (λ) of the controlling shallow soil layer. This factor, η, helps to screen the potential effects of topographic amplification on seismic motion [198,199]. Peak amplification typically occurs when H/λ is between approximately 0.2 and 1, a range where significant seismic wave amplification is most likely [185,199]. Additionally, the Diagnostic Companion Index (DCI) is another important metric used to assess the vulnerability of a system under topographic conditions. This index is defined as the ratio of the topographic height (H) to the ridge half-width (W) at mid-slope, helping to determine the impact of ridge geometry, particularly the height and width, on seismic performance [184,200]. For η values less than 0.1, topographic effects are generally negligible, resulting in little to no amplification of seismic waves. However, for η values between 0.2 and 0.6, ridge modes are more likely to occur, with spectral ordinates at the crest often increasing by a factor of 1.5 to 3 in specific frequency bands. In other frequency bands, deamplification may occur due to wave interference and scattering [185,198,199,202]. The interaction between the incidence and polarization of seismic waves, topographic curvature, and shallow soil layering all affect both the amplitude and bandwidth of seismic waves. Additionally, strong lateral gradients near ridge crests can induce torsion (twisting) and rocking (side-to-side motion) in structures located on irregular topographies [184,197,200,202]. The Eurocode 8 (EC8) provides a topographic multiplier (ST) used to adjust seismic forces for sites with significant topography. This multiplier is frequency independent and primarily intended for screening purposes, with typical values for pronounced relief ranging between 1.2 and 1.4. However, the EC8 multiplier has limitations as it cannot capture frequency-specific peaks and troughs in the seismic response, making it unsuitable for detailed analysis of complex topographic effects [47,203,204]. For sites with η ≥ 0.3 or areas with pronounced three-dimensional features like knolls, it is recommended to conduct site-specific two-dimensional (2D) or three-dimensional (3D) analyses with gradient-consistent input to better capture the effects of topography on seismic behavior [184,204].

Topographic amplification is most pronounced when seismic waves interact with terrain features like slopes and ridges, intensifying ground shaking, particularly near the crest. Maximum amplification occurs when seismic waves strike the slope at a vertical angle, causing constructive interference and significantly increasing seismic motion in these areas. Research confirms that amplification is influenced by both the angle of incidence and topographical relief, with steeper slopes concentrating seismic waves more than flatter regions [133,185,197,199]. This effect has been observed in past earthquakes: the 1999 Athens earthquake, for instance, caused severe damage along the crests of steep slopes [205]; the 2005 Kashmir earthquake saw much stronger shaking on ridgelines compared to adjacent valleys [201]; and during the 2010 Haiti earthquake, topographic amplification along the Pétionville ridge resulted in significantly greater ground movements and extensive structural damage [206]. Energy tends to accumulate at the crests of convex ridges and curved terrain, while lee slopes experience reduced motion [198,199,200]. Multiple scattering can extend shaking, and nonlinear soil behavior typically damps high-frequency components while shifting energy towards longer periods [197,207,208]. Topographic amplification, a localized increase in shaking as seismic waves traverse irregular ground, is particularly pronounced at crest sites, ridges, and convex slopes. These sites often record stronger motions within narrow frequency bands set by landform dimensions. When the characteristic frequencies of slopes or ridges align with nearby buildings, resonance can develop, raising shaking levels and increasing structural demand [133,184,197,201,207,209].

The depth of the foundation plays a crucial role in the seismic response of structures located on sloping terrains, particularly within the context of topographic–soil–structure interaction (TSSSI) [134,210,211]. Shallow foundations are more susceptible to seismic wave amplification at features like slopes and ridges, leading to increased lateral forces and settlement. This occurs because shallow foundations are more directly influenced by surface soil behavior, which is amplified by topographic features. In contrast, deep foundations provide greater stability by reducing surface shaking effects and energy focusing. Local topography, such as slopes or valleys, can concentrate seismic waves, amplifying seismic demand on structures in these areas [134,211,212,213]. The scale of amplification is influenced by both geology and geometry. Variations in soil and rock properties affect wave transmission, while the direction and angle of seismic waves can either amplify or attenuate the seismic motion, with canyons, basin edges, cliffs, and valleys redirecting energy and explaining sharp damage gradients over short distances [193,194,201]. Topography also alters frequency content and duration. Shallow soft layers can amplify motions, while elevated terrain tends to concentrate energy, and depressed ground may reduce it through reflection and dispersion [182,184,208]. When a single building is located on sloping ground, the problem extends beyond conventional SSI (soil–structure interaction). Topographic–soil–structure interaction (TSSI) captures the coupled response of the structure, the soil, and the terrain [42]. Slopes and ridges can focus or scatter seismic waves, altering lateral displacement, base shear, and acceleration at the foundation. Buildings closer to crests are generally more vulnerable than those situated farther back [199,214]. Compared with standard SSI, additional complications arise during strong shaking on steep or tall slopes. Shabani et al. [215] reported that mid- to high-rise buildings (10–15 stories) on slopes exhibited lateral displacements 10–125% greater than flat-ground SSI predictions. Simulations also indicate that amplification zones extend about two to three times the slope height behind the crest, where accelerations can reach twice those on level ground [184,199,201]. When multiple buildings are located on slopes or ridges, inter-building coupling combines with terrain effects. This topographic structure–soil–structure interaction (TSSSI) modifies the local wavefield and seismic demand distribution. The degree of amplification depends on slope geometry, soil stratigraphy, building spacing, and wave incidence [134,216]. Crest-adjacent mid- to high-rise buildings can show significant increases in displacement and drift, often ranging from 30 to 100%, with some cases approaching twice that of flat-ground cases [134,184,210]. Three-dimensional simulations and field-informed models frequently map crest amplification zones extending about one to three slope heights behind ridges, with the extent determined by geometry, soil stiffness, and input frequency [184,199]. Low-rise responses are typically smaller unless soils are soft and building-to-building interaction is strong [42,216]. Laboratory and numerical studies reveal wide variability in amplitude, duration, and frequency response based on terrain geometry, incidence, and soil–bedrock contrast [184]. SV-wave incidence on soft soils tends to produce stronger amplification and irregular, scattered wavefields near slopes and ridges [184,195]. PGA variations due to topography can reach ±50% relative to flat-reference sites, and crest-to-base differences can be even larger [201,202]. Records and simulations from the 2023 Kahramanmaraş sequence show that a neighboring building near a shallow slope can alter the response of another, highlighting the importance of building arrangement in hillside settings [217]. When structural periods approach those of ridges or slopes, clusters of buildings can radiate energy back into the soil and shift local amplification; parameters such as spacing ratio (η), plan coverage (φ), and floor-area ratio govern the strength of this feedback [141,161,175,191]. Reliable assessment and design in these settings require models that resolve terrain geometry, soil conditions, incidence, and polarization, as well as three-dimensional multi-building coupling [184]. Overall, TSSI and TSSSI are decisive factors for hillside cities. Beyond the fundamentals of SSI, codes and performance-based frameworks should incorporate topographic amplification, oblique incidence, and 3D coupling among multiple structures. The following are some of their key features.

• Dependence on Topography

Local relief and curvature set the interaction. Proximity to slope breaks, ridge crests, and valley edges changes the soil motion that reaches the foundation by altering wave paths and energy focusing. Key controls include H/λ, plan curvature, incidence angle, and polarization details, while well-established methods can be briefly described and appropriately cited [11,184,199,200].

• Amplification and Attenuation

Irregular ground can raise or reduce motion. Amplification tends to occur in narrow bands when terrain scales align with incoming wavelengths and, for buildings, when site frequencies are close to structural periods [184]. De-amplification appears on lee slopes or where scattering and damping dominate [201].

• Wave Transformations

At ridges, slopes, and valley margins, incident waves reflect, refract, and diffract; edge-generated surface waves can develop. These processes redistribute energy, shift phase, and change duration, which in turn alters soil–structure coupling and base input [134,198,199].

• Localized Site Effects

Topography, shallow layering, and incidence produce frequency-dependent patterns of amplification and shadowing. Soft near-surface soils often suppress high-frequency peaks while shifting energy to longer periods, yielding strong spatial variability over short distances [184,200,208].

• Combined Soil-Structure-Topography Response

Foundation type, stiffness contrast, and building period govern the degree of period lengthening, rocking, and drift relative to flat-ground SSI [92]. Responses near crests are commonly higher than farther back, so analyses should resolve 3D geometry and use site-specific input that captures incidence and polarization [184].

7. Conclusions

This seismic response in urban regions emerges from interactions acting at several scales: soil–structure interaction (SSI) at the component level, inter-building coupling (SSSI), cluster effects (SSCI), city scale, and site–city interaction (SCI). Terrain and geological features such as basins, slopes, and heterogeneity further shape these processes, often considered under topographic interaction (TSSI, TSSSI). No single parameter is sufficient to explain the range of behaviors observed in dense urban settings. Instead, the combined influence of near-surface shear-wave velocity and damping, slope and basin geometry, and urban-form descriptors such as plan coverage ratio (φ), floor area ratio (FAR), and normalized spacing (η = s/B) governs whether amplification, resonance, interference, or attenuation dominates.

For engineering and planning, three priorities follow:

• Inclusion of interactions in seismic assessments: Interaction effects must be accounted for in hazard and vulnerability studies, particularly in areas with soft deposits, significant relief, or dense building clusters. Site-specific shear velocity and damping data, together with φ, FAR, and η, should inform spectra and checks for resonance between adjacent structures.
• Accurate estimation of topographic and basin effects: Amplification linked to slopes and basins should be quantified with calibrated predictors or empirical models that reflect slope geometry, curvature, and wave incidence, enabling more reliable site-specific ground motion estimates.
• Adoption of nonlinear 3D analyses in critical zones: Where soft soils and close building spacing coincide, nonlinear three-dimensional models are essential. These analyses capture soil softening, energy dissipation, and foundation kinematics observed in strong shaking, providing realistic bounds on drift and base shear.

Numerical modeling and field studies are most effective when used together. Modeling can test mechanisms and explore parameter ranges, while observations ground those results and reveal their limits. Future progress will require linking detailed geotechnical data with descriptors of urban form and terrain in models that reflect heterogeneity and nonlinearity. With this approach, seismic assessment moves beyond single-building analysis toward frameworks that capture how cities respond collectively, supporting more resilient design in earthquake-prone regions