Behaviour of Structural Subassemblies of Steel Beams with Corrugated Webs Using Reverse Channel Connections
Abstract
1. Introduction
- Validate an ABAQUS model vs. the experimental results of Nie et al. [11].
- Develop a 3D finite element model using ABAQUS to study the behaviour of structural subassemblies of SBCW with different web corrugation configurations connected to CFT columns using an extended end-plate reverse channel connection.
- Perform a parametric study considering various factors, including web corrugation profiles (Trap, Rec, Sin and Tria), flange stiffeners at the point load, and web thickness.
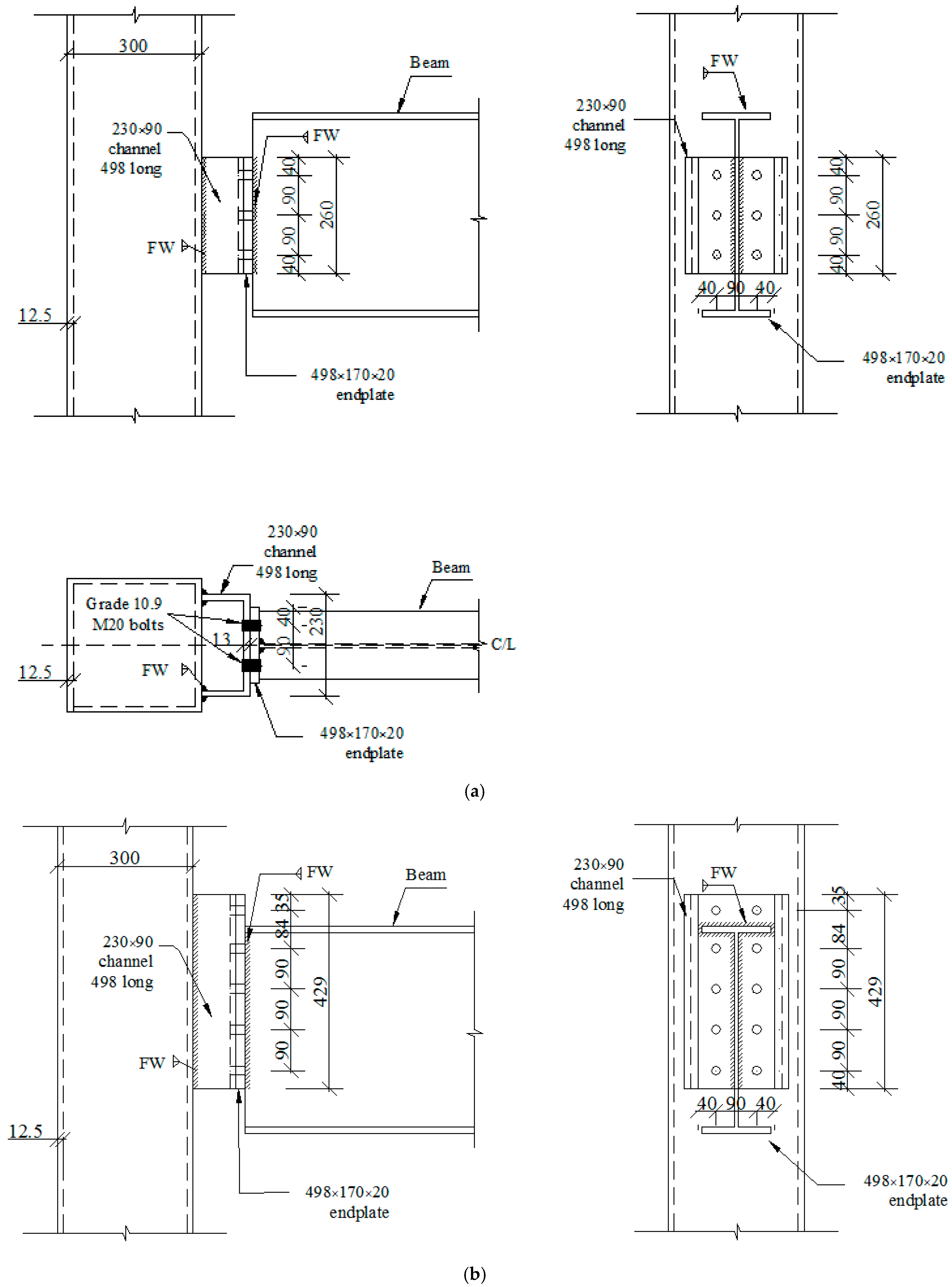
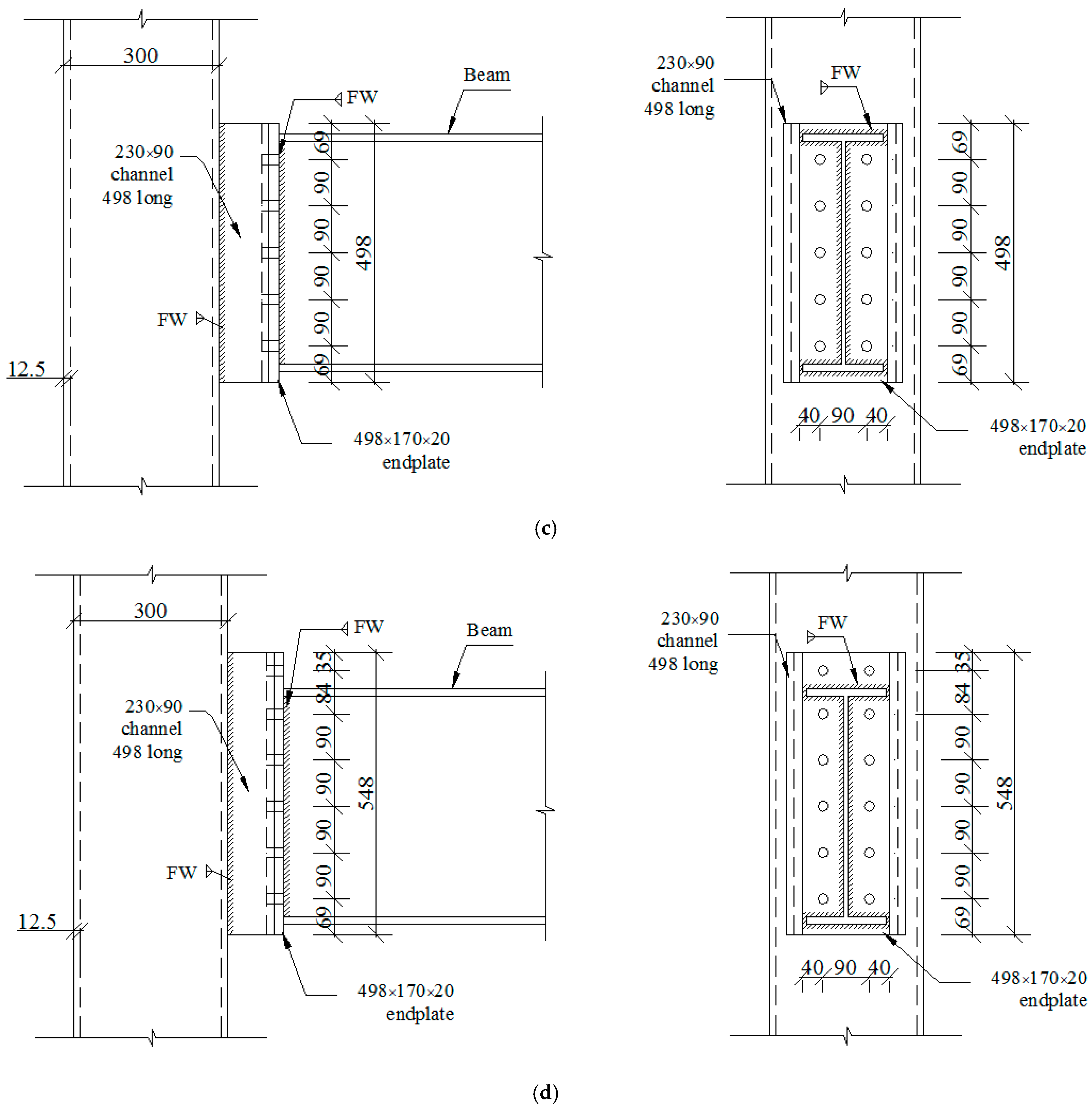
- Investigate the effects of four different joint types of reverse channel connection: extended endplate, flush endplate, flexible endplate, and hybrid extended/flexible endplate on the load-carrying capacity of SBCW.
2. Finite Element Model
- -
- -
- The beam was modelled using the FE shell element (S4R).
- -
- To model accurate beam behaviour, several simulations were performed using 50, 35, 20, and 10 mm mesh sizes. The results in Table 3 indicate that the finer mesh size of 10 mm exhibited a ≤3% Pu change relative to the experimental ultimate load. Accordingly, it was selected to simulate accurate beam behaviour.
- -
- Both geometric and material nonlinearities were considered to perform a nonlinear static analysis. A multilinear stress–strain curve was used to model steel material properties as an isotropic material (see Figure 2).
- -
- The following parameters were used throughout the analysis for the steel section based on the material property tests of Nie et al. [11]: yield strength of the web, 385.5 MPa; ultimate strength of the web, 461.2 MPa; elastic modulus, E = 2.06 × 105 MPa; and Poisson ratio, υ = 0.3.
- -
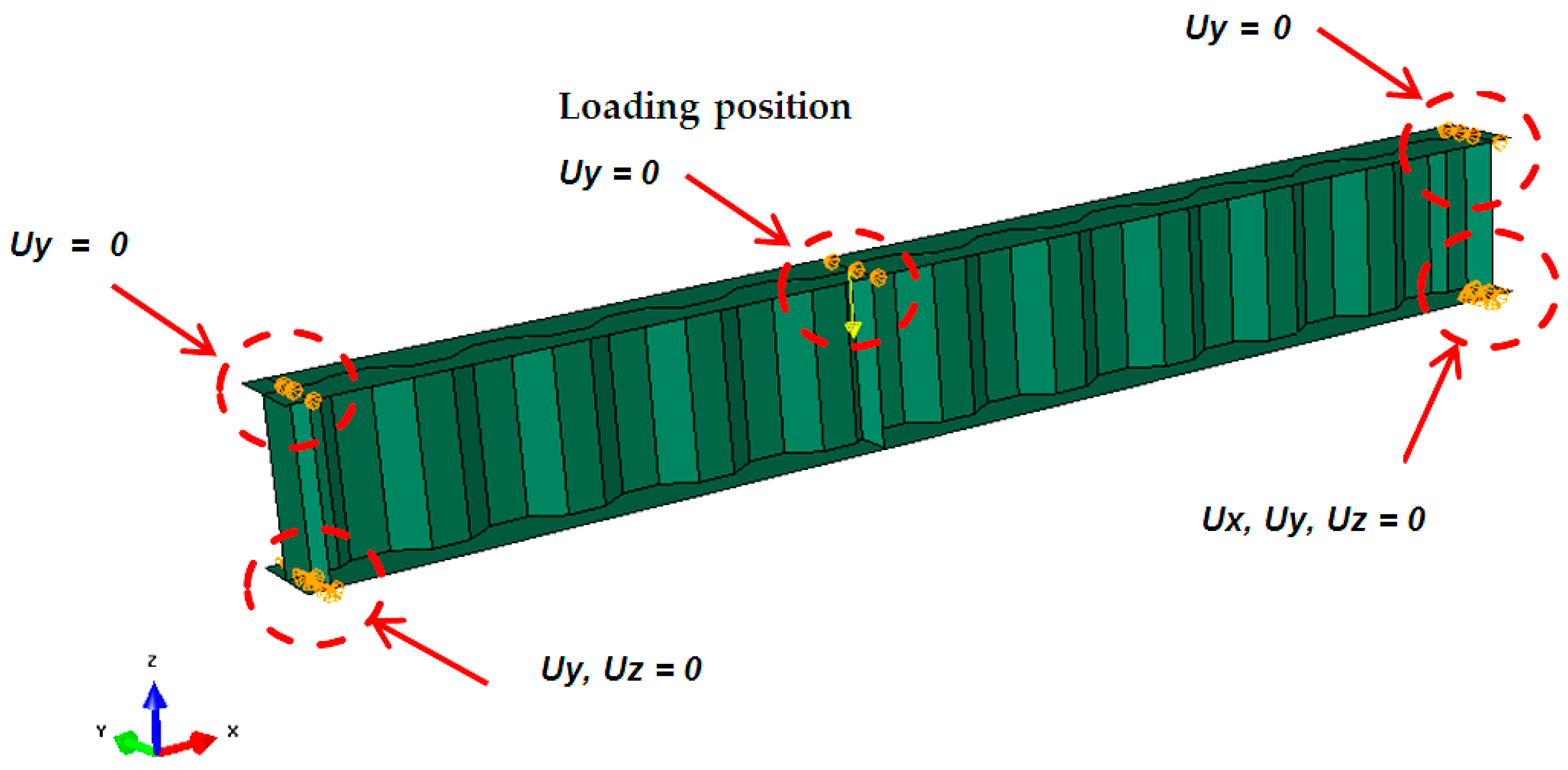
- Boundary conditions of the beam in numerical simulations were applied at the loading and supports as the experimental specimens; the left support was modelled as a hinged support and the right support as a roller support, as shown in Figure 1d. Figure 3 summarizes the constrained DOFs of the FE model at each support and load plate.
- -
- One load was applied across the top flange of the beam and increased gradually until failure.
- -
- Due to structural geometric imperfections and residual stresses during manufacturing, forming, and processing, geometric initial imperfections in the nonlinear FE models were established and validated. The equivalent geometric imperfections recommended by the standard EN 1993-1-5:2006 [32] were used for calculations of initial imperfections of the beam. Accordingly, geometric imperfections obtained from the first buckling mode based on eigenvalue buckling analysis were used and then scaled to simulate the initial imperfection. In simulation, the initial geometric imperfections in the web were estimated by scaling the first buckling mode by a value not more than L/350. The maximum value for the initial geometric imperfections used in validation for all tests was 5 mm. Table 4 shows the ultimate load capacity of test 2-2, using various values of initial geometric imperfections. The results in Table 4 indicate that Pu of the beam depends on initial geometric imperfections. Accordingly, the value that gave the least ΔPu% change relative to the experimental ultimate load was selected to simulate accurate beam behaviour.
- -
- Two load cases were applied to the beam. The first case was to stimulate the initial imperfection in the form of initial out-of-plane buckling over the web of the beam, when no external load was applied, and then, at the end of this case, after updating the geometry of the beam with the initial imperfection, the second case was applied, until the ultimate load was reached.
- -
- Static Riks is used for analysis with a minimum increment size of 1 × 10−5 and a maximum increment size of 0.1 with the default convergence tolerances in Abaqus.
- -
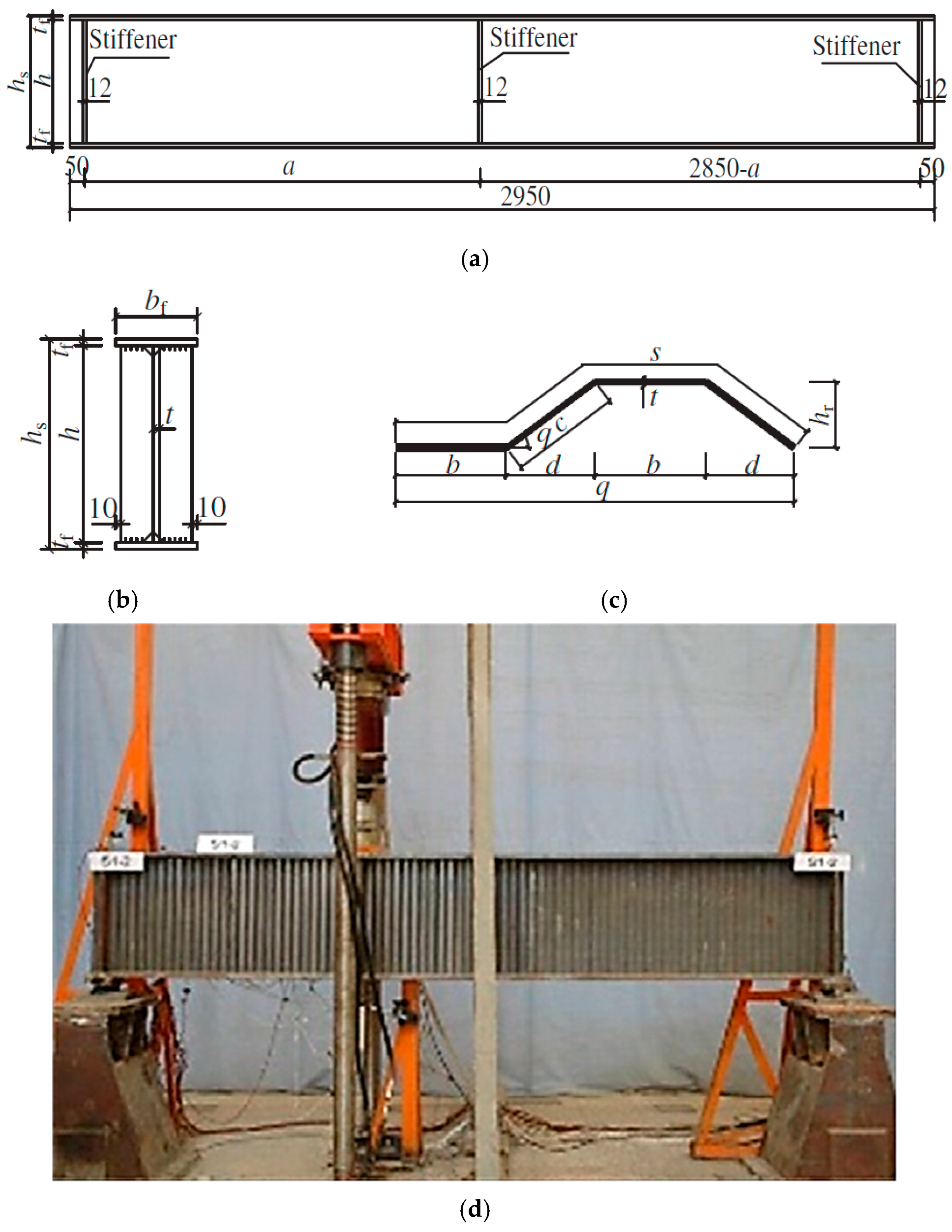

| Specimen | Flange Dimensions | Trapezoidal Corrugated Web Parameters | ||
|---|---|---|---|---|
| bf (mm) | t (mm) | a (mm) | h (mm) | |
| S1-2 | 150 | 12 | 1000 | 460 |
| S1-3 | 14 | 660 | ||
| S1-4 | 16 | 760 | ||
| S1-5 | 20 | 860 | ||
| S2-1 | 200 | 16 | 1200 | 260 |
| S2-2 | 20 | 360 | ||
| S2-3 | 25 | 460 | ||
| Corrugated Configuration | b (mm) | d (mm) | θ (o) | hr (mm) | s (mm) | c (mm) | t (mm) |
|---|---|---|---|---|---|---|---|
| S1 | 20 | 16 | 37 | 12 | 80 | 72 | 0.9 |
| S2 | 80 | 64 | 48 | 320 | 288 |
| Mesh Size (mm) | No. of Elements | Pu (Kn) | δmid (mm) | ΔPu% |
|---|---|---|---|---|
| 10 | 27609 | 68.55 | 3.30 | 0.96% |
| 20 | 6961 | 83.90 | 3.77 | 23.6% |
| 35 | 2068 | 106.54 | 4.59 | 56.9% |
| 50 | 1413 | 111.07 | 4.59 | 63.6% |
| Initial Geometric Imperfections (mm) | Pu (Kn) | δmid (mm) | ΔPu% |
| 1 | 75.74 | 3.26 | 11.38% |
| 2 | 70.4 | 3.25 | 3.53% |
| 3 | 64.87 | 3.38 | −4.60% |
| 4 | 62.14 | 3.24 | −8.62% |
| 5 | 58.46 | 3.38 | −14.03% |
3. Validation of the Finite Element Model
4. Numerical Model of the Behaviour of Restrained Structural Subassemblies of SBCW
- -
- Due to symmetry, half of the structure was modelled so that all nodes at the beam mid-section were fixed in the axial direction, preventing rotation about the two principal axes but allowing the beam to twist about its longitudinal axis. To account for the concrete slab, the beam was assumed to be fully laterally restrained.
- -
- The “tie” type constraint in ABAQUS was used to simulate the welds between connection components.
- -
- In modelling the end plate reverse channel connection, many contact pairs existed in the joints. These contact pairs occurred at the interfaces of the following contact points: the bolt shanks and web of the reverse channel and endplate, the bolt heads and web of the reverse channel, and the endplate and web of the reverse channel.
- -
- The ABAQUS contact function was used to simulate the interaction between the contact pairs. “Surface to surface” contacts with a small sliding option were defined for all contact relationships. The normal contact behaviour was assumed as “Hard contact”. A friction coefficient of 0.3 was assumed for the tangential direction of the contact pairs.
- -
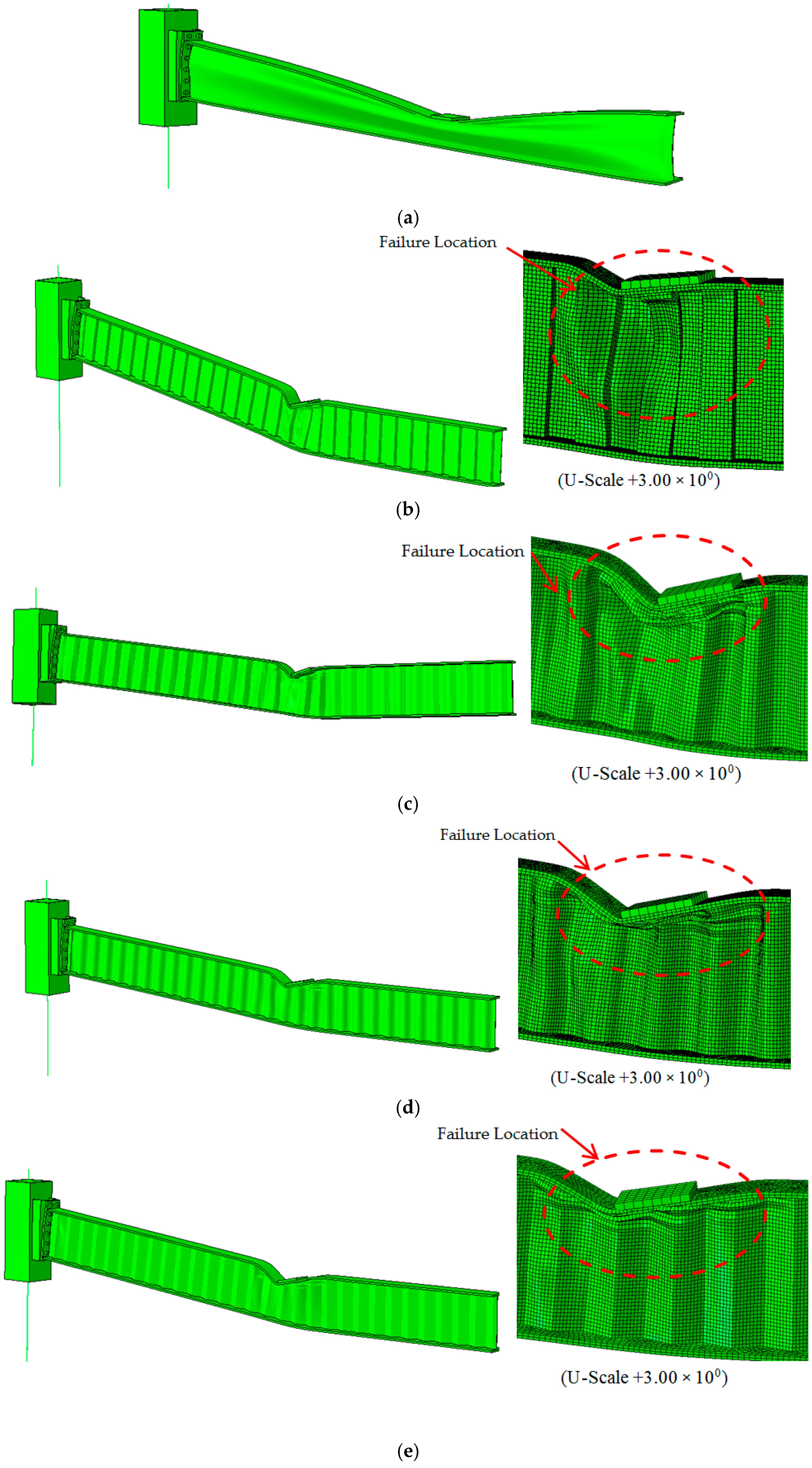
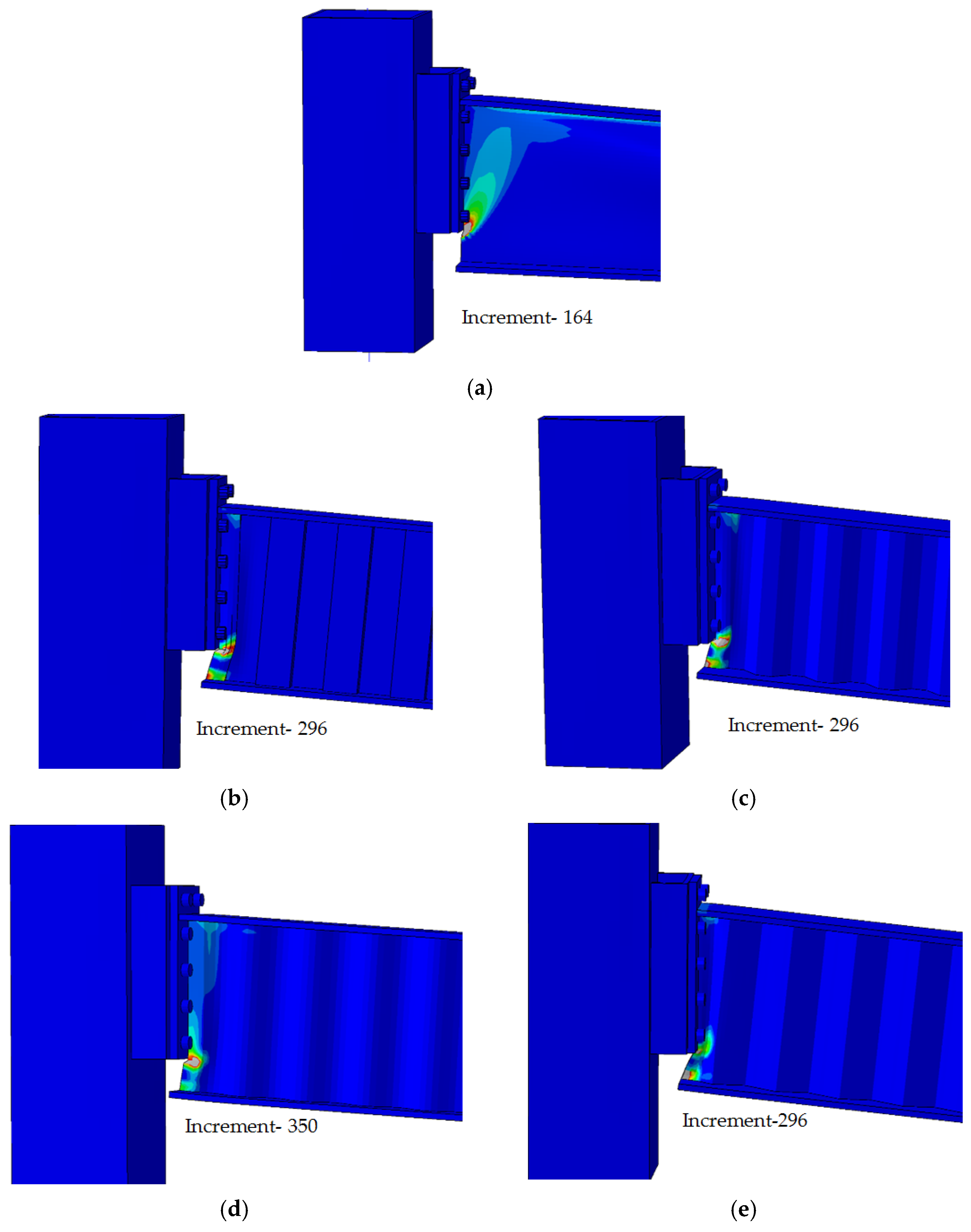
- As can be seen in Figure 2 (stress–strain curve), a localized reduction in the cross-sectional area of the material after the UTS (Necking) is reached at εp = 0.15. Therefore, the failure load was considered as a large deflection of the beam combined with the spread of plastic strain, exceeding 0.15 at the web and flange at which the beam failed to carry the load. Grey colour in the finite element models represents plastic strain exceeding 0.15.
- -
- -
- Generally, the simply supported SBCW failed by five different modes of failure:
- Global web shear buckling.
- Local shear web buckling.
- Local flange buckling.
- Vertical buckling into the web.
- Yielding of the compression flange.




| Corrugated Configuration | b (mm) | d (mm) | θ (o) | hr (mm) | s (mm) | q (mm) | t (mm) |
|---|---|---|---|---|---|---|---|
| Trap | 40 | 40 | 45 | 40 | 192 | 160 | 1.7 |
| Rec | 40 | 40 | 90 | 40 | 238 | 160 | 1.7 |
| Sin | 40 | 40 | 14 | 40 | 180 | 160 | 1.7 |
| Tria | 40 | 40 | 25 | 40 | 177 | 160 | 1.7 |
5. FE Results of Structural Subassemblies of SBCW Without Stiffener
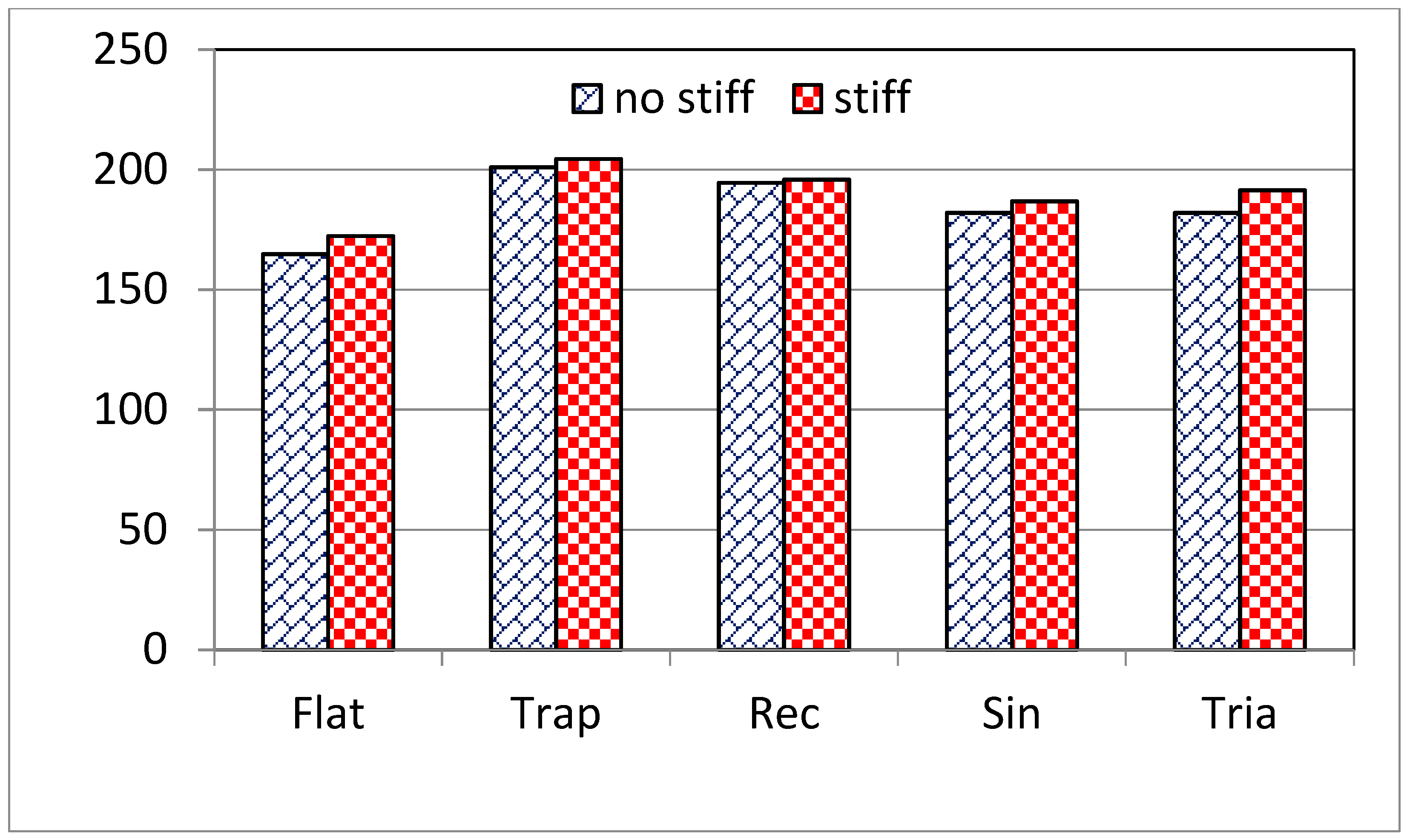
6. Effect of Transversal Stiffeners
7. Effect of Web Thickness
8. Effect of Type of Endplate Reverse Channel Connection
9. Limitations of the Study and Practical Implications
- -
- Elastic CFTC (concrete-filled tubular columns).
- -
- The SBCW overall height and flange dimensions are the same as the beam section size: 457 × 152 × 67 UB (hw = 428 mm, bf = 153.8 mm, and tf = 15 mm).
- -
- The web thickness: tw= 1.7 and 2.15 mm (hw/tw =250 and 200).
- -
- The SBCW is connected to CFTC using reverse channel end plate connections.
- -
- The connection is strong enough to transfer the failure to the beam (failure occurs in the beam before the connection).
- -
- Perfect bolt preload.
- -
- Ambient temperature (no elevated temperature).
- -
- The beam is applied by two monotonic concentrated loads (no cyclic load).
- -
- No residual stresses in flanges.
- -
- Using SBCW to increase the beam’s load capacity and enhance strength against shear buckling failure.
- -
- Using Rec and Trap web corrugation shapes for the beams without flange stiffener at point load.
- -
- Adding flange stiffener at point load for the beams of Tria and Sin web corrugation.
- -
- Using hw/tw = 200 for SBCW.
- -
- Using extended or flush endplate connections to connect SBCW to CFTC.
10. Conclusions
- -
- The behaviour of structural subassemblies of SBCW may require further experimental and numerical investigations, including elevated temperature behaviour, dynamic behaviour under extreme conditions and multi-hazard events.
- -
- The proposed FE model is in good agreement with the experimental observations and results in terms of the failure mode, deformed shape, and the measured vertical deflection–relationship. The FE model clearly captured the global and local shear buckling of the trapezoidal corrugated steel web at failure.
- -
- The common failure mode of structural subassemblies of steel beams with different corrugated webs subjected to two-point load is the compression flange buckling vertically into the web, then local buckling of the web under compressive loads.
- -
- The behaviour of I-beam sections can be improved by means of the web corrugation profiles. This is reflected in reported differences for different web corrugation shapes. On the other hand, adding a flange stiffener to the corrugated web beams introduces a slight improvement. To prolong the beam’s load-carrying capacity of corrugated web beam, increasing the web thickness slenderness ratio hw/tw can be an effective solution.
- -
- Among the four web corrugation shapes investigated, using the Rec and Trap web corrugation shapes gave the best behaviour for the beams without flange stiffener subjected to bending moment and shear. Beams with Trap and Rec web corrugations showed an increase of 22% and 18%, respectively. Meanwhile, beams with Tria and Sin web corrugations gave the least improvement. In this case, the ultimate load increases by 10.5%.
- -
- Adding a flange stiffener at the point load positions exhibited a relatively slight increase in the ultimate load of the beams. However, the stiffener increased the buckling resistance of the flanges and web. The best effect of the flange stiffener was for Tria and Sin web corrugations with an increase of about 5.1% and 2.6%, respectively, compared with those without a flange stiffener.
- -
- The web thickness has an important influence on the structural behaviour of the corrugated web beams. The increased web thickness from hw/tw = 250 to hw/tw = 200 increased the beam load-carrying capacity of the corrugated beam differently. For Sin and Rec web corrugations, the difference in beam load-carrying capacity was 28.8% and 24.9%, respectively. Meanwhile, for the Tria web corrugation, the difference was 20.1%. Finally, the difference reached 17.7% for Trap web corrugation.
- -
- Among the four connection types investigated, using the extended or flush endplate connections gave the best behaviour of SBCW connected to CFTC. Using a flexible endplate (or hybrid extended/flexible endplate) connection was not effective. Extended and flush endplate connections enhanced the beam’s ultimate load and showed an increase of (5.3–31.7%) and (25–30.9%) for flush endplate and extended endplate, respectively, compared to flexile endplate, depending on the web corrugation profile.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Kannoon, M.A.; Suhiel, I.A. Experimentally flexural behaviour study of steel beams with corrugated webs. IOP Conf. Ser. Mater. Sci. Eng. 2020, 888, 12084. [Google Scholar] [CrossRef]
- Elamary, A.S.; Alharthi, Y.; Abdalla, O.; Alqurashi, M.; Sharaky, I.A. Failure mechanism of hybrid steel beams with trapezoidal corrugated-web non-welded inclined folds. Materials 2021, 14, 1424. [Google Scholar] [CrossRef] [PubMed]
- Hasan, Z.K.; Hemzah, S.A.; Al-kannoon, M.A.-A.K. Behaviour of corrugated steel compact I-section beams. In Proceedings of the 2nd International Conference for Civil Engineering Science (ICCES). J. Phys. Conf. Ser. 2021, 1895, 012063. [Google Scholar] [CrossRef]
- Ammash, H.K.; Al-Bader, M.A. Shear behaviour of steel girder with web-corrugated core sandwich panels. IOP Conf. Ser. Mater. Sci. Eng. 2020, 1090, 012017. [Google Scholar] [CrossRef]
- Landolfo, R.; Mammana, O.; Portioli, F.; Di Lorenzo, G.; Guerrieri, M.R. Laser- welded built-up cold-formed steel beams: Experimental investigations. Thin-Walled Struct. 2008, 46, 781–791. [Google Scholar] [CrossRef]
- Kövesdi, B.; Dunai, L. Fatigue life of girders with trapezoidally corrugated webs: An experimental study. Int. J. Fatigue 2014, 64, 22–32. [Google Scholar] [CrossRef]
- Anami, K.; Sause, R.; Abbas, H.H. Fatigue of web-flange weld of corrugated web girders: 1. Influence of web corrugation geometry and flange geometry on web-flange weld toe stresses. Int. J. Fatigue 2005, 27, 373–381. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y.; He, J.; Xin, H.; Yao, H. Experimental study on cyclic behaviour of composite beam with corrugated steel web considering different shear-span ratio. Eng. Struct. 2019, 180, 669–684. [Google Scholar] [CrossRef]
- Emami, F.; Mofid, M.; Vafai, A. Experimental study on cyclic behaviour of trapezoidally corrugated steel shear walls. Eng. Struct. 2013, 48, 750–762. [Google Scholar] [CrossRef]
- Al-Mawashee, H.S.; Al-Kannoon, M.A.-A. Flexural strength of castellated beams with corrugated webs. J. Phys. IICESAT Conf. 2021, 1973, 012213. [Google Scholar] [CrossRef]
- Nie, J.-G.; Zhu, L.; Tao, M.-X.; Tang, L. Shear strength of trapezoidal corrugated steel webs. J. Constr. Res. 2013, 85, 105–115. [Google Scholar] [CrossRef]
- Elgaaly, M.; Hamilton, R.W.; Seshadri, A. Shear strength of beams with corrugated webs. J. Struct. Eng. ASCE 1996, 122, 390–398. [Google Scholar] [CrossRef]
- Elgaaly, M.; Seshadri, A.; Hamilton, R.W. Bending strength of steel beams with CWs. J. Struct. Eng. ASCE 1997, 123, 772–782. [Google Scholar] [CrossRef]
- Elamary, A.S.; Saddek, A.B.; Alwetaishi, M. Effect of corrugated web on flexural capacity of steel beams. Int. J. Appl. Eng. Res. 2017, 12, 470–481. [Google Scholar]
- Khalid, Y.A.; Chan, C.L.; Sahari, B.B.; Hamouda, A.M.S. Bending behaviour of corrugated web beams. J. Materials. Process. Technol. 2004, 150, 242–254. [Google Scholar] [CrossRef]
- Naji, R.N.; Chkheiwer, A.H. Study on the non-linear finite element analysis of corrugated webs in steel sections with varying thickness. Int. J. Mech. Eng. 2022, 7. [Google Scholar]
- Li, G.-Q.; Jiang, J.; Zhu, Q. Local bucking of compression flanges of H-beam with corrugated webs. J. Constr. Res. 2015, 112, 69–79. [Google Scholar] [CrossRef]
- Jáger, B.; Dunai, L.; Kövesdi, B. Flange buckling behaviour of girders with corrugated web part ii: Numerical study and design method development. Thin-Walled Struct. 2017, 118, 238–252. [Google Scholar] [CrossRef]
- Luo, R.; Edlund, B. Ultimate strength of girders with trapezoidally corrugated webs under patch loading. Thin-Walled Struct. 1996, 24, 135–156. [Google Scholar] [CrossRef]
- De’nan, F.; Choong, K.; Hashim, N.S. The effects of the depth of web on the bending behaviour of triangular web profile steel beam section. AIP Conf. Proc. 2017, 1892, 020022. [Google Scholar] [CrossRef]
- Kumar, U.M.; Reddy, D.P.; Patel, R.R.; Pandian, M.S.; Karthikeyan, K. A study on flexural capacity of steel beams with corrugated web. Int. J. Civ. Eng. Technol. (IJCIET) 2018, 9, 945–957. [Google Scholar]
- Mutalib, A.A.; Mussa, M.H.; Abdulghafoor, A.M. Finite element analysis of composite plate girders with a corrugated web. J. Eng. Sci. Technol. 2018, 13, 2978–2994. [Google Scholar]
- Chan, C.L.; Khalid, Y.A.; Sahari, B.B.; Hamouda, A.M.S. Finite element analysis of corrugated web beams under bending. J. Constr. Steel Res. 2002, 58, 1391–1406. [Google Scholar] [CrossRef]
- Al-Kanon, M.A.-A.; Suhiel, I.A. Flexural behaviour of steel beam with corrugated web. Int. J. Sci. Technol. Res. 2019, 10, 3004–3009. [Google Scholar]
- Sayed, A.M.; Elaraki, Y.G.; Elalaoui, O. Experimental and numerical analysis of steel beams’ efficiency with different shapes of corrugated webs under free vibrations. Metals 2022, 12, 938. [Google Scholar] [CrossRef]
- Tohamy, A.S.; Sadeek, R.A.; Saddek, A.B.; Badran, S.F.; El-Serwi, A.A. Behaviour of trapezoidal corrugated webs girders with cutouts: Experimental and analytical solution. J. Eng. Sci. 2022, 50, 146–159. [Google Scholar]
- Tohamy, A.S.; Badran, S.F.; EL-Serwi, A.A.; Sadeek, R.A.; Saddek, A.B. Efficiency of web cutouts for steel plate girders with corrugated webs versus flat webs under shear loading. Artic. Arab. J. Sci. Eng. 2022, 48, 5215–5228. [Google Scholar] [CrossRef]
- Almohamady, A. Opening in oriented corrugated web steel beams. IOP Conf. Ser. Earth Environ. Sci. 2024, 1326, 012028. [Google Scholar] [CrossRef]
- Hafsamol, S.; Abraham, R. Finite element analysis of corrugated web beams, column and slab connection under loading condition. Int. Res. J. Eng. Technol. (IRJET) 2019, 06, 5418–5422. [Google Scholar]
- Wang, Y.C.; Xue, L. Experimental study of moment–rotation characteristics of reverse channel connections to tubular columns. J. Constr. Steel Res. 2013, 85, 92–104. [Google Scholar] [CrossRef]
- ABAQUS Analysis User’s Manual, Version 6.6. ABAQUS Inc.: Palo Alto, CA, USA, 2006.
- EN 1993-1-5:2006; Eurocode 3—Design of Steel Structures—Part 1–5: Plated Structural Elements. European Committee for Standardisation: Brussels, Belgium, 2006; pp. 1–53.
































| Pu (Kn) | Δmid (mm) | ||||
|---|---|---|---|---|---|
| Test | Exp. | FE | ΔPu% | Exp. | FE |
| S1-2 | 103.86 | 107.55 | +3.55% | 4.74 | 3.96 |
| S1-3 | 123.53 | 122.27 | −1.02% | 3.17 | 3.168 |
| S1-4 | 120.79 | 119.55 | −1.03% | 3.17 | 2.91 |
| S1-5 | 127.33 | 127.4 | +0.05% | 4.105 | 2.37 |
| S2-1 | 43.59 | 42.83 | −1.93 | 2.85 | 3.77 |
| S2-2 | 67.90 | 68.59 | +1.02 | 2.96 | 3.21 |
| S2-3 | 117.47 | 112.8 | −3.98 | 2.33 | 3.25 |
| Web Corrugation | Pu (Kn) | ΔPu% |
|---|---|---|
| Flat | 164.8 | - |
| Trap | 201.1 | 22% |
| Rec | 194.4 | 18% |
| Sin | 182.2 | 10.5% |
| Tria | 182.1 | 10.5% |
| Web Corrugation | hw/tw = 250 | hw/tw = 200 | ||
|---|---|---|---|---|
| No Stiff | Stiff | No Stiff | Stiff | |
| Pu (Kn) | Pu (Kn) | Pu (Kn) | Pu (Kn) | |
| Flat | 164.8 | 172.3 | 205.8 | 225.0 |
| Trap | 201.0 | 204.5 | 227.8 | 240.6 |
| Rec | 194.5 | 195.8 | 230.7 | 244.6 |
| Sin | 182.0 | 186.8 | 223.1 | 240.6 |
| Tria | 182.0 | 191.4 | 218.5 | 227.8 |
| Web Corrugation | Type Reverse Channel Connection | |||||
|---|---|---|---|---|---|---|
| Flexible | Hybrid | Flush | Extended | ΔPu% (Flush/Flexible) | ΔPu% (Extended/Flexible) | |
| Pu (Kn) | ||||||
| Flat | 180.8 | 183.9 | 215.4.9 | 226 | 19.4 | 25.0 |
| Trap | 184.8 | 167 | 223.8 | 240.6 | 21.1 | 30.2 |
| Rec | 186.8 | 167.1 | 242.1 | 244.6 | 29.6 | 30.9 |
| Sin | 185.6 | 166.2 | 244.4 | 240.6 | 31.7 | 29.6 |
| Tria | 186.0 | 172 | 195.8 | 227.6 | 5.3 | 22.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsawaf, S.A.; Alshehri, F.S. Behaviour of Structural Subassemblies of Steel Beams with Corrugated Webs Using Reverse Channel Connections. Buildings 2025, 15, 4110. https://doi.org/10.3390/buildings15224110
Elsawaf SA, Alshehri FS. Behaviour of Structural Subassemblies of Steel Beams with Corrugated Webs Using Reverse Channel Connections. Buildings. 2025; 15(22):4110. https://doi.org/10.3390/buildings15224110
Chicago/Turabian StyleElsawaf, Sherif A., and Fahad S. Alshehri. 2025. "Behaviour of Structural Subassemblies of Steel Beams with Corrugated Webs Using Reverse Channel Connections" Buildings 15, no. 22: 4110. https://doi.org/10.3390/buildings15224110
APA StyleElsawaf, S. A., & Alshehri, F. S. (2025). Behaviour of Structural Subassemblies of Steel Beams with Corrugated Webs Using Reverse Channel Connections. Buildings, 15(22), 4110. https://doi.org/10.3390/buildings15224110





