Abstract
The Activity Concentration Index (ACI), defined in Directive 2013/59/Euratom, serves as a criterion for the radiological significance of Naturally Occurring Radioactive Materials (NORMs) concentrated in building materials, considering related exposures due to the external gamma radiation field but not due to radon concentration levels. This study proposes a simple way of applying the ACI to interior spaces when concrete is the dominant construction material. Three calculation methods were examined, using four spaces within existing buildings, namely Method A, using the building elements’ mass proportions as a weighting factor; Method B, using only the geometrical characteristics of the internal space; and Method C, combining the mass proportions and inverse square distances. This methodology proposes a way of calculating the ACI based on data provided by existing studies about NORM concentrations in building materials and, thus, no sampling and subsequent NORM concentration measurements were required. The spatial data could be easily determined using either building plans or in situ measurements, using a handheld laser distance meter. The advantages and disadvantages of all three methods were analyzed, along with a comparison to in situ gamma radiation field measurements, performed with a portable Geiger–Müller detector. All the methods showed proportionality to the measured values. Method C was found to be the most suitable, especially for existing buildings, and Method A is recommended for early-stage design assessments.
1. Introduction
The exposure of a person, living or working indoors, to ionizing radiation fields has multiple origins, as follows [,]: (a) exposure to an external gamma (ionizing) radiation field from objects (including building elements) present in a building’s interior spaces; (b) inhalation of the naturally occurring radioactive gas radon (Rn-222); (c) exposure to any ionizing radiation due to NORMs that have entered the human body by means other than the inhalation of radon; and (d) exposure to ionizing radiation fields due to artificial factors, such as the case of a person’s presence inside a hospital building or diagnostic center to undergo a diagnostic method using an X-ray device. The stochastic consequences due to radiation exposure (i.e., cancers) observed in concurrent populations, which means people who, at most, live or even work indoors, are attributed to all these types of exposure to ionizing radiation []. In addition, it must be taken into account that exposure to radionuclides is not the only cause of carcinogenesis, since factors such as alcohol consumption, smoking, exposure (inhalation) to asbestos fibers, and exposure to ultraviolet radiation are considered more important carcinogenic factors compared to occupational exposures to ionizing radiation (-γ and -X radiation) [].
When analyzing the special case of an individual’s exposure to -γ radiation fields due to the structural elements from which a building is constructed, it must be mentioned that the intensity of the exposure and its result (the dose of ionizing radiation that the individual receives) are determined according to the following aspects:
(a) The content (concentration) of radioisotopes in the structural elements of the building, and especially in the interior, which is analyzed for each element, can vary significantly, depending on the content of the radioisotopes in the building materials from which the building’s structural elements are made [,,,,,,,]. These radioisotopes are mainly K-40 and those belonging to the decay chains of Ra-226 and Th-232, which emit photons (γ-radiation) at a range of energies from 0.1 to 2.6 MeV [], not excluding other radioisotopes, such as cesium-137 [], that are found in significantly smaller amounts in common building materials. It should be noted that the architect’s decision on where to locate each building element is important. Two factors are very significant, especially in the case of where concrete elements, which normally consist of many individual components, are used in the structure, namely (i) the mix proportions of the used components (i.e., cement, aggregates, water), which is inextricably linked to the expected strength of the building’s structural elements [], and (ii) the choice of the components themselves, such as using building materials containing components listed in Annex XIII of Directive 2013/59/Euratom, the “Indicative list of types of building materials considered with regard to their emitted gamma radiation” (a typical example is cement to which fly ash has been added or concrete containing granodiorite (e.g., due to the recycling of waste material) [,].
(b) The duration of exposure, the distance from the radiation source, and the possible presence of shielding (the three dose limiting factors are time, distance, and shielding []):
(b1) Time: The dose received by a person in a space in which he is externally exposed to a certain dose rate from a -γ radiation field is, by definition, proportional to the time the person remains in that space. Therefore, it is a very important element to use when considering the interior space of a building. For example, a person who does not travel frequently for work typically spends about eight hours per day in the bedroom of their primary residence, approximately one-third of their daily life. On the other hand, a person who works in an office spends about eight hours per day, for at least 200 days per year, in that office. Therefore, it makes more sense to apply the ACI for each interior space in a building, combined with occupancy information, than to apply the ACI uniformly for the entire building.
(b2) Distance: The position of the building’s internal occupant is also a factor that is expected to influence the -γ radiation dose rate, at least, in combination with the factor concerning the concentration of radioisotopes in the materials of the surrounding building elements. In an extreme but typical example, the dose rate due to γ- radiation is expected to be significantly higher than usual at a point inside a building that is very close to a granite mass (e.g., a granite bench or a cover made of granite slabs).
(b3) Shielding: Other materials interposed between the occupant and a building element reduce the intensity of the -γ radiation field originating from that building element through the mechanism of “shielding”. Such cases include the following: (i) a floor cover between a concrete slab and the person standing on it, (ii) any cover (e.g., granite slabs) between the vertical building elements and the occupant, or even (iii) the presence of other objects (furniture, machinery, special structures, etc.) that may be present in the building’s internal space. Table 1 provides the values of the linear attenuation coefficient μ (which represents the fraction of a beam of photons, such as X-rays or gamma rays, that is absorbed or scattered per unit of thickness of the absorber), the mass attenuation coefficient μ/ρ (a measure of how easily a material can attenuate a beam of photons, such as X-rays or gamma rays, per unit mass of the material, and it is equal to the linear attenuation coefficient μ of the material divided by its density ρ), and Half-Value Layer (HVL) (the thickness of the material required to reduce the gamma-ray intensity by half, where HVL = ln2/μ) for materials typically used in buildings and interiors (e.g., furniture or closets). The values provided are at 662 keV, corresponding to the gamma-ray energy emitted by cesium-137, a common reference in radiation shielding studies.

Table 1.
Linear attenuation coefficient (μ in cm−1), mass attenuation coefficient (μ/ρ in cm2/g) and Half-Value Layer (HVL in cm−1) for materials typically used in buildings and interiors [,,].
According to the above, a 1 cm thick wood structure (e.g., furniture slab or closet door) would result in a 7.7% reduction in transmitted gamma radiation, when considered at an energy of 662 keV. The same calculation for a 1 cm thick marble slab (e.g., marble tiles) results in a 15.5% reduction at the same energy level. Finally, a 30 cm thick concrete slab attenuates 99.5% of the incident gamma radiation at 662 keV.
According to definition 9 of Directive 2013/59/Euratom [], “building material means any construction product for incorporation in a permanent manner in a building or parts thereof and the performance of which has an effect on the performance of the building with regard to exposure of its occupants to ionising radiation”. To assess whether the use of building materials (as defined above) should be the focus of a radiological assessment, Annex VIII of Directive 2013/59/Euratom defines the Activity Concentration Index, ACI:
In Equation (1), CRa-226 and CTh-232 are the concentrations of Ra-226 and Th-232, that is, the primary radioisotopes of the respective decay chains, not including their daughters, and CK-40 is the concentration of K-40. This formula was proposed to provide an estimate of the level of radiological risk to a person standing on a semi-infinite ground soil (which means of practically infinite depth) [,,]. Cases exceeding value 1 when this formula applies are identified as “building materials” that may cause an exceedance of the reference level of 1 mSv per year, as defined in par. 1 of article 75 of the Directive 2013/59/Euratom. It should be mentioned that this equation does not consider the level of exposure to the naturally occurring radioisotope gas Rn-222 [].
Equation (1) is a tool for evaluating the possible impact of the “building materials” used for the construction of any building. However, as discussed above, the final biological impact on humans due to the use of “building materials” cannot be assessed based only on the concentration of radioisotopes in every individual “building material”, separately. The report of the United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR) of the year 1993 [], in which the idea of an approach by means of an index, such as that of Equation (1), was first formulated, suggests that for complex exposure geometries, such as that of the external exposure to a -γ radiation field of a person inside a building, the index in question should be obtained after mass-weighting over the presence of the various materials in the evaluated construction.
UNSCEAR and Euratom models do not take into account the geometry of the internal space of a building. They are screening tools used to assess whether building materials might cause an excessive indoor gamma dose rate due to their content of naturally occurring radionuclides, but they do not provide an exact formula for calculation under real conditions. As we see in Equation (1), this index is independent of room size, shape, or wall thickness. This paper is the first to propose various simplified methods of weighting radioisotope concentrations in building elements, with the aim of calculating the value of the ACI for a specific interior space of a building where the dominant building material is concrete. The method reflects the nature of the internal space itself, without considering specific occupancy details—such as the exact arrangement or use of furniture at any given moment. In this way, the result of the index calculation serves as an indicator of the potential for the evaluated space to be classified as an area of radiological importance. At the same time, it is not reasonable to ignore the geometry of the interior space under evaluation.
Three different methods of weighting radioisotope concentrations were examined, in terms of their advantages and disadvantages, using (a) the ratio of the mass of the building materials included in the interior space of the building; (b) the geometry of the interior space, specifically with a weighting factor that is the inverse of the square of the distance from the center of the evaluated space to the closest point on the evaluated structural element, and (c) the combination of these two factors into a single weighting factor. These three methods of calculating ACI for indoor spaces were applied to the case of four indoor spaces in buildings where the main construction product is conventional concrete. The aim of this paper is to propose a simple way of calculating ACI that ensures (a) ease of calculations so that designers of new buildings and evaluators of existing buildings are not overly burdened and (b) the required sensitivity of the index when building internal spaces of radiological interest are evaluated.
2. Materials and Methods
2.1. Definition of the Building’s Internal Space Under Assessment
In all the following estimation methods, the point for which this estimation is performed is the center of the internal space under assessment. In more detail, a definition of this reference point could be the cross-section of lines connecting the diagonally opposite corners of the internal space (room or similar) at a height of 1 m above the standing level. This reference point is not considered as the exact representative of the exposure of the occupant. It is rather representative of the internal space itself, without considering the exact occupancy profile (e.g., the exact presence of furniture that is used at any specific time point). The method provides a broad, structural assessment rather than a dynamic, moment-to-moment one that includes movable or changeable interior features. In such a way, the result of the index calculation acts as an indicator of the potential of the under-assessment space to be characterized as a place of radiological significance. The proposed indicator values could lead to a characterization of the under-assessment space as is indicatively shown in Table 2. A similar characterization scale was suggested in a previous study [] per building material, but not for all those contributing to the under-assessment internal space.

Table 2.
Characterization of radiological significance for the under-assessment internal space when all contributing building materials are accounted for in the calculation of ACI according to Method C.
The above-mentioned definition of the reference point is easily realized in any case of a closed room surrounded by solid walls where, in the best case, adjacent walls are parallel to each other.
Considering the exposure geometry, a few more parameters should also be defined:
- When the exposure geometry is accounted for in the applied method (i.e., for Methods B and C), the distance of each building element accounted for in the calculation is defined as the distance from the reference point to the surface of the building element or to the closest edge to the reference point if the building element is not perpendicularly positioned to the line connecting it to the reference point (see d1 in Figure 1). In general terms, as shown in Figure 1, any contributing point source mass positioned at depth d2 in the building element emits gamma radiation that is self-attenuated by the building element’s material of thickness d2. As has been already studied [], this depth d2 cannot be more than approximately 30 cm. Any NORMs positioned at a depth of more than 30 cm do not contribute to the gamma dose rate at the reference point.
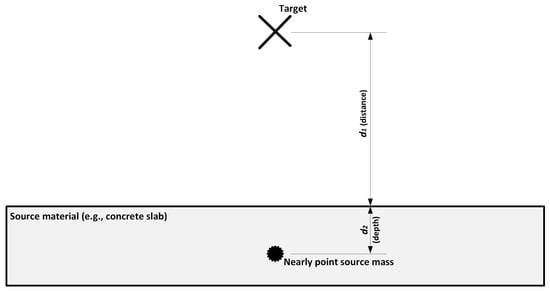 Figure 1. Self-attenuation effect on the gamma dose rate at the reference point.
Figure 1. Self-attenuation effect on the gamma dose rate at the reference point.
- Again, when the exposure geometry is accounted for in the applied method (i.e., for Methods B and C), the angular deviation θ of the building element’s point source mass (as shown in Figure 2) increases the distance from the point source mass to the reference point. In general, this distance equals √(dp2 + dh2) = dp·cos θ = (d1 + d2)·cos θ = dh·sin θ. In practice, this means that there is a maximum deviation dh beyond which any point source mass does not contribute to the gamma dose rate at the reference point, due to the law of the inverse square distance []. According to simple calculations using the inverse square distance laws, Figure 3 shows this maximum angular deviation, expressed as values of distance dh, which can be feasibly measured in an existing building element. Based on Figure 3, there is no meaning in accounting for building element parts that are positioned away by a length of twice dh.
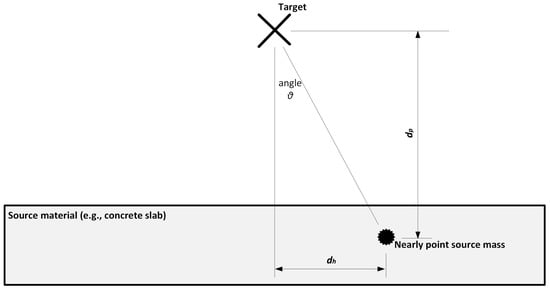 Figure 2. Angular deviation effect on the gamma dose rate at the reference point.
Figure 2. Angular deviation effect on the gamma dose rate at the reference point.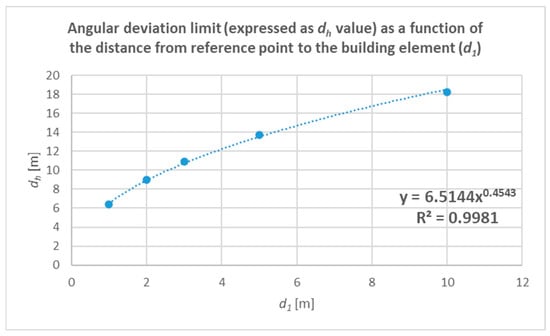 Figure 3. Maximum angular deviation, expressed as distance dh values, away from which no contribution to the gamma dose rate at the reference point is produced.
Figure 3. Maximum angular deviation, expressed as distance dh values, away from which no contribution to the gamma dose rate at the reference point is produced.
- The maximum depth of 30 cm and what is shown in Figure 3 are also interesting for the cases where the ACI calculation method accounts for the building elements’ mass proportions. These limitations define the maximum dimensions of any contributing building element that should be considered in the calculation method to estimate the volume of the building element’s contributing part. This volume, multiplied by the density of the building element’s material, defines the mass to be accounted for in the calculation method (mi). For example, if the internal space under assessment is an occupational space (e.g., a large floor of a concrete structure used as offices) and the floor slab is large enough to exceed a radius of 6 m around the reference point, practically, in a squared space, if the length of each wall exceeds approximately 8.5 m, then the dimensions of the slab to be accounted for in the calculation of ACI should be reduced accordingly.
- Figure 4 shows the geometry of human exposure when a person is standing on a semi-infinite ground soil due to activity concentration C of any radioisotope distributed in the soil. In the case of a building’s internal space, the exposed person is surrounded by building elements in addition to the standing ground (e.g., a concrete slab). Considering a concrete slab of maximum 30 cm thickness as producing the same field as a semi-infinite ground containing activity concentration C, this can be used as a reference mass to estimate the ratio of the mass of all other building elements present in the internal space under assessment. These building elements are limited to those having an internal surface in contact with the internal space air.
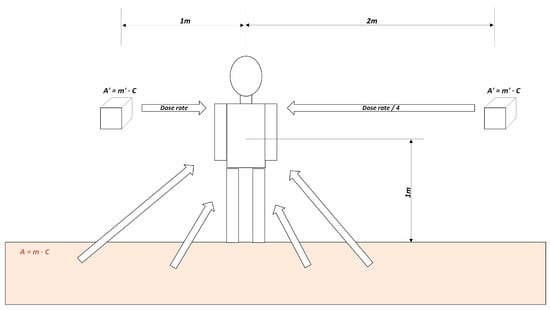 Figure 4. Geometry of human exposure when the person is standing on a semi-infinite ground soil due to activity concentration C of any radio isotope distributed in the soil. The arrows show the gamma field produced by materials near the exposed person (e.g., the ground soil where the person stands).
Figure 4. Geometry of human exposure when the person is standing on a semi-infinite ground soil due to activity concentration C of any radio isotope distributed in the soil. The arrows show the gamma field produced by materials near the exposed person (e.g., the ground soil where the person stands).
2.2. ACI Calculation Process
All three calculation methods involve the use of weighting factors to estimate a weighted mean of NORM concentrations within all building elements that form the interior of a living or working space. ACI is then calculated, using Equation (1). In the following equations, the symbol X denotes any of the three NORMs.
Method A:
Each NORM concentration is estimated using a weighting process based on the mass proportion of the building materials that are permanently present in the evaluated area.
NORM concentrations are weighted by the mass of all structural elements in contact with the interior space being examined each time (e.g., across the entire thickness of the underlying concrete slab).
In Equation (2), i and total number n denote the structural elements that contribute to the considered internal space. Obviously, the estimation of mi requires knowledge of the volume and specific gravity of the structural element.
Method B:
The index is calculated using the inverse of the square of the distance di of each structural element from a point located at the center of the interior space and at a height of 1 m above floor level.
In Equation (3), the distance di is calculated from the center of the interior space (i.e., the reference point for calculating the index) to the closest point of the interior surface in relation to the space under consideration, of the structural element under evaluation.
Method C:
The index is obtained by combining the factors used in the above Methods A and B.
In Equation (4) the mass m1 is the estimate for the mass of the underlying slab (typically, for this work, a reinforced concrete slab). In this way, an adjustment of the mass of the included structural element is achieved under the conditions of the geometry for which Equation (1) has been proposed, i.e., for a semi-infinite underlying soil, considering that a reinforced concrete slab at least 0.30 m thick can behave as a body of semi-infinite dimensions []. Equation (4) is practically a combination of Equations (2) and (3), as activity concentrations are weighted by a factor that incorporates both mass ratios and inverse square distances of building elements measured from the reference point.
2.3. Data on Activity Concentration of NORMs in Building Elements
For the application of the typology in the previous paragraph, the values for the concentrations of Ra-226, Th-232 and K-40 mentioned in relevant reports were used. For the slabs made of reinforced concrete and the vertical brick elements, values were taken from a survey conducted at the European level [,], which, however, includes individual activity concentration values for concrete and bricks obtained from product samples in the Greek market (as an example). Researchers attempting to perform this calculation for different areas (e.g., for a specific country) could rely on the results from other references providing naturally occurring radioactive material concentrations in construction products from those areas [,,,,,].
In this work, no further analysis of the accuracy of the data in Table 3 is carried out, as the aim is to evaluate the effectiveness of the proposed formulas for calculating the ACI, not to determine its values per se. For this purpose, and to make the calculations feasible, even if indicative, it was assumed that the specific weight of the clay bricks is equal to 1900 kg/m3. Also, the concentration of radioisotopes of natural origin contained in the polyurethane foam material was considered minimal, equal to concentrations that can be found in drinking water [], considering that these specific amounts may only occur due to radiopollution from the natural environment during the production process of polyurethane foam boards. This material is synthesized through the reaction of polyols and diisocyanates, both typically derived from petrochemical sources []. The specific weight of the polyurethane foam was taken as 60 kg/m3.

Table 3.
Characteristics of building elements (concentrations of naturally occurring radioisotopes and specific gravity) depending on their predominant building material (in parentheses the reported minimum and maximum value).
2.4. Description of the Analyzed Indoor Spaces
For the analysis carried out in this work, four indicative cases of spaces were chosen, presenting differences in the type, mass and geometry of the vertical structural elements and the superstructure, while all are based on a slab made of reinforced concrete. These spaces (three interior spaces and one pilotis space), for which the formula of Section 2.1 was tested, are as follows:
Space 1: Ground floor space pilotis (Figure 5), i.e., a space with an underlying reinforced concrete slab, an overlying concrete slab (with its lower surface at a height of 2.76 m from the floor surface) and minimal vertical structural elements (5 columns of standard dimensions made of reinforced concrete).
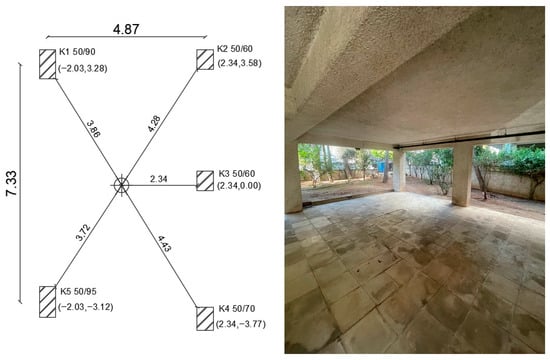
Figure 5.
Space 1: Pilotis.
Space 2: Office in a construction site/container (Figure 6), which is placed on a reinforced concrete slab and its internal height is 2.60 m.

Figure 6.
Space 2: Construction site office.
Space 3: A bedroom in a multi-storey apartment building (Figure 7), i.e., a space which has an underlying and overlying slab of reinforced concrete, but which is mainly surrounded by vertical elements of brick wall, at a short distance from the center of the room. The height of the interior is 2.76 m.
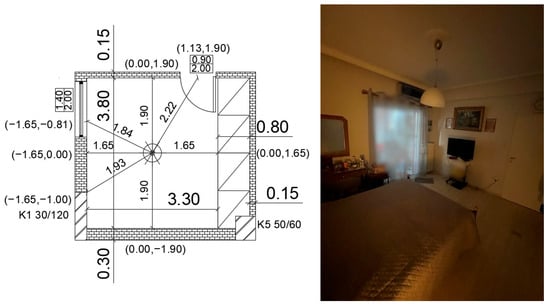
Figure 7.
Space 3: Bedroom.
Space 4: Underground parking area of an apartment building (Figure 8), i.e., an area that has an underlying and overlying slab of reinforced concrete and which is surrounded by vertical structural elements (walls) of reinforced concrete on three sides. The height of the interior is 2.97 m.
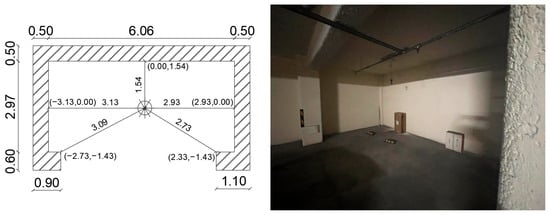
Figure 8.
Space 4: Underground vehicle parking area.
2.5. Method for Measuring the Gamma Dose Rate
A simple gamma dose rate measurement process was applied to validate that the estimated ACI values are compatible with the external gamma radiation exposure levels at the reference point. A Mirion Technologies, model RDS-32 handheld radiation survey instrument, utilizing an energy-compensated Geiger Müller tube as a detector, was used. According to the manufacturer, RDS-32 calibration accuracy in the reference calibration direction and in the Cs-137 calibration field (temperature 20 °C) is ±5%. Each measurement lasted for 12 min, while the equipment was set to log measurement results every 20 s. This means that each measurement result was based on a series of 36 subsequent measurements. Before each measurement, the operator located the reference point in the assessed space using a handheld laser distance meter Uni-T, model UT390H (Uni-Trend Technology Co., Ltd., Dongguan City, Guangdong Province, China) with a range of 0.05 m to 50 m and an accuracy of ±1.5 mm, as specified by the manufacturer. During the measurement, the operator was constantly rotated around his body axis, at such a rate that 4 complete rotations were made during the 12 min measurement period. At the same time, no other person was present in the assessed space.
3. Results and Discussion
3.1. ACI Calculation Results
Table 4 shows the results of calculations of the Activity Concentration Index for the four spaces examined, using all three Methods A–C as well as the in situ gamma dose rate measurements using a handheld Geiger–Müller detector.

Table 4.
Results of calculations of the Activity Concentration Index for the four indicative areas analyzed, using all three Methods A–C, and of in situ gamma dose rate measurements using a handheld Geiger–Muller detector.
The pilotis area and the office area on a construction site differ essentially in that the former has an overlying reinforced concrete slab. This comparison makes it clear that Method C shows a more representative sensitivity when the factor being considered has significant mass and is therefore likely to contribute to the dose received by the subject in that space. The index value with Method C successfully distinguishes the case of space 4 as more unfavorable compared to spaces 1 and 2. That is, the space is surrounded on almost all sides by concrete blocks in comparison to spaces surrounded by concrete blocks with smaller mass/dimensions.
Comparison of the values from Method A for spaces 1, 2 and 4 shows that this method does not exhibit sensitivity to the presence of additional structural elements such as the underlying slab.
The index value from Method B for space 3 shows excessive sensitivity when the evaluated site contains building material with increased concentrations of radioisotopes of natural origin, even if the specific building element considered is of low mass.
It should be mentioned that the above results are highly dependent on the definition of the geometrical characteristics of the internal space under assessment. For example, an alternative definition of the distance between the reference point and the building element could be measured from the center of the building element to better represent its position within the internal space. Such modifications should not cause significant deviations in the calculated values. As can be seen, the ACI by Methods B and C for the case of internal space 3 was estimated using this alternative distance definition, and the results were 0.930 and 0.412, respectively, showing no dramatic change.
3.2. Validation Through Comparison with In Situ Gamma Field Measurement Results
Figure 9 shows the results of ACI calculations in relation to the corresponding in situ gamma dose rate measurements performed in the assessed spaces. Table 5 shows statistical results of fitting a linear no-threshold model to the point sets presented in Figure 9.
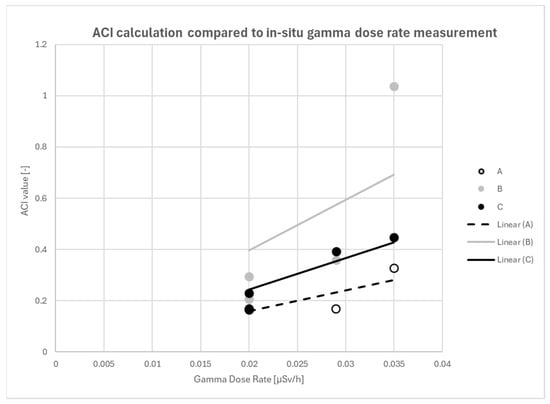
Figure 9.
ACI results for each calculation method in relation to the corresponding in situ gamma dose rate measurement results.

Table 5.
Fitting statistics for a linear no-threshold model for each of the three ACI calculation methods.
Considering that the main criterion for assessing exposure to ionizing radiation is the measure of effective dose, ACI should present values that correspond to specific ambient dose rate levels. The radiological interest of any building’s internal space depends on the gamma dose rate within it. Any ACI calculation method should be significantly correlated with the measured ambient dose rate in the internal space in order to be used as an estimator of the internal space’s radiological interest. It appears that all three calculation methods are proportional to measured values of gamma dose rate at the reference point; thus, ACI calculations are significantly correlated with the corresponding measurement results. Method C presents the best fitting quality. Although Method B is proportionate to the measured gamma dose rate, it seems to provide such high ACI values that the basic radiological reference value of ACI = 1 cannot be used. An example of this is the bedroom case, where brick walls resulted in increased ACI values. According to the literature, concentrations in brick are higher. The presence of brick in the space results in a higher value of the index (greater than 1), although this does not occur in Methods A and C. A new calibration and a new reference value for ACI should be investigated.
3.3. Uncertainty Analysis
The main uncertainty parameters, both for ACI calculation methods and for in situ gamma dose measurement, are identified and analyzed as follows:
- Definitional uncertainty for the determination of the reference point: In any case where the geometry of the internal space is simple, i.e., walls are solid and parallel to each other, the reference point is determined with minimal error. In other cases where difficulties exist, such as recesses, curved surfaces, open sides, etc., different people could determine the reference point with deviations. These deviations could be considered comparable to those dealt with by any operator performing in situ gamma dose rate measurement who tries to position the handheld survey meter in the middle of the internal space. A reasonable estimation of these deviations’ boundaries would be a radius of about 20–30 cm away from the actual center of the internal space, as these correspond to the physical boundaries of the human body (of the operator). Also, in such cases, this maximum shift of the point determined as the center of the internal space could be considered to produce minimal error. This could be attributed to the conflicting effects of the error in the di distances. This means that whenever di is underestimated for a certain building element, normally di for the opposite building element will be overestimated accordingly, so the produced errors nearly neutralize each other.
- Error in determining the mass of a building element: The uncertainty in determining the mass of each contributing building element depends on (a) uncertainty in estimating the volume of the building element, based on estimations of the exact shape and dimensions of the building element, and (b) uncertainty in estimating the density of the building element. A maximum error of not more than 1% could be attributed to any attempt to estimate the dimensions of a well-shaped building element. This means that even if the dimensions of a 3 m (height) × 4 m (length) wall are measured with a handheld laser distance meter, the maximum error for the actual 12 m2 area of the wall would be 0.0012 m2 (=12 cm2). Two specific cases could introduce significant error in estimating the volume of a building element: (i) the case where the cross-section of two perpendicular building elements (i.e., walls) is either double-counted or ignored, and (ii) the case where the “other side of the building element” is not visible (e.g., a concrete slab on ground soil, where its width to be accounted for in ACI calculations could vary between a minimum of 10 cm, reasonable for a carrying capacity of the structure, up to the maximum of 30 cm as per the ACI calculation restrictions introduced in this study).
- Uncertainty in determining the specific activity of NORMs in each building material: This uncertainty parameter is the most significant for existing structures, mainly in cases where no documentation on the used building materials exists. According to previous studies [,,,,,,,,,,,,,,,,,,,,,], NORM activity concentrations vary significantly, both among different countries of origin of the building materials and within the same country. This uncertainty source could be quantified using the intervals of activity concentrations for NORMs provided in previous studies. That means that when a study indicates that Ra-226 activity concentrations in concrete samples taken in a specific county of origin vary between 300 and 900 Bq/kg, then any attempt to use the proposed ACI calculation methods for buildings located in that country should account for an activity concentration equal to 600 ± 122 (a triangular distribution was assumed []). This means an uncertainty in activity concentration estimation of about 20%.
- Uncertainty of in situ dose rate measurement: This is a typical uncertainty level for an in situ measurement using a handheld Geiger–Müller survey meter. According to the measurement procedure followed (i.e., a sequence of 36 measurements, each 20 s long), repeatability, also shown in Table 4, does not exceed 4% of the measured value.
3.4. Methods’ Evaluation
The advantages and disadvantages of each of the methods considered are analyzed in Table 6.

Table 6.
Advantages and disadvantages of each method examined.
It should be noted that in all three methods, calculations represent the point located at the center of the indoor space under evaluation. The movement or way of working or living of the person inside a building is not limited to the center of these spaces. However, the feasibility that characterizes the proposed ACI calculation methods does not aim for an accurate radiological assessment of indoor spaces. That would require accurate dosimetry analysis, possibly through modeling methods (e.g., Monte Carlo analysis).
Also, for the sake of simplifying the calculations, the presence of bulky objects inside the interior spaces (e.g., wardrobes, furniture) was not considered. It is obvious that the presence of such objects acts as shielding to the radiation field produced by structural elements positioned behind them.
None of the indicators investigated (Methods A–C) consider:
- the phenomenon of self-absorption of radiation by the material of the structural element itself.
- the dimensions of the structural element along axes perpendicular to the distance vector of the interior reference point from the nearest point of the factored structural element.
The above could be considered in a practically feasible way only if the calculations are adjusted accordingly, which should, however, require support by 3D building software.
4. Conclusions
According to the above, two of the investigated methods are recommended for new building designers and for auditing existing buildings, respectively:
- Method A is recommended as a preliminary assessment of the radiological interest of a building under study, before finalizing its precise geometrical characteristics, based on rough estimates of construction materials’ quantities (mass estimates).
- Method C is recommended for verifying of the radiological interest of a newly constructed building or of an existing building.
In the context of further optimization of these methods, the following issues could be considered:
- Evaluation of the effect of the phenomenon of self-absorption of radiation by the building material itself. Calculations are proposed to estimate the maximum thickness of various building materials beyond which the contribution of radiation emitted by naturally occurring radioisotopes is not expected to affect the calculated ACI value.
- Further application of Method C to incorporate the presence of elements that are integral to the internal space under assessment (e.g., bedroom wardrobes).
- Investigation into how these methods could be adapted to also apply to exposures due to radon concentrations in internal building spaces.
Author Contributions
Conceptualization, G.P.; methodology, G.P.; investigation, G.P., N.N. and S.G.; writing—original draft preparation, S.G.; writing—review and editing, S.G.; supervision, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACI | Activity Concentration Index |
| NORM | Naturally Occurring Radioactive Material |
| UNSCEAR | United Nations Scientific Committee on the Effects of Atomic Radiation |
References
- IAEA Safety Standards Series No. SSG-32; Protection of the Public Against Exposure Indoors Due to Radon and Other Natural Sources of Radiation. Specific Safety Guide Jointly Sponsored by the IAEA, WHO. International Atomic Energy Agency: Vienna, Austria, 2015.
- United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR). Sources and Effects of Ionizing Radiation; UNSCEAR 1993 Report to the General Assembly, with Scientific Annexes; United Nations: New York, NY, USA, 1993. [Google Scholar]
- Papadakos, G. Stochastic Procedures and Relevant Quantitative and Qualitative Evaluation of Radioenvironmental Consequences in Cohorts Living on Hellenic Ground. Ph.D. Thesis, Section of Nuclear Engineering, School of Mechanical Engineering, National Technical University of Athens, Athens, Greece, 2012. [Google Scholar]
- Jemal, A.; Torre, L.; Soerjomataram, I.; Bray, F. The Cancer Atlas, 3rd ed.; American Cancer Society: Atlanta, GA, USA, 2019; Available online: www.cancer.org/canceratlas (accessed on 19 May 2025).
- Pavlidou, S.; Koroneos, A.; Papastefanou, C.; Christofides, G.; Stoulos, S.; Vavelides, M. Natural radioactivity of granites used as building materials. J. Environ. Radioact. 2006, 89, 48–60. [Google Scholar] [CrossRef] [PubMed]
- Ebaid, Y.Y.; Bakr, W.F. Investigating the effect of using granite and marble as a building material on the radiation exposure of humans. Radiat. Prot. Dosim. 2012, 151, 556–563. [Google Scholar] [CrossRef] [PubMed]
- Trevisia, R.; Leonardia, F.; Risicab, S.; Nuccetelli, C. Updated database on natural radioactivity in building materials in Europe. J. Environ. Radioact. 2018, 187, 90–105. [Google Scholar] [CrossRef] [PubMed]
- Garavaglia, M.; Bucci, S.; Caldognetto, E.; Candolini, G.; Ragani, M.F.; Giovani, C.; Magnoni, M.; Nuccetelli, C.; Peroni, I.; Rusconi, R.; et al. Use of NORM-containing products in construction: Radiological aspects for use of woodchip ashes in building industry. Constr. Build. Mater. 2018, 183, 264–269. [Google Scholar] [CrossRef]
- Gavela, S.; Papadakos, G. Activity Concentration Index Values for Concrete Multistory Residences in Greece Due to Fly Ash Addition in Cement. Eng 2023, 4, 2926–2940. [Google Scholar] [CrossRef]
- Tositti, L.; Masi, G.; Morozzi, P.; Zappi, A.; Bignozzi, M.C. Cleaner, sustainable, and safer: Green potential of alkali-activated materials in current building industry, radiological good practice, and a few tips. Constr. Build. Mater. 2023, 409, 133879. [Google Scholar] [CrossRef]
- Shrestha, A.K.; Shrestha, G.K.; Shah, B.R.; Koirala, R.P. Assessment of radioactivity and radiological hazards associated with bricks in eastern Nepal. Heliyon 2024, 10, e24844. [Google Scholar] [CrossRef]
- Fathy, I.N.; Elfakharany, M.E.; El-Sayed, A.A. Recycling of Waste Granodiorite Powder as a Partial Cement Replacement Material in Ordinary Concrete. Adv. Mater. Sci. 2024, 24, 56–88. [Google Scholar] [CrossRef]
- Fathy, I.N.; El-Sayed, A.A.; Elfakharany, M.E.; Mahmoud, A.A.; Abouelnour, M.A.; Mahmoud, A.S.; Mahmoud, K.A.; Hanafy, T.A.; Sayyed, M.I.; Nabil, I.M. Upgrading the compressive strength and radiation shielding properties of high strength concrete supported with nano additives of lead monoxide and granodiorite. Progress Nucl. Energy 2025, 180, 105562. [Google Scholar] [CrossRef]
- IAEA Safety Standards Series No. GSR Part 3; Radiation Protection and Safety of Radiation Sources: International Basic Safety Standards (BSS). IAEA: Vienna, Austria, 2014.
- Akkurt, I.; Altindag, R.; Gunoglu, K.; Sarıkaya, H. Photon attenuation coefficients of concrete including marble aggregates. Ann. Nucl. Energy 2012, 43, 56–60. [Google Scholar] [CrossRef]
- Najam, L.A.; Mheemeed, A.K.; Hassan, I.M. Using Gamma-Ray to Determine the Homogeneity of Some Building Materials. Int. J. Phys. 2014, 2, 23–29. [Google Scholar] [CrossRef][Green Version]
- Eke, C.; Agar, O.; Segebade, C.; Boztosun, I. Attenuation properties of radiation shielding materials such as granite and marble against γ-ray energies between 80 and 1350 keV. Radiochim. Acta 2017, 105, 851–863. [Google Scholar] [CrossRef]
- European Union. Council Directive 2013/59/Euratom of 5 December 2013 Laying Down Basic Safety Standards for Protection Against the Dangers Arising from Exposure to Ionising Radiation, and Repealing Directives 89/618/Euratom, 90/641/Euratom, 96/29/Euratom, 97/43/Euratom and 2003/122/Euratom. Available online: http://data.europa.eu/eli/dir/2013/59/oj (accessed on 8 April 2025).
- Kocsis, E.; Tóth-Bodrogi, E.; Peka, A.; Adelikhah, M.; Kovács, T. Radiological impact assessment of different building material additives. J. Radioanal. Nucl. Chem. 2021, 330, 1517–1526. [Google Scholar] [CrossRef]
- Nuccetelli, C.; Risica, S.; D’Alessandrο, M.; Trevisi, R. Natural radioactivity in building material in the European Union: Robustness of the activity concentration index I and comparison with a room model. J. Radiol. Prot. 2012, 32, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Senthilkumar, G.; Raghu, Y.; Sivakumar, S.; Chandrasekaran, A.; Prem Anand, D.; Ravisankar, R. Natural radioactivity measurement and evaluation of radiological hazards in some commercial flooring materials used in Thiruvannamalai, Tamilnadu, India. J. Radiat. Res. Appl. Sci. 2014, 7, 116–122. [Google Scholar] [CrossRef]
- Legasu, M.L.; Chaubey, A.K. Determination of dose derived from building materials and radiological health related effects from the indoor environment of Dessie city, Wollo, Ethiopia. Heliyon 2022, 8, e09066. [Google Scholar] [CrossRef]
- Abojassim, A.A.; Al-Taweel, M.H.; Abdulwahid, T.A. Evaluation of natural radioactivity levels for local and import of cement in Iraq. J. Sci. Eng. Res. 2014, 5, 218–220. [Google Scholar]
- Agbalagba, E.O.; Osakwe, R.O.A.; Olarinoye, I.O. Comparative assessment of natural radionuclide content of cement brands used within Nigeria and some countries in the world. J. Geochem. Explor. 2014, 142, 21–28. [Google Scholar] [CrossRef]
- Al-Jundi, J.; Ulanovsky, A.; Prohl, G. Doses of external exposure in Jordan house due to gamma-emitting natural radionuclides in building materials. J. Environ. Radioact. 2009, 100, 841–846. [Google Scholar] [CrossRef]
- Baykara, O.; Karatepe, S.; Dogru, M. Assessments of natural radioactivity and radiological hazards in construction materials used in Elazig, Turkey. Radiat. Meas. 2011, 46, 153–158. [Google Scholar] [CrossRef]
- Randall, D.; Lee, S. The Polyurethanes Book; Wiley: Hoboken, NJ, USA, 2002; ISBN 9780470850411. [Google Scholar]
- Chowdhury, M.; Alam, M.; Ahmed, A. Concentration of radionuclides in building and ceramic materials of Bangladesh and evaluation of radiation hazard, Turkey. J. Radioanal. Nucl. Chem. 1998, 231, 117–122. [Google Scholar] [CrossRef]
- Ibrahim, N. Natural activities of 238U, 232Th and 40K in building materials. J. Environ. Radioact. 1999, 43, 255–258. [Google Scholar] [CrossRef]
- Manic, V.M.; Manic, G.J.; Nikezic, D.R.; Krstic, D.Z. The dose from radioactivity of covering construction materials in Serbia. Nucl. Technol. Radiat. Prot. 2015, 30, 287–293. [Google Scholar] [CrossRef]
- Manic, G.; Manic, V.; Nikezic, D.; Krstic, D. The dose of gamma radiation from building materials and soil. Nukleonika 2015, 60, 951–958. [Google Scholar] [CrossRef][Green Version]
- Sonkawade, R.G.; Kant, K.; Muralithar, S.; Kumar, R.; Ramola, R.C. Natural radioactivity in common building construction and radiation shielding materials. Atmos. Environ. 2008, 42, 2254–2259. [Google Scholar] [CrossRef]
- ISO/IEC Guide 98-3:2008; Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995). ISO: Geneva, Switzerland, 2008.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).