Assessment of Price Adjustment Mechanisms in Romanian Public Construction Contracts: A Longitudinal Cost Impact Analysis (2018–2024)
Abstract
1. Introduction
2. Methodology
- -
- A review of legal documents and public procurement contracts between 2016 and 2024;
- -
- Statistical data sourced from the Romanian National Institute of Statistics (INS), including monthly indices for construction materials, labor, and fuel;
- -
- F1 will be assigned to the formula An = av + (1 − av) ∗ In/Io.Where:
- -
- “An” is the adjustment coefficient.
- -
- “av” is the percentage value of the advance payment.
- -
- “In” is the construction cost index (total) published by the National Institute of Statistics (INS) in the Statistical Bulletin of Prices, Table 15, for month “n”.
- -
- “Io” is the construction cost index (total).
- -
- F2 will be assigned to the formula An = av + m ∗ Mn/Mo + f ∗ Fn/Fo + e ∗ En/Eo.Where:
- -
- “An” is the adjustment coefficient.
- -
- “av” is a fixed coefficient representing the advance payment percentage.
- -
- “m”, “f”, and “e” are coefficients representing the estimated share of each relevant cost element in the execution of the works. (These cost elements are resources such as materials, labor, and equipment).
- -
- “Fn”, “En”, “Mn” are the current price/cost indices or reference prices for materials, labor, and equipment for month “n”, expressed in the contract currency, as applicable 60 days before the last day of month “n”. These price indices or reference prices correspond to the relevant cost elements.
- -
- “Lo”, “Eo”, “Mo”, and the base (reference) price/cost indices for materials, labor, and equipment, respectively (at contract commencement). The following equation will be checked: av + m + f + e = 1.
- -
- F3 will be assigned to the formula C = (ICCM)n/(ICCMian.2021) ∗ P + (1 − P).Where:
- -
- “P” is the proportion determined by the subject of the contract.
- -
- “ICCMn” is the construction cost index for materials for the month before the payment request (month “n”) for which official values are available.
- -
- “ICCMian.2021” is the construction cost index for materials for January 2021 (the base reference index for materials).
- -
- F4 will be assigned to the formula Va = Vo[(1 − p − a) ∗ ICCn/ICCdata referință + (p + a)].Where:
- -
- Va is the adjusted value of the payment request.
- -
- Vo is the value of the payment request according to the prices in the original contract offer;
- -
- a is the percentage of advance payment, determined as the ratio between the advance amount (unreimbursed) and the contract price;
- -
- p is the percentage of profit, determined as the ratio between the profit amount and the contract price;
- -
- ICC_n is the total construction cost index for the month of the payment request;
- -
- ICC_data referință is the total construction cost index for the month before the bid submission deadline (the reference index at contract baseline);
- -
- F5 will be assigned to the formula Valp = Vm ∗ [(%av + %p) + (1 − %av − %p) ∗ ICCmr/ICCmlr] + (Vpl − Vm) + (1 − %cpm) ∗ [(%av + %p) + (1 − %av − %p) ∗ ICCr/ICCplr] − (Vpl − Vm).Where:
- -
- Vapl is the updated value of the payment requested by the contractor at the submission date of the payment request;
- -
- Vpl is the value of the payment requested by the contractor at the submission date of the payment request;
- -
- Vm is the portion of the payment value corresponding to material expenditures, as per the contractor’s payment request;
- -
- ICCmr is the realized construction cost index for materials, published by the National Institute of Statistics, the first Statistical Bulletin of Prices—Table 15 cost indices in constructions by categories of objects and structural elements, applicable 60 days before the last day of the month “n”.
- -
- ICCmlr is the realized construction cost index for materials, published by the National Institute of Statistics, in the first Statistical Bulletin of Prices, for the reference month;
- -
- ICCr is the realized total construction cost index, published by the National Institute of Statistics, the first Statistical Bulletin of Prices, Table 15, applicable 60 days before the last day of the month “n”.
- -
- ICCplr is the total construction cost index, forecasted by the National Commission for Strategy and Forecast, valid in the reference month, for the date 60 days before the last day of the month “n” (according to Annex 4 of the relevant regulation);
- -
- %av is the percentage of advance granted by the client to the contractor as of the payment date;
- -
- %p is the percentage of profit included in the payment requests; if profit is not specified or cannot be identified, a default of 3% of the payment statement value is used;
- -
- %cpm is the weighting coefficient of materials used in calculating the total construction cost index, published by the National Institute of Statistics, the first Statistical Bulletin of Prices, Table 15A, determined according to the type of construction;
- -
- month “n” refers to the month of payment request submission.
- -
- F6 will be assigned to the formula An = av + m ∗ Mn/Mo.Where:
- -
- “An” is the adjustment coefficient to be applied to the value of material expenses within the work statements that will be presented for payment.
- -
- “av” is a fixed coefficient representing the percentage value of the advance payment according to the contract.
- -
- “m” represents the weight of the construction cost index for the cost of materials.
- -
- Mn represents the construction cost index for the cost of materials for the reference month “n”, applicable 60 days before the last day of the month “n”;
- -
- Mo is assimilated to the construction cost index for the cost of materials related to the month of the conclusion of the contract.
- -
- F7 will be assigned to the formula Y = [(1 + I)1/12 − 1] ∗ 100% resulting from the case study that will be published later after the completion of the analyzed data.Where:
- -
- I = the annual inflation rate expressed as a decimal place of 100 (i.e., 10% = 0.10).
- -
- Y = monthly inflation rate expressed as a percentage.
- -
- F8 will be assigned to the formula Va = V0 ∗ IPC/100 resulting from the case study No. 1 resulting from the case study which will be published later after the completion of the analyzed data.Where:
- -
- Va—updated price;
- -
- V0—initial price offered and specified at the signing of the contract;
- -
- IPC—monthly consumer price index.
- (a)
- Cost analysis for projects with a duration of 12 months of execution
- Hypothesis 1 for 2018 having the indicative I1_2018_12_E
- Hypothesis 2 for 2020 with the indicative I2_2020_12_E
- Hypothesis 3 for the year 2022 with the indicative I3_2022_12_E
- (b)
- Cost analysis for projects with a duration of 24 months of execution
- Hypothesis 1 with the start date of 2018 and end date of 2019 with the indicative I1_2018–2019_24_E
- Hypothesis 1 with the start date of 2020 and end date of 2021 with the indicative I2_2020–2021_24_E
- Hypothesis 3 with the start date of the year 2022 and the end date of 2023 with the indicative I3_2022–2023_24_E
- (c)
- Cost analysis for projects with a duration of 36 months of execution
- Hypothesis 1 with the start date of 2018 and end date of 2020 with the indicative I1_2018–2020_36_E
- Hypothesis 2 with the start date of 2020 and end date of 2022 with the indicative I2_2020–2022_36_E
- Hypothesis 3 with the start date of the year 2022 and the end date of 2024 with the indicative I3_2022–2024_36_E
3. Cost Analysis for Projects That Have the Execution Component
3.1. Hypothesis 1
- -
- New construction works—Non-residential buildings, according to Table 15A of the INSS bulletin; the share of material represents 45.82%
- -
- Bid submission date
- -
- Execution time 12 months/24 months/36 months
- -
- Contract signing date: January 2018
- -
- Date of submission of the offer (simplified procedure duration 3 months)—September 2017
- -
- Contract value: RON 10,000,000.00 without VAT
- -
- Monthly work situations will be issued
- -
- “av” is the percentage value of the advance payment compared to the Contract Price: 0.00
- -
- Profit: 5%
3.2. Hypothesis 2
3.3. Hypothesis 3
3.4. Comparison of the Hypotheses 1, 2 and 3
3.5. Comparative Analysis Using Mean Absolute Deviation
4. Conclusions
- In periods of moderate inflation (e.g., 2018–2020), some formulas (especially F1, F2, F4) tend to over-compensate for price changes, yielding adjustment rates higher than actual inflation. In contrast, formulas focusing only on specific cost components (F3, F6 for materials) or general consumer prices (F7, F8) may under-compensate relative to construction inflation.
- In periods of high or rapidly rising inflation (e.g., 2020–2022 and 2022–2024), all formulas struggled to fully match the actual inflation experienced. In our case studies, no formula produced an adjustment that exceeded the cumulative inflation of the period, and most fell well short. This indicates that extraordinary market conditions (sharp inflation spikes) can outpace the adjustment clauses unless those clauses are frequently updated or very responsive.
- Overall, F1—which adjusts the contract based on a broad construction cost index without fixed components (aside from an advance, if any)—provided results closest to actual inflation trends across different scenarios. This suggests F1 is generally the most robust formula for capturing market price evolution, especially if no advance payment is involved. When an advance payment is included, F1’s effectiveness diminishes, underscoring that large advance payments will reduce the contractor’s protection against inflation.
- Formulas that break down the price into multiple components (like F2, F4, F5) can be useful for fine-tuned adjustments, but their performance depends on the accuracy of the weight estimates and the behavior of each cost index. In our analysis, F2 (a weighted index formula) performed well in some cases (e.g., giving the highest adjustment in a high-inflation 36-month scenario), but in other cases, it either over or under-shot the inflation due to differential movements in labor, material, and equipment costs. F4 and F5, introduced by specific legislation in 2021–2022, provided intermediate results; they did not overshoot inflation as in earlier years but also did not fully catch up with the highest inflation spikes.
- Simpler formulas using generic inflation rates, such as F7 (monthly inflation derived from annual) and F8 (consumer price index adjustment), consistently gave the lowest adjustments. These may be too conservative for construction costs, which often rise faster than general consumer prices. Thus, such formulas might be more appropriate for contracts where price stability is expected, but they are not sufficient in a volatile market.
4.1. Discussion
4.2. Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ciurușniuc, C.A.; Ciurusniuc-Ichimov, I.; Șerbănoiu, A.A. Methods of Adjustments the Cost in Constructions. Bull. Politeh. Iași—Constr. Arhit. 2022, 68, 29–38. [Google Scholar] [CrossRef]
- Ciurușniuc, C.A.; Ciurusniuc-Ichimov, I.; Șerbănoiu, A.A. The Impact of Inflation on Construction Materials—An Overview. J. Eng. Res. 2024, 4, 2–6. [Google Scholar] [CrossRef]
- Babalola, A.J.; Aderogba, A.M.; Adetunji, O.O. Inflation and Cost Overrun in Public Sector Construction Projects in Nigeria. ECS Trans. 2022, 107, 16137–16147. [Google Scholar] [CrossRef]
- Pandey, R.K.; Khan, A.; Scholar, P. Impact of inflation rate on construction project: A review. Int. J. Sci. Res. Civ. Eng. 2023, 7, 23–29. [Google Scholar]
- Dabara, D.; Chiwuzie, A.; Omotehinshe, O.; Soladoye, J.O. Impact of inflation on indirect real estate investments in Nigeria. In Proceedings of the European Real Estate Society (ERES) Conference, Cergy-Pontoise, France, 3 July 2019. [Google Scholar]
- Akal, A.Y. Inflation and Reinforced Concrete Materials: An Investigation of Economic and Environmental Effects. Sustainability 2023, 15, 7687. [Google Scholar] [CrossRef]
- Romanian Government. Decision No. Law No. 907 of 29 November 2016 on the Stages of Elaboration and the Framework Content of the Technical-Economic Documentation Related to the Investment Objectives/Projects Financed from Public Funds; Romanian Government: Bucharest, Romania, 2016.
- Akalya, K.; Rex, L.K.; Kamalnataraj, D. Minimizing the Cost of Construction Materials through Optimization Techniques. IOSR J. Eng. (IOSRJEN) 2018, 1, 29–33. [Google Scholar]
- Rajguru, A.; Mahatme, P. Effective Techniques in Cost Optimization of Construction Project. Int. J. Res. Eng. Technol. 2015, 4, 464–469. [Google Scholar]
- Nițu, M.C.; Gasparotti, C. Evolution of the Construction Industry Based on the GDP Indicator in the Period 2008–2018 in Romania. J. Manag. Econ. Eng. 2020, 19, 426–431. [Google Scholar] [CrossRef]
- Meng, J.; Yan, J.; Xue, B.; Fu, J.; He, N. Reducing construction material cost by optimizing buy-in decision that accounts the flexibility of non-critical activities. Eng. Constr. Archit. Manag. 2018, 25, 1092–1108. [Google Scholar] [CrossRef]
- Alsugair, A.M.; Alsanabani, N.M.; Al-Gahtani, K.S. Forecasting the Final Contract Cost on the Basis of the Owner’s Cost Estimation Using an Artificial Neural Network. Buildings 2023, 13, 786. [Google Scholar] [CrossRef]
- Al-Hazim, N.; Salem, Z.A.; Ahmad, H. Delay and Cost Overrun in Infrastructure Projects in Jordan. Procedia Eng. 2017, 182, 18–24. [Google Scholar] [CrossRef]
- Mohamed, E.B.; Mahmoud, S.Y. An Assessment of the Impact of Inflation on the Prices of Selected Construction Materials in Sudan. Int. J. Multidiscip. Res. Publ. 2020, 2, 41–44. [Google Scholar]
- Halpin, D.W. Financial and Cost Concepts for Construction Management; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Holm, L.; Schaufelberger, J.E. Construction Cost Estimating; Routledge: Abingdon, UK, 2021. [Google Scholar]
- Peurifoy, R.L.; Oberlender, G.D. Estimating Construction Costs, 6th ed.; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Humphreys, K.K. Project and Cost Engineers’ Handbook, 4th ed.; Editura Marcel Dekker: New York, NY, USA, 2005. [Google Scholar]
- Lam, W.S.; Lam, W.H.; Jaaman, S.H. Portfolio Optimization with a Mean–Absolute Deviation–Entropy Multi-Objective Model. Entropy 2021, 23, 1266. [Google Scholar] [CrossRef] [PubMed]
- World Bank. Managing Public Procurement in Times of Crisis; Policy Note; World Bank: Washington, DC, USA, 2021. [Google Scholar]
- Albtoush, A.F.; Doh, S. A Review on causes of cost overrun in the construction projects. Int. J. N. Innov. Eng. Technol. 2019, 12, 15–22. [Google Scholar]
- Smith, J. The Economics of Inflation in Construction Projects. J. Constr. Econ. 2020, 45, 123–138. [Google Scholar]
- Ionescu, M.; Popescu, D. Post-pandemic Trends in Romanian Infrastructure. Procedia Eng. 2022, 198, 305–312. [Google Scholar]
- European Construction Sector Observatory (ECSO). Construction Cost Trends in the EU; European Construction Sector Observatory (ECSO): Brussels, Belgium, 2023. [Google Scholar]
- National Institute of Statistics. Available online: https://insse.ro/cms/ (accessed on 10 December 2023).
- Romanian Government. Decision No. 1/2018 of 10 January 2018 for the Approval of the General and Specific Conditions for Certain Categories of Procurement Contracts Related to Investment Objectives Financed from Public Funds; Romanian Government: Bucharest, Romania, 2018.
- Romanian Government. Emergency Ordinance No. 15 of 30 August 2021 on the Regulation of Some Fiscal-Budgetary Measures for Adjusting the Prices of Public Procurement Contracts; Romanian Government: Bucharest, Romania, 2021.
- Romanian Government. Emergency Ordinance No. 47 of 14 April 2022 on the Adjustment of the Prices of Public Procurement Contracts/Sectoral Contracts/Concession Contracts/Framework Agreements; Romanian Government: Bucharest, Romania, 2022.
- Romanian Government. Emergency Ordinance No. 64 of 9 May 2022 on the Adjustment of Prices and Value of General Estimates Within Projects Financed from Non-Reimbursable External Funds; Romanian Government: Bucharest, Romania, 2022.
- Yager, R.R.; Alajlan, N. A note on mean absolute deviation. Inf. Sci. 2014, 279, 632–641. [Google Scholar] [CrossRef]
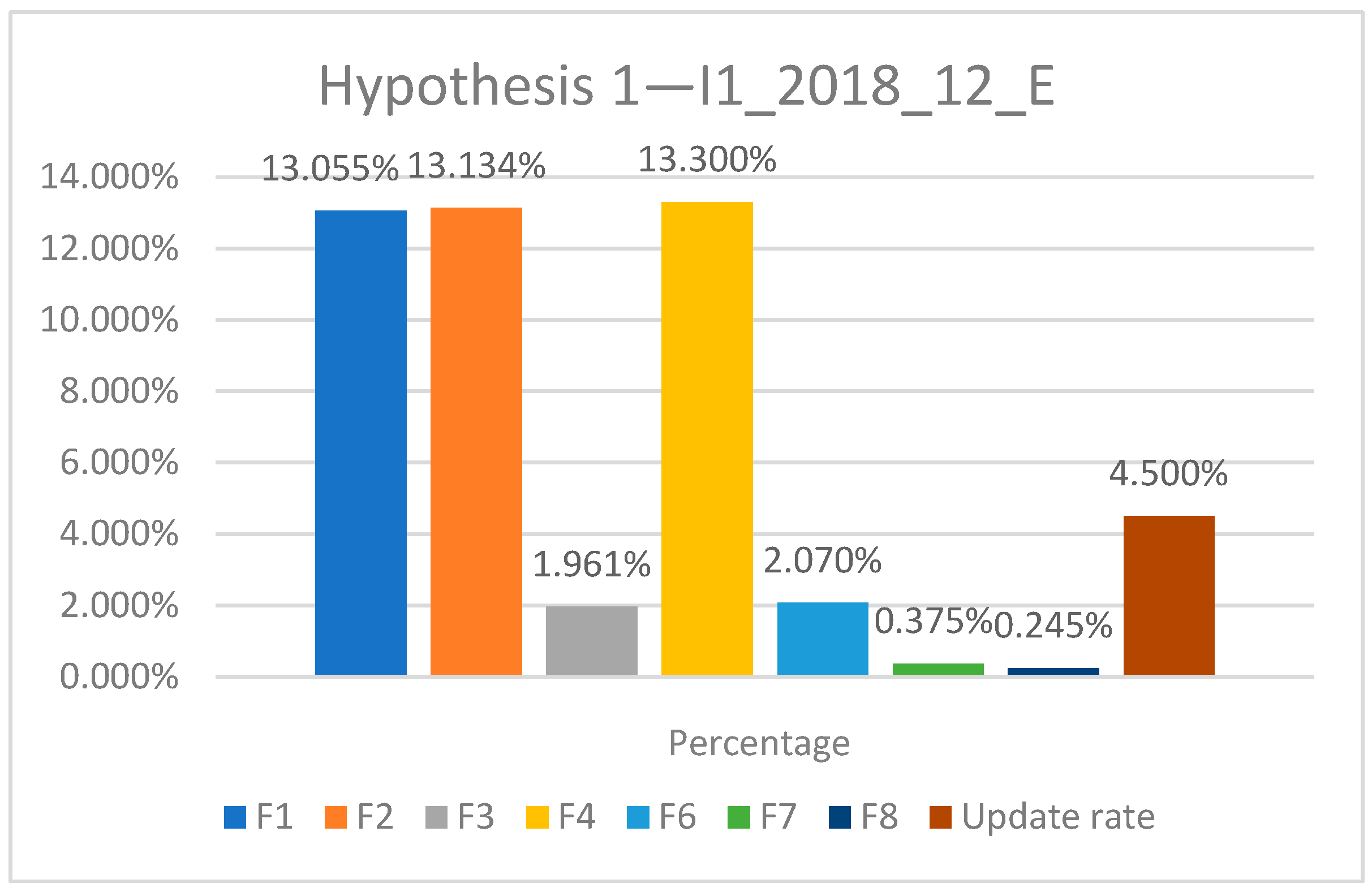

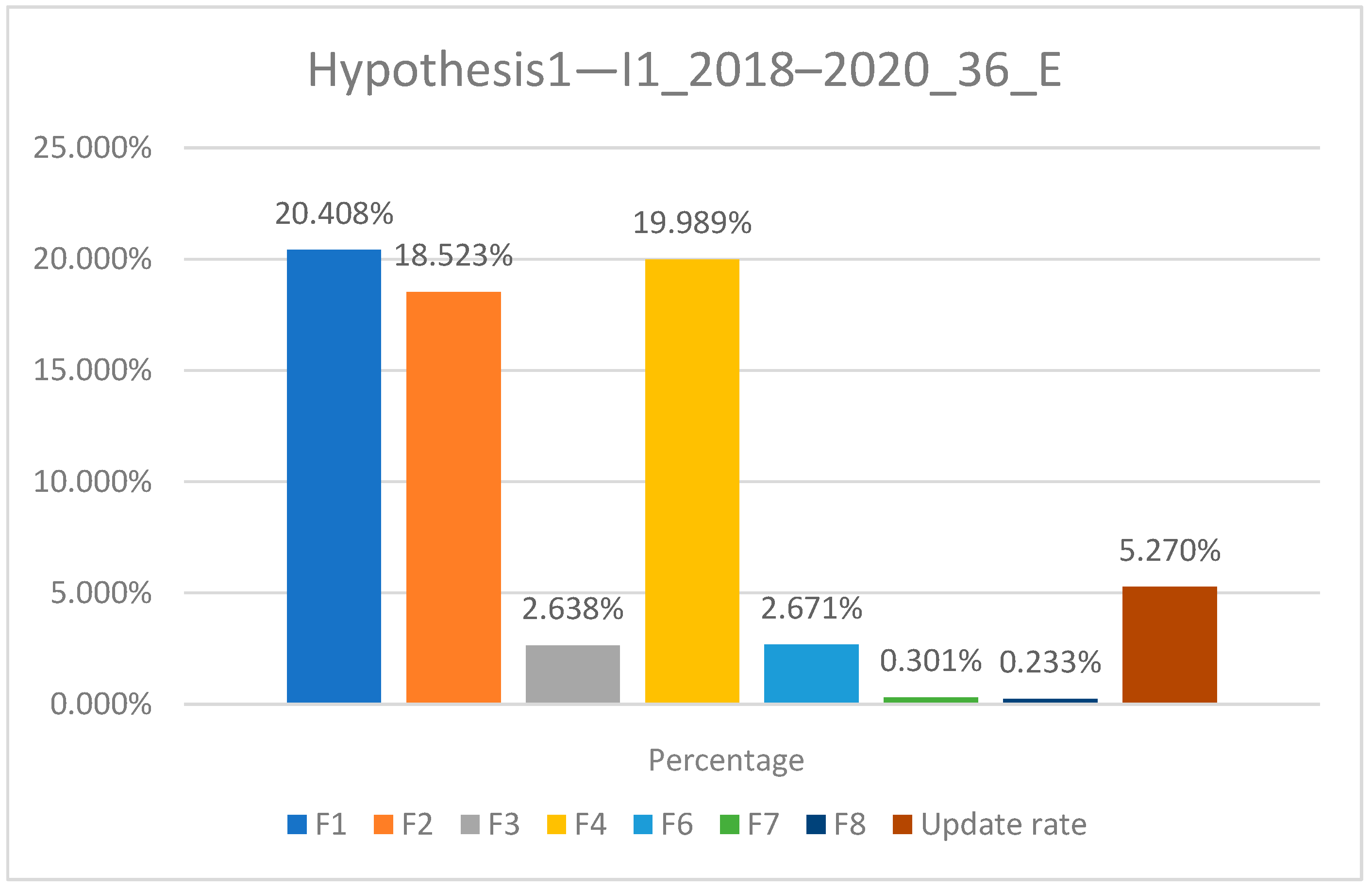
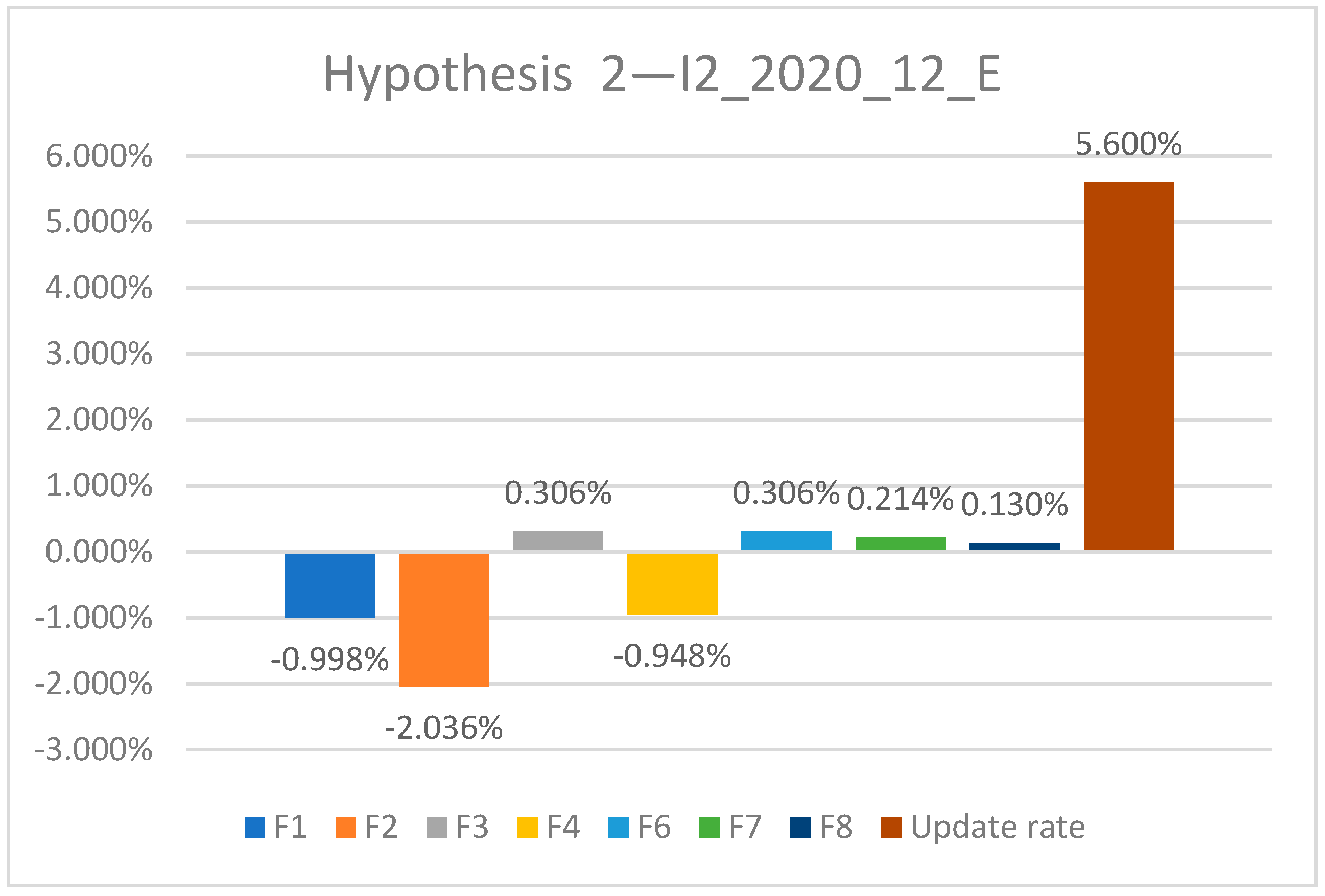


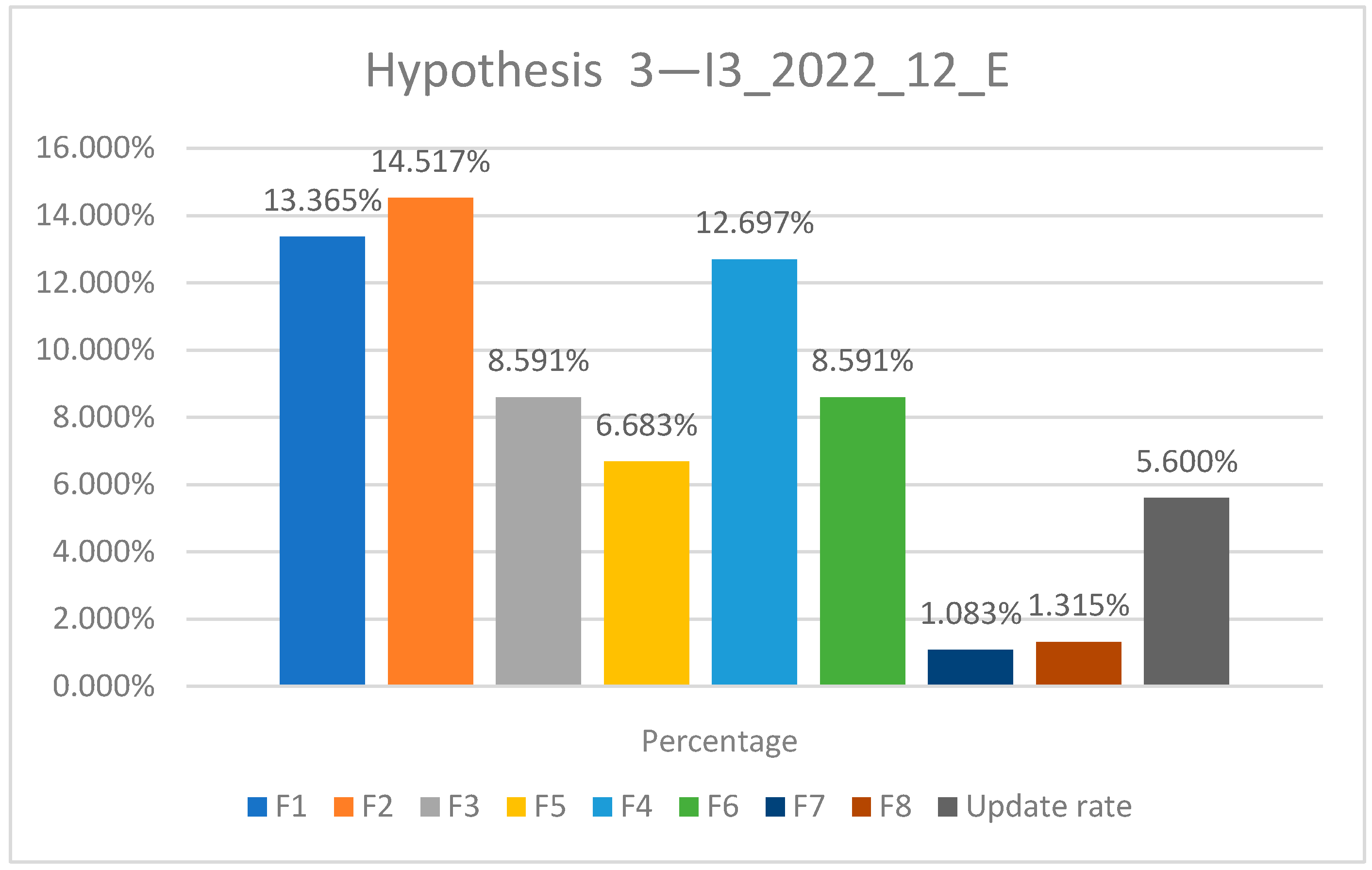

| Formula | Hypothesis 1—I1_2018_12_E | Hypothesis 1—I1_2018–2019_24_E | Hypothesis 1—I1_2018–2020_36_E |
|---|---|---|---|
| F1 | 13.06% | 18.09% | 20.41% |
| F2 | 13.13% | 17.30% | 18.52% |
| F3 | 1.96% | 2.66% | 2.64% |
| F4 | 13.30% | 17.94% | 19.99% |
| F6 | 2.07% | 2.80% | 2.67% |
| F7 | 0.38% | 0.34% | 0.30% |
| F8 | 0.25% | 0.25% | 0.23% |
| Update rate | 4.50% | 4.91% | 5.27% |
| Annual inflation rate | 4.60% | 3.80% | 2.60% |
| 11.00% (cumulative 2018–2020) | |||
| Formula | Hypothesis 2—I2_2020_12_E | Hypothesis 2—I2_2020–2021_24_E | Hypothesis 3—I2_2020–2022_36_E |
|---|---|---|---|
| F1 | −1.00% | 4.86% | 12.83% |
| F2 | −2.04% | 4.92% | 16.74% |
| F3 | 0.31% | 5.75% | 12.54% |
| F4 | −0.95% | 4.62% | 12.19% |
| F6 | 0.31% | 5.75% | 12.54% |
| F7 | 0.21% | 0.31% | 0.56% |
| F8 | 0.13% | 0.39% | 0.68% |
| Update rate | 5.60% | 5.55% | 5.56% |
| Annual inflation rate | 2.60% | 5.10% | 13.80% |
| 21.50% (cumulative 2020–2022) | |||
| Formula | Hypothesis 3—I3_2022_12_E | Hypothesis 3—I3_2022–2023_24_E | Hypothesis 3—I3_2022–2024_36_E |
|---|---|---|---|
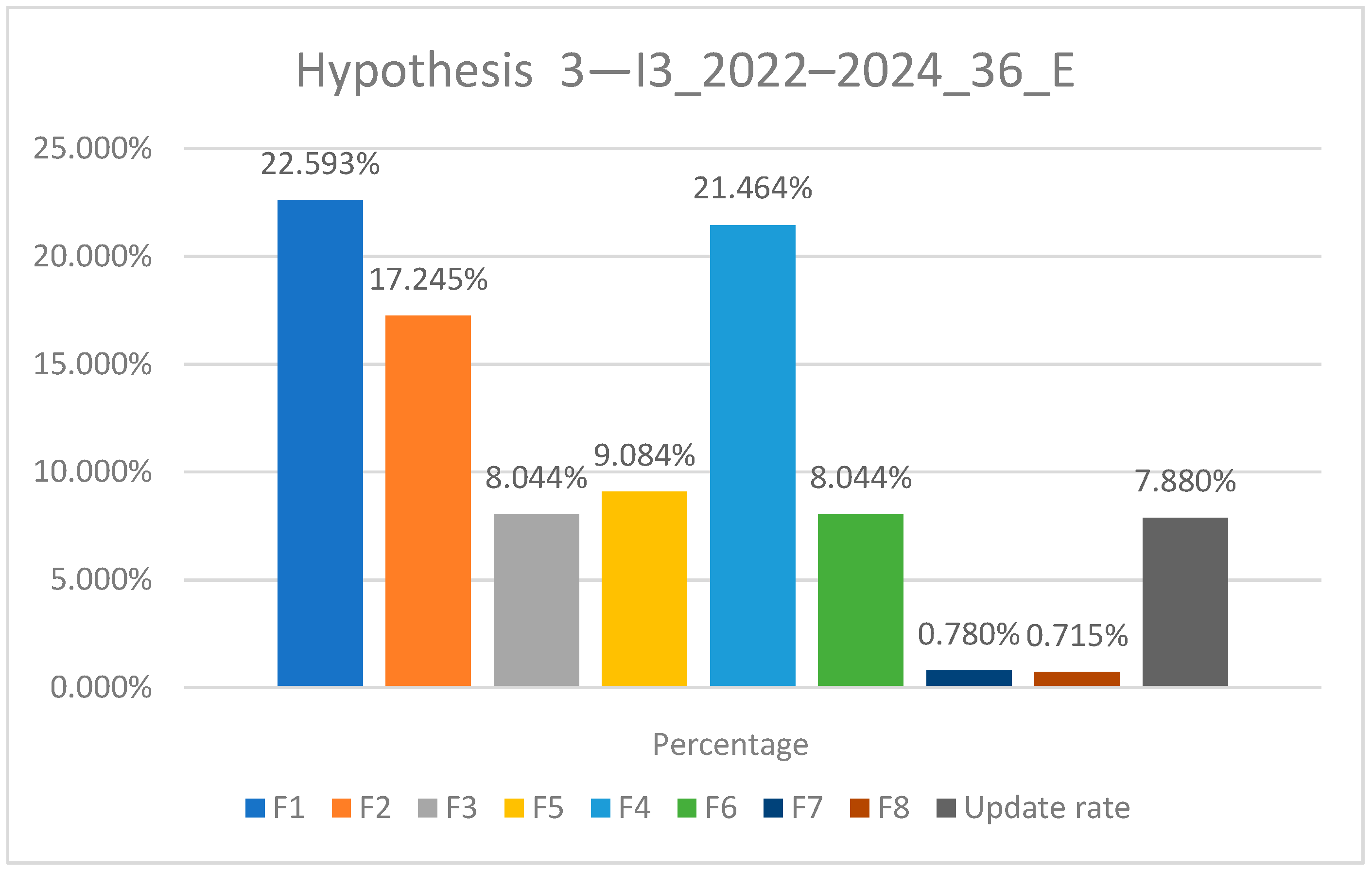
| F1 | 13.365% | 17.62% | 22.59% |
| F2 | 14.517% | 15.02% | 17.25% |
| F3 | 8.591% | 7.82% | 8.04% |
| F5 | 6.683% | 7.45% | 9.08% |
| F4 | 12.697% | 16.74% | 21.46% |
| F6 | 8.591% | 7.82% | 8.04% |
| F7 | 1.083% | 0.96% | 0.78% |
| F8 | 1.315% | 0.91% | 0.71% |
| Update rate | 5.600% | 7.55% | 7.88% |
| Annual inflation rate | 13.800% | 10.40% | 5.10% |
| 29.30% (cumulative 2023–2024) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciurușniuc, C.A.; Ciurușniuc-Ichimov, I.; Șerbănoiu, A.A. Assessment of Price Adjustment Mechanisms in Romanian Public Construction Contracts: A Longitudinal Cost Impact Analysis (2018–2024). Buildings 2025, 15, 2076. https://doi.org/10.3390/buildings15122076
Ciurușniuc CA, Ciurușniuc-Ichimov I, Șerbănoiu AA. Assessment of Price Adjustment Mechanisms in Romanian Public Construction Contracts: A Longitudinal Cost Impact Analysis (2018–2024). Buildings. 2025; 15(12):2076. https://doi.org/10.3390/buildings15122076
Chicago/Turabian StyleCiurușniuc, Cornel Adrian, Irina Ciurușniuc-Ichimov, and Adrian Alexandru Șerbănoiu. 2025. "Assessment of Price Adjustment Mechanisms in Romanian Public Construction Contracts: A Longitudinal Cost Impact Analysis (2018–2024)" Buildings 15, no. 12: 2076. https://doi.org/10.3390/buildings15122076
APA StyleCiurușniuc, C. A., Ciurușniuc-Ichimov, I., & Șerbănoiu, A. A. (2025). Assessment of Price Adjustment Mechanisms in Romanian Public Construction Contracts: A Longitudinal Cost Impact Analysis (2018–2024). Buildings, 15(12), 2076. https://doi.org/10.3390/buildings15122076






