Abstract
The behavior of structural elements, which is very important in structural engineering, can be determined non-destructively using ambient vibration tests. Composite elements used in structures can be formed by combining elements of different materials. It is much more difficult to predict the structural behavior of composite elements because they are made of different materials. Ambient vibration tests are one of the most important methods used to determine the dynamic characteristics of composite elements. In this study, composite cantilever beams were formed by combining wood and steel profiles in various combinations. The dynamic characteristics of these beams (natural frequency, mode shape, modal damping ratio) were determined by both the numerical method and operational modal analysis (OMA) method. Firstly, the initial analytical models of the beams were modeled using the finite element program. The natural frequencies and mode shapes of the models were determined using the modal analysis method. While creating the initial analytical model, the material properties of the beams were entered by taking into account the standard values in the literature. Then, the dynamic characteristics of the beams were determined using an experimental modal analysis method (operational modal analysis test). The dynamic characteristics obtained from tests and the analysis of the initial analytical models were compared. The analytical models were calibrated according to the test results. In this way, the modeled beams were provided with a more realistic dynamic behavior. Numerical models were modeled using the SAP2000 program. As a result of the analysis, the dynamic characteristics and structural properties of composite cantilever beams were compared. As the elasticity modules and cross-sections of the profiles used in the beams increase, the stiffness of the beams also increases. It was determined that the natural frequencies of the composite beams increase with the increase in their stiffness. When the frequencies of the first modes of the least rigid wood (W) beam and the most rigid steel–wood–steel (S-W-S) beam were compared, an increase of 47% was detected.
1. Introduction
Many engineering structures, such as buildings, bridges, and dams, are very important to people. For this reason, structures should not be damaged by external effects and disasters, such as earthquakes. Structural damages can cause both loss of life and major economic losses. From this perspective, it is very important to monitor especially important engineering structures. It is also very important to reveal possible changes in their structural behavior and the reasons for these changes [1,2].
Technological and electronic devices enable the observation of the behavior of structures. The responses of structures can be measured by means of technological accelerometers. By analyzing the acceleration signals measured for different situations and comparing the results obtained, it can be determined whether there is a change in the structure behavior. The method commonly used for this purpose is the Experimental Modal Analysis (EMA) method. The EMA method is used in many engineering fields. The first applications of this method were in the 1940s. In these applications, the method was used to determine damage to railway rails. The method was applied by observing the vibrations created by hitting the rails with sledgehammers. The EMA method is based on the principle of giving a vibration to the structure and measuring the reactions of the structure to this vibration. Depending on whether the effect applied to vibrate the structure is known or not, experimental modal analysis applications are divided into two groups as Traditional Experimental Modal Analysis (TEMA) and Operational Modal Analysis (OMA). In the TEMA method, the effect applied to the structure and the structure’s response to this effect must be known. The dynamic behavior of the structure is obtained by dividing the spectral functions of the response values by the spectral function of the effect values. This method is also called Forced Vibration Testing (FVT) because it also requires knowledge of the effect values. In the OMA method, it is not necessary to know the effect applied to the structure. In this method, it is assumed that the structure is vibrated under random effects, such as wind, vehicle load, and human movement. The dynamic characteristics of the structure can be determined by evaluating the spectral density functions of the response signals in both the time and frequency domains. Since random environmental vibrations are used to vibrate the structure in this method, it is also called the Ambient Vibration Test (AVT). Natural frequencies, mode shapes, and modal damping ratios, which are called the dynamic characteristics of the structure, are obtained from the measurements carried out using experimental modal analysis methods. Since these dynamic characteristics are the main parameters used in determining the dynamic behavior of the structure, it is very important to determine these characteristics realistically to reflect the current behavior of the structure [1,2].
In the design of structures, firstly, analytical models are created to represent the structures. Static and dynamic analyses are performed on these models for different loading conditions. However, analytical models generally cannot accurately represent the real structural behavior. The comparison of dynamic characteristics emerges as a practical solution to identify and eliminate differences in structural behavior. The dynamic characteristics of the current state of the structures can be determined using EMA methods. It is very important to calibrate the analytical models using test results. Thus, analytical models representing the real states of the structures can be obtained [1,2]. In addition, many assumptions are made in the theoretical analysis of structures (material properties, boundary conditions, etc.). Moreover, some mistakes can be made during the construction of the structure. Consequently, it is necessary to identify whether the theoretical design of the structure and the constructed structure have the same dynamic characteristics. Especially when complex structures are taken into consideration, the creation of finite element models in the theoretical analysis of structures may be insufficient and the structures may not be adequately represented. There is also a need to define the dynamic characteristics of historical buildings. However, it is very difficult to determine the material properties of historical structures accurately. Therefore, it is difficult to determine the dynamic characteristics of historical structures theoretically. It is necessary to determine the damage status and service life of structures, such as railway bridges, that were built in the past and are still in use. In addition, the dynamic characteristics of existing steel and reinforced concrete (RC) structures must be determined accurately for their earthquake safety. For these reasons, the necessity of an experimental method that takes into account the above-mentioned situations arises in order to determine and minimize the effects of vibrations on buildings. In addition, experimental methods are very important to determine whether there is damage in the structures, and if there is damage, to determine the location and size of the damage, and to determine the effect of the damage on the behavior of the structure. For this purpose, it is necessary to measure the structure in its current state, determine its dynamic characteristics, and take the necessary precautions [3].
Many studies and research have been carried out using the mentioned experimental methods, considering the vital situations. These situations can be summarized as follows: calibration of the model by comparing the dynamic characteristics of the finite element model with those obtained experimentally; determination of whether the assumptions made in the theoretical analysis are provided in reality; determination of the usability status of existing engineering structures after possible external effects, etc. Bayraktar et al. conducted a full-scale AVT (OMA testing) of a historical masonry minaret. They updated the 3D finite element (FE) model with the results they obtained from the test. In the FE model of the minaret, uncertain modeling parameters, such as material properties and boundary conditions, were changed to minimize the differences between the analytical and experimentally estimated modal properties. Then, earthquake analyses were performed using the calibrated FE model. At the end of the study, it was stated that the analytical and experimental results were compatible in terms of natural frequencies and mode shapes thanks to the calibration made in the model [4]. In another study, ambient vibration tests, mortar shear tests, and mechanical tests on the bricks and mortar of a historical minaret were conducted. Mechanical tests for bricks and mortars can be listed as follows: grout quality control test, moisture content of brick, water absorption test of brick, determination of brick density, determination of the elastic modulus of brick, the compressive strength of brick, the density of brick, determining the percentage of grout moisture, the grout water absorption test, and determination of the grout density. Then, a numerical analysis and risk analysis of the minaret were carried out. As a result of the study, it was observed that there was agreement between the analytical and experimental results. Proposals were made for the repair and strengthening of the Zein-o-din minaret using calibrated numerical models. It was stated that filling the gaps between the bricks and joints with high-strength mortars would be the best solution for the repair of the historical minaret [5]. Serhatoglu and Livaoglu investigated the dynamic characteristics and structural features of 18 Ottoman historical minarets in Bursa, Turkey. The modal vibration test and finite element program were used to obtain the dynamic characteristics of the minarets. The model calibration allowed for more realistic analyses. In addition, two empirical formulas were revealed for the first period of historical minarets. The formulas developed were compared with the literature [6]. Aymelek et al. conducted a structural evaluation of the historical minaret of İskenderpaşa in Turkey under earthquake and wind loads. Vibration tests were performed for the finite element model used in the study and the finite element model was calibrated according to the test results. In the model calibration process, both the material properties of the load-bearing masonry wall and the interaction between the structure and the ground were taken into consideration. It was determined that the analyses performed on the calibrated model produced more realistic structural behavior [7]. There are many studies similar to these studies on historical mosques and minarets in the literature [8,9,10,11,12]. Sanchez-Aparicio et al. determined methods for obtaining accurate numerical models that allow for determining the structural conditions of historical buildings. Laser scanning, photogrammetry, and OMA methods were used in the study. The purpose of the study was to reflect building damages and to reflect real behavior in the numerical model. It also aimed to prepare the numerical model correctly in terms of structural health monitoring. In the study, the Saint Torcato Church in Guimares, Portugal was examined as an example [13]. Torres et al. created a realistic model for the historic Metropolitan Cathedral of Santiago, Chile, which will allow for the evaluation of its current behavior and the future numerical study of the structure. An FE model of the church was created. OMA tests and mechanical tests were performed. The model was calibrated by considering the test results and the model was brought to a state where it can exhibit the real structural behavior [14]. Saisi et al. tried to reveal the structural condition of the historical Santa Maria del Carrobiolo Church, Monza, Italy and its towers. First, they examined the structure, and determined and evaluated the damages. They conducted ambient vibration tests and performed 1-year dynamic monitoring. They especially examined the effects of changing temperature on the natural frequencies of the tower [15]. Formisano et al. presented the seismic response assessment of two historical churches, Visitazione and San Giuliano, which were affected by the L’aquila earthquake in Italy in 2009. Experimental dynamic tests and numerical analyses were carried out. Similar to other studies, the FE model was updated using the results obtained from the tests conducted with the OMA method. Thus, the real structural behavior was transferred to the model. The analyses focused on damages and improvements [16]. Kita et al. presented a new method to rapidly identify earthquake-induced damage in historical masonry towers. This method, called DORI, attempted to combine OMA, FEM, fast modeling, and nonlinear dynamic analysis. The monumental bell tower of the Basilica di San Pietro in Perugia, Italy, was used in the study. It was determined that the general dynamic behavior of the tower, whose seismic status has been examined for a long time, changed after the earthquakes in the region. The studies revealed that the damages in situ, the general dynamic behavior of the tower, and the model-based damages were consistent with each other [17]. There are many studies similar to the studies mentioned above on churches and bell towers [18,19,20,21,22]. In their study, Aras and his colleagues determined the modal characteristics of the historical Beylerbeyi Palace in Istanbul, Turkey, using AVT. It was observed that the modes generally occurred in partial movements. It was thought that the main reason for this modal behavior was the irregular material properties and the lack of rigid diaphragm behavior. Since it is a historical building, the elasticity modules of the walls in different parts of the building emerged as different due to the deformations that occurred in the walls of the building. Then, the aim was to obtain a more accurate model by considering the test results. The elasticity modulus of the wall structure was changed step by step and similar results to the experimental ones were obtained in the numerical model. The analyses were used to try and reveal the differences in the material properties of the walls in different parts of the palace [23]. Many studies have been conducted to experimentally and analytically determine the dynamic characteristics of many historical structures, such as bridges, towers, and palaces. It was also aimed to evaluate structural damages and defects. In the studies, EMA methods and FE methods were generally used together [24,25,26]. Bayraktar and his colleagues examined the structures exposed to ground excitations caused by near-field blasting in their study. An RC building, a masonry building, a RC highway bridge, and a masonry arch bridge were preferred for the study. The vibration characteristics of the blasting were measured. Analytical modal analyses of the examined structures were performed. The experimental dynamic properties of the structures were determined using OMA tests. The FE model of the structures were updated by taking the test results into consideration. Nonlinear dynamic analyses were performed using FEM. As a result of the study, it is said that the OMA method can be safely used to determine the experimental dynamic properties of structures underground excitations caused by near-field blasting. In addition, it was stated in the study that the FE model update method can be taken into consideration for damage assessment and earthquake analyses of engineering structures [27]. In another study, Bayraktar et al. investigated the blast effects on an RC structure by taking into account the dynamic properties that were determined experimentally using the OMA method [28]. One of the most important points to be considered in the EMA methods is the measurement locations and measurement numbers. These parameters are very important with regard to the quality and accuracy of the results. Appropriate sensor placement is very important in determining structural dynamics, performing damage assessments, and investigating earthquake safety. In this context, there are many studies related to the optimum sensor number and placement [29,30,31]. In another study, OMA was performed on the 90-m-high RC minaret of the Faisal Mosque, which is considered an important engineering structure in Pakistan. The minaret was monitored for 3 days with 11 accelerometers. It was stated that the aims of the study were to observe the behavior of the minaret, to create a realistic FE model, and to provide basic data for structural health monitoring (SHM) studies [32]. SHM systems were used in many historical buildings or high-rise buildings in terms of determining and monitoring the dynamic characteristics with EMA methods [33,34,35]. Anuar and colleagues determined that printed circuit boards, which are part of electrical devices, are also exposed to various vibrations. They thought that the natural frequencies of these parts should be investigated in order to prevent damage and resonance. They obtained the natural frequencies by applying the EMA method to a printed circuit board in a free state [36]. In their study, Çakır and Uysal used the EMA method and the FE method. They produced masonry arches in the laboratory. They strengthened the arches from different parts with a polymeric composite material. They observed the changes in the dynamic characteristics of the arches [37]. Turker and his colleagues investigated the stiffness of the supports and joints of various steel beams and frames both analytically and experimentally [38]. A similar study was applied by TÜBİTAK and KTÜ. The EMA method was carried out on three-story steel frames that were reinforced and unreinforced with steel braces. The analytical model was calibrated using the test results [39]. Cevik modeled cross-layered and angled layered composite cantilever beams using the FE method. He compared the obtained natural frequencies with the results available in the literature. He found that increasing the number of layers decreased the natural frequency [40]. In this study, a new approach to beams was presented. In recent years, studies have been carried out that bring innovative approaches to beams. Ozdemir et al. obtained fibers from face masks in their study. Then, they designed RC beams using these fibers. They found that the addition of fibers to RC beams increased their load-carrying capacity, ductility, and energy absorption capacity. They carried out their studies both experimentally and numerically [41]. In another study, RC beams were designed and produced using automobile tire waste. The load-carrying capacities, rigidity, ductility, and energy-absorption capacities of the beams were investigated through experiments [42]. In their study, Özkılıç and colleagues designed and produced RC beams using aluminum waste. As a result of the experiments, the behavior of the beams under the effect of load was investigated [43].
In this study, five types of composite cantilever beams were used. Since there was one test sample from each type, a total of five experiments were carried out. Composite cantilever beams were formed by combining solid section wood and steel profiles. The profiles have a width of 3.00 cm and a height of 1.00 cm. Although there were many studies in the literature related to OMA, no studies have been found on the evaluation of composite beams formed in this way. No study has been found in the literature in which OMA tests have been performed on such composite cantilever beams. For this reason, the aim of this study was to investigate the dynamic behavior of composite cantilever beams both with OMA tests and analytically. In this way, changes in the dynamic characteristics of composite cantilever beams were examined. Composite cantilever beams were modeled in the finite element program using the material properties in the literature. Then, the dynamic characteristics of the beams were obtained using the operational modal analysis (OMA) method (ambient vibration test—AVT). The dynamic characteristics of the beams obtained using the experimental method and the analytical method were compared. The analytical models were calibrated using experimental data to provide more realistic results. In this way, the aim was to reveal the differences in the dynamic characteristics of composite cantilever beams. Additionally, the relationship between the experimental and analytical results was evaluated.
2. Properties of Composite Cantilever Beams
Cantilever beams were designed as single-profile wood (W), single-profile steel (S), double-profile wood–steel (W-S), triple-profile wood–steel–wood (W-S-W) and triple-profile steel–wood–steel (S-W-S) beams. The profiles had a 3.00 cm × 1.00 cm cross-section and were 100 cm long. The 3D drawing and dimensions of one profile are given in Figure 1. The length and cross-sectional properties of a profile are shown in Figure 1. The beams used in the experiments are given in Figure 2. Photographs of all the beams, the support, and the connection areas of the beams are given in Figure 2. L-shaped steel profiles were used to support the beams to the rigid concrete block (Figure 2a). For this reason, L-shaped steel profiles were screwed both to the beams and to the concrete block for support during the experiments. In addition, the profiles were screwed to each other at certain intervals in order to combine the profiles in the composite beams (Figure 2b). Since the intervals were determined as 20 cm, the profiles in the composite beams were connected to each other at a total of six points (Figure 2c).

Figure 1.
3D drawing and dimensions of a profile.

Figure 2.
Test samples.
3. Determination of the Dynamic Characteristics Using the Analytical Model Update (Calibration) Method
There are two methods for defining the dynamic behavior of structures: analytical and experimental. In the analytical method, natural vibration frequencies and mode shapes are determined using the mass, stiffness, and damping properties of the structure. In the experimental method, natural vibration frequencies, mode shapes, and damping ratios are obtained by measuring the vibrations of the structure.
3.1. Analytical Method
The FE method is used in the analytical determination of dynamic characteristics. For this purpose, firstly, the analytical model of the structure is created and then the material properties and boundary conditions are defined. Finally, the mass, damping, and stiffness matrices of the system are created and the modal analysis is performed.
In analytical models, it is very important to select elements that represent the real behavior of the structure. The types of elements that should be used in many engineering structures are known. Generally, one-dimensional elements are used for truss systems, two-dimensional elements are used for slabs and curtains, and three-dimensional elements are used for bridges and dams. The analytical model that geometrically represents the real structure is created by dividing each structural element into parts (mesh) and checking the mesh convergence. Accurate results cannot be obtained with analytical models that do not provide sufficient mesh convergence.
In analytical models, the material properties and boundary conditions of the structure must be defined accurately to represent the structure. Structure-ground interaction, support conditions, and bonding properties within the system should be taken into account. The analytical model should be created to reflect the real conditions as much as possible. Support and joint connections should be provided using spring or link elements.
The composite cantilever beams used in the study were analytically modeled using the FE method and modal analyses of the models were performed. The SAP2000 V 25.0.0 [44] program was used in the FE modeling of the beams. They were modeled as frame elements. The analytical models were divided into different numbers of elements to represent the real behavior of the cantilever beams. Then, mesh convergence control was performed. As a result, the analytical models were divided into ten equal parts and it was concluded that the results obtained in this case were sufficient. One end of the models is modeled as a fixed support. Link elements were used for the joint of the profiles in composite beam models. The SAP2000 model image of one of the beams is given in Figure 3. The figure showed the fixed support, link elements and profiles. Cross-sections of the initial analytical models of cantilever beams are given in Figure 4. Figure 4a shows the cross-sections of the S and W beams, Figure 4b shows the W-S beam, and Figure 4c shows the W-S-W and S-W-S beams. The standard values accepted in the literature were taken into account for the material properties of the wood and steel profiles [44,45,46,47,48]. Steel was defined as an isotropic material and wood was defined as an orthotropic material. The material properties are given in Table 1 and Table 2. The frequency values and modal participating mass ratios (MPMRs) obtained as a result of modal analysis are given in Table 3 and Table 4. The mode shapes obtained as a result of the modal analysis are given in Figure 5 and Figure 6. Since the mode shapes of all the beams were similar, the mode shapes of two beams from different angles are given as an example (Figure 5 and Figure 6). The frequency values of the first five modes for each beam were obtained from the experimental results. For this reason, the first five modes were also taken into account in the FE analyses. The total MPMRs of the first five modes for each beam were over 90%. In this case, it can be observed that the first five modes were sufficient to reflect the total behavior of the beam. In fact, it was observed from the MPMRs that the first three modes were sufficient to reflect the total behavior of the beam.

Figure 3.
Initial analytical model from SAP2000 (W-S-W).
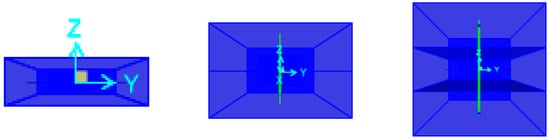
Figure 4.
Cross-sections of the initial analytical models from SAP2000.

Table 1.
Material properties of the initial analytical models for Steel (S235).

Table 2.
Material properties of the initial analytical models for Wood.

Table 3.
Natural frequencies obtained from the initial analytical models (Hz).

Table 4.
Modal participating mass ratios (MPMRs) obtained from the initial analytical models.
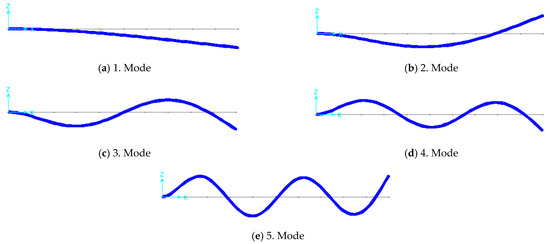
Figure 5.
Mode shapes obtained from the initial analytical model (S).
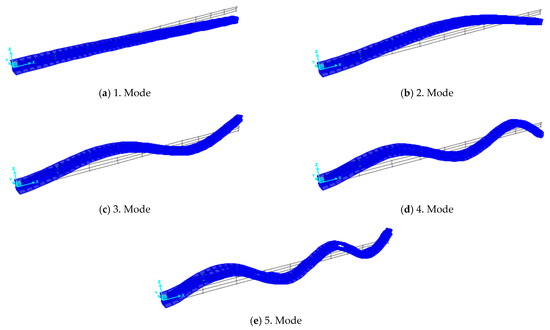
Figure 6.
Mode shapes obtained from the initial analytical model (W-S-W).
3.2. Experimental Method
It is known that the experimental modal analysis methods generate effective results in determining the dynamic characteristics of the structure. They are preferred because they do not cause damage to the structures. For these reasons, it is known that these methods are accepted. These methods are divided into two groups depending on whether the vibration effect used in the measurements is known or not: these are TEMA and OMA methods.
In the OMA method, the vibrations are measured from certain points of the structure. The dynamic characteristics of the structure are obtained using these data. In this case, the dynamic characteristics of the structures are determined using methods with algorithms in the frequency and time domains. Frequency domain methods are based on analyzing the signal measured at each point and the correlation between the signals. These methods are also called non-parametric methods. Time domain methods are based on the time history of the signal at each point or on model fitting with correlation functions.
In this study, experiments were carried out using the OMA method (AVT). For the measurements, the beams were first prepared to provide the desired boundary conditions. The beams were fixed to the concrete block by screwing. Five single-axis accelerometers were used in the experimental measurements. Accelerometers were placed on the test samples at equal intervals and in a way to measure the reactions in the vertical direction. The test setup is given in Figure 7. The data logger device and the recording computer were given in Figure 7a. The other photographs in Figure 7 were photographs of different beams taken from different angles to understand the experimental setup. In the measurements, the frequency range was selected as 0–800 Hz, and 10-min measurements were taken. Vibrations were produced by randomly hitting the concrete block to which the beams were attached with a plastic-tipped sledgehammer. Thus, it was aimed to provide a homogeneous vibration (from every point) in the cantilever beams. During the measurements, the signals from the accelerometers were simultaneously subjected to Fourier transformations in the PULSE [49] data acquisition interface program and recorded on the computer. The representative model and accelerometer placement created in the PULSE R 11.2 program are given in Figure 8. The figure contains a screenshot taken from the program. The figures shown with vertical arrows represent accelerometers (Figure 8).


Figure 7.
Sample measurement layout and accelerometer placement.
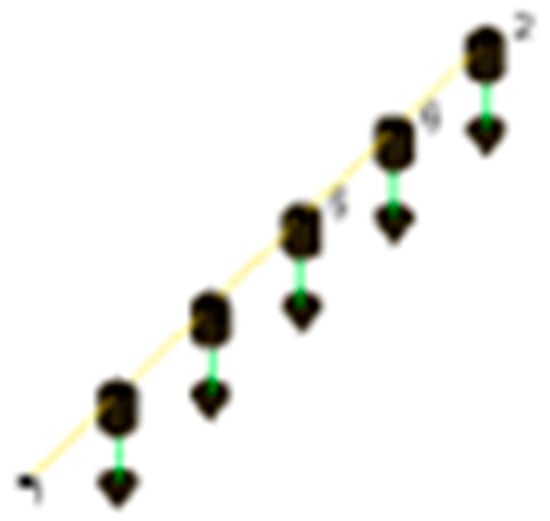
Figure 8.
Representative model and measurement setup in the PULSE program.
The filtering process was applied to the data obtained from the measurements with the help of weight functions in the OMA [50] program. Filtering methods should be used to separate the noise that prevents the accurate measurements from the structural vibrations of the test samples from the main vibrations. In this context, both Hanning windowing and a band-pass filter were used for signal processing in the study [51,52,53]. The modal parameters were obtained using the GFTAA method in the measurement carried out on cantilever beam models. The Enhanced Frequency Domain Decomposition (GFTAA) method is used to determine the dynamic characteristics from measurement data. In the OMA method, the measurements are taken from certain points of the structures. The dynamic characteristics are also obtained using these measurements. In this case, the dynamic characteristics of the structures are determined using methods with algorithms in the frequency and time domain. In the GFTAA method, the modes are obtained by selecting peaks in the spectral density functions obtained as a result of signal processing. Natural frequencies, mode shapes, and modal damping ratios can be obtained using this method. In the GFTAA method, the single degree of freedom Power Spectral The density function defined around a vibration peak can be transformed back to the time domain using the Inverse Discrete Fourier Transform. The natural frequency is obtained by determining the number of time-dependent zero crossings, and the damping is obtained using the logarithmic decay of the single degree of freedom normalized autocorrelation function [54,55,56]. As a result of using this method, the spectral density functions (SDFs) of the signals in each channel were obtained. As an example, the SDF of the steel and wood–steel–wood models from the test samples are given in Figure 9. The values enclosed in the boxes in the graphs are the frequency values of the five modes of the beams (Figure 9).
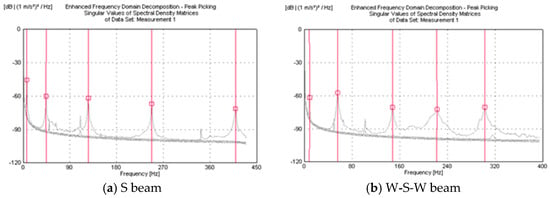
Figure 9.
Sample spectral density functions.
The natural frequencies and modal damping ratios were determined using SDF. The first five frequencies and modal damping ratios obtained from the measurements are given in Table 5 and Table 6. The mode shapes are given in Figure 10 and Figure 11.

Table 5.
Natural frequencies of the cantilever beam test specimens (Hz).

Table 6.
Modal damping ratios of the cantilever beam test specimens (%).
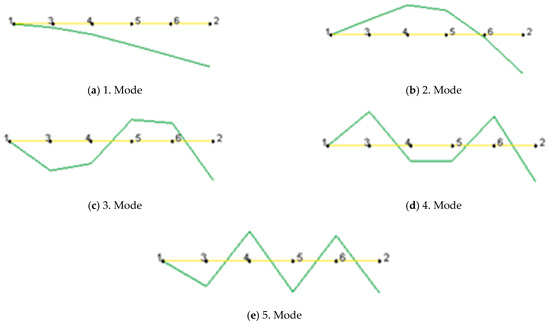
Figure 10.
Mode shapes obtained from measurements (S).
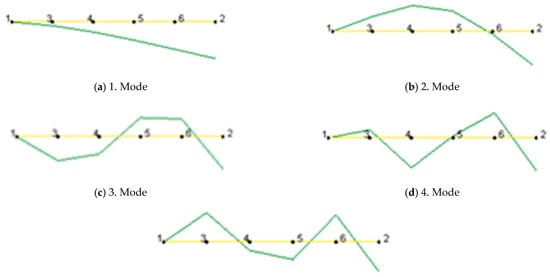
Figure 11.
Mode shapes obtained from measurements (W-S-W).
3.3. Calibration of Finite Element Models with Experimental Results
Some assumptions were made in the material properties and boundary conditions in the initial analytical models of the cantilever beams. In the initial analytical models, it was assumed that the support connections were fixed and the elastic modulus values were the values given in the standards. Changes were made to the initial analytical model according to the measurement results performed on the beams. In this way, the differences between the experimental dynamic characteristics and the analytical dynamic characteristics were minimized. This process is called model calibration. In the model calibration process, changes in the material properties, joint connections, and boundary conditions in the analytical model are taken into account. In this study, two parameters were focused on in the calibration of the analytical model according to the test results. The first parameter was the material properties. The material properties used in the initial analytical model were the material properties accepted in the literature. The difference between these material properties and the material properties of the test samples was investigated. The second parameter was the support conditions. In the initial analytical model, one end of the beam was defined as a fixed support. However, in the experiments, it was necessary to determine whether the beams were fixed to the concrete block completely. Considering all the parameters, the calibration process was first performed on wood (W) and steel (S) beams. In these beams, the material properties were determined as the material properties of the initial analytical model and a spring was assigned instead of a fixed support. Then, the stiffness of the spring was randomly changed and the modal analyses were performed. The frequency values obtained as a result of the analyses were compared with the frequency values obtained from the test results. As a result of the comparisons made for the W and S beams, the difference between the analysis results of the calibrated analytical models and the test results was reduced to less than 3% for all the modes. Since the difference was very small, the material properties were not changed and the calibration process was carried out for all the beams with the springs placed on the supports. In other words, the material properties in the literature were used in the calibration process. The analytical and experimental results were obtained very close to each other by changing only the support conditions in the steel (S) and wood (W) samples, where the main material properties can be determined. For this reason, there was no need to change the material properties. Springs were assigned to the supports for the support conditions. Calibration was performed by adjusting the stiffness values for each spring. In the tests, the cantilever beams were fixed to the concrete block. For this reason, one end of the beams was defined as a fixed support in the initial analytical models. Then, the initial analytical models and the test results were compared. The difference between the analysis results of the initial analytical models and the test results was found to be high. For this reason, the springs were assigned to one end of the beams in the calibration process (Figure 12). The supports were created with the stiffness of the springs. In this way, the analysis and test results were found to be close to each other. The accuracy of the boundary conditions was checked by the results being close to each other. Firstly, the experimental and initial analytical model results were compared (Table 7, Table 8, Table 9, Table 10 and Table 11). When the analysis results of the initial analytical models were compared with the experiment results for the first three modes of the beams, it was seen that the least differences were in the W beam. These differences were in the range of 0.8–3% for the W beam, 11–17% for the S beam, 10–19% for the W-S beam, 22–32% for the W-S-W beam, and 6–153% for the S-W-S beam (Table 7, Table 8, Table 9, Table 10 and Table 11). Then, changes were made to minimize the differences between the results (Table 12, Table 13, Table 14, Table 15 and Table 16). When the analysis results of the calibrated analytical models were compared with the test results for the first three modes of the beams, it was observed that the least differences were in the S beam. These differences were in the range of 1–3% for the W beam, 0.06–2% for the S beam, 3–5% for the W-S beam, 4–10% for the W-S-W beam, and 1–18% for the S-W-S beam (Table 12, Table 13, Table 14, Table 15 and Table 16). The diferences between the test results and the analytical models are given in Table 17. The MPMR values obtained from calibrated analytical models are given in Table 18. It was observed that the MPMRs of all the beams were over 60% for the first mode. It was also determined that the sum of MPMRs of the first three modes of the beams were over 85%.
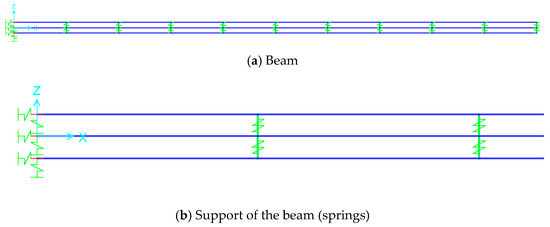
Figure 12.
Calibrated analytical model (S-W-S).

Table 7.
Natural frequencies of the experimental and initial analytical (W).

Table 8.
Natural frequencies of the experimental and initial analytical (S).

Table 9.
Natural frequencies of the experimental and initial analytical (W-S).

Table 10.
Natural frequencies of the experimental and initial analytical (W-S-W).

Table 11.
Natural frequencies of the experimental and initial analytical (S-W-S).

Table 12.
Natural frequencies of the experimental and calibrated analytical (W).

Table 13.
Natural frequencies of the experimental and calibrated analytical (S).

Table 14.
Natural frequencies of the experimental and calibrated analytical (W-S).

Table 15.
Natural frequencies of the experimental and calibrated analytical (W-S-W).

Table 16.
Natural frequencies of the experimental and calibrated analytical (S-W-S).

Table 17.
The differences between the tests (E) and initial (I)—calibrated (C) models (%).

Table 18.
Modal participating mass ratios (MPMRs) obtained from the calibrated analytical models (Hz).
4. Conclusions
Two cases related to composite beams were assessed in this study. First, the dynamic characteristics of composite beams were determined using the OMA method, which is a non-destructive test method. Then, the composite beams were modeled using the SAP2000 FE program. The FE models were calibrated taking into account the test results. Thus, we tried to obtain analytical models that were more suitable for the real structural behavior. Secondly, the dynamic characteristics of the composite beams were compared. Thus, it was examined how the dynamic characteristics of the beams changed when they became composite. The main conclusions from the study are given below:
- -
- MPMRs are ratios that express the total behavior of structures. For this reason, the sum of the MPMRs taken into account is very important. The fact that this sum is over 90% shows that it takes into account almost all the behavior of the structure. When the MPMRs of the beams obtained from the analyses were examined, it was observed that the sum of the first three modes of the beams was around 90%. Based on the MPMRs, it can be said that the first three modes were more important in the dynamic behavior of the beams. This situation was taken into consideration when the analytical model calibrations were performed according to the test results of the beams. Especially the first three modes were given more importance during the calibration.
- -
- In the initial analytical models, the material properties and boundary conditions were taken into consideration while performing the calibration according to the test results. Calibration in wood and steel models could be performed without changing the material properties by only changing the support conditions. In this case, it was found that the material properties of the wood and steel profiles used in the experiments were in accordance with the material properties in the literature. For this reason, the material properties of the wood and steel profiles were not changed in the calibrations of the initial analytical models. Calibration was performed using the material properties of the initial analytical models, defined by taking them from the literature. Support conditions were taken into consideration in the calibrations. Springs were assigned to the supports of the beams and the stiffnesses of these springs were evaluated and calibrations were performed.
- -
- When the differences between the frequency values obtained from the experimental results of the beams and the frequency values obtained from the calibrated analytical models of the beams were examined, it was observed that they were at acceptable levels, especially for the first three modes. The differences were less than 5% in almost all the beams for the first three modes. In addition, as a result of the calibration, the closest results to the test results were obtained for the S and W beams. The differences between the results for the first five modes of the S beam were obtained below 2% for the first mode and below 1% for the other four modes. For the first five modes of the W beam, the differences between the results were obtained below 2% for the first second, and fifth modes and below 3% for the third and fourth modes. It was determined that the differences were reasonable for the W, S, and W-S beams in the fourth and fifth modes of the beams, but the differences were high for the W-S-W and S-W-S beams in the fourth and fifth modes of the beams. In the modal analyses, the behavior of structures in higher modes becomes more complex. In such cases, more detailed and precise experiments may need to be performed to obtain higher mode behaviors. As the number of modes of the elements increases, their dynamic behaviors become more complex. In addition, as the number of elements connected in the composite beams increases, the joint areas also increase. Since the elements are composite, complex dynamic behaviors can vary greatly depending on the situation of the joint areas. In this case, the measurement sensitivity that can reveal complex behaviors in the experiments is of great importance. In addition, it becomes difficult to reflect the joint areas in the composite beams in the analytical model. This causes difficulties in the calibration of the analytical model, especially in complex dynamic behaviors. For these reasons, the differences were high in the W-S-W and S-W-S beams due to the effect of being composite and the effect of the fourth and fifth modes, where the dynamic behaviors become more complex.
- -
- When the frequency values of the beams were compared, it was observed that the smallest values were in the W beam and the largest values were in the S-W-S beam. Considering this situation, it can be said that the stiffness of the beams increases as they become composite. The frequency values of the composite beams increase with the increase in stiffness. As the cross-sections of the beams increase, their stiffness increases. For this reason, the stiffness of composite beams was greater. However, the masses of the composite beams were also greater. Both stiffness and mass are taken into account in the calculation of the frequency values. As the stiffness increases, the frequency values increase. However, as the mass increases, the frequency values decrease. The reason why the increase in frequency values were not very high can be explained in this way. In addition, the materials of the profiles used in the beams are very important, because as the elasticity modules of the materials used in the beams increase, the stiffness of the beams will also increase. Since the elasticity module of the steel is greater than the elasticity module of the wood, the stiffness of steel is greater than that of wood. For this reason, for example, the frequency values of the S-W-S beam were greater than the W-S-W beam. Considering the first three modes in particular, the order from the lowest frequency values to the highest frequency values was as follows: W, S, W-S, W-S-W, and S-W-S. According to the test results, an increase was calculated for the W beam with the lowest frequency values for the first mode. This increase was 9% for the S beam, 31% for the W-S beam, 35% for the W-S-W beam, and 47% for the S-W-S beam.
- -
- It is planned to make this study more comprehensive in the future. In the planned study, many parameters, such as the geometric properties of the profiles, the dimensions of the test samples, the properties of the joint areas in the composite beams, and the number of measuring instruments, will be taken into consideration. In addition, there is one sample of each type in this study. In future studies, it would be more appropriate to have three samples of each type in terms of both the reliability of the experiments and the statistical evaluation of the experimental results.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Türker, T. Structural Damage Detection and Evaluation by Using Ambient Vibration Data. Ph.D. Thesis, Karadeniz Technical University, The Graduate School of Natural and Applied Sciences, Trabzon, Türkiye, 2011; p. 218. [Google Scholar]
- Altunışık, A.C. Determination of Structural Behavior of Highway Bridges Using Analytical and Experimental Methods. Ph.D. Thesis, Karadeniz Technical University, The Graduate School of Natural and Applied Sciences, Trabzon, Türkiye, 2010; p. 190. [Google Scholar]
- Türker, T. Determination of Dynamic Characteristics of Steel Frames by Experimental Modal Analysis Method. Master’s Thesis, Karadeniz Technical University, The Graduate School of Natural and Applied Sciences, Trabzon, Türkiye, 2005; p. 100. [Google Scholar]
- Bayraktar, A.; Altunışık, A.C.; Sevim, B.; Türker, T. Seismic response of a historical masonry minaret using a finite element model updated with operational modal testing. J. Vib. Control. 2011, 17, 129–149. [Google Scholar] [CrossRef]
- Mirtaheri, M.; Abbasi, A.; Salari, N. A seismic behavior and rehabilitation of the historic masonry minaret by experimental and numerical methods. Asian J. Civ. Eng. 2017, 18, 807–822. [Google Scholar]
- Serhatoglu, C.; Livaoglu, R. A fast and practical approximations for fundamental period of historical Ottoman minarets. Soil Dyn. Earthq. Eng. 2019, 120, 320–331. [Google Scholar] [CrossRef]
- Aymelek, A.; Yanik, Y.; Demirtaş, B.; Yildirim, Ö.; Çalik, I.; Türker, T. Full-scale structural evaluations of ˙Iskenderpaşa minaret. Structures 2023, 55, 1028–1044. [Google Scholar] [CrossRef]
- Yanık, Y.; Türker, T.; Çalik, I.; Yildirim, Ö. Investigation of environmental and time depended effects on historical masonry minarets by vibration test. J. Fac. Eng. Archit. Gazi Univ. 2022, 37, 799–813. [Google Scholar] [CrossRef]
- Başaran, H.; Demir, A.; Ercan, E.; Nohutçu, H.; Hökelekli, H.; Kozanoglu, C. Investigation of seismic safety of a masonry minaret using its dynamic characteristics. Earthq. Struct. 2016, 10, 523–538. [Google Scholar] [CrossRef]
- Hökelekli, E.; Demir, A.; Ercan, E.; Nohutçu, H.; Karabulut, A. Seismic Assessment in a Historical Masonry Minaret by Linear and Non-linear Seismic Analyses. Period. Polytech. Civ. Eng. 2020, 64, 438–448. [Google Scholar] [CrossRef]
- Erdil, B.; Tapan, M.; Akkaya, İ.; Korkut, F. Effects of Structural Parameters on Seismic Behaviour of Historical Masonry Minaret. Period. Polytech. Civ. Eng. 2018, 62, 148–161. [Google Scholar] [CrossRef]
- Bayraktar, A.; Çalik, I.; Türker, T. A Simplified Fundamental Frequency Formulation Based on In-Situ Tests for Masonry Stone Minarets. Exp. Tech. 2022, 46, 225–238. [Google Scholar] [CrossRef]
- Sanchez-Aparicio, L.J.; Riveiro, B.; Gonzalez-Aguilera, D.; Ramos, L.F. The combination of geomatic approaches and operational modal analysis to improve calibration of finite element models: A case of study in Saint Torcato Church (Guimarães, Portugal). Constr. Build. Mater. 2014, 70, 118–129. [Google Scholar] [CrossRef]
- Torres, W.; Almazan, J.L.; Sandoval, C.; Boroschek, R. Operational modal analysis and FE model updating of the Metropolitan Cathedral of Santiago, Chile. Eng. Struct. 2017, 143, 169–188. [Google Scholar] [CrossRef]
- Saisi, A.; Gentile, C.; Ruccolo, A. Continuous monitoring of a challenging heritage tower in Monza, Italy. J. Civ. Struct. Health Monit. 2018, 8, 77–90. [Google Scholar] [CrossRef]
- Formisano, A.; Di Lorenzo, G.; Krstevska, L.; Landolfo, R. Fem Model Calibration of Experimental Environmental Vibration Tests on Two Churches Hit by L’Aquila Earthquake. Int. J. Archit. Herit. 2021, 15, 113–131. [Google Scholar] [CrossRef]
- Kita, A.; Cavalagli, N.; Venanzi, I.; Ubertini, F. A new method for earthquake-induced damage identification in historic masonry towers combining OMA and IDA. Bull. Earthq. Eng. 2021, 19, 5307–5337. [Google Scholar] [CrossRef]
- Osmancikli, G.; Uçak, Ş.; Turan, F.N.; Türker, T.; Bayraktar, A. Investigation of restoration effects on the dynamic characteristics of the Hagia Sophia bell-tower by ambient vibration test. Constr. Build. Mater. 2012, 29, 564–572. [Google Scholar] [CrossRef]
- Azzara, R.M.; Roeck, G.D.; Girardi, M.; Padovani, C.; Pellegrini, D.; Reynders, E. The influence of environmental parameters on the dynamic behaviour of the San Frediano bell tower in Lucca. Eng. Struct. 2018, 156, 175–187. [Google Scholar] [CrossRef]
- Yanık, Y.; Aymelek, A.; Çalik, I.; Türker, T. Vibration testing and performance evaluation of Hagia Sophia bell tower after recent restoration. Constr. Build. Mater. 2022, 347, 128617. [Google Scholar] [CrossRef]
- Milani, G.; Clementi, F. Advanced Seismic Assessment of Four Masonry Bell Towers in Italy after Operational Modal Analysis (OMA) Identification. Int. J. Archit. Herit. 2021, 15, 157–186. [Google Scholar] [CrossRef]
- Standoli, G.; Giordano, E.; Milani, G.; Clementi, F. Model Updating of Historical Belfries Based on Oma Identification Techniques. Int. J. Archit. Herit. 2021, 15, 132–156. [Google Scholar] [CrossRef]
- Aras, F.; Krstevska, L.; Altay, G.; Tashkov, L. Experimental and numerical modal analyses of a historical masonry palace. Constr. Build. Mater. 2011, 25, 81–91. [Google Scholar] [CrossRef]
- Türker, T.; Bayraktar, A. Structural safety assessment of bowstring type RC arch bridges using ambient vibration testing and finite element model calibration. Measurement 2014, 58, 33–45. [Google Scholar] [CrossRef]
- Shabani, A.; Feyzabadi, M.; Kioumarsi, M. Model updating of a masonry tower based on operational modal analysis: The role of soil-structure interaction. Case Stud. Constr. Mater. 2022, 16, e00957. [Google Scholar] [CrossRef]
- Altunisik, A.C.; Adanur, S.; Genc, A.F.; Gunaydin, M.; Okur, F.Y. An Investigation of the Seismic Behaviour of an Ancient Masonry Bastion Using Non-Destructive and Numerical Methods. Exp. Mech. 2017, 57, 245–259. [Google Scholar] [CrossRef]
- Bayraktar, A.; Altunisik, A.C.; Özcan, M. Safety assessment of structures for near-field blast-induced ground excitations using operational modal analysis. Soil Dyn. Earthq. Eng. 2012, 39, 23–36. [Google Scholar] [CrossRef]
- Bayraktar, A.; Türker, T.; Altunisik, A.C.; Sevim, B. Evaluation of blast effects on reinforced concrete buildings considering Operational Modal Analysis results. Soil Dyn. Earthq. Eng. 2010, 30, 310–319. [Google Scholar] [CrossRef]
- Pachon, P.; Castro, R.; Garcia-Macias, E.; Compan, V.; Puertas, E.E. Torroja’s bridge: Tailored experimental setup for SHM of a historical bridge with a reduced number of sensors. Eng. Struct. 2018, 162, 11–21. [Google Scholar] [CrossRef]
- Heo, G.; Wang, M.L.; Satpathi, D. Optimal transducer placement for health monitoring of long span bridge. Soil Dyn. Earthq. Eng. 1997, 16, 495–502. [Google Scholar] [CrossRef]
- Sunca, F.; Okur, F.Y.; Altunişik, A.C.; Kahya, V. Optimal Sensor Placement for Laminated Composite and Steel Cantilever Beams by the Effective Independence Method. Struct. Eng. Int. 2021, 31, 85–92. [Google Scholar] [CrossRef]
- Akhlaq, H.; Butt, F.; Alwetaishi, M.; Riaz, M.; Benjeddou, O.; Hussein, E.E. Structural Identification of a 90 m High Minaret of a Landmark Structure under Ambient Vibrations. Buildings 2022, 12, 252. [Google Scholar] [CrossRef]
- Chen, W.H.; Lu, Z.R.; Lin, W.; Chen, S.H.; Ni, Y.Q.; Xia, Y.; Liao, W.Y. Theoretical and experimental modal analysis of the Guangzhou New TV Tower. Eng. Struct. 2011, 33, 3628–3646. [Google Scholar] [CrossRef]
- Giordano, P.F.; Ubertini, F.; Cavalagli, N.; Kita, A.; Masciotta, M.G. Four years of structural health monitoring of the San Pietro bell tower in Perugia, Italy: Two years before the earthquake versus two years after. Int. J. Mason. Res. Innov. 2020, 5, 111797. [Google Scholar] [CrossRef]
- Gentile, C.; Guidobaldi, M.; Saisi, A. One-year dynamic monitoring of a historic tower: Damage detection under changing environment. Meccanica 2016, 51, 2873–2889. [Google Scholar] [CrossRef]
- Anuar, M.A.; Mat Isa, A.A.; Ummi, Z.A.R. Modal Characteristics study of CEM-1 Single-Layer Printed Circuit Board Using Experimental Modal Analysis. Procedia Eng. 2012, 41, 1360–1366. [Google Scholar] [CrossRef][Green Version]
- Cakir, F.; Uysal, H. Experimental modal analysis of brick masonry arches strengthened prepreg composites. J. Cult. Herit. 2015, 16, 284–292. [Google Scholar] [CrossRef]
- Türker, T.; Kartal, M.E.; Bayraktar, A.; Muvafik, M. Assessment of semi-rigid connections in steel structures by modal testing. J. Constr. Steel Res. 2009, 65, 1538–1547. [Google Scholar] [CrossRef]
- Türker, T.; Bayraktar, A. Finite element model calibration of steel frame buildings with and without brace. J. Constr. Steel Res. 2013, 90, 164–173. [Google Scholar] [CrossRef]
- Cevik, M. Free Vibration Analysis of Cross-ply and Angle-ply Laminated Composite Cantilever Beams. Sci. Eng. J Fırat Univ. 2007, 19, 139–145. [Google Scholar]
- Ozdemir, A.; Bozyigit, B.; Kılıç Demircan, R.; Mercimek, Ö.; Çelik, D.N.; Akkaya, S.T.; Kaplan, G. Innovative solutions on ductility and bearing capacity: Strengthening flexural performance of reinforced concrete beams with recycled mask fibers. Constr. Build. Mater. 2025, 458, 139717. [Google Scholar] [CrossRef]
- Yıldızel, S.A.; Özkılıç, Y.O.; Bahrami, A.; Aksoylu, C.; Başaran, B.; Hakamy, A.; Arslan, M.H. Experimental investigation and analytical prediction of flexural behaviour of reinforced concrete beams with steel fibres extracted from waste tyres. Case Stud. Constr. Mater. 2023, 19, e02227. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Karalar, M.; Aksoylu, C.; Beskopylny, A.N.; Stel’makh, S.A.; Shcherban, E.M.; Qaidi, S.; Pereira, I.S.A.; Monteiro, S.N.; Azevedo, A.R.G. Shear performance of reinforced expansive concrete beams utilizing aluminium waste. J. Mater. Res. Technol. 2023, 24, 5433–5448. [Google Scholar] [CrossRef]
- SAP2000; Version: 25.0.0; Structural Analysis Program. Computers and Structures Inc.: Berkeley, CA, USA, 2023.
- TEC-2018; Turkey Building Earthquake Code. 30364 Numbered the Official Newspaper of the Republic of Turkey (18 March 2018). Republic of Turkey Ministry of Interior Disaster and Emergency Management Authority: Ankara, Turkey, 2018.
- Eurocode 3; Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings (EN 1993-1-1). European Committee for Standardization: Brussels, Belgium, 2005.
- Green, D.W.; Winandy, J.E.; Kretschmann, D.E. Wood Handbook, Mechanical Properties of Wood-Chapter 4, General Technical Report FPL-GTR-113; United States Department of Agriculture Forest Service: Madison, Wisconsin, 1999. [Google Scholar]
- Kretschmann, D.E. Wood Handbook, Mechanical Properties of Wood-Chapter 5, General Technical Report FPL-GTR-190; United States Department of Agriculture Forest Service: Madison, Wisconsin, 2010. [Google Scholar]
- PULSE, Release 11.2. Analyzers and Solutions. Sound and Vibration Measurement A/S: Aalborg, Denmark, 2006.
- OMA, Release 4.0. Operational Modal Analysis. Structural Vibration Solution A/S: Aalborg, Denmark, 2006.
- Ahmadi, H.R.; Mahdavi, N.; Bayat, M. A new index based on short time Fourier transform for damage detection in bridge piers. Comput. Concr. 2021, 27, 447–455. [Google Scholar] [CrossRef]
- Ahmadi, H.R.; Momeni, K.; Jasemnejad, Y. A new algorithm and damage index for detection damage in steel girders of bridge decks using time-frequency domain and matching methods. Structures 2024, 61, 106035. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Sunca, F.; Sevim, B. Ambient vibration-based seismic evaluation of long-span prestressed concrete box-girder bridges under long-duration, near-fault and far-fault ground motions. J. Earthq. Tsunami 2024, 18, 2450019. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification from ambient responses using frequency domain decomposition. In Proceedings of the 18th International Modal Analysis Conference, San Antonio, TX, USA, 7–10 February 2000. [Google Scholar]
- Jacobsen, N.J.; Andersen, P.; Brincker, R. Using enhanced frequency domain decomposition as a robust technique to harmonic excitation in operational modal analysis. In Proceedings of the ISMA2006: International Conference on Noise & Vibration Engineering, Lueven, Belgium, 18–20 September 2006; International Conference on Noise&Vibration Engineering: Leuven, Belgium, 2006. [Google Scholar]
- Türker, T.; Bayraktar, A.; Kocaman, İ.; Çoruhlu, B. Experimental and analytical investigation of dynamic behavior of scaled masonry arch bridge model. In Proceedings of the Symposium on Strengthening and Preserving Historical Buildings and Cultural Heritage—5, Erzurum, Turkey, 1–3 October 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).