On the Penetration of Projectiles into Semi-Infinite Concrete Targets in a Coupled Deforming and Eroding Regime
Abstract
1. Introduction
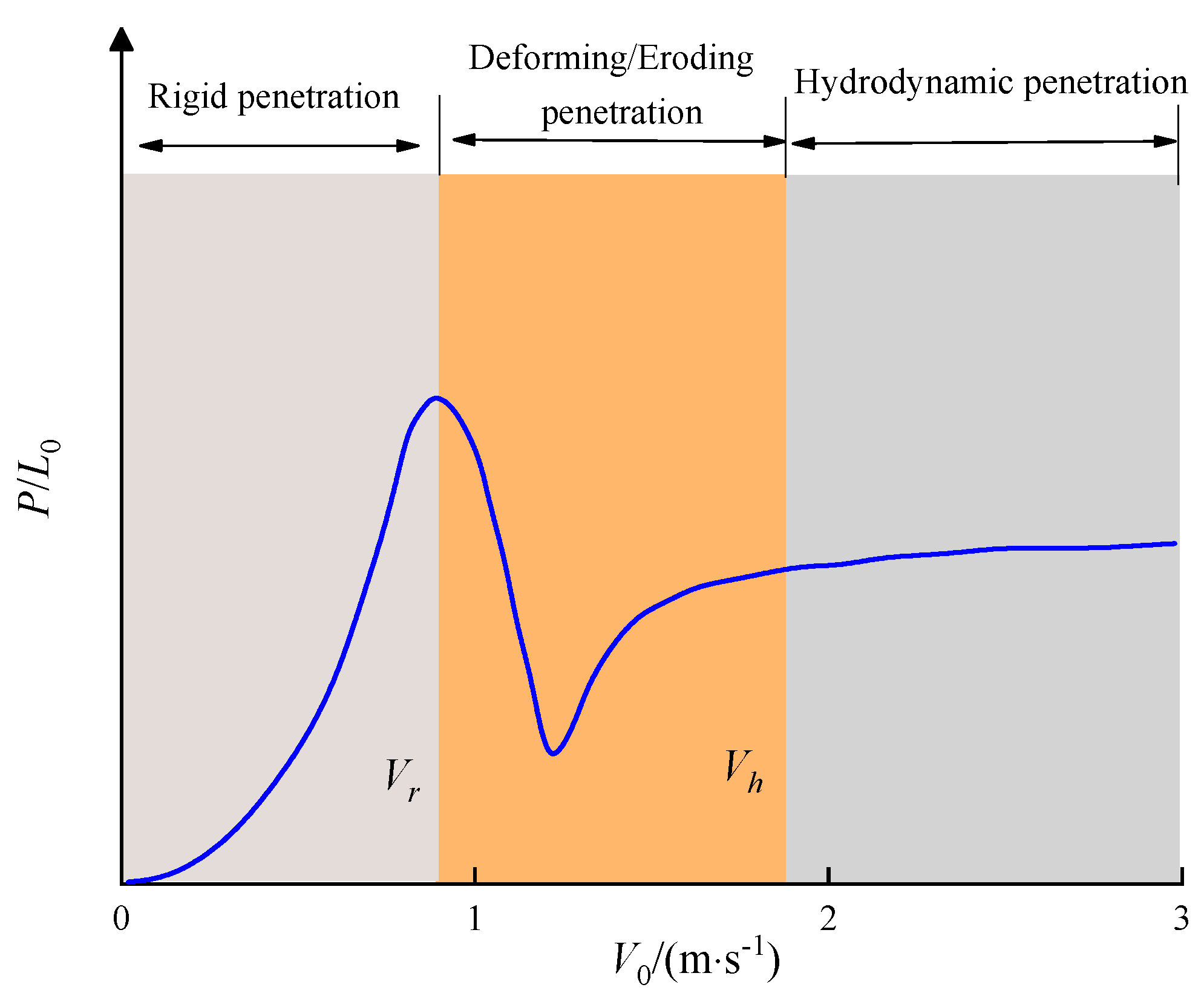
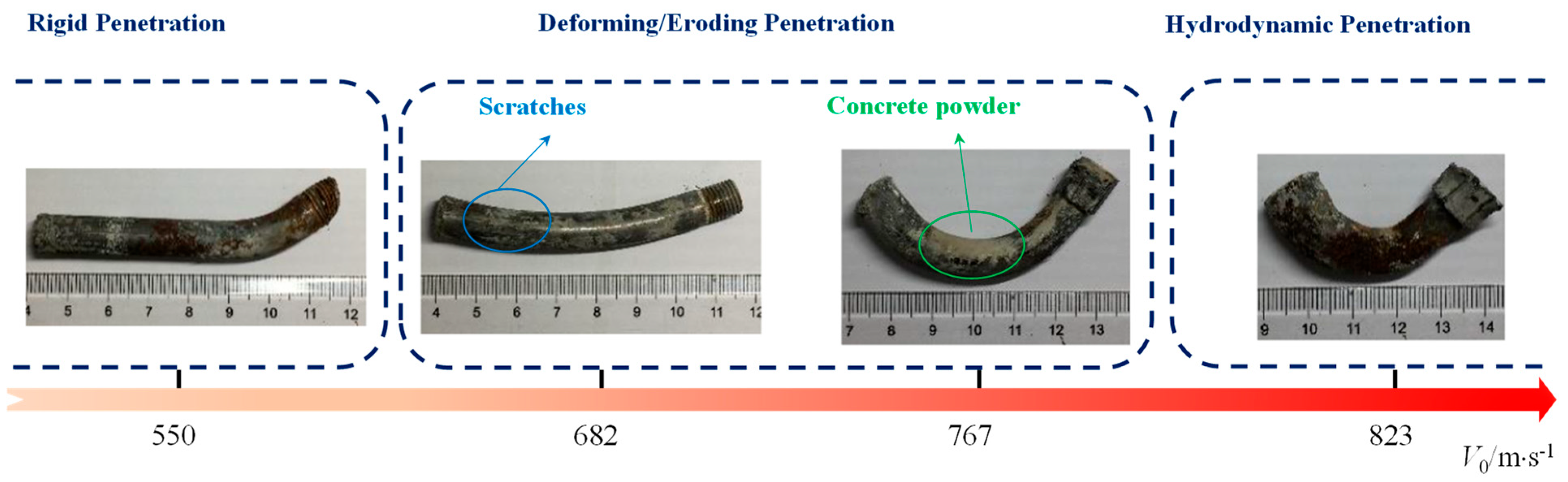
2. Penetration Regime
3. Critical Velocity
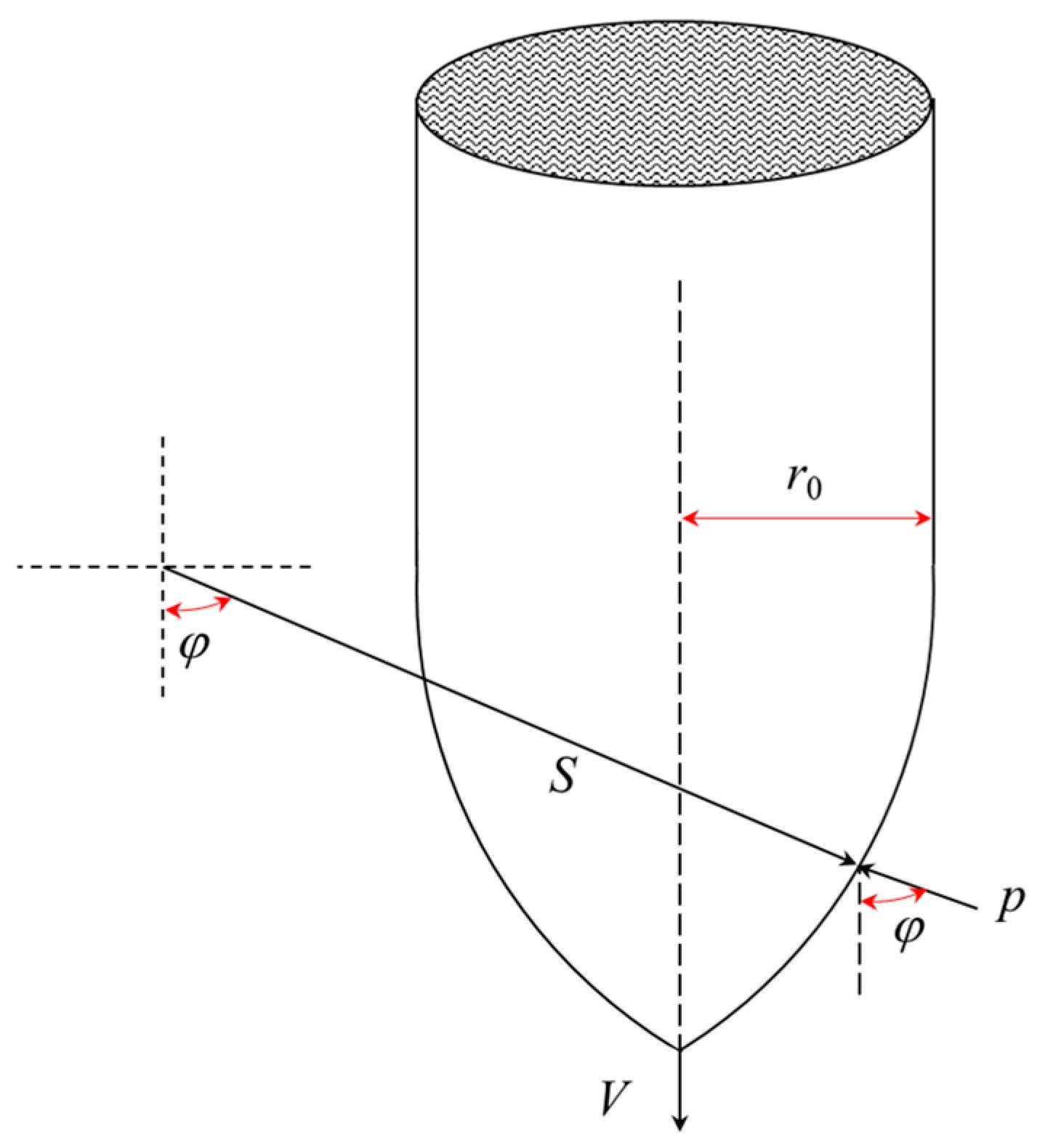
3.1. Rigid Velocity
3.2. Hydrodynamic Velocity
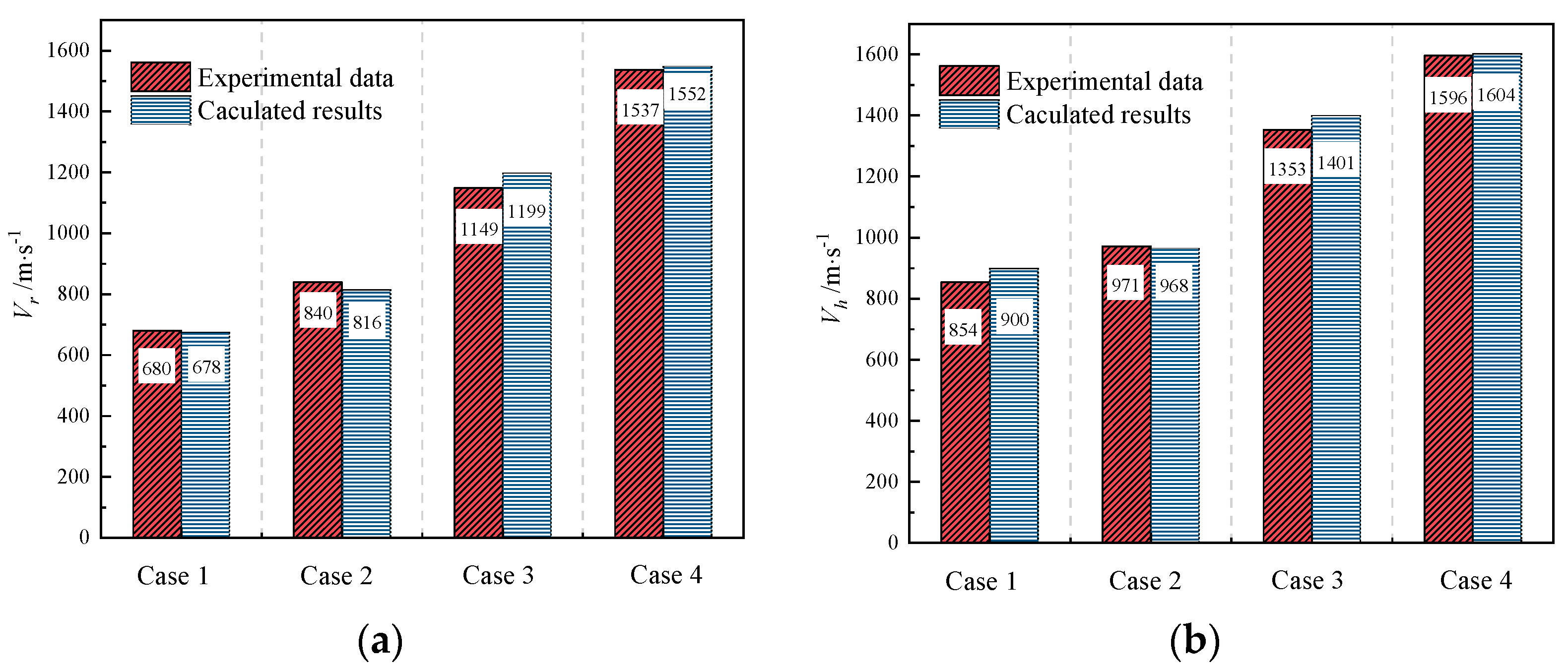
3.3. Reliability Validation of Critical Velocity Models
4. Cross-Sectional Area of the Projectile After Penetration
4.1. Fundamental Assumption
4.2. Construction of Caculated Model
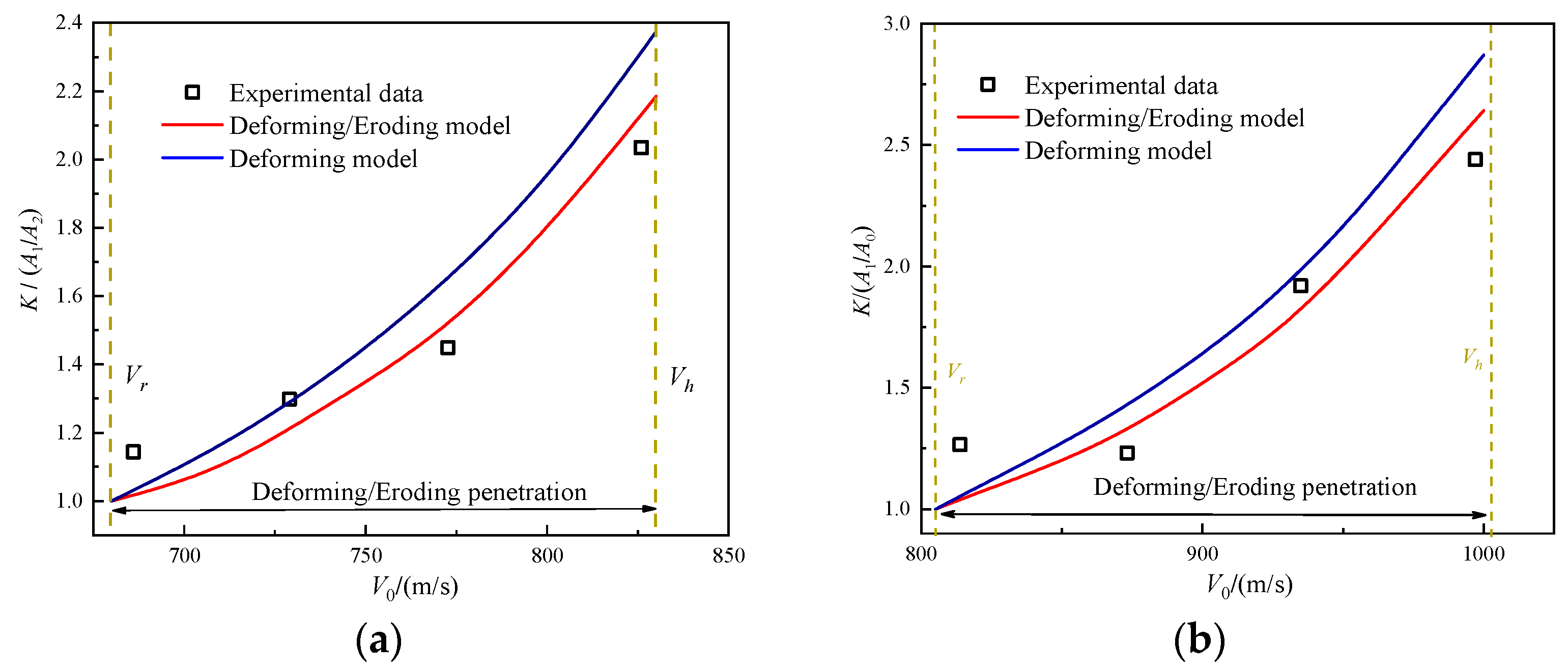
4.3. Comparison of Experimental Data and Calculated Results
4.4. Parametric Analysis of the Cross-Sectional Area
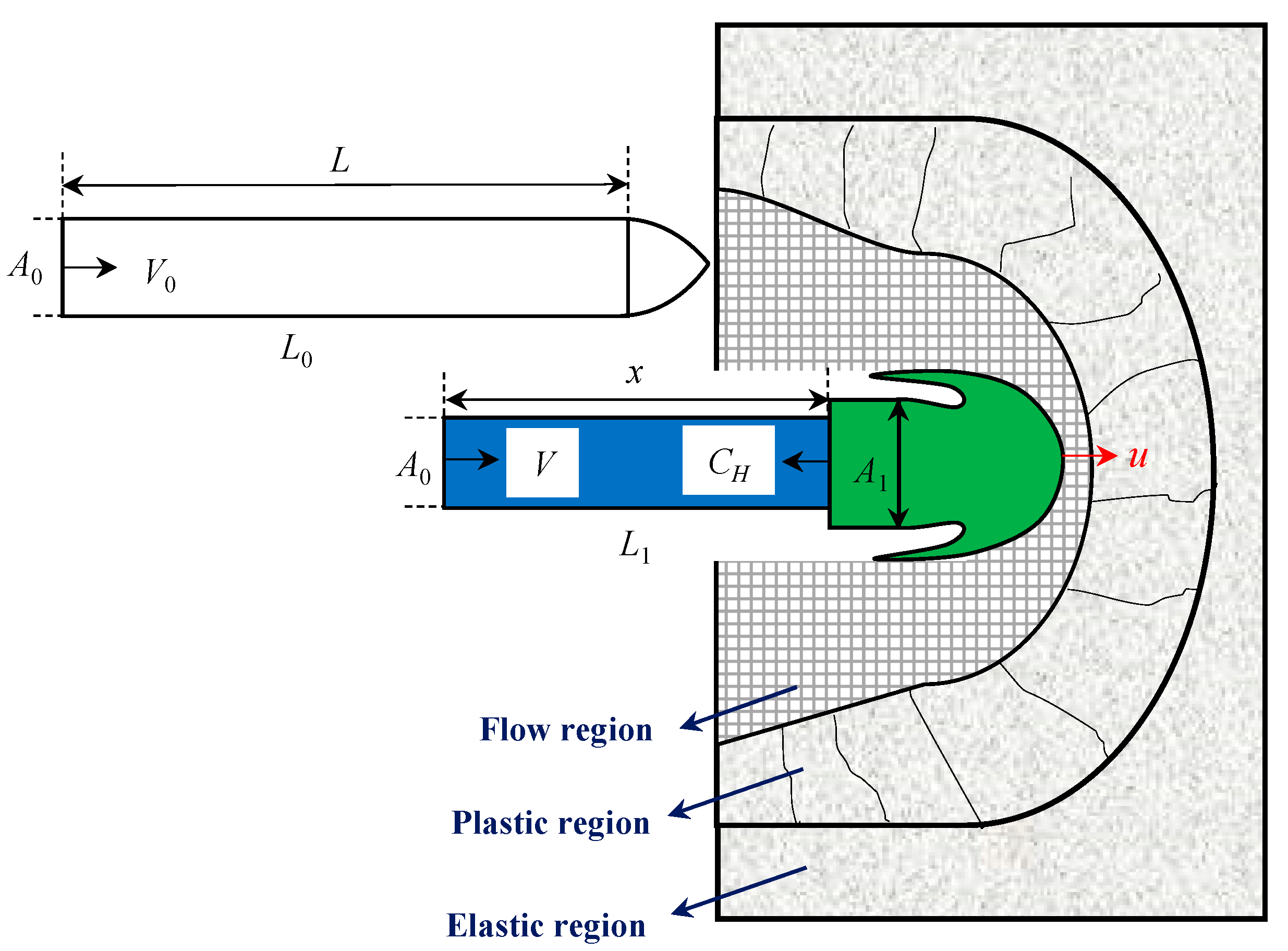
5. Theoretical Model of DOP
5.1. Rigid Penetration
5.2. Coupled Deforming/Eroding Penetration
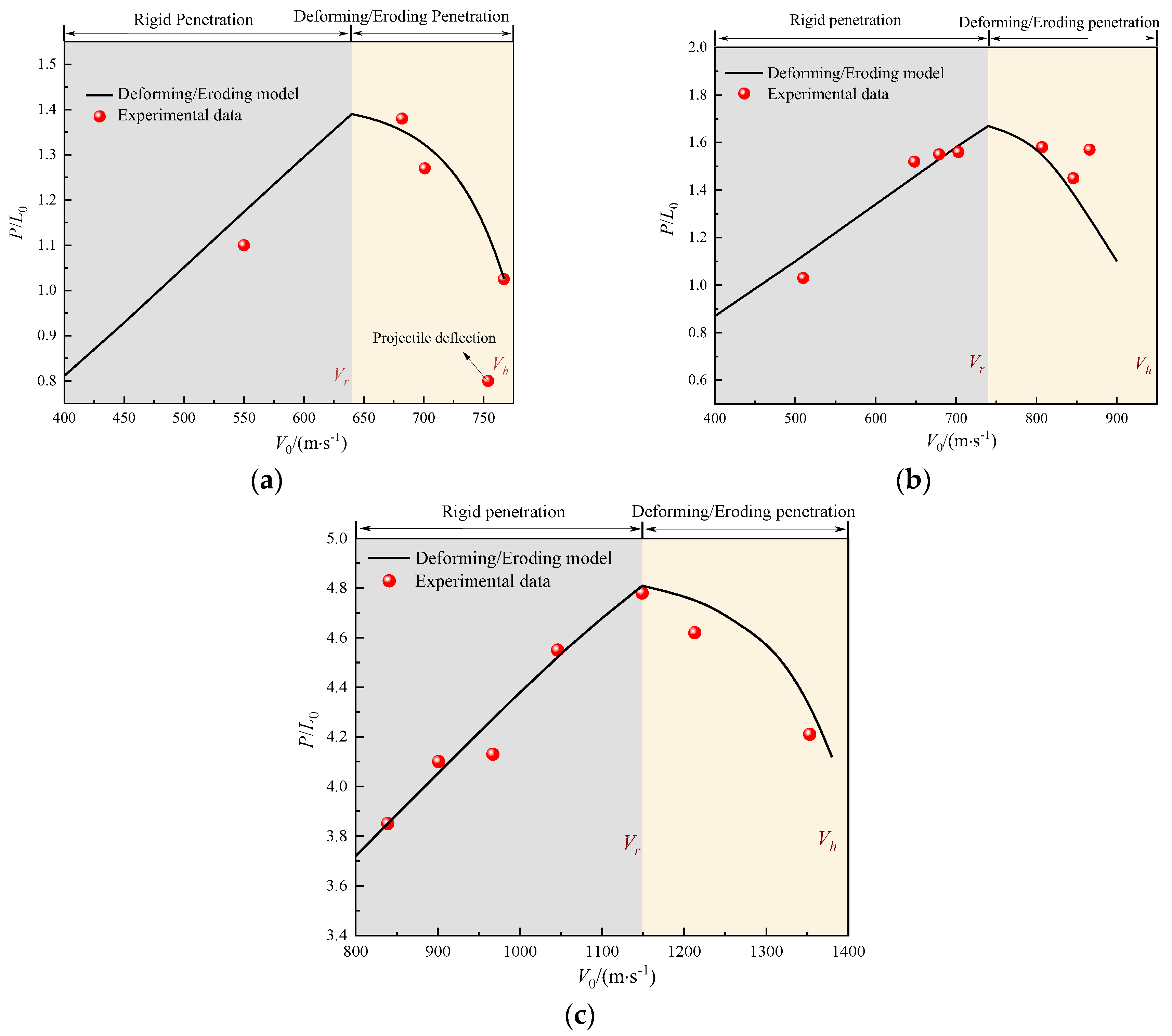
5.3. Comparison of Model Predictions with Experimental Data
6. Conclusions
- (1)
- The rigid velocity is defined as the critical initial impact velocity at which the projectile–target interfacial stress reaches the dynamic yield strength of the projectile, while the hydrodynamic velocity is defined as the critical impact velocity when the projectile’s erosion rate equals its internal plastic wave speed. These two critical velocities delineate the boundaries of the coupled deformation–erosion penetration regime.
- (2)
- The cross-sectional area evolution of projectiles is predominantly governed by material strength and plastic wave velocity. Specifically, the cross-sectional area demonstrates a negative correlation with material strength but exhibits a positive dependence on plastic wave velocity.
- (3)
- During the coupled deformation and erosion penetration process, the penetration depth decreases as the initial impact velocity increases. This is attributed to the increase in penetration resistance caused by the enlargement of the projectile’s cross-sectional area, as well as the significant dissipation of kinetic energy resulting from mass loss.
- (4)
- The theoretical framework shows good agreement with experimental data, with maximum errors of 9.5% for critical velocity prediction, 17.8% for residual projectile cross-sectional area prediction, and 24.4% for penetration depth prediction.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a0, a1, a2 | empirical coefficients related to the material properties of the target |
| A0 | cross-sectional area of the undeformed projectile |
| A1 | cross-sectional area of the deformed projectile |
| B0, B1, B2 | penetration resistance coefficients |
| CH | plastic wave velocity |
| CRH | caliber-radius-head |
| d | projectile diameter |
| Etp | plastic hardening modulus of the projectile |
| F | plastic hardening modulus of the projectile |
| fc | compressive strength of concrete |
| K | compressive strength of concrete |
| k1 | empirical mass loss coefficient |
| L0 | equivalent length of the projectile before penetration |
| L1 | equivalent length of the projectile during penetration |
| L | length of the projectile shank |
| M0 | initial mass of the projectile |
| Mr | residual mass of the projectile |
| M(V) | instantaneous mass of the projectile |
| ΔM | mass loss of the projectile |
| Prig | penetration depth of the projectile in rigid regime |
| Pres,r | penetration depth of the residual projectile in rigid regime |
| Pdef | penetration depth of the projectile in deformation and erosion regime |
| P | total penetration depth |
| p | cavity expansion stress |
| r0 | radius of the undeformed projectile |
| r1 | radius of the deformed projectile |
| Rt | strength of the target |
| S | radius of curvature of the ogive-nosed projectile |
| φ0 | shape parameter of the projectile nose |
| φ | angle between the normal to the projectile nose surface and the penetration central axis |
| u | penetration velocity |
| V0 | initial impact velocity |
| V | instantaneous velocity during penetration |
| Vr | rigid velocity |
| Vh | hydrodynamic velocity |
| x | length of the undeformed projectile |
| Yp | dynamic yield strength of the projectile |
| θ | angle between the surface normal of hemispherical nose and the penetration centerline |
| ψ | caliber-radius-head |
| ρt | density of the target |
| ρp | density of the target |
| φ | angle between the projectile nose surface normal and the penetration centerline |
| η(V) | instantaneous mass loss rate of the projectile |
| average resistance acting on the projectile nose |
References
- Ning, J.G.; Li, Z.; Ma, T.B.; Xu, X.Z. Failure behavior of projectile abrasion during high-speed penetrationinto concrete. Eng. Fail. Anal. 2020, 115, 104634. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Yan, J.B.; Shi, Z.Q.; Wang, H.F.; Xu, Y.L.; Huang, F.L. High-speed penetration of ogive-nose projectiles into thick concrete targets: Tests and a projectile nose evolution model. Def. Technol. 2024, 32, 553–571. [Google Scholar] [CrossRef]
- Li, Z.; Xu, X.Z. Theoretical investigation on failure behavior of ogive-nose projectile subjected to impact loading. Materials 2020, 13, 5372. [Google Scholar] [CrossRef]
- Gao, F.; Song, C.M.; Li, G.K.; Deng, S.X.; Wang, Z.; Liu, C.K. Experimental and analytical study on the penetration depth of mortar targets subjected to projectile impact in the hypervelocity regime. Int. J. Struct. Dyn. 2022, 22, 2250069. [Google Scholar] [CrossRef]
- Kong, X.Z.; Wu, H.; Fang, Q.; Zhang, W.; Xiao, Y.K. Projectile penetration into mortar targets with a broad range of striking velocities: Test and analyses. Int. J. Impact Eng. 2017, 106, 18–29. [Google Scholar] [CrossRef]
- Kong, X.Z.; Wu, H.; Fang, Q.; Peng, Y. Rigid and eroding projectile penetration into concrete targets based on an extended dynamic cavity expansion model. Int. J. Impact Eng. 2017, 100, 13–22. [Google Scholar] [CrossRef]
- Xing, H.Z.; Zhao, J.; Wu, G.; Duan, D.; Dehkhoda, S.; Lu, G.X.; Zhang, Q.B. Perforation model of thin rock slab subjected to rigid projectile impact at an intermediate velocity. Int. J. Impact Eng. 2020, 139, 103536. [Google Scholar] [CrossRef]
- Varnosfaderani, M.A.; Maghoul, P.; Wu, N. Modelling the penetration of subsonic rigid projectile probes into granular materials using the cavity expansion theory. Comput. Geotech. 2022, 141, 104546. [Google Scholar] [CrossRef]
- Alekseevskii, V. Penetration of a rod into a target at high velocity. Combust. Explos. Shock. Waves 1966, 2, 63–66. [Google Scholar] [CrossRef]
- Tate, A. A theory for the deceleration of long rods after impact. J. Mech. Phys. Solids 1967, 15, 387–399. [Google Scholar] [CrossRef]
- Lu, Y.Y.; Zhang, Q.M.; Xue, Y.J.; Guo, X.H.; Shang, C.; Liu, W.J.; Ren, S.Y.; Long, R.R. Hypervelocity penetration of concrete targets with long-rod steel projectiles: Experimental and theoretical analysis. Int. J. Impact Eng. 2021, 148, 103742. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, X.F.; Huang, C. Critical velocity theoretical model for hemispherical long rod projectiles’ penetrating semi-infinite thick target at high velocity. J. Vib. Shock 2019, 38, 8–14. [Google Scholar]
- Liu, C.; Zhang, X.; Chen, H.; Wang, J.; Wei, H.; Xiong, W. Experimental and theoretical study on steel long-rod projectile penetration into concrete targets with elevated impact velocities. Int. J. Impact Eng. 2020, 138, 103482. [Google Scholar] [CrossRef]
- Guo, L.; He, Y.; Pan, X.C.; He, X.; Tu, J.; Qiao, L.; Pang, C.X. Experimental study on mass loss of projectile subjected to high-velocity penetration into concrete target. J. Exp. Mech. 2020, 35, 82–90. [Google Scholar]
- Li, G.; Song, C.M.; Qiu, Y.Y.; Wang, M.Y. Theoretical and experimental studies on the phenomenon of reduction in penetration depth of hyper-velocity projectiles into granite. Chin. J. Rock Mech. Eng. 2018, 37, 60–66. [Google Scholar]
- Nia, A.A.; Zolfaghari, M.; Khodarahmi, H.; Nill, M.; Gorbankhani, A.H. High velocity penetration of concrete targets with eroding long-rod projectiles; an experiment and analysis. Int. J. Prot. Struct. 2014, 5, 47–63. [Google Scholar] [CrossRef]
- Qian, B.W.; Zhou, G.; Li, M.R.; Yin, L.X.; Gao, P.F.; Chen, C.L.; Ma, K. Study on the critical transformation speed of rigid body of highstrength steel projectile penetrating concrete target at high speed. Explo. Shock Waves 2024, 44, 147–157. [Google Scholar]
- Lu, Z.C.; Zhang, Y.D.; Wen, H.M.; Zhou, G.; Li, M.R.; Qian, B.W. Theoretical study on the penetration of long rods into semiinfinite concrete target. Mod. Appl. Phys. 2018, 9, 13–24. [Google Scholar]
- Zhang, Y.D.; Lu, Z.C.; Wen, H.M. On the penetration of semi-infinite concrete targets by ogival-nosed projectiles at different velocities. Int. J. Impact Eng. 2019, 129, 128–140. [Google Scholar] [CrossRef]
- Wen, H.M.; Lan, B. Analytical models for the penetration of semi-infinite targets by rigid, deformable and erosive long rods. Acta Mech. Sin. 2010, 26, 573–583. [Google Scholar] [CrossRef]
- Chen, X.W.; He, L.L.; Yang, S.Q. Modeling on mass abrasion of kinetic energy penetrator. Eur. J. Mech-A/Solids 2010, 29, 7–17. [Google Scholar] [CrossRef]
- He, L.L.; Chen, X.W.; He, X. Parametric study on mass loss of penetrators. Acta Mech. Sin. 2010, 26, 585–597. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, X.W.; Jin, F.N.; Xu, Y. Depth of penetration of high-speed penetrator with including the effect of mass abrasion. Int. J. Impact Eng. 2010, 37, 971–979. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, X.W.; Jin, F.N.; Xu, Y. Analysis on the bending of a projectile induced by asymmetrical mass abrasion. Int. J. Impact Eng. 2012, 39, 16–27. [Google Scholar] [CrossRef]
- Hao, O.; Chen, X.W. Modeling on mass loss and nose blunting of high-speed penetrator into concrete target. Int. J. Prot. Struct. 2019, 10, 3–25. [Google Scholar] [CrossRef]
- Guo, L.; He, Y.; Zhang, X.F.; He, Y.; Deng, J.; Guan, Z. Thermal-mechanical analysis on the mass loss of high-speed projectiles penetrating concrete targets. Eur. J. Mech.-A/Solids 2017, 65, 159–177. [Google Scholar] [CrossRef]
- Yao, Z.; Huang, F.L.; Li, J. Research on mass loss and nose shape evolution of kinetic energy projectiles penetrating concrete at high velocity. Acta Mech. Sin. 2024, 40, 423410. [Google Scholar] [CrossRef]
- Deng, Y.J.; Song, W.J.; Chen, X.W. Spherical cavity-expansion model for penetration of reinforced-concrete targets. Acta Mech. Sin. 2019, 35, 535–551. [Google Scholar] [CrossRef]
- Chen, X.W.; Li, Q.M. Deep penetration of a non-deformable projectile with different geometrical characteristics. Int. J. Impact Eng. 2002, 27, 619–637. [Google Scholar] [CrossRef]
- Chen, X.W.; Li, Q.M. Transition from nondeformable projectile penetration to semihydrodynamic penetration. J. Eng. Mech. 2004, 130, 123–127. [Google Scholar] [CrossRef]
- Lan, B.; Wen, H.M. Alekseevskii-Tate revisited: An extension to the modified hydrodynamic theory of long rod penetration. Sci. China Technol. Sci. 2010, 53, 1364–1373. [Google Scholar] [CrossRef]
- Tate, A. A possible explanation for the hydrodynamic transition in high speed impact. Int. J. Mech. Sci. 1977, 19, 121–123. [Google Scholar] [CrossRef]
- Zhang, L.S.; Huang, F.L. Model for long-rod penetration into semi-infinite targets. J. Beijing Inst. Technol. 2004, 13, 285–289. [Google Scholar]
- Tate, A. Long rod penetration models—Part II. Extensions to the hydrodynamic theory of penetration. Int. J. Mech. Sci. 1986, 28, 599–612. [Google Scholar] [CrossRef]
- Mu, Z.C.; Zhang, W. An investigation on mass loss of ogival projectiles penetrating concrete targets. Int. J. Impact Eng. 2011, 38, 770–778. [Google Scholar] [CrossRef]
- Silling, S.; Forrestal, M. Mass loss from abrasion on ogive-nose steel projectiles that penetrate concrete targets. Int. J. Impact Eng. 2007, 34, 1814–1820. [Google Scholar] [CrossRef]
- Wu, H.J.; Huang, F.L.; Wang, Y.N.; Duan, Z.P.; Shan, Y. Mass loss and nose shape change on ogive-nose steel projectiles during concrete penetration. Int. J. Nonlinear Sci. Numer. Simul. 2012, 13, 273–280. [Google Scholar] [CrossRef]
- Jiao, W.J.; Chen, X.W. Approximate solutions of the Alekseevskii–Tate model of long-rod penetration. Acta Mech. Sin. 2018, 34, 334–348. [Google Scholar] [CrossRef]
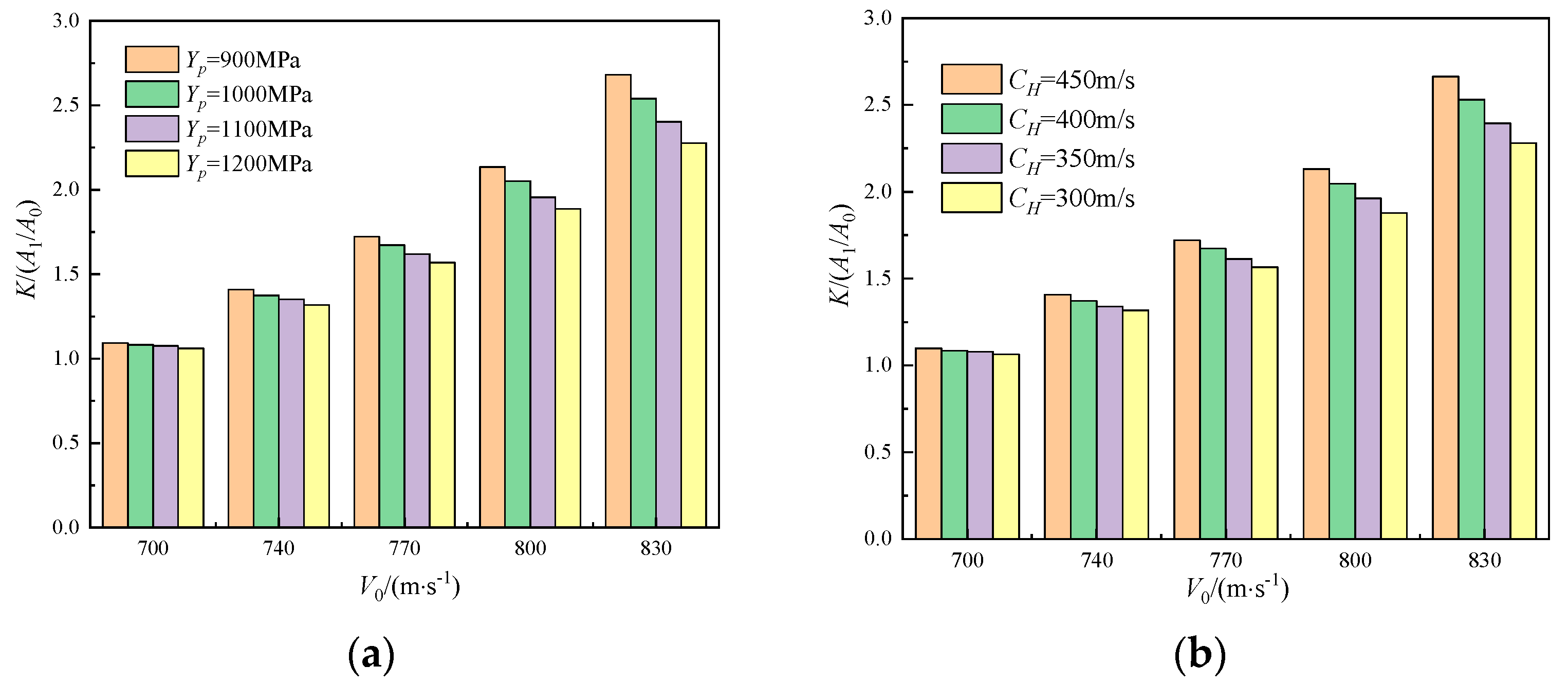

| Type | Projectile | |||||||
|---|---|---|---|---|---|---|---|---|
| ρp/(kg·m−3) | M0/g | CRH | d/mm | L0/mm | L/D | Ept/MPa | Yp/GPa | |
| Case 1 [13] | 7800 | 38.8 | 0 | 9 | 80 | 8.88 | 700 | 0.9 |
| Case 2 [5] | 7800 | 6.58 | 0 | 6 | 30 | 5 | 700 | 1.1 |
| Case 3 [14] | 7800 | 68.5 | 3 | 12 | 96 | 8 | 1200 | 1.45 |
| Case 4 [14] | 7800 | 322.5 | 3 | 30 | 90 | 3 | 1400 | 1.95 |
| Type | Target | ||||
|---|---|---|---|---|---|
| ρt/(kg·m−3) | fc/MPa | a0/(108 Pa) | a1/(106 kg·m−2·s−1) | a2/(103 kg·m−3) | |
| Case 1 [13] | 2400 | 45.4 | 4.07 | 1.56 | 1.48 |
| Case 2 [5] | 2400 | 50 | 4.48 | 1.63 | 1.48 |
| Case 3 [14] | 2200 | 42.8 | 3.83 | 1.45 | 1.36 |
| Case 4 [14] | 2200 | 42.8 | 3.83 | 1.45 | 1.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Lu, Y.; Li, J.; Chen, X.; Feng, X.; Lu, Z. On the Penetration of Projectiles into Semi-Infinite Concrete Targets in a Coupled Deforming and Eroding Regime. Buildings 2025, 15, 1607. https://doi.org/10.3390/buildings15101607
Xu H, Lu Y, Li J, Chen X, Feng X, Lu Z. On the Penetration of Projectiles into Semi-Infinite Concrete Targets in a Coupled Deforming and Eroding Regime. Buildings. 2025; 15(10):1607. https://doi.org/10.3390/buildings15101607
Chicago/Turabian StyleXu, Hengwei, Yonggang Lu, Junrun Li, Xing Chen, Xiaowei Feng, and Zhengcao Lu. 2025. "On the Penetration of Projectiles into Semi-Infinite Concrete Targets in a Coupled Deforming and Eroding Regime" Buildings 15, no. 10: 1607. https://doi.org/10.3390/buildings15101607
APA StyleXu, H., Lu, Y., Li, J., Chen, X., Feng, X., & Lu, Z. (2025). On the Penetration of Projectiles into Semi-Infinite Concrete Targets in a Coupled Deforming and Eroding Regime. Buildings, 15(10), 1607. https://doi.org/10.3390/buildings15101607




