A Dynamic Evaluation Method for the Development of Intelligent Construction Technology in the Construction Field Based on Structural Equation Model–System Dynamics Model

Abstract

In order to explore the development trends of intelligent construction technology in the field of construction, this paper constructs a system dynamics (SD) model of the application and development of BIM and the new-generation information technology in the construction industry based on SD theory and a structural equation model (SEM). Vensim DSS is used to explore the relationship between the SD model and six subsystems. The dynamic simulation and the sensitivity analyses are also conducted. Results show that during 2023–2050, as the time series advances, the effect value of the dynamic simulation gradually increases. From 2035, intelligent construction technology shows a trend of rapid development between various subsystems and the SD model. The adjusted model and the status of the subsystem are consistent with the SD model simulation curve. It is verified that intelligent construction technology has good development prospects in the construction field.

1. Introduction

With the rapid expansion of China’s economic construction scale, the construction industry is developing rapidly. In 2020, the total output value of China’s construction industry accounted for about 26% of the GDP with a year-on-year increase of 6.2%, and it will maintain a stable growth trend. However, there are many problems in China’s construction field, such as significant waste of resources [1], low economic benefits [2], serious environmental pollution [3], and extensive production management [4]. The Chinese government has promulgated a series of relevant policies to promote the application and development of intelligent construction technology in the construction field, aiming to vigorously promote the transformation and upgradation of the construction industry. For example, the “Guiding Opinions on Promoting the Coordinated Development of Intelligent Construction and Construction Industrialization” pointed out that it is necessary to use digitized and intelligent upgradation as a driving force, alongside innovate and break-through relevant core technologies, and increase the application of intelligent construction in all aspects of engineering construction. Intelligent transformation can improve the level of building management and construction efficiency, and reduce energy consumption, which is of great significance in promoting the reform of the construction industry [5,6,7].

Intelligent construction technology is an integrated technology with BIM technology at the core, and with the integrated development and application of BIM, the internet of things, cloud computing, big data, artificial intelligence, and other new-generation information technologies for the implementation of intelligent construction [8,9,10]. Intelligent construction has the advantage of the independent and interconnected characteristics of different new-generation information technologies and builds a complete intelligent construction technology system [11]. Intelligent construction fully empowers the engineering production and organization mode, which also promotes the interconnection of the engineering construction process, the integration of online and offline, and the coordination of resources and elements. Besides, intelligent construction can actively promote the formation of synergy between the construction industry and the information industry.

Structural equation modeling (SEM) is a method for quantitative and simplified research on complex data using the covariance between mathematical models and actual data through statistical theory. In recent years, the research around SEM has developed rapidly [12,13]. Oludolapo et al. [14] developed a partial least squares structural equation model (PLS-SEM) using questionnaire survey tools, and studied the impact of BIM technical barriers on BIM awareness throughout the project’s life cycle. Zhang et al. [15] established a SEM method to study the influence of environmental impact degree and product innovation on residents’ willingness to use photovoltaic systems. The research results show that there is a positive correlation between environmental impact degree, product innovation, and use intention.

System dynamics (SD) is an analysis method that integrates the comprehensive knowledge of information theory, system theory, control theory, and decision theory, which can track and simulate the current policy, and then provide a theoretical reference for decision makers [16,17]. Tang et al. [18] constructed an overall SD model framework based on the established causality diagrams among critical success factors, sustainable building completion criteria, and procurement system variables, and analyzed the impact of different procurement systems on sustainable building construction. Shi et al. [19] used SD to establish a public building carbon emission system simulation model, and used Vensim PLE simulation to simulate the changing trend of carbon emission data between 2020 and 2040. Then, based on the carbon emission simulation model of public buildings, the main carbon emission reduction paths such as the optimization of an energy structure, the application of energy-saving technology, and the application of renewable energy are obtained.

Gao et al. [20] embedded the ship owner’s psychological mechanism and behavior evolution into the dynamic model, and used empirical data to explore its evolution law. A Structural Equation Model (SEM) was constructed based on four variables, and the Three Gorges Project was taken as an example to conduct an empirical test on its influential relationship and degree. Finally, the SD model was used to simulate its dynamic evolution process. Ma et al. [21] proposed a dynamic laboratory safety assessment method integrating SEM and SD in view of the characteristics of insufficient and uncertain laboratory safety assessment data. Based on the questionnaire survey, the SEM was used to determine the influencing factors of laboratory safety, and their weights were embedded into the SD model. A sensitivity analysis was performed through a case study, identifying the variables that contributed most to improving laboratory safety. Albahri [22], utilizing a two-stage analysis combining Structural Equation Modeling (SEM) and Artificial Neural Networks (ANN), innovatively introduced a novel approach to linear and non-compensatory relationships. A comprehensive investigation across 11 industries over the past 6 years was conducted, involving the scrutiny of 239 articles, with meticulous screening and categorization resulting in 60 selected studies. The research findings highlighted the manufacturing and technology sectors as focal points, while the fields of construction and small-to-medium enterprises exhibited comparatively fewer studies. In discussing future work, the author proposed exploring determinants influencing the adoption of autism therapy in the healthcare domain. Upon contrasting the research outcomes, it is evident that the SEM-ANN model demonstrates significant advantages in static simulation, and it is adept at accommodating nonlinear factors within complex systems. However, it grapples with challenges such as overfitting and a decline in model interpretability. In comparison, the SEM-SD model focuses on causal relationships among variables and the dynamic evolution of systems, offering a more comprehensive consideration of both static and dynamic factors. It simulates policy impacts, providing theoretical references for decision makers.

Traditional project management focuses on phased, hierarchical and sequential management, which makes it difficult to change and creates low efficiency for information transmission [23]. Intelligent construction technology is characterized by informatization and intelligence. With the help of advanced technologies such as BIM, artificial intelligence, and big data analysis, the efficiency and adaptability of project collaboration are improved. The research shows that the organizational integration characteristics of BIM are helpful to overcome this conflict of interest, realizing the whole life cycle management, and improving the scientific nature of project management and the effectiveness of owner design management, and ensuring the orderly and efficient implementation of design work [24]. In addition, Yasin Celik proposed a BIM data traceability model based on a blockchain, which provides new technology for information exchange for construction projects. The bridge construction test shows that this method improves the BIM identification ability and improves the BIM implementation process [25]. Basem S designed a conceptual model for the integration of BIM and machine learning, which was applied to the final model for verification after use cases. It can predict the impact of design changes, assist decision making, and avoid time and cost waste [26].

From the above review, it can be seen that most of the current research explores the effectiveness of the integration of BIM and single information technology applied to a certain construction detail through practical engineering cases, and has limited contribution to the research on the overall development trend of intelligent construction technology in the construction field. At the same time, due to the large number of tasks, processes, and participants in engineering construction [27], it is less feasible to explore the impact of intelligent construction technology on the development of the construction industry with practical engineering as a case. Therefore, based on the theory of system dynamics and structural equation model, this paper constructs a system dynamics model (SD model of F7) for the application and development of BIM and new-generation information technology in the construction industry, and it uses Vensim DSS simulation to explore the relationship between six subsystems (F1-F6) and F7, and compares the simulation output results and sensitivity analyses under different conditions, so as to evaluate the development prospect of intelligent construction technology in the construction field.

2. System Dynamics’ Overview

2.1. Principles of System Dynamics

System dynamics (SD) combines qualitative and quantitative methods, information theory and cybernetics, and uses computer simulation technology to establish models to deal with complex nonlinear problems. SD judge the degree of fit of a data curve simulation and the similarity of a predicted development trend through the simulation curve formed by the evolution of the data along with the time series. The change of the trend of different curves will be an important sign of the behavioral characteristics of the system to deal with complex problems and carry out dynamic simulation for its future development.

2.2. System Dynamics Modeling Steps

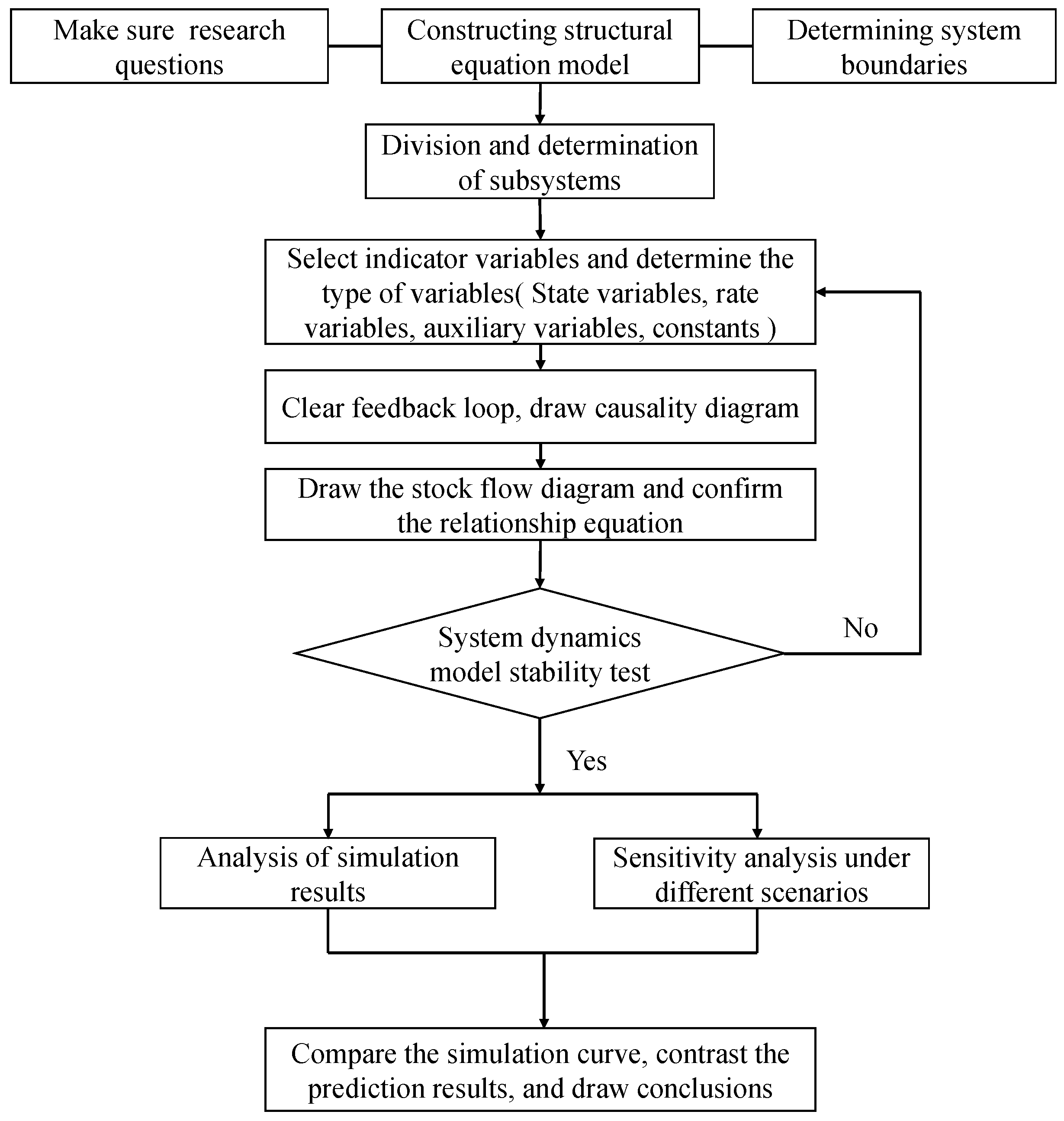
The establishment of a system dynamics model is generally carried out according to the following analysis process: (1) define the problem and divide the boundary of the system, (2) propose assumptions, (3) determine the influencing factors, (4) establish a causal relationship diagram, (5) analyze the causal relationship, (6) draw a stock flow diagram, (7) determine the model, (8) set the model parameters, (9) test the model, (10) analyze simulation results, and (11) perform sensitivity analysis under different scenarios [28]. The specific steps are shown in Figure 1.

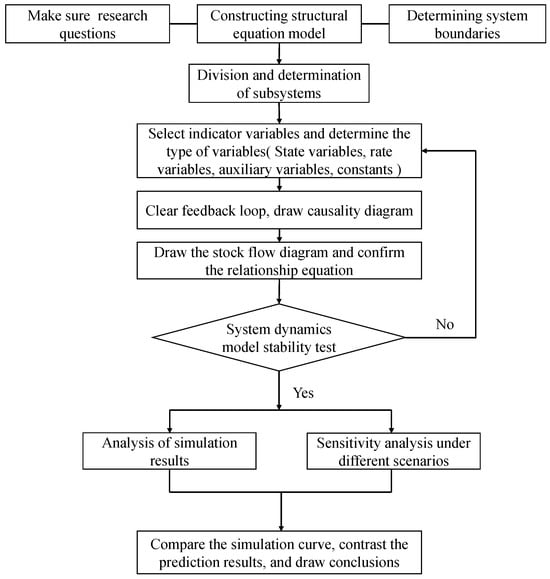
Figure 1. Process of system dynamics modeling.

3. System Dynamics Modeling

3.1. Construction of Structural Equation Model

This paper screened out the key variables affecting the intelligent transformation of the construction industry using the literature, research, and questionnaires. These variables were then condensed into six common factors using SPSS 26.0 software. Finally, AMOS 24.0 software was used to construct a structural equation model between the six common factors and the application and development of BIM and the new generation of information technology (F7) in the construction industry. At the same time, the factor analysis method is used to verify the results. The results show that the variables in this paper are scientific, and the structural equation model has good adaptability.

3.1.1. Data Sources

Online and offline surveys were conducted to experts, professors, and practitioners in the construction industry. The respondents were mainly from universities, design institutes, governments, construction, supervision, and other related sectors. The determination of the sample size is primarily contingent upon the specific circumstances of the questionnaire survey, taking into account factors such as the surveyed population, budget constraints, and acceptable error rates. Research results indicate that setting the sample size within the range of 200–400 is deemed appropriate [29]. A total of 280 questionnaires were sent out, and 265 responses were recovered, of which 251 were valid, with an effective recovery rate of 94.72%. The contents of the questionnaire and the basic data of the subjects are shown in Table 1 and Table 2.

Table 1. Contents of the questionnaire.

Influencing Factor	Symbol	Influencing Factor	Symbol	Influencing Factor	Symbol
The degree of building informatization product function understanding	X1	The popularity of the whole process, consulting businesses	X14	The smart contract function in ‘BIM + 6’ technology can provide a basis for investors to pay and settle	X27
The application degree of BIM technology in the construction industry	X2	The development prospect of building informatization in the whole process of consulting service	X15	‘BIM + 6’ technology fits the developing trend of construction project management	X28
The degree of cloud computing technology in the application scenario of the construction industry	X3	The whole process of engineering consulting service is worth developing	X16	A new model of blockchain + whole-process consultation	X29
The application degree of big data technology in the construction industry	X4	Construction companies’ understanding of professional informatization knowledge in the field of construction engineering	X17	The information-integrated service platform can realize the traceability, high transparency and non-tampering of the whole process of information flow and material flow, so as to improve the utilization rate of funds	X30
The application degree of Internet of Things technology in the construction industry	X5	The information of the construction process is not transparent	X18	The construction project uses the information integration service platform to collaborate in the project	X31
The application degree of 5G technology in the construction industry	X6	The construction companies’ trust the relevant stakeholders in the construction project	X19	The construction project uses the information integration service platform to realize the smart contract	X32
The application degree of artificial intelligence technology in the construction industry	X7	During the construction of the project, the investment unit pays the settlement on schedule	X20	The pre-job training module of the information integration service platform can improve workers’ construction skills and safety awareness	X33
The application degree of blockchain technology in the construction industry	X8	Strong scientific and technological means are needed in the process of engineering construction	X21	The information integration service platform can effectively guarantee the engineering quality	X34
The building informatization can improve the level of construction project management	X9	The function of ‘BIM + 6’ technology to optimize the design scheme	X22	The use of information integration service platform in construction projects can reduce material waste	X35
The application degree of building information technology in China	X10	The function of “BIM + 6” technology to reduce project cost	X23	Developing different information integration project management platforms meets the needs of the construction industry	X36
The development prospect of building informatization in China	X11	‘BIM + 6’ improves work efficiency, standardizes work flow and promotes cooperation among various professions in the construction stage.	X24	The information integration service platform can solve the problem of basic trust in engineering construction	X37
The use of building informatization products	X12	The blockchain in ‘BIM + 6’ realizes high transparency, traceability, and non-tampering of information data in construction	X25	The information integration service platform has strong technical barriers	X38
Long-term applicability of building information products	X13	Data analysis in ‘BIM + 6’ technology can assist decision making in the acceptance stage.	X26	It is difficult to popularize the use of the information integration service platform in the construction industry	X39

Table 2. Basic information of interviewees.

	Demographic Information	Amount	Proportion (%)		Demographic Information	Amount	Proportion (%)
Sexuality	Man	194	77.29	Qualifications	Licensed professional construction manager	9	3.59
	Woman	57	22.71		Registered cost engineers	1	0.40
Age	20–30	45	17.93
					Investment consulting engineer	2	0.80
	30–40	116	46.22		Other	164	65.34
	40–50	63	25.10	Job content	Real estate Development	4	1.59
	50–60	27	10.76		Construction	46	18.33
	Others	0	0.00		Design	56	22.31
Educational background	Undergraduate	78	31.08		Administration and management	5	1.99
	Master	60	23.90		Consultation	5	1.99
	Doctor	106	42.23		Project supervision	4	1.59
	Others	7	2.79		University teaching	104	41.43
Professional title	Professor	23	9.16		Software development	0	0.00
	Associate Professor	49	19.52		Cost management	2	0.80
	Professorate Senior engineer	10	3.98		Others	25	9.96
	Senior engineer	70	27.89	Work years	0–5	49	19.52
	Researcher	6	2.39		5–10	50	19.92
	Associate researcher	1	0.40		10–15	75	29.88
	Others	92	36.65		15–20	33	13.15
Qualifications	National 1st class certified architect	51	20.32		More than 20	44	17.53
	National 1st class certified structural engineer	23	9.16
	National 1st class certified geo-tech engineer	1	0.40

3.1.2. Sample Data Test

SPSS 26.0 was used to analyze the reliability of the sample data of this survey. The reliability coefficient of the questionnaire was 0.954, and the survey results had good reliability and internal consistency. Before using the factor analysis method, it is necessary to test whether the sample data is applicable, that is, using a validity test. A KMO test and Bartlett sphericity test were used to calculate the KMO value and significance probability value (p value) with SPSS 26.0 After testing, the KMO value of the sample data was 0.948, and the p value was 0. The calculation results show that there is a strong correlation between the various factors of the sample data, and the factor analysis method can be used for research and analysis.

3.1.3. Extracting Common Factors

Firstly, the principal component analysis method is used to solve the eigenvalues of the sample data, and then the total variance explanation is obtained using SPSS 26.0 analysis, as shown in Table 3. According to the extraction principle of an eigenvalue greater than one, the first six factors are extracted as common factors, and the cumulative variance contribution rate of the first six common factors is 73.54%, which can summarize most of the factor variables and basically reflect the essential information of the sample data.

Table 3. Total variance explanation.

Component	Initial Eigenvalue			Extract the Load Sum of Squares
	Total	Variance (%)	Accumulation (%)	Total	Variance (%)	Accumulation (%)
1	16.963	43.496	43.496	16.963	43.496	43.496
2	5.971	15.311	58.807	5.971	15.311	58.807
3	1.967	5.043	63.85	1.967	5.043	63.85
4	1.611	4.131	67.981	1.611	4.131	67.981
5	1.158	2.969	70.951	1.158	2.969	70.951
6	1.01	2.589	73.54	1.01	2.589	73.54
7	0.836	2.144	75.683
…	…	…	…

3.1.4. Common Factor Explanation

The rotated component matrix is obtained through the maximum variance orthogonal rotation transformation. Then, the index information carried by each common factor is obtained, and the important factor variables are identified. The relationship between the factor variables can be better understood. When the load value of the sample data is greater than 0.5, it has an effective explanatory power, and the relevant factor variables can be summarized as the corresponding common factors. In the component matrix after the rotation of the sample data, the load value of X16 has two factors that meet the requirements of interpretation, so there is a phenomenon of conceptual ambiguity. The X20 load values did not reach an effective explanation, so the X16 and X20 factor variables were deleted. Therefore, the factor variables contained in each common factor are shown in Table 4. The common factors F1-F6 represent the function of BIM and the new generation of information technology (F1); the application degree of the new generation of information technology in the construction industry (F2); the development trend of building informatization (F3); the characteristics of construction project management information products (F4); the actual situation of the construction process (F5); and the development of BIM-based information integration service platform (F6).

Table 4. Common factor explanation.

Common Factor	Factor Variables
F1	X21, X22, X23, X24, X25, X26, X27, X29, X30, X31, X32, X33, X34, X35, X37, X38, X39
F2	X2, X3, X4, X5, X6, X7, X8, X10
F3	X9, X11, X15
F4	X1, X12, X13, X14
F5	X17, X18, X19
F6	X28, X36

3.1.5. Establishment of a Second-Order Structural Equation Model

The maximum likelihood method is used to evaluate the parameters of the measurement model, and the fitting degree of the observed variables and the potential variables is judged according to the path coefficient and the fitting index. According to the correlation between the variables, the suitability of the measurement model is obtained. Hair et al. proposed that the test of ‘violation estimation’ must be carried out before evaluating the goodness of fit of the model. The measure of violation estimation is usually the presence of negative error variance and the standardization index that exceeds or is too close to one [30].

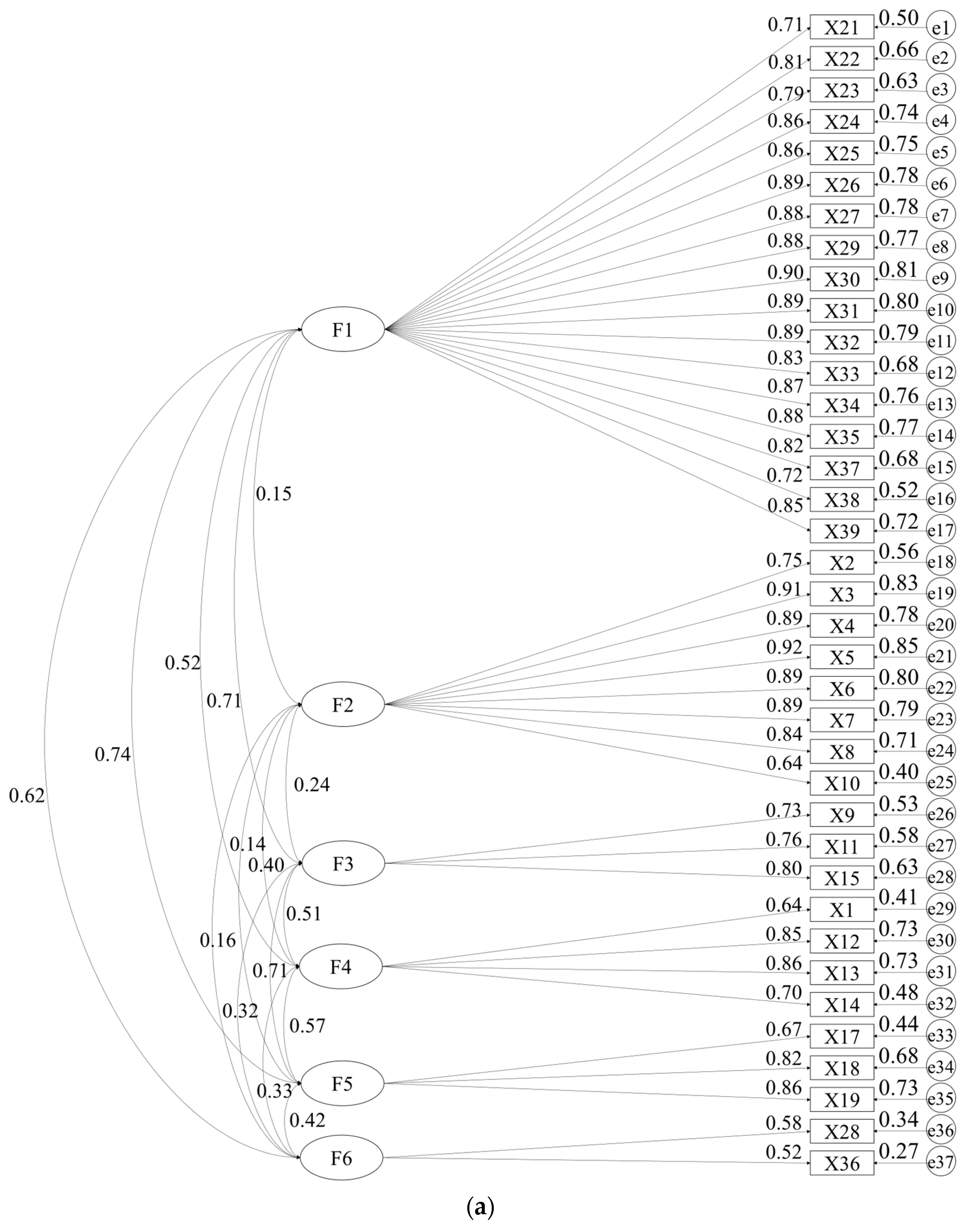
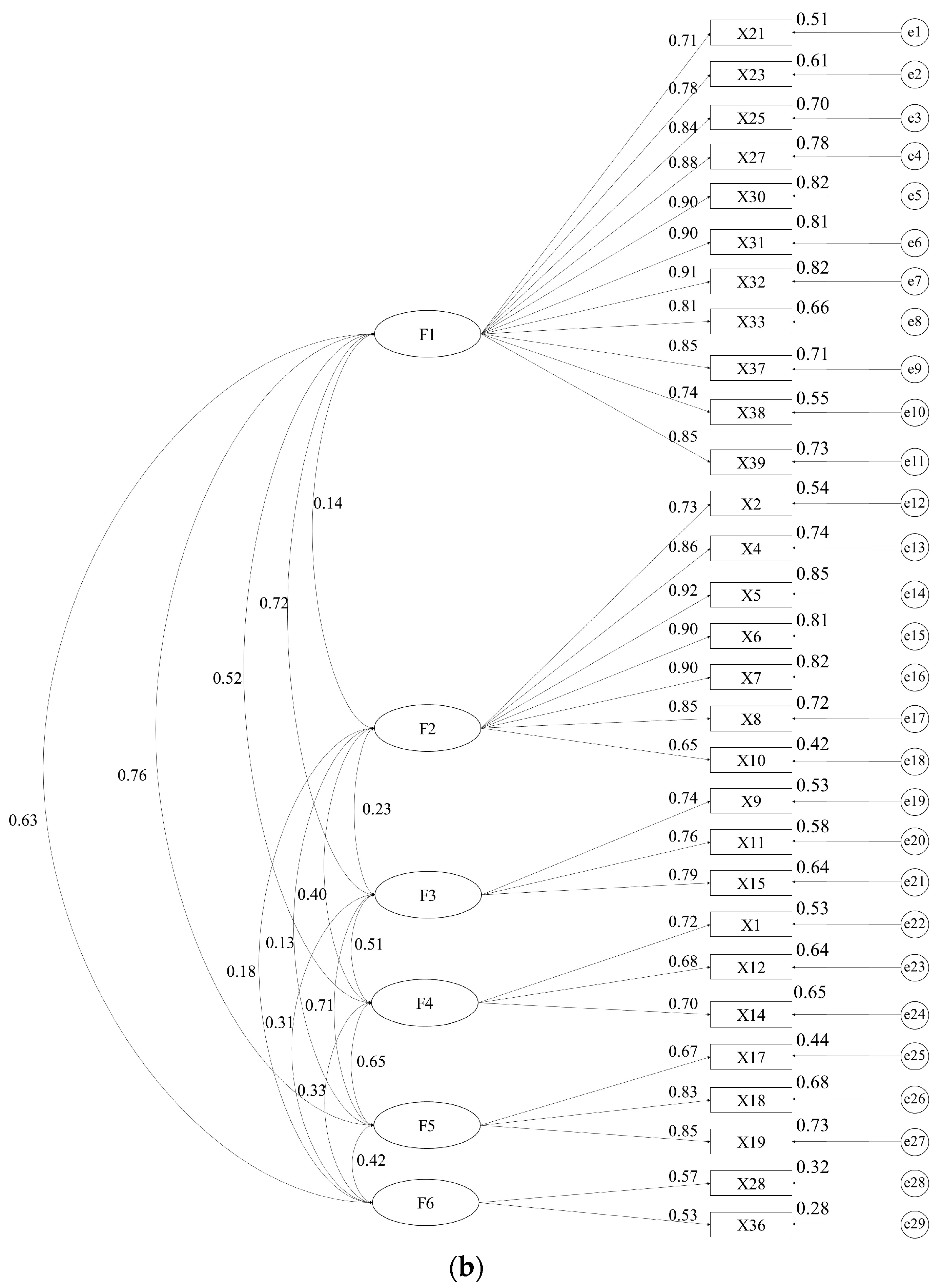
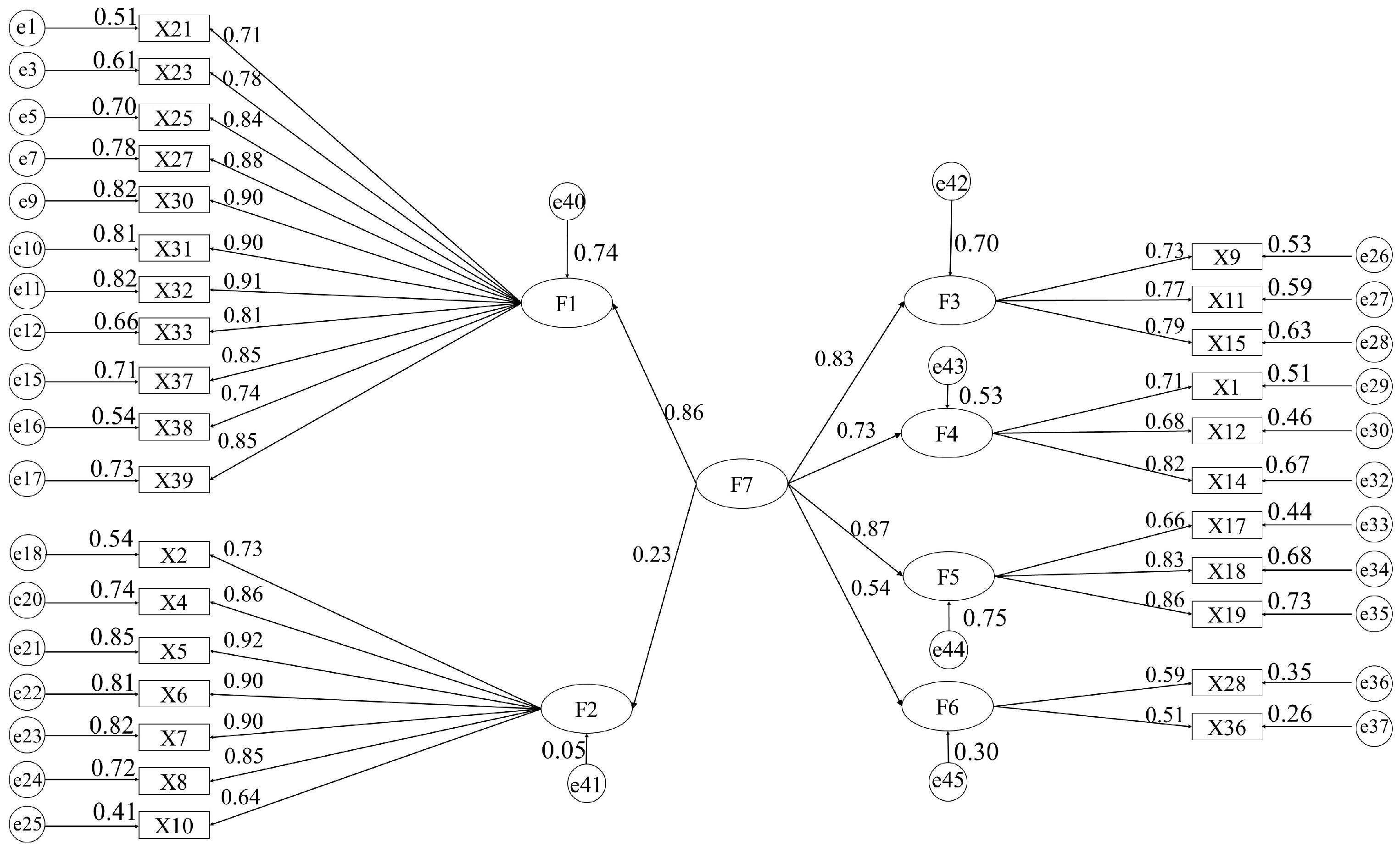
There is no negative error variance in the measurement model, and the absolute value of the standardized coefficient does not exceed 0.95, indicating that the model does not violate the estimation, and the overall model fitting degree can be tested, as shown in Figure 2. However, some of the indicators of the uncorrected measurement model did not meet the requirements, and the degree of adaptation was poor, as shown in Table 5. According to M.I. values provided by AMOS 24.0, the model is corrected one by one, from large to small, and the adaptation index of the corrected measurement model meets the adaptation standard. In the measurement model, e represents the residual term between variables, reflecting the part of the structural equation that has not been explained. If a negative value occurs, it indicates that the data processing is abnormal. At the same time, the residual term in the modified measurement model is positive, the path coefficient meets the standard, and the adaptation index meets the requirements. Therefore, the overall fitting degree of the model is good, as shown in Table 6.

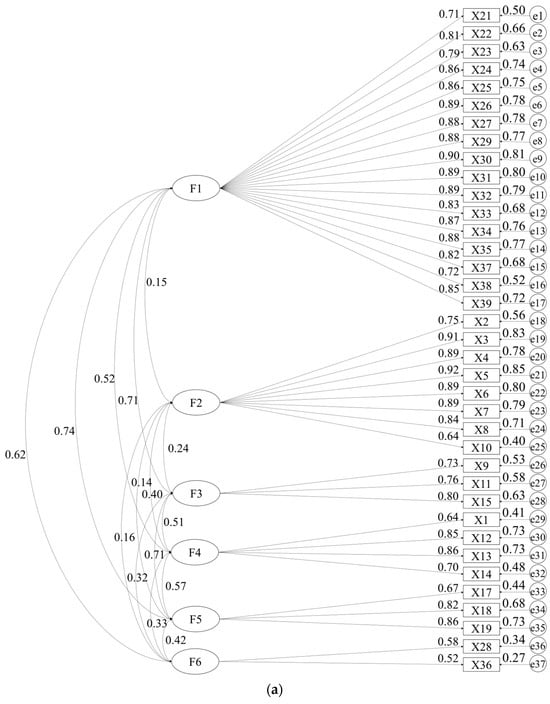
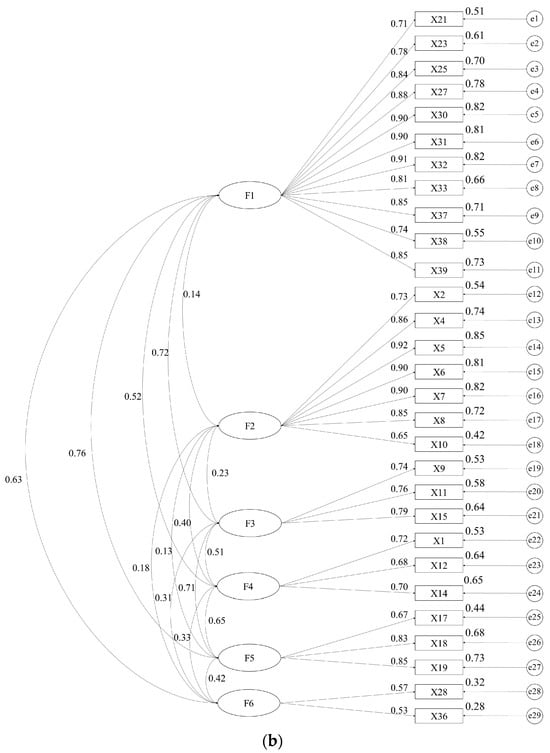
Figure 2. Confirmatory factor analysis model of measurement model. (a) Unmodified measurement model. (b) Modified measurement model.

Table 5. The overall adaptation index of the unmodified measurement model.

Statistical Test	Adaptation Standard	Measured Value	Adaptation
RMSEA	<0.08	0.08	No
CMIN/DF	<3	2.63	Yes
GFI	>0.8	0.73	No
TLI	>0.9	0.88	No
IEI	>0.9	0.89	No
CFI	>0.9	0.89	No

Table 6. The overall adaptation index of the modified measurement model.

Statistical Test	Adaptation Standard	Measured Value	Adaptation
RMSEA	<0.08	0.06	Yes
CMIN/DF	<3	2.03	Yes
GFI	>0.8	0.83	Yes
TLI	>0.9	0.93	Yes
IEI	>0.9	0.94	Yes
CFI	>0.9	0.94	Yes

Based on the revised measurement model, a first-order structural model was constructed. Utilizing first-order confirmatory factor analysis on the structural model, assumptions among various latent variables were tested, as illustrated in Figure 3. Following confirmatory factor analysis, the structural model exhibits favorable fit indices, including an RMSEA value of 0.065 (<0.08), CMIN/DF value of 2.060 (<3), GFI value of 0.821 (>0.8), TLI value of 0.924 (>0.8), IFI value of 0.931 (>0.9), and CFI value of 0.930 (>0.9). Upon examination, all model indicators meet the established standards, affirming the good fit of the structural equation model.

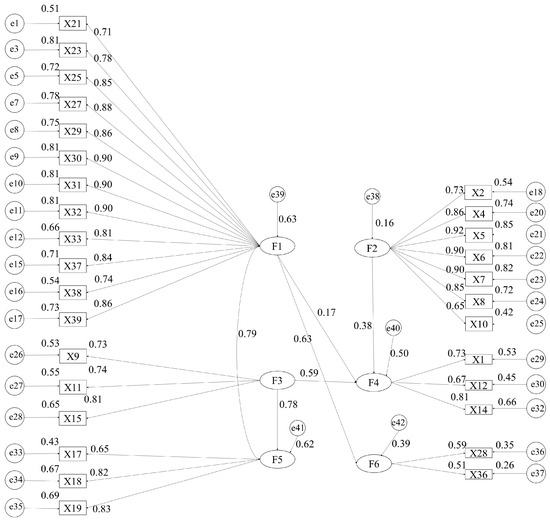
Figure 3. First-order confirmatory factor analysis on the structural model.

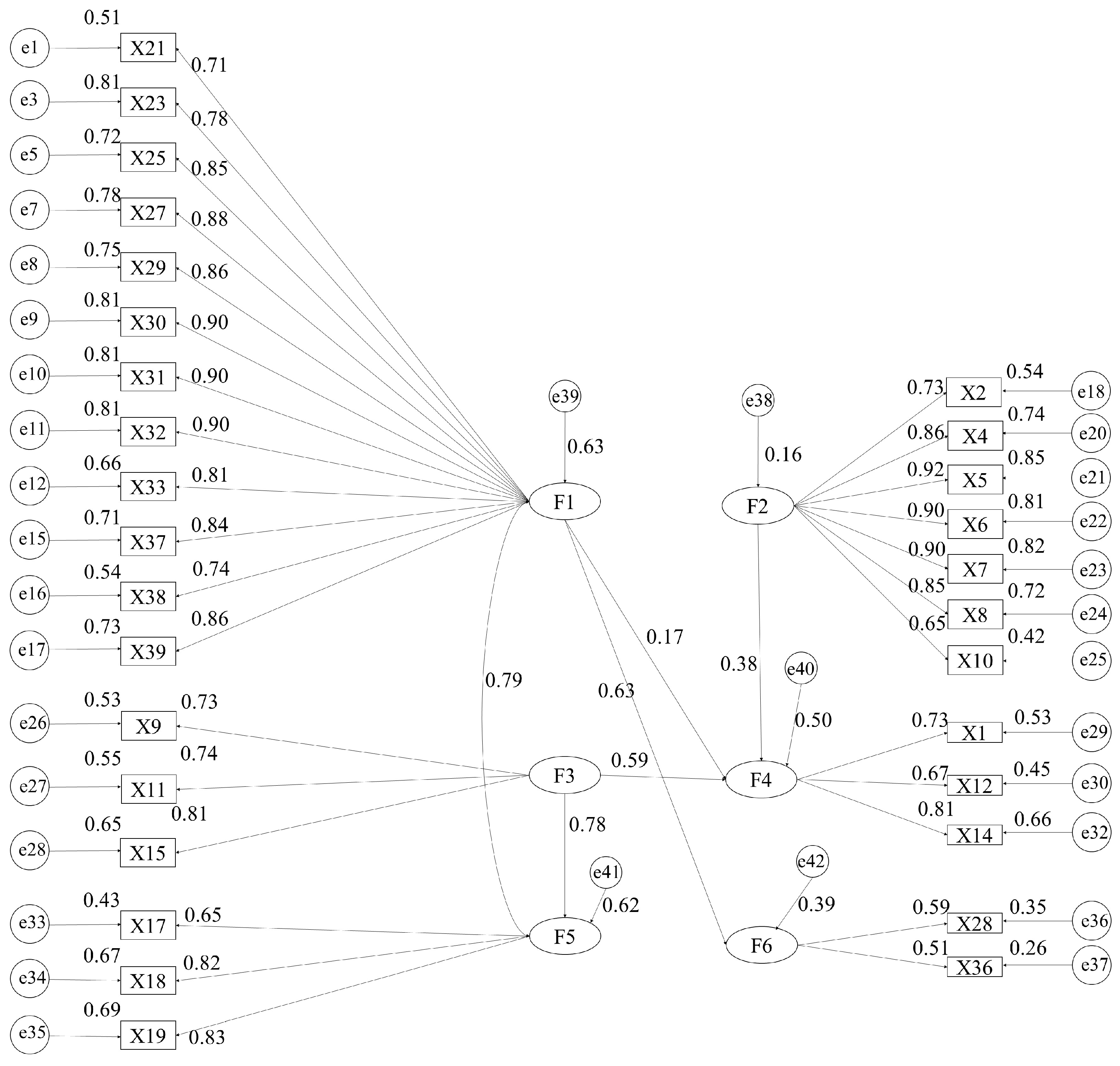
According to the standardized path coefficients between the latent variables in the modified first-order structural model, it is found that the correlation between the latent variables is strong, and the model with a good overall fitting degree after correction still has more observed variables. Therefore, there is a higher level of common factor in the six potential factors of the modified first-order structural model; that is, the external potential variable is the application and development of BIM and new-generation information technology in the construction industry (F7). Then, AMOS 24.0 is used to build the second-order confirmatory factor analysis model, and the maximum likelihood method is used to estimate the parameters. The analysis results are shown in Figure 4. As shown in Table 7, each index of the second-order confirmatory factor analysis model meets the standard [20], and the fitting degree of the structural equation model is good.

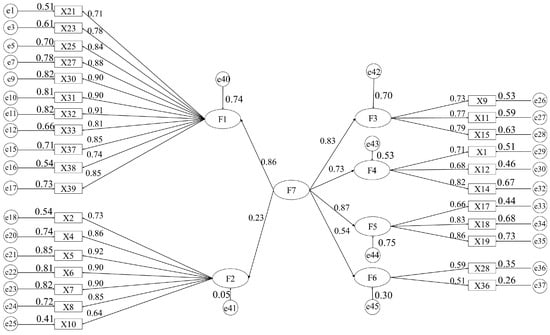
Figure 4. The second-order confirmatory factor analysis model of the structural model.

Table 7. The fitting index of the second-order confirmatory factor analysis model.

Statistical Test	Adaptation Standard	Measured Value	Adaptation
RMSEA	<0.08	0.07	Yes
CMIN/DF	<3	2.13	Yes
GFI	>0.8	0.83	Yes
TLI	>0.9	0.92	Yes
IEI	>0.9	0.93	Yes
CFI	>0.9	0.93	Yes

3.2. Boundary Determination

The determination of the system boundary is based on the system feedback structure and internal factors in the system behavior, while the external factors have little influence on its behavior. Therefore, the process of defining the system dynamics model mainly includes the division of systems and subsystems, and the determination of positive and negative correlations between related variables.

3.3. SD Model Construction

As shown in Figure 4, based on the relationship and the path distribution of nodes in the second-order SEM mathematical model, this paper divides the SD model of application and development of BIM and new-generation information technology (F7) into six subsystems which are the function of BIM and the new-generation information technology (F1); the application degree of new-generation information technology in construction industry (F2); the development trend of building informationization (F3); the characteristics of construction project management information products (F4); the reality of the engineering construction process (F5); and the development of an information integration service platform based on BIM (F6). The factors included in the SD model and subsystem are shown in Table 8, which is based on Table 1.

Table 8. The composition of the SD model.

SD Model (Symbol)	Subsystem (Symbol)	Influencing Factor (Symbol)	Positive Negative Correlation
F7	F1	X21	+
		X23	+
		X25	+
		X27	+
		X30	+
		X31	+
		X32	+
		X33	+
		X37	+
		X38	−
		X39	+
	F2	X2	+
		X4	+
		X5	+
		X6	+
		X7	+
		X8	+
		X10	+
	F3	X9	+
		X11	+
		X15	+
	F4	X1	+
		X12	+
		X14	+
	F5	X17	+
		X18	−
		X19	+
	F6	X28	+
		X36	+

3.4. Cause–Effect Diagram

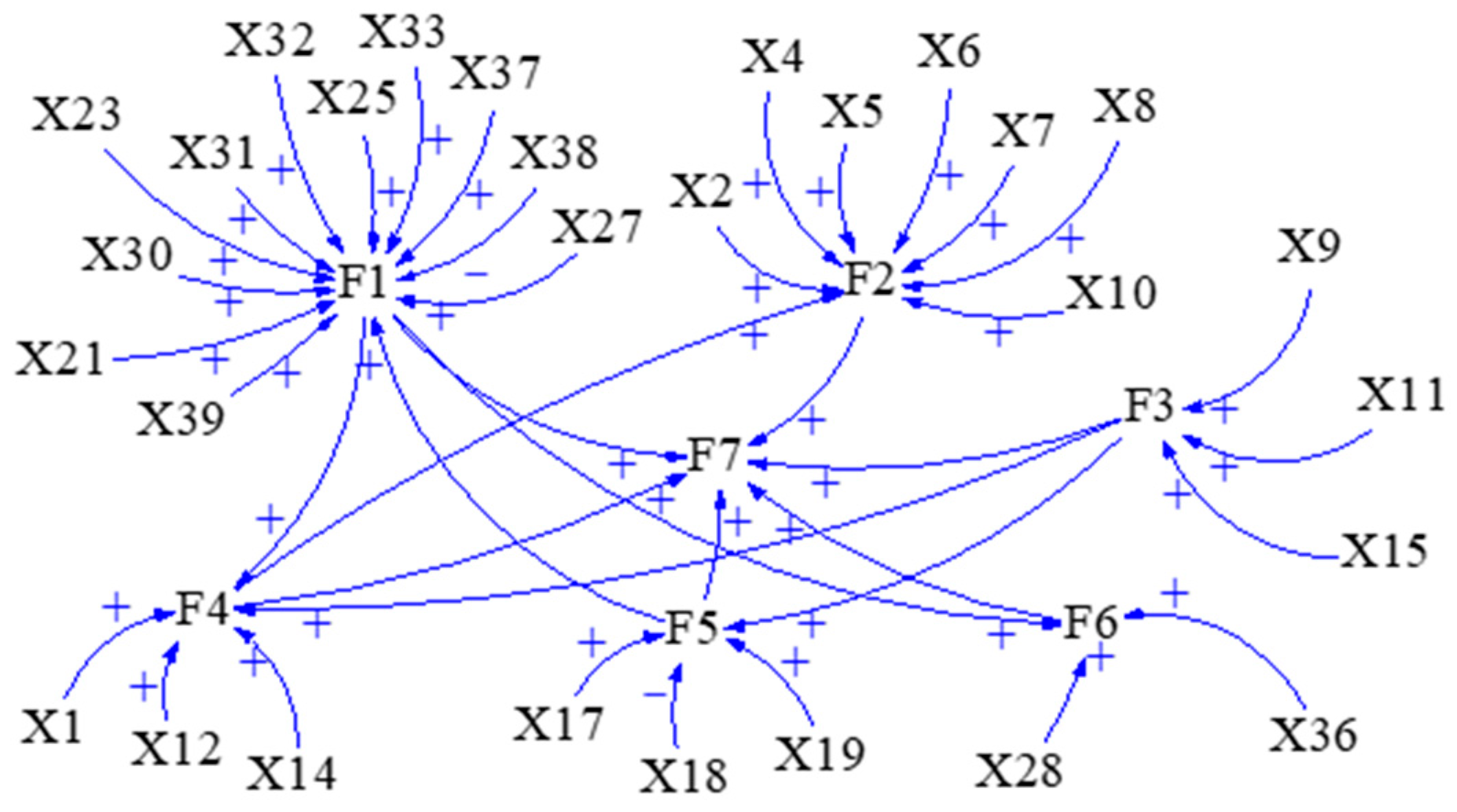
Based on the structural equation model of Figure 3 and Figure 4, the positive and negative correlations between SD models and subsystems which are shown in Table 8, the cause–effect diagram of the SD model is established (as shown in Figure 5), which provides the basis for drawing the stock–flow diagram and determining the model equations and parameters.

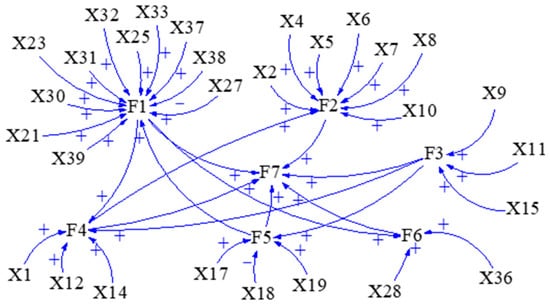
Figure 5. The cause–effect diagram of SD model.

3.5. Stock–Flow Diagram

3.5.1. Setting Variables in the System

Before drawing the flow diagram, it is necessary to clarify the variables in the system, which are classified into state variables, rate variables and constants, as shown in Table 9. The state variable in the table refers to the accumulation effect of the description system, reflecting the stock formed by the change of material flow or information flow over time. The rate variable refers to the change in the amount of stock per unit time.

Table 9. Variables in the SD model.

Variable Category	Variable Name
State	F1, F2, F3, F4, F5, F6, F7
Rate	f11, f12, f21, f31, f41, f51, f52, f61, f71
Constant	X1, X2, X4, X5, X6, X7, X8, X9, X10, X11, X12, X14, X15, X17, X18, X19, X21, X23, X25, X27, X28, X30, X31, X32, X33, X36, X3, X38, X39

3.5.2. Drawing the Stock–Flow Diagram

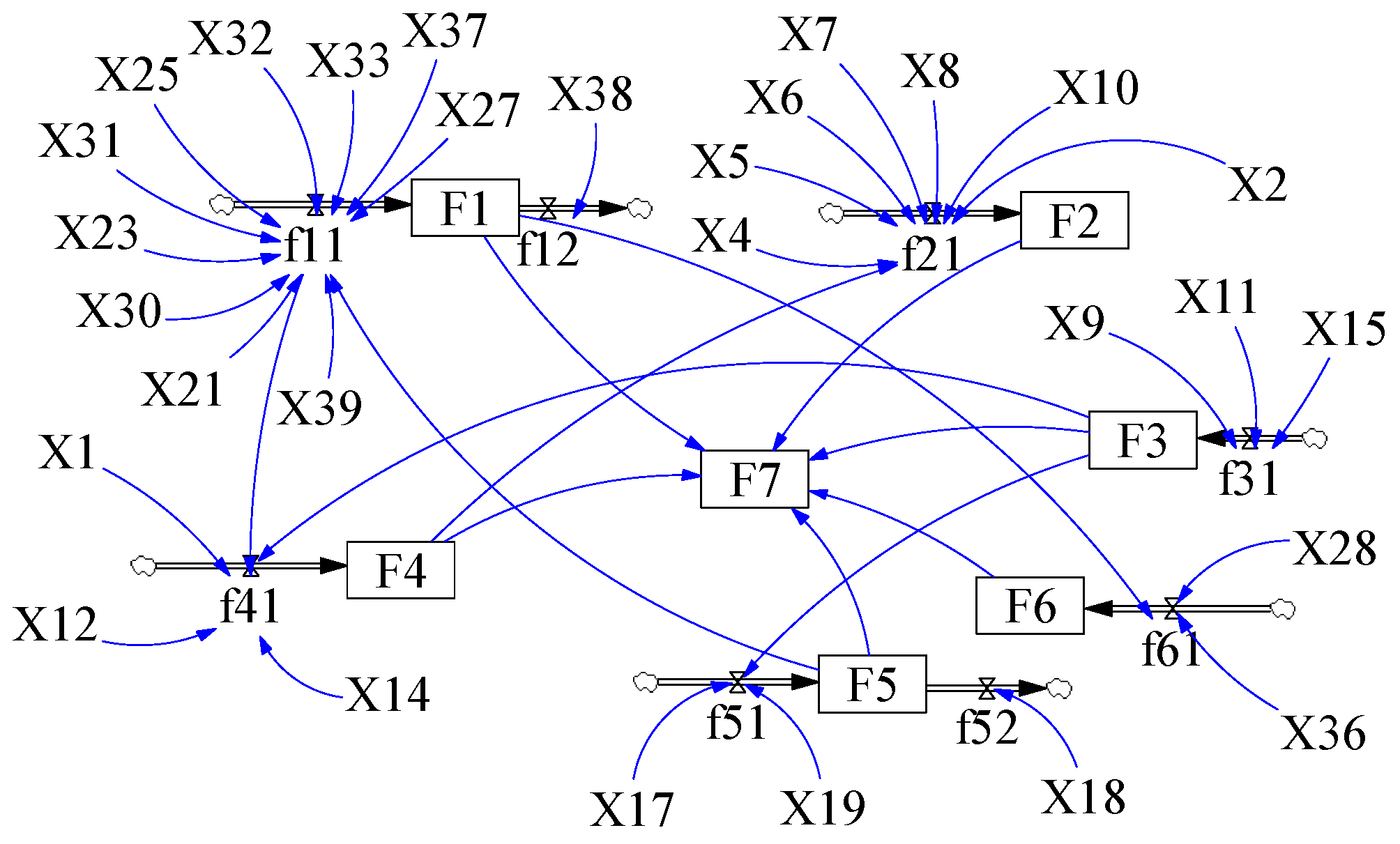
According to the cause–effect diagram in Section 3.2, combined with the set variables and six subsystems, the stock–flow diagram of SD model is drawn as shown in Figure 6.

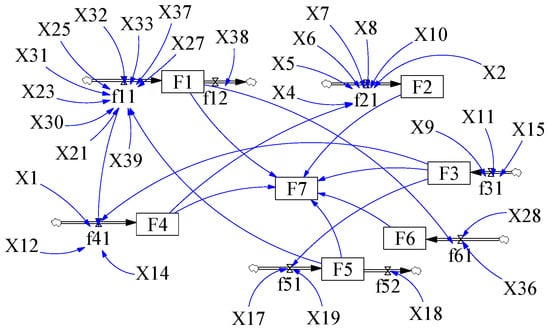
Figure 6. The stock–flow diagram of SD model.

3.6. Model Equation Setting

3.6.1. Weight Value and Mathematical Equation Determination

The relevant influence coefficients and weight values in the SD model are calculated based on the path coefficients and factor loads in the SEM. According to the second-order confirmatory factor analysis model, the weights of the relevant indicators are calculated using path coefficients to determine the weight coefficients (F_i) for each indicator. The formula is as follows:

$$F_i=\frac{k_i}{{\displaystyle \sum _{i=1}^{i=6}{k}_i}}$$

(1)

k_i represents the path coefficients of the six primary latent variables, and the denominator denotes the sum of the path coefficients of these six primary latent variables.

The weights of the state variables and constants in Table 10 provide a reference for determining the model equations. The mathematical equations in the SD model are shown in Table 11, where the initial value and unit of each subsystem are set to NA and Undefined, respectively.

Table 10. The weight of variables in the system model.

Level Variables	Weight	Constants	Weight
F1	0.212	X21	0.076
		X23	0.084
		X25	0.091
		X27	0.095
		X30	0.097
		X31	0.097
		X32	0.098
		X33	0.098
		X37	0.092
		X38	0.080
		X39	0.092
F2	0.057	X2	0.126
		X4	0.148
		X5	0.159
		X6	0.155
		X7	0.155
		X8	0.147
		X10	0.110
F3	0.204	X9	0.319
		X11	0.336
		X15	0.345
F4	0.180	X1	0.321
		X12	0.308
		X14	0.371
F5	0.214	X17	0.281
		X18	0.353
		X19	0.366
F6	0.133	X28	0.536
		X36	0.464

Table 11. Equation function.

Variable Category	Variable Name	Equation Function
Level	F1	F1 = f11 + f12 + 0.79 × F5
	F2	F2 = f21 + 0.38 × F4
	F3	F3 = f31
	F4	F4 = f41 + F1 × 0.17 + 0.59 × F3
	F5	F5 = f51 + f52 + 0.78 × F3
	F6	F6 = f61 + 0.63 × F1
	F7	F7 = f71
Rate	f11	f11 = 0.076 × X21 + 0.084 × X2 + 0.091 × X25 + 0.095 × X27 + 0.097 × X30 + 0.097 × X31 + 0.098 × X32 + 0.098 × X33 + 0.092 × X37 + 0.092 × X39
	f12	f12 = 0.08 × X38
	f21	f21 = 0.126 × X2 + 0.148 × X4 + 0.159 × X5 + 0.155 × X6 + 0.155 × X7 + 0.147 × X8 + 0.11 × X10
	f31	f31 = 0.319 × X9 + 0.336 × X11 + 0.345 × X15
	f41	f41 = 0.321 × X1 + 0.308 × X12 + 0.371 × X14
	f51	f51 = 0.281 × X17 + 0.366 × X19
	f52	f52 = −0.353 × X18
	f61	f61 = 0.536 × X28 + 0.464 × X36
	f71	f71 = 0.212 × F1 + 0.057 × F2 + 0.204 × F3 + 0.18 × F4 + 0.214 × F5 + 0.133 × F6

The paper takes F2 as an example of the formulation method for the equation functions in Table 11 which is as follows:

F2 = f21 variation + F2 initial value + F4 impact variable × 0.38

f21 variation = X2 × 0.126 + X4 × 0.148 + X5 × 0.159 + X6 × 0.155 + X7 × 0.155 + X8 × 0.147 + X10 × 0.11

F2 initial value = 0

In the above equation functions, the coefficient for F4 is derived from Figure 3, and the coefficients in the f21 change formula come from Table 10.

3.6.2. Parameter Value Determination

The parameter values used in this chapter come from the data obtained from the questionnaire survey. The calculation method of the parameter value of the state variable is obtained by multiplying the constant parameter value and its weight in each subsystem, and then adding them together. For example, the F3 parameter value = X9 (weight × parameter value) + X11 (weight × parameter value) + X15 (weight × parameter value). Meanwhile, the parameter value of the set constant is the sum of the mean statistics and mean error of the measurement index (influencing factor). Therefore, parameter values in the model are shown in Table 12.

Table 12. Parameter values in the model.

Level Variables	Parameter Values	Constants	Parameter Values
F1	4.422	X21	4.481
		X23	4.372
		X25	4.459
		X27	4.399
		X30	4.476
		X31	4.505
		X32	4.419
		X33	4.354
		X37	4.363
		X38	4.245
		X39	4.553
F2	3.397	X2	3.638
		X4	3.391
		X5	3.361
		X6	3.365
		X7	3.363
		X8	3.366
		X10	3.317
F3	4.496	X9	4.49
		X11	4.632
		X15	4.369
F4	3.841	X1	3.855
		X12	3.798
		X14	3.865
F5	4.082	X17	3.821
		X18	4.214
		X19	4.154
F6	4.444	X28	4.515
		X36	4.361
F7	4.204

3.7. SD Model Stability Test

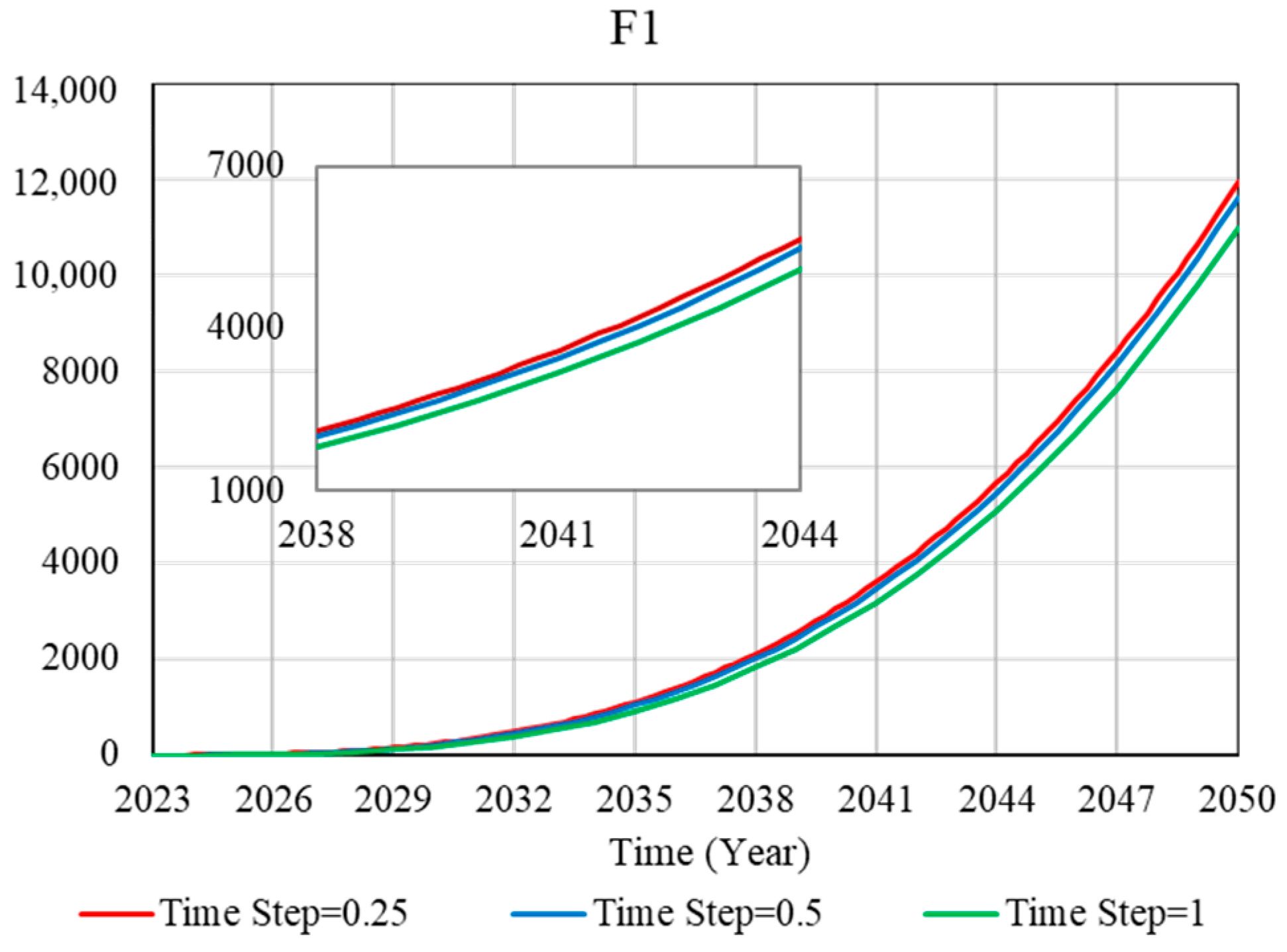
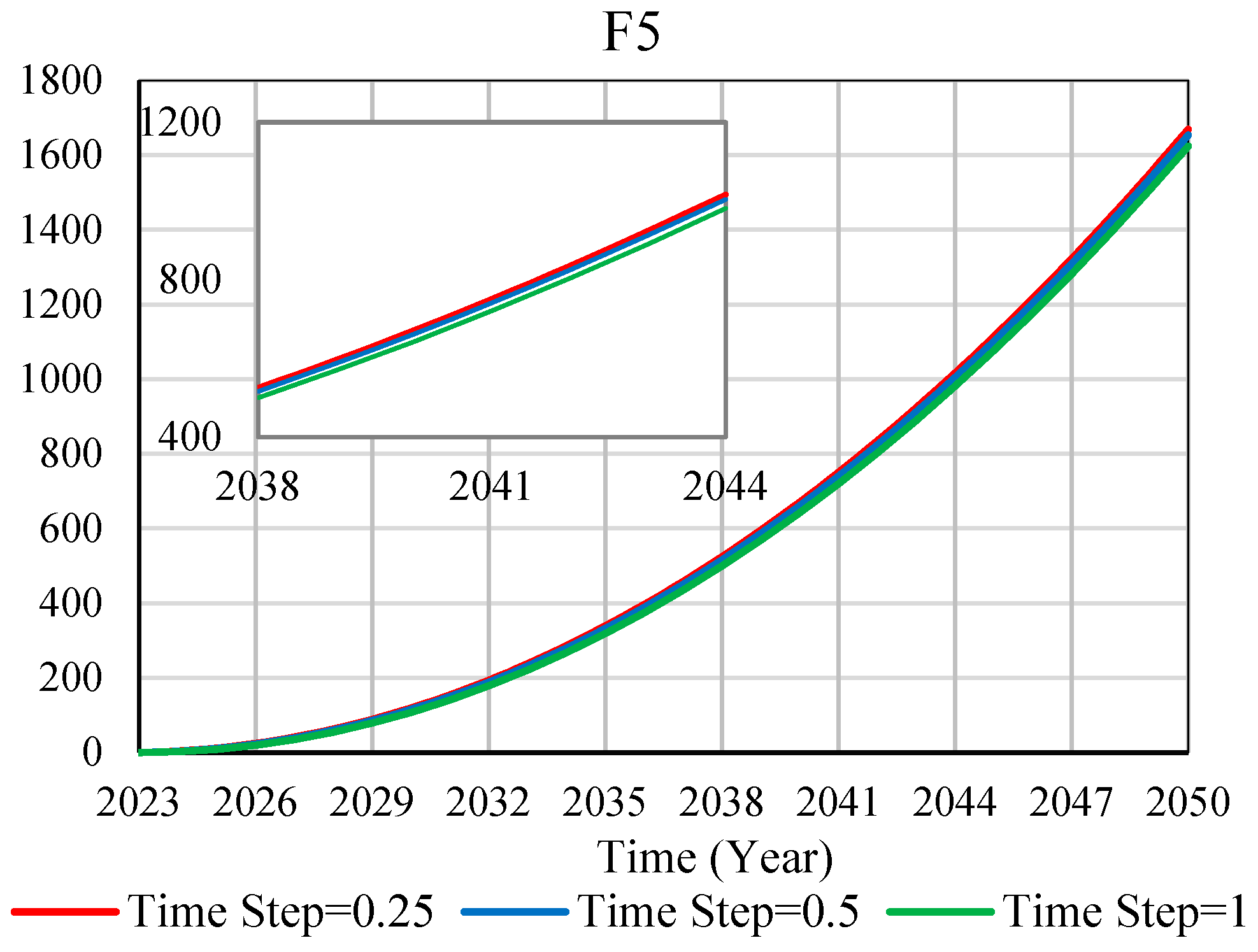
The stability test is to study the development trend of the curve in different situations and the stability of the fitting situation under different situation settings. The subsystem of BIM and new-generation information technology integration (F1) and the subsystem of the reality of the construction process (F5) are tested. Three different step sizes are set for them, namely 0.25, 0.5, and 1. The time unit of the test is the year, and the time interval starts from 2023 to 2050. The development trends of the two subsystems at different step lengths are highly consistent, indicating that the system has good stability (as shown in Figure 7).

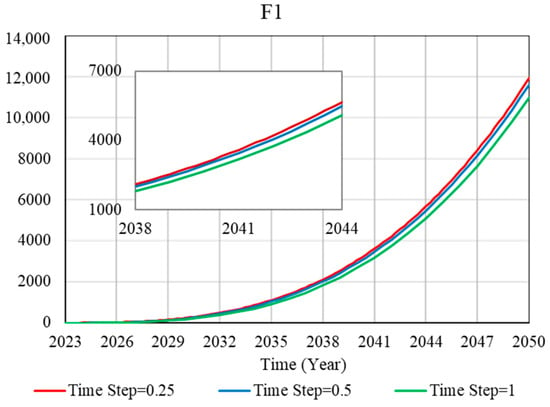
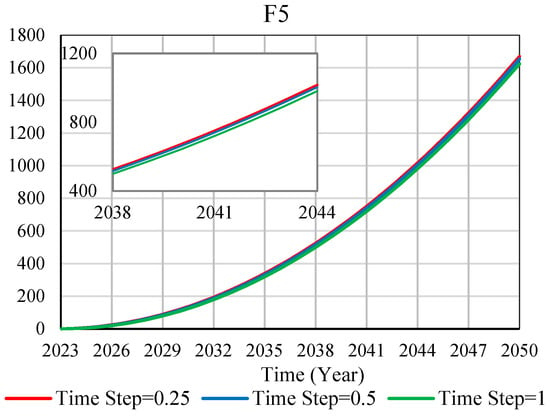
Figure 7. Stability test.

4. Dynamic Simulation Predictive Analysis

The SD model is tested using Vensim DSS, and the simulation results are analyzed. The SD model is set as follows: INITIAL TIME = 2023, FINAL TIME = 2050, TIME STEP = 1, Units for Time: Year. The set model parameters are substituted into the corresponding mathematical equations to observe the dynamic changes and development of each subsystem and SD model.

4.1. Evolution Trend of the System Dynamics Model

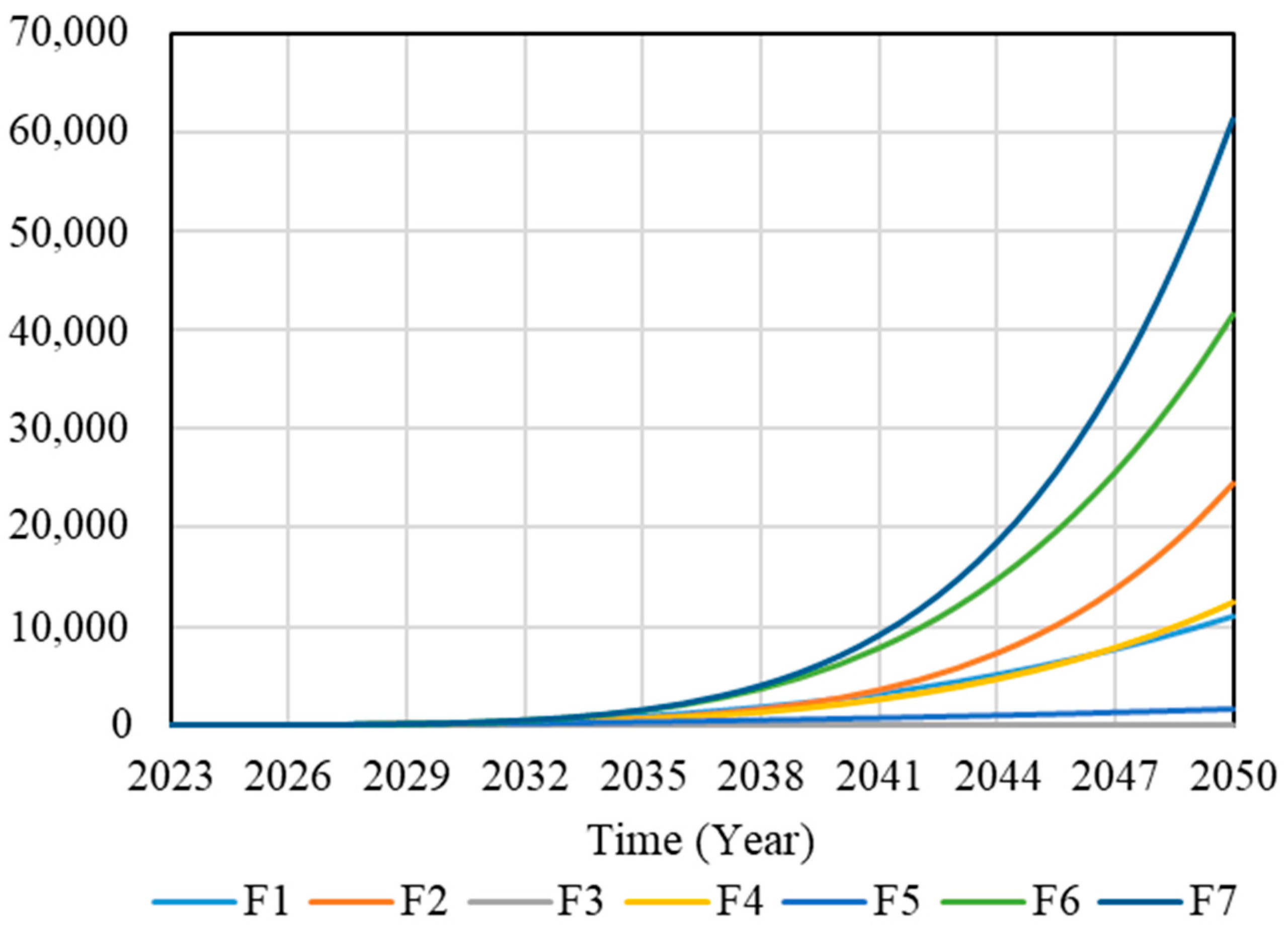
The dynamic simulation prediction of the established SD model of the application and development of BIM and the new-generation information technology (F7) and subsystems (F1-F6) in the construction industry is carried out within a set time period, as shown in Figure 8. F7 is a common index of F1-F6, and it can be seen from Figure 4 that the SD model of F7 includes the SD model of F1-F6 subsystems. According to Figure 8, as the abscissa time series advances, the corresponding ordinate effect value also gradually increases. The expression presented is an exponential growth generated by the positive feedback structure, and its growth trend is that the first growth is slower. The effect presented is still not obvious when it reaches 2033, indicating that the application of this technical means is not yet mature. However, every three years after 2035, the effect value will increase by multiples, which means that the application and development of technology at this time show a trend of rapid development. To sum up, the overall development trend of the F1-F6 subsystem and the F7 SD model during 2023–2050 is consistent, indicating that the application of BIM and the new generation of information technology is conducive to the transformation and development of the construction industry.

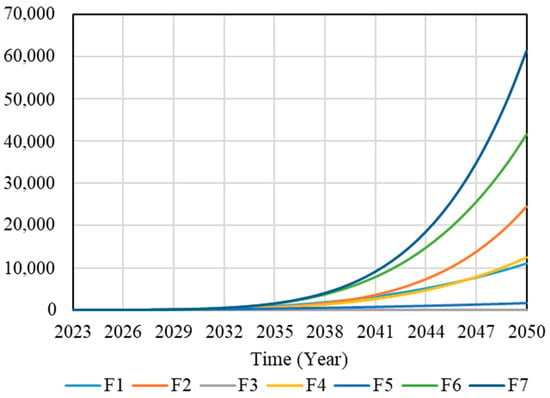
Figure 8. SD model dynamic simulation curve.

4.2. Sensitivity Analyses under Different Scenarios

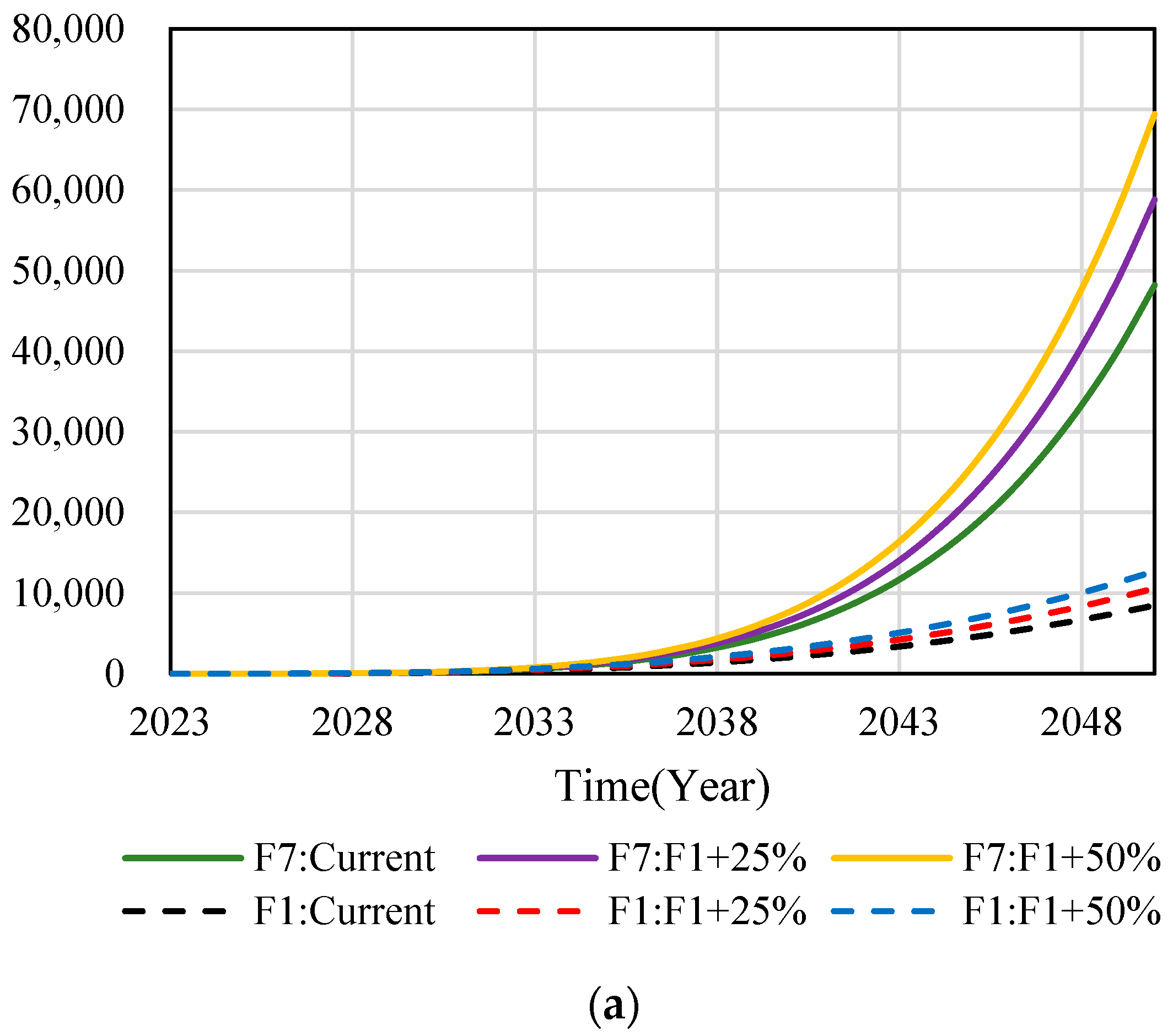
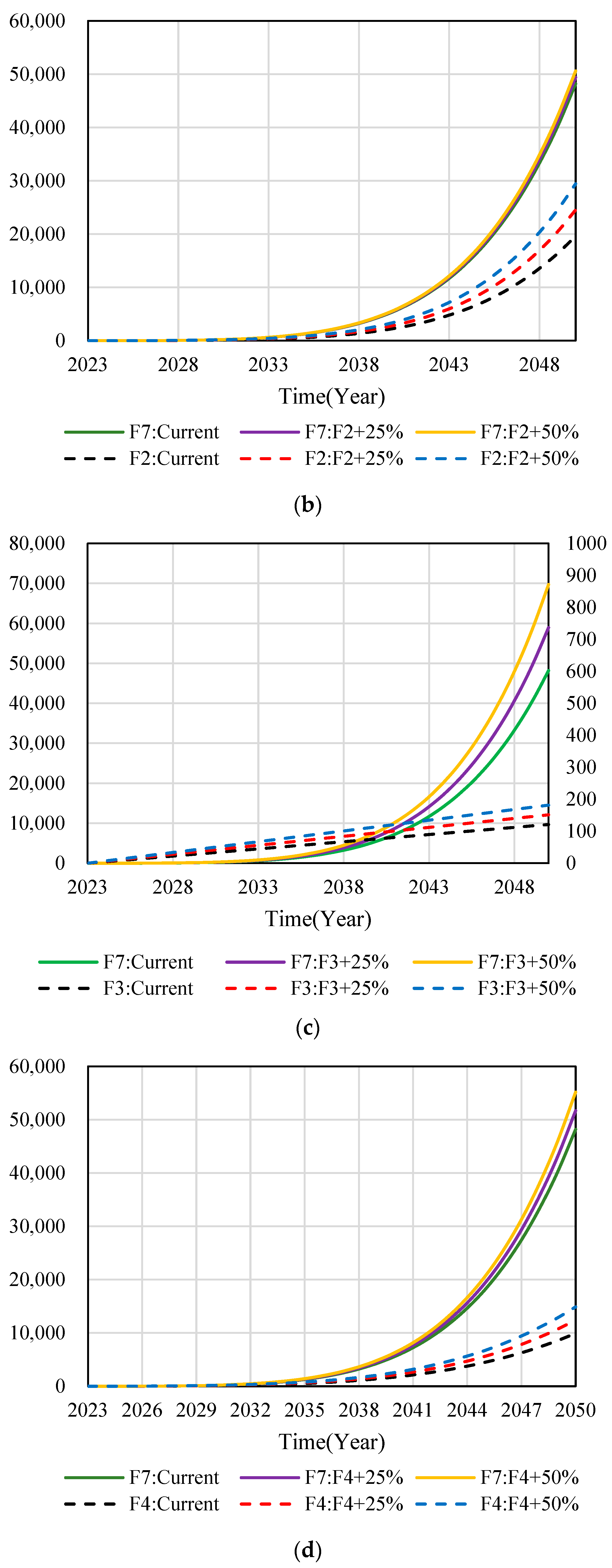
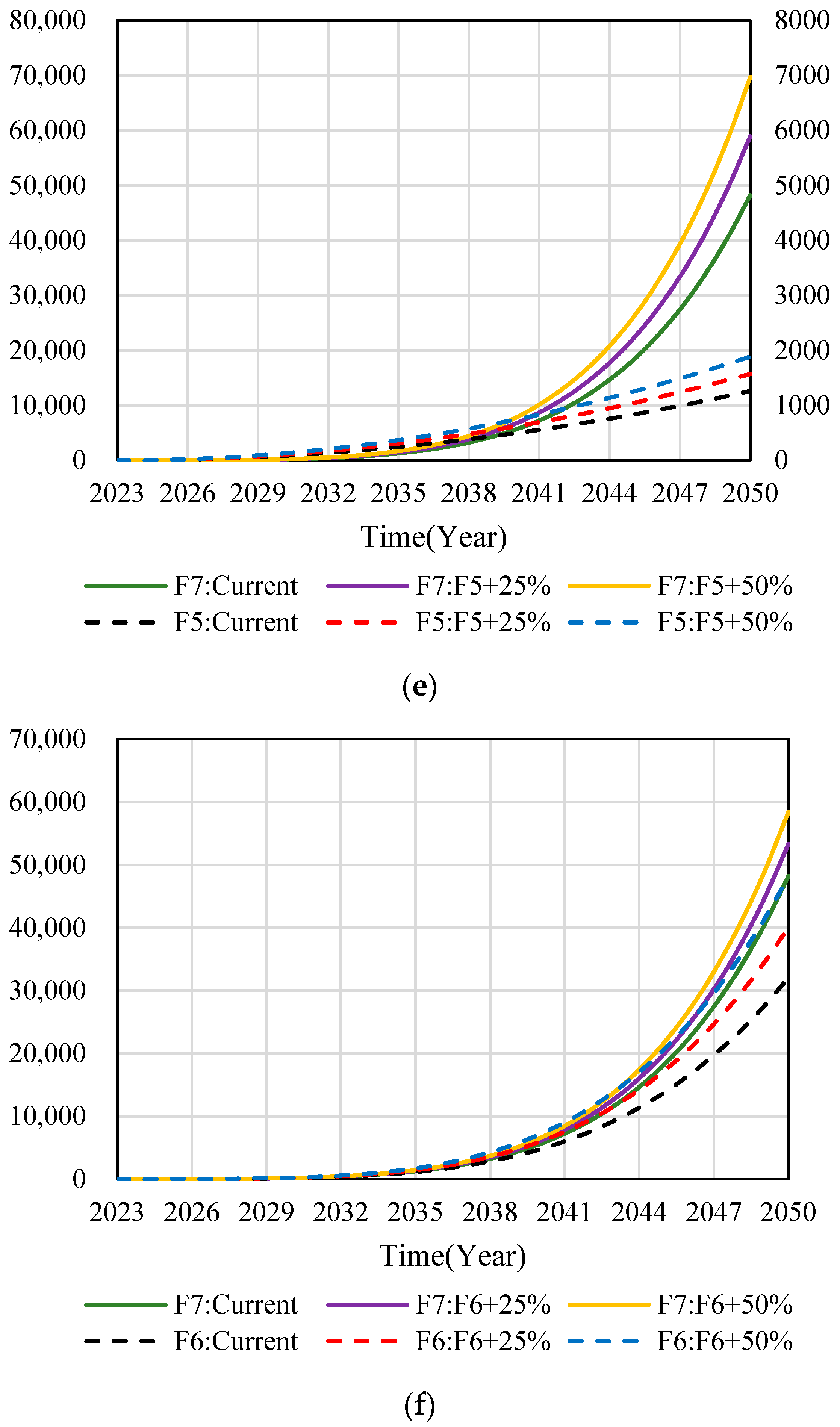
Sensitivity analysis is an effective evaluation method to study the sensitivity of simulation results of a SD model when parameters or conditions change. Through changing the mathematical equations in the subsystems, the changes of the dynamic simulation curves are shown in Figure 9:

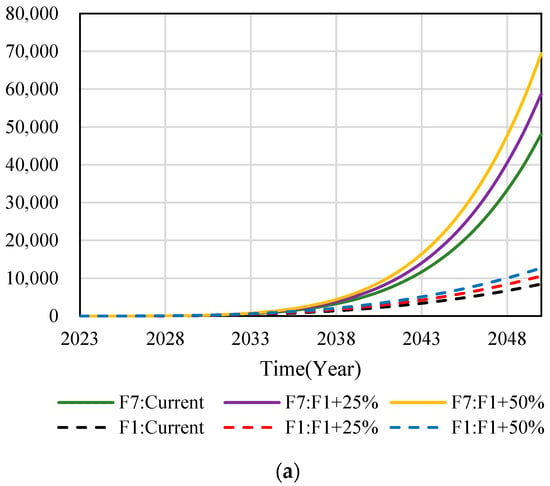
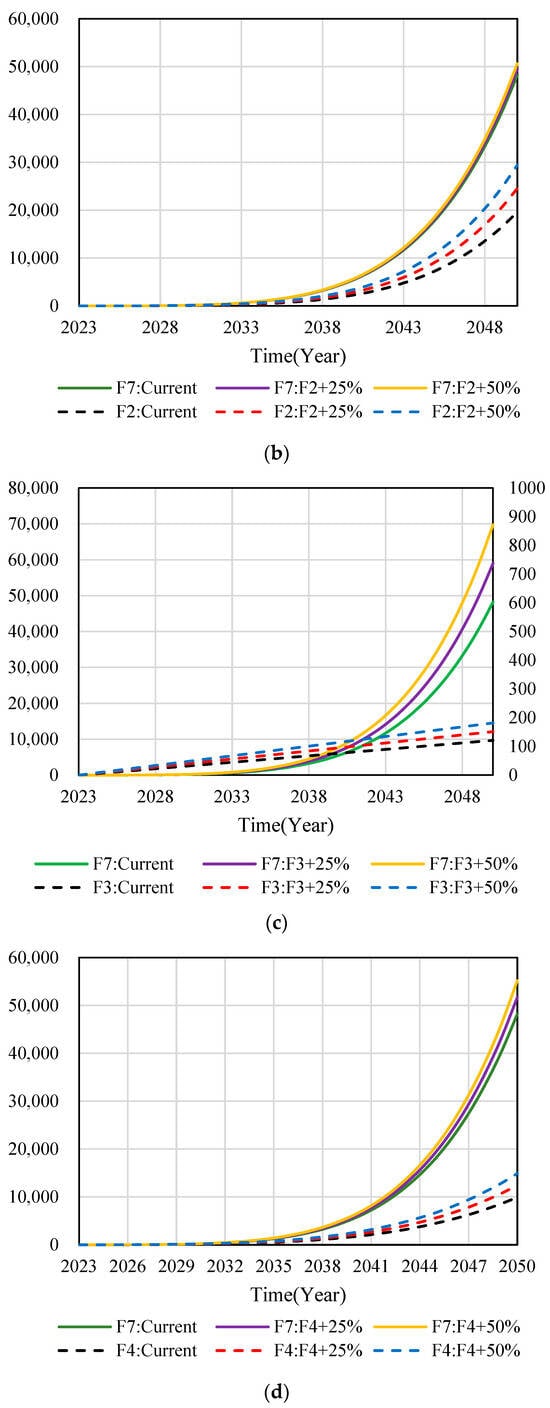
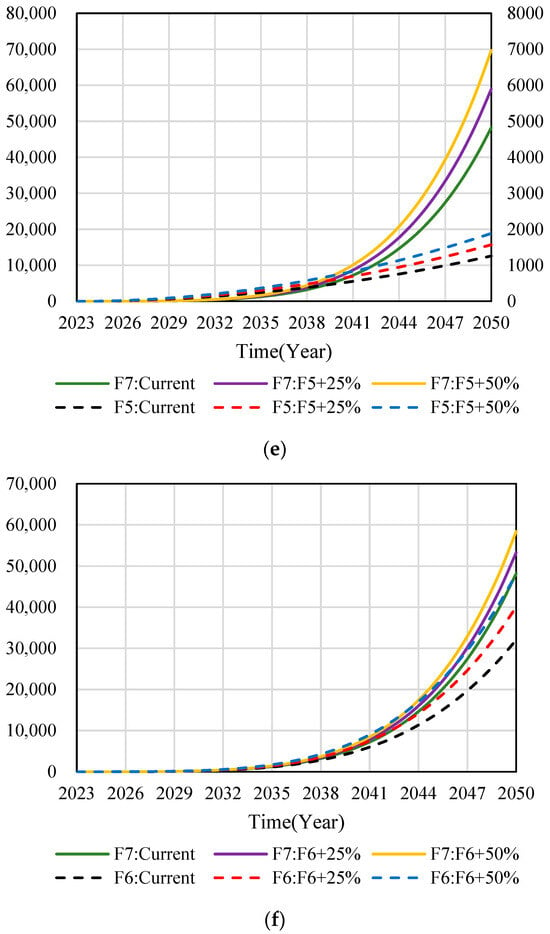
Figure 9. SD model sensitivity analysis. (a) Changes of simulation curve with adjusting F1. (b) Changes of simulation curve with adjusting F2. (c) Changes of simulation curve with adjusting F3. (d) Changes of simulation curve with adjusting F4. (e) Changes of simulation curve with adjusting F5. (f) Changes of simulation curve with adjusting F6.

The mathematical equations of F1-F6 subsystems are improved by 25% and 50%, respectively, when comparing their development trends with the current state of the subsystems, and comparing the adjusted subsystem model equations with the development trends of the F7 SD model. According to Figure 9, the dotted curves in Figure 9 represent the development status of the F1-F6 subsystem model and the dynamic simulation prediction of the adjusted development trend. The solid line curves represent the development status of the F7 SD model and the dynamic simulation prediction of the development trend of each subsystem after adjustment.

From the evolution of the dotted curves in Figure 9a,b,d,f after improving F1, F2, F4 and F6 subsystems by 25% and 50%, it is found that their predicted development trends are consistent, and the corresponding effect value increases with the enhancement of the subsystem. At the same time, it can be seen from the evolution law of the solid line curve that the adjusted F1, F2, F4, and F6 subsystem models maintain a similar growth pattern between 2023 and 2038. However, with the evolution of time between 2038 and 2050, the effect value of the subsystem also changed greatly, indicating that F1, F2, F4, and F6 subsystems all have important influences on the SD model of F7.

The dotted and solid curves in Figure 9c,e correspond to the left and right ordinate axes, respectively. From the development law of the dotted curves in Figure 9c,e, after improving the F3 and F5 subsystems by 25% and 50%, it is found that their predicted development trends are consistent, and with the enhancement of subsystems, the corresponding effect value increases, approximately showing a linear growth trend. At the same time, it can be seen from the development law of the solid line curve that the adjusted F3 and F5 subsystem models maintain a similar growth law between 2023 and 2041. However, with the evolution of time between 2041 and 2050, the effect value of the subsystem also changed greatly, indicating that both F3 and F5 subsystems have important influences on the SD model of F7.

To sum up, the changes of the dotted curve in Figure 9 represent the comparison between the adjusted subsystem model and the current status of the subsystem, which verifies that the development trend of the adjusted subsystem model is consistent with the simulation curve of the current status of the subsystem. Meanwhile, the changes of the solid line curve in Figure 9 represent the comparison between the adjusted subsystem and the SD model of F7, and it can be concluded that the impact of each subsystem on the SD model of F7 is positively correlated and has an important influence.

5. Conclusions and Prospect

This paper constructs a system dynamics model (F7 SD model), combined with system dynamics theory and structural equation model, for the application and development of BIM and new-generation information technology in the construction industry. After the stability test of the constructed system dynamics model, the evolution trend of the system dynamics model and the sensitivity analysis under different scenarios are carried out. The results show the following:

• The data collected through questionnaire surveys indicate that the majority of the respondents hold a positive attitude towards the application of intelligent construction technology in the field of construction. They believe it can protect and enhance productivity, reduce construction time, and decrease carbon emissions.
• Using Vensim DSS, the SD model (F7) of the application and development of BIM and the new generation of information technology in the construction field and the causality diagram, stock flow diagram, model parameters, and mathematical equations of the six subsystems are established.
• Through the stability test, different step sizes are set for the SD model. The development trend of the F1-F6 subsystem is highly consistent with that of the F7 system. Therefore, the SD model proposed in this paper has good stability.
• With the evolution of time (2023–2050), the corresponding effect values of the SD model constructed in this paper show an exponential growth trend. In the dynamic numerical simulation, the growth rate is slow before 2033, indicating that the application of the technical means is not yet mature. Since 2035, it has shown multiple growth states, which means that the technical application at this time shows a rapid development trend.
• Through the sensitivity test, the mathematical equations of F1, F2, F4, and F6 subsystems were increased by 25% and 50%, respectively. The effect values of the above subsystems and F7 system increased significantly, and showed an exponential growth trend after 2038. By increasing the F3 and F5 subsystems by 25% and 50%, respectively, the effect value growth of the F7 system is more significant than that of each subsystem, and after 2041, it shows an exponential growth trend. Therefore, intelligent construction technology has a good development prospect in the construction field.

The data collected in this paper are limited by region, time, and quantity. Therefore, it is suggested that the following research can adopt diversified data and use other computational technologies for deep mining analysis to verify the scientificity of the problem again.