Abstract
In this paper, we consider the optimization of temperature conditions and the thermo-stressed state of a concrete gravity dam made of extra lean roller-compacted concrete constructed in climate conditions corresponding to the Pskem HPP in the Republic of Uzbekistan. We show the need to take into account the effect of solar radiation on the heating of the concrete mass during the layer-by-layer construction of a gravity dam. A methodology was used to estimate solar radiation, considering cloud cover and the use of field and satellite observations. The seasonality of the concrete work and the terrain surrounding the construction site were also examined. We assessed the degree of influence of the factors acting on the formation of the temperature regime and the thermo-stressed state using the factor experiment technique. Regression equations, which allowed us to estimate the values of temperature and thermal stress arising in the structure during the construction period, were obtained. The created numerical model has been used for the estimation and optimization of the thermo-stressed state of the Pskem HPP dam option made of low-cement roller-compacted concrete. On the basis of calculations of the stress–strain state in elastic and elastic-plastic formulations, the possible cracking of concrete was evaluated. The competitiveness of the considered concrete option of the dam with the ground one is shown.
1. Introduction
Low-cement concrete dams have become widespread all over the world due to the high economic efficiency of this technology as well as the reliability and safety of the structures, including in regions with extreme climate and geotechnical conditions.
Low-cement concrete became widely used in the late 1940s in Great Britain for the construction of sub-base layers 150–250 mm thick in road buildings and in the construction of airfield runways. The cement content had already been reduced to 110–120 kg/m3, and the main drawback was considered to be the high risk of transverse cracking. This factor had a key influence on the selection of a low-cement mix, which was laid without expansion joints and compacted by rollers [1,2,3,4,5,6,7,8,9,10,11,12]. The idea of using low-cement concrete in gravity dam construction was proposed in 1960 as part of the discussion of the International Committee on Large Dams. In 1961 the first application of the technology took place on the cofferdam of the Shihmen dam on the island of Taiwan, where a central core was made of low-cement concrete. In 1970, a full-size test section was erected at Tims Ford Dam in the USA, and as early as 1983, the Willow Creek Dam was built in 5.5 months (52 m high, dam body concrete volume—333,000 m3).
During the construction of the Olivenhain Dam in the USA (97 m high, 1,140,000 m3 of concrete body), the maximum concrete work intensity was 12,250 m3/day, and the construction period was 12 months (Figure 1). The high intensity of the concrete works due to layer-by-layer mixture placing, the absence of formwork and dismantling, the reduction in labor costs to 0.15 man-days/m3 (Upper Stillwater Dam), and the associated reduction in overhead costs enabled more than 828 dams of this type to be realized, including gravity, arch, and buttressed dams as of 2019. Statistics on the cost per cubic meter of low-cement concrete poured as a function of construction volume in the USA are shown in Figure 2.

Figure 1.
Roller-compacted concrete dam Olivenhain, USA, 2004.
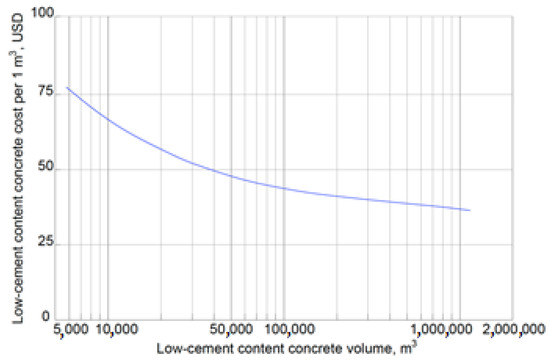
Figure 2.
Cost per 1 m3 of low-cement concrete by volume in the USA.
In Japan in 1974, a specially established research committee presented the results of its work on concrete dam design. Part of this work focused on rolled hydraulic concrete. Field tests conducted on the Ohawa dam (dam body volume—10,000 m3) in 1976 confirmed the possibility of the application of roller-compacted concrete in the construction of dams, the first of which, including the Shimazhiva dam (dam body volume—317,000 m3), was constructed in 1980. One of the largest low-cement concrete dams in the world is located in Japan. This is the Tamagawa dam (1987), which is 100 m high, and the volume of in situ roller-compacted concrete is 1,150,000 m3 [3,13].
The history of the development of roller-compacted concrete dams in the USSR started from the development and application of the technology of laying long blocks in the early 1970s during the construction of Toktogul HPP, then the dam of Tashkumyr HPP (Figure 3) on the Naryn river in Kyrgyzstan with 75 m height and 320 m length on the ridge (the volume of laid low-cement concrete—100 thousand m3). This was followed by Bukhtarminskaya HPP on the Irtysh river in Kazakhstan with 90 m height and 450 m length (the volume of laid low-cement concrete—587 thousand m3), Bureyskaya HPP on the Bureya river with 139 m height and 810 m length on ridge (volume of laid low-cement concrete—587 thousand m3), and also separate constructions or experimental plots at Kurpskay, Kureysky, Sayano-Shushensky HPPs. The Kapanda hydroelectric dam in Angola and the Son La hydroelectric dam in Vietnam was built in accordance with the designs developed by the Hydroproject Institute (Moscow, Russia).

Figure 3.
Low-cement concrete laying in the Tashkumyr hydroelectric power station dam.
In the late 1980s, the active development of technology began in China. A total of 45 dams were completed there as of 2019. China also has the highest low-cement concrete dam in the world, the Longtan, 217 m high (4.95 million m3 of in situ concrete), and the 121 m high dam (1.1 million m3 of low-cement concrete placed).
However, despite all of the above advantages, the structures in question may experience a number of problems related to filtration resulting from temperature cracking, which has been documented in a significant number of structures built. The problem of temperature cracking has not been completely solved, and there is also an underestimation of the contribution of certain influencing factors to the thermo-stressed state of structures, which demonstrates the relevance of the issue under consideration.
The present work focuses on the thermo-stressed state of low-cement concrete gravity dams during the construction and operational period under the influence of internal factors (cement consumption, cement heat release rate, the initial temperature of concrete mixture, layer thickness, erection speed, etc.) and environmental factors (season of work commencement, exposure of concrete mass surface to solar radiation or its temperature and radiation regime, reservoir temperature change by depth at different stages of its filling due to the schedule of building up the structure). Based on the results of this research, a numerical model of the thermo-stressed state of low-cement concrete gravity dams located in the climate conditions of the mountainous regions of the Republic of Uzbekistan and similar have been proposed. As a practical application of the proposed model, a prediction of the temperature regime and thermo-stressed state of the designed dam of the Pskem HPP in the Republic of Uzbekistan is presented.
Previous research on the topic. The problem of the temperature regime and thermo-stressed state of concrete gravity dams has been studied by a number of scientists both in the Russian Federation and abroad. The most famous works in this field are the ones by Aniskin N.A., J.M. Raphael, E.K. Schrader, M.R.H. Dunstan, G. Gentile, T. Hirose, J.P. Giroud, S.M. Ginzburg, Dzyuba K.I., Zaporozhets I.D., T.Y. Krat, Sh.N. Plyat, Orekhov V.G., Z. Bofang, V. Kuzmanovic, T. Fujisawa, Wang L., and others. However, even today, the problem has not been completely solved.
The objects of the research are the developed projects of low-cement concrete gravity dams of the Chirchik-Bozsu cascade HPPs in the Republic of Uzbekistan (Pskem HPP, Nizhnechatkal HPP, Mulallak HPP, etc.).
The subject of this research concerns predictive mathematical models and dependencies that allow the determination and forecasting of the temperature regime and thermo-stressed state of low-cement concrete dams.
2. Materials and Techniques
Calculations to determine the temperature conditions and thermo-stressed state of structures, considering the full range of internal and external factors, were carried out numerically using the ANSYS software version 19.2 package, through which some test problems were solved, and a numerical simulation of the field experiment was performed, followed by an assessment of the convergence of the results.
2.1. Methodology for Determining the Temperature Regime
The basic heat conduction Equation (1) and the basic heat release equation for an isothermal process (2) served as the basis for solving the problem by numerical methods:
where: thermal conductivity coefficient of low-cement concrete, its specific heat capacity, density, emperature, heat release during hydration of cement, time.
where: specific heat release of water in its reaction with the selected type of cement, amount of active water at the initial time, order of reaction, reaction rate constant, time.
The main external factor influencing the temperature regime of a concrete dam is the ambient air and water temperature. For the climate conditions under consideration (Republic of Uzbekistan), special attention should be paid to the impact of solar radiation on the temperature regime of the building due to a certain underestimation of this factor. Radiation has the most significant effect on the temperature behavior of concrete structures when they are erected in layers from 0.5 m to 1.5 m thick, as in this case, the heat generated by the heat evolution of the cement was added to the heat coming into the mass from the surface. Experience has proven that solar radiation can cause the temperature of a concrete mass to rise by up to 20 °C or more.
In the Russian literature [14,15,16,17], there are a number of references on the need to consider solar radiation when calculating the temperature-radiation regime of concrete surfaces; however, these sources mainly consider the surfaces of old concrete, while radiation has a significant impact on the temperature regime of fresh concrete (especially for low-height blocks). As a rule, recommendations considering solar radiation increases the temperature on the surfaces of the building and the amplitude of the temperature fluctuations of the external environment. Such methods, for example, have been considered by Chinese researchers [18,19,20,21].
Such techniques are based on field observations and do not answer the question of whether and how to account for the scattered part of solar radiation. They also contemplate the influence of some features by introducing generalization factors into the calculation, which does not allow the individual characteristics of the projects to be considered.
The existing methods for assessing the impact of solar radiation are outlined in the works of V. Ya. Kondratyev, Z.I. Pivovarova, S.M. Ginzburg, S.I. Sivkov et al. [22,23,24,25]. As part of ongoing work, existing techniques for considering solar radiation on the temperature regime of a structure have been improved, considering field and satellite observations, as well as the seasonality and the topography of the construction site.
The impact of solar radiation was assessed using the known dependencies (3) and (4):
where total daily solar radiation, sunrise time, sunset time, initial moment of solar radiation exposure time, final moment of solar radiation exposure time, intensity of direct radiation at time , intensity of scattered radiation at time .
The total solar radiation including cloud cover was determined as follows:
where: —cloudiness, %, —coefficient, taken depending on the latitude of the object location, —constant (for the considered climatic zone measured empirically).
In this paper, the accuracy of solar radiation was improved by using actinometric observations, hourly accounting for direct and diffused solar radiation intensities and hourly changes in the heating of the concrete surface, considering the characteristics of the location of the HPP and the topography of the directly selected pier for construction. The orientation of the dam in relation to the sides of the world, elevation, cloud cover, and geographical coordinates of the site was also considered. For higher accuracy, the scattered component of the solar radiation was contemplated in terms of its anisotropy (heterogeneity of the scattered radiation from the sky).
When solving the temperature problem through the numerical finite-element method using the ANSYS software package, an approximation model of the computational domain, including the unchangeable base mass under the structure and the gravity dam mass erected in layers, was created. In the elements included in the area of the layer-by-layer erected concrete massif, at each time step, the exothermic heat value was determined and calculated according to dependence (2).
In the nodes at the lower boundary of the foundation, boundary conditions of the first kind were used: temperature values were assumed to be constant in time and equal to the mean summer temperature for this climatic zone. The boundary conditions of the third kind were used in the nodes at the contact of the base and building with the air (including the time-varying boundary of the concrete mass to be erected): the law of heat exchange with the air environment, taking into account solar radiation, was set. Heat transfer coefficients for each time step were determined in accordance with the value of the additive and taking into account solar radiation for this moment in time.
The boundary condition of the first kind was used when taking into account the temperature impact of the reservoir and downstream water in the nodes along the “concrete-water” boundary, specifying in the nodes the value of water temperature corresponding in time to the law of water change in depth.
2.2. Methodology for Determining the Thermo-Stressed State
The impact of influencing factors in the low-cement concrete mass produces tensile stresses and plastic deformations, which may accumulate over time.
Under the elasticity theory, stresses and strains before a material enter the plastic stage are related according to the dependence (5):
where: components of the stress tensor, components of the strain tensor, components of the elasticity tensor.
In the plastic domain, the relationship between strain and stress is governed by the law of plastic fluidity, based on the assumption that under any loading, the strain consists of an elastic and a plastic part (6):
where: the elastic component of deformation, the plastic component of deformation. The modulus of elasticity in compression depending on the maturity of the concrete can be determined according to the dependence elaborated by N.Kh. Arutyunyan (7):
where: —the maximum value of the modulus of elasticity for the strength-gained concrete, MPa, —experimentally determined parameters.
As in the temperature problem, the process of constructing a concrete gravity dam in layers was modeled. As each successive layer was laid, the geometry of the structural changes and the elements of the approximation grid were recalculated for the modulus of elasticity and the compressive and tensile strength of the material. At the nodes along the boundary of the computational domain, the corresponding displacement boundary conditions were set. A vertical displacement constraint was set for the lower boundary of the base, and a horizontal displacement constraint was set for the vertical boundaries of the base area.
In order to verify the numerical calculation models, a field experiment was carried out, and a number of test calculations were performed. The results of computational studies using mathematical modeling in the ANSYS software package showed high reliability. Deviations in the maximum temperatures at the reference points did not exceed 1%.
3. The Setting and Results of the Research
The aim of this research was to find an optimum design for a low-cement concrete gravity dam that would satisfy the reliability and safety of the structure and maximize the cost-effectiveness of the project. The issues of the predictive modeling of the temperature regime and thermal stress state of concrete gravity dams were considered in several works carried out in the Moscow State University of Civil Engineering, JSC “VNIIG named after B.E. Vedeneev”, in the branch of JSC “Institute Hydroproject”—“NIIES” and other organizations [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,19,20,21,22,23,24]. Within the framework of this paper, numerical investigations by means of a finite element method with the application of ANSYS software took into account the topographical, engineering-geological, and climate conditions of the Pskem HPP construction region in the Republic of Uzbekistan [25,26,27,28,29], which were carried out. The result is a mathematical model of the structure that predicts the thermo-stressed state of the structure and maximizes design efficiency.
The results of variation calculations were performed to determine the degree of influence that acting factors had on the temperature and stress–strain state of the structure in the climate conditions of mountainous areas of the Republic of Uzbekistan, as presented below.
3.1. Consideration of Solar Radiation Effects
The main structures of the Pskem HPP are located in the mountain massif of the Western Tien Shan at elevations of (1100–1200) m. The construction area was characterized by sufficiently high solar activity, with an average of 250 sunny days per year. The average annual air temperature in the area was 9.5 °C. The absolute minimum recorded in January was minus 26.9 °C. The average temperature of the hottest month, July, was 22.0 °C. July also had an absolute maximum temperature of −41.7 °C. The coldest month was January, at minus 3.2 °C (Table 1). The data are given for the observation period from 1938 to 2016.

Table 1.
Climate characteristics of the Pskem HPP construction area.
The solar radiation characteristics were calculated considering the characteristics of the HPP area and the topography of the surrounding area selected for construction (Figure 4 and Figure 5). As a result of the calculations, the average monthly temperatures of the concrete surface of the dam were obtained, considering solar radiation (Figure 6b). For comparison, Figure 6 shows a graph of the change in surface temperatures without solar radiation. A rather large increase in surface heating can be observed. For the warmest period of the year (July-August), exposure to solar radiation increased the surface heating of the concrete to 41.0 °C, which was 17 °C higher than the temperature without solar radiation.
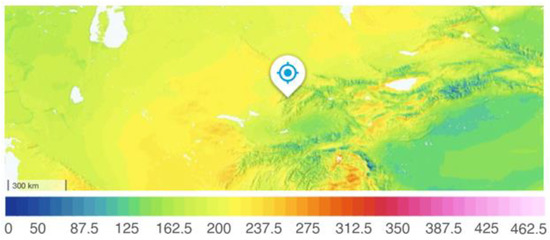
Figure 4.
Map of direct solar radiation intensity, kW/m2 in the area of the Pskem HPP (under construction).
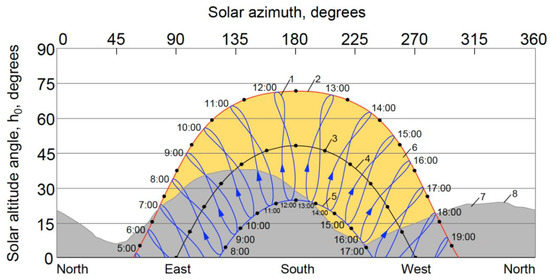
Figure 5.
Graph of changes in angular altitude ) and the azimuth of the sun, where: 1—local time in the construction area (time zone Tashkent, Uzbekistan, UTC+05:00); 2—movement of the sun at the summer solstice 21.07. 2021; 3—true solar time; 4—sun movement at the spring/autumn equinox; 5—sun movement at the winter solstice 21.12.2021; 6—zone of active solar exposure; 7—shading caused by surrounding terrain; 8—contour of the surrounding terrain at the construction site.
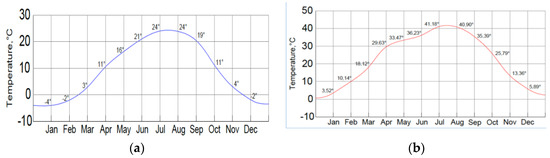
Figure 6.
Graph of changes in concrete surface temperature, taking into account the ambient temperature: (a) Without the influence of solar radiation; (b) Taking into account the influence of solar radiation.
3.2. Analysis of the Impact of Existing Factors Using the Methodology of a Factor Experiment
To assess the degree of influence of the main acting factors on the temperature regime and the thermo-stressed state of the structure in question, the method for factor analysis was used. The research was conducted for a full-factor experiment of type 2n, where the number of factors considered was n = 4. The total number of experiments needed for such a plan is N = 24 = 16. The response function as a regression equation for this experiment is as follows [30] (8):
The following factors and their ranges of variation were chosen for the calculation studies:
- —consumption of cement in the mixture (varies from 70 kg/m3 to 150 kg/m3).
- —thickness of the low-cement concrete layer to be placed (0.5 m to 1.5 m).
- —heat release of cement (from 339 kJ/kg (moderate) to 387.7 kJ/kg (elevated).
- —laying temperature of low-cement concrete (+10 °C to +30 °C).
The calculations according to the planning matrices made (the full-factor experiment 24 was considered) for the selected factors were performed for the following options:
- (1)
- Depending on the month when the construction work started: May or October with the corresponding ambient temperatures (according to the schedule, Figure 6).
- (2)
- (3)
- The responses chosen were: the absolute maximum temperature in the concrete mass (°C), maximum temperatures at characteristic points 2, 8, 14, 20, 26 in the center of the mass (°C), the maximum temperature gradient between the point in the center of the mass and the point on the pressure face (°C/m), the maximum value of the main tensile stress at characteristic points 2, 8, 14, 20, 26 in the center of the massif (MPa), the maximum value of equivalent plastic deformations at characteristic points 2, 8, 14, 20, 26 in the center of the massif (%). A diagram of the point locations is shown in Figure 7. All temperature calculations for all variants were carried out using the Ansys software package.
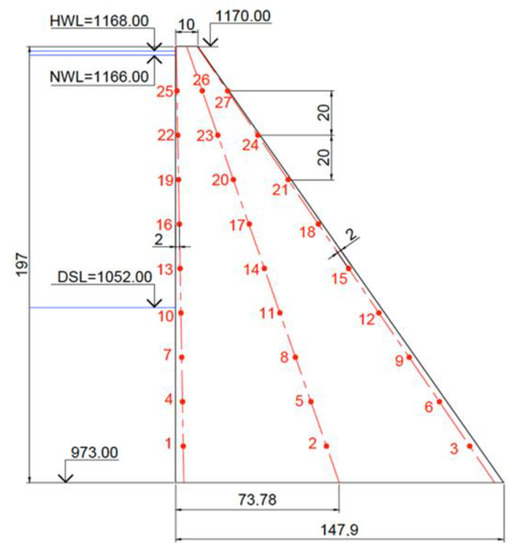 Figure 7. Location of fixed points for the values of the set responses across the cross section of the dam.
Figure 7. Location of fixed points for the values of the set responses across the cross section of the dam.
Regression equations were derived from the calculations to determine the values of the response functions, some of which are presented below (9–20):
- Option 1. Beginning of concreting in May excluding solar radiation.
- Option 2. Beginning of concreting in October excluding solar radiation.
- Option 3. Beginning of concreting in May taking into account solar radiation.
- Option 4. Beginning of concreting in October taking into account solar radiation.
By analyzing the equations derived from the solution of the temperature problem, the following conclusions can be drawn:
- All of the selected factors had a sufficiently strong influence on the values of the maximum temperature at the selected points. The cement consumption (factor ), the thickness of the concrete layer to be placed (), and the temperature of the concrete mix () had the greatest impact. Increasing cement consumption from 70 kg/m3 to 150 kg/m3 led to a significant (on average by 9.31 °C per fixing point) temperature increase in all points of the massif, reaching maximum values in the case of the concreting that started in May at point 2 (the temperature at the point with 70 kg/m3 cement content was 45.18 °C, with 150 kg/m3—54.42 °C).
- The degree and operator of the influence of the factor (the thickness of the concrete layer to be paved) depended on the placement area, the seasonality of the paving operation, and the solar radiation. When solar radiation was not taken into account and concreting started in May in massive areas of the dam, the temperature of the concrete mass decreased as the thickness of the layer of concrete that began to be placed increased (the regression equation coefficients with the clause are negative). However, for this option, the picture changed in the area at the crest of the dam, where the opposite was obtained: as the layer thickness increased the temperature rose as well. When concreting started in October, the picture was reversed: in the lower massive part of the dam, an increase in layer thickness led to a rise in temperature, while in the area near the crest, the opposite was true.
- For options with solar radiation in most areas of the dam, with an increasing layer thickness, there was a decrease in the mass temperature due to lower solar heating in thicker layers. The exception is the area near the base (point 2) for the option with the start of construction in low air temperatures during the autumn-winter period of the year. Paving in thin layers involved the intensive cooling of the concrete with cold air.
- For the climatic conditions considered, a consideration of solar radiation made a significant contribution to the increase in temperature warming of the structure during its construction (the temperature inside the concrete mass increases by 8.46 °C to 16.14 °C (Figure 8), depending on the fixing point.
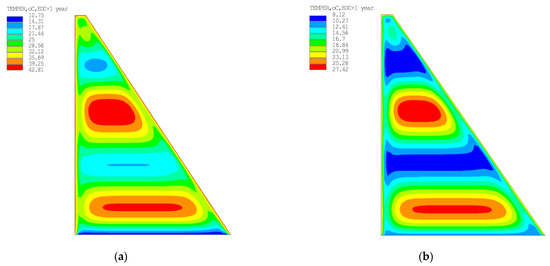 Figure 8. Example of calculating the maximum temperature in a concrete mass: (a) Calculation taking into account solar radiation; (b) Calculation excluding solar radiation.
Figure 8. Example of calculating the maximum temperature in a concrete mass: (a) Calculation taking into account solar radiation; (b) Calculation excluding solar radiation.
The resulting regression equations could be applied to a rapid assessment of the temperature behavior of massive low-cement concrete dams with a bottom width of at least 40 m in all climate conditions.
Based on the results of the various calculations, the most and least favorable design cases in terms of the temperature regime of the dam were identified (Figure 9).
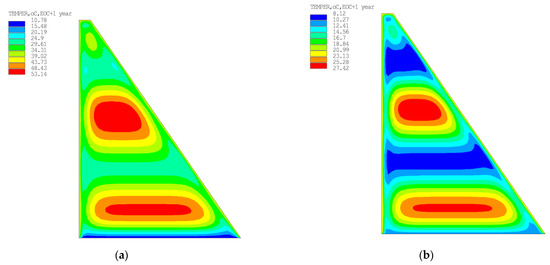
Figure 9.
Calculation results for maximum temperature in concrete mass: (a) The least favorable calculation case; (b) The most favorable calculation case.
The analysis of the obtained results shows that the most unfavorable in terms of the stress–strain state is the calculated case with the cement consumption of 150 kg/m3, a layer thickness of 0.5 m, increased heat generation, the initial temperature of the concrete mixture +10 °C, and the start of work in May. The most favorable temperature regime was obtained under the following conditions: cement consumption of 70 kg/m3, a layer thickness of 1.5 m, moderate heat dissipation, the initial temperature of concrete mixture +10 °C, and the start of work in October.
For these two cases, the stress–strain state of the structure was calculated by fixing the maximum values of the main tensile stress at points in the center of the mass and the equivalent plastic deformations at points both in the center of the massif and on the surfaces of the pressure and downstream faces (Figure 10).
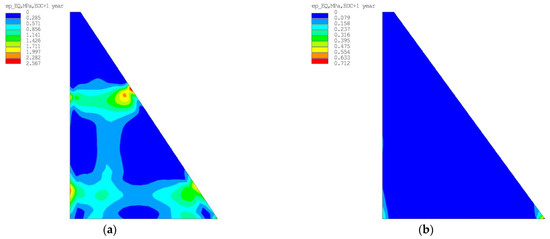
Figure 10.
Results of the determination of plastic deformation in a concrete mass: (a) The least favorable calculation case; (b) The most favorable calculation case.
The resulting numerical model of the temperature regime was applied to the dam under construction at the Pskem HPP site in the Republic of Uzbekistan. The calculations were made taking into account the schedule of the dam construction and reservoir filling (Figure 11) and the change in the reservoir water temperature by depth during each stage of the construction (Figure 12).
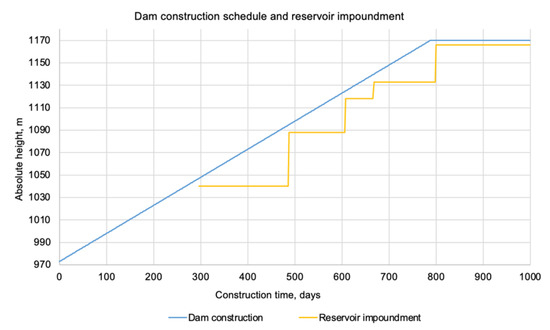
Figure 11.
History of dam construction and reservoir impoundment schedule.
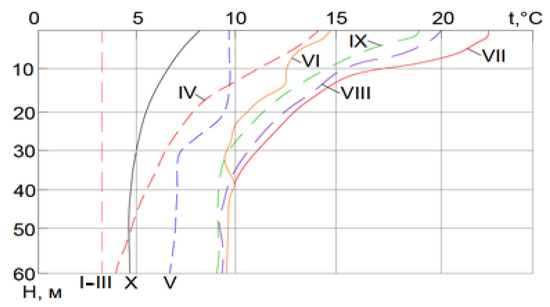
Figure 12.
Diagram of reservoir water temperature variation by depth, by month.
The dam was assumed to be built in 131 stages, with a low-cement concrete layer thickness of 1.5 m and 393 stages and a low-cement concrete layer thickness of 0.5 m. At the initial stage of the calculation, the natural stress–strain state of the dam foundation was modeled, after which a continuous layer-by-layer construction was calculated with a corresponding schedule of filling the reservoir. The total construction time for the design crest was 786 days. A special feature of the filling schedule was the time lag between the construction of the dam and the filling of the reservoir, which allowed the concrete to gain strength at the age of 28 days.
The division of the model into a large number of horizontal layers made it possible to accurately simulate the concrete laying process in layers. At each time step, the temperature at the point was set by reading it from the corresponding file with the results of the temperature problem at that time step, with the VAT calculation carried out on the temperature difference (T–Tref.), where Tref. was the initial temperature of the concrete mix.
Based on the results of the temperature calculations of the dam, including the influence of the reservoir, it was found that the reservoir had a significant impact on the temperature at the surface of the upstream face and in the area adjacent to it, but the temperature inside the concrete mass actually remained the same (32.2 °C in the most favorable calculation case and 53.1 °C in the least favorable calculation case, Figure 13).
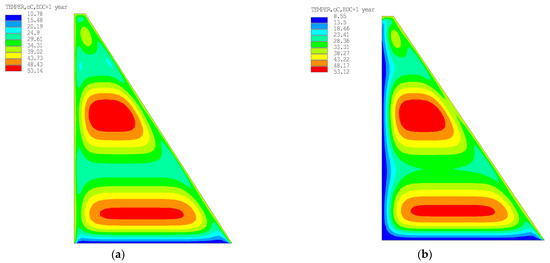
Figure 13.
Results of calculating the maximum temperature in the concrete mass in the least favorable calculation case: (a) Calculation excluding the effect of the reservoir; (b) Calculations considering the effect of the reservoir.
The most favorable (6) and least favorable (25) calculation cases with the following factor values and construction conditions were selected based on the results of the variation calculations of temperature conditions (Table 2).

Table 2.
Parameters of the calculation cases considered.
The model used allows the changes in strength parameters of low-cement concrete to be taken into account in time by applying special commands of the ANSYS software package [31,32], namely: the modulus of elasticity for the concrete ; the strength of concrete in uniaxial compression ; the strength of concrete in uniaxial compression ; the strength of concrete in uniaxial tension: . For each calculation option, a different material was created with its own construction time ( and ) and strength/stiffness curve.
The results of the calculations of the stress–strain state in the elastic and elastic-plastic formulations yielded stress and strain distribution patterns (Figure 14, Figure 15 and Figure 16).
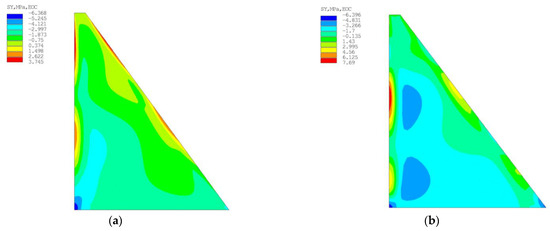
Figure 14.
Results of calculation of tensile stresses in the concrete mass at the time of completion of construction: (a) The most favorable calculation case; (b) The least favorable calculation case.
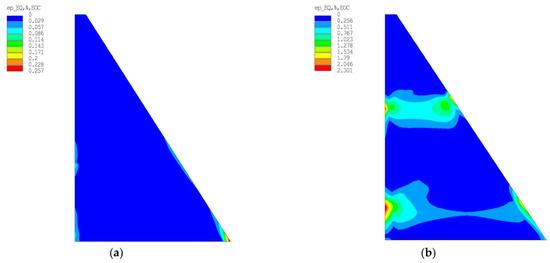
Figure 15.
Results of calculation of plastic deformation in concrete mass at the time of completion of construction with: (a) The most favorable design case; (b) The least favorable calculation case.
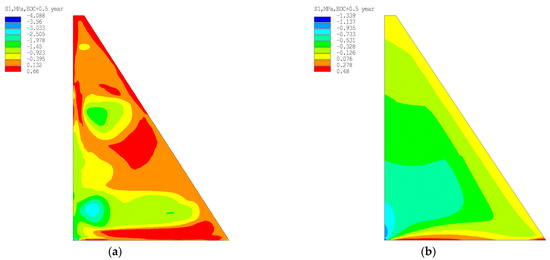
Figure 16.
The main maximum stresses in the dam: (a) Stresses when calculating with regard to temperature factors; (b) Stresses when calculating excluding temperature factors.
Potential fracturing was assessed using two methods:
1. The tensile stress fracture assessment.
Under the criterion laid down in the Russian standard SR 41.13330.2012, “Concrete and reinforced concrete structures of hydraulic structures,” no cracks are formed if the following condition for the value of maximum tensile stress is fulfilled [33]:
where: —maximum tensile stresses at time , a coefficient of structural conditions, a coefficient of working conditions for a solid structure, , maximum tension of concrete, factor entered to account for age of concrete, modulus of elasticity of concrete at time , MPa.
By substituting the parameters in (21): ; (SR 41.13330, Table B.6); the value of permissible tensile stress .
The results of the calculations (Figure 16) show that the opening of the contact joint at the time of completion of construction occurred in neither the most nor the least favorable calculation cases—contact joint— and that the tensile stresses in the concrete mass did not exceed the maximum permissible values. On the surface of the upstream face, local zones formed where the tensile stress exceeded the maximum permissible values , which may indicate possible cracking. In this case, the stress values in the concrete mass indicated that no through-cracking took place (Figure 14). Two years after the completion of construction, there was a reduction in the value of maximum tensile stresses (the absolute maximum value of tensile stresses has decreased by 28.65%). However, the estimation of the crack formation from an elastic calculation had some disadvantages. One of them was that the assessment of crack formation according to criterion (21) in SR 41.13330 was made without reference to time and did not take into account the accumulation of deformations with its course (all deformations in elastic operation are reversible). In addition, this criterion (21) was set for fluid-vibrated concrete, which had a different model of loading behavior than low-cement concrete.
2. Assessment of fracture formation by plastic deformation.
The pattern of tensile stress distribution across the cross-section was compared with a similar pattern for plastic strains (taking into account their accumulation over time). The plastic deformation cracking assessment criterion was determined in accordance with the US Army Corps of Engineers ETL-1110-2-542 [34] and the American Concrete Institute ACI 207.5R recommendations [35]. It has been experimentally established that for low-cement concrete, depending on cement consumption, the value of plastic deformation at which cracking occurs ranges from 0.6% to 0.9%.
For a cement consumption of 70 kg/m3 in the most favorable design case, the limit of deformation is 0.6%. For a cement consumption of 150 kg/m3 in the least favorable design case, the limit deformation is 0.85%.
The calculated maximum value of plastic deformation () (Figure 15) does not exceed the limit value, and cracking does not occur. At the same time, zones of plastic deformation development with values higher than those permissible could be observed on the surface of the upstream face, which may indicate the potential occurrence of cracks, but no through cracks were observed.
A comparison of the assessment of crack formation obtained using the two techniques (stress and plastic deformation) shows that they gave identical results.
The results of the study have shown that both options are suitable for erection in the engineering-geological, hydrological climatic, and actinometric conditions of the construction area and provide the safe and reliable operation of the structure; however, to prevent filtration processes in the dam body it is necessary to provide an external additional impervious element, as a synthetic impervious liner was considered in the present work.
An assessment of the influence of all temperature factors on the thermo-stressed state of the Pskem dam has shown that they fundamentally change the stress–strain state of the structure. The key factor is the heat dissipation of the concrete and other factors (especially the warming effect of solar radiation) that significantly increase its contribution to the thermo-stressed state of the structure (Figure 16).
3. Cost-effectiveness assessment.
The cost-effectiveness assessment was carried out based on the results of the financial calculations of cost and a comparison of a 197 m high earth dam option (central core impervious element) and a low cement concrete gravity dam option with a geocomposite impervious liner installed open on the surface of the upstream face. The design of such an element completely solves the problem of possible seepage through the dam body with possible fracturing on the upstream face.
The results of the comparison of options are presented in Table 3.

Table 3.
Assessment of the cost-effectiveness of dam design options.
Table 3 clearly illustrates the high cost-effectiveness of the proposed solution with a low-cement concrete gravity dam with an impervious liner.
As a methodological recommendation for performing calculations of the thermo-stressed state of a gravity dam made of low-cement concrete, a step-by-step algorithm was presented that could establish the order and sequence of actions for the optimal design of gravity dams made of low-cement concrete (Figure 17). The methodology used in this paper to optimize a low-cement concrete gravity dam using the example of the Pskem HPP in the Republic of Uzbekistan could be extended to other similar structures. The steps proposed in this algorithmic scheme are common to similar design objects regardless of their location and the climatic characteristics of the construction site. This principle is based on the mandatory requirements for the thermal stress state of the structure and the exclusion of temperature cracking.
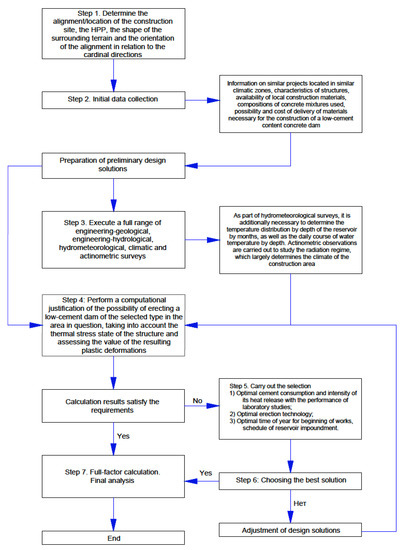
Figure 17.
Algorithm for the design of a low-cement concrete dam.
4. Findings
- The conducted research indicates the necessity of considering the influence of solar radiation on warming up the massive gravity dam made of low-cement concrete in the climate conditions of Pskem HPP in the Republic of Uzbekistan and similar ones. The methodology for accounting for the influence of solar radiation with respect to cloud cover makes it possible to predict the temperature and radiation regime of a massive gravity dam, taking into account field and satellite observations and determining the amount of absorbed solar energy and the associated heating of the concrete mass with respect to seasonality and the topography surrounding the construction site.
- The optimization of the temperature regime of the structure, carried out on the basis of the experimental planning theory with a numerical solution in the ANSYS software package, allowed the contribution of each to be evaluated in the internal and external environmental factors to the thermal stress state of the dam in the climate conditions of the construction area in the Republic of Uzbekistan.
- The created prediction model of the thermo-stressed state made it possible to estimate the values of absolute maximum temperature in the concrete mass; the maximum temperature at characteristic points; the maximum temperature gradient between a point in the mass center; and a point on the pressure face; values of the maximum main tensile stresses and plastic deformations. This enabled a comprehensive analysis to be carried out and the best design option to be selected.
- Regression equations have been derived from the results of the calculations to determine the values of the required indicators at any of the points under consideration. The equations can be applied to any solid, low-cement concrete dam with a minimum footprint of 40 m in all climate conditions.
- Based on the results of this work, a construction optimization algorithm was proposed for use in the engineering and justification of design solutions for low-cement concrete gravity dams.
- Recommendations and prospects for further development of the topic. Laboratory research on the determination of the optimum composition of the concrete mixture, a more detailed consideration of the influence of concrete strength growth in time and its influence on the state of the structure, a more detailed study of the thermal properties of different types of foundations and the general improvement of calculation models and methods are advisable. In addition, a promising direction is the study of cracking processes in massive structures made of low-cement concrete and the search for the new refinement of existing criteria for its assessment.
Author Contributions
Conceptualization, A.M.S.; Methodology, A.M.S.; Software, A.M.S.; Validation, N.A.A.; Investigation, A.M.S.; Writing—original draft, A.M.S.; Writing—review & editing, N.A.A.; Visualization, N.A.A.; Supervision, N.A.A.; Project administration, N.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bofang, Z. Thermal Stresses and Temperature Control of Mass Concrete; Butterworth-Heinemann: Oxford, UK, 2013; pp. 1–500. [Google Scholar]
- Gaspar, A.; Lopez, F. Methodology for a probabilistic analysis of an RCC gravity dam construction. Modelling of temperature, hydration degree and ageing degree fields. Eng. Struct. 2014, 65, 99–110. [Google Scholar] [CrossRef]
- GRI Guide GS12. Lifetime Prediction of Geosynthetics Using Time-Temperature Superposition (TTS) and Arrhenius Modeling; Geosynthetic Institute: Folsom, PA, USA, 2012. [Google Scholar]
- Hirose, T. Research and practice concerning RCD method. C.18. In Proceedings of the XIVth ICOLD Congress, Rio de Janeiro, Brazil, 3–7 May 1982; Volume 3. [Google Scholar]
- ICOLD Bulletin 165. Selection of Materials for Concrete Dams, ICOLD, Antalya. 1999. Available online: https://www.icold-cigb.org/GB/publications/bulletins.asp (accessed on 1 March 2023).
- Kuzmanovic, V.; Savic, L.; Mladenovic, N. Computation of Thermal-Stresses and Contraction Joint Distance of RCC Dams. J. Therm. Stress. 2013, 36, 112–134. [Google Scholar] [CrossRef]
- Midas GTS NX. User’s Guide; MIDAS Information Technology Co., Ltd.: Seongnam, Republic of Korea, 1989. [Google Scholar]
- Moutafis, N.I.; Thanopoulos, Y. The geomembrane faced hardfill dam. In Proceedings of the Hydro 2015, Bordeaux, France, 26–28 October 2015. [Google Scholar]
- Raphael, J.M. Tensile strength of concrete. J. Proc. 1984, 81, 158–165. [Google Scholar]
- Reeves, G.N.; Yates, L.B. Simplified Design and Construction Control for Roller-Compacted Concrete; Roller-Compacted Concrete: New York, NY, USA, 1985; pp. 48–61. [Google Scholar]
- Schrader, E.; Mckinnon, R. Construction and Operation of Willow Creek Dam. Concr. Int. 1984, 6, 38–45. [Google Scholar]
- Shaw, Q.H.W. The Early Behavior of RCC in Large Dams. Int. J. Hydropower Dams 2010, 17, 83–90. [Google Scholar]
- ICOLD Bulletin 117. The Gravity Dam—A Dam for the Future, ICOLD. 2000. Available online: https://www.icold-cigb.org/GB/publications/bulletins.asp (accessed on 1 March 2023).
- Ginzburg, S.M.; Rukavishnikova, T.N.; Sheinker, N.Y. Simulation models for estimation of temperature regime of concrete dam by example of Bureyskaya HPP. Vedeneev 2002, 241, 173–178. [Google Scholar]
- Ginzburg, S.M. Assessment of the Temperature Regime of Concrete Massifs during Their Construction, Taking into Account Random Factors; JSC “VNIIG named after B.E. Vedeneev”: St. Petersburg, Russia, 2002; Volume 241, pp. 188–192. [Google Scholar]
- Aniskin, N.A.; Hoang, N. Forecast of Cracking of Concrete Massive Dams during Construction in Severe Climatic Conditions; Bulletin of the Moscow State University of Civil Engineering: Moscow, Russia, 2014; pp. 165–178. [Google Scholar]
- Aniskin, N.A.; Truk Chong, N.; Bryansky, I.A.; Hung Huu, D. Determination of the temperature field and thermal stress state of the paving concrete mass by finite element. Vestnik MGSU 2010, 13, 1407–1418. [Google Scholar]
- ETL 1110-2-542; Thermal studies of mass concrete structures. US Army Corps of Engineers: Washington, DC, USA, 1997.
- Kehlbeck, F. Effect of Solar Radiation on Bridge Structures; Liu, X.F., Translator; China Railway Publishing House: Beijing, China, 1981. [Google Scholar]
- Nagayama, I.; Jikan, S. 30 years’ history of Roller-Compacted Concrete dams in Japan. In Roller Compacted Concrete Dams; Routledge: Milton Park, UK, 2018; pp. 27–38. [Google Scholar]
- Soroushian, P.; Choi, K.B.; Alhamad, A. Dynamic constitutive behavior of concrete. J. Proc. 1986, 83, 251–259. [Google Scholar]
- Grishin, M.M. Concrete Dams (On Rock Foundations); Grishin, M., Rozanov, N., Belyi, L., Vasilyev, P., Gordienko, P., Ivanishev, V., Orekhov, V., Eds.; Stroyizdat: Moscow, Russia, 1975. [Google Scholar]
- Semenov, K.; Konstantinov, I.; Savchenko, A.; Kokoreva, K.; Nesterov, A. The effect of temperature effects in calculating the thermal stress state of discretely built-up concrete bodies. Constr. Unique Build. Struct. 2015, 32, 18–28. [Google Scholar]
- Summary Report on the Study of Layer-by-Layer Method of Concreting in the Construction of the Toktogul HPP; JSC “Institute Hydroproject”: St. Petersburg, Russia, 1971.
- Sivkov, S.I. Methods for Calculating the Characteristics of Solar Radiation; Gidrometeoizdat: Moscow, Russia, 1968; 234p. [Google Scholar]
- Shakirov, V.A. Method of estimating the arrival of total solar radiation on inclined surfaces using multi-year archives of meteorological data. Syst. Methods Technol. 2017, 4, 115–121. [Google Scholar]
- Nikitin, A.M. Reservoirs of Central Asia; Gidrometeoizdat: Moscow, Russia, 1991. [Google Scholar]
- Aniskin, N.A.; Shaitanov, A.M.; Shaitanov, M.V.; Khokhotva, S.N. Influence of solar radiation on heating of massif of gravity dam erected from low-cement concrete. Hydraul. Eng. Constr. 2021, 11, 11–18. [Google Scholar]
- Aniskin, N.; Truk, N.T.; Anh, L.D. Influence of base elasticity modulus on thermal stress state of concrete block. Hydraul. Eng. Constr. 2019, 11, 4–9. [Google Scholar]
- Adler, Y.P. Planning the Experiment in the Search for Optimal Conditions; Stroyizdat: Moscow, Russia, 1976; 588p. [Google Scholar]
- Aniskin, N.; Shaytanov, A.; Shaytanov, M.; Khokhotva, S. Low-cement content gravity dam as an alternative for Pskem HPP. In Proceedings of the E3S Web of Conferences, St. Petersbourg, Russia, 17–19 November 2021; Volume 263, p. 02028. [Google Scholar]
- Lowe, J., III. Discussion to Utilization of soil cement as slope protection for earth dams. In Proceedings of the First ASCE Water Resources Engineering Conference, Omaha, NE, USA, 14–18 May 1962. [Google Scholar]
- SR 41.13330.2012; Concrete and reinforced concrete structures of hydraulic structures. Ministry of Regional Development of Russia: Moscow, Russia, 2012.
- Engineer Manual No. 1110-2-2006; Engineering and Design, Roller-Compacted Concrete. U.S. Army Corps of Engineers: Washington, DC, USA, February 1992.
- ACI Committee 207. Roller-Compacted Mass Concrete; ACI 207.5R-99; American Concrete Institute: Farmington Hills, MI, USA, 1999. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).