Abstract
Although some studies have been conducted to compute fragility surfaces of buildings using vector-valued seismic intensity measures (IMs), in all the cases, the first component of the vector usually is the spectral acceleration at first mode of vibration of the structure Sa(T1). In this study, fragility surfaces of three reinforced concrete buildings (RCB) subjected to narrow-band ground motions obtained from soft soil of Mexico City are computed considering vector-valued IMs based not only on Sa(T1), but also the velocity V(T1), pseudo-velocity Sv(T1), and normalized input energy by the mass EI/m(T1) as the first component. As second component of the vector-valued IMs, the Peak Ground Acceleration (PGA), Peak Ground Velocity (PGV), effective duration (tD), earthquake damage potential (ID) and four Np spectral shape-based parameters obtained through spectral acceleration (NpSa), velocity (NpV), pseudo-velocity (NpSv), and input energy (NpEI) have been analyzed. In order to obtain fragility surfaces, Multinomial Logistic Regression (MLR) was applied. It is observed that those vector-valued IMs based on the spectral shape proxies were more efficient to predict the probability of failure of RCB. For this reason, it is important to consider spectral shape vector-valued IMs in order to reduce uncertainty in the structural response of buildings under earthquakes. Thus, the use of two parameters instead of a single intensity measure improves the efficiency. Moreover, the fragility surfaces can be used for the seismic risk evaluation of buildings.
1. Introduction
One of the crucial parameters to define hazard, fragility and seismic risk studies are ground motion intensity measures. Most seismic design codes in the world use Sa(T1) as IM; however, several studies have shown serious limitations of this parameter since this parameter does not properly represent the inelastic effect [1] and therefore more advanced IMs have been proposed [1,2,3,4,5]; Then, some of these IMs were applied in the analysis of buildings [6]. As IMs have evolved, there was a tendency to incorporate new parameters that improve the prediction of structural response in buildings. For this reason, vector-valued IMs based on two or three components have been proposed in recent years to improve the efficiency of IMs [6,7,8,9,10,11,12,13,14], which consists of the ability of an IM to estimate the structural response with the least uncertainty. Over the last decade there has been a dedication to determining the seismic performance of vector-valued IMs [15,16,17,18,19]. The results of many researchers [20,21,22,23,24,25,26] highlight the use of more sophisticated IMs such as those based on spectral shape, since they have the ability to predict the structural response more properly and, above all, a lower uncertainty in buildings which are in the inelastic range [4,6]; therefore, in recent years, Np spectral shape-based IMs have been proposed [27,28,29]. On the other hand, they have not only studied the efficiency of these IMs in predicting the structural response but also in obtaining seismic fragility curves. Fragility surfaces are composed by a set of seismic fragility curves. These are used to assess the vulnerability of structures to earthquakes by estimating the levels of damage reached [30]. At the present time, they are used for multiple purposes in civil engineering (e.g., loss estimation, collapse risk assessment, design review, and others). They can be applied to different types of structures (e.g., irregular buildings, underground tunnels, docks, wind turbines, masonry structures, to name just a few). This makes them an important tool for evaluating structures [31]. Nevertheless, they only used traditional IMs or vector-valued IMs with Sa(T1) as the first component of the vector and Np based only on Sa(T1) as the second component; moreover, applying it only to bidimensional steel frames [10]. In other words, the key factor in a vector-valued IM is to determine the best combination of parameters to estimate the probability of failure, or seismic fragility, with the least uncertainty to reduce the limitations of traditional IMs [4,10]. It is precisely this need that has motivated the present research. Hence, in this study, the efficiency of 32 vector-valued IMs in predicting the probability of failure of three-dimensional reinforced concrete buildings is evaluated. The vector-valued IMs considered Sa(T1), V(T1), Sv(T1), and EI/m(T1) as the first component. As for a second component PGA, PGV, tD, ID, NpSa, NpV, NpSv, and NpEI have been selected. An incremental dynamic analysis (IDA) was performed by subjecting 30 narrow-band ground motions to three spatial reinforced concrete buildings considering the maximum inter-story drift ratio (MIDR) as an engineering demand parameter (EDP). On the other hand, MLR was applied to compute seismic fragility surfaces that determine which vector-valued IMs presents a better relation associated with seismic fragility in terms of probability of failure.
2. Methodology
This section shows the procedure carried out to obtain the seismic fragility surfaces of reinforced concrete buildings. The steps to follow can be summarized in the flow diagram of Figure 1. In the subsequent sections the procedure for each step is detailed.
2.1. Selected Seismic Intensity Measures
As it was indicated before, the vector-valued IMs considered are Sa(T1), V(T1), Sv(T1), and EI/m(T1) as the first component, while as the second component PGA, PGV, tD, ID, NpSa, NpV, NpSv, and NpEI are used. Where NpSa, NpV, NpSv, and NpEI represent the ratio between the average spectrum of pseudoacceleration (Saavg), velocity (Vavg), pseudovelocity (Svavg), and input energy (EIavg), for the range of periods from Ti to Tf (initial and final period, respectively) with respect to the corresponding spectrum at period j (within the range from Ti to Tf). The eight parameters selected as the second component of the vector-valued IMs are shown in Table 1 (including their mathematical formulation). It is important to emphasize that in this study not only the spectral acceleration at the fundamental period of the structure Sa(T1), from now on called only Sa, was used as the first component of the vector, but also the Velocity V, pseudo-Velocity Sv, and normalized input energy by the mass EI/m (from now on called only EI) were used, where m represents the mass of the structural system and EI is obtained according with the suggestion of Uang and Bertero [32]. The above means that the vector-valued IMs are composed as shown in Table 2.

Table 1.
Selected second component of the vector-valued IMs.

Table 2.
Set of vector-valued IMs used.
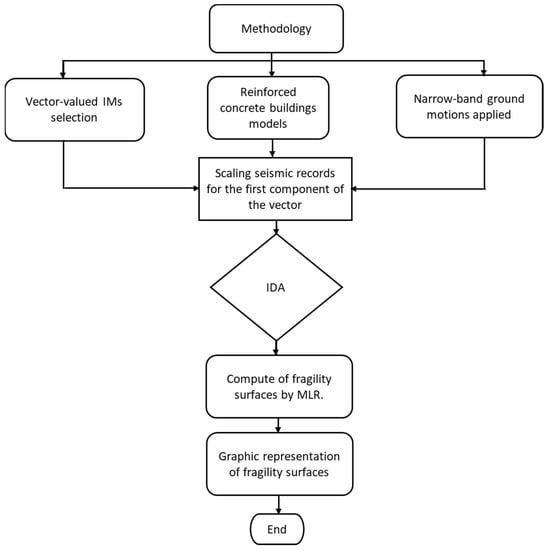
Figure 1.
Methodology to compute fragility surfaces.
2.2. Reinforced Concrete Buildings Models
Most of the buildings damaged by the well-known 1985 Mexican Earthquake correspond to reinforced concrete buildings located in the soft soil of Mexico City, particularly those buildings sensitive to the softening effects (structures with periods smaller to the soil period). Notice that in this case the soil period is about 2 sec. For this reason, the selection of the structural models was based on the indication given before. The models to be analyzed consist of three RCB of 4, 7, and 10 stories of 3.5 m height each, 3 bays in X and Y direction with 7 m length each. The buildings were designed according to the Mexico City Building Code (MCBC) [33] considering use for offices. In Figure 2 the general topology of the structures is illustrated. Some of the main characteristics of the reinforced concrete buildings are shown in Table 3. In Table 3, T1 corresponds to the structural vibration period, Cy and Dy are the seismic coefficient and displacement at yielding obtained from push-over analysis. The buildings were seismically analyzed with the nonlinear dynamic analysis computer program RUAUMOKO [34]. For the nonlinear dynamic analysis, the damping corresponding to all the frames is 5% of the critical damping. The base columns are assumed to be fixed. Beams and columns were modeled as frame elements which concentrate their inelastic response in plastic hinges located at their ends (lumped plasticity nonlinear frame elements). The Modified Takeda hysteretic behavior was used to model the nonlinearity of all the frame elements. More information about the Modified Takeda hysteretic model can be found in [34].
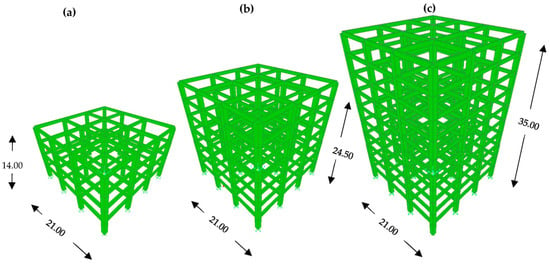
Figure 2.
RCB structural models for (a) 4, (b) 7, and (c) 10-story, dimensions in meters.

Table 3.
Important characteristics of the RCB.
2.3. Narrow-Band Ground Motions
The selection of seismic records was carried out taking into consideration earthquakes that were characteristic of México City (CDMX) and its outskirts, presenting magnitudes equal or greater than 6.8 in the moment magnitude scale (Mw) since these subject the structures to bigger demands compared to other types of earthquakes [35]. The search returned a total of 6 earthquakes (30 narrow-band time histories) that occurred on the Mexican Pacific coast, which were recorded at the different seismic stations in the city. Table 4 shows the selected earthquakes and some important data from them. Notice that the ground motion records have been obtained from the Mexican Strong Motion Database of the Mexican Society of Earthquake Engineering.

Table 4.
Selected Earthquake ground motions.
2.4. Incremental Dynamic Analysis
For the IDA curves, the approach proposed by Vamvatsikos and Cornell [36] was considered. The first step in the incremental dynamic analysis is to scale the 30 seismic records to a desired intensity level. In this study, the intensity level must correspond to the parameters selected as first component (Sa, V, Sv, and EI). Thus, the ground motion records are scaled at different values of Sa, V, Sv, and EI. Subsequently, the scaling factor necessary to reach the desired intensity at the fundamental period of the structure was obtained. Additionally, scaling factors were applied to the corresponding seismic records, to compute a total of 20 scaled seismic records, one for each scaling level, for each component of the selected seismic record. All the buildings are subjected to the ground motion records scaled for each intensity value and in terms of the IM under consideration (Sa, V, Sv, and EI) in order to assess the structural demand (engineering demand parameter). The EDP considered in this study was the MIDR, due to its wide use in current construction codes. The structural performance under seismic loads was obtained with the support of the RUAUMOKO 3D as it was indicated before. The most important parameters that were required for this software were the type of analysis (dynamic), the characteristics of the building (number of nodes, elements, cross sections, vibrating shapes, damping), the creation of each node and bar element of the structure with their respective arbitrary coordinates, the nodes where the inter-story drift are estimated, the properties of the cross sections (modulus of elasticity and shear, effective area, moment of inertia), the loads that are transmitted to the nodes according to the structural analysis carried out in accordance with the provisions of the construction code [33] and finally the time interval of 0.01 s as well as the duration of the time history of the earthquake that excites the structure. The reader is encouraged to review the manuals that the RUAUMOKO 3D software has in order to delve even deeper into all the functions that can be carried out with it. Finally, subjecting the RCB to the ground motions, it is possible to estimate the variation for the IM associated with the EDP for each scaling level. As an illustrative example, Figure 3 shows the IDA for the three RCB in terms of spectral acceleration as IM and MIDR as EDP.
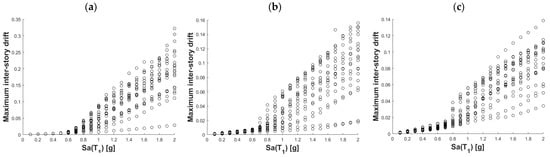
Figure 3.
IDA for frame (a) F4, (b) F7, and (c) F10 with Sa(T1) as IM and MIDR as EDP.
2.5. Seismic Fragility Surfaces
The fragility surfaces were estimated considering the probability of failure of the building when the EDP exceeded its reference value or exceedance rate. In the case of the MIDR, a limit value of 0.03 was considered, according to the current construction code [33], to evaluate the failure or no-failure of the structure. The probability of failure was indicated equal to 1 (failure) when the MIDR exceeded the limit value and 0 (no-failure) when it was lower. These values were then associated with the calculated IMs, PGA, PGV, tD, ID, NpSa, NpV, NpSv, and NpEI for each seismic record used. Finally, considering the values of each component of the vector-valued IMs, Equation (1) was applied to perform a MLR to obtain the fragility surfaces that estimate the behavior of the probability of failure when using an IM or another. Figure 4 shows an example of a seismic fragility surface and how the probability of failure varies as the values of the vector-valued IMs change.
where
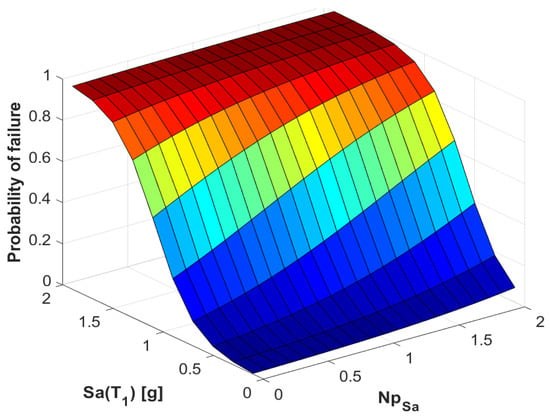
Figure 4.
Illustrative seismic fragility surface for the vector <Sa, NpSa>.
- PF = Probability of failure.
- x1 = First parameter of the vector or IM1 value.
- x2 = Secondary parameter of the vector or IM2 value.
- β0, β1 y β2 = Coefficients obtained from regression of the results for the scaled records variating both IM1 = x1 and IM2 = x2.
3. Numerical Results
For this section, it is important to mention that although the results are especially shown for the 10-story frame for the sake of brevity of the manuscript. Similar results are valid for all the selected reinforced concrete buildings. In addition, seismic fragility surfaces also are presented for the most efficient vector-valued IMs to predict fragility surfaces of all the buildings under consideration.
A total of 12 IDA were computed for the three reinforced concrete buildings, four first-component intensity measures and 30 ground motion records. As an example, the results of the IDA for the 10-stories RCB are shown in Figure 5 where the IMs associated with the EDP (MIDR) and the variation it presents for each scaling level is shown. From this IDA applied to the 10-stories RCB subjected to the 30 scaled seismic records, it can be seen the dispersion of the results of scaling for the MIDR when Sa and EI were used as intensity measure. For this reason, it is important to reduce the uncertainty in the prediction of the structural response using advances intensity measures as in the case of vector-valued ground motion intensity measures. Hence, this study computes seismic fragility surfaces of 3D reinforced concrete buildings using several vector-valued ground motion intensity measures. Figure 6, Figure 7, Figure 8 and Figure 9 illustrate the seismic fragility surfaces obtained for the 10 story RCB and all the selected 32 vector-valued intensity measures (with Sa, V, Sv and EI as the first component of the vector).
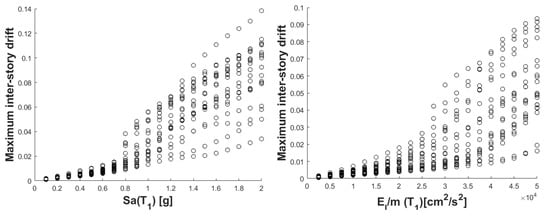
Figure 5.
IDA of the 10-story RCB subjected to scaled seismic records with Sa(T1) and EI/m (T1) as IM for MIDR as EDP.
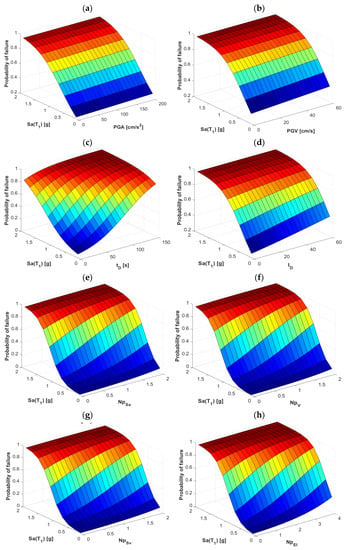
Figure 6.
Probability of failure for the frame F10 with Sa as the first component of the vector-valued IM and (a) PGA, (b) PGV, (c) tD, (d) ID (e) NpSa, (f) Npv, (g) NpSv and (h) NpEI, as the second component.
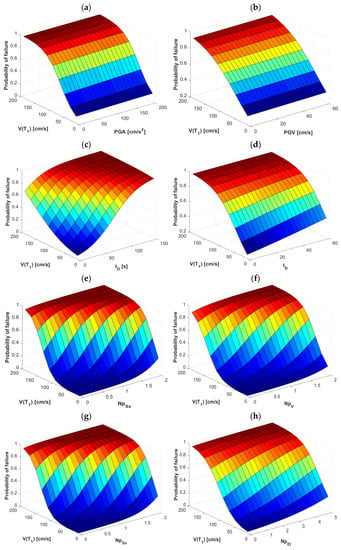
Figure 7.
Probability of failure for the frame F10 with V as the first component of the vector-valued IM and (a) PGA, (b) PGV, (c) tD, (d) ID, (e) NpSa, (f) Npv, (g) NpSv and (h) NpEI, as the second component.
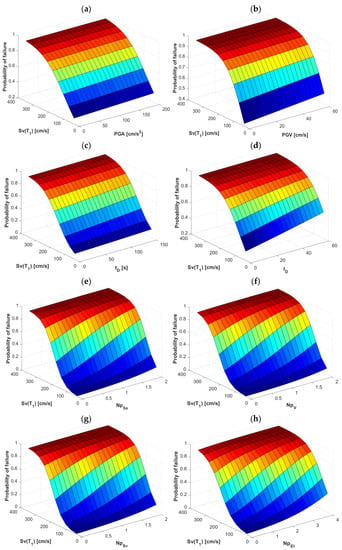
Figure 8.
Probability of failure for the frame F10 with Sv as the first component of the vector-valued IM and (a) PGA, (b) PGV, (c) tD (d) ID, (e) NpSa, (f) Npv, (g) NpSv and (h) NpEI, as the second component.
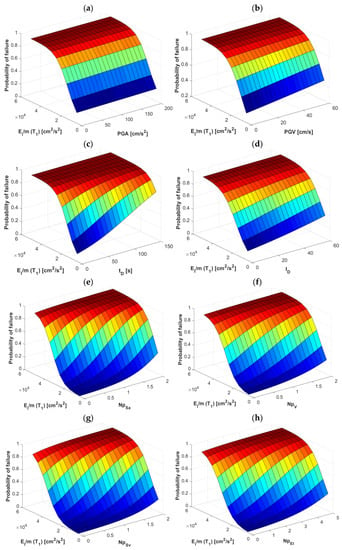
Figure 9.
Probability of failure for the frame F10 with EI as the first component of the vector-valued IM and (a) PGA, (b) PGV, (c) tD, (d) ID, (e) NpSa, (f) Npv, (g) NpSv, and (h) NpEI as the second component.
Regarding the fragility surfaces results, in Figure 6a,b, corresponding to PGA and PGV for the 10-story frame, we can see a very similar behavior between them where the trend seems to be flat along the vector-valued IMs, which represents a low influence on its ability to estimate fragility surfaces. The case improves for Figure 6c where a slight increase is seen as the effective duration tD increases. However, Figure 6d (ID) tends to behave like the first two vectors which seem to have little influence on the response (or the structural probability of failure). A significant change can be seen in Figure 6e, which represents a spectral shape-based parameter NpSa, noting a clear influence on the probability of failure when using this vector-valued IM. The same occurs for the case of Figure 6f,g (NpV and NpSv, respectively), although to a lesser extent since the regression is not so pronounced. Finally, for the case of Figure 6h (NpEI), it again presents a more appropriate, and even superior, behavior than the other vector-valued IMs, since the response is clearly influenced as the IM increases.
A similar behavior is observed for the case where V is used as the first component of the vector, since in Figure 7a the vector-valued IM again shows little influence as PGA increases, although with a slight improvement but does not represent a significant change in the result. In the case of PGV (Figure 7b), the surface continues to show low efficiency because its behavior remains flat as the vector-valued IM increases. In reference to tD (Figure 7c), which had shown good behavior in the previous figure, it seems to maintain it since its ability to influence the probability of failure increases at the same time as the vector-valued IM does, unlike ID who shows in Figure 7d a behavior more like the first two cases. Next, the vector-valued IM <V, NpSa> improves its performance and in fact outperforms the other vector-valued IMs in terms of its ability to better estimate the fragility surface (Figure 7e). NpV also has an acceptable behavior (Figure 7f) if we compare it with IMs based on peak ground response. In the case of NpSv, its graph shows a good surface when increasing the vector-valued IM (Figure 7g) and shows a very marked similarity to the case where Sa is used. Finally, in Figure 7h NpSa shows a good behavior but slightly lower than that of the other vector-valued IMs with spectral shape-based parameters. Likewise, we can perform an analysis for Figure 8 with Sv as the first component of the vector-valued, where it is observed that in Figure 8a,b (PGA and PGV, respectively) they are practically the same except that the latter has a more pronounced curvature, but for purposes of reliability as an estimator of the fragility surfaces it generates uncertainty due to its flat behavior despite the increase in vector-valued IMs. The same occurs with tD and ID (Figure 8c and Figure 8d, respectively) as they present improvements in the probability of failure but not enough to determine their use as vector-valued IMs in seismic fragility analysis. The interesting part comes again with the vector-valued IMs based on the spectral shape, since in Figure 8e a graph that estimates the probability of failure for <Sv, NpSa> in a good way is obtained. In Figure 8f corresponding to NpV, a better fragility surface is also obtained compared to the other vector-valued IM. For the case of NpSv (Figure 8g), it results in a considerable similarity with respect to the vector-valued IMs based on the Np parameter. Of the vector-valued Ims based on this spectral shape parameter, NpEI turns out to be the most consistent throughout the analyses, because in Figure 8h an appropriate behavior can be seen again on the fragility surface by significantly influencing the probability of failure as the vector-valued IM increases, this gives certainty to its efficiency as an estimator of the structural response when using these vector-valued Ims.
Finally, regarding the case of EI as the first component of the vector-valued Ims, the constant of the Ims based on peak ground response PGA and PGV (Figure 9a,b) and duration tD and ID (Figure 9c,d) is maintained where there is uncertainty about its efficiency to estimate the structural response due to the low influence that these parameters have in the estimation of fragility surfaces. On the other hand, the vector-valued Ims based on the spectral shape-Np parameter have a more appropriate behavior as we can see in Figure 9e with NpSa. The same occurs, although to a lesser extent, for Figure 9f (NpV) where a flatter but equally significant behavior is seen. In addition, in Figure 9g, corresponding to NpSv, it stands out for its similarity compared to the vector <EI, NpSa>, which translates into a desired behavior for this case as it has the same effects in estimating the probability of failure. Finally, we have Figure 9h where the probability of failure is clearly influenced as the vector <EI, NpEI> changes. For this reason, it has been established that the vector-valued Ims based on the spectral shape, in particular on the parameter Np addressed in this study, have a better relation as an estimator of the structural response and in this case in the estimation of seismic fragility surfaces.
In order to observe how the same vector-valued IM influences the different buildings analyzed in this study (F4, F7, and F10), Figure 10, Figure 11, Figure 12 and Figure 13 compare the fragility surfaces for all the buildings under consideration and the Np-based intensity measures. Figure 10 shows a similar behavior in the fragility surfaces for the three cases when the vector-valued IM <Sa, NpSa> is considered. The 4-story building seems to be more affected by the variation of the IMs that compose the vector. In the case of the 7-story frame, the fragility surface has a more stable behavior and is even better when we analyze the 10-story frame. However, in all three cases, there is a marked influence when varying the values of the vector-valued IMs, as noted in the previous section. Likewise, in Figure 11, we have the vector <Sa, NpV> with fragility surfaces where now the flattest behavior is obtained in the 7-story frame, while for buildings F4 and F10 the fragility surfaces are quite similar. We can also mention that the vector-valued IM <Sa, NpSv> is consistent with the previous cases and confirms that Sv behaves very similarly to Sa in this type of analysis (Figure 12). Finally, Figure 13 shows the behavior of the three buildings using <Sa, NpEI>, making it clear that this vector-valued IM does not change its ability to predict the response by analyzing the different types of buildings. This is useful because it infers that this vector could be efficient to analyze different types of buildings regardless of their height or even their topology.
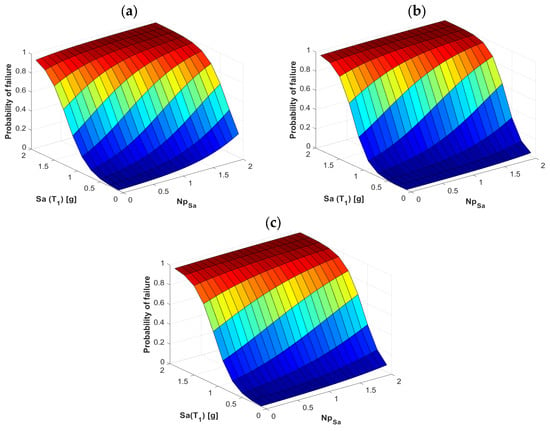
Figure 10.
Probability of failure comparison for the frames (a) F4, (b) F7, and (c) F10 using the vector-valued IM <Sa, NpSa>.
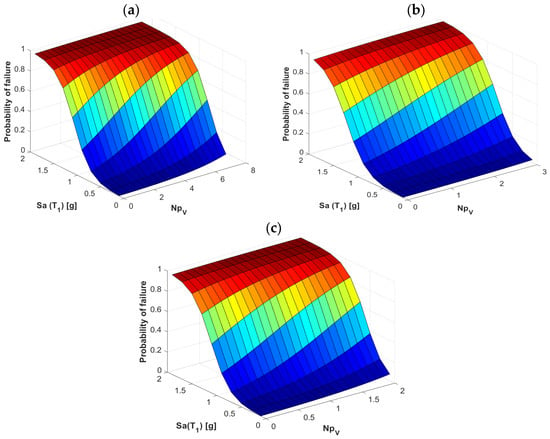
Figure 11.
Probability of failure comparison for the frames (a) F4, (b) F7, and (c) F10 using the vector-valued IM <Sa, NpV>.
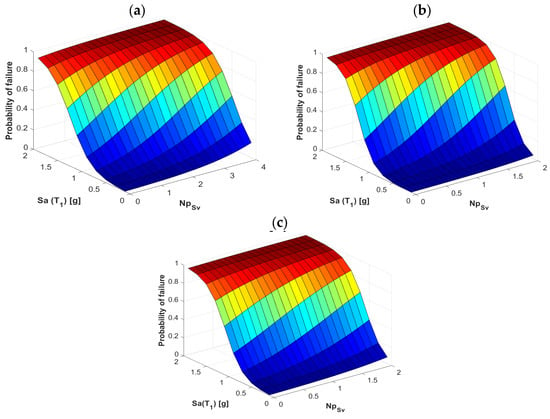
Figure 12.
Probability of failure comparison for the frames (a) F4, (b) F7, and (c) F10 using the vector-valued IM <Sa, NpSv>.
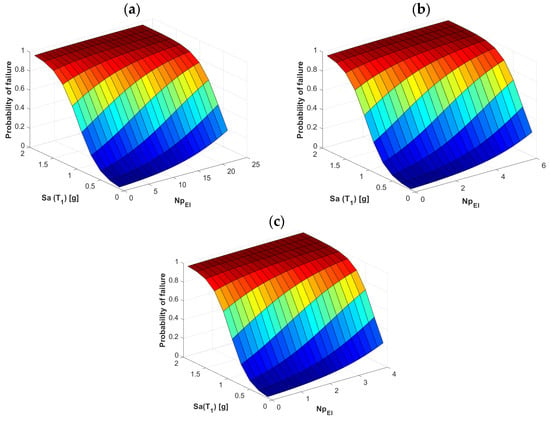
Figure 13.
Probability of failure comparison for the frames (a) F4, (b) F7, and (c) F10 using the vector-valued IM <Sa, NpEI>.
4. Discussion
The above results are consistent with previous works [8,12,15,37] regarding the efficiency of vector-valued IMs since it has been documented that vector-valued IMs based on peak ground response and duration do not obtain reliable results in estimating the structural response when analyze non-linear behavior or behavior beyond the elastic range. The usefulness of vector-valued IMs based on spectral shape, particularly those represented by the spectral shape parameter Np, has also been highlighted as more appropriate IM [11,29,38,39]. The importance of this study addresses spectral shape IM with different characteristics that present higher efficiency to estimate the structural response and apply its use in obtaining seismic fragility surfaces based on the probability of failure of the structure. Notice that this is the first time that fragility surfaces are obtained by using S, Sv and EI as the first component of the vector; moreover, this fragility surfaces consider Np based on different spectral shape parameters. Finally, the results of the study can be summarized as follows:
- In each of the cases of vector-valued IMs, PGA and PGV had low influence when they were used as the second component of the vector.
- tD tended to behave well in some cases, but it was inconsistent in others, so its reliability still requires further study; ID presented better results than PGA and PGV, but its use did not imply a clear advantage over other IMs with better results.
- The vector-valued IMs based on the spectral shape Np had higher influence on the structural response and were more appropriate parameters in the estimation of the probability of failure for trace seismic fragility surfaces.
- The IM with the best results as the first component of the vector were Sa(T1) and V(T1) since they generated the fragility surfaces that were most influenced by varying the vector-valued IMs. In addition, the vector <V, NpSa> had the best results and was established as the best estimator for seismic fragility surfaces based on the probability of failure of buildings.
- The vectors <Sa, NpSa>, <Sa, NpV>, <Sa, NpSv>, and <Sa, NpEI> were used to analyze the reinforced concrete buildings of 4, 7, and 10 stories. The results showed that in all cases, there was an important influence on the estimation of the probability of failure regardless of the building being analyzed. The above is valid only for the frames analyzed in this study; further investigation is required for buildings with different heights and topologies.
The present study has demonstrated the usefulness of using vector-valued IMs based on spectral shape over IMs based on peak ground response and duration. However, there is still uncertainty whether spectral shape-based IMs will be better estimators of the structural response when used as the first component in vector-valued IMs. This is precisely the aim of our future research with the implementation of new IMs and EDP as the reported for [40,41]. Finally, the fragility surfaces can be used for the seismic risk evaluation of buildings as we have seen in [42].
5. Conclusions
In the present work, seismic fragility surfaces were estimated considering the efficiency of 32 vector-valued IMs composed of the parameters Sa(T1), V(T1), Sv(T1), and EI/m(T1) as the first component of the vector while PGA, PGV, tD, ID, NpSa, NpV, NpSv, and NpEI were used as the second component. The study corresponded to three 3D reinforced concrete buildings subjected to 30 narrow-band ground motions, performing 12 incremental dynamic analysis considering the maximum inter-story drift as engineering demand parameter, and a total of 96 fragility surfaces were obtained. The present study has demonstrated the usefulness of using vector-valued IMs based on spectral shape over IMs based on peak ground response and duration. The efficiency to predict the probability of failure is increasing when spectral shape-based IMs based on the generalized spectral shape parameter Np is selected as second component of the vector. Notice that there is still uncertainty whether spectral shape-based IMs will be better estimators of the structural response when used as the first component in vector-valued IMs. This is precisely the aim of our future research with the implementation of new IMs and EDP. In the near future, it is interesting to work on this research field with intention of improving the IMs used in the design of structures in order to optimize costs and/or performance without compromising structural security. The results obtained here serve as a basis for future works and can be implemented to be applied in other types of structural systems in order to improve current building codes toward the perfect prediction of the structural response of buildings under earthquakes.
Author Contributions
Conceptualization, E.B.; methodology, E.B., N.Z. and J.T.; software, N.Z.; validation, E.B., J.B. and J.T.; formal analysis, J.B.; investigation, N.Z.; resources, M.B.; data curation, J.B.; writing—original draft preparation, N.Z.; writing—review and editing, A.V., J.C. (José Campos), R.S. and J.C. (Joel Carvajal); visualization, A.V. and J.C. (José Campos).; supervision, E.B. and M.B.; project administration, E.B. and M.B.; funding acquisition, E.B. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was developed thanks to the economic support provided by the Consejo Nacional de Ciencia y Tecnología (CONACyT) and the project financed by the SEP through the program from PRODEP. Finally, the support received from the Autonomous University of Sinaloa within the PROFAPI 2022 project is appreciated.
Data Availability Statement
Not applicable.
Acknowledgments
The first author appreciates the four-year doctoral scholarship granted by the CONACyT.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Cordova, P.; Deierlein, G.G.; Mehanny, S.S.F.; Cornell, C.A. Development of a Two-Parameter Seismic Intensity Measure and Probabilistic Assessment Procedure. J. Eng. Appl. Sci. 2001, 1, 51. [Google Scholar]
- Baker, J.W.; Cornell, A. Vector-valued intensity measures for pulse-like near-fault ground motions. Eng. Struct. 2008, 30, 1048–1057. [Google Scholar] [CrossRef]
- Riddel, R. On ground motion intensity indices. Earthq. Spectra 2007, 23, 147–173. [Google Scholar] [CrossRef]
- Bojórquez, E.; Iervolino, I. Spectral shape proxies and nonlinear structural response. Soil Dyn. Earthq. Eng. 2011, 31, 996–1008. [Google Scholar] [CrossRef]
- Tothong, P.; Luco, N. Probabilistic seismic demand analysis using advanced ground motion intensity measures. Earthq. Eng. Struct. Dyn. 2007, 36, 1837–1860. [Google Scholar] [CrossRef]
- Lucchini, A.; Mollaioli, F.; Monti, G. Intensity measures for response prediction of a torsional building subjected to bi-directional earthquake ground motion. Bull. Earthq. Eng. 2011, 9, 1499–1518. [Google Scholar] [CrossRef]
- Donaire-Ávila, J.; Mollaioli, F.; Lucchini, A.; Benavent-Climent, A. Intensity measures for the seismic response prediction of mid-rise buildings with hysteretic dampers. Eng. Struct. 2015, 102, 278–295. [Google Scholar] [CrossRef]
- Ge, P.; Zhou, Y. Investigation of efficiency of vector-valued intensity measures for displacement-sensitive tall buildings. Soil Dyn. Earthq. Eng. 2018, 107, 417–424. [Google Scholar] [CrossRef]
- Kiani, J.; Camp, C.; Pezeshk, S. Role of conditioning intensity measure in the influence of ground motion duration on the structural response. Soil Dyn. Earthq. Eng. 2018, 104, 408–417. [Google Scholar] [CrossRef]
- Bojórquez, E.; Iervolino, I.; Reyes-Salazar, A.; Ruiz, S.E. Comparing vector-valued intensity measures for fragility analysis of steel frames in the case of narrow-band ground motions. Eng. Struct. 2012, 45, 472–480. [Google Scholar] [CrossRef]
- Bojórquez, E.; Chávez, R.; Reyes-Salazar, A.; Ruiz, S.E.; Bojórquez, J. A new ground motion intensity measure IB. Soil Dyn. Earthq. Eng. 2017, 99, 97–107. [Google Scholar] [CrossRef]
- Yakhchalian, M.; Nicknam, A.; Amiri, G. Optimal vector-valued intensity measure for seismic collapse assessment of structures. Earthq. Eng. Eng. Vib. 2015, 14, 37–54. [Google Scholar] [CrossRef]
- Yang, C.; Xie, L.; Li, A.; Jia, J.; Zeng, D. Ground motion intensity measures for seismically isolated RC tall buildings. Soil Dyn. Earthq. Eng. 2019, 125, 105727. [Google Scholar] [CrossRef]
- Rajabnejad, H.; Hamidi, H.; Naseri, S.; Abbaszadeh, M. Effect of intensity measure on the response of a 3D-structure under different ground motion duration. Int. J. Eng. 2021, 34, 2219–2237. [Google Scholar]
- Zhou, Y.; Ge, P.; Han, J.; Lu, Z. Vector-valued intensity measures for incremental dynamic analysis. Soil Dyn. Earthq. Eng. 2017, 100, 380–388. [Google Scholar] [CrossRef]
- Tomeo, R.; Bilotta, A.; Pitilakis, D.; Nigro, E. Soil-structure interaction effects on the seismic performances of reinforced concrete moment resisting frames. Procedia Eng. 2017, 199, 230–235. [Google Scholar] [CrossRef]
- Kiani, J.; Camp, C.; Pezeshk, S. The importance of non-spectral intensity measures on the risk-based structural responses. Soil Dyn. Earthq. Eng. 2019, 120, 97–112. [Google Scholar] [CrossRef]
- Liu, T.-T.; Lu, D.-G.; Yu, X.-H. Development of a compound intensity measure using partial least-squares regression and its statistical evaluation based on probabilistic seismic demand analysis. Soil Dyn. Earthq. Eng. 2019, 125, 105725. [Google Scholar] [CrossRef]
- Javadi, E.; Yakhchalian, M. Selection of optimal intensity measure for seismic assessment of steel buckling. Restrained braced frames under Near-Fault ground motions. J. Rehabil. Civ. Eng. 2019, 7, 114–133. [Google Scholar]
- Buratti, N. A comparison of the performances of varios ground-motion intensity measures. In Proceedings of the 15th World Conference on Earthquake Engineering 2012, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Grigoriu, M. Do seismic intensity measures (IMs) measure up? Probabilistic Eng. Mech. 2016, 46, 80–93. [Google Scholar] [CrossRef]
- Kiani, J.; Pezeshk, S. Sensitivity analysis of the seismic demands of RC moment resisting frames to different aspects of ground motions. Earthq. Eng. Struct. Dyn. 2017, 46, 2739–2755. [Google Scholar] [CrossRef]
- Mollaioli, F.; Lucchini, A.; Cheng, Y.; Monti, G. Intensity measures for the seismic response prediction of base-isolated buildings. Bull. Earthq. Eng. 2013, 11, 1841–1866. [Google Scholar] [CrossRef]
- Palanci, M.; Senel, S. Correlation of earthquake intensity measures and spectral displacement demands in building type structures. Soil Dyn. Earthq. Eng. 2019, 121, 306–326. [Google Scholar] [CrossRef]
- Torres, J.I. Eficiencia de Medidas de Intensidad Sísmica Vectorial en la Predicción de la Respuesta de Edificios de C/R; Universidad Autónoma de Sinaloa: Culiacán, México, 2018; p. 102. [Google Scholar]
- Tsantaki, S.; Adam, C.; Ibarra, L. Intensity measures that reduce collapse capacity dispersion of P-delta vulnerable simple systems. Bull. Earthq. Eng. 2016, 15, 1085–1109. [Google Scholar] [CrossRef]
- Bojórquez, E.; Reyes-Salazar, A.; Ruiz, S. On the Use of Vector-Valued Intensity Measure to Predict Peak and Cumulative Demands of Steel Frames under Narrow-Band Motions. Appl. Mech. Mater. 2014, 595, 137–142. [Google Scholar] [CrossRef]
- Bojorquez, E.; Astorga, L.; Reyes-Salazar, A.; Teran-Gilmore, A.; Velazquez, J.; Bojorquez, J.; Rivera, L. Prediction of hysteretic energy demands in steel frames using vector-valued IMs. Steel Compos. Struct. 2015, 19, 697–711. [Google Scholar] [CrossRef]
- Torres, J.I.; Bojórquez, E.; Reyes, A.; Bojórquez, J. Vector-valued intensity measures to predict peak and hysteretic energy demands of 3D R/C buildings. Energy-Based Seism. Eng. 2021, 155, 274–289. [Google Scholar]
- Hosseinpour, F.; Abdelnaby, A. Fragility curves for RC frames under multiple earthquakes. Soil Dyn. Earthq. Eng. 2017, 98, 222–234. [Google Scholar] [CrossRef]
- Mai, C.; Konakli, K.; Sudret, B. Seismic fragility curves for structures using non-parametric representations. Front. Struct. Civ. Eng. 2017, 11, 169–186. [Google Scholar] [CrossRef]
- Uang, C.-M.; Bertero, V. Evaluation of seismic energy in structures. Earthq. Eng. Struct. Dyn. 1990, 19, 77–90. [Google Scholar] [CrossRef]
- RCDMX. Normas Técnicas Complementarias para el Diseño por Sismo; Gaceta Oficial de la Ciudad de México: Ciudad de México, México, 2017. [Google Scholar]
- Carr, A. Ruamoko 3D Manual; University of Canterbury: Christchurch, New Zealand, 2015. [Google Scholar]
- Teran-Gilmore, A.; Jirsa, J. The use of cumulative ductility strength spectra for seismic design against low cycle fatigue. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; Volume 889. [Google Scholar]
- Vamvatsikos, D.; Cornell, C. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Amiri, M.; Yakhchalian, M. Performance of intensity measures for seismic collapse assessment of structures with vertical mass irregularity. Structures 2020, 24, 728–741. [Google Scholar] [CrossRef]
- Minas, S.; Galasso, C. Accounting for spectral shape in simplified fragility analysis of case-study reinforced concrete frames. Soil Dyn. Earthq. Eng. 2019, 119, 91–103. [Google Scholar] [CrossRef]
- Chávez, R.; Bojórquez, E. Seismic hazard maps based on the intensity measure INp. KSCE J. Civ. Eng. 2017, 22, 247–256. [Google Scholar] [CrossRef]
- Ruggieri, S.; Calò, M.; Cardellicchio, A.; Uva, G. Analytical-mechanical based framework for seismic overall fragility analysis of existing RC buildings in town compartments. Bull. Earthq. Eng. 2022, 20, 8179–8216. [Google Scholar] [CrossRef]
- Ruggieri, S.; Vukobratovic, V. Acceleration demands in single-storey RC buildings with flexible diaphragms. Eng. Struct. 2023, 275 Part A, 115276. [Google Scholar] [CrossRef]
- Gehl, P.; Seyedi, D.; Douglas, J. Vector-valued fragility functions for seismic risk evaluation. Bull. Earthq. Eng. 2013, 11, 365–384. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).