Prediction of Bond-Slip Behavior of Circular/Squared Concrete-Filled Steel Tubes
Abstract
:1. Introduction
2. Experimental Database
3. Analysis of Variance (ANOVA)
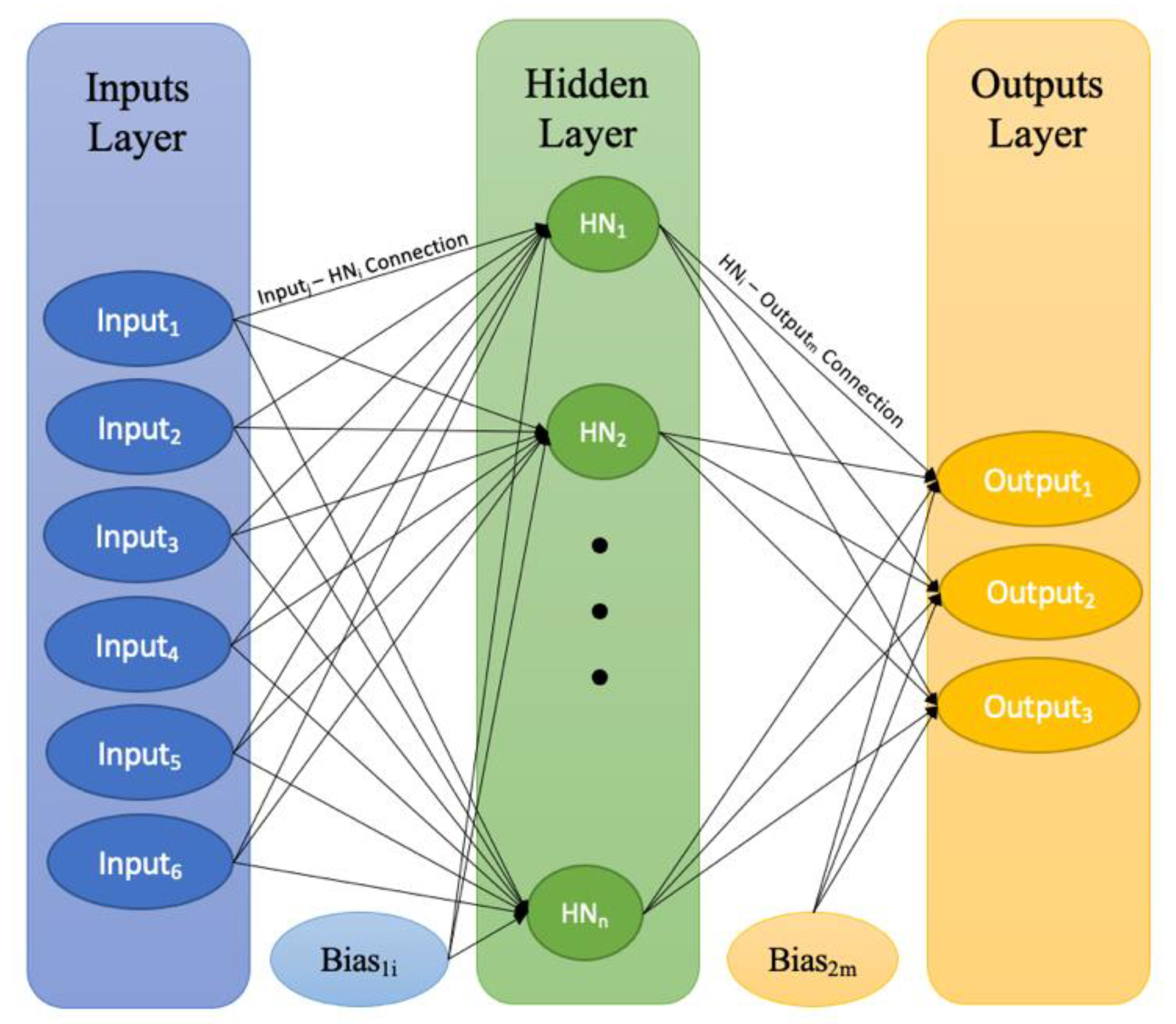
4. Artificial Neural Network (ANN)
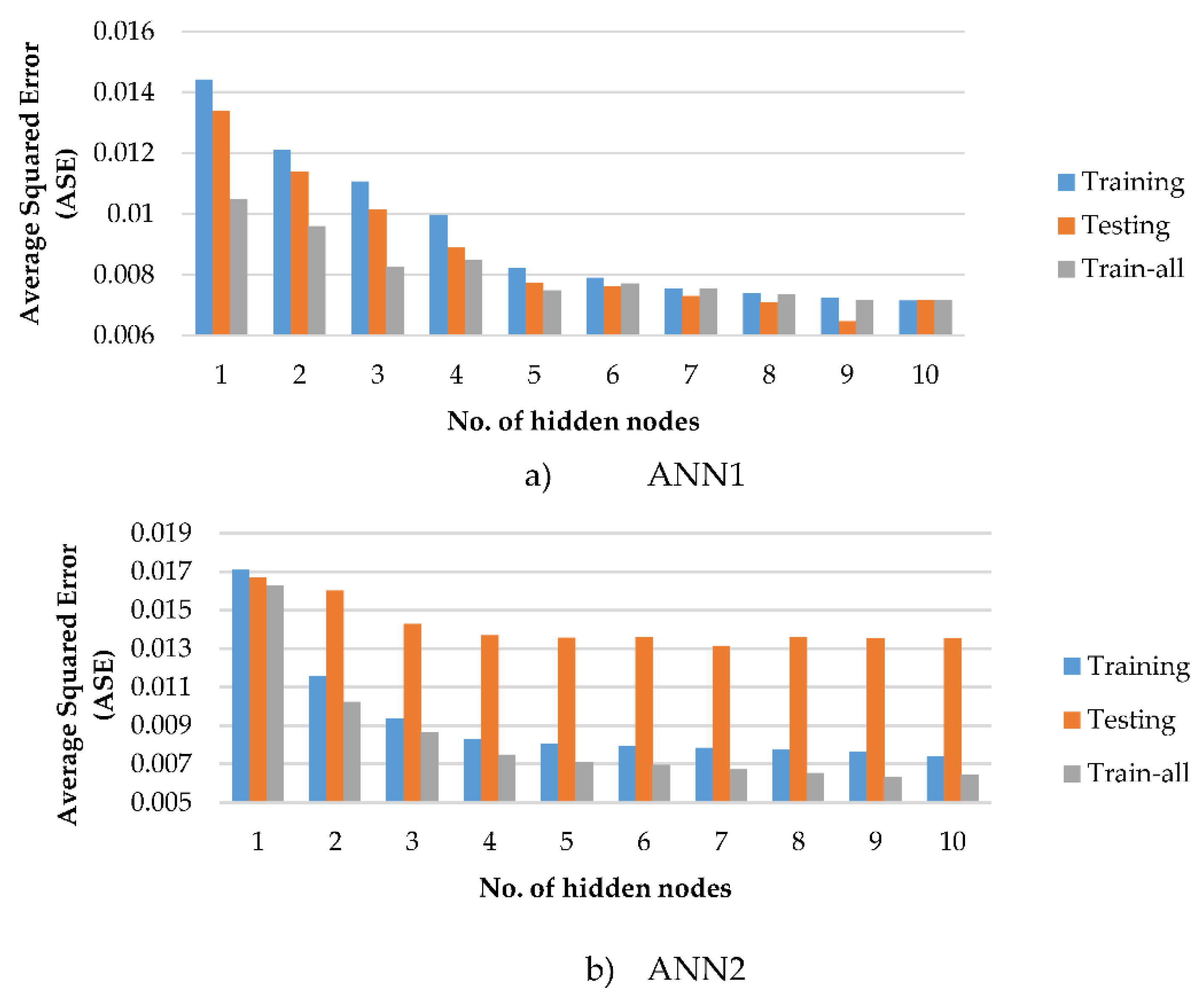
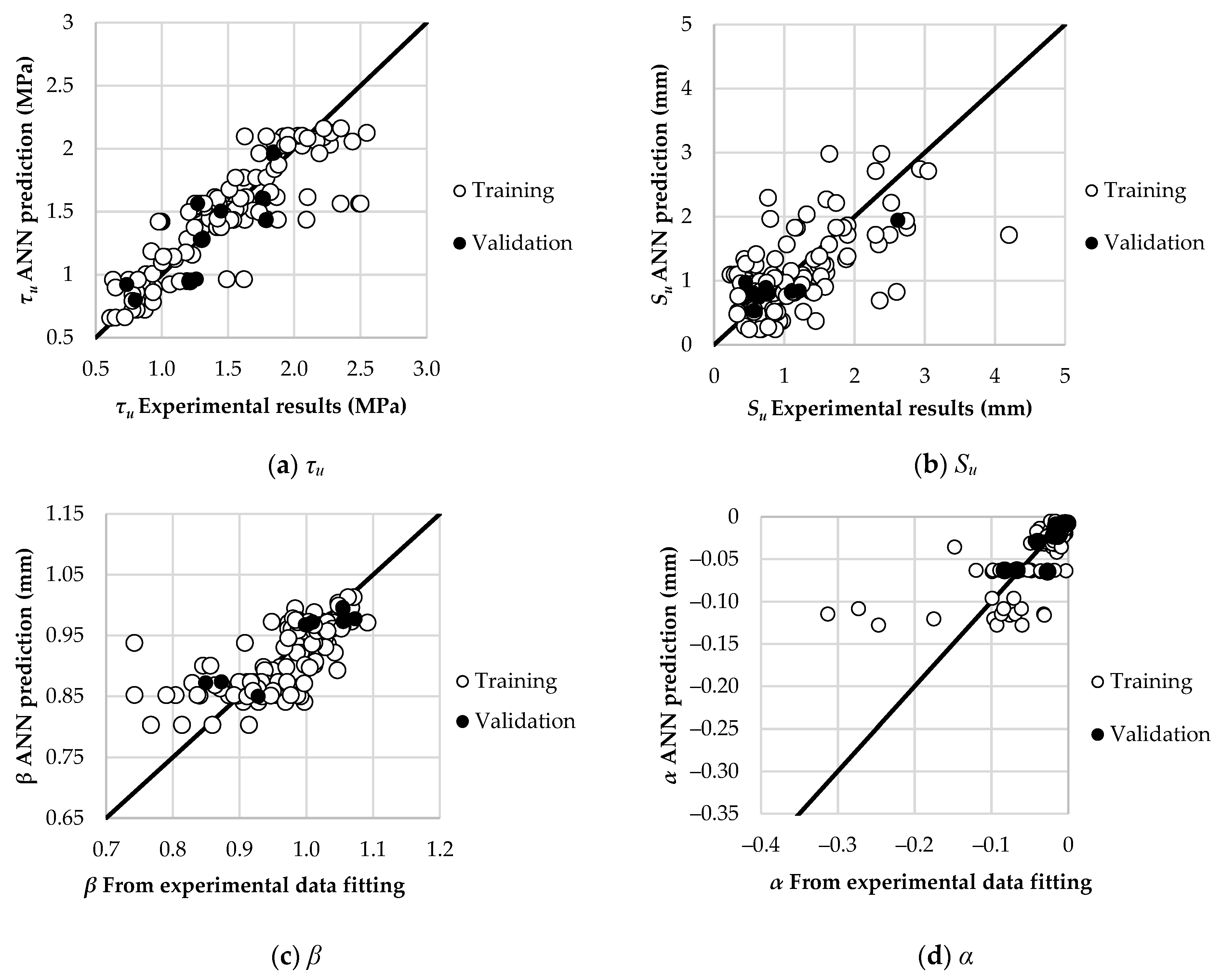
- ANN1 (for circular column): 157 datasets of circular columns are utilized. The datasets are divided into 117 training datasets, 30 testing datasets, and 10 validation datasets. ANN models’ ASEtraining, ASEtesting, ASEtrain-all, and ASEvalidation values are listed in Figure 5a. Based on the values shown in Figure 5a, the optimum number of hidden nodes for ANN1 is found to be 9; because it has the lowest ASEtesting value. Hence, ANN1 is denoted by its architecture as 5-9-4.
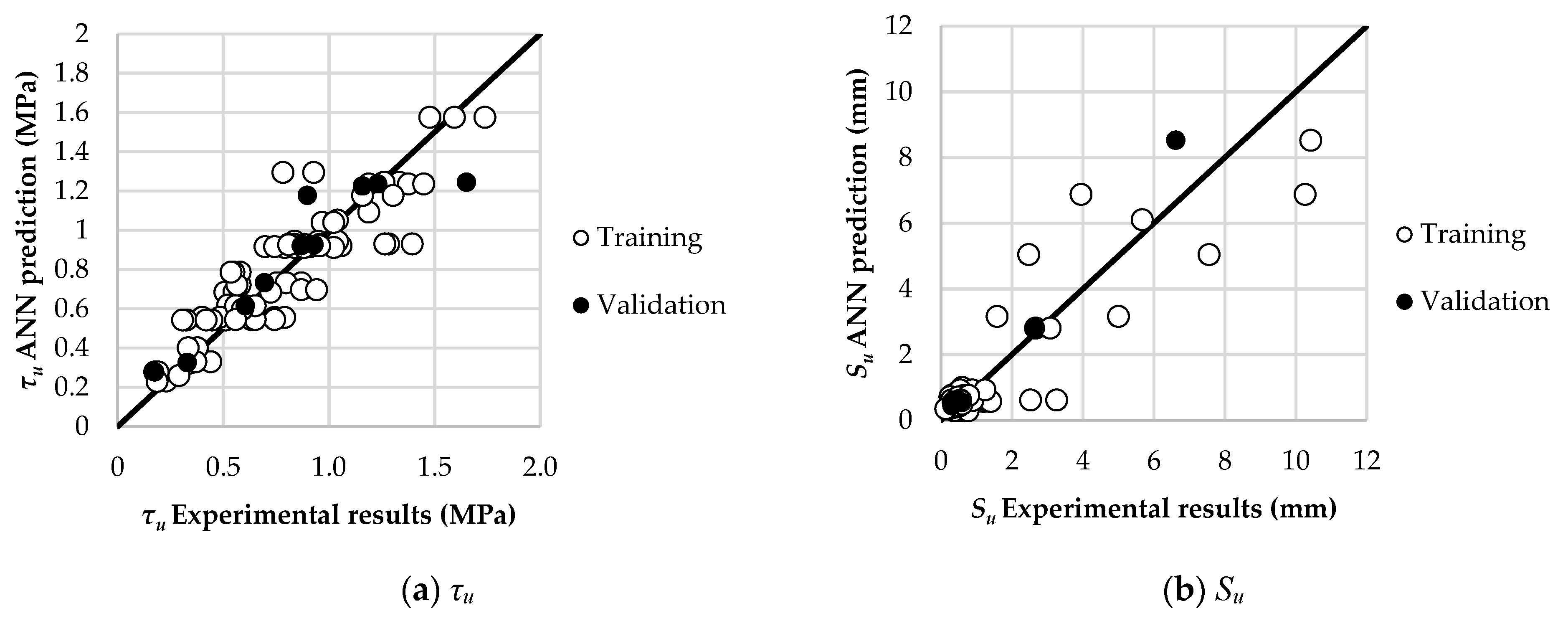
- ANN2 (for square column): 105 datasets of circular columns are utilized. The datasets are divided into 75 training datasets, 20 testing datasets, and 10 validation datasets. As shown in Figure 5b, the optimum number of hidden nodes for ANN2 is found to be 7. So, ANN2 is denoted by its architecture as 5-7-4.
5. Comparison and Discussion of Results
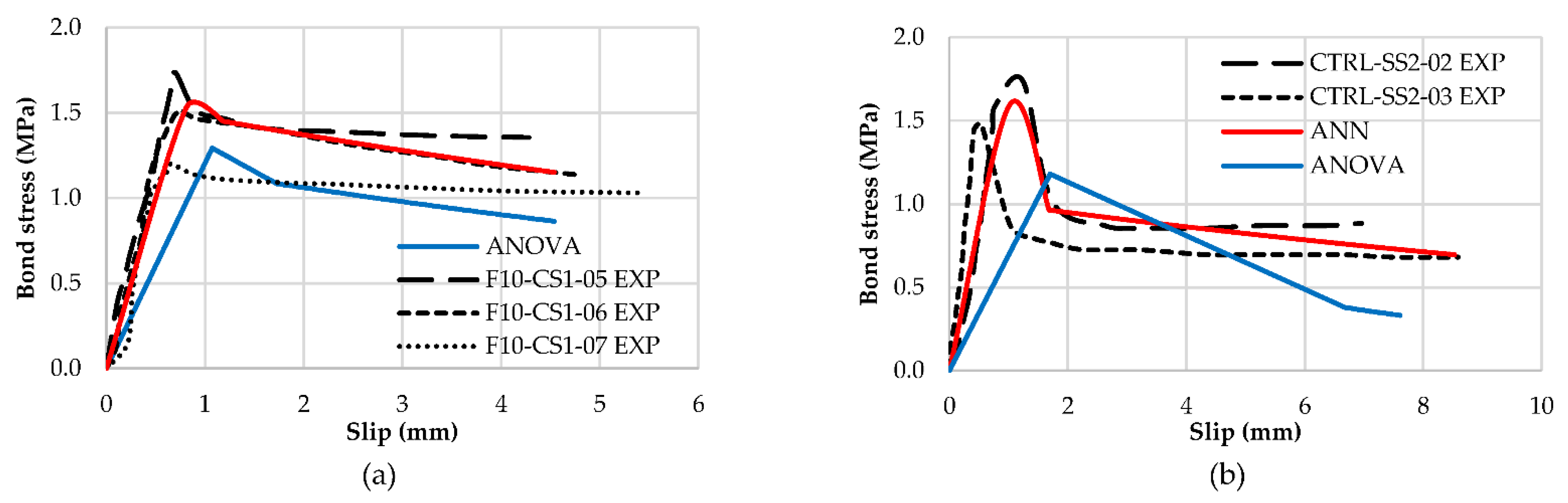
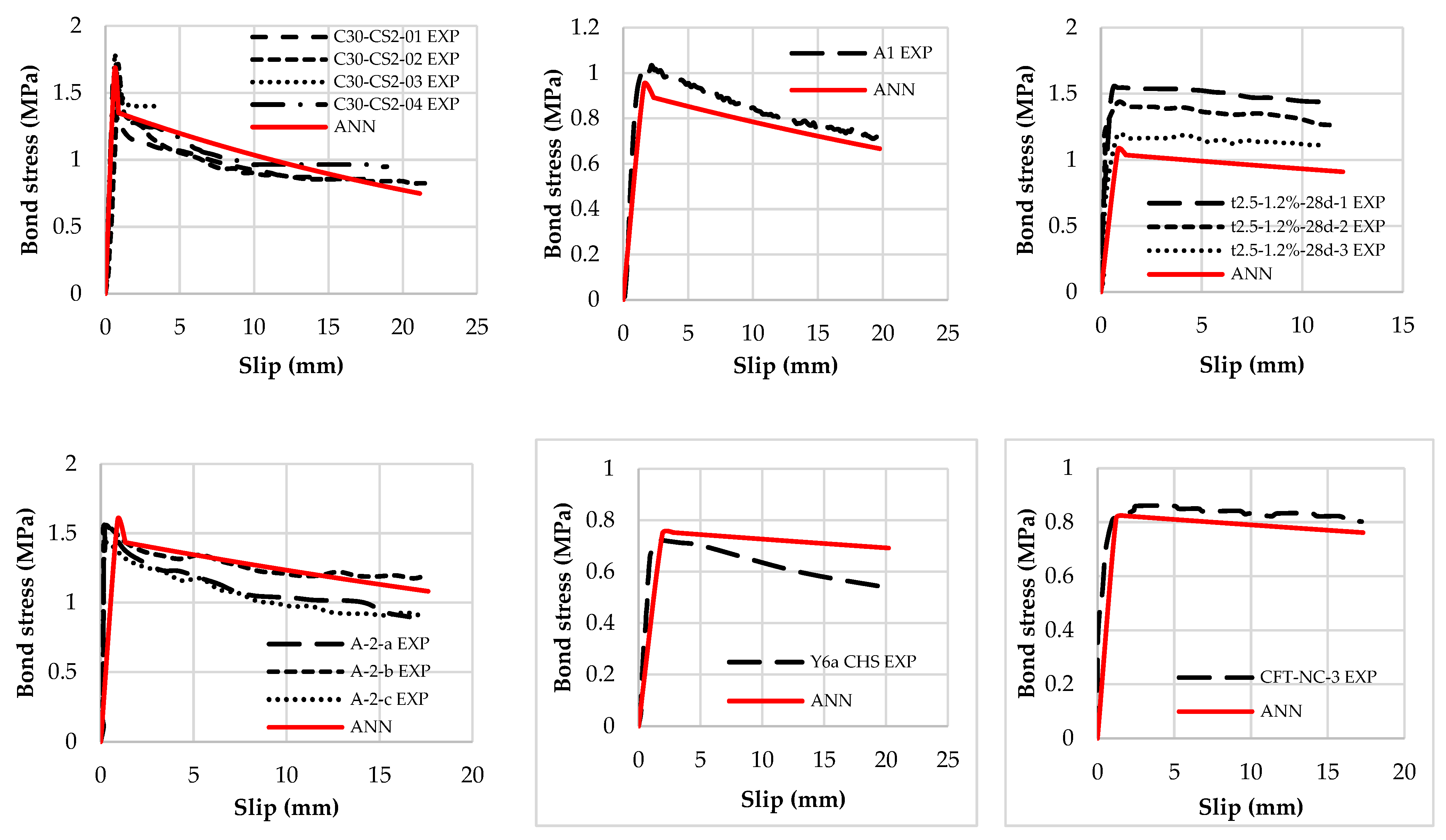
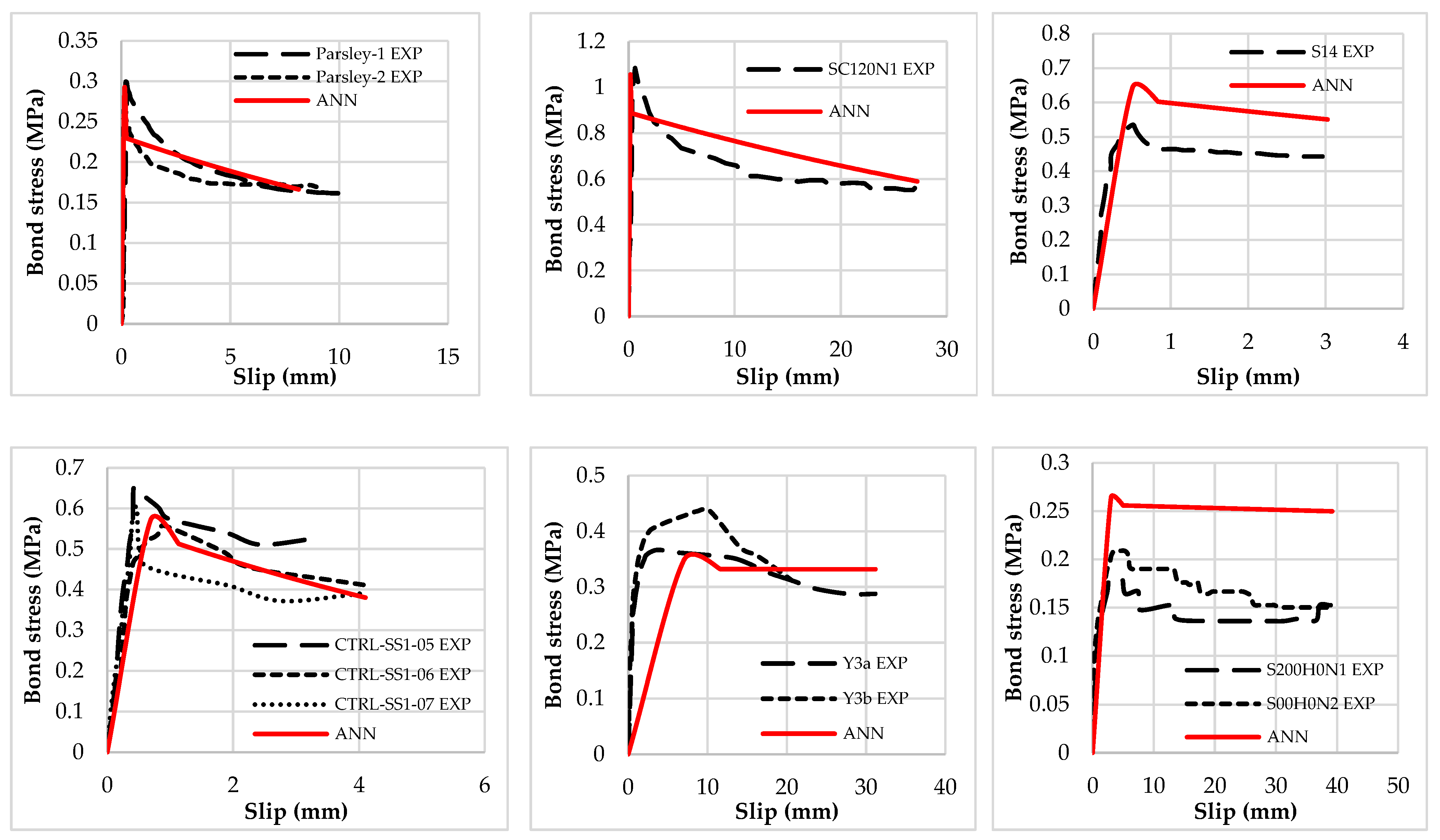
5.1. Comparison of Bond Strength Predicted by ANOVA and ANN with Existing Models
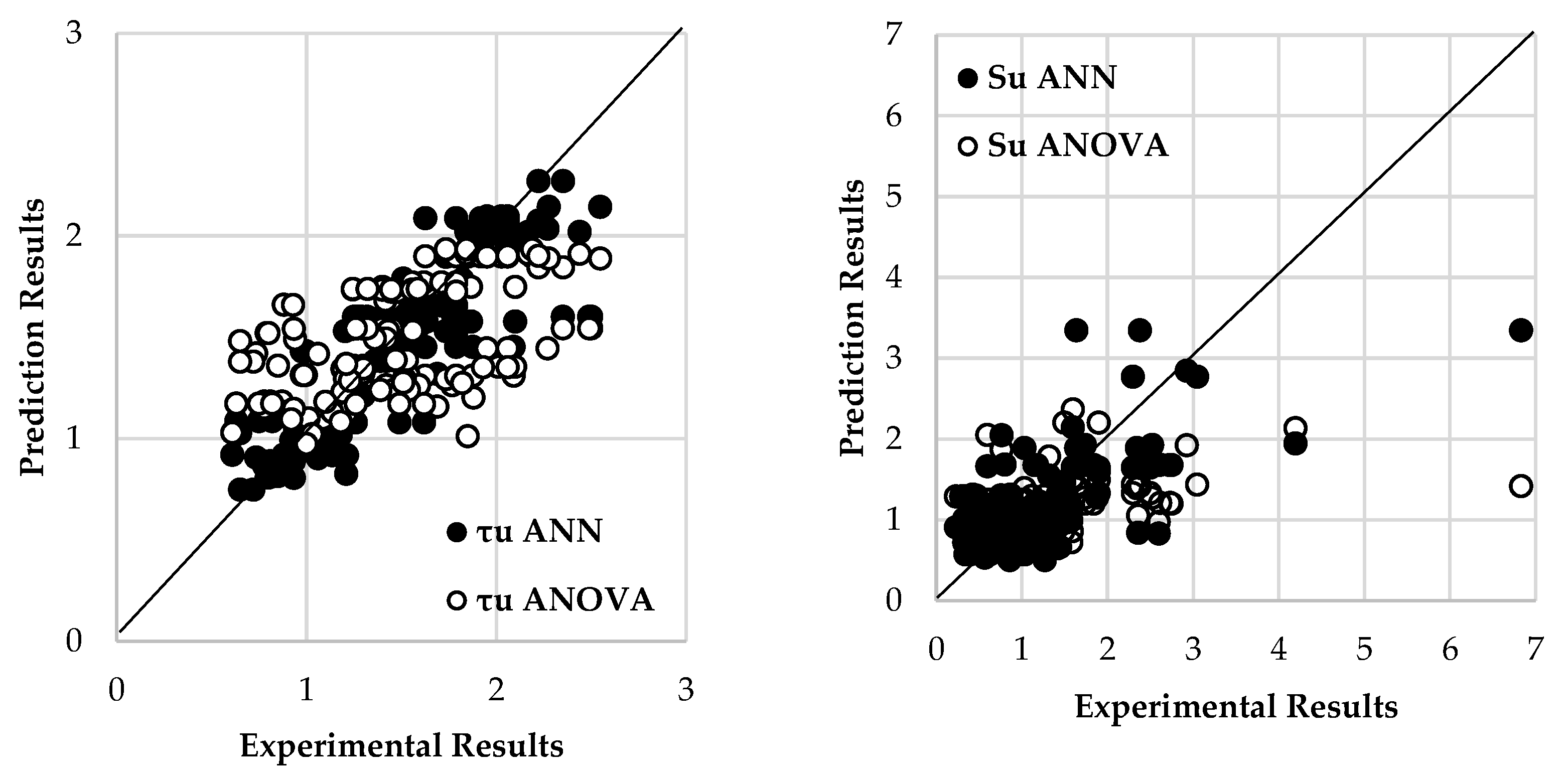
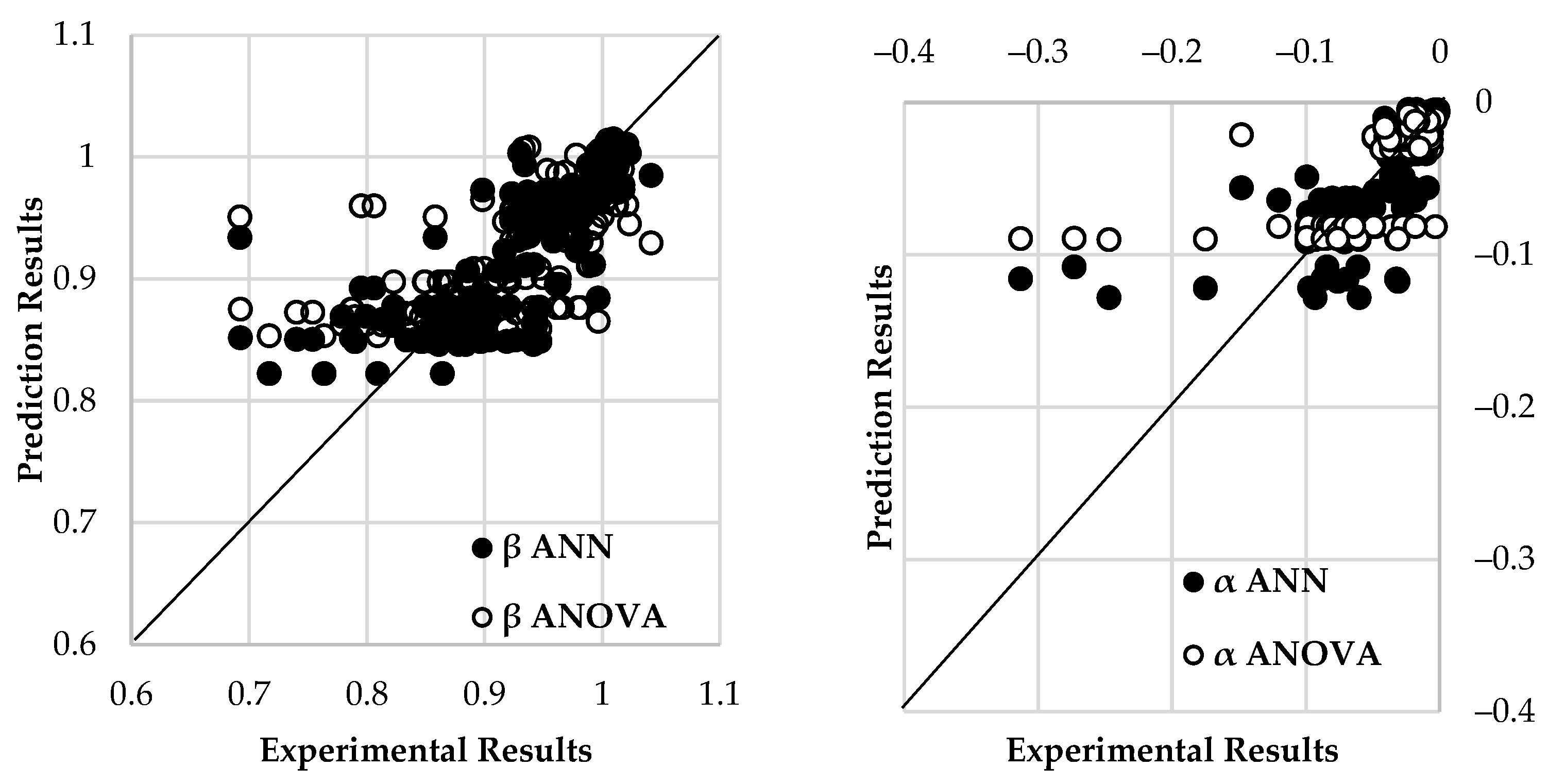
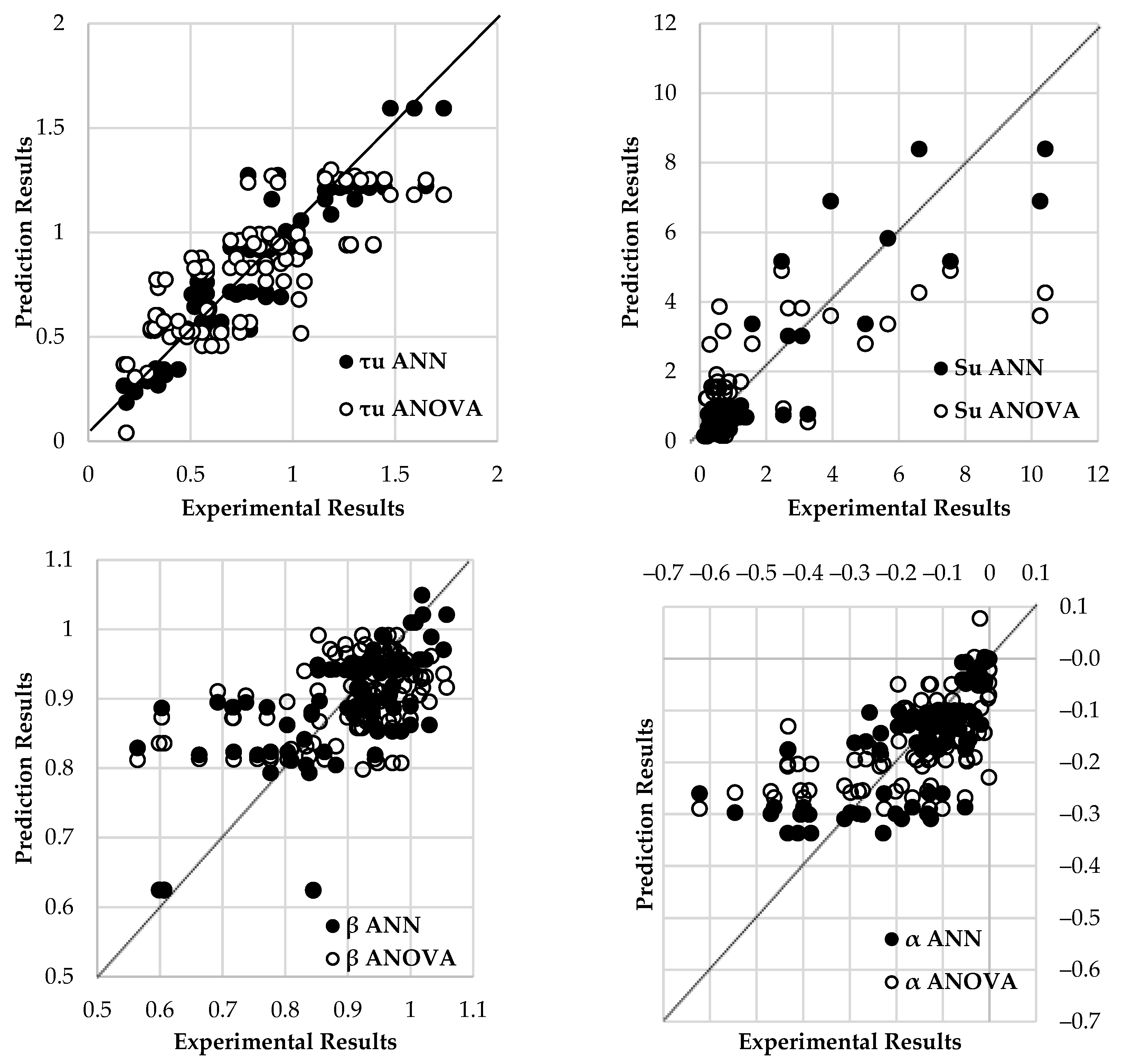
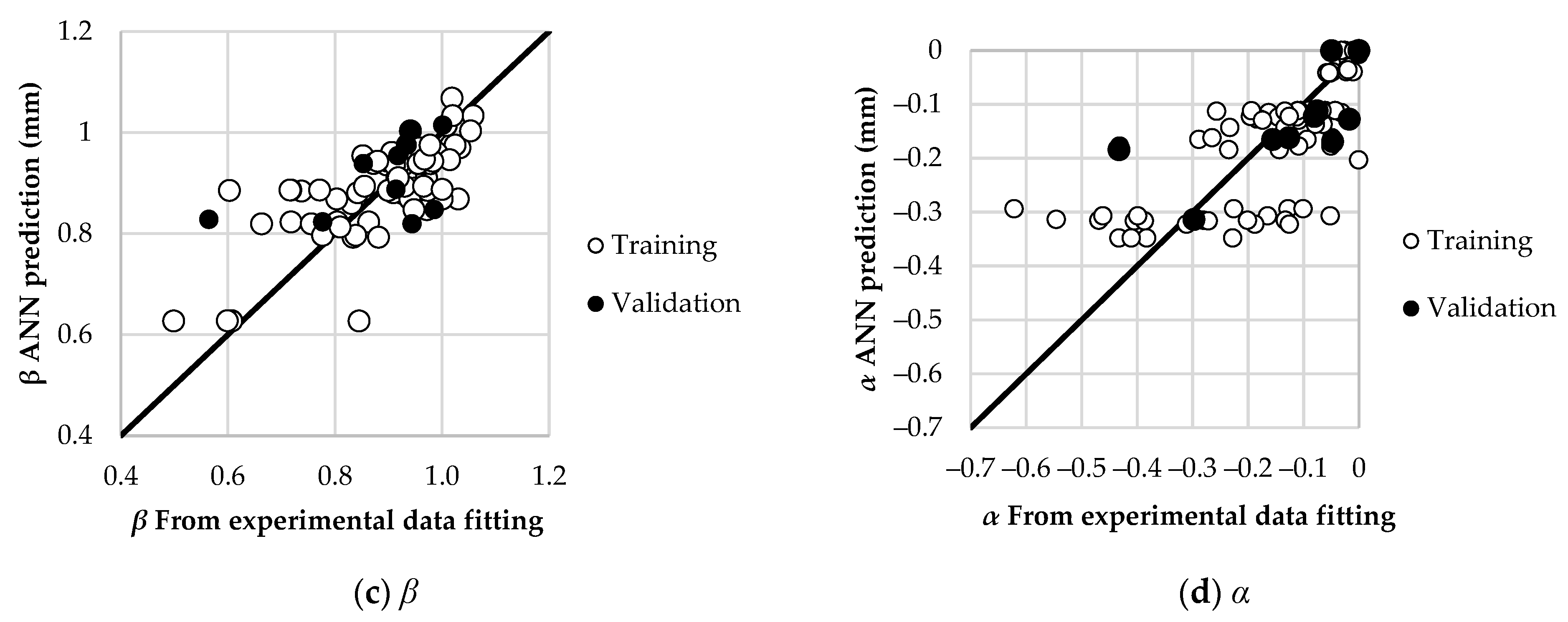
5.2. Comparisons of , , and α Predicted by ANOVA and ANN for Both Circular and Squared CFSTs
6. Finite Element Modeling of CFST’s Columns
6.1. Experimental Data for Calibration
6.2. Finite Element Discretization
6.3. Constitutive Models of Materials
6.4. Tube-Core Interface
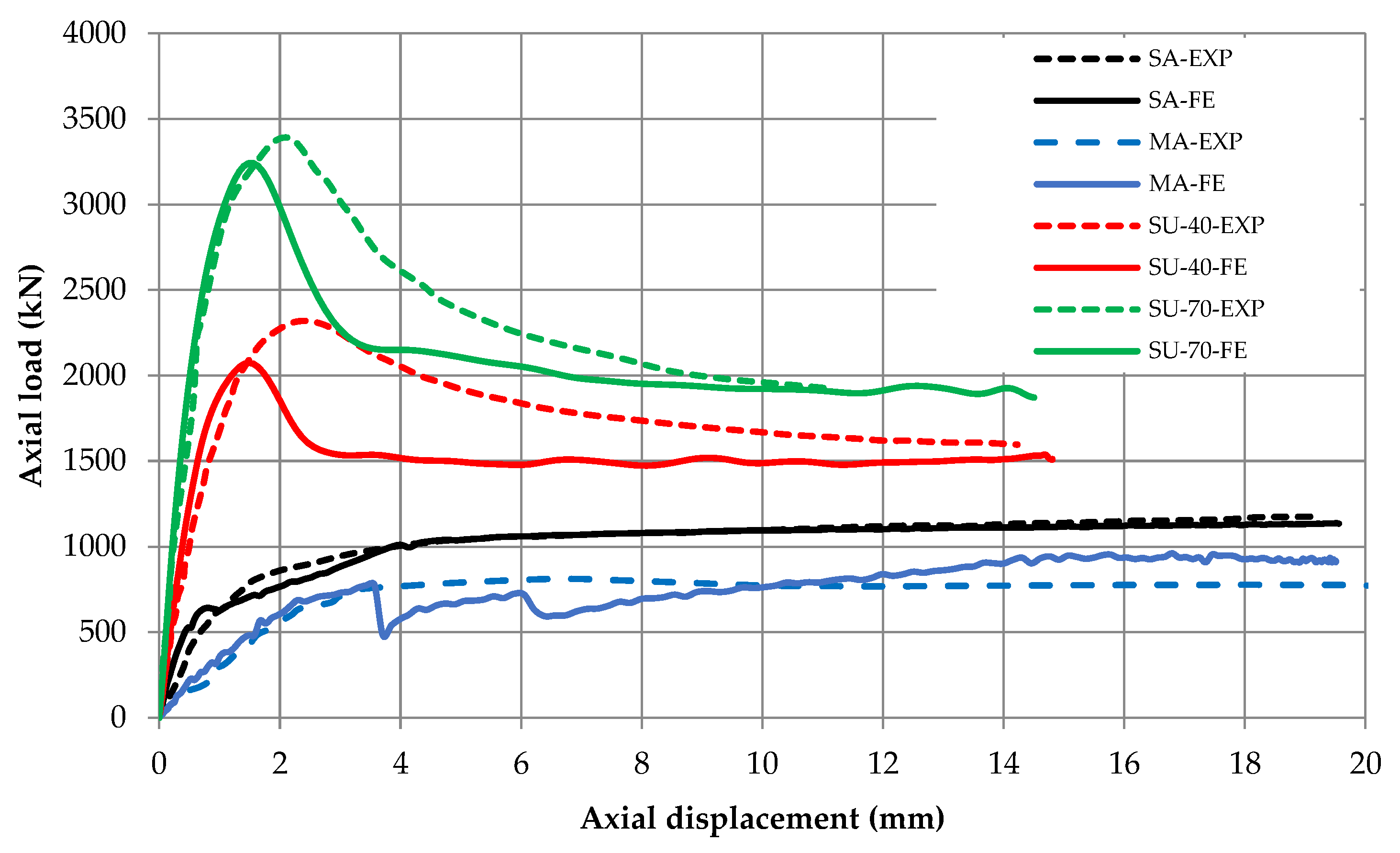
6.5. Finite Element Results
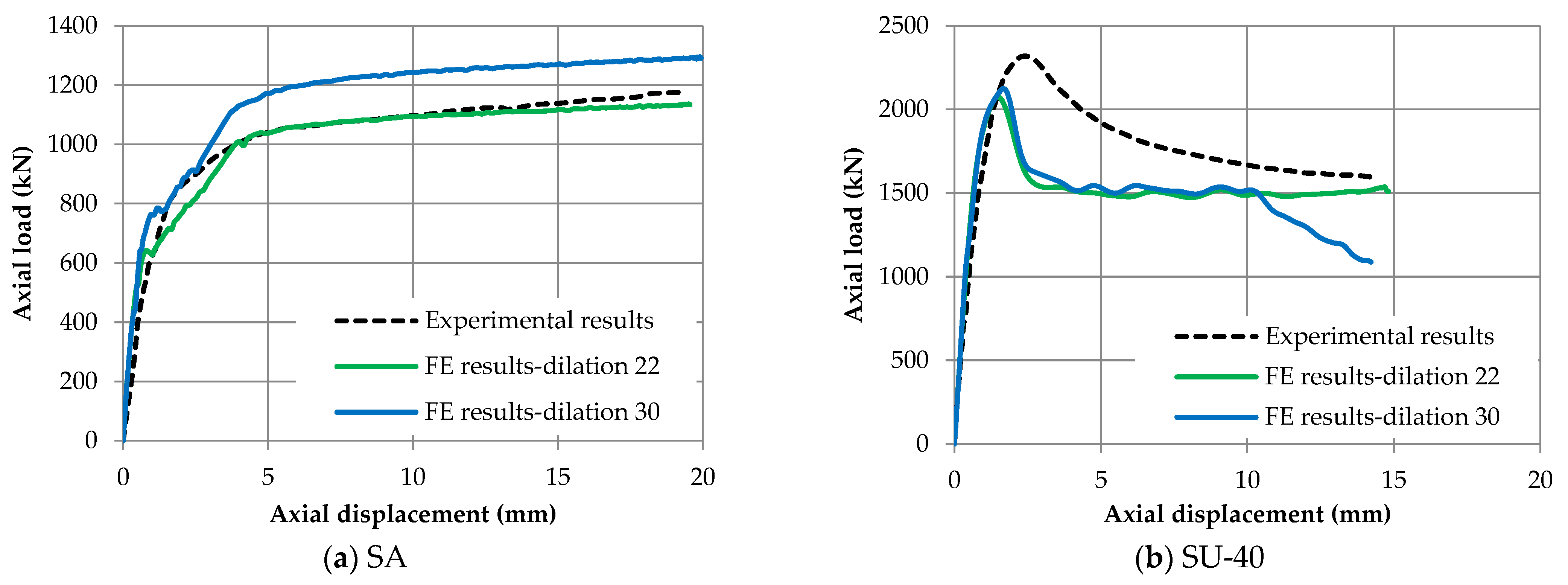
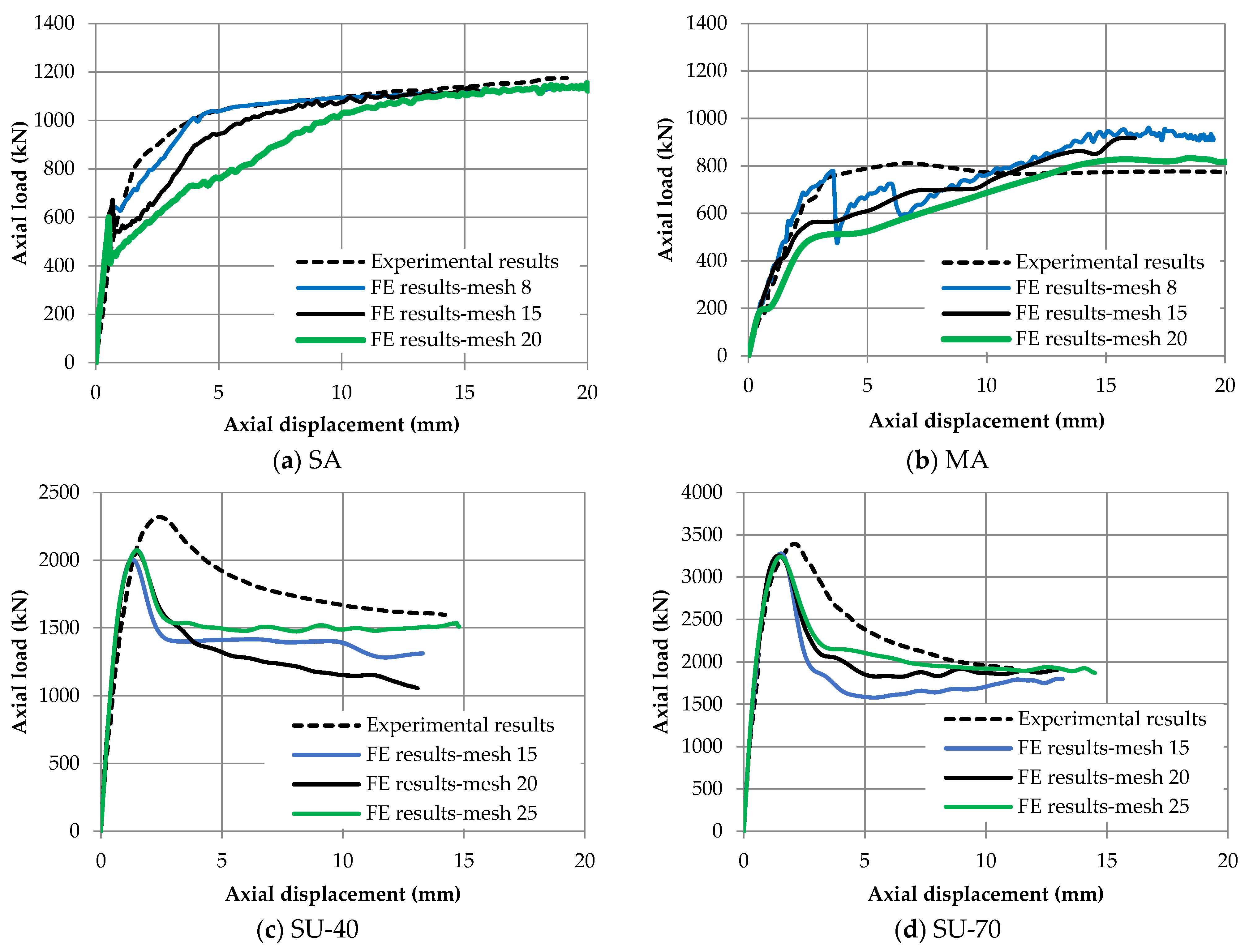
6.6. Sensitivity Analysis
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, F.; Yu, X.; Chen, B. The structural performance of axially loaded CFST columns under various loading conditions. Steel Compos. Struct. 2012, 13, 451–471. [Google Scholar] [CrossRef]
- Virdi, K.S.; Dowling, P.J. Bond Strength in Concrete Filled Circular Steel Tubes; Composite columns. CESLIC Report. CC11; Engineering Structures Laboratories, Civil Engineering Department, Imperial College London: London, UK, 1975. [Google Scholar]
- Morishita, Y. Experimental studies on bond strength in concrete filled square and octagonal steel tubular columns subjected to axial loads. Trans. Jpn. Concr. Inst. 1979, 1, 359–366. [Google Scholar]
- Tomii, M.; Yoshimura, K.; Morishita, Y. A method of improving bond strength between steel tube and concrete core cast in circular steel tubular columns. Trans. Jpn. Concr. Inst. 1980, 2, 319–326. [Google Scholar]
- Shakir-Khalil, H. Pushout strength of concrete-filled steel hollow sections. Struct. Eng. 1993, 71, 230–233. [Google Scholar]
- Shakir-Khalil, H. Resistance of concrete-filled steel tubes to pushoutforces. Struct. Eng. 1993, 71, 234–243. [Google Scholar]
- Roeder, C.W.; Cameron, B.; Brown, C.B. Composite Action in Concrete Filled Tubes. J. Struct. Eng. 1999, 125, 477–484. [Google Scholar] [CrossRef]
- Kilpatrick, A.E.; Rangan, B.V. Influence of interfacial shear transfer on behavior of concrete-filled steel tubular columns. Struct. J. 1999, 96, 642–648. [Google Scholar]
- Han, L.-H.; Yang, Y.-F. Influence of Concrete Compaction on the Behavior of Concrete Filled Steel Tubes with Rectangular Sections. Adv. Struct. Eng. 2001, 4, 93–100. [Google Scholar] [CrossRef]
- Xu, C.; Chengkui, H.; Decheng, J.; Yuancheng, S. Push-out test of pre-stressing concrete filled circular steel tube columns by means of expansive cement. Constr. Build. Mater. 2007, 23, 491–497. [Google Scholar] [CrossRef]
- Aly, T.; Elchalakani, M.; Thayalan, P.; Patnaikuni, I. Incremental collapse threshold for pushout resistance of circular concrete filled steel tubular columns. J. Constr. Steel Res. 2010, 66, 11–18. [Google Scholar] [CrossRef]
- Tao, Z.; Han, L.-H.; Uy, B.; Chen, X. Post-fire bond between the steel tube and concrete in concrete-filled steel tubular columns. J. Constr. Steel Res. 2011, 67, 484–496. [Google Scholar] [CrossRef]
- Qu, X.; Chen, Z.; Nethercot, D.A.; Gardner, L.; Theofanous, M. Load-reversed push-out tests on rectangular CFST columns. J. Constr. Steel Res. 2013, 81, 35–43. [Google Scholar] [CrossRef]
- Tahir, M.M.; Shek, P.N.; Tan, C.S. Push-off tests on pin-connected shear studs with composite steel–concrete beams. Constr. Build. Mater. 2009, 23, 3024–3033. [Google Scholar] [CrossRef]
- Chen, L.; Dai, J.; Jin, Q.; Chen, L.; Liu, X. Refining bond–slip constitutive relationship between checkered steel tube and concrete. Constr. Build. Mater. 2015, 79, 153–164. [Google Scholar] [CrossRef]
- Yan, J.-B.; Liew, J.Y.R.; Sohel, K.M.A.; Zhang, M.H. Push-out tests on J-hook connectors in steel–concrete–steel sandwich structure. Mater. Struct. 2013, 47, 1693–1714. [Google Scholar] [CrossRef]
- Virdi, K.S.; Dowling, P.J. Bond Strength in Concrete Filled Steel Tubes. IABSE Proc. 1980, 4, 125–139. [Google Scholar]
- Parsley, M.A.; Yura, J.A. Push-out behavior of rectangular concrete-filled steel tubes. Spec. Publ. 2000, 196, 87–108. [Google Scholar]
- Chen, Z.H.; Qu, X.S.; Wang, X.D.; Sun, R.R.; Li, L.M. Experimental Study on the Interface bearing capacity on concrete-filled square steel tube. J. Harbin Inst. Technol. 2009, 41, 27–32. [Google Scholar]
- Xue, L.H.; Cai, S.H. Bond strength at the interface of concrete-filled steel tube columns. Build. Sci. 1996, 12, 22–28. [Google Scholar]
- Lyu, W.-Q.; Han, L.-H. Investigation on bond strength between recycled aggregate concrete (RAC) and steel tube in RAC-filled steel tubes. J. Constr. Steel Res. 2019, 155, 438–459. [Google Scholar] [CrossRef]
- Martinelli, E. A general numerical model for simulating the long-term response of two-layer composite systems in partial interaction. Compos. Struct. 2020, 257, 112929. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia Corp. ABAQUS Analysis User’s Manual Online Documentation, Version (6.11); Dassault Systemes Simulia, Inc.: Providence, RI, USA, 2011; Available online: http://130.149.89.49:2080/v6.11/books/usb/default.htm (accessed on 30 March 2022).
- Fu, Z.Q.; Ge, H.B.; Ji, B.H.; Chen, J.J. Interface bond behaviour between circular steel tube and lightweight aggregate concrete. Adv. Steel Constr. 2018, 14, 424–437. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, H.; Raed, S.; Abendeh, M.; Hunaiti, Y.M. Evaluation of concrete–steel interfaces in steel tubes filled with chipped rubber–concrete. Proc. Inst. Civil Eng. Struct. Build. 2020, 1–23. [Google Scholar] [CrossRef]
- Abendeh, R.; Ahmad, H.S.; Hunaiti, Y.M. Experimental studies on the behavior of concrete-filled steel tubes incorporating crumb rubber. J. Constr. Steel Res. 2016, 122, 251–260. [Google Scholar] [CrossRef]
- Ke, X.; Sun, H.; Yang, Z. Calculation on bond strength of high-strength concrete filled steel tube. In 2015 4th International Conference on Sensors, Measurement and Intelligent Materials; Atlantis Press: Shenzhen, China, 2016; pp. 995–999. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Liu, Z.; Li, S.; Tang, W. Bond behavior of steel-fiber-reinforced self-stressing and self-compacting concrete-filled steel tube columns for a period of 2.5 years. Constr. Build. Mater. 2018, 167, 33–43. [Google Scholar] [CrossRef]
- Lv, J.; Zhou, T.; Du, Q.; Li, K.; Jin, L. Research on the Bond Behavior of Preplaced Aggregate Concrete-Filled Steel Tube Columns. Materials 2020, 13, 300. [Google Scholar] [CrossRef] [Green Version]
- Tao, Z.; Song, T.-Y.; Uy, B.; Han, L.-H. Bond behavior in concrete-filled steel tubes. J. Constr. Steel Res. 2016, 120, 81–93. [Google Scholar] [CrossRef]
- Zou, W.; Liang, J.; Zhang, G.; Yang, H. Bond Properties of RAC-Filled Square Steel Tubes after High Temperature. Adv. Mater. Sci. Eng. 2019, 2019, 2413613. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, R.A.; Slade, S.V.; Eperjesi, F. An introduction to analysis of variance (ANOVA) with special reference to data from clinical experiments in optometry. Ophthalmic Physiol. Opt. 2000, 20, 235–241. [Google Scholar] [CrossRef]
- Armstrong, R.A.; Eperjesi, F.; Gilmartin, B. The application of analysis of variance (ANOVA) to different experimental designs in optometry. Ophthalmic Physiol. Opt. 2002, 22, 248–256. [Google Scholar] [CrossRef] [Green Version]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- El Tabach, E.; Lancelot, L.; Shahrour, I.; Najjar, Y. Use of artificial neural network simulation metamodelling to assess groundwater contamination in a road project. Math. Comput. Model. 2007, 45, 766–776. [Google Scholar] [CrossRef]
- Javed, M.F.; Farooq, F.; Memon, S.A.; Akbar, A.; Khan, M.A.; Aslam, F.; Alyousef, R.; Alabduljabbar, H.; Rehman, S.K.U.; Rehman, S.K.U.; et al. New Prediction Model for the Ultimate Axial Capacity of Concrete-Filled Steel Tubes: An Evolutionary Approach. Crystals 2020, 10, 741. [Google Scholar] [CrossRef]
- Manasrah, A.; Masoud, M.; Jaradat, Y.; Bevilacqua, P. Investigation of a Real-Time Dynamic Model for a PV Cooling System. Energies 2022, 15, 1836. [Google Scholar] [CrossRef]
- Ilyas, I.; Zafar, A.; Javed, M.F.; Farooq, F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Forecasting Strength of CFRP Confined Concrete Using Multi Expression Programming. Materials 2021, 14, 7134. [Google Scholar] [CrossRef]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Basarir, H.; Elchalakani, M.; Karrech, A. The prediction of ultimate pure bending moment of concrete-filled steel tubes by adaptive neuro-fuzzy inference system (ANFIS). Neural Comput. Appl. 2019, 31, 1239–1252. [Google Scholar] [CrossRef]
- Tran, V.-L.; Thai, D.-K.; Nguyen, D.-D. Practical artificial neural network tool for predicting the axial compression capacity of circular concrete-filled steel tube columns with ultra-high-strength concrete. Thin-Walled Struct. 2020, 151, 106720. [Google Scholar] [CrossRef]
- Moradi, M.; Daneshvar, K.; Ghazi-Nader, D.; Hajiloo, H. The prediction of fire performance of concrete-filled steel tubes (CFST) using artificial neural network. Thin-Walled Struct. 2021, 161, 107499. [Google Scholar] [CrossRef]
- Najjar, Y.M. Quick manual for TR-SEQ1; Dept. of Civil Engineering, Kansas State University: Manhattan, KS, USA, 1999. [Google Scholar]
- Abu-Shamah, A.; Allouzi, R. Numerical investigation on the response of circular double-skin concrete-filled steel tubular slender columns subjected to biaxial bending. Steel Compos. Struct. Int. J. 2020, 37, 533–549. [Google Scholar] [CrossRef]
- Han, L.-H.; Yao, G.-H.; Tao, Z. Performance of concrete-filled thin-walled steel tubes under pure torsion. Thin-Walled Struct. 2007, 45, 24–36. [Google Scholar] [CrossRef]
- Effendi, M.K. The Effect of Concrete-Steel Interface Model on Finite Element Analysis of Concrete Filled Square Steel Tube Beam. Civ. Eng. J. 2020, 29, 135–146. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Hong, W.-K.; Ko, H.-J.; Kim, S.-K. Finite element model for the interface between steel and concrete of CFST (concrete-filled steel tube). Eng. Struct. 2019, 185, 141–158. [Google Scholar] [CrossRef]
- Alatshan, F.; Mashiri, F.R. Finite element modeling of concrete-filled steel tubes: Review and recent developments. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Baech, Switzerland, 2013; Volume 330, pp. 894–899. [Google Scholar] [CrossRef]
- Huang, C.S.; Yeh, Y.-K.; Liu, G.-Y.; Hu, H.-T.; Tsai, K.C.; Weng, Y.T.; Wang, S.H.; Wu, M.-H. Axial Load Behavior of Stiffened Concrete-Filled Steel Columns. J. Struct. Eng. 2002, 128, 1222–1230. [Google Scholar] [CrossRef] [Green Version]
- Tsai, W.T. Uniaxial Compressional Stress-Strain Relation of Concrete. J. Struct. Eng. 1988, 114, 2133–2136. [Google Scholar] [CrossRef]
- Popovics, S. A review of stress-strain relationships for concrete. J. Proc. 1970, 67, 243–248. [Google Scholar]
- Chang, G.A.; Mander, J.B. Seismic Energy Based Fatigue Damage Analysis of Bridge Columns: Part 1–Evaluation of Seismic Capacity; NCEER Technical Rep. No. NCEER-94-0006; University of Buffalo, The State University of New York: Buffalo, NY, USA, 1994. [Google Scholar]
- Li, X.-X.; Wang, C.; Sato, J. Framework for dynamic analysis of radioactive material transport packages under accident drop conditions. Nucl. Eng. Des. 2019, 360, 110480. [Google Scholar] [CrossRef]
| Shape | Output | ANN Results | ANOVA Results | ||||
|---|---|---|---|---|---|---|---|
| Mean Value, μ | Standard Deviation, σ | R2 | Mean Value, μ | Standard Deviation, σ | R2 | ||
| Circular | (MPa) | 0.999 | 0.166 | 0.876 | 1.001 | 0.277 | 0.328 |
| Su (mm) | 1.023 | 0.462 | 0.674 | 1.006 | 0.611 | 0.140 | |
| β | 1.000 | 0.052 | 0.742 | 1.000 | 0.062 | 0.394 | |
| α | 1.090 | 0.713 | 0.695 | 0.935 | 0.945 | 0.409 | |
| Square | (MPa) | 1.004 | 0.188 | 0.837 | 1.067 | 0.596 | 0.623 |
| Su (mm) | 1.160 | 0.658 | 0.809 | 0.338 | 2.932 | 0.442 | |
| β | 1.000 | 0.096 | 0.570 | 1.000 | 0.117 | 0.231 | |
| α | 1.175 | 0.985 | 0.548 | 0.907 | 1.922 | 0.358 | |
| Limit | fcu (MPa) | Age (days) | Li (mm) | T (mm) | B (mm) | D (mm) | α | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ANN1 | Max | 96.43 | 365 | 1095 | 6 | - | 219 | 2.55 | 6.83 | 1.04 | −1 × 10−3 |
| Min | 9.11 | 28 | 190 | 2.5 | - | 107.7 | 0.61 | 0.23 | 0.69 | −0.31 | |
| ANNmax | 120 | 450 | 1300 | 7 | - | 250 | 3 | 8 | 1.1 | 0 | |
| ANNmin | 0 | 0 | 0 | 1.5 | - | 75 | 0 | 0 | 0.6 | −0.35 | |
| ANN2 | Max | 58.31 | 365 | 1498.6 | 6.6 | 254 | - | 1.74 | 10.42 | 1.06 | −4 × 10−4 |
| Min | 9.11 | 28 | 190 | 3 | 90.85 | - | 0.17 | 0.13 | 0.5 | −0.62 | |
| ANNmax | 70 | 450 | 1750 | 7.5 | 310 | - | 2 | 12.5 | 1.25 | 0 | |
| ANNmin | 0 | 0 | 0 | 1.75 | 30 | - | 0 | 0 | 0.3 | −0.75 |
| Inputj | Connection Links Weights between Inputs and Hidden Nodes (Inputj–HNiConnection) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HN1 | HN2 | HN3 | HN4 | HN5 | HN6 | HN7 | HN8 | HN9 | ||
| Input1 D(mm) | −11.17 | −18.56 | −20.95 | −11.36 | −8.69 | −11.29 | −2.26 | −3.64 | −2.72 | |
| Input2 T(mm) | 11.47 | 0.96 | 30.81 | −8.25 | −18.52 | −7.72 | −4.56 | 5.32 | 1.46 | |
| Input3 Li(mm) | −6.08 | −15.98 | 0.44 | −5.25 | −4.93 | −12.12 | −4.70 | −2.71 | 0.74 | |
| Input4 fcu(MPa) | −15.35 | −15.39 | 1.55 | −3.66 | 20.37 | 1.73 | 1.55 | −5.55 | 0.90 | |
| Input5 A(days) | −16.51 | −0.93 | −6.22 | 9.25 | −0.62 | −6.42 | −2.36 | −3.37 | −3.67 | |
| Bias1 | 5.26 | 11.98 | −8.71 | 4.71 | 7.26 | 6.24 | 2.34 | −0.84 | −0.69 | |
| Outputm | Connection Links Weights between Hidden Nodes and Outputs (HNi–OutputmConnection) | |||||||||
| HN1 | HN2 | HN3 | HN4 | HN5 | HN6 | HN7 | HN8 | HN9 | Bias2 | |
| Output1 τu(MPa) | 4.28 | −2.75 | −3.64 | 1.46 | 0.65 | 6.97 | −6.84 | 2.22 | 0.36 | 0.72 |
| Output2 Su (mm) | −5.90 | −0.84 | 7.19 | 3.65 | 3.37 | 2.21 | −0.46 | 5.25 | 1.49 | −5.70 |
| Output3 | −3.21 | 0.31 | 4.45 | −0.11 | 1.36 | 2.51 | 0.19 | −1.23 | −3.11 | 0.20 |
| Output4 α | −5.13 | 3.49 | 3.70 | −5.49 | 1.50 | 0.01 | −1.90 | −0.06 | −0.06 | 2.44 |
| Inputj | Connection Links Weights between Inputs and Hidden Nodes (Inputj–HNiConnection) | |||||||
|---|---|---|---|---|---|---|---|---|
| HN1 | HN2 | HN3 | HN4 | HN5 | HN6 | HN7 | ||
| Input1 B(mm) | 3.49 | −24.58 | 5.49 | −7.53 | −2.29 | −1.42 | −0.37 | |
| Input2 T(mm) | −11.94 | 10.40 | −7.95 | 0.68 | 1.88 | −2.02 | −2.41 | |
| Input3 Li(mm) | 10.68 | 2.55 | 14.40 | −0.92 | −1.03 | −1.43 | −1.16 | |
| Input4 fcu(MPa) | 19.57 | 9.37 | −0.57 | 8.37 | −2.67 | −6.08 | 0.00 | |
| Input5 A(days) | 20.11 | −6.96 | 14.91 | 0.27 | 5.37 | −4.21 | −0.42 | |
| Bias1 | −11.30 | −5.28 | −4.33 | −2.57 | −1.66 | 1.15 | −0.39 | |
| Outputm | Connection Links Weights between Hidden Nodes and Outputs (HNi–OutputmConnection) | |||||||
| H1 | H2 | H3 | H4 | H5 | H6 | H7 | Bias2 | |
| Output1 τu(N/mm2) | −4.20 | 4.89 | 1.95 | 2.85 | 1.65 | −0.75 | −1.34 | −0.19 |
| Output2 Su(mm) | 5.75 | 8.42 | −6.37 | −0.78 | 1.96 | 0.86 | −0.81 | −3.70 |
| Output3 | 1.39 | −7.36 | −1.31 | 0.30 | 0.50 | 1.96 | 1.40 | 0.05 |
| Output4 α | 12.72 | 16.91 | −9.67 | −1.06 | −1.81 | 4.44 | 0.07 | 0.41 |
| Model | 5-9-4 ANN1 (Circular Column Model) | 5-7-4 ANN2 (Square Column Model) |
|---|---|---|
| ASEtraining | 0.00724 | 0.007836 |
| ASEtesting | 0.006465 | 0.01313 |
| ASEtrain-all | 0.007167 | 0.006721 |
| ASEvalidation | 0.007048 | 0.007940 |
| MAREtraining | 33. 648 | 41.586 |
| MAREtesting | 33.177 | 44.317 |
| MAREtrain-all | 33. 229 | 39.400 |
| MAREvalidation | 33.064 | 42.304 |
| R2training | 0.67767 | 0.59295 |
| R2testing | 0.54837 | 0.44174 |
| R2train-all | 0.74671 | 0.691078 |
| R2validation | 0.75730 | 0.631577 |
| References | Prediction Model | Mean Value, μ | Standard Deviation, σ |
|---|---|---|---|
| Circular CFST | |||
| Roeder et al. [7] | 1.197 | 0.524 | |
| Xue and Cai [20] | 4.316 | 1.809 | |
| Lyu and Han [21] | 1.212 | 0.549 | |
| Chen et al. [19] | 2.487 | 1.414 | |
| Proposed ANOVA | 1.001 | 0.277 | |
| Proposed ANN | 0.999 | 0.1660 | |
| Squared CFST | |||
| Parsley et al. [18] | 1.417 | 0.679 | |
| Lyu and Han [21] | 2.019 | 0.937 | |
| Xue and Cai [20] | 2.544 | 1.255 | |
| Proposed ANOVA | 1.067 | 0.596 | |
| Proposed ANN | 1.004 | 0.188 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allouzi, R.A.; Almasaeid, H.H.; Salman, D.G.; Abendeh, R.M.; Rabayah, H.S. Prediction of Bond-Slip Behavior of Circular/Squared Concrete-Filled Steel Tubes. Buildings 2022, 12, 456. https://doi.org/10.3390/buildings12040456
Allouzi RA, Almasaeid HH, Salman DG, Abendeh RM, Rabayah HS. Prediction of Bond-Slip Behavior of Circular/Squared Concrete-Filled Steel Tubes. Buildings. 2022; 12(4):456. https://doi.org/10.3390/buildings12040456
Chicago/Turabian StyleAllouzi, Rabab A., Hatem H. Almasaeid, Donia G. Salman, Raed M. Abendeh, and Hesham S. Rabayah. 2022. "Prediction of Bond-Slip Behavior of Circular/Squared Concrete-Filled Steel Tubes" Buildings 12, no. 4: 456. https://doi.org/10.3390/buildings12040456
APA StyleAllouzi, R. A., Almasaeid, H. H., Salman, D. G., Abendeh, R. M., & Rabayah, H. S. (2022). Prediction of Bond-Slip Behavior of Circular/Squared Concrete-Filled Steel Tubes. Buildings, 12(4), 456. https://doi.org/10.3390/buildings12040456








