The Magnetocaloric Properties and Critical Behavior of (Gd₄Co₃)_100−xGe_x Rapidly Quenched Alloys

Abstract

Gd₄Co₃ is a promising magnetocaloric material with a high magnetic entropy value. However, it undergoes a first-order magnetic transition, which hinders practical applications. Hence, (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) were studied to obtain high magnetic entropy values and a second-order magnetic transition. To investigate the effects of Ge addition on the thermal stability, magnetocaloric properties, and critical behavior of Gd₄Co₃-based alloys, (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) melt spun ribbons were prepared. Phase analysis showed these alloys are mainly amorphous, with a minority nanocrystalline phase. All alloys undergo a second-order ferromagnetic-to-paramagnetic transition. The Curie temperature (T_C) increases linearly from 211 K (x = 5) to 217 K (x = 15) with increasing Ge content. Under a magnetic field variation of 5 T, the alloys with x = 5, 10, and 15 exhibit peak magnetic entropy change (−ΔS_M) values of 7.15, 6.83, and 6.71 J/(kg·K), respectively, along with considerable refrigerant capacity (RC) in the range of 435–458 J/kg. These excellent magnetocaloric properties collectively demonstrate their great potential for magnetic refrigeration applications. Critical behavior analysis revealed critical exponents broadly consistent with mean-field theory (MFT, β = 0.5, γ = 1.0, δ = 3.0), indicating nanocrystals in the amorphous matrix induce long-range magnetic interactions.

1. Introduction

Driven by the demand for high energy efficiency and environmental protection, magnetic refrigeration (MR), with the magnetocaloric effect (MCE) as its core principle, has demonstrated great potential to replace conventional gas-compression refrigeration [1,2,3,4,5,6]. Since the discovery of the giant MCE in Gd₅Si₂Ge₂ [7], extensive efforts have been dedicated to investigating magnetocaloric materials (MCMs) with large or giant MCEs. However, MCMs associated with first-order magnetic transition (FOMT)—such as GdSiGe [7,8,9], MnAsSb [10], MnFePX(X = As, Si) [11,12], and NiMnX (X = Ga, In, Sn)-based Heusler alloys [13,14,15,16,17]—exhibit a giant magnetic entropy change (−ΔS_M) only over a narrow temperature range. Furthermore, significant thermal and magnetic hysteresis losses are commonly encountered in such FOMT alloys, leading to increased energy consumption and thereby impeding their practical application in refrigerator design [4].

For second-order magnetic transition (SOMT) magnetocaloric materials, the curves of (−ΔS_M) versus temperature (T) exhibit a peak around the transition point and a typical gentle “λ” shape. This λ-shaped profile broadens the transition temperature range, thereby contributing to a large refrigeration capacity (RC). As SOMT materials, amorphous alloys possess several superior properties compared to their crystalline counterparts, including unusually high electrical resistivity, low eddy current losses, high thermal conductivity, excellent corrosion resistance, and tunable magnetic ordering temperature. Additionally, they exhibit negligible thermal and magnetic hysteresis losses, which are favorable characteristics for magnetic cooling [18]. Although amorphous alloys typically show a smaller peak value of (−ΔS_M), their broader (−ΔS_M) peak width effectively enhances RC. These advantages make amorphous alloys—especially Gd-based amorphous alloys such as Gd₆₅Mn_35−xGe_x [19], Gd₆₀Co₃₀Al₁₀ [20], Gd₆₀Co_40−xMn_x [21], Gd₅₅Co₃₅M₁₀ (M = Mn, Fe and Ni) [22], (Gd₆₀Al₂₀Co₂₀)_100−xNi_x (x = 0, 1, 3, 5, 7, in at%) [23], and RE₂Co (RE = Gd, Ho) [24]—promising candidates for magnetic cooling applications.

Recently, Gd-Co-based amorphous alloys with good glass-forming ability (GFA) have received considerable attention. Gd-Co compounds exhibit strong magnetic exchange coupling, which arises from Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions between Gd atoms via conduction electrons [25]. For binary Gd-Co glassy ribbons, an increase in Co content relative to Gd leads to a higher Curie temperature (T_C), but at the cost of a decreased magnetic entropy change (−ΔS_M) [26].

With respect to the crystalline Gd₄Co₃ alloy, earlier studies have revealed two successive magnetic entropy changes. The first change is brought about by a spin-reorientation transition (SRT) at T_SR = 163 K, and the second by a transition from ferrimagnetic (FI) to paramagnetic (PM) at T_C = 220 K [27,28]. This double-peak feature in the (−ΔS_M) − T curve—attributed to the successive occurrence of T_SR and T_C—gives rise to an extraordinarily broad temperature range and a significant combined magnetocaloric effect (MCE) [28].

Zhang et al. [29] recently reported that, for the amorphous Gd₄Co₃ alloy under a magnetic field change of ΔH = 5 T, the Curie temperature (T_C) and the maximum magnetic entropy change (−ΔS_M)^max correspond to 208 K and 7.2 J/(kg·K), respectively. Previous reports [30,31] have shown that alloying with B or Si induces a ferromagnetic (FM) to PM transition at the T_C. For (Gd₄Co₃)_100−xB_x (x = 0, 5, 10, 15) amorphous alloys, increasing B content decreases T_C from 215 K to 197 K, while (−ΔS_M)^max increases from 6.7 J/(kg·K) to 7.8 J/(kg·K) (ΔH = 5 T) [30]. In contrast, for (Gd₄Co₃)_100−xSi_x glassy ribbons, Si addition initially lowers T_C (to 198 K at x = 0.05) but subsequently increases it substantially (to 213 K at x = 0.1). Under ΔH = 5 T, the (−ΔS_M)^max values for x = 0, 0.05, and 0.10 are 7.3, 7.2, and 6.4 J/(kg·K), respectively [31].

Notably, Si and Ge belong to the same group (Group 14) in the periodic table. As a Group 14 element, germanium (Ge) shares the same valence electron configuration (ns²np²) with silicon (Si)—a well-documented dopant in Gd-based magnetocaloric materials (MCMs). However, Ge has a larger atomic radius (122 pm) than Si (111 pm); importantly, this radius also differs from that of Co (116 pm), a key constituent of the Gd₄Co₃ matrix. This atomic size mismatch, combined with Ge’s distinct electronic structure, is hypothesized to modulate the alloy’s key material properties in a manner different from Si and boron (B)—two elements that have been previously investigated for alloying with Gd₄Co₃ [30,31]. Our previous work [19,32] indicated that a small amount of Ge or Si improves the GFA of the eutectic Gd₆₅Mn₃₅ alloy. For Gd₆₅Mn_35−xGe_x (x = 0, 5, 10) amorphous alloys, slightly higher Ge content increases T_C from 180 K to 229 K, along with an increased (−ΔS_M)^max [19]. In contrast, the presence of Si has no significant effect on the T_C or MCE of Gd₆₅Mn_35−xSi_x (x = 5, 10) amorphous alloys [32].

It is worth noting that while Si and Ge belong to the same group (i.e., are group homologs), the differences in their atomic radii and the respective electronic effects they exert on Gd-based amorphous alloys have not been systematically examined for the Gd₄Co₃ system. Existing literature lacks data on how Ge substitution impacts the thermal stability, MCE, and critical behavior (e.g., critical exponents governing ferromagnetic-to-paramagnetic transitions) of amorphous Gd₄Co₃. Thus, in this work, we studied the thermal stability, magnetic properties, and MCE of Ge-added Gd₄Co₃ rapidly quenched alloys. Additionally, the nature of the FM-to-PM phase transition was determined by analyzing the critical exponents.

2. Materials and Methods

Ingots of (Gd₄Co₃)_100−xGe_x (x = 5, 10, and 15) alloys were fabricated via arc melting, using high-purity elemental Gd (99.95 wt%), Co (99.995 wt%), and Ge (99.999 wt%) as raw materials under a high-purity argon protective atmosphere. To ensure compositional homogeneity, each ingot was remelted multiple times. The weight loss during arc melting was less than 1.0 wt%, indicating minimal compositional deviation. Subsequently, the ingots were crushed into small pieces, which were then processed into ribbons through single-roller melt spinning—with the process utilizing a copper wheel operating at a rotational speed of 50 m/s.

X-ray diffraction (XRD) was utilized to characterize the phase structure of the melt-spun ribbons, using an X-ray diffractometer (XRD, Philips X’pert Pro MPD, Panalytical, Almelo, The Netherlands) that operated with Cu-Kα1 radiation (λ = 1.54056 Å). Magnetic properties were measured using a physical properties measurement system (PPMS-9, Quantum Design, San Diego, CA, USA) in DC mode. For DC magnetic measurements, the temperature (T) dependence of magnetization (M) was recorded under an applied magnetic field of 0.01 T. The Curie temperature (T_C) of each alloy was determined as the temperature that corresponds to the peak value in the curves of |dM/dT| versus T. For the (Gd₄Co₃)_100−xGe_x rapidly quenched alloys, the temperature dependence of magnetic entropy change (−ΔS_M) was calculated from the magnetization isotherms measured near T_C, with the calculation following the Maxwell relation [4]:

$$\mathsf{\Delta }{S}_M(T,H)={\int }_0^H({\displaystyle \frac{\partial M}{\partial T}}{)}_{H}dH$$

(1)

where in T refers to the absolute temperature and H denotes the applied magnetic field.

For the study of critical exponents, magnetization (M) versus magnetic field (H) curves of the melt-spun ribbons were measured. The measurements spanned a temperature range of T_C ± 20 K, with a 1 K interval maintained between consecutive data points.

The uncertainties of the Curie temperature (T_C), crystallization onset temperature (T_x), magnetic entropy change (ΔS_M), and critical exponents in this work can be found in Supplementary Materials (Supplementary Data).

3. Results and Discussion

As shown in Figure 1, the XRD patterns of the as-spun (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) alloys exhibit clear broad humps—a characteristic feature of the amorphous phase—confirming that the alloys are predominantly amorphous. Nevertheless, weak diffraction peaks corresponding to crystalline Gd₄Co₃ are also detected, revealing that nanocrystals with a hexagonal Ho₄Co₃-type crystal structure (space group P6₃/m) precipitated in the amorphous matrix during the melt-spinning process.

Figure 1. X-ray diffraction (XRD) patterns of as-spun (Gd₄Co₃)_100−xGe_x ribbons (x = 5, 10, 15).

As presented in Figure 2, all the DSC curves of the as-spun (Gd₄Co₃)_100−xGe_x alloys (x = 5, 10, 15) show an exothermic peak in the 550–650 K range, which corresponds to the crystallization of the Ho₄Co₃-type phase. This assignment is verified by the XRD pattern of an initially amorphous (Gd₄Co₃)₉₀B₁₀ ribbon after annealing at 603 K for 10 min [30]. Notably, the crystallization onset temperature (T_x) of the alloys increases with Ge content: ~564 K for x = 5, ~582 K for x = 10, and ~603 K for x = 15. This upward trend in T_x confirms that the as-spun ribbons maintain excellent thermal stability at room temperature.

Figure 2. DSC curves of as-spun (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) ribbons (Heating rate: 20 K/min).

To analyze the magnetic properties of the as-spun (Gd₄Co₃)_100−xGe_x ribbons, their magnetization changes were tested in the temperature range of 5–300 K, and the corresponding M–T curves are displayed in Figure 3. Upon heating, a sharp drop in magnetization is detected—a hallmark of the ferromagnetic (FM) to paramagnetic (PM) phase transition. For the alloys where x = 5, 10, and 15, the corresponding Curie temperatures (T_C) are determined to be 211, 215, and 217 K, respectively. Notably, T_C exhibits an almost linear increase with higher Ge content, as illustrated in the inset of Figure 3. This trend aligns well with the behavior previously observed in Gd₆₅Mn_35−xGe_x (x = 5, 10) alloys [19].

Figure 3. Temperature dependence of magnetization (M–T) for as-spun (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) ribbons measured at an applied field of 0.01 T. The inset shows the dependence of Curie temperature (T_C) on Ge content for the as-spun ribbons; the value for x = 0 is adapted from Ref. [29]. Here, the red * denotes that x = 0 corresponds to the parent compound Gd₄Co₃ without Ge doping, which serves as a reference for the phase transition temperature.

Figure 4 presents the isothermal magnetization (M–H) curves of the as-spun (Gd₄Co₃)_100−xGe_x ribbons measured at 5 K with the applied field increasing from 0 to 5 T. All alloys reach magnetic saturation at low fields. The saturation magnetization (M_S) values, obtained by extrapolating the high-field magnetization data to zero field, are 188.4, 189.4, and 184.7 A·m²/kg for x = 5, 10, and 15, respectively—corresponding to 3.71, 3.55, and 3.29 μ_B per magnetic atom. The calculated magnetic moments per Gd atom are 6.83, 6.91, and 6.76 μ_B/Gd, respectively, which are slightly lower than the experimental M_S of the free Gd³⁺ ion (7.55 μ_B) [33]. This reduction is attributed to antiparallel spin coupling in the secondary Gd–Co sublattice [34].

Figure 4. Isothermal magnetization (M–H) curves of as-spun (Gd₄Co₃)_100−xGe_x (x = 5, 10 and 15) ribbons measured at 5 K (0–5 T field range).

The (−ΔS_M) vs. T curves of the as-spun (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) ribbons are presented in Figure 5 and summarized in Table 1. The peak (−ΔS_M) values for a field change from 0 to 5 T are 7.2, 6.8 and 6.7 J/(kg·K) for x = 5, 10 and 15, respectively—slightly lower than those for the amorphous Gd₄Co₃ alloy (7.2 J/(kg·K), 0–5 T) [31] and the amorphous (Gd₄Co₃)₉₀B₁₀ alloy (7.4 J/(kg·K), 0–5 T) [30]. However, these values are larger than those of the Gd₆₅Fe₂₀Al_15−xSi_x (x = 1, 3, 5, 7) glassy ribbons (4.68~4.80 J/(kg·K), 0–5 T) in a similar temperature range [35]. The large magnetocaloric effect makes the (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) amorphous alloys promising for magnetic cooling applications near 210 K.

Figure 5. (−ΔS_M) vs. T curves of as-spun (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) ribbons for magnetic field changes of 0–2 T and 0–5 T.

Table 1. Magnetocaloric performances and corresponding parameters of different materials under an applied magnetic field (H), with A denoting amorphous state and C crystalline state.

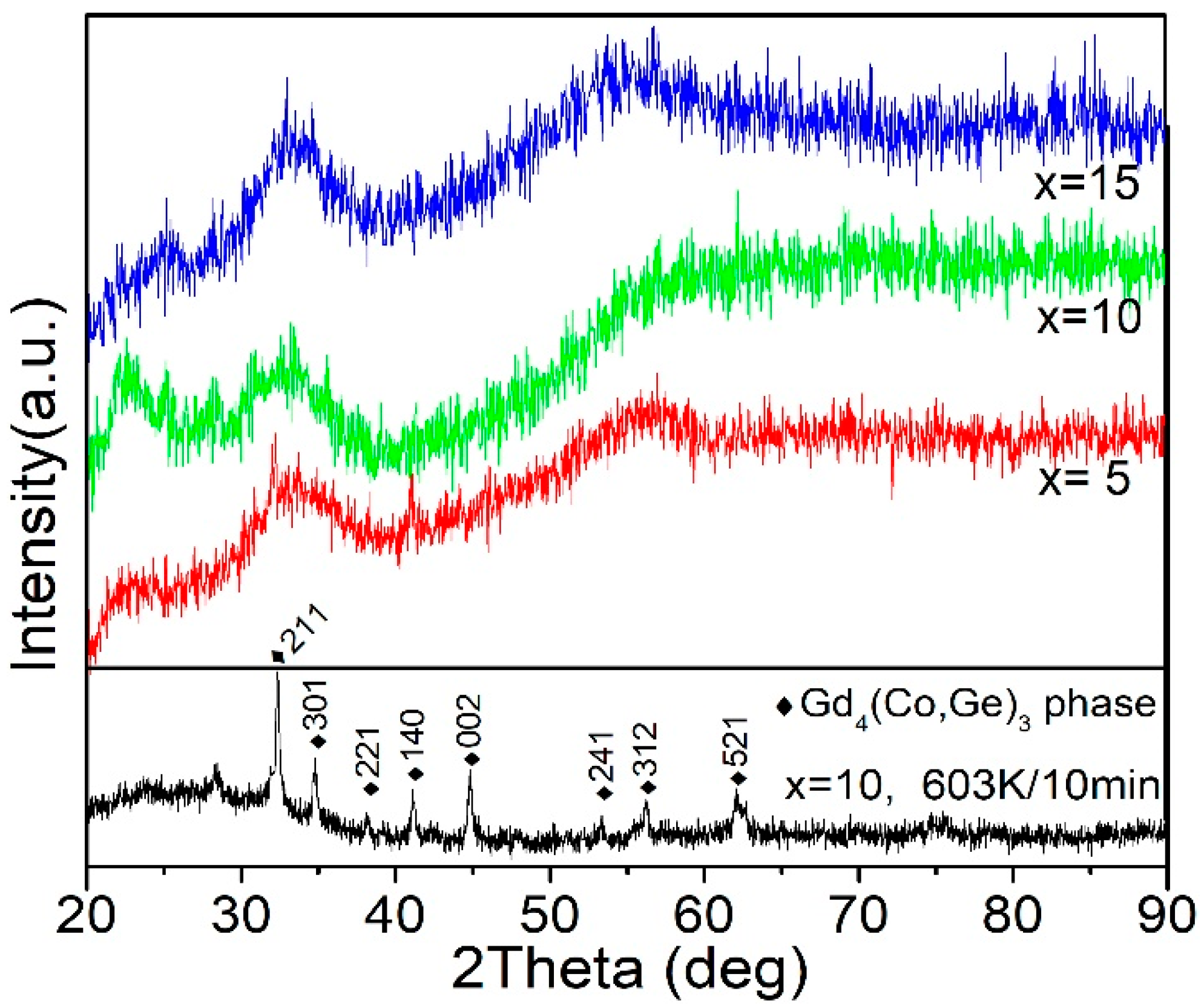
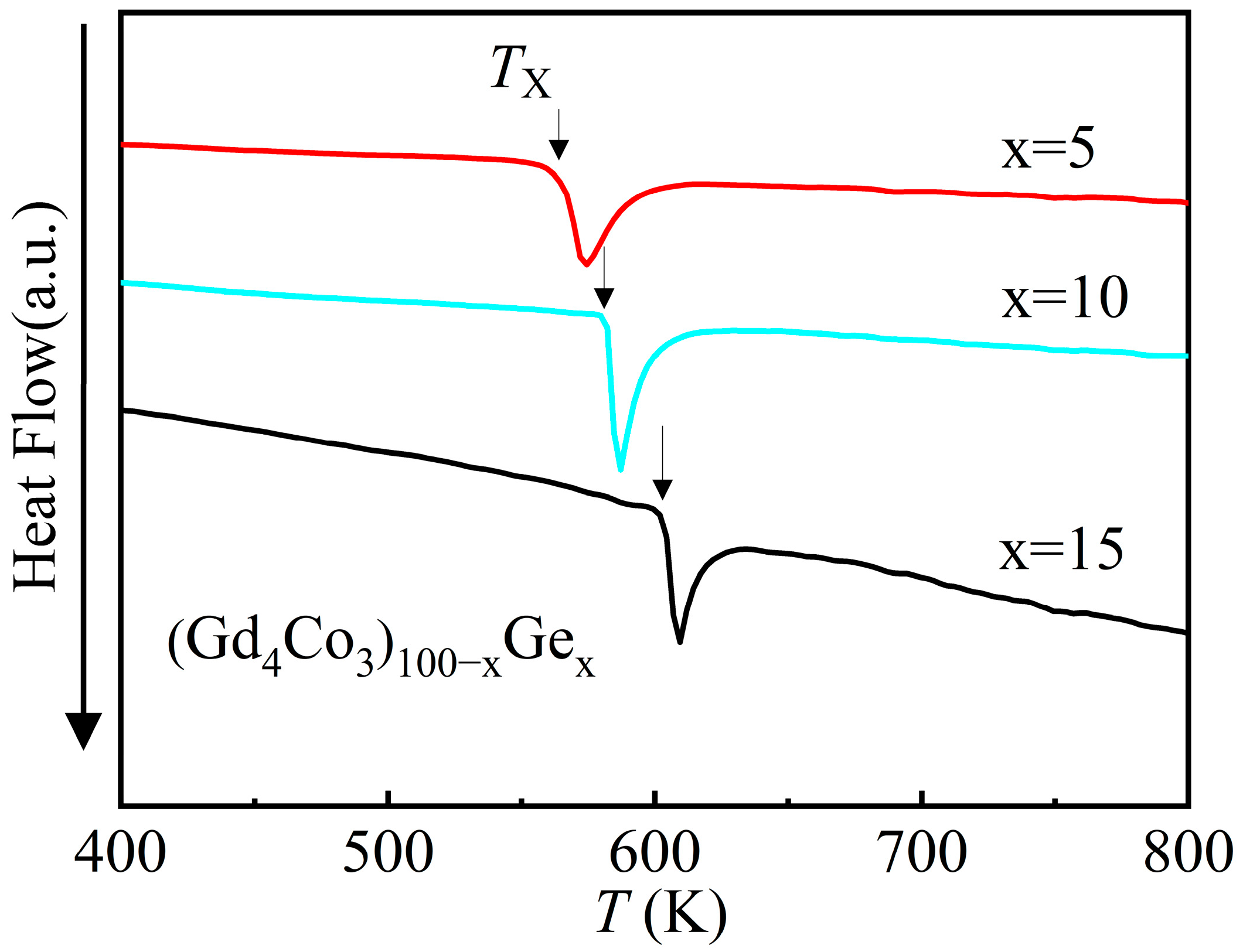
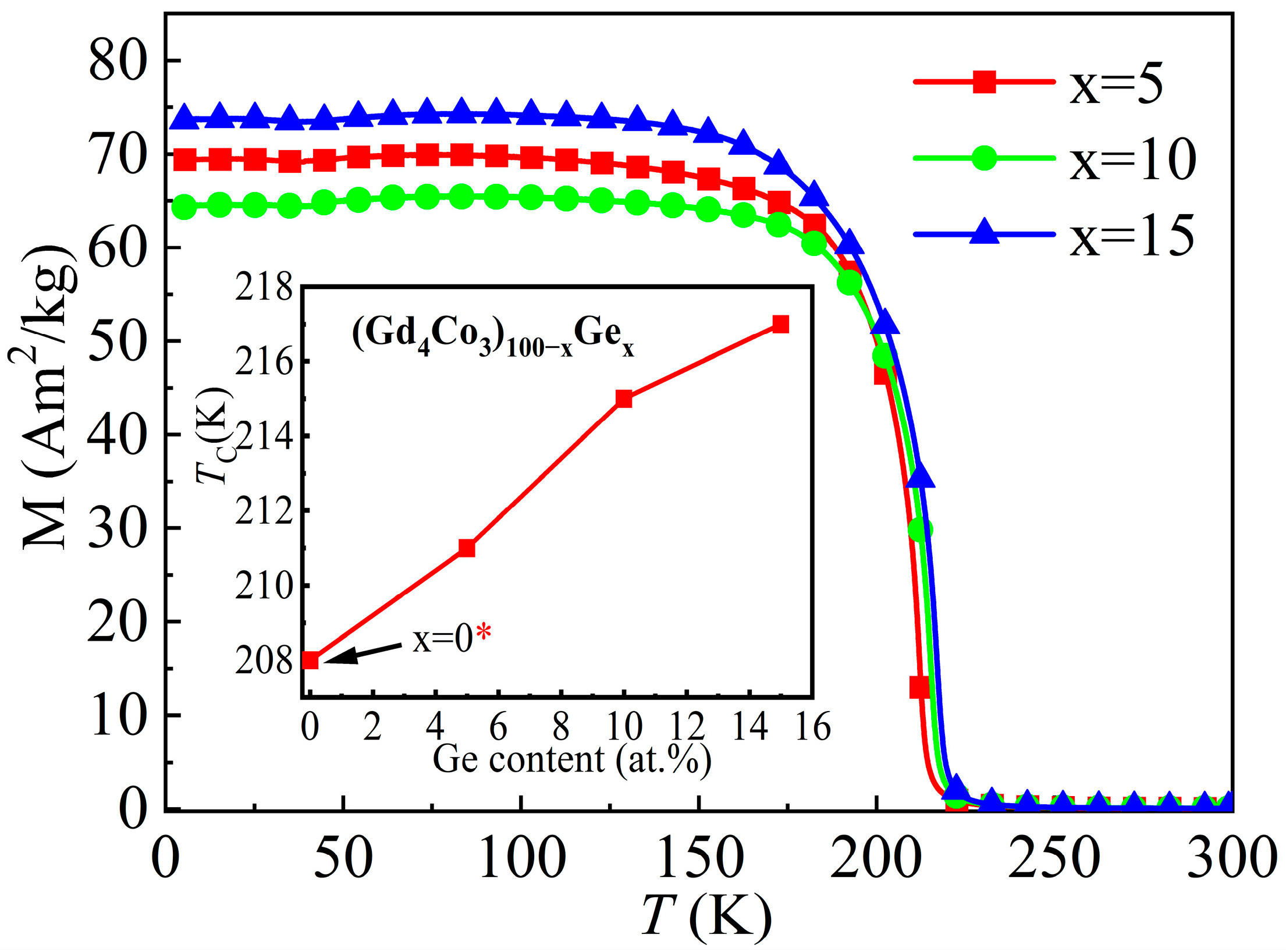
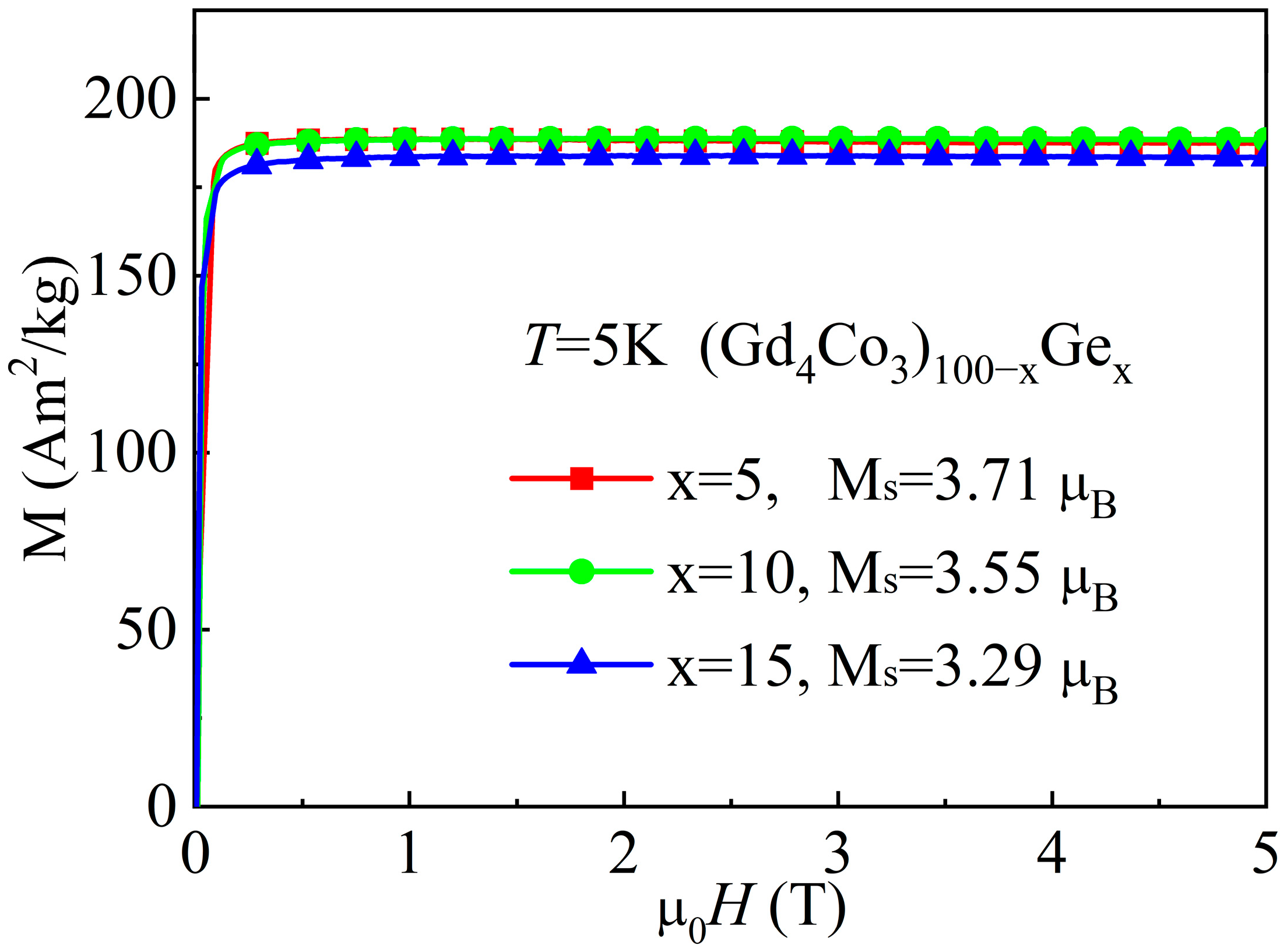
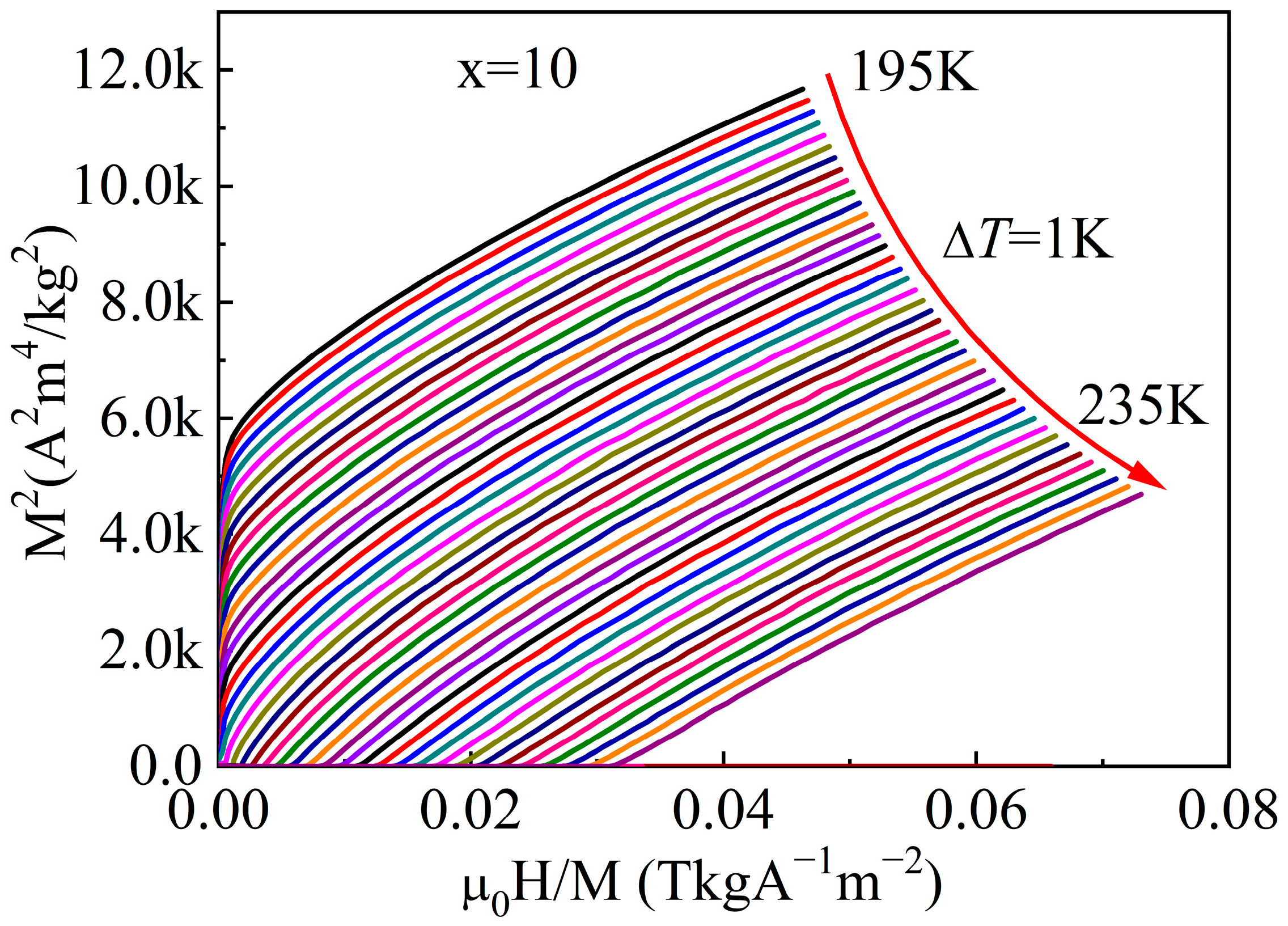
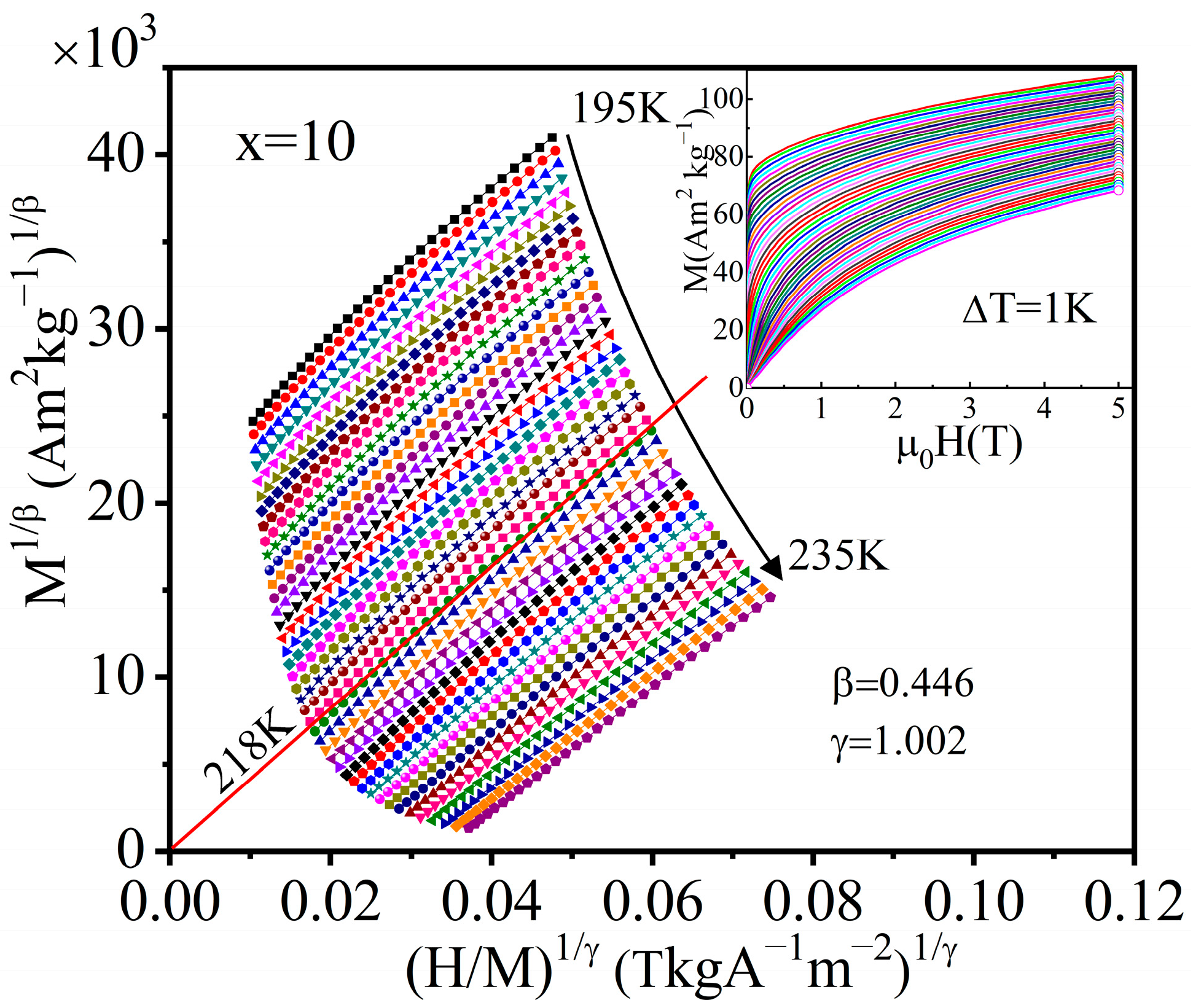
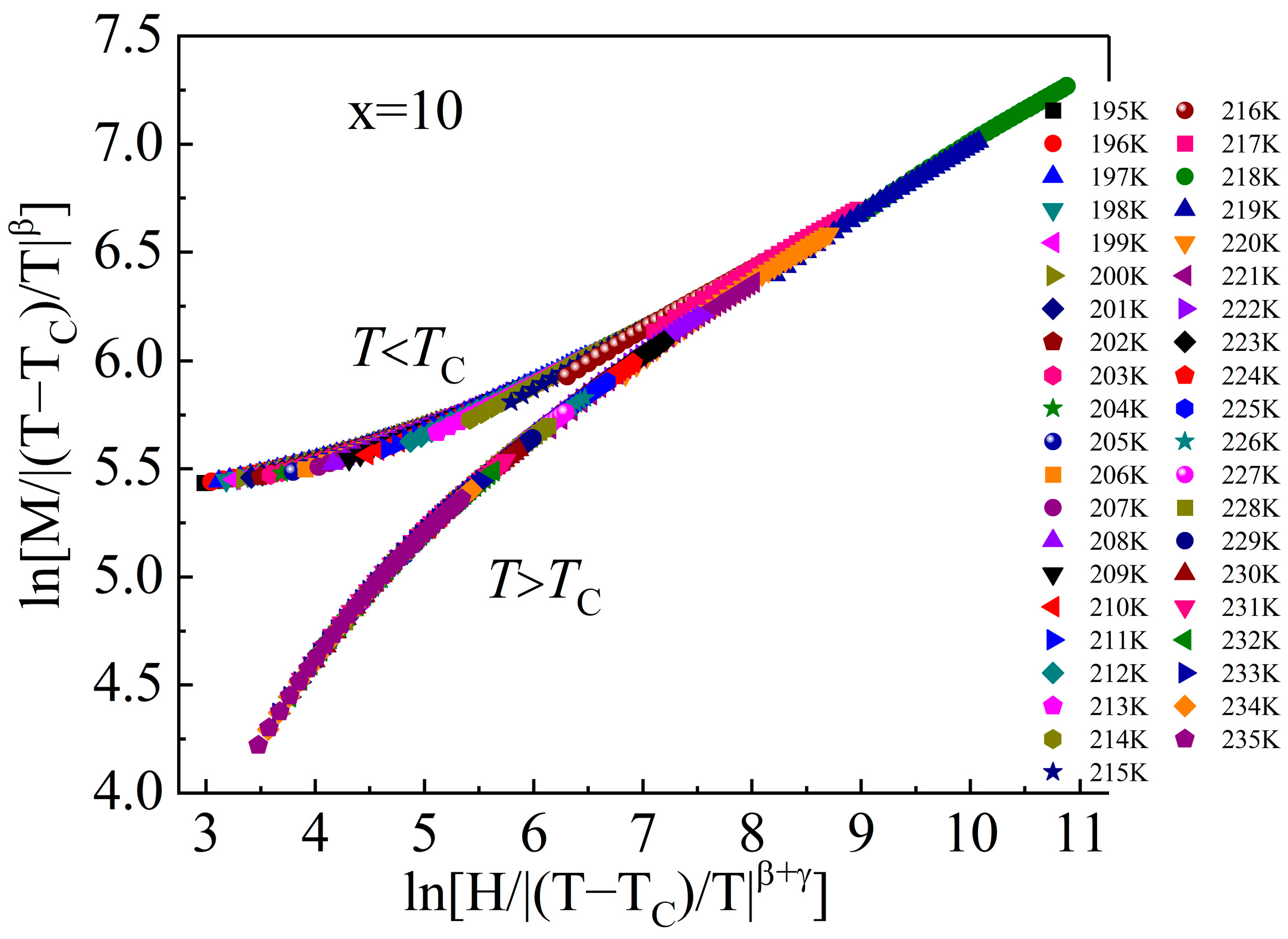
Material	State	TC (K)	(−ΔSM)max J/(kg·K), 0–5 T	RC J/kg, 0–5 T	References
(Gd4Co3)95Ge5	A	211	7.15	448	This work
(Gd4Co3)90Ge10	A	215	6.83	435	This work
(Gd4Co3)85Ge15	A	217	6.71	458	This work
(Gd4Co3)95B5	A	209	7.1	520	[30]
(Gd4Co3)90B10	A	203	7.4	527	[30]
(Gd4Co3)85B15	A	197	7.8	535	[30]
(Gd4Co3)0.95Si0.05	A	198	7.2	524	[31]
(Gd4Co3)0.9Si0.1	A	213	6.4	511	[31]
Gd4Co3	A	208	7.3	547	[31]
Gd4Co3	A	215	6.7	510	[30]
Gd4Co3	C	220	6.4	575	[30]
Gd4Co3	C	163 a/220	5.7	575	[28]
Gd60Co35Mn5	A	202	7.1	--	[21]
Gd65Fe20Al14Si1	A	210	4.77	762	[35]
Gd65Fe20Al12Si3	A	215	4.78	752	[35]
Gd65Fe20Al10Si5	A	220	4.68	713	[35]
Gd65Fe20Al8Si7	A	227	4.80	741	[35]
Gd55Co35Ni10	A	192	6.5	502	[36]
La(Fe0.88Si0.12)13	C	195	23	452	[37]

^a T_SR = 163 K.

The value of (−ΔS_M) is not the only parameter for characterizing magnetocaloric properties. Refrigeration capacity (RC) is another key quality factor for such materials when used as coolants in magnetic refrigeration, and its values were calculated following the method reported in Ref. [30].

$$RC={\int }_{T_{cold}}^{T_{hot}}{[-∆S_M]}_{T}dT$$

(2)

Typically, T_hot and T_cold are determined as the temperatures on either side of the half-maximum value of (−ΔS_M)^max.

For a 5 T field change, the as-spun (Gd₄Co₃)_100−xGe_x ribbons (x = 5, 10, 15) exhibit RC values of 448, 435, and 458 J/kg, respectively. These values are far lower than those of Gd₆₅Fe₂₀Al_15−xSi_x glassy ribbons in a similar temperature range [35]. However, they are comparable to or even larger than that of La(Fe_0.88Si_0.12)₁₃ under the same temperature condition [37] (Table 1). Combined with their large (−ΔS_M) values and high thermal stability, the relatively large RC of the as-spun (Gd₄Co₃)_100−xGe_x ribbons (x = 5, 10, 15) demonstrates their potential for magnetic cooling at ~210 K.

For the purpose of clarifying the magnetic phase transition mechanism in the as-spun (Gd₄Co₃)₉₀Ge₁₀ alloy, Arrott plots (M² vs. μ₀H/M) of the as-spun ribbon were constructed using M(H) isotherms measured over T_C ± 20 K with a 1 K temperature step (Figure 6). According to the Banerjee criterion [38], the presence of a positive slope in the Arrott plot confirms a second-order ferromagnetic (FM) to paramagnetic (PM) phase transition.

Figure 6. Arrott plots (M² vs. μ₀H/M) of as-spun (Gd₄Co₃)₉₀Ge₁₀ ribbon.

For such second-order magnetic transitions (SOMTs), a set of critical exponents is typically used for characterization [39,40,41]: β (describing the temperature dependence of spontaneous magnetization M_S), γ (characterizing the inverse initial susceptibility χ⁻¹), and δ (relating to the critical magnetization isotherm at T = T_C).

These critical exponents are defined as follows:

$$M_s=m_0{\left|t\right|}^{\beta } ,t>0,$$

(3)

$${\chi }^{-1}={\displaystyle \frac{h_0}{m_0}}{\left|t\right|}^{\gamma } ,t<0,$$

(4)

$$M=D{H}^{1/\beta } ,t=0,$$

(5)

Here, t represents the reduced temperature defined as t = 1 − T/T_C, while m₀, h₀ and D stand for critical amplitudes. Critical exponents, which can be derived from experimental measurements, satisfy the Widom scaling relation: δ = 1 + γ/β.

To obtain the critical exponents, the Kouvel–Fisher (KF) method [42,43] was applied (see Equations (6) and (7)). The advantage of the KF method is that no prior knowledge of T_C is required. In addition, only three free parameters need to be determined.

$$Y(T)=-M_S({\displaystyle \frac{\partial M_S}{\partial T}}{)}^{-1}=-{\displaystyle \frac{T-Tc}{\beta }}$$

(6)

$$X(T)={\chi }^{-1}({\displaystyle \frac{\partial {\chi }^{-1}}{\partial T}}{)}^{-1}={\displaystyle \frac{T-Tc}{\gamma }}$$

(7)

According to the mean-field theory [44], Arrott plots should consist of a series of parallel straight lines in the vicinity of T_C and pass through the origin at T = T_C. To construct such lines, modified Arrott plots (MAPs; see Equation (8)), which are based on the Arrott–Noakes equation of state [45], were employed. For the analysis, only the high-field linear region was adopted, since low-field plots show slight curvature caused by mutually misaligned magnetic domains [46].

The MAPs are reconstructed by starting from an initial estimate of the critical exponents β and γ, a process that ensures the MAPs yield straight lines.

$${\left({\displaystyle \frac{H}{M}}\right)}^{1/\gamma }=K+M^{1/\beta }$$

(8)

By performing linear extrapolation on the high-field regions of the MAPs, the spontaneous magnetization M_S(T) (plotted on the M^1/β axis) and inverse initial susceptibility χ₀⁻¹(T) (plotted on the (H/M)^1/γ axis) were obtained. These values were then used in conjunction with Equations (6) and (7) to obtain improved estimates of the critical exponents β and γ. This process was iterated until the exponents converged to stable values, yielding the final MAPs.

Figure 7 presents the final iteration step for the as-spun (Gd₄Co₃)₉₀Ge₁₀ alloy. Two fitted straight lines are observed, which intersect the abscissa at T = T_C with slopes −1/β and 1/γ, respectively. For the alloy with x = 10, the critical exponents were found to be β = 0.446, γ = 1.002, and T_C = 218 K; similarly, for x = 15, these values are β = 0.484, γ = 1.109, and T_C = 220 K.

Figure 7. Kouvel–Fisher plots of spontaneous magnetization (M_S) and inverse initial magnetic susceptibility (χ₀⁻¹) for the as-spun (Gd₄Co₃)₉₀Ge₁₀ alloy.

Figure 8 displays the modified Arrott plots (MAPs, M^1/β vs. (H/M)^1/γ) of the as-spun (Gd₄Co₃)₉₀Ge₁₀ alloy, constructed using the critical exponents β = 0.446 and γ = 1.002. The series of parallel lines confirms the high quality of these MAPs. Furthermore, T_C = 218 K is extracted from the line passing through the origin, which is consistent with the result obtained via the Kouvel–Fisher (KF) method (Figure 6). Additionally, the critical exponent was calculated using the Widom scaling relation [47,48]; for the as-spun alloy ribbons with x = 10 and x = 15, the δ values are 3.247 and 3.292, respectively.

Figure 8. Modified Arrott plots (M^1/β vs (H/M)^1/γ) for the as-spun (Gd₄Co₃)₉₀Ge₁₀ alloy. Solid lines are linear fit to the high-field of the isotherms. The critical isotherm at T_C = 218 K passes through the origin.

To further verify the reliability of the acquired critical exponents, scaling theory was employed. As per the scaling hypothesis [49], the magnetic equation of state within the critical region can be formulated as:

$$M(H,t)=t^{\beta }{f}_{\pm }(H/t^{\beta +\gamma })$$

(9)

where the scaling functions f₊ and f₋ correspond to temperatures above (T ˃ T_C) and below (T ˂ T_C) the critical point, respectively. True scaling behavior implies that all experimental isotherms in the critical region should collapse onto two universal curves (one for T ˃ T_C and one for T ˂ T_C) when plotted using appropriate scaling variables and with consistent values of β, γ, and δ.

By employing the renormalized magnetization m = t^−βM(H,t) and the renormalized field h = Ht^−(β+γ), the equation of state (9) transforms to

$$m=f_{\pm }(h)$$

(10)

The scaled plots of m versus h, constructed using the critical exponents β, γ, and δ obtained from the Kouvel–Fisher (KF) method, are presented in Figure 9. On a log-log scale, all data points collapse onto two distinct branches for T > T_C and T ˂ T_C, confirming the accuracy of the determined critical exponents.

Figure 9. ln-ln Scaling plots (renormalized m vs. h) of the as-spun (Gd₄Co₃)₉₀Ge₁₀ alloy in the critical region, with data collapse via β and γ from the KF method.

Table 2 lists the critical exponents derived from the KF method, alongside the theoretically predicted values for different models: mean-field theory (MFT), the three-dimensional Heisenberg (H3D) model, and the three-dimensional Ising (Is3D) model. A key distinction between these models is their underlying magnetic coupling: the H3D and Is3D models are based on short-range magnetic coupling [50], while the MFT model is based on long-range magnetic coupling [41]. Notably, the critical exponents of the alloys are broadly consistent with the MFT-predicted values; this consistency arises from the nanocrystals in the alloys, which generate long-range magnetic coupling.

Table 2. Comparison of critical exponents β, γ, and δ: KF method-determined values for (Gd₄Co₃)_100−xGe_x (x = 10, 15) alloys vs. theoretically predicted values for various universal classes.

Material	β	γ	δ	References
x = 10	0.446	1.002	3.247 *	This work
x = 15	0.484	1.109	3.292 *	This work
H3D	0.365	1.336	4.80 *	[50]
Is3D	0.325	1.24	4.82 *	[50]
MFT	0.5	1.0	3.0 *	[44]

* Obtained from the Widom scaling equation: δ = 1 + γ/β; H3D: Stands for the “three-dimensional Heisenberg model”; Is3D stands for the “three-dimensional Ising model”; MFT stands for “mean-field theory”.

4. Conclusions

In this work, (Gd₄Co₃)_100−xGe_x (x = 5, 10, 15) ribbons were fabricated via melt spinning. Phase analysis revealed that all as-spun ribbons are predominantly amorphous, with minor hexagonal Ho₄Co₃-type (space group P6₃/m) nanocrystals precipitated in the amorphous matrix during the melt-spinning process. The onset crystallization temperature (T_x) of the alloys increases with Ge content (from 564 K for x = 5 to 603 K for x = 15), demonstrating excellent thermal stability at room temperature.

All alloys undergo a second-order ferromagnetic (FM)-to-paramagnetic (PM) phase transition, with the Curie temperature (T_C) increasing linearly with rising Ge content—from 211 K (x = 5) to 215 K (x = 10) and further to 217 K (x = 15). For a 0–5 T field change, the (−ΔS_M)^max of the (Gd₄Co₃)_100−xGe_x alloys is 7.15 (x = 5), 6.83 (x = 10), and 6.71 (x = 15) J/(kg·K). These values are slightly lower than the corresponding values for amorphous Gd₄Co₃ and (Gd₄Co₃)₉₀B₁₀ but higher than Gd₆₅Fe₂₀Al_15−xSi_x glassy ribbons in the same temperature range. Combined with their large (−ΔS_M) values and high thermal stability, the relatively large RC of the as-spun (Gd₄Co₃)_100−xGe_x ribbons demonstrates their potential in magnetic cooling applications at ~210 K.

Critical behavior analysis was performed using the Kouvel–Fisher (KF) method and Widom’s scaling relation. The critical exponents of the alloys are β = 0.446, γ = 1.002, δ = 3.247 (x = 10) and β = 0.484, γ = 1.109, δ = 3.292 (x = 15), which are generally consistent with the predictions of mean-field theory (MFT, β = 0.5, γ = 1.0, δ = 3.0). This consistency indicates that the nanocrystals in the amorphous matrix induce long-range magnetic interactions.

Overall, the (Gd₄Co₃)_100−xGe_x amorphous–nanocrystalline ribbons combine favorable thermal stability, a tunable second-order FM-PM transition, and a considerable magnetocaloric effect, rendering them attractive candidates for low-temperature magnetic refrigeration applications.